1 引言
随着传感器分辨率的提高,一个目标在一个采样周期内至少产生一个量测,这种目标可视为扩展目标。近年来,扩展目标跟踪(extended target tracking, ETT)的研究逐渐成为目标跟踪领域的热点[1-2]。
传统跟踪算法需要对目标和量测进行数据关联,但随着目标数和量测数的增加,容易引起“组合爆炸”而使计算量呈指数增长。2004年,Mahler提出了随机有限集(random finite set, RFS)理论[3],随后把RFS应用到目标跟踪的研究中[4],该方法不需要对目标和量测进行数据关联,而是把所有的目标状态和量测建模为RFS,有效地降低了运算量,成为目标跟踪的主流框架。基于RFS的多目标跟踪滤波器包括概率假设密度(probability hypothesis density, PHD)滤波器[5]、集势PHD(cardinalized PHD, CPHD)滤波器[6-7]、势均衡的多目标多伯努利(cardinality balanced multi-target multi-bernoulli, CBMeMBer)滤波器[8]、以及广义化标记的多伯努利(generalized labeled multi-bernoulli, GLMB)滤波器[9]等。
为了对扩展目标进行建模,Gilholm等人提出了扩展目标的泊松分布模型,并给出了空间分布的似然函数[10]。2008年,Mahler在泊松分布模型的基础上提出了扩展目标概率假设密度(extended target PHD, ET-PHD)滤波器[11],并进行了理论推导,但没有给出具体实现过程。随后,在ET-PHD滤波器的基础上,为了解决不同背景下的ETT问题,Grans-trom等[12-14]和Zhang等[15-16]分别提出了基于不同的量测划分方法的扩展目标高斯混合PHD(extended target Gaussian mixture PHD, ET-GM-PHD)滤波器;Li等[17]提出了扩展目标粒子PHD(extended target particle PHD, ET-P-PHD)滤波器。此外,基于RFS的ETT算法研究还有:Lundquist[18]等提出了Gamma高斯逆Wishart实现的扩展目标CPHD滤波器;Lian[19]提出了顺序蒙特卡洛(sequen-tial montecarlo, SMC)实现扩展目标势均衡多目标多伯努利(cardinalized balanced multi-target multi-Bernoulli, CBMeMBer)滤波器;Beard[20]应用标签的RFS提出了扩展目标广义标签多伯努利(generalized labelled multi-Bernoulli, GLMB)滤波器等。
由于每个扩展目标产生多个量测,如何对多个量测进行划分,直接关系后续计算效率和精度。一般情况下,每个目标产生的多个量测在距离上相对集中,而杂波生成的量测相对分散,针对这种假设诸多学者提出了多种不同的量测集划分方法。但在ETT中每个采样时刻存在杂波以及目标产生量测数不确定性的问题,很难精准地对量测集进行划分,只能提出一些近似方法去替代:如Granstrom等[12-14]提出了距离划分方法,该方法可以有效地减少每个采样时刻的划分数使计算量降低;文献[17,21]提出了一种基于k-means聚类的量测集划分方法,但该方法易受初始聚类中心选取的影响;Zhang等[15-16]提出了一种基于模糊自适应共振理论(adaptive resonance theory, ART)的划分方法,在保证跟踪稳定性的前提下,该方法比距离划分和k-means聚类划分方法具有更小的计算复杂度,但ART方法中警戒参数的确定是一个难题;Yang[22]提出了基于谱聚类的量测集划分方法,但该方法存在聚类量测簇的数量需要人为确定且跟踪不稳定的问题。
目前所提出的量测集划分方法[23-27]基本都是根据某种相似度选取量测集所有划分的子集(为了有效跟踪目标,该子集中应包含信息最丰富最接近真实目标产生量测的量测集划分),但是该子集中包含的量测集划分数的多少将直接影响算法复杂度。为了降低运算量,在没有漏检和误检的同时,量测集子集的数量应尽可能少。
2014年,Rodriguez[28]提出一种基于密度峰值聚类(density peak clustering, DPC)算法,该算法对扩展目标的形状不敏感,可实现目标的任意展布形状的量测集划分。本文在DPC算法的基础上提出改进的DPC(improved DPC, IDPC)算法,首先对得到的量测集滤除杂波,然后得到目标的量测的簇并计算簇的中心,再根据每个采样时刻预测的权重较高疑似目标的高斯分量的位置与簇的中心距离矩阵的关系对目标的量测进行划分,得到最可能的量测集划分(本文也称其为信息最丰富的量测集划分),详见4.2。
本文其余部分安排如下:第2节简单介绍了ET-GM-PHD滤波器;第3节详细分析了量测集划分对目标跟踪的影响;第4节重点阐述了IDPC量测集划分算法;第5节对该算法进行了实验仿真及分析;第6节给出了本文的结论及未来工作展望。
2 ET-GM-PHD滤波器
Granstrom用空间分布模型描述ET-GM-PHD滤波器[12]中的扩展目标,其假设每个目标在每个采样时刻产生的量测数服从泊松分布,且量测在空间上服从以目标质心为均值的高斯分布。
假设ETT系统的运动模型和量测模型都是线性高斯的,根据RFS理论,扩展目标的状态方程为:
(1)
其中,![]() 表示k时刻真实的目标数,
表示k时刻真实的目标数,![]() 是均值为零、协方差为
是均值为零、协方差为![]() 的高斯过程噪声,Fk-1是状态转移矩阵。
的高斯过程噪声,Fk-1是状态转移矩阵。
扩展目标的量测方程为
(2)
其中,![]() 表示k时刻获得的量测数,
表示k时刻获得的量测数,![]() 是均值为零、协方差为Rk的高斯观测噪声,Hk是量测矩阵。
是均值为零、协方差为Rk的高斯观测噪声,Hk是量测矩阵。
在ET-GM-PHD滤波器中,k时刻的先验概率用高斯混合表示为
(3)
其中,![]() 和
和![]() 分别是高斯分量的权重、均值和协方差,Jk|k-1是预测高斯分量的个数,
分别是高斯分量的权重、均值和协方差,Jk|k-1是预测高斯分量的个数,![]() 是均值为m和协方差为P的高斯分布。
是均值为m和协方差为P的高斯分布。
使用与ET-PHD滤波相同的量测伪似然函数LZk(x)得到k时刻的后验概率为一个高斯混合
Dk|k(x|Zk)=LZk(x)Dk|k-1(x|Zk-1)
(4)
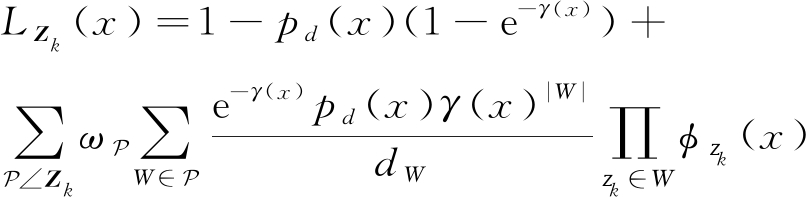
(5)
其中,1-e-γ(x)表示扩展目标至少生成一个量测的概率且扩展目标产生的量测数目服从泊松为γ(x)的泊松分布;pd(x)(1-e-γ(x))是扩展目标的有效检测概率;pd(x)是扩展目标的检测概率;![]() 和
和![]() 表示将k时刻获得的测量集Zk划分为
表示将k时刻获得的测量集Zk划分为![]() 类簇,每个划分是将量测集Zk划分为多个非空单元W,每个非空单元W代表源自同一扩展目标产生的量测集,|W|为单元W中的元素个数;λkck(zk)是服从泊松分布λk的杂波的强度函数;φzk(x)=p(zk|x)为扩展目标的观测空间分布函数。
类簇,每个划分是将量测集Zk划分为多个非空单元W,每个非空单元W代表源自同一扩展目标产生的量测集,|W|为单元W中的元素个数;λkck(zk)是服从泊松分布λk的杂波的强度函数;φzk(x)=p(zk|x)为扩展目标的观测空间分布函数。![]() 是划分
是划分![]() 的权值,dW是每一个划分中单元W的权值,具体计算如下
的权值,dW是每一个划分中单元W的权值,具体计算如下
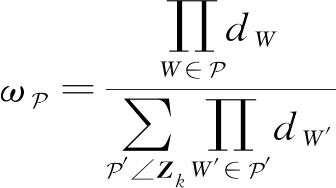
(6)
dW=δ|W|,1κW+![]()
(7)
其中κ(zk)=λkck(zk)(λk和ck(zk)分别为杂波生成量测的均值和空间分布),δi, j是Kronecker函数。
(8)
对于任意函数h(x),存在
(9)
为了进一步说明式(5)~式(7)中出现的划分![]() 和单元W之间的具体关系,假设当前时刻的量测集为Z={z1,z2,z3},则对量测集Z所有可能的划分及其包含的单元如下:
和单元W之间的具体关系,假设当前时刻的量测集为Z={z1,z2,z3},则对量测集Z所有可能的划分及其包含的单元如下:
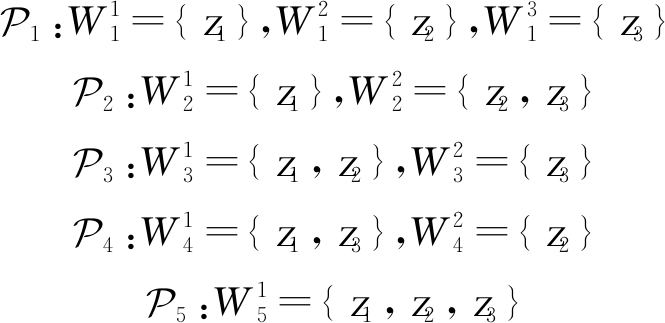
(10)
其中,![]() 是所有可能的划分中的第i个划分,
是所有可能的划分中的第i个划分,![]() 是第i个划分中的第j个量测集单元,
是第i个划分中的第j个量测集单元,![]() 表示该单元中包含的元素个数。显然,当扩展目标与杂波较多时就会产生大量的量测,而随着量测的增加量测集划分将急剧上升,这对扩展目标状态更新将造成计算负担并严重影响到扩展目标实时跟踪,所以,开发一种快速准确的量测集划分方法是解决扩展目标实时跟踪的关键。
表示该单元中包含的元素个数。显然,当扩展目标与杂波较多时就会产生大量的量测,而随着量测的增加量测集划分将急剧上升,这对扩展目标状态更新将造成计算负担并严重影响到扩展目标实时跟踪,所以,开发一种快速准确的量测集划分方法是解决扩展目标实时跟踪的关键。
3 量测集划分分析
由于精确计算量测集所有划分![]() 较难处理,为了提高计算速度,我们试图寻找一种
较难处理,为了提高计算速度,我们试图寻找一种![]() 尽量小的量测划分方法。在本节中,我们先分析不同情况下量测集所有可能的划分。其次寻找信息最丰富的量测集划分并尝试让其近似替代量测集所有划分,得出使用该类划分既可减少划分数目,又可降低ETT的计算复杂度的优势。
尽量小的量测划分方法。在本节中,我们先分析不同情况下量测集所有可能的划分。其次寻找信息最丰富的量测集划分并尝试让其近似替代量测集所有划分,得出使用该类划分既可减少划分数目,又可降低ETT的计算复杂度的优势。
3.1 无杂波的场景
为了分析如何划分目标生成的量测,本节假设一个无杂波且每个目标都能很好的分开的多扩展目标场景。令κ(zk)=0,则划分单元W的权值dW可以重新约简如下:
(11)
其中pd=pd(x)和γ=γ(x)。
量测伪似然函数LZk(x)重新计算如下:
LZk(x)=1-pd(1-e-γ)+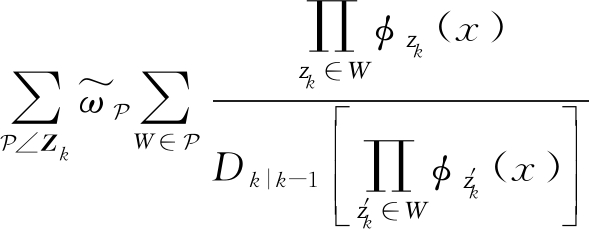
(12)
其中划分![]() 的权值
的权值![]() 为
为
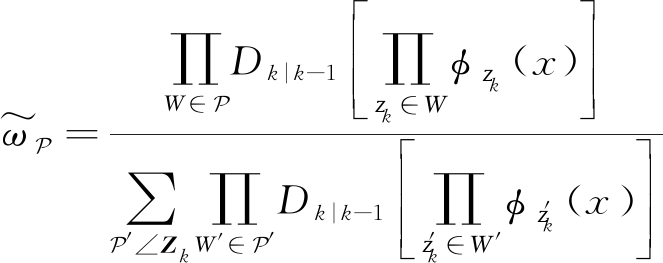
(13)
由于每个扩展目标都能很好地分开,量测集划分就可以简化为一个划分且该划分中的每个量测集单元W代表每个扩展目标生成的量测集,如下
(14)
其中![]() 代表只有一个划分;
代表只有一个划分;![]() 为第i个扩展目标生成的所有量测;m为划分单元的个数,即该采样时刻扩展目标的个数。
为第i个扩展目标生成的所有量测;m为划分单元的个数,即该采样时刻扩展目标的个数。
由于![]() 则由式(13)可看出
则由式(13)可看出![]() 故量测伪似然函数LZk(x)可简化为
故量测伪似然函数LZk(x)可简化为
LZk(x)=1-pd(1-e-γ)+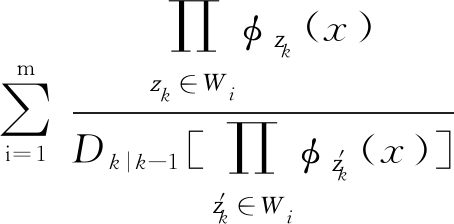
(15)
综上所述,当划分中的每个量测集单元包含扩展目标生成的所有量测时,该划分就是包含信息最丰富的划分,其可以近似替代量测集所有划分。
3.2 存在杂波的场景
实际场景中,ETT系统会存在杂波,如何对存在杂波的量测集进行划分是ETT系统中需要考虑的问题。为了分析如何划分杂波生成的量测,本节假设一个存在杂波且每个目标都能很好的分开的多扩展目标场景。另外,令目标生成的量测相对集中,杂波生成的量测相对分散,即杂波生成的量测远离目标的真实状态。
令zc为杂波量测,则杂波的强度函数为
Dk|k-1[φzc(x)]→0
(16)
当pd=pd(x)和γ=γ(x)时,由式(4)可得估计目标数量为

(17)
对于量测集Zk,假设存在一个划分![]() 且划分的单元为
且划分的单元为![]() 记
记
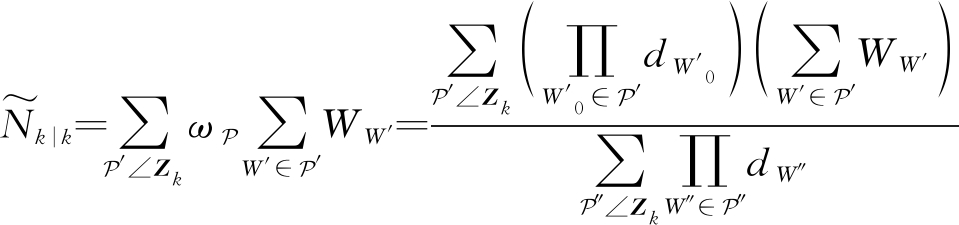
(18)
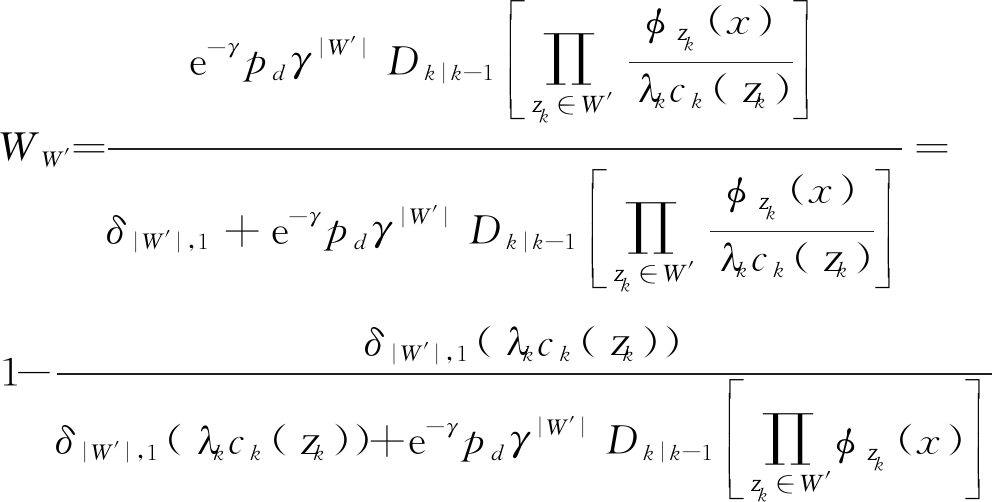
(19)
由式(18)可知,量测集划分中划分方法对目标数目估计及跟踪性能影响较大,为分析方便,记
(20)
由于扩展目标生成的量测较多且相对集中,而杂波随机分布(比较分散)在整个场景中,故可将每个杂波量测划分为一个量测单元。假设一个划分![]() 中包含m个单元,即
中包含m个单元,即![]() 对于
对于![]() 中第i个单元
中第i个单元![]() 具体分析如下:
具体分析如下:
(1)当![]() 时,即
时,即![]() 中的量测为杂波,则
中的量测为杂波,则![]() 且
且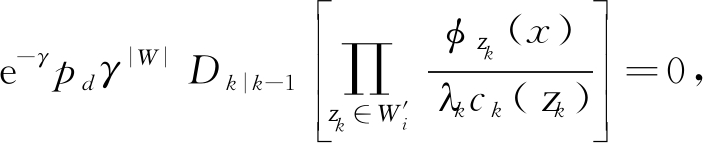 故
故![]() 且WW′→0,易知
且WW′→0,易知![]() 所以该划分中含有杂波的量测集单元对估计目标的数目没有影响,可将其删除,式(20)和式(6)可重新计算如下:
所以该划分中含有杂波的量测集单元对估计目标的数目没有影响,可将其删除,式(20)和式(6)可重新计算如下:
(21)
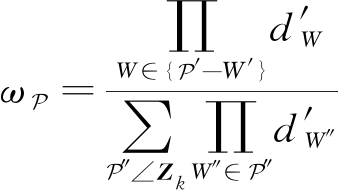
(22)
由式(21)和式(22)可得,如果杂波比较分散,可以对每一采样时刻得到的量测集先滤除杂波再进行划分,这样不但不影响估计目标数量还可以降低划分的复杂度。
(2)当![]() 时,①如果
时,①如果![]() 中的量测都由每个扩展目标生成的量测组成且不包含杂波,即此时杂波分布λkck(zk)=0,由式(19)可知,
中的量测都由每个扩展目标生成的量测组成且不包含杂波,即此时杂波分布λkck(zk)=0,由式(19)可知,![]() 那么该量测集单元是信息最丰富的单元;②如果
那么该量测集单元是信息最丰富的单元;②如果![]() 中的量测包含杂波,则
中的量测包含杂波,则![]() 且
且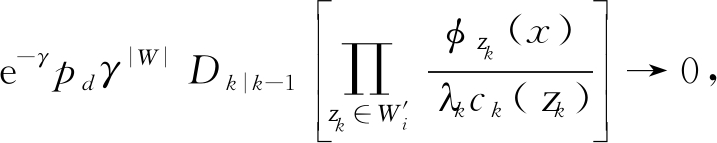 那么
那么![]() 由式(20)可知,
由式(20)可知,![]() 由①②分析可得,如果划分中每个量测集单元都是目标生成的量测,则该划分为信息最丰富的划分;如果划分中包含杂波,则该划分的
由①②分析可得,如果划分中每个量测集单元都是目标生成的量测,则该划分为信息最丰富的划分;如果划分中包含杂波,则该划分的![]() 近似为0,对目标跟踪性能没有影响。
近似为0,对目标跟踪性能没有影响。
综上所述,量测集划分的最终目的就是找到一个信息最丰富的划分去替代量测集所有划分,如①为了降低划分的复杂度,可先对量测集去除杂波;②对剩余量测集进行划分,使其每个量测集单元尽量包含一个目标生成的所有量测。
3.3 信息最丰富的划分
如上所述,由于每个目标生成的量测构成的量测集单元所组成的量测集划分对量测伪似然函数LZk(x)的影响最大,因此该划分称为信息最丰富的划分。但是,对去除杂波后的量测集进行正确的目标量测集划分是比较困难的。这时,我们可以通过在距离上或密度峰值上对每个目标产生的量测进行划分,并使其对应的量测集单元具有较高的权重。
假设去除杂波后的量测集可以找到信息最丰富的划分![]() 则只需要一个该划分就可以替代所有量测集划分的LZk(x),如
则只需要一个该划分就可以替代所有量测集划分的LZk(x),如
(23)
LZk(x)=1-pd(1-e-γ)+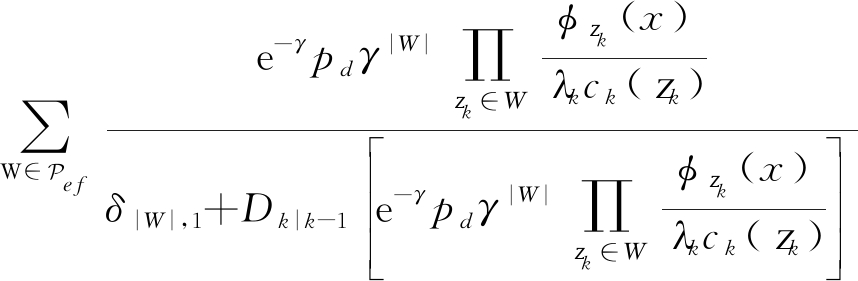
(24)
注意:
(1)信息最丰富的划分用近似的方法接近目标真实情况的量测集划分,其使ET-GM-PHD滤波器易处理并降低计算的复杂度,但其不能完全替代量测集所有划分。
(2)在上文中,为了有效去除杂波,我们假设杂波产生的量测与目标产生的量测相距较远。实际场景中,杂波量测有可能距离目标的真实位置较近且被归类为目标生成的量测,此时,由于杂波量测在目标的真实位置附近,可近似看作目标生成的量测,因此不会对ET-MD-PHD滤波器的跟踪性能产生严重影响。
(3)信息最丰富的划分在理想状态下具有最大的划分权重且![]() 但杂波和扩展目标产生的量测并不能完全分开,这导致划分的权重
但杂波和扩展目标产生的量测并不能完全分开,这导致划分的权重![]() 尽管这样,信息最丰富的划分仍具有最大的权重。
尽管这样,信息最丰富的划分仍具有最大的权重。
4 本文提出的量测集划分算法
2014年,Science期刊上发表了DPC算法[28],该算法简单灵活,可以高效地对大数据集进行分类,其主要思想为聚类中心比其邻域量测有较高的密度点,并且与其他较高密度的任何点有相对较大的距离。
4.1 DPC算法
对于k时刻的量测集Zk=![]() 中的每个量测,DPC算法需要计算局部密度ρi、量测点i与密度比其高的量测点j的最近距离δi两个参数,具体公式如下:
中的每个量测,DPC算法需要计算局部密度ρi、量测点i与密度比其高的量测点j的最近距离δi两个参数,具体公式如下:
(25)
(26)
其中dij是量测![]() 和
和![]() 的距离;dc是截断距离;如果x<0,则χ(x)=1,反之,χ(x)=0。因此,ρi为计算比dc更靠近量测
的距离;dc是截断距离;如果x<0,则χ(x)=1,反之,χ(x)=0。因此,ρi为计算比dc更靠近量测![]() 的量测个数,对于密度最高的量测点,δi取最大值即
的量测个数,对于密度最高的量测点,δi取最大值即![]()
由于密度为局部或全局最大值的量测点的δi远远大于最近邻量测点的距离,因此量测集的聚类中心具有ρi和δi都较大的特点。DPC算法是通过使用ρi-δi点集(ρi,δi)建立决策图,选取同时具有较高的密度ρi和较大的距离δi的量测点![]() 作为聚类中心,而把具有较高δi和较低ρi的量测点看作离群点或杂波,但该方法存在人为干预的缺点。
作为聚类中心,而把具有较高δi和较低ρi的量测点看作离群点或杂波,但该方法存在人为干预的缺点。
4.2 IDPC量测集划分算法
在IDPC算法中,为了减少杂波生成的量测对扩展目标生成的量测的聚类划分以及人为干预的影响,我们对k时刻的量测集Zk做以下四步处理:
(1)滤除杂波。选取截断距离dc为2倍的量测噪声标准差,局部密度阈值ρc为0.2倍目标泊松率(如γ=10时,ρc=2),对所有量测点的局部密度ρi进行筛选可以有效地去除距离目标较远的杂波,从而减少后续对量测集聚类的干扰。
(2)寻找密度较高的簇(量测集单元)。对于去除杂波[24]后的量测集![]() 引入一个变量a,使其满足a=ρi×δi,并对其进行降序排序,a值越大,其对应的量测点越有可能为聚类中心(也越有可能为扩展目标的运动质心),故可以自动选取a的前n个点作为密度峰值点,从而自动找出二维空间中疑似目标生成的量测形成簇及其簇的中心(也可称为聚类和聚类中心),簇的选取为密度峰值点的近邻(其小于阈值η且与截断距离dc相关)。簇的中心和簇可记为
引入一个变量a,使其满足a=ρi×δi,并对其进行降序排序,a值越大,其对应的量测点越有可能为聚类中心(也越有可能为扩展目标的运动质心),故可以自动选取a的前n个点作为密度峰值点,从而自动找出二维空间中疑似目标生成的量测形成簇及其簇的中心(也可称为聚类和聚类中心),簇的选取为密度峰值点的近邻(其小于阈值η且与截断距离dc相关)。簇的中心和簇可记为
![]() 当i≠j,i, j∈{1,2,…,n}时,ci≠cj。
当i≠j,i, j∈{1,2,…,n}时,ci≠cj。
![]() 当i≠j,i, j∈{1,2,…,n}时,
当i≠j,i, j∈{1,2,…,n}时,![]() 且Zk,ci∩Zk,cj=
且Zk,ci∩Zk,cj=![]() 。
。
其中,ci为目标i的运动质心,Zk,ci为目标i生成的量测集。这种划分记为![]() 且
且![]()
此时得到的簇,可能存在某个簇是两个或更多目标的量测混合(重叠簇)的现象,为了避免此类情况,可进行以下判断。
(3)通过预测的高斯分量判断步骤(2)的簇是否有重叠簇,并判断是否进行下一步划分。文献[29]提出了部分共识的概念,其主要思想为:权重高的高斯分量更可能为目标真实的估计。我们将预测的高斯分量中wk|k-1≥0.1的高斯分量的位置均值![]() (s为满足权重条件的均值数量)与步骤(2)的多个聚类中心计算距离矩阵:当聚类中心cj与
(s为满足权重条件的均值数量)与步骤(2)的多个聚类中心计算距离矩阵:当聚类中心cj与![]() 的距离小于η时,判定
的距离小于η时,判定![]() 在簇Zk,cj内;否则,判定
在簇Zk,cj内;否则,判定![]() 在簇Zk,cj之外。
在簇Zk,cj之外。
对s个预测位置![]() 与n个聚类中心
与n个聚类中心![]() 构建匈牙利分配的距离矩阵如下:
构建匈牙利分配的距离矩阵如下:
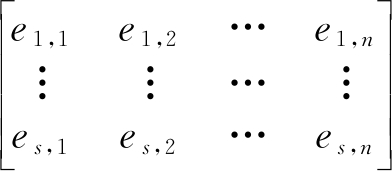
(27)
其中ei, j为第i个预测位置![]() 和第j个聚类中心cj的欧氏距离,其与η的比较用来判定
和第j个聚类中心cj的欧氏距离,其与η的比较用来判定![]() 是否在簇Zk,cj内。
是否在簇Zk,cj内。
通过判断簇内出现预测状态数量来识别簇是否为重叠簇,其计算如下:
(28)
(a)当mj>1时,说明有mj个预测目标在簇Zk,cj内,则该簇为重叠簇。此时对Zk,cj进行k-means计算,得到mj个较小的簇Zk,cj,l且l=1,2,…,mj,如
(29)
每个簇Zk,cj,l可作为划分中的一个量测集单元。
(b)当mj=1时,说明只有一个预测目标在簇Zk,cj内,则该簇为非重叠簇,即该时刻的簇Zk,cj可作为该目标产生的量测(对应一个量测集单元)。
(c)当mj=0时,说明无预测目标在簇Zk,cj内,此时可通过计算簇的大小|Zk,cj|来判断该簇是否保留。第一,如果|Zk,cj|较小,可当成杂波并将其删除。原因在于虽然我们假设杂波生成的量测是均匀分散在监视区域内的,但通过步骤(1)去除杂波后并不能保证杂波全部排除,也有可能会出现几个杂波相互靠近且被划分在同一个簇的情况,故如果|Zk,cj|值较小,则可认为簇Zk,cj是杂波产生的量测并将其删除。第二,如果|Zk,cj|较大,可当成漏检目标产生的量测并将其保留。原因在于步骤(3)是对目标的预测均值mk|k-1筛选后才与得到的聚类中心计算距离矩阵来判断其是否在某一簇内,但利用预测权重wk|k-1进行筛选难免会出现目标漏检情况,故如果|Zk,cj|较大,可认为簇Zk,cj是漏检目标产生的量测并保留。
(4)最后,重新得到一个新的量测集划分![]() (有且仅有一个该划分),使其包含以上分析得到的簇(量测集单元),此时所有量测集单元所组成的量测集
(有且仅有一个该划分),使其包含以上分析得到的簇(量测集单元),此时所有量测集单元所组成的量测集![]() 且
且![]()
由于IDPC算法对每个采样时刻得到的量测集进行的划分只得到一个划分,因此可以不对![]() 进行求和
进行求和![]() 且用式(6)求划分的权值恒为
且用式(6)求划分的权值恒为![]() 量测伪似然函数LZk(x)由式(5)可重新简化为
量测伪似然函数LZk(x)由式(5)可重新简化为
(30)
通过以上分析可知,使用IDPC算法划分得到的量测集单元中所包含的量测数目恒大于1,即|W|>1,故式(7)的每一个量测集单元W的权值也可以进行相应化简:
(31)
IDPC算法划分可得到一个最可能的量测集划分,这在要求实时性比较高的场景中具有重要意义。
4.3 IDPC算法总结
根据4.2节的分析,基于IDPC量测集划分的ETT算法基本步骤如下:
步骤1 已知k-1时刻目标的强度函数Dk-1|k-1(x|Zk-1),通过式(3)可得k时刻预测的目标强度函数Dk|k-1(x|Zk-1)。
步骤2 已知k时刻所有的量测集Zk,通过式(25)和式(26)得到每个量测点的局部密度ρi和距离δi。
步骤3 选取ρi>ρc,对量测集Zk去除分散的杂波,得到新的量测集![]()
步骤4 对量测集![]() 使用a=ρi×δi得到一种划分
使用a=ρi×δi得到一种划分![]() 使其可自动找出n个密度峰值近邻的量测集单元
使其可自动找出n个密度峰值近邻的量测集单元![]() 以及聚类中心
以及聚类中心![]()
步骤5 首先,对步骤1得到的预测均值mk|k-1根据权重wk|k-1进行筛选,得到筛选后的目标预测位置状态![]() 其次,用式(27)计算预测位置
其次,用式(27)计算预测位置![]() 与聚类中心
与聚类中心![]() 的成本矩阵,进而用式(28)计算预测位置
的成本矩阵,进而用式(28)计算预测位置![]() 落于第j个量测集单元Zk,cj的数量mj;最后,通过mj的大小以及量测集单元Zk,cj中包含元素个数来判别Zk,cj是进一步再划分为更小的mj个量测集单元
落于第j个量测集单元Zk,cj的数量mj;最后,通过mj的大小以及量测集单元Zk,cj中包含元素个数来判别Zk,cj是进一步再划分为更小的mj个量测集单元![]() 或是保持原有的量测集单元Zk,cj,还是将其删除。重新整理得到一种新的量测集划分
或是保持原有的量测集单元Zk,cj,还是将其删除。重新整理得到一种新的量测集划分![]() 并替代步骤4中的划分
并替代步骤4中的划分![]() 划分
划分![]() 中所有量测集单元所组成的量测集
中所有量测集单元所组成的量测集![]()
步骤6 将最新的划分![]() 及其包含的量测集单元代入式(4),得到更新的目标强度函数Dk|k(x|Zk)。
及其包含的量测集单元代入式(4),得到更新的目标强度函数Dk|k(x|Zk)。
步骤7 对更新的Dk|k(x|Zk)的高斯分量进行修剪合并等处理,获得扩展目标的状态估计。
5 模拟仿真及分析
本文在扩展目标出现交叉运动以及新生和衍生随机产生的场景下采用基于IDPC算法划分的ET-GM-PHD滤波器对目标进行跟踪,并与传统的距离划分和k-means划分方法进行了对比分析。
扩展目标都是在监视区域[-1000 m,1000 m]×[-1000 m,1000 m]内运动,每个扩展目标的运动服从高斯分布模型,其状态方程为:
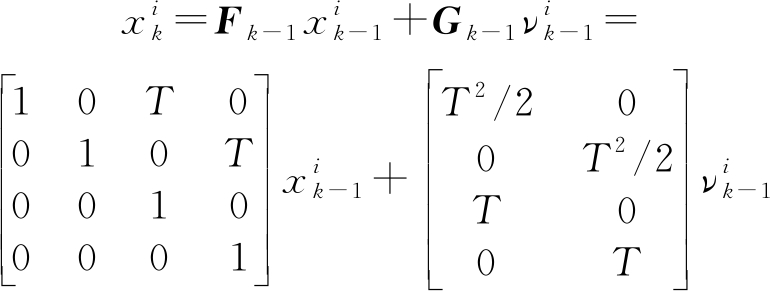
(32)
其中![]() 是扩展目标的状态,xk和yk是目标在二维空间中的平面位置,而
是扩展目标的状态,xk和yk是目标在二维空间中的平面位置,而![]() 和
和![]() 是其对应的速度(m/s),过程噪声是均值为零和协方差为Qk=(2 m/s)I2的高斯噪声,I2为二维单位矩阵。
是其对应的速度(m/s),过程噪声是均值为零和协方差为Qk=(2 m/s)I2的高斯噪声,I2为二维单位矩阵。
量测方程为:
(33)
其中![]() 是传感器在笛卡尔坐标系中得到的量测值,量测噪声是均值为零和协方差为Rk=(20 m/s)I2的高斯噪声,且每个扩展目标产生的量测相互独立同分布。
是传感器在笛卡尔坐标系中得到的量测值,量测噪声是均值为零和协方差为Rk=(20 m/s)I2的高斯噪声,且每个扩展目标产生的量测相互独立同分布。
场景中目标的存活概率和检测概率分别为ps=0.99和pd=0.99,背景杂波数服从均值为10的泊松分布且随机的分布在监视区域内,传感器的采样时间间隔为T=1 s,整个目标跟踪时长为100 s。仿真参数设置修剪门限Tprune=10-5,合并门限Uprune=4,最大高斯分量数Jmax=100。
新生目标强度:
![]()
![]()
Pbirth=diag([100 100 25 25])
(34)
衍生目标强度:
(35)
其中Pspawn=diag([100 100 400 400]),而ξ为本体状态。
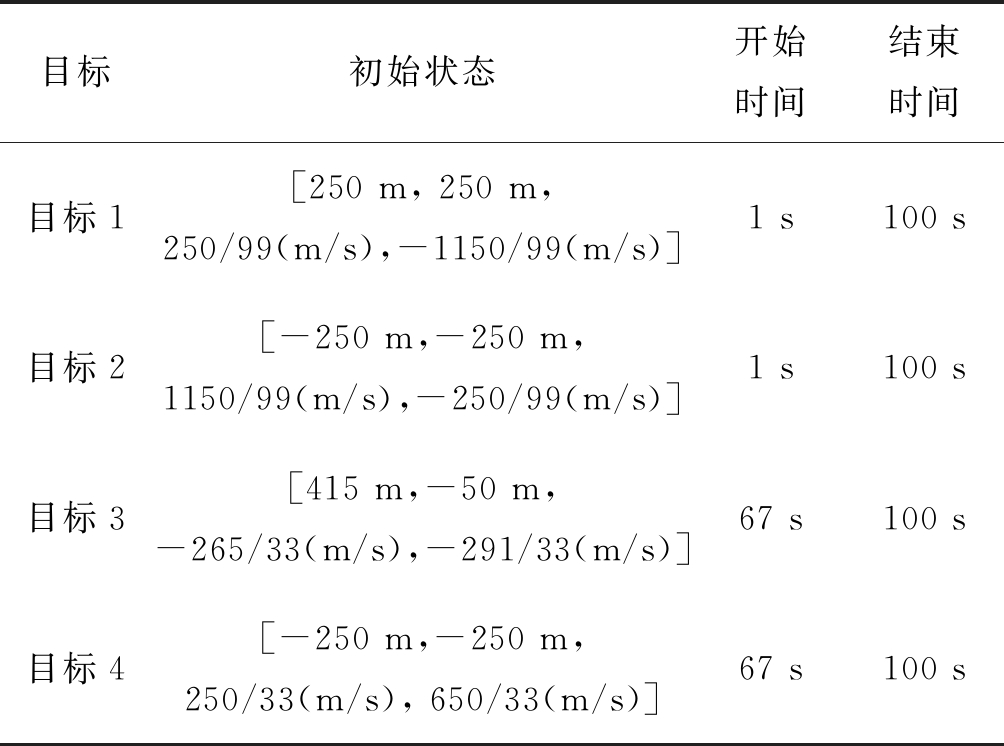
本场景包含四个扩展运动目标,其具体初始状态与起始时间如表1所示,每个目标的量测数目均服从均值为10的泊松分布。其中,在第56时刻出现两个扩展目标交叉运动,第67时刻出现一个新生目标和一个衍生目标,四个扩展目标的具体运动轨迹如图1所示。
表1 目标的初始状态与起始时间
Tab.1 Initial state, start and dead time of targets
目标初始状态开始时间结束时间目标1[250 m, 250 m,250/99(m/s),-1150/99(m/s)]1 s100 s目标2[-250 m,-250 m,1150/99(m/s),-250/99(m/s)]1 s100 s目标3[415 m,-50 m,-265/33(m/s),-291/33(m/s)]67 s100 s目标4[-250 m,-250 m,250/33(m/s), 650/33(m/s)]67 s100 s
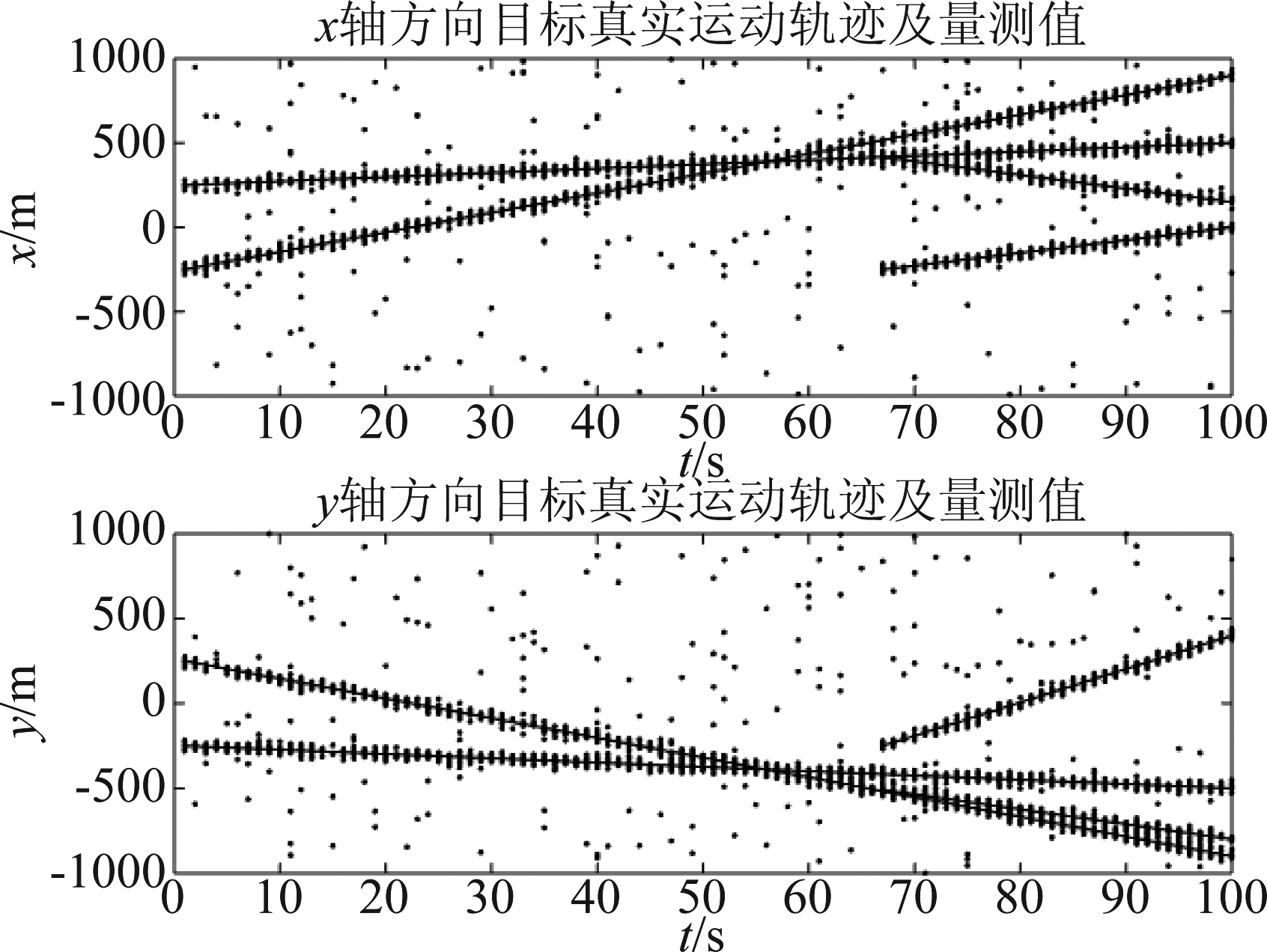
图1 在x和y轴上的真实位置及量测
Fig.1 The true x and y position and measurements
图2给出了目标在二维空间上的真实运动轨迹(如“-”所示)以及IDPC算法划分得到的估计轨迹(如“o”所示),从图中可以看出,IDPC算法对目标的跟踪效果与模拟仿真轨迹基本相同,没有出现明显的跟丢及偏离现象,具有很好地鲁棒性。
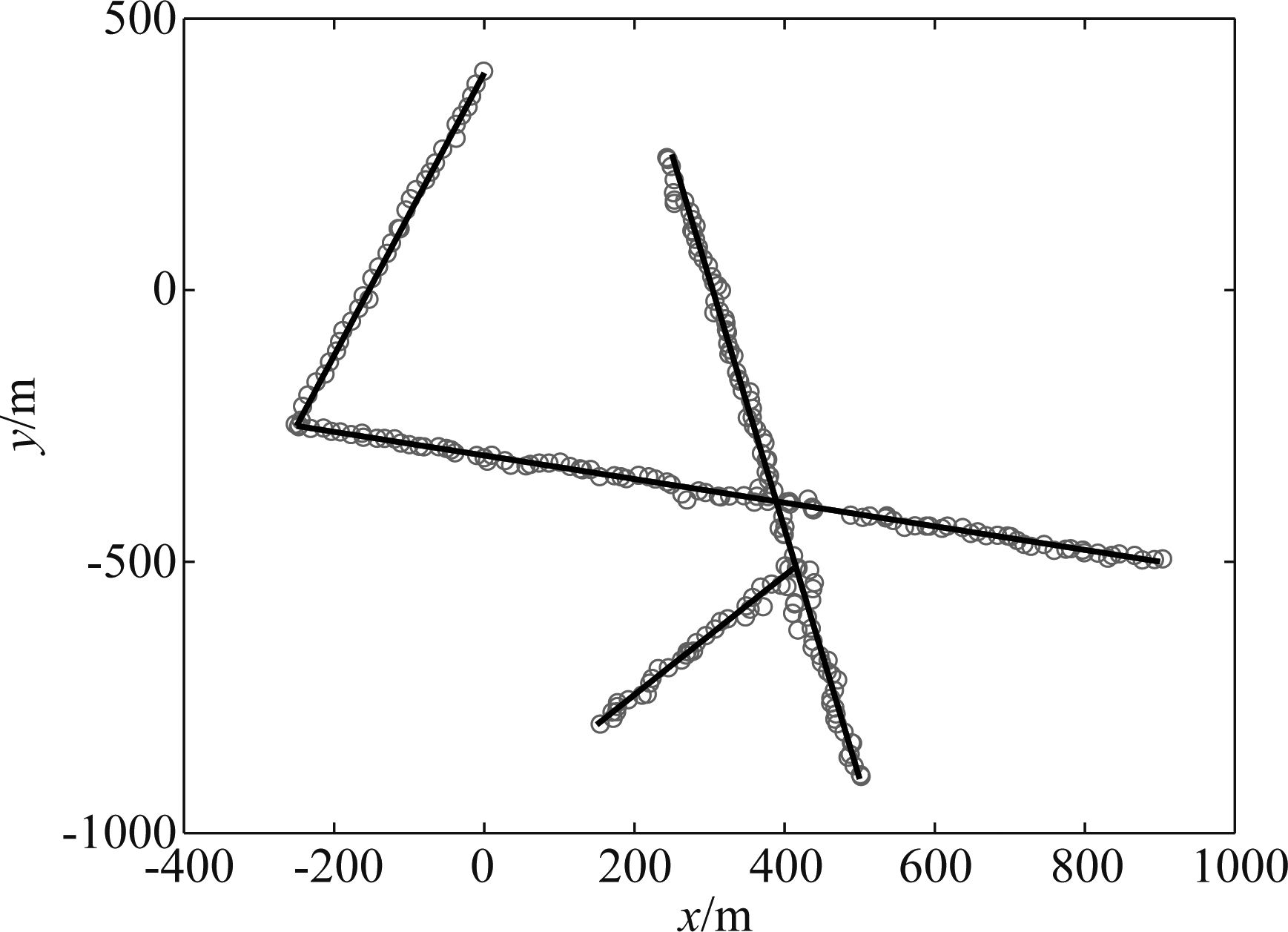
图2 真实和估计轨迹
Fig.2 Real and estimated trajectory
图3(a1)显示了第52时刻在空间上两个相互靠近的扩展目标和杂波产生的量测;图3(a2)是对图3(a1)的量测用IDPC算法进行量测集划分,得出该划分可以有效去除杂波并获得两个量测集单元的结论;图3(b1)显示了第68时刻四个扩展目标和杂波产生的量测,其中两个目标在空间上相互靠近;图3(b2)是对图3(b1)的量测用IDPC算法进行量测集划分,得出可以有效去除杂波并获得四个量测集单元的结论。从图3可看出,在空间上相互靠近的目标使用IDPC算法能够有效的区分。
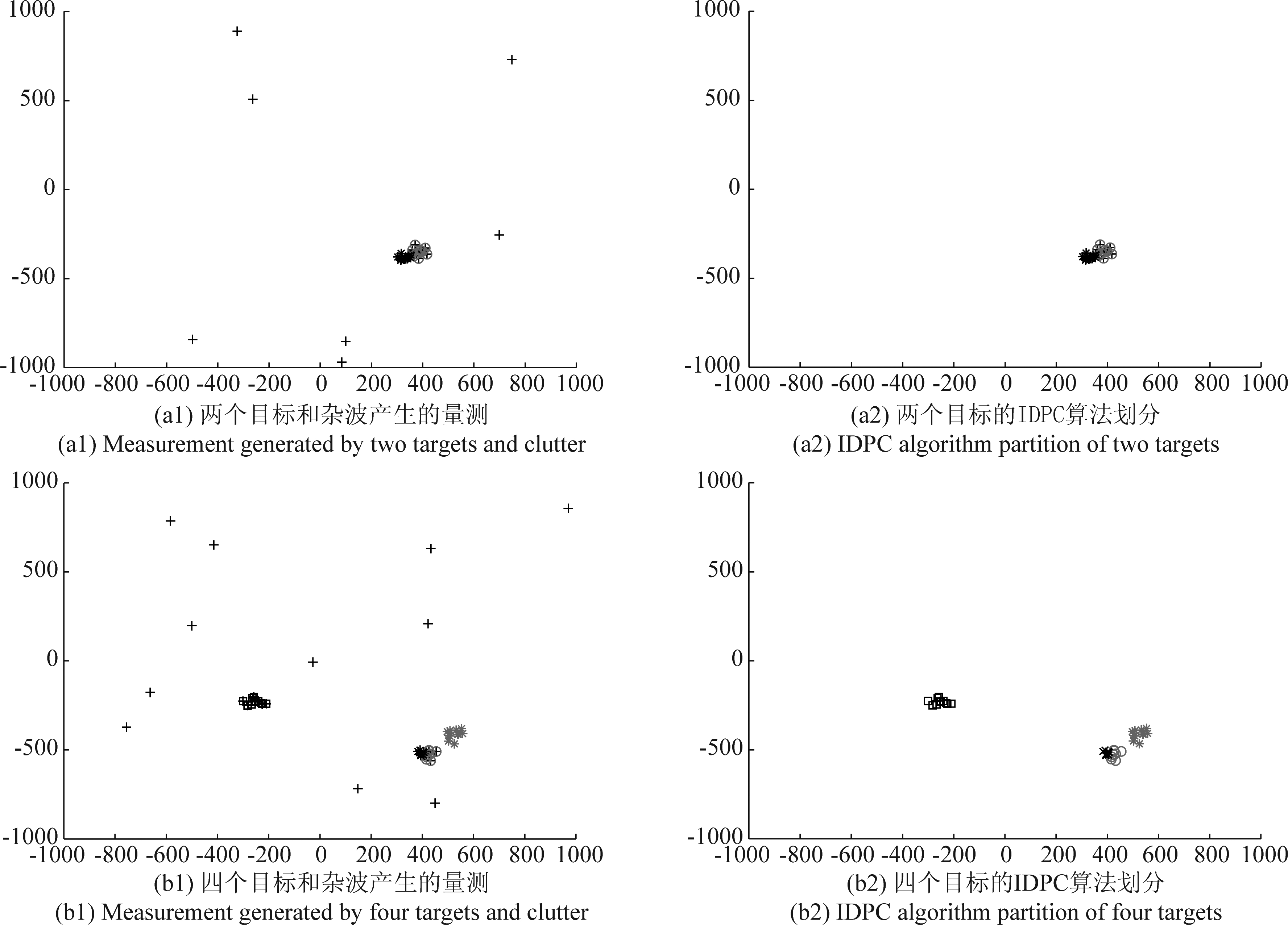
图3 IDPC算法划分结果
Fig.3 Result of the IDPC algorithm partition
为了进一步说明IDPC算法划分的优势,使其与距离划分方法进行比较效果如下:图4(a)是第68时刻四个扩展目标和杂波产生的量测,其中两个目标在空间上非常靠近;图4(b)显示了用距离阈值d=34.2359 m进行距离划分的结果,该划分可以得到七个量测集单元,其中杂波生成的量测明显地被分为量测集单元(如“▽”、“ ”和“◇”所示)以及两个靠近的扩展目标生成的量测分为一个量测集单元(如“o”所示);图4(c)显示了用距离阈值d=45.5512 m进行距离划分的结果,该划分可以得到六个量测集单元,与图4(b)显示结果相似,但一个量测集单元包含了其附近的杂波(如“×”所示);通过图4(b)和图4(c)分析可知,距离阈值的选择不恰当会出现把杂波分为量测集单元以及空间上相互靠近的目标产生的量测不能有效地区分的情况,且距离阈值范围的选取也会影响算法的复杂度;图4(d)显示了IDPC算法的划分结果,尽管存在两个目标产生的量测在空间上比较接近,但仍可以有效地划分出两个量测集单元,解决了距离划分的问题。
”和“◇”所示)以及两个靠近的扩展目标生成的量测分为一个量测集单元(如“o”所示);图4(c)显示了用距离阈值d=45.5512 m进行距离划分的结果,该划分可以得到六个量测集单元,与图4(b)显示结果相似,但一个量测集单元包含了其附近的杂波(如“×”所示);通过图4(b)和图4(c)分析可知,距离阈值的选择不恰当会出现把杂波分为量测集单元以及空间上相互靠近的目标产生的量测不能有效地区分的情况,且距离阈值范围的选取也会影响算法的复杂度;图4(d)显示了IDPC算法的划分结果,尽管存在两个目标产生的量测在空间上比较接近,但仍可以有效地划分出两个量测集单元,解决了距离划分的问题。
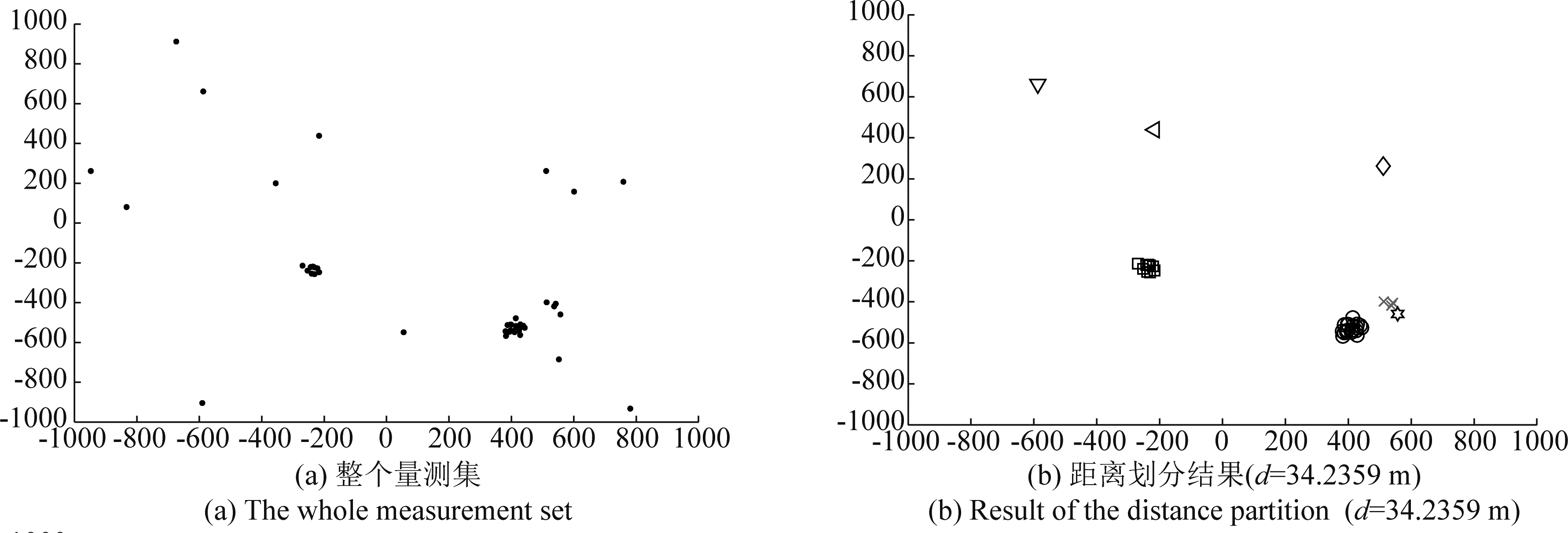
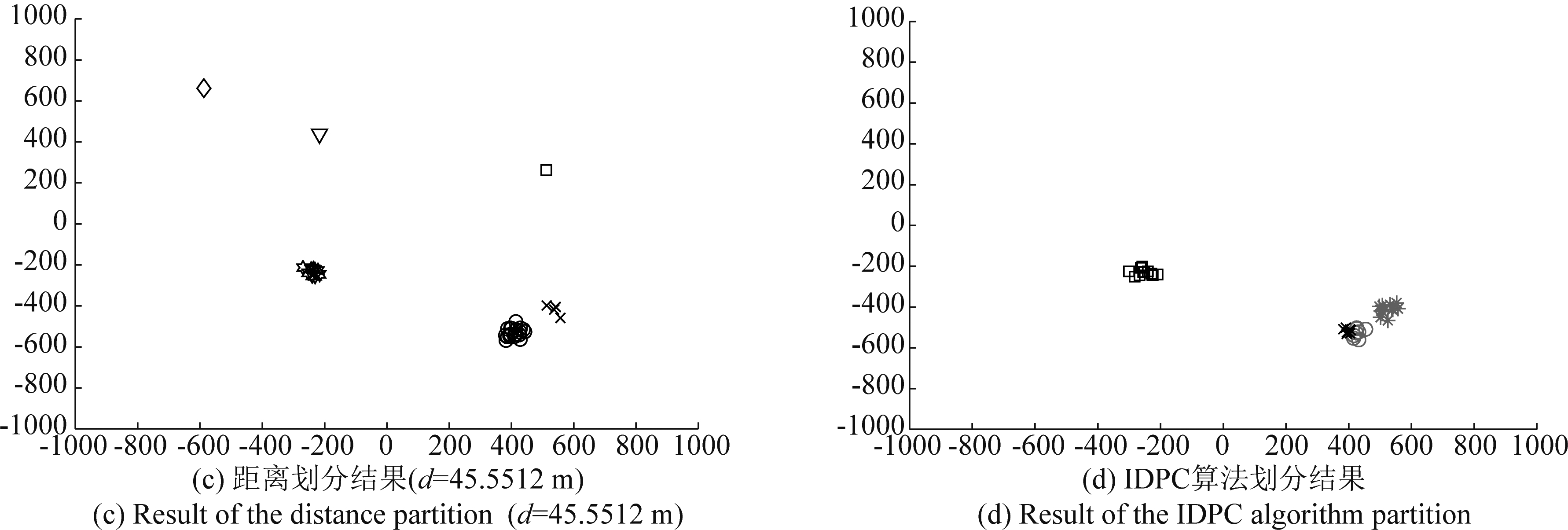
图4 IDPC算法划分和距离划分结果
Fig.4 Result of the IDPC algorithm and distance partition
由图4的分析和图5可以看出,在目标运动过程中存在交叉以及新生目标和衍生目标出现时,IDPC算法对量测集划分的结果明显优于距离划分和k-means划分。
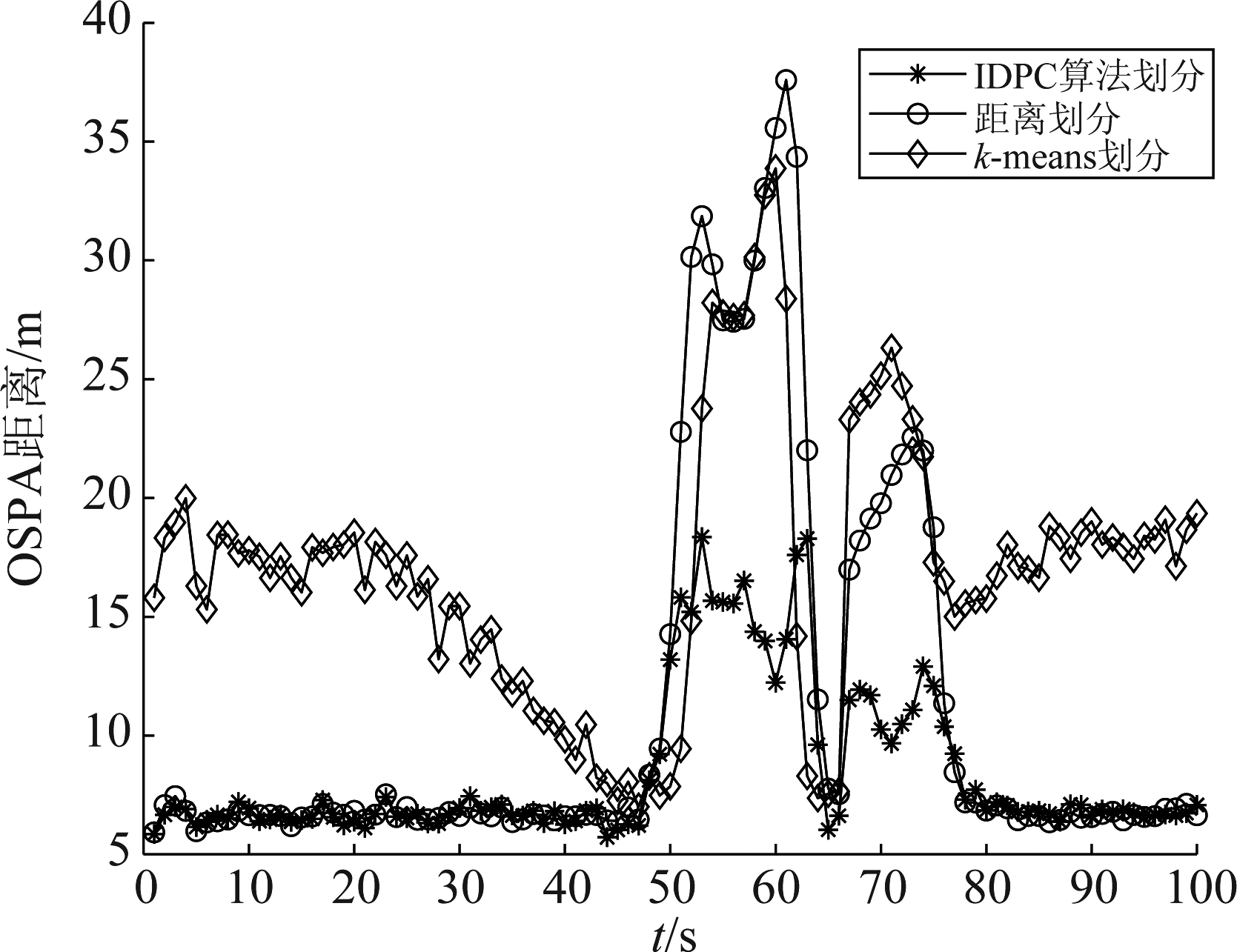
图5 平均OSPA距离
Fig.5 Average OSPA distance
图6表明了IDPC算法划分耗时相对距离划分和k-means划分较小,对于跟踪具有较大的优势,其原因为:IDPC算法仅通过一个截断距离得到最有可能的量测集划分,而距离划分根据多个截断距离以及k-means划分根据多个k值得到多个量测集划分。三种量测集划分方法得到不同的量测集划分![]() 使其在ET-GM-PHD状态更新步骤中运算耗时具有明显的差异,其中IDPC算法划分方法使整个滤波器的总耗时远小于后两者。
使其在ET-GM-PHD状态更新步骤中运算耗时具有明显的差异,其中IDPC算法划分方法使整个滤波器的总耗时远小于后两者。
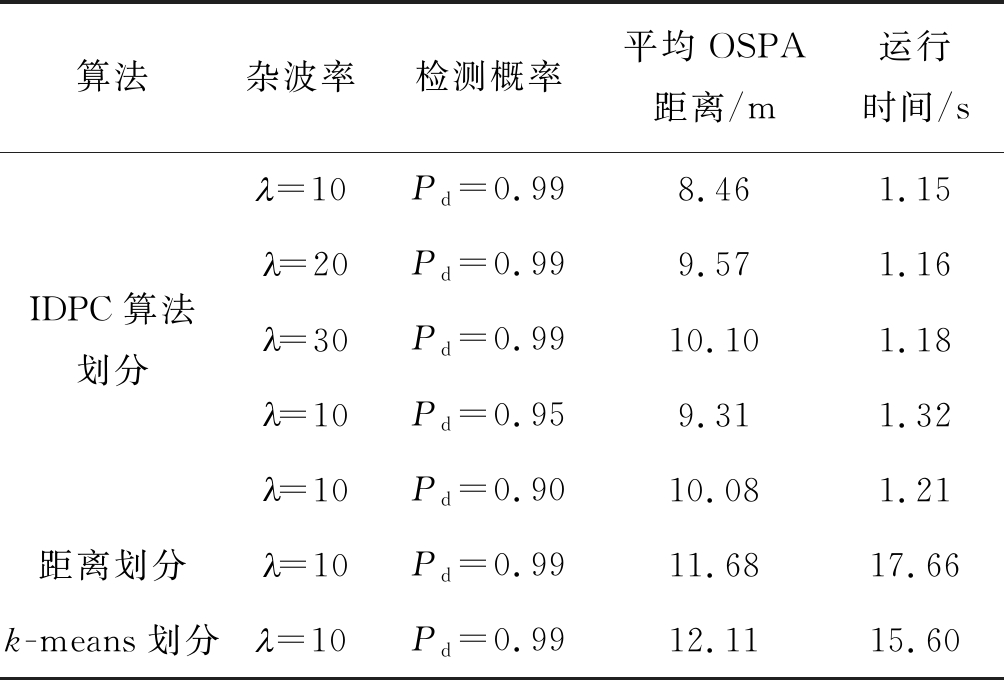
表2给出了不同杂波率和检测概率条件下三种量测集划分方法的平均OSPA距离和整体运行时间(主要说明IDPC算法划分的结果),明显得出低杂波和高检测率时IDPC算法的跟踪性能最好且运行速度最快。
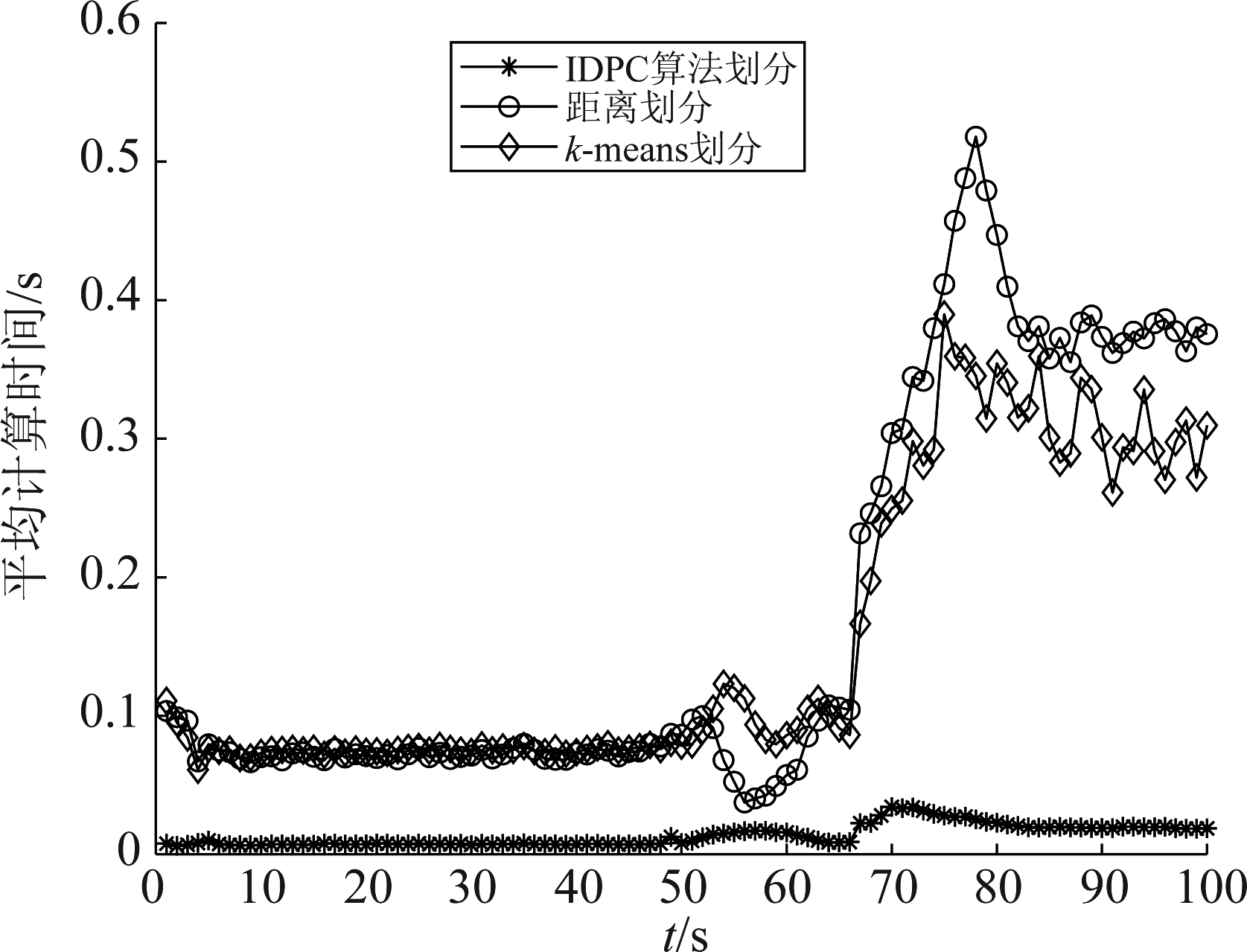
图6 平均计算时间
Fig.6 Average calculation time
表2 不同条件下的量测集划分的平均OSPA距离
Tab.2 Average OSPA distance of measurement set
partition under different conditions
6 结论
针对扩展目标中量测集划分难从而造成计算时间复杂问题,本文提出了一种IDPC量测集划分算法。该算法通过得到一个近似信息最丰富的划分去替代量测集所有划分。实验结果表明,在目标出现交叉、新生和衍生时,该算法均能够准确地对每个时刻的量测集进行划分,在保证目标稳定跟踪的同时又可以有效地缩短计算时间,使总体性能明显优于其他传统划分算法。本文没有考虑每个扩展目标产生的量测数目服从不同均值泊松分布的情况,下一步可以从该方面考虑并对IDPC算法进行优化。
[1] DEGERMAN J, WINTENBY J, SVENSSON D, et al. Extended target tracking using principal components[C]∥14th In-ternational Conference on Information Fusion, 2011: 1- 8.
[2] ANGELOVA D, MIHAYLOVA L. Extended object tracking using Monte Carlo methods[J]. IEEE Transactions on Signal Processing, 2008, 56(2): 825- 832.
[3] MAHLER R P S. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace and Electronic Systems, 2003, 39(4): 1152-1178.
[4] MAHLER R. Statistical multisource-multitarget information fusion[M]. Norwood, MA: Artech House, 2007.
[5] VO B N, MA W K. The Gaussian mixture probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4091- 4104.
[6] MAHLER R. PHD filters of higher order in target number[J]. IEEE Transactions on Aerospace and Electronic Systems, 2007, 43(4): 1523-1543.
[7] VO B T, VO B N, CANTONI A. Analytic implementations of the cardinalized probability hypothesis density filter[J]. IEEE Transactions on Signal Processing, 2007, 55(7): 3553-3567.
[8] VO B T, VO B N, CANTONI A. The cardinality balanced multi-target multi-bernoulli filter and its implementations[J]. IEEE Transactions on Signal Processing, 2009, 57(2): 409- 423.
[9] REUTER S, VO B T, VO B N, et al. The labeled multi-bernoulli filter[J]. IEEE Transactions on Signal Processing, 2014, 62(12): 3246-3260.
[10]GILHOLM K, SALMOND D. Spatial distribution model for tracking extended objects[J]. IEE Proceedings-Radar, Sonar and Navigation, 2005, 152(5): 364-371.
[11]MAHLER R. PHD filters for nonstandard targets, I: Extended targets[C]∥2009 12th International Conference on Information Fusion. Seattle, WA, USA. IEEE, 2009: 915-921.
[12]GRANSTRÖM K, LUNDQUIST C, ORGUNER U. A Gaussian mixture PHD filter for extended target tracking[C]∥2010 13th International Conference on Information Fusion. Edinburgh, UK. IEEE, 2010: 1- 8.
[13]GRANSTROM K, LUNDQUIST C, ORGUNER O. Extended target tracking using a Gaussian-mixture PHD filter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(4): 3268-3286.
[14]GRANSTROM K, ORGUNER U. A phd filter for tracking multiple extended targets using random matrices[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5657-5671.
[15]ZHANG Yongquan, JI Hongbing. A novel fast partitioning algorithm for extended target tracking using a Gaussian mixture PHD filter[J]. Signal Processing, 2013, 93(11): 2975-2985.
[16]ZHANG Yongquan, JI Hongbing. Gaussian mixture reduction based on fuzzy ART for extended target tracking[J]. Signal Processing, 2014, 97: 232-241.
[17]LI Yunxiang, XIAO Huaitie, SONG Zhiyong, et al. A new multiple extended target tracking algorithm using PHD filter[J]. Signal Processing, 2013, 93(12): 3578-3588.
[18]LUNDQUIST C, GRANSTRÖM K, ORGUNER U. An extended target CPHD filter and a gamma Gaussian inverse wishart implementation[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 472- 483.
[19]MA Dongdong, LIAN Feng, LIU Jing. Sequential Monte Carlo implementation of cardinality balanced multi-target multi-Bernoulli filter for extended target tracking[J]. IET Radar, Sonar & Navigation, 2016, 10(2): 272-277.
[20]BEARD M, REUTER S, GRANSTRÖM K, et al. Multiple extended target tracking with labeled random finite sets[J]. IEEE Transactions on Signal Processing, 2016, 64(7): 1638-1653.
[21]程艳云, 周鹏. 动态分配聚类中心的改进K均值聚类算法[J]. 计算机技术与发展, 2017, 27(2): 33-36,41.
CHENG Yanyun, ZHOU Peng. Improved K-means clustering algorithm for dynamic allocation cluster center[J]. Computer Technology and Development, 2017, 27(2): 33-36,41.(in Chinese)
[22]YANG Jinlong, LIU Fengmei, GE Hongwei, et al. Multiple extended target tracking algorithm based on GM-PHD filter and spectral clustering[J]. EURASIP Journal on Advances in Signal Processing, 2014, 2014(1): 1- 8.
[23]胡忠旺, 丁勇, 杨勇, 等. 基于时空关联—网格聚类的多扩展目标跟踪算法[J]. 传感器与微系统, 2019, 38(2): 129-132.
HU Zhongwang, DING Yong, YANG Yong, et al. Multiple extended target tracking algorithm based on spatiotemporal correlation and grid clustering[J]. Transducer and Microsystem Technologies, 2019, 38(2): 129-132.(in Chinese)
[24]迟珞珈, 冯新喜, 蒲磊, 等. 基于二级CFSFDP的扩展目标量测集划分算法[J]. 计算机工程, 2018, 44(5): 309-315.
CHI Luojia, FENG Xinxi, PU Lei, et al. Extended target measurement set partition algorithm based on second level CFSFDP[J]. Computer Engineering, 2018, 44(5): 309-315.(in Chinese)
[25]SHEN Xinglin, SONG Zhiyong, FAN Hongqi, et al. Fast density peak-based clustering algorithm for multiple extended target tracking[J]. Journal of Systems Engineering and Electronics, 2019, 30(3): 435- 447.
[26]苗露, 李鸿艳, 冯新喜. 基于CODHD聚类划分的多扩展目标跟踪算法[J]. 计算机工程与应用, 2018, 54(19): 261-265.
MIAO Lu, LI Hongyan, FENG Xinxi. Multiple extended target tracking algorithm based on CODHD clustering division[J]. Computer Engineering and Applications, 2018, 54(19): 261-265.(in Chinese)
[27]彭聪, 王杰贵, 朱克凡. 基于动态网格密度的SNN聚类的ET-GM-PHD滤波算法[J]. 弹箭与制导学报, 2019, 39(2): 152-158.
PENG Cong, WANG Jiegui, ZHU Kefan. ET-GM-PHD filtering algorithm based on dynamic grid density SNN clustering[J]. Journal of Projectiles,Rockets,Missiles and Guidance, 2019, 39(2): 152-158.(in Chinese)
[28]RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344(6191): 1492-1496.
[29]LI Tiancheng, CORCHADO J M, SUN Shudong. Partial consensus and conservative fusion of Gaussian mixtures for distributed PHD fusion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(5): 2150-2163.

