1 引言
交互式多模型算法(Interacting Multiple Model Algorithm,IMM)是非常有效的目标跟踪算法,获得了广泛的应用[1- 4],它采用多个固定的并行模型来描述目标的运动模式,通过加权计算各个子滤波器的滤波结果来获得最优状态估计。然而,其跟踪性能在很大程度上依赖所选取的模型集,在目标存在复杂机动的情况下,一种常见的思路是增加模型数目,来尽可能完整地包含目标的运动模式,但这会引起计算量的激增,而且,若所有模型均与目标机动不匹配、或模型之间区分度不明显,模型的增多反而可能会加剧模型间的竞争,导致跟踪性能下降。模糊逻辑方法在描述无法数学建模或准确估计参数的系统时具有优势[5],因此,研究人员将模糊逻辑运用到难以精确运动学建模的机动目标跟踪领域,提出了很多自适应IMM算法。
IMM算法中模型的匹配概率决定了各模型的滤波估计在融合输出中的权重,对目标的跟踪精度有很大影响。基于此,文献[6]利用模型概率和模型概率变化信息,通过模糊控制对IMM算法的模型概率更新模块进行改进,改善了传统算法在目标发生强机动时收敛速度慢的缺点。文献[7]则以当前量测值作为模糊系统输入,以模型当前时刻的滤波值分别作为隶属函数的中心,利用模糊逻辑方法计算各模型的匹配概率。文献[8]通过离线训练T-S(Takagi-Sugeno)模糊系统提取模型以及隶属函数,无需基于量测即可更新模型概率。模糊控制方法也能用于实时调整模型转换概率[9-12],提高算法收敛速度或降低滤波误差。
通过模糊推理调节各个子滤波器的过程噪声协方差以覆盖更大范围的机动,是模糊控制在IMM算法中另外一种典型的应用思路。模糊交互多模型算法(FIMM)[13]参考了军事专家总结的模糊规则[14],将模糊控制卡尔曼滤波器与IMM算法相结合,自适应地控制滤波器的过程噪声协方差大小。文献[15]同样是通过模糊控制过程噪声协方差,但区别于FIMM算法以机动新息和新息变化作为模糊系统输入,选择以模型概率为输入。文献[16]在FIMM算法基础上,将目标运动模式划分为机动与非机动两类,仅机动模式的子滤波器采用模糊控制调节过程噪声协方差,非机动模式下该参数设为固定值,进一步降低了计算量。文献[17]研究了FIMM算法模糊系统输入变量的归一化问题,提出了一种新的自适应归一化方式。文献[18]和文献[19]分别利用遗传算法和禁忌搜索算法优化模糊系统的隶属度函数参数,然而模型集始终固定的缺陷并未解决。
针对传统IMM及FIMM算法模型数目始终固定的问题,本文提出了一种基于模糊逻辑的改进自适应IMM算法(FAIMM)。通过对模型匹配概率的一种非线性映射处理,仅保留接近真实运动情况的模型子集,减少不必要的模型;并引入模糊推理,无需先验知识,即可完成过程噪声水平的实时自适应调整,从而降低模型集与目标机动的失配误差。最后,通过对气动目标轨迹的跟踪实验对比验证了所提算法的性能。
2 系统描述
对机动目标运动情况建立合适的数学模型,是目标跟踪中非常关键的问题。常用目标运动模型为
X(k+1)=F(k)X(k)+G(k)V(k)
(1)
传感器的观测方程为
Z(k)=H(k)X(k)+W(k)
(2)
其中,
表示目标状态向量,x(k),y(k),z(k)表示k时刻目标的位置分量,
表示速度分量,G(k)为系统扰动矩阵,F(k)为状态转移矩阵,对于不同的运动模型,F(k)一般是不同的。Z(k)=[x(k),y(k),z(k)]表示k时刻目标的观测值,一般只考虑位置量测,H(k)为量测矩阵, V(k)和W(k)分别表示过程噪声和观测噪声,它们是相互独立的零均值高斯白噪声,其协方差阵分别为Q(k)和R(k)。
2.1 含附加项的CV模型
该模型仅针对加速度的机动情况,假定目标的最大加速度为Amax,最小加速度为Amin。为了尽可能的反映目标的真实运动情况,模型集应当涵盖目标所有可能发生的状态变化,即:使用的多个模型应覆盖了整个模型空间,也就是Amin至Amax这一范围,同时,为了避免模型竞争,相邻的模型应该能很好的分离开来。因此,该模型在CV(恒速)模型基础上增加了一个平均加速度项[20]。每个模型以平均加速度为中心,只需覆盖特定的范围。模型状态方程为
X(k+1)=FX(k)+UAj(k)+GVj(k), j=1,...,r
(3)
其中,r为IMM算法中的模型数目,Aj(k)=[aj,x(k),aj,y(k),aj,z(k)]T是模型j的模型参数:平均加速度向量。Vj(k)为系统噪声,协方差为Qj(k)。
(4)
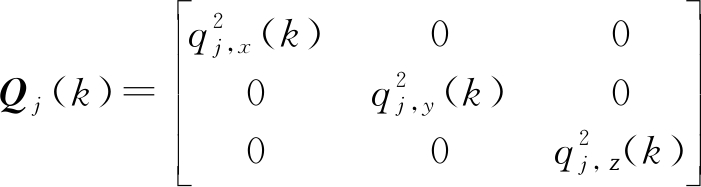
(5)
为了使模型集能够覆盖整个加速度范围,为每个模型设计不同的加速度均值,且在整个加速度范围内呈均匀分布;此外需设计适当的方差,以使相邻模型存在一定范围的交叉覆盖部分。如图1,通过选择适当的均值和方差,使得3个模型覆盖了整个模型空间,且特征明显,具有良好的模型分离度。
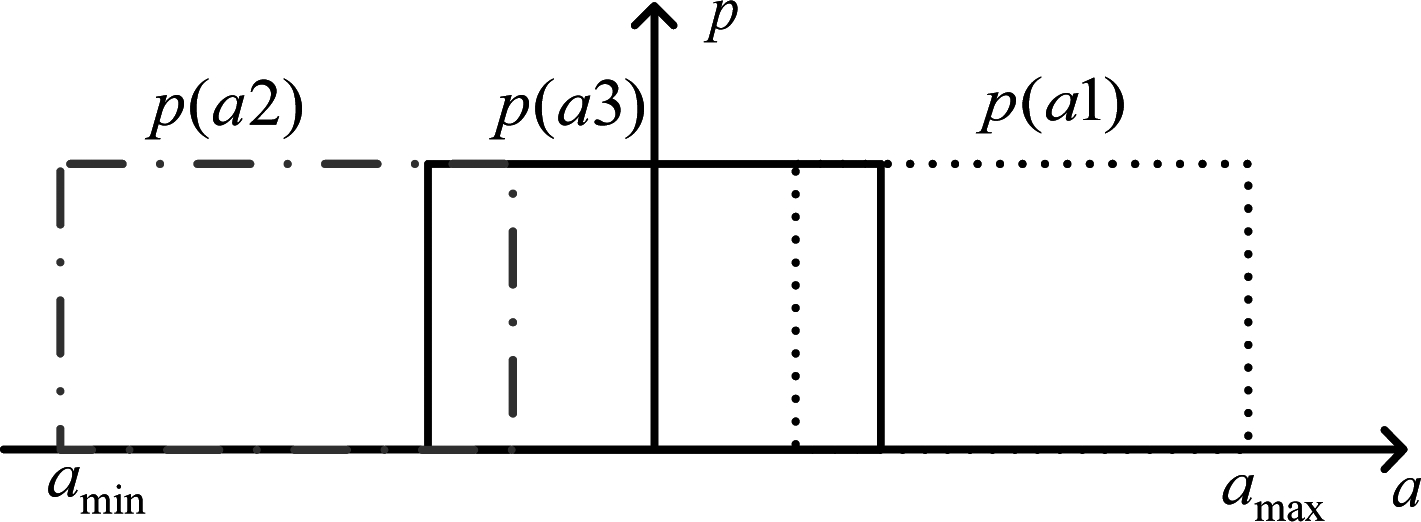
图1 模型分离度
Fig.1 The seperation of models
2.2 气动目标转弯模型
弧线飞行是非常典型的气动目标运动方式,其特点是目标在水平面内做机动转弯,同时在铅垂面上可以有升降运动。基于此,本文修改了协同转弯(CT)模型[21]。假设目标在水平面内以ω为转弯率做匀速圆周运动,在铅垂方向做匀速运动。则状态方程的离散化形式为
X(k+1)=FX(k)+GV(k)
(6)
式中,
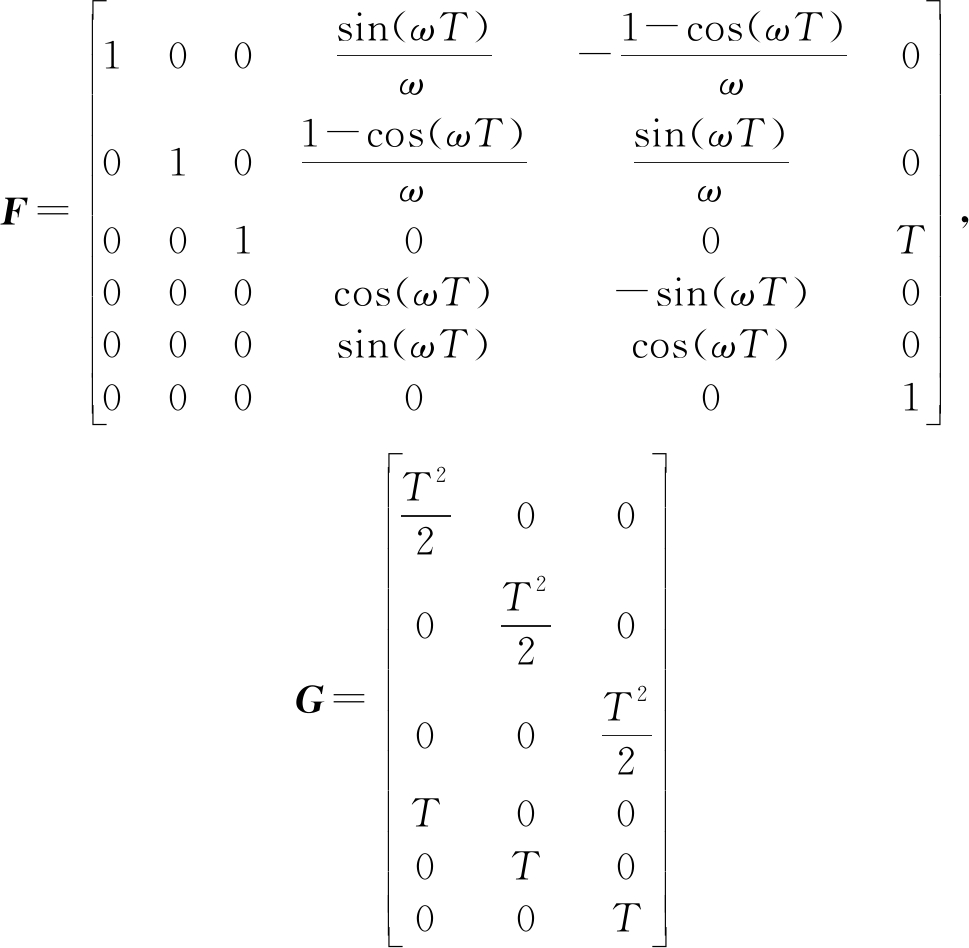
(7)
3 FIMM算法
过程噪声协方差是非常重要的滤波器参数,通常根据先验知识设置为固定值,在模型与运动模式匹配程度不同的情况下,该参数保持不变显然不够合理。因此,FIMM算法在IMM算法的基础上,通过模糊推理系统自适应地调整各个子滤波器的过程噪声协方差。如图2所示,模糊系统主要包括4个部分:输入变量模糊化、模糊知识库、模糊推理和输出变量反模糊化。下文给出了模糊系统的具体设计步骤。
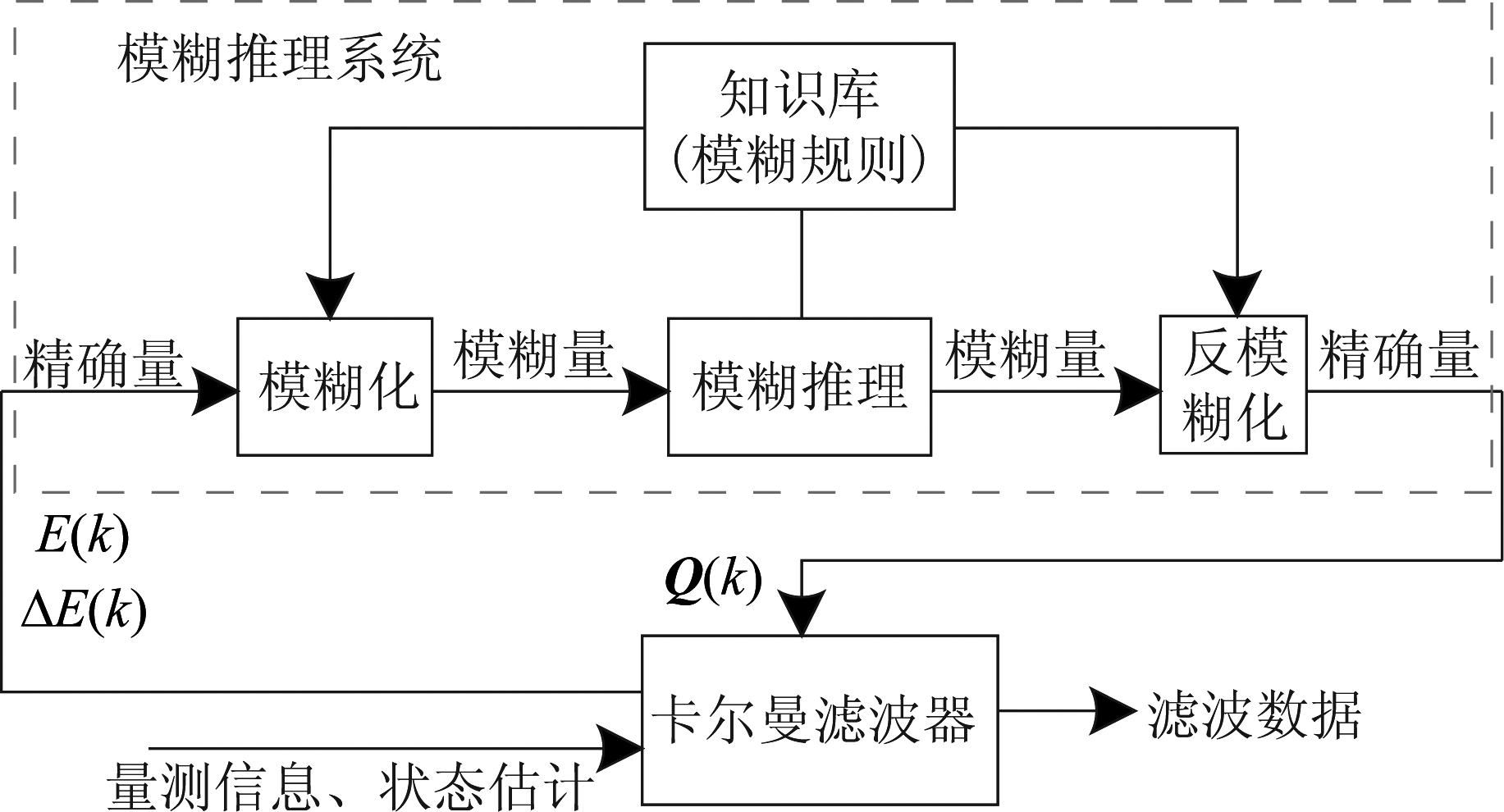
图2 模糊推理系统
Fig.2 Fuzzy inference system
(1)确定模糊系统的输入输出变量
选择估计误差E(k)和误差变化率ΔE(k)作为模糊系统的输入变量,这些信息能够有效地体现出对目标当前运动状态的估计情况,即反映出模型与目标状态的符合程度。以三维空间为例:
(8)
ΔE(k)=E(k)-E(k-1)
(9)
其中,
式中Ex(k),Ey(k),Ez(k)分别为相应方向的新息,zx(k),zy(k),zz(k)分别为k时刻目标的观测值,
分别为k时刻目标的预估值。显然,E(k)与ΔE(k)的取值范围会随目标机动的变化而变化。因此需要对输入变量进行归一化处理,使其取值始终在[0,1]区间内,归一化的思想如下式所示。
(10)
式中,y为待归一化量,y∈(ymin,ymax),y′为归一化后的结果。选择过程噪声水平q(k)作为模糊系统的输出变量,取值范围为[0,3]。
(2)模糊推理
定义归一化后的输入变量E′(k)与ΔE′(k)包含4个模糊集:LP(大),MP(中),SP(小),ZE(零),隶属度函数采用梯形函数。定义输出变量q(k)包含6个模糊集:EP(极大),VP(很大),LP(大),MP(中),SP(小),ZE(零),隶属度函数采用三角函数。
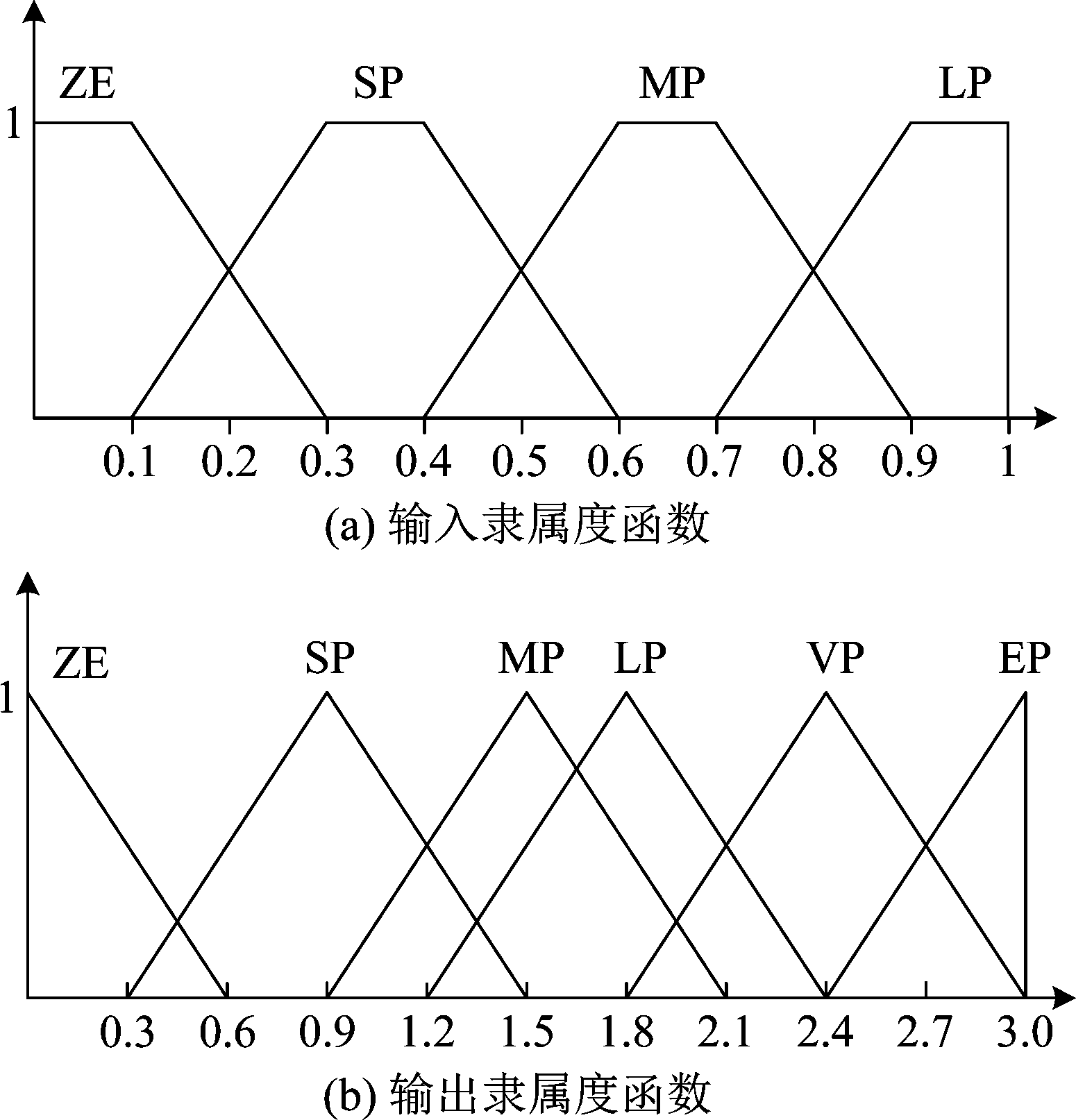
图3 隶属度函数
Fig.3 Membership functions
采用文献[13]给出的模糊规则,具体如表1所示。
表1 模糊规则表
Tab.1 Table of fuzzy logic rules
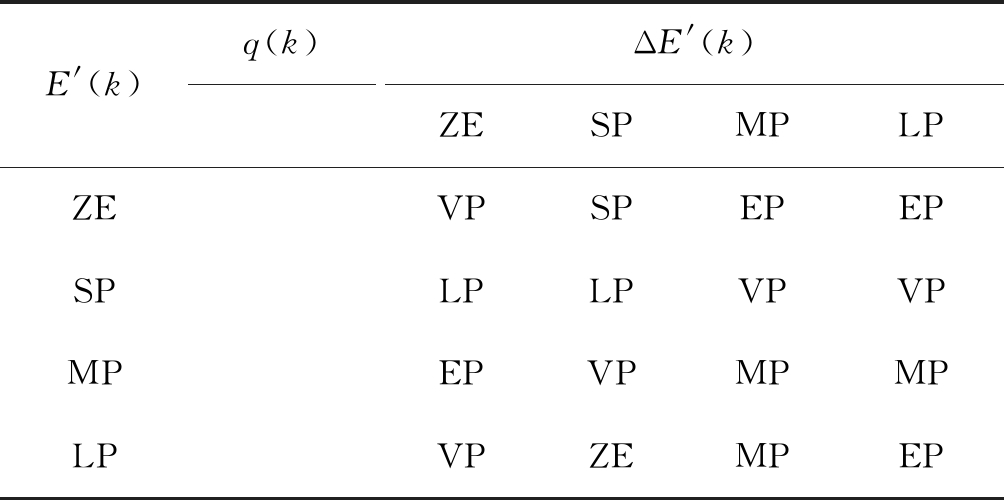
E'(k)q(k)ΔE'(k)ZESPMPLPZEVPSPEPEPSPLPLPVPVPMPEPVPMPMPLPVPZEMPEP
(3)反模糊化
采用重心法(Centroid)对模糊系统的输出变量进行解模糊,得到过程噪声水平q(k)的实际精确数值。此外,q(k)与过程噪声协方差矩阵Q(k)具有式(11)所示关系,其中λ为常数。
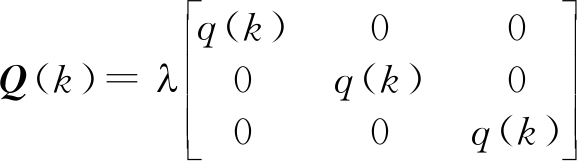
(11)
4 FAIMM算法
针对模型集固定及模型数目较多时存在的模型竞争问题,本文提出的FAIMM算法在FIMM算法的基础加以改进。如图4所示,FAIMM算法包括六个模块。具有N个模型的FAIMM算法的流程如图5所示。
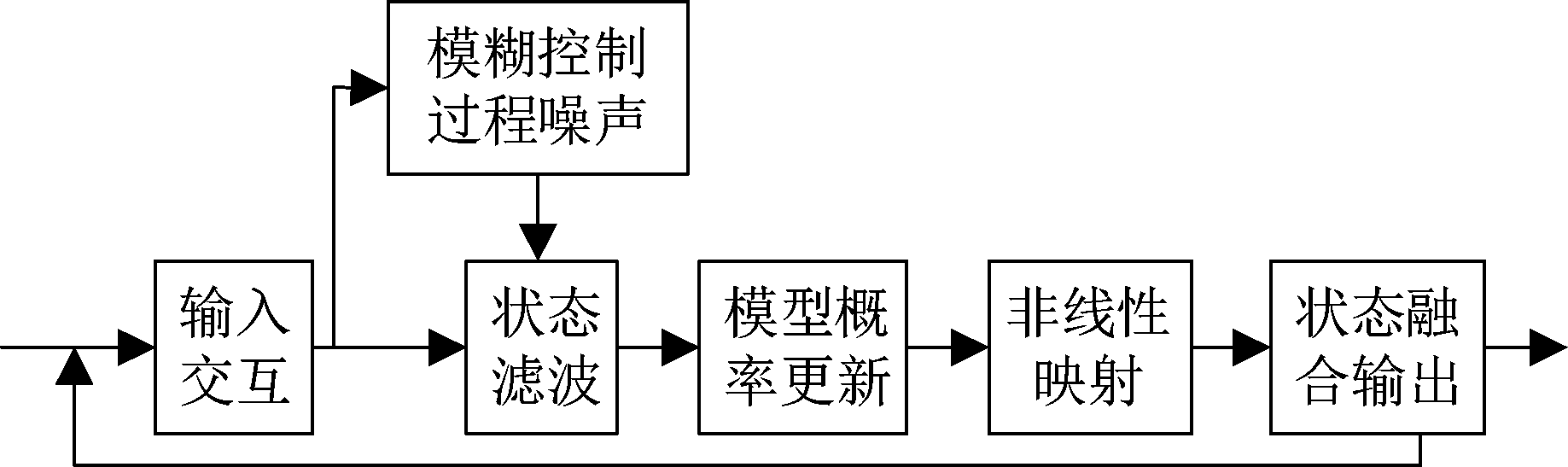
图4 FAIMM算法模块
Fig.4 Modules of FAIMM algorithm
以下给出具有N个模型的FAIMM算法从k-1时刻到k时刻的递推过程。
(1)输入交互
各模型之间的转移服从马尔科夫过程,假设N个模型之间的转移概率矩阵Ptij作为先验信息已经给定。
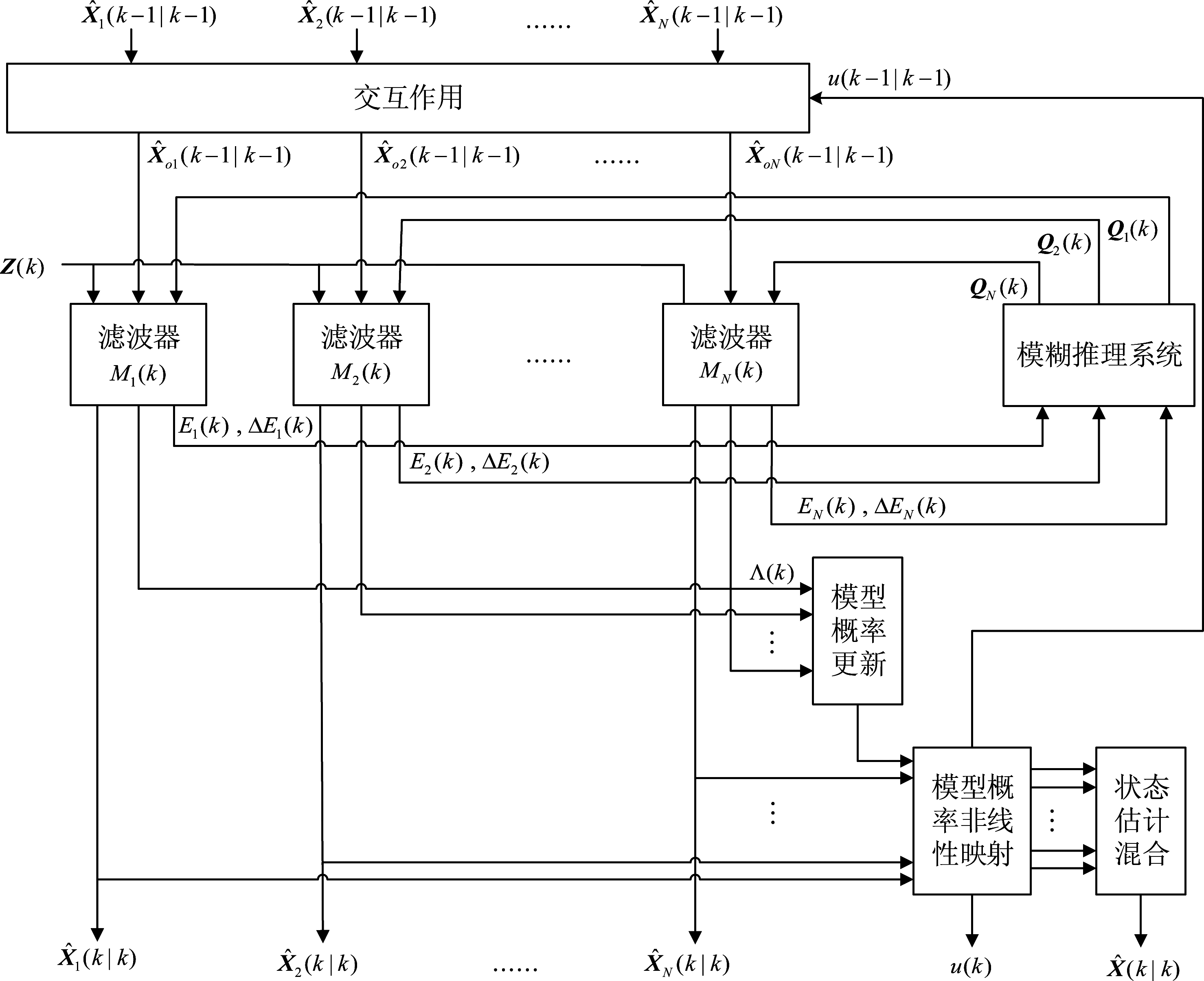
图5 FAIMM算法流程图
Fig.5 Proposed FAIMM algorithm
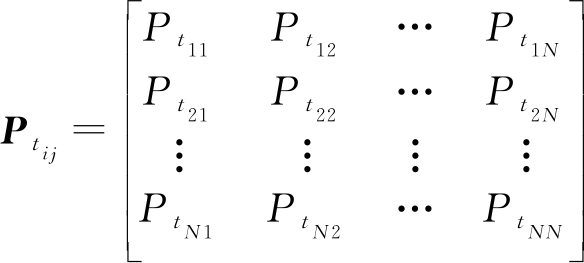
(12)
定义k-1时刻子滤波器j的状态估计为
相应的协方差矩阵为Pj(k-1|k-1),模型j的概率为μj(k-1),则交互后N个滤波器在k时刻的输入状态和协方差阵为
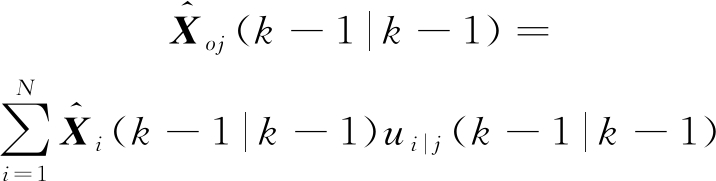
(13)
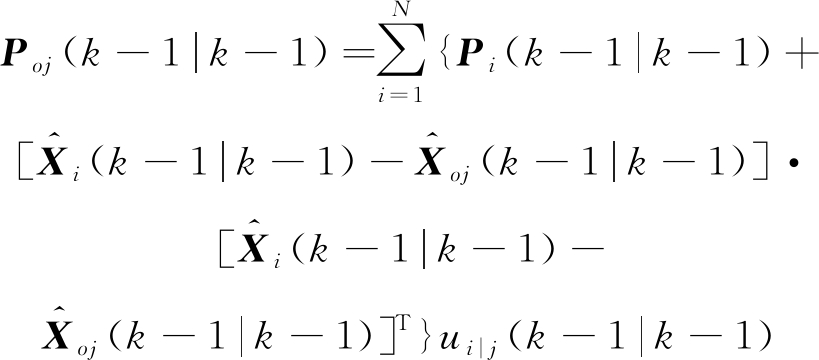
(14)
式中,ui|j(k-1|k-1)为混合概率,
为归一化常数,
(15)
(16)
(2)通过模糊系统确定过程噪声协方差
首先计算各个子模型的状态预测值
(17)
计算新息及新息变化率
(18)
Δεj(k)=εj(k)-εj(k-1)
(19)
由式(10)可知,归一化需要确定输入变量y的取值范围,以保证y∈(ymin,ymax),这一范围通常作为先验知识事先设定,这就存在两种弊端:(1)求得准确的先验知识是非常困难的;(2)这一参数可能要频繁调整。因此,考虑到模糊逻辑的通用性,采用如下无需先验知识的方式对输入变量进行自适应归一化处理。首先计算
可以看出它们的值均保持在[-1,1]。由于表示形式类似,这里仅给出
的计算方法。
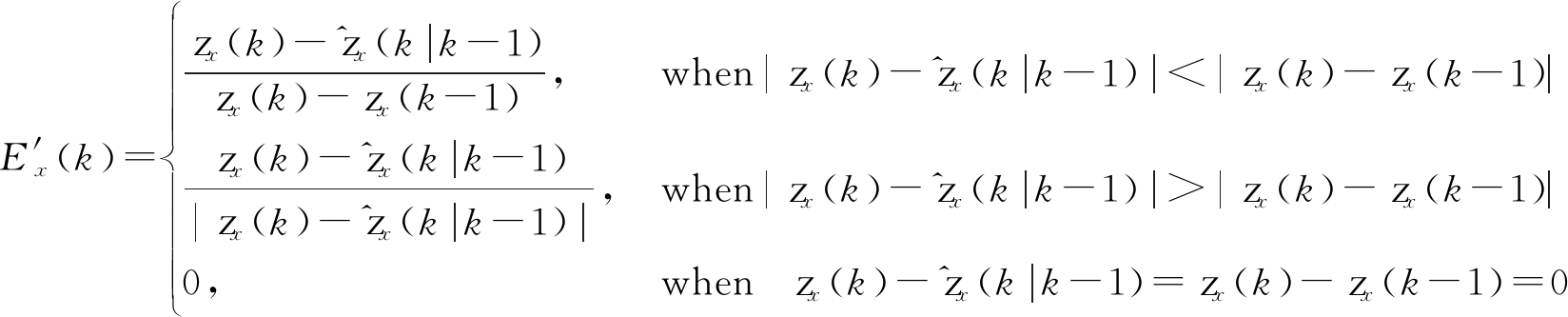
(20)
在
和
的基础上,定义
和
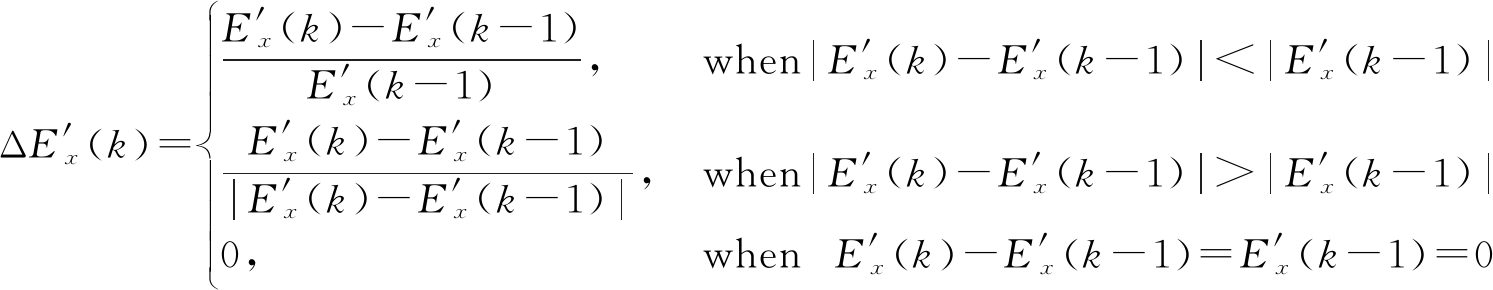
(21)
按式(22)、式(23)计算E′(k)和ΔE′(k),由此得到的E′(k)与ΔE′(k)都在[0,1]区间内,将其作为归一化后的输入变量用于后续的模糊推理。经模糊推理确定系统的输出qj(k),从而得到各个子滤波器的过程噪声协方差Qj(k)。
(22)
(23)
(3)滤波估计
状态预测协方差为
(24)
新息协方差矩阵为
(25)
滤波增益为
(26)
状态更新为
(27)
Pj(k|k)=[I-Kj(k)Hj(k)]Pj(k|k-1)
(28)
(4)模型概率更新
模型j的似然函数为
(29)
模型概率可估计为
(30)
其中,C为归一化常数,
(5)模型概率非线性映射
完成以上计算后,即可得到各模型的估计概率
由于随机干扰和模型竞争的存在,模型概率波动较强,存在较为明显的毛刺,因此本文首先对
进行均值平滑处理,能够较好地避免随机干扰导致的误判,然而,上述操作将会导致模型切换出现一定程度的滞后效应,为了尽可能地减少该不利影响,采用变长度的滑动窗口。设置窗口长度为f,即k时刻的模型概率
为及其之前f个时刻的概率的均值,设置一个阈值d,定义估计的概率与上一时刻的概率μj(k-1)差值为
若Δp超过阈值d,判定为存在模型切换,则将平滑窗口长度缩小为原来的一半。阈值d的取值范围为[0,1],若取值较大,则平滑效果好,滞后时间长;若取值较小,则滞后时间短,平滑效果差。
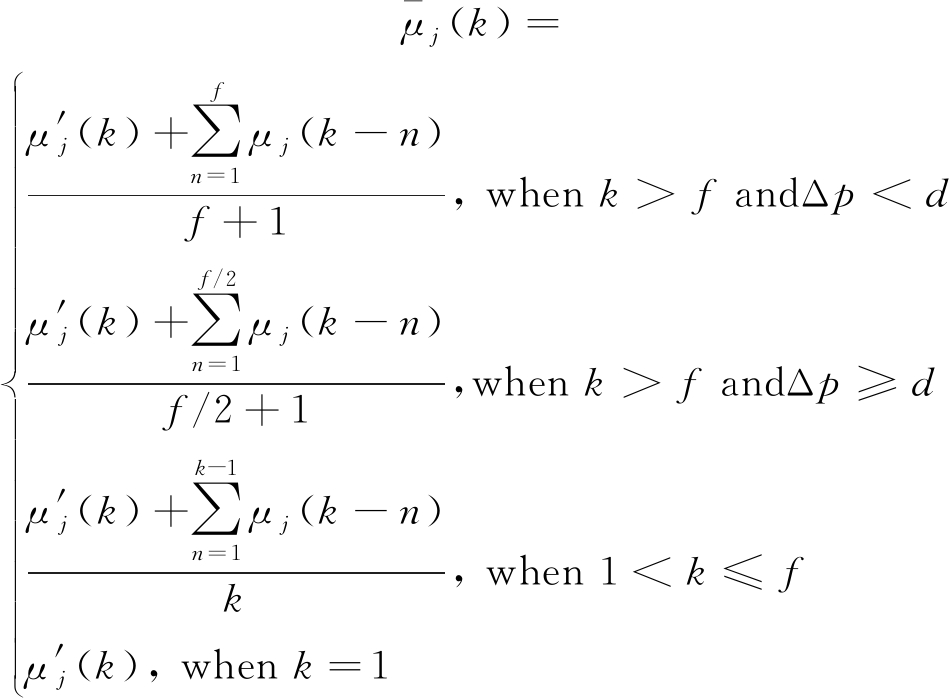
(31)
由于模型数目较多,FAIMM算法采用升半梯形的非线性映射函数处理各个模型的概率,以剔除无用模型,增大有用模型的权重,减少模型竞争。映射函数如下:
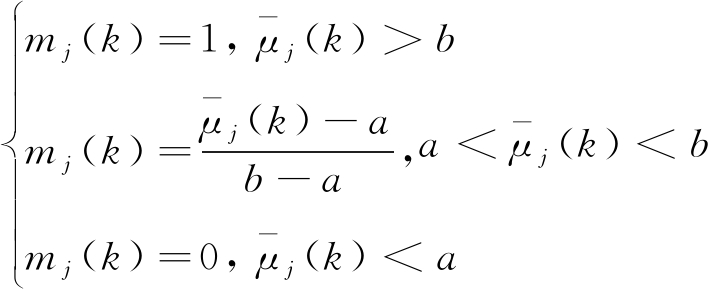
(32)
令
如式(33)对mj(k)进行归一化处理,得到的μj(k)为非线性处理后新的模型概率,将用于后续的交互融合估计。
(33)
(6)输出
根据上述处理后得到的模型概率μj(k),计算k时刻的输出
(34)
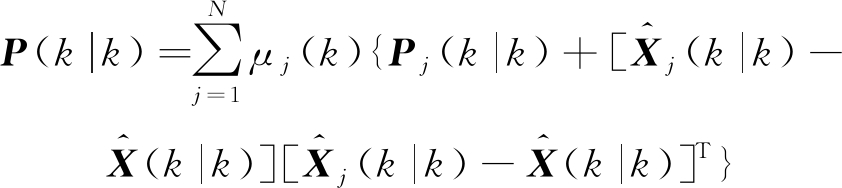
(35)
5 仿真分析
为了验证算法的有效性,在相同实验条件下,仿真对比基于固定模型数目的传统交互多模型算法(IMM)、基于模糊控制的交互多模型算法[13](FIMM)和本文提出的FAIMM算法的跟踪性能。
实验仿真气动机动目标的一段飞行过程,目标首先进行盘旋上升,然后做一段蛇形运动。真实航迹的初始位置为[0,0,500]m,初始速度为[100,100,100]m/s,采样周期为0.1 s,共计运动140 s。1～20 s目标以[-3,-3,-3]m2/s的加速度做匀加速直线运动,20～60 s目标在水平面上以5.73°/s的角速度转弯,在铅垂面上保持匀速运动,60～80 s目标以[3,3,3]m2/s的加速度做匀加速运动,80～120 s目标的加速度为[-3,-3,-3]m2/s,120～140 s目标的加速度为[9,9,9]m2/s。为了更好的比较算法的性能优劣,3种算法的距离量测误差相同,均设置为8 m,且采用同样的模型集合,包含3个含附加项的CV模型(附加加速度分别为9 m2/s,3 m2/s,-3 m2/s)和3个气动目标转弯模型(角速度分别为20°/s,5.73°/s,-11°/s)。各个模型初始概率相等,概率转移矩阵如下式。
(36)
算法参数设置方面,非线性映射函数式(32)中a取0.15,b取0.85,滑窗长度f为6,阈值d作为滑窗长度切换的条件,综合考虑平滑效果与滞后时间两个指标,折中选择了d=0.1这一参数。下图6分别表示无平滑、恒定滑窗长度f、变长度滑窗(d=0.1)、变长度滑窗(d=0.5)操作下某一时间段的模型概率变化曲线,可以看出,当阈值d=0.5时,平滑效果很好,但滞后时间较长,基本与恒定滑窗长度算法接近;当阈值d=0.1时,尽管平滑效果相较于d=0.5略有变差,但该参数设置能够在保证较好平滑效果的同时,尽量减少滞后效应。
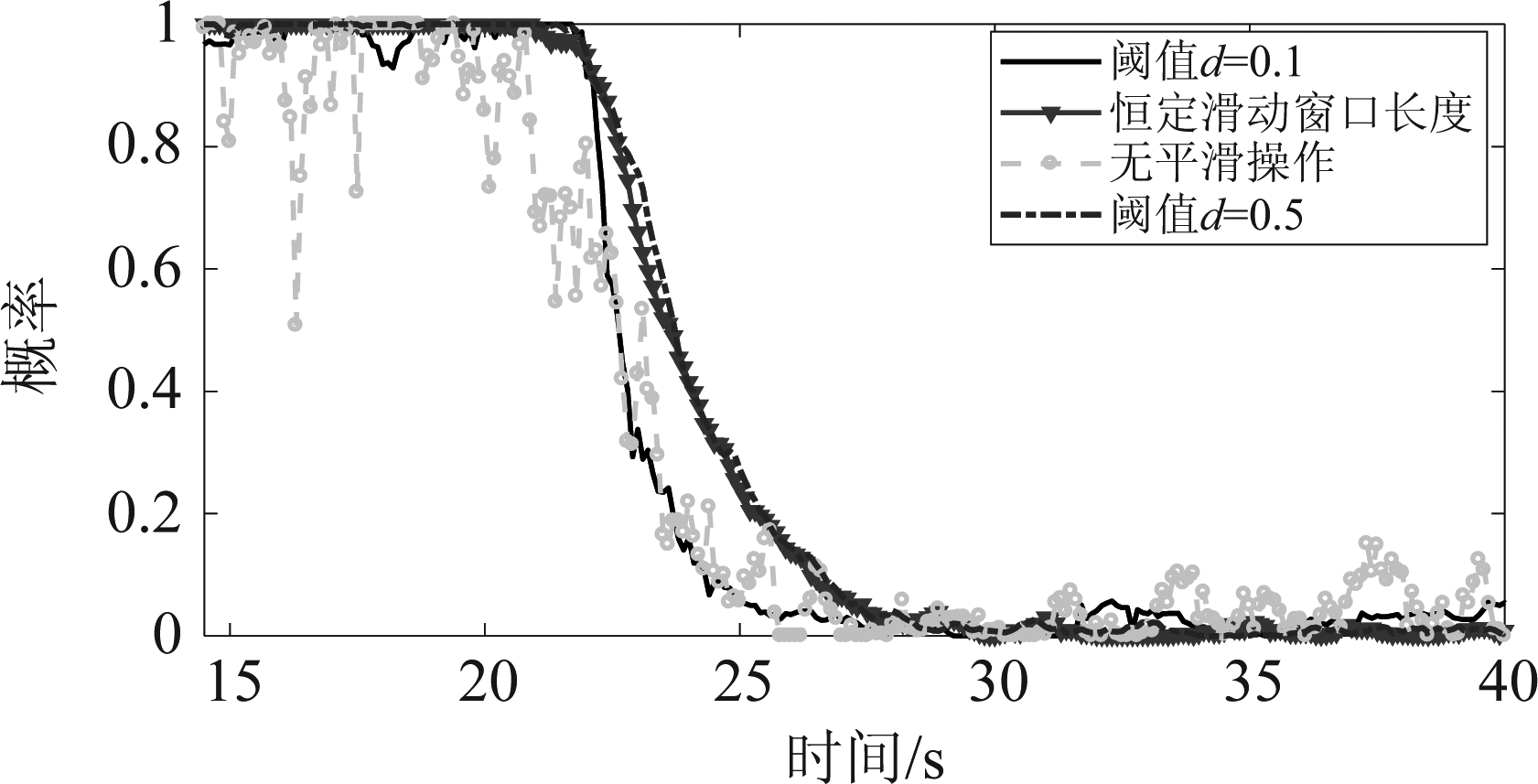
图6 不同阈值下的平滑效果及滞后效应
Fig.6 Smoothing effect and hysteresis effect under different settings
算法设置了6个不同形式或不同参数的模型,能够较为精细地覆盖机动模式,然而模型数目多也带来了模型竞争、模型之间切换不明显等问题。图7(a)～(f)为3种算法在单次仿真实验中6个模型的概率曲线变化。可见,传统IMM算法存在明显的模型竞争,模型概率曲线波动明显,毛刺现象严重,且某一运动模式下最优模型概率仅在0.5左右。FIMM算法相较于IMM算法而言性能略有提升,最优模型权重有所提高,但仍不理想。而FAIMM算法有效剔除了无用模型(模型4、6),其概率基本保持为0,并将有用模型(模型1、2、3、5)的概率提高至接近1的水平,因此,在整个跟踪阶段仅保留4个有用模型参与交互融合估计,减少了模型数目,避免了模型竞争;此外,算法通过变长度滑窗的均值平滑处理进一步消除了毛刺,实现了更为理想的模型切换效果,更好地反映了目标机动特性。
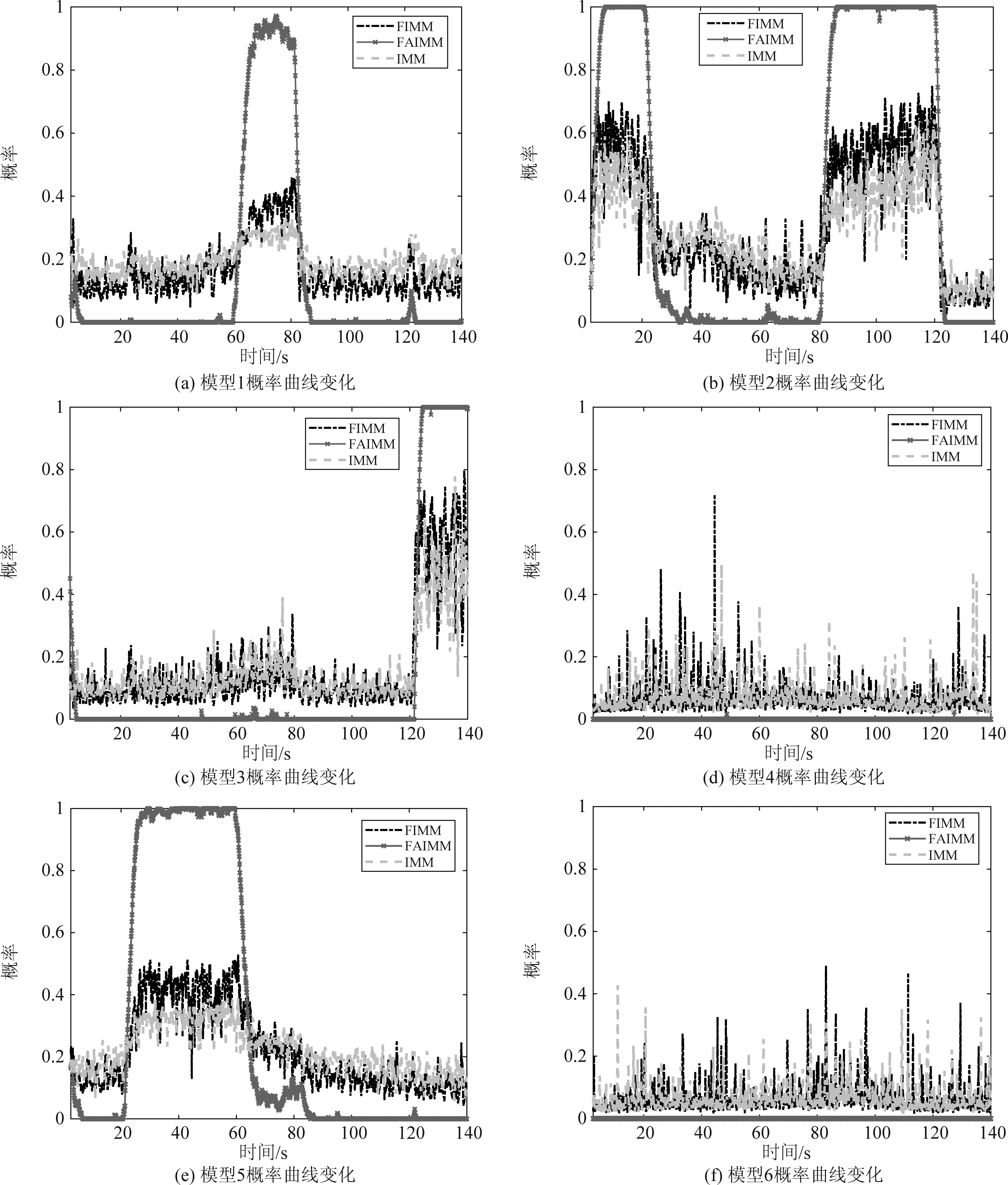
图7 各个模型的概率变化曲线
Fig.7 Model probability curves
进行300次蒙特卡洛仿真实验,3种算法的均方根误差曲线如下图8所示, 均方根误差值见表2。
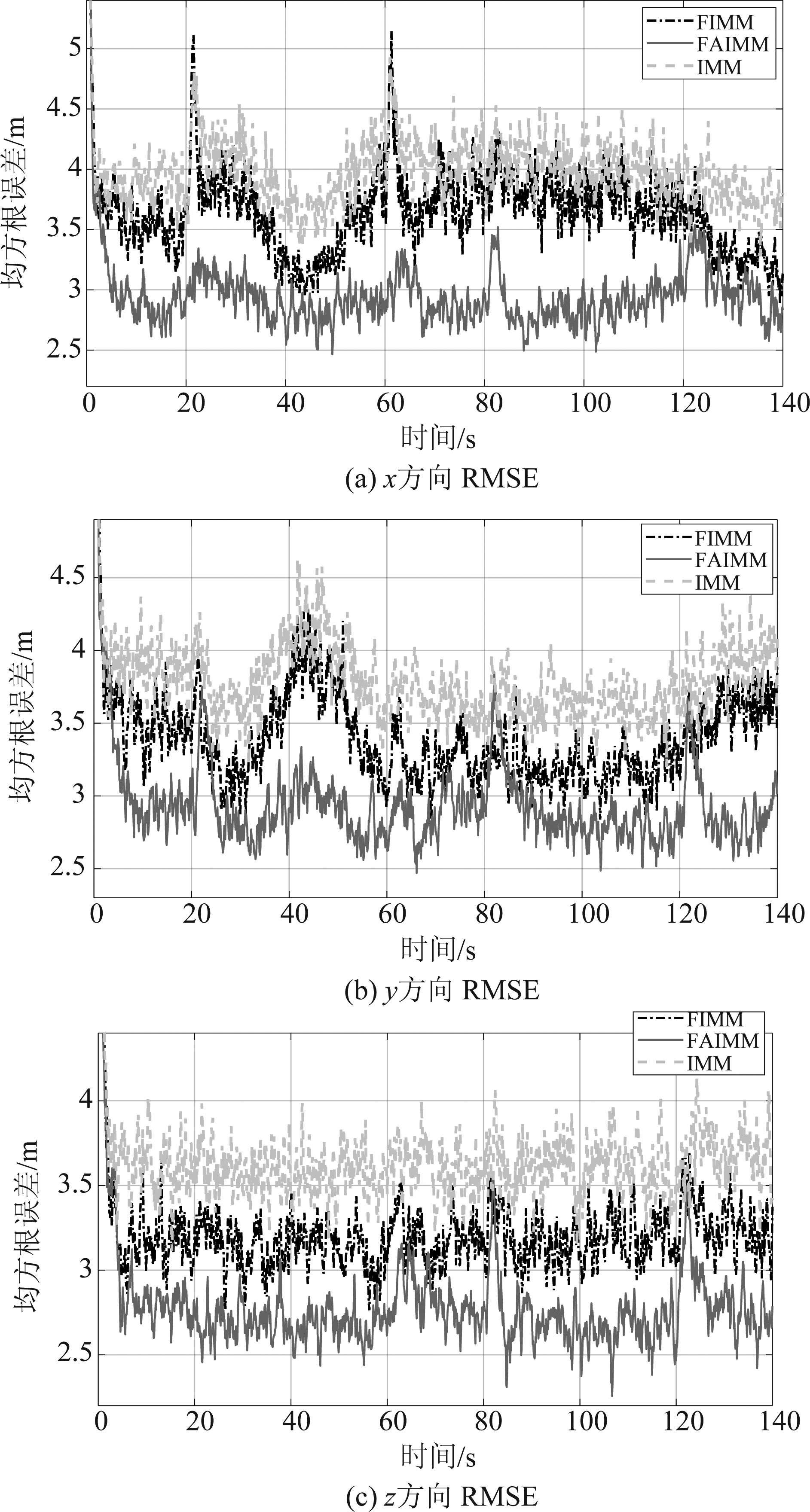
图8 均方根误差对比
Fig.8 Root mean square error comparision
表2 RMSE数值对比
Tab.2 RMSE value comparison
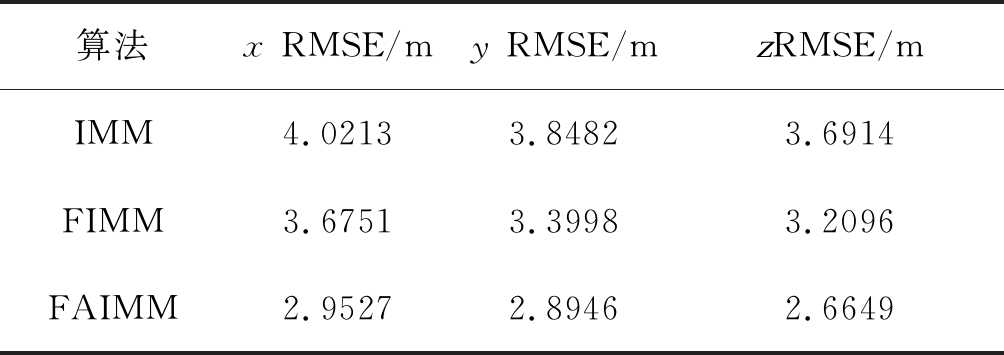
算法x RMSE/my RMSE/mzRMSE/mIMM4.02133.84823.6914FIMM3.67513.39983.2096FAIMM2.95272.89462.6649
由上述仿真结果可以看出,FAIMM算法相较于传统的IMM算法、FIMM算法滤波误差分别降低了26%和21%左右,在机动时刻和非机动时刻均有了更好的表现。在intel Core i7-7700K处理器、R2017a版本MATLAB的实验平台下,FIMM算法和FAIMM算法的运行时间分别为130.85 s和133.14 s,可以看出FAIMM算法在几乎不增加额外计算负担的前提下提升了算法性能。此外,FAIMM算法更适合于需要较多模型覆盖复杂机动的场景,由于对交互融合输出所使用的模型概率进行了处理,能够很好地解决模型数目较多带来的模型竞争问题;但即使在模型数目不足的情况下,FAIMM算法通过模糊推理系统自适应地调整过程噪声协方差,降低了模型集与目标机动的失配误差,仍能获得更好的跟踪效果。图9为目标真实航迹与FAIMM算法估计轨迹的对比,可以看出,估计结果与真实轨迹非常逼近,即使在机动转弯时刻也能够实现稳定跟踪,说明该算法能够有效地处理气动目标跟踪问题。
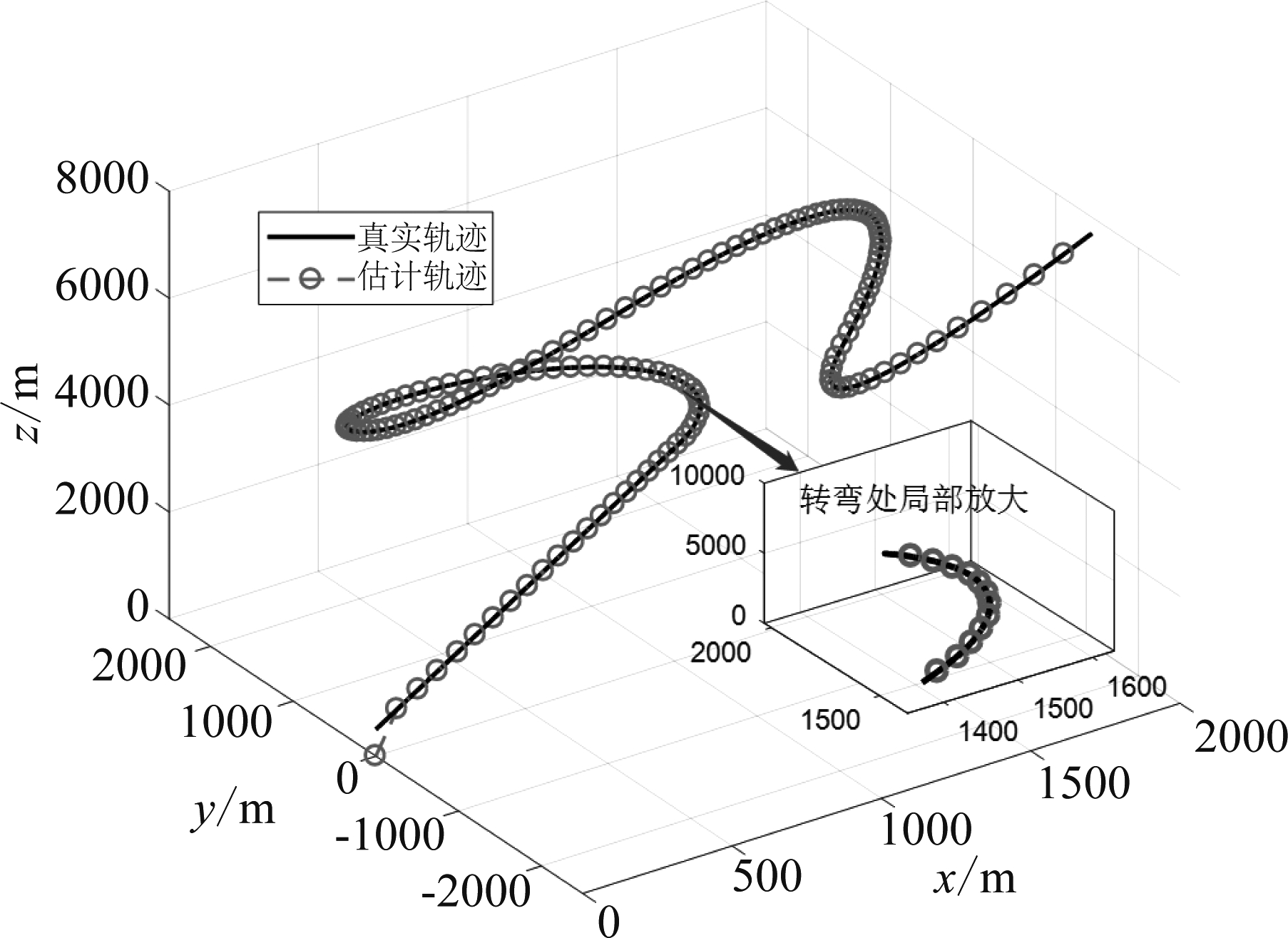
图9 估计轨迹与真实轨迹
Fig.9 Estimated trajectory and true trajectory
6 结论
FAIMM算法采用一种非线性映射的方式自适应地调整各个子模型的匹配概率,在提升有用模型概率的同时,减少了模型交互输出结构中的参与模型数量,有效避免了模型之间的竞争。同时,以归一化后的新息和新息变化为模糊系统输入,利用模糊推理机制自动调整过程噪声大小,使模型对目标机动有了更好的表现。最后,在气动目标飞行场景下,分别对FAIMM算法、FIMM算法、IMM算法进行实验仿真,结果表明FAIMM具有更高的跟踪精度。
[1] XIE Guotao, GAO Hongbo, QIAN Lijun, et al. Vehicle trajectory prediction by integrating physics-and maneuver-based approaches using interactive multiple models[J]. IEEE Transactions on Industrial Electronics, 2018, 65(7): 5999- 6008.
[2] XIE Guo, SUN Lanlan, WEN Tao, et al. Adaptive transition probability matrix-based parallel IMM algorithm[J]. IEEE Transactions on Systems, Man, and Cybernetics: Systems, 2019, PP(99): 1-10.
[3] 陈映, 程臻, 文树梁. 弹道导弹助推段同时跟踪和类型识别算法研究[J]. 信号处理, 2011, 27(5): 749-754.
CHEN Ying, CHENG Zhen, WEN Shuliang. Study on method for simultaneously tracking and classifying ballistic missile in boost and post-boost phase[J]. Signal Processing, 2011, 27(5): 749-754.(in Chinese)
[4] YOO K, CHUN J, SHIN J. Target tracking and classification for missile using interacting multiple model (IMM)[C]∥2018 International Conference on Radar (RADAR). Brisbane, QLD, Australia. IEEE, 2018: 1- 6.
[5] 王小梨, 李良群, 谢维信. UKF参数辨识的T-S模糊多模型目标跟踪算法[J]. 信号处理, 2019, 35(3): 361-368.
WANG Xiaoli, LI Liangqun, XIE Weixin. T-S fuzzy multiple model target tracking algorithm with UKF parameter identification[J]. Journal of Signal Processing, 2019, 35(3): 361-368.(in Chinese)
[6] 周卫东, 刘璐, 唐佳. 基于模糊逻辑的交互式多模型滤波算法[J]. 北京航空航天大学学报, 2018, 44(3): 413- 419.
ZHOU Weidong, LIU Lu, TANG Jia. Interactive multiple model filtering algorithm based on fuzzy logic[J]. Journal of Beijing University of Aeronautics and Astronautics, 2018, 44(3): 413- 419.(in Chinese)
[7] WANG Qicong, CHEN Xiaoqiang, ZHANG Lin, et al. Fuzzy interacting multiple model H∞ filter algorithm based on current statistical model[J]. International Journal of Fuzzy Systems, 2019, 21(6): 1894-1905.
[8] COSME L B, CAMINHAS W M, D’ANGELO M F S V, et al. A novel fault-prognostic approach based on interacting multiple model filters and fuzzy systems[J]. IEEE Transactions on Industrial Electronics, 2018, 66(1): 519-528.
[9] 国强, 贺紫兰. 一种新的模糊控制多模型算法在目标跟踪中的应用[J]. 哈尔滨工业大学学报, 2016, 48(11): 123-128.
GUO Qiang, HE Zilan. A novel fuzzy control multiple model algorithm in target tracking[J]. Journal of Harbin Institute of Technology, 2016, 48(11): 123-128.(in Chinese)
[10]EUN Y, JEON D. Fuzzy inference-based dynamic determination of IMM mode transition probability for multi-radar tracking[C]∥Proceedings of the 16th International Conference on Information Fusion. Istanbul, Turkey. IEEE, 2013: 1520-1525.
[11]LI Liangqun, ZHAO Da, LUO Chengda. A novel interacting T-S fuzzy multiple model by using UKF for maneuvering target tracking[C]∥2019 22th International Conference on Information Fusion (FUSION). Ottawa, ON, Canada. IEEE, 2019: 1-7.
[12]KIM H S, PARK J G, LEE D. Adaptive fuzzy IMM algorithm for uncertain target tracking[J]. International Journal of Control, Automation and Systems, 2009, 7(6): 1001-1008.
[13]DING Zhen, LEUNG H, CHAN K, et al. Model-set adaptation using a fuzzy Kalman filter[J]. Mathematical and Computer Modelling, 2001, 34(7/8): 799- 812.
[14]CHAN K C C, LEE V, LEUNG H. Radar tracking for air surveillance in a stressful environment using a fuzzy-gain filter[J]. IEEE Transactions on Fuzzy Systems, 1997, 5(1): 80- 89.
[15]刘政, 马增强, 柳晓云, 等. 基于模糊推理的改进的交互式多模型算法[J]. 济南大学学报(自然科学版), 2017, 31(2): 129-135.
LIU Zheng, MA Zengqiang, LIU Xiaoyun, et al. Improved interacting multiple model algorithm based on fuzzy inference[J]. Journal of University of Jinan (Science and Technology), 2017, 31(2): 129-135.(in Chinese)
[16]申斌, 董朝阳, 陈宇, 等. 一种模糊自适应交互多模型算法[J]. 系统仿真学报, 2005, 17(10): 2345-2348.
SHEN Bin, DONG Chaoyang, CHEN Yu, et al. Fuzzy adaptive interacting multiple model algorithm[J]. Journal of System Simulation, 2005, 17(10): 2345-2348.(in Chinese)
[17]刘瑞兰, 陈小惠. 基于模糊交互多模型的机动目标被动跟踪算法[J]. 电子测量与仪器学报, 2012, 26(10): 846- 850.
LIU Ruilan, CHEN Xiaohui. Maneuvering target tracking algorithm based on fuzzy interacting multiple model[J]. Journal of Electronic Measurement and Instrument, 2012, 26(10): 846- 850.(in Chinese)
[18]PENG Dongliang, GUO Yunfei. Fuzzy-logic adaptive variable structure multiple-model algorithm for tracking a high maneuvering target[J]. Journal of the Franklin Institute, 2014, 351(7): 3837-3846.
[19]TURKMEN I. IMM fuzzy probabilistic data association algorithm for tracking maneuvering target[J]. Expert Systems With Applications, 2008, 34(2): 1243-1249.
[20]DING Z, HONG L. An interacting multiple model algorithm with a switching Markov chain[J]. Mathematical and Computer Modelling, 1997, 25(1): 1-9.
[21]YUAN Xianghui, LIAN Feng, HAN Chongzhao. Models and algorithms for tracking target with coordinated turn motion[J]. Mathematical Problems in Engineering, 2014, 2014: 1-10.
