1 引言
自适应波束形成能够在干扰方向自动生成零陷以提高波束输出的信干噪比(Signal to Interference and Noise Ratio,SINR),能够有效抑制动态干扰,在雷达、声纳、无线通信等方面有着广泛的应用。Capon波束形成[1],又称最小方差无失真响应(Minimum Variance Distortion-less Response, MVDR)波束形成,是一种经典的自适应波束形成器,其能够在阵列导向向量、目标来波方向(Direction of Arrival,DOA)以及估计的干扰加噪声自相关矩阵不存在误差理想条件下达到最优性能。然而,一方面,实际中目标来波方向以及对应的阵列导向向量一定存在误差,Capon波束形成器的性能会因为此类误差急剧下降;另一方面,当输入信噪比过高或者干扰来波方向快速变化时,估计的干扰加噪声自相关矩阵误差也会增大,导致Capon波束形成器的性能恶化。
为了解决Capon波束稳健性不佳的问题,学界提出了多种方法。
基于对角加载的方法通过在协方差矩阵上加载或等效加载一个对角矩阵以移除其过小的特征值,减小矩阵病态条件的影响。原始对角加载法[2]的问题主要是很难根据实际情况确定合适的对角加载量。稳健Capon波束形成(Robust Capon Beamforming,RCB)[3]方法通过构建并最小化拉格朗日函数的方式,求解给定目标方向导向向量误差界时的约束最优化问题,并利用特征值分解将其转化为易于求解的多项式求根问题。近年来,有学者提出了一种自动计算加载量的三对角加载方法[4],可以在标准Capon波束形成的基础上额外付出仅2M2+6M次浮点运算的代价以取得较RCB更好的性能。
为了在干扰来波方向快速变化时,仍有能力对其有效抑制,可以对波束进行预成型以在干扰源活动范围内形成凹槽。基于零点展宽的方法[5-7],又称协方差矩阵锥化法,通过人为在协方差矩阵中引入等效的虚拟干扰源以使MVDR波束形成器自动形成凹槽;线性约束最小方差(Linear Constrained Minimum Variance,LCMV)[8]方法通过在Capon波束形成方法中添加对波束输出施加线性约束来获取需要的波束形状,如平坦的主瓣响应以及宽凹槽等以容许来波方向的较大变化;这两类方法的主要问题是未考虑到目标来波方向导向向量误差,稳健性不足。线性约束稳健Capon波束形成(Linear Constrained Robust Capon Beamforming,LCRCB)[9]方法综合使用RCB方法与LCMV方法,将波束分解为两个正交子空间以分别成型,可以在保证一定稳健性的同时获取所需的波束形状,也能零陷凹槽外的干扰。基于二阶锥规划(Second-Order Cone Programming,SOCP)的方法[10-12]以凸优化的方式求解给定稳健性、旁瓣级、凹槽、主瓣形状等参数时的最优波束加权值,具备良好的通用性。近来有研究引入了压缩感知技术[13],在阵元数一定的情况下,提供了更多的自由度,可用以提升波束形成器的性能。
然而,上述的方法时间复杂度均为O(M3)级别,在阵列较大、采样率较高时,很难在快拍间隙完成计算。一种思路是使用子空间追踪/估计方法。考虑到实时自适应波束形成器往往是单快拍迭代工作的,系统在每个快拍来到时更新波束加权值。利用单快拍更新下协方差矩阵更新量秩仅为1的特性,直接对特征值分解进行O(M2)秩1更新的方法需要阵元数目M非常大时才会具有优势[14]。对特征空间进行主成分提取以缩减计算量的方法[15]能够有效削除求取全部特征空间以及求逆的计算量,然而在低信噪比下,难以分离特征空间的主成分。另一个思路是使用迭代算法追踪拉格朗日函数的极值点。最差情况-迭代梯度(Worst Case Iterative Gradient,WC-IG)方法[16]使用梯度下降法来在先前解的基础上求解新的极值点,因梯度下降法简单可靠,具有较好的通用性,如用于圆阵的模态域波束形成[17]等。这些方法均为求解标准RCB问题的方法,无法应用于存在波束预成型的场景。
针对上述问题,本文提出了一种基于单快拍更新和迭代梯度方法的线性约束稳健Capon波束形成快速算法。首先将波束加权值分解到两个正交子空间,再推导出计算波束加权值线性约束部分所使用的逆矩阵的秩1更新公式,同时使用迭代梯度方法求解自适应部分的加权值,将两部分根据无失真约束结合生成输出的波束加权值,最后给出新方法的时间复杂度分析。
2 信号建模
有一个窄带目标信号和J个窄带干扰分别从θ0与[θ1,…,θJ]角度入射到一个由各向同性阵元组成的M元阵列。该阵列接收到的信号快拍可以建模为:
k=1,2,…,K
(1)
其中x(k)∈CM×1是阵列的输出矢量,[a(θ0),a(θ1),…,a(θJ)]为阵列在信号或干扰方向[θ0,θ1,…,θJ]上的导向向量。[s0(k),s1(k),…,sJ(k)]表示第k个采样时刻的信号和干扰波形,n(k)表示对应时刻阵列接收到的噪声矢量。假定n(k),si(k)(i=0,1,…,J)之间互不相关且均值为零,那么阵列输出的自相关矩阵可以表示为:
(2)
(3)
其中,
为信号/干扰的功率,Qx为干扰加噪声自相关矩阵。
记波束形成器的加权值为w,则波束的输出信号以及输出信干噪比定义如下:
xout(k)
wHx(k)
(4)
(5)
3 线性约束稳健波束形成算法
在(1)所述的阵列信号模型下,RCB问题可以建模为一个变量为真实目标方向导向向量a的约束极值问题[3]:
(6)
其中,
表示预先指定的理想的目标方向导向向量,误差限
其中E∈CM×M为表征导向向量误差在不同方向上大小的矩阵;同时,通常假定
以避免a=0的平凡解。
设求出的解为
波束形成器的加权值wRCB为:
(7)
LCMV问题可以建模为变量为波束加权值w的约束极值问题[8]:
(8)
其中,C∈CM×L为线性约束的系数矩阵,g∈CL为约束值,L为约束个数。它的解为
(9)
LCRCB方法希望在满足线性约束的情况下,容许目标方向导向向量有一定误差。因而波束加权值被分解为两部分[9]:
wLCRCB=wC+wa
(10)
其中wC是一个满足线性约束的LCMV解,wa则是剩余自由度下的一个RCB解。
首先考察wC。对于L(L<M)个线性约束
(11)
其中
及
定义同(8)中C与g。
希望找到与(11)等价的线性约束wHC=gH以及一组对应的wC、wa,使得wC成为LCMV问题(8)的解,亦即
而
为一个给定标量。为此,将
分解到
张成的空间及其正交补空间上,记在的正交补空间上分量为C。
当
时,由于
构造
显然
则存在L×L可逆矩阵
使得
约束(11)等价于
(12)
其中gH取
的后L-1个分量组成的行矢量,而
取的第一个分量。
当
根据(9),wC的解为
(13)
其次,考察wa。为了使
需要
亦即wa属于C的正交补空间
为了在
上构造RCB问题以求解wa,需要将信号投影到为此,构造的一组正交基,记为GC∈CM×N,N=M-rank(C),令
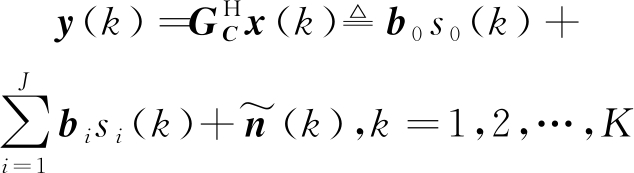
(14)
其中
则
上的RCB问题(以下称为MRCB问题)描述如下:
(15)
其中
本文取导向向量误差模值平方最大为ε的球形不确定集亦即
那么
约束
退化成为
记问题(15)的解为
则对应的MRCB问题的解为:
(16)
当rank(C)=L-1时,为了保证约束(12)成立,对wMRCB进行缩放以得到
(17)
其中,上标*表示取标量的共轭;记v为wC在上的分量,有
以及
当rank(C)=L时,为了使约束(11)及
成立,对wMRCB进行缩放得到
(18)
其中,
4 迭代梯度解
实际系统中,真实的阵列输出自相关矩阵Rx是不可知的,通常使用
来估计Rx。在每接收到一个快拍,需要更新一次波束加权值的工作情形下,需要对阵列输出的自相关矩阵进行如(19)的秩1更新。
(19)
这里
表示共接收到k个快拍之后的自相关矩阵的估计
在计算中,为了尽量减少乘除法次数,一般用
来代替
进行计算,μ取1-1/K。此时,对应的秩1更新为:
(20)
与之对应,
的秩1更新为:
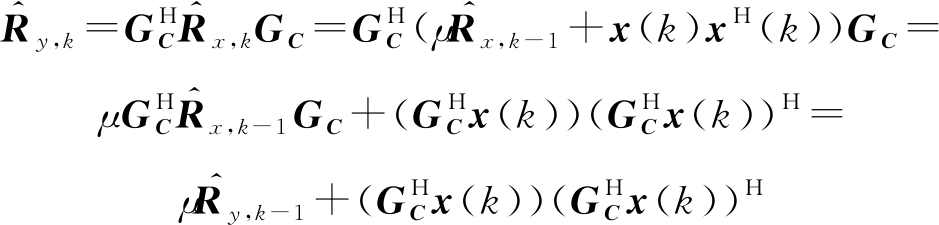
(21)
第k个快拍到来后,LCRCB问题的迭代解为:
(22)
或
(23)
其中αk,βk,γk的定义与(17)、(18)中α,β,γ分别对应。
将(20)代入(13),得到wC的迭代解:
(24)
为了在O(M2)时间复杂度下计算wC,k,需要维护
与
两个逆矩阵。
由矩阵求逆引理:
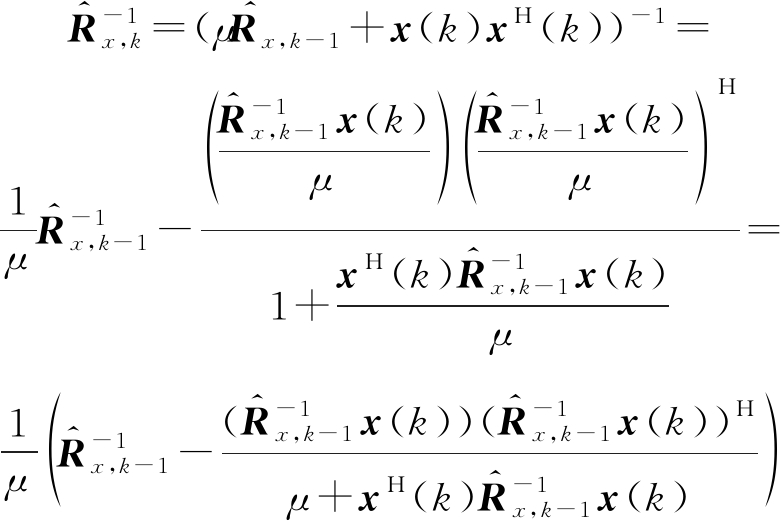
(25)
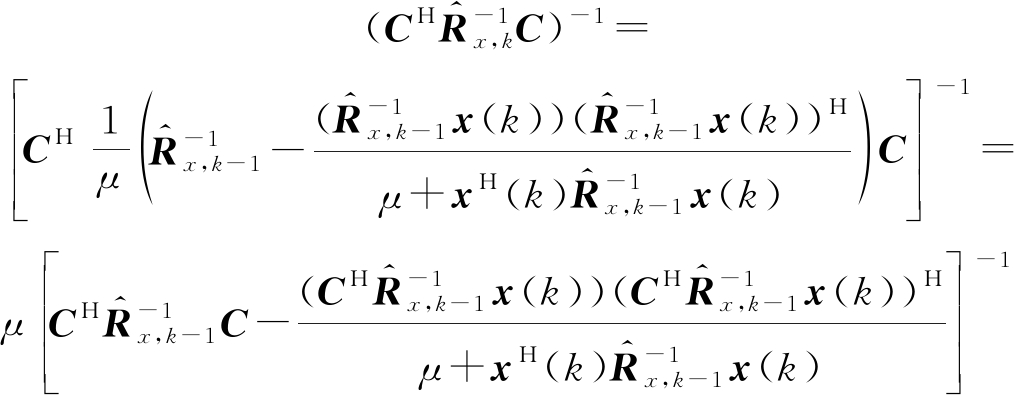
(26)
令
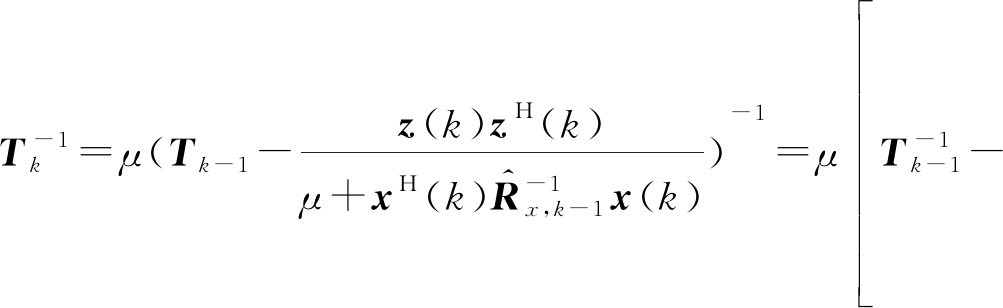
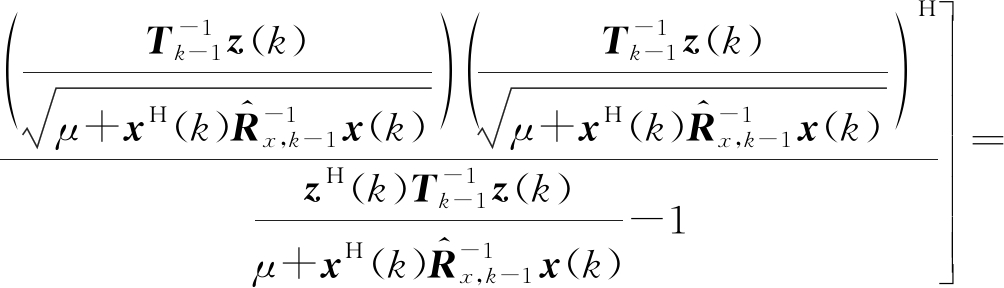
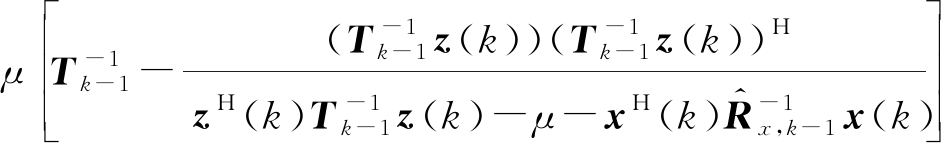
(27)
对于wMRCB的秩1更新,可以通过迭代梯度方法求解。
首先需要使用(21)对
进行更新亦即维护
由[3]中所述,问题(15)等价于以下WC-RAB问题的求解:
(28)
为使问题(28)的拉格朗日函数
达到极小值,使用梯度下降法进行w的迭代[16],有:
wk=wk-1-μkδk
(29)
其中
(30)
(31)
这里0<α≤1为梯度下降法的步长控制参数。
令
(32)
(33)
代入(29)得到
(34)
这里
是无约束条件下的最小化结果,pk是约束条件下的修正量。如果能够满足(28)中的约束,则有
(35)
否则,需要求解
(36)
即
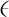
(37)
这是一个关于λ的二元一次方程,它的解为:
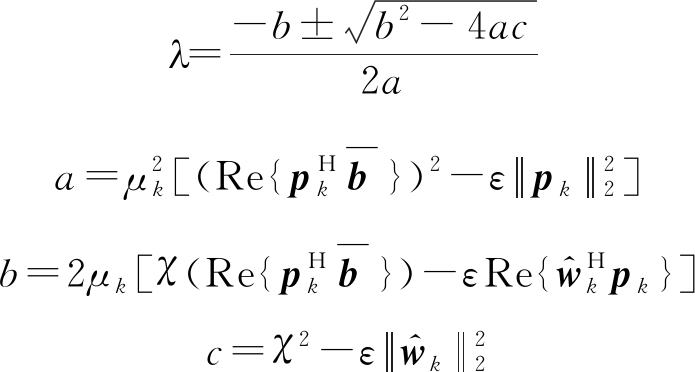
(38)
其中
实数λ可能有两个根,遵循表1所示的原则[16]取其中一个以尽量保证数值稳定性。
在求出wk后,令wMRCB,k=GCwk,由(22)或(23)即得wLCRCB,k。
由此,算法LCRCB-IG总结如表2。
每次迭代的总时间复杂度为O(5M2+5L2+5N2+2ML+2MN+4M+2L+10N)。这里时间复杂度为rank(C)=L时的情况,rank(C)=L-1时情况与之类似。算法中第7步的时间复杂度采用[14]中的结果。
而LCRCB方法每次更新
均需要重新计算加权值。在使用标准Cholesky分解求逆的情况下,计算wC需要的时间复杂度为O(2/3M3+2/3L3+5ML2+2L2);原始RCB方法需要的时间复杂度也为O(N3)级别。LCRCB-IG较之有数量级上的提升。
表1 λ的选择原则
Tab.1 Rules to choose λ
表2 LCRCB-IG算法
Tab.2 The LCRCB-IG algorithm
算法 LCRCB-IG时间复杂度 输入:新的数据快拍x(k) 输出:新的波束加权值wLCRCB,k1. 计算R^-1x,k-1x(k),μ+xH(k)R^-1x,k-1x(k)O(M2+M)2. 使用(25)更新R^-1x,kO(3M2+M)3. 计算z(k),T-1k-1z(k),zH(k)T-1k-1z(k)O(ML+L2+L)4. 使用(27)更新T-1kO(3L2+L)5. 使用(13)计算wC,kO(L2+M2+ML)6. 使用(21)更新R^y,kO(3N2+MN)7. 使用(29)更新wkO(2N2+10N)8. 计算wMRCB,kO(MN)9. 根据(22)或(23)计算wLCRCB,kO(2M)
5 数值仿真
本节使用LCRCB-IG、LCRCB、DAS(Delay and Sum, 时延求和)方法,对静止干扰、运动干扰两种情形进行了仿真,并对比了输出信干噪比在不同条件下的变化情况。仿真使用阵元数M=20的半波长间距均匀线列阵,观测空间为[-90°,90°],期望来波角度为
两个干扰角度分别为θ1,θ2,干扰强度分别为INR1=35 dB,INR2=20 dB。其中,θ1∈[-30°,-10°],期望波束设置为在该区间具有-35 dB深度的宽凹槽。
5.1 线性约束的简化
为了形成所需的凹槽,在[-30°,-10°]内间隔1°采样,构成约束:
wHS=f H S∈CM×P, f∈CP×1
(39)
其中S的每一列为采样点的导向向量, f的每个元素值均为10-35/10。由于P>M,为了削减计算量,采用[18]中的方法,对S进行奇异值分解S=UΣ VH,提取前L个最大的奇异值及对应的奇异向量,构成缩减后的奇异值矩阵ΣL=diag{σ1,…,σL},以及对应的UL和VL,使得:
(40)
其中,0<ξ<1为一个预定的阈值。
使用
代替(39)中的S,可得
(41)
这时,取
以及
即可得到L(一般L<M)个近似约束以削减计算量。这里取ξ=10-40/10,得到L=8。
5.2 导向向量误差建模
在仿真中,使用目标、干扰的真实来波角度导向向量生成输入的阵列信号。记真实目标来波角度为
在第k个快拍时,真实的目标来波角度的导向向量建模为:
(42)
其中δθ为表示目标信号来波方向误差的参数,eS,k是一个模为1的M维高斯分布随机变量,
表示目标来波角度导向向量在每次快拍迭代中随机变化量的方差。
真实的第i个干扰来波角度的导向向量建模为:
(43)
其中θi,k是第k个快拍到来时对应的干扰来波角度,eI,i,k是一个模为1的M维高斯分布随机变量,
表示干扰来波角度导向向量在每次快拍迭代中随机变化量的方差。
5.3 快拍迭代的实现细节
在迭代中,根据(1),构造仿真输入信号
x(k)=a0,ks0(k)+a1,ks1(k)+a2,ks2(k)+n(k)
(44)
其中s0(k),s1(k),s2(k)分别为能量为SNRin,INR1,INR2的高斯白噪声,n(k)的每个分量均为能量为0 dB的高斯白噪声,信号/干扰/噪声之间互不相关。使用(20)计算阵列输出自相关矩阵, 非迭代算法在每个快拍到达时使用与LCRCB-IG中相同的自相关矩阵进行计算。
由(3),评估算法性能需要的对应的干扰加噪声自相关矩阵Qx,k使用(44)计算:
(45)
为了考察迭代算法在新出现信号/干扰时的收敛性能,假定初始时,阵列只接收到噪声,无干扰和信号,对应的自相关矩阵初值为:
(46)
IM为M阶单位矩阵,与给定的μ相对应的K=1/(1-μ)称为计算自相关矩阵时的等效快拍数目。
对于wMRCB的初值,实验表明,取
能够最快收敛到标准RCB解。
5.4 信噪比的计算
根据(4)、(5),波束的输出信干噪比为
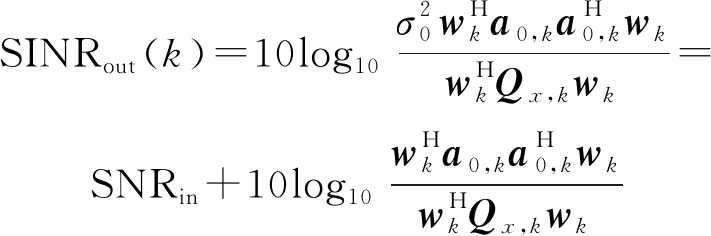
(47)
其中wk为第k个快拍来到后的波束加权值。
对于一定的Qx,k,理想的输出信干噪比定义如下:
(48)
5.5 固定的干扰
固定θ1,k=-20°,θ2,k=50°,令
参考[9]取4。蒙特卡洛仿真次数为200。以下除非特殊说明,信干噪比均取100次快拍迭代后的值。
取σ2=0,μ=0.95,SNRin=0 dB,在100次快拍迭代后,δθ=0°,2°时输出的波束图分别如图1,可以看到在两种情况下,LCRCB-IG算法与LCRCB算法生成的波束图仅有轻微差异,尤其是在主瓣以及凹槽区域高度一致;图中使用了DAS与标准RCB算法的波束输出作为对比参考。
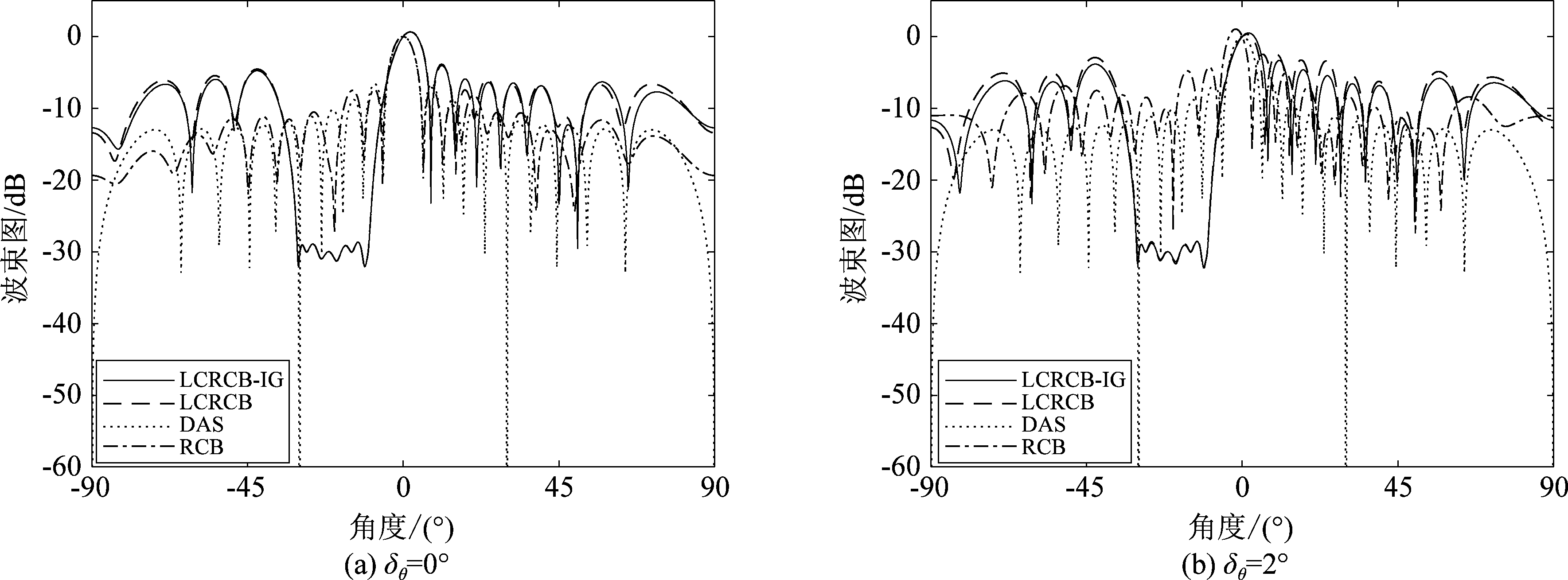
图1 固定干扰下的波束图
Fig.1 Beam pattern under fixed interferences
图2表示了不同SNRin、σ2以及μ的情况下,输出信干噪比随迭代快拍数变化情况。可以看到,LCRCB-IG与LCRCB方法的输出信干噪比非常接近,差距在1 dB以内,且收敛速度一致。值得注意的是,在低信噪比以及σ2=0.1的条件下,虽然输出信干噪比波动较大,但μ相同的LCRCB与LCRCB-IG输出信干噪比曲线差异很小。
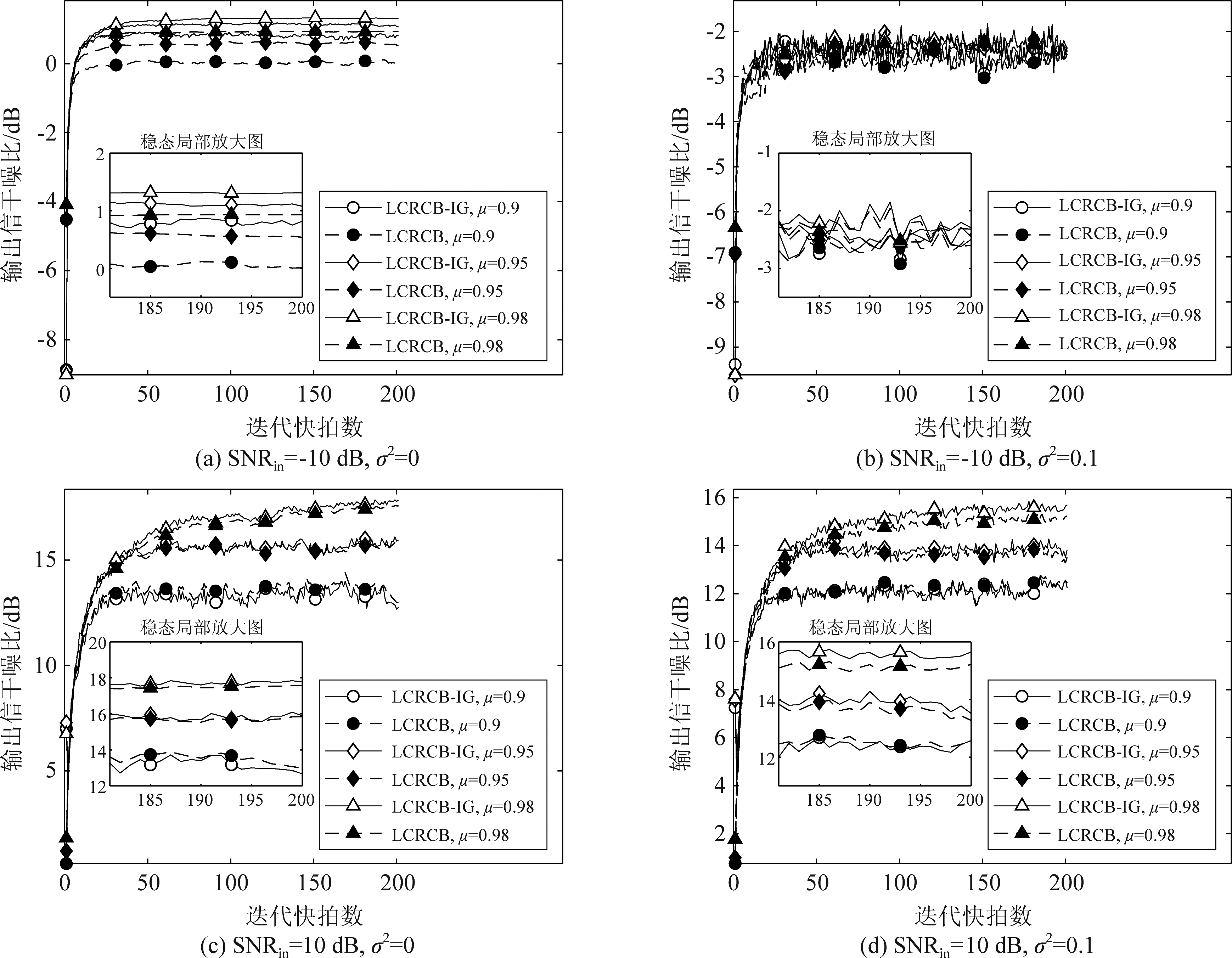
图2 输出信干噪比随迭代快拍数变化
Fig.2 The output SINR vs with the number of iterative snapshots
在不同SNRin和σ2条件下,输出信干噪比随计算自相关矩阵时的等效快拍数目K的变化见图3。可以看到,在低信噪比、σ2=0的情况下,K过小时LCRCB-IG较LCRCB输出信干噪比稍大,其余情况下均较为一致,这也与图2中的观察一致。
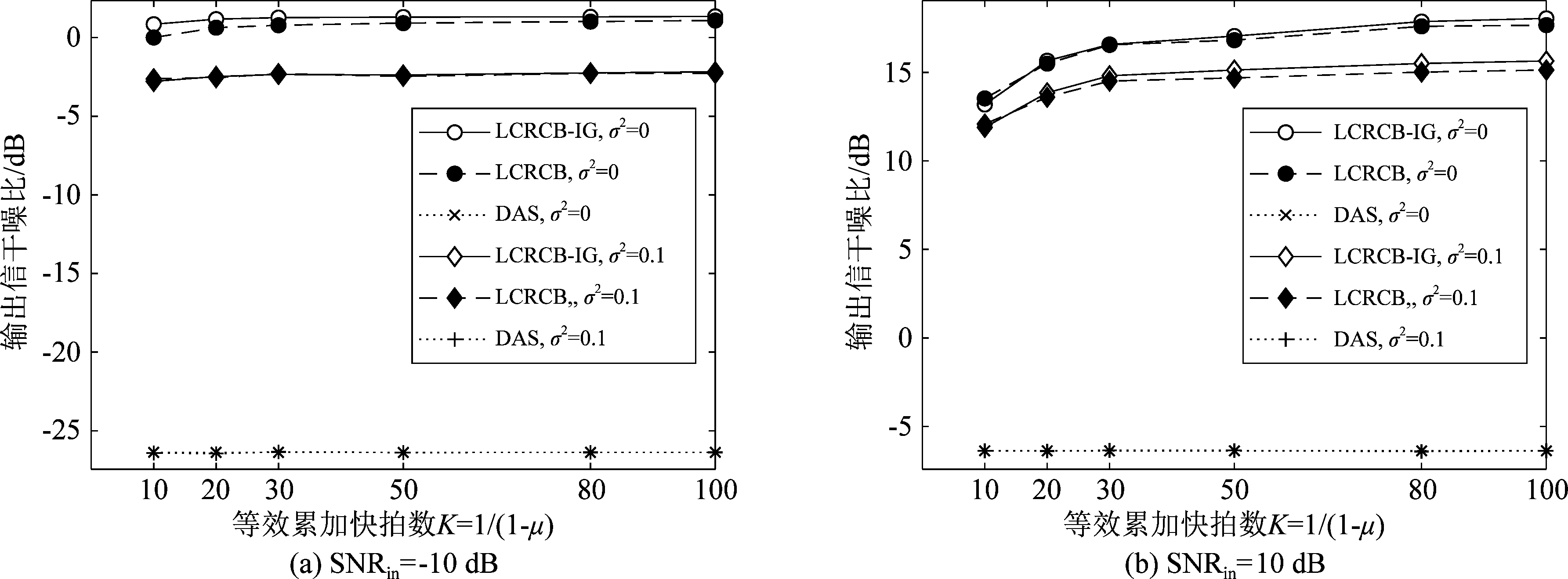
图3 输出信干噪比随K变化
Fig.3 The output SINR vs K
图4说明了在不同μ与σ2的情况下,输出信干噪比随输入信噪比的变化。值得注意的是,在输入信噪比达到20 dB时,LCRCB-IG的性能急剧下降,原因可能是当包含了较多目标信号成分时,梯度下降法的方向偏向于减去过多的目标信号成分,导致输出信干噪比下降。
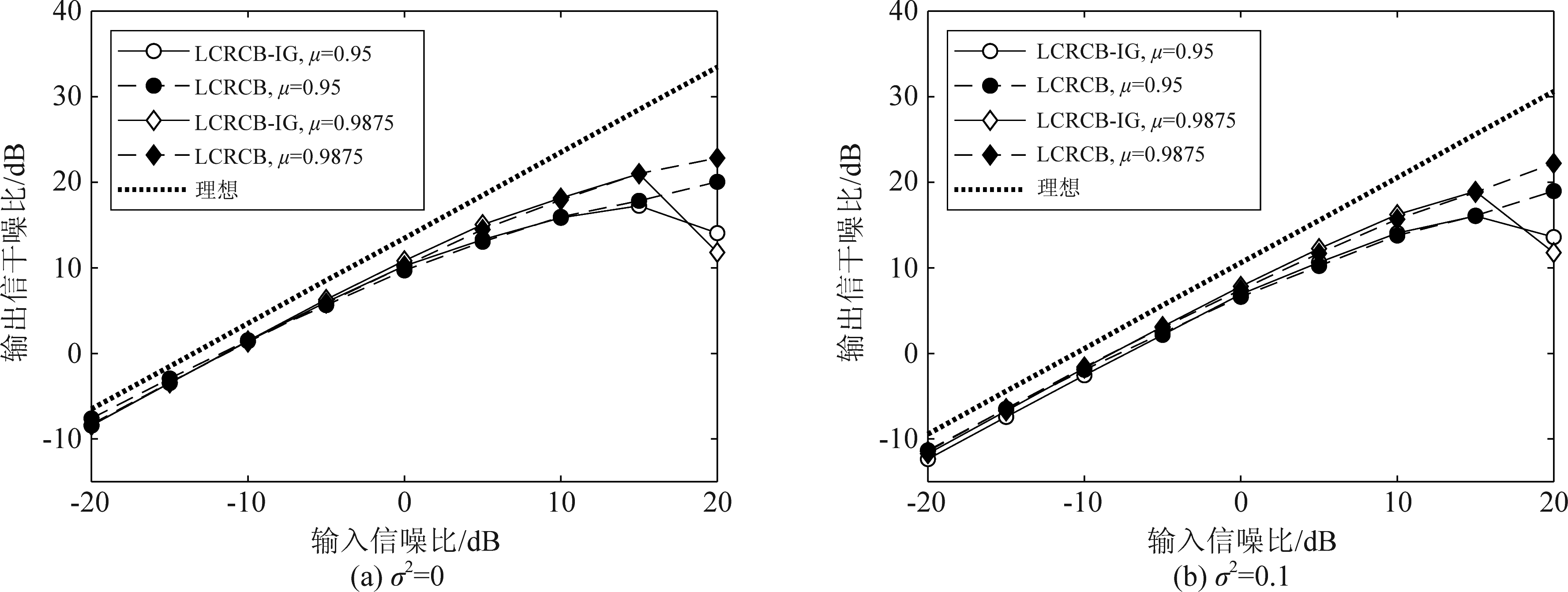
图4 输出信干噪比随输入信噪比变化
Fig.4 The output SINR vs the input SNR
在不同SNRin和μ的情况下,输出信干噪比随σ2变化如图5所示,可见LCRCB-IG与LCRCB方法的性能对σ2的响应几乎一致。
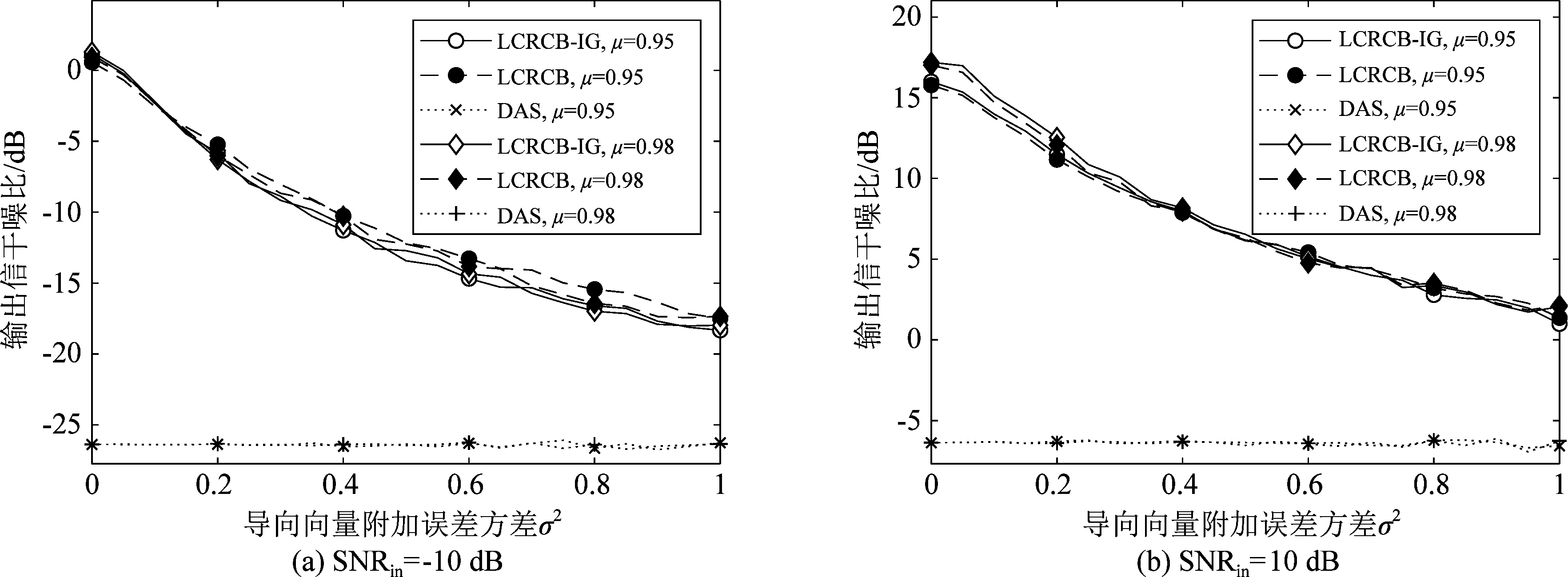
图5 输出信干噪比随导向向量附加误差方差变化
Fig.5 The output SINR vs variance of additional error for steering vector
5.6 运动的干扰
在1000次快拍迭代的时间内,θ1,k可在[-15°,-25°]区间匀速往复运动,θ1,0=15°,θ1,500=25°,θ1,1000=15°;θ2,k可在[-49°,-51°]区间以同样的方式匀速往复运动。这里蒙特卡洛仿真次数为200,
与前一节中一致,μ取0.95。在不同的SNRin、σ2以及干扰运动情况下,输出信干噪比随迭代快拍数变化如图6。在低输入信噪比下,LCRCB与LCRCB-IG性能几乎相同;在高输入信噪比下,LCRCB-IG相对LCRCB有微弱优势。
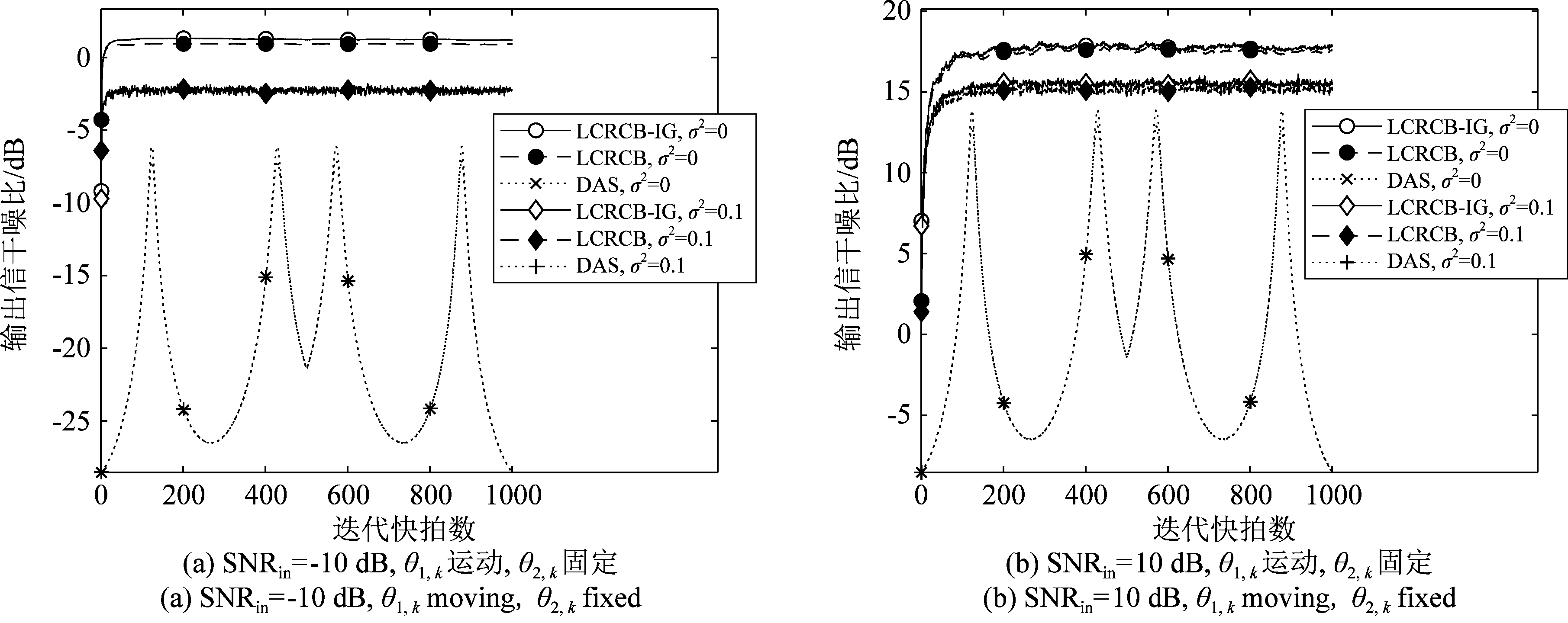
图6 输出信干噪比在干扰运动情况下随迭代快拍数变化
Fig.6 The output SINR vs the number of iterative snapshots under interference movement
在θ1,k,θ2,k均运动时,取σ2=0,不同SNRin情况下第500次快拍迭代的波束图对比如图7。其中竖直虚线代表该时刻两个干扰源的位置θ1,500=-25°,θ2,500=51°。与干扰固定的情况相同,LCRCB与LCRCB-IG的波束图仅有轻微差异。
5.7 相干源干扰
LCRCB基于RCB与LCMV,这两种方法均在干扰与期望信号相干时存在性能下降的问题,从而使得LCRCB对相干干扰敏感。有必要考察LCRCB-IG在相干源干扰存在时的性能是否与LCRCB一致。在式(44)中,分别取s1(k)=s0(k)(干扰1相干),s2(k)=s0(k)(干扰2相干)两种情况,与5.5节中取相同的固定θ1,k,θ2,k以及σ2定义,μ=0.95。考察不同σ2下算法输出信干噪比随输入信噪比的变化。如图8所示,当s1(k)=s0(k),亦即相干源处于凹槽内时,算法的性能没有改变。而当s2(k)=s0(k),亦即相干源不在预先形成的凹槽内时,算法的性能极大下降。在相干干扰下,LCRCB与LCRCB-IG性能完全一致。
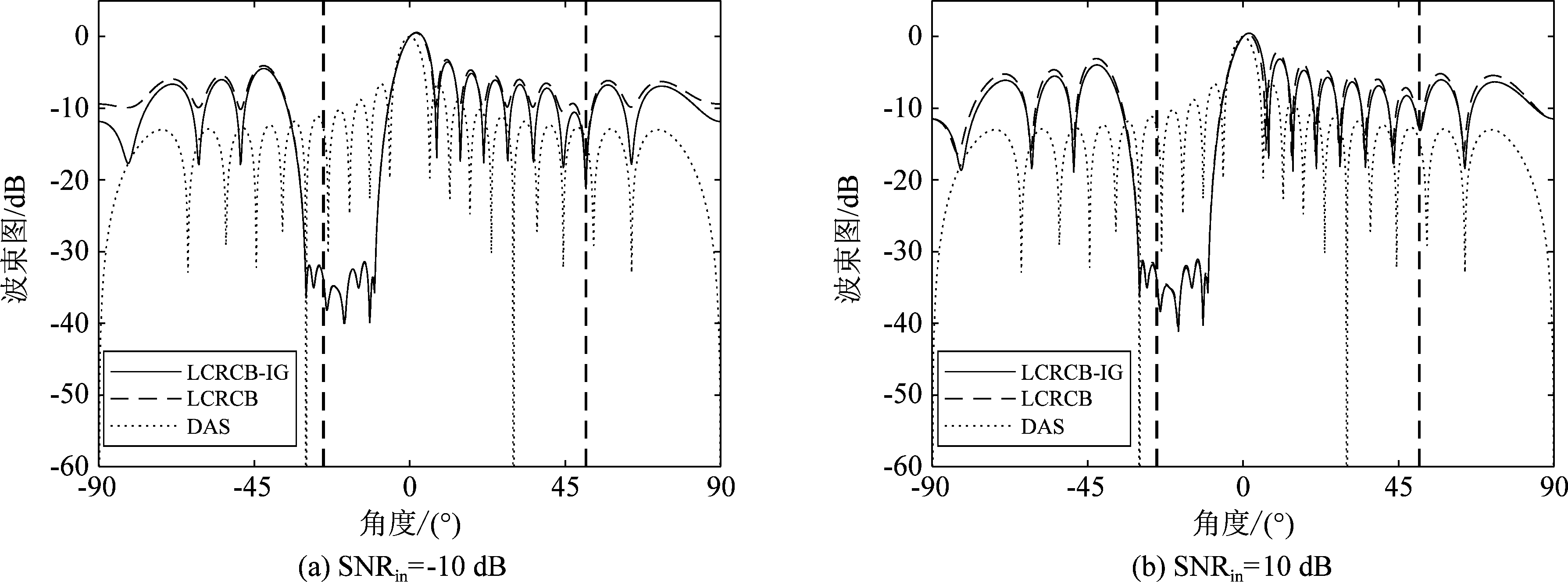
图7 干扰运动情况下波束图
Fig.7 Beam pattern under interference movement
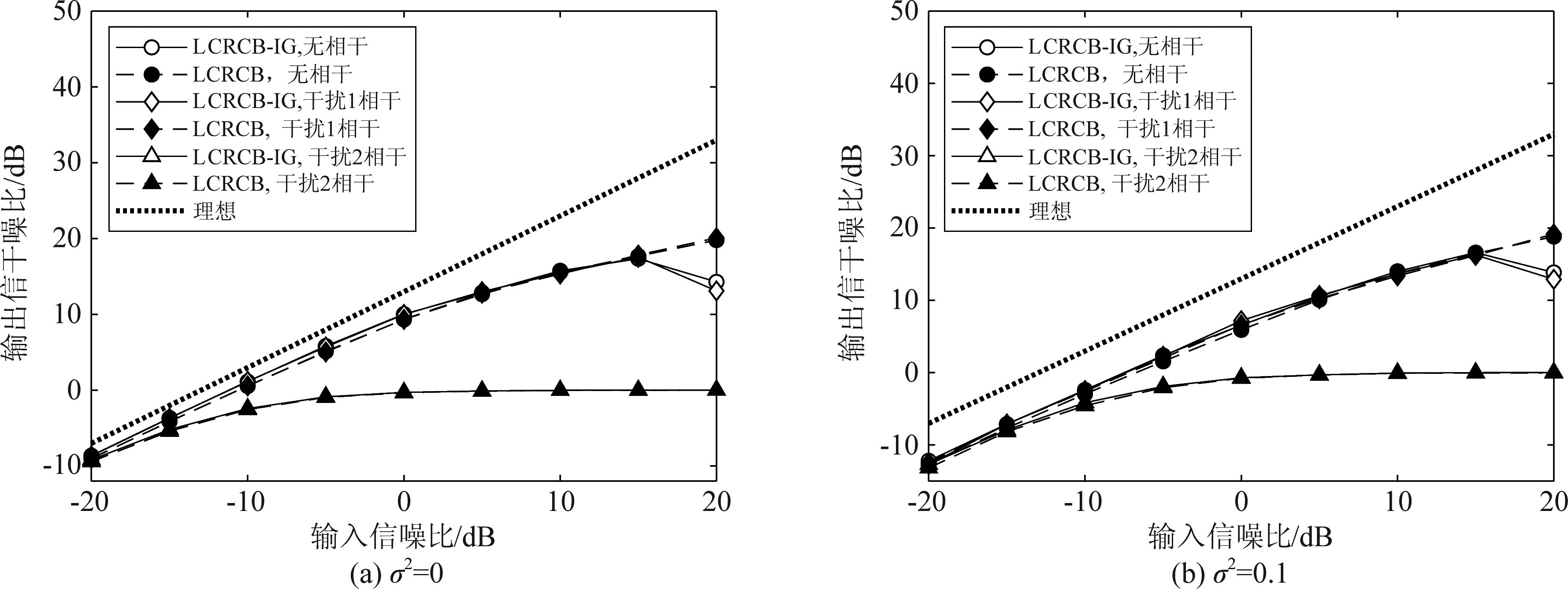
图8 相干条件下输出信干噪比随输入信噪比变化
Fig.8 The output SINR vs the input SNR with coherent interference
6 结论
针对带线性约束的稳健自适应波束形成算法计算量过大,难以应用于实时信号处理系统中的问题,提出了一种线性约束稳健Capon波束形成快速算法。该算法利用秩1更新维护计算代价较大的逆矩阵,使用梯度下降方法来更新波束加权值,实现了较小常系数的O(M2)时间复杂度的线性约束稳健自适应波束形成。仿真实验表明,本文中的算法在静态干扰、动态干扰下和原始的LCRCB算法在波束形状以及输出信干噪比性能上均几乎一致,能够用于实时信号处理系统。
[1] CAPON J. High-resolution frequency-wavenumber spectrum analysis[C]∥Proceedings of the IEEE. U.S.A.: IEEE, 1969: 1408-1418.
[2] CARLSON B D. Covariance matrix estimation errors and diagonal loading in adaptive arrays[J]. IEEE Transactions on Aerospace and Electronic Systems, 1988, 24(4): 397- 401.
[3] LI Jian, STOICA P, WANG Zhisong. On robust Capon beamforming and diagonal loading[J]. IEEE Transactions on Signal Processing, 2003, 51(7): 1702-1715.
[4] ZHANG Ming, CHEN Xiaoming, ZHANG Anxue. A simple tridiagonal loading method for robust adaptive beamforming[J]. Signal Processing, 2019, 157: 103-107.
[5] 马远良. 任意结构形状传感器阵方向图的最佳化[J]. 中国造船, 1984, 25(4): 78- 85.
MA Yuanliang. Pattern optimisation for sensor arrays of arbitrary configuration[J]. Shipbuilding of China, 1984, 25(4): 78- 85.(in Chinese)
[6] YANG Xiaopeng, LI Shuai, LONG Teng, et al. Adaptive null broadening method in wideband beamforming for rapidly moving interference suppression[J]. Electronics Letters, 2018, 54(16): 1003-1005.
[7] 曹运合, 郭勇强, 刘帅, 等. 基于旁瓣对消器的自适应零陷优化设计[J]. 电子与信息学报, 2020, 42(3): 597- 602.
CAO Yunhe, GUO Yongqiang, LIU Shuai, et al. Adaptive null broadening algorithm based on sidelobes cancellation[J]. Journal of Electronics & Information Technology, 2020, 42(3): 597- 602.(in Chinese)
[8] FROST O L. An algorithm for linearly constrained adaptive array processing[C]∥Proceedings of the IEEE. U.S.A.: IEEE, 1972: 926-935.
[9] SOMASUNDARAM S D. Linearly constrained robust capon beamforming[J]. IEEE Transactions on Signal Processing, 2012, 60(11): 5845-5856.
[10]鄢社锋, 马远良, 孙超. 任意几何形状和阵元指向性的传感器阵列优化波束形成方法[J]. 声学学报, 2005, 30(3): 264-270.
YAN Shefeng, MA Yuanliang, SUN Chao. Beampattern optimization for sensor arrays of arbitrary geometry and element directivity[J]. Acta Acustica, 2005, 30(3): 264-270.(in Chinese)
[11]SUN Dajun, JIA Zixuan, TENG Tingting, et al. Strong coherent interference suppression based on second-order cone null steering beamforming[C]∥MATEC Web of Conferences. EDP Sciences, 2019, 283.
[12]刘倩, 朱安珏. 基于二阶锥规划的稳健低旁瓣自适应波束形成[J]. 声学技术, 2020, 39(3): 379-384.
LIU Qian, ZHU Anjue. Second-order cone programming based robust low sidelobe adaptive beamforming[J]. Technical Acoustics, 2020, 39(3): 379-384.(in Chinese)
[13]陈力恒, 马晓川, 李璇, 等. 结合压缩感知模型的稀疏阵列波束形成方法[J]. 信号处理, 2020, 36(4): 475- 485.
CHEN Liheng, MA Xiaochuan, LI Xuan, et al. Sparse array beamforming method combined with compressed sensing model[J]. Journal of Signal Processing, 2020, 36(4): 475- 485.(in Chinese)
[14]SOMASUNDARAM S D, BUTT N R, JAKOBSSON A, et al. Low-complexity uncertainty-set-based robust adaptive beamforming for passive sonar[J]. IEEE Journal of Oceanic Engineering, 2015.
[15]ASL B M, DEYLAMI A M. A low complexity minimum variance beamformer for ultrasound imaging using dominant mode rejection[J]. Ultrasonics, 2018, 85: 49- 60.
[16]ELNASHAR A. Efficient implementation of robust adaptive beamforming based on worst-case performance optimisation[J]. IET Signal Processing, 2008, 2(4): 381-393.
[17]SONG Xin, HAN Xiuwei, WANG Feng, et al. Recursive updating algorithm for robust adaptive beamforming in a uniform circular array[J]. International Journal of Wireless Information Networks, 2019, 26(4): 331-343.
[18]SOMASUNDARAM S D, JAKOBSSON A, PARSONS N H. Robust and automatic data-adaptive beamforming for multidimensional arrays[J]. IEEE Transactions on Geoscience and Remote Sensing, 2012, 50(11): 4642- 4656.
