1 引言
根据雷达发射信号形式可以将雷达分为脉冲体制雷达与连续波体制雷达[1]。脉冲体制雷达收发分时,隔离性好,发射信号瞬时功率大,适用于远距离成像。而在近距离成像中,由于收发分时的特点,脉冲雷达需要在短时间内进行收发切换,工程上实现难度较大[2-3]。线性调频连续波(Linear Frequency Modulation Continuous Wave,LFMCW)雷达是在连续波雷达的基础上发展起来的一种高分辨率雷达。这种雷达由于采用连续波体制,因此发射机只需要较低的发射峰值功率[4]。而且,针对LFMCW雷达,采用Dechirp接收方式还能极大地降低对接收机AD采样的要求。因此这种雷达具有结构简单,成本较低的优势。再加上连续波雷达不存在近距离测距盲区的优点,因此LFMCW雷达在民用近距离成像,如车载毫米波雷达成像中,具有独特优势[5- 6]。
近距离成像由于探测范围小,往往对成像分辨率要求更高。就距离向而言,更高的分辨率意味着要求更大的发射信号带宽,通常需要达到GHz量级。然而,随着发射信号带宽的增加,LFMCW雷达发射机要产生严格的线性调频信号变得越来越困难。当信号中的非线性调频分量变得不可忽略时,基于Dechirp的脉冲压缩结果将出现主瓣展宽、旁瓣升高、主瓣峰值下降等问题[7- 8],影响目标距离聚焦效果。而且,这种散焦效应是空变的,Dechirp参考点无散焦,但随着目标偏离参考点距离增加,散焦程度将逐步增大。
为了解决非线性调频误差带来的距离向散焦问题,目前解决的方法主要从硬件的精细设计[9-10]和信号处理误差补偿[7,13-16]两个方面出发。硬件上的精细化设计是解决发射信号频率非线性问题的根本途径。然而,一方面,这种方式往往会极大地增加雷达的复杂度,从而提高系统成本,另一方面,受现有理论和工程水平限制,即使进行了更精细化的设计,这种方式也可能无法完全满足实际精度需求。而信号处理误差补偿方法则是针对雷达回波信号进行分析和处理,试图从信号中提取误差参数并进行补偿,是一种成本相对较低的误差补偿实现方法[11]。本文主要研究基于信号处理的非线性调频误差补偿方法。
由于Dechirp接收后的残余相位误差具有空变性,即误差的大小与目标位置相关[12]。因此,如何实现这种空变误差的统一校正是非线性调频误差校正的关键点和难点。目前也有很多的文献对此展开研究。针对非线性调制误差的补偿包括误差的估计和校正两个过程。对于非线性调频相位误差的估计,通常采用实延迟线的方法,即利用实延迟线模拟得到单点目标的差频回波信号,再从该模拟回波信号中提取误差。对于具体的误差估计方法,许多文献提出了不同的方法。其中文献[7]采用分段线性拟合的方法估计信号的调频非线性。文献[13]利用高阶模糊函数拟合误差相位,文献[14]基于泰勒展开与相位积分思想在短延迟线情况下估计误差相位。而对于非线性调频误差的校正,文献[7]对三阶误差进行了推导,提出准确校正各个距离门的误差方法。该方法需要逐像素点进行,效率太低。文献[15]尝试在频域上对误差进行一致校正,但低采样率使其无法直接进行傅里叶变换,需要通过升采样进行处理,这使得处理量增加。文献[16]提出使用重采样进行校正,在一定条件下忽略了相位误差随目标距离变化的部分,对空不变部分进行补偿。现有的补偿方法大都难以兼顾补偿精度和计算效率。
为了高效且精确地补偿非线性调频相位误差,本文从Dechirp与匹配滤波的内在联系入手,在不提高数据采样率的前提下恢复目标回波信号的频谱,然后利用匹配滤波的方式实现距离向脉冲压缩。由于匹配滤波实现过程中,无需考虑误差的空变性,因此利用该方法可以克服Dechirp方式脉冲压缩面临的空变补偿问题,实现高精度高效率非线性调制相位误差补偿。
本文安排如下:第2节分别介绍了匹配滤波与Dechirp的原理,并且揭示了两种脉冲压缩方法的等效性;第3节推导了非线性调频误差对Dechirp处理结果的空变性影响;第4节针对非线性调频误差提出了基于频谱恢复的校正方法;第5节通过仿真验证了理论分析的正确性与新方法的有效性;第6节对全文进行总结。
2 Chirp信号的脉冲压缩原理
对于Chirp信号,可以采取两种方式实现脉冲的压缩。一种是匹配滤波方式,另一种是Dechirp方式。下面我们先分别介绍这两种方法的实现原理,然后将揭示两者的本质联系。
2.1 匹配滤波原理
假设LFMCW雷达发射的理想线性调频信号为
(1)
其中A表示信号的振幅, fc表示信号载频,k表示调频斜率,t表示限制在一个脉冲内的时间变量,即快时间。
匹配滤波处理针对的是直接接收的Chirp回波信号。忽略天线传播等幅度效应,接收信号为发射信号的一个时间延时。假设目标延迟时间为τ,则接收信号可以表示为
(2)
在对接收信号采样前,通常会将射频信号解调到视频,解调后的视频信号可以表示为
r(t)=Bexp{jπk(t-τ)2}
(3)
其中,B=Aexp{-j 2πfcτ}为复常数。
匹配滤波本质上是将回波信号与发射信号做相关。根据相关与卷积的关系,也可以表示为将接收信号与发射信号的共轭反转做卷积,即[17]
y(t)=r(t)⊗s*(-t)
(4)
实际实现时,为了提高计算效率,通常会在频域实现卷积,即
y(t)=IFFT{FFT{r(t)}·FFT{s*(-t)}}
(5)
从上述公式推导中可以看出,匹配滤波对信号的波形没有要求,发射信号存在非线性调频误差不会影响匹配滤波结果。但匹配滤波做脉冲压缩需要对回波直接采样。接收宽带信号时,对AD采样要求过高,将大大提高应用成本。
2.2 解线性调频(Dechirp)原理
Dechirp是针对线性调频信号提出的,通过消除时间的二次相位使得信号的能量集中在单一频点上,以达到脉冲压缩的目的。
对于LFMCW雷达成像,一般使用发射信号作为Dechirp参考信号,接收雷达回波信号为
![]()
exp{-j(πkτ2-2πkτt+2πfcτ)}
(6)
其中rect(·)表示矩形窗。此差频信号为单频信号,信号频率与目标距离成正比,此时对该信号直接做傅里叶变换即可得到脉冲压缩结果。目标与雷达之间的距离为
(7)
其中τi和fi分别为不同目标所对应的时延与频点。当存在多个目标时,该差频信号的带宽与场景大小成正比。由式(7)可知差频信号带宽与目标发射信号带宽的关系[18]:
(8)
其中ΔR表示成像场景大小,Tp表示脉冲宽度,c表示电磁波传播速度,Bif与Br分别表示差频信号与目标发射信号带宽。当成像场景较小,使得时延范围![]() 比信号的脉宽Tp小时,Dechirp接收可以有效地降低接收信号带宽,从而降低对采样率的要求。Dechirp原理也可由如图1形象地说明[19]。
比信号的脉宽Tp小时,Dechirp接收可以有效地降低接收信号带宽,从而降低对采样率的要求。Dechirp原理也可由如图1形象地说明[19]。
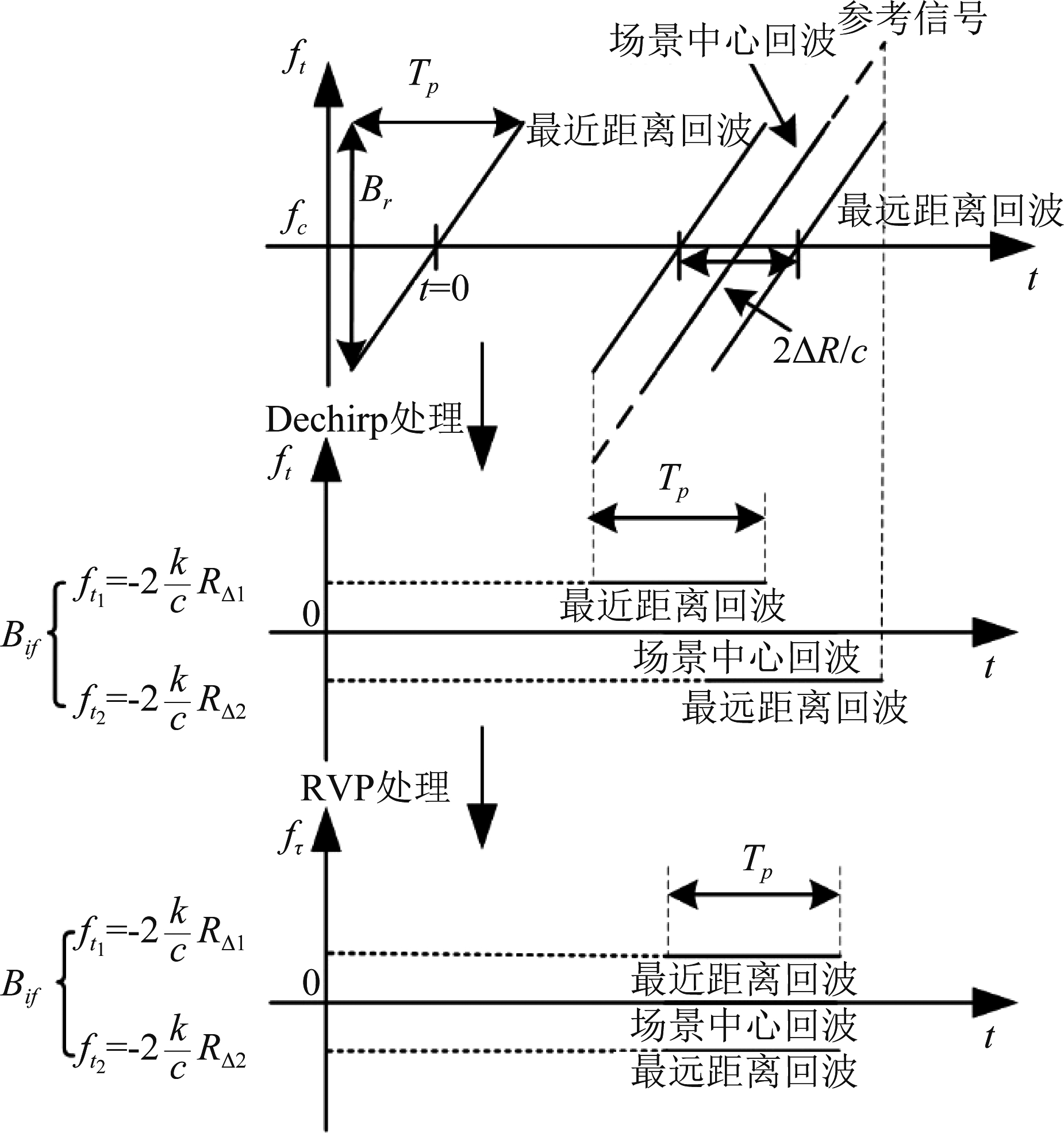
图1 解线性调频原理
Fig.1 The Principle of Dechirp
从式(6)的包络项和图1均可看到,Dechirp后信号在时间上是错位的。而且从式(6)中还可以看到有一个跟目标位置有关的常数相位,常称为残留视频相位项(Residual Video Phase, RVP),该项虽然不影响距离向聚焦结果,但当其大小不能忽略时会对方位向聚焦产生影响。为了去除该相位影响,可以增加一个RVP去除的后处理过程。该RVP去除处理顺便还能完成不同目标回波信号时域上的对齐。去RVP处理可以通过在频域乘以如下滤波器传递函数实现
(9)
从上述分析中得知,Dechirp技术通过混频使得接收信号的带宽大大降低。针对宽带信号而言,Dechirp可以极大程度的降低AD采样的要求。这一技术使得LFMCW雷达极易获得高分辨率图像。
2.3 Dechirp与匹配滤波的内在联系分析
从上面分析可知,完整的Dechirp处理包含三个过程,即Dechirp接收、傅里叶变换和RVP去除,用公式表示即
(10)
对上式,如果我们定义一个新的时间变量η,并令ft=-kη,然后将其代入公式(10)可以得到
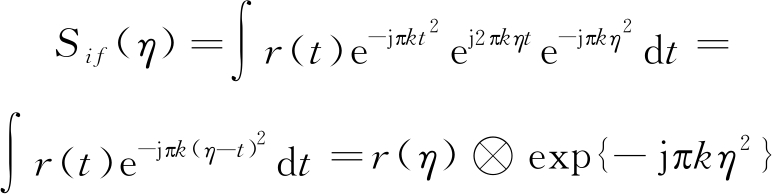
(11)
上式表明,Dechirp处理后的结果,实际上就是将接收信号和发射信号的共轭反转相卷积后的结果,也即匹配滤波过程。因此,Dechirp处理和匹配滤波处理虽然看起来采取了完全不同的实现方式,但其本质上是完全等同的。
3 非线性调频对解线性调频处理的影响
FMCW雷达由于硬件老化、温漂和相噪等因素会导致发射的线性调频信号存在一定的非线性调频误差,假设含有误差的发射信号模型为
(12)
其中,ε(t)为调频时产生的误差相位。因此Dechirp接收得到的差频信号可以表示为
sεif(t)=Aexp{j(πkτ2-2πkτt+2πfcτ)}×
exp{j(ε(t-τ)-ε(t))}
(13)
从ε(t-τ)-ε(t)项可知,差频信号的相位误差大小受到非线性调频误差相位形式以及目标距离的影响。文献[20]的结论也佐证了这一点,假设非线性频率服从均值为0,标准差为σ的平稳高斯分布,可以求得此时距离分辨率为
(14)
其中L为均方根线性度:![]() ρ(t)为ε(t)与ε(t-τ)的相关系数。线性度L的大小与误差相位形式有关,相关系数ρ(t)与时间延迟有关。
ρ(t)为ε(t)与ε(t-τ)的相关系数。线性度L的大小与误差相位形式有关,相关系数ρ(t)与时间延迟有关。
为了更直观的体现误差的空变性。产生一个脉宽为30 μs的信号并将发射信号误差相位设置为![]() 比较距雷达0 m、40 m、80 m和120 m四个目标的相位误差大小以及变化趋势。图2中可以看到在参考距离(即距雷达0 m处目标)没有误差,随着距离增大,误差相位逐渐增大。
比较距雷达0 m、40 m、80 m和120 m四个目标的相位误差大小以及变化趋势。图2中可以看到在参考距离(即距雷达0 m处目标)没有误差,随着距离增大,误差相位逐渐增大。
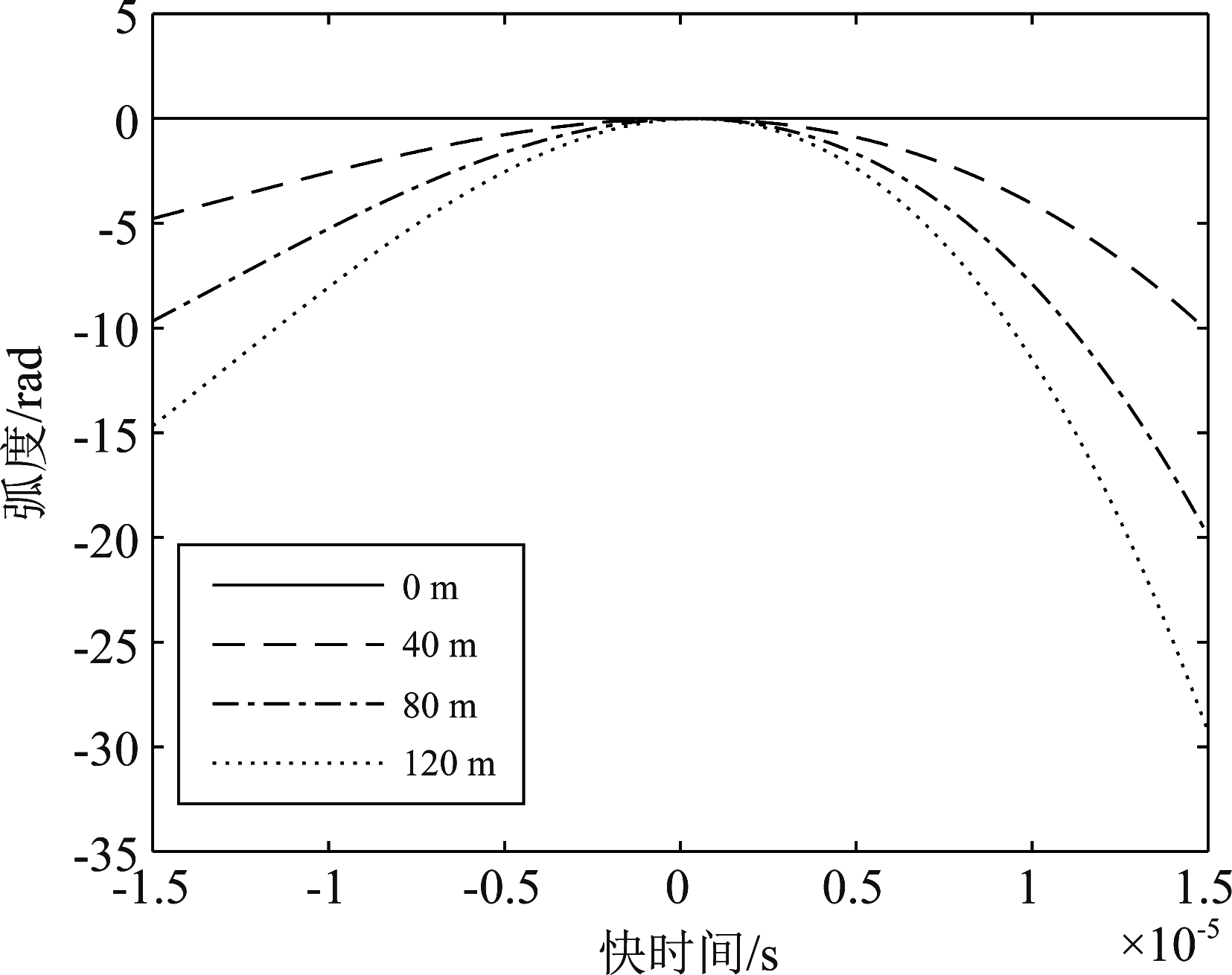
图2 Dechirp后的残留误差空变性
Fig.2 Residual Error Variability after Dechirp
图3展示了调频存在非线性对于Dechirp结果的影响。可以看到误差使得脉冲压缩结果存在严重散焦,相对应的,参考信号处点目标可以正确成像。
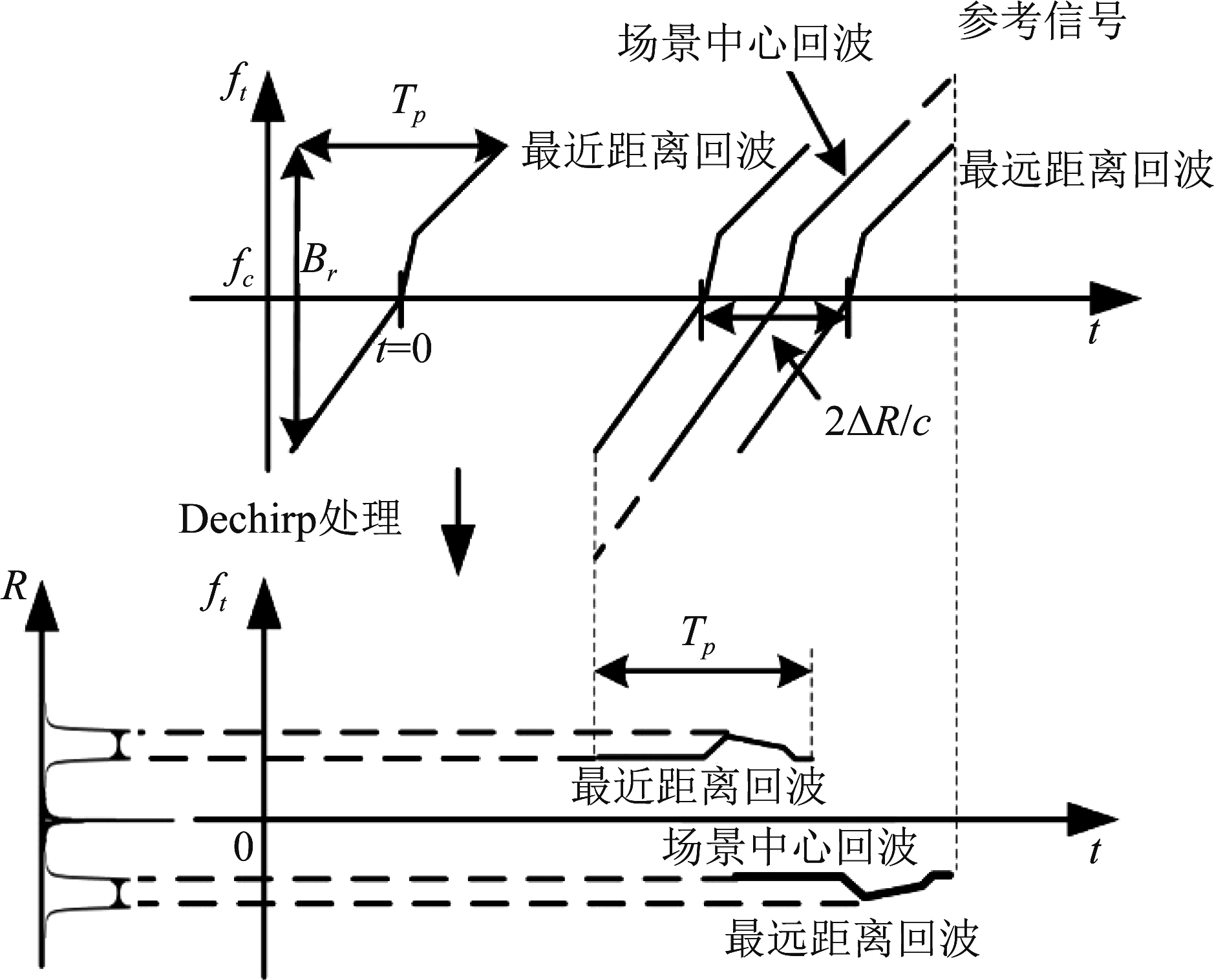
图3 非线性调频误差对Dechirp的影响
Fig.3 The Influence of Nonlinear Frequency Modulation Error on Dechirp
4 非线性调频误差的估计与校正
由前文分析可知,要实现高分辨率成像,非线性调频引起的相位误差不能忽视。非线性调频补偿算法主要从两个方向入手。针对发射信号相位误差大小,需要设计精确的非线性调频误差估计算法对其进行估计。针对目标延时引起的误差空变性,能否统一地校正非线性调频误差是衡量校正方法有效性的重要因素。
4.1 基于最小二乘拟合的误差估计方法
文献[14]提出的非线性调频误差估计方法采用延迟线的方式,即设置一段等效距离为Rref,延迟为τref的射频延迟线,将该延迟线与发射信号混频得到参考信号,利用该参考信号估计非线性调频误差。该延迟线得到的差频信号相位误差可以表示为
![]()
ε(t-τref)-ε(t)
(15)
当τref取得较小时,在τref=0点进行泰勒展开,可以得到误差相位的一阶近似模型
Δφ(t,τref)=ε(t-τref)-ε(t)≈τrefε′(t)
(16)
整理上式即可得到误差相位的估计
(17)
此方法引入延迟线技术,对于延迟距离的大小有一定的要求,若参考延迟距离太近,误差太小,在工程上容易被噪声淹没,无法提取出所需延迟相位误差,导致无法对其进行估计,而当延迟线距离太大时,式(16)的一阶泰勒展开又存在较大误差。
为了解决该方法的不足,本文利用最小二乘算法拟合Δφ(t,τref)。为简化分析,假设信号频率调制满足低阶模型(可以很容易扩展到更高阶模型),误差相位为:
(18)
将式(16)利用多项式拟合,表示为
Δφ(t,τref)=ε(t-τref)-ε(t)=
2π(A1t2+A2t+A3)
(19)
式(18)与式(19)系数存在以下关系
A1=-a3τref![]()
![]()
(20)
整理上式可得
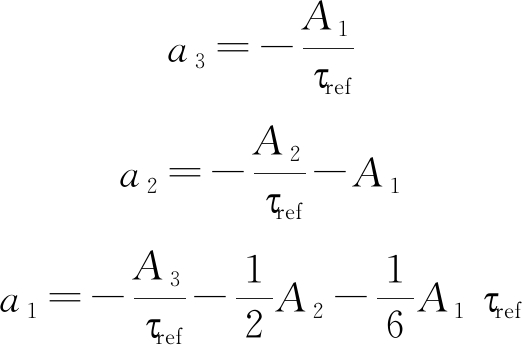
(21)
利用最小二乘拟合法能够得到系数A1,A2,A3。并通过式(21)得到误差相位的各项系数,该方法避免了当延迟线较大时泰勒展开带来的估计误差。
此外,现有的方法通常都是采用单个延迟线进行误差估计。前面提到当噪声较大时,近距离延迟线产生的误差容易被噪声淹没。因此,可以利用多延迟线技术(也可以用角反等效实现)以获得更加精确的误差估计结果,利用多个延迟线数据,获得更多的样本数据。在不同延迟线数据内,由于τref不同,因此调频斜率不同,但都跟误差相位的系数相关。利用所有数据,做总体最小二乘可以获得系数的更鲁棒性的估计。
4.2 基于频谱恢复的误差校正方法
从上一节的分析我们知道,Dechirp后的残留误差是空变的,即不同位置的目标回波信号具有不同相位误差,偏离参考点越远,误差越大。这种误差的空变性给误差补偿处理带来了极大挑战,现有方法大多难以兼顾补偿精度与计算效率。需要指出的是,这种误差的空变性是由Dechirp处理本身带来的,如果采用匹配滤波处理就不存在这种空变补偿问题。但是,对于低成本雷达,如果采用直接接收并基于匹配滤波处理又会由于过高的采样率而带来成本的急剧增加。为此,本文提出一种新的处理策略。该方法基于Dechirp接收信号,然后利用Dechirp处理和匹配滤波处理的等效原理,首先直接恢复回波信号的频谱(为了避免提高采样率,实际恢复的是去除标准线性调频项后的频谱),然后利用匹配滤波方式实现脉冲压缩。这种处理既保留了Dechirp接收的低采样率,又避免了空变误差的补偿。
假设含有非线性调频误差的差频信号模型如式(14)所示,首先根据估计得到的误差相位将差频信号中的发射信号相位误差去除,即
s1(t)=sεif(t)ejε(t)=rε(t)e-jπkt2
(22)
由于Dechirp处理和匹配滤波处理的等效性表现在处理线性调频信号时。因此将Dechirp信号中的发射信号非线性调频相位误差去除后,得到的是接收回波信号与标准线性调频信号的Dechirp处理结果。将式(22)信号做傅里叶变换并去RVP处理,得到
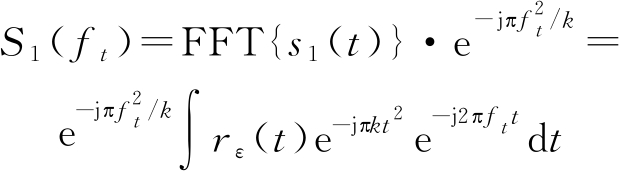
(23)
将ft=-kη代入式(23),可以表示为
![]()
rε(η)⊗e-jπkη2
(24)
再对新的时间变量η进行傅里叶变换得到
(25)
至此,已经恢复出了去除标准调频项后的频谱,将该信号乘以![]() 即可得到接收信号的频谱。由于恢复的频谱不满足奈奎斯特采样定理,不能通过逆傅里叶变换直接得到接收信号。
即可得到接收信号的频谱。由于恢复的频谱不满足奈奎斯特采样定理,不能通过逆傅里叶变换直接得到接收信号。
为实现频域匹配滤波,还需要发射信号的频谱作为匹配滤波器。发射信号的频谱可以通过以下两种方式获取。
第一种方法是在信号处理过程中人为提高采样率,产生一个高采样率的发射信号,再通过傅里叶变换得到频谱。该方法在信号处理时进行,无需提高AD的采样率。但由于新方法恢复出的频谱采样率较低,在获得了高采样率的发射信号频谱后,又要对其进行降采样,并且在人为提高采样率后还会增加一定的处理量。
第二种方法是对发射信号利用新方法获得去除标准调频项后的发射信号频谱,如此一来,既不需要提高采样率又可以直接获得去除调频项后的发射信号频谱,省去了最后补偿标准调频项以获得完整的信号频谱过程。第二种方法获得的发射信号去调频项后的结果为
(26)
其中S(fη)为发射信号频谱,利用式(26)与式(25)做频域匹配滤波得到
![]()
IFFT{Rε(fη)·S*(fη)}
(27)
至此,目标已经聚焦到精确的位置。该方法利用Dechirp与匹配滤波的关系,在低于信号带宽的采样率前提下恢复得到信号的频谱。且该方法的优势在于整个过程中没有引入与目标位置相关的参数,因此该方法可以对不同位置目标进行统一地误差校正。整个非线性调频误差的估计与校正流程图如图4。
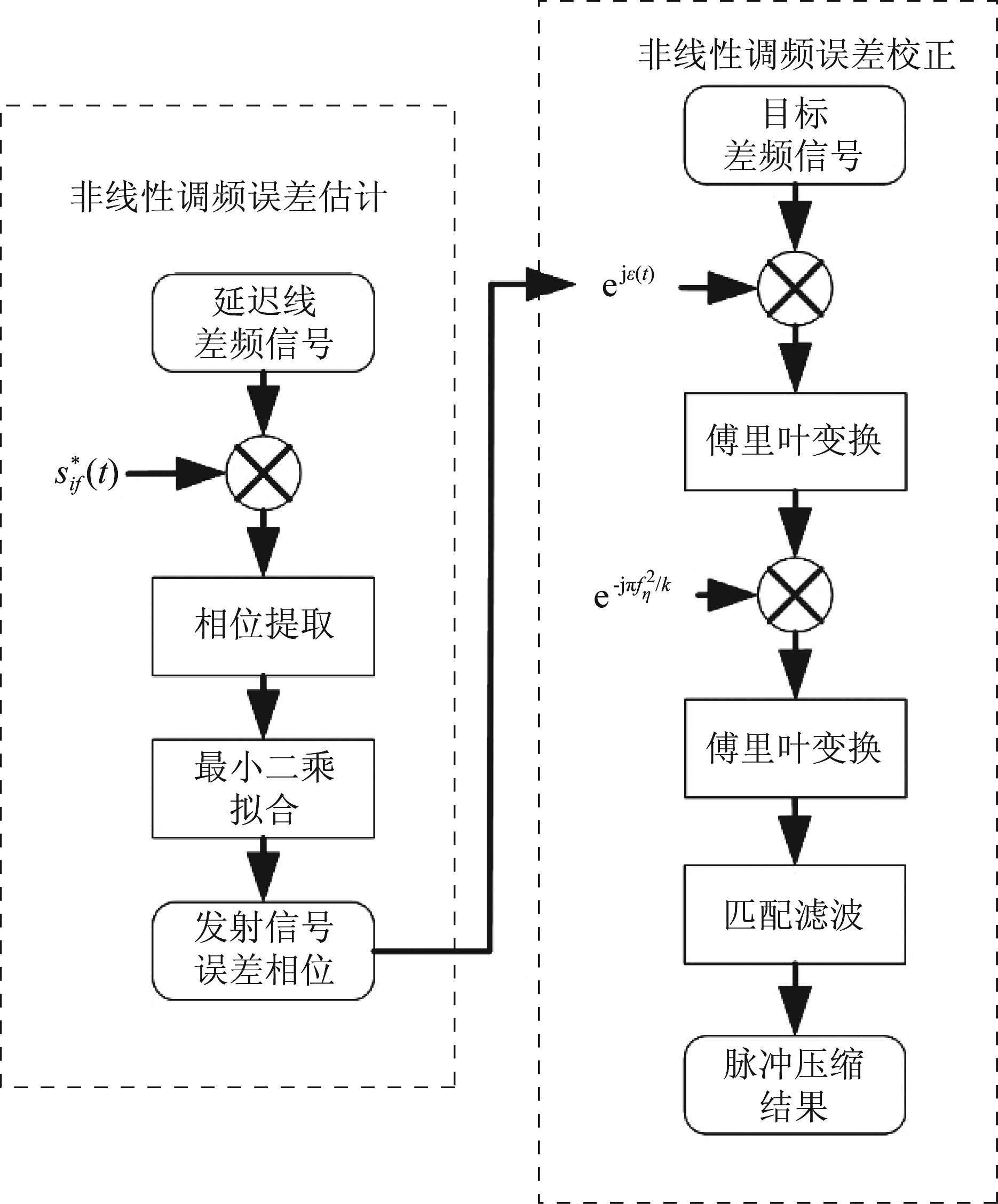
图4 非线性调频误差估计与校正过程
Fig.4 Non-linear Frequency Modulation Error Estimation and Correction Process
5 实验验证
我们通过对仿真数据处理来验证理论分析的正确性以及算法的有效性。主要的雷达参数如表1所示。由于缺少误差较大的实测数据,为了更接近于实际LFMCW雷达应用(例如车载雷达)的情况,对雷达前方目标进行脉冲压缩处理。在雷达前方25 m,50 m,75 m,100 m,125 m,150 m处设置六个点目标。值得一提的是,为了易于观察非线性调频误差空变性,仿真选取的场景相较一般短程成像场景较大。在发射信号中加入非线性调频误差![]()
表1 仿真参数
Tab.1 Simulation Parameters

参数参数值脉冲宽度30 μs带宽4 GHz载频77 GHz信号采样频率160 MHz成像范围0 m~180 m
LFMCW雷达在AD采样过程中通常仅对所有信号重叠的部分进行采样,舍弃重叠部分外的信号。因此虽然发射信号为4 GHz带宽,但实际有效带宽比发射信号带宽小,在本次实验中实际接收信号有效带宽为3.84 GHz。在图5中给出了该操作的示意图,图中τmax为最远目标与雷达之间的时延。
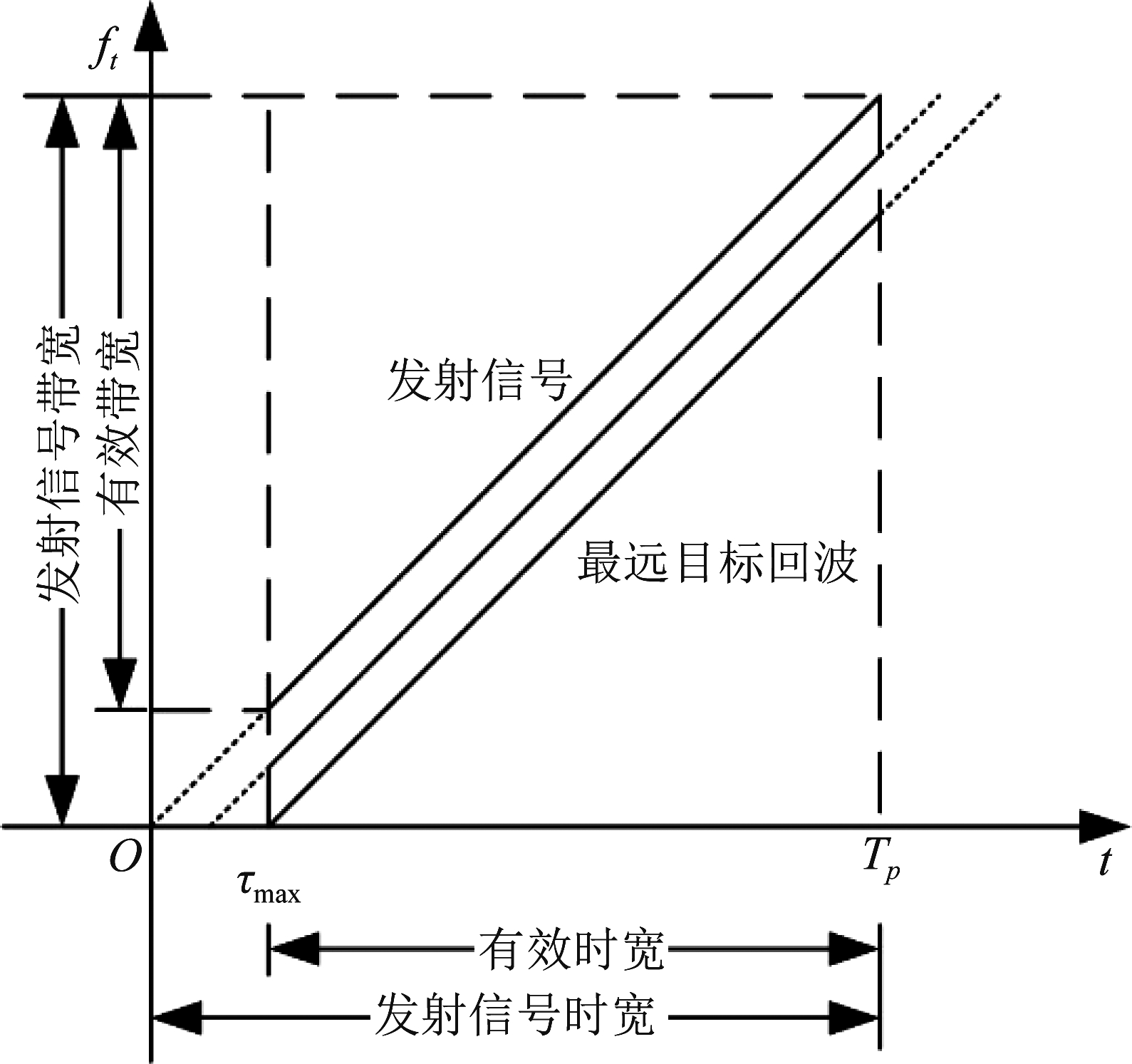
图5 LFMCW雷达信号有效带宽示意图
Fig.5 Schematic Diagram of LFMCW Radar Signal Effective Bandwidth
本文提出的频谱恢复校正法利用匹配滤波进行校正,匹配滤波器的设计是该方法的关键步骤,本实验利用上一节所提到的第二种方法,即将发射信号通过频谱恢复法来产生匹配滤波器的传递函数。该函数包络即相位如图6所示,通过新方法可以恢复出带宽约为3.84 GHz的信号频谱,该频谱的相位与频率成二次关系。
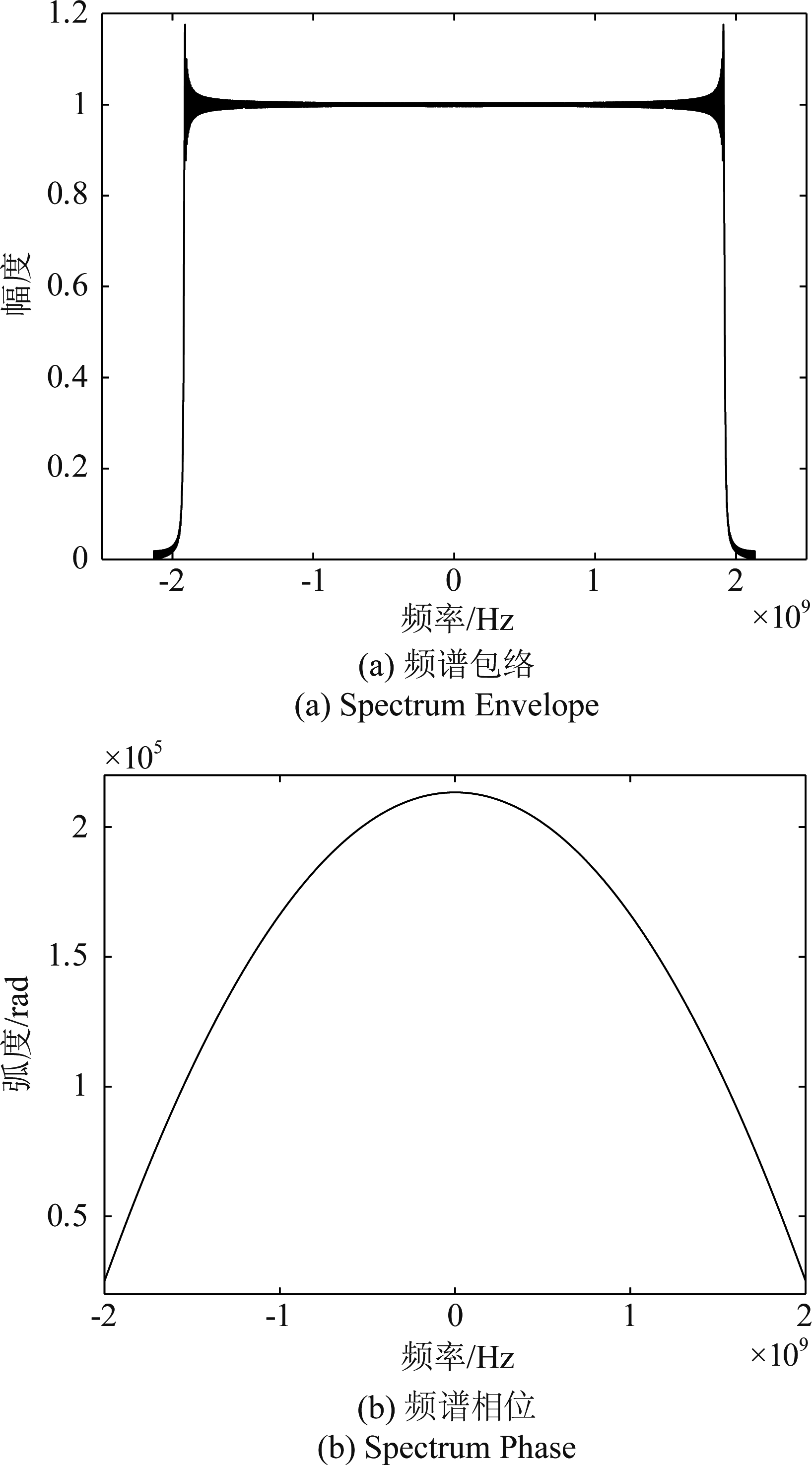
图6 新方法恢复得到的匹配滤波器频谱
Fig.6 The Matched Filter Restored by New Method
利用频谱恢复法进行校正第一步是去除发射信号的误差项并进行傅里叶变换,通过该操作得到的信号相位误差是非空变的。图7给出了此处的结果,此时所有目标的散焦程度相同。后续的步骤对该信号进行处理,这也从另一方面说明了为什么该方法能够统一地校正非线性调频误差。
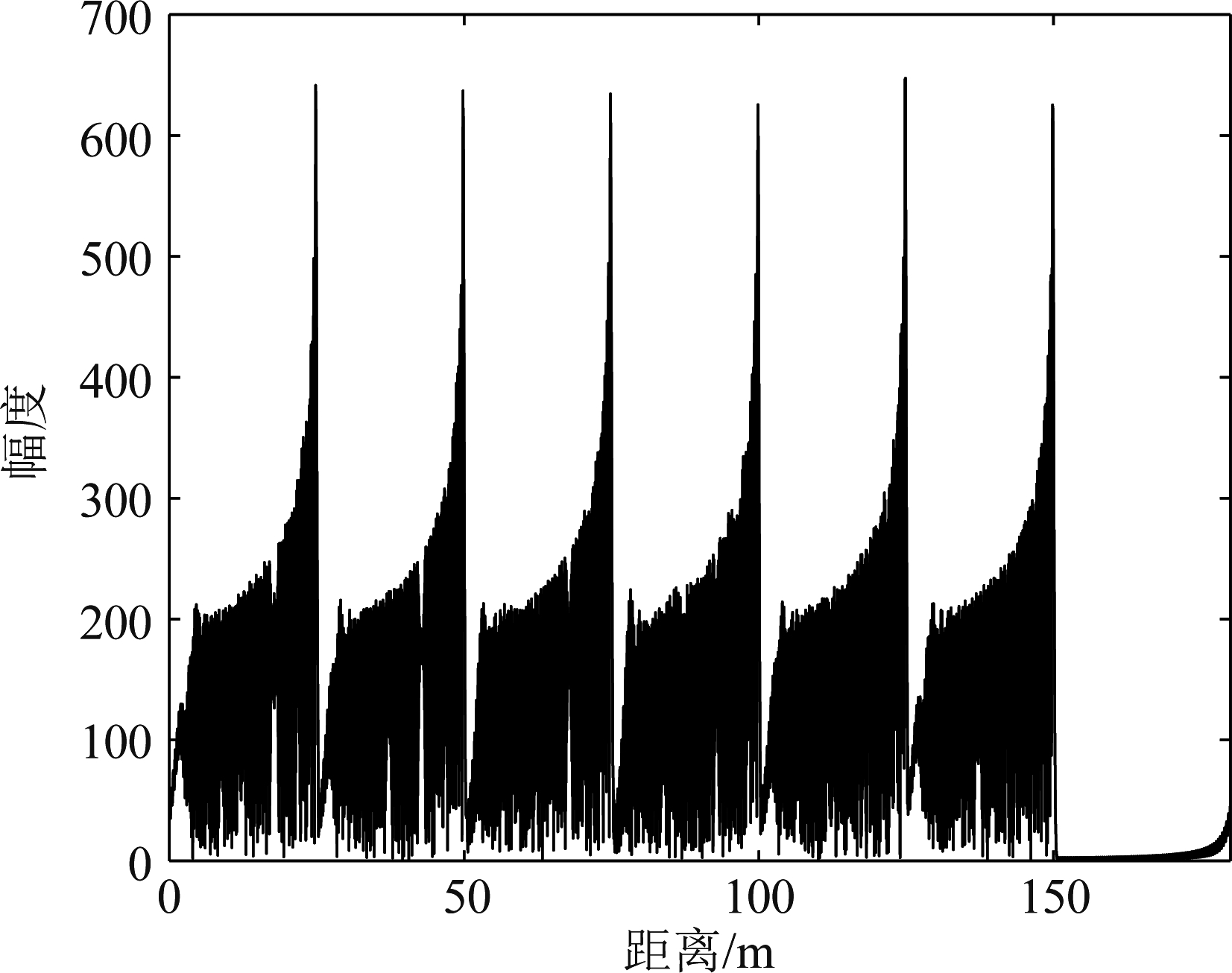
图7 去除发射信号误差相位后的结果
Fig.7 The Result after Removing the Transmitted Signal Error Phase
为了更加直观的体现本文提出的方法在非线性调频误差校正方面的优势,图8给出了三个成像结果,图8(a)为直接对差频信号进行傅里叶变换得到的脉冲压缩结果。由于非线性调频误差的影响,随着与雷达之间的距离增大,空变误差对信号脉压的影响越来越大。这些影响主要表现为峰值幅度降低,主瓣展宽以及成对旁瓣升高。
利用文献[16]中提出的重采样方法对误差进行校正,该方法在一定的假设条件下忽略了目标距离对相位误差的影响。图8(b)中可以看到,当与雷达距离较小时能够改善成像结果。但随着距离增大,校正效果逐渐变差甚至无法校正。
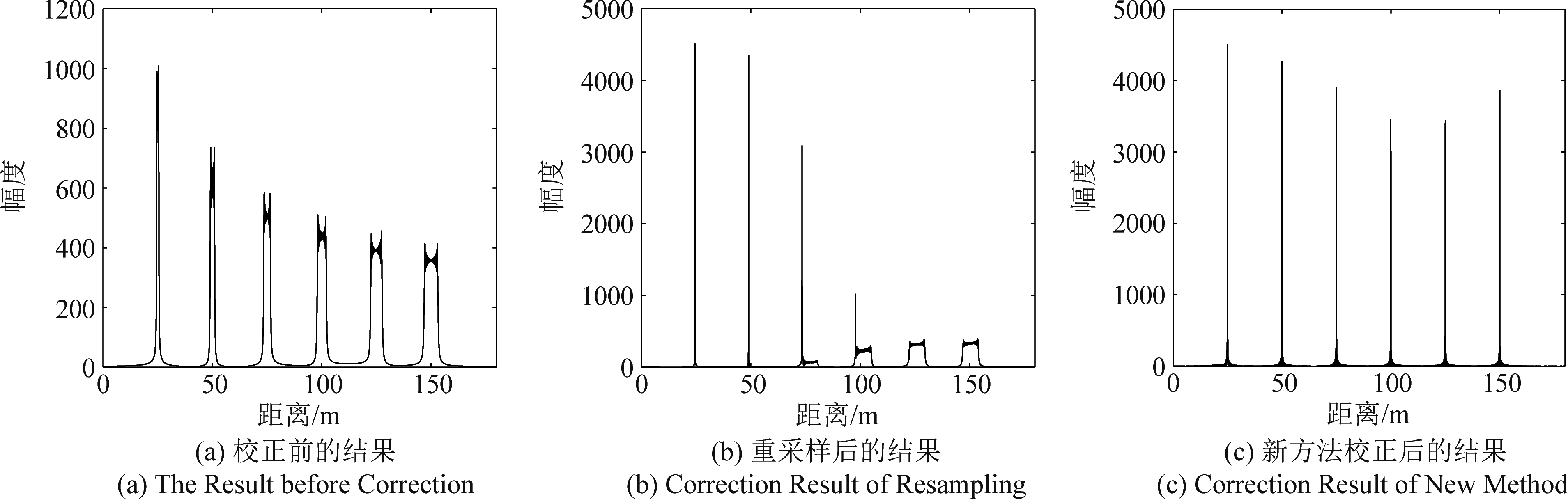
图8 成像结果
Fig.8 Imaging Results
频谱恢复法得到的校正结果如图8(c)所示,不同距离处的目标脉压结果与理想结果相近,主瓣展宽得到了抑制,峰值抬高,成对旁瓣消失。与图8(b)对比,可以说明该方法能够更加有效地校正线性调频误差。
为了进一步体现该方法的有效性,将图8中各个点目标成像结果放大如图9所示,其中虚线表示校正前的压缩结果,实线为频谱恢复法的校正结果,点线为重采样法的校正结果。图9(a)和(b)为50 m内的两个点目标校正效果,重采样法此时能够消除散焦现象,但是目标位置存在一定的偏移,这是由于其重采样规则导致的。随着距离增加,重采样的校正效果恶化,甚至比校正前的散焦程度更加严重。而频谱恢复法能够对所有点目标进行准确校正。
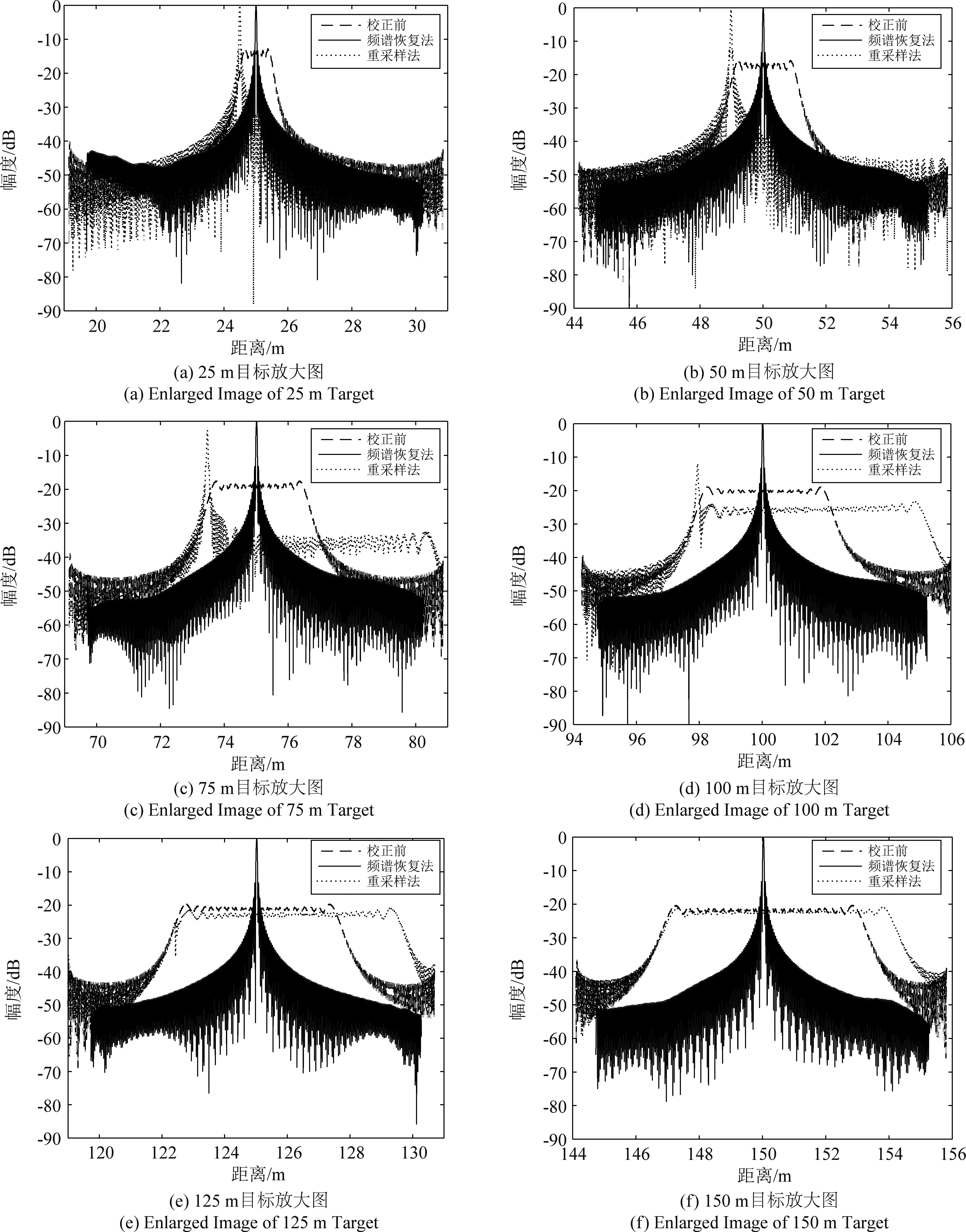
图9 各个点目标放大图
Fig.9 Enlarged View of Each Point Target
利用校正结果的峰值旁瓣比(Peak Side Lobe Ratio, PSLR)、积分旁瓣比(Integral Side Lobe Ratio,ISLR)和分辨率来评估新方法的校正效果,如表2所示。在该信号不加窗的情况下对应的理论分辨率为0.0346 m,峰值旁瓣比理论值的-13.26 dB,积分旁瓣比理论值为-9.80 dB。从表中结果可以看到,各项指标基本符合理论值。
表2 校正结果的PSLR、ISLR与分辨率
Tab.2 PSLR, ISLR and Resolution of the Correction Result
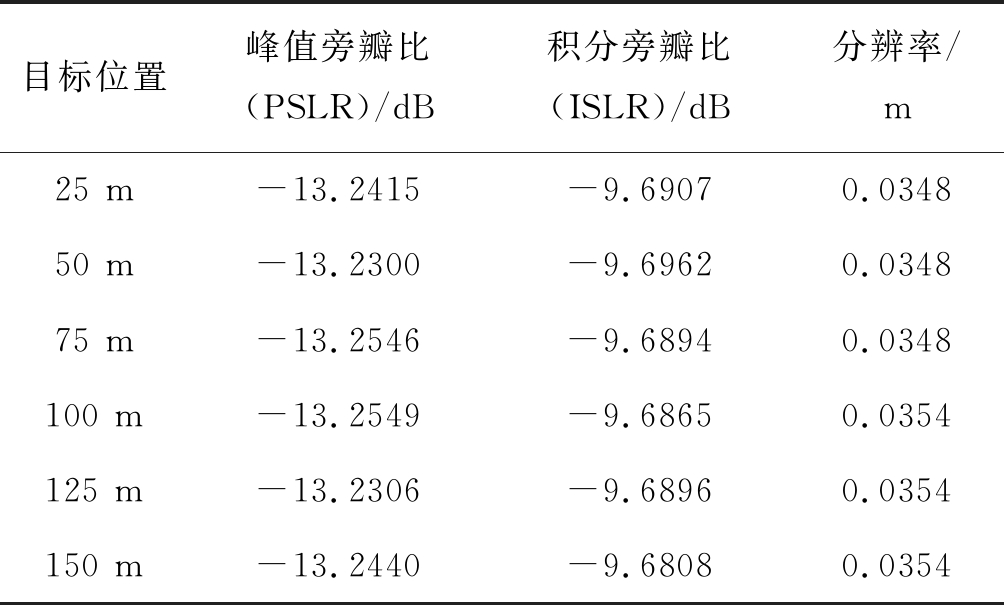
目标位置峰值旁瓣比(PSLR)/dB积分旁瓣比(ISLR)/dB分辨率/m25 m-13.2415-9.69070.034850 m-13.2300-9.69620.034875 m-13.2546-9.68940.0348100 m-13.2549-9.68650.0354125 m-13.2306-9.68960.0354150 m-13.2440-9.68080.0354
考虑到实际应用中不可避免的噪声干扰,通过仿真验证新方法的抗噪声性能。新方法是通过匹配滤波来实现脉冲压缩处理,因此在噪声环境下,新方法具有较强的鲁棒性。在前面实验中分别加入信噪比为-5 dB与-10 dB的高斯白噪声。图10展示了在加入信噪比为-5 dB的噪声时的压缩结果,校正前能够明显的观察到每个散焦目标的位置,新方法能够准确的校正各个目标。图11为加入信噪比为-10 dB的噪声的脉冲压缩结果,在大噪声环境下,校正前的严重散焦目标已经被噪声淹没,而新方法还能够准确的对误差进行校正。仿真结果说明,该方法存在较强的鲁棒性,在大噪声的环境下也可以得到较为准确的校正结果。
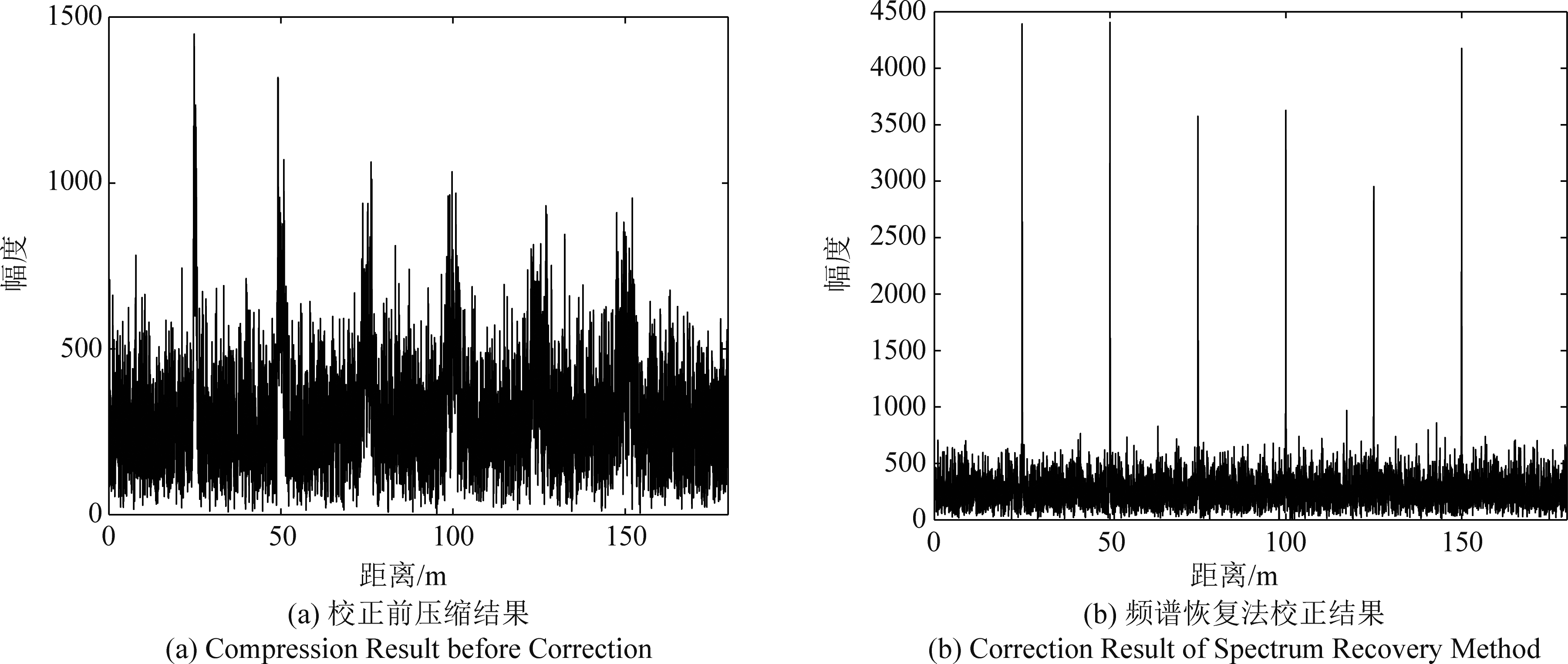
图10 处理结果(SNR=-5 dB)
Fig.10 Processing Result (SNR=-5 dB)
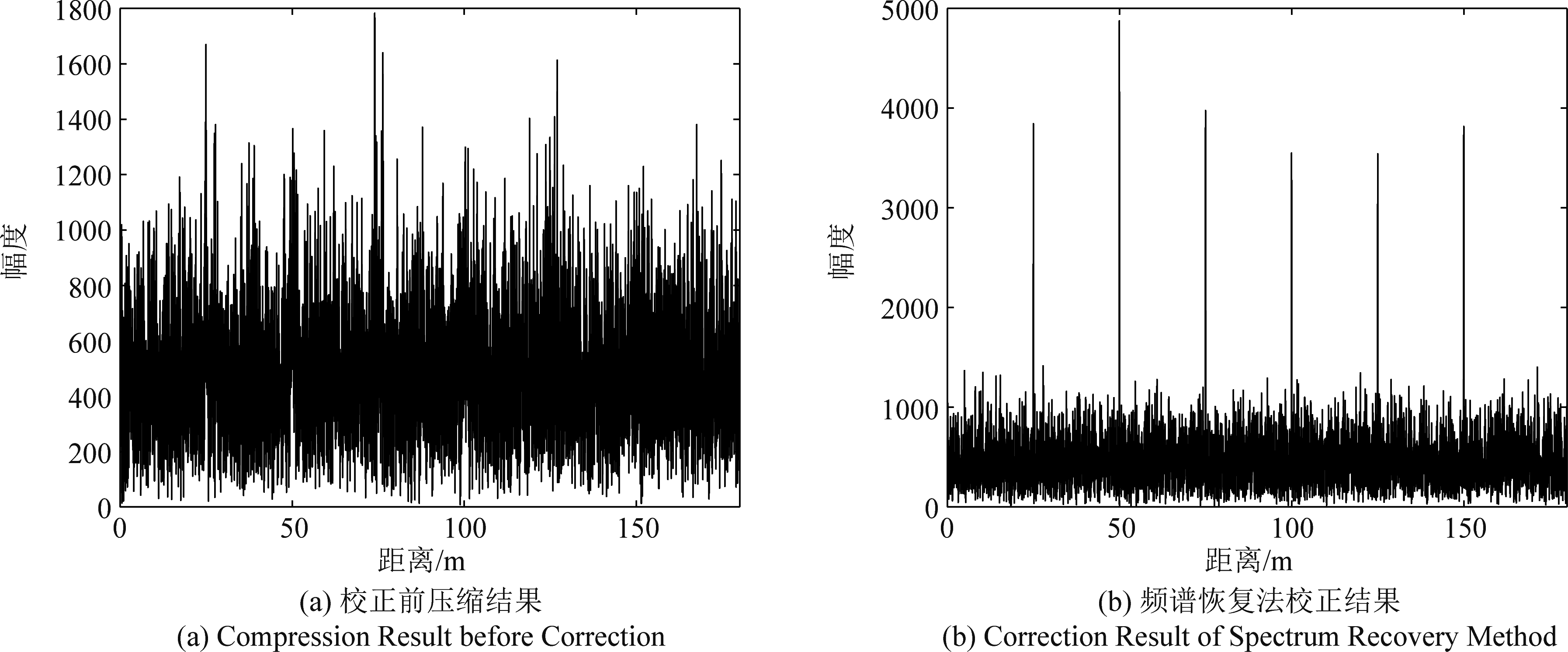
图11 处理结果(SNR=-10 dB)
Fig.11 Processing Result (SNR=-10 dB)
6 结论
本文针对LFMCW雷达信号调频非线性问题,提出了一种基于频谱恢复的误差估计与校正方案。主要结论如下:
(1)推导了匹配滤波与Dechirp两种脉冲压缩方式的等效原理,在LFMCW雷达采样率低的前提下,利用这种原理从低采样率的差频信号中恢复了发射信号以及目标回波的频谱。
(2)算法利用了信号波形不影响匹配滤波压缩结果的特点,有效地解决了Dechirp接收信号残留相位误差空变性的问题。算法可以统一地对不同位置目标进行校正。在保证校正精度的前提下提高了校正效率。
(3)算法使用了匹配滤波进行脉冲压缩,在大噪声的环境下也能够得到较好的成像效果。具有较好的鲁棒性。
本文所提方案在车载毫米波雷达等小目标近距离成像场合具有广泛的应用前景。
虽然如此,本文所提方法在误差较大的情况下,对于场景边缘的点目标误差校正存在一定的难度。场景边缘点目标由于非线性调频误差导致的主瓣展宽,可能会使得部分主瓣发生混叠现象,此时恢复出的频谱不再是该目标回波的频谱,导致方法失效。未来主要将对误差大小对场景边缘点的影响进行分析,通过在信号处理过程中适当提高采样率以扩大场景来保证所需场景内的点目标能够精确校正,信号处理过程中采样率如何设置是需要解决的关键问题。
[1] 曾维棋. 基于FMCW雷达的高精度测距定位算法研究与实现[D]. 成都: 电子科技大学, 2019: 1-2.
ZENG Weiqi. Research and implementation of high-precision ranging and positioning algorithm based on FMCW radar[D]. Chengdu: University of Electronic Science and Technology of China, 2019: 1-2.(in Chinese)
[2] ANGHEL A, VASILE G, CACOVEANU R, et al. Short-range wideband FMCW radar for millimetric displacement measurements[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(9): 5633-5642.
[3] 王世峰, 戴祥, 徐宁, 等. 无人驾驶汽车环境感知技术综述[J]. 长春理工大学学报(自然科学版), 2017, 40(1): 1- 6.
WANG Shifeng, DAI Xiang, XU Ning, et al. Overview on environment perception technology for unmanned ground vehicle[J]. Journal of Changchun University of Science and Technology (Natural Science Edition), 2017, 40(1): 1- 6.(in Chinese)
[4] 夏赛强, 向龙, 毛辉煌, 等. 两种脉冲压缩实现方式对微动目标回波影响的研究[J]. 空军预警学院学报, 2017, 31(6): 407- 412.
XIA Saiqiang, XIANG Long, MAO Huihuang, et al. Effect of two pulse compression approaches on micro-motion target[J]. Journal of Air Force Early Warning Academy, 2017, 31(6): 407- 412.(in Chinese)
[5] 单文秋. 车载毫米波雷达前视成像系统研究[D]. 呼和浩特: 内蒙古工业大学, 2018: 2-3.
SHAN Wenqiu. Study on vehicle-mounted millimeter wave radar forward looking imaging system[D]. Hohhot: Inner Mongolia University of Technology, 2018: 2-3.(in Chinese)
[6] 李名玮. 调频连续波雷达射频前端的设计与实现[D]. 西安: 西安电子科技大学, 2018: 1-3.
LI Mingwei. Design and implementation of radio frequency front-end of frequency modulated continuous wave radar[D]. Xi’an: Xidian University, 2018: 1-3.(in Chinese)
[7] 曲长文, 王颖, 苏峰, 等. LFMCWSAR非线性校正成像方法研究[J]. 中国电子科学研究院学报, 2009, 4(1): 50-53.
QU Changwen, WANG Ying, SU Feng, et al. Research on nonlinearity correction imaging method of LFMCW SAR[J]. Journal of China Academy of Electronics and Information Technology, 2009, 4(1): 50-53.(in Chinese)
[8] 齐艳丽, 赖涛, 赵拥军, 等. 短程宽带FMCW雷达信号非线性校正方法研究[J]. 信号处理, 2016, 32(5): 590-597.
QI Yanli, LAI Tao, ZHAO Yongjun, et al. Research on nonlinearity correction of short-range wideband FMCW radar signal[J]. Journal of Signal Processing, 2016, 32(5): 590-597.(in Chinese)
[9] 刘志强. 高性能微波频率源与毫米波FMCW射频前端关键技术研究[D]. 南京: 东南大学, 2019: 53-76.
LIU Zhiqiang. Research on key technology of high performance microwave frequency synthesizer and millimeter wave FMCW RF front-end[D]. Nanjing: Southeast University, 2019: 53-76.(in Chinese)
[10]申江江, 何勰, 于志军, 等. LFMCW雷达频率源扫频线性度与距离分辨率研究[J]. 兵器装备工程学报, 2020, 41(11): 95-99.
SHEN Jiangjiang, HE Xie, YU Zhijun, et al. Analysis of frequency sweep linearity error and range resolution of LFMCW radar[J]. Journal of Ordnance Equipment Engineering, 2020, 41(11): 95-99.(in Chinese)
[11]赵志勇, 常文革, 黎向阳, 等. 去调频处理中空变相位误差补偿方法[J]. 国防科技大学学报, 2014, 36(3): 169-176.
ZHAO Zhiyong, CHANG Wenge, LI Xiangyang, et al. Range-dependent phase error compensation of dechirp[J]. Journal of National University of Defense Technology, 2014, 36(3): 169-176.(in Chinese)
[12]META A, HOOGEBOOM P, LIGTHART L P. Signal processing for FMCW SAR[J]. IEEE Transactions on Geoscience and Remote Sensing, 2007, 45(11): 3519-3532.
[13]ANGHEL A, VASILE G, CACOVEANU R, et al. FMCW transceiver wideband sweep nonlinearity software correction[C]∥2013 IEEE Radar Conference (RadarCon13). Ottawa, ON, Canada. IEEE, 2013: 1-5.
[14]VOSSIEK M, HEIDE P, NALEZINSKI M, et al. Novel FMCW radar system concept with adaptive compensation of phase errors[C]∥1996 26th European Microwave Conference. Prague, Czech Republic. IEEE, 1996: 135-139.
[15]ZHANG Yixiong, HONG Rujia, PAN Pingping, et al. Frequency-domain range sidelobe correction in stretch processing for wideband LFM radars[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(1): 111-121.
[16]SCHEIBLHOFER S, SCHUSTER S, STELZER A. Signal model and linearization for nonlinear chirps in FMCW Radar SAW-ID tag request[J]. IEEE Transactions on Microwave Theory and Techniques, 2006, 54(4): 1477-1483.
[17]LIU Jiafang, ZHANG Yunhua, DONG Xiao. Dechirping compression method for nonlinear frequency modulation waveforms[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(3): 377-381.
[18]金丽花. 斜视聚束合成孔径雷达成像算法研究[D]. 上海: 上海交通大学, 2008: 18-19.
JIN Lihua. Study on the imaging algorithm of squint spotlight synthetic aperture radar[D]. Shanghai: Shanghai Jiaotong University, 2008: 18-19.(in Chinese)
[19]保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 25-26.
BAO Zheng, XING Mengdao, WANG Tong. Radar imaging technology[M]. Beijing: Publishing House of Electronics Industry, 2005: 25-26. (in Chinese)
[20]张立志, 汪学刚, 向敬成. 调频线性度与FMCW雷达距离分辨力的关系[J]. 信号处理, 1999, 15(S1): 3-5.
ZHANG Lizhi, WANG Xuegang, XIANG Jingcheng. The relationship between FM linearity and range resolution in FMCW radar[J]. Signal Processing, 1999, 15(S1): 3-5. (in Chinese)



