1 引言
线性调频(Linear frequency modulated, LFM)信号又称Chirp信号,是信号处理领域中常用的信号形式,在雷达、声呐等探测系统中,均得到广泛应用[1]。面对日益复杂的任务需求,探测系统通常使用宽带的LFM信号以保证其优越的性能。但信号带宽的拓展,使得信号频率提高,在Nyquist采样定理下,探测系统前端的A/D转换器需要工作在较高的频率以保证采样过程不造成信息丢失。同时,采样频率的提高,将会产生大量的数据信息,从而增加探测系统数据存储及传输压力。
压缩感知理论的提出为宽带LFM信号的采集提供了新的思路[2]。在压缩感知理论下,信号的采集过程取决于信号本身的信息量,相较于Nyquist采样定理,压缩感知理论可以在信号采集的同时直接实现信号的压缩,有效降低信号的采样频率与采样点数,进而缓解数据的存储与传输压力。鉴于压缩感知理论在信号采集过程中体现的巨大优势,国内外众多学者对基于压缩感知理论的模拟信息转换(Analog-to-Information Conversion, AIC)系统展开了研究。比较成熟的系统包括调制宽带转换器(Modulated Wideband Converter, MWC)[3]以及随机解调器(Random Demodulator, RD)[4]。MWC系统通过将不同频率切片合入基带,使得信号能够在基带内以较低的频率进行采样。基于MWC系统,文献[5]研究了宽带LFM信号的数字接收以及参数识别算法,有效降低了接收机的采样频率以及采样点数。文献[6]将短时傅里叶变换应用到MWC系统中,通过加窗MWC获得对LFM信号的调频率估计,再利用经典MWC系统对去调频后的信号完成压缩采样过程。但是当LFM信号具有多分量或占据两多个子带时,上述方法均存在采样通道增加,采样系统复杂等问题。相比于MWC系统,RD系统结构较为简单,能够通过单通道的方式实现信号的压缩采样,因而得到广泛的应用。基于RD系统,文献[7]提出了分段积分型RD系统实现雷达回波LFM信号的采样,并通过构造波形延时字典,保证原始信号的精确重构,但分段积分型RD系统改变了传统RD系统单通道的结构特性,一定程度上增加了系统构造复杂度,同时,波形时延字典需要较多的LFM信号先验信息,并易受噪声干扰。针对字典构造问题,文献[8]提出了基于分数阶离散傅里叶正交字典的LFM信号压缩感知重构,该方法利用传统RD系统完成压缩采样过程,并利用信号在分数阶傅里叶变换下的稀疏性完成重构,取得了良好效果。
分数阶傅里叶变换能够介于时域和频域之间多视角地分析和处理信号。频域连续的LFM信号在分数阶傅里叶变换下能够表现为一种冲激形式,从而呈现出良好的稀疏性。分数阶傅里叶逆变换,则为原始信号的精确重构提供了理论支撑。目前,在基于分数阶傅里叶变换的信号压缩感知中,分数阶傅里叶变换主要用于稀疏字典的构造,而模拟信息转换过程则采用RD系统[8]。但离散的分数阶傅里叶正交字典构造过程相对复杂,一定程度上增加了LFM信号的重构过程复杂度。针对这一问题,本文从模拟信息转换系统设计的角度出发,提出了一种基于α-随机解调器的LFM信号模拟信息转换方法。一方面,该方法保留了传统RD系统单通道的工作方式,具有传统RD系统结构简单的特点,另一方面,通过改进通道内基本结构,该方法避免了重构阶段分数阶离散傅里叶正交字典复杂的构造过程,在保证原始信号准确重构的同时,能够有效降低重构过程的复杂度。
2 基本理论
2.1 分数阶傅里叶变换
分数阶傅里叶变换(Fractional Fourier transform, FrFT)[9]是一种广义的傅里叶变换,对于给定的信号x(t),其FrFT可以表示为:
Xα(u)=![]() Kα(t,u)x(t)dt
Kα(t,u)x(t)dt
(1)
Kα(u,t)为FrFT核函数,定义为:
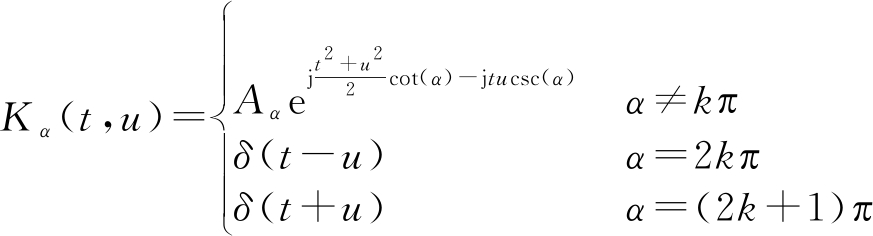
(2)
式中,α为FrFT旋转角,![]() 表示整数域。
表示整数域。
FrFT逆变换可以表示为:
(3)
式中(·)*为共轭运算。
假设LFM信号中包含了K个不同中心频率的信号成分,则信号模型为:
(4)
其中fi,Ai分别为第i个成分的中心频率以及幅度,k为调频率。当旋转角度α满足α=-arccot(2π·k)时,LFM信号在u=2πfisin(α)处表现为冲激函数。
2.2 传统的随机解调器
为将压缩感知应用到模拟信号的压缩采样当中,国内外学者对基于压缩感知理论的模拟信息转换系统展开了广泛研究[10-11]。其中,RD系统的结构较为简单,易于硬件实现,具有广阔的应用前景[12-13]。RD系统结构如图1所示。

图1 RD系统模型
Fig.1 Schematic diagram for RD system
信号pc(t)为具有伪随机性的连续信号,其表达式为:
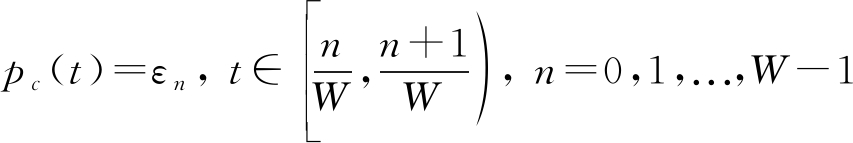
(5)
式中W为Nyquist频率,εn以等概率取自±1。RD系统针对的是多音信号,并不适用于本文LFM信号。为此,本文提出了基于α-随机解调器(α-Random Demodulator, α-RD)的LFM信号模拟信息转换方法。
3 基于α-随机解调器的模拟信息转换方法
3.1 α-随机解调器系统描述
本文所提的α-RD系统模型如图2所示,与传统RD相比,本文所提α-RD系统包含两个乘法器。经过两次乘法器后的信号y(t)可以表示为
(6)
式中![]()
积分器和采集器一方面实现对信号y(t)的采样,另一方面具有低通抗混叠的作用。经过采集器采集后,离散的采样序列y[m]可以表示为:
(7)
α-RD系统采样频率为R,远远低于Nyquist频率W,而采样频率的降低也使得采样点数显著减少,因此α-RD系统保留了传统RD系统在采样点数以及采样频率方面所具有的优势。
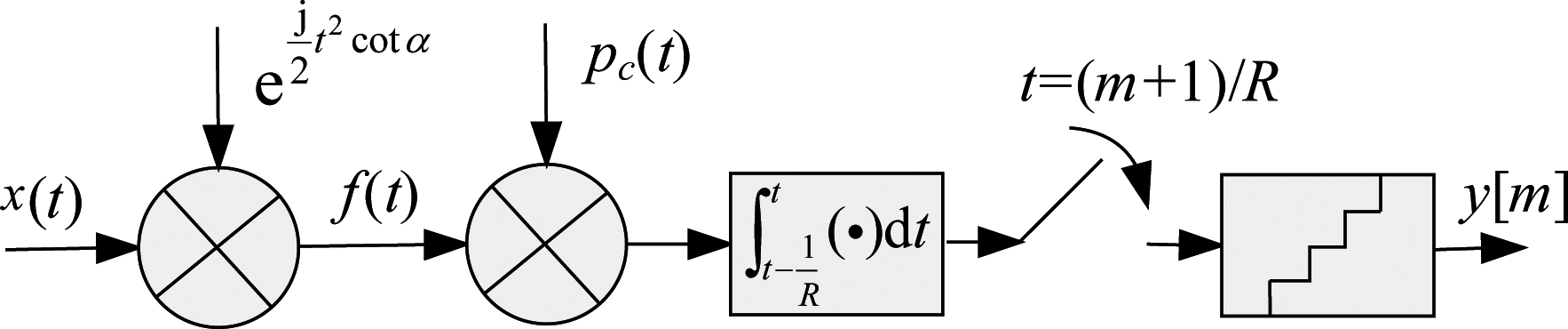
图2 α-RD系统模型
Fig.2 Schematic diagram for α-RD system
3.2 α-随机解调器工作原理
对于时域t∈[0,1)的LFM信号,分数阶傅里叶变换可表示成级数[14]形式:
(8)
其中,Z∈{0,±1,±2,...,±(W/2-1),W/2}为K个整数的集合,系数an′为:
(9)
考虑到pc(t)信号特点,对图2中的信号f(t)在1/W的时间段内取积分。假设tn=n/W, fn为信号f(t)在时间间隔[tn, tn+1/W)内的积分,则fn可以表示为:
(10)
将式(8)带入,可得:
fn=![]()
![]()
![]()
(11)
其中,bn′可以表示为:
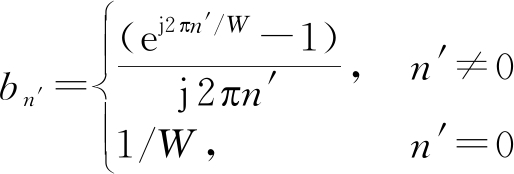
(12)
令![]() 则式(11)可以表达为:
则式(11)可以表达为:
(13)
定义向量f=[fn]n=0,1,2,...,W-1,向量s=![]() 以及标准正交的离散傅里叶矩阵
以及标准正交的离散傅里叶矩阵![]() 则式(13)可以表达成矩阵形式:
则式(13)可以表达成矩阵形式:
f=Es
(14)
由于pc(t)以Nyquist速率(即W)在±1之间随机切换,因此信号y(t)的离散时间表示为:
yn=εnfn
(15)
在1/R的时间段内对yn进行求和,得到采样序列y[m]:
y=HDf
(16)
其中,y是由采样序列y[m]构成的向量,m=0,1,...,R-1。H为R×W维矩阵,矩阵中第m行元素从第mW/R+1开始有连续W/R个1,其余为0。D为W×W的对角阵:
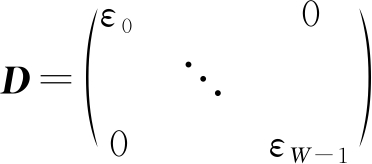
(17)
对于向量s中的元素sn′,当an′=0时,sn′=0。因此,原始信号在分数阶傅里叶变换下的稀疏性,决定了向量s的稀疏性。此时,经过压缩采样后,稀疏向量s的重构模型可以表示为[15]:
(18)
式中Θ=HDE,||·||0为l0范数。该重构问题可利用优化算法求解,本文中采用了快速迭代收缩阈值算法(fast iterative shrinkage-thresholding algorithm, FISTA)[16]。
构造对角矩阵![]() 以及向量a=[an′]n′=0,±1,±2,...,±(W/2-1),W/2,由于对角阵B可逆,因此;
以及向量a=[an′]n′=0,±1,±2,...,±(W/2-1),W/2,由于对角阵B可逆,因此;
a=B-1s
(19)
则原始信号x(t)可通过式(8)得到精确重构。
4 实验与分析
4.1 仿真LFM信号
为验证α-RD系统压缩采样以及重构效果,进行LFM信号的仿真实验。仿真信号由式(4)产生,调频率为k=-500 MHz/μs,信号持续时间t∈[0,1 μs),Nyquist频率设置为1000 MHz。实验中仿真信号为复数形式,图3(a)、(b)给出了仿真信号实部波形,信号中心频率个数分别为2、4,中心频率分别为{250 MHz,450 MHz}、{100 MHz,200 MHz,300 MHz,400 MHz}。两种信号的傅里叶变换以及分数阶傅里叶变换如图3(c)~( f )。可以看出,LFM信号在傅里叶变换下并不具有稀疏性,但是在分数阶傅里叶变换下却具有良好的稀疏性,图3(e)、( f )中两种信号的稀疏度分别为K=2以及K=4。
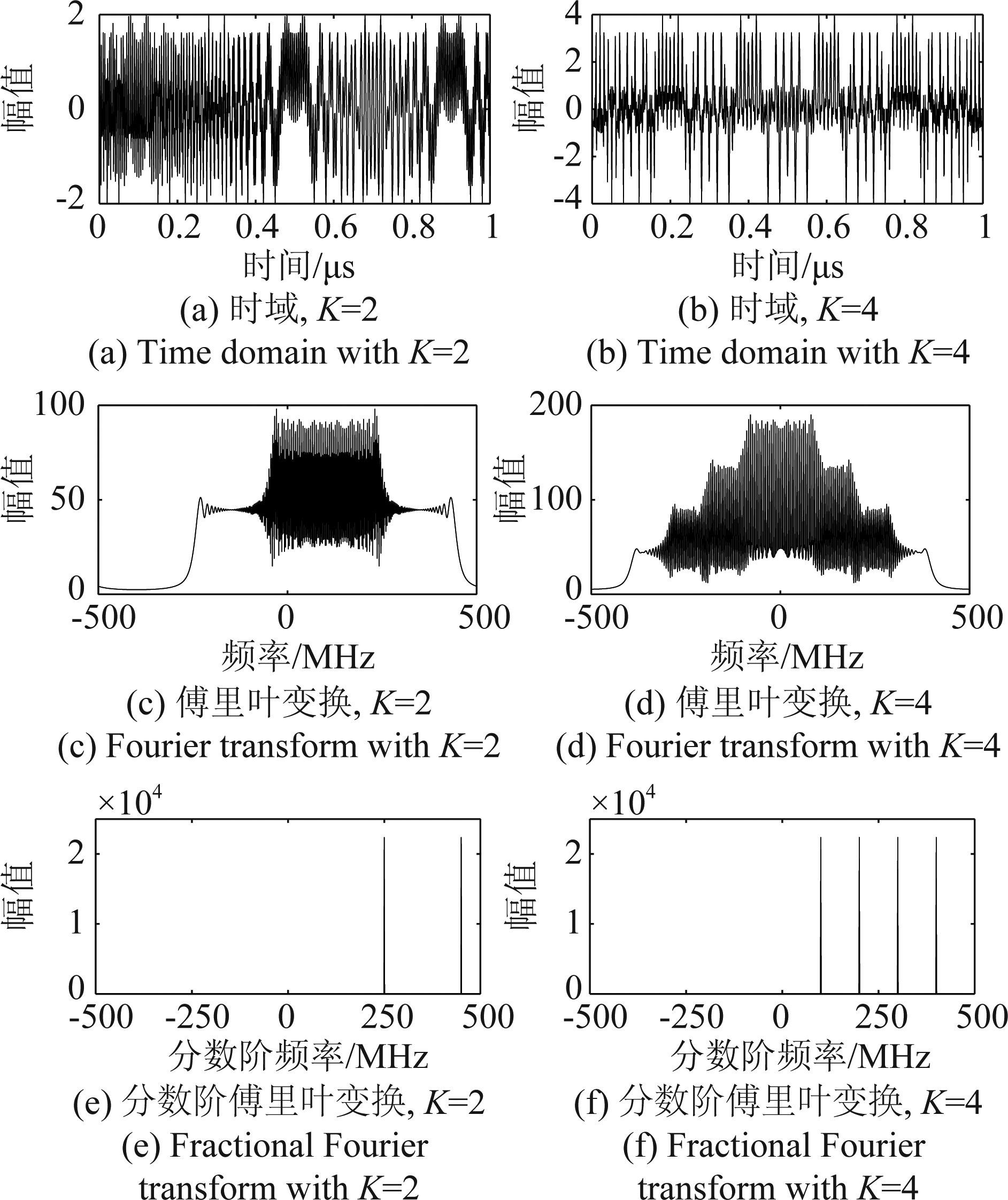
图3 仿真信号
Fig.3 Simulated signals
4.2 模拟信息转换及信号重构
利用α-RD系统对上述LFM信号进行压缩采样,并利用采样后的信号进行原始信号的重构。重构过程中分别采用了以下几种算法:
(1)FISTA;
(2)ISTA;
(3)正交匹配追踪(Orthogonal Matching Pursuit, OMP)[17];
(4)压缩传感匹配追踪(Compressive Sampling Matching Pursuit, CoSaMP)[18]。
利用相对误差(Relative Error, RE)衡量重构效果,其计算公式为:
(20)
要保证高概率的信号重构,α-RD系统采样速率R必须满足一定的条件。不同R值条件下,信号的重构概率如图4所示。每个R值进行200次蒙特卡洛仿真实验,当重构相对误差低于0.1时,认为信号得到准确重构。
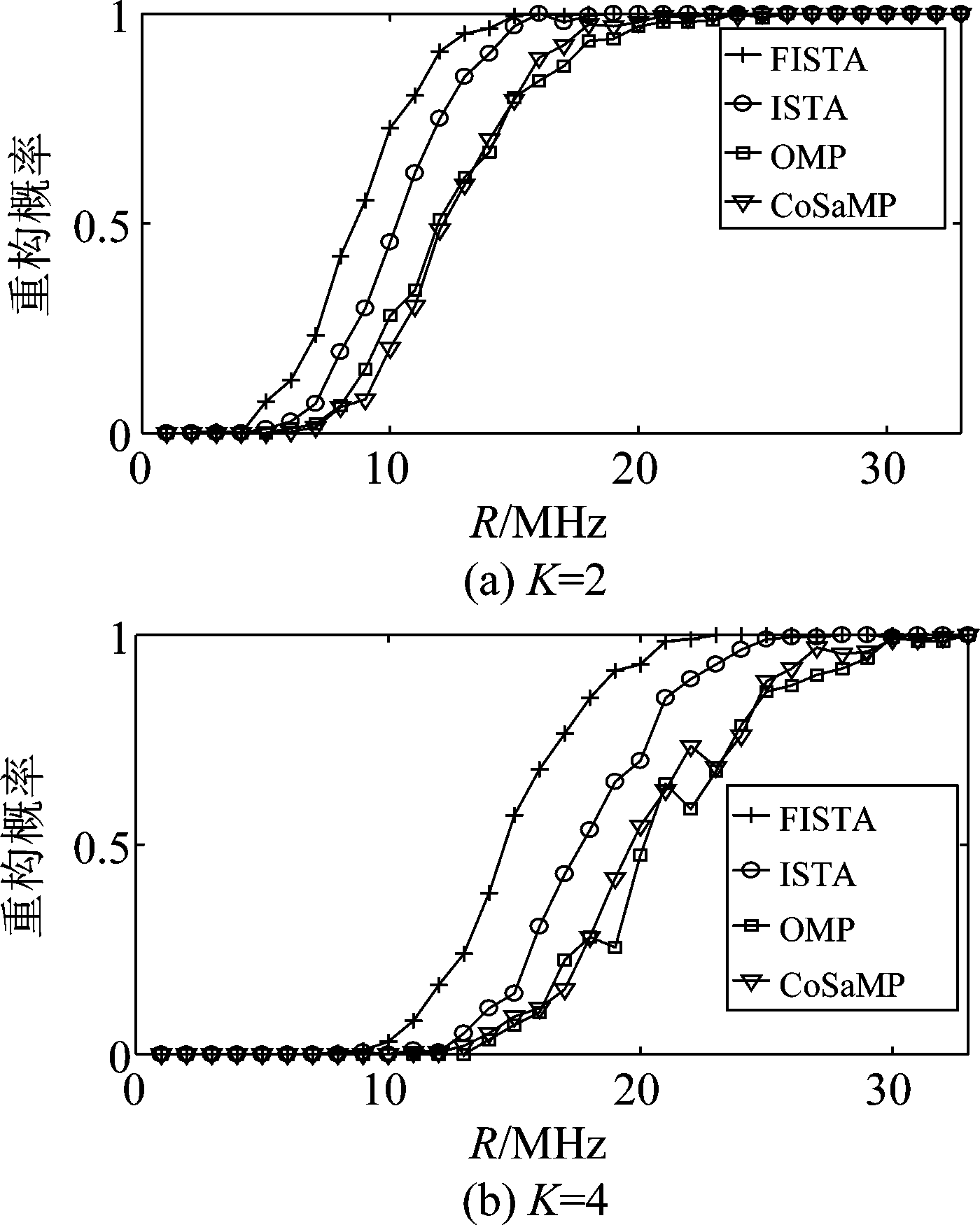
图4 重构概率
Fig.4 Reconstruction probability
对比四种不同重构算法,可以看出,OMP与CoSaMP重构效果相似,FISTA、ISTA的重构效果要明显好于OMP与CoSaMP,而FISTA重构效果最佳。一方面,FISTA能够有效降低α-RD系统的最低工作频域,在要求重构概率高于90%的条件下,FISTA所需要的最低R值低于ISTA、OMP与CoSaMP。另一方面,在采样不充分的条件下,FISTA重构概率要高于其他算法。例如,在图(a)中,当4 MHz<R<16 MHz时,FISTA重构概率要高于其他三种算法。因此,FISTA更适合用于α-RD系统的原始信号重构。
4.3 不同采样方法对比
为进一步验证本文模拟信息转换方法的有效性,引入不同采样方法进行对比实验,分析不同采样方法下LFM信号的采样与重构效果。对比方法包括:
(1)Nyquist采样;
(2)传统RD模拟信息转换;
(3)传统RD模拟信息转换+分数阶傅里叶字典;
(4)本文α-RD模拟信息转换。
方法(2)、(3)、(4)均为模拟信息转换方法,方法(3)采样文献[8]所提方案。在对比实验中,方法(2)、(3)、(4)中压缩采样系统采样频率均设置为50 MHz。重构信号时域波形如图5、图6所示,表1中则给出了不同采样方法的性能对比。其中,信号1、2的稀疏度分别为K=2,K=4,Nyquist采样方法的重构误差忽略不计。
表1 采样与重构效果对比
Tab.1 Comparison for sampling and reconstruction
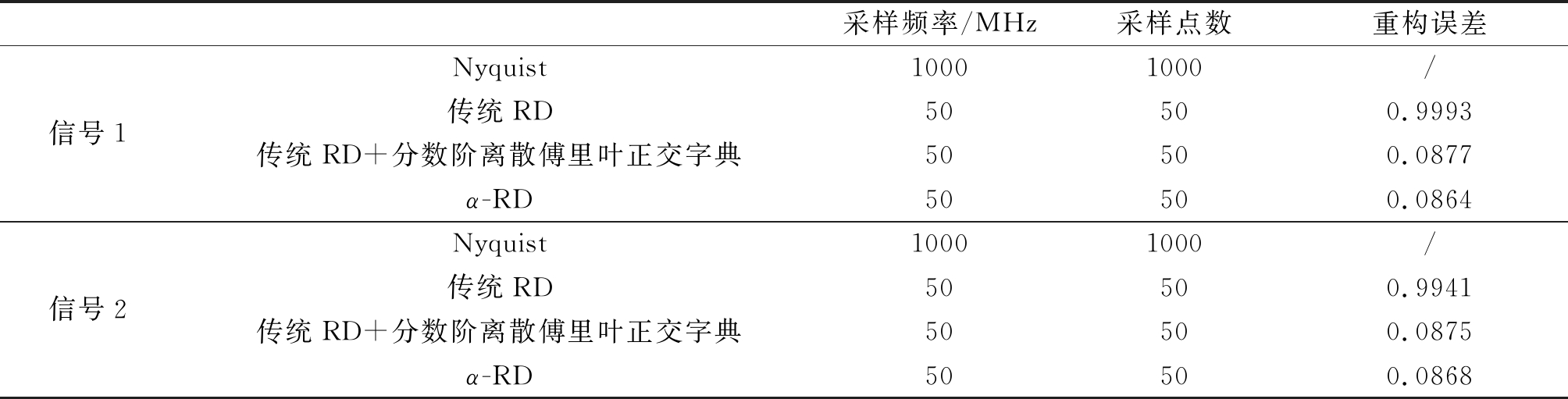
采样频率/MHz采样点数重构误差信号1Nyquist10001000/传统RD50500.9993传统RD+分数阶离散傅里叶正交字典50500.0877α-RD50500.0864信号2Nyquist10001000/传统RD50500.9941传统RD+分数阶离散傅里叶正交字典50500.0875α-RD50500.0868
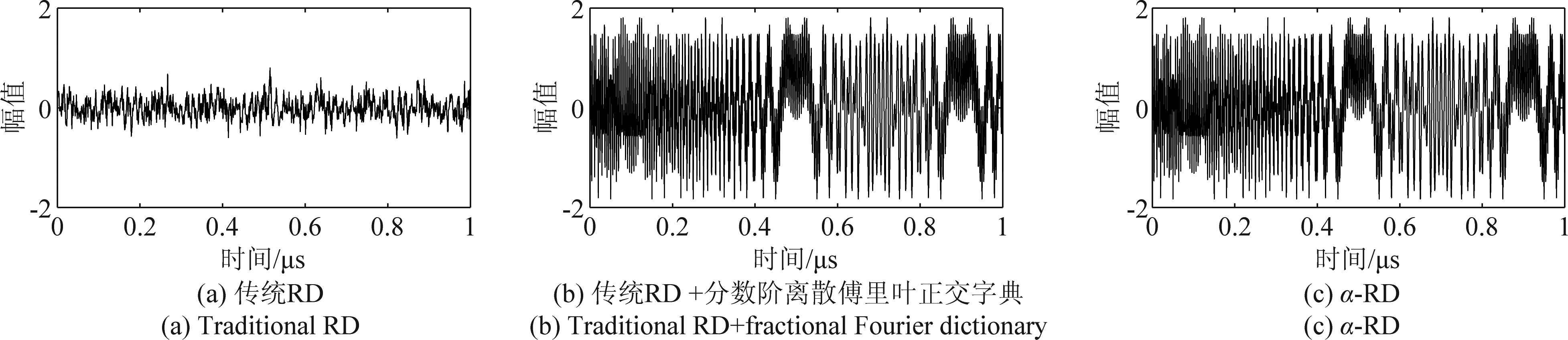
图5 信号1的重构效果对比
Fig.5 Comparison of reconstruction for signal 1
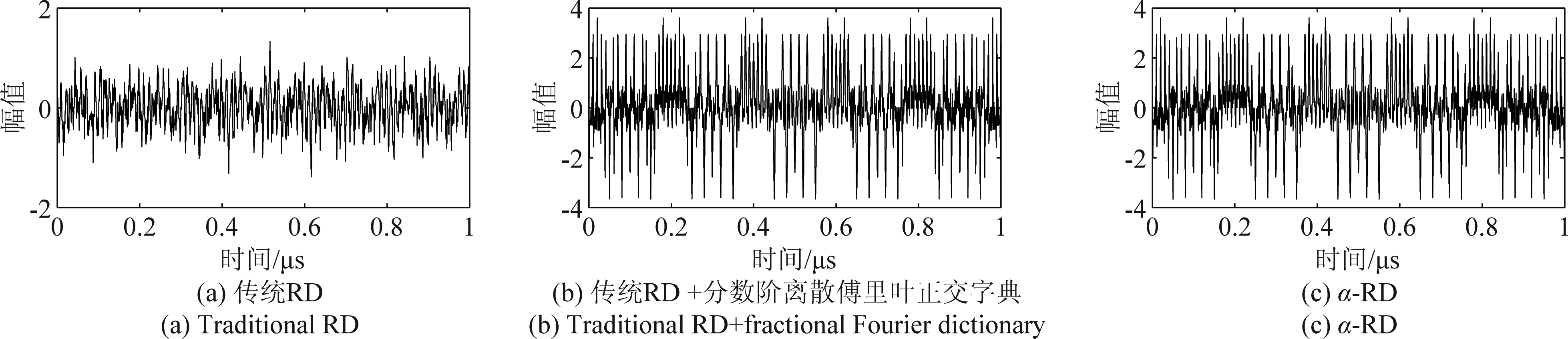
图6 信号2的重构效果对比
Fig.6 Comparison of reconstruction for signal 2
在采样效果上,三种模拟信息转换方法的采样频率远远低于Nyquist采样方法。对比三种模拟信息转换方法,方法(2)的重构效果较差,在图5、图6中的重构波形均产生明显失真。分析其原因,主要是因为传统RD系统的信号重构过程依赖于原始信号在频域所具有的稀疏性。本文所研究的LFM信号频域稀疏性较差,因此在传统RD模拟信息转换方法下,信号不能得到有效重构。
方法(3)与方法(4)的重构效果相近,表1中两种方法的重构误差均低于0.1,在图5、图6中两种方法下的重构波形未发生明显失真。这两种方法本质上均利用了原始信号在分数阶傅里叶域的稀疏性来进行重构,而LFM信号在该变换下具有良好的稀疏性,因此信号得到有效重构。
与传统RD模拟信息转换方法相比,方法(3)中的分数阶离散傅里叶正交字典的构造过程相对复杂,并且复杂度随着信号长度的增加而不断增加,因此当要求重构信号维度较高时,方法(3)并不适用。而本文所提的方法(4)则能够有效改善这一问题。本文方法中重构阶段采用了与传统RD系统相同的离散傅里叶正交字典,假设重构信号维度为N,离散傅里叶与分数阶离散傅里叶正交字典的构造计算量如表2所示。从表中可以看出,在字典构造过程中,分数阶离散傅里叶正交字典的乘法运算量是离散傅里叶正交字典的三倍,同时额外增加了2N2次加法运算。
为进一步分析不同字典对计算复杂度的影响,图7给出了分数阶离散傅里叶正交字典以及离散傅里叶正交字典在不同重构信号维度下,字典构造的时间消耗对比。从图中可以看出,随着信号维度的增加,字典构造时间消耗不断增加,对比两种字典,可以看出,离散傅里叶正交字典的时间消耗要明显低于分数阶离散傅里叶正交字典,并且重构信号维度越高,差别越明显。因此本文方法重构过程中的字典构造复杂度更低,更适合进行高维信号的重构。
表2 字典构造计算量对比
Tab.2 Computational comparison for dictionary construction

加法运算乘法运算指数运算离散傅里叶正交字典/N2N2分数阶离散傅里叶正交字典2N23N2N2
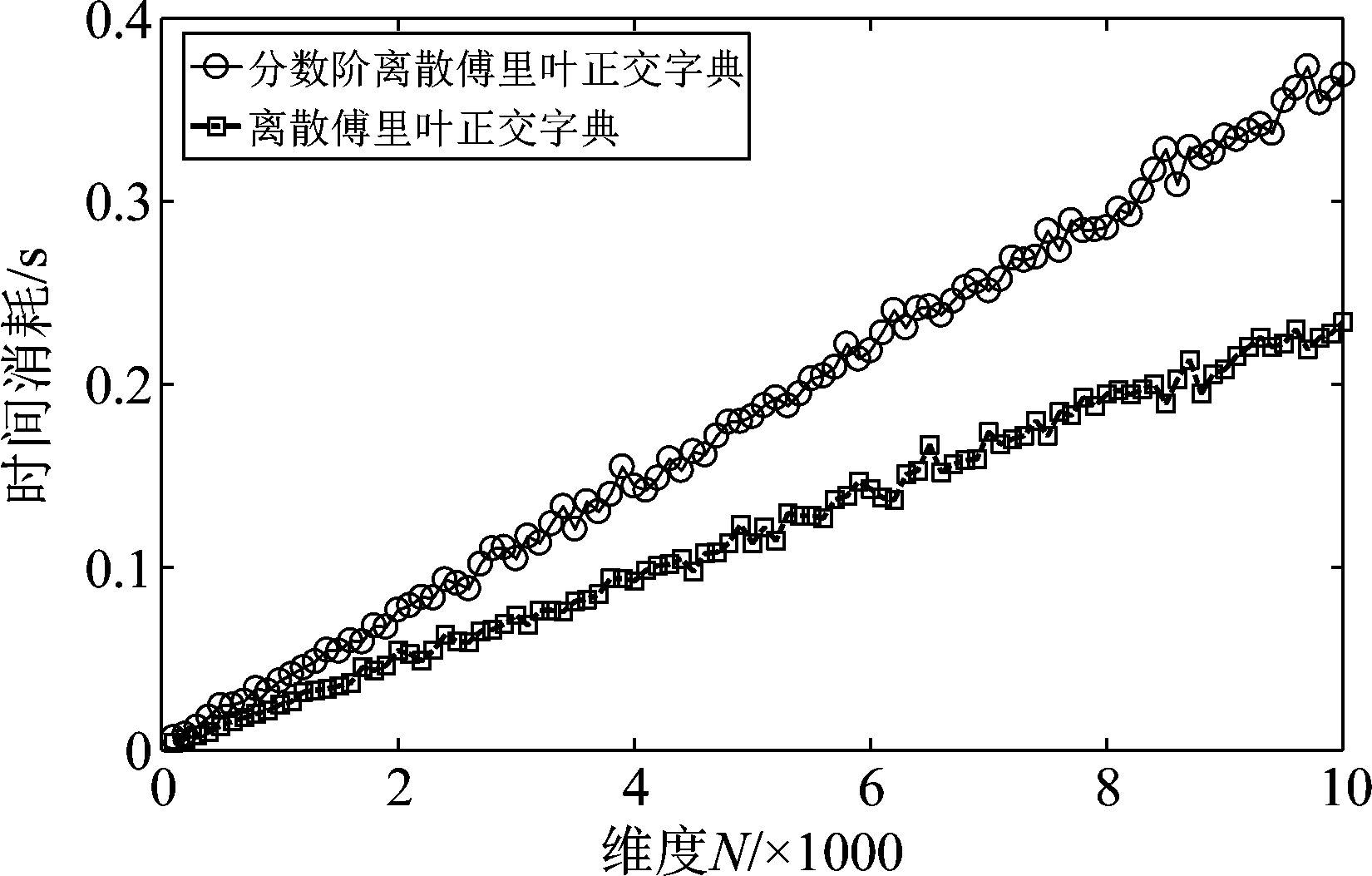
图7 时间消耗对比
Fig.7 Comparison of time consumption
4.4 实测信号分析
为进一步验证本文压缩采样系统性能,利用实测的LFM信号进行压缩采样与重构仿真实验。LFM信号发生与采集设备如图8所示。图中同一个机箱内安装有M9381A以及M9391A两套PXI设备。M9381A矢量信号发生器作为信号源,用来产生LFM信号,M9391A矢量信号分析仪通过线接线与M9381A连接,用来接收LFM信号。软件系统中, M9381A SFP用来完成对LFM信号的参数设置,89600 VSA用来记录M9391A中采集到的信号,并对采集到的信号进行基本的频谱分析。

图8 M9381A矢量信号发生器以及M9391A矢量信号分析仪
Fig.8 M9381A vector signal generator and M9391A vector signal analyzer
实验过程中,LFM信号带宽分别设置为100 MHz、120 MHz以140 MHz,信号以射频周期信号的形式发出,调制频率为1.3 GHz,三种信号的周期分别为20.41 μs、17.08 μs以及14.62 μs。在接收端,信号经解调后,再经过M9391A采集,信号采集频率为204.7 MHz,单周期内采集得到的信号时域图如图9所示,图中为复数信号的实部波形图。利用89600 VSA对信号进行频谱分析,如图10所示。
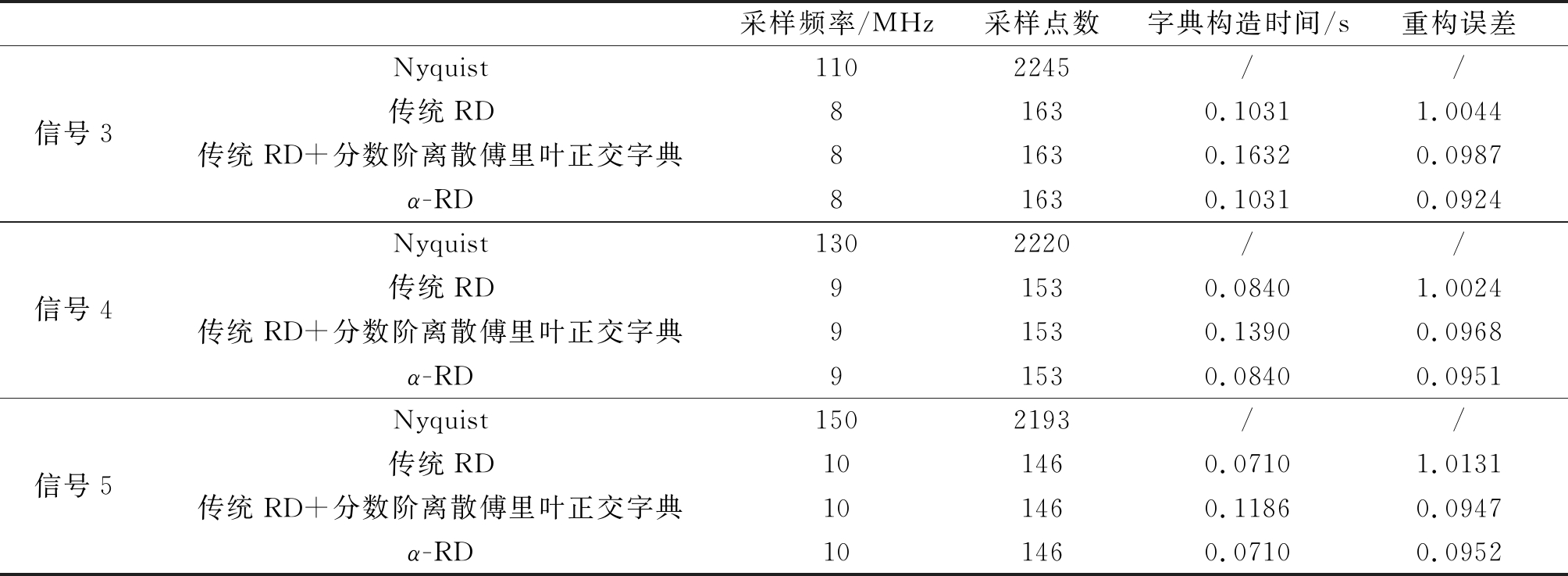
根据图10中信号频谱特性,Nyquist采样方法中三种信号的最低采样频率分别设定为110 MHz、130 MHz以及150 MHz。利用方法(1)~(4)对上述三种实测LFM信号进行采样与重构仿真实验。对于方法(2)~(4),三种信号的采样频率分别设定为8 MHz、9 MHz以及10 MHz。采样与重构效果如表3所示,表中信号3、信号4、信号5分别表示带宽为100 MHz、120 MHz以140 MHz的三种实测LFM信号。图11~图13则给出了三种信号重构后的时域波形图。
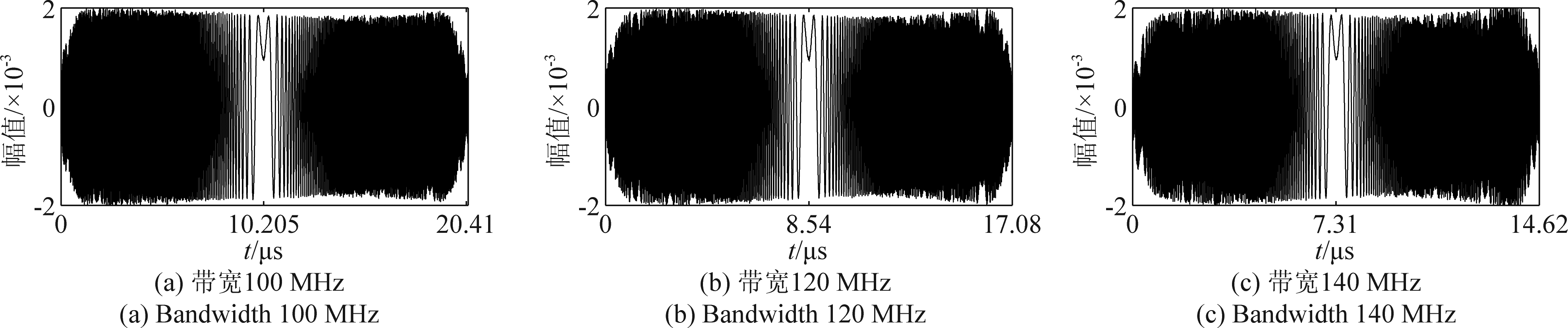
图9 实测信号时域波形 Fig.9 Measured signals in time


图10 实测信号频谱
Fig.10 Spectrum for measured signals
从表3中可以看出,三种模拟信息转换方法的采样频率与采样点数均明显低于Nyquist采样方法。在重构误差上,方法(3)与方法(4)的重构误差较低,而方法(2)的重构误差较大。在字典构造时间上,方法(2)与方法(4)字典构造时间消耗相对较低,而方法(3)的字典构造时间明显高于方法(2)与方法(4)。综上所述,本文提出的基于α-RD的LFM信号模拟信息转换方法既实现了LFM信号的有效重构,又保留传统RD系统结构简单、复杂度低的特点,能够有效降低LFM信号的采样频率与采样点数。

图11 信号3的重构效果对比
Fig.11 Comparison of reconstruction for signal 3
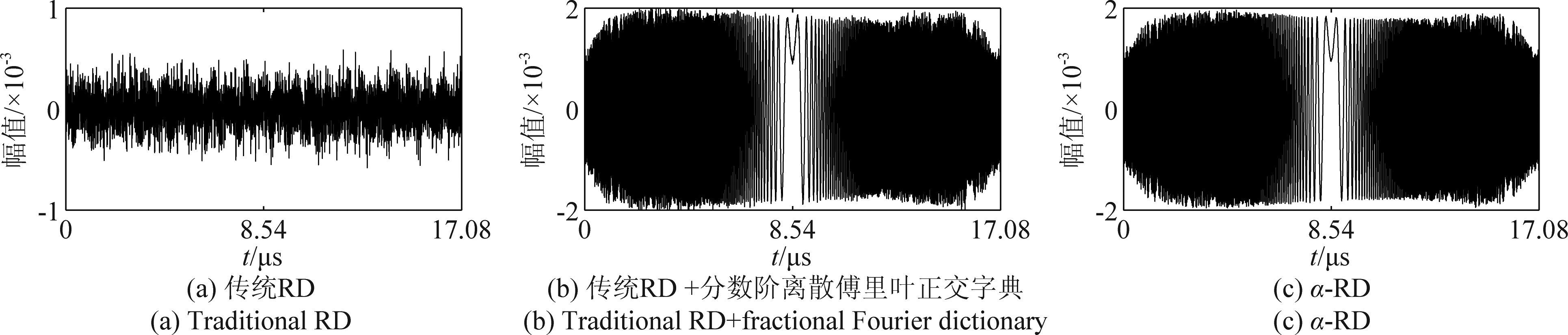
图12 信号4的重构效果对比
Fig.12 Comparison of reconstruction for signal 4

图13 信号5的重构效果对比
Fig.13 Comparison of reconstruction for signal 5
表3 采样与重构效果对比
Tab.3 Comparison for sampling and reconstruction
采样频率/MHz采样点数字典构造时间/s重构误差信号3Nyquist1102245//传统RD81630.10311.0044传统RD+分数阶离散傅里叶正交字典81630.16320.0987α-RD81630.10310.0924信号4Nyquist1302220//传统RD91530.08401.0024传统RD+分数阶离散傅里叶正交字典91530.13900.0968α-RD91530.08400.0951信号5Nyquist1502193//传统RD101460.07101.0131传统RD+分数阶离散傅里叶正交字典101460.11860.0947α-RD101460.07100.0952
5 结论
本文针对LFM信号带宽提升所带来的采集、存储、传输困难问题,提出了一种基于α-RD系统的LFM信号模拟信息转换方法。本文提出的α-RD系统通过模拟乘法器、积分器等基本电路结构实现LFM信号的压缩采样功能,具有结构简单,易于硬件电路实现的特点。原始信号的重构过程利用了LFM信号在分数阶傅里叶变换下的稀疏性,而利用本文提出的α-RD系统,重构阶段能够避免分数阶离散傅里叶正交字典复杂的构造过程。通过仿真信号以及实测信号实验,本文分析了采样速率、采样方法以及重构算法等因素对信号采样与重构过程的影响,实验结果表明,本文基于α-RD系统的LFM信号模拟信息转换方法能够有效降低LFM信号的采样频率与采样点数,从而有效缓解采样系统的存储与传输压力。
[1] ARAB H, DUFOUR S, MOLDOVAN E, et al. Accurate and robust CW-LFM radar sensor: Transceiver front-end design and implementation[J]. IEEE Sensors Journal, 2018, 19(5): 1943-1950.
[2] 梁胜浴, 黄建军, 黄敬雄, 等. 一种雷达信号的单样本压缩采样方法[J]. 信号处理, 2019, 35(6): 1011-1017.
LIANG Shengyu, HUANG Jianjun, HUANG Jingxiong, et al. A single sample compressive sampling method for radar signals[J]. Journal of Signal Processing, 2019, 35(6): 1011-1017.(in Chinese)
[3] MISHALI M, ELDAR Y C. From theory to practice: Sub-nyquist sampling of sparse wideband analog signals[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 375-391.
[4] TROPP J A, LASKA J N, DUARTE M F, et al. Beyond nyquist: Efficient sampling of sparse bandlimited signals[J]. IEEE Transactions on Information Theory, 2010, 56(1): 520-544.
[5] 陈涛, 王思超, 郭立民. 离散压缩采样结构下的宽带LFM信号识别及参数估计[J]. 哈尔滨工程大学学报, 2018, 39(8): 1415-1421.
CHEN Tao, WANG Sichao, GUO Limin. Recognition and parameter estimation of wideband LFM signal based on MWC discrete compressive sampling structure[J]. Journal of Harbin Engineering University, 2018, 39(8): 1415-1421.(in Chinese)
[6] 杨恩蘋. 非平稳信号压缩采样与重构算法研究[D]. 成都: 电子科技大学, 2018.
YANG Enping. Research on compressive sampling and reconstruction algorithm of the non-stationary signal[D]. Chengdu: University of Electronic Science and Technology of China, 2018. (in Chinese)
[7] 邱培培. 基于AIC的压缩感知雷达接收机信号重构算法研究[D]. 哈尔滨: 哈尔滨工程大学, 2019.
QIU Peipei. Research on signal reconstruction algorithm of compressed sensing radar receiver signal basing on AIC[D]. Harbin: Harbin Engineering University, 2019. (in Chinese)
[8] 方标, 黄高明, 高俊, 等. FRFT域LFM雷达回波信号的压缩采样模型[J]. 西安电子科技大学学报, 2015, 42(1): 200-206.
FANG Biao, HUANG Gaoming, GAO Jun, et al. Compressive sensing of linear frequency modulated echo signals in fractional Fourier domains[J]. Journal of Xidian University, 2015, 42(1): 200-206.(in Chinese)
[9] 陈小龙, 关键, 于晓涵, 等. 雷达动目标短时稀疏分数阶傅里叶变换域检测方法[J]. 电子学报, 2017, 45(12): 3030-3036.
CHEN Xiaolong, GUAN Jian, YU Xiaohan, et al. Radar detection for moving target in short-time sparse fractional Fourier transform domain[J]. Acta Electronica Sinica, 2017, 45(12): 3030-3036.(in Chinese)
[10]ZHAO Haoran, QIAO Liyan, ZHANG Jingchao, et al. Generalized random demodulator associated with fractional Fourier transform[J]. Circuits, Systems, and Signal Processing, 2018, 37(11): 5161-5173.
[11]王朋. 宽带压缩感知接收机关键技术研究[D]. 成都: 电子科技大学, 2020.
WANG Peng. Research on key technologies of broadband compressed sensing receiver[D]. Chengdu: University of Electronic Science and Technology of China, 2020. (in Chinese)
[12]郑仕链, 杨小牛, 赵知劲. 用于随机解调器压缩采样的重构判定方法[J]. 物理学报, 2014, 63(22): 410- 414.
ZHENG Shilian, YANG Xiaoniu, ZHAO Zhijin. Reconstruction verification for random demodulator based compressed sampling[J]. Acta Physica Sinica, 2014, 63(22): 410- 414.(in Chinese)
[13]宋维斌, 张圣儒, 邓忆秋, 等. 分数傅里叶变换域稀疏带限信号的模拟信息转换[J]. 光电工程, 2018, 45(6): 50-58.
SONG Weibin, ZHANG Shengru, DENG Yiqiu, et al. Analog to information conversion for sparse signals band-limited in fractional Fourier transform domain[J]. Opto-Electronic Engineering, 2018, 45(6): 50-58.(in Chinese)
[14]沙学军, 史军, 张钦宇. 分数傅里叶变换原理及其在通信系统中的应用[M]. 人民邮电出版社, 2013.
SHA Xuejun, SHI Jun, ZHANG Qinyu. Fractional fourier transform theory and its applications in communication systems[M]. Posts and Telecommunications Press, 2013.(in Chinese)
[15]DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[16]BECK A, TEBOULLE M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202.
[17]MENG Zong, SHI Ying, CHEN Zijun, et al. Adaptive block forward and backward stagewise orthogonal matching pursuit algorithm applied to rolling bearing fault signal reconstruction[J]. The Journal of the Acoustical Society of America, 2019, 146(4): 2385-2394.
[18]黄振, 柏正尧, 莫禹钧. 采用压缩采样匹配追踪算法的频谱感知[J]. 信号处理, 2014, 30(9): 1086-1090.
HUANG Zhen, BAI Zhengyao, MO Yujun. Spectrum sensing using the algorithm of compressive sampling matching pursuit[J]. Journal of Signal Processing, 2014, 30(9): 1086-1090.(in Chinese)




