1 引言
为了满足不断增长的高速数据业务需求,提高频谱利用率对于无线移动通信系统变得尤为重要。作为5G关键技术之一的大规模MIMO(Massive MIMO)技术,因其能够大幅度提高系统的频谱效率(Spectrum Efficiency, SE)而广受业界关注[1-2]。然而,传统的蜂窝网络架构中存在的小区间干扰问题始终无法得到很好的解决。因此,由分布式大规模MIMO技术演变而来的无小区大规模MIMO(Cell-Free Massive MIMO)系统逐渐走进了人们的视野[3]。
无小区大规模MIMO系统通过在一片区域部署大量接入点(Access Point, AP),这些AP通过回程链路(Backhaul)与中央处理单元(Central Processing Unit, CPU)相连,从而实现在同一时频资源块内为系统中多个用户进行服务。由于打破了传统小区的概念,无小区大规模MIMO系统中不存在所谓的边缘用户,因此可实现更加均匀的覆盖[4],而且AP具有体积小、重量轻等特点,部署起来非常灵活。
由于小区边界的取消,系统中总用户数远大于原来单个小区内的用户数,导致在单个相干时间内无法向系统中所有用户分配正交导频资源,从而引起严重的导频污染问题[5]。为此,文献[6]以最大化复用相同导频的用户间距为目标,提出了一种结构化的导频分配策略,但其实现难度相对较高。Sabbagh R等人在对用户进行配对的基础上,以最大化用户的上行和速率为目标,设计了一种动态导频复用方法[7];文献[8]则结合非正交多址接入(Non-Orthogonal Multiple-Access, NOMA)思想对用户进行分簇,为处于同一簇的用户分配同一导频序列,然而该方法无法有效地解决处于同一簇内的用户间的导频污染问题。与此同时,一些学者则通过对AP进行选择划分来减轻用户受到的干扰。Nguyen T H等人基于负载均衡的思路,设计了一种迭代算法来逐步剔除为某个用户服务的AP集合中贡献相对较小的AP,以达到减小发送功率的目的[9]。文献[10]提出了一种随机排序和分组算法对AP进行分组,从而提升系统的能量效率。作者在文献[11]中,通过优化上行导频信号的发送功率加权因子来降低导频污染的影响,进而提高信道估计精度;由于该方法采用近似来简化优化问题的处理,导致最终效果并不理想。
上述针对导频污染问题的解决方案均是在常规的时分复用导频(Multiplexed Pilot, MP)配置模式下进行的,即在一个相干时间内,用户的导频信号和数据信号分别在不同的时隙内进行发送,这样的导频配置方式存在一个问题:若导频长度过短,则可分配的正交导频数过少,复用相同导频的用户数将增多,由此会加剧导频污染问题,进而降低系统SE;反之,若导频长度过长,导频开销增大,用户数据信号所占用的带宽将大大缩减,由此也会降低系统SE。因此,以上导频优化策略只能在一定程度上缓解导频污染问题。与MP配置模式不同的另一种导频配置方式是叠加导频(Superimposed Pilot, SP)配置模式,在这种模式下,用户的导频信号和数据信号将被混合起来在整个相干时间内进行发送,这样做的好处有两点:一是导频信号长度变长,正交导频资源增加;二是导频信号不再单独占用系统带宽,数据信号带宽占比变大。这两点都能起到提高系统频带利用率的效果,因此,研究SP配置模式下无小区大规模MIMO系统的性能更具有意义。
综上分析,在本文中,我们摒弃传统的MP配置模式,采用SP配置模式,在上行阶段,AP首先基于线性最小均方误差(Linear Minimum Mean Square Error, LMMSE)准则,对信道进行估计;然后将接收到的多用户叠加信号发送给CPU进行信号检测,CPU则根据估计得到的信道采用最大比合并(Maximum Ratio Combining, MRC)技术对叠加信号进行处理,以分离出与各用户对应的有用信号和干扰信号,进而从理论上推导出各用户的上行信干噪比(Signal to Interference plus Noise Ratio, SINR)及对应的上行SE。在相同的相干时间内,相较于基于MP的导频配置模式,SP导频配置模式可供分配的正交导频数目将大幅度增加,从而为有效地解决导频污染问题提供了可能,进而上行SE得到明显地提升。数值仿真结果验证了该理论分析的正确性。
本文所使用的符号定义如下:大写斜体加粗字母表示矩阵,小写斜体字母表示标量,小写斜体加粗字母表示矢量,IA表示一个维度为A×A的单位矩阵;(·)*,(·)H分别表示共轭、共轭转置,
分别表示模的运算、期望运算和方差运算;[·]l表示矢量的第l个元素(或矩阵的第l列);z～CN(0,σ2)表示一个循环对称复高斯分布的随机变量z,其均值为0,方差为σ2;C表示复数集。
2 系统模型
考虑如图1所示由K个单天线用户、L个AP组成的无小区大规模MIMO系统,其中每个AP上配有M根天线,满足ML≫K;用户和AP随机分布在一广阔区域内,AP通过回程链路与CPU相连。假设AP和用户均处于时分双工(Time Division Duplex, TDD)模式,根据信道互易性,仅需进行上行信道估计[12];同时,在单个相干间隔内,本文仅考虑上行信号传输阶段,在此阶段内,AP完成信道估计,CPU完成信号检测。至于下行数据传输阶段,根据信道的互易性,CPU根据上行信道的统计信息对下行信号进行预编码,此研究将在后续工作中展开。
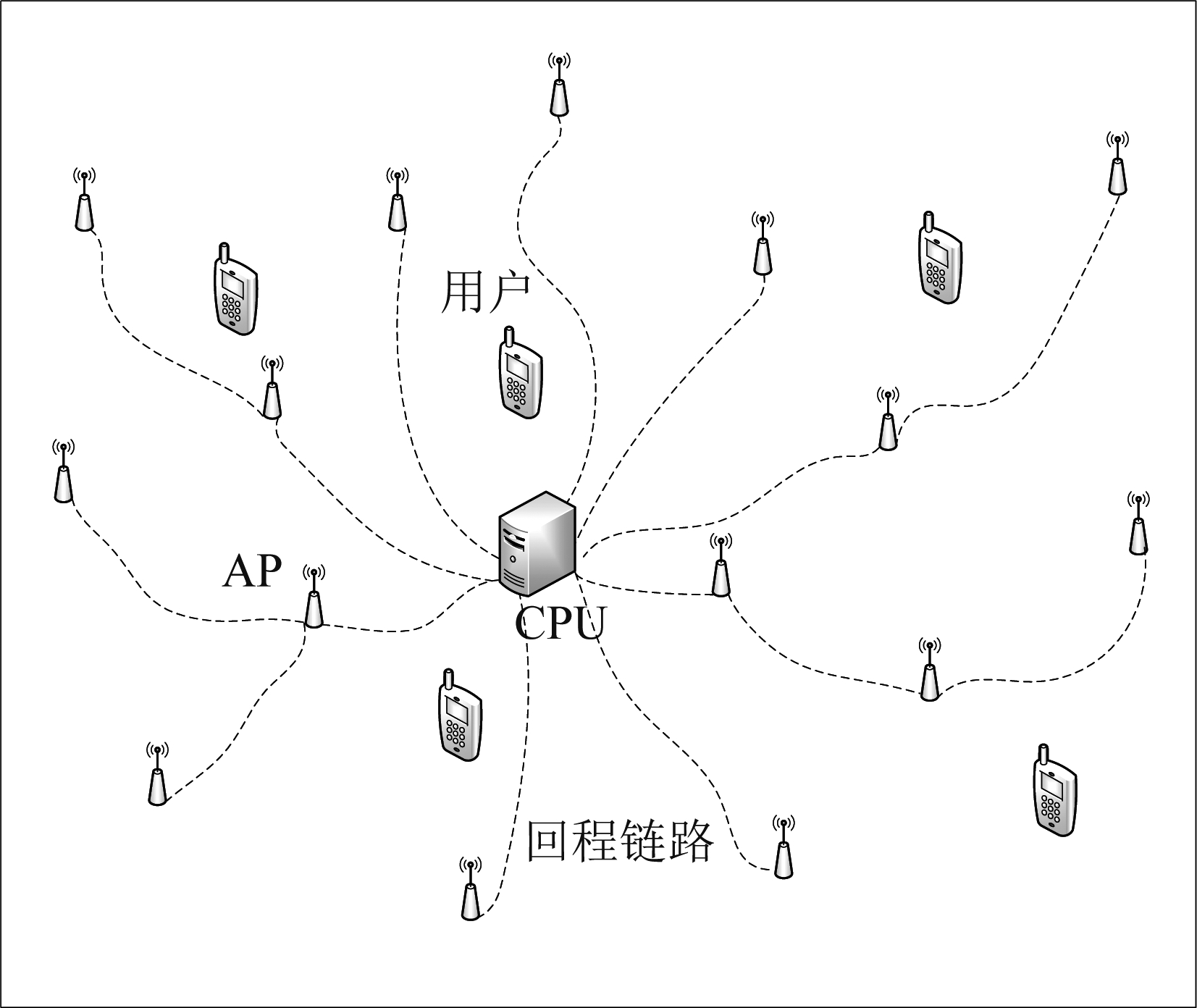
图1 无小区大规模MIMO系统
Fig.1 Cell-Free Massive MIMO system
假设所有AP均参与系统中用户的通信,令第k个用户和第l个AP之间的信道矢量为
(1)
其中βlk表示CPU处已知的大尺度衰落系数,其值变化非常缓慢,通常在几个相干时间内保持不变;hlk表示小尺度衰落系数,假设hlk,l=1,2,…,L,k=1,2,…,K是独立同分布的随机矢量,且满足hlk～CN(0,IM),其值在每个相干时间内保持不变。
3 基于叠加导频配置模式的上行信号传输
叠加导频配置模式如图2所示,其中T表示相干间隔长度。在上行阶段,用户向AP发送上行叠加信号,其中包括第k个用户发送的导频信号,记为φk∈CT×1,满足
图2 叠加导频配置模型
Fig.2 Superimposed pilot configuration mode
(2)
其中
表示与用户k使用相同导频的用户集合(包括自身在内);同时还包括第k个用户发送的数据信号,记为sk∈CT×1,假设各用户的发送数据信号相互独立,且满足sk～CN(0,IT),则
(3)
为了简化后续分析,假设各用户发送的导频信号功率相等,数据信号功率也相等,则第l个AP接收到的信号Yl∈CM×T可以表示为
(4)
其中P表示发射信号的总功率,α表示用户数据信号占总发送功率的比例因子,Wl∈CM×T为附加背景噪声矩阵,其元素相互独立,服从均值为0,方差为σ2的复高斯分布。
在用户向各AP发送完上行叠加信号后,AP将在本地采用LMMSE方法[13]进行信道估计。具体来说,第l个AP先将接收到的混合信号Yl投影到φk的方向上,即
(5)
进而利用
来估计glk。令估计信道
其中clk,SP可按下述方法求得。
由信道估计的贝叶斯均方误差
(6)
最小化,则有
(7)
于是得到
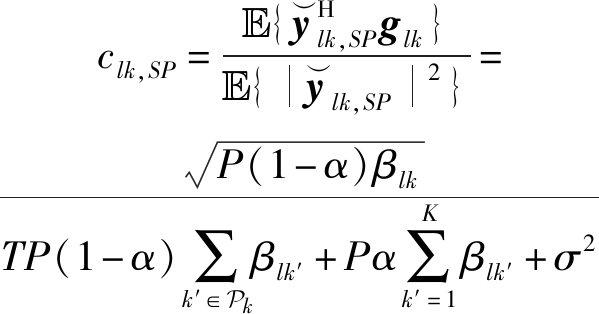
(8)
进而得到估计信道
根据前述假设,
其中
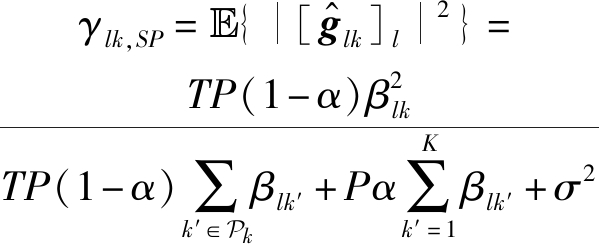
(9)
对应的信道估计误差为
满足
待本地信道估计完成后,各AP将接收到的上行信号发送给CPU进行集中译码,本文采取MRC进行译码接收。用户k在j时刻的发送数据为[sk]j,对应的接收信号则由Yl中的第j列给出。通常AP确知用户k发送的导频信号,同时,文中我们主要推导无小区大规模MIMO系统的谱效理论上限,于是类似文献[14],假设从CPU处的接收信号中可完美消除导频信号对接收信号的贡献,则CPU在时刻j(j∈{1,2,…,T})的接收信号为
(10)
然后,CPU通过对rk,SP中期望信号与干扰信号进行分离即可完成译码,具体过程将在下一节进行分析。
4 叠加导频配置模式下无小区大规模MIMO系统上行频谱效率分析
将式(4)中的噪声矩阵Wl改写为Wl=[w1,w2,…,wT],由于wi与wj当i≠j时相互独立,且满足wi～CN(0,σ2IM),代入式(10)有
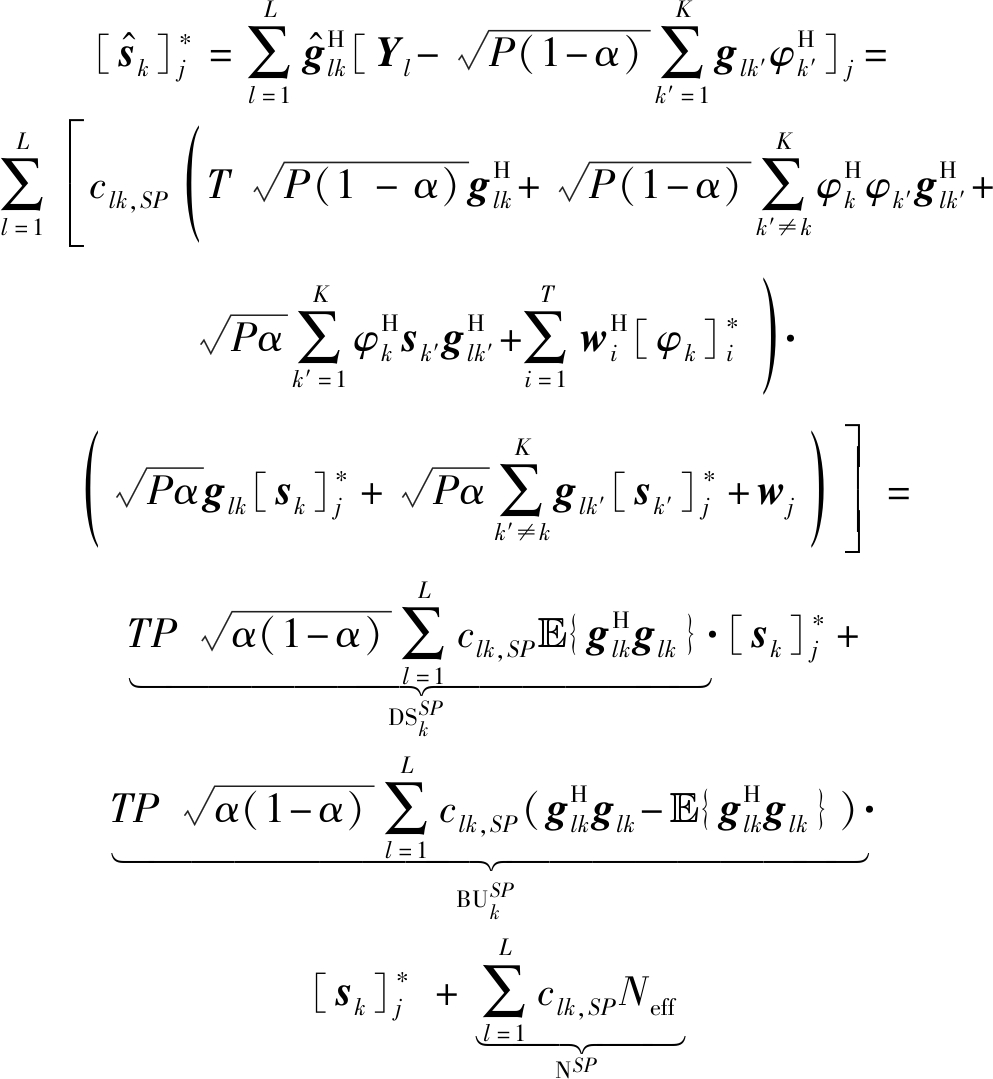
(11)
其中
表示CPU检测到用户k的在j时刻的发送信号。由三部分组成,其中
表示用户k的期望信号强度,
表示由波束成形增益不确定性带来的误差项,NSP表示干扰和噪声项,且
其中
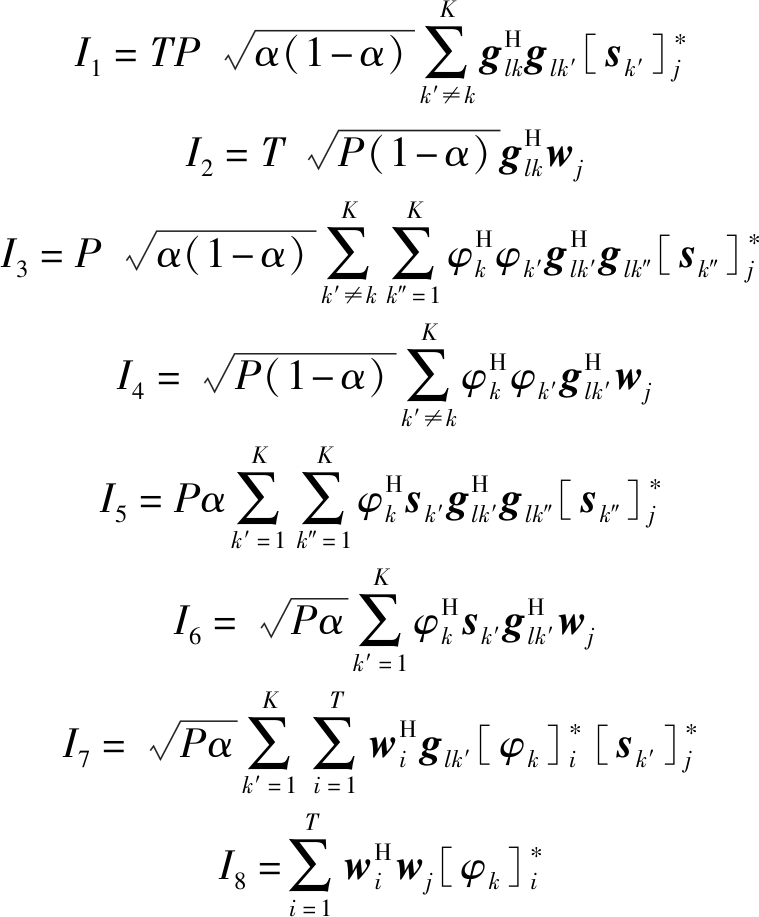
(12)
由于sk与glk相互独立,所以[sk]j与和均相互独立,故有
因此,式(11)中第一项与第二项不相关,同理可得式(11)中第一项与第三项也不相关。于是,SP配置模式下,用户k的上行SE的上限可表示为
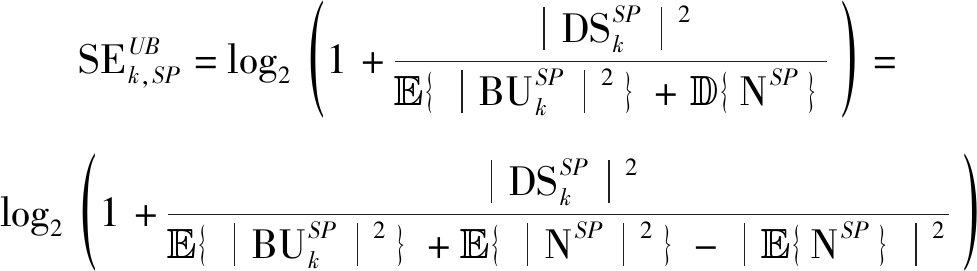
(13)
定理1 对于任意有限M和K,第k个用户的上行SE满足
(14)
其中
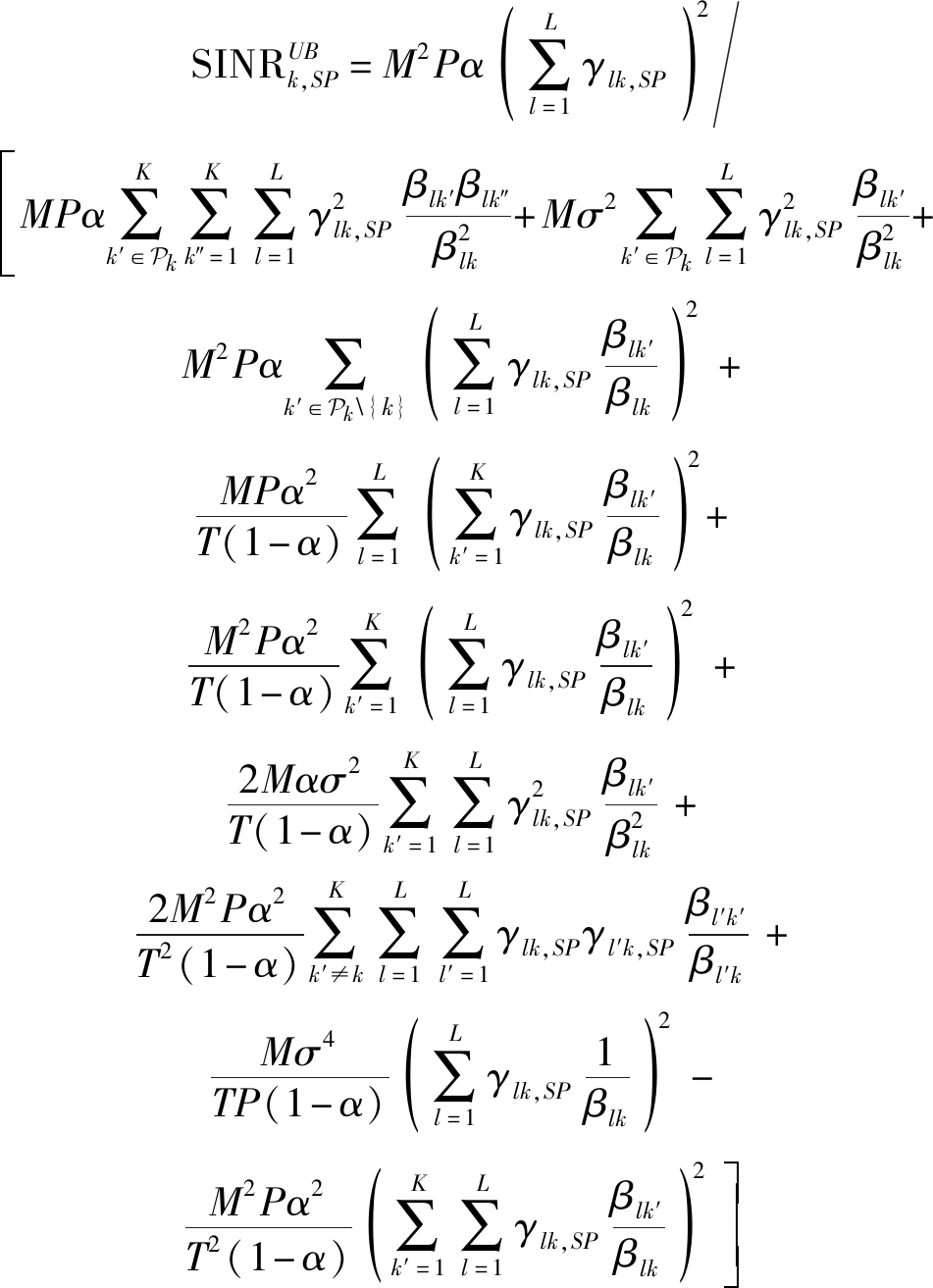
(15)
式(15)的证明过程见附录A。
5 仿真结果
在本节,通过数值仿真对SP配置模式下无小区大规模MIMO系统的SE进行评估,并与MP配置模式下系统的SE进行对比。仿真中,假设用户和AP随机分布在一个边长为D的正方形区域内。在关于无小区大规模MIMO系统的早期文献中,关于大尺度衰落系数的建模通常采用COST-Hata模型[11,15],然而其并不适合无小区大规模MIMO的系统架构[16],因此本文按照文献[17]对大尺度衰落系数进行建模,即
(16)
其中dlk表示用户和AP之间的距离,Xlk表示阴影衰落,满足
噪声功率按照下式计算
σ2=B×kB×T0×NF
(17)
其中B表示系统带宽,kB=1.381×10-23为玻尔兹曼常数,T0=290为噪声温度,NF为噪声系数,其余仿真参数如表1所示。
表1 部分仿真参数
Tab.1 Some simulation parameters
D/m2000 AP与用户高度差/m10 B/MHz20 NF/dB7 P/mW200 σsh/dB10
为了使SP/MP配置模式下均能考虑到导频污染的影响,以保证性能对比的公平性,参考文献[8-9,11,15],对信道相干间隔T取值适当地减小。图3给出K=100,L=200,T=50时,SP配置模式下无小区大规模MIMO系统中平均每用户的SE随有用信号功率因子α的变化曲线。从图中可看出,在AP天线数M取不同值时,SE随α的变化的趋势基本一致。SE先随着α的增大而增大,当α增大到某一定值时,SE达到最大值,然后随着α的增大而减小,这说明,SP配置模式下存在一特定的最优的功率分配因子;根据图中显示,在当前参数配置下,其最优功率分配因子α*约为0.3;这里需要指出,对于其他配置,也会有类似的结论。
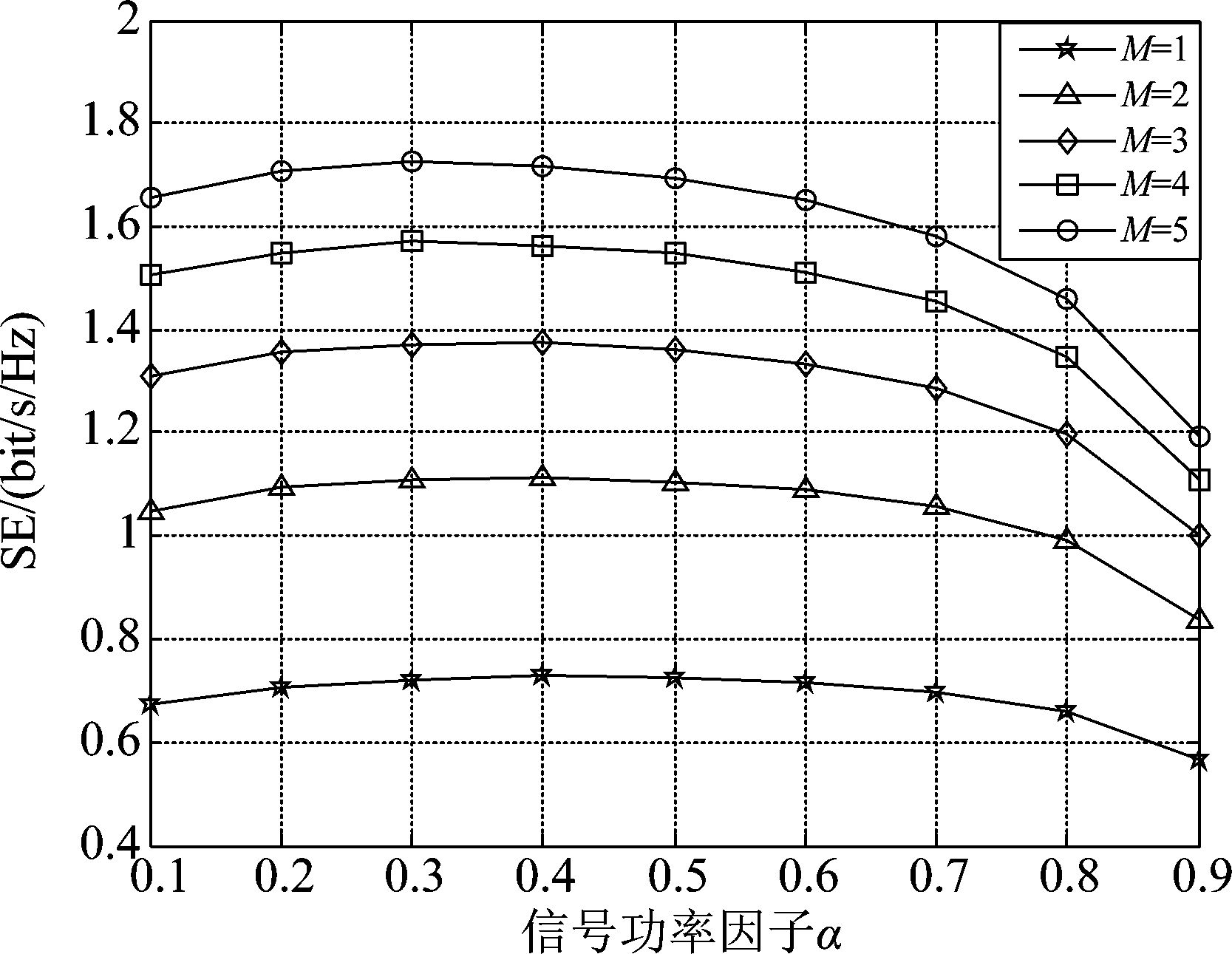
图3 SP模式下系统SE随数据信号功率因子α的变化曲线
Fig.3 Curve of system SE with power factor of data signal in SP mode
当α*=0.3,结合表1中给定的总发送功率P,可知在SP配置模式下,期望信号最优功率为60 mW,导频信号最优功率均为140 mW。于是,为了后续有效地对比SP/MP配置模式下无小区大规模MIMO系统的性能差别,图4给出K=100,L=200,T=50,导频信号功率和数据信号功率分别取值140 mW、60 mW时,MP配置模式下无小区大规模MIMO系统的平均每用户SE随导频长度τp的变化曲线。从图中可看出,在AP配置不同天线数的情况下,SE随τp的变化的趋势基本一致,即当τp较小时,SE随着τp的增大而增大,这是因为随着τp的增大,系统中可用的正交导频资源增多,信道估计结果变得精确,导致SE上升;而随着τp继续增大到某一定值时,SE达到最大,之后便随着τp的增大而减小,这是因为,相比于信道估计精度的增加,在一个相干间隔内期望信号所占比重的减小对系统SE的影响占主导地位,因此,随着τp的进一步增大,SE反而减小。更为重要的是,从图中可以看出,对于MP配置模式,在当前参数配置下,其最优正交导频长度值
约为5。
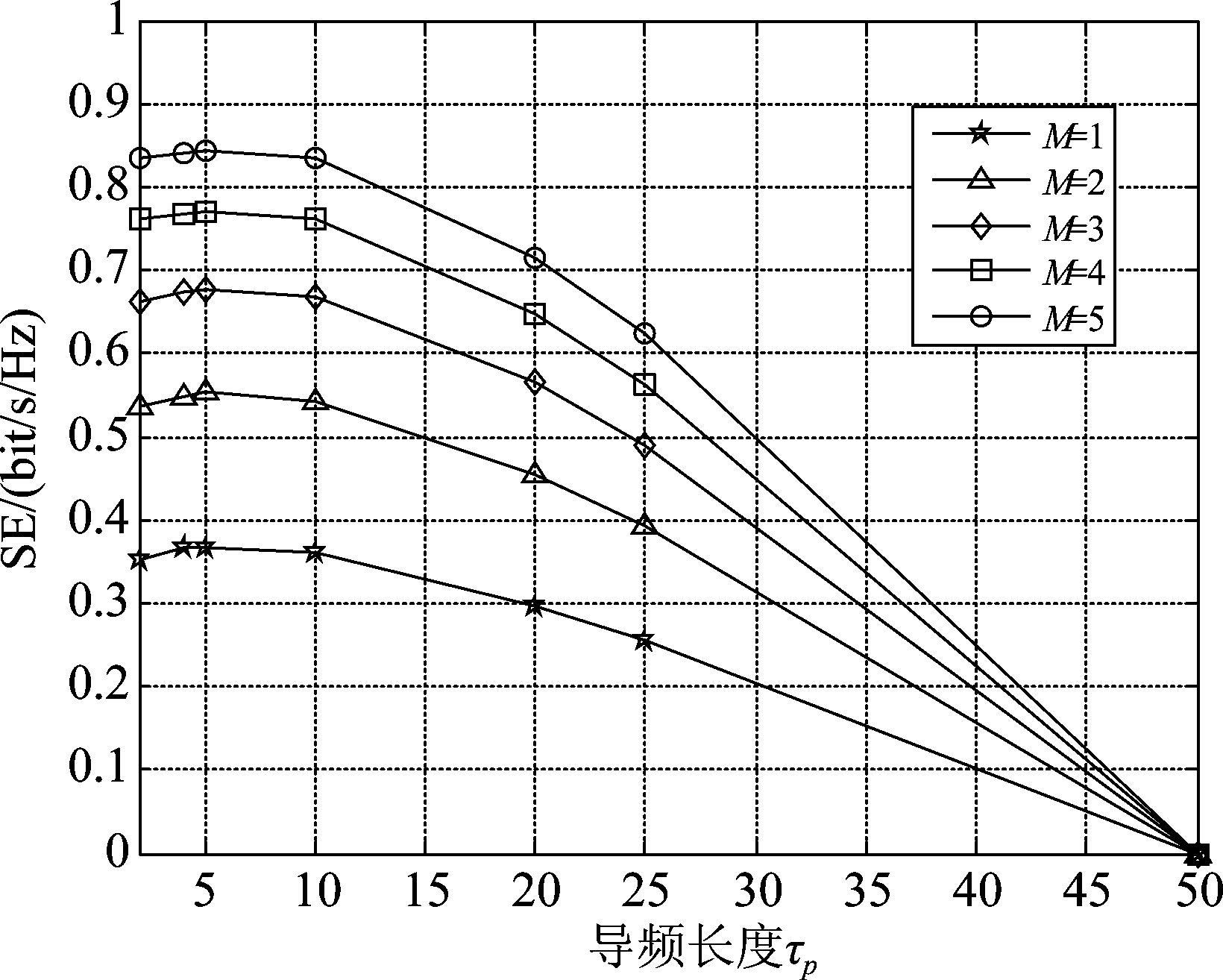
图4 MP模式下系统SE随导频长度τp的变化曲线
Fig.4 Curve of system SE with the length of pilot in MP mode
在图4仿真结果的基础上,图5给出了K=100,L=200,M=5,α=0.3,T=50,导频信号功率和数据信号功率分别取值140 mW、60 mW时,SP配置模式和MP配置模式下系统中平均每用户SE的累计分布函数(Cumulative Distribution Function, CDF)对比情况。从图中可看出,在存在导频污染,即T<K时,而其他条件相同的情况下,SP配置模式下系统中平均每用户的SE明显高于MP配置模式下系统的SE;同时,对于MP配置模式,在相同条件下,最优导频长度
的SE明显要高于τp=20时的SE,从而进一步验证了图4结论的正确性。
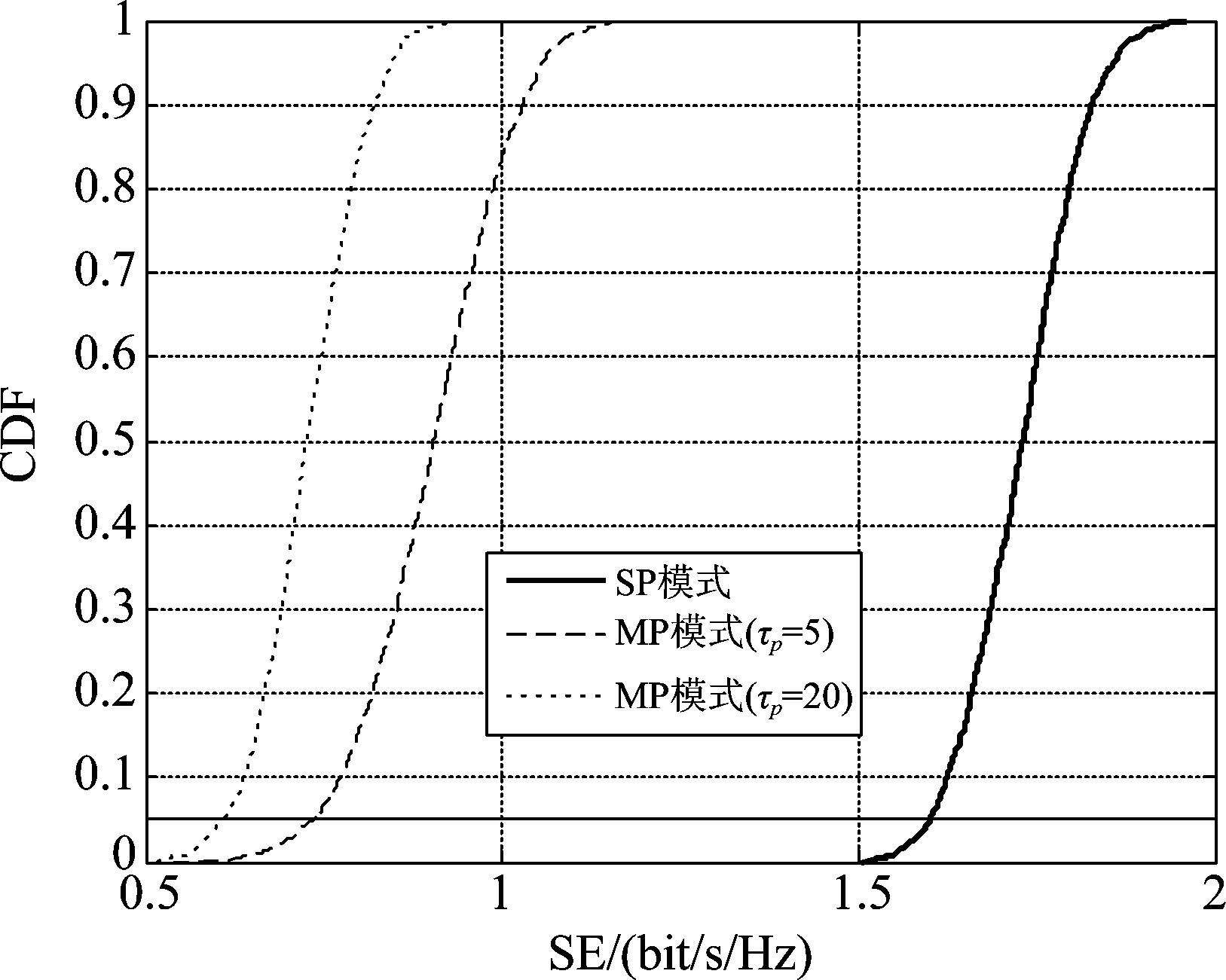
图5 三种配置下系统SE的CDF曲线
Fig.5 CDF curve of system SE in three configurations
6 结论
在无小区大规模MIMO系统中,目前关于导频污染问题的研究通常基于MP配置模式展开;受有限信道相干时间的制约,这些研究工作所提出的解决方案的效果并不是特别明显。因此,本文基于SP配置模式,推导了多用户无小区大规模MIMO系统SE的上限表达式,并将其与基于MP配置模式进行对比。仿真结果表明,在导频污染存在情况下,基于SP配置模式的无小区大规模MIMO系统的95%-likely用户SE(即图5中纵坐标为0.05时对应的横坐标值,表示系统中95%的用户平均SE高于该值)约为基于MP配置模式下的2.2倍。因此,在信道相干时间受限的无小区大规模MIMO系统中,SP配置模式将为有效减轻导频污染并提高系统SE提供了一种可行的解决思路。
附录A 式(15)的证明
式(13)中分子
根据式(11),可进一步写作
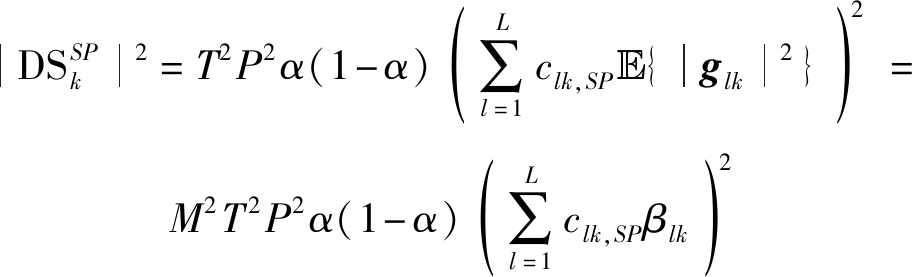
(18)
根据式(8)和式(9),有
(19)
代入式(18),可得
(20)
式(13)中分母第一项
根据式(11),有
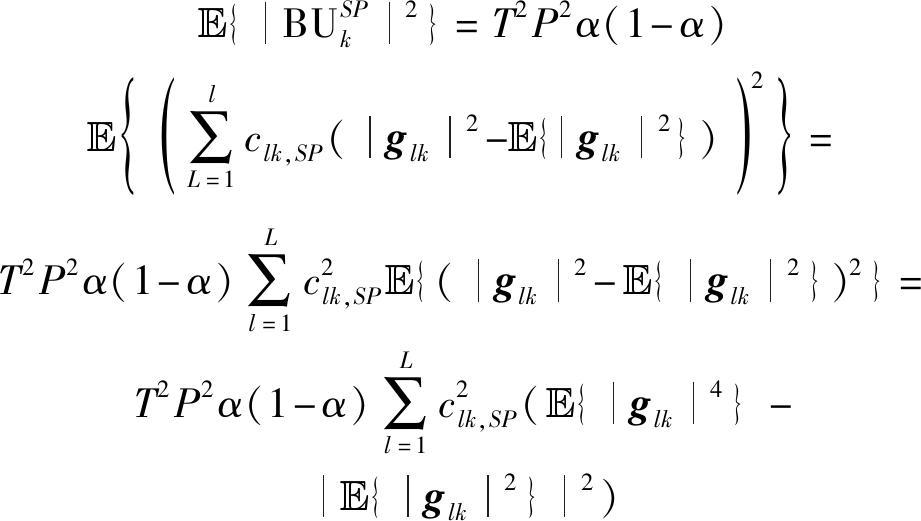
(21)
对于
由于
其中χ2(2M)表示自由度为2M的卡方分布,所以
(22)
代入式(21),可得
(23)
式(13)中分母中第二项
先计算
(24)
再计算
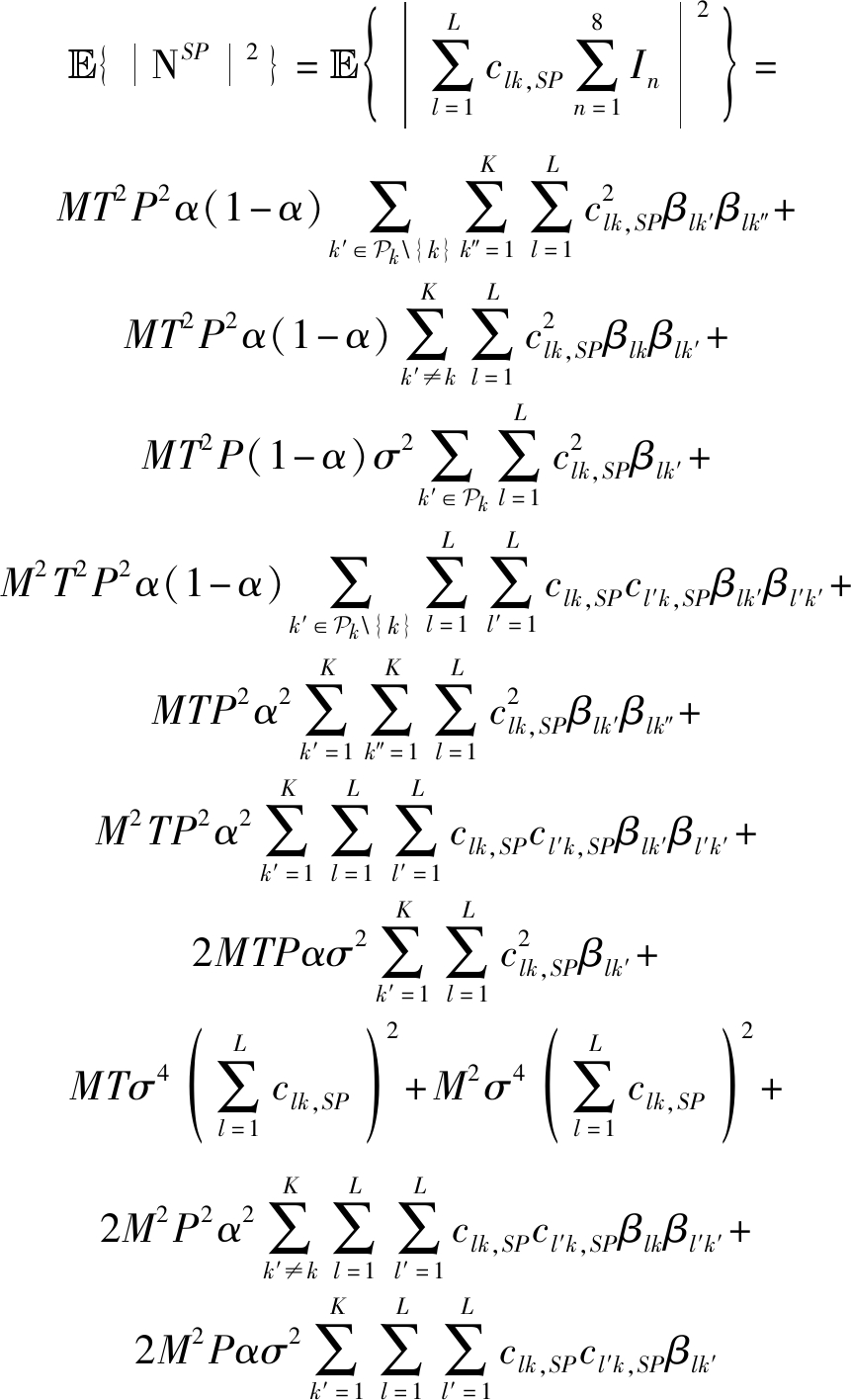
(25)
将式(20)、(23)、(24)、(25)代入式(13),结合(14)、(19)两式,即可证得式(15)。
[1] WANG Chengxiang, HAIDER F, GAO Xiqi, et al. Cellular architecture and key technologies for 5G wireless communication networks[J]. IEEE Communications Magazine, 2014, 52(2): 122-130.
[2] RUSEK F, PERSSON D, LAU B K, et al. Scaling up MIMO: Opportunities and challenges with very large arrays[J]. IEEE Signal Processing Magazine, 2013, 30(1): 40- 60.
[3] NAYEBI E, ASHIKHMIN A, MARZETTA T L, et al. Cell-free massive MIMO systems[C]∥2015 49th Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA. IEEE, 2015: 695- 699.
[4] INTERDONATO G, BJÖRNSON E, QUOC NGO H, et al. Ubiquitous cell-free Massive MIMO communications[J]. EURASIP Journal on Wireless Communications and Networking, 2019, 2019(1): 1-13.
[5] JOSE J, ASHIKHMIN A, MARZETTA T L, et al. Pilot contamination problem in multi-cell TDD systems[C]∥2009 IEEE International Symposium on Information Theory. Seoul, Korea (South). IEEE, 2009: 2184-2188.
[6] ATTARIFAR M, ABBASFAR A, LOZANO A. Random vs structured pilot assignment in cell-free massive MIMO wireless networks[C]∥2018 IEEE International Conference on Communications Workshops (ICC Workshops). Kansas City, MO, USA. IEEE, 2018: 1- 6.
[7] SABBAGH R, PAN Cunhua, WANG Jiangzhou. Pilot allocation and sum-rate analysis in cell-free massive MIMO systems[C]∥2018 IEEE International Conference on Communications (ICC). Kansas City, MO, USA. IEEE, 2018: 1- 6.
[8] LI Yikai, ARUMA BADUGE G A. NOMA-aided cell-free massive MIMO systems[J]. IEEE Wireless Communications Letters, 2018, 7(6): 950-953.
[9] NGUYEN T H, NGUYEN T K, HAN H D, et al. Optimal power control and load balancing for uplink cell-free multi-user massive MIMO[J]. IEEE Access, 2018, 6: 14462-14473.
[10] PANDA S. Performance optimization of cell-free massive MIMO system with power control approach[J]. AEU-International Journal of Electronics and Communications, 2018, 97: 210-219.
[11] MAI T C, NGO H Q, EGAN M, et al. Pilot power control for cell-free massive MIMO[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 11264-11268.
[12] 杜福德, 谢威, 夏晓晨. 频分双工大规模MIMO系统时变信道估计[J]. 信号处理, 2020, 36(3): 397- 406.
DU Fude, XIE Wei, XIA Xiaochen. Time-varying channel estimation for frequency-division duplex massive MIMO systems[J]. Journal of Signal Processing, 2020, 36(3): 397- 406.(in Chinese)
[13] SENGUPTA S K, KAY S M. Fundamentals of statistical signal processing: Estimation theory[J]. Technometrics, 1995, 37(4): 465.
[14] VERENZUELA D, BJÖRNSON E, SANGUINETTI L. Spectral and energy efficiency of superimposed pilots in uplink massive MIMO[J]. IEEE Transactions on Wireless Communications, 2018, 17(11): 7099-7115.
[15] NGO H Q, ASHIKHMIN A, YANG Hong, et al. Correction to “cell-free massive MIMO versus small cells” [mar 17 1834-1850][J]. IEEE Transactions on Wireless Communications, 2020, 19(5): 3623-3624.
[16] BJÖRNSON E, SANGUINETTI L. Making cell-free massive MIMO competitive with MMSE processing and centralized implementation[J]. IEEE Transactions on Wireless Communications, 2020, 19(1): 77-90.
[17] BJÖRNSON E, SANGUINETTI L. Scalable cell-free massive MIMO systems[J]. IEEE Transactions on Communications, 2020, 68(7): 4247- 4261.
