1 引言
跑道容量分为实际容量和最大容量。实际容量是指对应于一个可接受的延误水平,单位时间内跑道可服务的飞机架数。最大容量是指在持续服务请求,不违反空中交通管理规定,不考虑延误水平的情况下,单位时间跑道系统可服务的最大航空器架次。按照航空器起降状态的不同,又可分为跑道离港容量和跑道着陆容量。本文分析的跑道容量均为理论最大着陆容量。跑道容量优化是指通过一定的措施提升跑道容量或合理分配跑道抵离港流量、缓解拥堵和延误。根据优化措施的不同,可以分为三类:基于线性规划的流量分配优化[1-3]、基于飞机排序的容量提升优化[4-7]和基于尾流间隔缩减的跑道容量优化[8-10]。在基础设施一定的情况下,尾流间隔往往决定了机场跑道单位时间内的航空器起降架次,即跑道的运行容量。因此尾流间隔的大小成为提升跑道系统容量最直接的关键要素之一。研究基于尾流间隔缩减的跑道容量优化对提升跑道容量、应对航空交通量极速增长具有重要意义。
针对通过缩减尾流间隔提升跑道容量,2007年,欧洲航空安全导航组织(EUROCONTROL)提出航空器再分类(RECAT)的概念,通过合理地重新划分航空器类别来安全谨慎地缩减尾流间隔,进而提高跑道容量和管制运行效率。美国联邦航空局(FAA)于2009年与国际民航组织(ICAO)、EUROCONTROL以及欧洲航空安全局(EASA)联合开展RECAT技术的研究工作,分两个阶段试验RECAT技术,第一阶段的工作(RECAT I)已经在2011年完成,现在正在开展第二阶段的研究工作(RECAT1.5)。中国在这方面的研究起步较晚,目前,我国没有提出自己的航空器再分类计划,但是中国民航局明确表示,要基于欧美运行经验和国内研究成果,结合国内机场的交通流特点,确定中国民航的航空器再分类标准。
据此,在中国的机场运行环境下,研究欧洲航空器再分类标准(RECAT-EU)及美国航空器再分类标准(FAA RECAT1.5)对跑道容量的影响具有重要意义。针对航空器再分类标准的改变对跑道容量的提升,国内已有部分文献展开讨论。但是,他们将航空器间隔作为离散事件而不是随机过程来处理,并不能充分反映跑道在发生风险概率方面的性能和安全性[11],且未考虑SRO对跑道容量的影响。事实上,ROT通过与航空器着陆间隔共同作用来影响跑道容量,当航空器间隔小于前机的ROT时,便会发生SRO的风险[12-14],一旦SRO发生,后机需按照指定程序复飞或推迟进近,这对跑道容量以及着陆安全有着不容忽视的影响[15]。
针对该研究领域的不足之处,本文立足国内天津滨海国际机场的实际运行状况,深入挖掘ADS-B(Automatic Dependent Surveillance-Broadcast)数据统计得到该机场着陆航空器ROT,再根据尾流间隔标准由Monte Carlo仿真生成航班流,理论分析了在该机场运行环境下尾流间隔标准的改变对SRO和跑道容量的影响,定量计算了SRO在其中造成的偏差,分析了ROT和LTI对SRO及跑道容量的影响。本文的研究工作可为中国民航确定自己的航空器再分类标准以及空管人员合理规划航空器间隔优化跑道容量提供参考依据。
2 发生SRO的概率及其对跑道容量的影响
SRO是指当连续进近航空器降落在同一条跑道时,后机在前机离开跑道之前抵达跑道入口的情形。此时,两架飞机的LTI小于前机的着陆ROT,如图1所示。
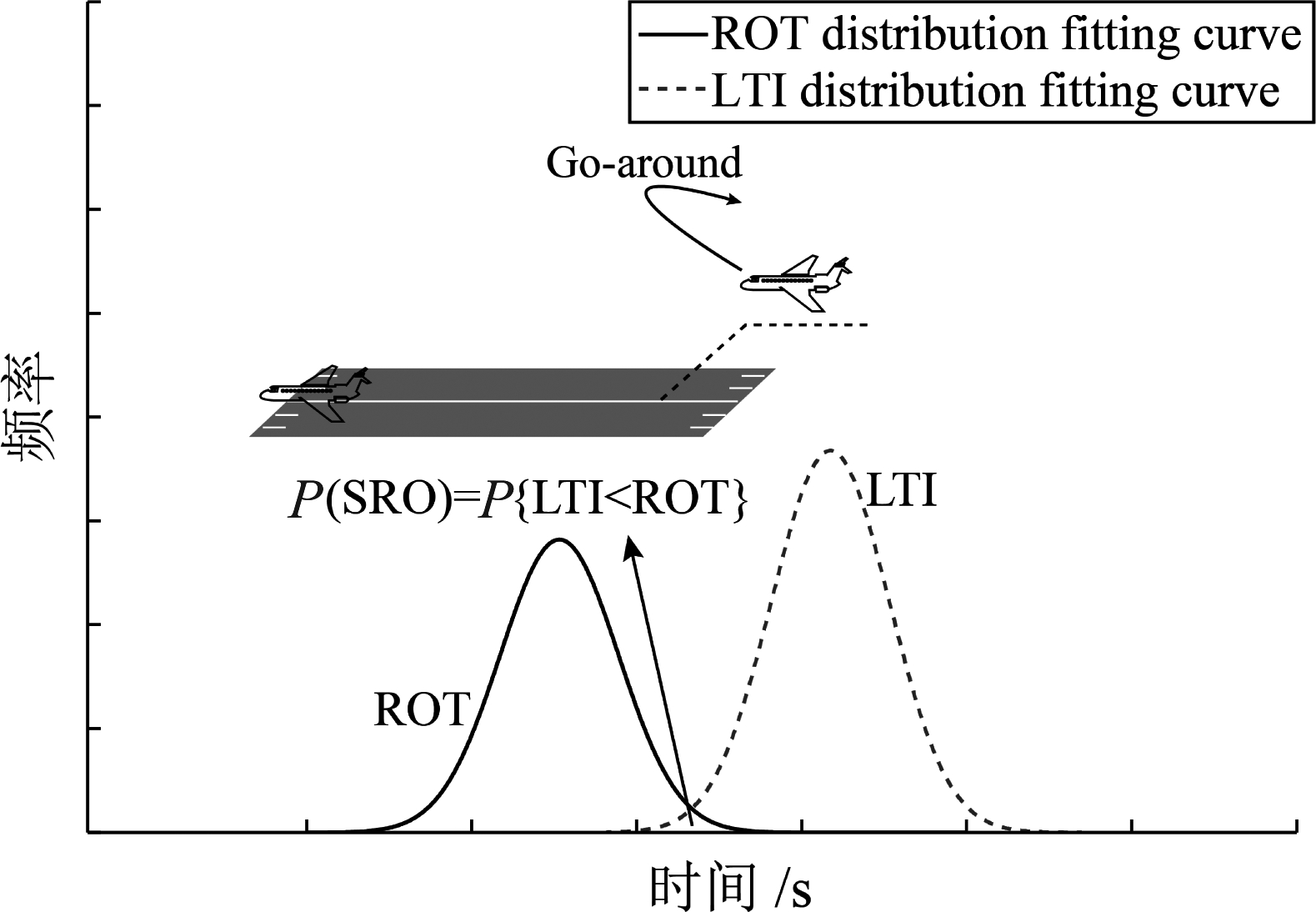
图1 发生SRO情形的示意图
Fig.1 Schematic diagram of SRO situation
图1中,ROT和LTI分布拟合后的两条曲线与横轴所构成区域的重叠部分表示发生SRO的情形,其面积大小为理论上发生SRO的概率大小,记为P(SRO),计算公式如式(1)所示,
P(SRO)=P{LTI![]() fLTI(x)dx+
fLTI(x)dx+![]() fROT(x)dx
fROT(x)dx
(1)
其中, fROT表示ROT分布拟合概率密度曲线函数, fLTI表示LTI分布拟合概率密度曲线函数,X为两者交点的横坐标。ROT及LTI分布拟合后的概率密度曲线形状取决于该机场ROT及LTI历史数据的频率分布情况。作为表征ROT及LTI特征的曲线,能够反映在该机场运行环境下航空器的历史运行状况。
本文分析的跑道容量是以着陆单跑道模型[16]为基础,在持续服务请求不间断的情况下,单位时间跑道系统理论上可服务的最大航空器架次。为了安全考虑,当SRO发生时后机需按照规定程序执行复飞,这会影响后续进近的航空器,进而影响跑道容量。公式(2)给出了航空器执行复飞过程对跑道容量造成的影响。
(2)
其中,C为跑道容量,T为平均间隔时间,pg(T)为执行复飞的概率。根据诱发复飞的原因可将复飞分成两类[14],第一类是由于遭遇尾涡流造成的复飞(wake-vortex go-around),第二类是由于同时跑道占用造成的复飞(well-known go-around)。故有公式(3)成立,
pg(T)=P(SRO)+Pwake-vortex
(3)
其中,Pwake-vortex为航空器遭受尾涡流风险而发生复飞的概率大小,P(SRO)是由于发生同时跑道占用而复飞的概率大小。由于Pwake-vortex往往数值很小[12],故有pg(T)≈P(SRO)。所以,公式(2)近似转化为公式(4),
(4)
公式(4)表明,P(SRO)的大小决定了SRO对跑道容量的影响程度。根据前面的分析,P(SRO)取决于LTI和ROT的频率分布情况,由于ROT受机型比例及跑道出口设计的影响较大,对于某一个机场而言,ROT的频率分布相对固定,而LTI则跟尾流间隔标准密切相关,因为采用新尾流间隔标准后的航空器LTI得以整体缩减,LTI频率分布较之前会向左移动,不同尾流间隔标准下ROT与LTI重叠部分的面积不同,发生SRO的概率也就不同。因此,有必要分析不同尾流间隔标准下SRO对跑道容量的影响程度。
3 不同尾流间隔标准下SRO对跑道容量的影响
以国内现阶段尾流间隔标准CCAR-93TM-R5和尾流再分类标准FAA RECAT1.5为依据,分别分析不同尾流间隔标准下SRO对跑道容量的影响。根据第2节的分析, CCAR-93TM-R5尾流间隔标准下的跑道容量为:
(5)
其中,CCN为CCAR-93TM-R5尾流间隔标准下的跑道容量,PCN(SRO)为该标准下发生SRO的概率,TAVG_CN为该标准下连续进近航空器平均间隔时间。
FAA RECAT1.5尾流间隔标准下的跑道容量为:
(6)
其中,CUS为FAA RECAT1.5尾流间隔标准下的跑道容量,PUS(SRO)及TAVG_US分别为该尾流间隔标准下发生SRO的概率及连续进近航空器平均间隔时间。由公式(5)、(6)可知,SRO对不同尾流间隔标准下的跑道容量影响程度取决于该尾流间隔标准下发生SRO的概率大小。
不考虑SRO的影响,尾流间隔标准的改变对跑道容量的提升为:
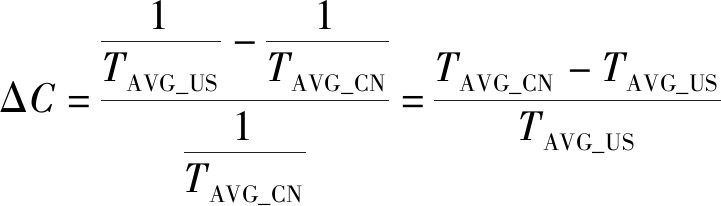
(7)
实际上,SRO对跑道容量的影响不能忽视,考虑SRO的影响,尾流间隔标准的改变对跑道容量的提升为:
(8)
将式(5)、式(6)代入式(8),整理得
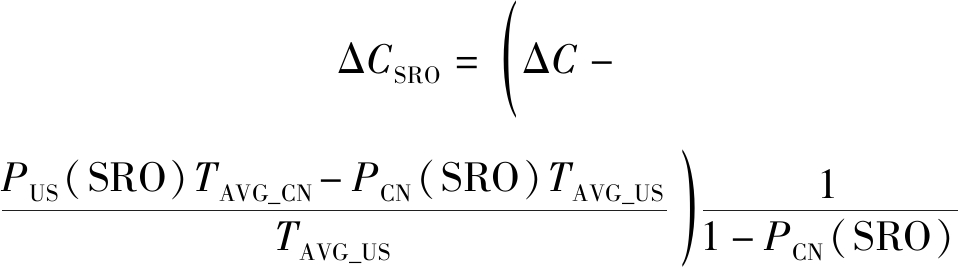
(9)
在CCAR-93TM-R5尾流间隔标准下,发生SRO概率的极低,几乎可以忽略不计,即PCN(SRO)≈0,SRO对由尾流间隔缩减提升跑道容量造成的偏差Cd约为:
(10)
4 ROT及LTI分布拟合及参数估计
ADS-B是一种利用全球卫星定位系统实现精确定位,将飞机位置、速度、身份和飞行状态信息向地面站和其他航空器进行周期性广播的新监视技术[17]。ADS-B解析数据地表位置信息详细记录了飞机经纬度、运动状况和朝向/地面航迹等信息。本文基于ADS-B解析数据地表位置信息表(TYPE05TO08),统计了2019年8月1日至8月6日9:00-24:00时段内的着陆航空器ROT。
4.1 单一分布拟合ROT
将由ADS-B解析数据统计得到的天津滨海国际机场着陆航空器ROT绘制频率密度直方图并进行分布拟合,取拟合程度较高的四种类型,结果如图2所示,每种拟合类型的估计参数值如表1所示。
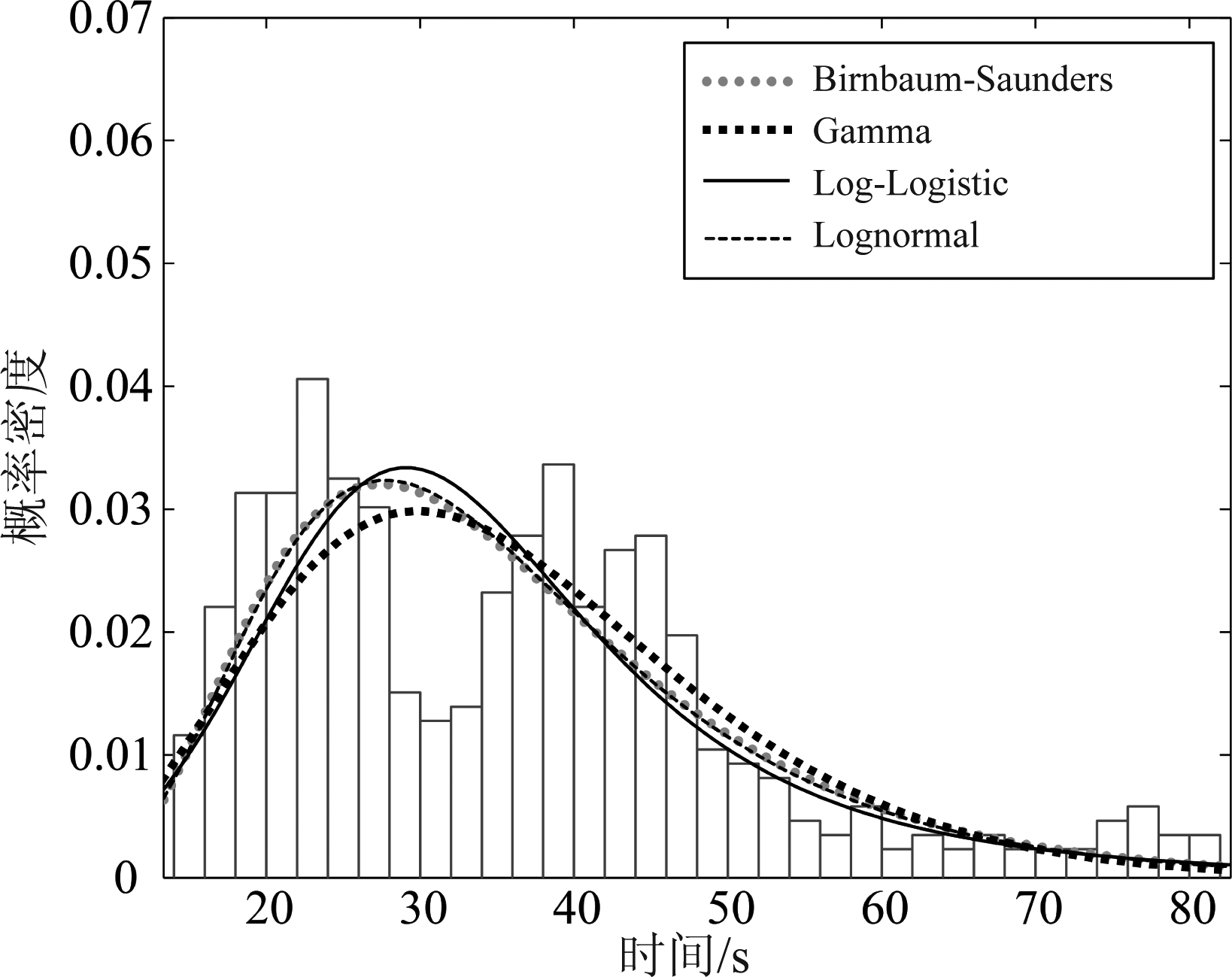
图2 ROT分布拟合
Fig.2 ROT distribution fitting
表1 ROT分布拟合类型及估计参数
Tab.1 ROT distribution fitting types and estimated parameters
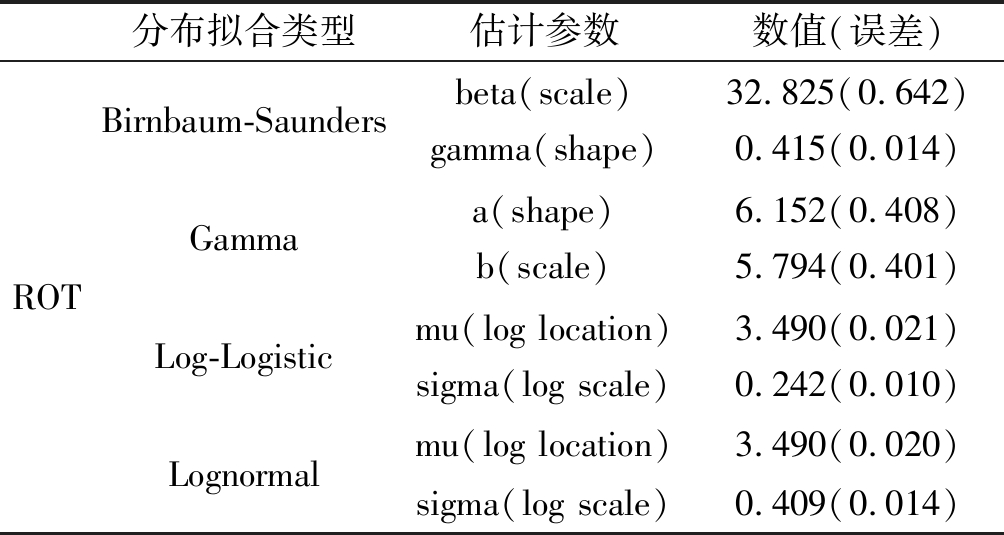
分布拟合类型估计参数数值(误差)ROTBirnbaum-SaundersGammaLog-LogisticLognormalbeta(scale)gamma(shape)32.825(0.642)0.415(0.014)a(shape)b(scale)6.152(0.408)5.794(0.401)mu(log location)sigma(log scale)3.490(0.021)0.242(0.010)mu(log location)3.490(0.020)sigma(log scale)0.409(0.014)
从图2可以看出,天津滨海国际机场ROT分布是双峰分布,用单一分布做拟合较难满足ROT分布的多峰特性。一般来说,峰的个数与跑道出口的个数是一致的,不同峰所在位置体现了不同跑道出口的航空器数量,反映了通过该出口的航空器跑道占用时间的集中性。不同机场的跑道出口个数不同,ROT分布峰的个数也就不同。
为了更好地描述ROT分布的多峰性和有偏性。本文用混合偏态分布模型[18]来拟合上述ROT分布。
4.2 混合偏态分布模型拟合ROT
混合偏态分布模型可以用于拟合非常丰富的分布,能够更好地描述ROT分布的有偏性和多峰性。混合偏态分布是多个偏态分布的线性组合,基于K个偏态分布线性加权的混合偏态分布概率密度函数为
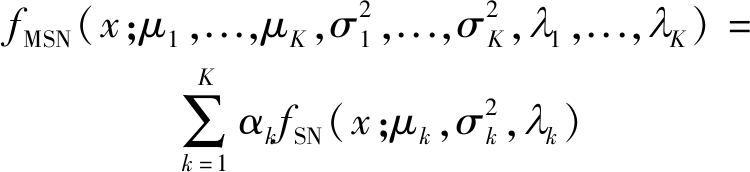
(11)
式中,αk为权重系数,表明不同偏态分布在混合偏态分布中的权重。![]() 表示第k个偏态分布的概率密度函数,
表示第k个偏态分布的概率密度函数,
(12)
其中,![]() 分别为偏态分布的位置参数、尺度参数和偏度参数。式中φ(·)和Φ(·)分别为标准正态分布的概率密度函数和分布函数。
分别为偏态分布的位置参数、尺度参数和偏度参数。式中φ(·)和Φ(·)分别为标准正态分布的概率密度函数和分布函数。
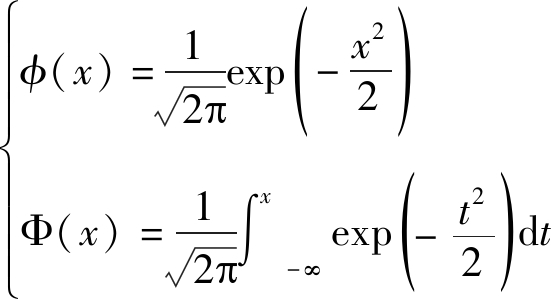
(13)
根据文献[18],用最小二乘法对ROT分布进行非线性拟合,即求取模型参数使得分布模型和频率(数)密度曲线之间的残差平方和最小,满足:
min(fMSN(X,C)-Y)(fMSN(X,C)-Y)Τ
(14)
式中,C为待估计参数向量,包含混合模型中每个模型的四个参数;向量对(X,Y)为频率(数)密度直方图的描点,X、Y均为行向量。
本文借助matlab中lsqnonlin函数对ROT频数分布进行拟合,通过设置拟合初始参数、多次调参,最终拟合结果如图3所示,拟合估计参数见表2。
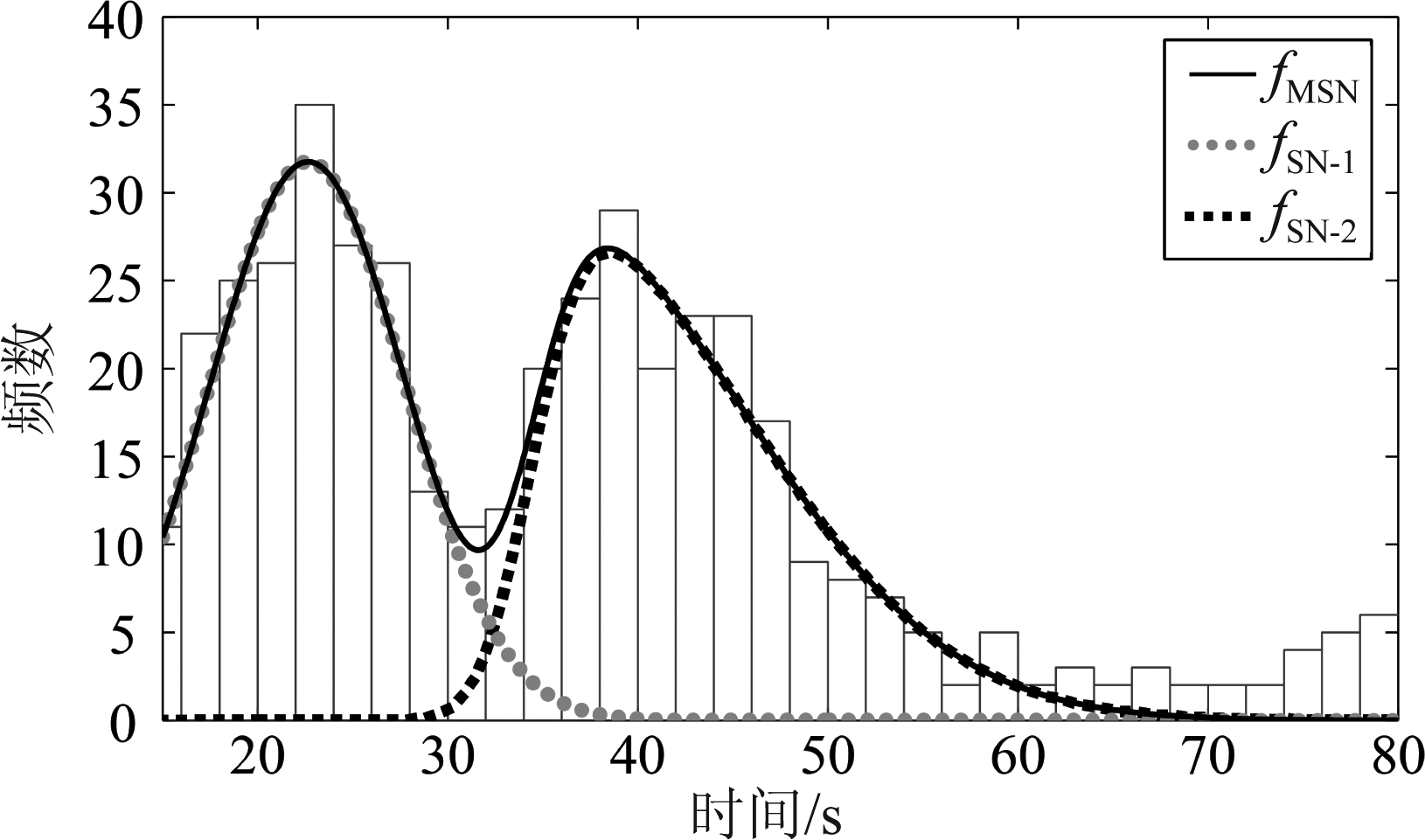
图3 混合偏态分布模型拟合ROT
Fig.3 Mixed skew distribution model to fit ROT
表2 混合偏态分布拟合估计参数
Tab.2 Estimated parameters of mixed skew distribution

图3中, fSN-1与fSN-2分别为两个偏态分布, fMSN为由两个偏态分布线性加权得到的混合偏态分布。可以看到,较单一分布拟合ROT,混合偏态分布用每个偏态分布拟合一个单峰,从而在整体上可以较好地描述ROT分布的多峰性。
4.3 LTI分布拟合及参数估计
为了分析不同尾流间隔标准下SRO对跑道容量的影响,本文根据FAA RECAT1.5机型分类标准、天津滨海国际机场的机型统计比例、各种机型的平均进近速度及文献[11]设置的相关参数,用Monte Carlo仿真生成不同尾流间隔标准下的航班流。(注:FAA RECAT1.5机型分类标准、天津滨海国际机场的机型比例、各种机型的平均进近速度见附录E)。将CCAR-93TM-R5标准下连续进近航空器间隔LTICN和FAA RECAT1.5标准下连续进近航空器间隔LTIUS绘制频率密度直方图并进行分布拟合,如图4所示;分布拟合类型及估计参数如表3所示。
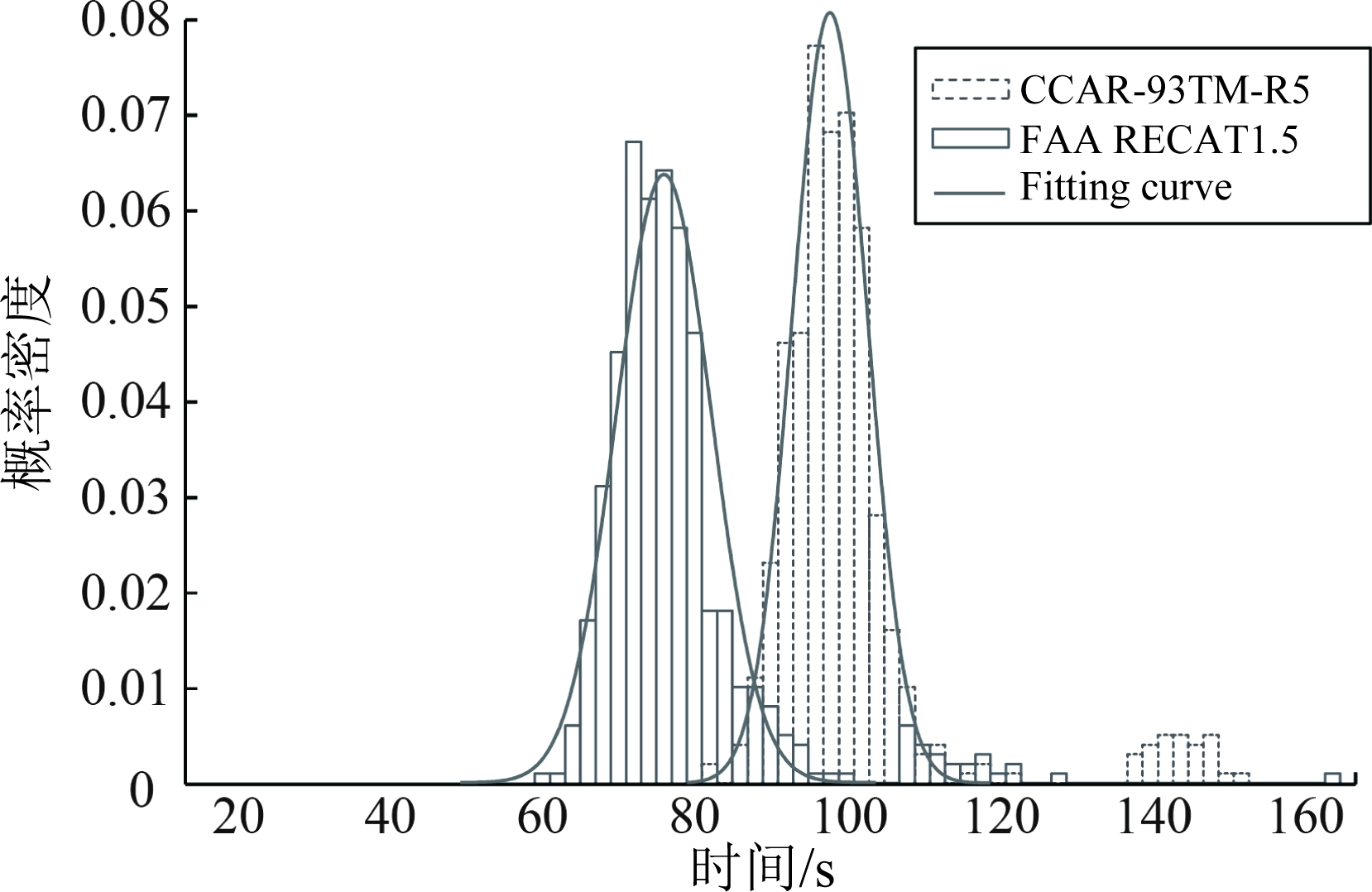
图4 不同尾流间隔标准下LTI分布拟合
Fig.4 LTI distribution fitting under different wake separation
表3 LTI分布拟合类型及参数
Tab.3 LTI distribution types and parameters of the fitting

分布拟合类型拟合参数及误差LTICNNormalμ=98.837(0.227)σ=4.947(0.161)LTIUSNormalμ=76.809(0.288)σ=6.269(0.204)
从表3可以看出,不同尾流间隔标准下LTI分布可以用正态分布来拟合。尾流间隔标准变化前后,LTI的期望值有着明显减小,这是因为当尾流间隔缩减后,部分航空器机型之间的间隔减小,使得航空器间隔总体均值减小。
5 计算发生SRO的概率
为了定量评估SRO对跑道容量的影响,需要首先计算发生SRO的概率大小。综合图2、图3的分布拟合结果,依据表1、表2和表3的拟合估计参数,根据第2节的分析及公式(1),用Matlab计算不同尾流间隔标准、不同ROT分布拟合类型发生SRO的概率大小,如图5所示,计算数值见表4。
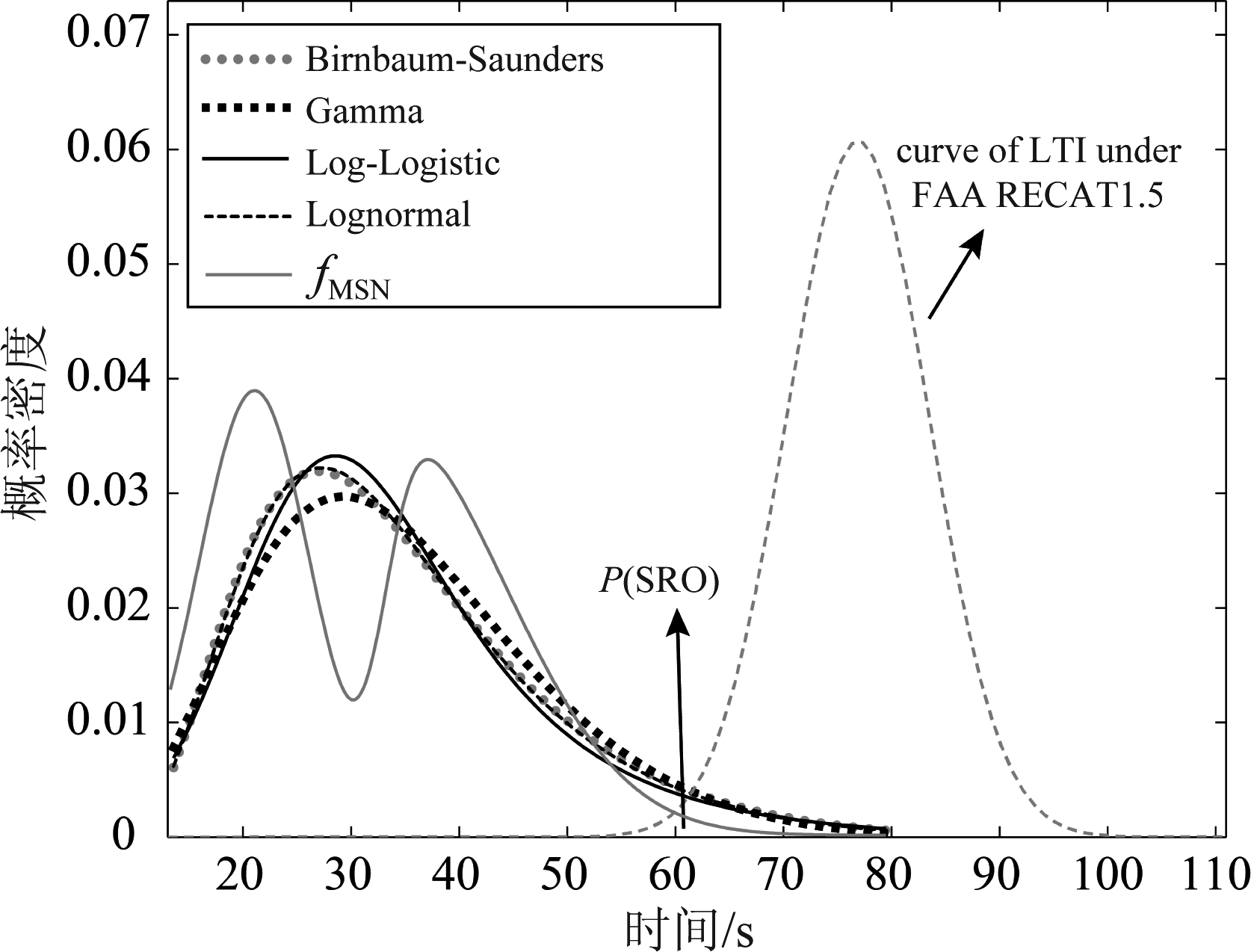
图5 发生SRO的概率计算
Fig.5 The probability calculation of SRO
表4 不同尾流间隔标准下发生SRO的概率计算
Tab.4 The probability calculation of SRO under different wake separation
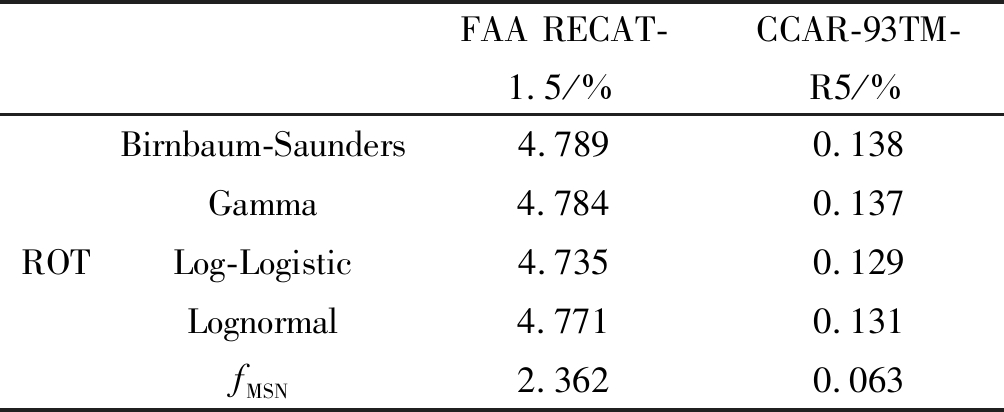
FAA RECAT-1.5/%CCAR-93TM-R5/%ROTBirnbaum-Saunders4.7890.138Gamma4.7840.137Log-Logistic4.7350.129Lognormal4.7710.131fMSN2.3620.063
由于CCAR-93TM-R5尾流间隔标准下发生SRO的概率极低,反映在图中LTICN与不同类型ROT分布重叠部分几乎不可见,故图5仅绘制了FAA RECAT1.5尾流间隔标准下不同ROT分布拟合类型对应发生SRO的概率。从表4可以看出,尾流间隔标准的变化使得发生SRO的概率成倍增加,新尾流间隔标准下,SRO对跑道容量的影响不能忽视。且用单一分布拟合ROT所得到的发生SRO的概率大小接近,但用混合偏态分布模型所拟合得到的数值要低,这是因为ROT分布总体上呈现多峰、偏态的特性,因此用单一分布拟合ROT总会存在一定的偏差。本文以混合偏态分布模型拟合ROT所得结果为例,经公式(7)~(10)分析计算可知,不考虑SRO的影响,尾流间隔标准的变化使得跑道容量的增长率为28.69%;实际上,跑道容量增长率为25.74%,SRO对跑道容量的提升会造成2.95%的偏差。
6 ROT和LTI对SRO及跑道容量的影响分析
空管导航新技术(GBAS、PBN、MLS),监视新技术(ADS-B),进近离场新程序(SOIA、HALS/DTOP)的使用,以及TBO(Trajectory based Operation)、TBS(Time based Separation)的实施,使得航空器的实际航迹与预定航迹的偏离变小、到达指定空域点的实际时间与预计时间偏差变低,从而使得机场系统运行误差降低、航行精度提高。新技术、新举措的实施通过优化跑道占用时间以及航空器缓冲间隔,影响了ROT及LTI的频率分布状况。由前面的分析可知,SRO及跑道容量与ROT和LTI密切相关,由ROT和LTI数据频率分布状况所决定,受分布拟合概率密度曲线参数影响。分析ROT、LTI对SRO及跑道容量的影响,能够在一定程度上反映并量化新技术、新举措在机场的应用对SRO及跑道容量所带来的潜在改变。由于不同机场的ROT和LTI分布不同,针对不同机场的情况进行定量分析可能有所差异,但为了给出一般性的结论,本节以正态分布为例,分析μROT、σROT、μLTI、σLTI对SRO和跑道容量的影响。其中,μROT、σROT、μLTI、σLTI分别为ROT和LTI的期望值、标准差。
6.1 ROT对SRO及跑道容量的影响
根据第2节的分析及公式(1),经附录A推导得:
(15)
为分析μROT、σROT对SRO的影响,计算P(SRO)对μROT、σROT的偏导数,经附录B推导可知,
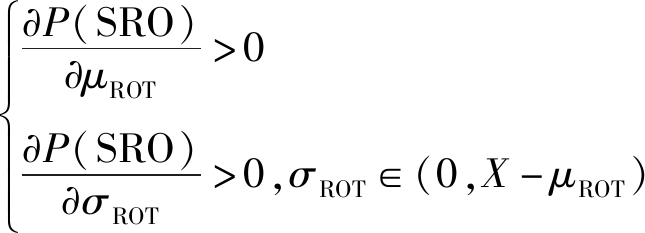
(16)
有式(16)恒成立。式(16)表明发生SRO的概率与μROT、σROT∈(0,X-μROT)为递增关系。
根据公式(4)及T的含义可知,T在数值上应等于LTI概率分布的期望值μLTI,故有式(17)成立。
(17)
根据式(16)、式(17)可知:跑道容量与μROT、σROT∈(0,X-μROT)为递减关系,μROT、σROT越大,跑道容量越小。
6.2 LTI对SRO及跑道容量的影响
为分析μLTI、σLTI对SRO的影响,计算P(SRO)对μLTI、σLTI的偏导数,经附录C推导可知,
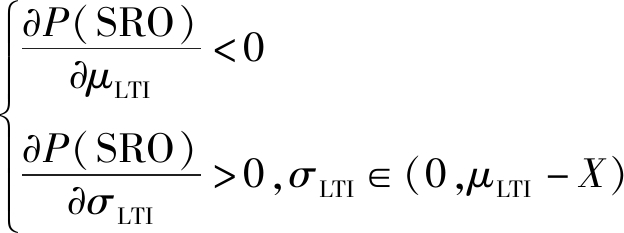
(18)
有式(18)恒成立。式(18)表明发生SRO的概率与μLTI为递减关系,与σLTI∈(0,μLTI-X)为递增关系。μLTI越小,发生SRO的概率越大;σLTI∈(0,μLTI-X)越小,发生SRO的概率越小。
为分析μLTI、σLTI对跑道容量的影响,根据式(17)计算跑道容量C对σLTI的偏导数,经分析可知![]() 在σLTI∈(0,μLTI-X)时恒成立,故跑道容量与σLTI∈(0,μLTI-X)为递减关系。
在σLTI∈(0,μLTI-X)时恒成立,故跑道容量与σLTI∈(0,μLTI-X)为递减关系。
根据式(17)计算跑道容量对μLTI的偏导数,经附录D推导可知,存在使得跑道容量最大的μLTI,其值为:
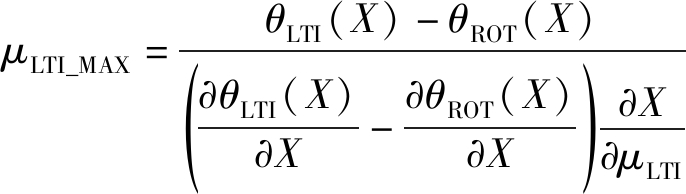
(19)
其中,
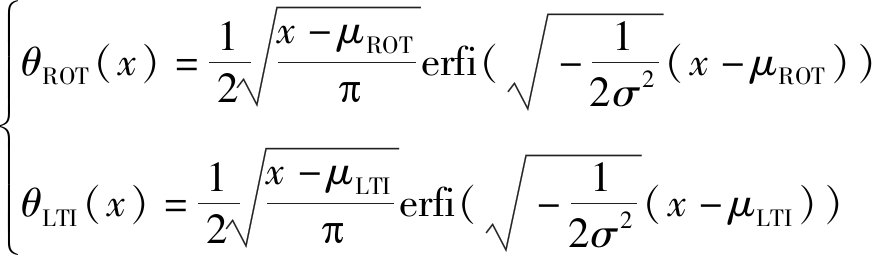
(20)
式(19)表明,只有当μLTI=μLTI_MAX时,跑道容量才为最大;高于或者低于这个值,跑道容量都会降低。
7 评估ROT和LTI对SRO及跑道容量的影响
由第6节的分析可知,影响参数的变动都会在一定程度上使得发生SRO的概率和跑道容量发生改变,为分析不同影响参数对SRO及跑道容量的影响程度,分别将影响参数减小20%[12],分析发生SRO的概率及跑道容量的变化量,记两者的改变量分别为ΔP(SRO)和ΔC,分析结果如图6所示。(注:“20%”参数值的设置对应新程序新举措在机场实施后对整个系统误差的影响,参数的设置具有实际意义。)
图6条形图的长度表示四个影响参数分别减小原来的20%后对发生SRO的概率和跑道容量的影响程度,长度越长表示影响越大。从中可以看出,参数的变化都会影响发生SRO的概率和跑道容量,但μLTI对两者的影响最大。分析结果符合我们的经验和预期,因为μLTI由尾流间隔标准决定,而P(SRO)和跑道容量主要受不同尾流间隔标准下的LTI决定,故μLTI对两者的影响最大。
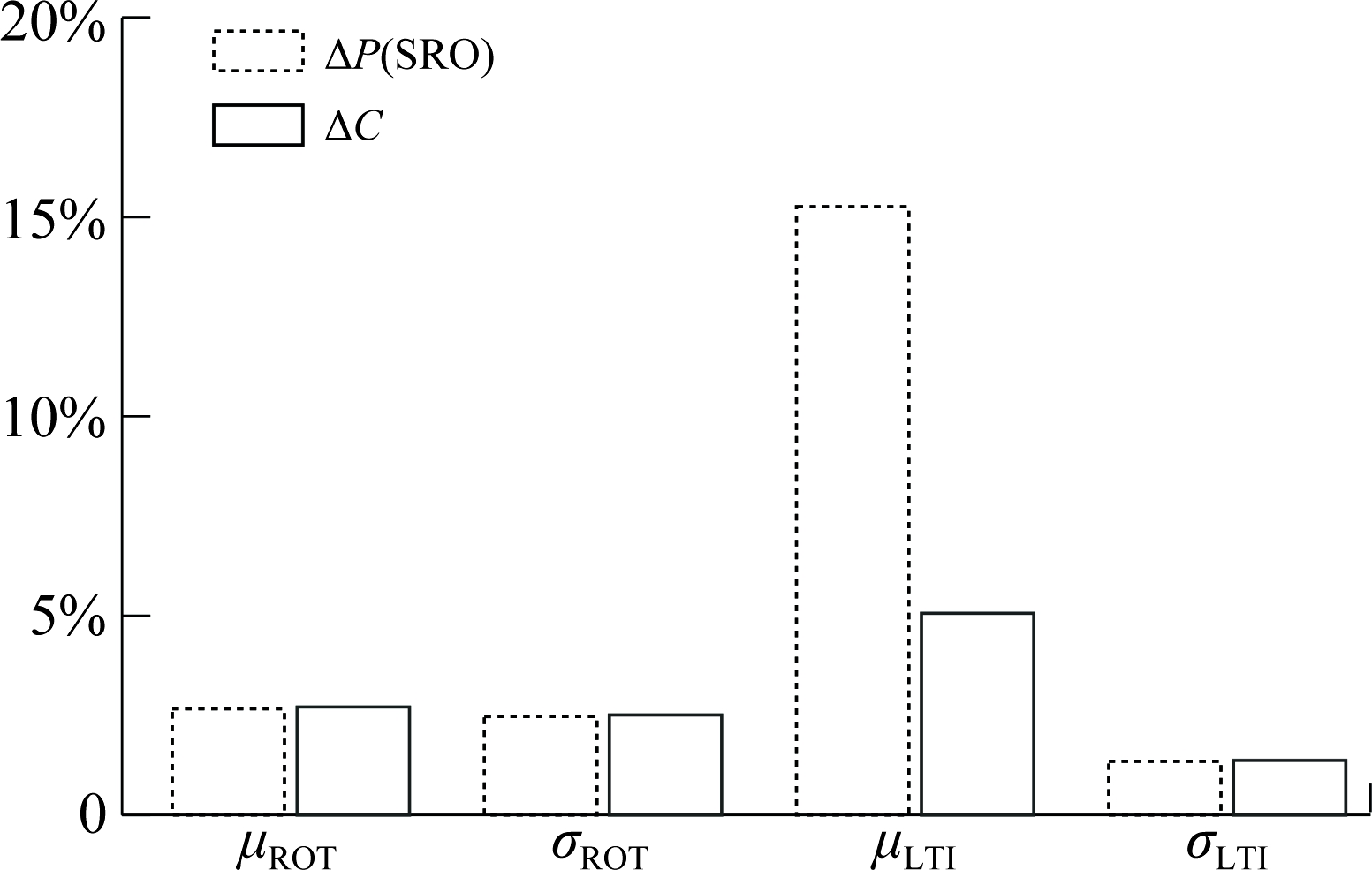
图6 影响参数减小20%对P(SRO)和跑道容量的影响
Fig.6 Impact parameters reduced by 20% on runway capacity and P(SRO)
为评估μROT、σROT对SRO和跑道容量的影响,根据第6节的分析及ROT的分布拟合结果,将σROT从14开始按步长为2的规则递减,以μROT为横轴、P(SRO)为纵轴分析μROT、σROT对SRO的影响,如图7所示;以μROT为横轴、跑道容量为纵轴分析μROT、σROT对跑道容量的影响,如图8所示。
从图7可以看出,P(SRO)与μROT和σROT的关系与第6节理论分析的结果一致,当μROT低于30后,发生SRO的概率几乎为0,从图8可以看出,这时的跑道容量也随之接近极限。这表明通过减小ROT来增加跑道容量是可能的措施之一。例如,1、采用锐角跑道出口替代传统的90°跑道出口2、对于多出口跑道,优化停机位分配等。这些措施都会通过降低ROT,来减小发生SRO的概率,提高跑道容量。
综合图7、图8来看,由于μROT增大会使发生SRO的概率增大,故跑道容量受SRO的影响会随着μROT的增加而下降,但当μROT减小时,发生SRO的概率趋于0,跑道容量会缓慢增大到一个最大值。这表明,通过减小ROT来增加跑道容量是可能的措施之一,但容量的提升是有限的。
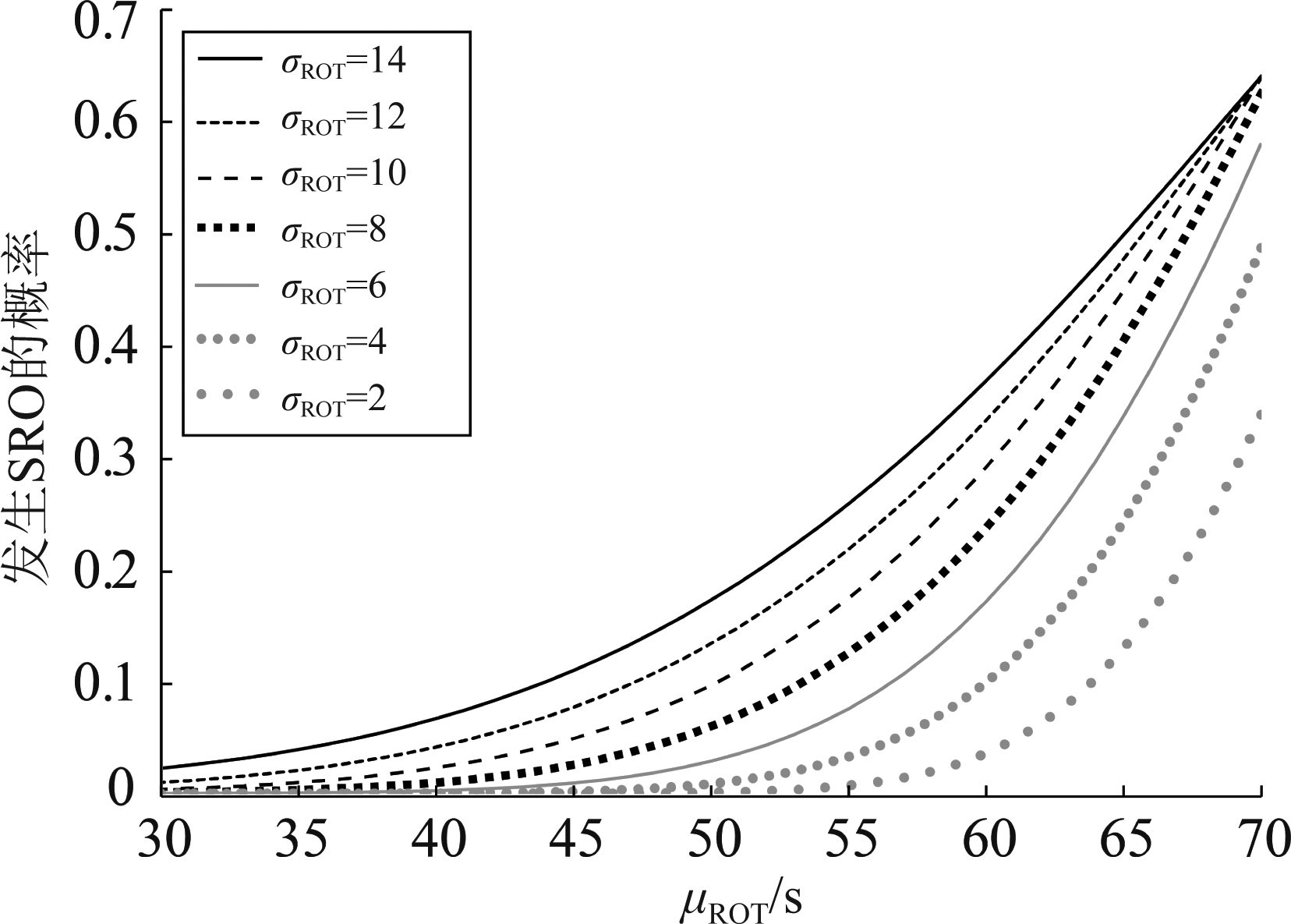
图7 ROT参数对P(SRO)的影响
Fig.7 Effect of ROT parameters on P(SRO)
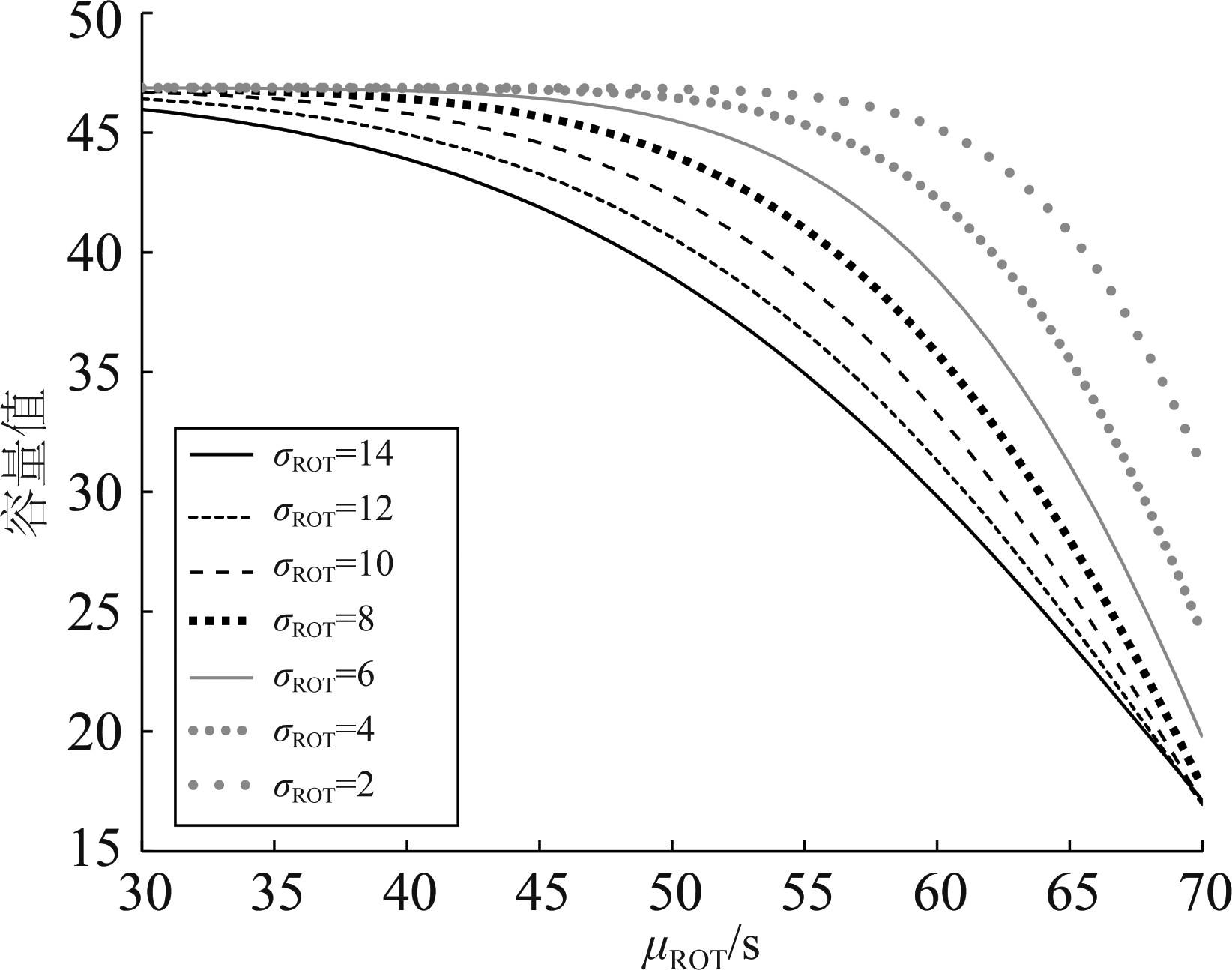
图8 ROT参数对跑道容量的影响
Fig.8 Effect of ROT parameters on runway capacity
为评估μLTI、σLTI对SRO和跑道容量的影响,根据第6节的分析及LTI的分布拟合结果,将σLTI从6开始按步长为1的规则递减,以μLTI为横轴、P(SRO)为纵轴分析μLTI、σLTI对SRO的影响,如图9所示;以μLTI为横轴、跑道容量为纵轴分析μLTI、σLTI对跑道容量的影响,如图10所示。
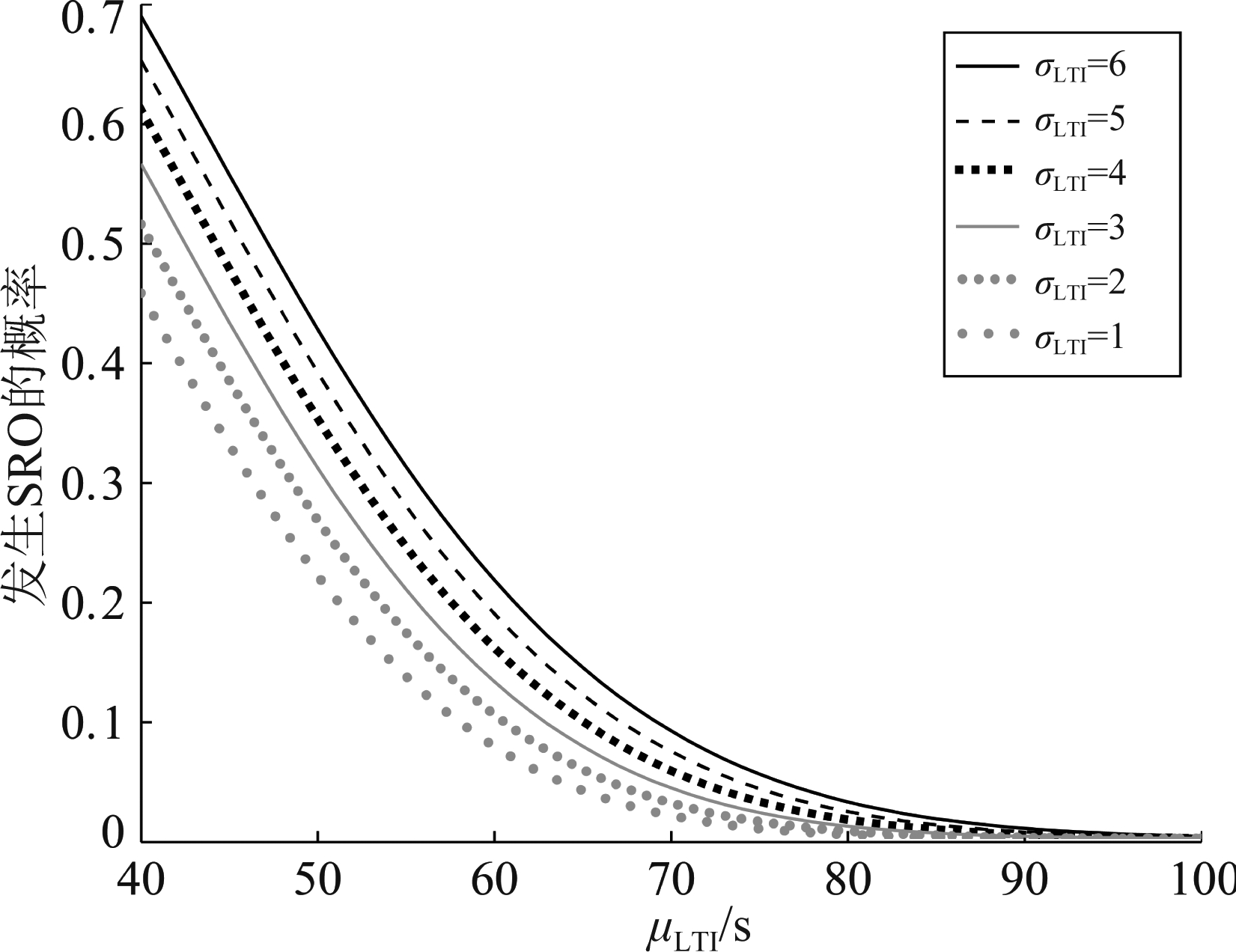
图9 LTI参数对P(SRO)的影响
Fig.9 Effect of LTI parameters on P(SRO)
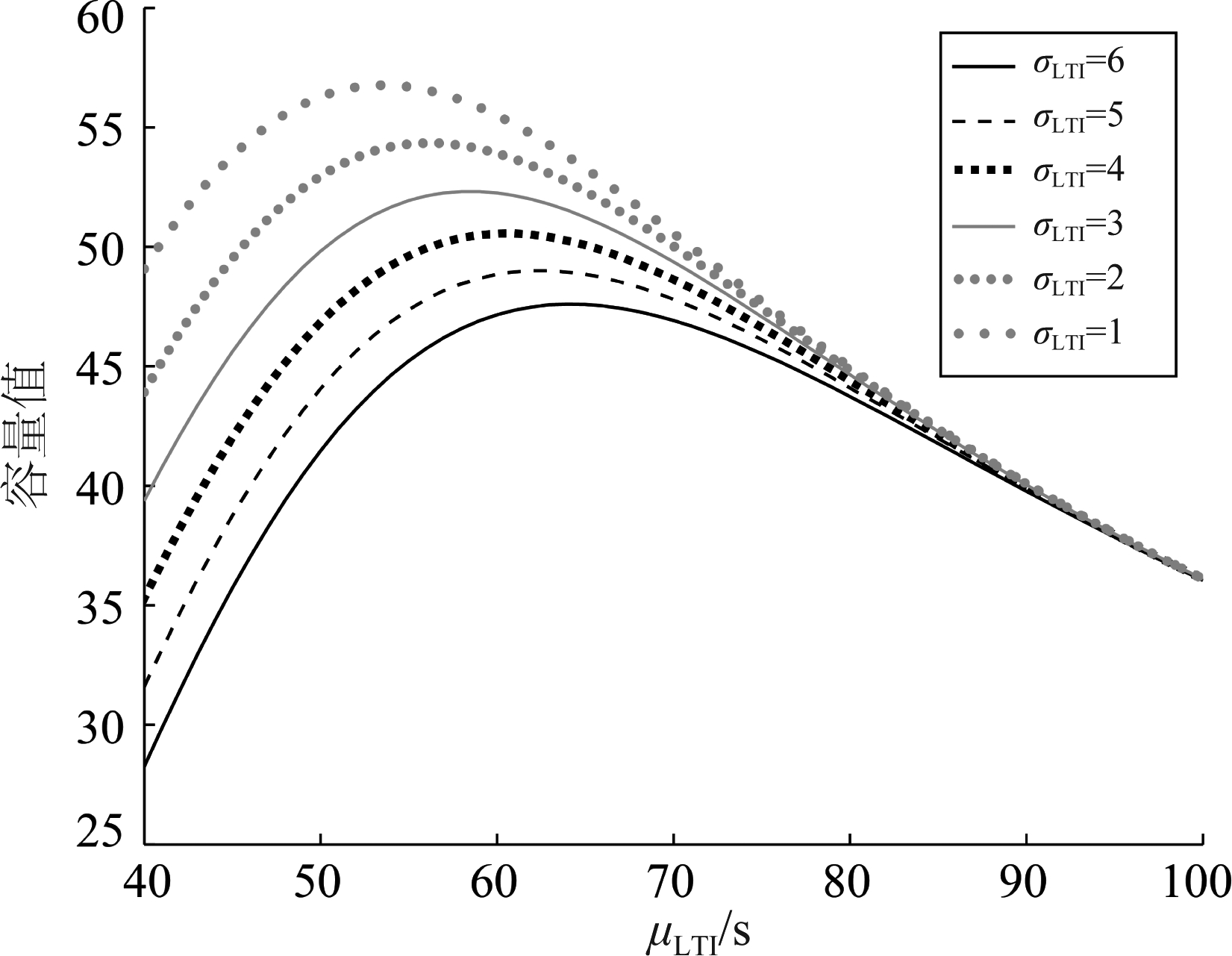
图10 LTI参数对跑道容量的影响
Fig.10 Effect of LTI parameters on runway capacity
从图9可以看出,P(SRO)与μLTI、σLTI的关系与第6节理论分析的结果一致。综合图7、图9来看,影响参数的标准差(σROT、σLTI)越小,发生SRO的概率越低,而标准差的改变与航行精度及机场系统运行误差密切相关,根据第6节的分析,通过引用新的导航、监视和通信技术可以降低航行误差、提高航行精度,进而减小影响参数的标准差,降低发生SRO的概率,在一定程度上提高跑道容量。
综合图9、图10来看,μLTI越大,SRO发生的概率越低,但是跑道容量会因单位时间内可服务的航空器数量下降而降低;μLTI越小,SRO发生的概率越大,跑道容量会因发生SRO而降低。这表明,可以通过合理安排航空器间隔使得跑道容量趋于最大。
8 结论
本文定量计算了不同尾流间隔标准下发生SRO的概率,分析了尾流间隔缩减前后跑道容量的变化情况,计算了ROT及LTI参数对SRO及跑道容量的影响。研究结论如下:
(1)在现阶段尾流间隔标准下,SRO的影响微乎其微,发生SRO的概率为0.063%;在新尾流间隔标准下,发生SRO的概率为2.362%。
(2)不考虑SRO对跑道容量的影响,尾流间隔标准的改变使得跑道容量提升28.69%。事实上,SRO的影响不能忽视,跑道容量实际提升25.74%,SRO会造成2.95%的偏差。
(3)通过分析ROT和LTI参数对SRO和跑道容量的影响可知,减小ROT、缩减尾流间隔、引用空管新技术都可以在一定程度上降低发生SRO的概率并提高跑道容量。通过减小ROT来提升跑道容量,该措施对容量的提升是有限的;存在使得跑道着陆容量最大的航空器间隔,空管人员可根据实际情况适当调整航空器间隔,使得容量趋于最大;引用新技术能够在一定程度上通过降低系统误差、提高航行精度,来降低发生SRO的概率并提升跑道容量。
附录A
XCN为fROT(x)与fLTICN(x)交点的横坐标,XUS为fROT(x)与fLTIUS(x)交点的横坐标。
(A1)
(A2)
(A3)
令fROT(x)=fLTICN(x),解得:
(A4)
令fROT(x)=fLTIUS(x),解得:
(A5)
说明:附录A的推导计算是将不同尾流间隔标准下的X分别求出,而第4节关于X的计算结果为该部分推导结果的一般形式,两者本质上是一致的。
附录B
设F(X,μROT,σROT,μLTI,σLTI)=0为ROT与LTI共同确定的方程式,对各个参数求导数,结果如下:
(B1)
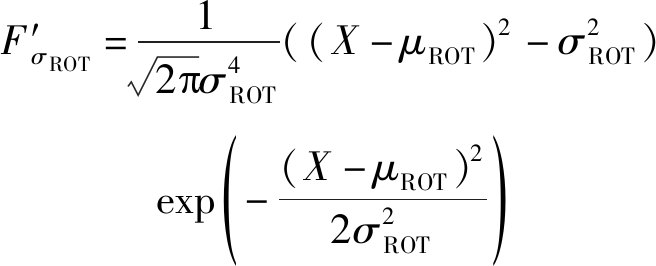
(B2)
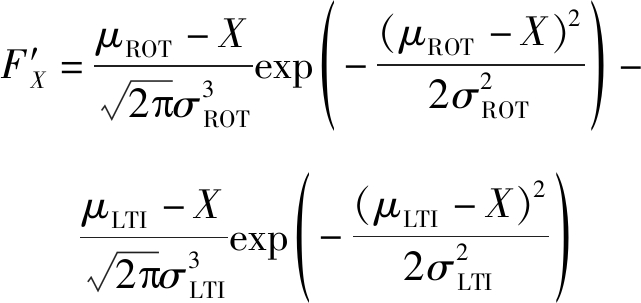
(B3)
根据隐函数微分法则,有
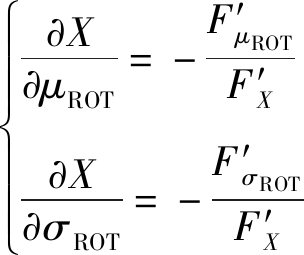
(B4)
因为μLTI>X>μROT,所以![]() 恒成立,而当σROT位于区间(0,X-μROT)之内时,
恒成立,而当σROT位于区间(0,X-μROT)之内时,![]() 成立。
成立。
因为
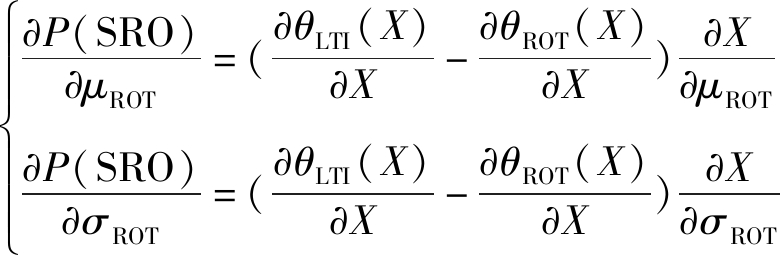
(B5)
其中,
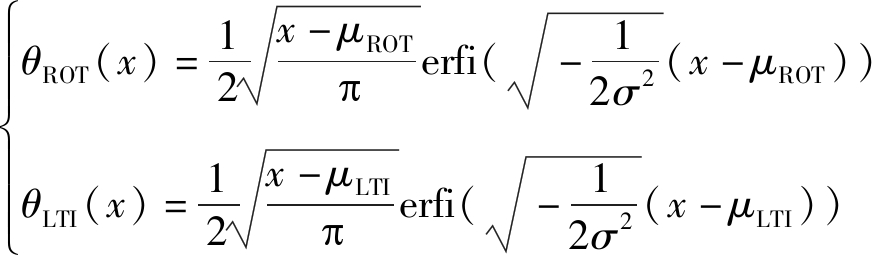
(B6)
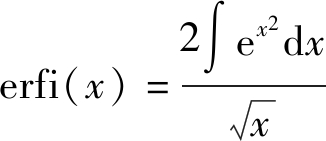
(B7)
而![]() 恒成立,故
恒成立,故![]() 在σROT∈(0,X-μROT)时恒成立。
在σROT∈(0,X-μROT)时恒成立。
附录C
对F(X,μROT,σROT,μLTI,σLTI)=0参数求偏导得:
(C1)
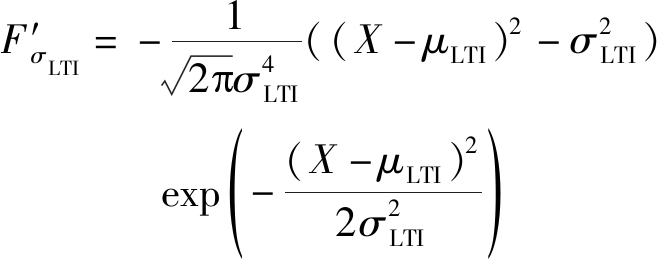
(C2)
因为
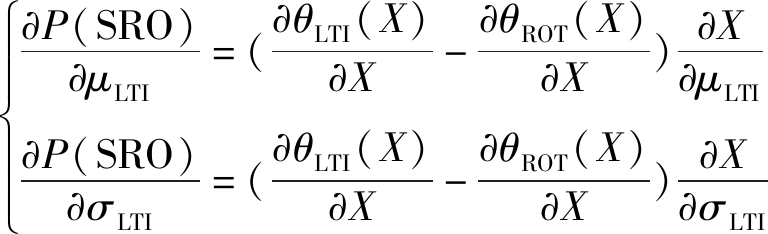
(C3)
且有![]() 恒成立,而当σLTI位于区间(0,μLTI-X)之内时,
恒成立,而当σLTI位于区间(0,μLTI-X)之内时,![]() 成立。故
成立。故![]() 在σLTI∈(0,μLTI-X)时恒成立。
在σLTI∈(0,μLTI-X)时恒成立。
附录D
![]() 增大,C减小;μLTI减小,P(SRO)增大,C减小。故存在最合适的μLTI值使得跑道容量最大。令
增大,C减小;μLTI减小,P(SRO)增大,C减小。故存在最合适的μLTI值使得跑道容量最大。令
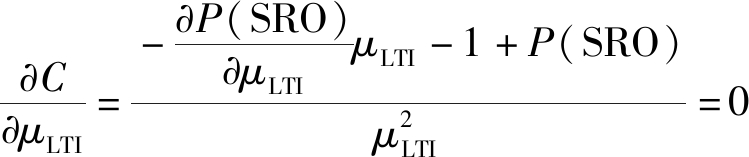
(D1)
这是一个一阶线性微分方程,用积分因子法求得
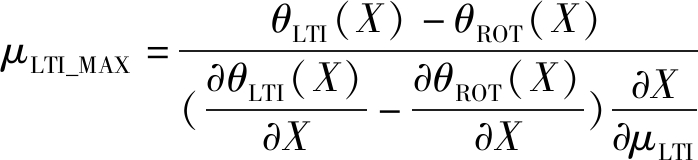
(D2)
μLTI_MAX便是使得跑道容量最大的值。
经求导得,
(D3)
由C3可知,![]() 在σLTI∈(0,μLTI-X)时恒成立,所以
在σLTI∈(0,μLTI-X)时恒成立,所以![]() 在σLTI∈(0,μLTI-X)时恒成立。
在σLTI∈(0,μLTI-X)时恒成立。
附录E
FAA RECAT1.5航空器分类标准如表5所示,天津滨海国际机场的机型比例如表6所示。
表5 机型分类标准
Tab.5 Type classification standard
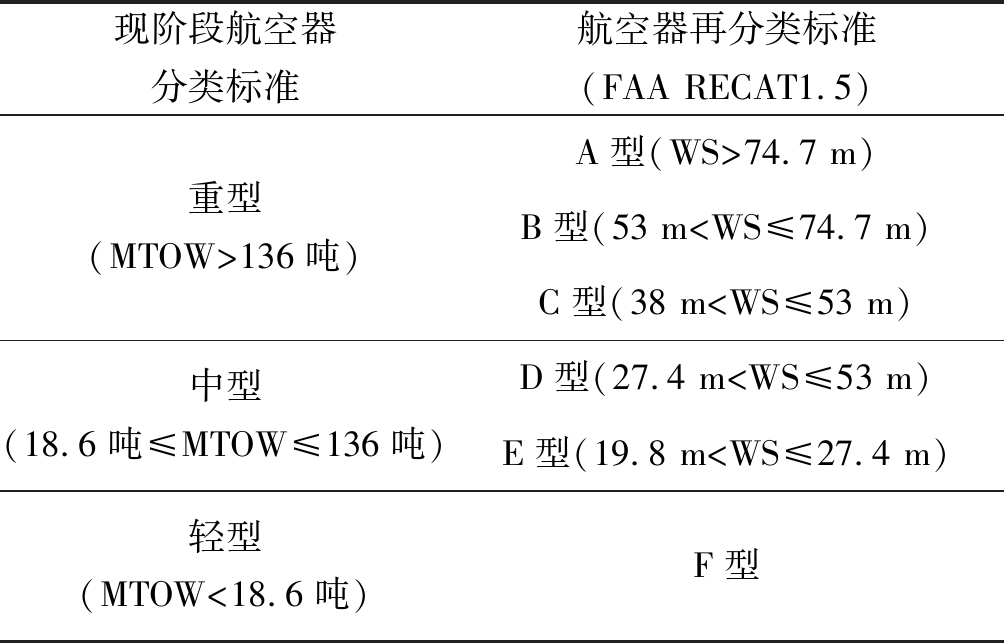
现阶段航空器分类标准航空器再分类标准(FAA RECAT1.5)重型(MTOW>136吨)A型(WS>74.7 m)B型(53 m 注:最大起飞重量(maximum take-off weight, MTOW),翼展(wingspan, WS)。
表6 机型比例统计
Tab.6 Type ratio statistics

CCAR-93TM-R5FAA RECAT1.5重型 6%B型 6%中型94%D 型86%E 型8%
FAA RECAT1.5雷达尾流间隔标准如表7所示(由于天津滨海国际机场仅有B、D及E型航空器运行,故仅统计B、D及E型航空器)。
表7 RECAT-EU/FAA RECAT1.5雷达尾流间隔
Tab.7 Radar wake separation of RECAT-EU or FAA RECAT1.5
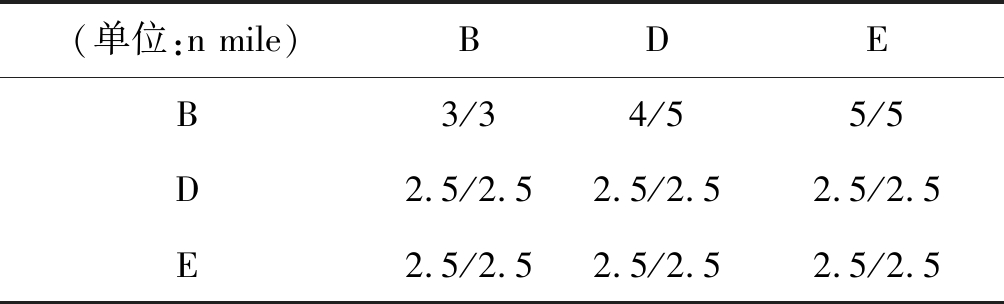
(单位:n mile)BDEB3/34/55/5D2.5/2.52.5/2.52.5/2.5E2.5/2.52.5/2.52.5/2.5
从表7可以看出,FAA RECAT1.5给出的是雷达尾流间隔标准,需转换成时基尾流间隔标准。转换方法用到雷达尾流间隔标准和各个机型的平均进近速度,资料表明:B、D和E型航空器的平均进近速度分别为270 km/h、255 km/h和210 km/h。转换之后的时基尾流间隔标准如表8所示。
表8 FAA RECAT1.5 时基尾流间隔
Tab.8 Wake separation based on time
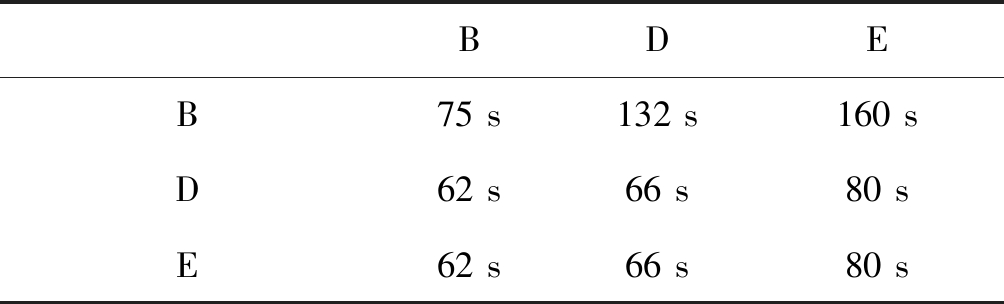
BDEB75 s132 s160 sD62 s66 s80 sE62 s66 s80 s
[1] GILBO E P. Airport capacity: Representation, estimation, optimization[J]. IEEE Transactions on Control Systems Technology, 1993, 1(3): 144-154.
[2] GILBO E P. Optimizing airport capacity utilization in air traffic flow management subject to constraints at arrival and departure fixes[J]. IEEE Transactions on Control Systems Technology, 1997, 5(5): 490-503.
[3] YANG Shangwen, TONG Ming. Applied technology with robust optimization of airport capacity dynamic system[J]. Applied Mechanics and Materials, 2014, 540: 507-511.
[4] MA Ji, SBIHI M, DELAHAYE D. Optimization of departure runway scheduling incorporating arrival crossings[J]. International Transactions in Operational Research, 2021, 28(2): 615- 637.
[5] AHMED M, ALAM S, BARLOW M. A cooperative co-evolutionary optimisation model for best-fit aircraft sequence and feasible runway configuration in a multi-runway airport[J]. Aerospace, 2018, 5(3): 85.
[6] LIEDER A, BRISKORN D, STOLLETZ R. A dynamic programming approach for the aircraft landing problem with aircraft classes[J]. European Journal of Operational Research, 2015, 243(1): 61- 69.
[7] 张军峰, 葛腾腾, 郑志祥. 多机场终端区进离场航班协同排序研究[J]. 交通运输系统工程与信息, 2017, 17(2): 197-204.
ZHANG Junfeng, GE Tengteng, ZHENG Zhixiang. Collaborative arrival and departure sequencing for multi-airport terminal area[J]. Journal of Transportation Systems Engineering and Information Technology, 2017, 17(2): 197-204.(in Chinese)
[8] 厉耀威. 尾流间隔缩减及其碰撞安全性分析[D]. 南京: 南京航空航天大学, 2015.
LI Yaowei. Wake vortex separation reduction and its analysis of collision safety[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2015. (in Chinese)
[9] 冯志勇. 尾流对飞行的影响及安全间隔研究[D]. 成都: 西南交通大学, 2007.
FENG Zhiyong. How wake vortexes affect the flights and safety separation research[D]. Chengdu: Southwest Jiaotong University, 2007. (in Chinese)
[10] 徐肖豪, 赵鸿盛, 王振宇. 尾流间隔缩减技术综述[J]. 航空学报, 2010, 31(4): 655- 662.
XU Xiaohao, ZHAO Hongsheng, WANG Zhenyu. Overview of wake vortex separation reduction systems[J]. Acta Aeronautica et Astronautica Sinica, 2010, 31(4): 655- 662.(in Chinese)
[11] BAKER M, MEGERSA D, PANLILIO A. Runway operational quality assurance[C]∥2013 IEEE Systems and Information Engineering Design Symposium. Charlottesville, VA, USA. IEEE, 2013: 1- 6.
[12] SHORTLE J, SHERRY L. A model for investigating the interaction between go-arounds and runway throughput[C]∥2013 Aviation Technology, Integration, and Operations Conference. Los Angeles, CA. Reston, Virginia: AIAA, 2013.
[13] JEDDI B G ,DONOHUE G L, SHORTLE J F. A statistical analysis of the aircraft landing process[J]. Journal of Industrial and Systems Engineering, 2009, 3(3):152-169.
[14] JEDDI B G,SHORTLE J F.A model for runway landing flow and capacity with risk and cost benefit factors[J].Journal of Industrial and Systems Engineering, 2012, 6(1):1-19.
[15] HU Junqi, MIRMOHAMMADSADEGHI N, TRANI A. Runway occupancy time constraint and runway throughput estimation under reduced arrival wake separation rules[C]∥AIAA Aviation 2019 Forum. Dallas, Texas. Reston, Virginia: AIAA, 2019
[16] 李华融. 多跑道机场容量研究[D]. 南京: 南京航空航天大学, 2013.
LI Huarong. Multi-runway airport capacity research[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2013. (in Chinese)
[17] 陈蕾, 吴仁彪, 卢丹. 利用多普勒效应的ADS-B欺骗式干扰检测方法[J]. 信号处理, 2018, 34(6): 722-728.
CHEN Lei, WU Renbiao, LU Dan. ADS-B spoofing detection method using Doppler effect[J]. Journal of Signal Processing, 2018, 34(6): 722-728.(in Chinese)
[18] 刘燕华, 李伟花, 刘冲, 等. 短期风电功率预测误差的混合偏态分布模型[J]. 中国电机工程学报, 2015, 35(10): 2375-2382.
LIU Yanhua, LI Weihua, LIU Chong, et al. Mixed skew distribution model of short-term wind power prediction error[J]. Proceedings of the CSEE, 2015, 35(10): 2375-2382.(in Chinese)


