1 引言
稀疏恢复问题作为压缩感知中研究和讨论的重要问题之一,被广泛应用于信号处理[1]、医学成像[2]以及雷达系统[3- 4]等跨学科领域中。理论上,由受噪声干扰的低维观测向量重构原始稀疏信号,通常是一个欠定和病态的问题,目前主要有三类算法对其进行优化求解,它们分别是:贪婪算法[5- 6]、凸松弛算法[7- 8]和迭代阈值算法[9-12]。贪婪算法主要包括各类匹配追踪算法,通过多次迭代从过完备原子库里寻找稀疏向量的支撑集,并使用最小二乘估计重构信号。这类算法通常需要的测量数据多,计算量大,收敛速度也较慢。凸松弛算法主要通过凸优化方法解决凸或拟凸优化问题, 从而恢复出稀疏信号。相对于贪婪算法,该类算法大大减少了重构信号所需的观测次数,得到的解是满足条件的最稀疏解。迭代阈值算法通过阈值确定迭代中的保留项,进一步更新待恢复信号。文献[11]中提出的迭代软阈值算法(Iterative Soft-Thresholding Algorithm,ISTA)通过一个软阈值操作更新信号,复杂度小且结构简单,受到广泛的研究与应用。但ISTA收敛速度较慢。文献[12]基于ISTA的框架提出一种快速迭代软阈值算法(Fast Iterative Soft-Thresholding Algorithm,FISTA),该算法选择前两次迭代点的线性组合作为下一次迭代时近似函数的起始点,进一步提高收敛速率,但收敛速度依旧有限。
近年来,许多国内外学者开始将深度学习技术应用到稀疏恢复求解中。文献[13]介绍了一种迭代软阈值学习算法(Learned Iterative Soft-Thresholding Algorithm,LISTA),将ISTA展开为递归前馈神经网络,通过学习的方式优化更新字典矩阵,可更快地趋向最优解。文献[14]提出一种快速迭代软阈值学习算法(Learned Fast Iterative Soft-Thresholding Algorithm,LFISTA),构建了与LISTA类似的递归神经网络,进一步提高了算法的收敛速度。文献[15-16]基于LISTA分别引入了不同的约束条件以达到加速收敛的目的。文献[15]利用LISTA结构中两个可学习矩阵的耦合性,并采取了多种阈值选取方案,在简化网络结构的同时加快了稀疏恢复的速度。文献[16]选取了一个可解析的自由权值矩阵,优化并固定该解析矩阵,通过学习调整权值步长和阈值参数即可加速收敛。从上述研究内容可知,深度学习技术的引入可以有效地提高ISTA的收敛速度,在此基础上,通过增加约束条件可进一步加速收敛。
实际上,稀疏恢复优化问题属于约束最小化问题的一种情况,一阶迭代固定步长算法[17-19]一般适用于解决该类问题。文献[20]利用李雅普诺夫函数证明了一阶迭代固定步长算法可线性收敛。受到该思想启发,本文提出一种引入多状态记忆机制的改进LISTA(Learned Iterative Soft-Thresholding Algorithm with Multi-state Memory,LISTA-MM)算法。该算法设置了一个状态连接度数,连接多个先前迭代点,学习迭代点的权重矩阵,从而灵活地利用稀疏信息,确保了稀疏估计过程中信息被正确传递并充分利用,能够有效提高收敛速度,并且优化稀疏恢复性能。此外,本文还将LISTA-MM的卷积形式应用在图像超分辨率中,训练了一个图像超分辨率网络模型,并将该网络的重构结果和其他几种图像超分辨率网络的结果进行比较。实验结果表明,基于LISTA-MM的网络在图像质量评估指标上优于其他几种网络,并且重构图像的可视化结果受伪影影响小,具有更接近原始图像的清晰规则纹理。
本文贡献如下:(1)本文提出一种引入多状态记忆机制的改进迭代软阈值学习算法,设置状态连接度数,灵活利用多个迭代状态点信息,提高了算法的收敛速度;(2)通过仿真实验验证了本文算法在保证稀疏恢复精度的同时有效提高了收敛速度;(3)将LISTA-MM扩展为卷积形式,训练了一个图像超分辨率网络模型,探索其在图像超分辨率中的应用,实验结果表明该网络比其他几种图像超分辨率网络具有更好的性能。
本文安排如下:第2节介绍稀疏恢复的求解问题并且详细叙述本文提出的改进迭代软阈值学习算法LISTA-MM;第3节介绍了LISTA-MM的卷积形式及其在图像超分辨率中的应用;第4节展示了本文改进算法与几种迭代软阈值学习算法的对比结果,以及基于LISTA-MM的网络与其他几种图像超分辨率网络的重构结果对比;第5节为本文的结论。
2 引入多状态记忆机制的迭代软阈值学习算法
2.1 稀疏恢复问题的求解
在稀疏恢复问题中,令待恢复信号为z∈RN,假设其非零元素不超过K个(K-稀疏性),D∈RM×N为测量矩阵或过完备字典矩阵(M≪N),则需要从低维观测向量中恢复未知的稀疏信号:
y=Dz+n
(1)
其中,y∈RM是观测向量,n∈RM为噪声向量。上述问题是一个欠定且病态的问题,不能通过简单的线性运算直接求解,常见求解方式是把噪声条件下的稀疏恢复问题表述为下列无约束最小化问题:
(2)
其中||z||1表示稀疏正则项,λ是正则系数。上述问题是一个经典的LASSO问题,ISTA是求解该问题的典型一阶算法,该算法利用第k次迭代时近似函数取得最小值的点zk作为下一次迭代的起始点,每一步的迭代仅涉及矩阵和向量的乘积及软阈值的计算。
ISTA算法被认为是梯度算法的一种自然延伸,首先考虑连续可导的无约束最小化问题:
min{g(z):z∈RN}
(3)
用梯度下降法求解的迭代形式为:
zk+1=zk-tk∇g(zk)
(4)
这里tk>0是迭代步长,梯度下降法可以表示成g在点zk处的近端正则化,其等价形式表示为:
![]() ∇
∇![]()
(5)
令![]() 将这个思想应用于无约束最小化问题(2)得到:
将这个思想应用于无约束最小化问题(2)得到:
![]() ∇g(zk)〉+
∇g(zk)〉+![]()
(6)
忽略式(6)中的常数项可以得到:
zk+1=![]()
(7)
由于l1范数是可分的,式(6)最终可写为
zk+1=hλtk(zk-tk∇g(zk))
(8)
这里hθ(x)=sign(x)max(|x|-θ,0)是以θ为参数的软阈值函数。将![]() 代入式(7),可得到ISTA算法求解问题(2)的具体迭代形式为:
代入式(7),可得到ISTA算法求解问题(2)的具体迭代形式为:
(9)
其中zk表示第k次迭代的稀疏估计值,L通常作为DTD的最大特征值,T表示转置运算符。
受到深度学习技术的启发,文献[13]中的LISTA用![]() 分别替代公式(9)中的
分别替代公式(9)中的![]() 和λ/L,将ISTA展开为一个递归结构神经网络,本质上实现了ISTA的K次截断迭代形式:
和λ/L,将ISTA展开为一个递归结构神经网络,本质上实现了ISTA的K次截断迭代形式:
zk+1=hθ(Szk+Wey),k=1,…,K
(10)
其中两个字典矩阵We、S和阈值参数θ可通过最小化重构误差的方式来学习优化。
2.2 引入多状态记忆机制的迭代软阈值学习算法
值得注意的是,公式(2)中的稀疏恢复问题的目标函数是凸函数,该问题属于约束最小化问题的一种情况:
(11)
其中f:RN→R表示包括l-光滑函数和u-强凸函数在内的一系列问题[20],一阶迭代固定步长算法[17-19]一般适用于解决上述问题。类似于加速近端梯度法的思想,一阶迭代固定步长算法利用先前V次迭代中近似函数取得最小值的点,将这些点通过步长γ加权表示为新点yk,作为下一次迭代的起始点,使得下一步的梯度更新方向与当前的梯度方向不要相差太大,能够有效加速迭代点的收敛,其具体求解形式为:
![]() ∇f(yk)
∇f(yk)
(12)
其中α,βj,γj是(固定)步长,V(≥0)被称为度数。基于一阶迭代固定步长算法的求解思想,本文提出多状态记忆机制并应用到LISTA框架中,其具体数学表达式为:
zk+1=hθ(Sqk+Wey)
(13)
其中权系数γi和矩阵S是相互独立的可学习参数,VLISTA-MM被定义为模型的状态连接度数。本文将每一次更新的迭代点称为一个迭代状态,状态连接度数决定每次迭代需要记忆的先前状态个数。多状态记忆机制是一种信息记忆与传递机制,针对LISTA每次迭代只依赖于前一迭代状态对算法收敛速度的限制,通过状态连接度数设置需要记忆的状态个数,在模型迭代更新时,灵活地记忆并传递多个迭代状态的信息,并利用权系数γ加权得到新状态点qk,将其作为下一次迭代的起始点,确保了迭代过程中不会出现过大的偏差,加快了迭代点向期望值收敛的速度。
将上式软阈值函数中的qk用状态加权和代入,并合并权系数γi和矩阵S,式(13)可重新表示为:
(14)
式中Wi=γiS是迭代点zi的可学习权值矩阵。与LISTA相同,通过最小化重构误差优化更新矩阵We和Wi。图1展示了LISTA-MM的网络部分展开结构。为了方便观察,图中只保留了与迭代点zk+1有关的连接。可以看出,先前的迭代状态通过权值矩阵被选择和传递到当前迭代中,灵活地组合这些迭代状态的信息,从而减小了迭代过程中的估计偏差带来的影响,提高稀疏估计的效率和正确性。
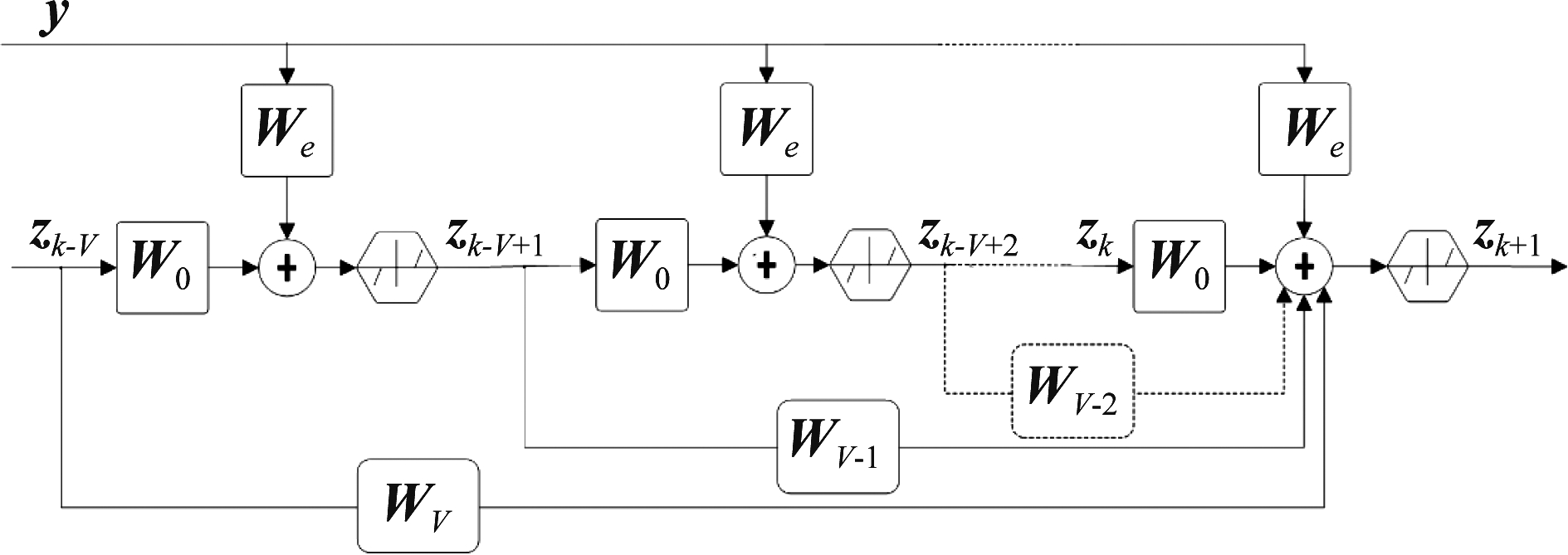
图1 LISTA-MM网络的部分展开结构
Fig.1 The partially unfolded network structure of LISTA-MM
3 LISAT-MM在图像超分辨率的应用
图像超分辨率的目的是由一张低分辨率图像ILR重构出对应的高分辨率图像ISR。从稀疏的角度来看,低分辨图像(高分辨图像)可以被表示为过完备字典Dl(Dh)中少量原子的线性组合,这些原子被称为线性稀疏系数gl(gh)∈RN。当字典Dl和Dh被正确定义时,假设每个低分辨图像/高分辨图像对共享相同的稀疏编码,图像超分辨率可以表示为形如公式(2)的稀疏编码问题,本节将探索卷积形式的LISTA-MM在图像超分辨率中的应用。
利用卷积运算符代替矩阵乘法,公式(14)可以被重新表述为卷积结构形式,其类似于文献[21]提出的一个稀疏自动编码器模型:
(15)
为了简化计算和提高效率,这里令所有迭代层都共享同一个卷积算子S,分离出相互独立的权重系数分别用w0,w1,w2,…,wV表示。在非负稀疏编码的假设下,非负软阈值函数和ReLU激活函数被认为是等效函数。因此,将hθ(x)替代成ReLU(x-θ),卷积LISTA-MM模块可以采用深度学习技术训练:
(16)
此时⊗表示卷积算子,y∈Rb×c×h×w表示通道数为c、尺寸为h×w的b幅图像,We∈Rm×c×s1×s1和S∈Rm×c×s1×s1是两个互不相关的可训练变量,s1表示卷积滤波器的卷积核大小。卷积LISTA-MM的展开结构如图2所示,这里以第k+1次迭代的展开为例。
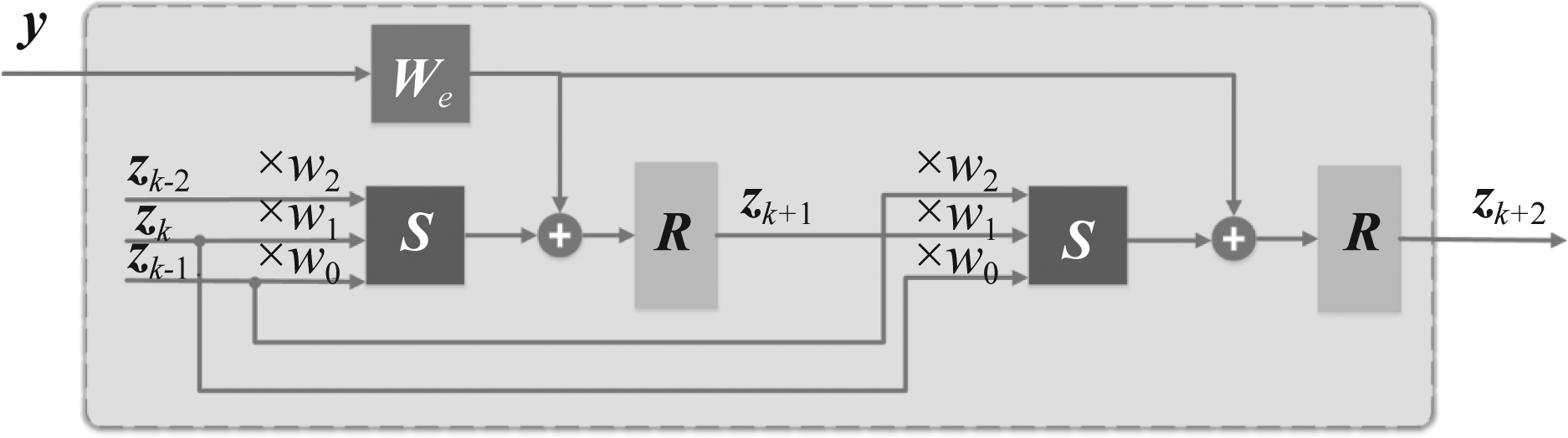
图2 卷积LISTA-MM的部分展开结构
Fig.2 The partially unfolded architecture of the convolutional LISTA-MM
图像超分辨率网络的整体构成如图3所示,主要分为特征提取、LISTA-MM和重构三大模块。特征提取模块和重构模块均由卷积层和ReLU激活算子组成,分别提取图像的低维特征和高维特征。中间LISTA-MM模块通过递归方式学习更新特征图的稀疏编码。该网络的初始输入是插值后的低分辨率图像ILR,经过网络重构出期望的高分辨率图像ISR。
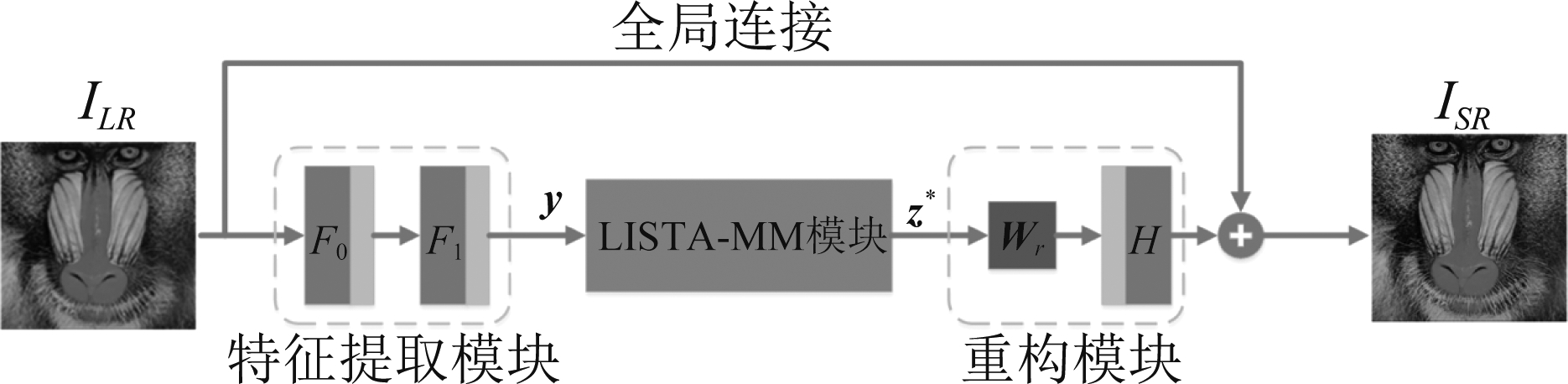
图3 图像超分辨率网络的整体结构
Fig.3 The architecture of the image super-resolution network
4 实验结果及分析
为了验证本文所提算法的有效性,本文将选取仿真数据和自然场景图像数据集[22-23]分别进行实验。实验分为两个部分:首先,本文所提LISTA-MM算法与LISTA及其衍生的几种迭代软阈值学习算法进行比较,验证多状态记忆机制在提高稀疏恢复收敛速度方面的有效性。其次,本文将卷积LISTA-MM应用到图像超分辨率网络中,并与现有的一些图像超分辨率网络进行比较。
4.1 仿真信号稀疏恢复4.1.1 数据集及实验细节
实验使用随机生成满足高斯分布的仿真信号,观测信号和重构信号的长度分别设置为100和200。测量矩阵D为随机生成矩阵,D中每一列被归一化,且服从零均值高斯分布![]() (Q为观测信号的长度)。在实验中考虑加性高斯白噪声na,则将信噪比(Signal-to-Noise Natio,SNR)定义为:
(Q为观测信号的长度)。在实验中考虑加性高斯白噪声na,则将信噪比(Signal-to-Noise Natio,SNR)定义为:
(17)
其中z是作为参照的稀疏信号, [||·||]表示能量的期望值。本节实验采用归一化均方误差(Normalized Mean Square Error,NMSE)作为主要评价指标,以便更直观地反映稀疏恢复算法的性能:
[||·||]表示能量的期望值。本节实验采用归一化均方误差(Normalized Mean Square Error,NMSE)作为主要评价指标,以便更直观地反映稀疏恢复算法的性能:
NMSE=10log10
![]()
(18)
其中![]() 是重构信号,NMSE的值越低,重构信号和参照信号之间的偏差越小,重构效果更好。
是重构信号,NMSE的值越低,重构信号和参照信号之间的偏差越小,重构效果更好。
为了验证本文所提LISTA-MM在仿真数据上的有效性,实验将公式(14)中的状态连接度数VLISTA-MM分别设置为1~4,训练不同的LISTA-MM模型(分别表示为LISTA-MM1,LISTA-MM2,LISTA-MM3,LISTA-MM4),讨论了多状态记忆机制对收敛速度的影响,并且将其与LISTA和文献[15-16]提出的稀疏恢复算法(本文分别称之为LISTA-CP[15],LISTA-CPSS[15],TiLISTA[16])进行比较。实验环境为PyTorch和MATLAB R2017b,模型建立在PyTorch上,采取Adam优化器并将初始学习率设为0.02。
4.1.2 仿真信号稀疏恢复结果
为了探究多状态记忆机制对稀疏恢复收敛速度的影响,本节实验首先预训练LISTA模型,并将预训练参数固定,从头训练LISTA-MM模型,只更新公式(14)中的权重矩阵Wi。图4展示了不同噪声条件下LISTA-MM与LISTA算法的稀疏恢复性能结果,其中x轴表示迭代次数,y轴表示NMSE,以分贝(dB)为单位。从图4可以看出,在不同SNR水平下,与LISTA相比,LISTA-MM达到同等大小的NMSE值所需的迭代次数更少,从而验证其在加快收敛速度方面的有效性,且随着SNR的增大,这种优势更为明显。另外,从图4 (d)可以看出,当稀疏恢复结果开始趋于稳定时,LISTA-MM的恢复误差比LISTA低3~10 dB。
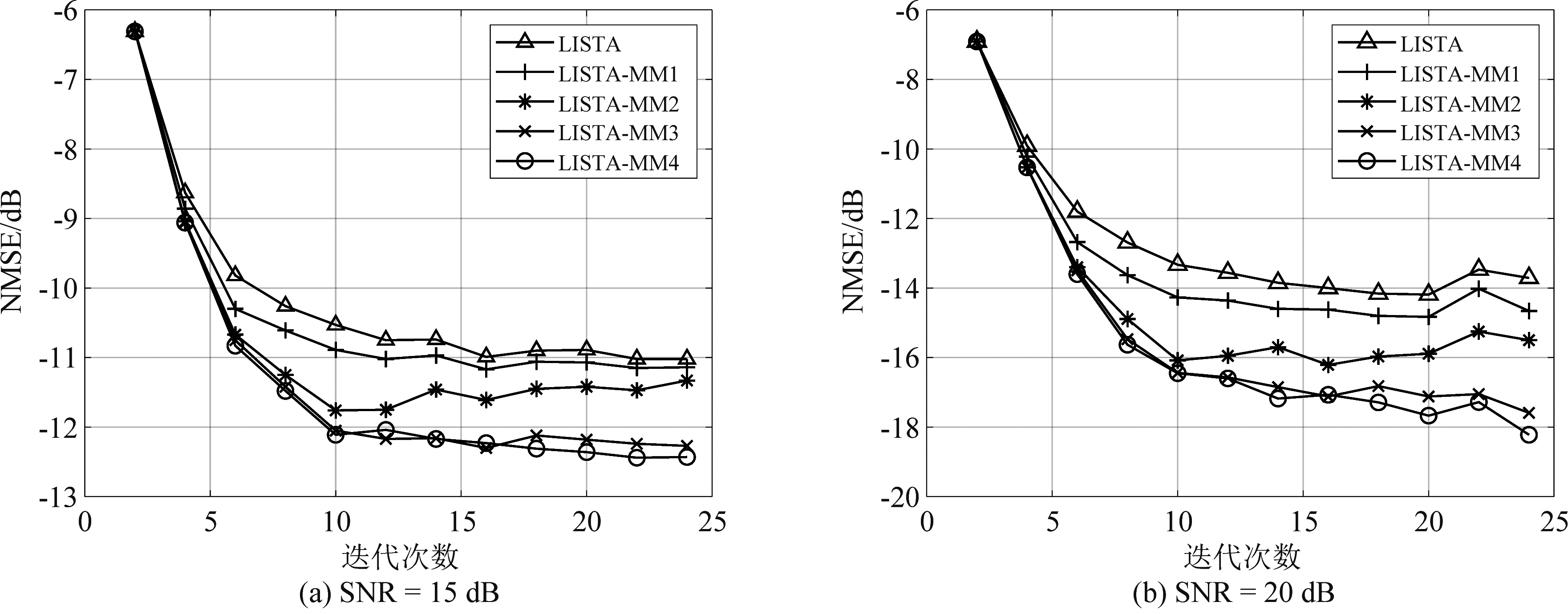
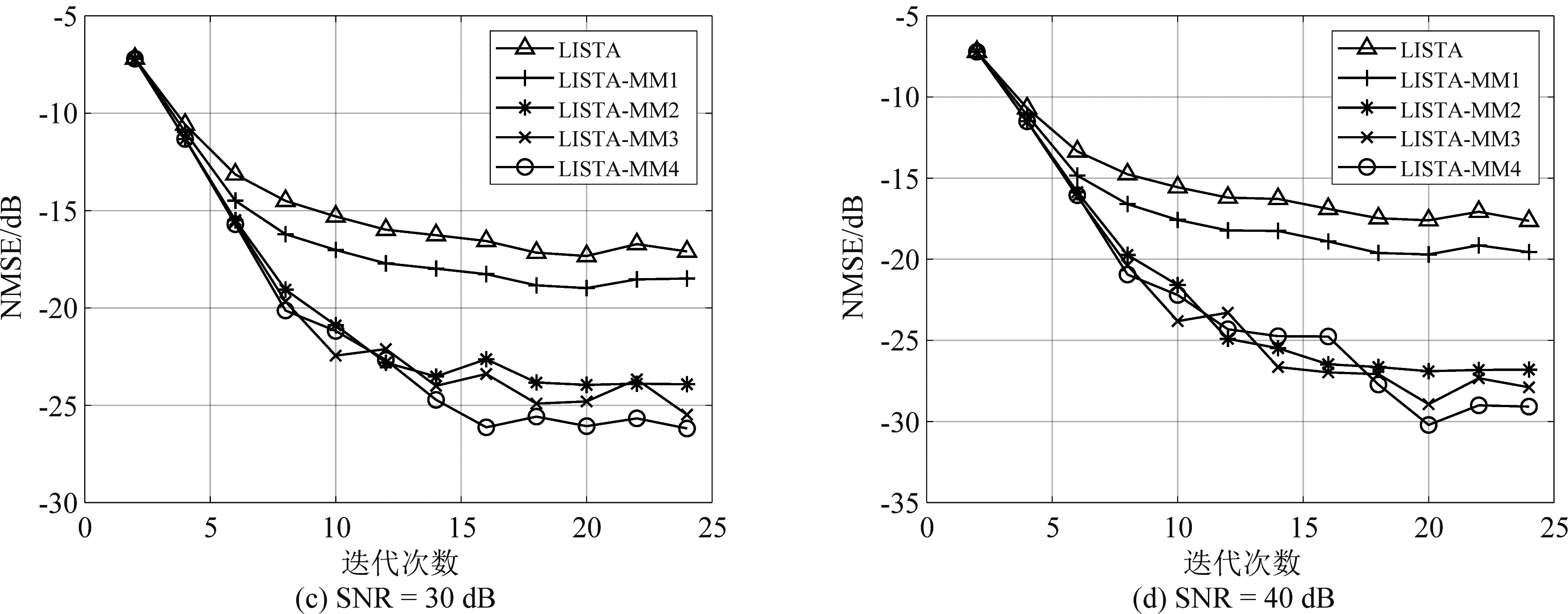
图4 不同信噪比水平下,LISTA-MM和LISTA的稀疏恢复性能结果(LISTA-MM模型的数字后缀表示状态连接度数)
Fig.4 Sparse recovery performance results of LISTA-MM and LISTA at different SNR levels (the digital suffix of LISTA-MM model represents the state connection degree)
为了进一步探究LISTA-MM的性能表现,本文进行无预训练模型实验,分别从头训练LISTA模型和LISTA-MM模型,并与LISTA-CP、LISTA-CPSS、TiLISTA进行比较。图5展示了不同噪声条件下上述算法的稀疏恢复性能结果。从图中可知,当SNR=15 dB,LISTA-MM的收敛速度明显优于其他四种算法。当SNR≥20 dB时,LISTA-MM和LISTA-CP的NMSE结果较为接近,收敛速度相当,且性能明显优于其他三种算法。
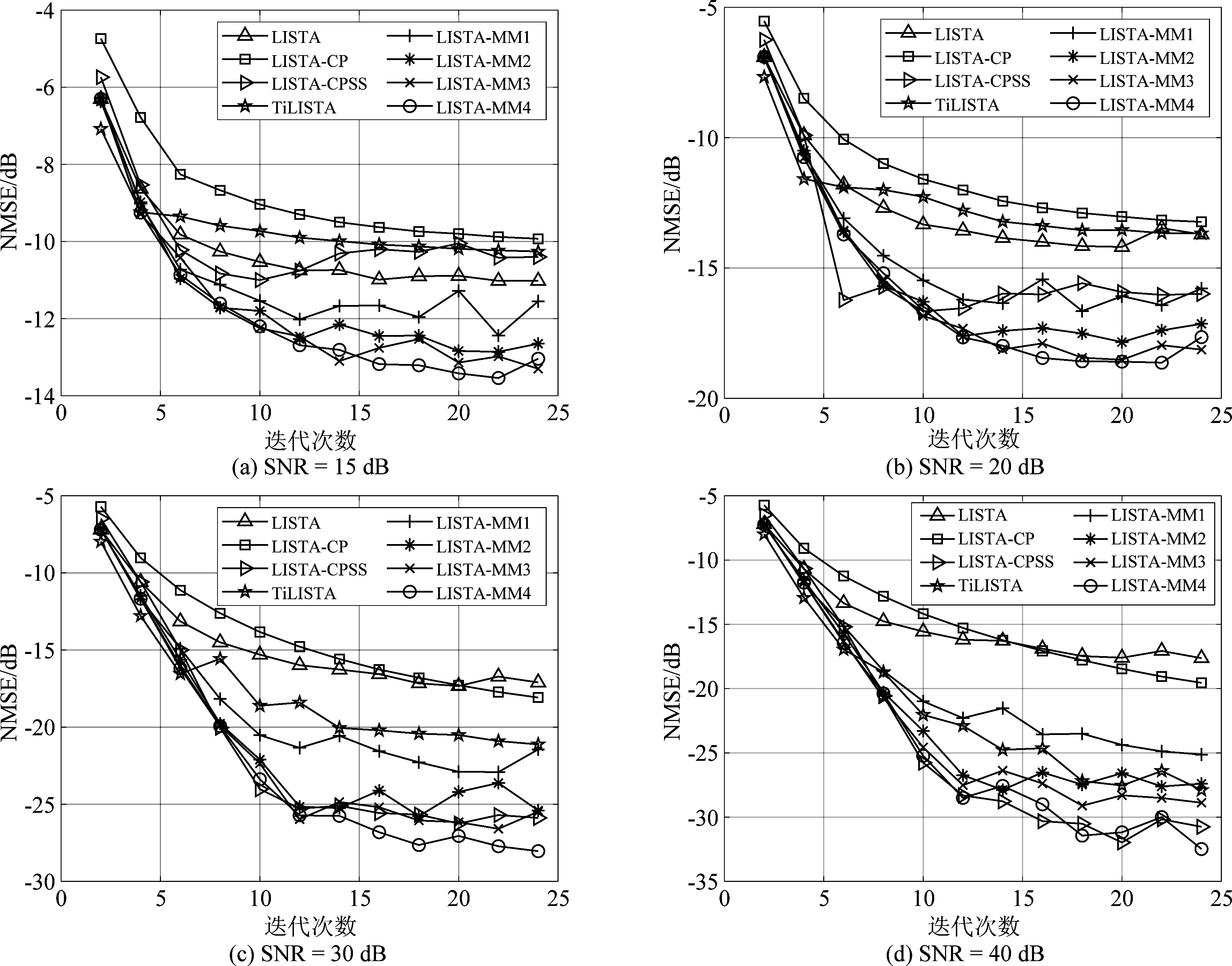
图5 不同信噪比水平下,LISTA-MM和LISTA,LISTA-CP,LISTA-CPSS,TiLISTA的稀疏恢复性能结果(LISTA-MM模型的数字后缀表示状态连接度数)
Fig.5 Sparse recovery performance results of LISTA-MM and LISTA,LISTA-CP,LISTA-CPSS,TiLISTA at different SNR levels (the digital suffix of LISTA-MM model represents the state connection degree)
此外,本文还展示了LISTA和LISTA-MM算法重构信号的可视化对比结果,如图6所示,其中x轴表示序列长度,y轴表示信号幅度。从图中可以看出,LISTA-MM算法的重构信号基本恢复了信号的稀疏信息,并且相较于LISTA,其信号幅度更接近原始稀疏信号,重构误差更低。综上所述,实验结果表明,多状态记忆机制的引入不仅可以加快算法的收敛速度,还能提高信号的稀疏恢复精度。
4.2 图像超分辨率重建结果
参照现有的图像超分辨率网络,本节实验使用与文献[28]相同的训练集。该训练集共291张自然场景图像,分别来自文献[22]和Berkeley分割数据集[23]。由于训练图像具有局限性,训练前本文采用数据增强方式,使用MATLAB R2017a对训练集进行不同尺度(×2,×3,×4)的下采样,并训练了一个图像超分辨率网络模型。实验使用的测试集是Set5[24],Set14[25],BSD100[23],Urban100[26],并将图像由RGB颜色空间变换到YCbCr颜色空间,在Y通道上计算峰值信噪比(Peak Signal-to-Noise Ratio,PSNR)和结构相似性(Structural Similarity,SSIM)作为实验评价指标,其中PSNR值越大表示重构图像失真越少,SSIM值越大表示两幅图像相似度越高,重构图像质量越好。
本节实验采用卷积LISTA-MM(状态连接度数VLISTA-MM设置为4)搭建图像超分辨率网络,将该网络的重建图像和实验评估指标与现有的一些图像超分辨率网络进行比较。本节实验中网络迭代层数设置为25,实验环境为PyTorch,在NVIDIA Titan Xp gpu下进行训练,使用Adam优化器和图像超分辨率网络训练常用的l1损失函数,初始学习率设置为4×10-4,每训练10个阶段减半,共训练了35个阶段。
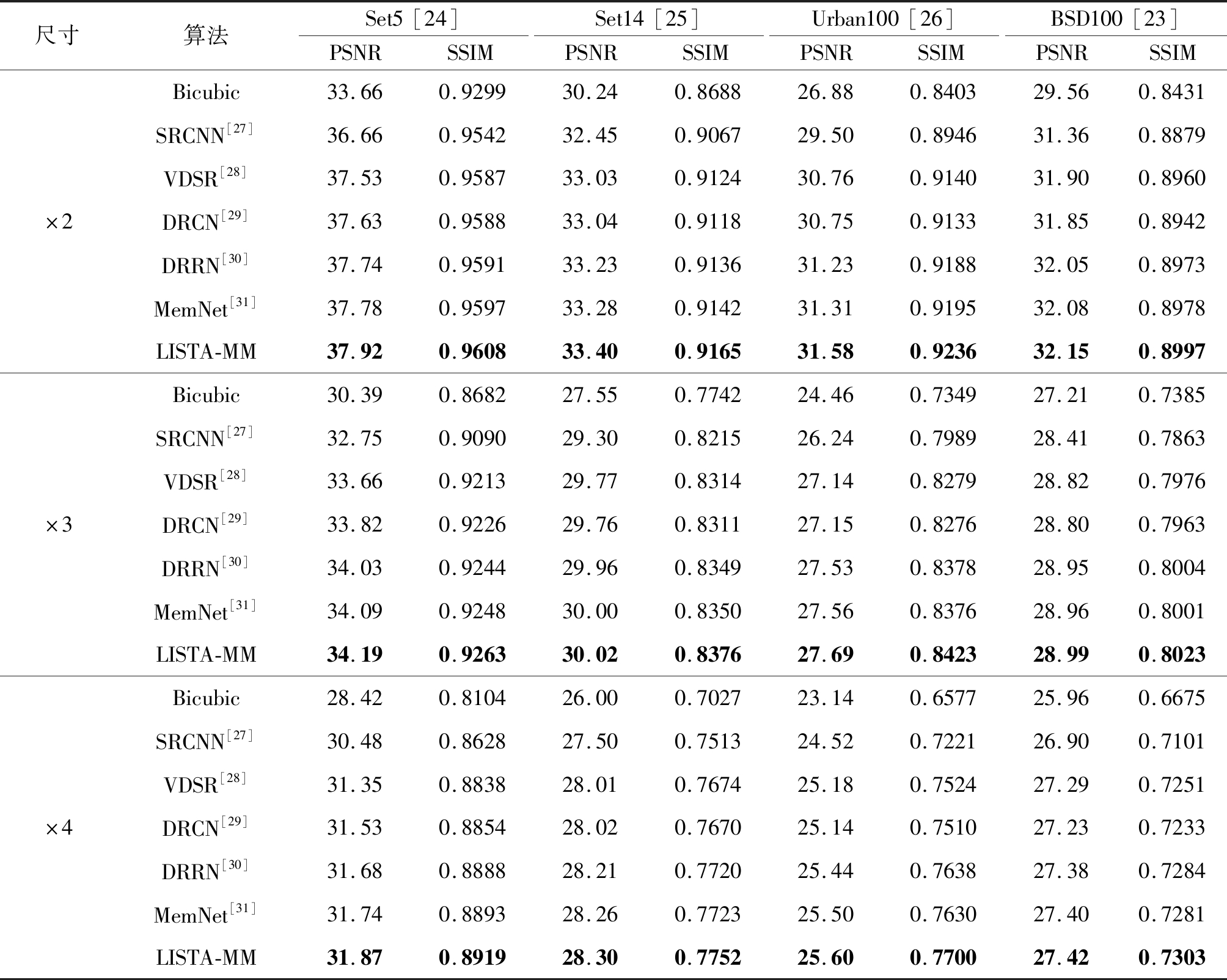
实验对LISTA-MM与双三次插值算法,以及文献[27-31]中的图像超分辨率网络进行比较(本文分别依次称为Bicubic、SRCNN[27]、VDSR[28]、DRCN[29]、DRRN[30]和MemNet[31]),实验评估指标在MATLAB中计算。表1总结了上述网络在标准数据集上的实验定量结果(在尺度因子分别为2,3,4时,数据集Set5,Set14,BSD100和Urban10的PSNR/SSIMs平均值),最佳性能用加粗数字表示。从表中可以看出,基于LISTA-MM的图像超分辨率网络在四个数据集上的评价指标均优于其他六种网络。此外,图7展示了不同网络下图像超分辨率的可视化结果。从图中可以看出,其他六种网络容易被明显的伪影影响,重建图像出现不正确的纹理和过于平滑的边缘。相较其他六种网络,LISTA-MM的重构图像更清晰,细节纹理信息更丰富准确。实验结果表明,基于LISTA-MM的网络在评价指标和可视化效果上均优于其他网络,证明了卷积LISTA-MM在图像超分辨率中的优势。
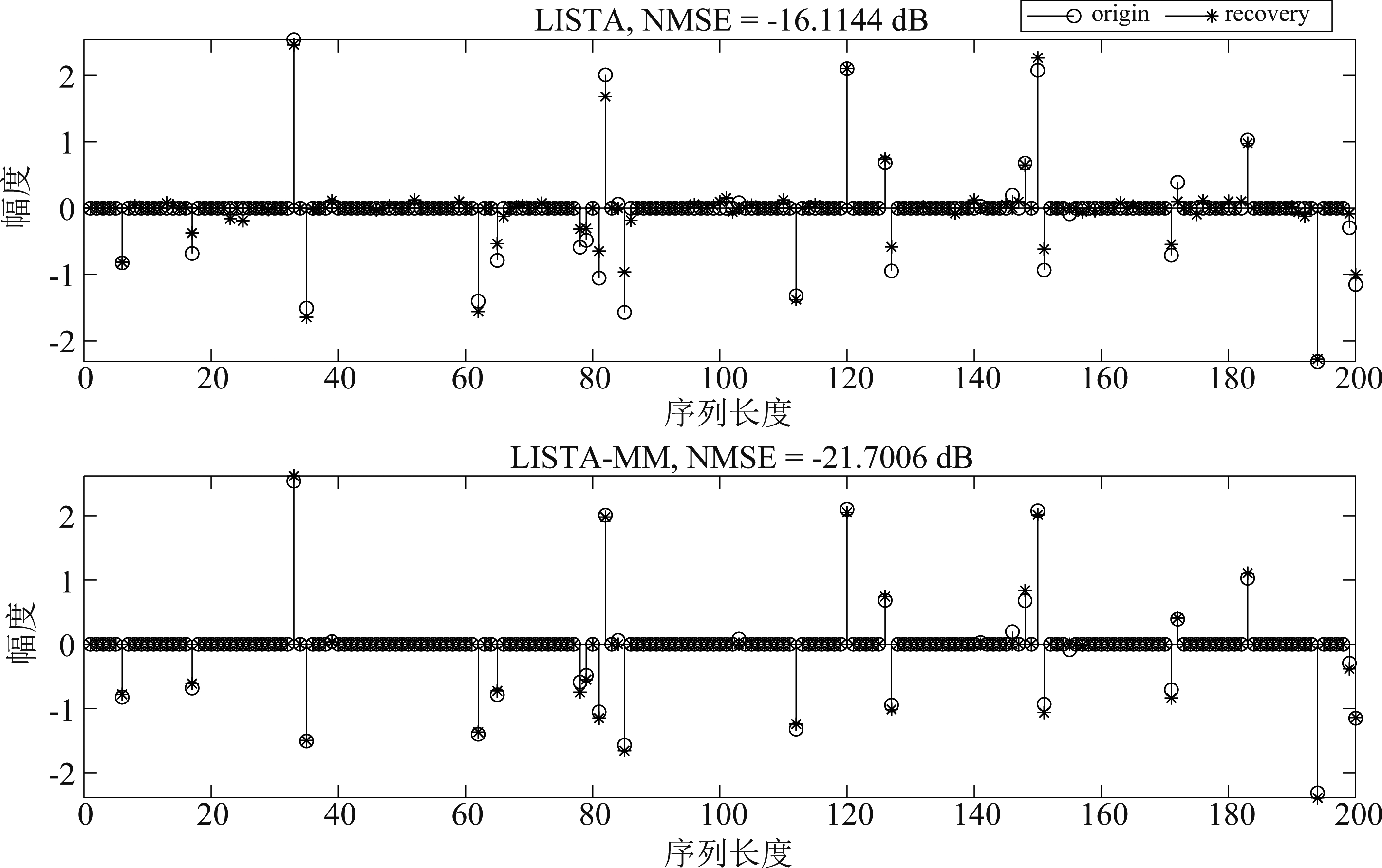
图6 LISTA和LISTA-MM算法的重构信号可视化结果(SNR=25 dB,迭代层数等于20)
Fig.6 Visualization of recovered signal of LISTA and LISTA-MM (SNR=25 dB,iterative layer equals to 20)
表1 不同网络下标准数据集测试结果(最佳性能用加粗数字表示)
Tab.1 Test results of standard datasets under different networks (Bold Number indicates the best performance)
尺寸算法Set5[24]PSNRSSIMSet14[25]PSNRSSIMUrban100[26]PSNRSSIMBSD100[23]PSNRSSIM×2Bicubic33.660.929930.240.868826.880.840329.560.8431SRCNN[27]36.660.954232.450.906729.500.894631.360.8879VDSR[28]37.530.958733.030.912430.760.914031.900.8960DRCN[29]37.630.958833.040.911830.750.913331.850.8942DRRN[30]37.740.959133.230.913631.230.918832.050.8973MemNet[31]37.780.959733.280.914231.310.919532.080.8978LISTA-MM37.920.960833.400.916531.580.923632.150.8997×3Bicubic30.390.868227.550.774224.460.734927.210.7385SRCNN[27]32.750.909029.300.821526.240.798928.410.7863VDSR[28]33.660.921329.770.831427.140.827928.820.7976DRCN[29]33.820.922629.760.831127.150.827628.800.7963DRRN[30]34.030.924429.960.834927.530.837828.950.8004MemNet[31]34.090.924830.000.835027.560.837628.960.8001LISTA-MM34.190.926330.020.837627.690.842328.990.8023×4Bicubic28.420.810426.000.702723.140.657725.960.6675SRCNN[27]30.480.862827.500.751324.520.722126.900.7101VDSR[28]31.350.883828.010.767425.180.752427.290.7251DRCN[29]31.530.885428.020.767025.140.751027.230.7233DRRN[30]31.680.888828.210.772025.440.763827.380.7284MemNet[31]31.740.889328.260.772325.500.763027.400.7281LISTA-MM31.870.891928.300.775225.600.770027.420.7303

图7 图像可视化结果比较
Fig.7 Comparison of image visualization results
5 结论
本文基于LISTA框架引入一种多状态记忆机制,设置状态连接度数,使多个先前迭代点通过可学习权值矩阵组合连接到当前迭代,从而确保了信息利用的正确性与高效性,达到加速算法收敛的目的。实验结果表明,在同等误差范围内,LISTA-MM所需的迭代次数少于LISTA及其衍生算法,从而验证LISTA-MM在加快收敛速度方面的有效性。此外,本文扩展LISTA-MM的卷积形式并将其应用于图像超分辨率中,相应的实验结果展示出该网络在重构高分辨率图像中的优势。
[1] 王友华, 张建秋. 联合稀疏信号恢复的贪婪增强贝叶斯算法[J]. 电子学报, 2016, 44(4): 780-787.
WANG Youhua, ZHANG Jianqiu. A greedy refinement Bayesian approach to joint sparse signal recovery[J]. Acta Electronica Sinica, 2016, 44(4): 780-787.(in Chinese)
[2] 王林元, 李磊, 闫镔, 等. 稀疏信号恢复理论在CT图像重建中的应用[J]. CT理论与应用研究, 2009, 18(3): 22-29.
WANG Linyuan, LI Lei, YAN Bin, et al. The application of sparse signal recovery theory in CT image reconstruction[J]. Computerized Tomography Theory and Applications, 2009, 18(3): 22-29.(in Chinese)
[3] 谢前朋, 王伦文. 基于连续稀疏恢复循环平稳信号的DOA估计[J]. 现代雷达, 2017, 39(1): 32-36,55.
XIE Qianpeng, WANG Lunwen. DOA estimation method for cyclostationary signals based on continuous sparse reconstruction[J]. Modern Radar, 2017, 39(1): 32-36,55.(in Chinese)
[4] 杨磊, 李慧娟, 李埔丞, 等. 基于贪婪-快速阈值迭代的SAR地面动目标稀疏表征算法[J]. 信号处理, 2019, 35(11): 1844-1852.
YANG Lei, LI Huijuan, LI Pucheng, et al. Sparse representation for SAR ground moving target imaging based on greedy FISTA[J]. Journal of Signal Processing, 2019, 35(11): 1844-1852.(in Chinese)
[5] MALLAT S G, ZHANG Zhifeng. Matching pursuits with time-frequency dictionaries[J]. IEEE Transactions on Signal Processing, 1993, 41(12): 3397-3415.
[6] TROPP J, GILBERT A. Signal recovery from partial information via orthogonal matching pursuit[J]. IEEE Transactions on Information Theory, 2007, 53(12):4655- 4666.
[7] CHEN S S, DONOHO D L, SAUNDERS M A. Atomic decomposition by basis pursuit[J]. SIAM Review, 2001, 43(1): 129-159.
[8] SILVA T C, RIBEIRO A A, PERIÇARO G A. A new accelerated algorithm for ill-conditioned ridge regression problems[J]. Computational and Applied Mathematics, 2018, 37(2): 1941-1958.
[9] BLUMENSATH T, DAVIES M E. Normalized iterative hard thresholding: Guaranteed stability and performance[J]. IEEE Journal of Selected Topics in Signal Processing, 2010, 4(2): 298-309.
[10] BLUMENSATH T, DAVIES M E. Iterative hard thresholding for compressed sensing[J]. Applied and Computational Harmonic Analysis, 2009, 27(3): 265-274.
[11] DAUBECHIES I, DEFRISE M, DE MOL C. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457.
[12] BECK A, TEBOULLE M. A fast Iterative Shrinkage-Thresholding Algorithm with application to wavelet-based image deblurring[C]∥2009 IEEE International Conference on Acoustics, Speech and Signal Processing. Taipei, Taiwan, China. IEEE, 2009: 693- 696.
[13] GREGOR K, LECUN Y. Learning fast approximations of sparse coding[C]∥ICML'10: Proceedings of the 27th International Conference on International Conference on Machine Learning. 2010: 399- 406.
[14] MOREAU T, BRUNA J. Understanding trainable sparse coding with matrix factorization[C]∥International Conference of Learning Representation (ICLR), 2017.
[15] Chen X, Liu J, Wang Z, et al. Theoretical linear convergence of unfolded ISTA and its practical weights and thresholds[C]∥In Proceedings of the 32nd International Conference on Neural Information Processing Systems (NIPS′18).Curran Associates Inc,Red Hook, NY,USA, 2018:9079-9089.
[16] Liu J,Chen X,Wang Z,et al. ALISTA: Analytic weights are as good as learned weights in LISTA[C]∥International Conference of Learning Representation (ICLR),2019.
[17] POLYAK B T. Some methods of speeding up the convergence of iteration methods[J]. USSR Computational Mathematics and Mathematical Physics, 1964, 4(5): 1-17.
[18] CYRUS S, HU Bin, VAN SCOY B, et al. A robust accelerated optimization algorithm for strongly convex functions[C]∥2018 Annual American Control Conference (ACC). Milwaukee, WI. IEEE, 2018: 1376-1381.
[19] VAN SCOY B, FREEMAN R A, LYNCH K M. The fastest known globally convergent first-order method for minimizing strongly convex functions[J]. IEEE Control Systems Letters, 2018, 2(1): 49-54.
[20] TAYLOR A, SCOY B V, LESSARD L. Lyapunov functions for first-order methods: tight automated convergence guarantees[C]∥Proceedings of the 35th International Conference on Machine Learning (ICML),2018:7810-7823.
[21] SRETER H, GIRYES R. Learned convolutional sparse coding[C]∥2018 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Calgary, AB, Canada. IEEE, 2018: 2191-2195.
[22] YANG Jianchao, WRIGHT J, HUANG T S, et al. Image super-resolution via sparse representation[J]. IEEE Transactions on Image Processing, 2010, 19(11): 2861-2873.
[23] MARTIN D, FOWLKES C, TAL D, et al. A database of human segmented natural images and its application to evaluating segmentation algorithms and measuring ecological statistics[C]∥Proceedings Eighth IEEE International Conference on Computer Vision. ICCV 2001. Vancouver, BC, Canada. IEEE, 2001: 416- 423.
[24] BEVILACQUA M, ROUMY A, GUILLEMOT C, et al. Low-complexity single-image super-resolution based on nonnegative neighbor embedding. British Machine Vision Conference (BMVC), 2012.
[25] ZEYDE R, ELAD M, PROTTER M. On single image scale-up using sparse-representations[C]∥7th International Conference, Curves and Surfaces, 2012:711-730.
[26] HUANG Jiabin, SINGH A, AHUJA N. Single image super-resolution from transformed self-exemplars[C]∥2015 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Boston, MA, USA. IEEE, 2015: 5197-5206.
[27] DONG Chao, LOY C C, HE Kaiming, et al. Image super-resolution using deep convolutional networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2016, 38(2): 295-307.
[28] KIM J, LEE J K, LEE K M. Accurate image super-resolution using very deep convolutional networks[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA. IEEE, 2016: 1646-1654.
[29] KIM J, LEE J K, LEE K M. Deeply-recursive convolutional network for image super-resolution[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA. IEEE, 2016: 1637-1645.
[30] TAI Ying, YANG Jian, LIU Xiaoming. Image super-resolution via deep recursive residual network[C]∥2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, HI, USA. IEEE, 2017: 2790-2798.
[31] TAI Ying, YANG Jian, LIU Xiaoming, et al. MemNet: A persistent memory network for image restoration[C]∥2017 IEEE International Conference on Computer Vision (ICCV). Venice, Italy. IEEE, 2017: 4549- 4557.


