1 引言
盲源分离已成为信号处理领域的一个热门研究主题,其起源于人们对鸡尾酒会问题的研究[1- 6]。“盲”表示在没有先验知识的条件下,仅从观测到的混合信号中提取出源信号。随着盲源分离理论研究的深入,基于盲源分离的麦克风阵列多路语音信号处理的应用研究逐渐引起人们的关注。
根据麦克风阵元和声源相对数量,盲源分离可分为两类:第一类属于超定或正定的情况,即麦克风阵元数大于或等于声源数,第二类是欠定情况,即麦克风阵元数小于声源数。独立成分分析(Independent Component Analysis, ICA)是有效解决第一类盲源分离问题最为流行的方法[1]。该方法通过找到非高斯数据的线性表示形式,以使得组成部分在统计上独立或尽可能独立。对于欠定情况,由于受固有不利条件的限制,混合矩阵无法直接求逆,导致ICA方法将失效。近年来,随着语音信号处理研究的深入,学者们通过利用时频域中语音信号的稀疏性来实现信源分离已得到广泛应用[4-7]。然而上述方法都是在窄带假设下进行的,即从声源到麦克风之间的冲激响应的长度小于短时傅里叶变换(short-time Fourier transform, STFT)的窗长,例如时频域中的瞬时混合模型。但是,这种窄带近似在高混响环境中并不能很好地发挥作用;而且有研究发现:基于窄带近似的方法在高混响环境中的性能会急剧下降[8-9]。为了减轻这个问题,文献[4]引入了源信号的满秩空间协方差矩阵,但是在高混响场景中分离性能仍不够理想。文献[8]提出了一种半盲条件下的宽带凸方法,该方法在混响环境下表现出良好的分离性能,但是其运算量高。最近,文献[10]提出了基于卷积传输函数和频域套索优化模型的声源半盲分离算法,该研究结果表明:在混响场景中,采用时频域中的卷积混合模型更合适。受文献[10]的启发,文献[11]深入研究了高混响环境下的盲源分离,并取得非常不错的分离性能。
由上述讨论可看出,大多数基于时频域处理的盲源分离算法都只是将时域中的卷积混合信号利用STFT变换到时频域中,进而采用窄带近似转换为时频域中的瞬时混合形式来进行处理,因而在高混响环境下性能并不理想。于是,本文针对高混响场景,将时频域中的瞬时模型扩展到卷积模型,即信号模型在时频域依旧是卷积混合的形式,结合房间冲激响应(RIR)[14]的统计特性,构建一时频域联合优化问题;进而充分利用优化问题的线性可分离且为凸函数的特性,我们采用了交替方向乘子法(ADMM)[12]对该优化问题进行求解。仿真结果表明:与现有盲源分离算法相比,本文算法具有非常明显的性能优势。
2 问题表述
在时域中,麦克风阵列接收信号遵循如下混合模型:
(1)
其中sj(t)和xi(t)分别表示源信号和观测信号,I和J分别为麦克风和声源的数量,aij(t)表示从第j个声源到第i个麦克风之间的房间冲激响应(RIR),*代表卷积运算,ei(t)为背景噪声。
2.1 瞬时窄带近似
令xi(f,n),sj(f,n),ei(f,n)分别代表式(1)中xi(t),sj(t),ei(t)的STFT系数,其中f=0,…,F-1和n=0,…,N-1分别表示频率和时间帧的索引,F和N分别为频点的数目和时间帧的数目。根据窄带假设,将式(1)中的卷积混合模型转换为时频域中的瞬时混合模型[7,9],即
(2)
其中x(f,n)=[x1(f,n),…,xI(f,n)]T,aj( f )=[a1j( f ),…,aIj( f )]T,e(f,n)=[e1(f,n),…,eI(f,n)]T。由于算法在每个频点上进行操作,简洁起见,下文讨论中将略去频率索引f。于是,在各频点f上,式(2)用矩阵形式表示:
X=AS+E
(3)
其中X∈CI×N,A∈CI×J,S∈CJ×N,E∈CI×N分别表示观测信号,混合矩阵,源信号以及噪声。文献[11]中还提出了模型(3)的另一种形式:
X=Aα+E
(4)
值得注意的是(4)中的α∈CJ×N和式(3)中的S是不同的,这里的α是综合STFT系数,用来避免分析STFT系数S带来的附加约束[13]。通过时频表示,选择从合成信号中表示系数族,而不是分析系数族。综合方法提供了一种将先验信息或约束引入表示形式的通用方法,考虑到这种利用先验知识的尝试,因此问题就变成了“如何更好地合成信号,使其合成系数的某些行为具有特权？”。于是,利用α的稀疏性,可以通过求解如下无约束优化问题来实现盲源分离:
(5)
其中||·||F,||·||1,λ分别表示Frobenius范数,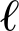
1范数以及正则化参数。λ用来平衡数据保真项
||X-Aα
和正则项
为一示性函数,可避免不必要的解并且减轻缩放模糊问题。一种常用的示性函数为:
(6)
其中aj表示矩阵A的第j列。
2.2 卷积窄带近似
从理论上讲,瞬时窄带近似仅在RIR长度小于STFT窗长时才有效;因此,当RIR的长度大于STFT的窗长时,式(2)中的模型无效;但这种情况在实际中很少见,通常对STFT的窗长采取限制以确保音频信号的局部平稳性[10]。因此在高混响的情况下,时频域中的卷积模型更为合适[11],其具体形式如下
(7)
其中
表示时频域中卷积核的长度,
包含了时频域中与第j个源关联的冲激响应。
式(7)中的卷积窄带近似实际上为式(2)中瞬时窄带近似的推广,因为它考虑了沿时间索引的信息发散。当卷积核长度
它就退化成了瞬时窄带近似。时频域中的卷积核
与时域中的aij(t)直接关联,具体如下式所示:
(8)
式(8)代表对应时间索引t的卷积,其中k0表示STFT帧步长,
(9)
其中LF是频带数,φ(k′)和
分别表示STFT的分析窗和综合窗。
利用矩阵表达,对于每个频点f,式(7)中的卷积近似可写成
(10)
其中
是通过连接冲激响应长度形成的混合系统,*代表卷积混合过程。与时域中的原始混合过程相比,卷积近似式(10)大大减少了卷积核的长度。与2.1节类似,将分析STFT系数S替换为综合STFT系数α,则
(11)
为了联合估计混合系统和源信号,设计如下优化问题:
(12)
其中
是为了避免缩放模糊的归一化项,具体形式为:
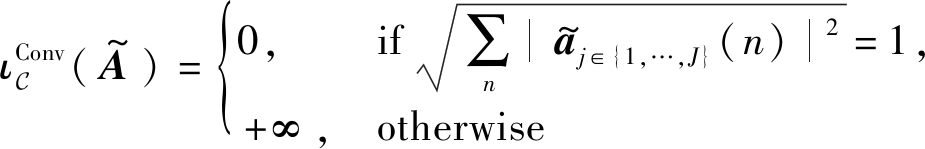
(13)
是附加在卷积核上的惩罚项[14]。在文献[14]中,作者假设混合信号和源信号均已知的条件下,研究了RIR估计问题,文中采用可微惩罚项,
(14)
其中ρ(t)表示房间冲激响应的幅度包络,它取决于混响时间RT60:
ρ(t)=σ10-3t/RT60
(15)
其中σ是缩放因子。显然,惩罚项式(14)被设计为迫使RIR呈指数下降,从而满足房间冲激响应的声学统计。由于时频域中的卷积核通过式(8)与时域中的房间冲激响应相关联,因此在本文中,时频域的惩罚项我们采取相同的形式,即
(16)
其中
是时频域中的衰减系数,它取决于ρ(t)和STFT变换。
3 提出的算法
为了求解式(5)和式(12)的两个优化问题,本文选择使用交替方向乘子法(ADMM)作为优化算法来求解。首先从模型式(5)开始,基于ADMM算法,推导相应的求解过程,文中称作窄带ADMM(narrowband ADMM, N-ADMM)算法。类似地,基于式(12)的卷积模型,我们也给出了相应的求解过程,文中称为卷积ADMM(convolutive ADMM, C-ADMM)算法。
3.1 窄带ADMM
为了应用ADMM算法对优化问题式(5)进行求解,引入辅助变量Z1,于是,优化问题式(5)可表示为
subject to α=Z1
(17)
对应地,式(17)的增广拉格朗日函数为
(18)
其中η1是对偶变量,γ1是惩罚项参数。窄带ADMM通过使用以下更新规则迭代更新原始变量和对偶变量来最小化增广拉格朗日函数:
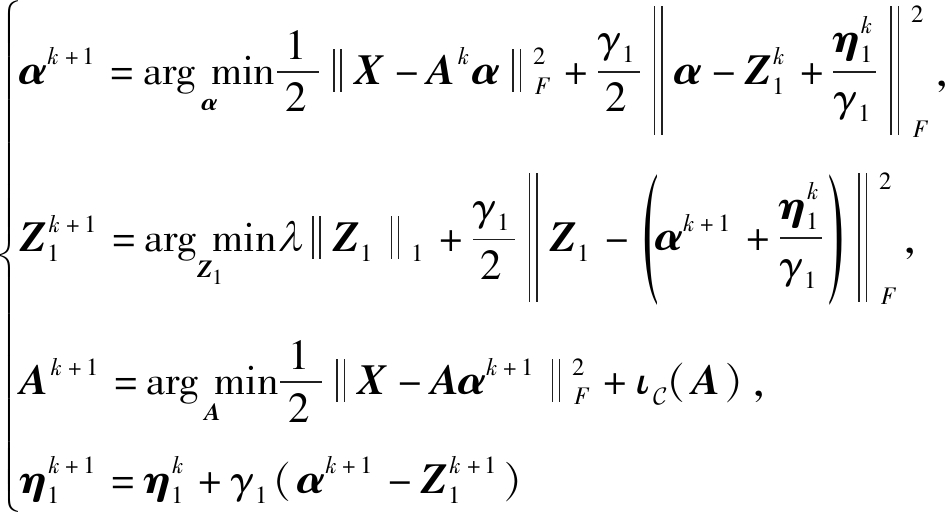
(19)
为了解决式(19)中第一个子问题,引入以α为自变量的函数
(20)
对式(20)在αk处采用二阶泰勒展开到二次项,则有
(21)
其中
是▽αF的Lipschitz常数,于是α可通过梯度下降法求解。于是,所有子问题的解总结为式(22)。
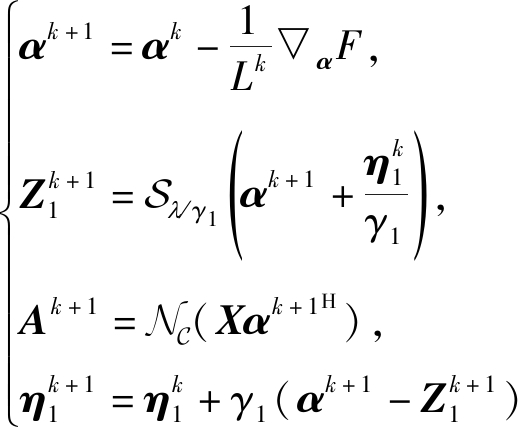
(22)
值得注意的是,求解(19)中的第二个和第三个子问题都采用了近端方法[20],其中1范数的近端算子是软阈值算子
的近端算子由归一化算子
给出。
3.2 卷积ADMM
同样地,对于优化问题式(12),引入辅助变量Z2,得到如下约束受限的优化问题:
subject to α=Z2
(23)
优化问题(23)的增广拉格朗日函数如下:
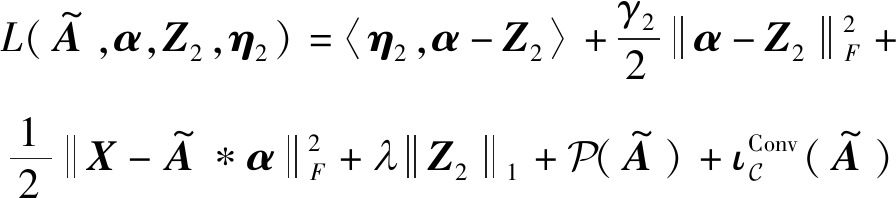
(24)
其中η2和γ2分别为对偶变量和惩罚项参数。
观察到式(24)的增广拉格朗日函数和式(18)很相似,这意味着利用N-ADMM算法求解式(18)的步骤同样适用于C-ADMM算法,于是在表1中,C-ADMM算法的步骤总结如下,并进行了适当的修改。
表1 C-ADMM算法步骤
Tab.1 Convolutive ADMM algorithm steps
在表1中,更新αk+1和
的方法与解决式(19)中第一个子问题的方法类似,首先进行二阶泰勒展开,然后采用梯度下降法进行求解,但是里面包含卷积运算会增大运算量。这两个最小化问题都需要相应的Lipschitz常数,分别用Lα和
来表示。其中Lα可以通过功率迭代算法[8]来得到,采用文献[11]中提出的命题来计算,
则利用上文中提到的软阈值方法求解。
4 仿真实验
在该节,针对4种不同条件下的分离性能对比,其中包括不同混响时间,不同的信噪比,不同的声源个数,以及不同的噪声类型,对文中提出的混响环境下基于卷积模型的欠定盲源分离算法进行性能评估,并将其与四种传统盲源分离算法对比,包括卷积近端近似线性最小化(用C-PALM表示)[11],退化解混估计技术(用DUET表示)[6],1范数最小化方法(用L1-MIN表示)[7],满秩空间协方差矩阵方法(用Full-rank表示)[4]。需要指出的是,由于所有实验均考虑了混响,因此N-ADMM仅用于初始化C-ADMM。
4.1 实验设置
仿真中,正则化参数λ在[4e-3,5e-2]范围内取值,算法开始时设定一较大的值,然后在每一次迭代中减小λ的值[11];惩罚项参数γ1和γ2均采用γ1,2=1.01×γ1,2的更新规则,上界设为6[15-17]。同时,为了更为公平地进行性能对比,其余参数设置均与C-PALM相同。由于混响时间是未知的,分别将卷积核长度预定义为3,衰减系数
预定义为[3.03,3,2.97]。为了验证提出算法的有效性,分别对模拟合成混合信号和实际录音进行了实验。对于混响环境,我们使用工具箱[18]模拟房间冲激响应,然后将语音信号作为源与房间冲激响应进行卷积以获得观测信号,图1展示了模拟房间的配置信息,所有的实验数据均来源于SISEC 2013数据集。
各种算法的分离性能通过信号失真比(signal to distortion ratio, SDR),信号干扰比(signal to interference, SIR),源图像空间失真比(source image to spatial distortion ratio, ISR),以及信号伪像比(signal to artifact ratio, SAR)[19]来评价。其中SDR体现了每个估计源的整体质量,SIR衡量了来自其他源的干扰程度,ISR度量了空间失真量,SAR主要是评估了算法本身产生的一些伪像对信号的干扰。
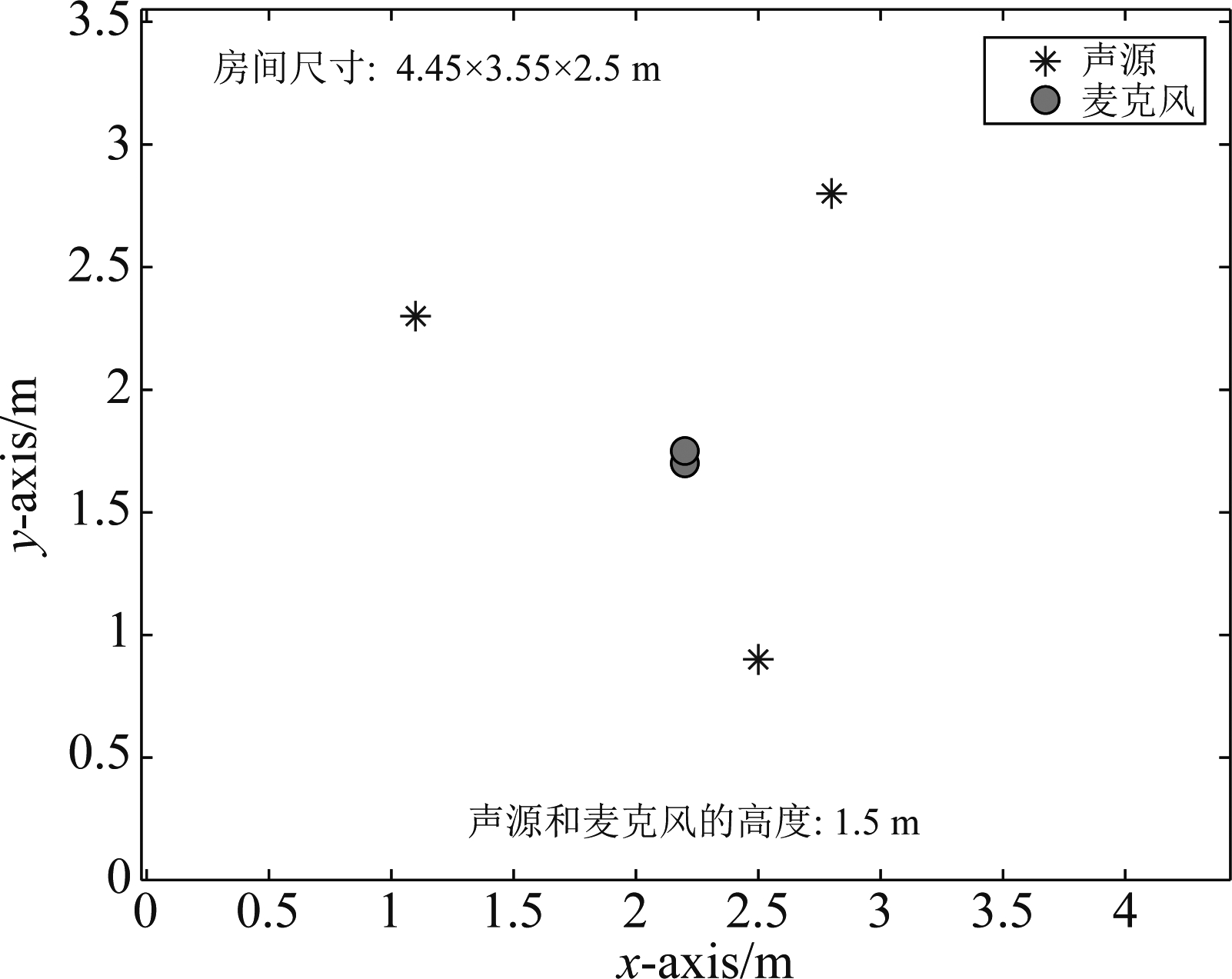
图1 合成混合信号的房间配置
Fig.1 Room configuration for synthesized mixtures
4.2 采用模拟合成数据的仿真实验对比
根据欠定情况,仿真时,将麦克风阵元数和声源数分别设为2和3。图2显示了在无噪声环境中各种算法在不同混响时间下的分离性能。显然,由于采用了卷积近似模型和ADMM优化框架,所提出的算法C-ADMM在SDR,SIR,ISR和SAR这四个性能指标上均优于其他方法,Full-rank,DUET,以及L1-MIN这三种算法在混响较高时性能普遍变差,主要是因为它们的信号模型只考虑了瞬时混合情况,无法适用于混响高的环境。当混响时间为50 ms到550 ms时,C-ADMM在所有指标上均比C-PALM提升将近1 dB。值得注意的是,在低混响条件下,满秩方法(Full-rank)的SAR比C-PALM高,这是因为满秩空间协方差模型更适用于混响较低的情况。由于瞬时窄带近似不再适用于房间冲激响应的长度超过STFT窗长的情况,因此DUET和L1-MIN在混响情况下的效果较差。从图2中的各个性能指标可以看出,采用卷积模型的算法性能要优于瞬时模型。
接下来对比了不同算法在不同信噪比下的性能表现,仿真中选择高斯白噪声作为背景噪声,混响时间固定为130 ms,结果如图3所示。从图3可看到,当输入信噪比为0 dB的时候,所有方法都展示出了较差的性能,尤其是SDR和SAR均为负值。在低信噪比的情况下,C-ADMM的分离性能优于C-PALM,其中在SIR指标上提升的较多。在高信噪比的情况下,C-ADMM在四个性能指标上相比C-PALM有1 dB左右增益,这显示了所提出算法对抗噪声的鲁棒性。
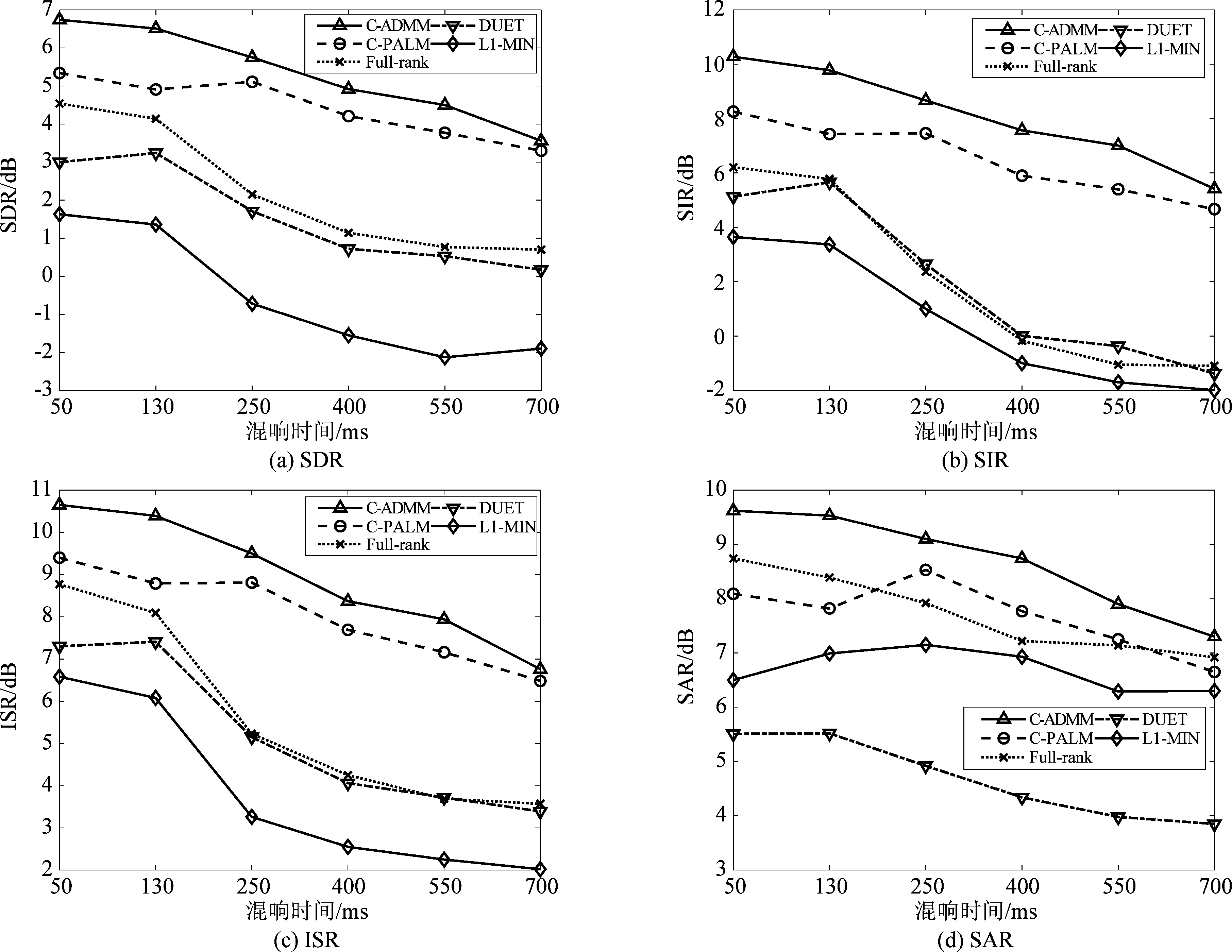
图2 不同算法在不同混响时间下的分离性能
Fig.2 Separation performance of different algorithms under different reverberation time
表2中对比了不同声源数量下的分离性能,仿真中将麦克风阵元数设定为2,混响时间设定为130 ms。正如预料,所有算法性能均随声源数的增加而下降,但是文中所提出算法的性能仍优于其他算法,因此所提算法相比于其他算法更加稳健。
表2 不同声源数量的性能对比(SDR/SIR/ISR/SAR,单位:dB)
Tab.2 Performance comparison of different numbers of sound sources (SDR/SIR/ISR/SAR in dB)
声源数量345C-ADMM5.12/9.09/9.14/9.292.74/3.75/6.38/6.472.27/2.94/5.36/5.25C-PALM2.9/6.13/7.27/7.372.24/3.22/5.88/5.931.99/2.81/5.15/4.68Full-rank3.73/5.13/7.56/8.892.11/1.87/5.94/7.51.41/0.77/4.46/6.37DUET0.5/-0.26/4.13/3.94-0.48/-1.74/2.85/3.15-0.53/-3.42/2.27/2.07L1-MIN-0.58/-0.73/3.76/3.86-1.2/-2.46/2.62/4.77-1.02/-3.97/2.28/4.18
最后,比较了各种算法在不同噪声类型下的分离性能,用来验证所提出算法在各种场景下的有效性,结果如表3所示。分别在0 dB,5 dB,10 dB,以及15 dB测试了5种类型的噪声,混响时间固定为130 ms,其中babble指餐厅内嘈杂噪声,volvo指车内噪声,leopard指军用车辆噪声,m109指坦克内部噪声,pink指粉红噪声。结果显示:各种算法的分离性能均随噪声的增加而降低,并且在不同的噪声类型下性能也会有所不同。但是无论哪种情况,文中所提算法C-ADMM的性能始终要优于其他算法。此外,通过分析表3中的实验结果,不难发现:不同噪声类型对算法性能的影响是有差别的,尽管提出算法相比于其他算法依旧保持着良好的性能优势。
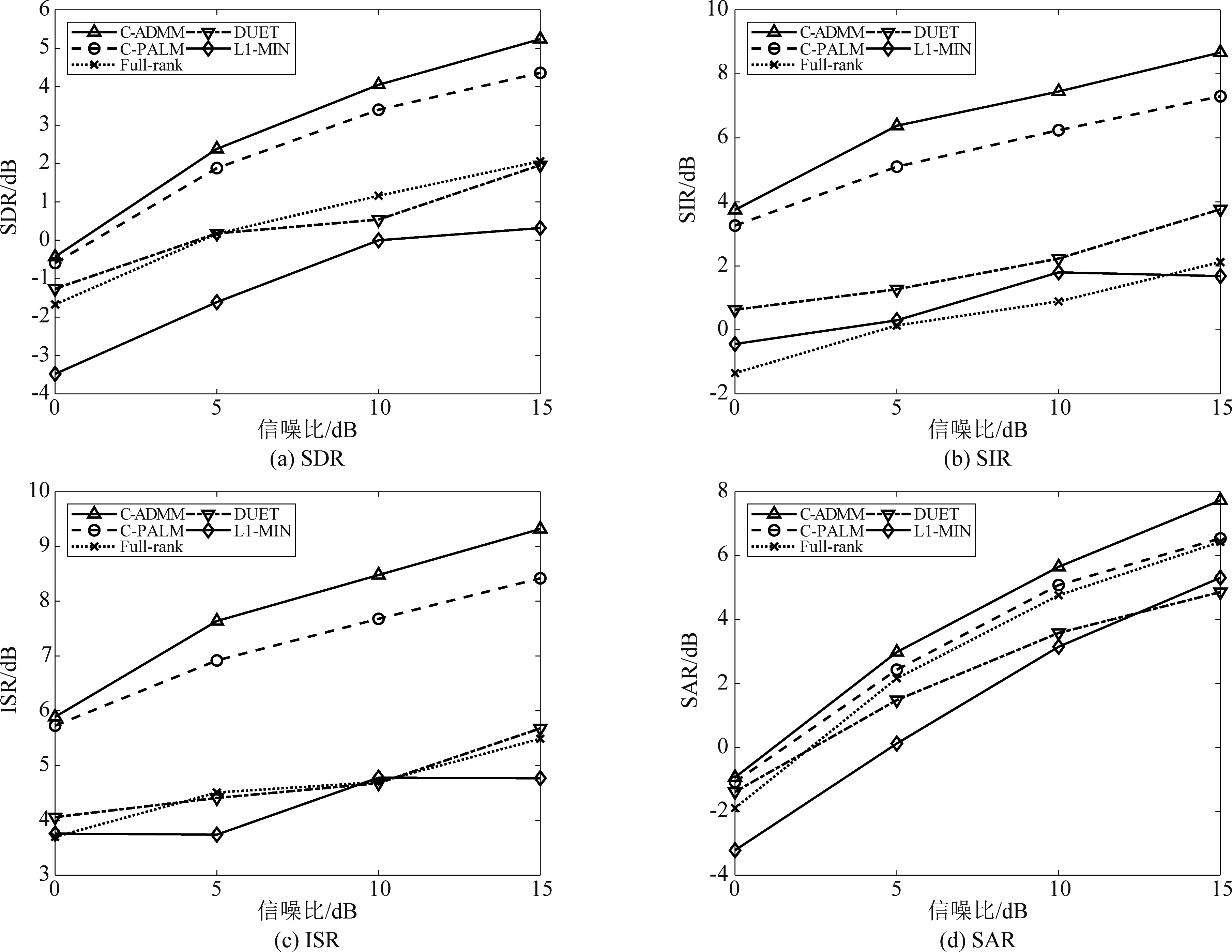
图3 不同算法在不同信噪比下的分离性能
Fig.3 Separation performance of different algorithms under different signal-to-noise ratios
表3 不同噪声类型下的性能对比(SDR/SIR,单位:dB)
Tab.3 Performance comparison under different noise types (SDR/SIR in dB)
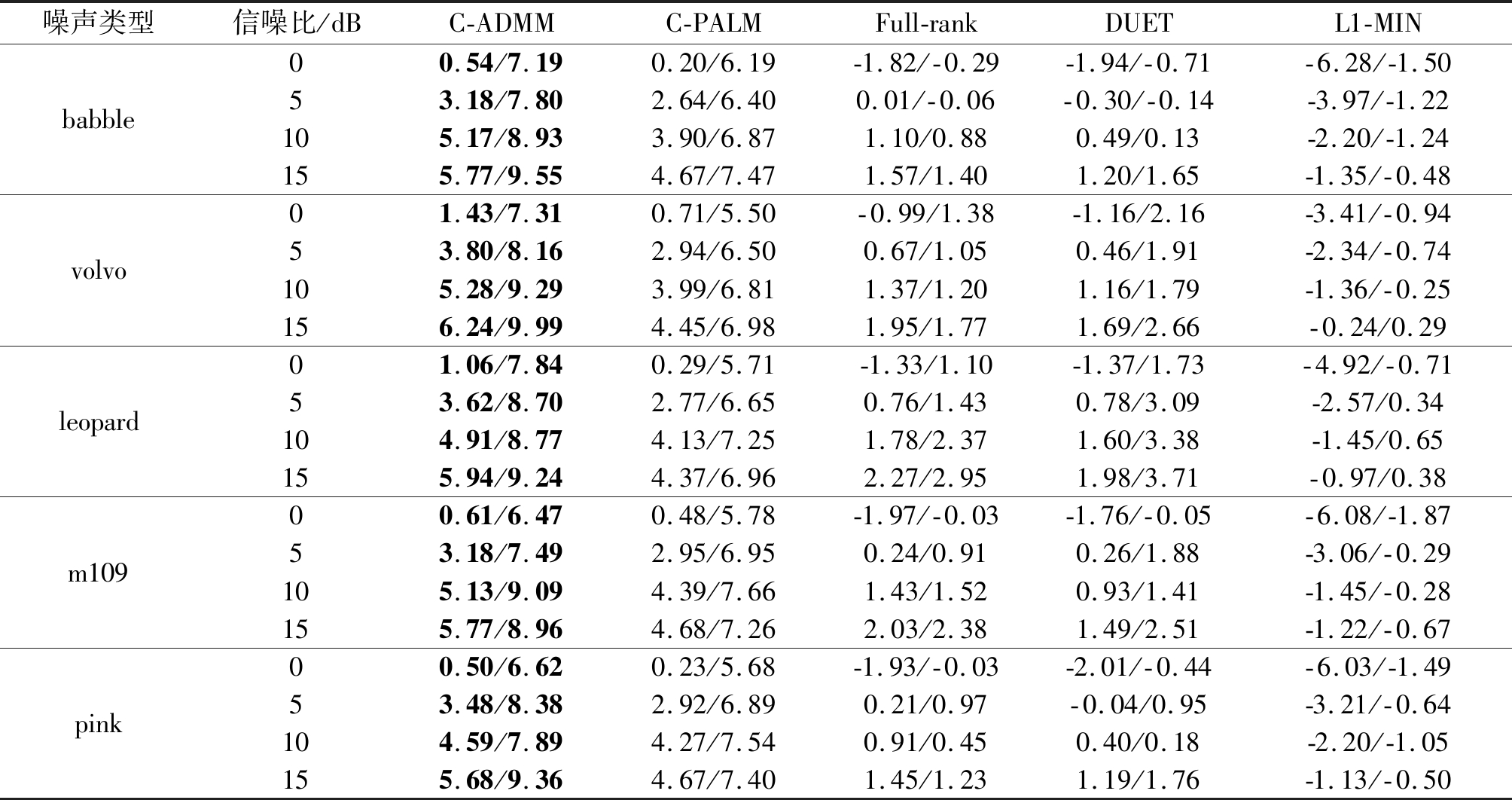
噪声类型信噪比/dBC-ADMMC-PALMFull-rankDUETL1-MINbabble00.54/7.190.20/6.19-1.82/-0.29-1.94/-0.71-6.28/-1.5053.18/7.802.64/6.400.01/-0.06-0.30/-0.14-3.97/-1.22105.17/8.933.90/6.871.10/0.880.49/0.13-2.20/-1.24155.77/9.554.67/7.471.57/1.401.20/1.65-1.35/-0.48volvo01.43/7.310.71/5.50-0.99/1.38-1.16/2.16-3.41/-0.9453.80/8.162.94/6.500.67/1.050.46/1.91-2.34/-0.74105.28/9.293.99/6.811.37/1.201.16/1.79-1.36/-0.25156.24/9.994.45/6.981.95/1.771.69/2.66-0.24/0.29leopard01.06/7.840.29/5.71-1.33/1.10-1.37/1.73-4.92/-0.7153.62/8.702.77/6.650.76/1.430.78/3.09-2.57/0.34104.91/8.774.13/7.251.78/2.371.60/3.38-1.45/0.65155.94/9.244.37/6.962.27/2.951.98/3.71-0.97/0.38m10900.61/6.470.48/5.78-1.97/-0.03-1.76/-0.05-6.08/-1.8753.18/7.492.95/6.950.24/0.910.26/1.88-3.06/-0.29105.13/9.094.39/7.661.43/1.520.93/1.41-1.45/-0.28155.77/8.964.68/7.262.03/2.381.49/2.51-1.22/-0.67pink00.50/6.620.23/5.68-1.93/-0.03-2.01/-0.44-6.03/-1.4953.48/8.382.92/6.890.21/0.97-0.04/0.95-3.21/-0.64104.59/7.894.27/7.540.91/0.450.40/0.18-2.20/-1.05155.68/9.364.67/7.401.45/1.231.19/1.76-1.13/-0.50
4.3 采用实际录音的实验对比
分别测试了SISEC 2013提供的一些真实混合录音,其中包含了3个声源和4个声源的情况,表4列出了不同算法得到的SDR和SIR。对于3个声源的混合语音,C-ADMM算法与C-PALM相比,SDR在混响时间为130 ms和250 ms时分别提升了0.27 dB和0.36 dB,而SIR分别提升了0.49 dB和0.65 dB。对于4个声源的混合语音,C-ADMM算法与C-PALM相比,SDR分别提升了0.34 dB和0.41 dB,SIR分别提升了0.58 dB和1 dB。这些指标都展示了所提算法C-ADMM具有出色的分离性能。
表4 在SISEC 2013实测数据上的分离性能(SDR/SIR,单位:dB)
Tab.4 Separation performance over real-world test data of SISEC 2013(SDR/SIR in dB)
混响时间方法3个源的混合语音4个源的混合语音130 msC-ADMM4.73/7.153.10/4.71C-PALM4.46/6.662.76/4.13Full-rank0.29/-1.300.15/-2.07DUET0.07/-1.260.54/-0.23L1-MIN-1.84/-1.24-0.47/-1.35250 msC-ADMM4.30/6.293.28/5.11C-PALM3.94/5.642.87/4.11Full-rank0.97/-0.350.54/-1.54DUET0.56/-0.59-0.20/-2.25L1-MIN-1.13/-1.27-1.22/-2.84
5 结论
针对欠定情况下的盲源分离问题,本文基于时频域中的卷积近似模型,提出了源信号和混合系统的联合估计,最终的优化问题由ADMM优化框架交替求解。通过对比实验发现,提出算法均比C-PALM,Full-rank,L1-MIN以及DUET等方法性能优越,这表明卷积窄带近似模型比瞬时窄带近似模型更适合于高混响的场景,同时,ADMM优化框架可取得更接近原优化问题的最优解。随着近几年深度学习的发展和应用,在未来工作中,我们将研究如何将深度学习应用到声源分离中,并将其与基于信号处理的经典算法进行比较。
[1] COMON P. Independent component analysis, A new concept?[J]. Signal Processing, 1994, 36(3): 287-314.
[2] JIA Yinjie, XU Pengfei. Convolutive blind source separation for communication signals based on the sliding Z-transform[J]. IEEE Access, 2020, 8: 41213- 41219.
[3] LI Yibing, WANG Yifan, DONG Qianhui. A novel mixing matrix estimation algorithm in instantaneous underdetermined blind source separation[J]. Signal, Image and Video Processing, 2020, 14(5): 1001-1008.
[4] DUONG N Q K, VINCENT E, GRIBONVAL R. Under-determined reverberant audio source separation using a full-rank spatial covariance model[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2010, 18(7): 1830-1840.
[5] SAWADA H, ARAKI S, MAKINO S. Underdetermined convolutive blind source separation via frequency Bin-wise clustering and permutation alignment[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(3): 516-527.
[6] YILMAZ O, RICKARD S. Blind separation of speech mixtures via time-frequency masking[J]. IEEE Transactions on Signal Processing, 2004, 52(7): 1830-1847.
[7] WINTER S, KELLERMANN W, SAWADA H, et al. MAP-based underdetermined blind source separation of convolutive mixtures by hierarchical clustering and-norm minimization[J]. EURASIP Journal on Advances in Signal Processing, 2006, 2007: 024717.
[8] KOWALSKI M, VINCENT E, GRIBONVAL R. Beyond the narrowband approximation: Wideband convex methods for under-determined reverberant audio source separation[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2010, 18(7): 1818-1829.
[9] FENG Fangchen, KOWALSKI M. Revisiting sparse ICA from a synthesis point of view: Blind Source Separation for over and underdetermined mixtures[J]. Signal Processing, 2018, 152: 165-177.
[10] LI Xiaofei, GIRIN L, HORAUD R. Audio source separation based on convolutive transfer function and frequency-domain lasso optimization[C]∥2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). New Orleans, LA. IEEE, 2017: 541-545.
[11] FENG Fangchen, KOWALSKI M. Underdetermined reverberant blind source separation: Sparse approaches for multiplicative and convolutive narrowband approximation[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 27(2): 442- 456.
[12] BOYD S, PARIKH N, CHU E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers [J]. Foundations & Trends in Machine Learning, 2010, 3(1):1-122.
[13] BALAZS P, DOERFLER M, KOWALSKI M, et al. Adapted and adaptive linear time-frequency representations: A synthesis point of view[J]. IEEE Signal Processing Magazine, 2013, 30(6): 20-31.
[14] BENICHOUX A, SIMON L S R, VINCENT E, et al. Convex regularizations for the simultaneous recording of room impulse responses[J]. IEEE Transactions on Signal Processing, 2014, 62(8): 1976-1986.
[15] GU Shuhang, XIE Qi, MENG Deyu, et al. Weighted nuclear norm minimization and its applications to low level vision[J]. International Journal of Computer Vision, 2017, 121(2): 183-208.
[16] LI Chunna, SHAO Yuanhai, YIN Wotao, et al. Robust and sparse linear discriminant analysis via an alternating direction method of multipliers[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 31(3): 915-926.
[17] ZHANG Xia, LIU Ding, YU Fei, et al. A distributed alternating direction method of multipliers algorithm for consensus optimization[C]∥2019 Chinese Automation Congress (CAC). Hangzhou, China. IEEE, 2019: 4104- 4107.
[18] LEHMANN E A, JOHANSSON A M. Prediction of energy decay in room impulse responses simulated with an image-source model[J]. The Journal of the Acoustical Society of America, 2008, 124(1): 269-277.
[19] VINCENT E, GRIBONVAL R, FEVOTTE C. Performance measurement in blind audio source separation[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2006, 14(4): 1462-1469.
[20] BOLTE J, SABACH S, TEBOULLE M. Proximal alternating linearized minimization for nonconvex and nonsmooth problems[J]. Mathematical Programming, 2014, 146: 459- 494.
