1 引言
随着目标跟踪相应的算法不断地进步,在计算机视觉领域引起越来越广泛的关注和研究[1-2]。目标跟踪算法涵盖了图像处理、机器学习和模式识别等方面的技术,在人机交互、军事制导、智能监控以及智能交通等领域的应用越来越广泛[3]。但在现实场景中的复杂情况使得目标跟踪的效果受到一定的影响。这些影响因素主要包括光照、运动模糊、形变、遮挡、尺度变化、快速运动和相似背景干扰等。如何在复杂的背景环境下提高算法的跟踪精度和稳定性成为目标跟踪研究领域的重点研究内容。
根据不同的观测模型可以将跟踪算法分成两大类模型,分别是生成式模型和判别式模型。生成式模型只是针对目标的外观特征进行建模,因此在处理目标被遮挡和目标快速运动等问题时,跟踪效果不是很理想。目前比较流行的是判别式模型,判别式模型将目标跟踪问题转化成二分类问题,用分类实现目标的定位,通过辨别特征差异,对前景和背景进行有效区分,从而将背景和跟踪目标区分开。两种模型进行对比判别式模型的跟踪效果更稳定,稳定性更强。
近年来,依据判别式模型的相关滤波(Correlation Filter)算法发展越来越广泛[4]。相关滤波在2010年初次被应用在跟踪领域,Bolme等提出了最小均方误差滤波器MOSSE(Minimum Output Sum of Squared Error)相关滤波器[5],在该算法中依据样本图像对目标外观进行建模,大幅度提高了目标跟踪的速度和准确度。针对训练样本不足的问题,Henriques等人[6]在2012年提出了核循环结构跟踪算法CSK(Circulant Structure of Tracking-by-detection with Kernels),在该算法中通过循环移位进行密集采样,使得整张图片的信息得到充分的利用。并结合FFT(Fast Fourier Transform)进行分类器的快速训练,极大地提高了算法的性能。2014年Henriques等[7]在CSK的基础上提出核相关滤波算法KCF(Kernel Correlation Filter),该算法将多通道的HOG特征[8]作为选取的目标特征,大大提高了滤波器的判别能力;通过核函数将线性空间的零回归问题映射到非线性空间,使得样本分类速度在高维特征空间中得到提高。同年,文献[9]提出用颜色空间CN(Color Name)[10]替换CSK中的灰度特征,并采用PCA(Principal Component Analysis)降维[11]的方式,将特征空间中的冗余信息去除,有效的提升算法的实时性。Danelljan等提出了多尺度空间滤波跟踪算法DSST[12](Discriminative Scale Space Tracker),该算法以MOSSE算法为基础,提取HOG特征,构建三维滤波器,其中分为一维尺度滤波器和二维位置滤波器。该算法能够很好的适应目标的尺寸变化,尺度滤波器具有很好的移植性。SRDCF算法的提出有效的解决循环移位产生的边界效应[13]问题。
特征的选择和提取是目标跟踪算法中的重要部分,选取特征的优劣对跟踪器的精度和鲁棒性起着非常重大的作用。随着近些年人们对特征提取的越来越丰富,涌现出许多把多种特征进行融合的算法。Li等[14]提出了多特征尺度自适应滤波器SAMF(Scale Adaptive Multiple Feature),该算法在特征层面上把梯度特征HOG、灰度特征和CN特征进行串联,从而得到多特征的融合特征,相比较于单特征的目标跟踪算法,在跟踪精度和鲁棒性上得到很大提升;但跟踪速度上效果欠佳。Bertinetto等[15]提出互补学习相关滤波器Staple,HOG特征在目标形变是稳定性差,但是对光照变化具有鲁棒性;CN特征对光照变化敏感,但对物体形变和快速运动的跟踪稳定性十分出色,因此该方法将HOG特征和CN特征进行互补融合,从而有效的提高了跟踪的精度。文献[16]提出对不同特征按照特征响应图的可信度来分配权重,通过求得FHOG特征和LBP(Local Binary Pattern)特征[17]的特征响应图,之后进行自适应加权融合,对目标部分遮挡、尺度变化等多种问题具有较好的稳定性和准确率。
虽然以上基于相关滤波的算法都已经取得了不错的跟踪效果,但还存在因光照变化、尺度变化、运动模糊和目标遮挡等导致跟踪过程中出现不同程度的跟踪漂移,甚至是跟丢目标的问题。在跟踪速度能够满足实时性要求的情况下,本文提出一种多特征自适应融合的跟踪算法。本文算法将梯度特征HOG、灰度特征和CN特征作为本算法提取特征。首先分析三种不同特征的跟踪性能表现,在特征层面上把CN特征、GRAY特征融合成颜色特征矩阵。随后在决策层面对颜色特征和HOG特征分别进行训练,训练得到两组独立的相关滤波器,之后在决策层面把训练所得到的两种滤波器的响应值分配不同的权重,通过线性加权的运算得到多个具有不同偏向的特征值,选取得分值最高的融合特征作为跟踪特征,保障了跟踪效果的准确性;引入遮挡判别策略和目标重定位机制,实现对目标遮挡的有效识别,抑制跟踪漂移。在标准数据集OTB50[18]和OTB100[19]上进行实验,并和近年来一些流行跟踪方法进行对比,结果表明,本文所用算法具有更高的有效性和稳定性。
2 目标跟踪算法
2.1 MOOSE相关滤波算法
MOOSE相关算法主要思想是通过卷积滤波方法将时域卷积变换成频域乘法,为了实现算法运算速度的提升,加入快速傅里叶变换进行快速计算。所对应的公式如下:
f(x,y)⊗h(x,y)⟺F(u,ν)⊙H(u,ν)
(1)
式中:⊗是卷积符号,表示两个函数在空间上的卷积,⊙表示两个矩阵中对应元素的乘积。
在目标跟踪算法中,卷积滤波的核心思想是把输入图像和相应的滤波器进行卷积运算,输出结果得到陡峭的两维高斯分布图形,恰好峰值正处在输入图像的中心位置,最高峰值位置就是目标的中心位置[20],因此在后续的跟踪过程中就可以通过判断卷积滤波后的峰值位置来定位每一帧图像目标的跟踪位置。
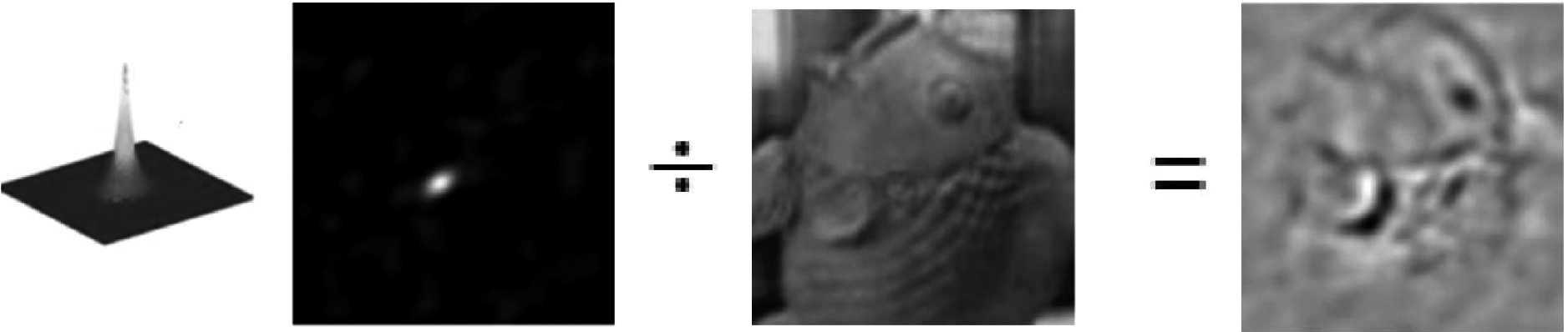
图1 卷积滤波过程
Fig.1 Convolution filtering process
MOSSE算法选取灰度特征提取样本fi,…, ft,经过滤波后的结果为gi,…,gt,其所在对应的时刻所得到的滤波器ht应满足最小均方误差和:
(2)
图像的尺寸大小为M×N,等式的左边是空间域方程,根据Parseval定理[21]导出等式右边。由此,可以得到求解上式最小值得方程式:
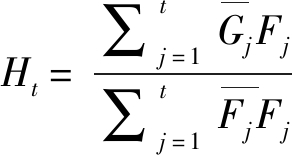
(3)
式中,分子和分母根据样本fi并加入一定的权重进行更新。对于下一帧尺寸大小为M×N的样本Z,得到的相关值y表示为:
(4)
y取得最大值所在位置就是样本Z中目标的位置。
MOSSE算法结构简单,利用相关滤波思想,提高了算法的跟踪精度。然而,算法仅仅使用了灰度特征,对一些复杂的背景、目标形变以及尺度变化跟踪效果不是很理想。
2.2 FDSST目标跟踪算法
DSST目标跟踪算法是由MOSSE算法改进的,将特征由一维的灰度特征改为多维的HOG特征,大大提高了跟踪的效果。在DSST算法中包含两个滤波器,分别是位置滤波器和尺度滤波器,用来分别预测目标的尺度和位置。FDSST算法[22]是在DSST算法的基础上,对滤波后的数据进行插值和维数的压缩,达到提升算法跟踪速度的效果。
首先,该算法根据选定目标的第一帧f,用循环矩阵算法生成一系列的样本,通过样本训练得到最优的滤波器,用来估计下一帧目标的位置所在。该算法把梯度特征HOG作为该算法采用的特征,针对目标提取d维特征, f l,其中l∈{1,2,…,d},代表的第l通道特征, f(n)∈Rd。每个通道都有所对应的滤波器hl。得到的样本输出g为期望中的以正样本为中心的二维高斯函数。对应的目标函数方程式表示为:
(5)
式中:*表示循环相关,λ为引入的正则项系数,防止分母项为零和避免滤波器过拟合。
为加速运算,用Parseval公式将运算转换到复频域进行运算求解得到滤波器为:
(6)
式中:![]() 是由f和g经过DFT变换后得到的复共轭。
是由f和g经过DFT变换后得到的复共轭。
将按照时间顺序的每一帧加入对滤波器的训练中,根据每帧的训练结果决定模型更新与否。为了确保每个通道的滤波器hl都有很强的鲁棒性,对滤波器模型采用如下策略更新:
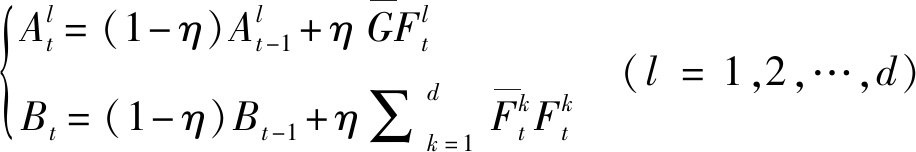
(7)
式中:t表示视频帧序列的帧数,![]() 和Bt分别是每个样本ft在滤波器
和Bt分别是每个样本ft在滤波器![]() 上的分子和分母,
上的分子和分母,![]() 表示为第t帧、第k维的复共轭,η是所选取的学习率。
表示为第t帧、第k维的复共轭,η是所选取的学习率。
第t帧图像根据t-1帧的位置情况,在指定的背景区域提取不同的维度的特征样本,经压缩后得到以预测目标位置为中心的图像zt经过傅里叶变换得到选定的正样本区域![]() 得到最终响应分数yt的复频域表示为:
得到最终响应分数yt的复频域表示为:
(8)
式中,响应值越大,是目标位置的可能性越大。最终可以求得![]()
为了对目标尺度的变化进行良好的适应,用一维高斯函数作为尺度滤波器期望输出,将尺度池中的尺度通过滤波器,得到不同的响应值,得到值最大的尺度即为当前帧目标的最佳尺度。假设当前帧目标大小为P×R,尺度池中的尺度因子为![]() 其中S为压缩后特征维数,n为滤波器的大小,尺度响应表示为:
其中S为压缩后特征维数,n为滤波器的大小,尺度响应表示为:
Sscale=σn×P×σn×R
(9)
其中:σ是尺度系数,Sscale为尺度响应。在尺度滤波过程中,通过对17维的特征进行插值得到33维响应向量,判定响应值最大的尺度作为选取的最合适尺度。
3 自适应多特征融合目标跟踪算法
本文是在FDSST的算法框架上进行改进的。目标的特征选择对目标跟踪成功与否取着决定性作用,本文采用HOG、CN和灰度特征,通过设置不同的融合因子,得到五种不同权重组合的融合特征,通过选取最大响应值判断出最优融合特征;加入遮挡判断策略和目标重定位机制,提高了算法的抗遮挡能力,防止跟踪过程中发生漂移现象,有效地提高了跟踪的稳定性和准确性。
3.1 特征融合和自适应选择
HOG特征是对图像局部特征的表现,CN特征是对图像全局特征的描述,局部特征HOG对光照的变化不敏感,但对目标的快速移动和程度比较大的形变比较敏感;CN特征对形变和快速移动有很好的鲁棒性。但在灰度图像中,灰度特征对目标的判定效果要比CN特征好,所以在本文中,首先对图像进行判断,如果输入图像为灰度图像,就只提取图像的灰度特征和HOG,不对CN特征进行提取;如果图像为彩色图像,则分别对图像的三类特征进行提取,随后把灰度特征和CN特征在特征层面融合在一起,称为颜色特征。其表示为:
(10)
式中:Ugray代表所提取的灰度特征,UCN表示CN特征,Ucl表示两种特征在特征层面上的融合。cat()函数用于构造多维矩阵。
之后分别计算HOG特征fhog和颜色特征fcl的响应图,通过线性加权的方式对两种响应在决策层面进行融合,得到融合响应。
F=τFhog+(1-τ)Fcl
(11)
式中:Fhog和Fcl分别是两种特征的得分响应函数;τ为融合因子。最终得到融合特征的响应F。
在跟踪过程中,目标和背景都在发生一定的变化,如果设定融合特征偏向为某一固定值,则没有应对不断变化的目标和背景的选择适应能力。因此本文通过设定几种不同的融合因子,得到不同程度的偏向,可以有效地应对目标和背景的变化,并增强了对不同跟踪场景的适应能力。经过大量实验论证,选出五种使本文算法跟踪效果最优的融合因子,如表1所示。
表1 融合因子分配方式
Tab.1 Allocation of fusion factors
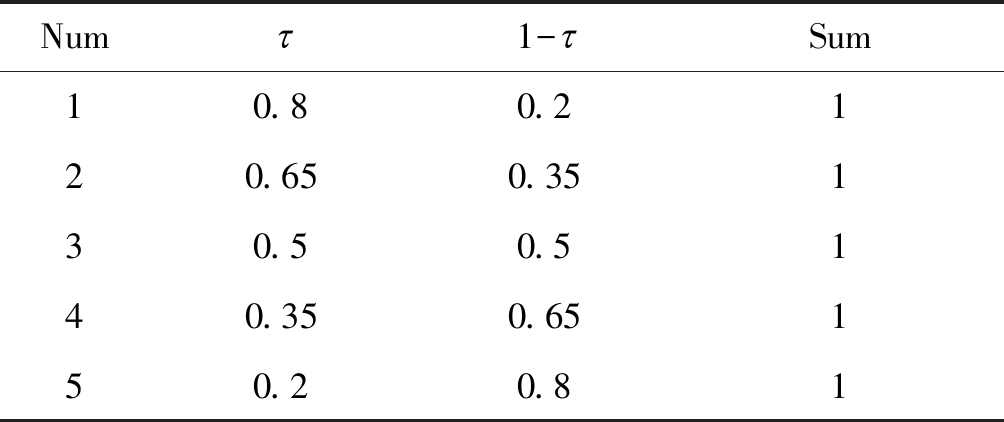
根据表1的融合因子,得到五种不同的融合响应值F={F1,F2,F3,F4,F5},并采用文献[4]提出的平均峰值相关能量(APCE)计算五种融合的可信度,平均峰值相关能量越大,跟踪效果越稳定。计算公式表示为:
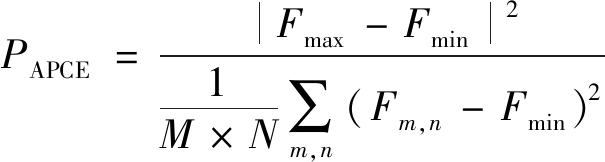
(12)
式中:Fmax表示最大响应值,Fmin表示最小响应值,Fm,n是位置(m,n)的元素值。选择可信度最大值所对应的融合特征作为当前帧的融合特征。
如图2所示,是分别以Basketball序列和Deer序列为例,给出了不同融合因子下融合特征的可信度值曲线图。图中五种不同颜色的曲线表示不同的融合特征。在basketball序列中,经常存在快速移动,目标遮挡的现象,可以看出,随着跟踪过程中目标和背景的不断变化,最大可信度所对应的融合因子也有所不同。Deer序列中,存在目标快速移动问题,但随着目标的移动,融合特征也在根据可信度的大小发生调整从而适应跟踪过程中的变化。因此本文所提出的特征自适应融合保障了每一帧的可信度值是最大的,为后续帧的跟踪提供了比较可靠的依据。
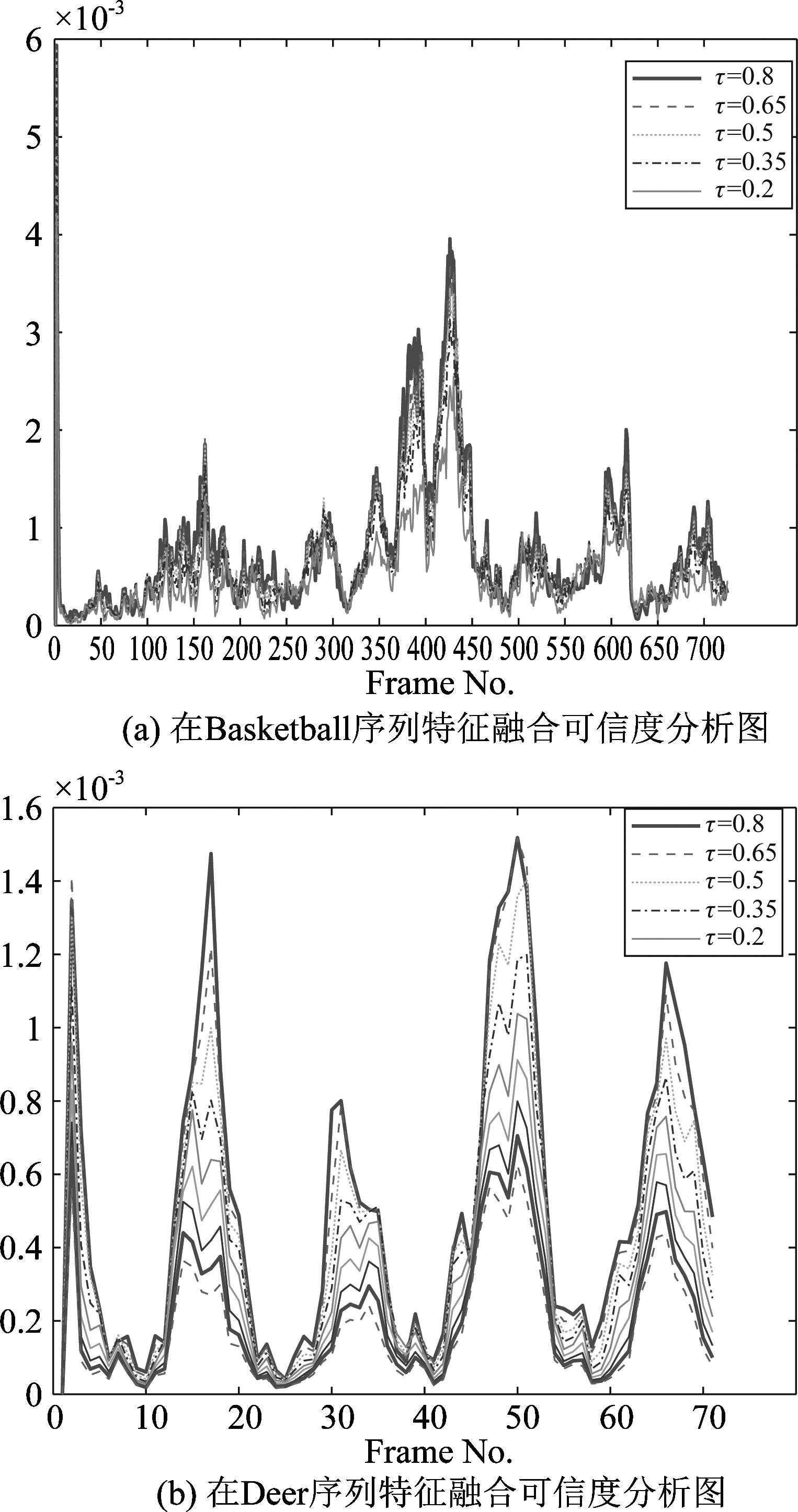
图2 特征选择结果分析
Fig.2 Analysis of feature selection results
3.2 遮挡判断策略
目标遮挡是目标跟踪过程中常见的问题。在跟踪过程中,提取的目标外观特征会随着被遮挡而受到污染,目标跟踪模型会出现不同程度的跟踪漂移,导致跟踪结果不准确。如果目标被严重遮挡或是全部遮挡,可能会导致跟踪失败。当目标跟踪的过程没有干扰时,其响应图是一个具有稳定峰值的高斯分布图。如果发生目标遮挡或丢失等干扰情况,响应图就会出现多峰值状态。如图3所示。
本文采用峰值旁瓣比(PSR)和平均峰值相关能量(APCE)[4]的结合作为遮挡评判能够更大程度的对目标的遮挡做出准确判断。PSR作为跟踪置信度,寻找其最大的峰值,将最大峰值周围的区域作为旁瓣,如下式表示:
(13)
式中:Fmax表示最大响应值,μ表示峰值旁瓣的均值,δ表示峰值旁瓣的方差。通常会设定阈值,如果计算得到的PSR值大于设定阈值,则认定为跟踪成功,否则,跟踪失败。
但目标在连续视频帧中被遮挡情况下,出现多峰值现象,响应图各点的响应值会出现波动,均值会被拉大,相差值效果不明显,减弱PSR对遮挡判断能力。在这种情况下可以使用最大响应峰值和多个峰值之间的关系,用APCE来衡量跟踪的结果。

图3 目标正常和被遮挡的跟踪响应图
Fig.3 Normal and occlusion tracking response maps
PAPCE的值是对响应结果的波动情况反映。随着PAPCE的值越大,跟踪效果越趋于稳定。但目标小部分被遮挡时,APCE变化不明显,此时PSR效果比较好。因此本文采用两者的结合作为评判尺度。
在第t帧中,定义的遮挡状态置信度θ(t)如下:
(14)
式中:当APCE的值PAPCE小于设定阈值Ptha,PSR值小于设定阈值Pthp时,θ(t)值为1,目标跟踪出现丢失,需要进行目标的重定位。
3.3 目标重定位
在目标跟踪过程中,由于较长时间的遮挡或干扰,跟踪模型会学习到遮挡物或干扰物的特征,影响跟踪器做出准确的判断,出现跟踪漂移现象。为防止后续跟踪漂移现象加重或是目标丢失,需要增加目标的候选区域,重新确定目标的准确位置。因此,本文提出一种目标重新定位的方法。通过对发生目标遮挡的视频帧增加目标候选区域的方法,实现对目标的重新定位。目标重定位的示意图如图4所示。

图4 目标检测到遮挡后重定位
Fig.4 Target relocation after occlusion detection
在目标重新定位的过程中,本文算法以遮挡前的目标所在位置为基准,通过将中心位置分别向左上方、正上方、右上方、左下方、正下方和右下方移动一定距离得到候选区域。在当前帧中增加了6个不同的候选区域来增加搜索范围。这6个区域和原区域彼此之间都有重合,对每个区域进行独立的目标搜索。这些区域表示为a={a1,a2,a3,a4,a5,a6}。随后对这些区域做原有跟踪算法的目标跟踪操作,得到每个区域的相关响应值,选取响应峰值最大的区域m作为本次重定位选定的最终区域。
Fm=max{F1,F2,F3,F4,F5,F6}
(15)
之后,使用3.2节中所提出的遮挡判断策略对选定的区域进行判断,如果满足式(14)的判定条件,则认为成功跟踪到目标,否则,认为当前帧目标跟踪失败。
由图5可知,通过3.2节中所提到的算法进行目标遮挡检测,当检测出目标被遮挡后,立即启动重定位机制,在遮挡过后成功地跟踪到目标。

图5 重定前后对比图
Fig.5 Comparison before and after reset
3.4 本文算法步骤
本文算法具体步骤如下所示。
①建立初始化模型。根据第一帧图像所提供的信息,分别训练颜色滤波器、HOG滤波和一维尺度滤波器。
②特征提取。根据t-1帧训练得到的滤波器对第t帧图像进行特征提取。获得HOG特征向量和颜色特征向量。
③特征融合。对步骤②得到的特征向量进行响应求解,由表1所提供的融合因子进行融合,得到不同偏向的融合特征响应。选取可信度最大的特征作为跟踪特征,取得目标位置。
④遮挡判断。根据遮挡判断策略对步骤③得到的目标位置进行判断,判断此帧是否出现目标遮挡或是丢失。
⑤目标重定位。如果在步骤④中判定目标跟踪过程出现遮挡或是目标丢失,则进行目标重新定位,否则,跳过本步骤,直接转到步骤⑥。
⑥尺度估计。根据当前帧所确定的目标位置,由方程式(9)构建尺度金字塔,通过尺度滤波器计算得到尺度响应。选取最大响应值作为当前帧t的最佳估计尺度。
⑦模型更新。根据前面步骤所得到的最佳跟踪结果进行模型更新。
⑧跟踪结果可视化。将跟踪窗口进行可视化呈现,如果不是最后一帧转到步骤②继续执行下一帧图像跟踪,否则,结束。
本文算法框图如图6所示。
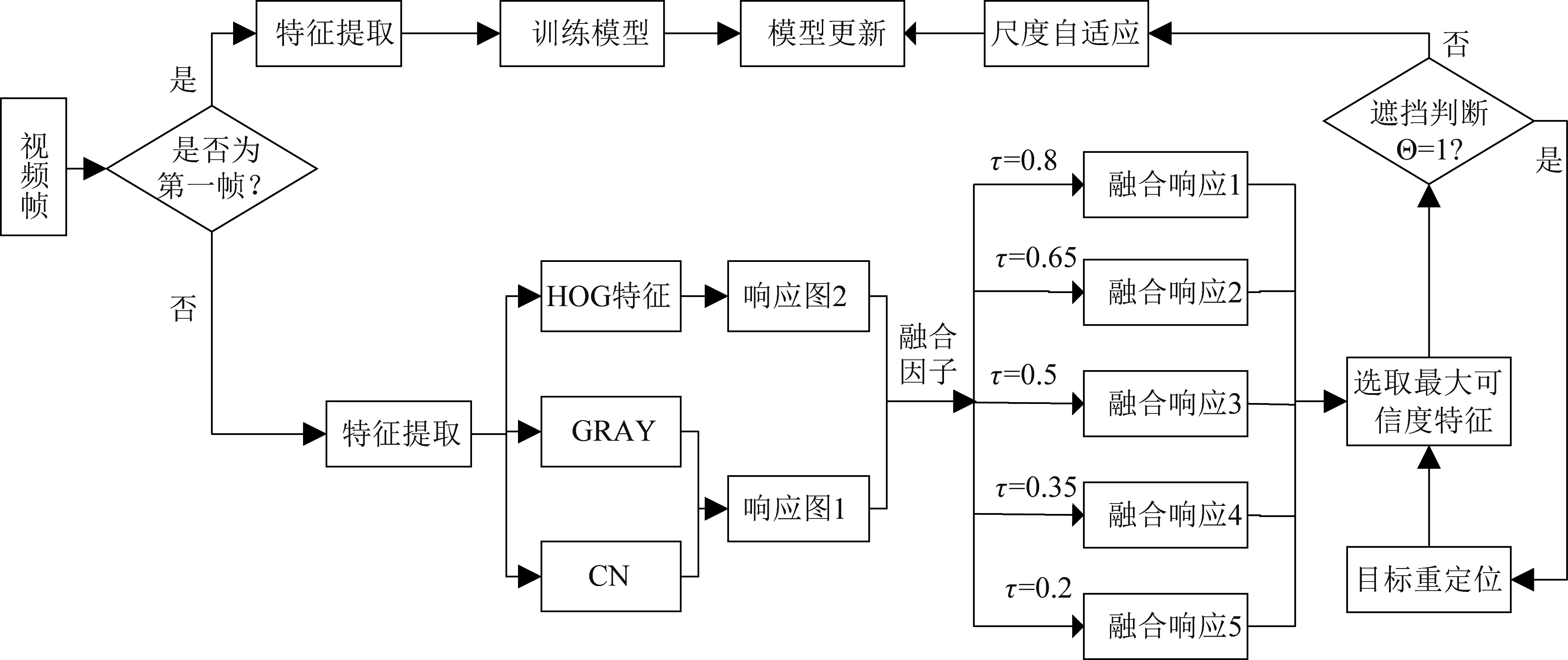
图6 本文算法流程图
Fig.6 Algorithm flow chart
4 实验结果及分析
4.1 实验环境及配置
本文所提算法的实验是在Intel(R) Core(TM) i5- 6500 CPU,主频3.2GHz,内存8GB的台式电脑上进行的,实现本文算法的平台为MATLAB R2017a。
本文选取OTB50和OTB100大型基准数据集作为本文实验的测试序列。其中包括物体遮挡、尺度变化、光照变化、快速移动和背景干扰等多种具有挑战性的影响因素。为了验证本文算法的鲁棒性和有效性,选取了CSK、KCF、CN、FDSST、SAMF和STAPLE等6种近几年跟踪效果比较好的算法进行对比。
本文采取准确率和成功率作为评价标准。使用一次性通过评估(OPE)评价准则对准确率和成功率进行计算。设定准确率的阈值p=20 pixel,准确率(DP)表示的是跟踪中心点位置误差小于设定阈值p的相对帧数所占总帧数的比值,其定义公式表示如下:
![]()
(16)
成功率(OP)用跟踪方框Bt和预测方框Bgt的交并比(重叠率)大于阈值的帧数与总帧数的比值表示,一般阈值设定为S=0.5。重叠率和成功率计算公式如下:
(17)
(18)
本文算法实验的参数设置情况为:学习率为0.025,正则化参数为0.01,HOG通道为32维,CN是10维,灰度特征维1维特征;在一维尺度滤波器中,尺度因子的参数设置为1.02,维数为17维。
4.2 算法结果比较分析
本文算法在OTB50和OTB100两个数据集上测试了包括本文算法在内的7种算法,得到了7种算法在OTB50和OTB100上的跟踪成功率和精确率曲线如图7和图8所示。7种算法的准确率和成功率对比如表2所示。
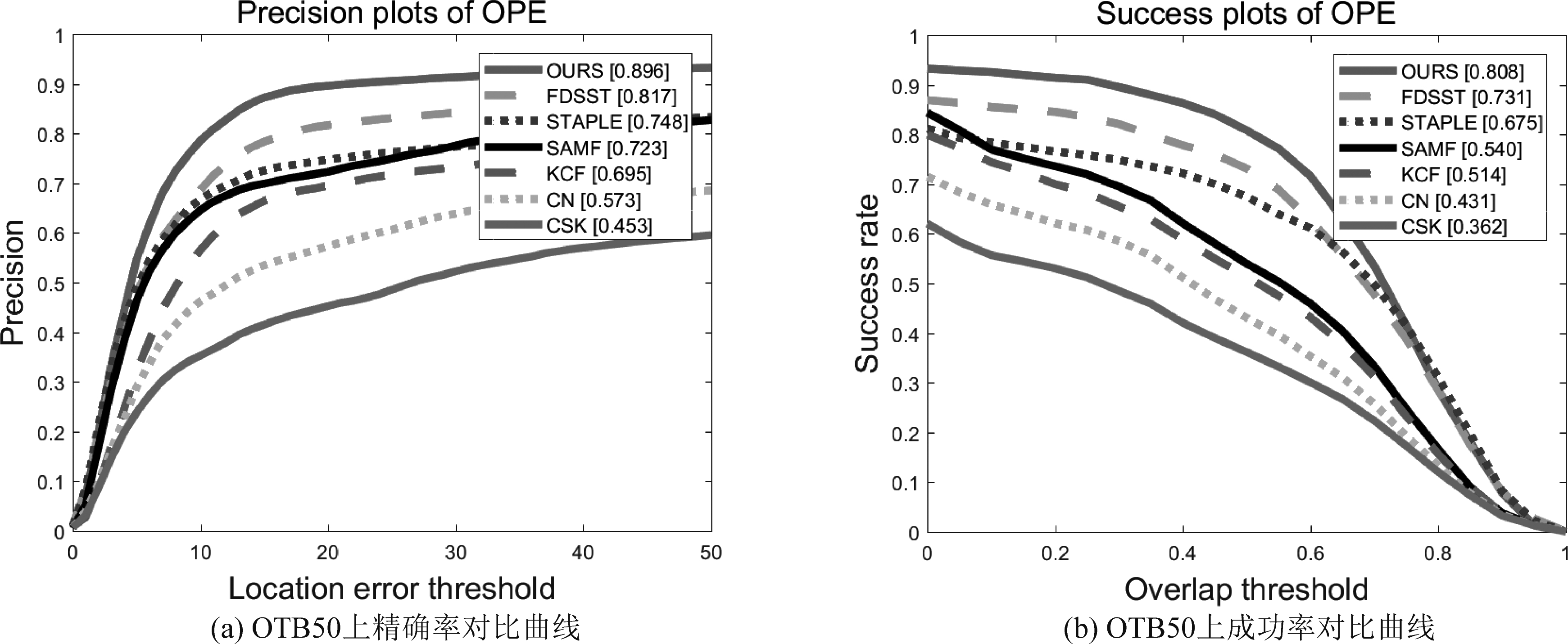
图7 在OTB50数据集上的一次性评估结果
Fig.7 One time evaluation results on OTB50 data set
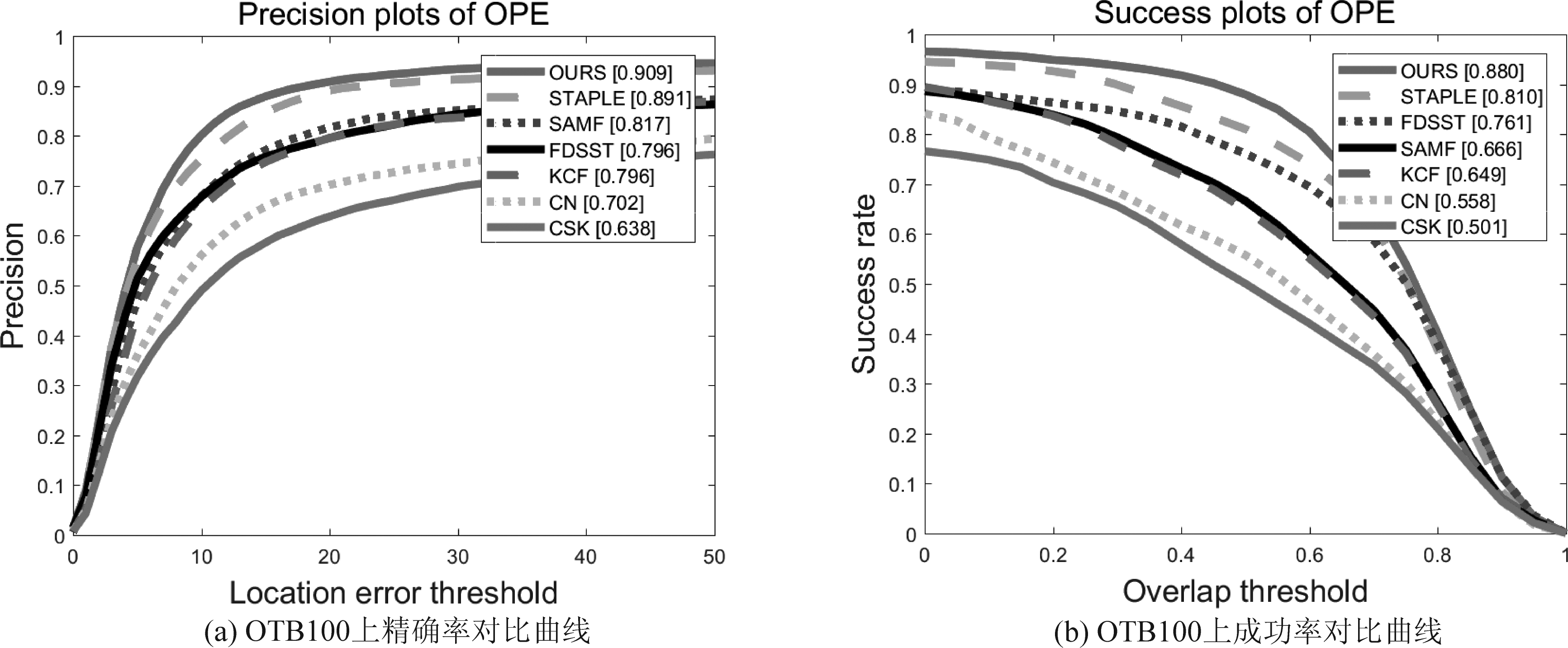
图8 在OTB100数据集上的一次性评估结果
Fig.8 One time evaluation results on OTB100 data set
表2 7种算法性能比较
Tab.2 Performance comparison of 7 algorithms

AlgorithmCSKKCFCNFDSSTSAMFSTAPLEOURSMeanDPOTB500.4530.6950.5730.8170.7230.7480.896OTB1000.6380.7960.7020.7960.8170.8910.909MeanOPOTB500.3620.5140.4310.7310.5400.6750.808OTB1000.5010.6490.5580.7610.6660.8100.880MeanFPS305.795169.67299.085266.547315.22164.062930.830
分析图5、图6和表2的数据可得,在OTB50数据集上进行测试的7种算法中,本文算法的精确率和成功率分别是0.896和0.808,排名第二的算法FDSST精确率和成功率分别为0.817和0.731,本文算法比排名第二的算法精确率和成功率分别提高了7.9%和7.7%;在OTB100数据集上,本文算法精确率和成功率分别为0.909和0.880,排名第二的算法STAPLE精确率和成功率分别为0.891和0.810,比排名第二的算法STAPLE分别提高了1.8%和7%。在跟踪速度上,本文算法在OTB50和OTB100上的平均跟踪速度为30.830FPS,比SAMF算法提高了15.609FPS;但相较于其他五种算法,本文跟踪速度相对比较慢。通过上述对比,本文所提出的算法在和其他6种对比算法相比较在整体性能上表现最优。
本文算法优点主要在于以下几点:(1)对HOG特征、CN特征和灰度特征在特征层面和决策层面进行融合,有效的解决了只有单一特征HOG特征时对运动模糊、快速移动的敏感性和CN特征对光照变化的敏感,极大地增强了特征的表达能力。(2)通过大量实验,设定了5组最佳融合因子,选取响应值最高的融合特征,提高了跟踪的准确性。(3)引入遮挡判断策略和目标重定位机制,能够很大程度上提高抗遮挡能力,有效抑制跟踪漂移。(4)引入尺度滤波器,在跟踪过程中能够自适应目标尺度的变化,增强了跟踪效果的稳定性和准确性。
4.3 其他性能比较
我们对目标跟踪中经常遇到的运动模糊和遮挡性等问题上的跟踪性能进行比较。相应的精确率和成功率的对比曲线图如图9和图10所示。
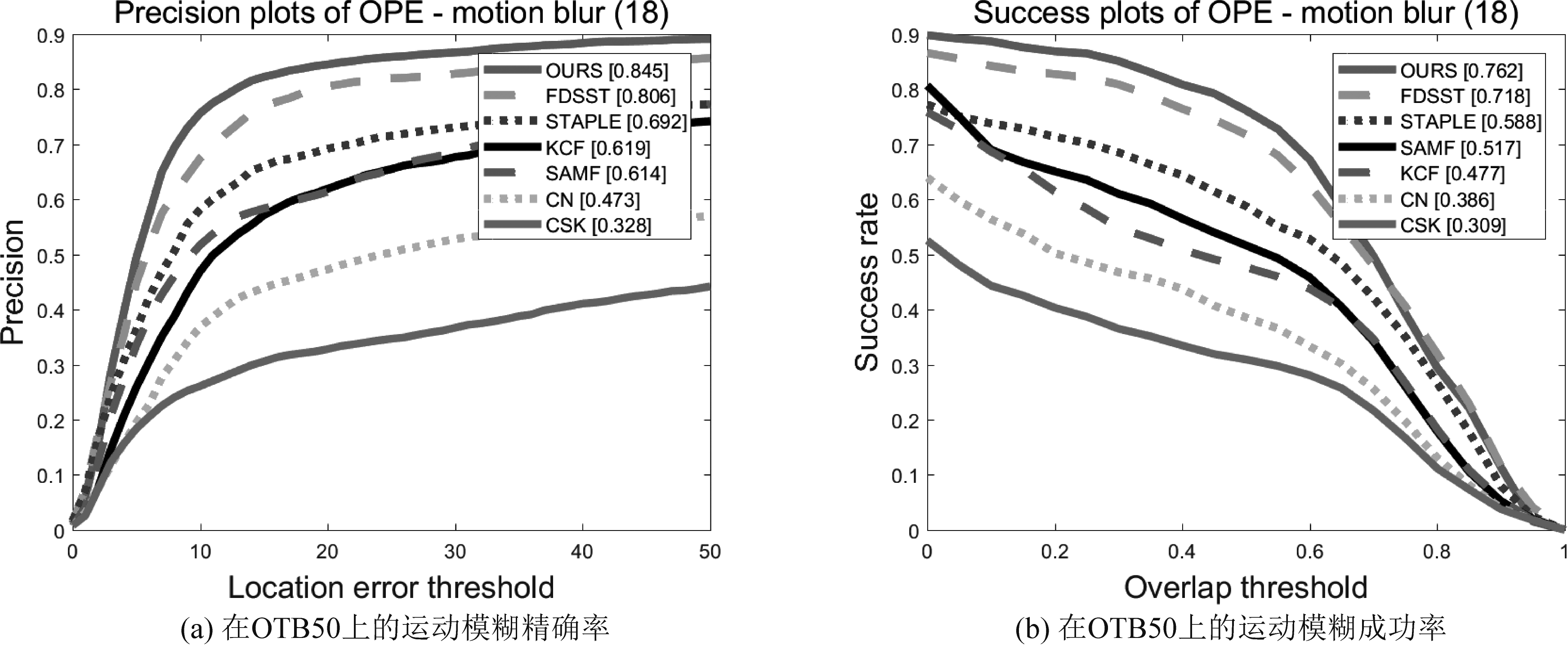
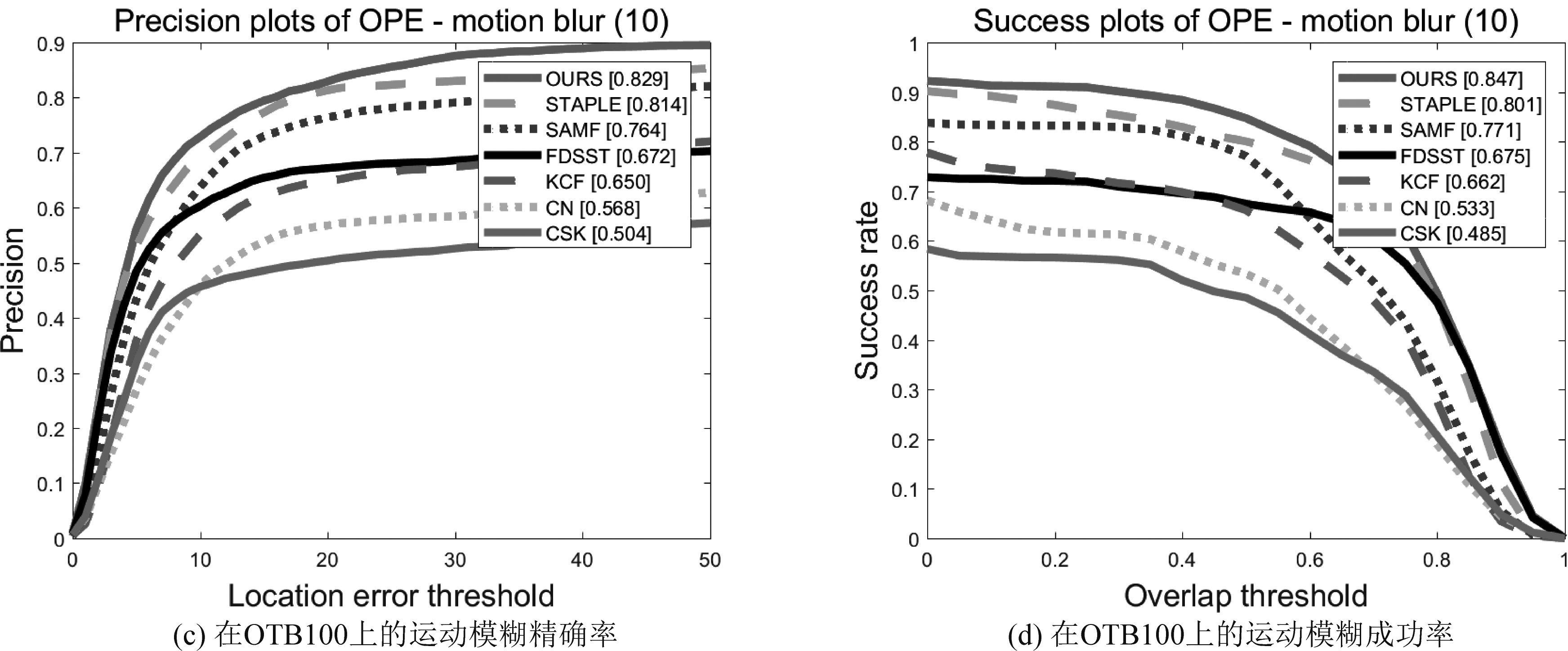
图9 在运动模糊视频序列上的精确率和成功率
Fig.9 Accuracy rate and success rate on motion blurred video sequence
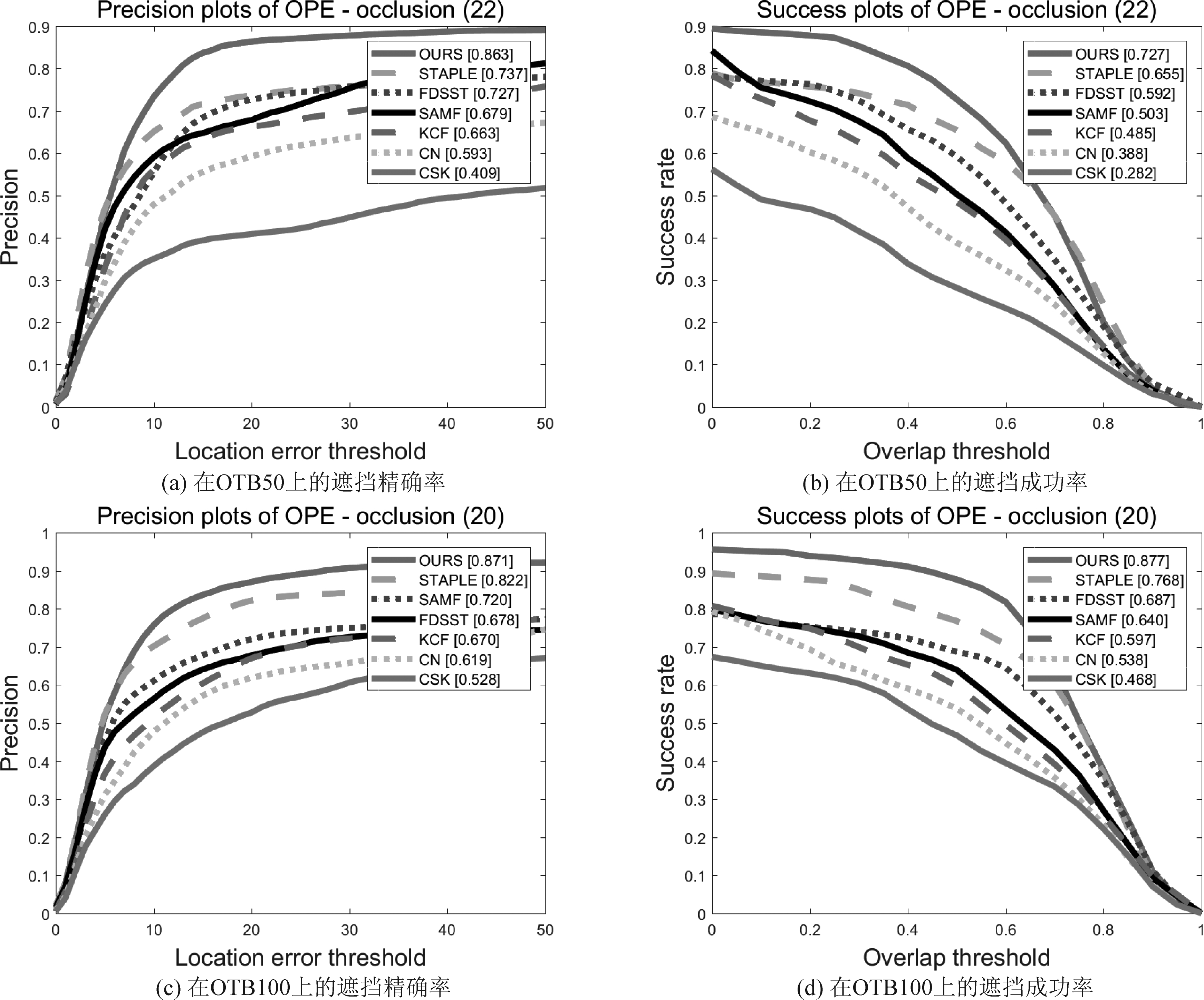
图10 在遮挡视频序列上的精确率和成功率
Fig.10 Accuracy rate and success rate on occluded video sequence
4.4 定性分析
在实验过程中,我们抽取五组具有代表性的视频进行比较,其中前两组都有严重的目标遮挡问题。后面每组视频都存在快速移动、运动模糊和目标遮挡等特点,对比结果如图11所示。
Jogging视频序列中存在严重的遮挡问题,当目标在第50帧左右时,开始出现较为严重的遮挡,在此时本文算法能够稳定跟踪,SAMF和STAPLE开始发生轻微的跟踪漂移,其他算法发生的漂移更严重;到第65帧时,只有本文算法还能持续稳定跟踪直至跟踪结束,其他六种算法均由于跟踪漂移严重而跟踪失败。说明本文算法对遮挡问题具有很好的鲁棒性,能够十分有效的抑制跟踪漂移。

图11 本文算法在Jogging,Human7,DragonBaby,Bird2,Soccer视频序列中与其他算法进行对比
Fig.11 Algorithm in this paper is compared with other algorithms in the video sequences of Jogging,human7, dragonbaby, bird2 and soccer
Soccer视频序列存在目标遮挡和背景复杂的情况,在104帧到108帧,随着目标位置被遮挡的越来越严重,其他对比算法逐渐出现跟踪漂移的情况,有的算法甚至是丢失跟踪目标。本文算法得益于采用了遮挡判断策略和目标重新定位机制,能够有效的判断出遮挡的存在,并进行目标的重定位,大大提高了跟踪的准确性和稳定性;在145帧到247帧中,大部分算法已经跟踪丢失目标,本文算法依然能够准确的跟踪到目标。说明本文算法对目标遮挡和背景复杂有很好的鲁棒性,对跟踪漂移具有良好的抑制作用。
Human7视频序列中目标具有运动模糊和视频抖动的属性,在33帧到122帧的过程中,CSK、KCF、CN、FDSST和SAMF都出现了跟踪丢失的现象,只有SATPLE和本文算法能够准确的跟踪到目标,在207帧和224帧中,STAPLE算法发生了轻微的漂移。本文算法在尺度和精度上都能够很好的定位目标。说明本文算法对目标运动模糊具有很好的适应性和稳定性。
DragonBaby视频序列具有运动模糊、快速移动等特点。在第33和34帧时,FDSST、KCF、CSK等算法已经跟踪失败,其他算法都出现一定的漂移,只有本文算法准确的跟踪到目标区域。在第50帧和85帧中,除本文算法和STAPLE外,其他算法全部跟丢,STAPLE算法出现较大的漂移,本文算法跟踪准确。这说明本文算法在快速移动和运动模糊的场景下可以实现对目标的稳定跟踪。
Bird2视频序列主要包含目标遮挡和背景复杂的情况。在Bird2中,第62帧其他算法在存在遮挡的情况下发生了跟踪漂移,只有本文算法精确地跟踪到目标所在位置。在第93帧和96帧,CSK算法和FDSST算法已经跟丢目标。由上述情况说明本文算法能够在目标发生遮挡或背景复杂的情况下对目标的跟踪具有很好的稳定性。
以上实验结果表明,本文的算法在目标运动模糊、目标遮挡和快速移动等情况下,能够稳定的跟踪到目标,具有很强的鲁棒性和稳定性。
5 结论
本文算法通过将三种不同的特征在特征层面和决策层面进行融合,并结合不同的融合因子,得到五种不同的融合响应值,通过最大响应值选取最佳融合特征,从而提高了目标的特征表达能力;引入遮挡判断策略,能够有效的判断出遮挡现象行的存在;采用目标重定位机制,有效的抑制了跟踪漂移和防止目标丢失;引进了单独的尺度滤波器,对目标尺度变化具有良好的适应性。我们的实验结果表明,本文所提出的算法在目标跟踪过程中,对目标跟踪过程中存在的运动模糊、光照变化和部分遮挡等干扰因素具有很好的鲁棒性和准确性;跟踪速度能够满足实际使用要求。在后续工作中,打算改进算法的运算效率,在保证稳定性和准确性的同时进一步提升算法的跟踪速度。
[1] 张哲, 孙瑾, 杨刘涛. 融合相关滤波与关键点匹配的跟踪算法[J]. 光学学报, 2019, 39(2): 259-267.
ZHANG Zhe, SUN Jin, YANG Liutao. Tracking algorithm based on correlation filter fusing with keypoint matching[J]. Acta Optica Sinica, 2019, 39(2): 259-267.(in Chinese)
[2] 卢湖川, 李佩霞, 王栋. 目标跟踪算法综述[J]. 模式识别与人工智能, 2018, 31(1): 61-76.
LU Huchuan, LI Peixia, WANG Dong. Visual object tracking: A survey[J]. Pattern Recognition and Artificial Intelligence, 2018, 31(1): 61-76.(in Chinese)
[3] 李军伟, 周小龙, 产思贤, 等. 基于自适应卷积神经网络特征选择的视频目标跟踪方法[J]. 计算机辅助设计与图形学学报, 2018, 30(2): 273-281.
LI Junwei, ZHOU Xiaolong, CHAN Sixian, et al. A novel video target tracking method based on adaptive convolutional neural network feature[J]. Journal of Computer-Aided Design & Computer Graphics, 2018, 30(2): 273-281.(in Chinese)
[4] 孙紫君, 黄福珍. 基于改进核相关滤波算法的目标跟踪[J]. 上海电力学院学报, 2019, 35(5): 442- 448.
SUN Zijun, HUANG Fuzhen. Target tracking based on improved kernel correlation filtering[J]. Journal of Shanghai University of Electric Power, 2019, 35(5): 442- 448.(in Chinese)
[5] BOLME D S, BEVERIDGE J R, DRAPER B A, et al. Visual object tracking using adaptive correlation filters[C]∥2010 IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco, CA, USA. IEEE, 2010: 2544-2550.
[6] HENRIQUES J F, CASEIRO R, MARTINS P, et al. Exploiting the circulant structure of tracking-by-detection with kernels[C]∥Computer Vision-ECCV 2012, 2012: 702-715.
[7] HENRIQUES J F, CASEIRO R, MARTINS P, et al. High-speed tracking with kernelized correlation filters[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(3): 583-596.
[8] WANG Xiaoyu, HAN T X, YAN Shuicheng. An HOG-LBP human detector with partial occlusion handling[C]∥2009 IEEE 12th International Conference on Computer Vision. Kyoto, Japan. IEEE, 2009: 32-39.
[9] DANELLJAN M, KHAN F S, FELSBERG M, et al. Adaptive color attributes for real-time visual tracking[C]∥2014 IEEE Conference on Computer Vision and Pattern Recognition. Columbus, OH, USA. IEEE, 2014: 1090-1097.
[10] CHIN T J, SUTER D. Incremental kernel principal component analysis[J]. IEEE Transactions on Image Processing, 2007, 16(6): 1662-1674.
[11] VAN DE WEIJER J, SCHMID C, VERBEEK J. Learning color names from real-world images[C]∥2007 IEEE Conference on Computer Vision and Pattern Recognition. Minneapolis, MN, USA. IEEE, 2007: 1- 8.
[12] DANELLJAN M, H GER G, SHAHBAZ KHAN F, et al. Accurate scale estimation for robust visual tracking[C]∥Proceedings of the British Machine Vision Conference 2014. Nottingham. British Machine Vision Association, 2014: 1-11.
GER G, SHAHBAZ KHAN F, et al. Accurate scale estimation for robust visual tracking[C]∥Proceedings of the British Machine Vision Conference 2014. Nottingham. British Machine Vision Association, 2014: 1-11.
[13] DANELLJAN M, H GER G, KHAN F S, et al. Learning spatially regularized correlation filters for visual tracking[C]∥2015 IEEE International Conference on Computer Vision (ICCV). Santiago, Chile. IEEE, 2015: 4310- 4318.
GER G, KHAN F S, et al. Learning spatially regularized correlation filters for visual tracking[C]∥2015 IEEE International Conference on Computer Vision (ICCV). Santiago, Chile. IEEE, 2015: 4310- 4318.
[14] LI Yang, ZHU Jianke. A scale adaptive kernel correlation filter tracker with feature integration[C]∥Computer Vision-ECCV 2014 Workshops, 2015: 254-265.
[15] BERTINETTO L, VALMADRE J, GOLODETZ S, et al. Staple: complementary learners for real-time tracking[C]∥2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Las Vegas, NV, USA. IEEE, 2016: 1401-1409.
[16] 纪纲, 高富东, 范加利. 基于改进的MOSSE相关滤波的目标跟踪[J]. 计算机测量与控制, 2018, 26(6): 236-238,243.
JI Gang, GAO Fudong, FAN Jiali. Object tracking algorithm based on improved MOSSE correlation filter algorithm[J]. Computer Measurement & Control, 2018, 26(6): 236-238,243.(in Chinese)
[17] 齐永锋, 王梦媛. 基于LBP与核相关滤波器的运动目标跟踪算法[J]. 红外技术, 2019, 41(6): 572-576.
QI Yongfeng, WANG Mengyuan. Moving target tracking algorithm based on LBP and kernel correlation filter[J]. Infrared Technology, 2019, 41(6): 572-576.(in Chinese)
[18] WU Yi, LIM J, YANG M H. Online object tracking: A benchmark[C]∥2013 IEEE Conference on Computer Vision and Pattern Recognition. Portland, OR, USA. IEEE, 2013: 2411-2418.
[19] WU Y, LIM J, YANG M H. Object tracking benchmark[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2015, 37(9): 1834-1848.
[20] WANG Mengmeng, LIU Yong, HUANG Zeyi. Large margin object tracking with circulant feature maps[C]∥2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR). Honolulu, HI, USA. IEEE, 2017: 4800- 4808.
[21] 李小平, 牛旭. Parseval定理在广义积分中的应用[J]. 塔里木大学学报, 2009, 21(3): 30-32.
LI Xiaoping, NIU Xu. Parseval theorem in the application of solving the generalized integrals[J]. Journal of Tarim University, 2009, 21(3): 30-32.(in Chinese)
[22] DANELLJAN M, H GER G, KHAN F S, et al. Discriminative scale space tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1561-1575.
GER G, KHAN F S, et al. Discriminative scale space tracking[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(8): 1561-1575.

