1 引言
自适应陷波器(ANF)频率估计方法在卫星导航定位、工业控制与仪表以及医学工程中有着较为广泛的应用[1-5]。该频率估计方法同基于FFT离散频谱校正的频率估计方法[6-7]相比,具有无频谱泄漏、计算简单的优点,但也存在易受噪声影响,频率估计结果有偏的问题。ANF频率估计方法按照陷波器传递函数的不同,大致可分为两类[8],一类是基于有限冲激响应自适应陷波器(FIR-ANF)的频率估计方法,该类方法的结构较为简单,但易受噪声干扰,估计结果往往存在较大的偏差;另一类是基于无限冲激响应自适应陷波器(IIR-ANF)的频率估计方法,该类方法虽然抗噪性较好,频率估计精度有一定的提升,但其结构较为复杂,且存在收敛速度慢的缺点。针对上述问题,相关的文献开展了一些研究。如文献[9]针对FIR-ANF的频率估计问题进行了研究,一定程度上提高了频率估计精度,具备了一定的抗噪性,但其频率估计有偏和收敛速度不快的问题还有待解决。文献[10]则主要针对IIR-ANF的频率估计问题开展研究,虽然提高了频率估计精度,但其频率估计偏差依然存在,且收敛速度慢的问题仍较为严重,亟待进一步改善。
为此,本文以结构较为简单的FIR-ANF为基础,利用误差函数的性能分析结果,推导出频率估计递推表达式,提高其频率估计方法的收敛速度。在分析递推表达式频率估计性能的基础上,提出偏差补偿项,有效提高FIR-ANF频率估计方法的精度和抗噪性能,获得无偏的频率估计结果。
2 方法原理
设正弦输入信号为:
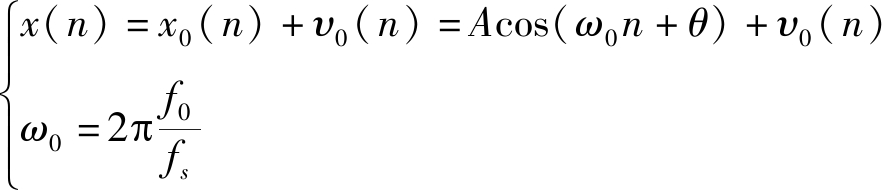
(1)
式中,A为信号幅值,θ为信号相位;ω0为信号频率,单位rad, f0为信号实际频率,单位Hz, fs为采样频率;υ0(n)为高斯(正态)白噪声,其均值为0,方差为σ2。
FIR-ANF的传递函数为
H(z)=1+az-1+z-2
(2)
其中a=-2cos ω,ω为陷波频率,当x(n)通过式(2)所示的ANF后,其值y(n)如式(3)和式(4)所示。当ANF收敛后,此时a→a0=-2cos ω0,即ω→ω0,陷波频率等于输入信号频率。
x(n)→(1+az-1+z-2)→y(n)
(3)
y(n)=x(n)+ax(n-1)+x(n-2)
(4)
根据文献[11],则式(3)和式(4)的误差函数为
J=y2(n)
(5)
使其最小化
![]() =2y(n)x(n-1)
=2y(n)x(n-1)
(6)
常见的基于FIR-ANF的频率估计是在式(6)的基础上形成如下的基于梯度下降的频率迭代递推计算式,
(7)
式(7)所示的梯度下降频率估计方法,在y(n)中包含有待估计参数a值,即梯度下降的速度与估计参数a值的关联性较大,会导致整个频率估计方法出现收敛速度偏慢的问题。
为此,将式(6)展开后取0,可得
![]() =2y(n)x(n-1)=2(x(n)+
=2y(n)x(n-1)=2(x(n)+
ax(n-1)+x(n-2))x(n-1)=0
(8)
即在稳态条件下,存在式(9)的关系
(9)
式(9)中,r1(n)=x(n-1)(x(n)+x(n-2)),r0(n)=x2(n-1),与估计参数a完全没有关联,只与输入信号有关,而输入信号一般来说相对固定,可以有效的提高整个频率估计方法的收敛性,在实际计算中,为保证计算结果平滑,可以采用式(10)所示的迭代计算方式。
r1(n)=λr1(n-1)+
(1-λ)[x(n-1)(x(n)+x(n-2))]
r0(n)=λr0(n-1)+(1-λ)x2(n-1)
(10)
式(10)中λ是遗忘因子。
3 无偏性与方差分析
3.1 无偏性分析
为分析所提FIR-ANF频率估计方法的性能,验证其偏差性,需要求取式(9)的期望,由于其计算时是按照分子分母分别迭代计算,故其期望值为:
(11)
在式(11)中对其中各项分别计算,可得
E[r1(n)]=E[x(n-1)(x(n)+x(n-2))]
(12)
E[r0(n)]=E[x2(n-1)]
(13)
为计算式(11),需要分别计算出E[r1(n)]、E[r0(n)],为此将式(1)代入式(12)~式(13),在计算过程中注意噪声及其在不同时刻的自相关性和互相关性,可得
E[r1(n)]=E[x(n-1)(x(n)+x(n-2))]=A2cos ω0
(14)
E[r0(n)]=E[x2(n-1)]=![]()
(15)
将式(14)~式(15)代入式(11)可得,
(16)
式(16)中,影响频率估计均值的关键因素是其中的噪声σ2,如果在无噪声的情况下,即σ2=0时,则式(16)可简化为:
(17)
为获得无偏的频率估计结果,需要将r0(n)中的σ2消除。由文献[12]可知,当FIR-ANF处于收敛的稳定状态下时,即a0→-2cos ω0,可得
E[x(n)y(n)]=E[x(n)(x(n)+ax(n-1)+![]()
(18)
将式(18)所示的偏差补偿项代入式(15)可得,
E[r1(n)]=E[x(n-1)(x(n)+
x(n-2))]=A2cos ω0![]()
![]()
(19)
由此可将于r0(n)中的σ2消掉,则对式(9)和式(10)所示方法进行偏差补偿后的频率估计方法为
(20)
r1(n)=λr1(n-1)+
(1-λ)[x(n-1)(x(n)+x(n-2))]![]()
(21)
对式(20)所示的频率估计方法求取期望,可得
(22)
由此可见所提的频率估计方法为无偏的,为进一步分析所提方法的方差性能,对式(9)和式(20)进行方差分析。
3.2 方差分析
针对式(9),为求取其方差,需要按照文献[13]对其进行处理,
(23)
将f1在点T10=E[T1]=μ1=[E[r1(n)] E[r0(n)]]T附近用一阶泰勒级数展开[13],可得

(24)
对式(24)求取方差可得,
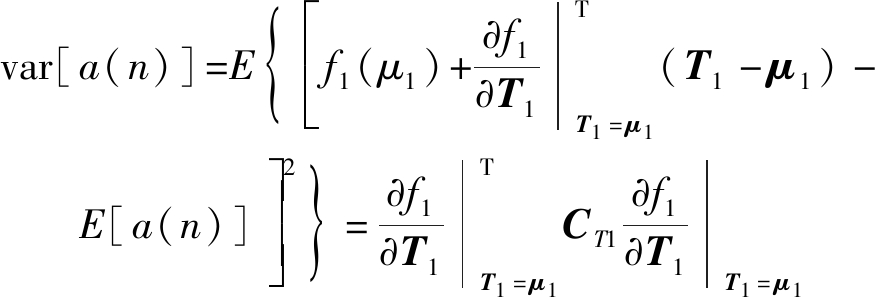
(25)
其中,
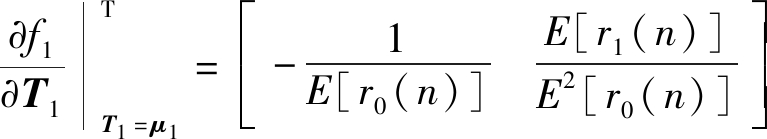
(26)
CT1为协方差矩阵,其值为
(27)
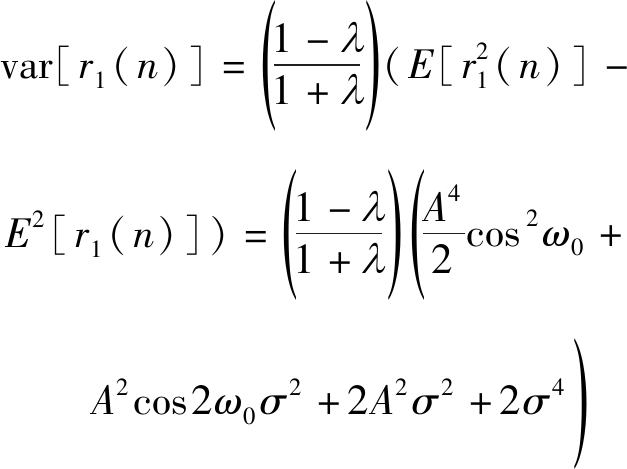
(28)
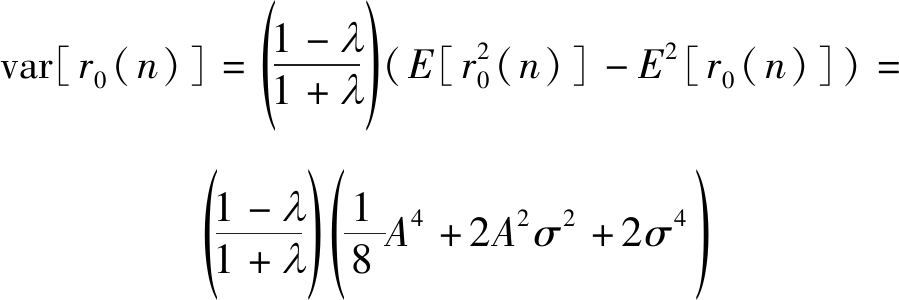
(29)
同理,对式(22)进行处理,可得
(30)
同样,将f2在点![]() 对其进行泰勒级数展开
对其进行泰勒级数展开
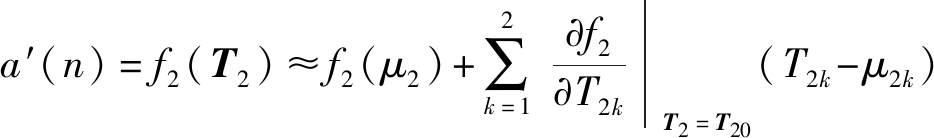
(31)
对式(31)求取方差可得
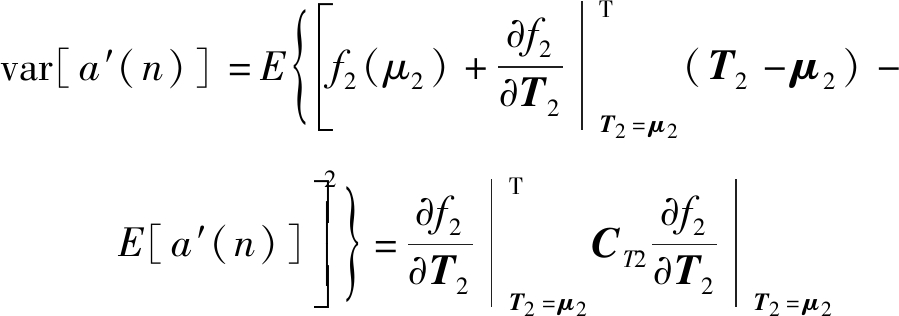
(32)
其中,
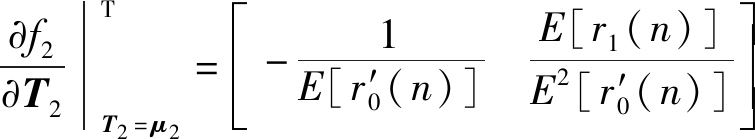
(33)
CT2为协方差矩阵,其值为
(34)
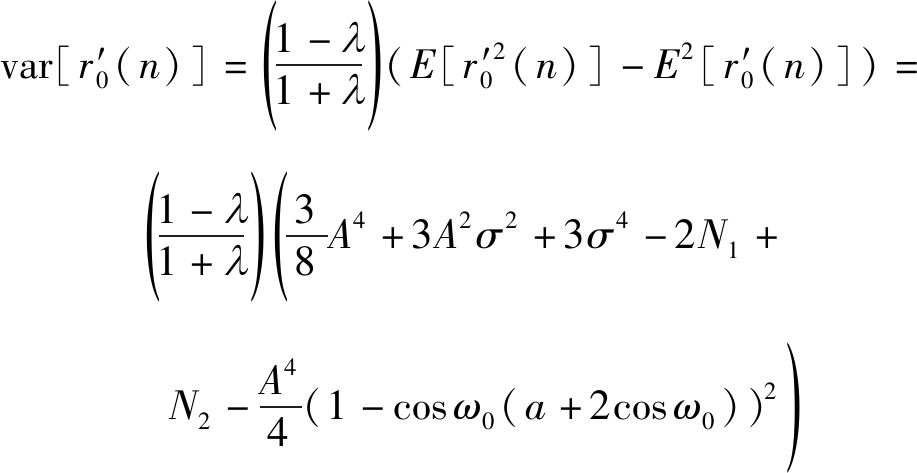
(35)
其中,
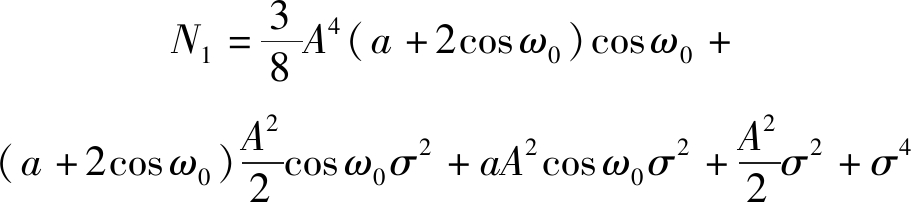
(36)
![]()
![]()
(4+a2)σ4+2(a+2cos ω0)A2cos ω0σ2
(37)
![]()
(a+2cos ω0)A2σ2+aσ4
(38)
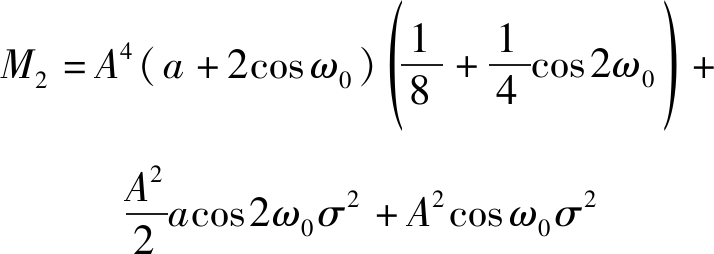
(39)
4 计算验证
为了验证式(9)和式(20)所提频率估计方法之间的差异和有效性,在MatLab R2018环境下,给出不同信号参数下的频率估计结果。令A=1,ω=0.1π,θ在区间(0, 2π)上服从均匀分布,λ=0.9999,频率初值a(0)=0,信噪比SNR=5 dB和20 dB,独立运行50次,则式(9)、式(20)和文献[9]、[10]和[12](参数设置ρ=0.95,μ=10-4)所提的频率估计结果如图1所示。由图1可知,当信噪比较高时,式(9)、式(20)和文献[9]、[10]和[12]所提方法都可以较准确的给出频率估计结果,但式(20)方法的收敛性能最佳;当信噪比较低时,则只有式(20)和文献[9]、[10]可以给出较满意的频率估计结果,而式(9)和文献[12]所给频率估计结果都已经偏离了频率真值。
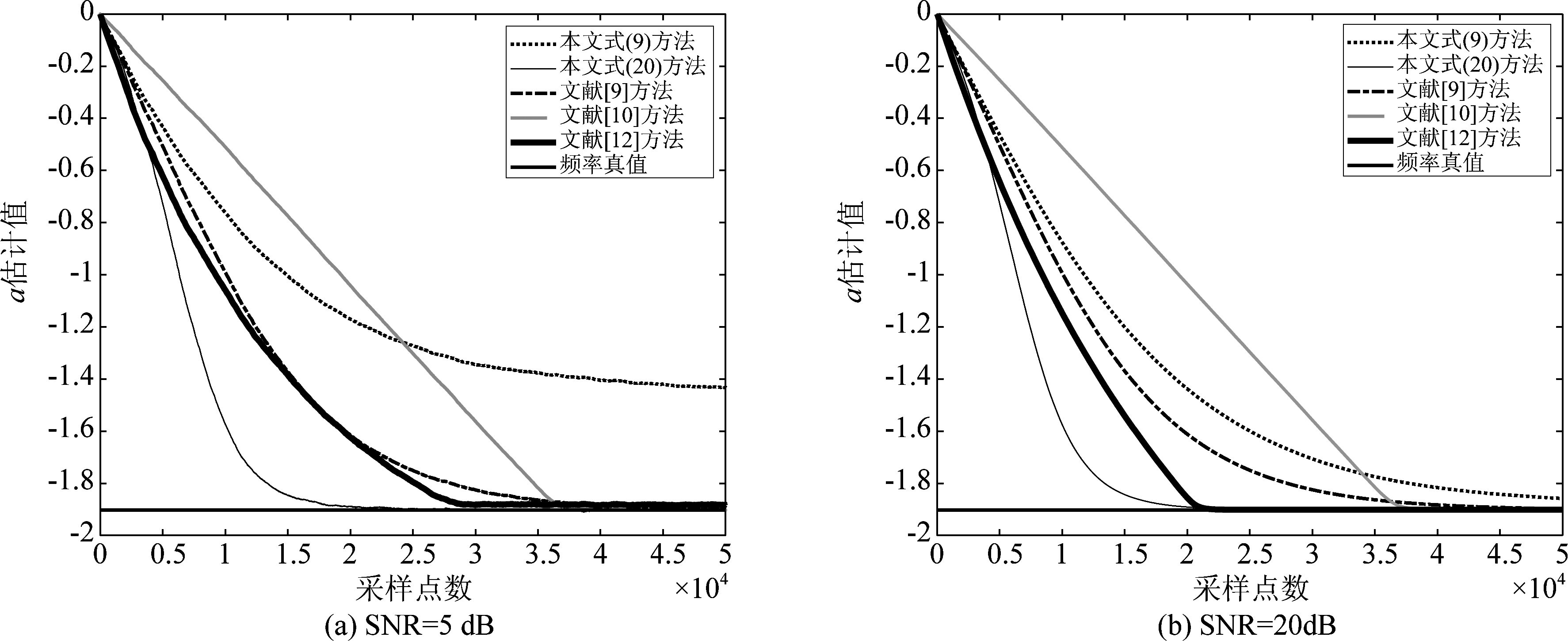
图1 A=1,ω=0.1π,θ∈(0, 2π),λ=0.9999,ρ=0.95,μ=10-4,a(0)=0,SNR分别为5 dB和20 dB时,独立运行50次,不同方法的频率估计结果
Fig.1 A=1, ω=0.1π, θ∈(0, 2π), λ=0.9999, ρ=0.95, μ=10-4, a(0)=0, SNR is 5 dB or 20 dB,frequency estimation results by different methods, 50 runs
为进一步分析式(9)和式(20)方法在ω∈(0, π)范围内的频率估计性能,其频率估计期望与均方差如图2所示。其中A=1,θ∈(0, 2π),λ=0.9999,a(0)=0,SNR=5 dB,独立运行50次。由图2可知,在整个频率范围内,式(20)比式(9)的频率估计精度要高,特别是在频谱的两端,即ω→0或ω→π时,此时式(20)的频率估计精度要优于式(9)的频率估计精度,但式(20)的方差要略大于式(9)的方差,这是式(20)的不足之处,有待深入研究加以改善。值得注意的是,当ω处于频率的中段,即ω在0.5π附近时,此时式(9)和式(20)频率估计精度相当。
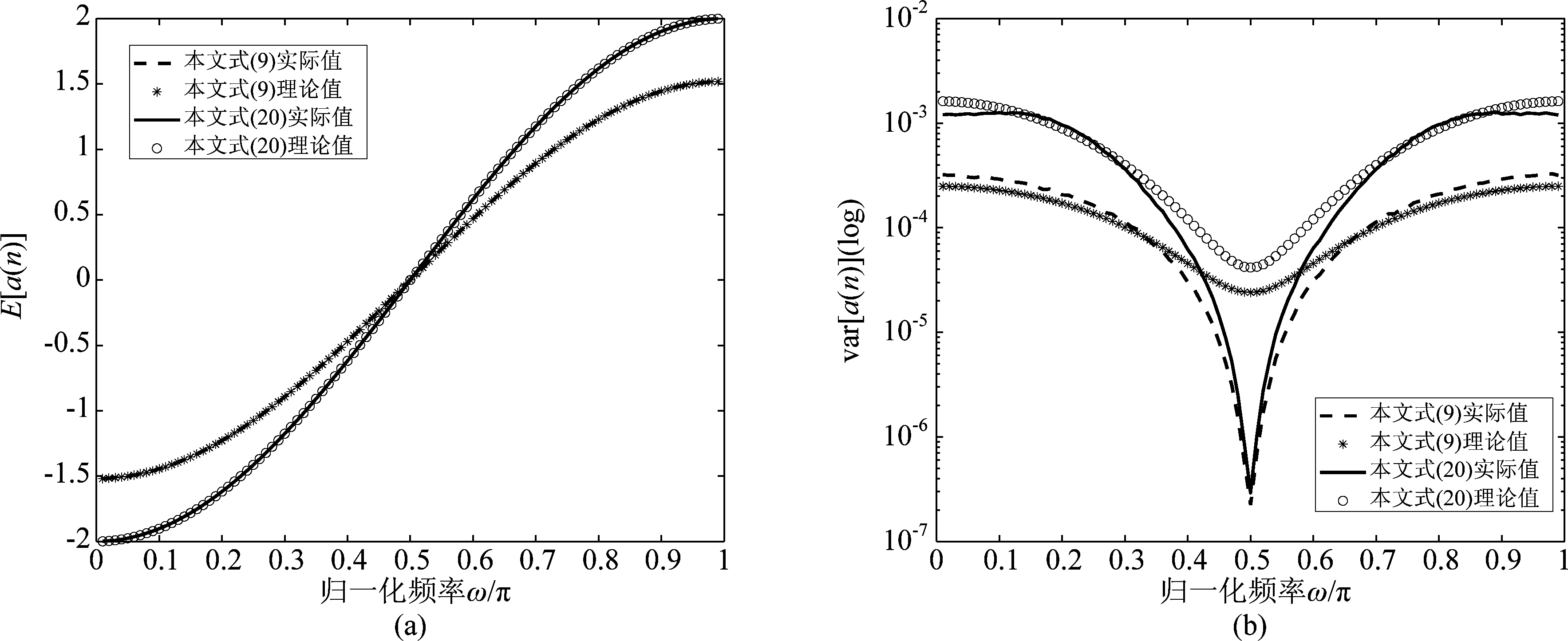
图2 A=1,θ∈(0, 2π),λ=0.9999,a(0)=0,SNR=5 dB,ω在(0, π)的范围内时,独立运行50次的频率估计结果
Fig.2 A=1, θ∈(0, 2π), λ=0.9999, a(0)=0, SNR=5 dB,ω in (0, π), frequency estimation results, 50 runs
为进一步分析式(9)和式(20)方法在λ∈[0.96, 1)范围内的频率估计性能,其频率估计期望与均方差如图3所示。其中A=1,ω=0.1π,θ∈(0, 2π),a(0)=0,SNR=5 dB,独立运行50次。由图3可知,式(9)对λ值的选取不敏感,受λ值的影响较小;但式(20)则对λ值的选取非常敏感,存在不稳定的现象,其选择的区间相对较小,且越接近于1时其频率估计精度越高,但过于接近1会导致收敛速度变慢,在实际应用中需综合考虑。
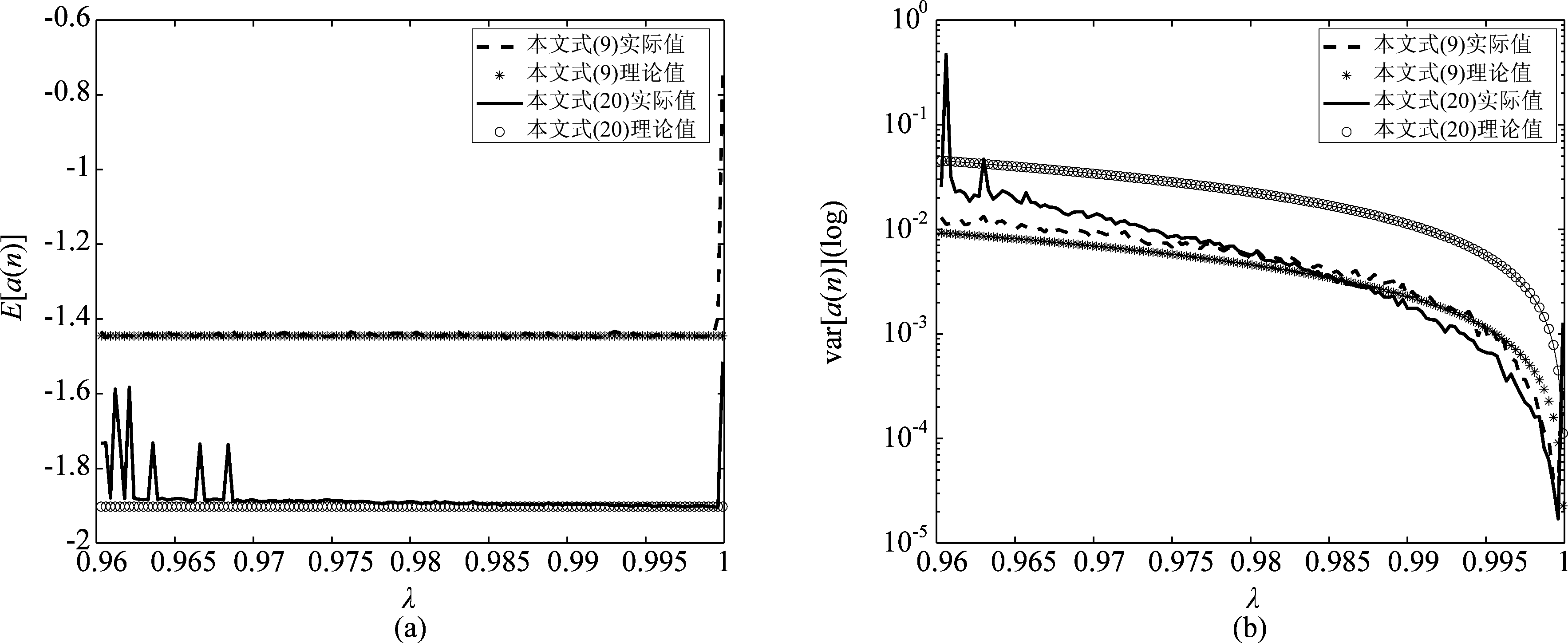
图3 A=1,ω=0.1π,θ∈(0, 2π),a(0)=0,SNR=5 dB,λ在[0.96, 1)的范围内时,独立运行50次的频率估计结果
Fig.3 A=1, ω=0.1π, θ∈(0, 2π), a(0)=0, SNR=5 dB,λ in [0.96, 1), frequency estimation results, 50 runs
为进一步分析式(9)和式(20)方法在信噪比SNR∈[-10, 20]时的频率估计性能,其频率估计期望与均方差如图4所示。其中A=1,ω=0.1π,θ∈(0, 2π),λ=0.9999,a(0)=0,独立运行50次。由图4可知,式(20)和式(9)的期望与实际计算值吻合较好,但方差的分析实际值与理论值有一定的差距,需下一步深入研究。式(20)相比式(9)方差要大,这与前面的分析基本一致,但式(20)的频率估计方法的估计准确度较好,具有无偏的特性。综上所述,本文所提的FIR-ANF频率估计方法具有收敛速度快、抗噪性能好的特点,且其频率估计结果无偏。
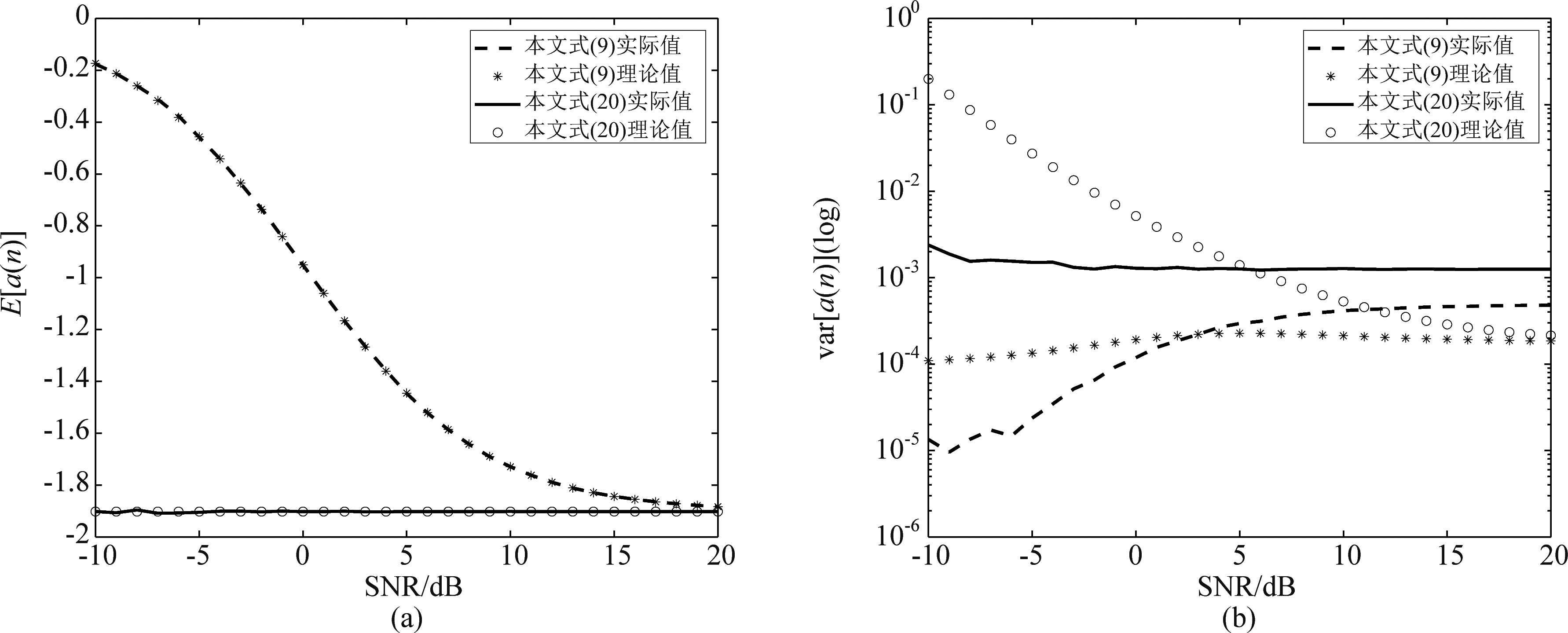
图4 A=1,ω=0.1π,θ∈(0, 2π),λ=0.9999,a(0)=0,SNR在[-10, 20]dB的范围内时,独立运行50次的频率估计结果
Fig.4 A=1, ω=0.1π, θ∈(0, 2π), λ=0.9999, a(0)=0, SNR in [-10, 20], frequency estimation results, 50 runs
5 结论
论文针对现有自适应陷波器频率估计方法存在结构复杂、收敛速度慢、抗噪性弱和频率估计结果有偏的问题,以结构较为简单的FIR自适应陷波器为基础,在分析其误差函数性能的基础上,提出了一种频率无偏估计的FIR-ANF频率估计方法。研究表明有如下结论:
(1)收敛性能好。在保证频率估计精度前提下,所提方法的收敛速度较快,具备较好的实时性。
(2)抗噪性能好。在不同信噪比条件下,都可以取得满意的频率估计结果,对噪声不敏感。
(3)频率估计结果无偏。所提方法可以给出无偏的频率估计结果,且结构简单,具备较为广泛的应用前景。下一步将针对调制后的正弦信号频率估计开展研究,进一步提升所提频率估计方法的应用范围。
[1] LV Q, QIN Honglei. A novel algorithm for adaptive notch filter to detect and mitigate the CWI for GNSS receivers[C]∥2018 IEEE 3rd International Conference on Signal and Image Processing (ICSIP). Shenzhen, China. IEEE, 2018: 444- 451.
[2] GAMBA M T, FALLETTI E. Performance comparison of FLL adaptive notch filters to counter GNSS jamming[C]∥2019 International Conference on Localization and GNSS (ICL-GNSS). Nuremberg, Germany. IEEE, 2019: 1- 6.
[3] WANG Han, SUN Hongling, SUN Yunping, et al. A narrowband active noise control system with a frequency estimation algorithm based on parallel adaptive notch filter[J]. Signal Processing, 2019, 154: 108-119.
[4] BAHN W, KIM T I, LEE S H, et al. Resonant frequency estimation for adaptive notch filters in industrial servo systems[J]. Mechatronics, 2017, 41: 45-57.
[5] RANA K P S, KUMAR V, GUPTA A. A pole-radius-varying IIR notch filter with enhanced post-transient performance[J]. Biomedical Signal Processing and Control, 2017, 33: 379-391.
[6] 丁康, 谢明, 杨志坚. 离散频谱分析校正理论与技术[M]. 北京: 科学出版社, 2008: 58- 65.
DING Kang, XIE Ming, YANG Zhijian. The theory and technology of discrete spectrum correction Theory and technology of discrete spectrum correction[M]. Beijing: Science Press, 2008: 58- 65.(in Chinese)
[7] 毛育文, 涂亚庆, 张海涛, 等. 计及负频率的极高频信号离散频谱校正新方法[J]. 振动、测试与诊断, 2012, 32(3): 477- 482,519.
MAO Yuwen, TU Yaqing, ZHANG Haitao, et al. New discrete spectrum correction method with negative frequency contribution for ultra high frequency signals[J]. Journal of Vibration, Measurement & Diagnosis, 2012, 32(3): 477- 482,519.(in Chinese)
[8] 李明, 涂亚庆, 沈廷鳌, 等. 二阶自适应陷波器频率估计方法统计性能分析[J]. 信号处理, 2013, 29(6): 734-742.
LI Ming, TU Yaqing, SHEN Tingao, et al. Statistical performance analysis of frequency estimation method with second order adaptive notch filter[J]. Journal of Signal Processing, 2013, 29(6): 734-742.(in Chinese)
[9] PUNCHALARD R, LORSAWATSIRI A, LOETWASSANA W, et al. Direct frequency estimation based adaptive algorithm for a second-order adaptive FIR notch filter[J]. Signal Processing, 2008, 88(2): 315-325.
[10] PUNCHALARD R. Mean square error analysis of unbiased modified plain gradient algorithm for second-order adaptive IIR notch filter[J]. Signal Processing, 2012, 92(11): 2815-2820.
[11] KANG C H, KIM S Y, PARK C G. A GNSS interference identification using an adaptive cascading IIR notch filter[J]. GPS Solutions, 2014, 18(4): 605- 613.
[12] 李明, 涂亚庆, 沈艳林, 等. 自适应陷波器噪声统计性能与相关性分析[J]. 电子学报, 2018, 46(9): 2108-2114.
LI Ming, TU Yaqing, SHEN Yanlin, et al. Noise analysis of statistical performance and correlation for adaptive notch filter[J]. Acta Electronica Sinica, 2018, 46(9): 2108-2114.(in Chinese)
[13] 涂亚庆, 李明, 沈廷鳌, 等. 计及负频率的DFT与DTFT相位差测量误差分析[J]. 振动与冲击, 2015, 34(20): 85-91.
TU Yaqing, LI Ming, SHEN Tingao, et al. Error analysis of DFT or DTFT based phase difference measurement considering the negative frequency contribution[J]. Journal of Vibration and Shock, 2015, 34(20): 85-91.(in Chinese)




