1 引言
目标检测目前已广泛应用于民用和国防安全领域,受复杂杂波背景和复杂运动的影响,目标回波往往表现出较低的可观测特性,增加了雷达探测的难度[1-2]。因此,杂波背景下运动目标的快速可靠检测一直是雷达信号处理中的一个热点和难点。随着相控阵雷达、MIMO雷达等新型雷达系统的出现,通过延长了目标的观测时间,有利于提高杂波背景下的积累增益,提高弱目标的检测性能。MIMO雷达在目标定位、跟踪与检测等诸多方面展现出了优异的性能,是当今雷达领域的前沿研究热点[3-5]。
MIMO雷达在目标检测中已有不少研究[6- 8],但在目前研究的模型中,考虑多径的情况还较少,城市环境或低角度的目标检测中存在的大量多径[9-10],多径效应的存在会影响接收信号的信噪比,降低检测概率。为了解决检测中的多径问题,文献[11]研究了一种基于熵理论的多路径环境下MIMO雷达检测模型,该模型定义了多径距离差的概念,通过多径回波功率来提高检测性能;文献[12]提出了一种基于估计信噪比的新型加权MIMO检测器,克服低空环境下的负面多径效应。然而,上述文献对于复杂的传播环境时,建立精确的多径信道模型是困难的,并且当环境存在大量多径时,无法有效减少多径效应带来的影响。因此,除了考虑减少多径对检测性能的不利影响外,找到一种利用多径本身特性的方法来提高检测性能是有研究意义的。
近年研究发现,物理学领域的时间反演(Time reversal, TR)[13]理论,同样适用于无线电磁波领域[14]。在时域上对信号进行逆序操作,等同于在频域上的共轭运算,可以对散落在多径上的能量信号实现在特定的空间能量聚焦,表现出空时聚焦特性[15]。文献[16]中时间反演技术将接收到的信号功率集中在时域和空间域上,以提高信噪声比和多径信道的能量效率。文献[17]已将时间反演运用到水下声源的检测中,实验证明时间反演在不仅可以减少多径效应带来的影响,同时聚焦多径信号携带的能量。
基于以上学者的研究,时间反演在对抗多径上有着十分优越的表现,因此,针对由于存在多径效应和复杂杂波背景等导致目标检测性能下降的问题,本文提出一种基于时间反演优化的运动目标检测方案,利用时间反演的空时聚焦性,将散落在多径中的目标运动信号能量聚焦,同时减少了多径对目标检测带来的影响。仿真结果表明:在杂波环境具有相同信噪比情况下,所提方案比传统MIMO的检测方法有较好的性能提升。
2 系统模型
2.1 多径环境
假设存在一个静止的环境,且目标无法主动发出信号,用探测信号记录整个环境的信道状态信息。在目标出现运动后环境产生变化,接收天线分别记录两个状态下的信道状态信息,再将两种背景环境相减,可得到目标运动所产生的信号[18]。发送天线发出探测信号进入到环境中。如图1所示,信号经过建筑物或其他物体产生的反射、折射等,会以不同的角度到达接收天线。
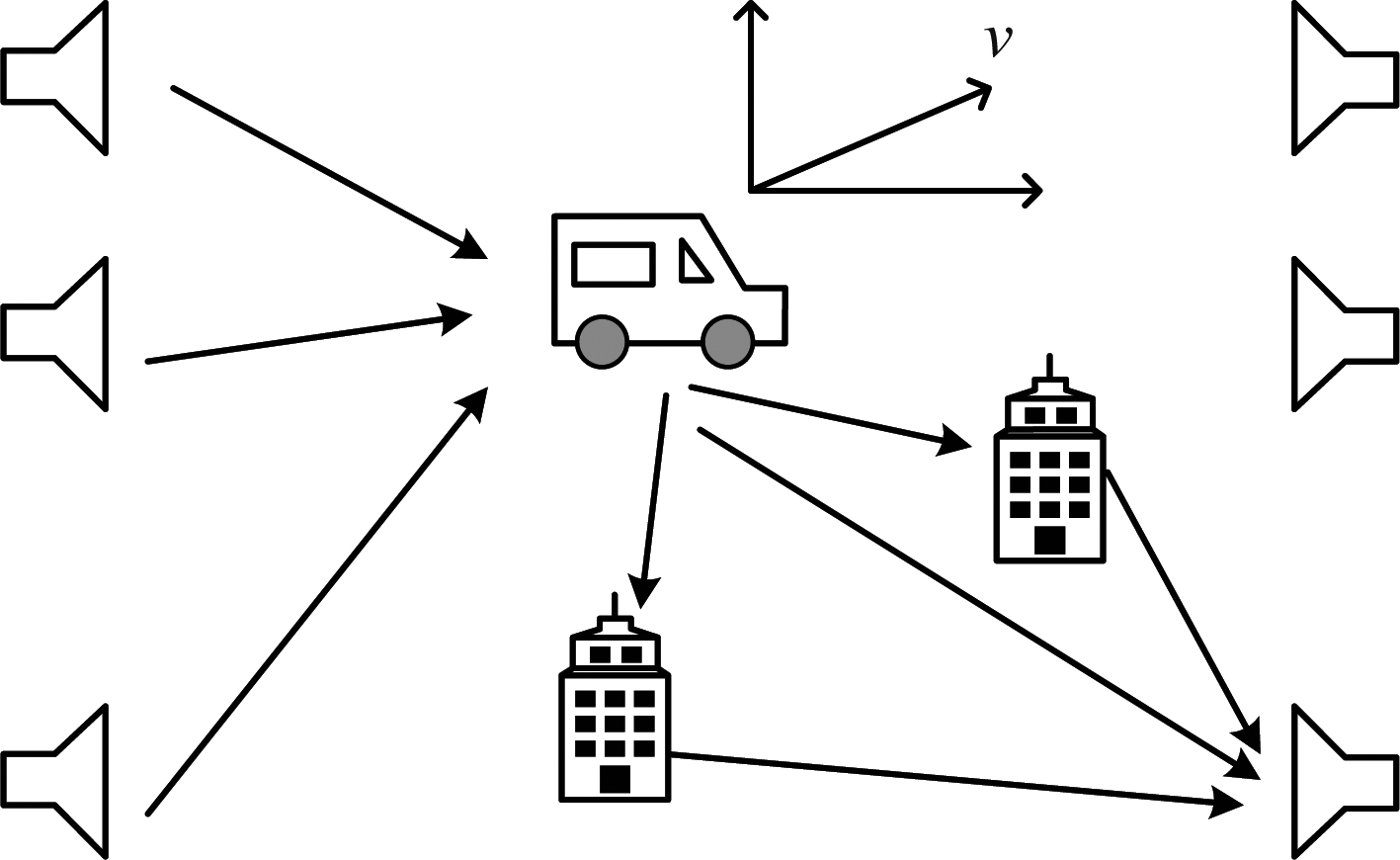
图1 系统模型
Fig.1 System model
2.2 信号模型
在本系统中,所发送的探测信号为宽带正交波形,探测信号用sm表示,代表第m个发送天线所发出的信号,这里发送信号使用相互正交波形[19],即不同发送天线发送的信号是相互正交的,表示为:
(1)
假设目标出现相对于收发天线以恒定的速度运动,v=(|v|cos θ,|v|sin θ)。每条路径产生不同的多普勒因子,且每条路径以不同的角度到达天线,用ul=(cos φl,sin φl)表示到达角,且φl∈[0,2π],l=0,…,L-1。
由此可以推出多普勒因子为βl,且
(2)
上式,c为电磁波传播速度,〈·,·〉表示向量空间的内积运算。
3 探测过程
探测过程系统流程图2如下所示,分为向前传输过程和接收端时间反演后重传过程,下文分别分析两个过程的具体推导。
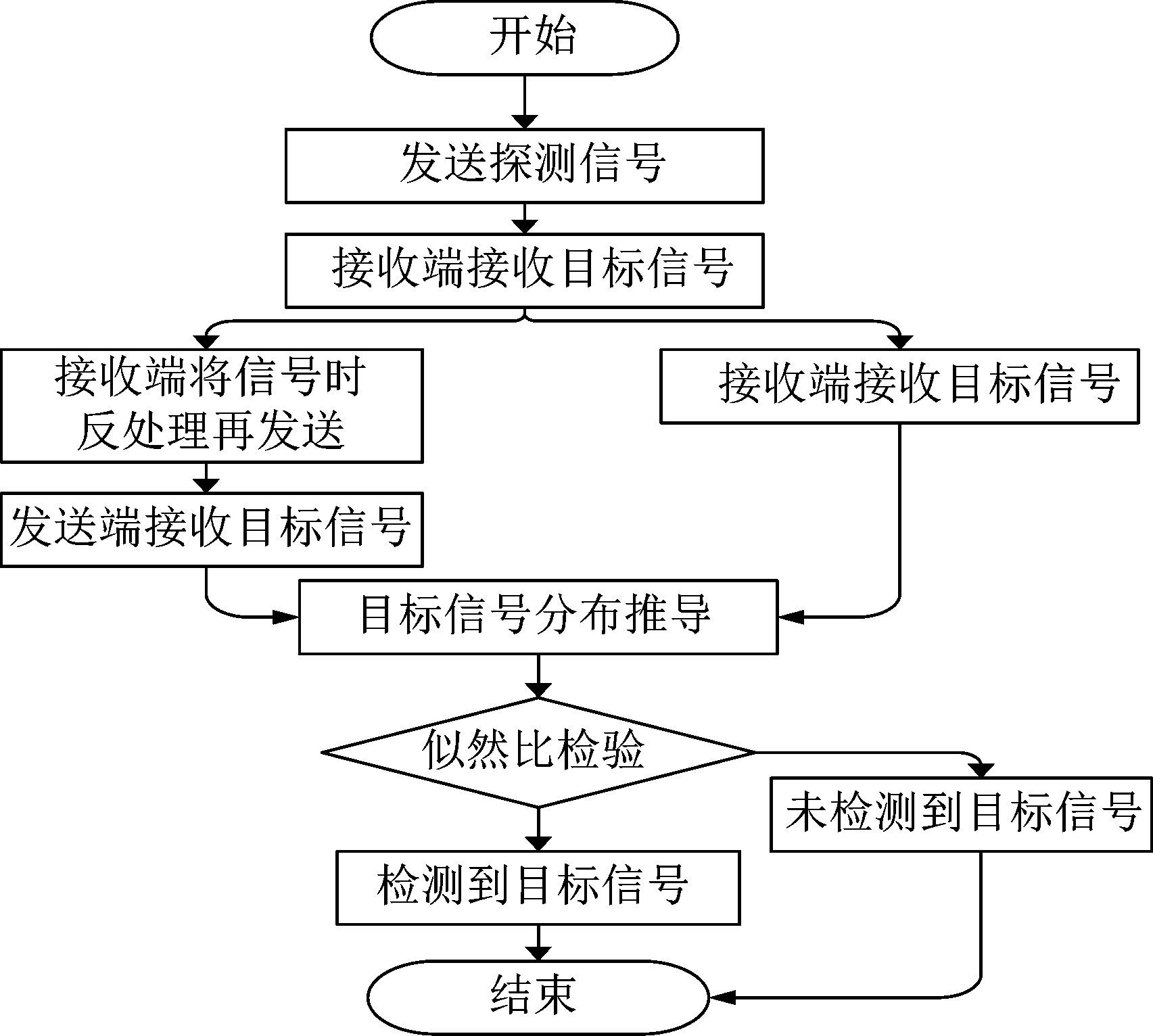
图2 系统流程图
Fig.2 System flow chart
3.1 传统探测
首先表示出MIMO雷达发送端与接收端的信道冲击响应,在发送端发射天线m∈(1,M)与合法接收端接收天线n∈(1,N)之间的信道冲击响应(channel impulse response, CIR)可记为:
(3)
其中L表示可识别多径条数,
分别表示发送天线m到合法接收端接收天线n的第l条路径的幅度与时延。
发送天线发送探测信号sm,在第n个接收天线端接收到的信号rn可以表示为:
(4)
式中,v(t)表示白噪声,且
为目标运动对接收信号产生的相位变化。具体写出上式:
(5)
为了直观了解整个过程,写成如下矩阵形式:
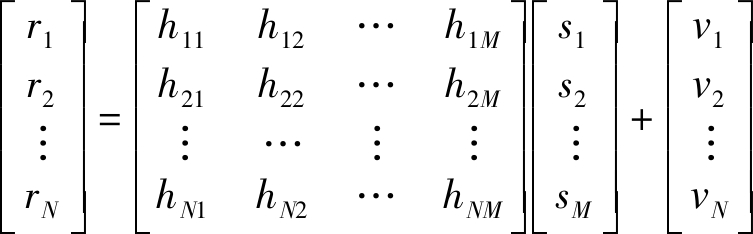
(6)
3.2 时间反演-重传过程
在接收端将接收信号进行时间反演处理,即进行时间取反,能量归一化。得到的信号表示为
为能量归一化因子,再将信号回传到发送端,假设当目标运动缓慢时,往返信道具有互易性,所以发送端接收到的信号可以表示为:
(7)
进一步如下运算得:
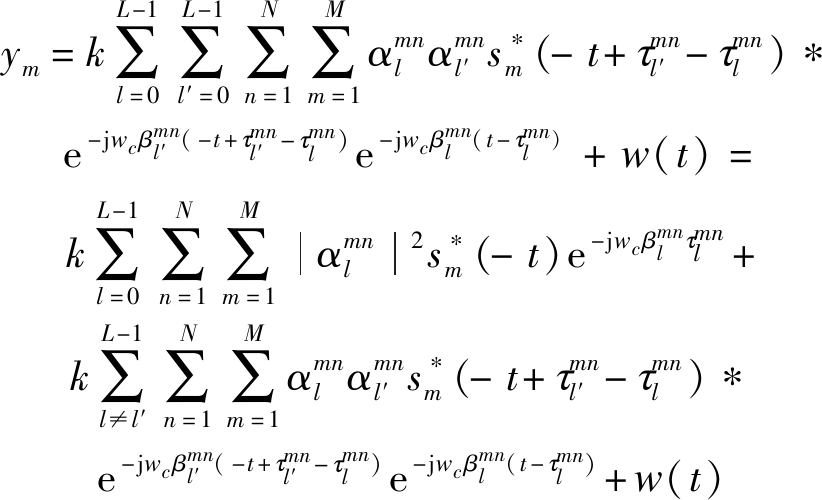
(8)
公式(8)中,等号右边的第一项为各个路径的自相关函数之和,第二项为往返不同路径的互相关函数之和,非相干多径卷积会相互抵消使得第二部分值会很小,第三项为高斯白噪声。为了便于分析,取第一项用作主要的到达信号,上式可以写为:
(9)
为了方便表达,将Gl令为:
(10)
4 检测分析
在分析信号的检测概率之前。为了方便数学分析,做出如下假设:1.假设环境中有丰富的多径数L;2.到达角0≤φ≤2π是均匀分布的;3.路径增益因子αl是服从均值为0,方差为
的复高斯分布;4.在考虑近似问题时,忽略能量归一化因子k带来的影响[18]。
4.1 MIMO检测
在向前传输阶段接收到的信号可以写为:
(11)
令
(12)
此时,假设多径数L足够大,运用中心极限定理,Al可以近似看为一个正态分布。
假设信道
服从循环对称复高斯,所以:
(13)
传输过程接收天线会收到M个发送天线的独立同分布的复高斯信号,所以可以推出:
(14)
(15)
化简得
运用二元假设检验的方法,用H0表示目标没有运动;H1表示目标出现运动;
(16)
下面根据奈曼皮尔逊准则来计算检测概率,列出概率密度函数求取似然比,
(17)
(18)
上式T表示转置运算, IN代表N阶单位矩阵,且
似然比函数为:
(19)
去除无关项得,
(20)
上式化简得:
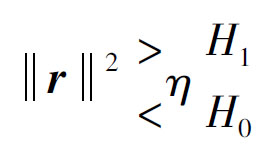
(21)
上述式子表示为,当||r||2大于门限η时,判为目标出现运动;||r||2小于门限η时,判为目标静止。||r||2的分布可以如下表示:
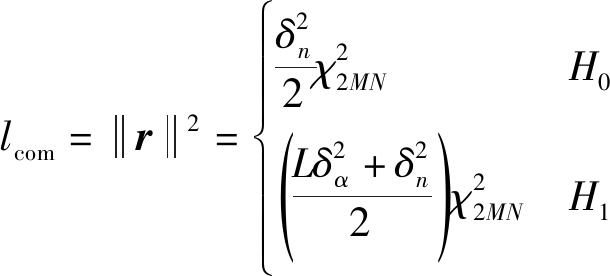
(22)
其中
表示自由度为d的卡方分布。
虚警概率可表示为:
(23)
判决门限η为:
(24)
表示以自由度为2MN的卡方分布随机变量为参数的反累积分布函数。检测概率有如下公式给出:
(25)
4.2 TR+MIMO检测
经过时间反演重传后,接收信号可以写成:
(26)
当多径足够大时,根据中心极限定理,Gl可以近似看作一个正态分布,所以,
(27)
可以得到
(28)
(29)
显然,
是服从
分布,其中
是自由度为2的卡方分布,所以方差可以算出为
所以
令
所以可以推出,
(30)
同样运用二元假设法可以表示为:
(31)
H0表示目标未出现运动;H1表示目标出现了运动。
下面依然运用奈曼皮尔逊检测准则,可以推出似然比ltr,即:
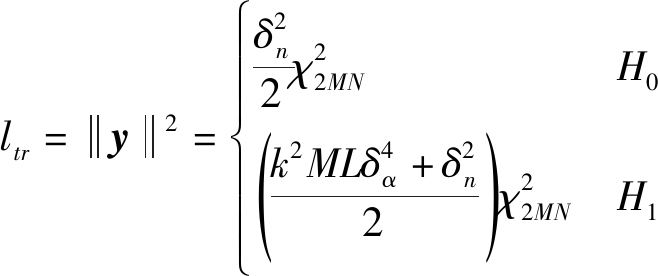
(32)
虚警概率可以推出为:
(33)
因此判决门限推出为:
(34)
最后的检测概率就可以表示为:
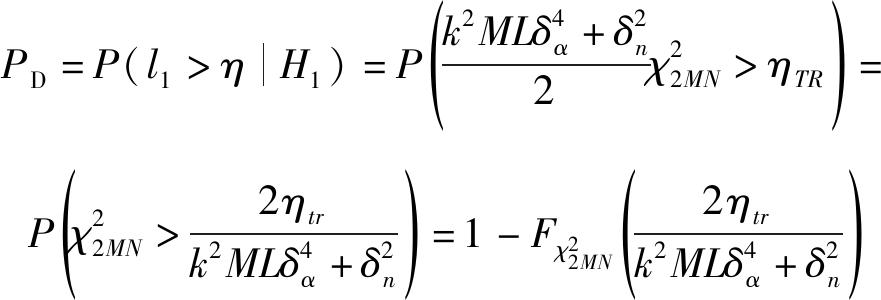
(35)
5 仿真与分析
本节采用MATLAB工具对本文提出的方法进行仿真验证。
为了直观表示杂波环境和噪声对目标信号所产生的影响和TR技术对目标信号的聚焦特性,此部分仿真对接收到的杂波、噪声和目标信号进行了模拟。
如图3所示,仿真部分的杂波是随机产生,并且服从方差为1的瑞利分布,探测信号采用高斯双脉冲信号。
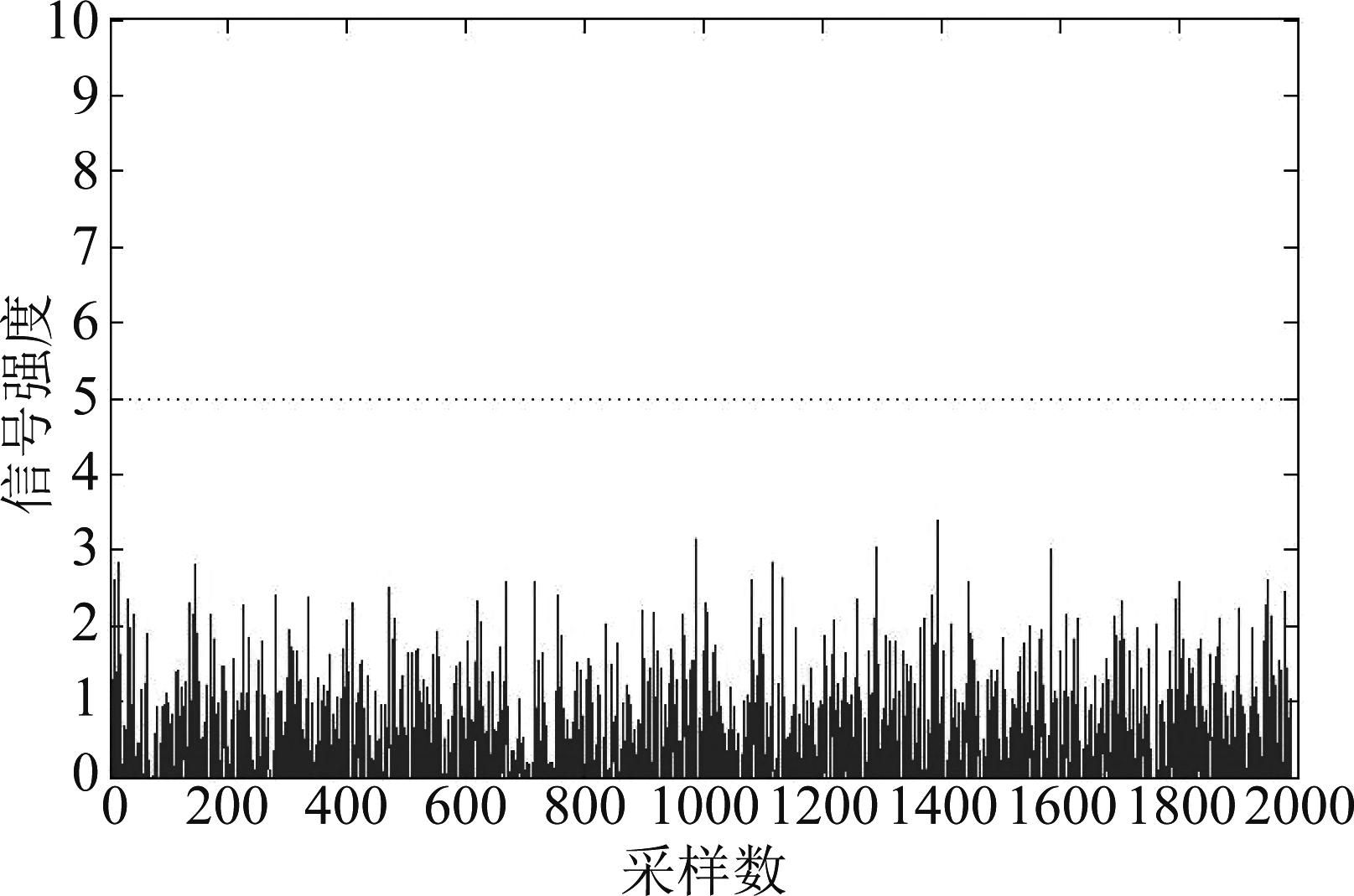
图3 杂波环境
Fig.3 Clutter environment
如图4,探测信号经过目标后在接收端得到目标信号,在图4中已用红色圆圈画出。在随机杂波中,目标信号可能会淹没在杂波环境中,影响检测性能。
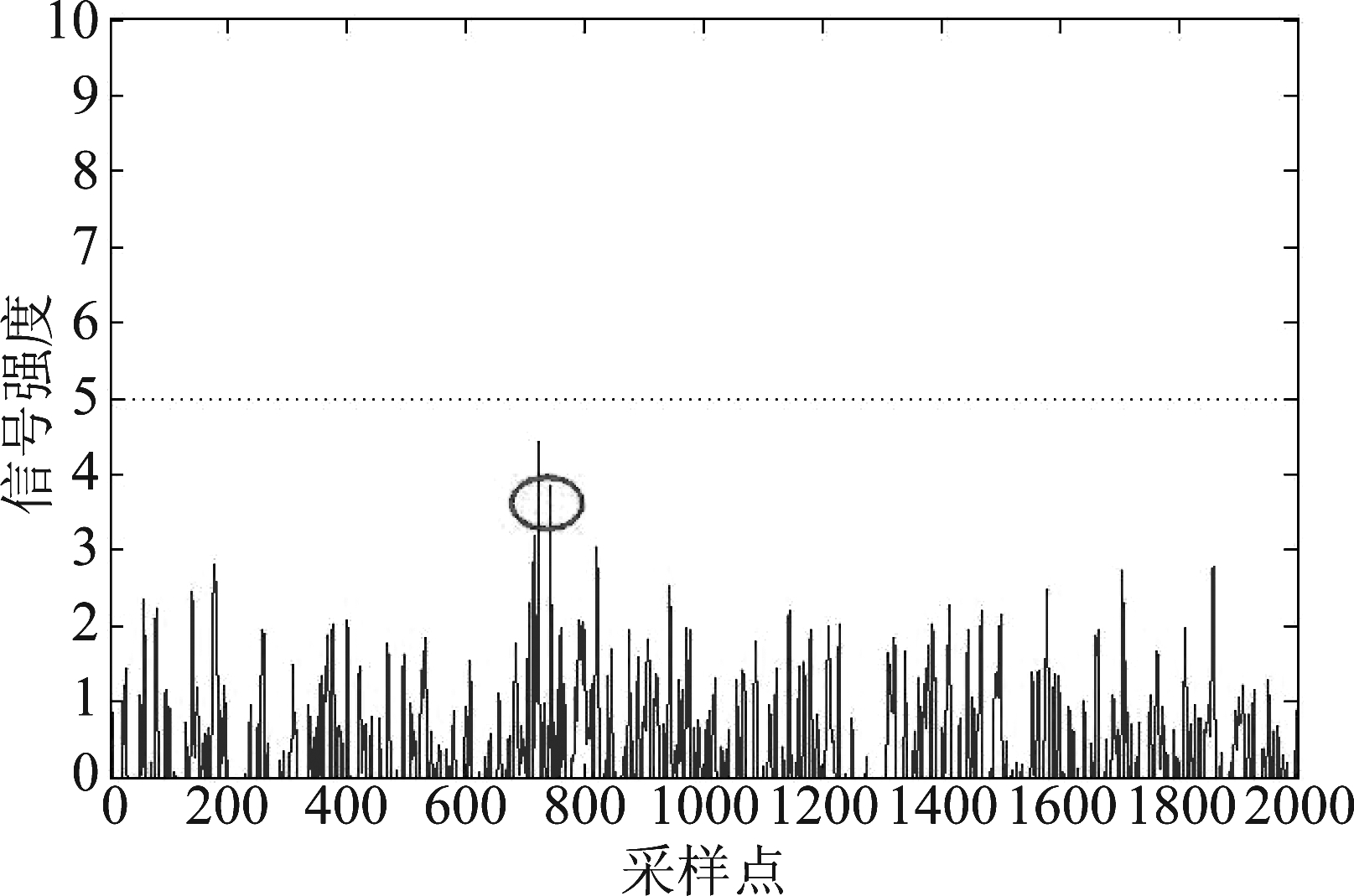
图4 传统MIMO系统
Fig.4 Traditional MIMO system
如图5所示,利用时间反演的空时聚焦特性,将散落在多径的目标信号的能量聚焦,能够减少杂波环境对目标信号检测带来的干扰,由图5可以看出,目标信号强度明显优于传统MIMO系统,且在时间反演处理后,目标信号在对抗杂波干扰的能力增强。
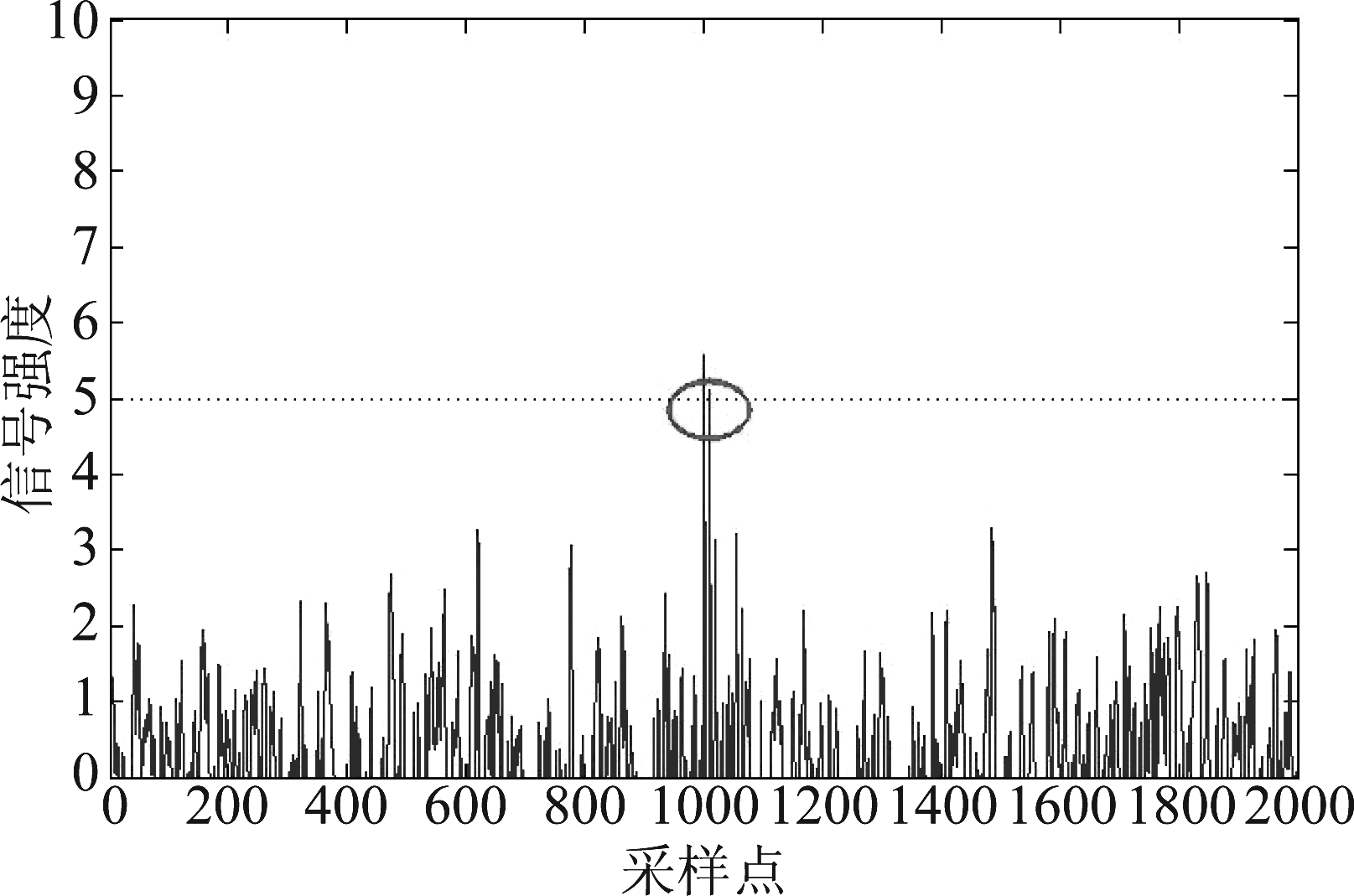
图5 TR+MIMO系统
Fig.5 TR+MIMO system
接下来的部分仿真针对MIMO和TR+MIMO两种雷达系统的检测概率进行仿真。采用检测概率随信噪比的变化来描述检测性能,信噪比定义为
单位为dB。系统无线传输信道的设置为均值E=0,方差δa=2。能量归一化因子设置为k=1,即忽略能量归一化因子的影响。采用了恒虚警概率的方法,即虚警概率PFA取为定值,求出判决门限η,根据判决门限求出检测概率PD。仿真部分分别进行了在不同的多径数、不同的虚警概率和不同天线数量组合的系统中,时间反演对系统检测性能的影响,最后还计算了MIMO和TR+MIMO两个系统的时间复杂度,并对复杂度进行了分析。
图6为虚警概率PFA=10-5下,不同多径数L=[4,8,12]的性能仿真图,可以看出MIMO和TR+MIMO两种系统的检测概率都随着信噪比的增大而提高。在相同的路径数和信噪比SNR时,TR+MIMO系统检测性能优于文献[19]中传统MIMO系统。在L=8,两种系统在检测概率PD同时达到0.5时,信噪比增益约为7.5 dB。
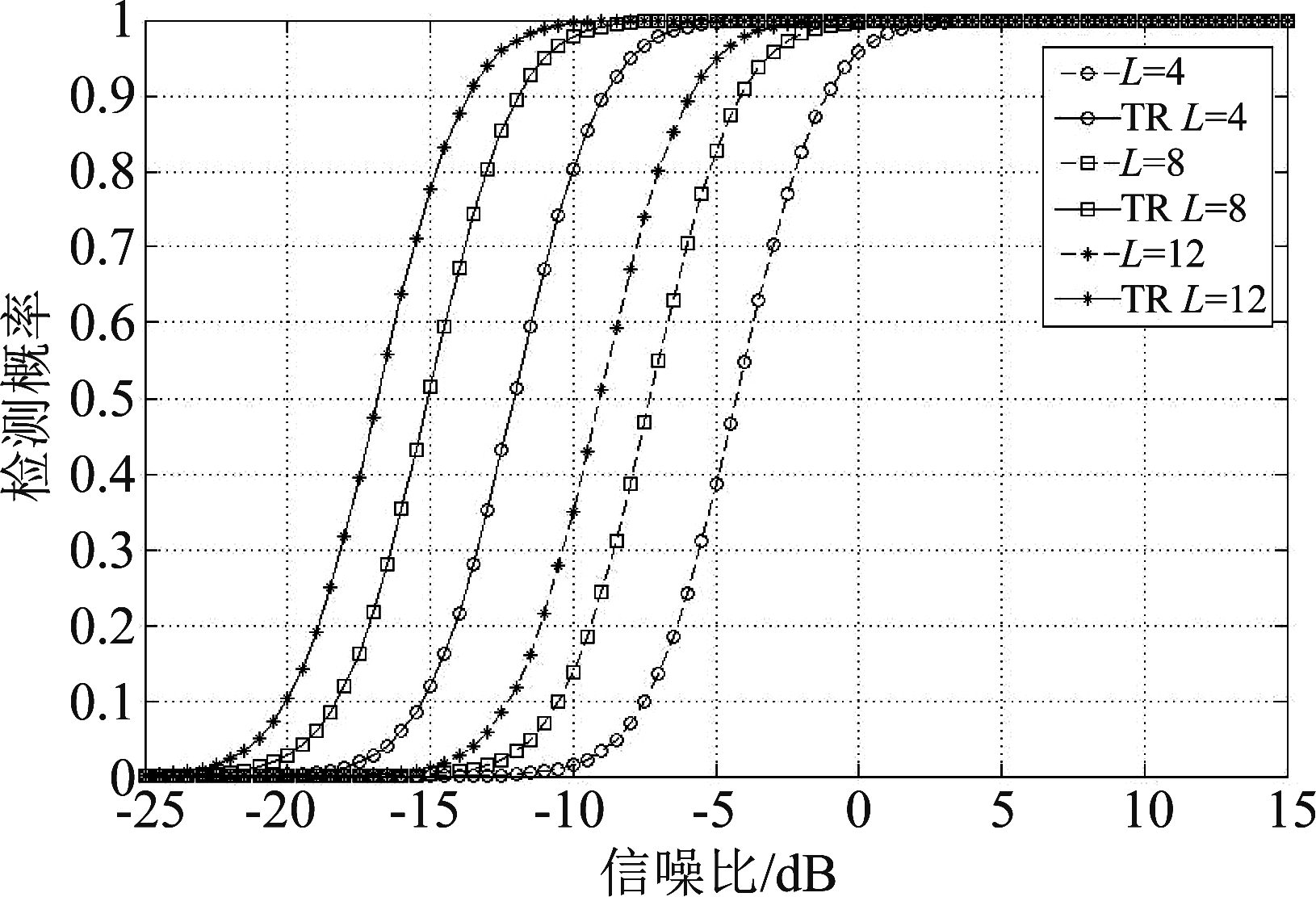
图6 不同多径的对比
Fig.6 Comparison of different multipath
图7为多径数L=8,发送天线M=2,接收天线N=3下,不同虚警PFA=[10-5,10-4,10-3]的性能仿真图。如图7所示,在虚警概率PFA增大时,对比同一信噪比,检测概率PD有所上升。
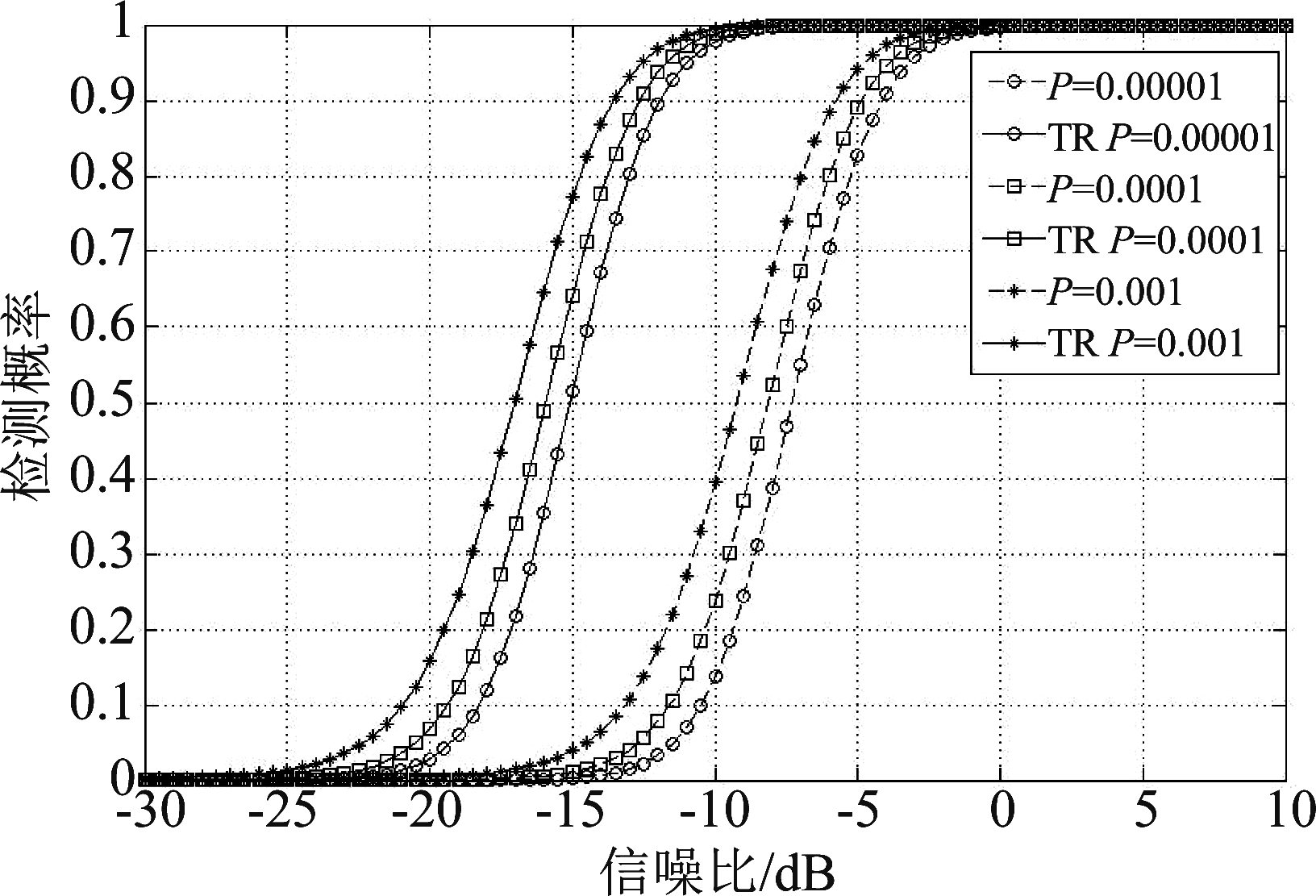
图7 不同判决门限的对比
Fig.7 Comparison of different decision thresholds
由图8对比了不同天线配置下的检测性能时,设置同一虚警概率PFA=10-5和同一路径数L=8。分别仿真了两个系统下不同天线配置的检测性能,和对文献[20]中采用的单天线系统进行了仿真对比。仿真结果显示,MIMO雷达比单天线雷达在检测目标的性能上有较好提升;加入时间反演后,检测性能进一步提高;在同一信噪比情况下,天线数增多,检测性能越好。
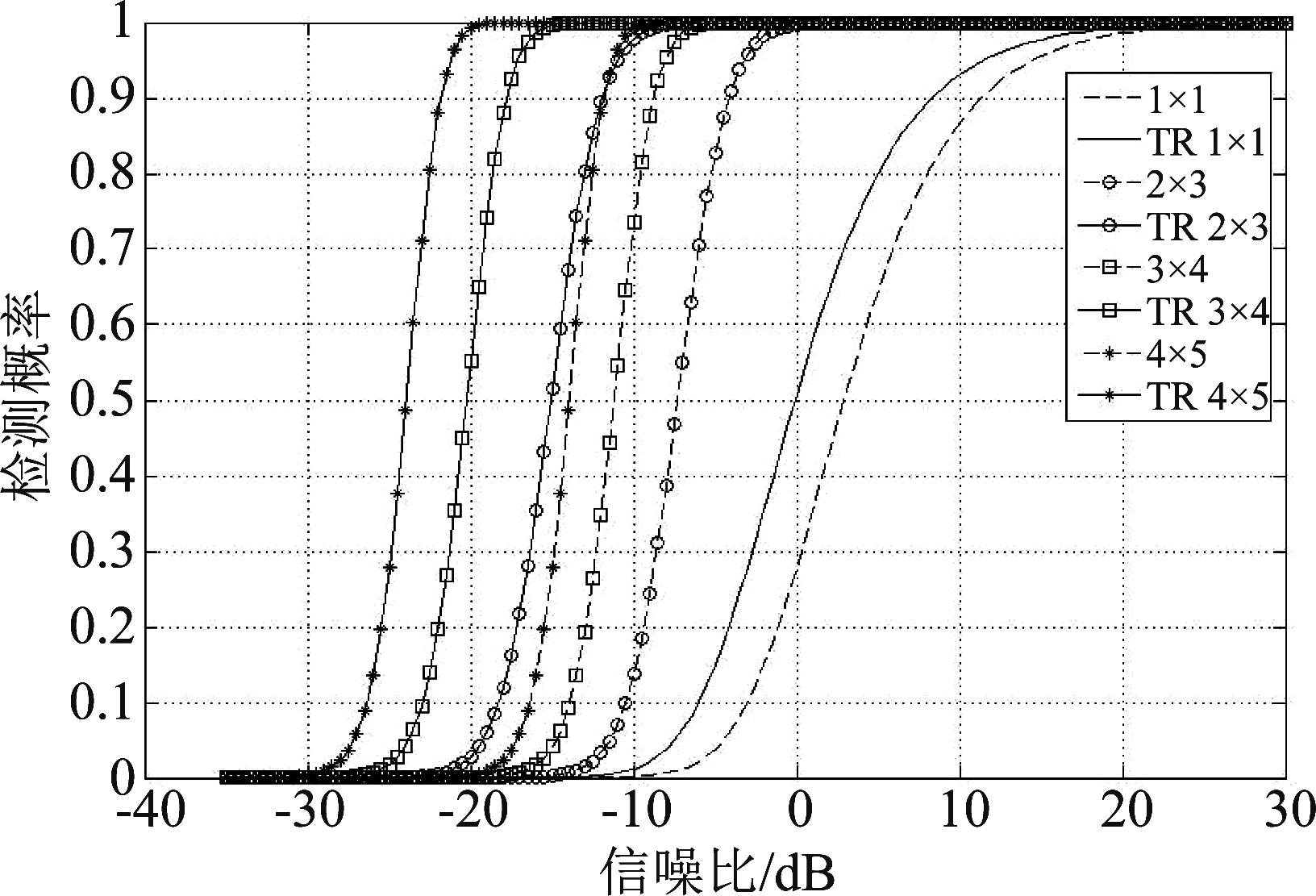
图8 不同天线组合的对比
Fig.8 Comparison of different antenna combinations
图9在同一虚警概率PFA=10-5、同一路径数L=8和同一天线配置下,对比了不同现有方法下的检测性能。由图9可以看出,在同一信噪比下,MIMO雷达的检测性能优于相控阵雷达(Phased array radar, PAR)和MISO(Multiple input single output,MISO)雷达,频率分集阵列(Frequency diverse array, FDA)优于MIMO雷达;在加入TR技术以后,TR-MIMO的性能已有明显提升,虽然TR-MIMO在低信噪比时检测性能逊于FDA,原因是在信噪比较低时,MIMO雷达的多天线特性使其总噪声能量是各个接收天线之和,但随着信噪比的增大,TR技术的聚焦效果更加明显,并且MIMO雷达具有更高的自由度,TR-MIMO的检测性能优于FDA。
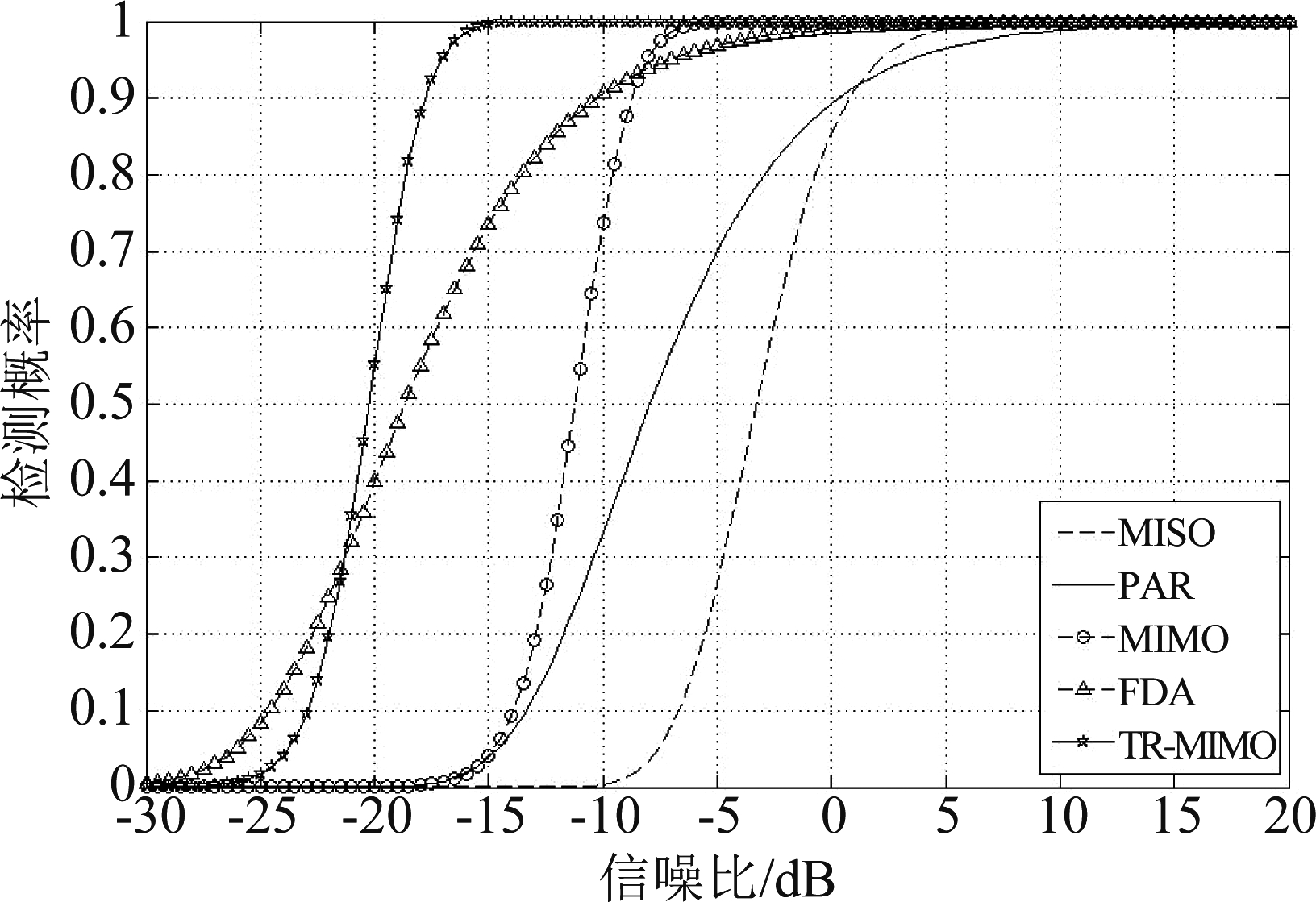
图9 不同现有方法的对比
Fig.9 Comparison of different existing methods
6 复杂度分析
目标检测的复杂度由信号收发处理和检测性能分析两部分组成,检测部分都采用奈曼皮尔逊准则设计的检测算法,因此,两种系统复杂度的对比体现在信号收发处理的复杂度中。在算法复杂度的计算当中,算法复杂度根据复数乘法的次数计算得到,因此本文需要分别分析MIMO与TR+MIMO两种传输系统的复杂度。
传统MIMO系统的矩阵过程可以表示为R=HS,R是一个N×1维的矩阵,H是一个N×M维的矩阵,S是一个M×1维的矩阵,因此在R=HS的运算中需要进行M×N次乘法,因此算法复杂度为M×N。
在TR+MIMO系统中,所用的算法表达式用矩阵可写为Y=HHTRS,在传统MIMO系统上,增加一次矩阵运算,Y是一个M×1的矩阵,S是一个M×1维的矩阵,H是一个M×N维的矩阵,HTR表示为时间反演矩阵,是一个N×M的矩阵,TR+MIMO系统运算了2M×N次乘法。
经过上述的算法复杂度的计算,所提出的运用TR技术方法增加了较少的算法复杂度,但换来了系统对运动目标更好的检测性能。
7 结论
本文针对MIMO系统下对运动目标检测性能下降的问题,提出一种基于时间反演的优化方案,并分别推导了常规的MIMO系统和结合时间反演技术的MIMO系统对运动目标检测的具体过程,求得两个系统的检测概率表达式。通过仿真结果表明,运用时间反演技术的时空聚焦技术,减少了多径效应的干扰,增强了目标信号的能量,使得其目标信号杂波环境中更容易检测,在提高较少系统复杂度的同时,较好的提升系统的检测性能。
[1] YI Wei, ZHOU Tao, AI Yue, et al. Suboptimal low complexity joint multi-target detection and localization for non-coherent MIMO radar with widely separated antennas[J]. IEEE Transactions on Signal Processing, 2020, 68: 901-916.
[2] HASSANIEN A, HIMED B, METCALF J, et al. Moving target detection in spatially heterogeneous clutter using distributed MIMO radar[C]∥2018 International Conference on Radar (RADAR). Brisbane, QLD, Australia. IEEE, 2018: 1- 6.
[3] 徐峰, 薛珺亓, 杨小鹏. 相控阵MIMO雷达抗干扰波束形成算法[J]. 信号处理, 2017, 33(12): 1531-1535.
XU Feng, XUE Junqi, YANG Xiaopeng. Phased-MIMO radar anti-jamming beamforming algorithm[J]. Journal of Signal Processing, 2017, 33(12): 1531-1535.(in Chinese)
[4] 王珍, 何茜. 合作式MIMO雷达通信一体化系统的检测与互信息增益[J]. 信号处理, 2020, 36(10): 1654-1661.
WANG Zhen, HE Qian. Target detection and mutual information improvement for cooperative MIMO radar-communication systems[J]. Journal of Signal Processing, 2020, 36(10): 1654-1661.(in Chinese)
[5] 隋凯凯, 李宏, 李欣欣. 杂波加噪声环境下MIMO雷达检测性能分析[J]. 计算机系统应用, 2013, 22(9): 230-233,101.
SUI Kaikai, LI Hong, LI Xinxin. MIMO radar detection performance analysis in clutter and noisy environments[J]. Computer Systems and Applications, 2013, 22(9): 230-233,101.(in Chinese)
[6] SUN Guohao, ZHANG Wei, TONG Jun, et al. Knowledge-aided target detection for multistatic passive radar[J]. IEEE Access, 2019, 7: 53463-53475.
[7] ZHANG Xin, SW
RD J, LI Hongbin, et al. A sparsity-based passive multistatic detector[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(6): 3658-3666.
[8] YANG Yang, SU Hongtao, HU Qinzhen, et al. Centralized adaptive CFAR detection with registration errors in multistatic radar[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(5): 2370-2382.
[9] CHEN Xiaolong, CHEN Baoxin, XUE Yonghua, et al. Space-range-Doppler focus processing: A novel solution for moving target integration and estimation using FDA-MIMO radar[C]∥2018 International Conference on Radar (RADAR). Brisbane, QLD, Australia. IEEE, 2018: 1- 4.
[10] XIANG Houhong, CHEN Baixiao, YANG Minglei, et al. A novel phase enhancement method for low-angle estimation based on supervised DNN learning[J]. IEEE Access, 2019, 7: 82329- 82336.
[11] SHI Junpeng, HU Guoping, ZHOU Hao, et al. Novel detection model for MIMO radar in multipath environment[C]∥2016 IEEE Chinese Guidance, Navigation and Control Conference (CGNCC). Nanjing, China. IEEE, 2016: 1525-1529.
[12] ZHOU Hao, HU Guoping, SHI Junpeng, et al. Weighted target detector via estimated SNR in a multipath environment[J]. The Journal of Engineering, 2019, 2019(20): 7119-7124.
[13] LEROSEY G, DE ROSNY J, TOURIN A, et al. Focusing beyond the diffraction limit with far-field time reversal[J]. Science, 2007, 315(5815): 1120-1122.
[14] LIAO Peng, HU Binjie, LIN Zhiwu, et al. Effect of signal characteristics on focusing property of time reversal electromagnetic wave[C]∥2019 International Conference on Microwave and Millimeter Wave Technology (ICMMT). Guangzhou, China. IEEE, 2019: 1-3.
[15] 张冉. 时间反演超分辨率聚焦的建模和实现研究[D]. 成都: 电子科技大学, 2017.
ZHANG Ran. Study on modeling and implementation of time reversal super-resolution focusing[D]. Chengdu: University of Electronic Science and Technology of China, 2017. (in Chinese)
[16] AN Hongsun, PARK H. Time reversal scheme using multiple transmit antennas for SWIPT in indoor channel[C]∥2018 IEEE 29th Annual International Symposium on Personal, Indoor and Mobile Radio Communications (PIMRC). Bologna, Italy. IEEE, 2018: 296-300.
[17] LIU Kuanwen. Detection of underwater sound source using time reversal mirror[C]∥2019 IEEE Underwater Technology (UT). Kaohsiung, Taiwan, China. IEEE, 2019: 1-5.
[18] MOURA J M F, JIN Yuanwei. Detection by time reversal: Single antenna[J]. IEEE Transactions on Signal Processing, 2007, 55(1): 187-201.
[19] QIAN Huang. Target detection of MIMO radar[C]∥Proceedings of 2011 Cross Strait Quad-Regional Radio Science and Wireless Technology Conference. Harbin, China. IEEE, 2011: 1082-1084.
[20] ON B, IM S, KARGL S G, et al. Bottoming target detection using time reversal processing[C]∥OCEANS 2017-Anchorage. Anchorage, AK, USA. IEEE, 2017: 1-5.
