1 引言
工业无线传感器网络(Industrial Wireless Sensor Networks,IWSN)的自组织和无线特性给工业生产领域带来了极大的便利性[1-3]。相对于普通消费类WSN将成本作为重要属性而言,工业级WSN一般将安全性和隐私性放在最重要的位置。然而,在IWSN中,无线介质同时开放给合法和非法用户访问,这导致IWSN比传统工业定制的有线传感器网络更容易受到窃听攻击[4- 6]。由于传感器节点有限的计算能力和能量,建立在计算量上的传统密码学上的安全方式,已难以适应对数据汇聚的实时性和低功耗属性要求更为严格的IWSN应用场景[7- 8]。尤其是现在越发复杂的加解密技术将使得硬件性能提升不大的IWSN瘫痪,极大地降低工厂生产的效率。
针对IWSN的安全问题和计算资源有限的矛盾,物理层安全(Physical Layer Security,PLS)技术以窃听信道模型[9]为基础,利用协同干扰技术、中继转发技术、编码技术等提高物理层安全速率[10-13],增强整个通信系统的保密性能[14-15]。
博弈论应用于PLS研究,为节点间的安全协作提供了功率控制框架。文[16]对蜂窝网中的D2D通信进行Stackelberg博弈建模,通过优化D2D链路的功率控制和信道访问,最大程度地提高D2D链路的物理层安全速率。文[17]利用Stackelberg博弈对传感器与控制器之间的兴趣分配关系进行建模,以防御信息物理运输系统中的干扰和窃听攻击。文[18]研究基于联盟博弈的多小区下行链路保密协作算法, 通过设计联盟加入和退出规则,实现下行链路对子载波的高效选择和保密协作联盟的自组织生成。文[19]针对协作中继采用协同压缩感知放大转发技术,研究基于联盟博弈论的最优中继选择联盟形成算法,以提高系统安全速率。文[20]提出基于演化博弈机制的物理层安全协作方法, 通过求解获得使发送端达到协作稳定策略的条件,使网络从不稳定状态向协作稳定状态演化,从而提高系统的安全速率。但对于多跳IWSN大规模传输模型,在有机械障碍,金属摩擦和发动机振动存在的工业环境中,无线衰落急剧波动导致多跳IWSN主干网的物理层安全速率随着传输规模的增大而下降得更为剧烈。上述两跳以内的功率控制博弈模型,因只考虑到一跳或两跳的安全速率,使得功率分配不均衡,出现浪费能量且无法提高甚至可能降低多跳IWSN主干网的安全速率的问题。
本文以提高IWSN簇头节点构成的主干网安全速率和节点能量效率为出发点,同时考虑IWSN中节点的自私性、数据多跳性和节点能耗等因素,研究一种反馈Stackelberg博弈功率控制方案。本文方案基于全双工目的节点的协同干扰方案,在发送节点的效用函数中引入反馈代价函数,以优化每跳中协同干扰功率的分配,并提高IWSN主干网安全速率和降低目的节点发送协同干扰功率的能耗。
2 网络系统模型及其安全速率
2.1 网络系统模型
本文研究从簇头节点到基站一次数据完整传输过程的物理层安全问题。设IWSN采用多跳LEACH-C协议聚簇结构[21],IWSN簇间主干网通信模型如图1所示。
传感器节点在采集到数据后发送给本簇内的簇头节点,簇头节点(Cluster Head Node, CH)负责收集并且传输簇内传感器节点采集的数据。设簇头节点依次沿着主干网节点有序传输数据,直到传输到基站,完成一次完整的数据传输[22-23],从当前簇头节点传输数据到下一簇头节点的过程为一跳通信,如CHi将数据发送给下一个簇头节点CHi+1的过程。
设主干网中簇头节点集合为:
CH={CH1,…,CHi,…,CHn},i=1,2,…,n
(1)
其中,n为簇头节点的数量。
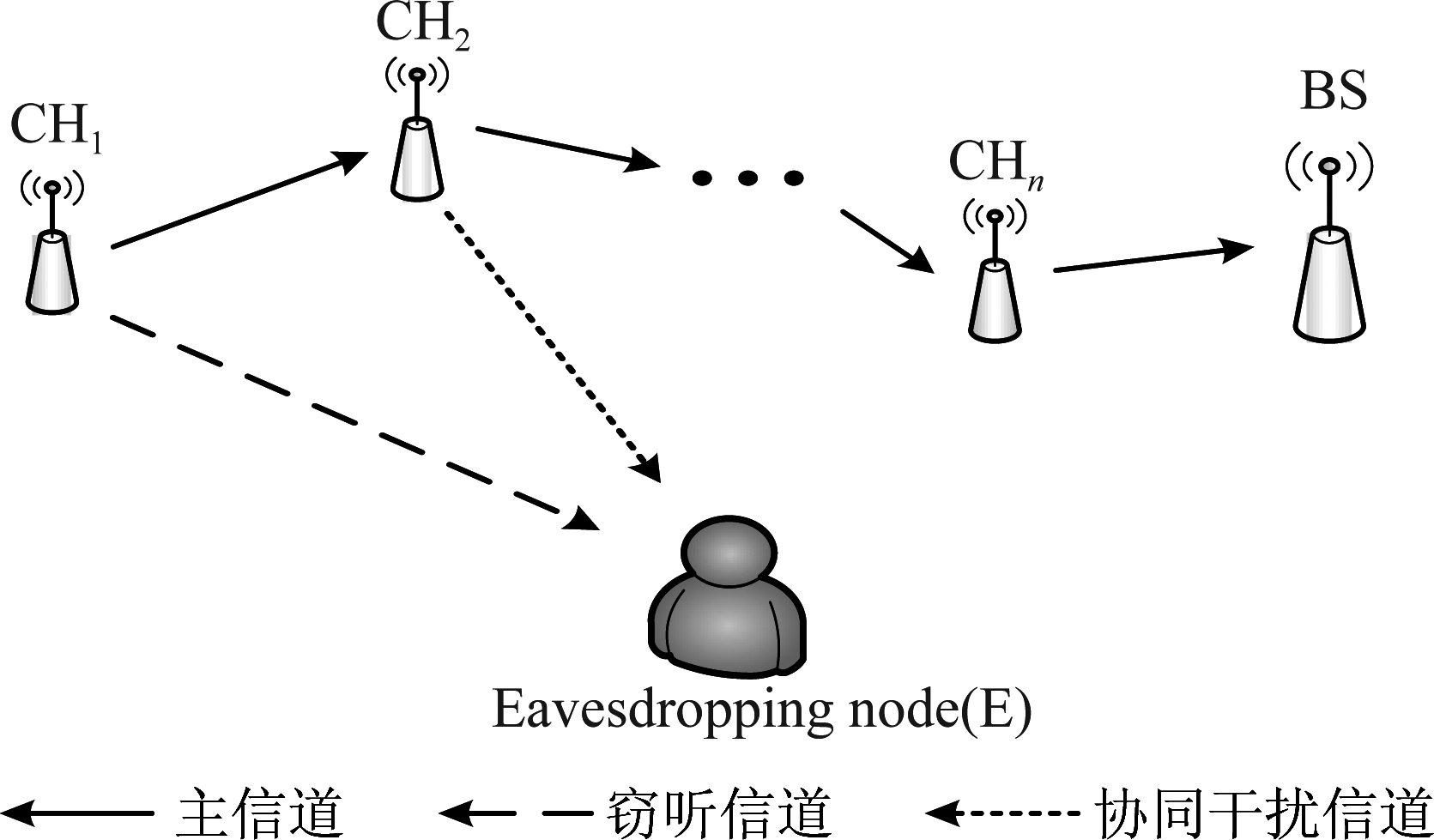
图1 IWSN主干网簇间通信窃听模型
Fig.1 IWSN backbone network intercluster communication
eavesdropping model
假设以下条件成立:(1)簇头节点CHi仅掌握相邻簇头节点的信道状态信息(Channel State Information, CSI),相邻簇头节点之间通过控制信道交换各自的CSI[10-12],且窃听节点掌握所有合法节点的CSI。(2)IWSN中各节点的热噪声均为独立分布且具有相同的方差σ2的加性高斯白噪声。(3)在整个通信中,窃听节点E都处于窃听状态。(4)每个簇头节点有相同增益的发送和接收天线,并以全双工方式工作,且每一跳中发送节点的发射功率相同。
在第i跳通信中,发送节点CHi向目的节点CHi+1发送信号Xi,i+1,全双工目的节点在接收发送节点信号Xi,i+1的同时发送协同干扰信号Xi+1,E对窃听节点E实施干扰。目的节点接收到混合信号后,利用自干扰消除(Self-interference Cancellation,SIC)技术对自身发送的协同干扰信号进行自干扰消除[24-26]。
引入SIC技术后,目的节点和窃听节点接收到的信号分别为Yi+1和YE:
(2)
(3)
其中Pi、Pi+1分别为发送节点CHi的信号发射功率和目的节点CHi+1的协同干扰信号发射功率。Hi,i+1、Hi,E、Hi+1,E分别表示第i跳的发送节点-目的节点、发送节点-窃听节点、目的节点-窃听节点的信道增益,Hi+1,i+1为目的节点的自干扰信道增益。ρ为目的节点的线性自干扰因子,ρ越小对自干扰信号的消除能力越强。N为目的节点和窃听节点端的热噪声,且满足N~CN(0,σ2)。
2.2 安全速率
发送节点与目的节点之间的信道容量与发送节点到窃听节点之间的信道容量,从一定程度上体现了通信的安全性,与信道容量相关的安全速率可用于衡量通信的保密性能。
(1)信道容量
由经典窃听信道模型可得从发送节点到目的节点的主信道容量Ci,i+1为[9]:
(4)
同理可得从发送节点到窃听节点的窃听信道容量Ci,E为:
(5)
由公式(5)可知窃听信道容量Ci,E随着目的节点发送的协同干扰功率Pi+1增大而减小,可通过控制协同干扰功率Pi+1的大小来改变窃听信道容量的大小。
(2)安全速率
安全速率表征网络中合法节点传输信息的能力与非法的窃听节点窃取信息的能力大小关系,也间接地表征发送节点到目的节点的通信保密性能。
定义1 若某跳中主信道容量大于窃听信道容量,则安全速率为两信道容量之差,否则为零[27]。
第i跳的安全速率(Secrecy Rate,SR)SRi可以表示为:
SRi=max{Ci,i+1-Ci,E,0}, i=1,2,…,n
(6)
安全速率值越大,表示发送节点到目的节点的通信保密性就越高。仅当安全速率SRi值大于零即主信道容量大于窃听信道容量时,通信才可能有保密性[9]。
定义2 某跳的历史安全速率(History Secrecy Rate,HSR)为数据在某条主干网中完成从第一跳传输到该跳的前一跳所经过的跳数中安全速率的最小值。
第i跳的历史安全速率HSRi为:
HSR1=SR1
(7)
定义3 某跳的当前安全速率(Current Secrecy Rate,CSR)为数据从第一跳传输到该跳后所经过的全部跳数中安全速率的最小值。
第i跳的当前安全速率为CSRi:
(8)
定义4 主干网安全速率为数据在主干网中完成从第一跳传输到最后一跳后所经过的全部跳数中安全速率的最小值[27]。
主干网安全速率SR为:
(9)
要提高第i跳的安全速率SRi,即保证主信道容量始终大于窃听信道容量,对窃听信道引入具有差异化的协同干扰。由公式(6),在主信道容量不变时,可通过降低窃听信道容量来提高安全速率;而由公式(5),可通过增大目的节点发送的协同干扰功率来降低窃听信道容量。
由定义3和定义4,公式(9)可表示为:
(10)
由公式(10),SR的值取决于整个n跳中当前安全速率的最小值,因此通过提高整个n跳中当前安全速率的最小值可提高主干网安全速率SR。
由定义1~3,CSRi与SRi及HSRi之间存在关联:
CSRi=min{HSRi,SRi}
(11)
从保证安全通信和降低能耗的角度,分析公式(11):
(1)当SRi>HSRi,即第i跳的安全速率大于其历史安全速率时,当前安全速率取决于历史安全速率,而与第i跳的安全速率无关。因此,为了尽可能地降低目的节点发送协同干扰功率的值,可在保证SRi大于HSRi的前提下,尽可能地降低SRi的值,使得(SRi-HSRi)的值尽可能小。
(2)当SRi
假设发送节点和目的节点为最大化自身收益,两节点间存在博弈,为此引入协同干扰服务付费激励机制。发送节点为了尽可能地提高安全速率,向目的节点购买尽可能多的协同干扰功率,但也需向目的节点支付更多的报酬。目的节点选择一个合适的协同干扰功率单价,使得协同干扰的报酬尽可能地高于其成本。此外,发送节点考虑购买协同干扰功率对提高主干网安全速率的贡献,在提高本跳安全速率的同时,应尽量减小自身安全速率与其历史安全速率的差值。两者之间的干扰功率买卖过程可建模为博弈问题。
3 Stackelberg博弈功率控制模型
将每跳中发送节点和目的节点之间对协同干扰功率单价和协同干扰功率策略的选择过程建模为Stackelberg博弈过程。Stackelberg博弈是一种完全信息动态博弈模型[28-29]:(1)博弈方分为主导者和跟随者,主导者往往具有“先动优势”。(2)博弈双方掌握的信息是对称的,即博弈双方拥有相同的共同知识。本方案设置目的节点为博弈的主导者,而发送节点为跟随者。
3.1 Stackelberg博弈功率控制建模
第i跳的Stackelberg博弈可以表示为:
Gi=〈{CHi,CHi+1},{Pi+1,μi},{Ui,Ui+1}〉
(12)
其中,Stackelberg博弈模型的三要素如下:
(1){CHi,CHi+1}为第i跳中参与博弈的发送节点和目的节点集。
(2){Pi+1,μi}为博弈双方各自的策略空间集合。![]() 为发送节点策略空间,即选择购买协同干扰功率的范围。
为发送节点策略空间,即选择购买协同干扰功率的范围。![]() 为目的节点策略空间,即选择协同干扰功率单价的范围。
为目的节点策略空间,即选择协同干扰功率单价的范围。
(3){Ui,Ui+1}为博弈双方的效用函数集合。Ui(Pi+1,μi)为发送节点的效用函数,Ui+1(Pi+1,μi)为目的节点的效用函数。
3.1.1 发送节点的效用函数
发送节点支付目的节点相应的报酬,购买协同干扰功率以有效地提高安全速率;此外,考虑主干网的整体安全速率和目的节点能耗,避免片面追求本跳节点效用函数最大化。效用函数包括三方面因子:
(1)收益函数:收益函数表示发送节点在安全速率下对通信安全性的满意水平,安全速率越高,通信的安全性就越高。
(2)代价函数:代价函数表示发送节点购买干扰功率必须支付给目的节点的报酬。
(3)反馈代价函数:安全速率与历史安全速率间的差值。反馈代价函数提高主干网安全速率和降低能耗,引导主干网中各跳间的不合作博弈下趋向于合作。
发送节点效用函数Ui:
(13)
其中b×SRi为收益函数,b为安全速率单位收益调节因子;μiPi+1为代价函数,μi表示协同干扰功率单价;![]() 为反馈代价函数,a为反馈代价函数调节因子,a的取值如下:
为反馈代价函数,a为反馈代价函数调节因子,a的取值如下:
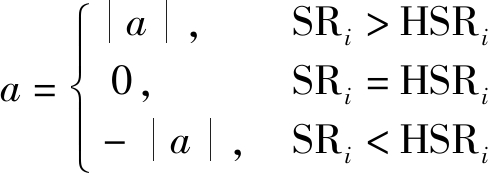
(14)
当a=0时,表示对各跳间的调节效果为零。
3.1.2 目的节点效用函数设计
目的节点效用函数包括两个方面因子:
(1)收益函数:目的节点发送协同干扰功率获得的报酬。
(2)代价函数:目的节点发送协同干扰功率所需的能耗成本。
目的节点效用函数Ui+1:
Ui+1(Pi+1,μi)=μiPi+1-cPi+1
(15)
其中,μiPi+1为收益函数;cPi+1为代价函数,c为发射协同干扰功率的成本调节因子。
3.2 Stackelberg博弈功率控制模型均衡点求解
Stackelberg博弈的纳什均衡点表示博弈双方在该点的收益达到帕累托最优。发送节点根据给定的协同干扰功率单价决定最佳协同干扰功率;目的节点根据发送节点的协同干扰功率,决定最佳协同干扰功率单价。Stackelberg博弈功率控制模型的均衡点为发送节点和目的节点的效用函数取最大值时,所对应的最佳协同干扰功率![]() 和最佳协同干扰功率单价
和最佳协同干扰功率单价![]() 组成的策略点
组成的策略点![]()
采用后向归纳法,当达到Stackelberg均衡点时,![]() 和
和![]() 应满足:
应满足:
(16)
(17)
3.2.1 最佳协同干扰功率分析
根据协同干扰功率对安全速率的提升效果,在博弈中发送节点的策略选择可分为两种情况:
(1)当ρPi+1(Hi+1,i+1)2≥Pi+1(Hi+1,E)2时,即ρ(Hi+1,i+1)2≥(Hi+1,E)2,即协同干扰信号对窃听信道的干扰小于主信道的干扰,使得每跳的安全速率降低。因此发送节点将退出博弈,即![]()
(2)当ρPi+1(Hi+1,i+1)2<Pi+1(Hi+1,E)2时,即ρ(Hi+1,i+1)2<(Hi+1,E)2,此时与上述(1)中的情况相反。目的节点选择最佳协同干扰功率,以最大程度地干扰窃听信道,使得每跳的安全速率最大化,因此发送节点效用函数(13)转化为:
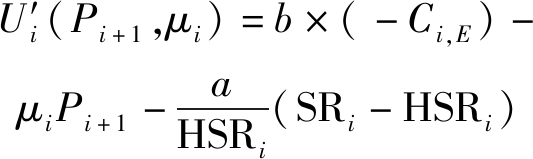
(18)
由(18),求解最佳协同干扰功率公式(16)转化为:
(19)
重点对在ρ(Hi+1,i+1)2<(Hi+1,E)2时发送节点参与博弈的情况进行分析。根据式(18),把发送节点的效用函数看作协同干扰功率Pi+1的一元方程,发送节点的干扰功率优化问题进而可转换为求该一元方程的极值问题。
对发送节点效用函数![]() 求Pi+1的偏导数:
求Pi+1的偏导数:
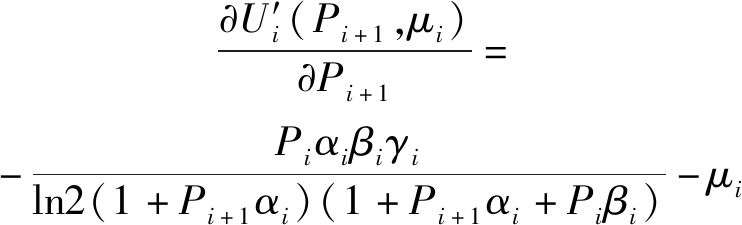
(20)
其中![]()
令公式(20)等于0,整理后得到关于协同干扰功率Pi+1的一元二次多项式:
(21)
根据多项式(21)以及协同干扰功率Pi+1边界条件![]() 解得μi对应的
解得μi对应的![]() 的闭式解为:
的闭式解为:
(22)
其中![]() 由(20)可知,
由(20)可知,![]() 为μi连续的单调递减函数。
为μi连续的单调递减函数。
3.2.2 最佳协同干扰功率单价分析
根据公式(17),为求得最佳协同干扰功率单价![]() 将公式(22)的
将公式(22)的![]() 代入Ui+1(Pi+1,μi),利用目的节点效用函数
代入Ui+1(Pi+1,μi),利用目的节点效用函数![]() 对功率单价μi求一阶偏导,可得:
对功率单价μi求一阶偏导,可得:
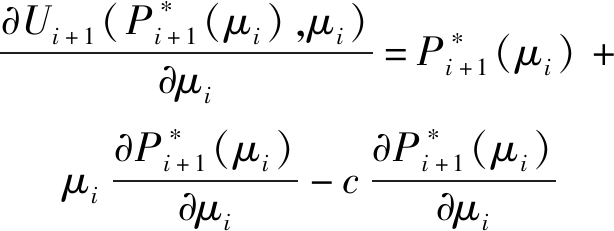
(23)
令公式(23)等于0,可解得最优协同干扰功率单价闭式解:
(24)
4 FSPC算法
基于Stackelberg博弈功率控制模型,设计一种可提高主干网安全速率的博弈功率控制算法FSPC。
4.1 FSPC算法描述
FSPC算法流程图如图2所示,主要步骤为:
(1)初始化:当跳数i=1时,设置a=0使得反馈代价函数为零;
(2)循环迭代:求安全速率SRi,并取SRi与历史安全速率HSRi的较小值作为其当前安全速率CSRi;
(3)循环终止:重复步骤(2),直到数据传输到基站,即跳数i=n,输出主干网安全速率。
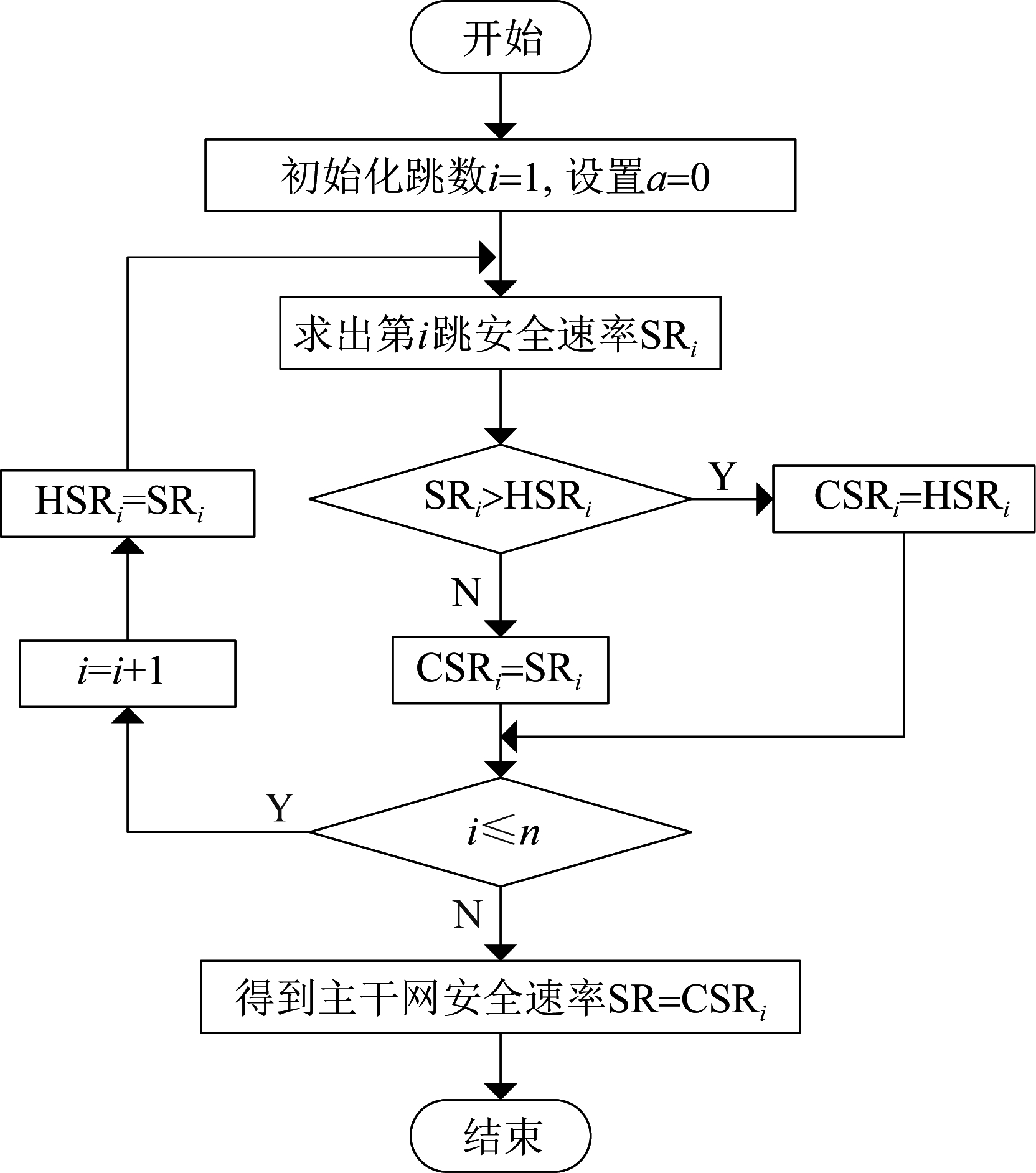
图2 FSPC算法流程图
Fig.2 FSPC algorithm flow chart
4.2 博弈均衡迭代求解
为得到SRi,需要先求解出该跳博弈模型的均衡解,为此设计博弈均衡交叉迭代求解算法,如图3。
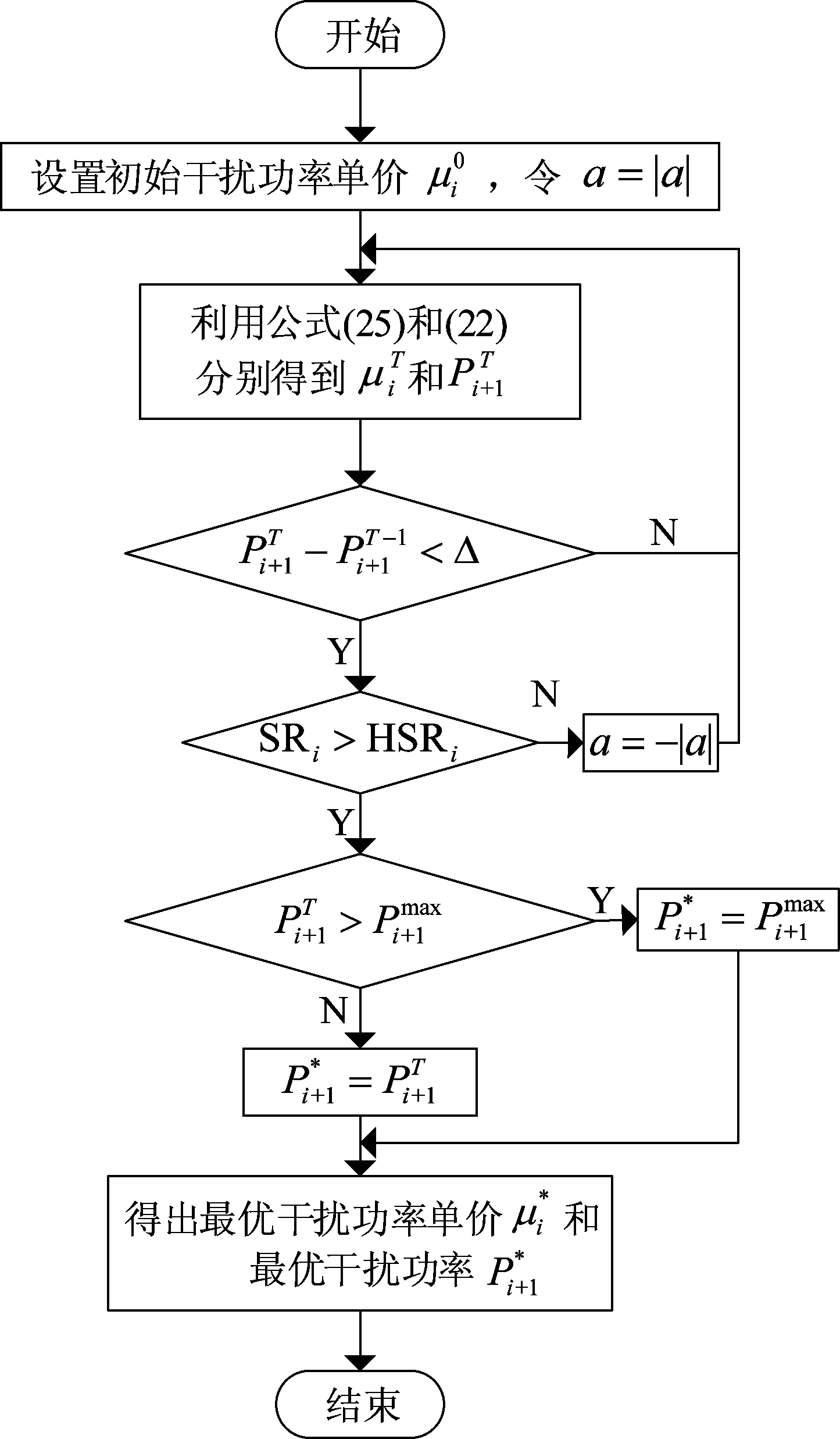
图3 交叉迭代算法流程图
Fig.3 Flow chart of cross iteration algorithm
根据公式(24),得到协同干扰功率单价的迭代公式:
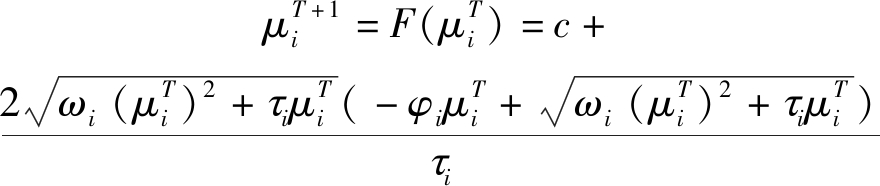
(25)
其中T表示迭代次数。
首先设置初始协同干扰功率单价![]() 利用公式(25)计算出迭代次数为T时的协同干扰功率单价
利用公式(25)计算出迭代次数为T时的协同干扰功率单价![]() 将
将![]() 代入公式(22)得到协同干扰功率
代入公式(22)得到协同干扰功率![]() 直到相邻两次迭代的
直到相邻两次迭代的![]() 变化近似相等时,算法停止迭代,输出Stackelberg博弈功率控制模型的均衡点。
变化近似相等时,算法停止迭代,输出Stackelberg博弈功率控制模型的均衡点。
5 仿真与分析
使用Matlab2018a仿真平台对本文方法进行仿真。仿真主要从两个方面进行,一是根据发送节点和目的节点的效用函数,分析合适的收益调节因子b和成本调节因子c;二是对比分析本文采用的方法与其他功率分配方案在安全性能、节省能耗等方面的性能对比。
5.1 仿真环境及其参数设置
不失一般性,假设所有信道具有单一功率的平坦准静态瑞利衰落环境,且将信道的高斯噪声方差进行归一化为1。将路径损耗因子M设定为3,阴影衰落A设定为2[30]。总的参数配置如表1所示。
表1 仿真参数
Tab.1 Simulation parameters
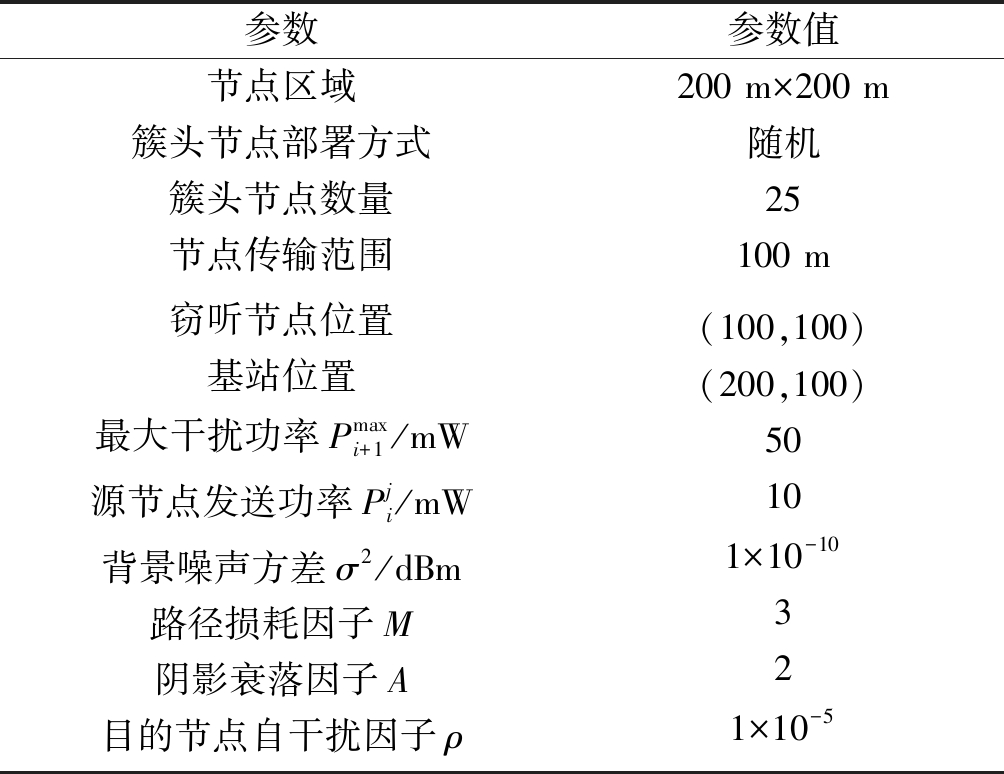
参数参数值节点区域200 m×200 m簇头节点部署方式随机簇头节点数量25节点传输范围100 m窃听节点位置基站位置最大干扰功率Pmaxi+1/mW源节点发送功率Pji/mW背景噪声方差σ2/dBm路径损耗因子M阴影衰落因子A目的节点自干扰因子ρ(100,100)(200,100)50101×10-10321×10-5
5.2 确定调节因子
对不同成本调节因子c和不同收益调节因子b对应的发送节点和目的节点效用函数进行仿真,结果如图4、图5。在c相同的情况下,b越大,发送节点和目的节点的效用越大;而对于相同b,c越小,发送节点和目的节点的效用函数越大。综合考虑发送节点和目的节点效用函数,c取1,b取5。
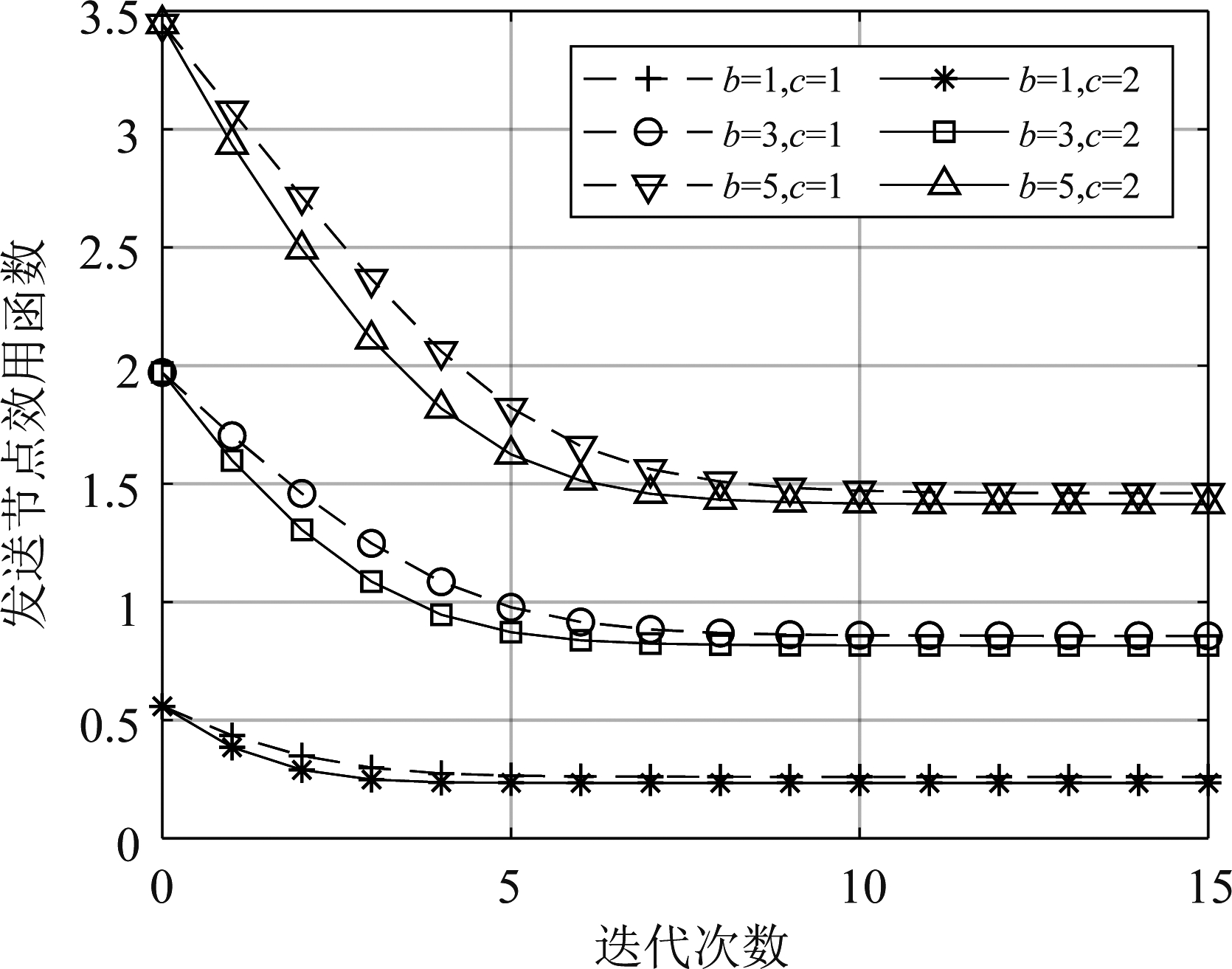
图4 不同参数下的发送节点效用函数
Fig.4 Utility function of sending node under different parameters
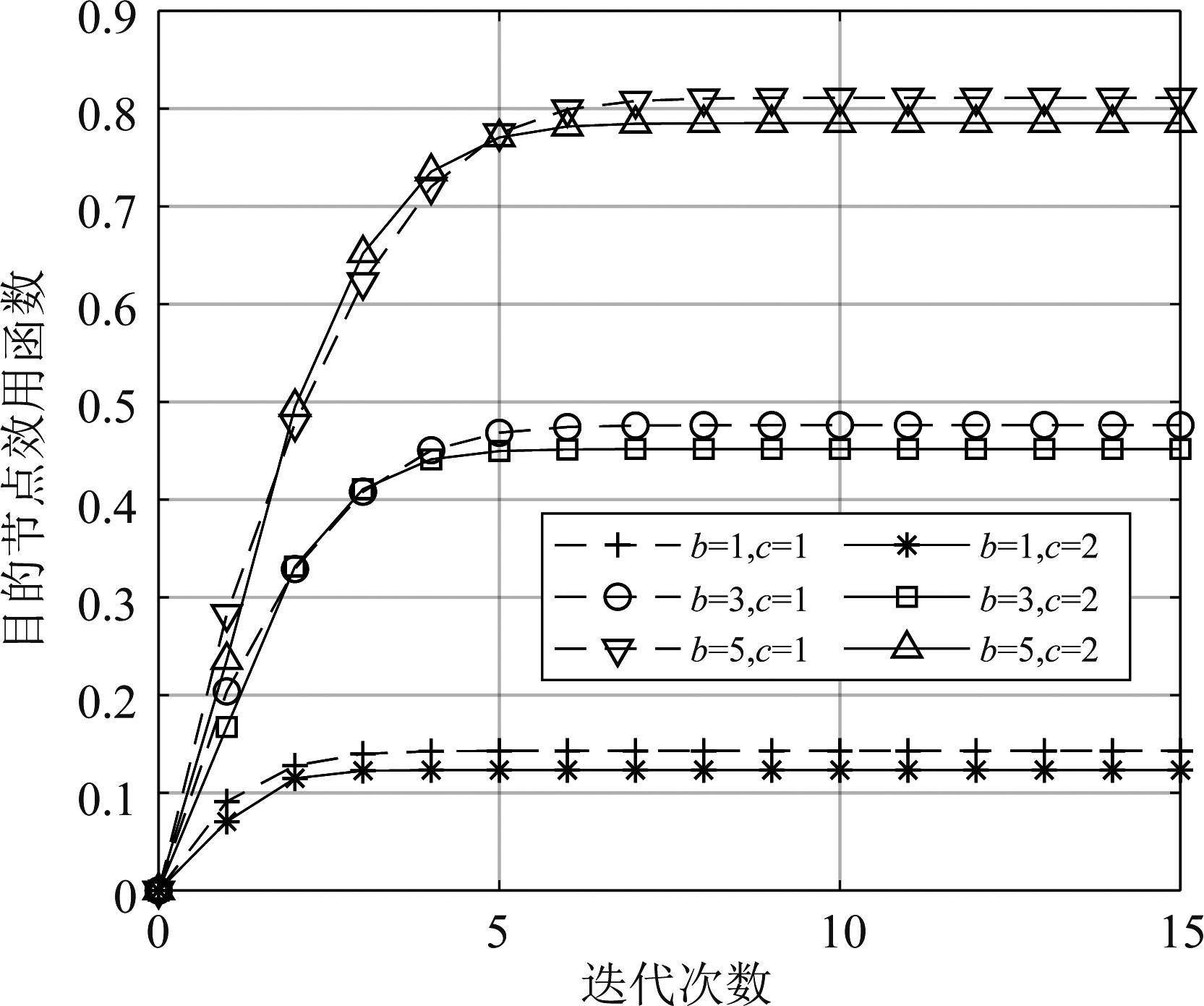
图5 不同参数下的目的节点效用函数
Fig.5 Utility function of destination node under different parameters
5.3 性能分析5.3.1 交叉迭代算法收敛性分析
对发送节点和目的节点处于不同位置的收敛性能及迭代出的协同干扰功率对比分析。选取发送节点和目的节点基点坐标对(60,60)和(140,60)。在仿真中,协同干扰功率相邻迭代次数变化值小于10-4时,算法停止迭代,对比结果如图6所示。
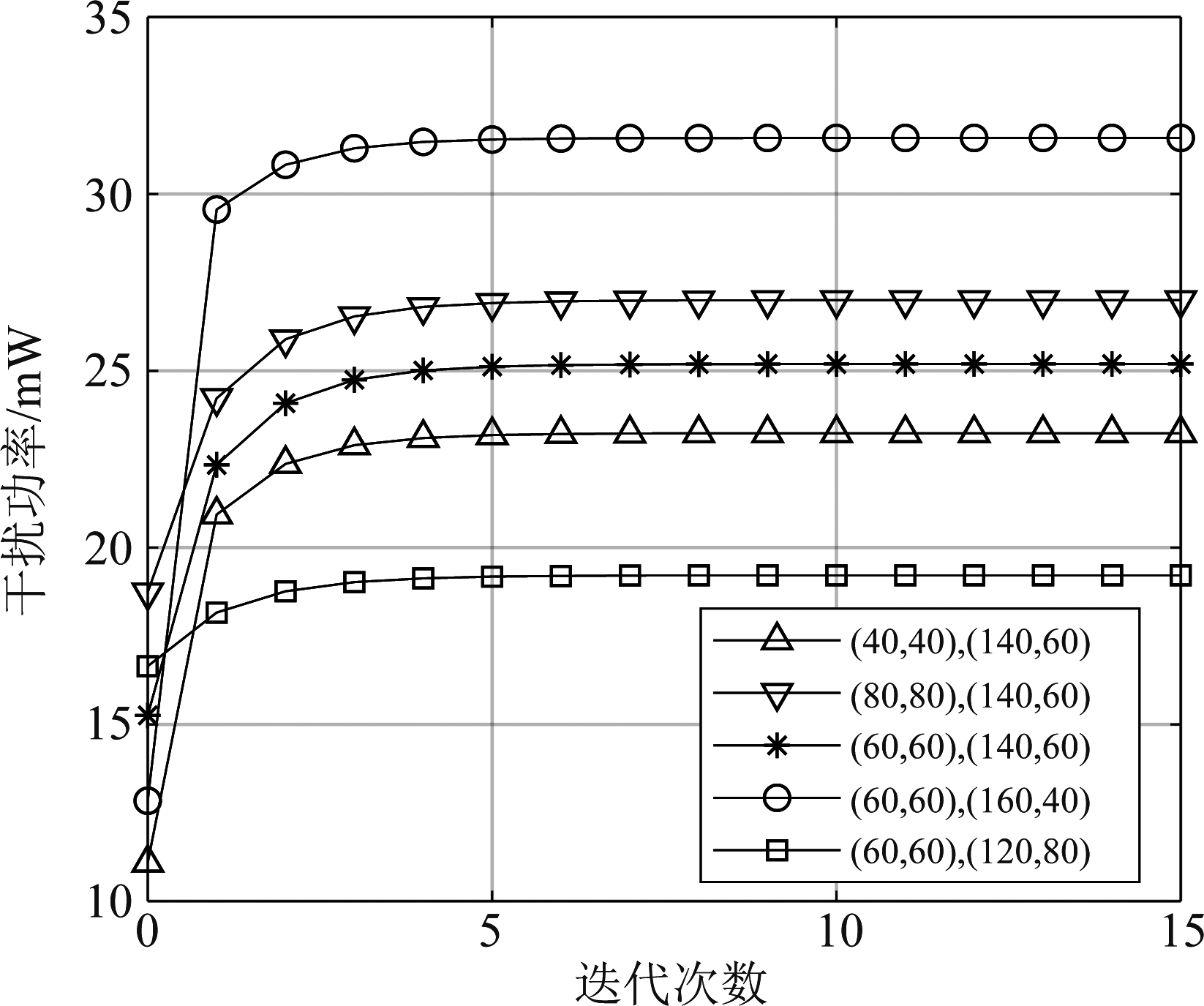
图6 不同位置下的协同干扰功率
Fig.6 Cooperative jamming power in different locations
图6为不同位置下的协同干扰功率迭代对比图。对于不同发送节点和目的节点位置对,约经过5次迭代收敛于不同的协同干扰功率值,交叉迭代算法具有理想的收敛性能,且根据合法节点与窃听节点不同的位置来收敛于不同的最佳协同干扰功率。选取坐标对(40,40)和(140,60)、(80,80)和(140,60),比较发送节点与窃听节点的距离对协同干扰功率的影响,由对应的收敛曲线可知,发送节点离窃听节点越近,迭代出的最佳协同干扰功率越大;选取坐标对(60,60)和(160,40),(60,60)和(120,80),比较目的节点与窃听节点距离对协同干扰功率的影响,由对应的收敛曲线可知,目的节点离窃听节点越远,迭代出的最佳协同干扰功率越大。这是因为发送节点靠近窃听节点、或目的节点远离窃听节点,窃听节点都将窃听到更多的信息,需通过增大协同干扰功率来提高本跳的安全速率。
5.3.2 安全性能和能耗分析
随机选取一条跳数为5的主干网进行仿真,分析反馈调节因子a的值对提升主干网安全速率和降低能耗的影响,结果如表2和表3所示。SR为主干网安全速率,即五跳中最小一跳安全速率;P2~P5分别为第一跳到第五跳的协同干扰功率,![]() 为五跳的平均协同干扰功率。
为五跳的平均协同干扰功率。
由表2,当a为1时,对主干网安全速率的提升效果最好,相对无反馈时提升了0.012 bit/s/Hz。由表3,a值越大![]() 就越小。综合考虑主干网安全速率和能耗,将反馈调节因子a设为1。
就越小。综合考虑主干网安全速率和能耗,将反馈调节因子a设为1。
(1)安全性能分析:选取主干网安全速率作为指标,和RISA方案(RISA方案就是当a取0时的本文方案)[17]、随机功率控制(Random Power Control, RAND)方案、无协同干扰方案(No Cooperative Jamming, NCJ)进行仿真对比分析,结果如图7所示。RAND方案中发送节点和目的节点随机地选择策略,NCJ方案每跳中的目的节点不提供协同干扰服务。
表2 不同反馈调节因子下的安全速率
Tab.2 The security rate under different feedback adjustment factors

aSR1/(bit/s/Hz)SR2/(bit/s/Hz)SR3/(bit/s/Hz)SR4/(bit/s/Hz)SR5/(bit/s/Hz)SR/(bit/s/Hz)0.00.51.01.50.5290.5290.5290.5290.4380.4420.4500.4580.4590.4560.4510.4400.5260.5220.5150.5010.5040.5030.5000.4930.4380.4420.4500.440
表3 不同反馈调节因子下的协同干扰功率
Tab.3 Optimum cooperative jamming power under different feedback adjustment factors

aP2/mWP3/mWP4/mWP5/mWP6/mWP-/mW00.51.01.522.422.422.422.420.520.921.722.926.726.225.423.736.335.233.530.215.215.014.714.124.223.923.522.6
由图7,各方案的第二跳安全速率最低,即各方案的主干网安全速率取各自第二跳的安全速率。本文FSPC的主干网安全速率明显高于RAND和NCJ,略高于RISA。这是因为RAND采用随机选择策略,NCJ目的节点不提供协同干扰。而相比于RISA,本文方案在安全速率最小的那跳中会增加对协同干扰功率的购买,使得主干网安全速率在RISA方案基础上略微提高,因此本文方案具有更高的安全性。

图7 不同方案下的安全速率
Fig.7 The security rate under different algorithms
(2)能耗分析:假设每跳中目的节点发送协同干扰信号的时间相同,选取同一主干网中的平均协同干扰功率![]() 作为指标。因RAND方案和NCJ方案在安全性能方面不可靠,所以重点选取RISA方案进行分析和对比。
作为指标。因RAND方案和NCJ方案在安全性能方面不可靠,所以重点选取RISA方案进行分析和对比。
由表3可知,本文方案的a为1时对应的![]() 等于23.5 mW,a为0时对应的
等于23.5 mW,a为0时对应的![]() 等于24.2 mW。RISA方案的
等于24.2 mW。RISA方案的![]() 与a取0时的本文方案是相同的,因此本文方案的能耗要低于RISA。这是因为本文方案在非最小安全速率的其他跳中会减小对协同干扰功率的购买,这些跳中协同干扰功率降低量的和要大于在最小安全速率的那跳中协同干扰功率增加的量,最后综合导致本文方案的能耗更低。
与a取0时的本文方案是相同的,因此本文方案的能耗要低于RISA。这是因为本文方案在非最小安全速率的其他跳中会减小对协同干扰功率的购买,这些跳中协同干扰功率降低量的和要大于在最小安全速率的那跳中协同干扰功率增加的量,最后综合导致本文方案的能耗更低。
6 结论
针对多跳IWSN中主干网的物理层安全问题,利用FSPC算法有效地提高了主干网安全速率并且降低了整体能耗。首先,为保证各跳通信安全,采用了目的节点协同干扰方案,引入了向提供协同干扰服务的目的节点付费的激励机制;其次,考虑多跳主干网安全速率,在发送节点的效用函数引入了反馈代价函数;利用了Stackelberg博弈对每跳中的发送节点和目的节点的策略选择过程建模,并求出了Stackelberg博弈的均衡解。仿真结果表明,FSPC算法较其他功率控制算法,优化了各跳中对协同干扰功率的控制性能,减小了各跳的安全速率的差值,进一步提高了主干网通信安全和能耗降低。
[1] SALAM H A, KHAN B M. IWSN-standards, challenges and future[J]. IEEE Potentials, 2016, 35(2): 9-16.
[2] JYOTHI A P, USHA S. Interstellar-based topology control scheme for optimal clustering performance in WSN[J]. International Journal of Communication Systems, 2020, 33(8):1-16.
[3] DUAN Ying, LI Wenfeng, FU Xiuwen, et al. A methodology for reliability of WSN based on software defined network in adaptive industrial environment[J]. IEEE/CAA Journal of Automatica Sinica, 2018, 5(1): 74- 82.
[4] 杨冬, 马剑, 张宏科. 智慧协同工业无线传感器网络[J]. 电子学报, 2017, 45(6): 1537-1544.
YANG Dong, MA Jian, ZHANG Hongke. Smart and cooperative industrial wireless sensor network[J]. Acta Electronica Sinica, 2017, 45(6): 1537-1544.(in Chinese)
[5] 蒋俊正, 李杨剑, 赵海兵, 等. 一种大规模传感器网络节点分布式定位算法[J]. 电子与信息学报, 2019, 41(12): 3022-3028.
JIANG Junzheng, LI Yangjian, ZHAO Haibing, et al. A distributed node localization algorithm for large scale sensor networks[J]. Journal of Electronics & Information Technology, 2019, 41(12): 3022-3028.(in Chinese)
[6] 孙东旭, 曹建福, 郑辑光. 面向工业测控的无线传感器网络分簇路由算法[J]. 信息与控制, 2012, 41(6): 779-785.
SUN Dongxu, CAO Jianfu, ZHENG Jiguang. A clustering routing algorithm of WSN for industrial measurement and control[J]. Information and Control, 2012, 41(6): 779-785.(in Chinese)
[7] ANASTASOV J A, ![]() D M, et al. On physical layer security in WSN over GK fading channels during intercept events[J]. Telecommunication Systems, 2020, 74(1): 95-102.
D M, et al. On physical layer security in WSN over GK fading channels during intercept events[J]. Telecommunication Systems, 2020, 74(1): 95-102.
[8] ZHONG Yi, GE Xiaohu, HAN Tao, et al. Tradeoff between delay and physical layer security in wireless networks[J]. IEEE Journal on Selected Areas in Communications, 2018, 36(7): 1635-1647.
[9] WYNER A D. The wire-tap channel[J]. The Bell System Technical Journal, 1975, 54(8): 1355-1387.
[10] 李元健, 赵睿, 谭星, 等. 全双工目的端加扰安全传输系统中的天线模式切换[J]. 信号处理, 2018, 34(4): 457- 464.
LI Yuanjian, ZHAO Rui, TAN Xing, et al. Antenna mode switching for full-duplex at a destination of a jamming secure transmission system[J]. Journal of Signal Processing, 2018, 34(4): 457- 464.(in Chinese)
[11] 王东, 李永成, 白铂, 等. 放大转发中继网络中绿色的物理层安全通信技术[J]. 电子与信息学报, 2016, 38(4): 841- 847.
WANG Dong, LI Yongcheng, BAI Bo, et al. Green communications based on physical-layer security for amplify-and-forward relay networks[J]. Journal of Electronics & Information Technology, 2016, 38(4): 841- 847.(in Chinese)
[12] 黄博阳, 方彦军, 孔政敏. 中继辅助的干扰信道中总体MSE最小化的安全波束成形[J]. 信号处理, 2019, 35(2): 200-207.
HUANG Boyang, FANG Yanjun, KONG Zhengmin. Total MSE maximization beamforming for secure communications in relay aided interference systems[J]. Journal of Signal Processing, 2019, 35(2): 200-207.(in Chinese)
[13] FANG He, XU Li, ZOU Yulong, et al. Three-stage Stackelberg game for defending against full-duplex active eavesdropping attacks in cooperative communication[J]. IEEE Transactions on Vehicular Technology, 2018, 67(11): 10788-10799.
[14] JUNG H, LEE I H. Secrecy performance analysis of analog cooperative beamforming in three-dimensional Gaussian distributed wireless sensor networks[J]. IEEE Transactions on Wireless Communications, 2019, 18(3): 1860-1873.
[15] PANDEY A, YADAV S. Performance evaluation of amplify-and-forward relaying cooperative vehicular networks under physical layer security[J]. Transactions on Emerging Telecommunications Technologies, 2018, 29(12):1-18.
[16] QU Junyue, CAI Yueming, WU Dan, et al. Stackelberg game based power allocation for physical layer security of device-to-device communication underlaying cellular networks[J]. Frequenz, 2014, 68(5/6): 285-295.
[17] WANG Kun, YUAN Li, MIYAZAKI T, et al. Jamming and eavesdropping defense in green cyber-physical transportation systems using a Stackelberg game[J]. IEEE Transactions on Industrial Informatics, 2018, 14(9): 4232- 4242.
[18] 李明亮, 郭云飞, 黄开枝. 基于联盟博弈的多小区下行链路保密协作算法[J]. 电子与信息学报, 2017, 39(6): 1271-1277.
LI Mingliang, GUO Yunfei, HUANG Kaizhi. Coalition game based secrecy downlink cooperation algorithm in multi-cell networks[J]. Journal of Electronics & Information Technology, 2017, 39(6): 1271-1277.(in Chinese)
[19] LI Jialun, CHANG Shuai, FU Xiaomei, et al. A coalitional formation game for physical layer security of cooperative compressive sensing multi-relay networks[J]. Sensors, 2018, 18(9): 2942.
[20] 黄开枝, 洪颖, 罗文宇, 等. 基于演化博弈机制的物理层安全协作方法[J]. 电子与信息学报, 2015, 37(1): 193-199.
HUANG Kaizhi, HONG Ying, LUO Wenyu, et al. A method for physical layer security cooperation based on evolutionary game[J]. Journal of Electronics & Information Technology, 2015, 37(1): 193-199.(in Chinese)
[21] LONG Chengzhi. An improved LEACH multi-hop routing protocol based on intelligent ant colony algorithm for wireless sensor networks[J]. Journal of Information and Computational Science, 2014, 11(8): 2747-2757.
[22] 叶润, 王缓缓. 能量均衡多跳分簇路由算法[J]. 智能系统学报, 2014, 9(5): 608- 612.
YE Run, WANG Huanhuan. WSN energy balance multi-hop clustering routing algorithm[J]. CAAI Transactions on Intelligent Systems, 2014, 9(5): 608- 612.(in Chinese)
[23] 徐倩, 胡艳军. 一种基于反馈的K-means分簇算法研究[J]. 信号处理, 2017, 33(8): 1145-1151.
XU Qian, HU Yanjun. A research on K-means clustering algorithm based on feedback[J]. Journal of Signal Processing, 2017, 33(8): 1145-1151.(in Chinese)
[24] LI Chenxing, LIU Ying, XU Qiang, et al. Self-interference cancellation with frequency offset and nonlinear distortion suppression for cooperative jamming communications[J]. IEEE Communications Letters, 2019, 23(11): 2091-2094.
[25] ZHOU Yongkai, XIANG Zhengzheng, ZHU Yan, et al. Application of full-duplex wireless technique into secure MIMO communication: Achievable secrecy rate based optimization[J]. IEEE Signal Processing Letters, 2014, 21(7): 804- 808.
[26] LI Lingxiang, CHEN Zhi, ZHANG Duo, et al. A full-duplex bob in the MIMO Gaussian wiretap channel: Scheme and performance[J]. IEEE Signal Processing Letters, 2016, 23(1): 107-111.
[27] LEUNG-YAN-CHEONG S, HELLMAN M. The Gaussian wire-tap channel[J]. IEEE Transactions on Information Theory, 1978, 24(4): 451- 456.
[28] MANZOOR A K, HAMIDOU T, ATHANASIOS V V. Evolutionary Coalitional Games: Design and Challenges in Wireless Networks[J]. IEEE Wireless Communications, 2012, 19(2):50-56.
[29] MYERSON R B. Game Theory: Analysis of Conflict[M]. Cambridge, Massachusetts, USA: Harvard University Press, 1997.
[30] 金鑫. 无线信道传播模型的研究与实现[D]. 北京: 北京邮电大学, 2010.
JIN Xin. Research and realization of wireless communication channel propagation model[D]. Beijing: Beijing University of Posts and Telecom, 2010. (in Chinese)

