1 引言
当今世界,弹道导弹技术实现了快速地发展[1],对各国产生了重大影响。为了应对弹道导弹的威胁,各国都在抓紧研究如何对弹道导弹进行拦截。对于弹道导弹防御这项技术来说,首要的是对弹道导弹进行准确识别[2],识别出真假弹头。然而,随着分导式多弹头以及导弹诱饵技术的日益成熟[3],在飞行过程中,弹道导弹会释放假弹头以及诱饵,同时自身也会产生许多碎片,对雷达形成干扰。因此,对于依靠传统特征进行识别的方法来说,很难从群目标中准确识别出真弹头,从而使得很难依靠传统的识别技术获得弹头的相关参数。然而,物体的微小运动是独一无二的,因此可以利用该特性对弹道导弹进行识别[4]。Victor C. Chen首先提出了微多普勒的概念[5],并将其引入到目标识别领域中。之后,利用微多普勒信息识别目标成为新的研究热点。
一般情况下,弹道导弹在飞行中,其运动由平动和微动组成。其中,平动会导致散射点回波多普勒曲线出现倾斜,影响弹道导弹微动信息的提取。因此,为了提取微动信息,应该进行平动补偿。目前,对平动分量的补偿已经进行了大量的研究并取得了一定的成果。文献[6]采用高阶模糊函数,搜索图像峰值估计出平动参数,实现了目标的平动补偿,但求解需要相对较长的观测时间。文献[7]通过Radon变换,对目标整体微多普勒曲线进行投影变换,进而实现平动补偿。文献[8]提出了一种延迟共轭相乘的方法,消除微动保留平动,对目标进行平动补偿。文献[9]利用Viterbi算法,根据多普勒率与微多普勒关系得到微动参数,进而实现平动补偿。文献[10]通过提取交叉点信息,得到平动参数,实现了对目标的平动补偿。
基于上述的研究现状,本文提出了Shi-Tomasi角点检测算法[11],进行平动补偿。同时,针对检测时间较长的问题,本文对算法进行了优化,更好的估计出平动参数,实现了较高精度的平动补偿。
2 锥体弹道目标的进动模型
在飞行的过程中,弹道目标的飞行姿态受到多种因素的影响。为了简化分析,本文只考虑重力对飞行姿态的影响。若重力作用在导弹的质心上,则飞行姿态仅仅为自旋;若重力没有作用在导弹的质心上,则弹道目标的飞行姿态为一方面绕着自身的对称轴进行自旋,另外一方面绕着空间某一定轴做锥旋运动。自旋和锥旋的叠加,最终形成了进动的飞行姿态[12]。
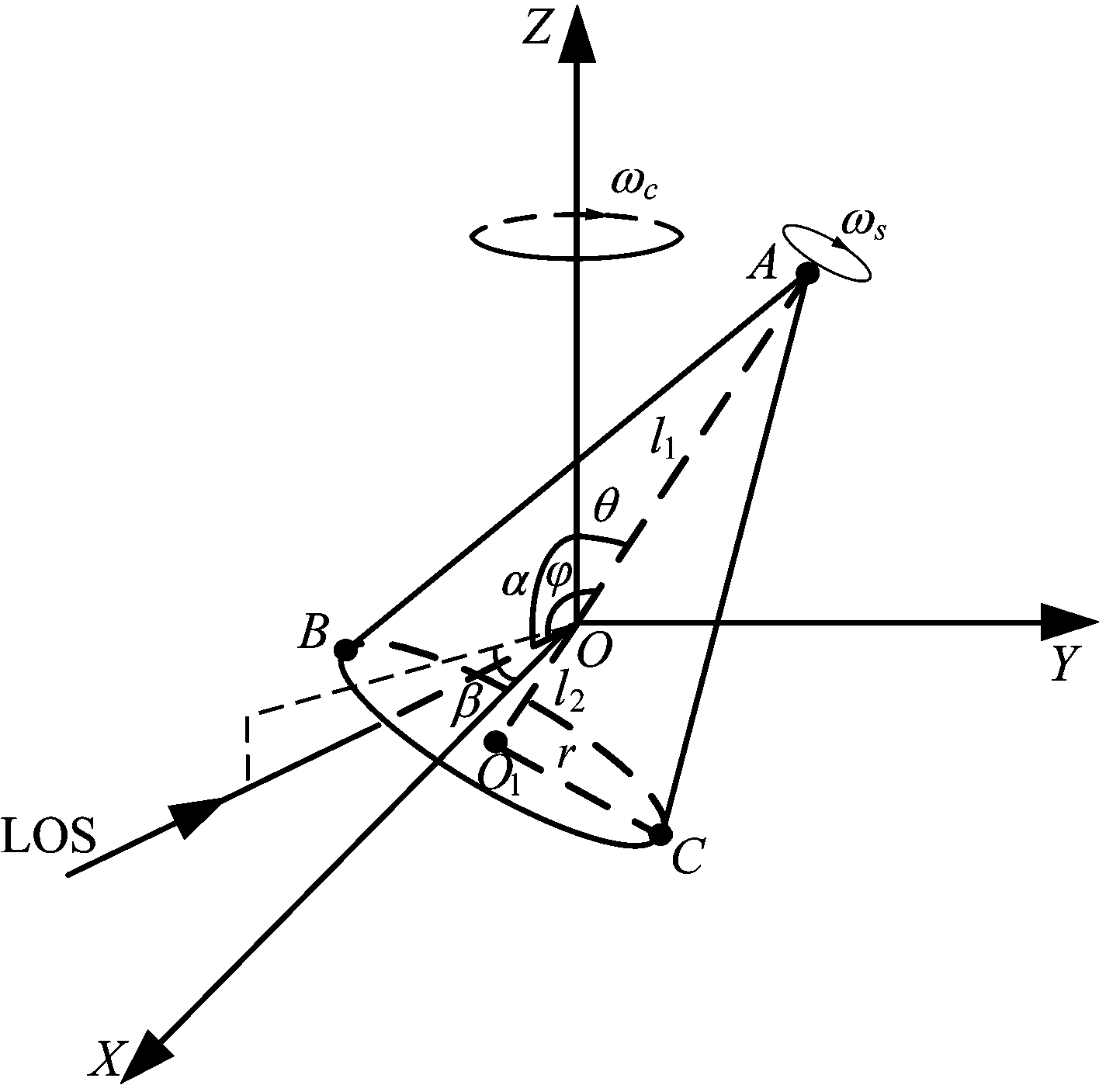
图1 进动锥体弹道目标的散射模型
Fig.1 Scattering model of precession cone ballistic target
如图1所示,坐标系O-XYZ为锥体目标的参考坐标系,其原点O为锥体弹道目标的质心,坐标系中的Z轴为锥体运动的进动轴。在目标运动的起始时刻,雷达视线LOS在参考坐标系O-XYZ中的方位角和仰角分别为α和β,与自旋轴的夹角为φ,锥旋角与自旋角的夹角,即进动角为θ,目标质心与雷达的初始距离为R0(这里没有在图中标明)。目标的锥旋角速度为ωc,自旋角速度为ωs,平动速度为ν。质心到散射点A的距离为l1,到底面圆圆心距离为l2。
根据文献[13],可以得到,散射点的微动距离变化公式如下所示,即
rA=l1cos β(t)
rB=-l2cos β(t)-rsin β(t)
rC=-l2cos β(t)+rsin β(t)
(1)
其中:
cos β(t)=cos θcos α+sin θsin αsin(ωct-φ0)
φ0为初始时刻t=0时,目标对称轴在面XOY内的投影与OX轴的夹角。由于夹角φ0仅仅影响微多普勒的初相,对周期以及幅值没有影响,因此我们可以取任意一数值,不失一般性,可以令φ0=0[14]。
当雷达波束照射到目标的时候,目标会形成三个典型散射点,锥顶散射点A点,底面边缘滑动散射点B点、C点,如图1所示。在实际应用中,由于存在遮挡效应,三个散射点不一定同时被雷达观测到。根据文献[15],我们可以得到相关散射点的可见角度,如下表1所示,其中ε为锥体目标的半锥角。
表1 散射点的可见角度
Tab.1 The visible angle of the scattering point
本文对角度在0<β<(ε∩(π-ε))的范围内进行分析,此时三个散射点均可产生回波,对每个散射点产生的回波进行叠加,形成一个总的回波[16]。下面对散射点的频率与运动之间的关系进行分析。其他情况均可照此分析,这里不在赘述。
图2 雷达与锥体目标散射点之间距离示意图
Fig.2 Schematic diagram of the distance between the radar and the cone target scattering point
本文以散射点A为例。如图2所示,雷达位于O′点位置。在实际的飞行过程中,弹道目标距离雷达较远,因此O′O与O′A的夹角比较小,此时我们可以近似得到|O′A|≈|O′H|、|O′A|≈|O′O|+|OA|,即|O′H|=RA=R+rA。
多普勒频率可以由下式得到
(2)
式中:fd为多普勒频移,νr为散射点沿雷达视线方向的径向速度,λ为载波波长。
当目标向着雷达运动时,νr>0,回波载频比发射的载频大,反之νr<0,回波载频比发射的载频小。因此,雷达只要能够测出散射点径向距离的变化率,即可得到散射点的频率[17]。
根据图2可以得到
因此散射A点的多普勒频率为
(3)
式中:νrA散射点A沿雷达视线方向的径向速度, ft和fm分别为目标平动与微动导致的多普勒频率。
在目标的运动过程中,弹道目标的平动分量数学表达式可以近似用多项式来描述[9],即
(4)
若时间比较短,采用低阶的多项式数学模型就可以较好的描述平动分量。本文采用3阶多项式数学模型来对平动分量进行描述,即:
R=R0+a1t+a2t2/2+a3t3/6
(5)
式中:R0表示锥体目标距雷达的初始距离,a1表示锥体目标沿雷达视线的径向速度,a2表示锥体目标沿雷达视线的径向加速度,a3表示锥体目标沿雷达视线的2阶径向加速度。
因此,锥体目标运动产生的频率为
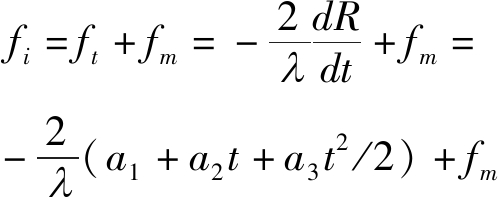
(6)
假设雷达发射载频为f0的单频信号,即
st(t)=exp(j 2πf0t)
(7)
则雷达接收到的各个散射点回波为
(8)
式中:Ai为散射点回波的系数,Ri(t)为t时刻散射点与雷达间的距离。
接收的回波信号包含载频信号exp(j 2πf0t),在采样之前,可以通过正交解调予以去除[18]。解调后的散射点的基带信号可以表示为
(9)
根据上式,可以得到散射点的时频曲线图。通过观察目标散射点的时频曲线图,可以看出在时频曲线图上存在多个交点。
在实际中,弹道目标的平动速度比较大,产生的多普勒频率要远远大于雷达脉冲重复频率,得到的回波频率远大于基带[-PRF/2,PRF/2],从而会发生模糊或折叠[10]。若仅仅考虑多普勒模糊情况,可以将目标多普勒频率fi拆分如下式所示
fi=n·PRF+fn
(10)
式中:n·PRF为模糊项,n=round(fi/PRF)为模糊数, fn为剩余项。根据式(6)和(10)得到
(11)
由式(1)、(2)以及
可知,当ωct-φ0=(k+1/2)π(k=0,1,2,...)时, fm=0,则
(12)
此时,锥顶散射点A点,底面边缘滑动散射点B点、C点具有相同的频率值,也即时频曲线图的交点。在这些交点处,由式(12)可知,频率值仅仅与平动项有关。因此,可以通过对交点信息的提取得到平动分量,进而实现对散射点的平动补偿[10]。
3 时频方法
由于时频对仿真实验存在相关影响,因此对时频方法进行分析。
3.1 短时傅里叶变换
短时傅里叶变换(short-time Fourier transform, STFT)的基本原理是用时宽很窄的窗函数提取信号,这时可以将取出的信号看作是平稳的,用傅里叶变换进行分析,得到频率信息[19]。
信号s(t)的短时傅里叶变换定义为
STFTs(t, f)=
s(τ)g*(τ-t)e-j2πfτdτ
(13)
式中g(t)为一个时间宽度很短的窗函数。
3.2 Gabor变换
Gabor展开可以表示为
(14)
式中:amn称为Gabor展开系数,g(t)为Gabor基函数,ΔT和Δf分别表示时间和频率采样间隔。
amn可以用下面式子求出
amn=s(t)γ*(t-mΔT)e-jn2πΔftdt
(15)
式中:γ(t)是与g(t)双正交对偶的基函数[20]。
3.3 Cohen类时频分布
Cohen类时频分布可以统一写成
φ(τ,ν)e-j2π(tν+τf-uν)dudνdτ=
(16)
式中:
f)可以看成是一个平滑函数。
Cohen类时频分布还可以用模糊函数表示,即
(17)
式中:F是∏(t, f)的二维傅里叶变换[21]。
Rihaczek分布定义为:
Rx(t, f)=x(t)x*( f )e-j2πft
(18)
它对应于在Cohen类时频分布中取F(τ,ν)=ejπ ντ[22]。
Page分布定义为:
(19)
它表示信号在时间t之前的能量谱密度的微分,也是Cohen类时频分布的一种,对应取F(τ,ν)=e-jπν|τ|[22]。
4 提取角点的图像特征
4.1 角点检测算法
根据第2节所述,为了实现平动补偿,需要确定时频曲线中交点的位置,为此引入角点检测算法。角点一般可以定义为两条边的交点,或者可以理解为在角点的周围内具有两个不同区域的不同方向的边界。角点检测算法(Corner Detection Algorithm)是用来获得图像中特征点的一种方法,也称为特征点检测算法[23]。算法的基本原理是选取某一区域,在图像上任意移动选取的区域。通过对比移动前后,区域中像素点灰度值变化来确定是否存在角点。任意移动所选取的区域,如果图像的灰度值产生较大变化,那么可以认为在该区域中存在角点[24]。
Moravec角点检测算法是最早应用的算法。首先,该算法以某一像素点为中心确定一个区域,每个像素点都会形成一个区域。算法通过计算相邻区域的平方差之和,检测相邻区域的相关性,进而确定是否存在角点。然而,该算法有明显的缺陷。算法只是单纯计算了几个确定方向的像素值,未实现各向同性。同时由于所取的范围简单的正方形区域,很容易产生噪声。为了解决上述相关问题,提出了Harris算法。首先,Harris算法计算矩阵行列式值与迹的差值,求出角点响应函数,之后进行阈值处理,得到局部极大值。但是该算法不具有尺度不变性,同时检测所需的时间较长,实际应用较差。
Shi-Tomasi算法是Harris算法的改进。相对于Harris算法来说,Shi-Tomasi算法通过计算自相关矩阵的特征值,用所得特征值与设定的阈值进行比较。若特征值均大于阈值,则可以确定角点。Shi-Tomasi算法具有良好的可重复性,比较简单,检测效率较高,同时解决了Moravec算法无法对图像进行各向性计算等问题。在很多情况下,可以得到更好的结果。
如图3所示,窗口在平面上移动。若在光滑平面上,如图3(a),窗口在任意方向上没有发生任何变化;若在边缘区域上,如图3(b),窗口在边缘所对应的方向没有发生变化;若在角点区域上,如图3(c),窗口在各个方向均发生变化。根据图3,Shi-Tomasi算法利用窗口移动判断在任意方向上是否发生变化,对图像中的角点进行检测。
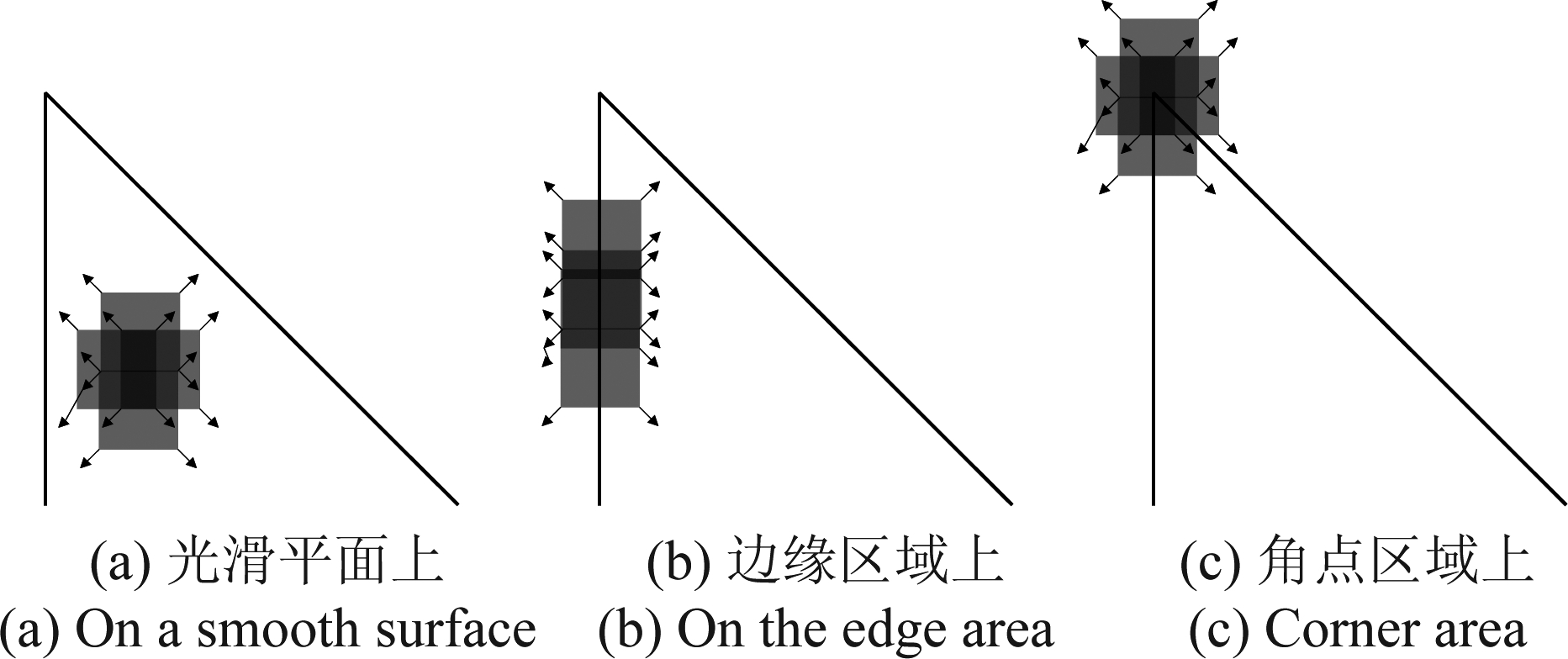
图3 窗口运动示意图
Fig.3 Schematic diagram of window movement
在图像(x,y)处,对窗口进行平移,平移量为[u,ν],则移动前后的图像灰度值变化为
(20)
式中:w(x,y)为加权函数,位于(x,y)处的窗口,I(x,y)为(x,y)处像素点灰度值大小,I(x+u,y+ν)为(x+u,y+ν)处像素点灰度值大小。
根据全微分公式可以得到:
I(x+u,y+ν)=I(x,y)+Ixu+Iyν+o(u2,ν2)
(21)
带入式(20)中得到
(22)
将上式改为矩阵形式,如下式所示
(23)
记:
(24)
M为2×2维矩阵,则式(23)可以化简为
(25)
设矩阵M的特征值为λ1、λ2,定义
R=min(λ1,λ2)
(26)
对函数R进行阈值处理,即
R>threshold
(27)
即可提取R的局部最大值。根据局部最大值R进行非极大值抑制,实现对角点的检测。
根据上述所述的原理,Shi-Tomasi算法对图像中所有的像素点进行检测,得到大量角点,但是多数角点并不是我们需要的,同时导致检测时间较长。为此对该算法进行改进,剔除不需要的角点,缩短检测时间。
具体主要是在计算响应函数之前,对图像中的像素点进行初步筛选,确定候选的角点。算法将检测区域内中心像素点与边缘像素点的灰度值进行比较,确定两者的相似度。若两者的灰度值之差在一个给定的范围之内,那么这两个像素点是相似的,反之,是不相似的。计算每个边缘像素点与中心像素点灰度值之差,可以得出检测区域内与中心像素点相似的个数n,根据n的值确定是否为候选角点。
通过该方法,可以将大量无关的像素点剔除,大大缩短后续程序所需要的时间,提高了算法的效率。具体算法步骤如下:
步骤1 设定图像(x,y)处的灰度值I(x,y),通过差分方程对每个像素点进行滤波,得到Ix、Iy,进而求出
以及IxIy。
步骤2 对
以及IxIy进行高斯滤波,消除图像中的孤立点,得到的结果作为矩阵M中的元素。
步骤3 确定候选角点。对窗口内边缘像素点与中心像素点灰度值进行比较,判断是否在所给出的阈值之内,得到相似像素点的个数,进而确定是否为待选角点。
步骤4 利用公式(26)计算像素点的响应函数R。
步骤5 进行非极大值限制,判断像素点是否存在角点。
4.2 回归分析
在前文的叙述中,平动分量利用3阶多项式模型描述即可,即
R=R0+a1t+a2t2/2+a3t3/6
(28)
由公式(2)可知多普勒频率fd与目标的径向速度νr正相关,即
fd∝νr
(29)
而νr=-dR/dt,因此,在时频曲线图曲线中的交点应该成抛物线分布。根据角点的参数,对上述的交点进行回归分析,得出平动分量的相关参数。
假设在一直角坐标系中,有n个点,其坐标分别为(x1,y1),(x2,y2),…,(xn,yn)。现在对这n个点进行k阶多项式拟合,即
f(x)=a0+a1x+a2x2+...+akxk
(30)
将上述点的横坐标代入k阶多项式中得
...
(31)
为了让拟合效果更好,我们需要使多项式计算出来的f(xi)与真实yi之间最小。这里可以利用下式进行评价:
(32)
即
(33)
此时,利用偏导求出最小值。下面将z分别对a0、a1、a2、…、ak求偏导,得到下面的式子。令式子均为0,求解可得到a0、a1、a2、…、ak的值。
...
(34)
化简整理得到如下多个方程式
...
(35)
将其转换成矩阵形式,令
(36)
(37)
则矩阵形式如下所示
XTXa=XTY
(38)
解得
a=(XTX)-1XTY
(39)
5 仿真实验
5.1 时频方法对检测效果的影响
假设雷达发射的信号载频为f=6 GHz,脉冲重复频率为PRF=600 Hz。锥体目标的质心到顶点的距离l1=2.7 m,到底面中心的距离l2=0.9 m,底面半径r=0.6 m。雷达视线与锥旋轴的夹角
进动角
锥旋频率ωc=4π。假设锥体目标距离雷达的初始距离R0=10 km,径向速度a1=-2 m/s,径向加速度a2=2 m/s2,2阶径向加速度a3=1 m/s3。假设信噪比为SNR=10 dB。根据前文所得的距离公式以及相关参数进行仿真。将结果与假设值对比,计算相对误差。若相对误差在可接受的范围之内,则算法是有效的,可以实现平动补偿。
利用短时傅里叶变换对信号进行分析,得到图4(a)。利用Gabor变换,对信号进行时频分析得到散射点时频曲线图,如图4(b)所示。利用Rihaczek分布,对信号进行时频分析得到散射点时频曲线图,如图4(c)所示。利用Page分布,对信号进行时频分析得到散射点时频曲线图,如图4(d)所示。
从图4(b)可以看出时频效果较差。这是由于在实际的临界采样情况下,窗函数不能构成标架,不能保证其时域和频域的紧支撑性能,无法反映信号在时频平面能量的分布[20]。从图4(c)、(d)可以看到,交叉项比较严重,时频曲线图中交点无法清晰反映出来,后续检测会产生较大误差。而根据图4(a)可以看出,对于短时傅里叶变换,交叉项的影响较小,可以较好提取出角点进行检测。因此本文选择短时傅里叶变换进行仿真实验。
图4(a)是利用短时傅里叶变换仿真的锥体目标在飞行的过程中三个散射点产生回波的时频曲线图,从图中我们可以看到是时频曲线图不是水平的,而是带有一定倾斜角度的,说明这里面存在着平动分量。同时还可以观察到,三条曲线有多个相交点,根据前文所述,这些交点只包含平动分量信息,因此可以利用这些交点进行平动分量的补偿。
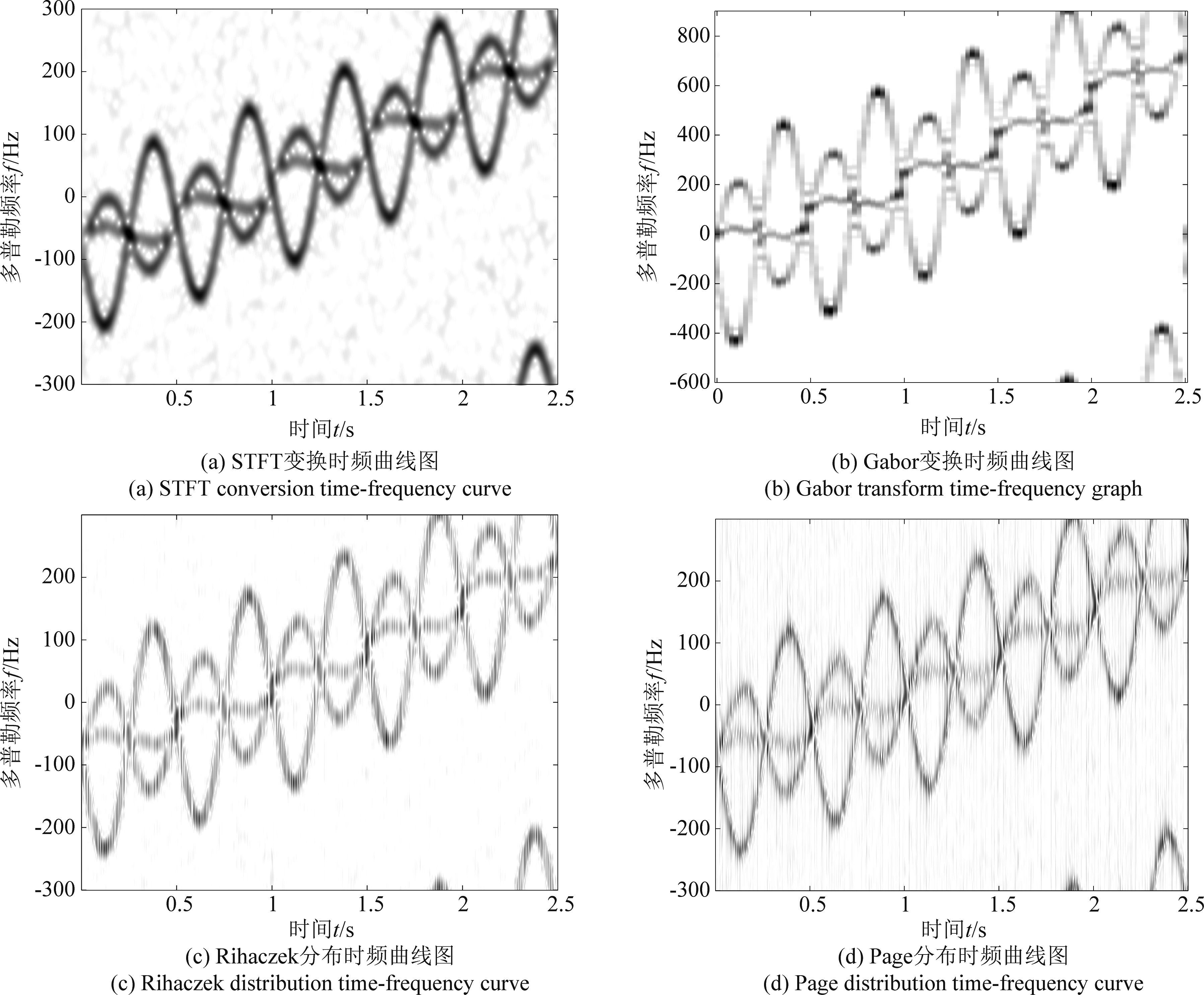
图4 散射点时频曲线图
Fig.4 Time-frequency curve of scattering points
采用高斯平滑滤波,对图4(a)进行平滑处理得到二值化图像,如图5所示。之后再对图5进行骨架抽取,如图6所示。
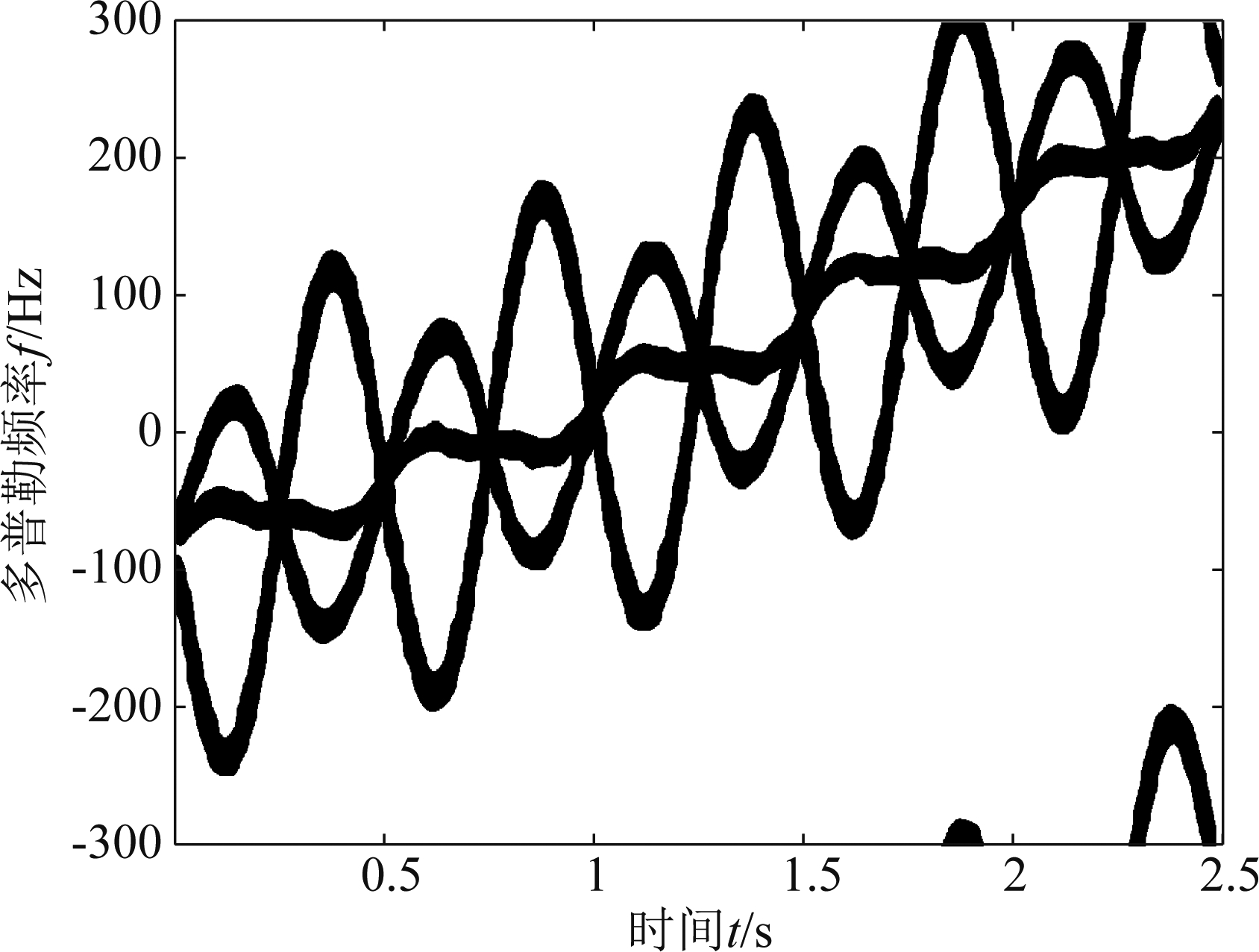
图5 二值化图像
Fig.5 Binarized image
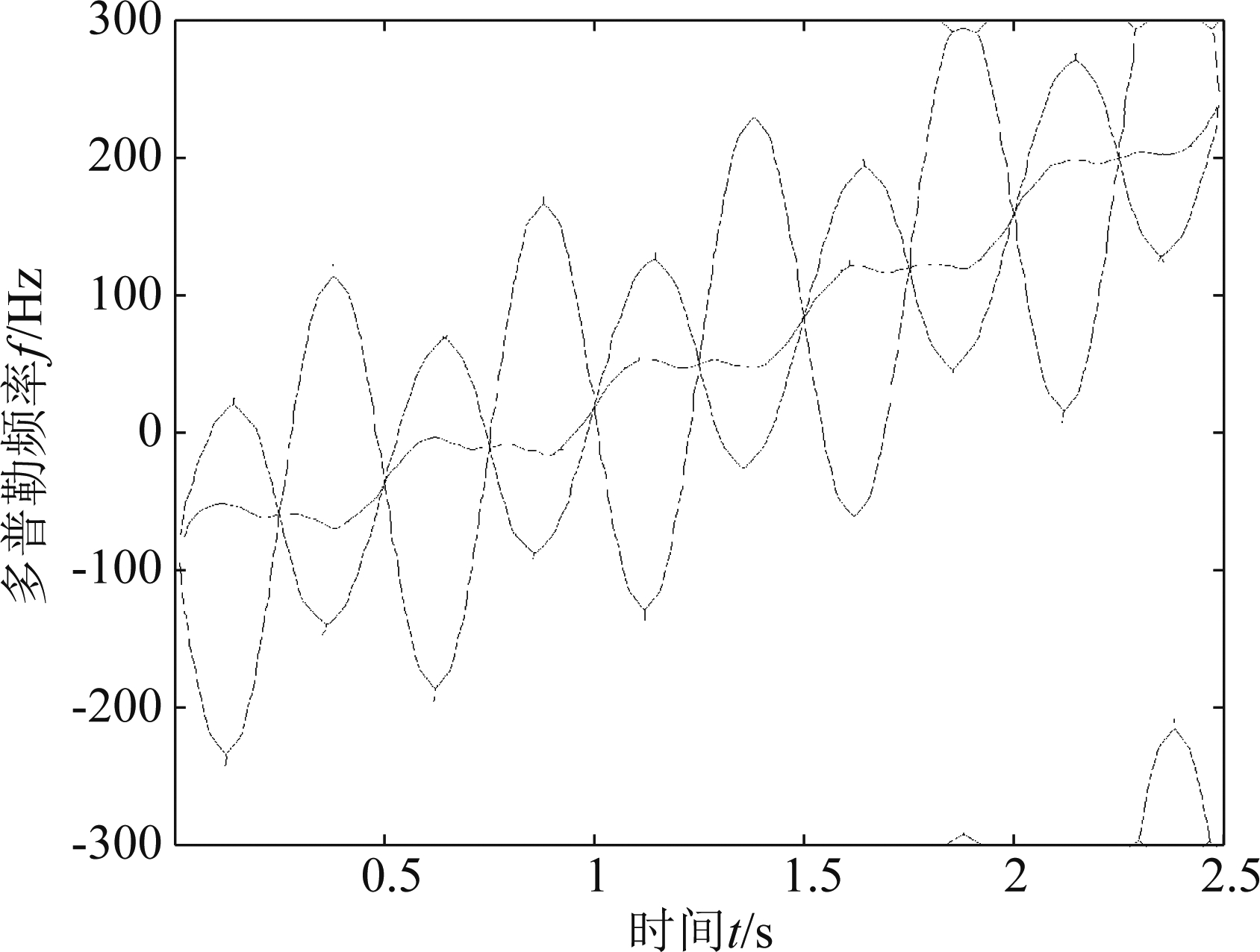
图6 骨架提取图像
Fig.6 Skeleton extraction image
根据上文所述的角点检测算法,对图6的时频曲线图进行角点检测,提取相关角点,如图7所示。观察图7,算法检测出大量的角点。利用2.1小节的改进方法对算法进行改进,剔除不需要的角点,得到新的角点分布图,如图8所示。通过观察,曲线有9个交点,其中第4个、第6个、第8个交点检测存在较大误差,其余6个交点均可通过算法准确检测出来,确定出相关交点的位置信息。由于交点只包含平动分量信息,根据所得的交点位置信息可以得出平动分量信息。根据图像行列数与时频图坐标对应关系,将确定的位置转化成时间-频率信息。图5～图8是进行一次仿真得到的仿真图。实验中进行多次蒙特卡罗仿真。通过实验条件仿真观察时频图,每个离散时间对应一个角点,这为利用多项式回归分析估计平动分量提供了可能。根据式(6)与式(39)可以估计得到径向速度a1=-2.0009 m/s,径向加速度a2=1.97915 m/s2,2阶径向加速度a3=0.9976 m/s3。对比假设的数据,计算相对误差分别为εa1=0.045%、εa2=1.0425%、εa3=0.24%。
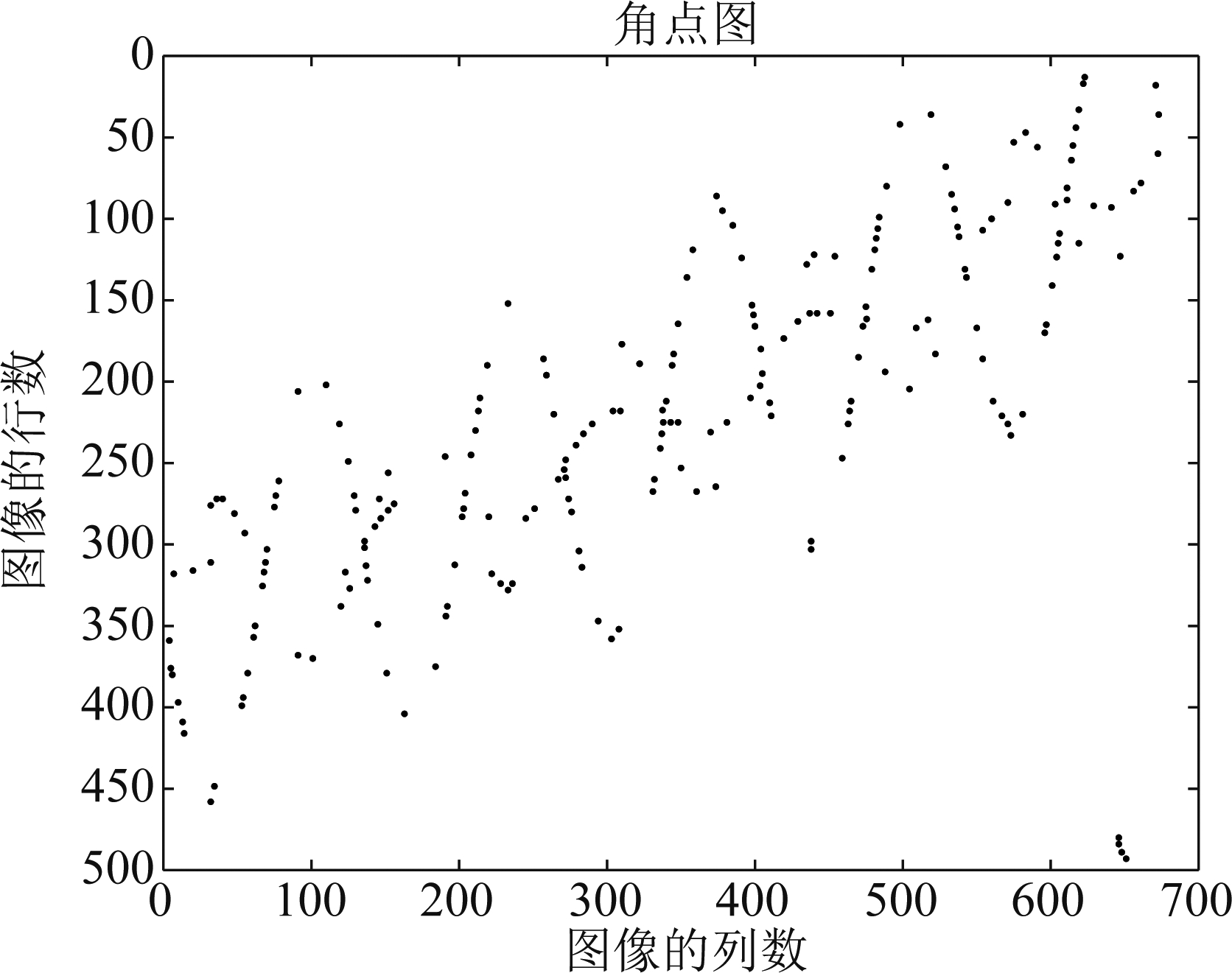
图7 角点图
Fig.7 Corner diagram
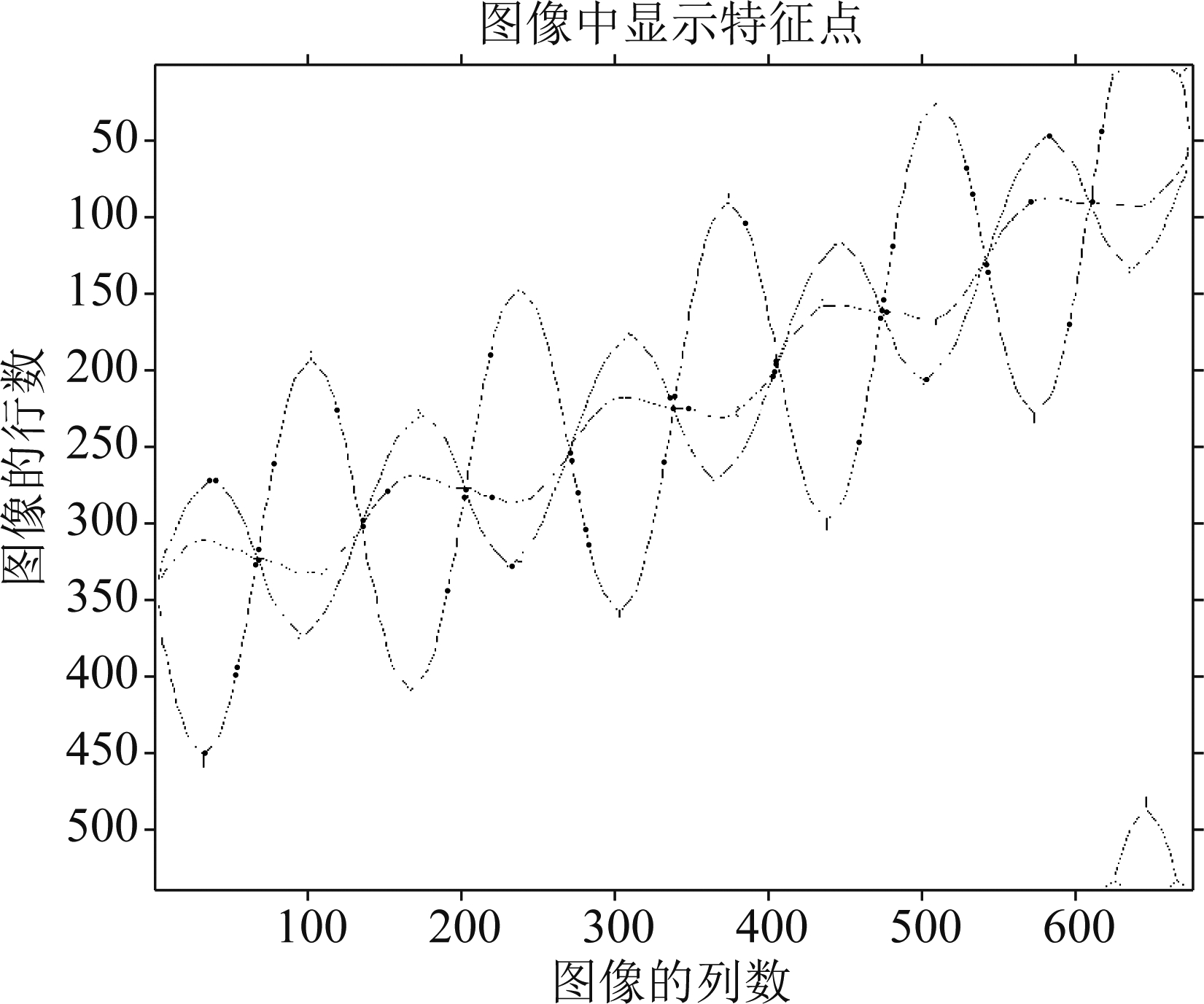
图8 图像中显示特征点
Fig.8 Feature points displayed in the image
同时,在进行提取的过程中,比较改进前后的Shi-Tomasi算法计算响应函数R以及确定角点所耗费时间。在改进之前,其所耗费的时间为0.728964 s,在改进之后,其所耗费的时间为0.022917 s。通过对比,可以看到改进之后的算法所需时间大约为原算法的3.14%,大大缩短了相关的计算时间,更有利于在实际中进行应用。
上述实验均是在同一台计算机上进行的,计算机的硬件配置参数:处理器Intel i5-10210U、内存16G、显卡型号MX250。
根据公式(6),减去估计出的平动分量,得到散射点的微动分量。图9为减去平动分量之后的锥体目标散射点的时频曲线图。根据图像所示,平动分量已经去掉,得到了较好的微动分量时频曲线图。验证了该算法的有效性。
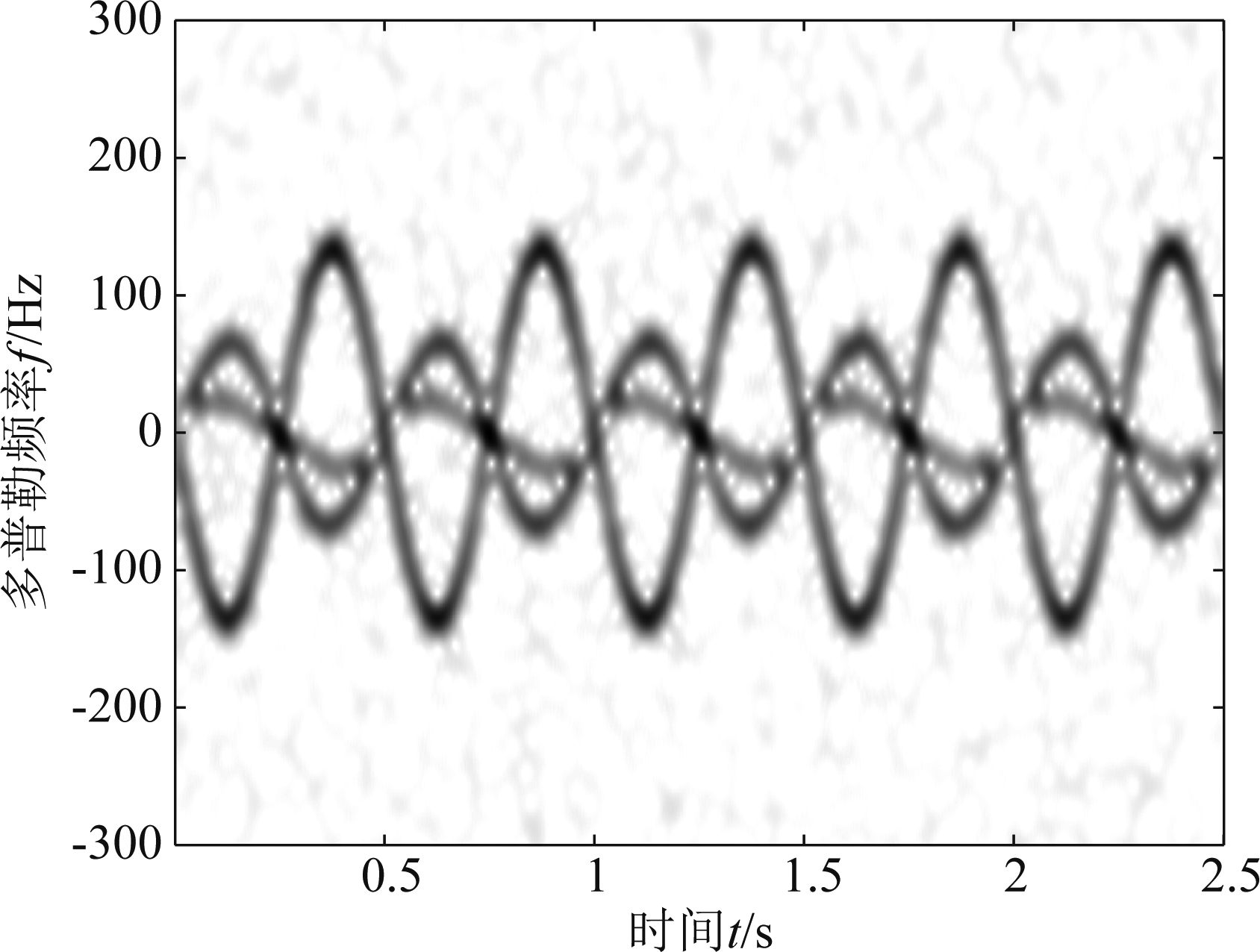
图9 平动补偿后的散射点时频曲线图
Fig.9 Time-frequency curve of scattering points after translation compensation
5.2 不同参数下算法的检测效果
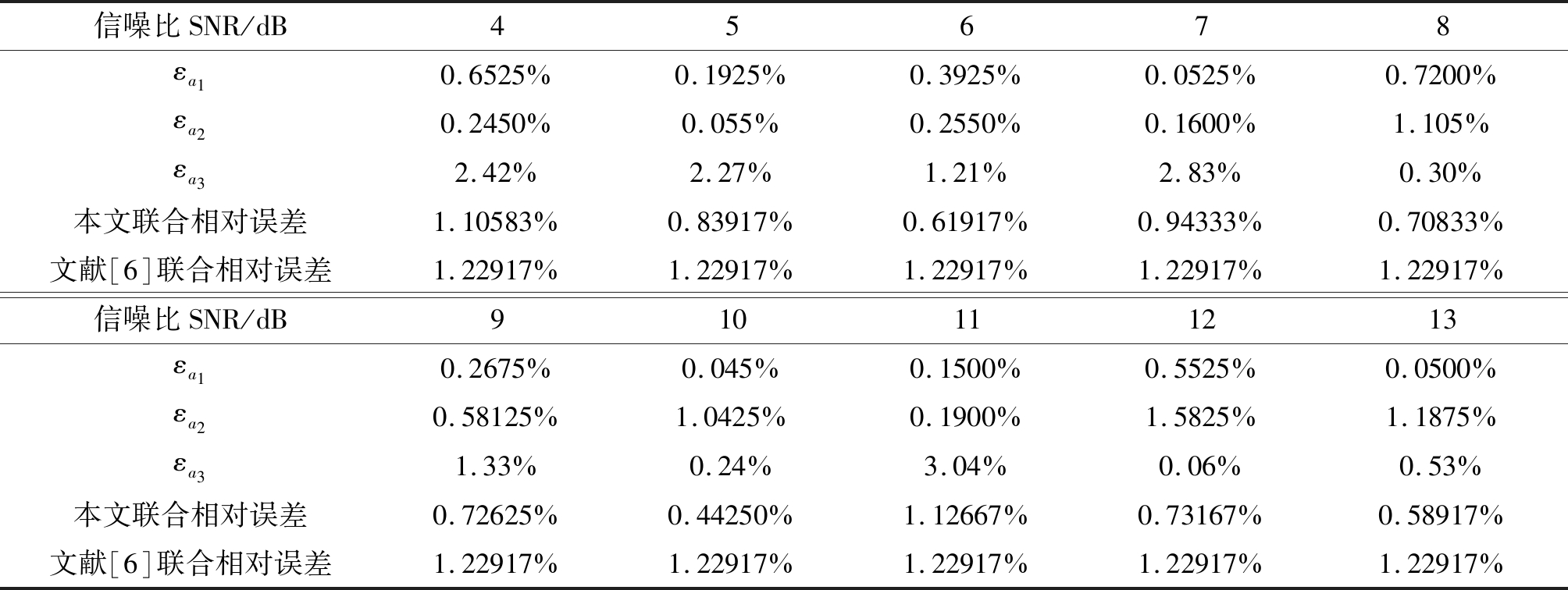
下面在不同信噪比下,对本文所提出的算法的检测效果进行进一步分析。接下来在不同的信噪比条件下进行多次蒙特卡罗仿真,其他仿真参数与上面设置一致。在不同的信噪比条件下仿真,每个离散时间对应一个角点,利用多项式拟合得到的仿真结果如表2所示。同时,对平动参数a1、a2、a3进行整体的误差分析,可以得到参数的联合相对误差,如表2所示。
表2 不同信噪比下的相对误差
Tab.2 Relative error under different signal-to-noise ratio
信噪比SNR/dB45678εa10.6525%0.1925%0.3925%0.0525%0.7200%εa20.2450%0.055%0.2550%0.1600%1.105%εa32.42%2.27%1.21%2.83%0.30%本文联合相对误差1.10583%0.83917%0.61917%0.94333%0.70833%文献[6]联合相对误差1.22917%1.22917%1.22917%1.22917%1.22917%信噪比SNR/dB910111213εa10.2675%0.045%0.1500%0.5525%0.0500%εa20.58125%1.0425%0.1900%1.5825%1.1875%εa31.33%0.24%3.04%0.06%0.53%本文联合相对误差0.72625%0.44250%1.12667%0.73167%0.58917%文献[6]联合相对误差1.22917%1.22917%1.22917%1.22917%1.22917%
根据表2所得到的数据可以看出,在不同的信噪比下,平动分量所产生的相对误差,基本保持稳定,因此该算法具有良好的鲁棒性。表中有极个别数据波动较大,可能是由于提取的角点偏差较大。
同时,相较于文献[6]的方法,可以看出本文所提的算法,参数估计的精度较好,补偿的效果更好。
针对不同的弹头特性及系统参数对图像灰度的影响,通过改变弹头的自旋频率以及雷达发射信号的脉冲重复频率进行仿真实验,其结果如表3、表4所示。
表3 不同自旋频率下的相对误差
Tab.3 Relative error at different spin frequencies
表4 不同脉冲重复频率下的相对误差
Tab.4 Relative error under different pulse repetition frequency
根据仿真实验结果可以得到,增大自旋频率以及脉冲重复频率可以提高实验结果的检测精度。
6 结论
弹道目标的雷达时频曲线图是由多个散射点叠加而成,但由于目标存在平动运动,因此为了实现对弹道目标的识别,分析相关特性,需要进行平动补偿。为此,本文提出了Shi-Tomasi角点检测算法,通过分析角点的特性对平动分量进行了补偿。仿真实验验证了该算法的有效性、鲁棒性。该算法实现了对图像的各向性进行检测,比较简单,同时又对算法进行了优化,缩短了运行时间,提高了在实际应用中的效率。
根据表2可以看出,由于提取的角点不精确,进而导致在估计平动补偿的相关参数时产生较大的误差。因此,接下来可以继续对算法进行改进,使提取的角点更加精确。表3针对不同的弹头特性对图像灰度的影响进行了仿真,随着自旋频率的增大,检测的点数随之增加,角点检测精度提高,误差变小。而表4针对系统参数对图像灰度的影响进行了仿真,随着脉冲重复频率的增大,时频效果更好,角点检测精度提高,误差变小。
在实际中,目标的散射点特性都比较复杂,同时在目标的飞行过程中,伴随着目标飞行的行程中,还存在大量的弹头碎片以及诱饵。因此,下一步,可以对在复杂散射点情况下对群目标的微动特性进行研究。
同时,对中段弹道目标进行平动补偿之后,下一步工作就是对得到的信号进行分离。通过对散射点时频曲线的研究,得到弹道目标的特性。
[1] 梁蕾. 洲际弹道导弹突防技术发展历程[J]. 飞航导弹, 2018(1): 33-37.
LIANG Lei. Development history of intercontinental ballistic missile penetration technology[J]. Aerodynamic Missile Journal, 2018(1): 33-37. (in Chinese)
[2] DODGE M. U.S.-Czech ballistic missile defense cooperation: Lessons learned and way forward for others[J]. Comparative Strategy, 2020, 39(3): 288-298.
[3] MENQ J Y, TUAN P C, LIU Tasheng. Discrete Markov ballistic missile defense system modeling[J]. European Journal of Operational Research, 2007, 178(2): 560-578.
[4] GAO Hongwei, XIE Lianggui, WEN Shuliang, et al. Micro-Doppler signature extraction from ballistic target with micro-motions[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 1969-1982.
[5] CHEN V C, LI F, HO S S, et al. Analysis of micro-Doppler signatures[J]. IEE Proceedings-Radar, Sonar and Navigation, 2003, 150(4): 271-276.
[6] 许旭光, 冯存前, 苏于童, 等. 基于高阶模糊函数的进动目标平动补偿[J]. 探测与控制学报, 2019, 41(1): 113-118.
XU Xuguang, FENG Cunqian, SU Yutong, et al. Translational motion compensation of precession target based on high-order ambiguity function[J]. Journal of Detection & Control, 2019, 41(1): 113-118.(in Chinese)
[7] 韩立珣, 许丹, 田波, 等. 基于Radon变换的弹道目标平动补偿[J]. 火力与指挥控制, 2019, 44(11): 16-19.
HAN Lixun, XU Dan, TIAN Bo, et al. Translational motion compensation of ballistic target based on radon transform[J]. Fire Control & Command Control, 2019, 44(11): 16-19.(in Chinese)
[8] 贺思三, 赵会宁, 张永顺. 基于延迟共轭相乘的弹道目标平动补偿[J]. 雷达学报, 2014, 3(5): 505-510.
HE Sisan, ZHAO Huining, ZHANG Yongshun. Translational motion compensation for ballistic targets based on delayed conjugated multiplication[J]. Journal of Radars, 2014, 3(5): 505-510.(in Chinese)
[9] 杨有春, 童宁宁, 冯存前, 等. 利用最强散射点信息的平动补偿与微多普勒提取[J]. 西安电子科技大学学报, 2012, 39(6): 147-153.
YANG Youchun, TONG Ningning, FENG Cunqian, et al. Translation compensation and micro-Doppler extraction by using the information on the strongest scatter[J]. Journal of Xidian University, 2012, 39(6): 147-153.(in Chinese)
[10] 束长勇, 黄沛霖, 姬金祖. 进动锥体目标平动补偿及微多普勒提取[J]. 系统工程与电子技术, 2016, 38(2): 259-264.
SHU Changyong, HUANG Peilin, JI Jinzu. Translation compensation and micro-Doppler extraction of the precessional cone target[J]. Systems Engineering and Electronics, 2016, 38(2): 259-264.(in Chinese)
[11] 朱思聪, 周德龙. 角点检测技术综述[J]. 计算机系统应用, 2020, 29(1): 22-28.
ZHU Sicong, ZHOU Delong. Review on image corner detection[J]. Computer Systems & Applications, 2020, 29(1): 22-28.(in Chinese)
[12] 雷腾, 刘进忙, 李松, 等. 弹道目标进动周期特征提取新方法[J]. 计算机工程与应用, 2013, 49(1): 265-270.
LEI Teng, LIU Jinmang, LI Song, et al. Novel micro-Doppler signature extraction method of ballistic midcourse target[J]. Computer Engineering and Applications, 2013, 49(1): 265-270.(in Chinese)
[13] MA Liang, LIU Jin, WANG Tao, et al. Micro-Doppler characteristics of sliding-type scattering center on rotationally symmetric target[J]. Science China Information Sciences, 2011, 54(9): 1957-1967.
[14] 马梁. 弹道中段目标微动特性及综合识别方法[D]. 长沙: 国防科学技术大学, 2011.
MA Liang. The micro-motion characteristic and combining classification of ballistic target[D]. Changsha: National University of Defense Technology, 2011. (in Chinese)
[15] 韩立珣, 田波, 冯存前, 等. 进动弹道目标平动补偿与分离[J]. 北京航空航天大学学报, 2019, 45(7): 1459-1466.
HAN Lixun, TIAN Bo, FENG Cunqian, et al. Translation compensation and resolution of ballistic target with precession[J]. Journal of Beijing University of Aeronautics and Astronautics, 2019, 45(7): 1459-1466.(in Chinese)
[16] 赵双, 鲁卫红, 冯存前, 等. 多视角微多普勒融合的进动目标特征提取[J]. 信号处理, 2016, 32(3): 296-303.
ZHAO Shuang, LU Weihong, FENG Cunqian, et al. Feature extraction of precession targets based on multi-aspect micro-Doppler fusion[J]. Journal of Signal Processing, 2016, 32(3): 296-303.(in Chinese)
[17] 丁鹭飞, 耿富录, 陈建春. 雷达原理[M]. 第5版. 北京: 电子工业出版社, 2014: 2- 4.
DING Lufei, GENG Fulu, CHEN Jianchun. Radar principles[M]. 5th Edition. Beijing: Publishing House of Electronics Industry, 2014: 2- 4.(in Chinese)
[18] IAN G C, FRANK H W. Digital processing of synthetic aperture radar data: algorithms and implementation[M]. [S.l.]: Artech House, 2004: 93-98.
[19] SAMIEE K, KOV
CS P, GABBOUJ M. Epileptic seizure classification of EEG time-series using rational discrete short-time Fourier transform[J]. IEEE Transactions on Biomedical Engineering, 2015, 62(2): 541-552.
[20] 张群, 罗迎. 雷达目标微多普勒效应[M]. 北京: 国防工业出版社, 2013: 99-106.
ZHANG Qun, LUO Ying. Micro-Doppler effect of radar targets[M]. Beijing: National Defense Industry Press, 2013: 99-106.(in Chinese)
[21] COHEN L. Generalized phase-space distribution functions[J]. Journal of Mathematical Physics, 1966, 7(5): 781-786.
[22] 葛哲学, 陈仲生. Matlab时频分析技术及其应用[M]. 北京: 人民邮电出版社, 2006: 82-90.
GE Zhexue, CHEN Zhongsheng. Matlab Time-Frequency Analysis Technology and Its Application[M]. Beijing: People Post Press, 2006: 82-90.(in Chinese)
[23] 王军华. 基于单目视觉的人形机器人避障策略研究[D]. 合肥: 中国科学技术大学, 2015.
WANG Junhua. A study on obstacle avoidance strategy for humanoid robot based on monocular vision[D]. Hefei: University of Science and Technology of China, 2015. (in Chinese)
[24] 关静, 楼飞. 基于角点检测的规则几何图形识别算法研究[J]. 现代信息科技, 2019, 3(24): 71-73.
GUAN Jing, LOU Fei. Research on recognition algorithm of regular geometry based on corner detection[J]. Modern Information Technology, 2019, 3(24): 71-73.(in Chinese)
