1 引言
随着遥感技术的发展,高光谱图像(Hyperspectral image,HSI)因其具有高光谱分辨率及丰富光谱信息的特点而广泛应用,如目标检测、环境监测、农林业、军事等。分类是高光谱遥感图像研究中的一个热点内容,学者提出了许多的分类方法,如随机森林[1-2]、支持向量机[3- 4]、神经网络[5-7]、稀疏表示[8]等。
稀疏表示通过较少训练样本的线性组合来表达大量的待测样本,最后通过重构残差对待测样本进行分类判别,目前稀疏表示已经广泛应用于HSI分类。文献[9]将稀疏表示应用于HSI分类,考虑到同质区域的存在,相应提出了联合稀疏表示的方法,假设相邻像元具有共同的稀疏模式,即位于同一邻域内的相邻像元由相同的训练样本稀疏表示,但稀疏向量不一定相同;文献[10]根据待测中心像元与邻域像元的结构相似度给各个邻域像元赋予相应的权重,构建加权联合稀疏表示;固定的邻域窗口存在一定的局限性,不能完全反映空间信息,文献[11]采用核函数度量待测像元与邻域像元间的相似性,使联合稀疏表示的邻域窗口自适应。另外文献[12-14]通过提取空间-光谱特征利用空间信息用于稀疏表示HSI分类。以上文献都在一定程度上利用了空间信息提升分类精度,但是,基于稀疏表示的HSI分类精度一定程度上依赖于训练样本的质量和数量,训练样本越多,字典包含的地物特征越丰富,训练样本的获取主要依靠专家人为标记,成本昂贵,在实际分类中,存在因训练样本量少而分类精度低的问题。
针对上述问题,本文提出了基于字典优化的联合稀疏表示高光谱图像分类(joint sparse representation hyperspectral image classification based on dictionary optimization, DO-JSRC)算法。结合空间信息将HSI划分为多个子集;利用已知标签信息的训练样本标记子集中可能成为训练样本的像元,组成备选集;通过光谱相似性准则筛选备选集形成优化字典。通过优化字典方式扩大了训练样本的数量,用于联合稀疏表示提高HSI分类精度。此外,HSI的成像机制使它包含了数百个连续波段的光谱信息,高维数据在带来丰富信息的同时,也使得在处理数据时计算量大幅度增加;连续波段间的信息可能会造成数据冗余,降低数据分析效率。为了降低高光谱数据维度的同时保留有用的光谱信息,相应的提出了许多基于特征提取[15]和波段选择[16-17]的降维方法。由于噪声波段与其他波段间的差异较大,基于聚类的波段选择方法通常对噪声波段比较敏感,容易使噪声波段单独聚类,影响选择结果。因此,本文采取基于层次聚类的波段选择方法,利用自适应距离计算方式改善噪声对波段选择的影响。
2 联合稀疏表示
本文的HSI分类是基于联合稀疏表示的分类方法,联合稀疏表示可以结合邻域像元的空间信息,提升HSI分类精度,其过程如下:
原始高光谱数据集X=[x1 x2 ... xn ... xN]∈RB×N表示该HSI包含N个像元,每个像元由B个光谱波段组成。若HSI由C个地物类别组成,已知地物标签信息的训练样本组成的字典可以表示为D=[D1 ... D2 ... Dc ... DC],第c类地物包含Nc个训练样本,则属于第c类地物的训练样本集合为![]() 在联合稀疏表示中,待测像元x1与其邻域像元集合X1=[x1 x2 ... xl]可以构建为:
在联合稀疏表示中,待测像元x1与其邻域像元集合X1=[x1 x2 ... xl]可以构建为:
X1=[x1 x2 ... xl]=[Da1 Da2 ... Dal]=DS
(1)
式(1)中的al表示对应像元xl的稀疏向量,al中元素只有少数非0项,S为稀疏向量组成的稀疏矩阵。
待测像元x1可以通过稀疏矩阵和字典进行重建,联合稀疏表示重建可表示为:
S=arg min ‖S‖row,0 s.t. DS=X1
(2)
‖S‖row,0表示稀疏矩阵S的非零行行数。为了解决式(2)中非确定性多项式的问题,许多学者对此进行了研究并提出解决方案,本文采用文献[9]提出的同时正交匹配追踪(simultaneous orthogonal matching pursuit, SOMP)算法。得到稀疏矩阵后重建待测像元可得到重构残差,则使用第c类字典得到稀疏重构残差可以表示为:
(3)
其中,‖·‖F表示Frobenius范数,![]() 表示第c类重构原子对应的稀疏矩阵。将待测像元的标签类别归属为重构残差最小的类,即
表示第c类重构原子对应的稀疏矩阵。将待测像元的标签类别归属为重构残差最小的类,即
(4)
3 基于字典优化的联合稀疏表示高光谱图像分类
本文提出基于字典优化的联合稀疏表示高光谱图像分类方法改善由于训练样本少而分类精度低的问题。考虑到HSI数据维度高,存在冗余,在字典优化前采用层次聚类的波段选择对原始HSI数据降维。整体算法框架如图1所示。

图1 DO-JSRC算法框架
Fig.1 DO-JSRC algorithm framework
3.1 波段选择
本文利用层次聚类的方式实现波段选择,用于HSI数据降维。层次聚类采用自下而上的方式构建波段层次,可将HSI的波段划分为簇数量Ncluster∈(1, 2, ...,B)任意的多个波段簇,将相似度高的波段聚类成簇,各个簇之间的波段差异较大。在每个簇内选取最具代表性的波段形成新的高光谱数据,从而降低HSI维度。
本文基于层次聚类的波段选择主要分为三个步骤:相互近邻搜索、合并相邻簇、选择波段。对于原始HSI数据处理如下:
用无向图G=(V,E)来表示HSI数据,其中顶点V=[b1 b2 ... bB]∈RN×B表示光谱波段,这里将每个波段看作一棵树。考虑HSI光谱波段的连续性,相邻波段间联系紧密、相似性大的特点,边es表示第s个簇和第s+1个簇之间的相似度量,不计不相邻簇之间的边,所以,边的集合可表示为E=[e1,e2, ...,es, ...,eS],S∈[1,B-1],第一个簇和最后一个簇形成的顶点只有一条与相邻簇的边,其他簇均有两条边,如图2所示。
图2 高光谱图像的无向图
Fig.2 Undirected image of hyperspectral image
(1)相互近邻搜索
在聚类过程中引入相互近邻的概念,假设存在4个相邻簇s-1、s、s+1、s+2之间的三条边es-1、es、es+1,若同时满足es<es-1和es<es+1,则第s个簇和第s+1个簇成为相互近邻。
(2)合并相邻簇
在一次合并过程中,若存在相互近邻簇,满足合并条件则按照边从小到大合并两个相互近邻簇;若不存在相互近邻簇,满足合并条件则合并边最小的两个簇。
将聚类过程中某次合并形成的S个簇表示为C=[C1 C2 ... Cs ... CS],其中CS中包含ns(1≤ns≤B)个波段,由式(5)更新第s个簇的聚类中心。欧式距离是度量两个变量之间差异的基本度量,通过式(6)计算第s个簇和第s+1个簇之间的距离。
(5)
(6)
式(5)中![]() 表示第s个簇中的第i个波段。
表示第s个簇中的第i个波段。
考虑到波段中可能存在噪声的情况,只利用欧式距离可能使噪声波段单独形成一个簇,因为噪声波段通常与相邻波段差距较大,为此提出了一种自适应距离计算方式。在第s个簇和第s+1个簇之间的距离计算过程中引入内类散度矩阵,将Cs与Cs+1包含的波段视为同一个类,类中心可用式(7)得到,并通过式(8)计算类内离散度,则第s个簇和第s+1个簇之间的自适应距离定义为式(9)。类内散度值越大,两个簇形成的类越离散,波段间相似性越低,式(9)将簇包含的波段数加入计算是为了改善噪声单独成簇的问题。
(7)
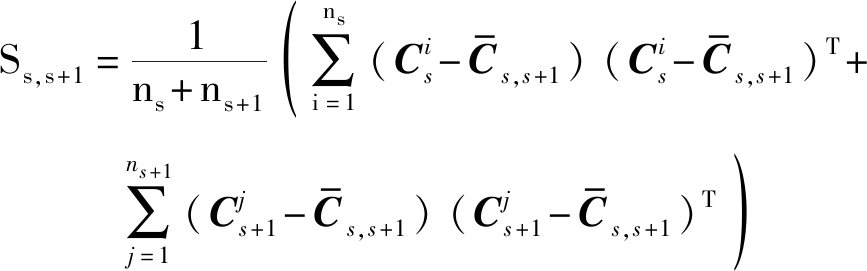
(8)
es=ds,s+1×Ss,s+1×ns×ns+1
(9)
上述相互近邻搜索和合并相邻簇是基于层次聚类思想对HSI数据处理的过程,HSI层次聚类流程图如图3所示。
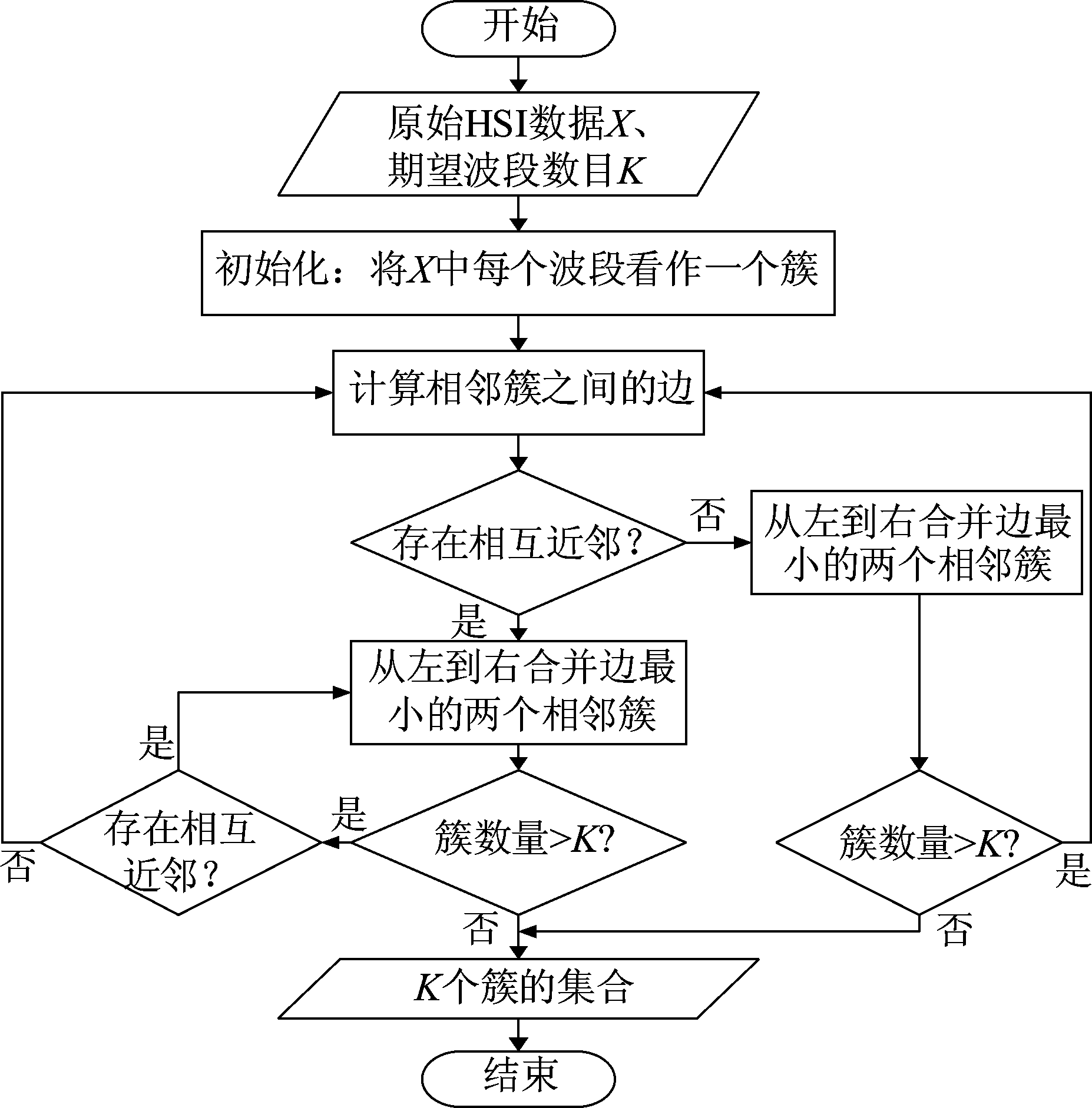
图3 HSI层次聚类流程图
Fig.3 HSI Hierarchical clustering flowchart
(3)选择波段
经过层次聚类将B个波段划分为K个簇,每个簇内的波段相似性较高,可能存在冗余,从每个簇中选择最具代表性的波段组成期望波段子集,本文采取基于排序的方法从每个簇中选取信息量最大的波段。波段的信息量可以通过峰度度量,对于任意波段b:
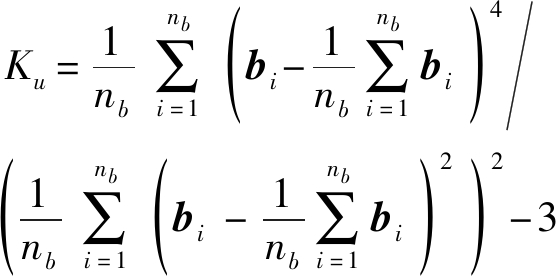
(10)
式(10)中Ku表示波段b的峰度,峰度越大,波段数据越偏离正态分布,波段包含的信息量越大。
基于层次聚类的波段选择具体过程如表1所示。
表1 基于层次聚类的波段选择
Tab.1 Band selection based on hierarchical clustering

算法1 基于层次聚类的波段选择1.输入:原始HSI数据X=[x1x2...xn...xN]∈RB×N,期望选取波段数目K。2.初始化:将高光谱图像中的每个波段看作一个簇,C=XT=[C1C2...Cs...CS]∈RN×B,S=B。3.当形成簇数量S>K时,执行以下步骤:步骤1 根据式(9)计算得到E=[e1,e2,...,es, ...,eS],S∈[1,B-1],并执行相互近邻搜索;步骤2 合并相邻簇If 存在Num个相互近邻 While Num 从左到右合并相互近邻中边e最小的两个簇,簇数量S减一,Num减一; If S=K 终止聚类; End End 更新C,返回步骤1;EndIf 不存在相互近邻 从左到右合并E中边e最小的两个簇 If S=K 终止聚类; End 更新C,返回步骤1;End4.当聚类结束后,得到聚类结果C=[C1C2...Ck...CK],根据公式(10)计算簇中每个波段的信息量,选择信息量最大的波段组成期望波段集。5.输出:波段选择后的HSI数据XBS=[x1x2...xn...xN]∈RK×N。
3.2 字典优化
为了解决训练样本量少的问题,本文提出了相应的字典优化方案,主要分为以下三个步骤:
(1)第一步:通过聚类利用HSI中每个像元的光谱信息和像元间的空间信息,将波段选择后的HSI数据集XBS拆分成多个子集,使每个子集自适应的包含一定数量的像元。其中,每个像元与聚类中心间的距离计算公式(11)和聚类中心更新公式(12)如下:
像元xi和第t个聚类中心xCt的空间坐标分别表示为![]() 和
和![]() 当xi位于聚类中心xCt的搜索范围内时它们之间的距离定义为:
当xi位于聚类中心xCt的搜索范围内时它们之间的距离定义为:
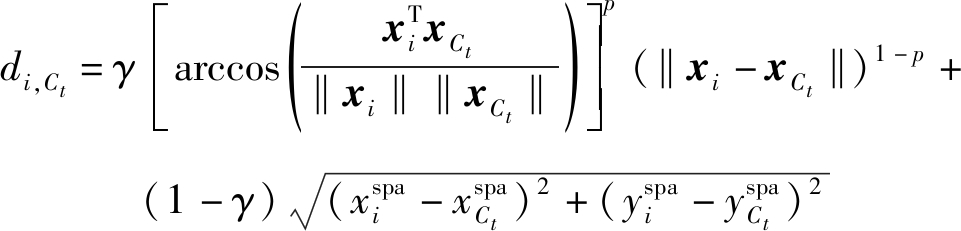
(11)
式(11)中,p用于平衡光谱角距离和欧式距离,γ用于平衡光谱信息和空间信息。
(12)
式(12)中,Xt表示第t个子集,NCt表示该子集包含的像元数量。
(2)第二步:利用已知标签信息的训练样本标记子集内可能成为训练样本的像元,形成训练样本备选集。
(3)第三步:通过光谱相似性准则筛选备选集形成优化字典。具体实现方法如表2所示。
表2 结合聚类的字典优化
Tab.2 Dictionary optimization combined with clustering

∑1。 2)计算Ac中每一个像元xAic与训练样本聚类中心的相似度qc(i)=exp -‖xAic-d-c‖2δ2()。 3)设置阈值η,若qc(i)>η,将备选集合Ac中的像元xAic加入第c类训练样本组成的字典集合形成新的字典D′。End6.输出:优化后的字典D′=[D′1D′2...D′c...D′C]∈RK×M。
3.3 基于字典优化的联合稀疏表示高光谱图像分类
为了减少HSI数据冗余,本文采用基于层次聚类进行波段选择降低数据维度,将处理后的HSI数据用于后续的分类;由于稀疏表示的分类方法依赖于训练样本,本文提出字典优化改善训练样本少而分类精度低的问题;最后,将字典优化后得到训练字典用于联合稀疏表示,对HSI进行稀疏重构,判断HSI中每个像元所属地物类别,得到分类结果。具体实现过程如表3所示。
表3 DO-JSRC算法
Tab.3 DO-JSRC algorithm

算法3 DO-JSRC算法1.输入:原始HSI数据X=[x1x2...xn...xN]∈RB×N,期望选取波段数目K,聚类数量T,稀疏度K0,选取邻域阈值η1和η2。2.通过算法1的波段选择得到XBS=[x1x2...xn...xN]∈RK×N。3.初始化:从XBS中随机选取一定数量的像元组成的字典D=[D1...D2...Dc...DC],将余下的像元组成测试集Test,稀疏像元索引集Λ0=ϕ,迭代记数q=1。4.算法2利用已知训练样本标记未知像元得到优化后的字典D′=[D′1D′2...D′c...D′C]∈RK×M。5.For 待测像元y∈Test1)根据K-JSRC算法中邻域的选取方式找到待测像元的邻域组成集合Y=[yy1y2...yNn]∈RK×Nn, R0=Y。
续表3

4 实验分析
本次实验仿真条件:电脑的运行内存8 GB、主频3 GHz、处理器为Inter(R)Core(TM)i5- 8500,仿真平台为MATLAB R2014a。通过Indian Pines数据集和Pavia University数据集验证本文提出的基于字典更新的联合稀疏表示高光谱图像分类方法的分类效果,体现分类性能的评价指标有:总体分类精度(Overall Accuracy, OA)、平均分类准确率(Average accuracy,AA)和Kappa系数。将本文提出的算法DO-JSRC与SD-JSRC[18]、K-JSRC[11]、CODL[19]和cdSRC[20]四个算法进行对比。
4.1 数据集
Indian Pines数据集:该HSI数据包含145×145个像元,200个波段,由16个类别的地物组成。本文主要选取其中9个类别的地物进行实验仿真,它们分别为Buildings-Grass-Trees-Drives、Corn-Mintill、Grass-Pasture、Grass-Trees、Hay-Windrowed、Wheat、Soybean-Mintill、Soybean-Clean、Woods,总共包含7425个像元,该地物分布如图4所示。

图 4 Indian Pines地物分布
Fig.4 Indian Pines feature distribution
Pavia University数据集:该数据集包含610×340个像元,除去噪声波段剩余103个波段,共包含9类地物,分别为Asphalt、Gravel、Bitumen、Meadows、Trees、Painted metal sheets、Bare Soil、Self-Blocking Bricks、Shadows。
4.2 参数设置
采用基于稀疏表示的分类方法在仿真实验时,若每一类字典原子的个数Nclass≥10,则将稀疏度设置为K0=10,若Nclass≤10,则K0=Nclass。SD-JSRC算法的参数设置参照文献[18],其中α=0.96。参照文献[11],K-JSRC算法采用余弦型指数核函数,相关参数设置为:![]() 算法的参数设置参照文献[19],其中λ=5和β=0.5。根据文献[20]将cdSRC算法中λ设置为0.001。
算法的参数设置参照文献[19],其中λ=5和β=0.5。根据文献[20]将cdSRC算法中λ设置为0.001。
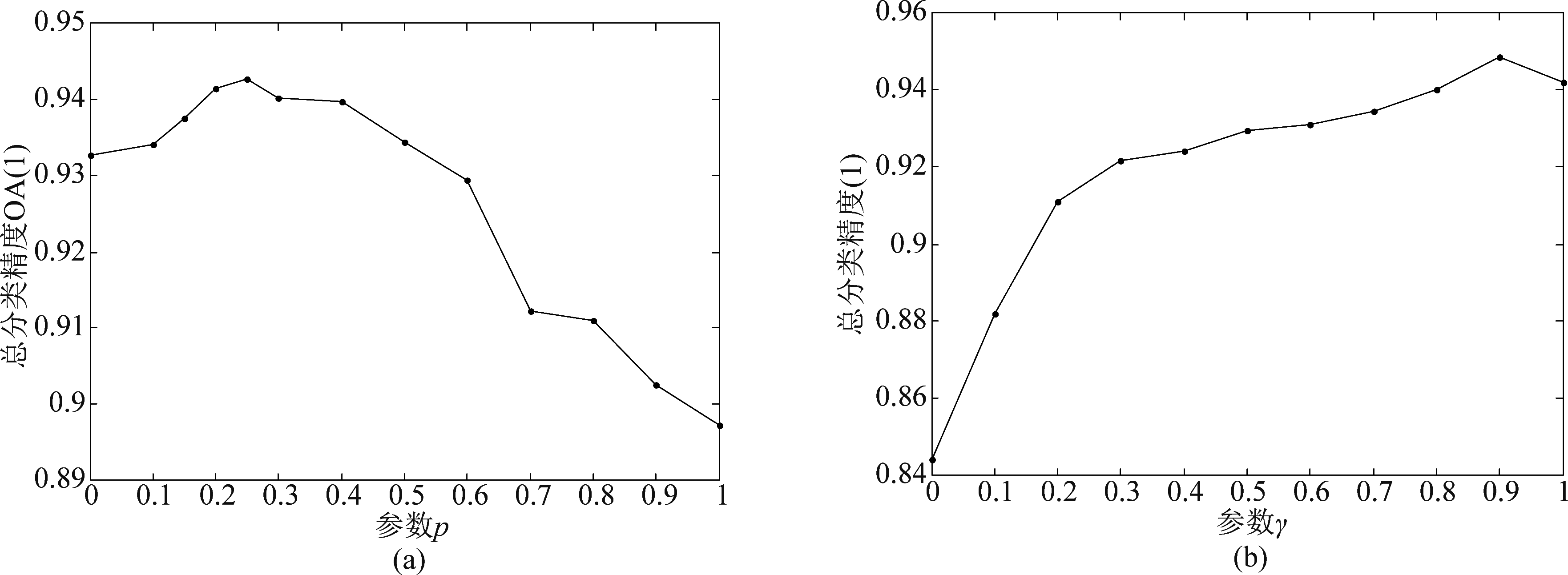
图5 Indian Pines数据集参数p、γ对总分类精度的影响
Fig.5 The influence of Indian Pines data set parameters p and γ on the total classification accuracy
本文提出算法的相关参数设置:字典优化中设置聚类迭代次数S=10。在Indian Pines数据集仿真实验时,固定平衡空间信息与光谱信息的参数γ=1,如图5所示,依据光谱角距离和欧式距离间的平衡参数p对总体分类精度影响,选定参数p=0.25;固定参数p=0.25,如图5所示,依据参数γ对总体分类精度影响,选定参数γ=0.9,两次实验中训练样本数目均为30,子集个数设置为T=2500。
图6展示了字典优化中不同子集数量时的总分类精度,将后续仿真实验中Indian Pines数据集和Pavia University数据集的子集个数设置为T=2000和T=20000。在基于层次聚类的波段选择方法中期望选取波段数目K对HSI分类的影响可通过总分类精度来验证,根据图7(a)选定Indian Pines数据集中基于层次聚类的波段选择中的波段数量为K=60,根据图7(b)选定Pavia University数据集中期望波段数K=40,两个数据集的训练样本均为10。
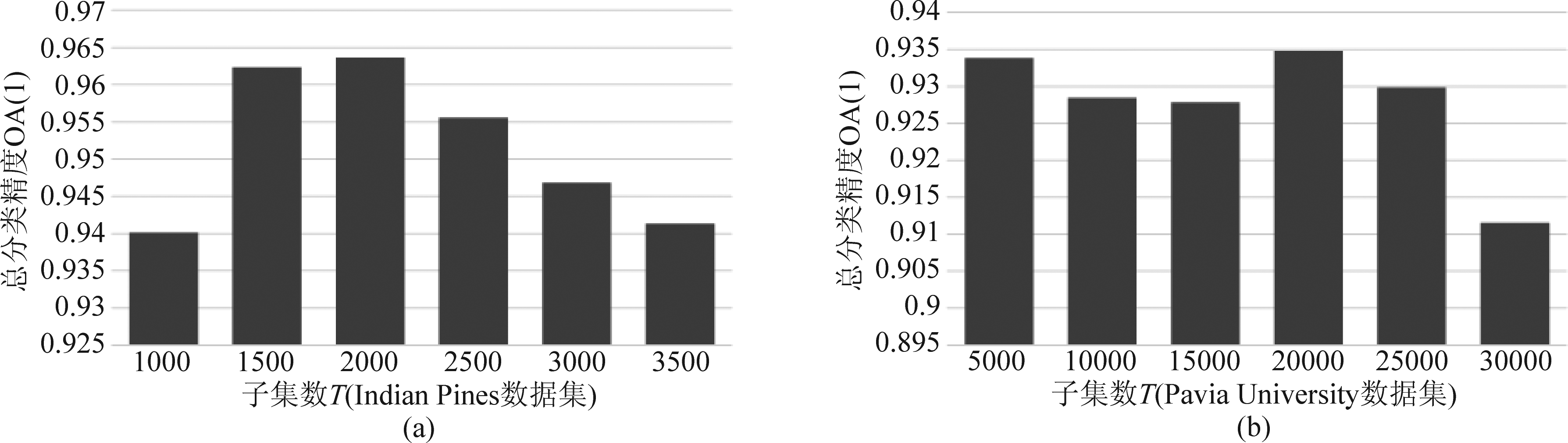
图6 字典优化中子集数量对总分类精度的影响
Fig.6 The impact of the number of subsets in dictionary optimization on the total classification accuracy
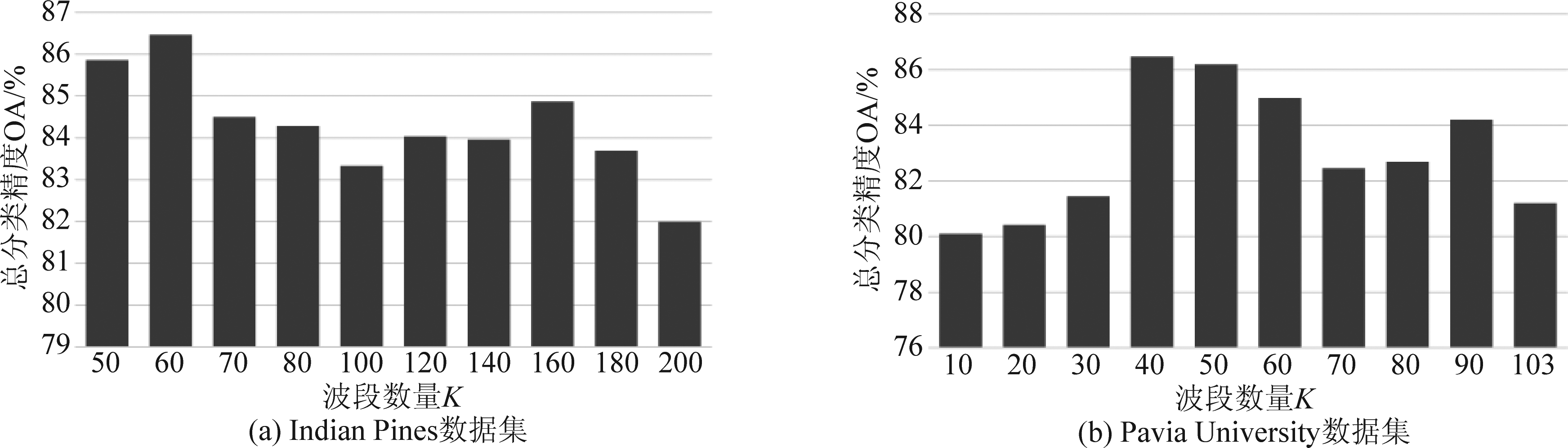
图7 波段数量对分类效果的影响
Fig.7 The influence of the number of bands in the Indian Pines data set on the classification effect
4.3 仿真分析4.3.1 Indian Pines数据集
仿真实验中,通过选取不同数量的训练样本组成字典对比几个算法的分类效果,如表4所示,选取1、5、10、20、30、50、100、200八种不同原子个数的像元作为训练样本,对应剩余地物像元作为测试样本,对比各个算法的分类效果。由于训练样本的选取是随机的,不同训练样本的样本质量不同会影响分类效果,因此本文的实验结果均是重复10次实验并对结果取平均值。将表4中的数据绘制成图8所示的折线图,可以更加直观地展示不同字典原子对各个分类算法的影响,以及对比各个算法间的分类效果。使用不同的灰度值表示各个地物类别,生成对应的假色图像,图9是选取30个类字典原子时各个算法的分类结果。
从图8可以清晰地看出每个算法的总分类精度均随着字典原子个数的增加而提高,类字典原子个数从1个增加30个的过程中,各个算法的总分类精度的增幅较大,而后平缓。
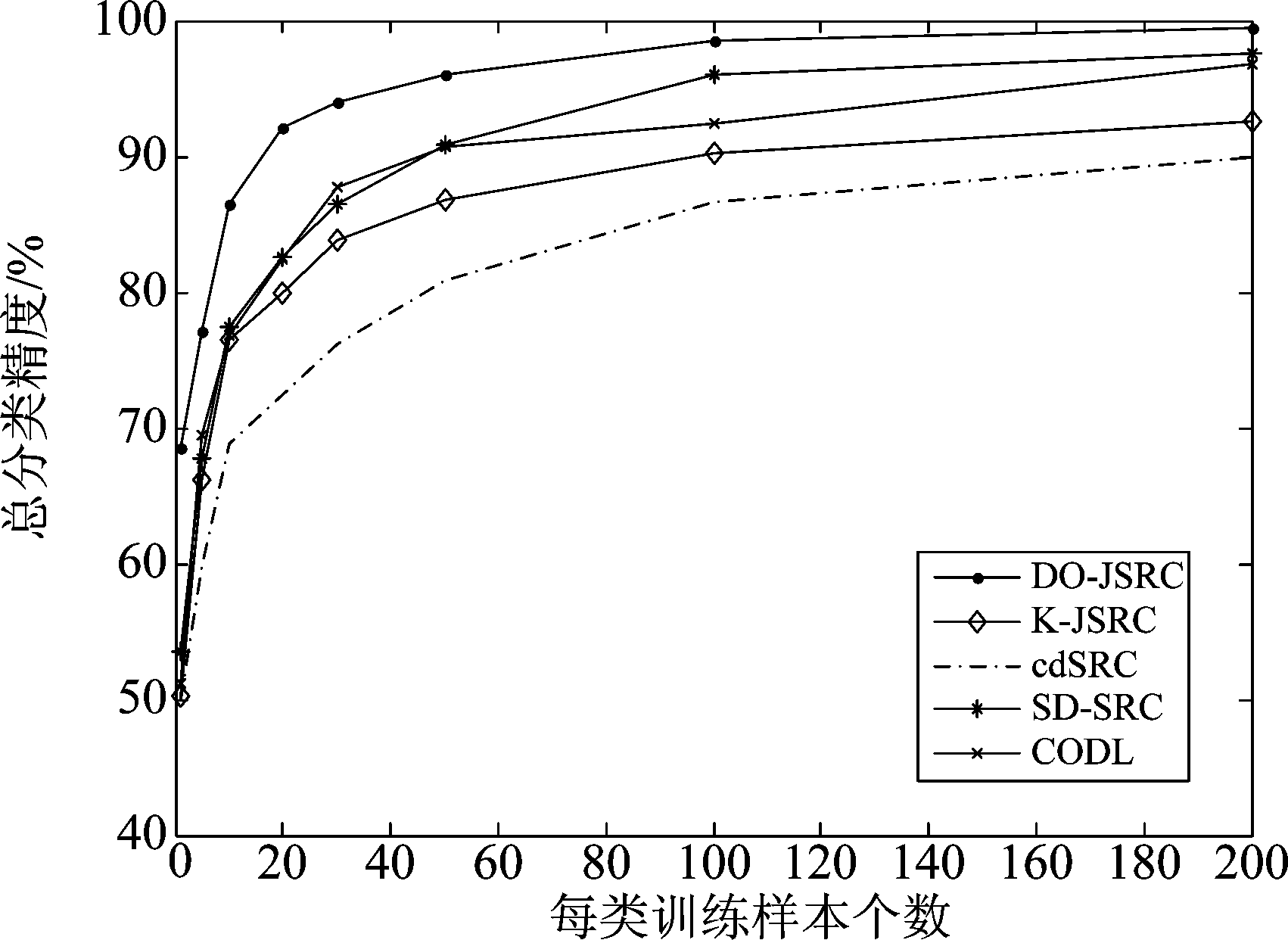
图8 Indian Pines 9类地物总分类精度
Fig.8 The total classification accuracy of
Indian Pines 9 features
在类字典原子个数为1时,本文算法的总分类精度可以达到68.58%,相较于SD-JSRC、K-JSRC、CODL、cdSRC算法分别高出15.07%、18.38%、17.34%、18.71%,当类字典原子个数为5时,相较于SD-JSRC、K-JSRC、CODL、cdSRC算法分别高出9.35%、10.91%、7.71%、17.35%,当类字典原子个数达到10时,本文算法的总分类精度达到86.47%。从表4实验仿真数据可以看出本文提出算法在已知地物类别的训练样本数量较少时也能够达到较好的分类效果。
图9展示了类字典原子个数为30时各个算法的分类效果,从图中可以看出cdSRC算法每个类都存在错分的现象,K-JSRC、CODL和SD-JSRC算法存在分类正确的类。而本文所提出算法能够完全正确分类的地物类别相较于K-JSRC、CODL和SD-JSRC进一步提升,这里完全正确分类的地物类别有3类,可以看到本文算法的分类效果与标准地物分类更加接近。
表4 Indian Pines总体分类精度(%)
Tab.4 Overall classification accuracy of Indian Pines (%)
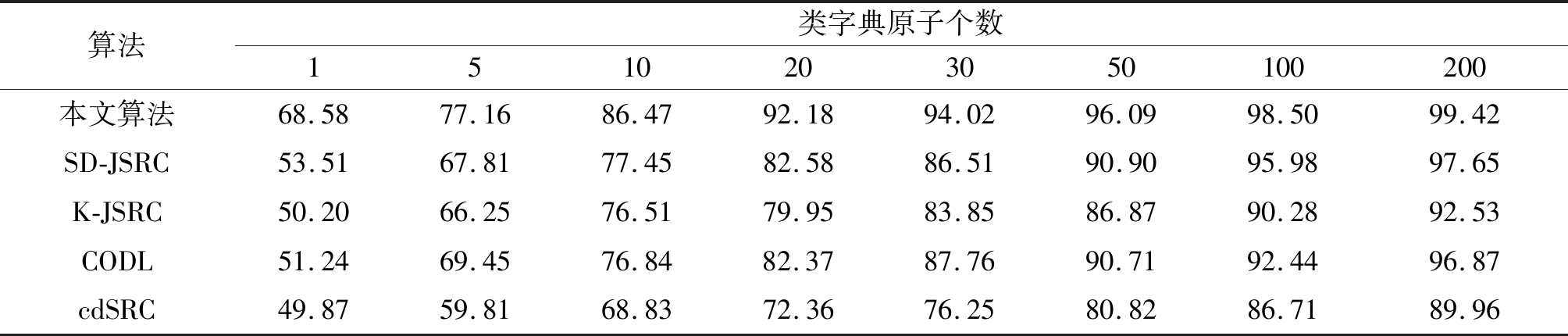
算法类字典原子个数1510203050100200本文算法68.5877.1686.4792.1894.0296.0998.5099.42SD-JSRC53.5167.8177.4582.5886.5190.9095.9897.65K-JSRC50.2066.2576.5179.9583.8586.8790.2892.53CODL51.2469.4576.8482.3787.7690.7192.4496.87cdSRC49.8759.8168.8372.3676.2580.8286.7189.96
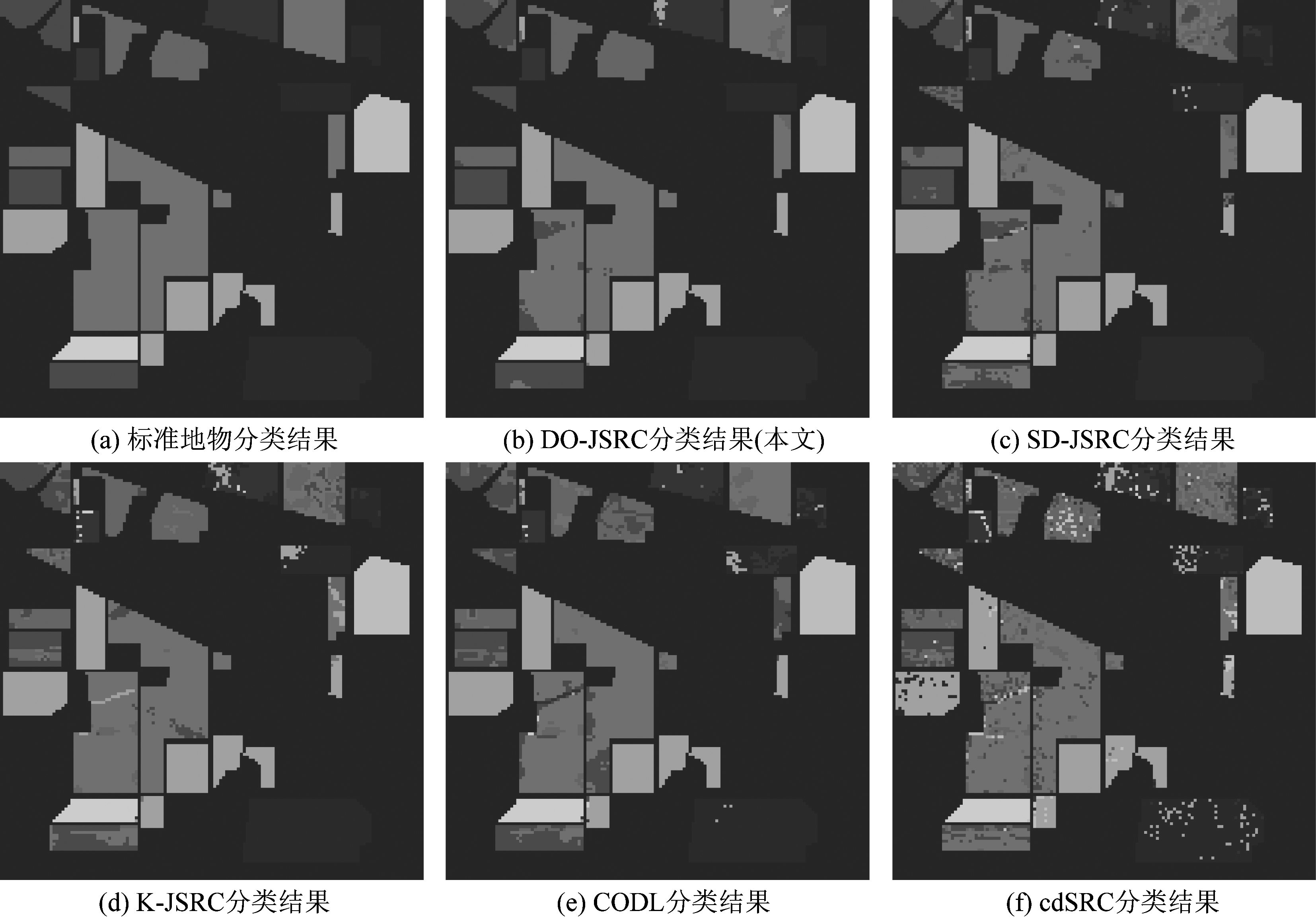
图9 Indian Pines数据集分类结果
Fig.9 Classification results of Indian Pines dataset
4.3.2 Pavia University数据集
本文选取类字典原子个数为30对各个分类算法进行验证,如表5所示,通过平均分类准确率、总体分类精度和Kappa对比本文算法和SD-JSRC、K-JSRC、CODL和cdSRC几个算法间的分类效果。图10是各个算法分类结果生成的假色图像,直观地展示了分类效果。由于训练样本的选取是随机的,实验过程中对10次实验结果取均值。

图10 Pavia University数据集分类结果
Fig.10 Classification results of Pavia University dataset
表5中可以看到相较于cdSRC算法和CODL算法,本文算法得到的Pavia University数据集的9种地物绝大部分的平均分类精度均有所提升,如:对于地物Gravel,本文算法的平均分类精度比SD-JSRC算法和K-JSRC算法、CODL算法、cdSRC算法分别提高1.86%、10.86%、2.87%、20.48%。本文算法的总分类精度达到93.04%,比SD-JSRC算法、K-JSRC算法、CODL算法、cdSRC算法分别提高了1.04%、3.77%、1.47%、15.18%,同样Kappa也相应提升了1.24%、4.69%、1.89%、18.44%。
图10展示了类字典原子个数为30时各个算法的分类效果,从图中可以看出cdSRC算法的分类效果较差。K-JSRC算法、CODL算法和SD-JSRC算法的分类效果较cdSRC提升较大,本文的DO-JSRC算法通过对训练样本组成的字典进行选择优化,进一步提升了分类精度,分类效果更接近真实地物。
表5 Pavia University数据集总体分类精度(%)
Tab.5 Overall classification accuracy of the Pavia University dataset (%)
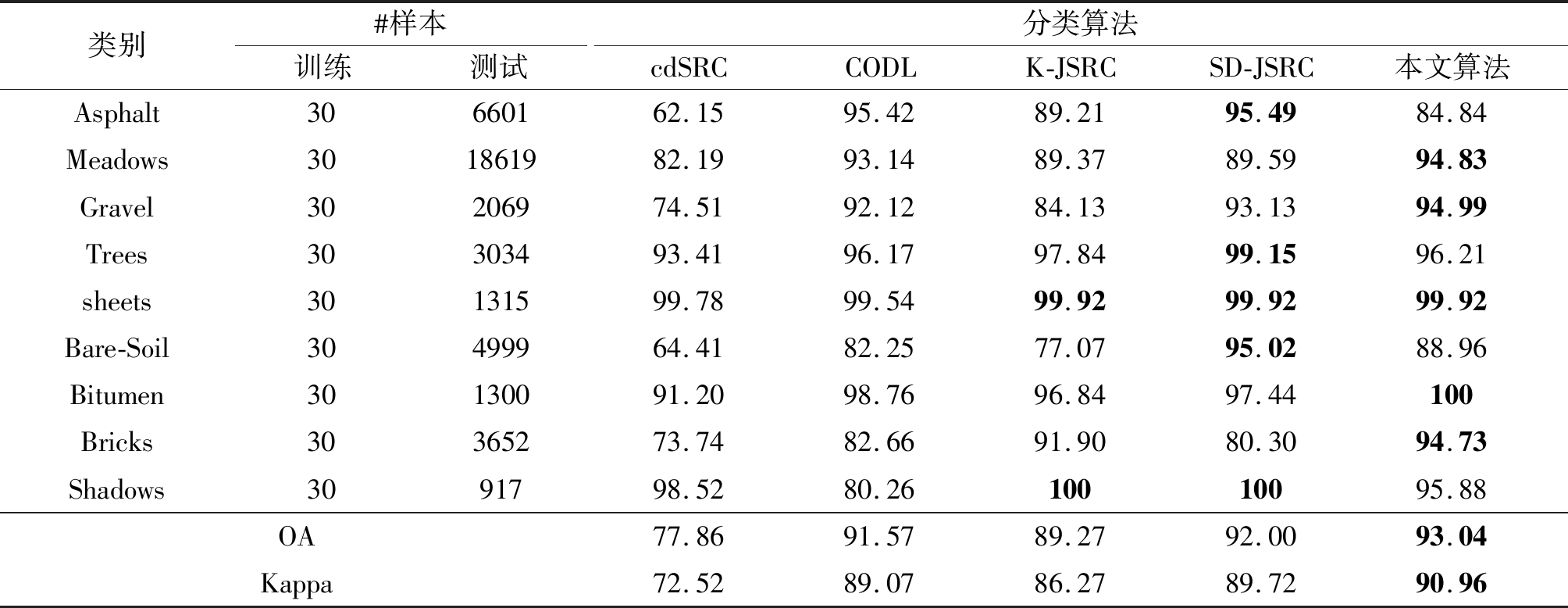
类别#样本训练测试分类算法cdSRCCODLK-JSRCSD-JSRC本文算法Asphalt30660162.1595.4289.2195.4984.84Meadows301861982.1993.1489.3789.5994.83Gravel30206974.5192.1284.1393.1394.99Trees30303493.4196.1797.8499.1596.21sheets30131599.7899.5499.9299.9299.92Bare-Soil30499964.4182.2577.0795.0288.96Bitumen30130091.2098.7696.8497.44100Bricks30365273.7482.6691.9080.3094.73Shadows3091798.5280.2610010095.88OA77.8691.5789.2792.0093.04Kappa72.5289.0786.2789.7290.96
5 结论
本文提出了基于字典优化的联合稀疏表示高光谱图像分类算法。一方面,由已知标签信息的训练样本标记可能加入训练样本备选集的像元,通过光谱相似度准则对备选集进行筛选优化字典;另一方面,为了降低高光谱数据维度,减少冗余,本文采取一种基于层次聚类的波段选择方法,通过自适应距离增加聚类可靠度,减少噪声波段的影响。在Indian Pines数据集和Pavia University数据集上进行实验仿真,验证本文提出的算法和几个对比算法的分类效果,实验结果表明本文提出算法能够有效地提高分类精度,并且在训练样本较少的情况下也能获得很好的分类效果。本文还有许多值得进一步研究的地方,例如,如何进一步增强算法的稳定性,减少由训练样本质量差异带来的影响等。
[1] LIU Bing, GUO Wenyue, CHEN Xin, et al. Morphological attribute profile cube and deep random forest for small sample classification of hyperspectral image[J]. IEEE Access, 2020, 8: 117096-117108.
[2] XIA Junshi, GHAMISI P, YOKOYA N, et al. Random forest ensembles and extended multiextinction profiles for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 202-216.
[3] 高恒振, 万建伟, 王力宝, 等. 基于谱域-空域组合核函数的高光谱图像分类技术研究[J]. 信号处理, 2011, 27(5): 648- 652.
GAO Hengzhen, WAN Jianwei, WANG Libao, et al. Research on classification technique for hyperspectral imagery based on spectral-spatial composite kernels[J]. Signal Processing, 2011, 27(5): 648- 652.(in Chinese)
[4] 王立国, 王雪君, 郝思媛. 引入负相似的高光谱图像半监督分类[J]. 信号处理, 2015, 31(4): 414- 422.
WANG Liguo, WANG Xuejun, HAO Siyuan. Dissimilarity in semisupervised classification of hyperspectral image[J]. Journal of Signal Processing, 2015, 31(4): 414- 422.(in Chinese)
[5] FENG Jie, YU Haipeng, WANG Lin, et al. Classification of hyperspectral images based on multiclass spatial-spectral generative adversarial networks[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(8): 5329-5343.
[6] MOU Lichao, LU Xiaoqiang, LI Xuelong, et al. Nonlocal graph convolutional networks for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(12): 8246- 8257.
[7] LIU Qichao, XIAO Liang, YANG Jingxiang, et al. Content-guided convolutional neural network for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(9): 6124- 6137.
[8] PENG Jiangtao, LI Luoqing, TANG Yuanyan. Maximum likelihood estimation-based joint sparse representation for the classification of hyperspectral remote sensing images[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(6): 1790-1802.
[9] CHEN Yi, NASRABADI N M, TRAN T D. Hyperspectral image classification using dictionary-based sparse representation[J]. IEEE Transactions on Geoscience and Remote Sensing, 2011, 49(10): 3973-3985.
[10] ZHANG Hongyan, LI Jiayi, HUANG Yuancheng, et al. A nonlocal weighted joint sparse representation classification method for hyperspectral imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2014, 7(6): 2056-2065.
[11] 陈善学, 周艳发, 漆若兰. 基于核函数的联合稀疏表示高光谱图像分类[J]. 系统工程与电子技术, 2018, 40(3): 692- 698.
CHEN Shanxue, ZHOU Yanfa, QI Ruolan. Joint sparse representation of hyperspectral image classification based on kernel function[J]. Systems Engineering and Electronics, 2018, 40(3): 692- 698.(in Chinese)
[12] TANG Yuanyan, YUAN Haoliang, LI Luoqing. Manifold-based sparse representation for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(12): 7606-7618.
[13] GAN Le, XIA Junshi, DU Peijun, et al. Multiple feature kernel sparse representation classifier for hyperspectral imagery[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(9): 5343-5356.
[14] FANG Leyuan, WANG Cheng, LI Shutao, et al. Hyperspectral image classification via multiple-feature-based adaptive sparse representation[J]. IEEE Transactions on Instrumentation and Measurement, 2017, 66(7): 1646-1657.
[15] DEEPA P, THILAGAVATHI K. Feature extraction of hyperspectral image using principal component analysis and folded-principal component analysis[C]∥2015 2nd International Conference on Electronics and Communication Systems (ICECS). Coimbatore, India. IEEE, 2015: 656- 660.
[16] SONG Meiping, SHANG Xiaodi, WANG Yulei, et al. Class information-based band selection for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8394- 8416.
[17] YU Chunyan, WANG Yulei, SONG Meiping, et al. Class signature-constrained background-suppressed approach to band selection for classification of hyperspectral images[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(1): 14-31.
[18] 陈善学, 陈雯雯. 基于二级字典的联合稀疏表示高光谱图像分类[J]. 系统工程与电子技术, 2020, 42(3): 550-556.
CHEN Shanxue, CHEN Wenwen. Joint sparse representation of hyperspectral image classification based on secondary dictionary[J]. Systems Engineering and Electronics, 2020, 42(3): 550-556.(in Chinese)
[19] FU Wei, LI Shutao, FANG Leyuan, et al. Contextual online dictionary learning for hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(3): 1336-1347.
[20] CUI Minshan, PRASAD S. Class-dependent sparse representation classifier for robust hyperspectral image classification[J]. IEEE Transactions on Geoscience and Remote Sensing, 2015, 53(5): 2683-2695.

