1 引言
波达方向角(Direction of Arrival, DOA)的估计性能受限于阵列的测向分辨率[1]。提高DOA估计分辨率的研究一直备受学界关注。通常,阵列的有效孔径越大,测向分辨率越高[2]。由于阵元间距必须满足空间采样定理的约束(即阵元间距Δd≤0.5λ),因此传统扩大阵列孔径的思路是保证阵元间距小于半波长的同时增加阵元数目。相较于传统阵列,稀疏阵列(阵元间距Δd>0.5λ)能够使用较少阵元获得更大的阵列孔径,具有低成本、布阵灵活、高分辨率等优势[3]。但由于其违背了空间采样定理的约束,因此存在测向模糊问题[2-5]。
为解决上述问题,学界对稀疏阵列进行了深入研究,从阵列设计和算法角度提出了多种解模糊方法。基于算法的解模糊方法一般利用了信号中的某些特征作为判断真实DOA的判据,并需要较为复杂的运算:例如Kastinen D通过计算理论模糊集,再通过模式匹配的方法排除掉模糊角以解模糊[6];He Z等人构建了一个用于估计谱峰处信号功率的代价函数,用来识别真实峰和虚假峰,以解模糊[7]等;文献[8-9]使用压缩感知的方法对阵列进行虚拟插值以解模糊,这类方法不仅运算量较大,往往还需要一些先验信息(如信号入射方向的范围)作为插值依据。
相较于算法层面的解模糊方法,基于阵列设计的解模糊方法通常利用了稀疏均匀线阵(Sparse Uniform Linear Array, SULA)的几何特征或阵列流形特征,具有低复杂度和处理简便等优势:例如He Z等通过在SULA阵元上放置不同厚度和不同折射率的介质基片,通过改变信号的等效波长以解模糊[10];Yang K等通过优化SULA各向异性的阵元朝向,以改变阵列可能产生的模糊导向矢量以解模糊[11];Hai-Lang S等通过小幅度移动稀疏阵的阵元,通过对比阵元移动前后获得的DOA估计谱以解模糊[12];Chen T等通过限制非均匀阵列的最小阵元间距,并使用接收信号的四阶累积量构建单快拍测量的稀疏信号模型以得到解模糊的DOA估计[13]。这些方法的核心思路都是改变导向矢量的性质,使其不产生模糊角,或产生的模糊角在同一坐标系下不重合。通过将阵列进行旋转也可以改变其流形特征,文献[14-17]利用了信源方向固定时信源相对阵列的“旋转不变性”,通过将阵列旋转前后的采样数据融合处理,以提高DOA估计的精度和自由度,但并未将该技术用于稀疏阵列解模糊方法的研究。Lin M等也应用了这种思路,通过旋转阵列,比较阵列旋转前后获得的DOA估计谱以解模糊[18-19]。但该方法并未深入研究阵列旋转角度对模糊角的影响,未给出旋转前后模糊角不重合时旋转角所应满足的条件。此外,该方法需要对阵列进行旋转操作,这些问题增加了上述研究的应用难度。
基于上述原因,本文首先研究了SULA的模糊导向矢量,发现模糊角与转动角度间的非线性关系。并从这种非线性关系出发,研究和论证了SULA旋转前后不出现重叠模糊角时旋转角应满足的条件,提出了旋转模糊对消准则。为解决实际应用中线阵一旦布好无法旋转的问题,本文基于上述准则,提出一种稀疏X-形阵列多重联合MUSIC方法(Multiple-Joint MUSIC, MJ-MUSIC)方法,通过构造X-形阵列来代替阵列的旋转。该方法充分利用了阵列上的接收信号,使虚假峰相互交错,并进一步利用提出的准则增大真实峰与虚假峰之间的差值,提高了DOA解模糊的正确率。当满足旋转模糊对消准则时,该方法的DOA解模糊正确率与非稀疏情况下传统MUSIC算法的估计正确率一致。
2 SULA的模糊问题
如图1所示,一个N阵元的ULA(Uniform Linear Array, ULA),对于DOA为θm∈(0°,180°)的入射信号(0°为阵元1处端射,90°为垂直入射,180°为阵元N处端射),该阵列对应的导向矢量为:
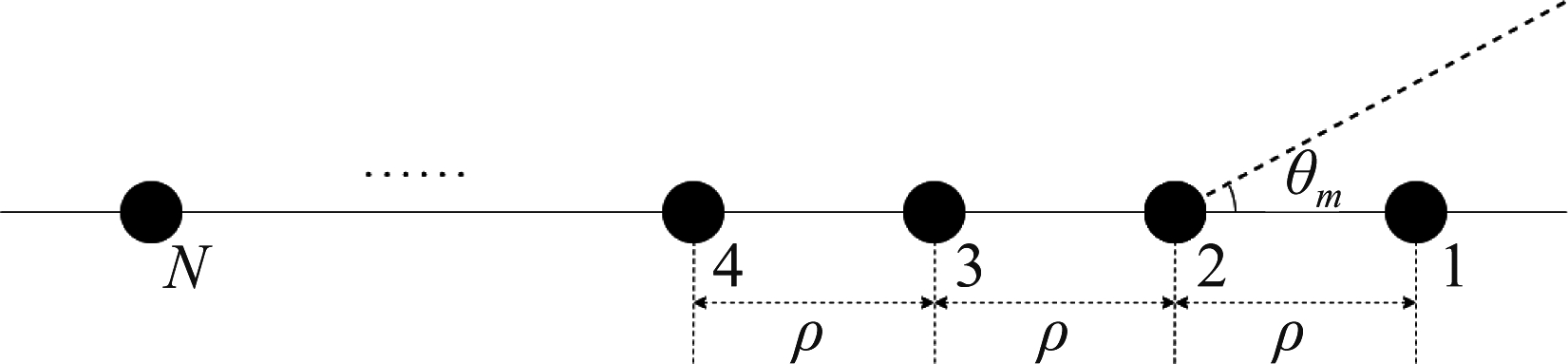
图1 ULA示意图
Fig.1 Illustration of ULA geometry
a(θm)=[1 e-j2πρcos θm … e-j2π(N-1)ρcos θm]T
(1)
其中
为阵元间距Δd对信号波长λ的比值,(·)T为向量或矩阵的转置。
假设有M个非相干的远场窄带信号,其到该阵列的DOA分别为{θ1,θ2,…，θM},则这些信号对该阵列的流形矩阵为:
(2)
在子空间类的DOA估计方法中,如多重信号分类(MUtiple SIgnal Classification, MUSIC)算法,通过对接收信号的自相关矩阵进行分解,得到信号子空间span(Us)与噪声子空间span(Un)。由于入射信号导向矢量a(θm)∈span(Us)且span(Us)⊥span(Un),则可通过计算不同角度的导向矢量对噪声子空间的性来获得DOA估计谱[20],即:
(3)
其中,(·)H为向量或矩阵的共轭转置。
将式(2)中的矩阵A增广,令
为除DOA之外其他角度上的导向矢量,即
且
有:
(4)
当ρ≤0.5时,复函数f(θ)=e-j2πρcosθ是θ∈(0,180°)上的单值函数,式(4)中的矩阵为范德蒙特矩阵,
列满秩,即该矩阵各列向量之间互相线性独立。由于a(θm)⊥span(Un),当且仅当θ=θm,m=1～M时式(3)取得极大值,即DOA估计谱峰。
当ρ>0.5时,定义该阵列为SULA。由于复函数f(θ)=e-j2πρcosθ不再是θ∈(0,180°)上的单值函数,因此当
取某个角度时,
是列秩亏损的,即存在导向矢量可由真实方向上导向矢量线性表示[2]:
(5)
此时,由于a(θm)⊥span(Un),因此它们的线性组合
即式(3)不仅在θ=θm,m=1～M处取得谱峰,还会错误地在处取得谱峰。测向角称为模糊角,错误谱峰称为虚假峰,该现象称为DOA估计的模糊问题。当式(5)中的复系数γm有且仅有一个不为零时,称为一般模糊问题;当有多个不为零时,称为复杂模糊问题[2]。
3 旋转模糊对消准则
假定信源位置不变,SULA以其几何中心为轴在信源和阵列构成的平面上旋转,转动的角度记为φ(φ>0时顺时针旋转,φ<0时逆时针旋转)。则阵列旋转前后的测向角有如下线性映射关系:
θφ=θ+φ
(6)
相应地,记aφ(·)为旋转后阵列的导向矢量,根据式(6),该导向矢量与原阵列导向矢量有如下关系:
aφ(θφ)=a(θ+φ)
(7)
若为阵列原位置时的模糊角,对于阵列旋转后的测向角
其对应的导向矢量也满足式(7)所示的关系。由式(1)可知,复函数f(θ)=e-j2πρcosθ是关于自变量θ的非线性函数。当模糊角的导向矢量为式(5)所示的线性组合时,并不能保证导向矢量
也为旋转后阵列DOA处导向矢量的线性组合,即:
(8)
其中,θm,φ为阵列旋转后的第m个DOA。
式(8)表明,当原阵列发生旋转后,其原模糊角映射在旋转后阵列的测向角
不一定为模糊角。记
和
分别为原SULA和经过旋转的SULA上的模糊角集合,若能找到特定条件,使
则便可利用上述性质解模糊。
考察一种SULA对称旋转的情况,即当旋转角φ分别等于φ和-φ(φ>0°)时,根据式(1)和式(6),经过对称旋转的SULA的导向矢量应满足:
(9)
其中bφ(θ)∈CN×1与导向矢量的结构类似,可表示为:
(10)
旋转模糊对消准则:当阵元间距与信源波长的比值ρ和对称旋转角φ满足:
(11)
时,有:
(12)
其中
是旋转角为φ时SULA上的模糊角集合,
是旋转角为-φ时SULA上的模糊角集合。式(12)表明,当ρ与φ满足式(11)的约束时,上述两个模糊角集合映射在同一坐标下的交集为空集。
旋转模糊对消准则的证明(反证法):
假设
若假设1为真,则
根据式(5)有:
(13)
此外,根据假设1和式(5)、(9)可得:
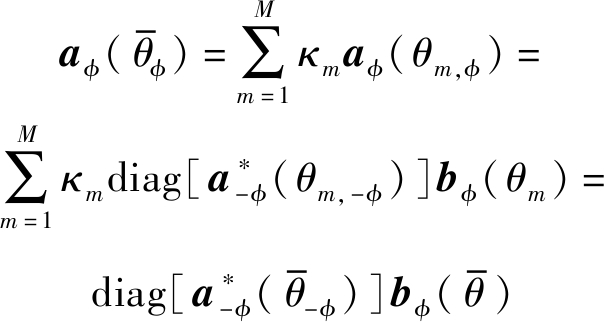
(14)
其中,线性组合的复系数由式(5)所定义,为不失一般性,且与式(13)中的复系数加以区分,使用κm表示该复系数。
将式(13)代入式(14),有:
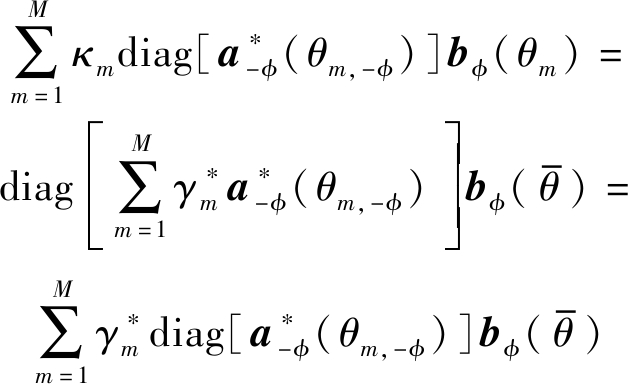
(15)
式(15)表明,向量
是向量组{bφ(θm)},m=1～M的线性组合。令bφ(θ)=e-j2πρcosφcosθ。则矩阵
可表示如下:
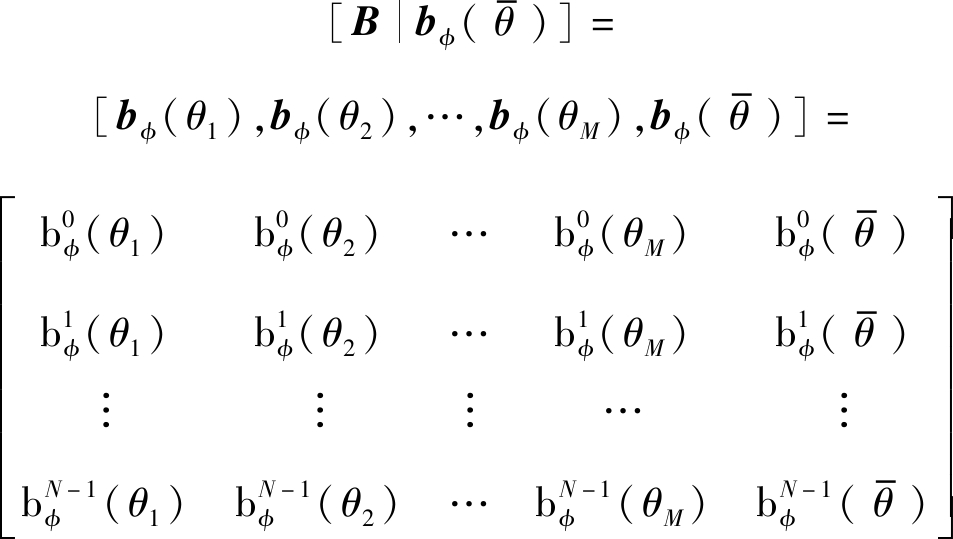
(16)
由式(16)可知,当ρ2cosφ<0.5时,复函数bφ(θ)=e-j2πρcosφcosθ为θ∈(0,180°)上的单值函数,则
为范德蒙特矩阵,其列满秩,各列向量之间线性独立。此时,向量不可能为向量组{bφ(θm)},m=1～M的线性组合。此处结论与上述推论矛盾,因此当ρ2cosφ<0.5时,假设1为假命题。旋转模糊对消准则得证。
4 MJ-MUSIC方法
根据旋转模糊对消准则,当SULA满足该定理的约束时,
可利用该性质设计一种能够解模糊的DOA估计方法。
如图2,考虑两个交叉放置的相同的SULA,阵元间距与信号波长的比值为ρ,以2φ为夹角相交于它们的几何中心,构成一个X形稀疏阵。其中,
该稀疏X形阵两臂上接收到的阵列信号可分别记为:
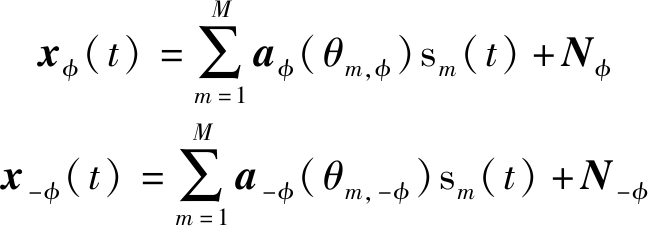
(17)
其中,sm(t)为第m个DOA的信源函数,Nφ和N-φ分别为稀疏X形阵两臂上的噪声矢量,每个噪声矢量中的元素均为独立同分布的零均值加性白噪声,记Nφ的平均功率为
的平均功率为
对式(17)中的两项接收信号进行求和,有:
xc(t)=xφ(t)+x-φ(t)=
CφS(t)+Nφ(t)+ N-φ(t)
(18)
其中,cφ(θm)=aφ(θm,φ)+a-φ(θm,-φ),Cφ=[cφ(θ1),cφ(θ2),…,cφ(θM)],S(t)=[s1(t),s2(t),…,sM(t)]。
对于合并的接收信号xc,其自相关矩阵
为:
(19)
式(19)中的矩阵Cφ类似于式(2)的阵列流形矩阵,可将Rc进一步分解,得到其噪声子空间span(Uc,n),同样类似于子空间类的DOA方法,Uc,n由Rc最小的N-M个特征值所对应的特征向量构成。
由式(19)可知,由实际DOA导向矢量构成的Cφ(θm)⊥span(Uc,n),且当该稀疏X形阵的夹角满足旋转模糊对消准则的约束时,即
对于
且
不同时为稀疏X形阵两臂上的模糊角,也就是在
和
中,只有一项为其对应DOA上导向矢量的线性组合,即:
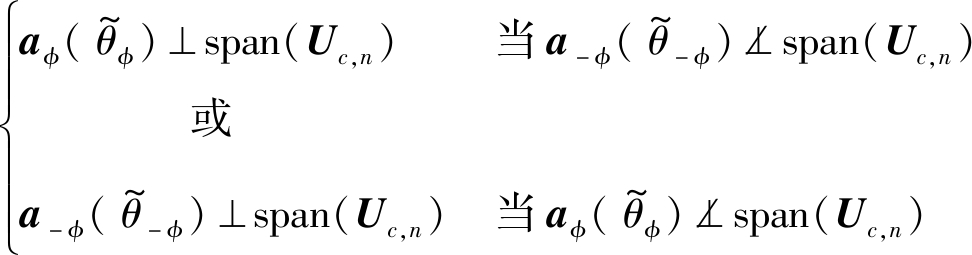
(20)
因此,可推出:
(21)
可利用式(3)的方式使用cφ(θ)对噪声子空间span(Uc,n)进行扫描,得到联合MUSIC估计谱:
(22)
注意到,如式(20)所示,由于和中只有一项为其对应DOA上导向矢量的线性组合。因此,有:
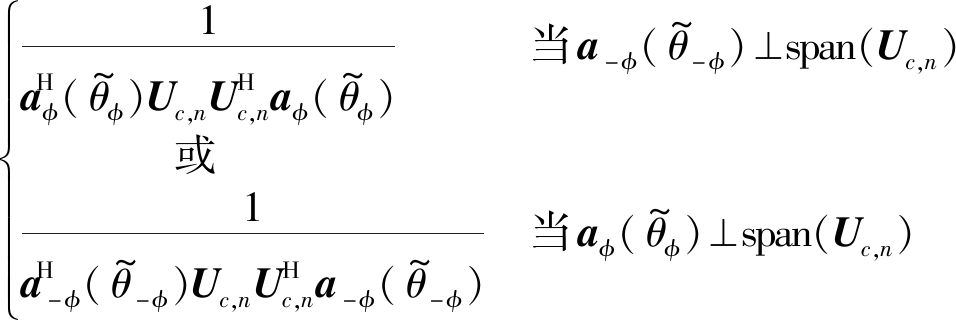
(23)
此时,根据式(23)可知,
为θ在
附近的局部极大值。且由于Cφ(θm)⊥span(Uc,n),因此有:
(24)
其中
为附近非模糊的测向角。
式(24)表明,虽然联合MUSIC利用旋转模糊对消准则减弱了谱中的虚假峰,但若局部极大值(即幅度弱化的虚假峰)
的幅度大于谱峰检测门限时,会影响谱峰搜索的准确性。为进一步减弱虚假峰,增大真实DOA谱峰和虚假峰之间的差值,可并行利用稀疏X形阵两臂上的信号,从每个阵列臂上分别获得一组MUSIC估计谱。在满足旋转模糊对消准则时,当把得到的两组MUSIC-DOA估计谱根据式(6)映射到同一坐标(即映射到图2中虚线所表示的“参考SULA”上的测向角)时,可保证谱峰只在真实DOA测向角上重合。此时,可利用这两组MUSIC-DOA估计谱对联合MUSIC谱中的虚假峰进行“二次减弱”,即将这两组MUSIC估计谱与式(22)得到的联合MUSIC估计谱相乘开立方,得到MJ-MUSIC谱Pm(θ):
(25)
其中,Pφ(θ)和Pφ(-θ)分别为顺时针和逆时针夹角方向阵列臂上得到的MUSIC估计谱。MJ-MUSIC方法的原理框图如图2所示。
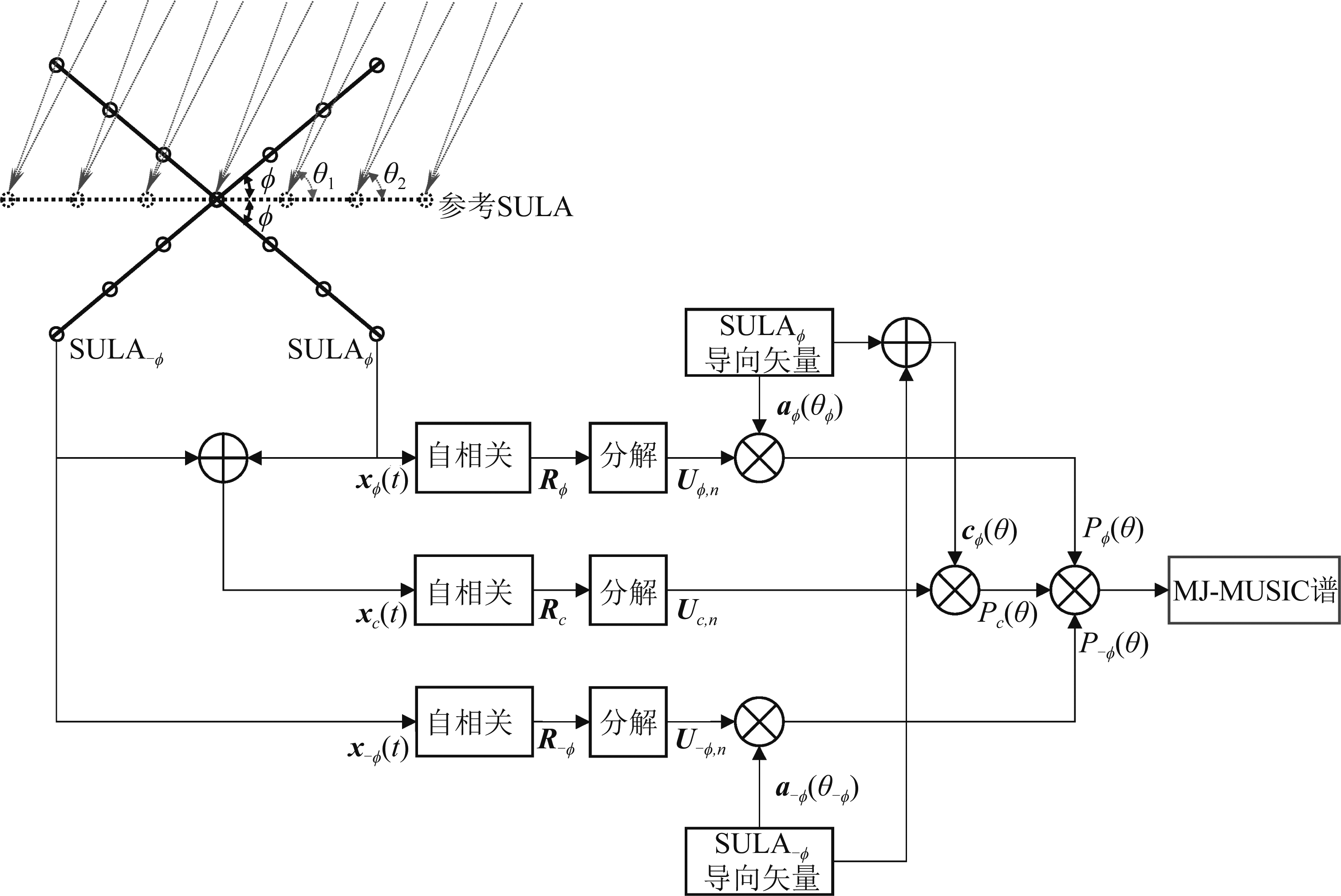
图2 MJ-MUSIC方法原理
Fig.2 Block diagram of MJ-MUSIC method
综上所述,MJ-MUSIC方法再次利用了旋转模糊对消准则,对联合MUSIC谱中的虚假峰进行了“二次减弱”,可降低谱峰检测门限,以更灵敏,更准确地进行谱峰搜索,得到解模糊的DOA估计结果。
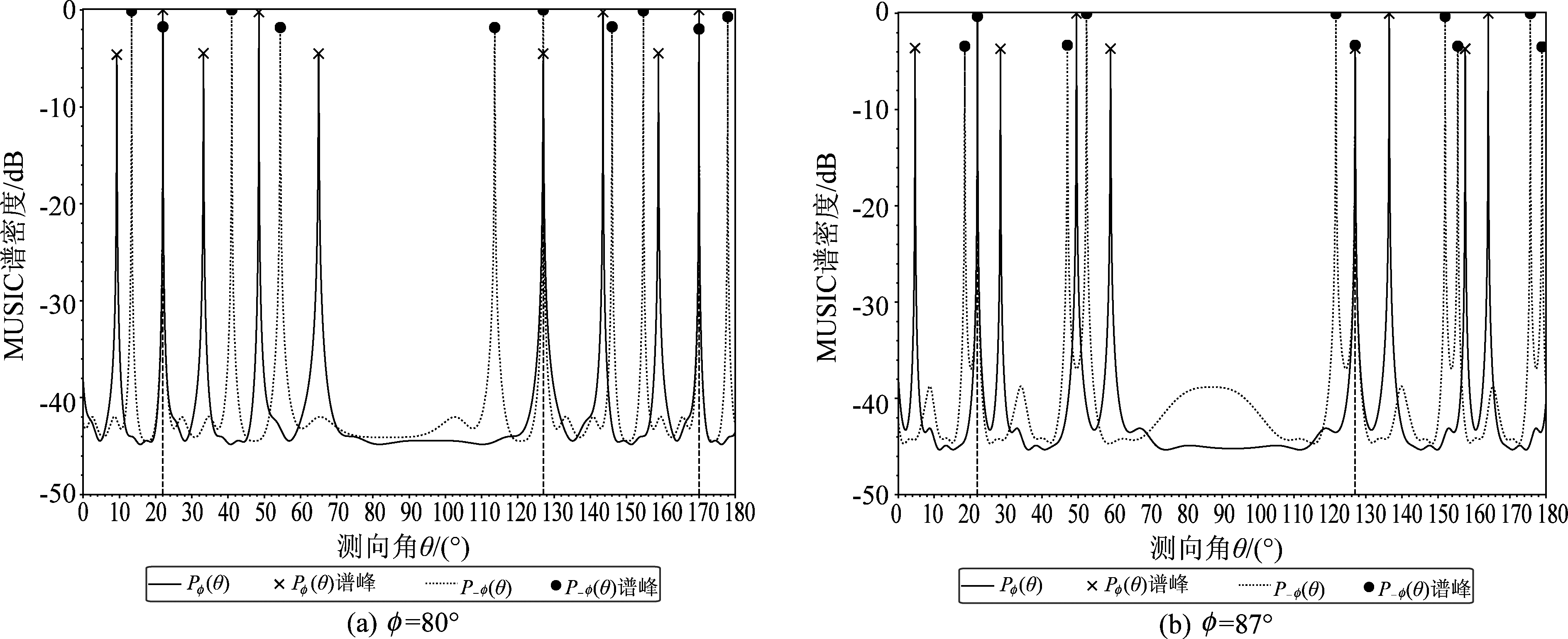
图3 传统MUSIC算法在φ不同取值时的DOA估计结果
Fig.3 DOA estimated by conventional MUSIC on different φ
5 仿真验证
实验1 两个窄带非相干信号分别从22°和127°入射至一个稀疏X形阵,该阵列共有7个阵元,阵元间距Δd=2.5λ。快拍数为200,SNR=15 dB。实验分别取φ=80°和φ=87°时X形阵两臂上得到的传统MUSIC估计谱进行对比。实验结果如图3所示。图中,X-轴表示测向角,Y-轴表示MUSIC谱密度,谱峰重叠处使用虚线进行了标记。
根据旋转模糊对消准则,当ρ=2.5时,只有当φ∈(84.26°,90°)时可确保稀疏X形阵两臂上的模糊角在同一坐标下不互相重叠。
图3(a)中,φ=84°∈/ (84.26°,90°),两个MUSIC谱均存在很多谱峰,其中含有真实峰和虚假峰。可以看到,当映射到同一坐标下,两个MUSIC谱的谱峰在22°、127°和170°处均出现了重叠。而真实DOA为22°和127°,170°处的谱峰重叠是由于此时的阵列夹角φ和阵元间距ρ不满足旋转模糊对消准则的约束,使它们同时在170°出现了模糊。
图3(b)中,φ=87°∈(84.26°,90°)。可以看到,当映射到同一坐标下,两个MUSIC谱的谱峰仅在22°和127°处重叠,在其他角度上都互相交错。
上述实验结果表明,当阵列夹角φ和阵元间距ρ满足旋转模糊对消准则的约束时,得到的两个MUSIC谱不会出现相同的模糊角。
实验2 三个窄带非相干信号分别从25°、78°和152°入射至一个稀疏X形阵,该阵列共有7个阵元,阵元间距Δd=3λ。快拍数为200,SNR=20 dB。实验分别取φ=80°和φ=87°时该稀疏X形阵上得到的联合MUSIC估计谱和MJ-MUSIC估计谱进行对比。实验结果如图4所示。图中,X-轴表示测向角,Y-轴表示谱密度,谱峰检测门限取值为-20 dB,使用水平虚线进行标记,真实DOA使用垂直虚线进行标记。
根据旋转模糊对消准则,当ρ=3时,只有当φ∈(85.22°,90°)时可确保稀疏X形阵两臂上的模糊角在同一坐标下不互相重叠。
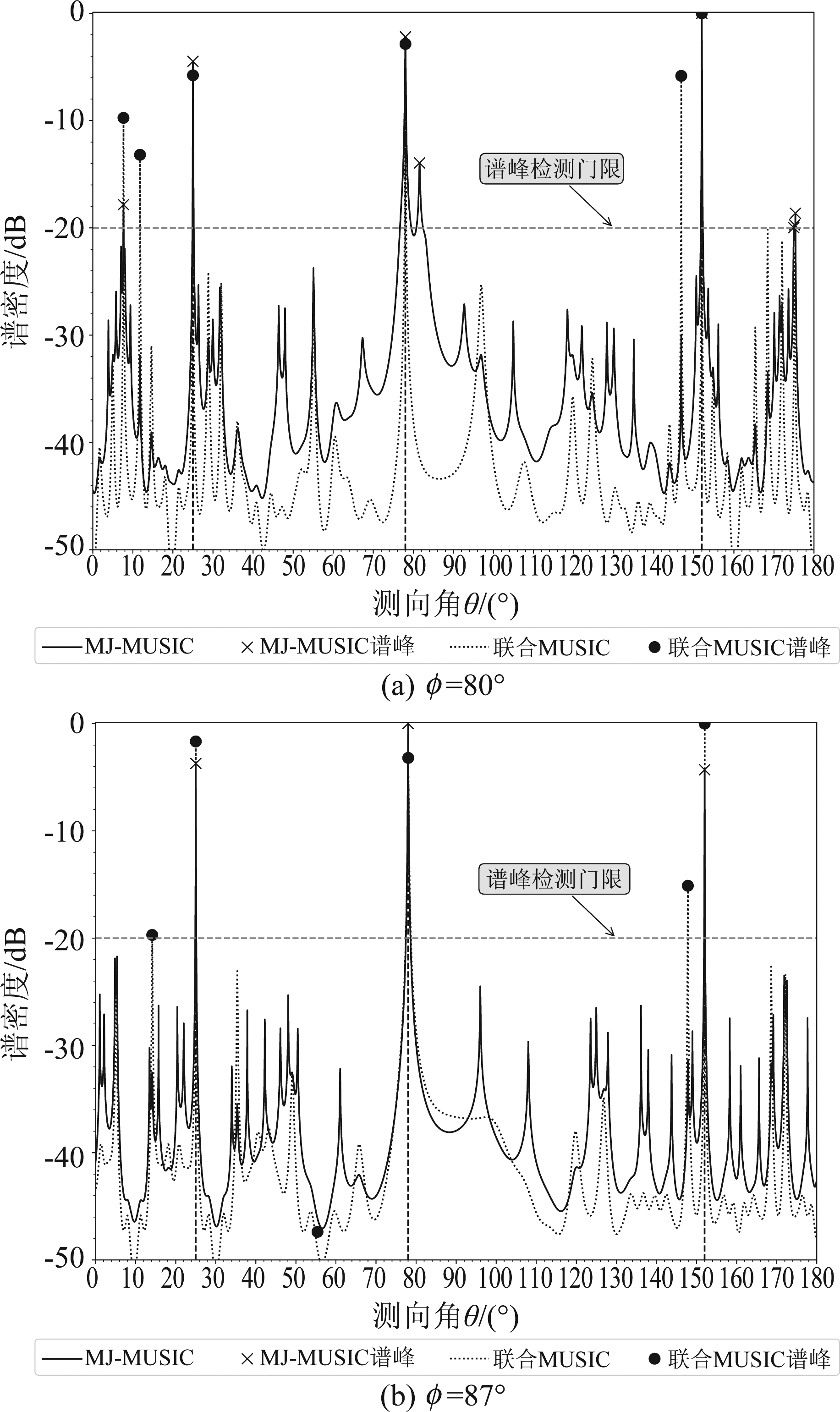
图4 MJ-MUSIC和联合MUSIC在φ不同取值时的DOA估计结果
Fig.4 DOA estimated by MJ-MUSIC and Combined MUSIC on different φ
图4(a)中,φ=80°∈/ (85.22°,90°)。可以看出,联合MUSIC谱和MJ-MUSIC谱除了在25°、78°和152°处有显著高于检测门限以上的谱峰,还有很多其他略高于谱峰检测门限的虚假峰。这是因为此时阵列夹角φ不满足旋转模糊对消准则的约束,产生了互相重合的模糊角,进而影响了式(21)中联合导向矢量cφ(θ)对噪声子空间的非正交性。由于虚假峰的干扰,两种方法均无法估计出正确的DOA。
图4(b)中,φ=87°∈(85.22°,90°)。可以看出,联合MUSIC谱和MJ-MUSIC的估计谱在25°、78°和152°处有显著高于检测门限以上的谱峰。此外,联合MUSIC的估计谱还在14°和148°处有略高于检测门限的虚假峰,这些虚假峰的高度和数量均少于图3(a)所示的结果。这是因为旋转模糊对消准则虽然能够保证模糊角在此时不互相重合,但由于式(24)的影响,联合MUSIC谱在14°和148°处出现了局部极值。此时,通过谱峰搜索,可由MJ-MUSIC估计谱得到正确的DOA。
上述实验结果表明,当阵列夹角φ和阵元间距ρ满足旋转模糊对消准则的约束时,MJ-MUSIC估计性能优于联合MUSIC,可通过MJ-MUSIC估计谱得到正确的DOA。
实验3 两个非相干窄带信号从随机角度入射至稀疏X形阵,入射角度服从(0°,180°)的均匀分布。快拍数为200,SNR=15 dB。该稀疏X形阵共有5个阵元,阵元间距ρ=2,夹角φ以Δφ=0.1°为增量变化,变化范围为(80°,90°)。每个夹角φ取值处进行1000次蒙特卡洛实验,用以统计MJ-MUSIC的平均DOA估计正确率(谱峰检测门限取值为-15 dB),以测试其解模糊的性能。同时也统计了联合MUSIC(Combined MUSIC)、稀疏情况下MUSIC算法取重合谱峰(Overlap,文献[18-19]方法)以及非稀疏情况下MUSIC算法(Δd=0.5λ)的平均DOA估计正确率作为参考,实验结果如图5所示。图中,X-轴表示夹角φ的取值,Y-轴表示DOA估计正确率,φopt所标注的垂直虚线为旋转模糊对消准则约束的φ取值下界。
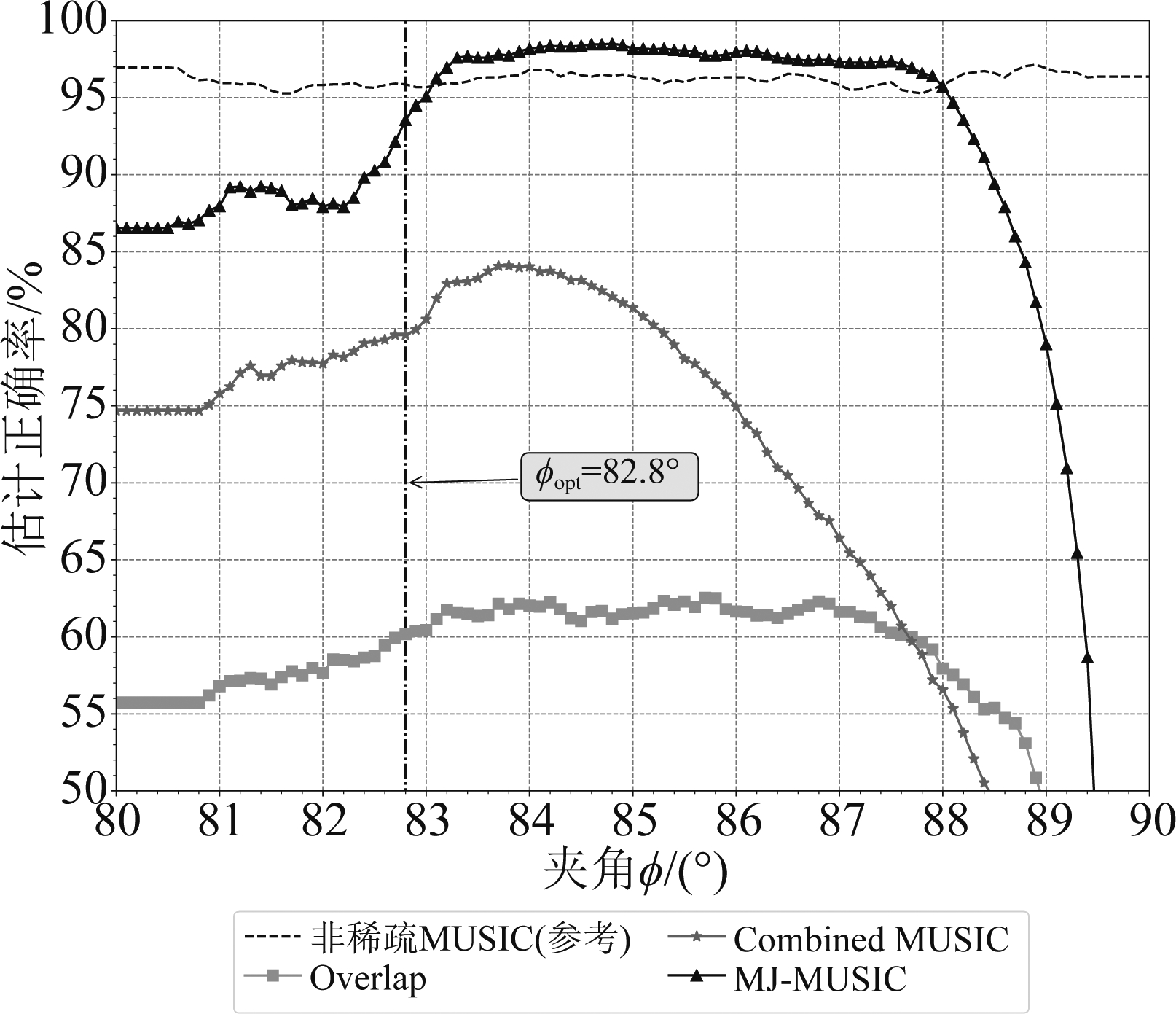
图5 各方法在φ不同取值时的DOA估计正确率
Fig.5 DOA estimation correct rate of different methods respect to φ
图5展示了各方法在不同φ取值时的DOA估计平均正确率。根据旋转模糊对消准则,ρ=2时φ应在(φopt,90°)范围内,其中
可以看到,在φ取到82.8°后,Overlap、联合MUSIC和MJ-MUSIC方法的估计正确率均有显著提高,验证了旋转模糊对消准则的有效性。
从图5可也看出,在(φopt,90°)范围内,MJ-MUSIC方法的估计正确率最高,且在(83°,88°)范围内略微超过了用于参考的非稀疏情况的MUSIC估计正确率,这是因为MJ-MUSIC的阵列孔径((5-1)×2λ=8λ),高于非稀疏情况的阵列孔径((5-1)×0.5λ=2λ),因此前者的DOA估计准确率较高;联合MUSIC次之,这是由于其估计谱由于式(24)的影响,出现了高于检测门限的虚假峰;Overlap方法由于会受到MUSIC分辨率、谱峰搜索误差等因素的影响,因此正确率最低。
此外,在φ>88°后,三种方法的估计正确率快速下降至0。从数值角度上看,由于φ→90°,aφ(θφ)→
使cφ(θ)退化为2Re{a-φ(θ-φ)},不再具有解模糊的能力。
上述实验结果表明,提出的旋转模糊对消准则是有效的,基于该准则的MJ-MUSIC方法能有效解模糊。
6 结论
本文研究了SULA的模糊角与转动角之间的关系,并根据模糊角与转动角度间的非线性关系,提出了旋转模糊对消准则,该准则揭示了SULA旋转前后不出现重叠模糊角时旋转角应满足的条件。基于此准则,本文提出了MJ-MUSIC方法,该方法应用于稀疏X形阵列,用其夹角代替了SULA的旋转,并进一步利用提出的准则构建了联合MUSIC谱,使其与X形阵两臂上得到的MUSIC相乘,得到MJ-MUSIC谱,进一步增大真实峰与虚假峰之间的差值,提高了DOA解模糊的正确率。最后,仿真结果验证了旋转模糊对消准则的正确性,当MJ-MUSIC满足其约束时,该方法的DOA估计正确率与非稀疏情况下传统MUSIC算法的DOA估计正确率一致,具有较好的操作性和有效性,可以为工程应用提供参考。
[1] KRIM H, VIBERG M. Two decades of array signal processing research: The parametric approach[J]. IEEE Signal Processing Magazine, 1996, 13(4): 67-94.
[2] PROUKAKIS C, MANIKAS A. Study of ambiguities of linear arrays[C]∥Proceedings of ICASSP ′94. IEEE International Conference on Acoustics, Speech and Signal Processing. Adelaide, SA, Australia. IEEE, 1994: IV/549-IV/552.
[3] 何子远. 稀疏阵DOA估计及模糊特性研究[D]. 成都: 电子科技大学, 2012.
HE Ziyuan. Research on DOA estimation and the ambiguities for sparse arrays[D]. Chengdu: University of Electronic Science and Technology of China, 2012. (in Chinese)
[4] FLIELLER A, LARZABAL P, CLERGEOT H. Study of ambiguities in array manifold: A general framework[C]∥Proceedings of 8th Workshop on Statistical Signal and Array Processing. Corfu, Greece. IEEE, 1996: 574-577.
[5] TAN C M, FOO S E, BEACH M A, et al. Ambiguity in MUSIC and ESPRIT for direction of arrival estimation[J]. Electronics Letters, 2002, 38(24): 1598.
[6] KASTINEN D. Determining all ambiguities in direction of arrival measured by radar systems[J]. URSI Radio Science Bulletin, 2018, 2018(365): 20-28.
[7] HE Ziyuan, ZHAO Zhiqin, NIE Zaiping, et al. Method of solving ambiguity for sparse array via power estimation based on MUSIC algorithm[J]. Signal Processing, 2012, 92(2): 542-546.
[8] ZHOU Nan, LUO Lingen, SHENG Gehao, et al. Direction of arrival estimation method for multiple UHF partial discharge sources based on virtual array extension[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2018, 25(4): 1526-1534.
[9] CUI Ao, XU Teng, YU Weichuang, et al. An array interpolation based compressive sensing DOA method for sparse array[C]∥2019 3rd International Conference on Imaging, Signal Processing and Communication (ICISPC). Singapore. IEEE, 2019: 24-27.
[10] HE Ziyuan, ZHAO Zhiqin, NIE Zaiping, et al. Resolving manifold ambiguities for sparse array using planar substrates[J]. IEEE Transactions on Antennas and Propagation, 2012, 60(5): 2558-2562.
[11] YANG Kai, ZHAO Zhiqin, ZHU Xiaozhang, et al. Resolving ambiguities in DOA estimation by optimizing the element orientations[C]∥2013 IEEE Antennas and Propagation Society International Symposium (APSURSI). Orlando, FL, USA. IEEE, 2013: 1326-1327.
[12] SUN Hailang, TAO Haihong, HAO Rongchang. Method of resolving ambiguity for sparse array via modified sparse even array based on MUSIC algorithm[C]∥2009 2nd Asian-Pacific Conference on Synthetic Aperture Radar. Xi’an, China. IEEE, 2009: 246-249.
[13] CHEN Tao, SHI Lin, GUO Limin. Sparse DOA estimation algorithm based on fourth-order cumulants vector exploiting restricted non-uniform linear array[J]. IEEE Access, 2019, 7: 9980-9988.
[14] 司伟建, 吴娜, 蓝晓宇, 等. 基于阵列基线旋转的多目标DOA估计算法[J]. 系统工程与电子技术, 2014, 36(5): 809- 815.
SI Weijian, WU Na, LAN Xiaoyu, et al. Multiple DOA estimation algorithm based on array rotation method[J]. Systems Engineering and Electronics, 2014, 36(5): 809- 815.(in Chinese)
[15] 刘月婵, 孙超, 何元安. 旋转式阵列声源定位技术研究[J]. 声学技术, 2011, 30(3): 31-33.
LIU Yuechan, SUN Chao, HE Yuan’an. Research on sound source localization technology using rotating array[J]. Technical Acoustics, 2011, 30(3): 31-33. (in Chinese)
[16] LAN Xiaoyu, WAN Liangtian, HAN Guangjie, et al. A novel DOA estimation algorithm using array rotation technique[J]. Future Internet, 2014, 6(1): 155-170.
[17] LAN Xiaoyu, WAN Liangtian, HAN Guangjie, et al. A fast modified DOA estimation algorithm with rotation array for vehicle security in intelligent transportation system[C]∥2015 IEEE 12th Intl Conf on Ubiquitous Intelligence and Computing and 2015 IEEE 12th Intl Conf on Autonomic and Trusted Computing and 2015 IEEE 15th Intl Conf on Scalable Computing and Communications and Its Associated Workshops (UIC-ATC-ScalCom). Beijing, China. IEEE, 2015: 484- 489.
[18] LIN Mingtuan, LIU Peiguo, LIU Jibin. Rotary way to resolve ambiguity for planar array[C]∥2014 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC). Guilin, China. IEEE, 2014: 170-174.
[19] LIN Mingtuan, LIU Peiguo, LIU Jibin. DOA ambiguity suppressing by rotating the array[C]∥2015 IEEE 4th Asia-Pacific Conference on Antennas and Propagation (APCAP). Bali, Indonesia. IEEE, 2015: 165-167.
[20] SCHMIDT R. Multiple emitter location and signal parameter estimation[J]. IEEE Transactions on Antennas and Propagation, 1986, 34(3): 276-280.
