1 引言
融合前向纠错(Forward Error Correction, FEC)编码与高阶调制的编码调制技术可以实现更高的频谱效率和高可靠传输的误码率[1]。低密度奇偶校验(Low-Density Parity-Check, LDPC)码因其吞吐量高、错误平层低以及译码延时小等优势成为第三代FEC编码方案的候选码之一[2]。其中,多进制低密度奇偶校验(Non-Binary LDPC,NB-LDPC)码与二进制LDPC码相比,在中短码长下具有更优越的纠错性能,且易与高阶调制结合以实现更高频谱效率的传输,从而有效改善系统性能[3]。
正交幅度调制(Quadrature Amplitude Modulation, QAM)相比于相移键控(Phase-Shift Keying, PSK)调制,具有更好的抗噪声性能以及更高的带宽利用率,所以在光网络、卫星通讯等场景中多被研究[4]。迄今为止,QAM的研究主要集中于相位数与信号点数为22p(p≥2)的高阶或高维的星座设计[5- 8]。然而,在相同信道条件下,若只采用22p阶QAM,调制阶数为22p和22(p+1)的调制系统要实现相同的误码率,其所要求的信干比(Signal Interference Ratio, SIR)的差异约为6 dB,这将导致自适应调制时可选调制方式之间的性能跨度过大,从而降低系统的传输效率[9]。因此,介于22p与22(p+1)之间的非标准QAM技术具有潜在的应用价值[10]。由于非标准QAM的星座点数并非2的幂次,如何将2进制信息分配给QAM星座是研究的主要难点。针对素数阶调制,文献[11]提出了一种适用于光纤通信系统的非均匀5-QAM与7-QAM星座图,采用哈夫曼预编码实现2进制比特序列到符号的映射,并为星座点符号设置不等发送概率,获得了一定的成型增益。针对非素数阶的调制,文献[13]研究了3×2p(p<2)即6进制QAM,采用文献[12]提出的3×2p进制的转换方法,将5个2进制比特转换为2个6进制符号,由5位2进制比特表示的31个信号状态与一对6进制符号相对应,然而这种传输方法的效率为2.5比特/符号,与最大传输效率
比特/符号相比,每个符号传递的信息有将近0.1比特的损失。文献[14]将同样的转换方法应用于6-PSK调制,提出了差分编码与6-PSK相结合的方案。但与未编码相比,6-PSK与差分编码结合方案有0.2 dB的性能损失。
多进制LDPC码与对应阶的高阶调制结合可以实现符号级的匹配,避免比特与符号转换带来的性能损失,进一步优化误码率性能以保证信息传输的可靠性[15]。多进制LDPC码与对应阶的高阶调制结合主要分为两类,即有限域GF(2p)LDPC码与2p阶高阶调制的结合[16-18]和非2的幂次的高阶调制与对应进制的LDPC码的结合[11,19-20]。第一类采用比特交织、多级网格编码方法或者非均匀星座调制与多进制LDPC码结合的方法,将编码比特和高阶调制星座融合在一起以获得性能的优化。但随着调制阶数2p的增加,多进制LDPC码的编译码复杂度会大幅提高,导致译码时间过长,实用性较低[16]。第二类结合方法通常针对调制阶数较低的非标准QAM星座图,相应的多进制LDPC码的编译码复杂度较低。对于素数阶的编码调制,文献[11]将提出的非均匀5-QAM与7-QAM调制分别与对应进制的LDPC码编码结合,进一步提高了编码调制方案的整体性能。文献[19]提出了一种适用于卫星通信系统的7-QAM与GF(7) NB-LDPC码结合的编码调制方案,该方案将7-QAM与7进制的LDPC码结合,实现了符号级的匹配,有效地降低了对非线性失真的影响。对于非素数阶的编码调制,文献[20]提出了一种与18-QAM匹配的多级编码调制方案,该方案将1位2进制与2位3进制符号映射为1位18进制符号,将18-QAM与多级Turbo编码结合以实现匹配,但其误码率性能与基于16-QAM的编码调制方案相比仍存在0.6 dB的差距。对于3×2p进制,目前与3×2p阶调制匹配的LDPC码编码方案仍缺乏研究。
由于多进制LDPC码是二进制LDPC码在有限域GF(q)(q>2)上的扩展,有限域的阶数为素数或素数的幂[21]。因此,针对3×2p进制,难以在有限域上实现3×2p进制的LDPC码编码。针对6进制调制,提出了一种结合6-QAM与双层LDPC码的编码调制传输方案。本文采用GF(2) LDPC码与GF(3) LDPC码分层编码实现6进制编码,并在接收端迭代执行双层LDPC码的译码。提出的迭代译码方法通过GF(2) LDPC码译码信息与GF(3) LDPC码译码信息的互相传递,提高了系统的整体性能。在加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道下,一方面,与先执行GF(2) LDPC码译码后执行GF(3) LDPC码译码相比,先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码的编码调制方案实现了一定的性能增益。另一方面,在相同的频谱效率下,执行一次整体迭代译码时,采用先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码时,与基于6-PSK的编码调制方案相比,结合6-QAM与双层LDPC码的编码调制方案有更优的纠错性能。随着整体迭代次数的增加,在带来一定译码延时的同时,双层LDPC码的迭代译码性能获得了有效改善。
本文其余部分的安排如下。第2节介绍了6-QAM星座图的设计方法。第3节提出了面向6-QAM的双层编码调制传输方案,介绍了发送端的双层编码调制方案以及接收端的双层迭代译码方法。仿真结果与分析在第4节中给出。最后第5节总结了本文的工作。
2 6-QAM星座图设计与分析
针对进制数为非2的幂次的调制,一种新型的将元素0放在原点的QAM星座图受到关注。文献[11]设计的5-QAM星座图如图1(a) 所示,其中一个点位于原点,其余四个点分布在外圆上。5-QAM与GF(5) NB-LDPC码的结合提高了系统的整体性能。此外,文献[19]提出了一种7-QAM星座图,如图1(b)所示,7-QAM星座图为原点加正六边形的构型。7-QAM与GF(7) NB-LDPC码相结合有效地抵抗了卫星通信中存在的非线性失真。本文设计了一种如图1(c)所示的6-QAM星座图,其中一个星座点位于原点,其余五个星座点均匀分布于相邻相位差为2π/5的外圆上,其中,6-QAM星座图的半径
将第a个星座点表示为Sa, 则Sa的位置由2进制符号ba与3进制符号ta共同决定。Sa可表示为bata的形式,即每个星座点携带一位2进制符号与一位3进制符号的信息。
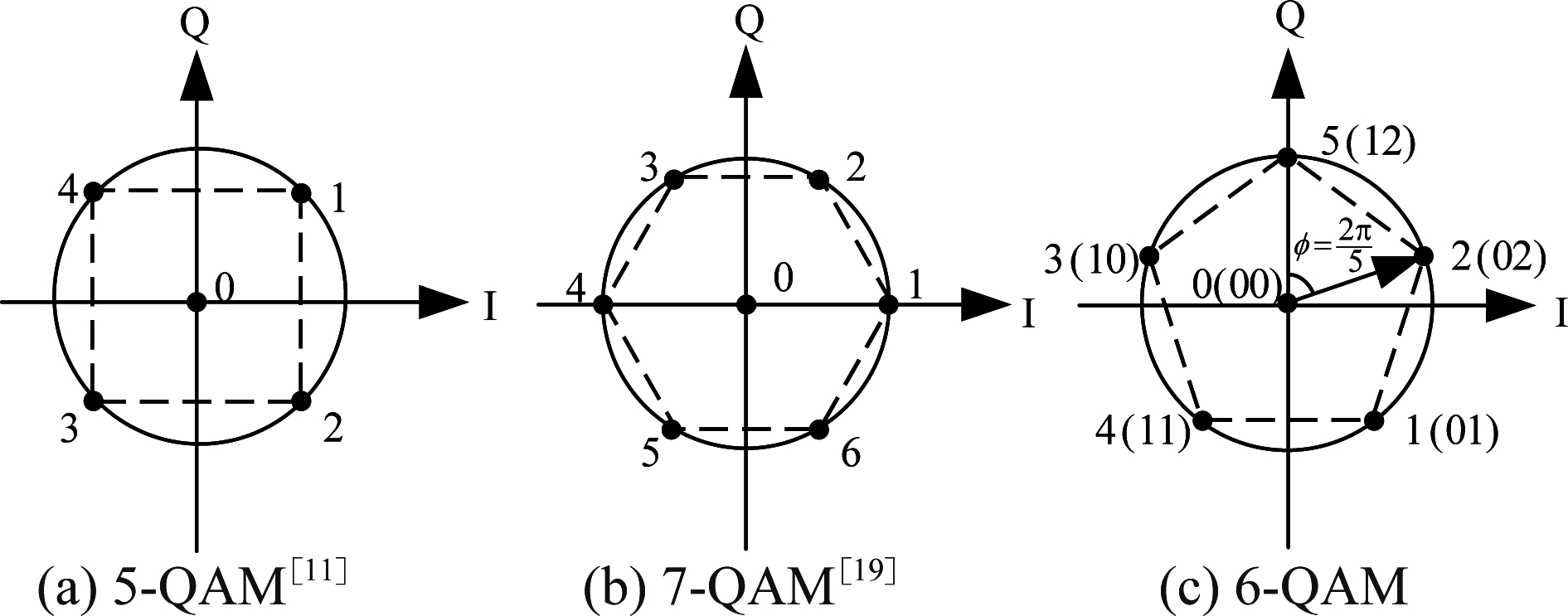
图1 星座图
Fig.1 Constellation diagram
首先,由图1所示的星座图分布,可计算得到三种星座图的最小欧氏距离dmin,计算结果如表1所示。θmin表示除符号‘0’外的最小相位差,dmin的值由功率归一化后计算得到。由表1可得,6-QAM的最小欧氏距离dmin比7-QAM的最小欧氏距离高10log(1.0954/1.0801)≈0.06 dB,比5-QAM的最小欧氏距离dmin低10log(1.1180/1.0954)≈0.09 dB。因而,在相同的平均功率下,6-QAM的抗噪声性能优于7-QAM的抗噪声性能。
表1 三种星座图的基本参数
Tab.1 Parameters of three constellations
其次,由最小欧氏距离dmin可以推导出QAM的误符号率的上界,M-QAM的误符号率Ps(M-QAM)上界如式(1)所示[20],其中Q函数表示为
表示调制阶数,α表示与最小欧氏距离对应的相邻星座点的数量。由图1易知,对于5-QAM、6-QAM与7-QAM的星座图,α的取值分别为4、5和6。由式(1)可得,6-QAM的误符号率介于5-QAM与7-QAM的误符号率之间。
(1)
6-PSK的误符号率计算公式如式(2)所示[13],其中erfc函数表示为
(2)
3 面向6-QAM的双层编码调制传输方案
本节首先给出了发送端基于GF(2) LDPC码与GF(3) LDPC码的分层编码方法;然后介绍了接收端双层LDPC码间的迭代译码方法。
3.1 发送端的双层编码调制方案
多进制编码阶数与高阶调制阶数匹配时,通信系统获得的译码性能最佳[11]。为实现与6-QAM匹配的多进制编码,本文提出了一种组合GF(2) LDPC码与GF(3) LDPC码的分层编码方法,两种LDPC码编码均采用基于重复累加(Repeat Accumulate, RA)结构的校验矩阵[22]。
图2给出基于6-QAM的编码调制方案发送端框图。在发送端,首先,信息序列U经过串并转换分为GF(2)信息序列UB和GF(3)信息序列UT两部分;然后,将UB和UT分别输入GF(2) LDPC码编码器和GF(3) LDPC码编码器,分层执行GF(2) LDPC码编码与GF(3) LDPC码编码,GF(2)的信息序列为UB={ub0,ub1,…,ubk-1}, GF(2) LDPC码编码所需的校验矩阵用HB表示,执行UB与HB的编码计算得到GF(2) LDPC码的码字CB={cb0,cb1,…,cbn-1}。同理,GF(3)信息序列为UT={ut0,ut1,…,utk-1},对应的校验矩阵表示为HT,执行UT与HT的编码运算,得到GF(3) LDPC码的码字CT={ct0,ct1,…,ctn-1}。进一步,按照设计的映射关系将CB与CT映射为6进制码字C;最后,将6进制码字C采用前面所述的6-QAM进行调制,调制后得到的符号序列X经噪声方差为σ2的AWGN信道传输。
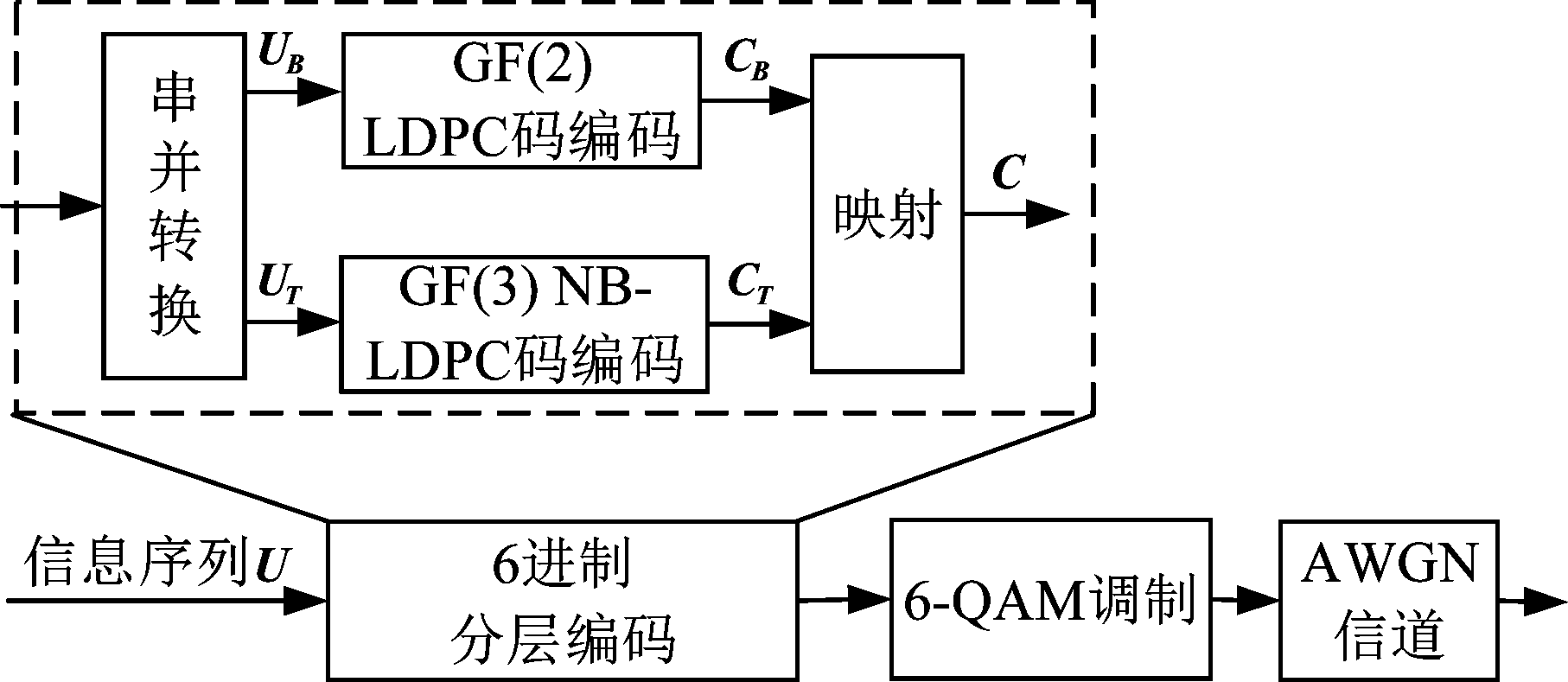
图2 基于6-QAM的编码调制方案发送端框图
Fig.2 The transmitter block diagram of coded modulation
scheme with 6-QAM
为使相邻星座点对应的符号间具有最小的平均符号差,本文设计了如图3所示的映射规则,相邻的6进制符号之间相差一位符号。图3中第一列表示GF(2)元素即0和1,第二列表示GF(3)的元素0、1和2。6进制码字中每个6进制符号由两位符号构成,其中第一位表示GF(2) LDPC码的码字符号,第二位表示GF(3) LDPC码的码字符号。GF(2)符号与GF(3)符号的组合共有6种。这6种组合与6进制元素0～5一一对应。
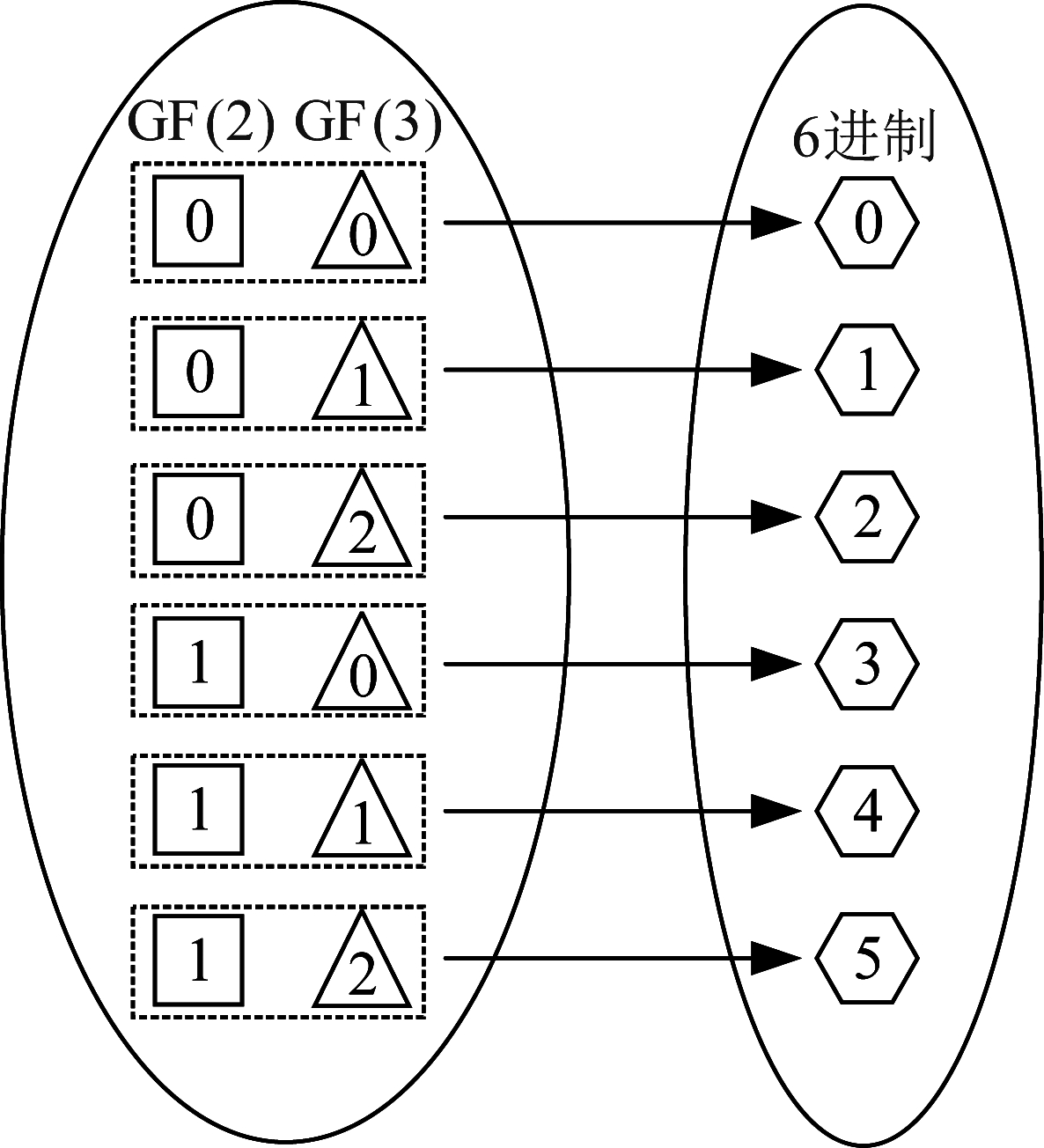
图3 GF(2)、GF(3)与6进制的符号映射关系
Fig.3 Mapping relationship between GF(2),GF(3) and senary symbols
3.2 接收端的双层迭代译码方法
集分割方法是编码调制方案设计的重要手段,通过将符号集合划分为更小的子集,使得子集内最小平方欧氏距离递增，从而实现更低的误码率[23]。本小节介绍了双层LDPC码间的迭代译码方法,对二进制集分割与三进制集分割方法进行了分析。
首先,介绍二进制集分割方法,6-QAM的二进制集分割示意图如图4所示,根据2进制符号ba的值将6个星座点的集合S划分为2个子集
和
每个子集包含3个符号,若ba=0,则子集为
若ba=1,则子集为
根据3进制符号ta的值将和
对应至6个星座点。由图5可知,相较于二进制集分割前，集合的最小欧氏距离为集合S的最小平方欧氏距离为6/5=1.2，二进制集分割后，子集S′0内星座点间的最小平方欧氏距离为1.2，子集的最小平方欧氏距离为1.6584。
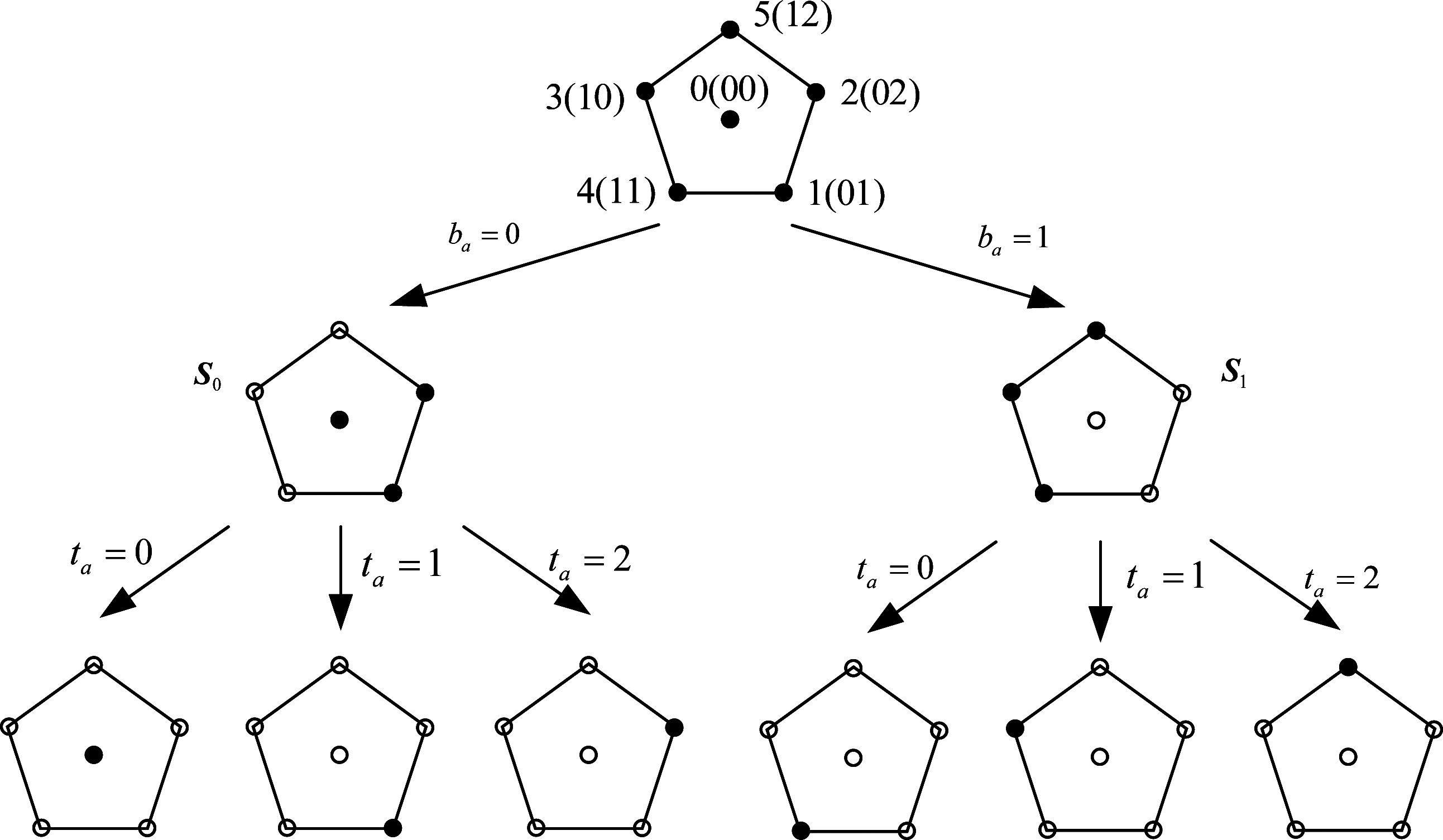
图4 6-QAM的二进制集分割示意图
Fig.4 Binary set partition diagram for 6-QAM
与二进制集分割对应的迭代译码方法先执行GF(2) LDPC码译码后执行GF(3) LDPC码译码,其框图如图5所示。首先,计算接收到的6进制符号的软解调概率信息P,然后执行两种LDPC码间的迭代译码。具体来说,首先在①处根据软解调概率P计算GF(2) LDPC码译码初始概率,执行GF(2) LDPC码的译码;然后在②处根据GF(2) LDPC码译码的后验概率与软解调概率P计算GF(3) LDPC码译码的初始概率,并执行GF(3) LDPC码的译码,至此完成一次整体迭代。此时,若达到预设的最大整体迭代次数,则停止迭代,将所得GF(2) LDPC码的译码码字
与GF(3) LDPC码的译码码字
映射为6进制译码码字;否则,返回①处,根据GF(3) LDPC码译码的后验概率与软解调概率信息P更新GF(2) LDPC码译码的初始概率,继续执行GF(2) LDPC码译码。
图5 基于二进制集分割的迭代译码方法框图
Fig.5 Block diagram of iterative decoding method based on binary set partition
具体地,与二进制集分割对应的迭代译码方法流程图如图6所示,其中,GF(2) LDPC码译码采用对数域的置信度传播(Log-BP)算法[24],GF(3) LDPC码译码算法采用多进制BP算法[25]。GF(2) LDPC码与GF(3) LDPC码间的译码最大迭代次数表示为Iterout。GF(2) LDPC码译码最大迭代次数与GF(3) LDPC码译码最大迭代次数均表示为Iterin。具体步骤如下:
在接收端,首先,对接收到的6进制符号根据6-QAM星座图进行符号解映射, 输出符号Y的似然信息值的计算公式如式(3)所示:
a=0,1,…,5
(3)
其中,yl表示第l个接收到的6进制符号坐标,l=1,2,…,n。xa表示6-QAM星座点的复数坐标。将第l个接收的符号为a的概率记为
的计算公式如式(4)所示:
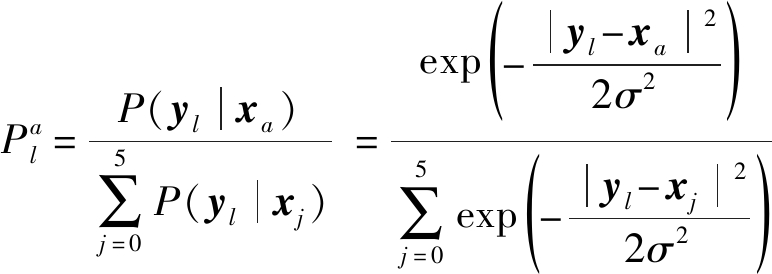
(4)
根据6进制符号的软解调信息
计算GF(2) LDPC码译码的初始概率PB,并执行GF(2) LDPC码译码,得到GF(2) LDPC码的译码码字
具体计算公式如式(5)所示。2进制符号为0的初始概率为接收到第l个6进制符号是0、1和2的概率之和,记为
则2进制符号为1的初始概率为接收的第l个6进制符号是3、4和5的概率之和,记为
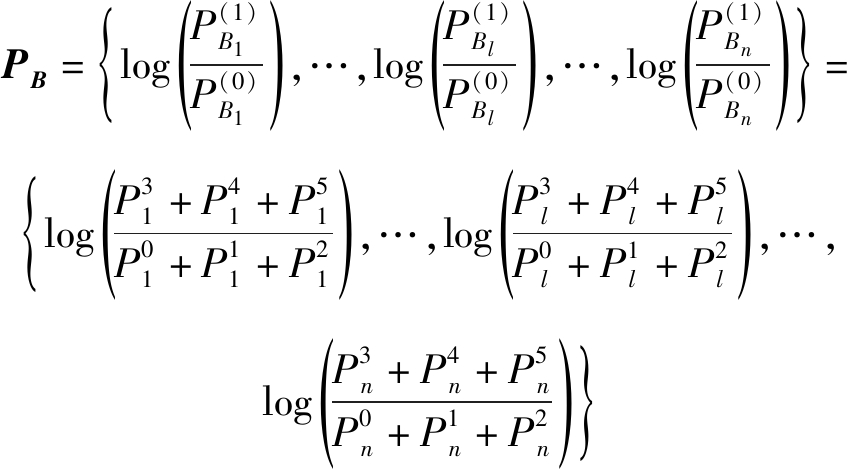
(5)
进一步,依据GF(2) LDPC码译码后验概率postB与6进制符号的软解调概率,计算GF(3) LDPC码译码初始概率PT,并执行GF(3) LDPC码译码,得到GF(3) LDPC码码字
译码过程中,若满足校验方程
或达到设定的最大迭代次数Iterin,则结束GF(3) LDPC码译码迭代。第l个GF(3) LDPC码的码字符号的译码初始概率PTl计算公式如式(6)所示,其中
和
分别表示第l个GF(3) LDPC码码字符号为0、1和2的概率。
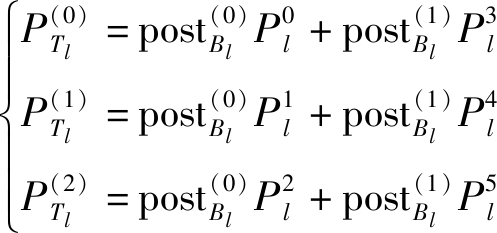
(6)
执行一次GF(2) LDPC码译码与GF(3) LDPC码译码即完成一次双层LDPC码间的整体迭代。此时,若达到最大整体迭代次数Iterout,则停止译码;否则,更新GF(2) LDPC码译码的初始概率PB,继续执行GF(2) LDPC码译码。进一步,PB由GF(3) LDPC码译码的后验概率postT与6进制符号的软解调信息进行更新。具体而言,第l个GF(2) LDPC码的码字符号的译码初始概率PBl更新规则如式(7)所示,第l个GF(3) LDPC码码字为0、1和 2的后验概率分别表示为
和
(7)
整体迭代结束后,将GF(2) LDPC码译码码字
与GF(3) LDPC码译码码字
按照图3所示的规则映射为6进制码字
得到恢复后的信息序列。
图6 基于二进制集分割的六进制码迭代译码方法流程图
Fig.6 Flow chart of iterative decoding method for senary code based on binary set partition
其次,6-QAM的三进制集分割示意图如图7所示,根据ta的值将6个星座点集合S划分为三个子集S0、S1和S2。若ta=0,则子集为S0={0,3},若ta=1,则子集为S1={1,4}。若ta=2,则子集为S2={2,5}。进一步,根据ba的值将S0、S1和S2对应至6个星座点。三进制集分割后，子集S0的最小平方欧氏距离为1.2，子集S1与S2的最小平方欧氏距离均为1.6584。
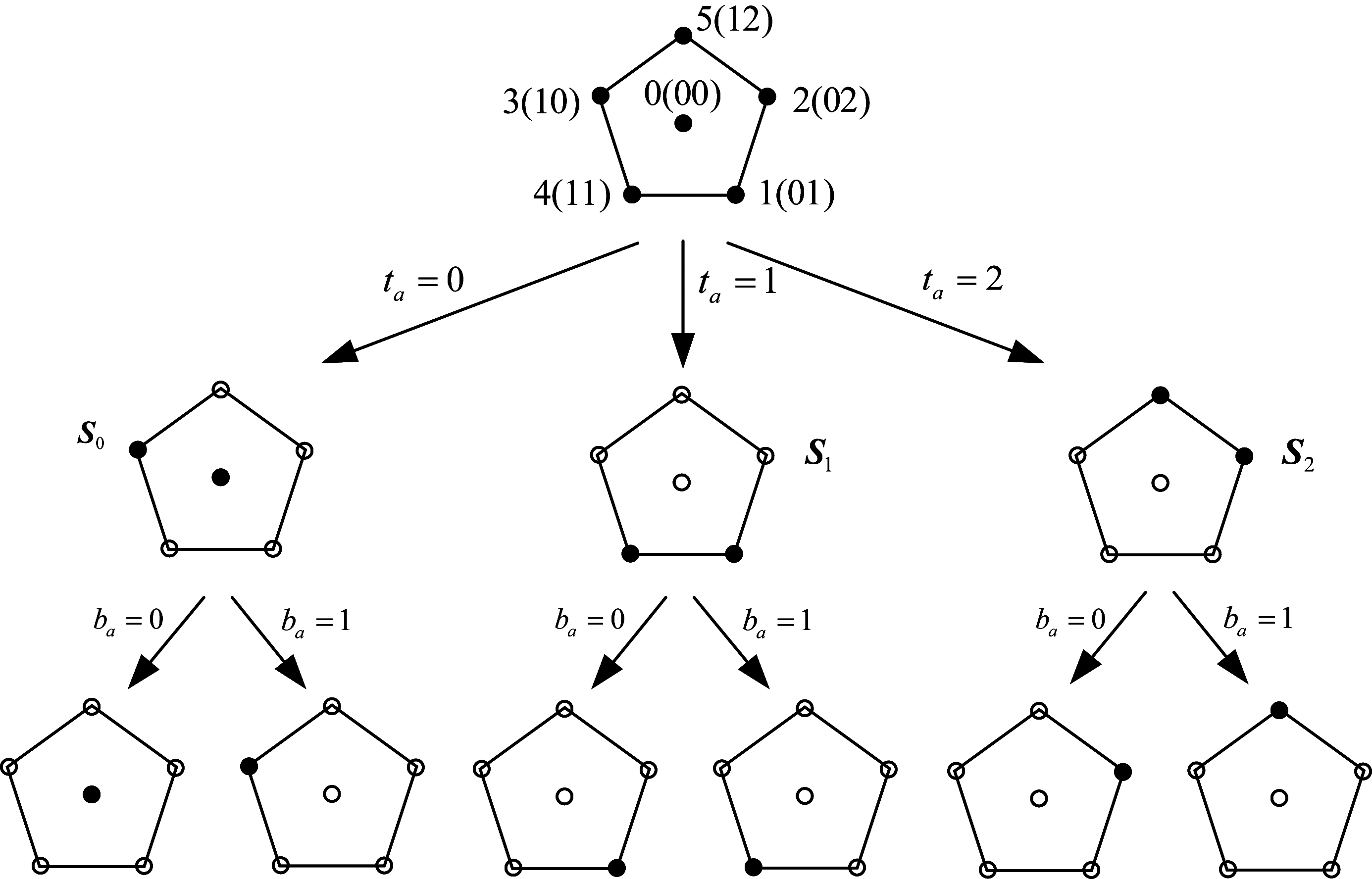
图7 6-QAM的三进制集分割示意图
Fig.7 Ternary set partition diagram for 6-QAM
与三进制集分割对应的迭代译码方法先执行GF(3) LDPC码的译码后执行GF(2) LDPC码的译码,其流程具体如下,其中,GF(2) LDPC码译码和GF(3) LDPC码译码算法以及相关参数值的设置与二进制集分割对应的迭代译码方法相同,此处不再详述。在接收端,首先根据式(3)、式(4)计算接收到的6进制符号的软解调概率信息,然后执行迭代译码过程。
首先根据6进制符号的软解调概率计算GF(3) LDPC码译码初始概率PT,并执行GF(3) LDPC码译码,得到GF(3) LDPC码码字
LDPC码译码时,第l个符号的初始概率PTl的计算公式如式(8)所示。
(8)
然后,依据GF(3) LDPC码译码的后验概率postT与6进制符号的软解调信息,计算GF(2) LDPC码译码的初始概率PB,执行GF(2) LDPC码译码,得到GF(2) LDPC码译码码字
具体而言,GF(2) LDPC码译码时,第l个符号的初始概率PBl的计算公式如式(9)所示,
(9)
至此,完成一次双层LDPC码间的整体迭代。此时,若达到最大整体迭代次数Iterout则停止迭代,否则,继续执行GF(3) LDPC码译码。GF(3) LDPC码译码初始概率PT通过GF(2) LDPC码译码的后验概率postB与6进制符号的软解调信息计算更新。第l个3进制符号的概率更新规则如式(10)所示,
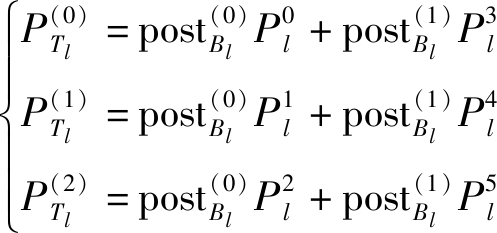
(10)
整体迭代结束后,将GF(2) LDPC码译码码字
与GF(3) LDPC码译码码字
映射为6进制码字得到恢复的信息序列。
4 仿真结果
本节对提出的结合6-QAM与双层LDPC码的编码调制方案进行了性能仿真,在AWGN信道下,首先仿真了不同调制的软解调性能,其次,分析了采用不同译码顺序的双层迭代译码方法的误符号率(Symbol Error Rate, SER)性能;进一步,分别在AWGN信道下和瑞利衰落信道下,与结合6-PSK的双层LDPC码的编码调制方案以及其他进制的编码调制方案的性能进行了比较。为方便起见,先执行GF(2) LDPC码译码后执行GF(3) LDPC码译码的迭代译码方法称为方案一,先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码的迭代译码方法称为方案二。作为比较的几种编码调制方案均采用相同结构的校验矩阵,LDPC码的码率均为0.5,码长为6000个对应进制的符号。如GF(5) NB-LDPC码的码长为6000个5进制符号,GF(7) NB-LDPC码的码长为6000个7进制符号。GF(5) NB-LDPC码与GF(7) NB-LDPC码译码迭代次数设置为20次。Iter表示GF(2) LDPC码与GF(3) LDPC码整体迭代的次数。GF(2) LDPC码译码的最大迭代次数与GF(3) LDPC码的最大迭代次数均设为20。
4.1 不同调制的软解调性能
本部分仿真了AWGN信道下6-QAM与5-QAM、7-QAM及6-PSK未编码时的误符号率,仿真结果如图8所示。由图8可知,6-QAM的软解调性能介于5-QAM与7-QAM之间,与理论分析一致。SER为10-5时,与7-QAM,6-PSK的解调信噪比(Signal to Noise Ratio,SNR)门限相比,6-QAM的解调SNR门限分别有0.3 dB和0.8 dB的增益。
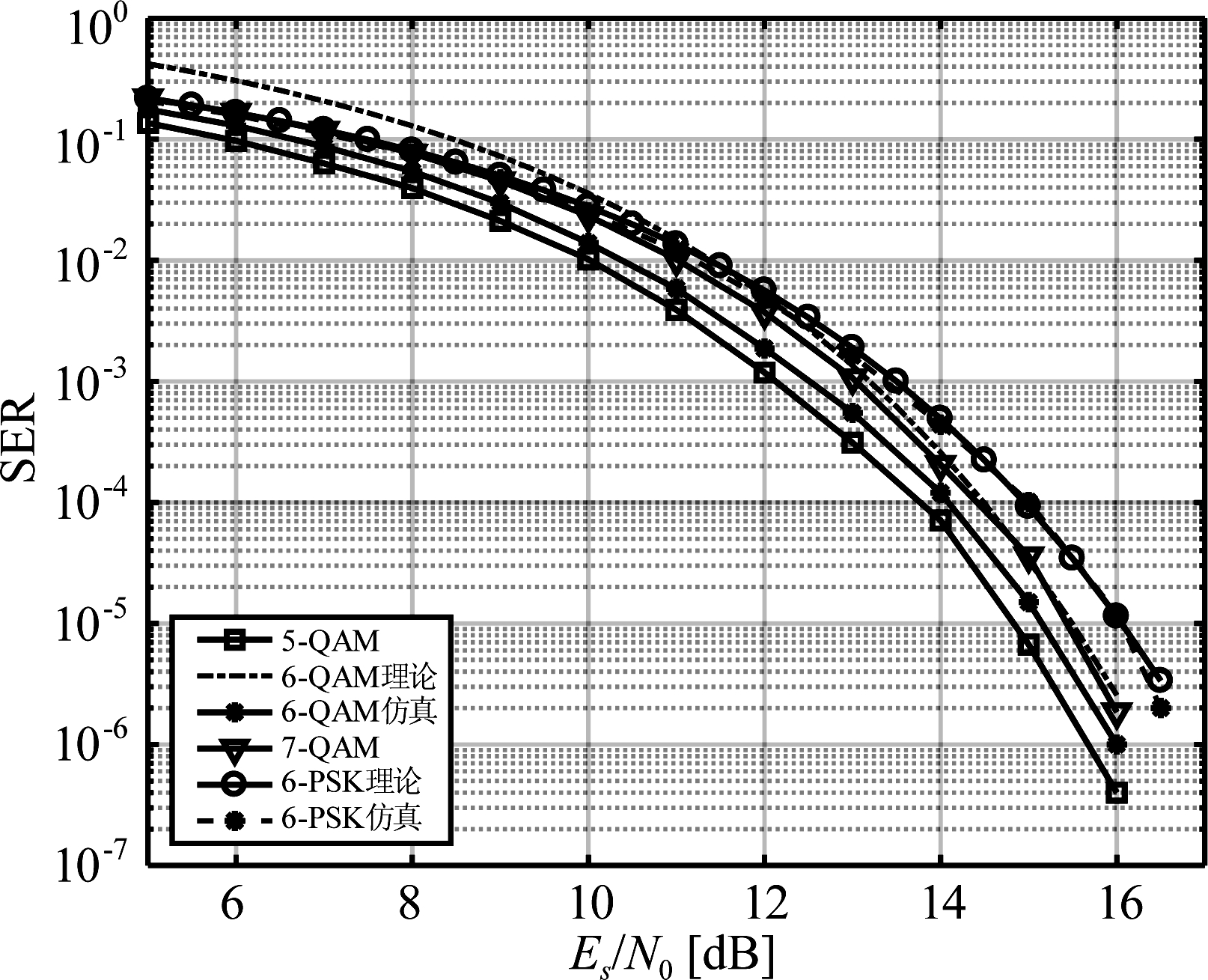
图8 AWGN信道下不同调制的误符号率性能
Fig.8 SER performance of various modulations under the AWGN channel
4.2 基于6-QAM的双层LDPC码在不同译码顺序下的性能
首先,仿真验证了采用不同译码顺序时基于6-QAM的双层编码方案的SER性能。如图9所示,一方面,整体迭代次数相同时,方案二与方案一相比,获得了更大的性能增益;另一方面,随着迭代次数的增加,两种方案的误码性能均得到了进一步改善。SER为10-6时,与整体迭代1次相比,迭代2次时,方案一与方案二分别获得了0.1 dB与0.2 dB的增益。
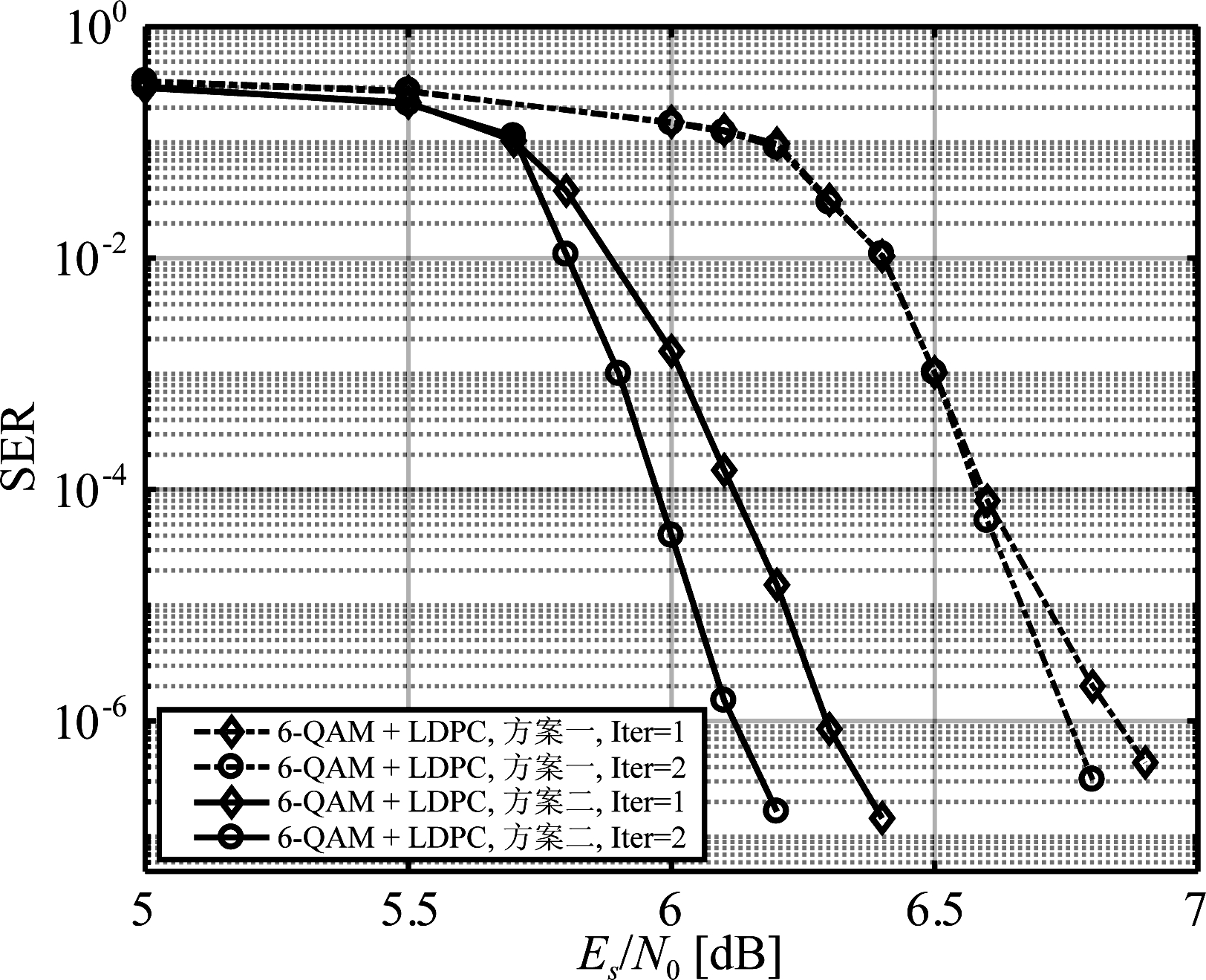
图9 基于6-QAM的双层编码调制方案的SER性能
Fig.9 SER performance of two-level coded modulation schemes for 6-QAM
为进一步分析两种方案中LDPC码的纠错性能,图10给出了不同整体迭代次数下,两种编码调制方案中GF(2) LDPC码与GF(3) LDPC码的译码性能。图10中横坐标Es/N0指的是整体方案的符号信噪比。由图10可以观察到,不同的集分割方法与译码方法对纠错性能的影响较大。一方面,方案一首先执行GF(2) LDPC码的译码,方案二首先执行GF(3) LDPC码的译码,整体迭代一次时,SER为10-5时,图10(b)所示方案二中第一级GF(3) LDPC码的误码率低于图10(a)所示方案一中第一级GF(2) LDPC码的误码率,这验证了三进制集分割方法的有效性。另一方面,图10(a)中,随着迭代次数的增加,GF(2) LDPC码有较小的增益,GF(3) LDPC码几乎没有性能增益,而在图10(b)中,随着迭代次数的增加,GF(2) LDPC码与GF(3) LDPC码之间实现了译码信息的有效传递,两者的SER性能均有明显改善。因而,对于本文提出的基于6-QAM的两种编码调制方案,采用三进制集分割的方法对星座图进行划分,对应的先执行GF(3) LDPC码译码,后执行GF(2) LDPC码译码的迭代译码方法获得了更优的译码性能。
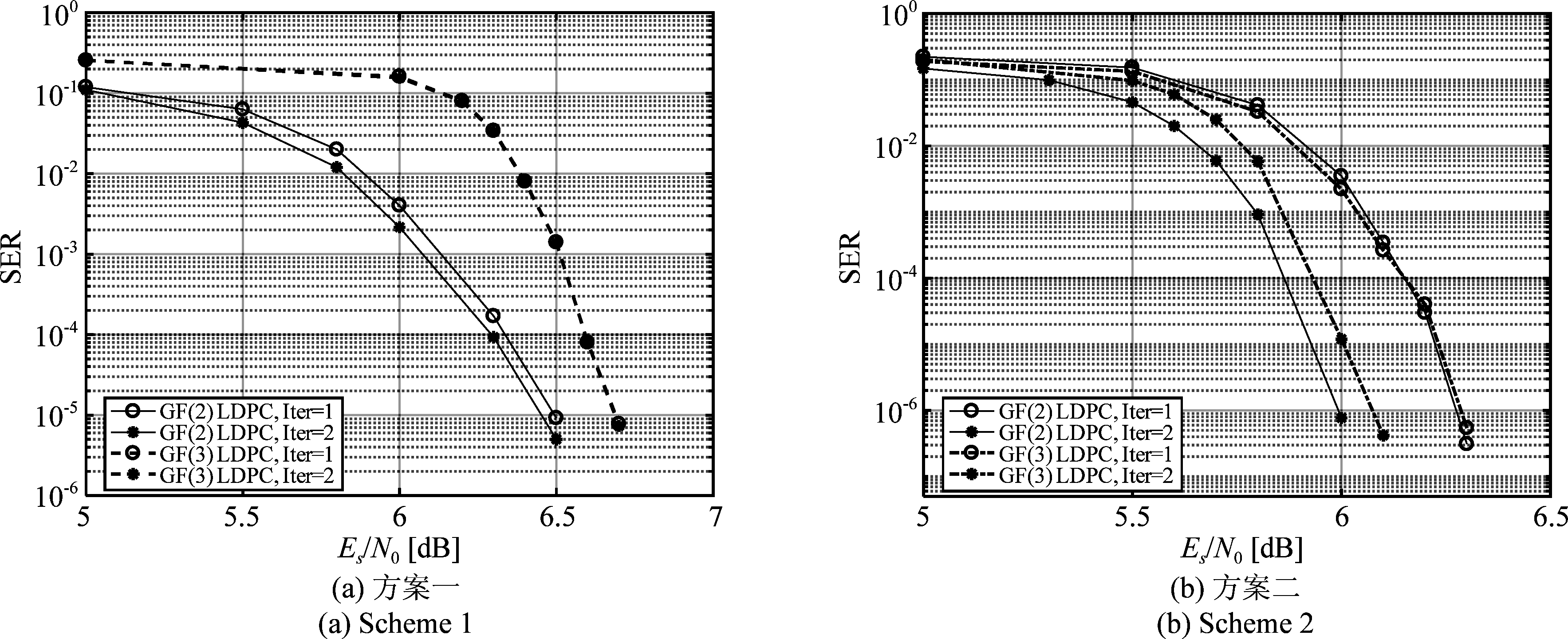
图10 GF(2) LDPC码与GF(3) LDPC码的SER性能
Fig.10 SER performance of GF(2) LDPC code and GF(3) LDPC code
4.3 双层编码调制与其他方案的比较
图11给出了AWGN信道及瑞利衰落信道下,先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码时,提出的6-QAM的双层编码调制方案与基于6-PSK的编码调制方案和相邻进制的编码调制方案的SER性能。基于6-PSK的编码调制方案采用本文提出的编译码方法,其中瑞利衰落信道下假设每个符号的衰落独立同分布。首先在AWGN信道下,星座点间最小平方欧氏距离即
是影响编码调制方案性能的主导因素,6-QAM星座的最小平方欧氏距离为1.2,而6-PSK星座中最小平方欧氏距离为1,因而采用相同结构的LDPC码时,由图11(a)可知,基于6-QAM的编码调制方案获得了更优的性能。具体地,SER为10-5时,先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码时,与基于6-PSK的编码调制方案相比,6-QAM结合双层LDPC码的传输方案获得了约1.3 dB的增益。另一方面,从图11(a)可以观察到,GF(2) LDPC码与GF(3) LDPC码分别执行1次译码时,与7-QAM和GF(7) NB-LDPC码结合的编码调制方案相比,SER为10-5时,6-QAM的双层编码调制方案有更优性能。迭代2次时,与5-QAM和GF(5) LDPC码结合的编码调制方案相比,仅有约0.3 dB的性能损失。其次,由图11(b)可以观察到,执行一次译码时,采用先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码的6-QAM编码调制方案与采用先执行GF(2) LDPC码译码后执行GF(3) LDPC码译码的6-PSK编码调制方案和7-QAM结合GF(7) NB-LDPC码的两种方案相比,在瑞利衰落信道下同样获得了更优的误码性能。
图11 不同编码调制方案的SER性能
Fig.11 SER performance of different coded modulation schemes
在复杂度方面,针对基于GF(q)的不同进制的LDPC码,当译码采用多进制BP算法时,其运算复杂度为O(q2),随着进制数的增加,多进制LDPC码的译码复杂度呈指数增长[25]。但是,由于6进制不是素数或素数的幂,难以实现基于GF(q)的6进制编码[21]。因此,本文采用GF(2) LDPC码与GF(3) LDPC码组合实现双层编译码,从而实现与6进制调制的匹配。但是,双层迭代译码随着整体迭代次数的增加,在提高译码性能的同时也会增加译码复杂度,带来一定的译码延时。对于图11中基于6-PSK和6-QAM的编码调制方案,均采用双层LDPC码的编译码方法,因而二者的复杂度是相当的。综上所述,本文提出的基于双层LDPC码的编译码方法与6-QAM实现了匹配,且采用先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码的迭代译码方法获得了更优的纠错性能。
5 结论
为实现与非标准多进制QAM调制匹配的编码,本文提出了结合6-QAM与双层LDPC码的双层编码调制传输方案,并对其SER性能进行了仿真。在发送端,通过GF(2) LDPC码与GF(3) LDPC码分层编码的方式,组合映射得到6进制码字,从而实现与6-QAM的匹配。在接收端,提出了两种针对编码调制的双层迭代译码方法,通过GF(2) LDPC码与GF(3) LDPC码之间译码信息的循环迭代,不断修正各自译码所需的概率信息,提高了译码成功的概率,进而有效改善了整体传输方案的SER性能。仿真结果表明,AWGN信道下,本文提出的基于双层LDPC码的编译码方法实现了与非标准6-QAM的匹配,采用先执行GF(3) LDPC码译码后执行GF(2) LDPC码译码的编码调制方案与采用先执行GF(2) LDPC码译码后执行GF(3) LDPC码译码编码调制方案相比,获得了更优异的纠错性能。随着迭代次数的增加,提出的编码调制方案的纠错性能有进一步改善。
[1] DJORDJEVIC I B. On advanced FEC and coded modulation for ultra-high-speed optical transmission[J]. IEEE Communications Surveys & Tutorials, 2016, 18(3): 1920-1951.
[2] TZIMPRAGOS G, KACHRIS C, DJORDJEVIC I B, et al. A survey on FEC codes for 100 G and beyond optical networks[J]. IEEE Communications Surveys & Tutorials, 2016, 18(1): 209-221.
[3] WANG Zhihui, WANG Liqian, WANG Dongdong, et al. Superposition Construction of NB-QC-LDPC Codes for optical communication systems[C]∥2019 18th International Conference on Optical Communications and Networks (ICOCN). Huangshan, China. IEEE, 2019: 1-3.
[4] BEYGI L, AGRELL E, KAHN J M, et al. Rate-adaptive coded modulation for fiber-optic communications[J]. Journal of Lightwave Technology, 2014, 32(2): 333-343.
[5] 周林, 卢进, 彭盛亮, 等. 可变速率多元LDPC码高阶调制系统[J]. 信号处理, 2013, 29(10): 1368-1375.
ZHOU Lin, LU Jin, PENG Shengliang, et al. Non-binary rate-compatible LDPC-coded High order modulation system[J]. Journal of Signal Processing, 2013, 29(10): 1368-1375.(in Chinese)
[6] SINGYA P K, KUMAR N, BHATIA V, et al. On performance of hexagonal, cross, and rectangular QAM for multi-relay systems[J]. IEEE Access, 2019, 7: 60602- 60616.
[7] ARABACI M, DJORDJEVIC I B, XU Lei, et al. Four-dimensional nonbinary LDPC-coded modulation schemes for ultra-high-speed optical fiber communication[J]. IEEE Photonics Technology Letters, 2011, 23(18): 1280-1282.
[8] LIN Changyu, DJORDJEVIC I B, CVIJETIC M, et al. Mode-multiplexed multi-Tb/s superchannel transmission with advanced multidimensional signaling in the presence of fiber nonlinearities[J]. IEEE Transactions on Communications, 2014, 62(7): 2507-2514.
[9] SVENSSON A. An introduction to adaptive QAM modulation schemes for known and predicted channels[J]. Proceedings of the IEEE, 2007, 95(12): 2322-2336.
[10] CONTI A, WIN M Z, CHIANI M. Slow adaptive M-QAM with diversity in fast fading and shadowing[J]. IEEE Transactions on Communications, 2007, 55(5): 895-905.
[11] LIN Changyu, ZOU Ding, LIU Tao, et al. Capacity achieving nonbinary LDPC coded non-uniform shaping modulation for adaptive optical communications[J]. Optics Express, 2016, 24(16): 18095-18104.
[12] NODA S, SAITO Y, YOSHIDA T. Configuration and error ratio performance of M-QAM whose number of signal points is not a power of 2[J]. Electronics and Communications in Japan (Part I: Communications), 2007, 90(2): 46-57.
[13] LE A T, ARAKI K. A group of modulation schemes for adaptive modulation[C]∥2008 11th IEEE Singapore International Conference on Communication Systems. Guangzhou, China. IEEE, 2008: 864- 869.
[14] NODA S, KOIKE S. Optimum binary to symbol coding for 6PSK and bit error rate performance[C]∥2007 IEEE Wireless Communications and Networking Conference. Hong Kong, China. IEEE, 2007: 509-513.
[15] LI Ge, FAIR I J, KRZYMIEN W A. Density evolution for nonbinary LDPC codes under Gaussian approximation[J]. IEEE Transactions on Information Theory, 2009, 55(3): 997-1015.
[16] PAN Xiaoqing, JIANG Ming. A hybrid symbol mapping for non-binary LDPC coded modulation with QAM signaling[C]∥2016 8th International Conference on Wireless Communications & Signal Processing (WCSP). Yangzhou, China. IEEE, 2016: 1-5.
[17] WANG Liqian, WANG Dongdong, NI Yongjing, et al. Design of irregular QC-LDPC code based multi-level coded modulation scheme for high speed optical communication systems[J]. China Communications, 2019, 16(5): 106-120.
[18] WU Zhanji, KANG Weimin. A time sharing hybrid probabilistic shaping scheme for nonbinary LDPC codes[J]. IEEE Access, 2020, 8: 65488- 65497.
[19] LIU Yanyan, CHEN Weigang, WANG Anguo, et al. Combination of high-order modulation and non-binary LDPC codes over GF(7) for non-linear satellite channels[J]. Electronics, 2019, 8(12): 1396-1411.
[20] TANAHASHI M, OCHIAI H. A multilevel coded modulation approach for hexagonal signal constellation[J]. IEEE Transactions on Wireless Communications, 2009, 8(10): 4993- 4997.
[21] 史治平, 李少谦, 周亮. 多元LDPC码及其在无线通信中的应用[M]. 北京: 国防工业出版社, 2012：18-25.
SHI Zhiping, LI Shaoqian, ZHOU Liang. Non-binary low-density parity-check codes and their applications in wireless communications[M]. Beijing: National Defense Industry Press, 2011: 18-25. (in Chinese)
[22] CHEN Weigang, LIANG Chenchi, GUO Tai, et al. Encoder implementation with fpga for non-binary LDPC codes[C]∥2012 18th Asia-Pacific Conference on Communications(APCC).Jeju,Korea(South).IEEE,2012: 980-984.
[23] WACHSMANN U, FISCHER R F H, HUBER J B. Multilevel codes: Theoretical concepts and practical design rules[J]. IEEE Transactions on Information Theory, 1999, 45(5): 1361-1391.
[24] CHEN Jinghu, FOSSORIER M P C. Near optimum universal belief propagation based decoding of low-density parity check codes[J]. IEEE Transactions on Communications, 2002, 50(3): 406- 414.
[25] DECLERCQ D, FOSSORIER M. Decoding algorithms for nonbinary LDPC codes over GF(q) [J]. IEEE Transactions on Communications, 2007, 55(4): 633- 643.
