1 引言
合成孔径雷达(Synthetic aperture radar, SAR)由于其全天时、全天候工作的能力,在军事和民用领域得到了广泛的应用[1]。但是,传统的线性阵列雷达只能对阵列单元前方区域进行单一视角观测,不能对大视角大场景区域进行感知。针对其在广域观测中的不足,一种基于弧形阵列天线的SAR成像系统被提出,与线性阵列成像方式相比,其具有大视角的观测能力[2-9]。弧形阵列SAR(Arc array SAR)通过在方位向上沿圆弧向布置的天线阵元实现了弧形孔径合成,其指向沿圆弧逐渐移动,既能实现孔径合成,又能扩大阵列向成像观测范围。但是,传统的单基弧形阵列SAR的发射机与接收机被放置在同一平台,这不仅使雷达很容易于被探测到,也影响了其目标探测与识别的能力。
双基SAR(Bistatic SAR)克服了传统单基SAR的不足,在这种模式下,雷达的发射机和接收机被安置在两个不同的平台,减少了接受机和发射机系统复杂度,设备安装也更为简单,还能提供更多目标双基地反射率中包含的附加信息[10-18]。双基弧形阵列SAR(Arc array bistatic SAR)是一种新的机载高分辨率阵列雷达成像模式,其继承了弧形阵列SAR与双基SAR的优点,在实现平台周围全方位快速观测,大视场高分辨率成像的同时,减小了接收机被发现的概率,大大提高了被动接收雷达的战场生存能力。而且,多角度多方位的观测提供了观测目标的更多的信息,使双基弧形阵列SAR具备了三维成像的能力[19-21]。
但是,由于双基弧形阵列SAR天线特殊的圆弧型构造的影响,常规的用于线性阵列的成像方法无法满足成像要求,而在成像算法的设计过程中,其驻定相位点也无法用传统的驻定相位原理来解析出,因此其回波信号的二维频谱也无法得到。文献[22]将斜距模型进行二阶泰勒级数展开,所引入的误差较大,会对成像结果产生影响,因此需要寻找一种新的适用于双基弧形阵列SAR的频谱推导方法。本文引入了隐函数导数(Derivatives of an Implicit Function, DIF)的思想,将驻定相位点当作多普勒频率(方位频率)的隐函数,通过对该隐函数进行求导得到驻定相位点关于多普勒频率的各阶导数表达式,然后在方位频率为零处将驻定相位点展开成距离频率的泰勒级数,进而求解出该驻相点,这样一来,就可以直接运用驻定相位原理来推导出其二维频谱表达式。
本文内容结构安排如下,第2节首先详细介绍了双基弧形阵列SAR的天线结构、基本工作原理、成像几何与回波信号模型,然后引入隐函数思想推导出了的双基弧形阵列SAR回波信号的二维频谱,第3节基于求出的二维频谱提出了一种适用于双基弧形阵列SAR的成像处理方法;第4节通过点目标的仿真验证了提出的成像处理方法的有效性;第5节对本文进行了总结。
2 双基弧形阵列SAR
2.1 成像几何
双基弧形阵列SAR作为一种新型的机载SAR观测系统,它采用了一种广域圆环的波束扫描方式,具有更大的观测区域,加快了雷达获取场景信息的速度。其中,无源的弧形阵列接收天线是该系统中最重要的组成部分,它关系到整个成像系统能否实现全方位的快速成像。无源弧形阵列天线的结构如图1所示,“AB”代表无源接收天线单元,多个天线单元沿着圆弧均匀排列,每个天线单元之间的角度间隔被设置为ΔθInterval,弧形阵列天线的半径为Rr,θs是弧形阵列天线的合成孔径角度,θa代表沿着天线阵列方向的方位向波束宽度,Nr是天线阵列中被用来合成孔径的天线单元的数量。在双基弧形阵列SAR系统中,无源弧形阵列天线利用微波开关控制天线单元,使其指向沿圆弧逐渐移动,既能实现孔径合成,又扩大了阵列向成像观测范围,另外,与现有线性阵列SAR相比,双基弧形阵列SAR天线采用刚性基线结构,很大程度上降低了飞机机身震颤对天线的影响,有利于系统的实现[5]。
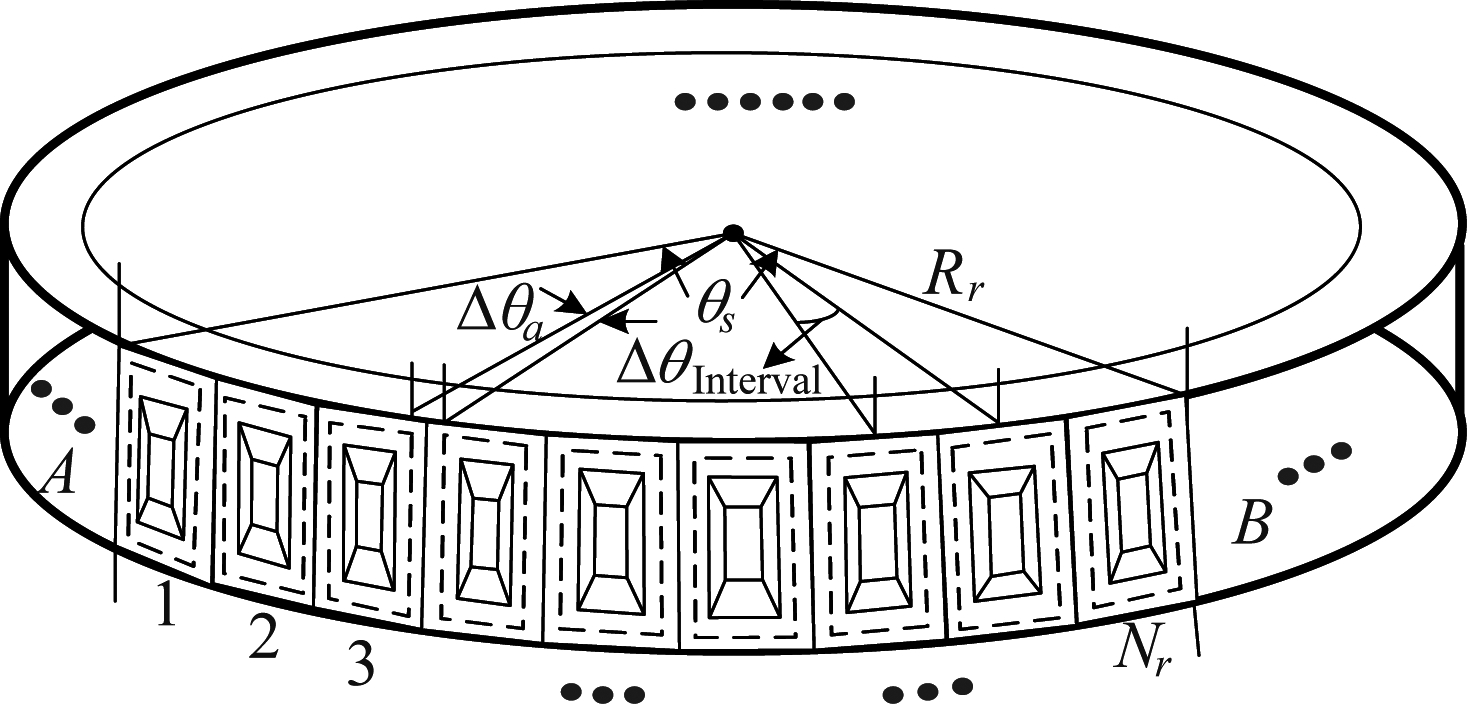
图1 无源弧形阵列接收天线的结构
Fig.1 Configuration of arc array antenna
双基弧形阵列SAR简化后的工作模式如图2所示。直升机接收平台向固定在静止平台上的发射机发送请求信号,然后,发射机向目标区域发射高功率线性调频(LFM)信号,接着,无源弧形阵列接收天线用高速微波开关控制天线上各个天线单元的开/关,沿圆弧逐渐移动,实现孔径合成,从而控制回波信号的接收。双基弧形阵列SAR的发射机可以被放置在远离目标区域的地方,这样就降低了其在战场上被打击的概率,而无源接收机被安装在直升机的腹部,这样可以做到接收平台的完全无源,也就不会因为发射无线电信号而被探测到。同时,利用时间和频率标准在两个平台之间的连续传输,实现了双基地平台的同步。此外,因为发射斜距地变化几乎不会对双基弧形阵列SAR的方位向分辨率产生影响,所以双基弧形阵列SAR可以被应用到自主紧急着陆、物资空投、末端制导与动目标探测等领域[15-18]。
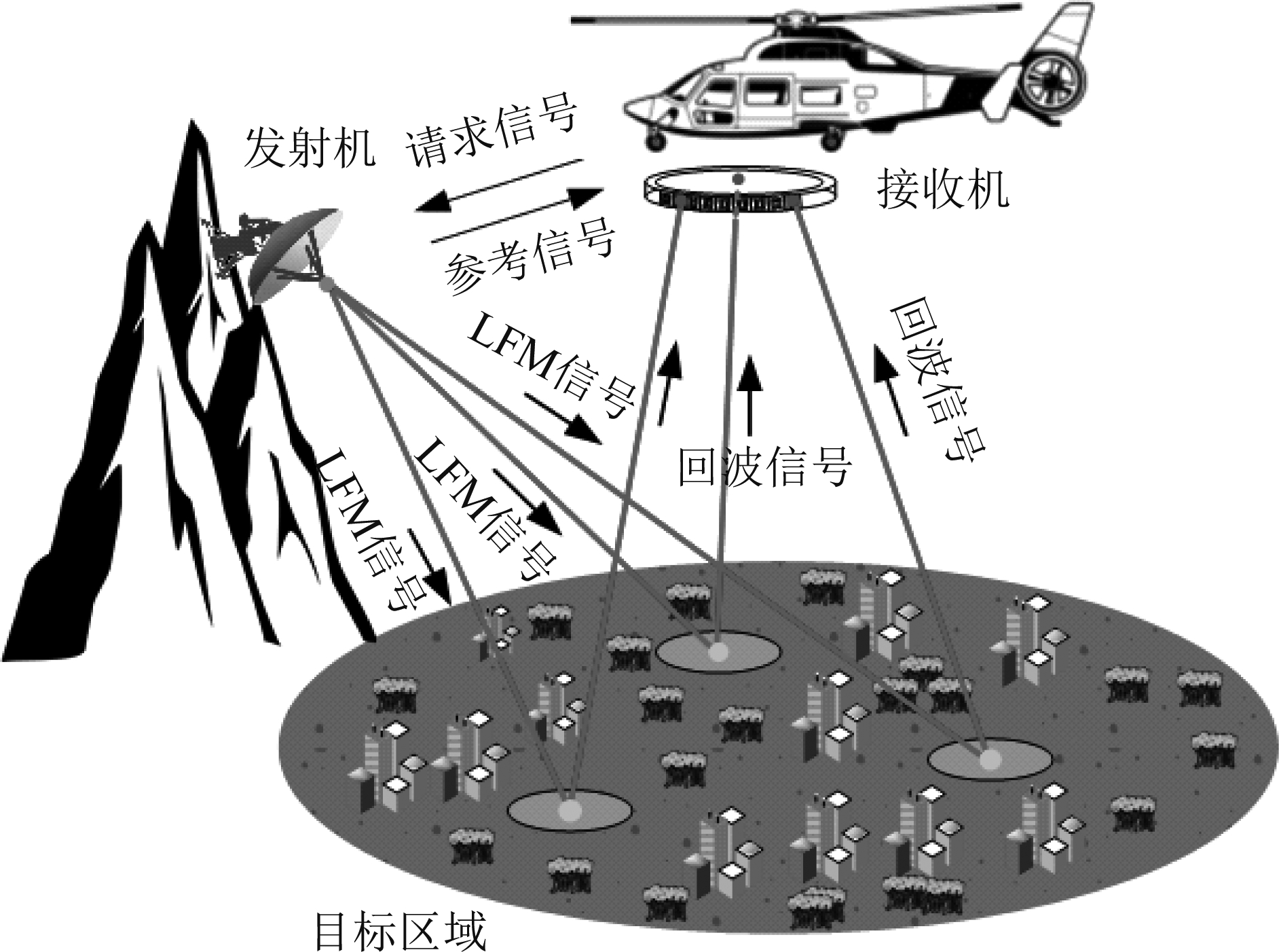
图2 双基弧形阵列SAR工作模式示意图
Fig.2 The work mode of arc array BiSAR
双基弧形阵列SAR的成像几何如图3所示。图中数学符号定义如表1所示。
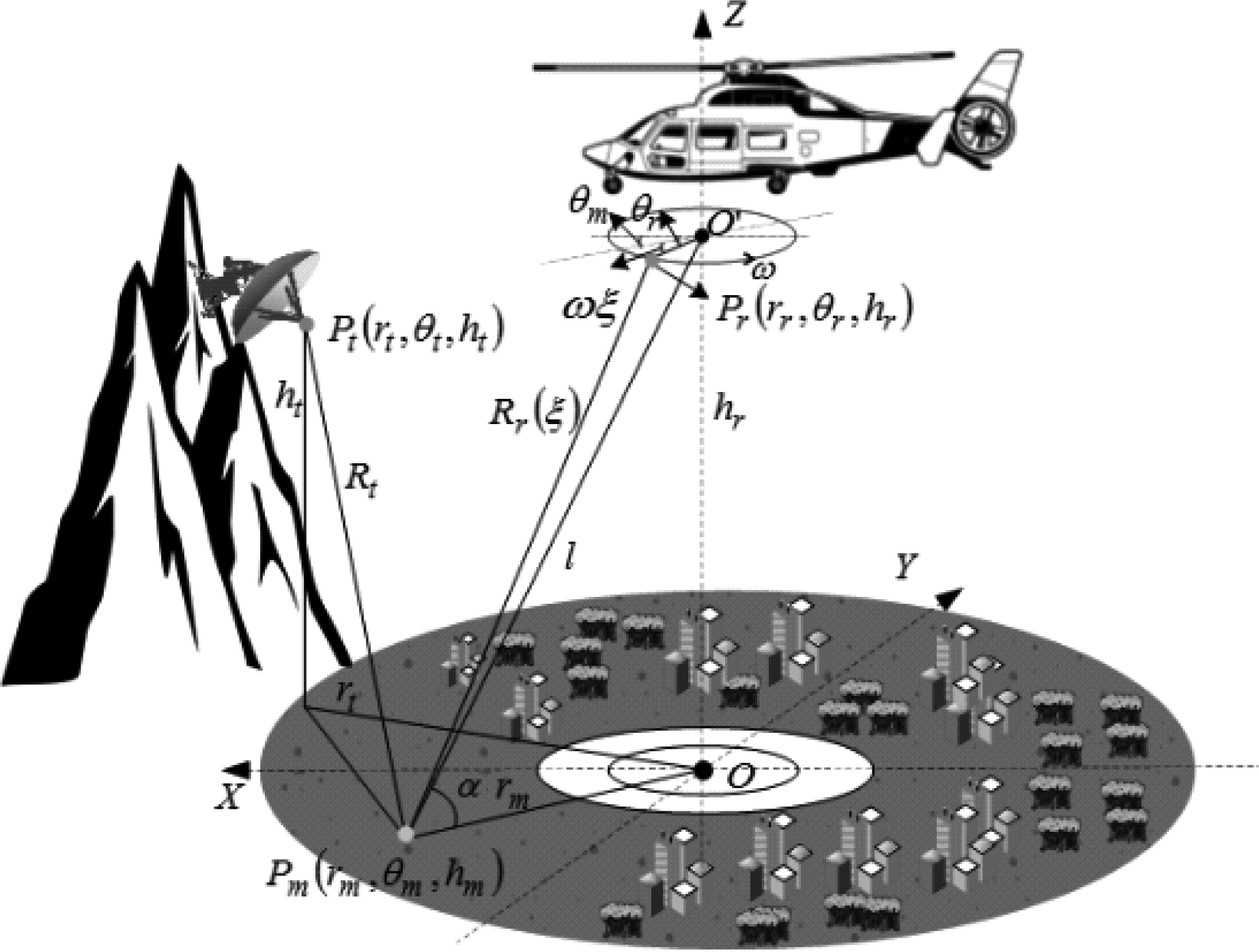
图3 双基弧形阵列SAR成像几何
Fig.3 The imaging geometry of arc array BiSAR
表1 数学符号定义
Tab.1 The mathematical symbol definition

O坐标系原点。O′无源弧形阵列接收天线的中心。Pm(rm,θm,hm)地面上任意点目标位置坐标。rm为点目标与O之间的距离;θm为Pm方位角(定义与X正半轴的夹角)角度;hm为点目标的高度。Pr(rr,θr,hr)弧形阵列天线等效采样点位置坐标。rr为天线半径;θr为Pr方位角角度,其中θr=θm+ωξ,ω为天线单元开关移动的角速度,ξ为方位向慢时间;hr为接收平台和天线的高度。Pt(rt,θt,ht)静止发射机位置坐标。rt为发射机与O之间的地面距离;θt为Pt方位角角度;ht为发射平台和发射机的高度。l目标Pm与弧形阵列天线中心O之间的距离αO′Pm与地面之间的角度,且cosα=l2-h2r/l。Rt发射机与点目标之间的距离。Rr(ξ)接收天线与点目标之间的距离。
2.2 信号模型
设发射机与接收机之间的双基瞬时斜距为Rb(ξ),利用余弦定理可以得到以下关系:
Rb(ξ)=Rt+Rr![]()
![]()
(1)
则Rb(ξ)的精确表达式为:
(2)
Rb(ξ)可被展开为泰勒级数得:
Rb(ξ)=B0+B1ξ+B2ξ2+B3ξ3+B4ξ4+…
(3)
其中,BN,N=0,1,2,...是泰勒级数的系数。
设发射机发射线性调频(LFM)信号,脉冲宽度为Ts,调频率为K,解调至基带后,点目标的回波信号可表示为:
ss(tτ,ξ)=σmar(tτ-Rb(ξ)/c)aa(ξ)·
exp{jπK[tτ-Rb(ξ)/c]2}·exp(-j 2π/λ·Rb(ξ))
(4)
其中,σm是散射系数,ar(·)和aa(·)分别为雷达(LFM)信号的距离向包络和方位向包络,c为光速,λ为中心频率所对应的波长。
2.3 基于隐函数导数法的二维频谱
将式(4)所示的回波信号变换到距离频域-方位时域,得:
Ss(fτ,ξ)=σmAr(fτ)aa(ξ)·![]()
(5)
其中, fc为载频, fτ为距离向频率,Ar(fτ)代表距离频率包络。可见在式(2)斜距公式中存在根号下三角函数形式的表达式,给双基弧形阵列SAR回波信号的二维频谱推导带来了较大的困难,很难用驻定相位原理来精确求解其二维频谱。下面将结合隐函数导数法来解决这一问题。对式(5)作FFT,得
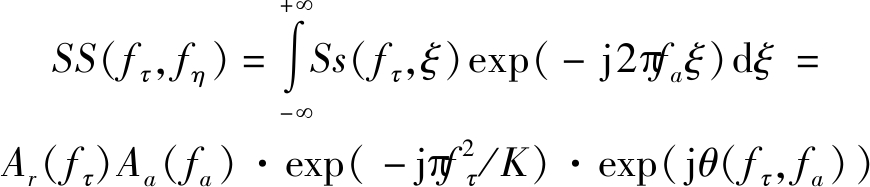
(6)
其中,
(7)
其中, fa是方位频率。对θ(fτ,ξ)关于ξ求导得:
dθ(fτ,ξ)/dξ|ξ=ξ0=![]()
(8)
驻定相位点ξ0满足dθ(fτ,ξ)/dξ|ξ=ξ0=0,经过移项整理可得:
(9)
令fχ为:
(10)
利用驻定相位点ξ0,二维频谱的相位项可以表示为:
(11)
可以看出,此驻相点ξ0的解析表达式不能通过代数的方法精确得到。但是显然,ξ0是fχ的一个隐函数,可以代数方法来得到。将ξ0在fχ=0处展开为泰勒级数,可以得到:
![]()
C0+C1[-cfa/(fτ+fc)]+C2[-cfa/(fτ+fc)]2+
C3[-cfa/(fτ+fc)]3+…
(12)
其中,![]() 则系数Ci为:
则系数Ci为:
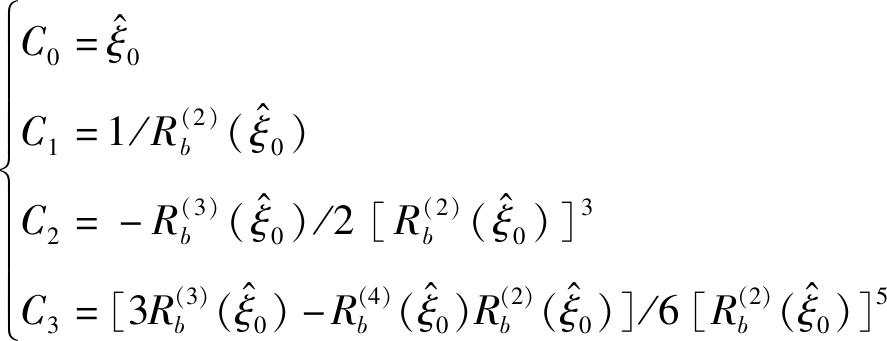
(13)
其中,![]()
为了得到ξ0泰勒展开系数,则需求解出![]() 的值,下面给出求解
的值,下面给出求解![]() 的步骤。由式(2)可知,双基斜距表达式为:
的步骤。由式(2)可知,双基斜距表达式为:
(14)
则其导数可被表示为:
(15)
在点![]() 处,式(15)为0,即:
处,式(15)为0,即:
(16)
由cos x=1-x2/2+x2/24+…和rm≫rr,式(16)可被进一步近似为以下多项式:
(17)
其中,![]() 为了方便后续计算,将式(17)写为:
为了方便后续计算,将式(17)写为:
(18)
其中,μ=ωrrrm(ω3/6q1/2+ω3rrrm/2q3/2),ε=ω2rrrm/6q1/2,则可以解出[24]:
![]()
16[η+(μη-ε)/(8η+μ2)1/2]}1/2
(19)
其中,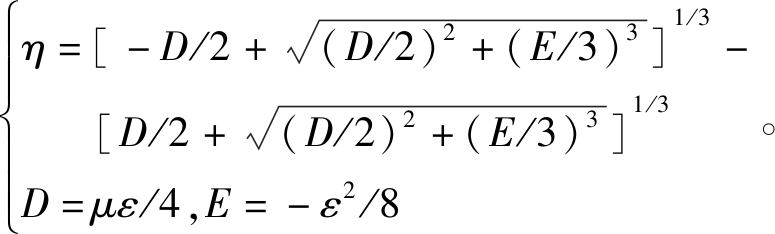
3 基于隐函数导数法的成像算法
3.1 成像算法
前面通过引入隐函数导数法推导出了双基弧形阵列SAR的二维频谱,现在将前面得到的频谱应用到成像算法上。先从式(4)开始,相位项![]() 和距离向调频有关,而且仅仅与fτ有关,故可以通过距离压缩将该项除去。然后,为了解决距离频率fτ和多普勒频率fa之间存在耦合的问题,这里将ξ0和Rb(ξ0)展开为fτ的级数,可以得到:
和距离向调频有关,而且仅仅与fτ有关,故可以通过距离压缩将该项除去。然后,为了解决距离频率fτ和多普勒频率fa之间存在耦合的问题,这里将ξ0和Rb(ξ0)展开为fτ的级数,可以得到:
(20)
(21)
由式(12)可解出:
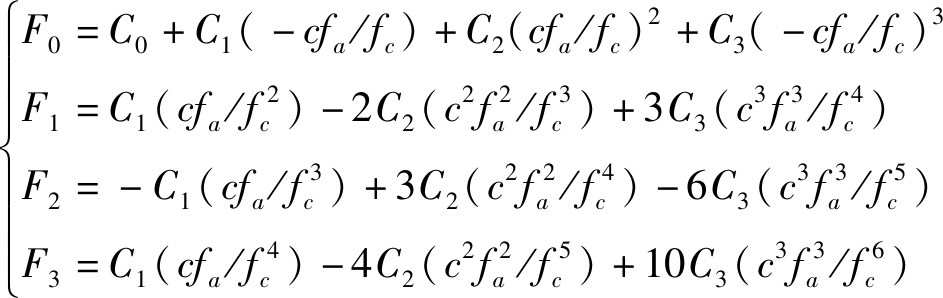
(22)

(23)
其中,![]()
将式(22)和式(23)带入到式(11)可得:
θ(fr, fa)≈φaz+φrcm+φsrc+φres
(24)
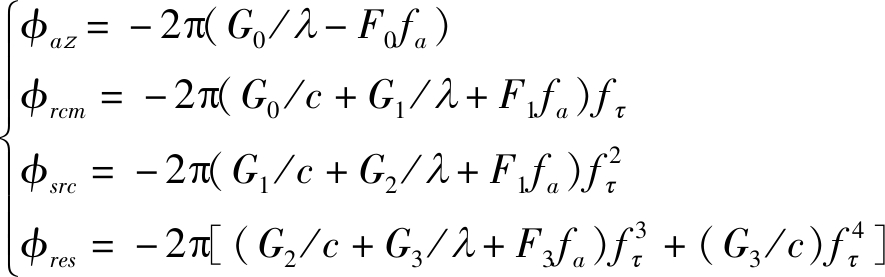
(25)
其中,φac与方位向调频有关,φrcm与距离徙动有关,φsrc代表距离和方位向的耦合相位,而φrcm则是双基弧形阵列SAR中残余的高阶指数项。根据之前的分析,首先雷达回波信号需要在二维频域中去除耦合相位项和残余相位项,然后在距离多普勒域完成距离徙动项校正,校正距离徙动之后,同一距离单元的所有点目标会有相同的方位向调频率。接着完成方位脉冲压缩,对信号做方位IFFT得到最终的聚焦信号。
具体的算法流程如下:
1)对回波信号进行距离压缩,除去和距离向调频有关的相位项![]() 然后对信号做二维FFT,将信号转换至二维频域。
然后对信号做二维FFT,将信号转换至二维频域。
2)对距离徙动项φrcm、耦合相位项φsrc和残余相位项φres进行补偿,补偿函数为:
(26)
3)然后将柱坐标系下的二维频谱插值变换到直角坐标系,坐标映射关系如下:
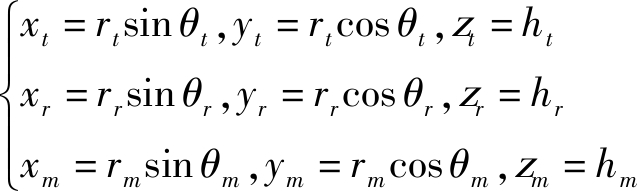
(27)
其中,(xt,yt,zt),(xr,yr,zr),(xm,ym,zm)分别为静止发射机位置坐标Pt,弧形阵列天线等效采样点位置坐标Pr,地面上任意点目标位置坐标Pm在直角坐标系下的坐标。
4)沿距离向对信号进行逆傅里叶变换,将数据变换到距离多普勒域,然后构造滤波器H2(fa)通过方位向压缩去除φaz,滤波器表达式为:
H2(fa)=exp{-jφaz}
(28)
5)沿方位向进行逆傅里叶变换,完成最终的信号聚焦。至此完成了整个双基弧形阵列SAR成像算法,流程图如图4所示。
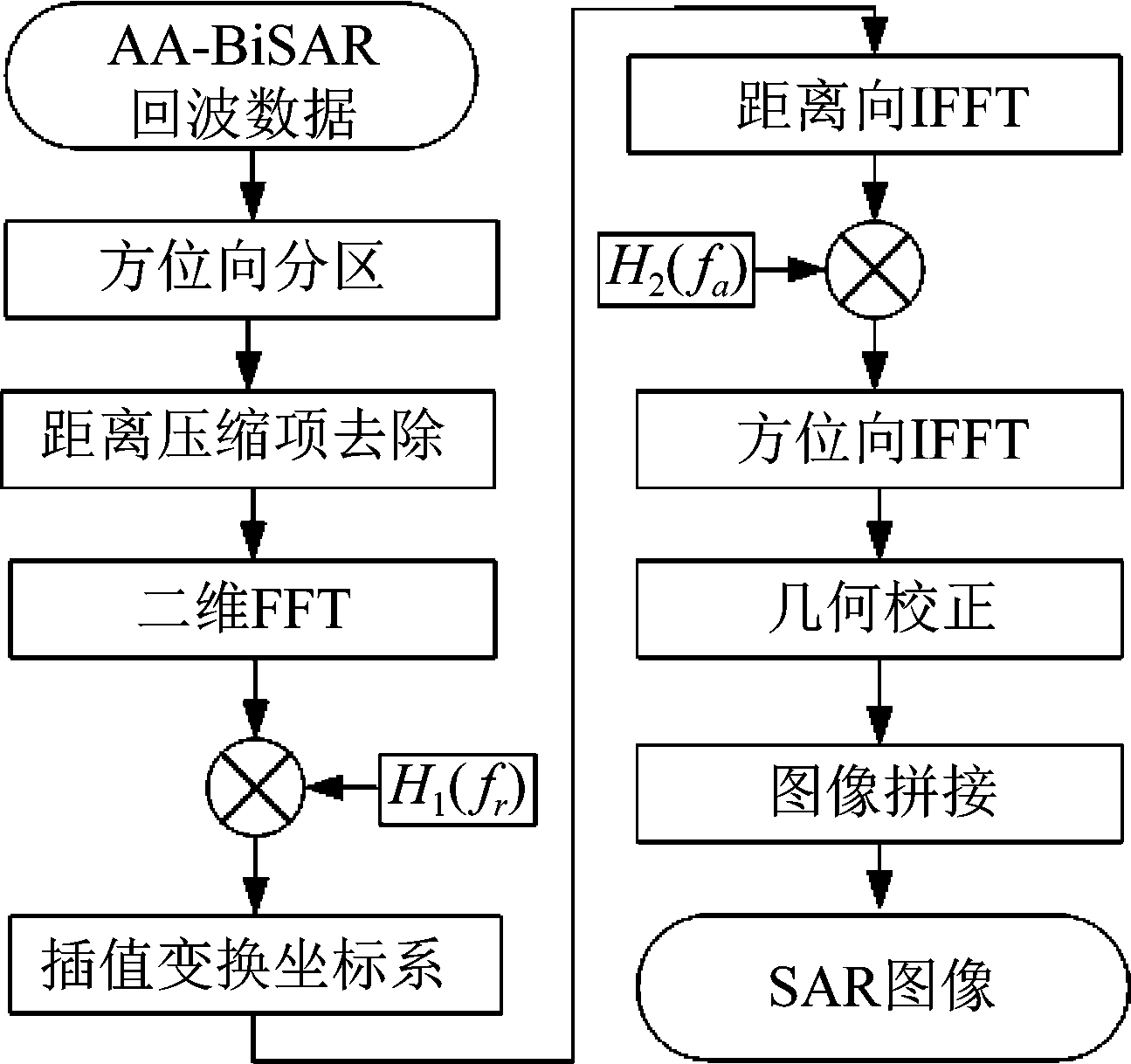
图4 成像算法流程图
Fig.4 The flowchart of imaging algorithm
3.2 成像分辨率分析
对于线性调频信号的双基弧形阵列SAR,其瞬时方位频率为:
fa=∂{arg[ss(tτ,ξ)]}/∂ξ=2πrrcos αsin(ωξ)/λ=
2πrrcos αsin(θr-θm)/λ
(29)
则双基弧形阵列SAR的方位向角分辨率可表示为[2,9]:
ρa=2π/[max{fa}-min{fa}]≈
λ/[2rrsin(θa/2)cos α]=![]()
(30)
其中,rr为天线半径,λ是信号的波长,θs是方位合成孔径的角度,hr为天线平台高度。
与单基弧形阵列SAR不同的是,在双基模式中,由于接收平台和发射平台被安装在不同的两个地方,所以,瞬时双基斜距和包括两个不同的方向上的距离[2,12]。因此,本文将直接考虑双基弧形阵列SAR的地距分辨率,其表达式为:
(31)
其中,Br是信号的带宽,
(32)
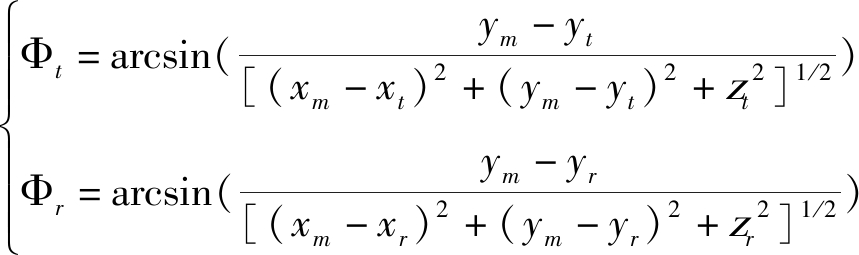
(33)
4 仿真实验
4.1 相位误差分析
不同于传统的线性阵列SAR模式,由于特殊的圆弧形天线结构和工作方式,双基弧形阵列SAR的方位向分辨率与方位合成孔径角度的大小有关[2,9],由式(2)知方位合成孔径角度的越大,斜距中的余弦项展开要求的阶次越高,而当忽略级数中的高阶项所引入的相位误差小于π/4时,那么其对成像结果的影响也就可以忽略不计。文献[22]方法引入的相位误差三维图如图5(a)所示,以方位向角度为横坐标的二维图如图5(b)所示,其中虚线为π/4。选取特定目标点(600,0°),具体系统参数选择见表2所示,可见点目标斜距在进行二阶泰勒级数展开时,为了获得聚焦质量较好的目标点,方位合成孔径角度的取值范围需在-19°到+19°内;而本文方法在进行双基斜距展开时将泰勒级数展开到四阶,相位误差如图6所示,可见其相位误差远小于π/4,同时这也说明在对双基弧形阵列SAR斜距进行泰勒级数展开时,四阶近似已经能够满足成像的要求,同时在图6(a)与图6(b)中运用级数反演法(Method of Series Reversion, MSR)[23]与本文隐函数导数法(DIF)所引入的相位误差进行了对比,可以看出因二者均将斜距展开到了四阶,故所引入的相位误差相差很小,说明二者方法所求的频谱精度相当,但需要说明的是,本文隐函数导数法比级数反演法适用于更多的特殊方程的近似求解,级数反演法将驻相点在多普勒中心处展开,就推导思路来说,二者是完全不一样的,若方程中存在耦合,那么级数反演法就失去了作用,而隐函数导数法仍然适用,在以后的对更多构型的双基弧形阵列SAR的研究中,隐函数导数法将具有很大优势[24-27]。
表2 仿真参数
Tab.2 Simulation parameters
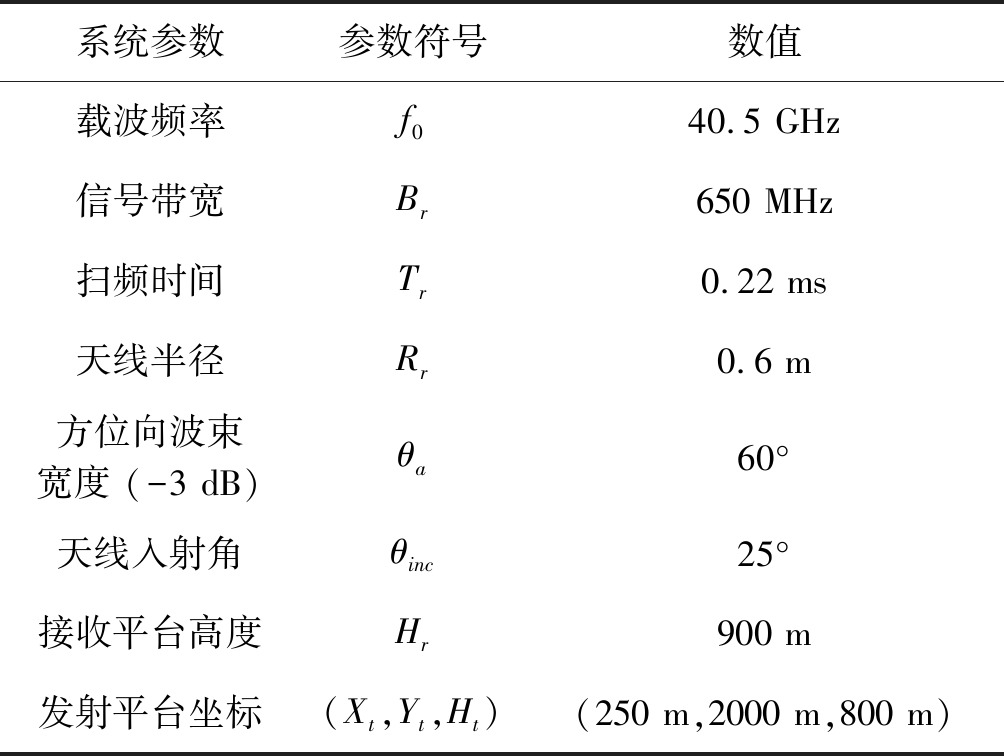
系统参数参数符号数值载波频率f040.5 GHz信号带宽Br650 MHz扫频时间Tr0.22 ms天线半径Rr0.6 m方位向波束宽度 (-3 dB)θa60°天线入射角θinc25°接收平台高度Hr900 m发射平台坐标(Xt,Yt,Ht)(250 m,2000 m,800 m)
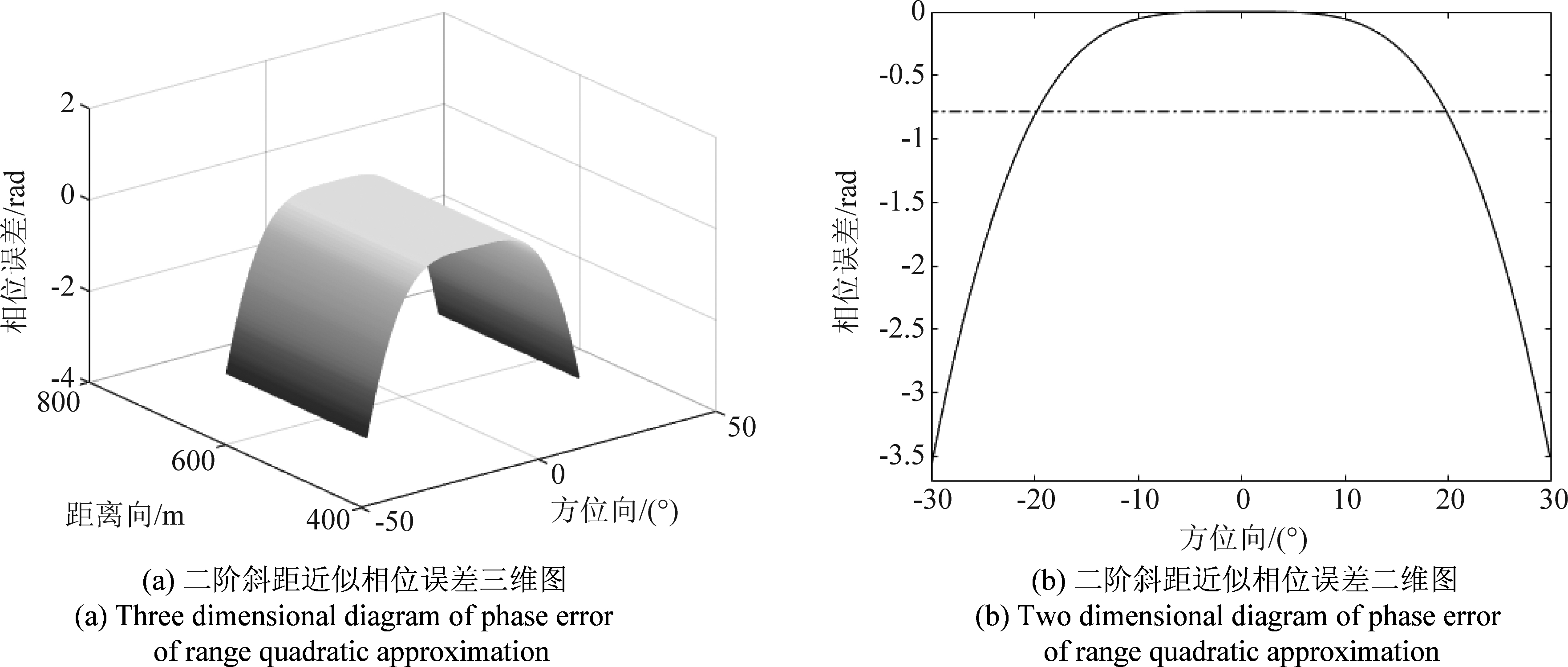
图5 二阶斜距近似相位误差图
Fig.5 Phase error of range quadratic approximation
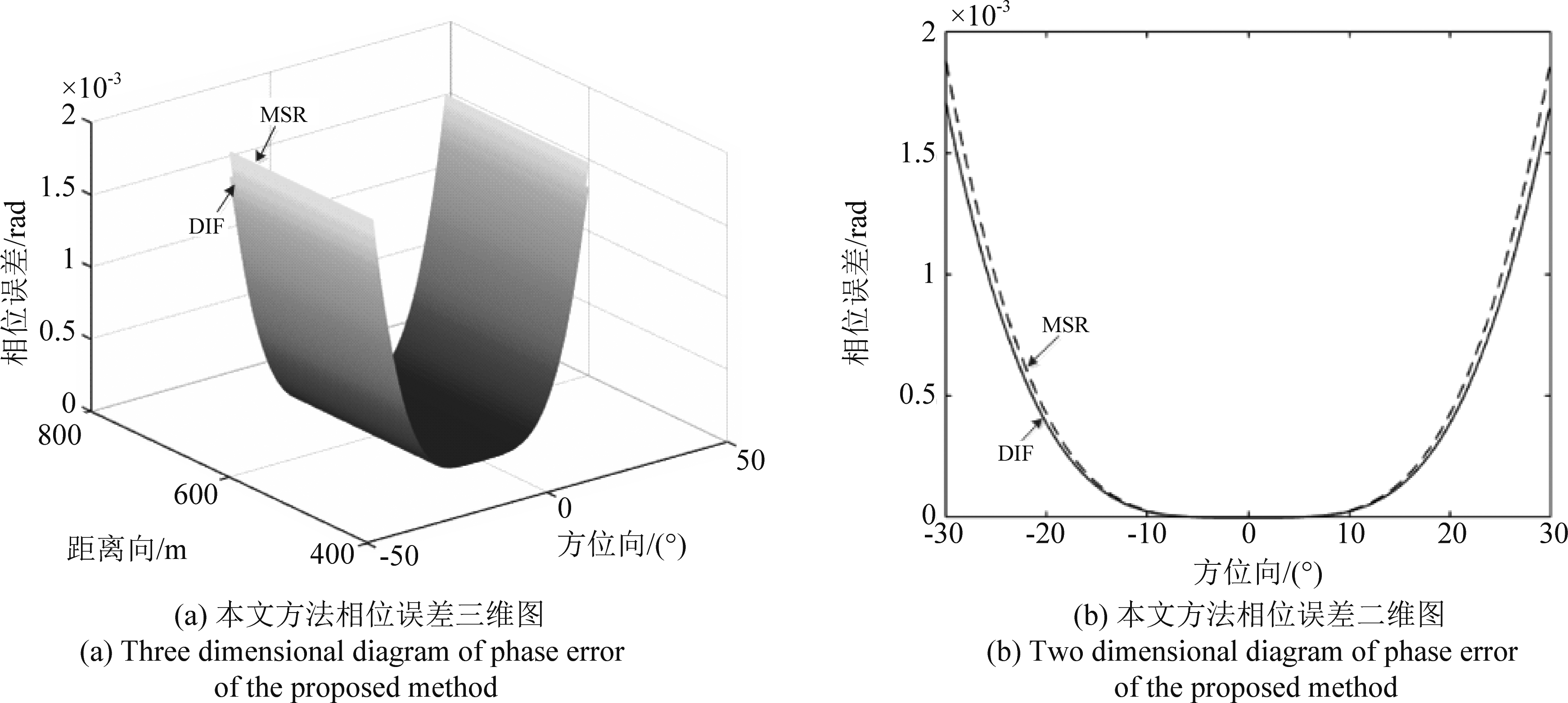
图6 本文方法相位误差
Fig.6 Phase error of the proposed method
4.2 成像结果
为了验证本文提出方法的成像效果,下面分别采用本文推导的方法与文献[22]中所述的子孔径划分成像算法进行点目标成像仿真对比,仿真参数选择如表2所示。在仿真实验中,设置了一个点阵目标场景,其位置如图7所示。采用本文的成像处理算法对点目标回波进行仿真验证,其聚焦图像如图8所示,选取目标区域中P1(200,25°),P2(250,0°),P3(300,-25°)三个点目标做进一步分析,其等高线图如图9所示,并给出了所对应的方位向和距离向响应脉冲,可以看出,不同距离和角度处的3个点目标都得到了很好的聚焦效果。同样,运用文献[22]算法对点P1进行成像并对结果作对比,从图10中可以看出,在双基弧形阵列SAR模式下,斜距的二阶次近似已经无法表征足够的相位变化信息,进而造成点目标的聚焦效果下降,难以满足成像的要求。而本文提的算法在进行级数展开时将双基斜距近似到四阶,推导得到的二维频谱中能够体现出更多的斜距变化信息,因而提高了成像质量,获得了更高的图像精确度,聚焦效果较好。
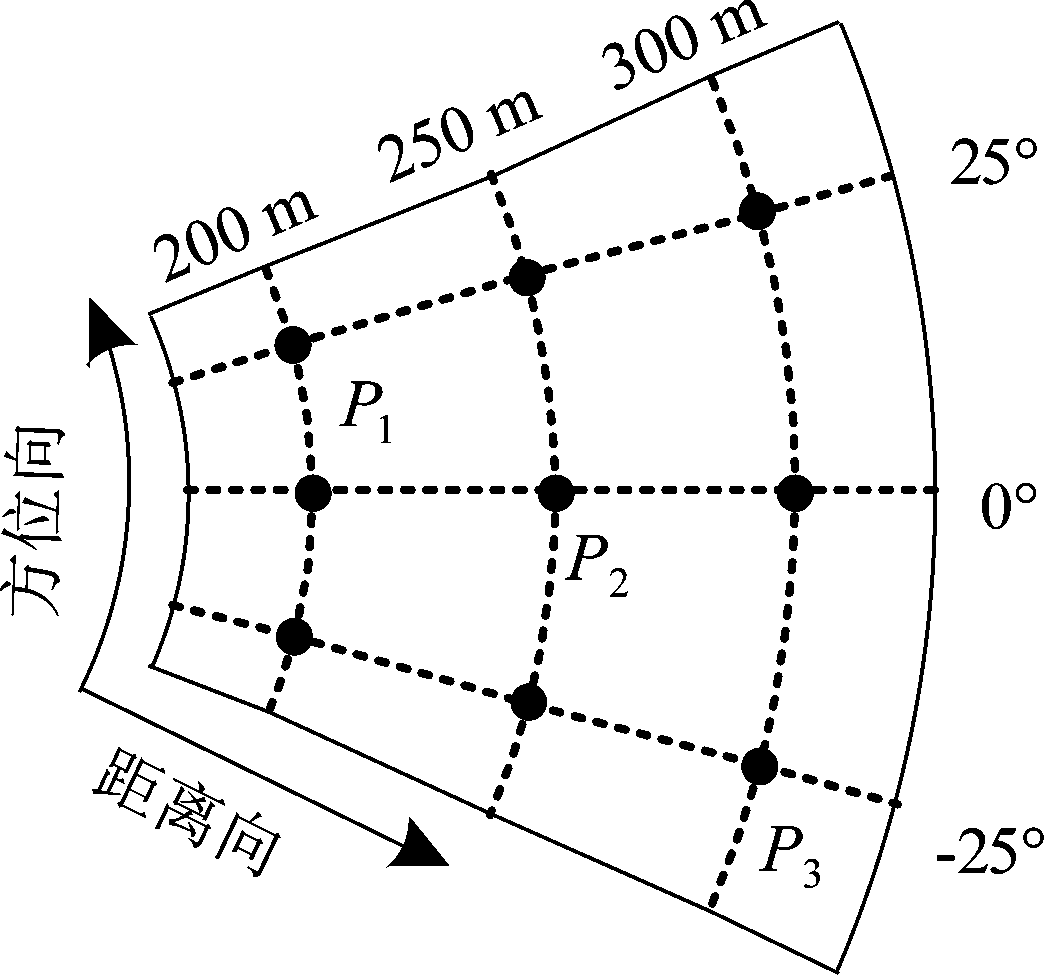
图7 点目标位置分布
Fig.7 The positions of point target
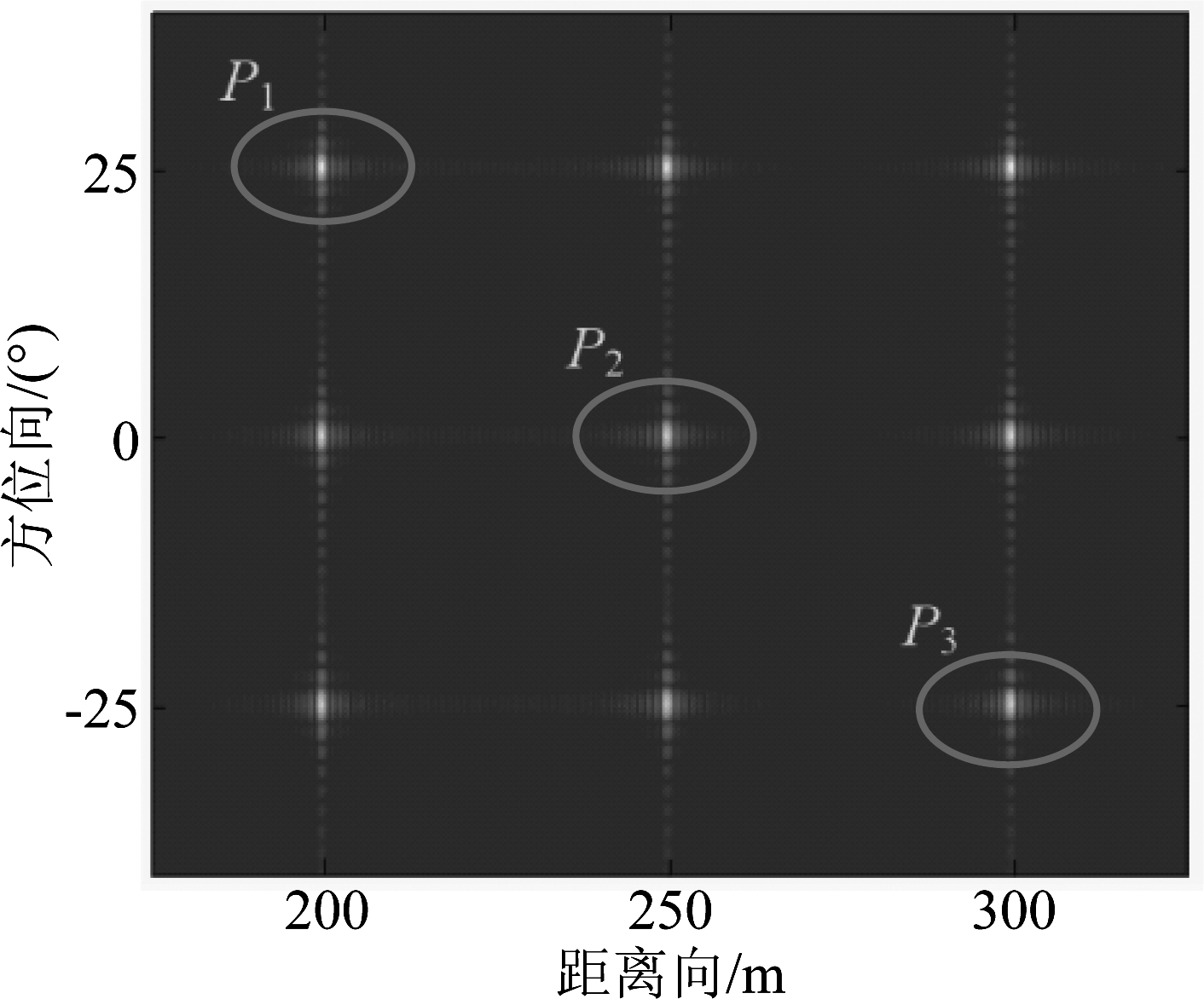
图8 点目标成像结果
Fig.8 Point target imaging results
为了更进一步对成像结果进行分析,由表3给出了点目标P1、P2和P3的具体的测量参数,其中,PSLR和ISLR分别表示峰值旁瓣比和积分旁瓣比。P1、P2和P3距离(地距)向分辨率的理论值分别为0.556 m、0.497 m和0.432 m,沿方位(阵列)向角分辨率的理论值分别为0.928°、0.752°和0.637°,由表中的数据可以看出,各点成像性能测量参数值与理论分析基本吻合,可见本文提出的基于隐函数导数法的双基弧形阵列SAR成像算法的有效性。

图9 点目标的等高线与脉冲响应图
Fig.9 The contour and impulse response of point target
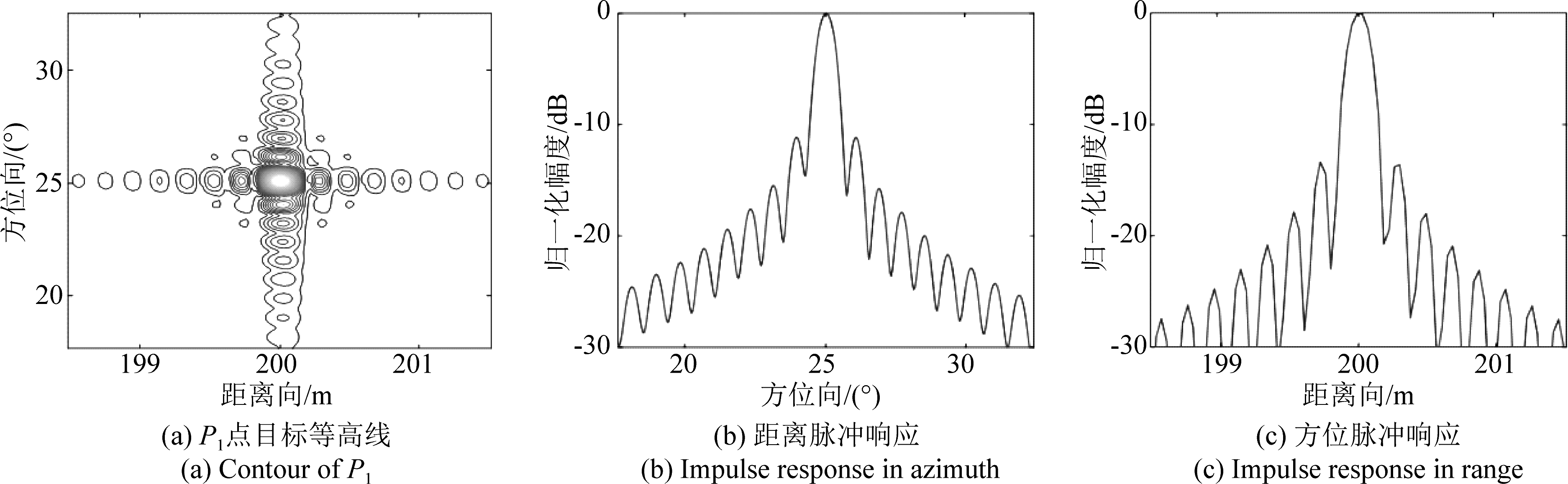
图10 采用传统子孔径方法P1的等高线与脉冲响应图
Fig.10 The contour and impulse response of P1using sub-aperture partition
表3 点目标测量参数
Tab.3 Measured parameters of the selected targets.

目标距离向分辨率/mPSLRISLR方位向分辨率/(°)PSLRISLRP10.564-13.139-9.360.943-12.636-8.802P20.548-13.224-9.410.808-12.683-8.859P3 0.435-13.357-9.580.759-12.703-8.945
5 结论
双基弧形阵列SAR成像模式具有观测范围广且不易被侦测的优点,可用于直升机的着陆、侦察、搜救和起飞等领域。但由于双基弧形阵列SAR特殊的弧形阵列天线结构的影响,其回波信号的二维频谱表达式很难用传统的驻定相位原理来推导。为了解决这一问题,本文引入隐函数导数法,求解出了回波信号的二维频谱的驻定相位点,然后通过代数运算,得到了双基弧形阵列SAR的二维频谱。在此频谱基础上,本文研究了一种适用于双基弧形阵列SAR的成像方法,文中给出了该算法完整的推导过程,最后通过不同点目标的仿真验证了提出的算法的有效性。
[1] CUMMING I G, WONG F H. Digital signal processing of synthetic aperture radar data; artech house [M]. Norwood, MA, USA, 2005.
[2] HUANG Pingping, LI Kai, XU Wei, et al. Focusing arc-array bistatic synthetic aperture radar data based on keystone transform[J]. Electronics, 2019, 8(12): 1389.
[3] 杜欣, 黄平平, 徐伟, 等. 基于斜距高阶近似的弧形阵列SAR成像方法[J]. 信号处理, 2019, 35(5): 809- 815.
DU Xin, HUANG Pingping, XU Wei, et al. Imaging approach for arc array SAR based on high-order approximation of slant range[J]. Journal of Signal Processing, 2019, 35(5): 809- 815.(in Chinese)
[4] 黄增树, 孙进平, 谭维贤, 等. 弧形阵列3D-SAR成像处理算法研究[J]. 信号处理, 2019, 35(4): 523-530.
HUANG Zengshu, SUN Jinping, TAN Weixian, et al. Research on arc array 3D-SAR imaging algorithm[J]. Journal of Signal Processing, 2019, 35(4): 523-530.(in Chinese)
[5] HUANG Pingping, TAN Weixian, SU Ying. MIMO-SAR imaging technology for helicopter-borne based on ARC antenna array[C]∥2015 IEEE International Geoscience and Remote Sensing Symposium (IGARSS). Milan, Italy. IEEE, 2015: 1801-1804.
[6] HUANG Zengshu, SUN Jinping, TAN Weixian, et al. Investigation of wavenumber domain imaging algorithm for ground-based arc array SAR[J]. Sensors, 2017, 17(12): 2950.
[7] LUO Yunhua, SONG Hongjun, WANG R, et al. Arc FMCW SAR and applications in ground monitoring[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(9): 5989-5998.
[8] LEE H, LEE J H, KIM K E, et al. Development of a truck-mounted arc-scanning synthetic aperture radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(5): 2773-2779.
[9] 黄平平, 谭维贤, 苏莹, 等. 直升机载弧形阵列MIMO微波成像技术研究[J]. 雷达学报, 2015, 4(1): 11-19.
HUANG Pingping, TAN Weixian, SU Ying, et al. Research on helicopter-borne MIMO microwave imaging technology based on arc antenna array[J]. Journal of Radars, 2015, 4(1): 11-19.(in Chinese)
[10] 范宇杰, 温育涵, 卫扬铠, 等. 连续目标双基地调频连续波SAR回波建模方法[J]. 信号处理, 2018, 34(11): 1345-1354.
FAN Yujie, WEN Yuhan, WEI Yangkai, et al. Continuous target bistatic FMCW SAR echo modeling method[J]. Journal of Signal Processing, 2018, 34(11): 1345-1354.(in Chinese)
[11] 王晶阳, 田卫明, 卢晓军, 等. 地基双基地MIMO成像雷达空间分辨特性分析[J]. 信号处理, 2018, 34(11): 1286-1296.
WANG Jingyang, TIAN Weiming, LU Xiaojun, et al. Analysis on spatial resolutions of ground-based bistatic MIMO imaging radar[J]. Journal of Signal Processing, 2018, 34(11): 1286-1296.(in Chinese)
[12] 仇晓兰,丁赤飚,胡东辉. 双站SAR成像处理技术 [M]. 北京: 科学出版社, 2010.
QIU Xiaolan, DING Chibiao, HU Donghui. Bistatic SAR data processing algorithms[M]. Beijing: Science Press, 2010. (in Chinese)
[13] 刘荦锶, 吴立薪, 胡程, 等. 一静一动双基地SAR改进非线性CS算法[J]. 信号处理, 2013, 29(3): 342-350.
LIU Luosi, WU Lixin, HU Cheng, et al. Improved NLCS imaging algorithm of bistatic SAR with a stationary receiver[J]. Journal of Signal Processing, 2013, 29(3): 342-350.(in Chinese)
[14] 张振华. 双/多基SAR成像算法研究[D]. 西安: 西安电子科技大学, 2007.
ZHANG Zhenhua. Study of Bi-and MultiStatic SAR image formation[D]. Xi’an: Xidian University, 2007. (in Chinese)
[15] ZHANG Qianghui, WU Junjie, LI Zhongyu, et al. PFA for bistatic forward-looking SAR mounted on high-speed maneuvering platforms[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(8): 6018- 6036.
[16] WANG R, LOFFELD O, NEO Y L, et al. Focusing bistatic SAR data in airborne/stationary configuration[J]. IEEE Transactions on Geoscience and Remote Sensing, 2010, 48(1): 452- 465.
[17] MIAO Yuxuan, WU Junjie, LI Zhongyu, et al. A generalized wavefront-curvature-corrected polar format algorithm to focus bistatic SAR under complicated flight paths[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 3757-3771.
[18] AN Hongyang, WU Junjie, SUN Zhichao, et al. A two-step nonlinear chirp scaling method for multichannel GEO spaceborne-airborne bistatic SAR spectrum reconstructing and focusing[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(6): 3713-3728.
[19] 李婷婷, 黄平平, 徐伟, 等. 一种两维稀疏的3D-SAR成像方法[J]. 信号处理, 2019, 35(5): 850- 859.
LI Tingting, HUANG Pingping, XU Wei, et al. A two-dimensional sparse 3D-SAR imaging algorithm[J]. Journal of Signal Processing, 2019, 35(5): 850- 859.(in Chinese)
[20] 谭维贤. 合成孔径雷达三维成像理论与方法研究 [D]. 北京:中国科学院研究生院, 2009.
TAN Weixian. Study on theory and algorithms for three-dimensional synthetic aperture radar imaging [D]. Beijing: Graduate University of Chinese Academy of Sciences, 2009. (in Chinese)
[21] 杜磊. 阵列天线下视合成孔径雷达三维成像模型、方法与实验研究[D]. 北京:中国科学院大学,中国科学院研究生院, 2010.
DU Lei. Study on model, algorithm and experiment for downward-looking synthetic aperture radar three-dimensional imaging based on linear array antennas [D]. Beijing: University of Chinese Academy of Sciences, Graduate University of Chinese Academy of Sciences, 2010. (in Chinese)
[22] 孙兵周, 荫清, 陈杰, 等. 广域观测圆轨迹环扫SAR成像模式研究[J]. 电子与信息学报, 2008, 30(12): 2805-2808.
SUN Bingzhou, YIN Qing, CHEN Jie, et al. Operation mode of circular trace scanning SAR for wide observation[J]. Journal of Electronics & Information Technology, 2008, 30(12): 2805-2808.(in Chinese)
[23] NEO Y L, WONG F, CUMMING I G. A two-dimensional spectrum for bistatic SAR processing using series reversion[J]. IEEE Geoscience and Remote Sensing Letters, 2007, 4(1): 93-96.
[24] XIONG Tao, XING Mengdao, WANG Yong, et al. Using derivatives of an implicit function to obtain the stationary phase of the two-dimensional spectrum for bistatic SAR imaging[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6):1165-1169.
[25] ERIC W. CRC Concise Encyclopedia of Mathematics[M]. Boca Raton, FL, USA: CRC Press, 2002.
[26] LIAO Yi, WANG Wenqin, LIU Qinghuo. Two-dimensional spectrum for circular trace scanning SAR based on an implicit function[J]. IEEE Geoscience and Remote Sensing Letters, 2016, 13(7): 887- 891.
[27] 熊涛. 双基SAR成像算法研究[D]. 西安: 西安电子科技大学, 2012.
XIONG Tao. Study on imaging algorithms for bistatic SAR[D]. Xi’an: Xidian University, 2012. (in Chinese)




