1 引言
无线声传感网络(Wireless Acoustic Sensor Networks, WASNs)一般由多个节点组成,每个节点包括一个或多个传声器、一个处理单元和一个能够实现节点之间交换数据的无线通信模块[1-2]。相比于传统的单传声器阵列,WASNs可以覆盖更大范围的区域,增加了存在靠近目标源的节点的可能,因此一些节点可以拾取到具有更高信噪比和直达混响比的信号[3- 4]。作为下一代的音频获取和处理技术,WASNs有许多潜在的应用,例如声学事件监测[5- 6]和智能家居系统[7- 8]。
复高斯混合模型(Complex Gaussian Mixture Model, CGMM)是常用的多说话人分离模型,其利用语音信号的统计特性来进行多说话人分离。相比单传声器阵列,WASNs提供了更加丰富的空域信息,有望提升CGMM的分离性能。常规的集中式的CGMM要求每个节点发送自己的接收信号向量以便每个节点都能获得WASNs的所有接收信号向量,因此在每个节点形成了维度非常高的信号向量。在CGMM用期望最大化(Expectation Maximization, EM)算法迭代估计后验概率和模型参数的过程中,每个节点需要多次对该高维信号向量进行处理,例如空域协方差矩阵求逆[9-11],导致了非常高的计算复杂度和非常高的能量消耗。此外,CGMM迭代估计的分离性能与EM算法的初始值密切相关[12]。当只有一个说话人存在时,通常可以用接收信号的相关矩阵进行空域协方差矩阵的初始化。当有多个说话人存在时,通常需要预先对训练数据集进行处理来实现不同说话人的空域协方差矩阵的初始化;而在实际应用场景中,训练数据集通常很难获取。
本文提出了一个复高斯混合模型下的分布式多说话人分离及其基于到达角度(Direction of Arrival, DOA)量测自聚类的空域协方差矩阵初始化方法。在不同节点之间的接收信号向量条件独立的前提假设下[13-14],本文推导出分布式CGMM迭代过程中的所有接收信号向量对应的空域协方差矩阵的求逆和后验概率等参数的估计可以逐节点进行;然后,每个节点融合其他节点的接收信号向量对应的空域协方差矩阵和后验概率等参数来更新全局的相关参数。基于此,本文提出用基于DOA的导向矢量的相关矩阵来初始化每个节点的空域协方差矩阵。考虑该方法存在DOA模糊问题,即不同节点上具有相同索引的DOA并不一定对应同一个说话人。为了解决DOA模糊问题以使不同节点能够协同工作,本文进一步提出了基于DOA量测自聚类的方法来从不同节点上选出对应同一个说话人的DOA量测值组合。同时,这个方法从空域上区分了不同的说话人,避免了分离问题中常见的排序问题[15-16]。最后的实验结果证实了本文提出的方法的有效性。
2 信号模型
设一个WASNs含有J个节点,第j个节点有Mj个传声器。因此,该WASNs中的传声器的总数是
所有接收信号向量由不同节点的接收信号向量组成,在短时傅里叶变换域(Short-Time Fourier Transform, STFT),所有接收信号向量y(f,l)可表示为
(1)
其中, f代表频率索引,l代表帧索引,上标T代表转置,yj(f,l)是第j个节点的接收信号向量。
若有K个说话人,y(f,l)可建模如下:
(2)
其中,s(k)(f,l)是第k个说话人的信号,n(f,l)是噪声向量,
是第k个说话人到M个传声器的声学传递函数(Acoustic Transform Function, ATF)。考虑足够短时间内,说话人不移动,因此h(k)(f,l)时不变,可重新表示为h(k)( f )。
3 集中式复高斯混合模型
考虑到语音信号在时频域的稀疏性[17],即每个时频点至多只有一个说话人,接收信号可聚集到K+1个类别,其中每个类别只包含一个说话人的含噪语音或者只包含噪声。因此,式(2)中的信号模型可表示为[9]:
y(f,l)=h(ν)( f )s(ν)(f,l) (ν=d(f,l))
(3)
其中,d(f,l)代表时频点(f,l)的类别索引。ν可以取值k+n 或n,其对应的类别分别为第k个说话人的含噪语音s(k+n)(f,l)或噪声s(n)(f,l)。
假设s(ν)(f,l)服从一个复高斯分布:
(4)
其中,φ(ν)(f,l)对应信号方差。因此,当已知时频点(f,l)的类别索引时,接收信号y(f,l)的条件分布为:
(5)
其中,R(ν)( f )为空域协方差矩阵且对应h(ν)( f )h(ν)H( f )。通过对类别索引d(f,l)求边缘分布,可得接收信号y(f,l)服从的CGMM为
(6)
其中,α(ν)( f )为混合权重,且满足
CGMM的参数α(ν)( f ),φ(ν)(f,l)和R(ν)( f )可以通过最大似然法估计。最大似然法估计可以通过EM算法实现。根据[9],代表d(f,l)=ν的后验概率λ(ν)(f,l)可以通过下式计算:
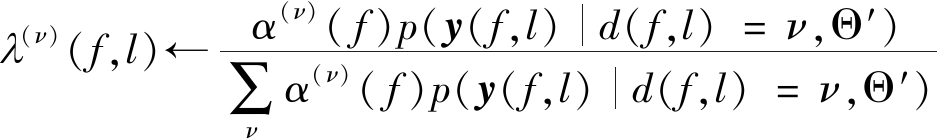
(7)
其中,Θ′代表上一次参数估计的集合。在M-step中,CGMM的参数更新如下:
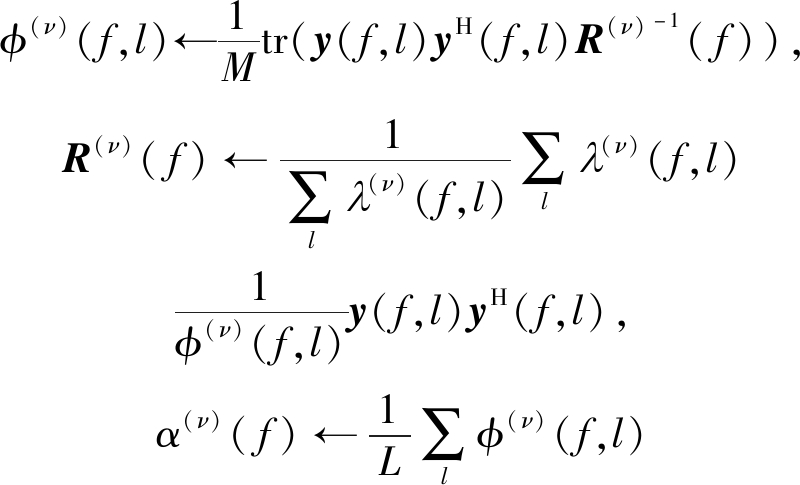
(8)
在收敛以后,λ(ν)(f,l)可以作为时频点(f,l)的掩蔽的估计。
集中式CGMM要求每个节点发送自己的接收信号向量以使每个节点都能获得WASNs的所有接收信号向量,因此在每个节点形成了M×1的高维信号向量y(f,l)。在式(7)和式(8)的迭代过程中,需多次对该高维信号向量对应的不同类别的R(ν)( f )求逆,计算复杂度高且能量消耗大。
4 分布式复高斯混合模型
复高斯混合模型下的分布式多声源分离算法(Distributed Complex Gaussian Mixture Model, DCGMM)利用了不同节点之间的接收信号向量条件独立的前提假设[13-14],使得EM算法迭代过程中的空域协方差矩阵的求逆、信号方差和后验概率的估计可以逐节点局部进行。然后,每个节点融合其他节点对应的参数来更新全局的参数。最后,EM算法收敛后即可获得全局后验概率λ(ν)(f,l)。
4.1 分布式复高斯混合模型推导
根据不同节点之间的接收信号向量条件独立的前提假设,式(6)中的所有接收信号向量对应的空域协方差矩阵即R(ν)( f )有如下的块对角形式:
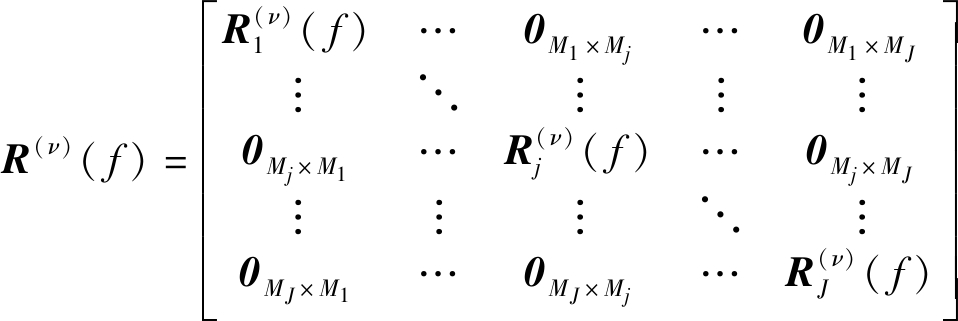
(9)
其中,
是第j个节点的接收信号向量对应的空域协方差矩阵。把上式代入式(6)中,经过EM算法处理后,可得:
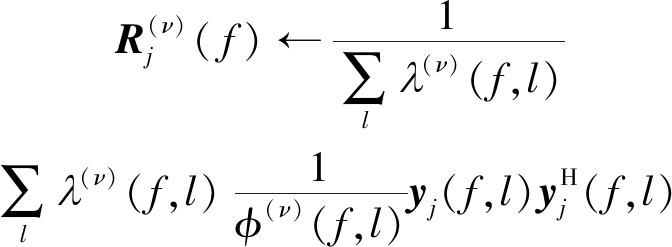
(10)
定义局部后验概率
和信号方差
如下:
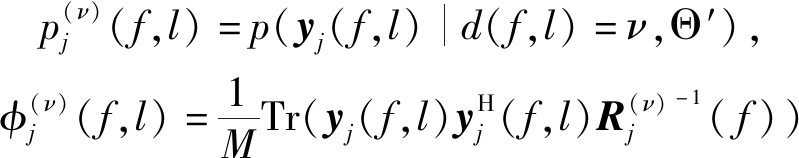
(11)
此时,对于DCGMM来说,其E-step为:
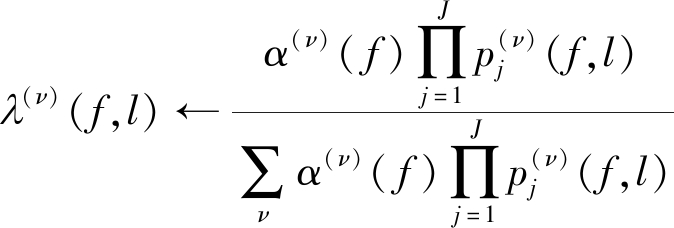
(12)
其M-step为:
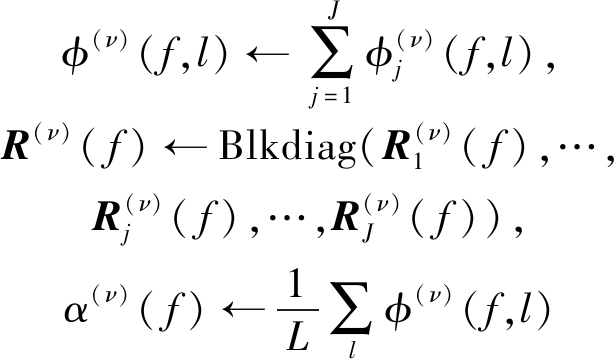
(13)
其中,Blkdiag(·)表示R(ν)( f )具有式(9)的块对角形式。
在式(7)和式(8)中,需对M×M的矩阵R(ν)( f )求逆;而在式(12)和式(13)中,只需对Mj×Mj的矩阵
求逆。计算复杂度由原来的
降低到了
如表1,可极大降低计算复杂度。
表1 计算复杂度对比
Tab.1 Computational complexity of different methods
方法计算复杂度J=4,Mj=6CGMM (M3) (13824)DCGMM (M3j) (216)
4.2 分布式复高斯混合模型的空域协方差矩阵初始化
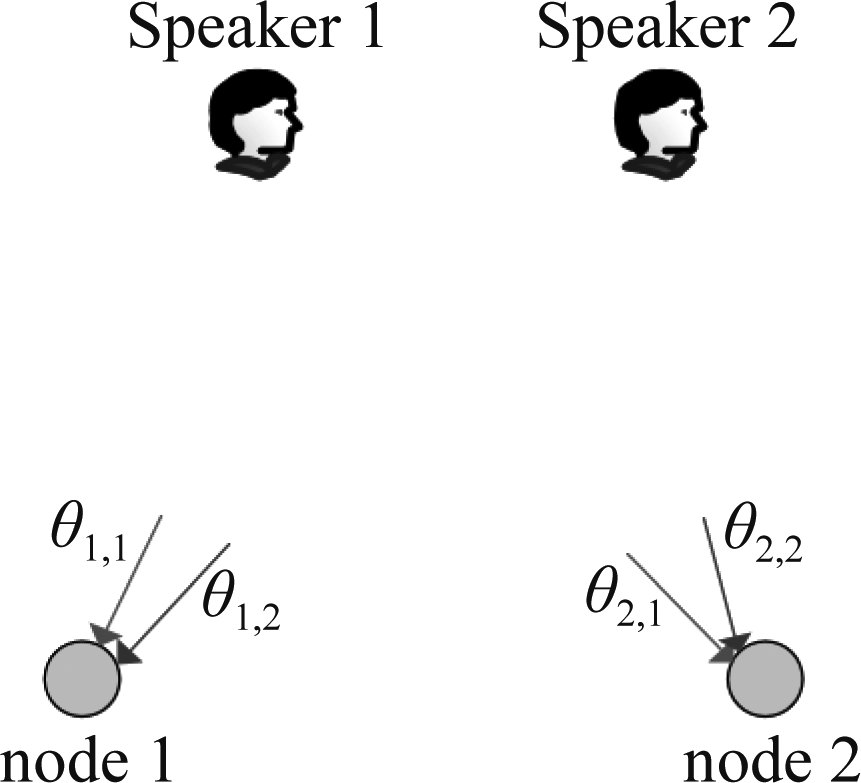
图1 DOA模糊示意图.θ1,1,θ1,2和θ2,1,θ2,2分别是node 1和node 2估计的两个说话人的DOA.但是,node 1和 node 2并不知道对方的哪个DOA量测值和自己的DOA量测值对应同一个说话人
Fig.1 The illustration of DOA ambiguity. θj,k, j∈[1,2],k∈[1,2] are the DOA measurements about the two speakers including speaker 1 and speaker 2 at node j. However, it is unclear that which DOA measurements from different nodes correspond to the same speaker
空域协方差矩阵初始化对DCGMM的性能有重要影响,为了解决多说话人空域协方差矩阵初始化问题,本文提出用基于DOA的导向矢量的相关矩阵对每个节点的进行初始化的方法。然而,直接用基于DOA的导向矢量会存在DOA模糊问题,即不同节点上具有相同索引的DOA并不一定对应同一个说话人,如图1。为了解决DOA模糊问题以使不同节点协同工作,本文提出了基于DOA量测自聚类组合的方法来从不同节点上选出对应同一个说话人的DOA组合。从原理上来说,这个方法通过衡量一个DOA组合的子集对应的说话人位置估计的发散程度来判断该组合的DOA是否对应同一个说话人。
设pj是第j个节点的位置且已知,uk是第k个说话人的位置且未知,
是第j个节点上的第κj个DOA量测值,且该量测值对应第k个说话人。如果一个DOA量测值组合对应同一个说话人,例如,
那么,说话人的位置估计
可以通过下面的最小二乘算法获得:
(14)
其中,A(j,∶)代表矩阵A的第j行,b(j)代表向量b的第j个元素。
说话人的位置估计
近似服从一个正态分布,其均值为uk,协方差矩阵为
对应该正态分布的样本点会形成一个聚类,其中心和形状分别由向量uk和协方差矩阵Σk决定。样本点和聚类中心的平方马氏距离
的定义如下[18]:
(15)
对应固定密度,即rk固定的样本点分布椭圆上。这个椭圆的面积Vk衡量了样本点相对于中心的分散程度,且可以表示为:
(16)
因此,行列式det(Σk)1/2与Vk在数学意义上等价,可以用作衡量样本点分散程度的代价函数,越大的det(Σk)1/2意味着样本点越发散。
对于一个给定的DOA量测值组合,如果其中的DOA量测值对应同一个说话人,例如,
那么对应该集合子集,例如,
的位置估计将聚集到以说话人位置uk为中心的聚类内。否则,对应不同子集的位置估计将偏离uk,并且更加发散。
为了方便描述,去掉DOA量测值
中的说话人索引k,并设参考节点(第1个节点)上的第k个DOA量测值θ1,k对应第k个说话人。对于第k个说话人的某一个候选组合Ck,p={θ1,k,…,θj,κj,…,θJ,κJ},p∈[1,KJ-1],假定
是对应它的B个子集的位置估计。那么,该组合对应的椭圆面积近似为:
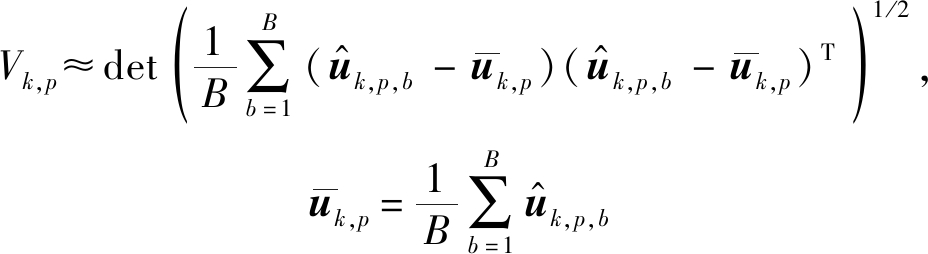
(17)
我们的目标是寻找最优的DOA量测值组合:
(18)
在找到最优的DOA量测值组合(也即对应同一个说话人的DOA量测值组合)后,可以获得第k个说话人在第j个节点上的基于DOA的导向矢量
然后,式(10)中的
可以用方程
(19)
去进行初始化。
4.3 3-step启发式聚类算法
穷举最大似然方法需要计算所有可能的DOA量测值组合对应的椭圆面积来寻找对应同一个说话人的DOA量测值组合。随着说话人个数K或节点个数J的增加,组合个数将急剧增加,导致计算复杂度不能接受。因此,本文提出了一个基于自聚类量测组合的3-step启发式聚类算法。它首先选择初始节点,并且组合它们的DOA量测值来获得潜在的说话人位置。然后,用潜在说话人位置去匹配剩余节点的DOA量测值来预先拒绝错误的组合。最后,使用不同说话人的被选中的DOA量测值组合去构造分组矩阵,以便最终选择对应同一个说话人的DOA量测值组合。
4.3.1 选择初始节点去估计潜在说话人位置
首先选择m,m≥3个节点(式(14)的闭式解要求至少有3个节点),并且组合它们的DOA量测值,如Algorithm 1。然后,对于每个说话人的DOA量测值组合,通过使用式(14)可以获得Km-1个潜在说话人位置
Algorithm 1 组合m个初始节点的DOA量测值for k=1 to K q=0 Bk是一个空矩阵 for κ2=1 to K ︙ for κm=1 to K q=q+1 Row (Bk)q=[k,κ2,…,κm]∥m个索引被存储在匹配矩阵Bk的第q行 end endend
4.3.2 匹配剩余节点的DOA去预先拒绝错误的组合
逐个添加剩余节点并用潜在说话人位置去匹配它们的DOA量测值以便预先拒绝掉许多错误的DOA量测值组合。
从潜在说话人位置
到节点对(1, j), j=m+1的角度差αk,q, j的定义如下:
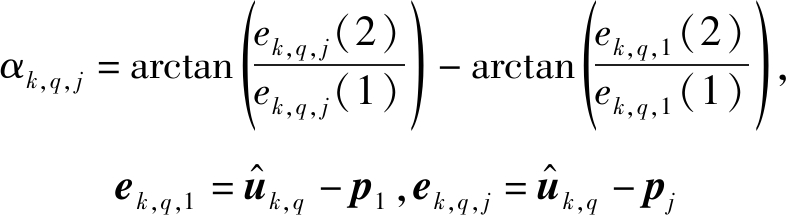
(20)
角度差的误差βk,q, j的定义如下:
βk,q, j=|αk,q, j-(θj,κj-θ1,k)|,
(21)
对于一个DOA量测值组合{θ1,k,θ2,κ2,θ3,κ3,…,θj,κj},这个组合中的DOA量测值对应同一个说话人的置信度可以用βk,q, j表示。βk,q, j越小,置信度越高。因此,对Km-1个βk,q, j按从小到大的顺序排列,并只把前ρ个βk,q, j对应的组合的索引
保留在匹配矩阵Bk中。为了避免丢失掉对应同一个说话人的DOA量测值组合,ρ通常取一个比较大的值,例如,ρ=Km-1/2。
对节点j∈[m+2,J]重复上面的匹配过程,同时,更新Bk和ρ。对每个说话人k∈[1,K]执行该步骤,从而极大降低错误的DOA组合数目。
4.3.3 构造分组矩阵去最终选择对应同一个说话人的DOA量测值组合
经过上面的匹配步骤后,对于每一个说话人,有ρ个被选中的组合,即Bk∈Nρ×J。根据式(17),可以获得Bk中的每个组合对应的椭圆面积。把Bk对应的ρ个椭圆面积按从小到大的顺序排列,然后只保留前ρ2个椭圆面积对应的组合(为了避免丢失对应同一个说话人的DOA量测值组合,ρ2通常需要取较大的值,例如,ρ2=2K)。
从每个匹配矩阵Bk,k∈[1,K]中挑选一个DOA量测值组合去构造一个K×J的分组矩阵,该矩阵的第k行对应第k个说话人。由于一个说话人只能使用每个节点的一个DOA量测值,因此,如果一个分组矩阵的某一列中有重复的索引,那么该分组矩阵将被删除,如 Algorithm 2。对于每一个分组矩阵,求它的K个椭圆面积的和。最终,对应最小和的分组矩阵将被选中。基于被选中的分组矩阵中每一行的DOA索引,可以选出对应K个说话人的DOA量测值组合,并根据式(19)对DCGMM的空域协方差矩阵进行初始化。
Algorithm 2 构造K个说话人的分组矩阵q=0 for q1=1 to ρ2 ︙ for qk=1 to ρ2 ︙ for qK=1 to ρ2 F=Row(B1)q1︙Row(Bk)qk︙Row(BK)qKéëêêêêêêêùûúúúúúúú∥构造一个K×J的分组矩阵 ifF 的每一列中没有重复的索引 then q=q+1 Gq=F end end endend
5 算法测试与分析
仿真房间的长宽高分别是5 m、5 m和3 m。WASNs有J=4个节点,分别为node 1～node 4,每个节点有Mj=6个传声器,这些传声器组成了阵元间距为3 cm的均匀线阵。房间内有K=2个说话人,且这2个说话人功率相等。图2展示了节点和说话人的位置。除语音信号外,还有高斯白噪声,输入信噪比记为SNR。
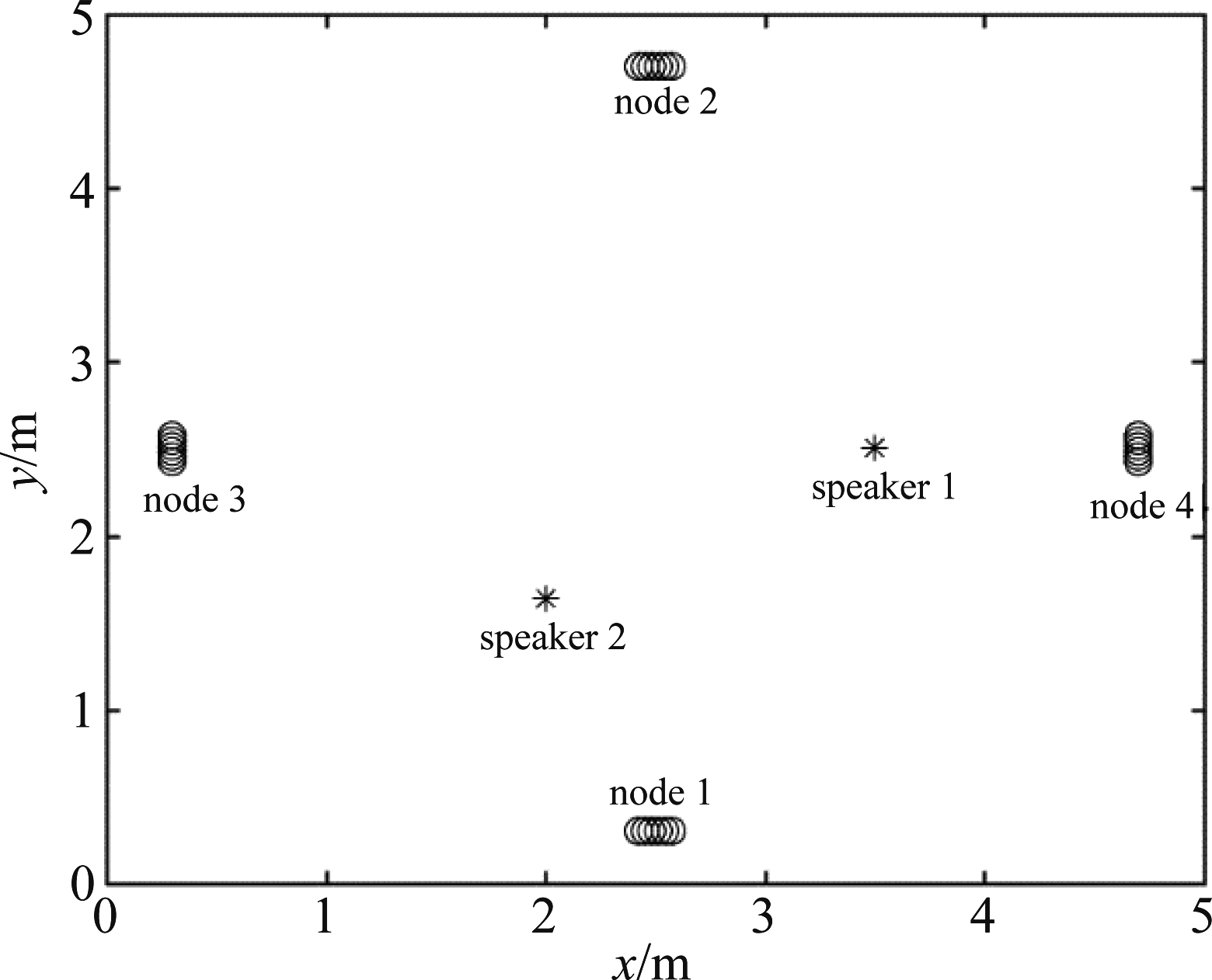
图2 仿真用到的声学场景.每个节点位于每面墙的中央,且距墙30 cm,节点和说话人距地面的高度为1.5 m
Fig.2 The acoustic scenario used in the simulation. The nodes are located at the center of each of the four walls, 30 cm from the walls. All nodes and all sources are in the same horizontal plane, 1.5 m above ground level
观察图3(a)发现,node 1、node 3与node 2、node 4上具有相同索引的DOA并不对应同一个说话人,即存在DOA模糊问题。图3(b)展示了不同的DOA量测误差下的失配比例,即没有从不同节点上找到对应同一个说话人的DOA量测值组合的次数与Monte-Carlo次数的比例。当DOA量测值误差项的标准差σ不超过4°时,在每一次的Monte-Carlo中,自聚类量测组合方法总能找到对应同一个说话人的DOA量测值组合。当σ大于4°时,开始出现失配,并且随着误差项的增大,失配比例也增大;这是因为对应同一个说话人的DOA量测值组合的子集对应的位置估计的误差增大,导致不同子集对应的位置估计的发散程度,即式(16)中的椭圆面积增大,甚至大于不是对应同一个说话人的DOA量测值组合的椭圆面积。
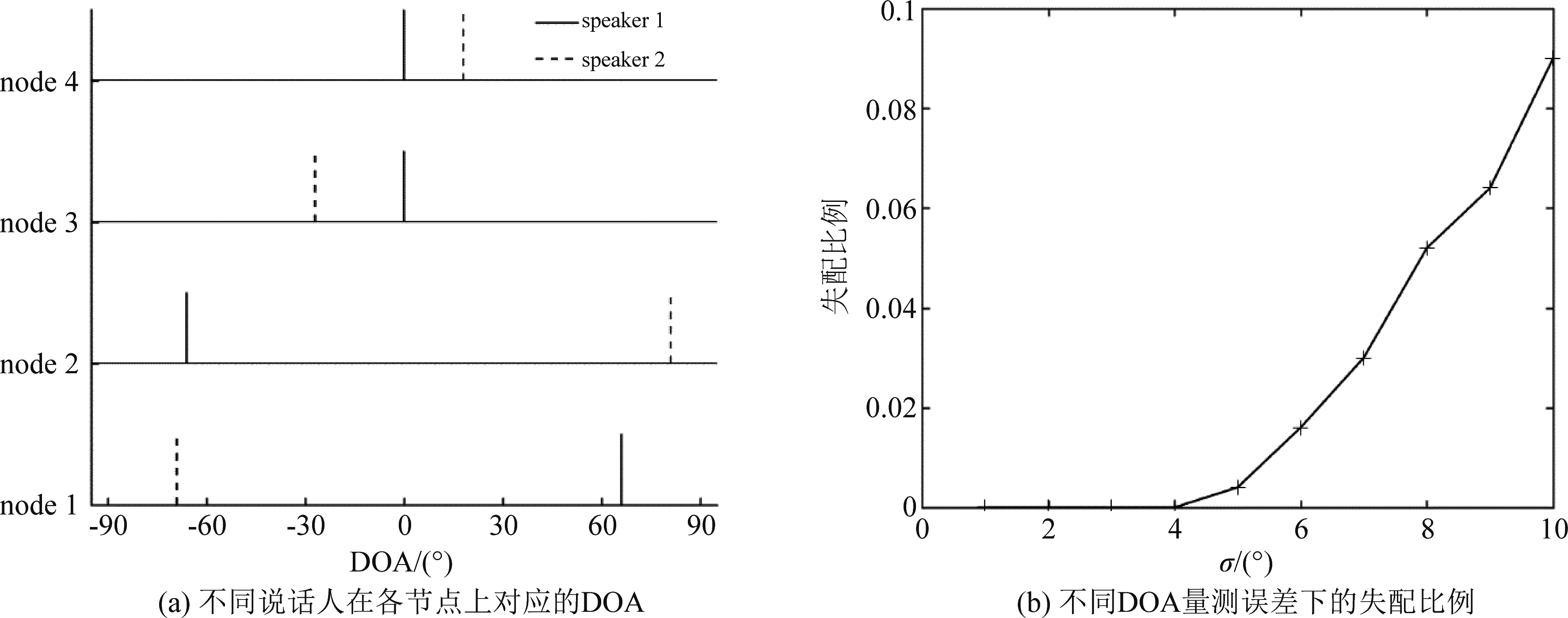
图3 自聚类量测组合方法解决DOA模糊问题的结果
Fig.3 The result of the self-clustering measurement combination method to solve the DOA ambiguity problem
具有理想初始值(每个说话人对应的空域协方差矩阵已知)的集中式算法和本文提出的分布式算法分别记为Oracle 1和Oracle 2,使用本文提出的初始化方法的分布式算法记为SC-MC。图4对比了在混响时间T60=0.3 s和 SNR=30 dB的情况下,不同方法在60次Monte-Carlo运行下分离的说话人信号的平均SDR、STOI和PESQ。图5对比了某一次Monte-Carlo运行下不同方法分离的说话人信号的语谱图。观察发现,当具有理想初始值时,本文提出的分布式算法的性能要优于集中式算法,这得益于在分布式算法的推导过程中使用了式(9)中的具有块对角形式的空域协方差矩阵,这个结果与[19- 20]中的结论一致。当使用本文提出的初始化方法时,分布式算法的性能接近具有理想初始值的集中式算法,且几乎没有随DOA误差的增大而下降,这表明了本文提出的初始化方法的鲁棒性。
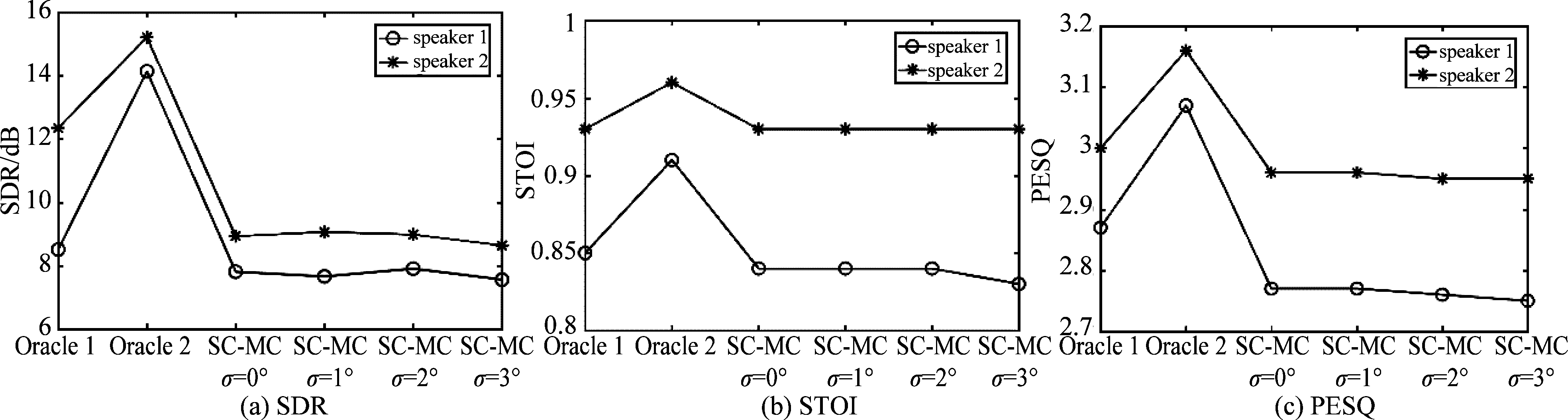
图4 不同方法分离的说话人信号的SDR,STOI和PESQ (T60=0.3 s, SNR=30 dB)
Fig.4 SDR, STOI, and PESQ of the speech signals obtained by different methods under T60=0.3 s and SNR=30 dB
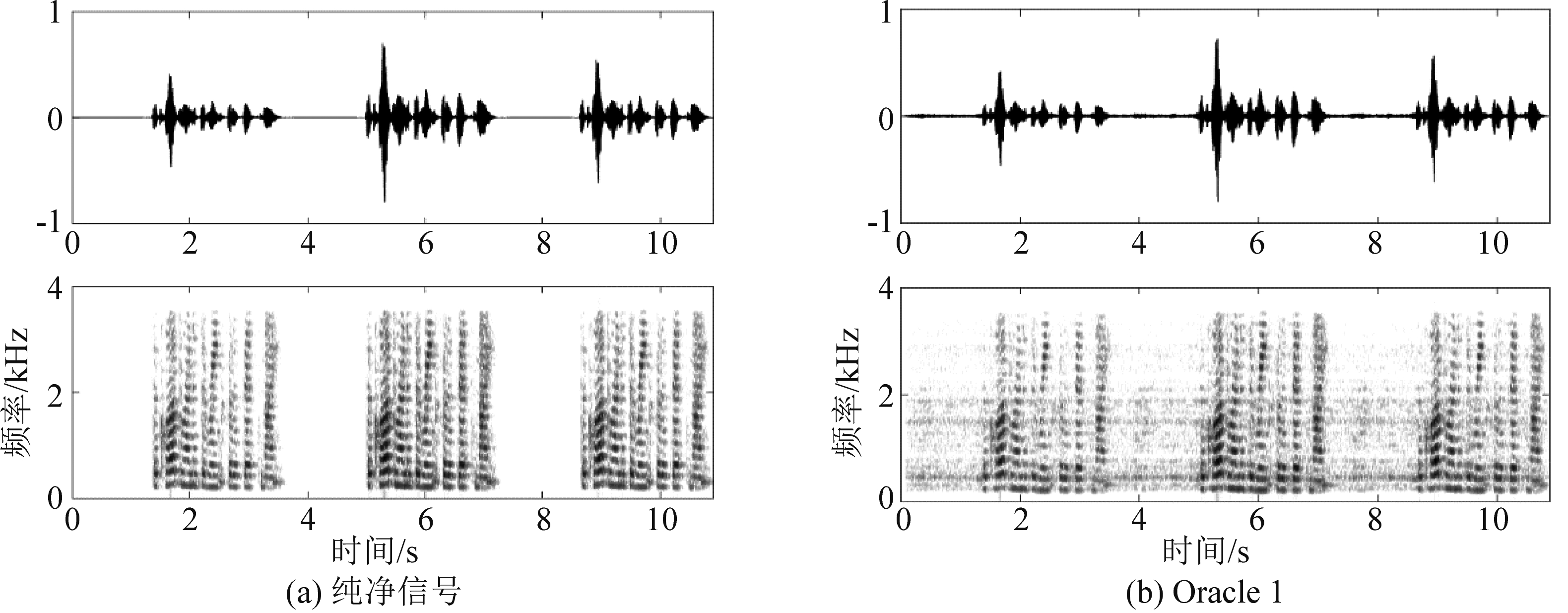
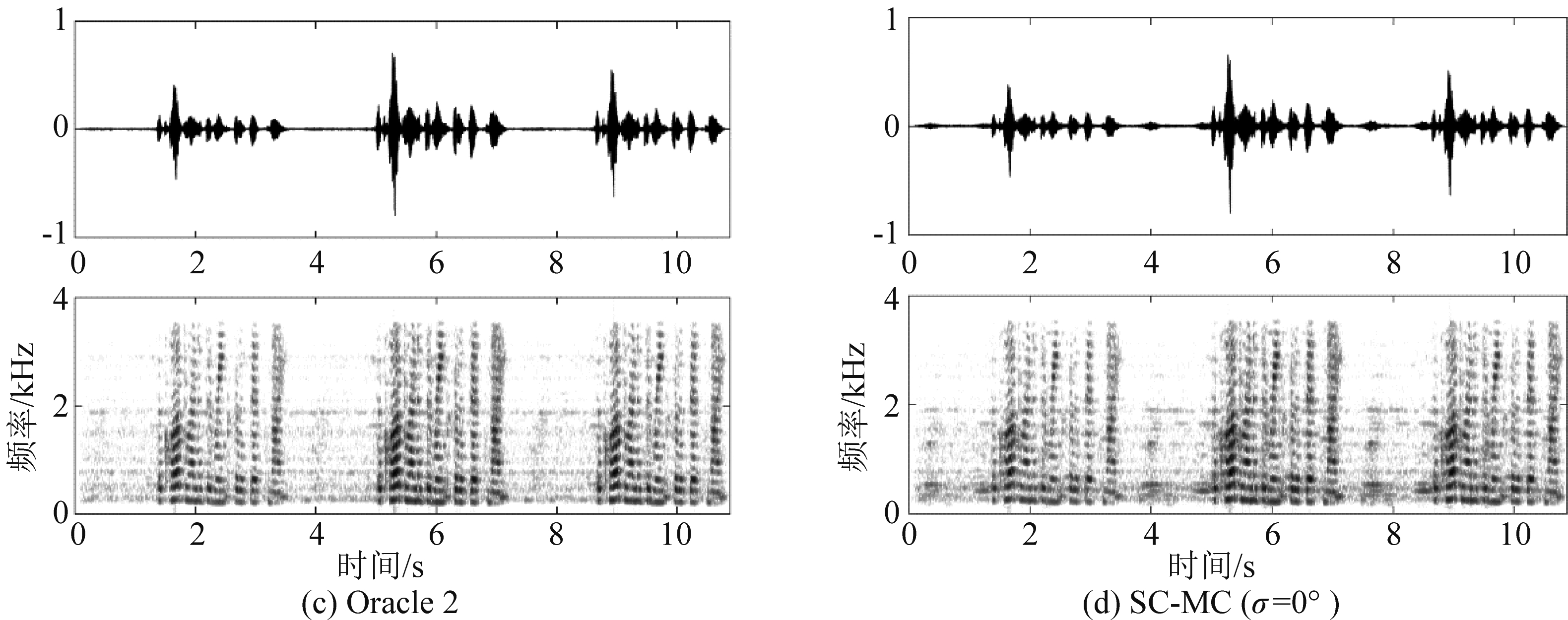
图5 不同方法分离的第2个说话人信号的语谱图(T60=0.3 s,SNR=30 dB)
Fig.5 The spectrograms of the speaker 2 obtained by different methods under T60=0.3 s and SNR=30 dB
图6对比了在混响时间T60=0.5 s和 SNR=30 dB的情况下,不同方法分离的说话人信号的平均SDR、STOI和PESQ。可以发现,本文提出的SC-MC甚至比具有理想初始值的集中式算法Oracle 1具有更好的性能。
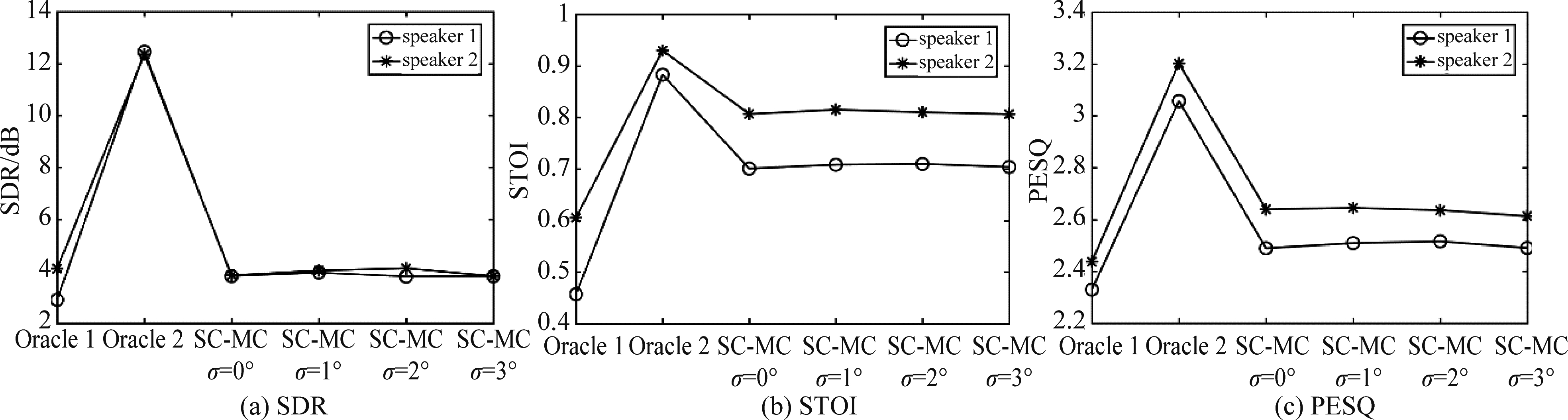
图6 不同方法分离的说话人信号的SDR,STOI和PESQ (T60=0.5 s, SNR=30 dB)
Fig.6 SDR, STOI, and PESQ of the speech signals obtained by different methods under T60=0.5 s and SNR=30 dB
图7对比了在混响时间T60=0.3 s和 SNR=10 dB的情况下,不同方法分离的说话人信号的平均SDR、STOI和PESQ。可以发现,相比于Oracle 1和 Oracle 2, 本文提出的SC-MC的性能有一些降低,这表明SC-MC对噪声比较敏感。
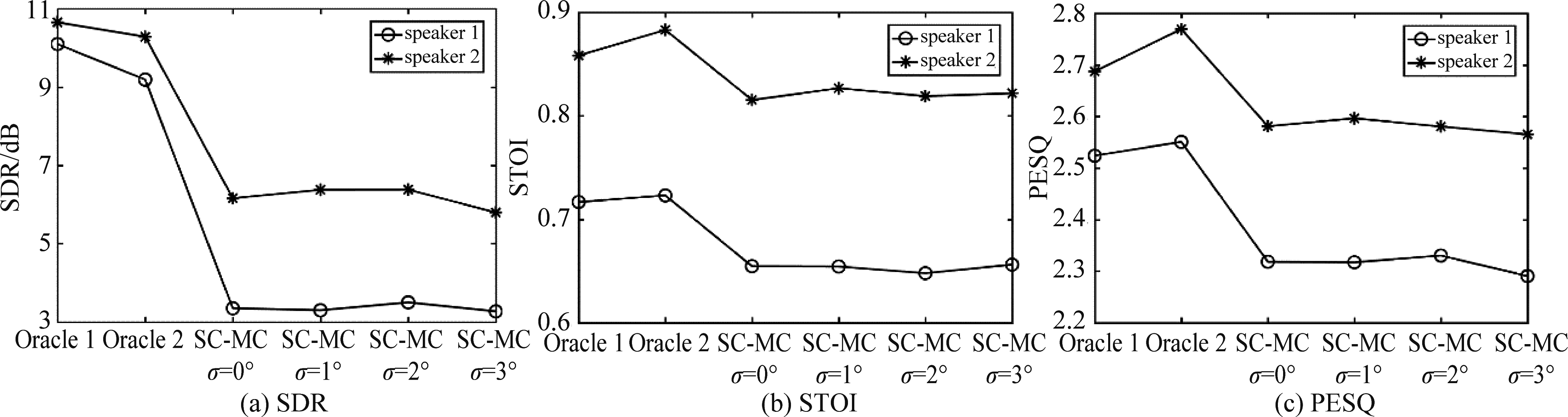
图7 不同方法分离的说话人信号的SDR,STOI和PESQ (T60=0.3 s, SNR=10 dB)
Fig.7 SDR, STOI, and PESQ of the speech signals obtained by different methods under T60=0.3 s and SNR=10 dB
6 结论
本文研究了CGMM下的分布式语音分离及其空域协方差矩阵初始化的问题。通过使用块对角形式的空域协方差矩阵,降低了CGMM参数迭代估计过程中的计算复杂度。DOA量测自聚类方法确保了用基于DOA的导向矢量的相关矩阵去初始化每个节点对应的空域协方差矩阵时,不同节点仍能协同工作。这种初始化方法从空域角度区分了不同的说话人,避免了排序问题,而且获得了与具有理想初始值的集中式算法十分接近的性能。
[1] BERTRAND A. Applications and trends in wireless acoustic sensor networks: A signal processing perspective[C]∥2011 18th IEEE Symposium on Communications and Vehicular Technology in the Benelux (SCVT). Ghent, Belgium. IEEE, 2011: 1- 6.
[2] ZHANG Guoqiang, HEUSDENS R. Distributed optimization using the primal-dual method of multipliers[J]. IEEE Transactions on Signal and Information Processing Over Networks, 2018, 4(1): 173-187.
[3] HASSANI A, BERTRAND A, MOONEN M. GEVD-based low-rank approximation for distributed adaptive node-specific signal estimation in wireless sensor networks[J]. IEEE Transactions on Signal Processing, 2016, 64(10): 2557-2572.
[4] ZHANG Jie, HEUSDENS R, HENDRIKS R C. Rate-distributed spatial filtering based noise reduction in wireless acoustic sensor networks[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 26(11): 2015-2026.
[5] GUO Xinwei, CHEN Zhifei, HU Xiaoqing, et al. Multi-source localization using time of arrival self-clustering method in wireless sensor networks[J]. IEEE Access, 2019, 7: 82110- 82121.
[6] ALEXANDRIDIS A, MOUCHTARIS A. Multiple sound source location estimation in wireless acoustic sensor networks using DOA estimates: The data-association problem[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 26(2): 342-356.
[7] JIA Ying, LUO Yu, LIN Yan, et al. Distributed microphone arrays for digital home and office[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP).France (Toulouse):IEEE, 2006:V1065-V1068.
[8] HASSANI A, PLATA-CHAVES J, BAHARI M H, et al. Multi-task wireless sensor network for joint distributed node-specific signal enhancement, LCMV beamforming and DOA estimation[J]. IEEE Journal of Selected Topics in Signal Processing, 2017, 11(3): 518-533.
[9] HIGUCHI T, ITO N, ARAKI S, et al. Online MVDR beamformer based on complex Gaussian mixture model with spatial prior for noise robust ASR[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2017, 25(4): 780-793.
[10] HIGUCHI T, ITO N, YOSHIOKA T, et al. Robust MVDR beamforming using time-frequency masks for online/offline ASR in noise[C]∥2016 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). Shanghai, China.IEEE, 2016: 5210-5214.
[11] ZHANG Jie, KOUTROUVELIS A I, HEUSDENS R, et al. Distributed rate-constrained LCMV beamforming[J]. IEEE Signal Processing Letters,2019,26(5):675- 679.
[12] DEMPSTER A P, LAIRD N M, RUBIN D B. Maximum likelihood from incomplete data via the EM Algorithm[J]. Journal of the Royal Statistical Society: Series B (Methodological), 1977, 39(1): 1-22.
[13] GU Dongbing. Distributed EM algorithm for Gaussian mixtures in sensor networks[J]. IEEE Transactions on Neural Networks, 2008, 19(7): 1154-1166.
[14] SOUDEN M, KINOSHITA K, DELCROIX M, et al. Distributed microphone array processing for speech source separation with classifier fusion[C]∥2012 IEEE International Workshop on Machine Learning for Signal Processing. Santander, Spain. IEEE, 2012: 1- 6.
[15] WANG Lin, DING Heping, YIN Fuliang. A region-growing permutation alignment approach in frequency-domain blind source separation of speech mixtures[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(3): 549-557.
[16] 冷艳宏, 郑成诗, 李晓东. 功率比相关子带划分快速独立向量分析[J].信号处理,2019,35(8):1314-1323.
LENG Yanhong, ZHENG Chengshi, LI Xiaodong. Fast independent vector analysis using power ratio correlation-based bands partition[J]. Journal of Signal Processing, 2019, 35(8): 1314-1323.(in Chinese)
[17] ITO N, ARAKI S, YOSHIOKA T, et al. Relaxed disjointness based clustering for joint blind source separation and dereverberation[C]∥2014 14th International Workshop on Acoustic Signal Enhancement (IWAENC). Juan-les-Pins, France. IEEE, 2014: 268-272.
[18] STORK David G, DUDA Richard O, HART Peter E. Pattern Classification[M]. New York:Wiley, 2001:17-19.
[19] ZHENG Chengshi, DELEFORGE A, LI Xiaodong, et al. Statistical analysis of the multichannel Wiener filter using a bivariate normal distribution for sample covariance matrices[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 26(5): 951-966.
[20] KOUTROUVELIS A I, SHERSON T W, HEUSDENS R, et al. A low-cost robust distributed linearly constrained beamformer for wireless acoustic sensor networks with arbitrary topology[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2018, 26(8): 1434-1448.
