1 引言
物联网通过各类传感器采集的物理信息建立起物物、物人和物与过程的泛在连接,从而形成各物理对象均能互联互通的网络。物联网的物理信息需通过传感器采集才能传输至网络,进而完成信息交互,而近距离无线通信是物联网中传感通信的常用技术,如NFC、WSN、RFID、WiFi和蓝牙等[1-2]。物联网中近距离无线传感通信多是一传感节点对多物理节点的情形,例如物品识别,门禁出入和人员定位等[3]。为了提高近距离无线传感通信的实时性和高效性,需具备短时间内成功识别多信息能力,而无线通信通常采用共享信道,因此多个信源短时内一起传输通信必导致冲突发生。通常,该冲突分解在媒体访问控制(Media Access Control, MAC)层上采用随机多址解决,常用的方法如ALOHA和树形分类等[4-9],其基本思想为,信息随机发送,当发生冲突时再被随机重传,直到信息传送成功。虽然随机多址的冲突分解操作简单,但是当信息增多,重传也增多,不可避免导致通信效率降低。其实,冲突信号为各信源信号的叠加,在物理层中可直接从冲突的叠加信号中分离出各信息源。这种带有信号分离的冲突分解[10-11]不再视冲突信号为无效信号,通过冲突分解以提高通信效率,因此一直都受到较多的关注。
近距离无线通信网络经常采用信号编解码技术来减少通信干扰,冲突分解本质是一种去干扰技术,因此良好的编解码能够有效提高冲突分解性能。无线通信中,信号频率漂移是一普遍现象,以FM0和Miller码为代表的延迟编码[12-13]也常被用于近距离无线通信中以对抗频率漂移[13]。区别于匹配滤波器的解码,延迟码并不需要知道信号的频率信息,仅依靠信号的相位是否发生改变就可解码数字0或1。由于信号的相位改变并不因为频率改变而发生改变,因此延迟码可以较好地解决频率漂移中的解码问题。
分离型冲突分解中,解码对象为冲突叠加信号,如果仅通过判断相位来解码将比较困难。一种较为简单的解码方法是对叠加信号分离后再判断相位的改变。信号分离可采用无监督k均值聚类方法[14],但该方法当信号源数增多时,信号簇存在不确定性,导致聚类存在多个可能性。为解决分离的不确定性,可采用有监督分离,先将信号源的衰减系数估计出以确定聚类中心点[15],然后再对信号分离,但如何估计衰减系数也比较困难,因为无论是导频还是盲估计都会增加系统的复杂度[16-18]。另外一种冲突分解方法是不对信号分离,而是从叠加信号中直接解码出源信号,如采用Viterbi和连续干扰消除[19]。该方法通过最大似然准则寻找与观测值最相似的数据作为解码数据,然而,该方法寻找相似度需要计算距离,这仍需要知道信号的衰减度,不准确的信号估计不可避免导致较低的解码性能。
针对以上分离型冲突分解方法存在的问题,本文提出一种有限符号分离的Viterbi解码(Finite-symbol Separation Viterbi Decoder,FSVD)冲突分解方法,该方法采用最小方差准则来消除信号簇的不确定性,同时又不需估计信道信息,据此可得到更准确的似然距离,从而提高Viterbi解码的准确性。我们通过估计簇数目[11,20]以确定冲突信源数,当冲突信源较少时,由于分离结果属于一有限集,因此可将初步的似然结果存储起来,每次搜索最小误差时可调用存储的数据以减少计算量。实验中,我们采用跨层的思想,在MAC层采用动态帧时隙的方法使初始帧长与冲突时隙数相同,继而在物理层根据EPC C1 Gen2标准[21]分别用仿真和软件无线电构建了一个基于FM0码的超高频短距离无线通信系统[22],将各冲突分解嵌入至ALOHA协议中进行测试。实验结果表明,本文的FSVD算法在信噪比超过15 dB时,解码冲突信源为2,3时的解码效率已接近100%,其吞吐量性能接近假定信号衰落系数已知的解码算法性能,而好于信号衰落系数未知的传统算法性能。
2 相关工作
传统MAC层冲突分解采用随机多址网络,例如ALOHA,如图1(a)所示,信号随机选择时隙发送,若发生冲突则在下一个帧中重传。然而,MAC层方法将冲突时隙视为无效时隙,通信效率并不高。分离型冲突分解图1(b)所示,可将MAC层的冲突时隙中各信号进行恢复。由于其将冲突时隙视为有效通信时隙,因此通信效率得到了提高。
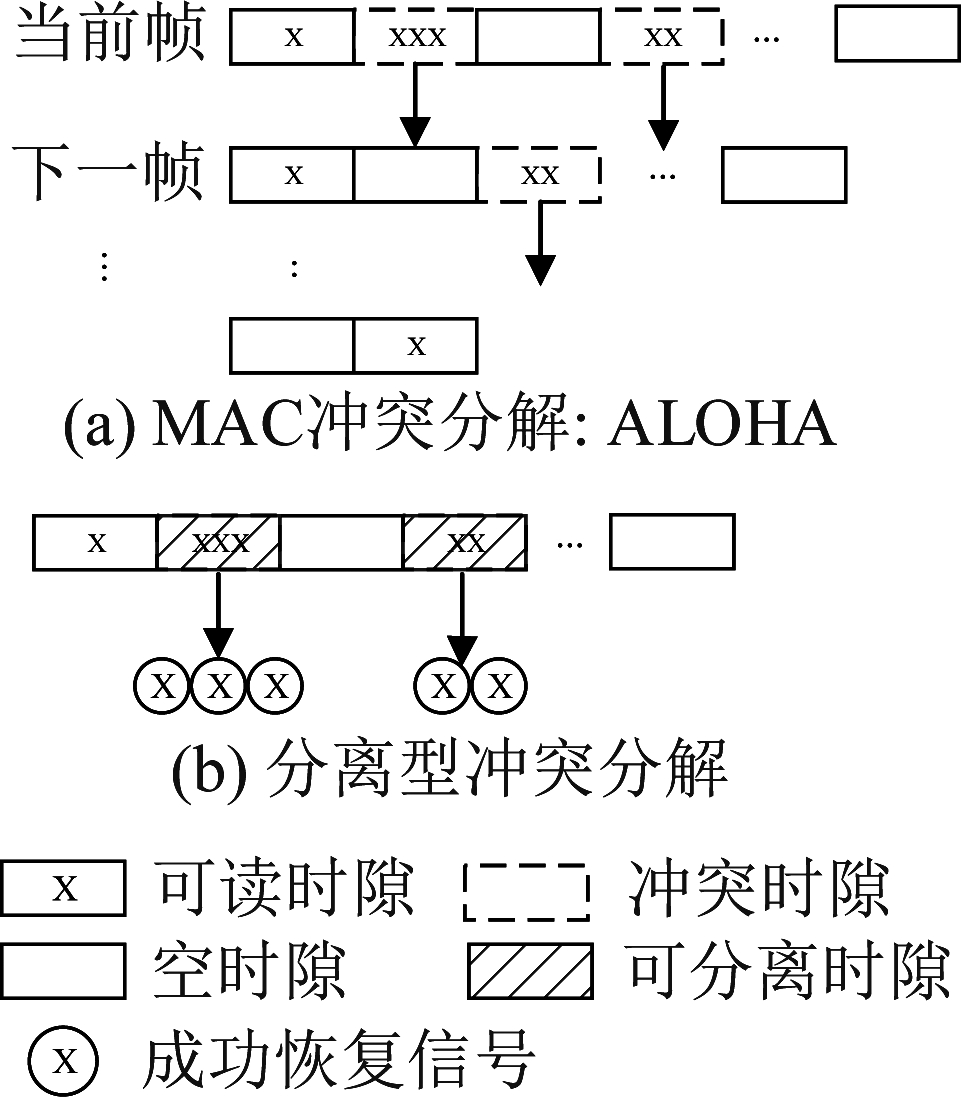
图1 MAC层冲突分解和分离型冲突分解
Fig.1 MAC-layer collision resolution and separated collision resolution
冲突信号实为各信源信号的叠加信号,一种分离型冲突分解方法是对冲突信号分离后再解码,图(a)中给出了两个信源叠加后成为冲突信号。通常,具有N个信源的二进制数字单极性码经同相正交相(Inphase Quadrature, IQ)解调后,各采样点投射至一复平面后会呈现M=2N个簇,由该簇中心点构成的集合可表示为[14]
…, hN-1+hN,…, h1+h2+…+hN}
(1)
其中h1, h2, …hN分别为各信号源衰减复系数。经聚类后,任何一个采样点均可根据(1)中的中心点分离成N个信源点矢量,分离结果构成的集合表示为
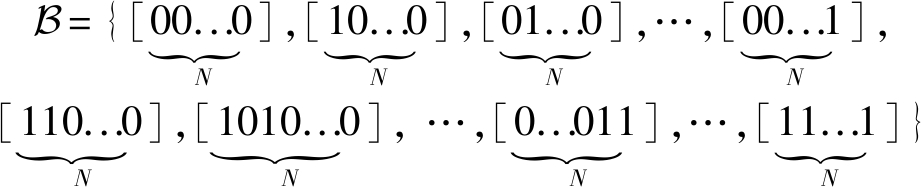
(2)
其中
和
的每一元素构成一一对应关系,例如0和h1就分别对应于[00…0]和[10…0]。图2(b)为两个信号源冲突信号投至复平面的例子。
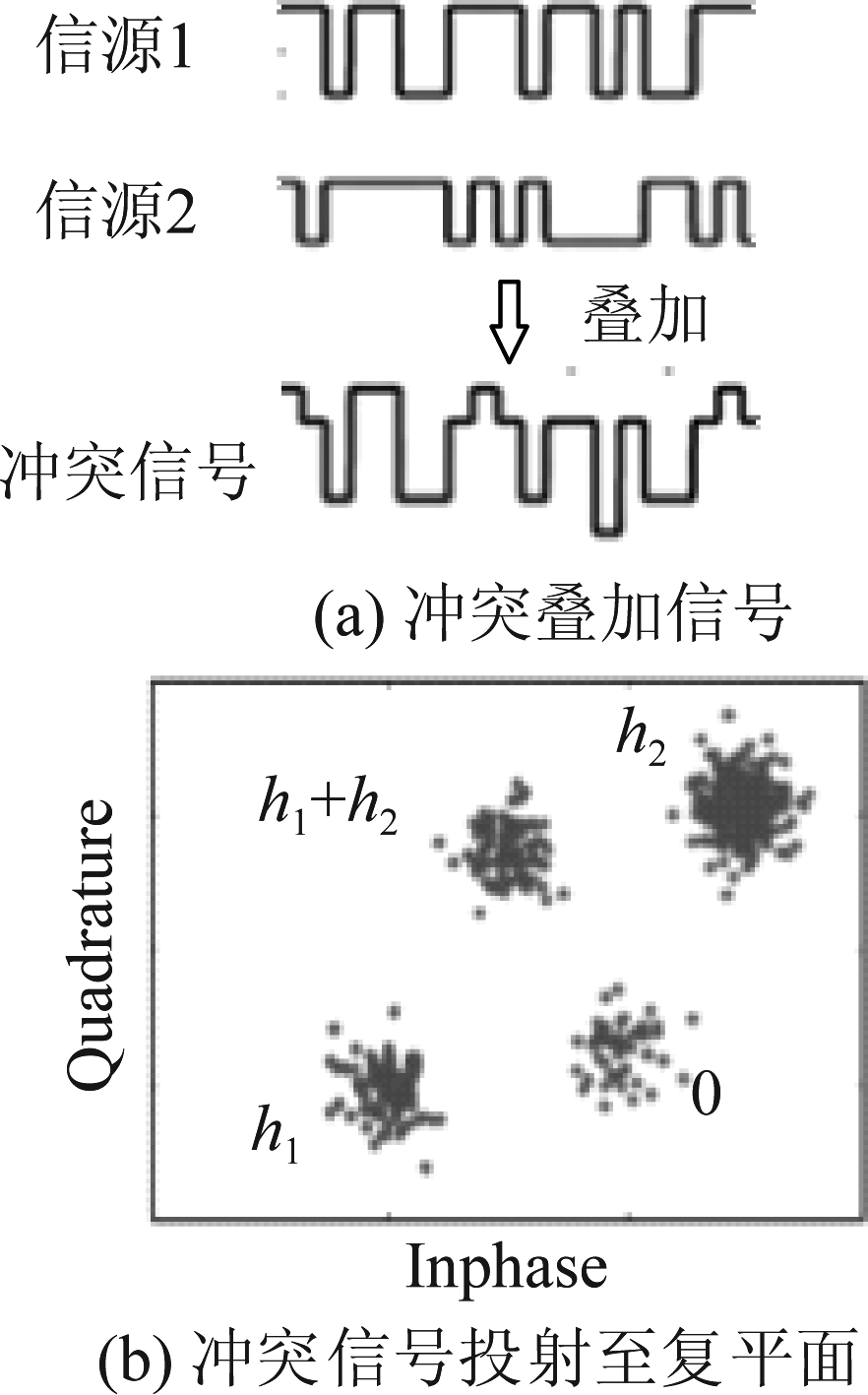
图2 冲突信源为2个时,投射到复平面示例图
Fig.2 An example for a collision signal with two signal sources projected to a complex plane
另外一种分离型冲突分解方法是根据信源的编码直接从冲突信号中解码出各个信源信号,例如FM0和Miller码[12],其仅通过码元之间相位反转就可检测出原始码元,因此可对抗频率漂移而被广泛用于近距离无线通信中。图3为FM0码状态转化图及对应的码型,从图中可以看到,FM0码可看作一个有限状态机图,据此可画出如图4的网格图。FM0解码其实就是利用Viterbi算法[19]从该网格图中寻找一条最大似然路径,以此消除其他信源对本信源的干扰,然后再用连续干扰消除逐次解码各个信源。
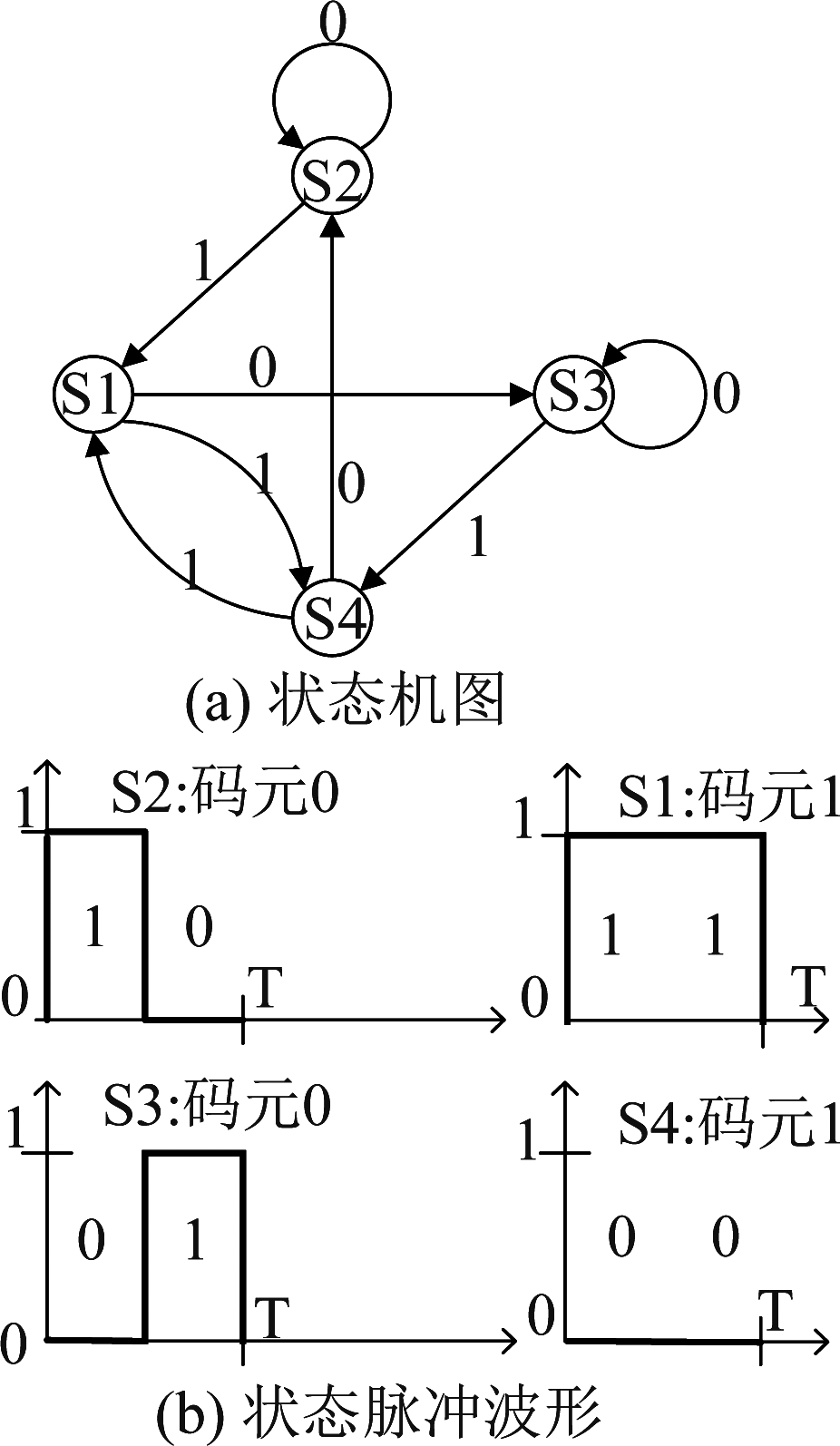
图3 FM0状态机及其波形图
Fig.3 FM0 state machine and its waveform
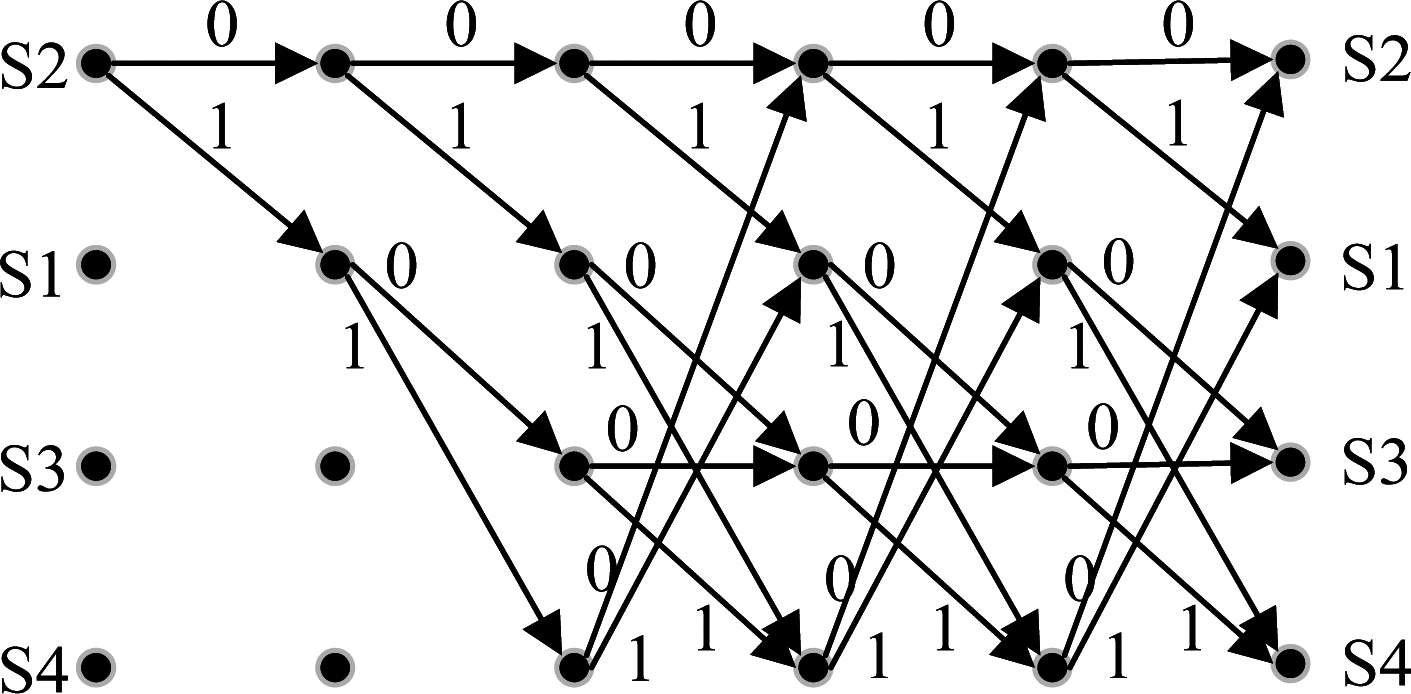
图4 FM0编码对应网格图
Fig.4 Grid for Viterbi algorithm in FM0 coding
3 问题提出
对于分离型冲突分解方法,其分离信号需知各簇中心位置,然而各中心点存在不确定性,如图2(b)中,中心点从0开始沿顺时针依次为h1,h1+h2和h2,但各个衰减系数的大小和相位预先并不知道,因此也可能依次为h1+h2,h2和h1,甚至是其他的排列。若存在M个信源,那么中心点可能有
种排列,当M较大时,排列数将是一个庞大值。若中心点位置无法确定,则信号分离将难以进行。最直接的解决方法是对信号衰减系数进行估计后再确定位置,然而估计该系数也存在一定问题。若采用导频的方法估计[18],需要设计导频,这将导致系统复杂度升高,同时,导频还会降低通信效率。若不降低通信效率采用盲估计的方法,算法的复杂度会增加,同样会导致系统成本增加。
对于直接解码的分离冲突分解方法,其寻找最大似然路径需要计算距离,但是若不准确估计信号衰减系数仍会导致误判。图5给出了一信道衰减系数为hn的二进制单极性码信号,若hn较小,则容易被误判为数字0,从而导致似然路径计算失效。估计出信道衰减系数hn,再归一化后与参考信号计算距离是一种方法,但如前所述,信道系数的估计会给系统带来一定的复杂度。
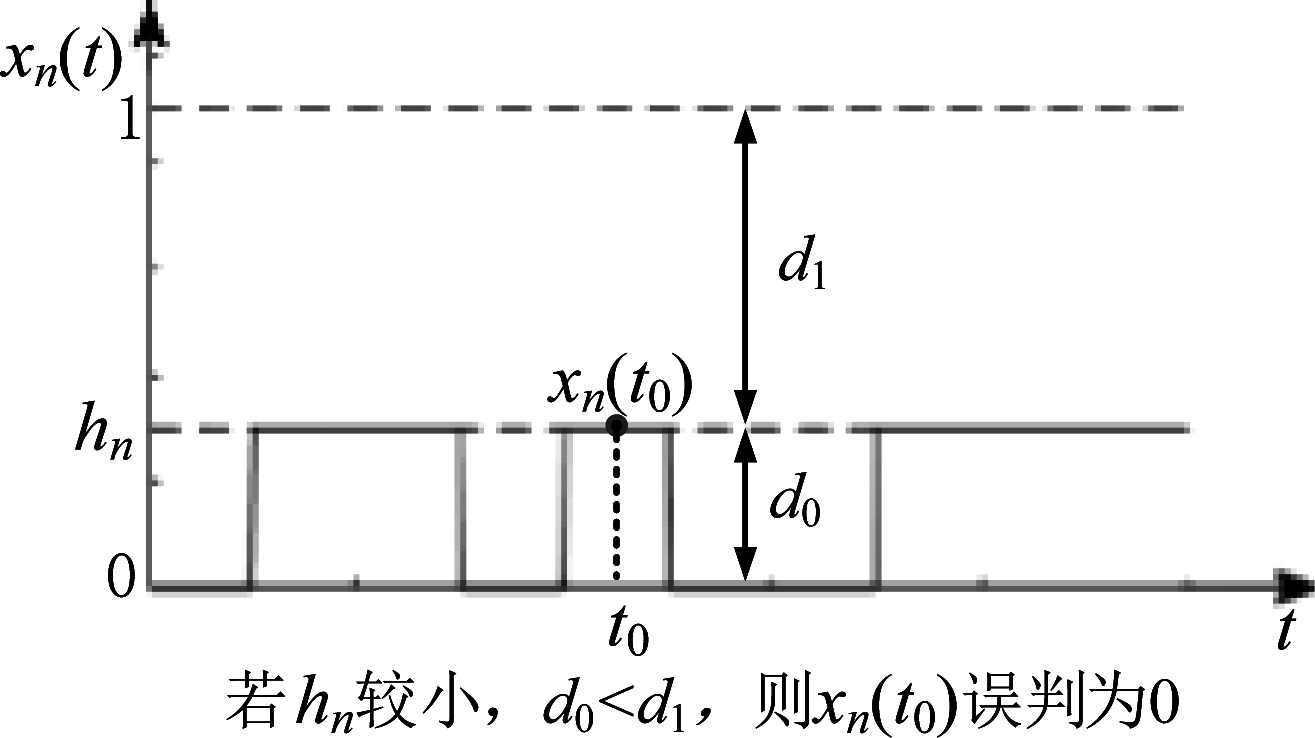
图5 似然距离计算错误示例图
Fig.5 An example of misjudgment for a symbol
本文研究的分离型冲突分解将从系统复杂性的角度去研究簇中心不确定性问题,将信号唯一分离后得到一个具有0、1电平的数字信号,然后再计算与参考信号的似然距离以降低计算的错误率。
4 系统模型
本文研究的近距离无线通信网络系统模型如图6所示,模型中若干个节点采用共享无线信道向中心节点发送数据,系统采用随机多址的ALOHA协议解决冲突,当一个时隙内有多个节点发送的信号则采用分离型冲突分解方法。假设在这样一个时隙内有N个节点信源发送的K个二进制码元un,k∈{0,1},n=1, 2, …N, k=1, 2, …K,经编码后得到编码序列νn,k′∈{0,1},n=1, 2, …N, k′=1, 2, …K′ (通常,K≠K′,例如图3的FM0编码,码元0将被编码至01或10,则K=K′/2[21])。若L表示为载波泄露[21,23],则接收端经I/Q调制后的接收信号y(t)表示为
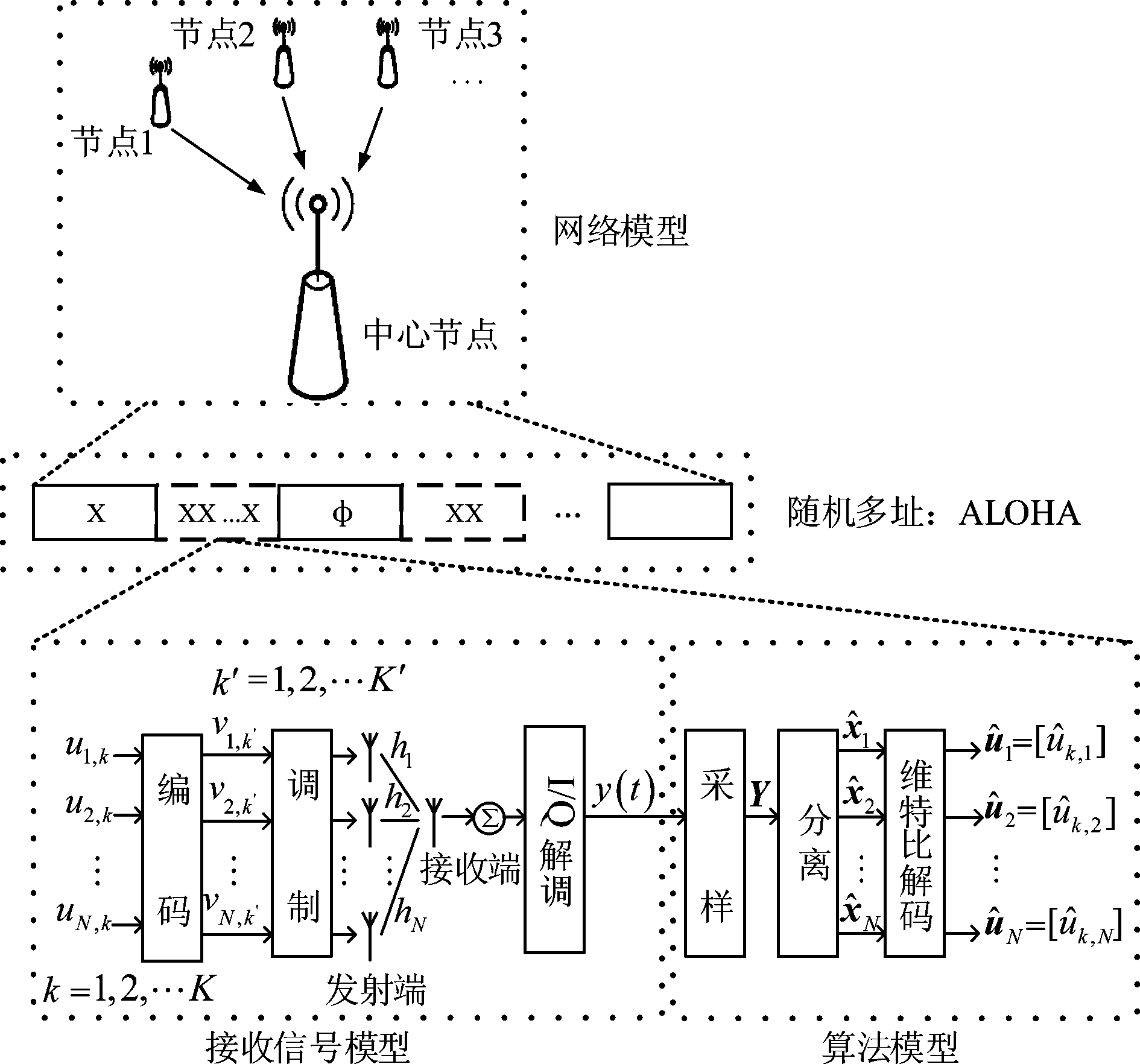
图6 短距离无线通信系统模型
Fig.6 System model for a short-range wireless network
(3)
其中,hn为第n个信源到接收端的复衰落系数,在近场通信中,该衰落系数在很短的一个通信时间内可视为平坦性衰落的线性时不变信
代表第n个源信号,an和bn分别为码元周期和码元时延,gan(t)为调制的方波波形,即当0≤t≤an,gan(t)=1,否则为0,η(t)为噪声信号。
对接收信号进行解码时,先对接收信号进行采样。设T为采样周期,做I次采样可得接收信号矢量
其中
为复数集,yi=y(iT),i=1, 2, …I。然后,采用最小方差分离得到N个信源信号矢量
最后,利用维特比解码得到N个信源的码元序列矢量
5 FSVD算法
本部分给出信号分离算法,图7给出了该算法框架图。将接收信号Y投射至复平面中,聚类后可得M个中心点
进而判断,当簇的数目为4或8时,分离算法启动;否则,分离算法不启动。如图2所示,估计器通过该聚类中心点可得一估计字典矩阵
此外,聚类后对任意采样点有
若
表示聚类后第m个簇中各点的集合。由字典矩阵和聚类结果可确定分离函数fdict(·),从而得到分离的信源信号矢量
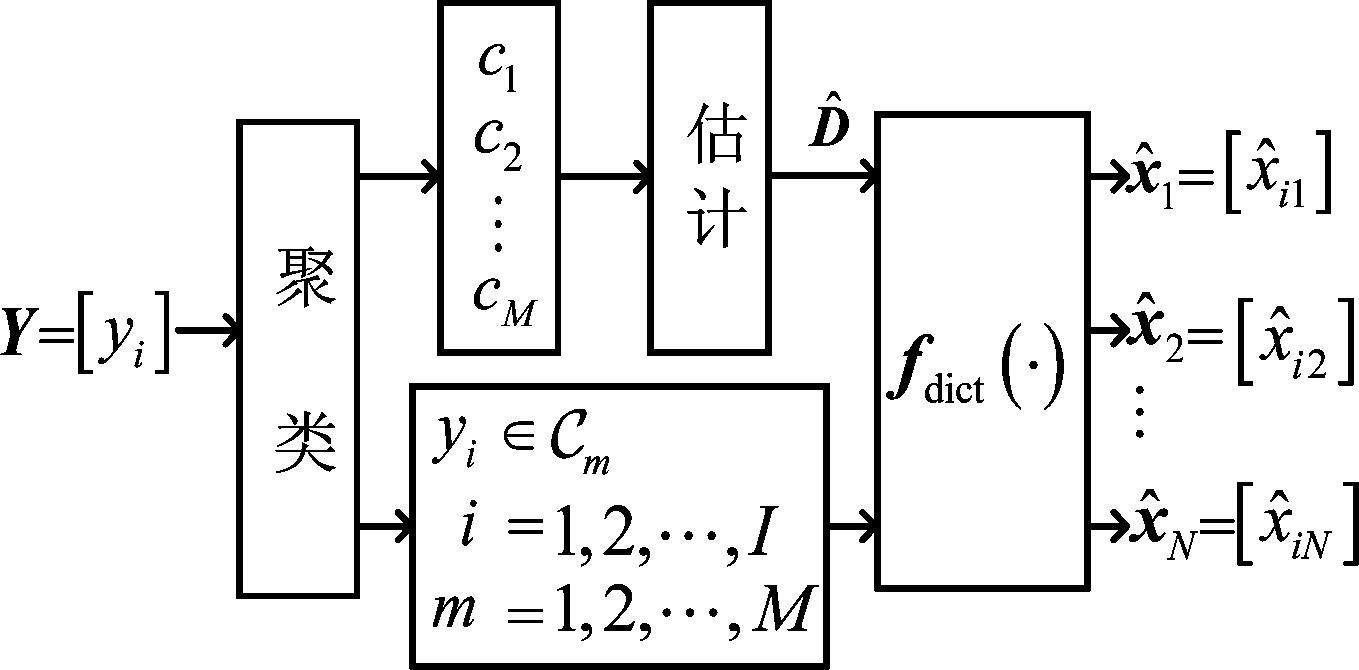
图7 分离算法图
Fig.7 Flow chart of separation algorithm
5.1 聚类中心的矩阵表达
令D=[dm]∈{0,1}M×N为行向量dm所构成的字典矩阵,其中
且dm≠dn当m≠n,那么聚类中心矢量
可表示为
C=DH
(4)
其中H=[h1, h2, …hN]T。若字典矩阵D确定,则由(4)可得到中各点和dm间的映射关系fsep(·),表示为
(5)
例如,若d2=[0 1 0 1],yi经聚类后为
那可分解为四个信源采样点0,1,0和1。
5.2 字典矩阵估计
为确定式(5)的函数,需对字典矩阵D进行估计,可建立如下目标函数
f(C|D)=||DD†C-C||2
(6)
得到如下估计(证明见附录1)
(7)
为行矢量
构成矩阵D的集合,(·)†表示为伪逆。由于为一有限集,因此D的集合也是有限集,因此通过全局搜索可得到(6)的估计结果。注意到(7)中的估计结果并不需预先知道信号衰减系数H的信息,因此可避免估计H给信号分离所带来的不确定问题。
去掉了载波泄露的零点,因此搜索集减少,搜索次数也从M!降至(M-1)!。在进行求伪逆时,因为将预先计算的结果存储,因此乘法次数从M3降至M×N。
表1 算法复杂度
Tab.1 Signal fading coefficient setting
穷尽搜索低复杂搜索伪逆求解预先存储求解搜索次数O(M!)O((M-1)!)//乘法次数//O(M3)O(M×N)
5.3 低复杂度的分离算法
由(7)和(2)可知
直接对(7)进行计算将导致较多计算量,可做如下处理。由于簇中心点00…0可预先确定,该中心点为静默期时对应的载波强度L,此时可更新C和D分别为
(8)
(9)
由
可减至(M-1)!,将其代入(6～7),当N为2和3时,搜索次数可减至3!=6和7!=5040。由于D可预先设置,因此可将(6)改写为
(10)
其中
为D′=DD†-I所构成的矩阵集合,可预先计算后放至存储器中以减少计算复杂度。
5.4 维特比解码
利用(5)的函数关系可将信号向量Y分解成一行向量ξi构成的信号矩阵X=[ξi]∈{0,1}I×N,其中ξi=fdict(yi),该分解过程表示为
(11)
将信号矩阵
写成由列向量
所构成的
其中
为第n个信源的第i个采样点。那么,通过FM0码规则(见图4)或米勒码规则,采用维特比算法fvit(·)可由xn得到第n个信源的解码结果
(12)
其中
注意到分离后的xn是二进制0、1序列,因此在计算似然路径时,将可避免图5中由衰减系数hn造成无效幸存路径的情况。最后,给出FSVD算法步骤,如表2所示。
表2 FSVD算法步骤
Tab.2 FSVD algorithm steps
输入:接收信号向量Y=[yi]∈ 1×I。输出:第n个信源序列向量u^n=[u^k,n]∈{0,1}K×1, n=1, 2, …N。已知条件:载波泄露L;维特比解码函数fvit(·)。步骤:①聚类:得到中心点矢量C=[cm]∈ M×1;
续表2
②字典矩阵估计:由(10)得到D^;③信号分离:由(11)和(5)得到信号分离矩阵X^=[ξi]∈{0,1}I×N;④解码:由(12)得到各信源信号向量u^n=[u^k,n]∈{0,1}K×1, n=1, 2, …N。
6 实验设置
本实验中,我们依据EPC C1 Gen2标准[21]中的主要参数构建一个超高频的短距离无线通信网络,以测试提出算法的性能。在该网络中,中心节点的功能由一阅读器完成,其他节点由若干标签充当,阅读器让标签采用随机多址方法随机选择时隙来发送信号,当某一时隙发生冲突后再对时隙中的冲突信号进行解码。实验分别用模拟数据和实测数据给出了算法性能的结果,具体的实验设置如下所述。
6.1 数据产生
6.1.1 仿真数据
在仿真实验中,随机多址采用ALOHA方法,其中帧长与节点数均为128。由于节点数与帧长数目相等,可得到平均一个冲突时隙中冲突节点数约为2.33[9],因此我们主要仿真了冲突时隙内有2,3节点冲突的信号。模拟的冲突信号依据(3)得到,为基带信号加高斯白噪声,主要参数依据EPC C1 Gen2标准,具体设置如表3所示。
表3 仿真数据参数设置
Tab.3 Parameters for simulation data
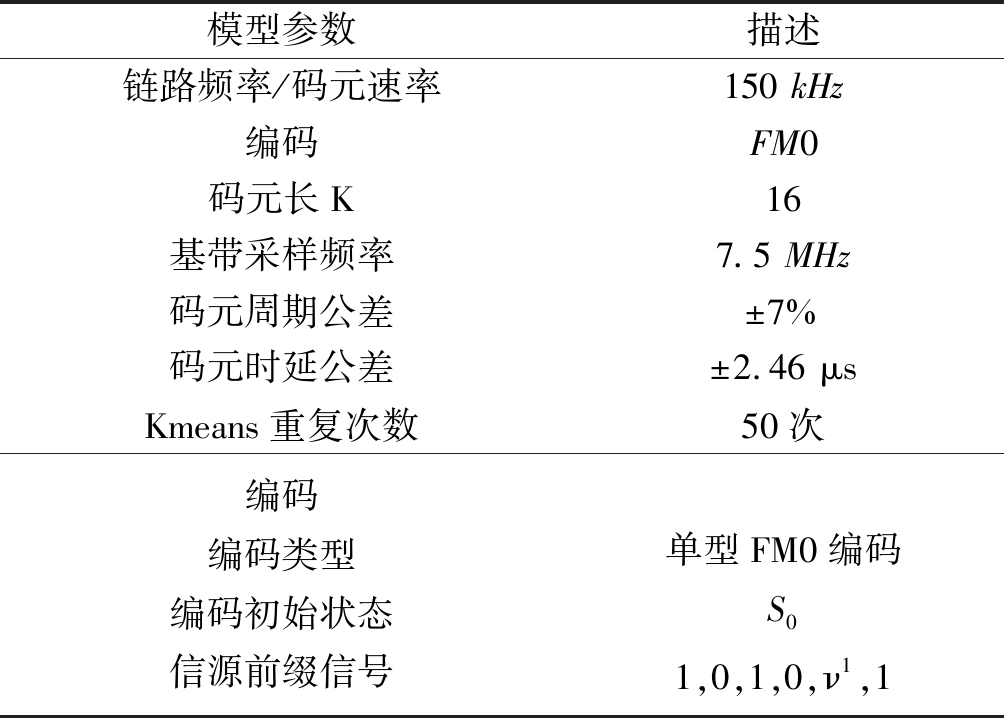
模型参数描述链路频率/码元速率150 kHz编码FM0码元长K16基带采样频率7.5 MHz码元周期公差±7%码元时延公差Kmeans重复次数±2.46 μs50次编码编码类型编码初始状态信源前缀信号单型FM0编码S01,0,1,0,ν1,1
注:1. “ν”指FM0偏移即应发生相位跳变其实没有。
另外,传统维特比的解码性能与信道系数相关,某些信道系数值会使维特比搜索的幸存路径失败,表4给出的信道系数值将可区分传统维特比[19]和本文FSVD算法在解码性能上的区别,分别给出了标签数为2、3时的系数值,其中,标签数为3以上的系数值未给出,由于其出现概率较小,具体见图14。
表4 信号衰落系数参数设置
Tab.4 Signal fading coefficient setting
注:1. 给出两组信号衰落系数,其中图9和图11采用第一列系数,图12选用第二列。
6.1.2 实测数据
在实测实验中,我们采用USRP软件构建了一个超高频近距离通信网络,该网络仍依据EPC C1 Gen2标准构建,软件采用GNU Radio实现,详细参数参见文献[22],代码下载地址为https:∥github.com/nkargas/Gen2-UHF-RFID-Reader。USRP平台使用了一块USRP N200主板和RXF900子板来完成中心节点功能,其他节点则有EPC C1 Gen2标准的标签来充当。同时,子板带有两个圆极化天线,一个用于发送命令,另一个用于接受命令。表5给出了上述软件无线电的相关设置。
表5 USRP系统设置
Tab.5 Parameters for USRP
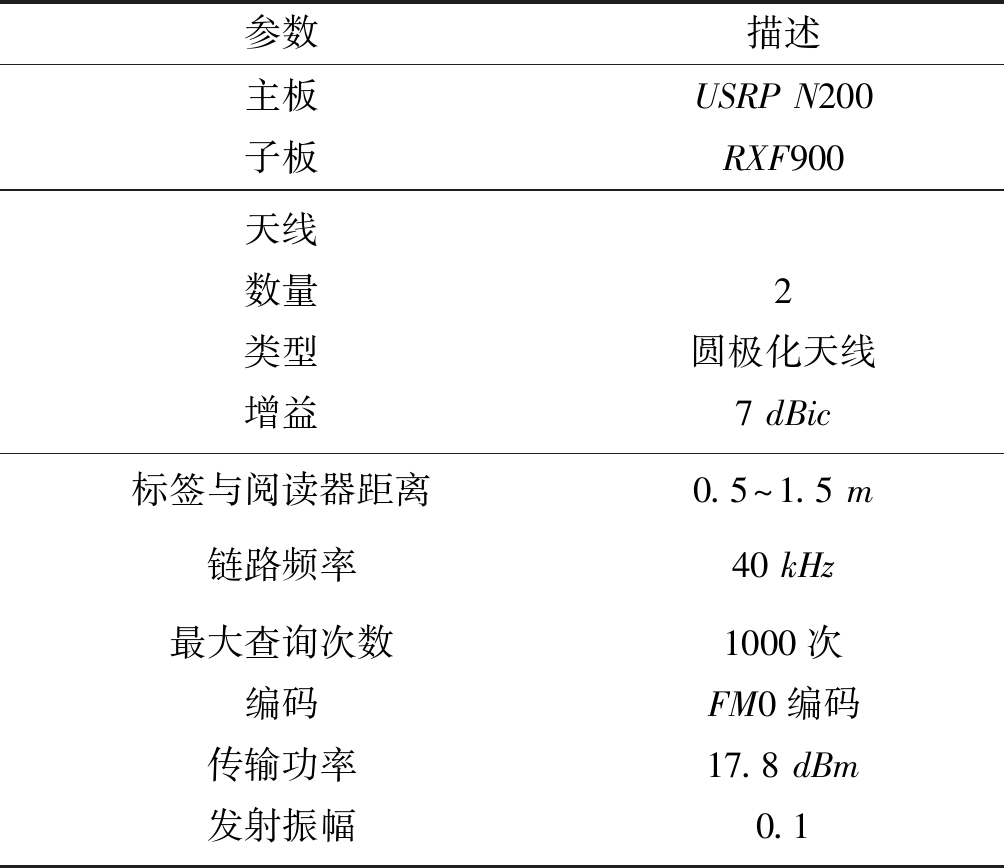
参数描述主板USRP N200子板RXF900天线数量类型增益2圆极化天线7 dBic标签与阅读器距离0.5～1.5 m链路频率40 kHz最大查询次数编码传输功率发射振幅1000次FM0编码17.8 dBm0.1
6.2 实验算法
为了评估算法性能,本文采用四种算法进行性能对比。第一种为本文的FSVD算法,算法步骤已在表2中给出;第二种为传统维特比算法[19],用C-Viterbi表示,该算法运用连续干扰消除技术,先解码出信道衰减系数最大的信源,进而解码出信道系数次大的信源,直至结束;第三种为信道预知的维特比算法,用H-Viterbi表示,该算法假设信道系数已知,然后根据信道系数对冲突信号分离后通过Viterbi解码出原始信源;第四种为信道未知通过FSVD算法分离信号的相位跳变解码(FS-Jump),该算法先通过FSVD算法分离信号,再根据FM0编码的相位跳变原则解码信源。以上算法的具体参数设置如表6所示。另外,注意到FSVD和FS-Jump均采用两种聚类方法,Kmeans和网格聚类,分别用于仿真数据和实测数据,原因在于,Kmeans在低信噪比有较好的聚类性能但复杂度高,而网格聚类[19]的复杂度较低,在较高信噪比下也具有较好性能。
表6 各算法设置
Tab.6 Evaluated algorithm setting
算法描述FSVD聚类方法解码信道Kmeans1, 网格聚类2Viterbi未知C-Viterbi解码信道连续干扰消除的Viterbi解码假定已知H-Viterbi解码信道Viterbi解码假定已知FS-Jump聚类方法解码信道Kmeans1, 网格聚类2相位跳变解码未知
注:1. 仿真数据采用Kmeans。
2. 实测数据采用网格聚类[19]。
6.3 性能指标
实验中我们将测试以下几种指标的变化,以衡量算法的性能。
误码率定义为每个信号解码的错误码元数NS比上解码的总码元数NT的均值,表示为
(13)
解码效率定义为一个冲突时隙内平均成功解码的信源数KS比上冲突信源数KT,表示为
(14)
其中当且仅当一个码元块中所有码元均成功解码才能记为成功解码块。
吞吐量定义为一个帧中平均成功解码的码元块数LS比上帧长LT,表示为
(15)
解码时间TD,定义为各算法解码一个冲突时隙内各冲突信号所花费的平均时间以衡量算法的复杂度,所有数据处理均在ASUS FL8000U PC电脑下进行,CPU为Intel Core i7- 8550U。
7 实验结果与分析
实验中,我们主要对H-Viterbi,FSVD,FS-Jump和C-Viterbi四种算法进行对比。H-Viterbi算法假定信道系数已知,以此进行有监督的冲突信号分离,FSVD算法则在信道系数未知下进行无监督冲突信号分离,二者皆使用Viterbi解码,因此若FSVD算法性能接近H-Viterbi则FSVD的无监督分离将接近信道已知的有监督分离。FS-Jump与FSVD算法采用同种算法进行冲突分离,均无需知道信道系数,只是前者通过相位反转解码信源,后者采用Viterbi解码,以此对比FSVD算法的解码性能。C-Viterbi算法不对冲突信号分离,仅通过连续干扰消除的Viterbi解码方式得到信源,在某些信道系数下,该方法会得到错误的幸存路径。在实验中,我们采用这些信道系数,将C-Viterbi方法与其他方法进行对比,以此说明误判的情形。
7.1 仿真数据
在仿真实验中,我们使用MATLAB软件测试以下指标,以衡量各算法性能。
当信噪比取值-20 dB到25 dB时,我们给出了信源为2、3的情况下的误码率曲线图,如图8、图9所示。由图8所见,SNR在-5 dB到5 dB时,FSVD算法误码率曲线在H-Viterbi和FS-Jump算法之间,即FSVD算法的性能接近信道已知的H-Viterbi算法,好于采用相同分离算法的FS-Jump算法。该结果说明,在无需要估计信道的情况下,FSVD聚类性能接近有监督的聚类性能。由于FSVD算法的分离方法和FS-Jump算法相同,因此该结果也说明Viterbi解码好于相位反转的解码方法。另外,当SNR在5 dB到25 dB时,C-Viterbi的曲线在约10-2趋于水平,这说明即使信噪比增大其误码率也无法降低,原因在于,信源在一些特定的衰减系数下,如表4,C-Viterbi会搜索到无效的幸存路径致使无法解码出更多信源。图9结果与图8类似,FSVD误码率曲线图仍在H-Viterbi和FS-Jump算法之间,同时C-Viterbi也无法解码出更多的正确信源。对于C-Viterbi,其误码率虽然随着SNR的增大而降低,但是由于信道系数的影响,当信噪比增大时,该算法仍然无法解码出更多信源。
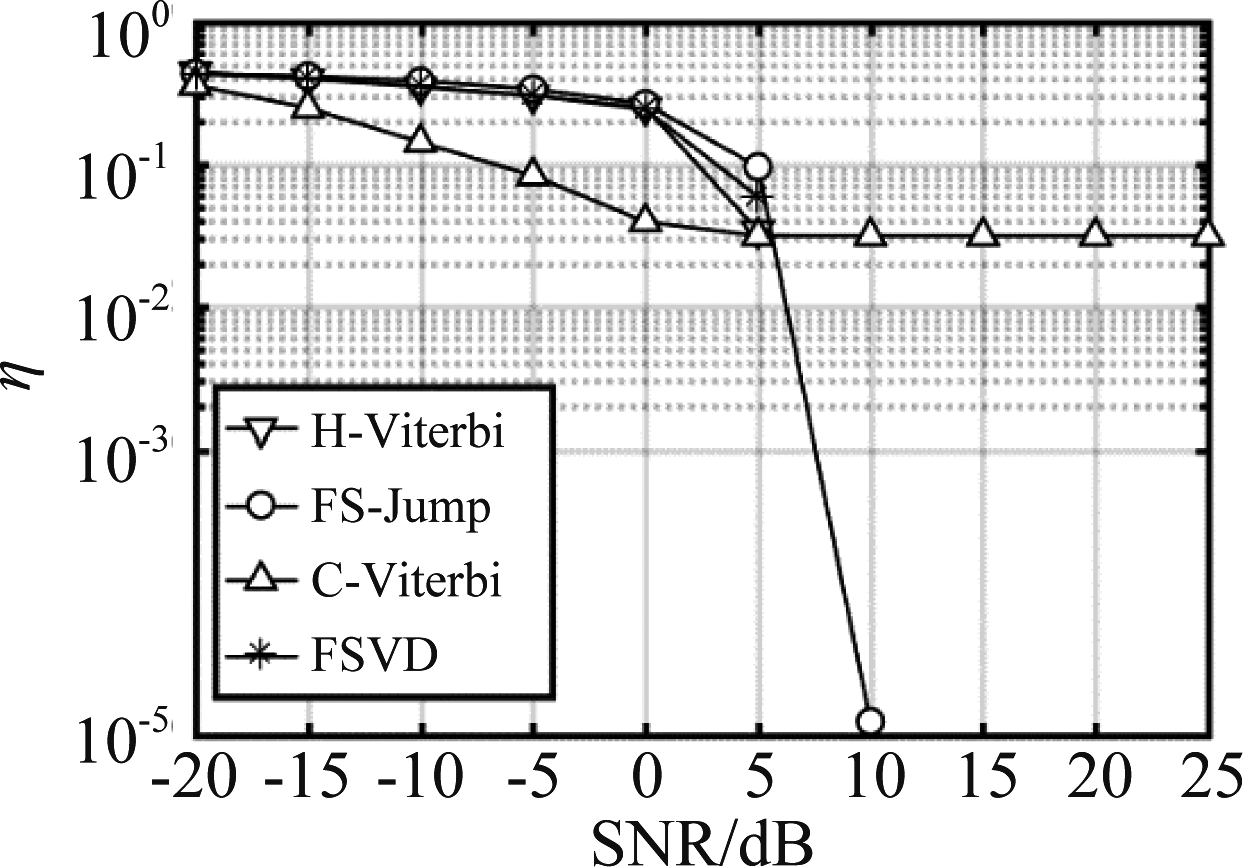
图8 冲突信源数为2的误码率
Fig.8 Bit error rate with 2 collision sources
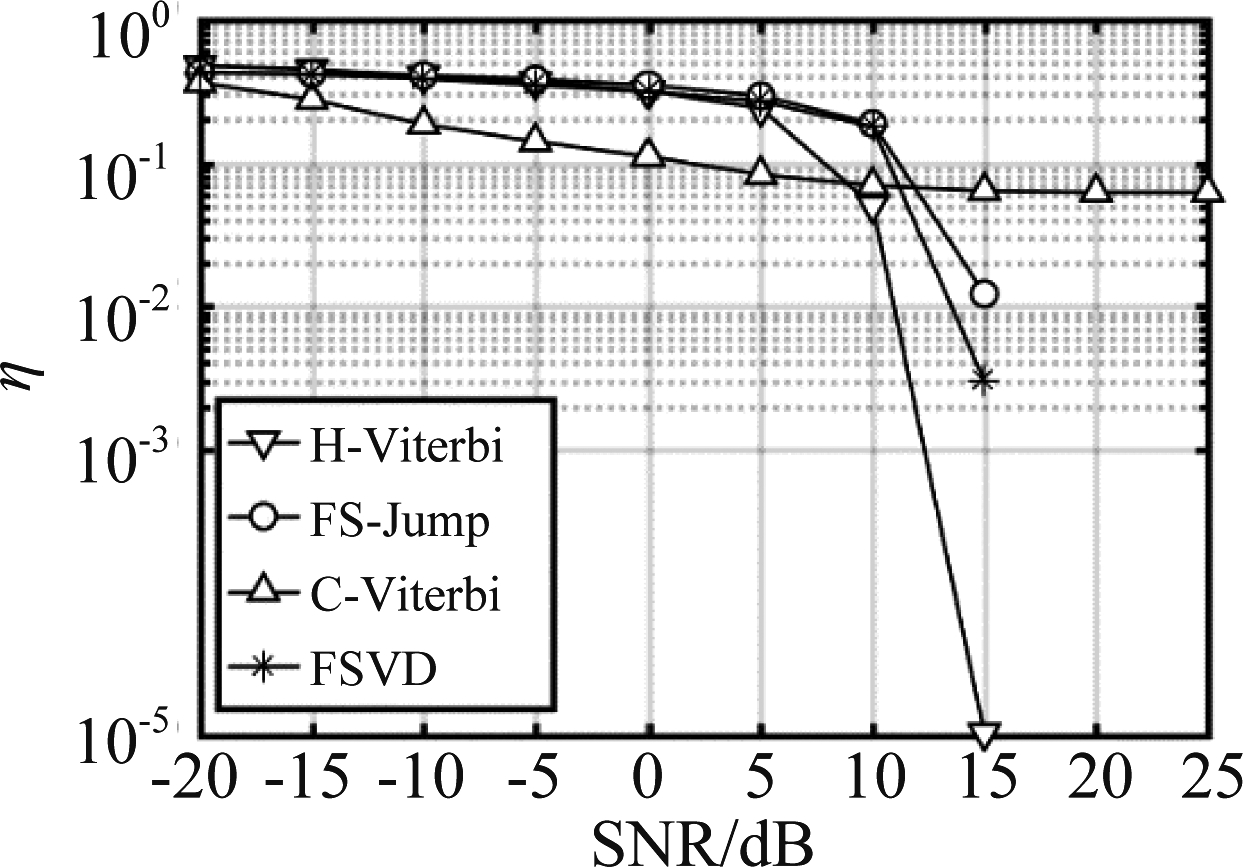
图9 冲突信源数为3的误码率
Fig.9 Bit error rate with 3 collision sources
当信噪比取值-20 dB到25 dB时,我们给出了信源为2、3的情况下的解码效率曲线图,如图10,图11所示。与误码率曲线类似,FSVD算法解码效率曲线在H-Viterbi和FS-Jump算法之间,同时C-Viterbi的解码效率始终不能达到100%。该结果说明,FSVD的解码效率的高低与信噪比或者冲突信源数的影响,在增大信噪比或者冲突信源数降低,其解码效率会提高,而C-Viterbi的性能却与冲突信源的衰减系数相关,特定的衰减系数如表4,会致使某些冲突信源无法被正确解码。图12给出了一种更特殊的解码效率图,该图中的信号衰落系数见表4。相比图11,此时C-Viterbi解码效率为0,且随着信噪比的增大,其解码性效率始终无法提升。该结果说明,在该信号衰落系数下,无一信源可以被解码出。
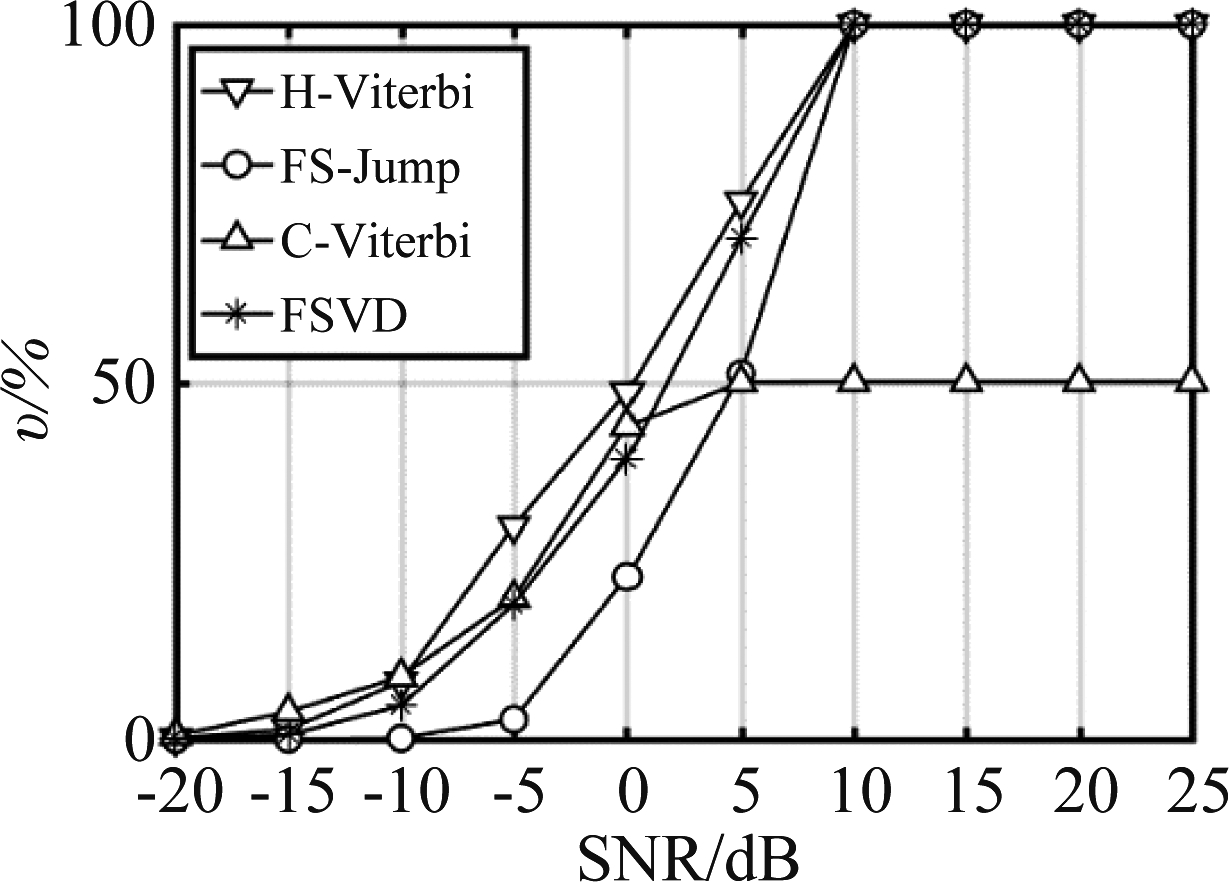
图10 冲突信源数为2的解码效率
Fig.10 Decoding efficiency with 2 collision sources
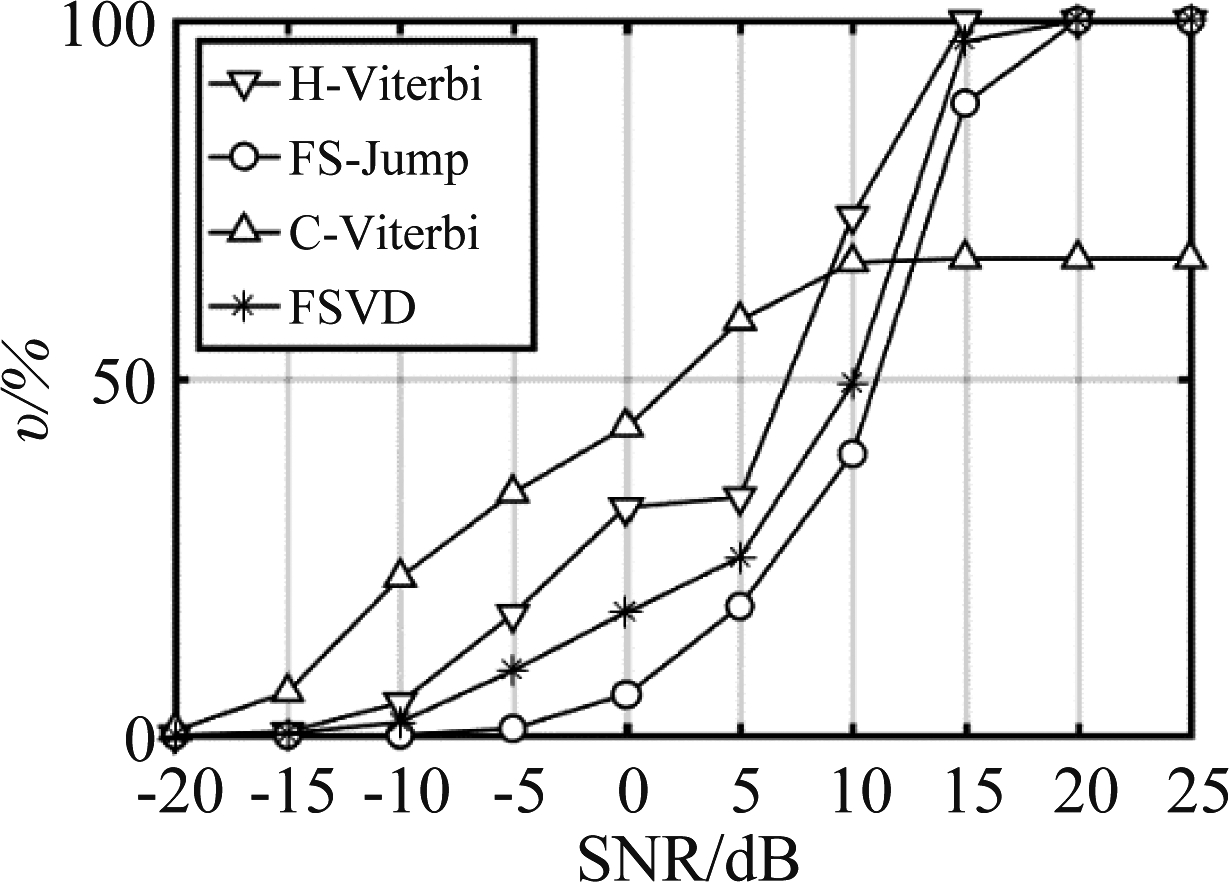
图11 冲突信源数为3的解码效率
Fig.11 Decoding efficiency with 3 collision sources
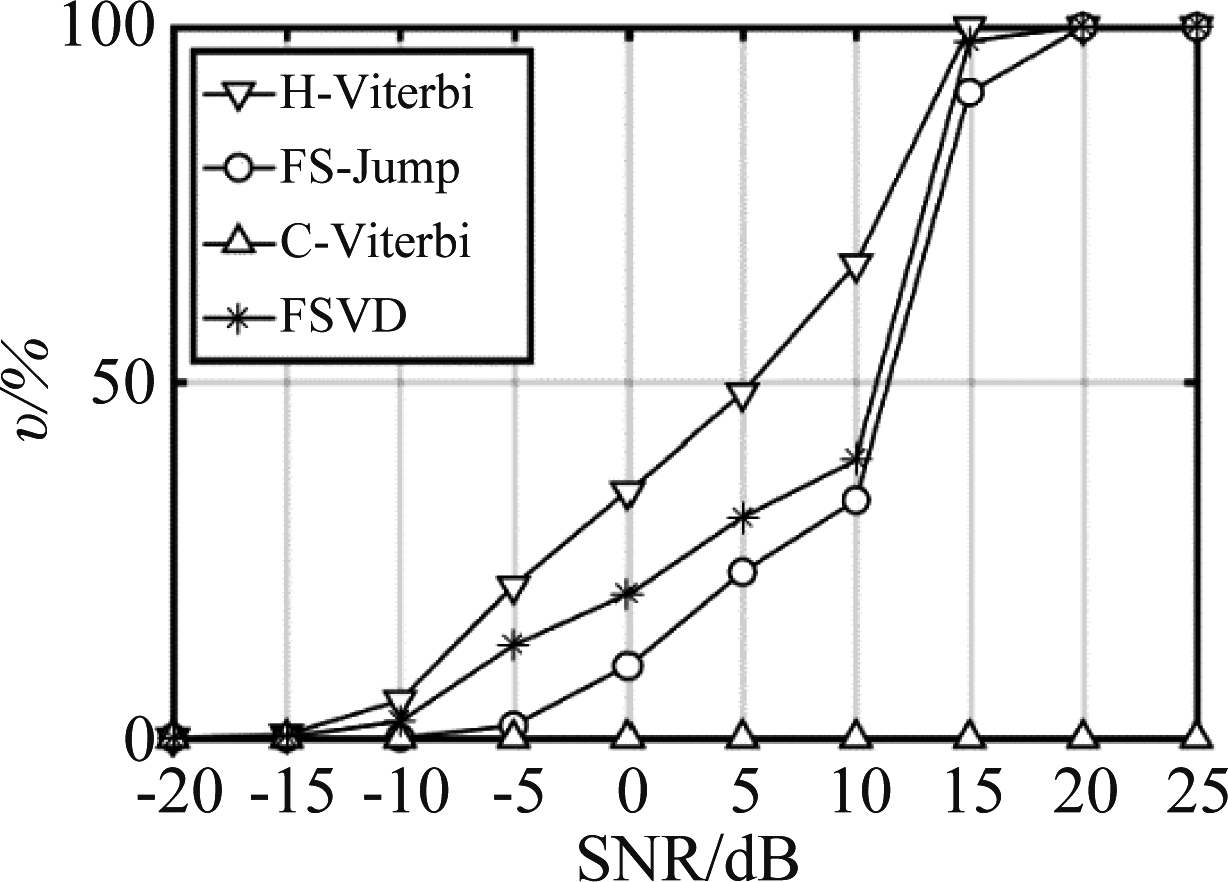
图12 冲突信源数为3的解码效率
Fig.12 Decoding efficiency with 3 collision sources for another group of fading signal coefficients
当信噪比为-20 dB到25 dB时,我们给出了ALOHA随机多址中各算法的吞吐量,如图13所示。并且,图中还给出未采用分离型冲突分解的纯ALOHA系统吞吐量,其吞吐量接近理论值0.367。图13显示了当信噪比逐渐增大时,各分离型冲突分解算法的吞吐量均大于纯ALOHA系统吞吐量,这说明分离型冲突分解算法确实可增大ALOHA系统的吞吐量。与误码率和解码效率的结果图类似,FSVD算法的吞吐量也是介于H-Viterbi和FS-Jump算法之间,而C-Viterbi算法的吞吐量最终只能达到约0.5。
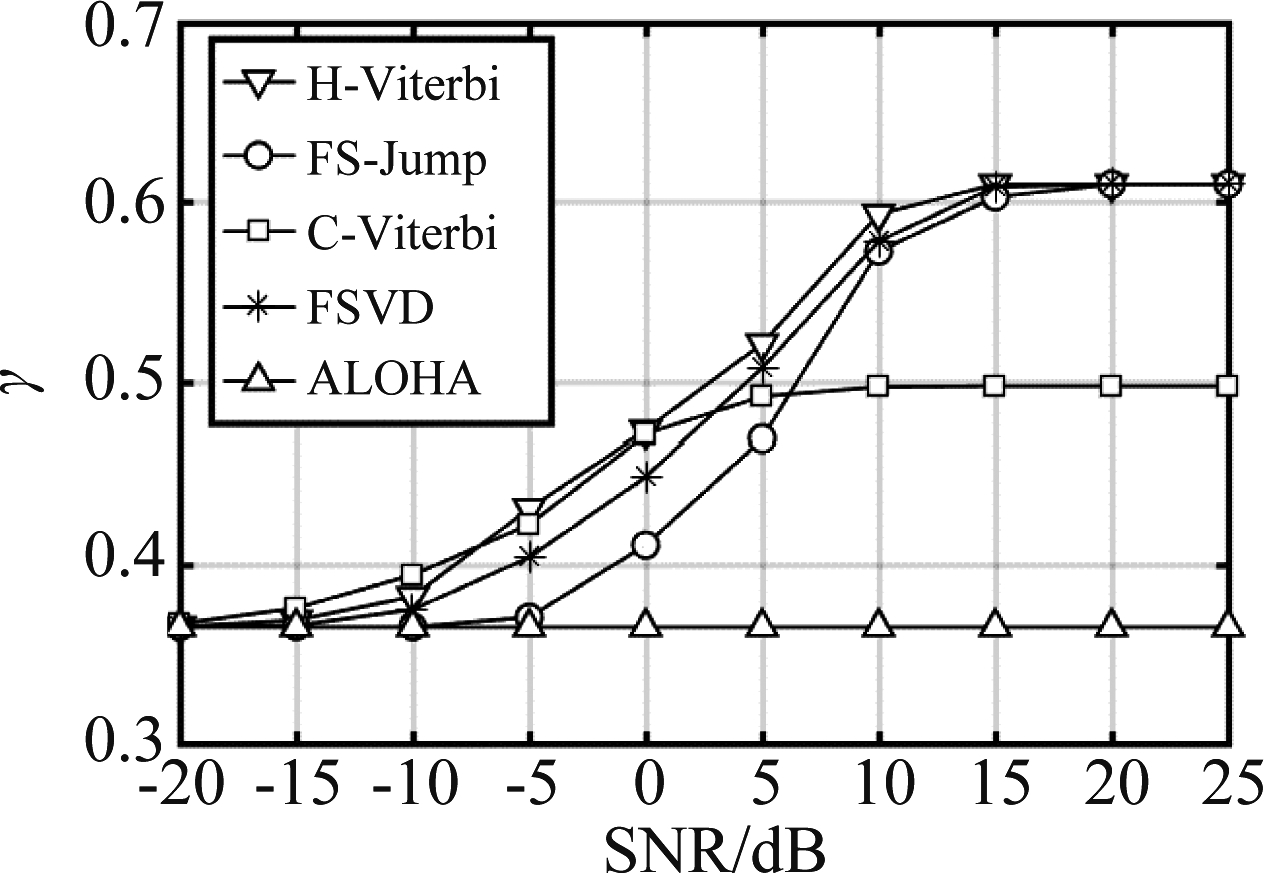
图13 ALOHA系统中各算法吞吐量
Fig.13 Throughput of separated collision resolutions in ALOHA system
另外,注意到图8～图11的实验结果仅给出了冲突信源数为2、3的仿真结果,原因在于,当帧长和冲突信源数相等时,一个冲突时隙中有3个以上信源的情况较少。图14给出了帧长和冲突时隙均为128时,各冲突时隙的个数,如图14所示,从中可以看到冲突的时隙数随冲突信源数的增大而减小,特别冲突信源数超过3的时隙数已经非常小了,因此,我们在计算如图13的吞吐量时,超过3个标签时视为无法成功分离。
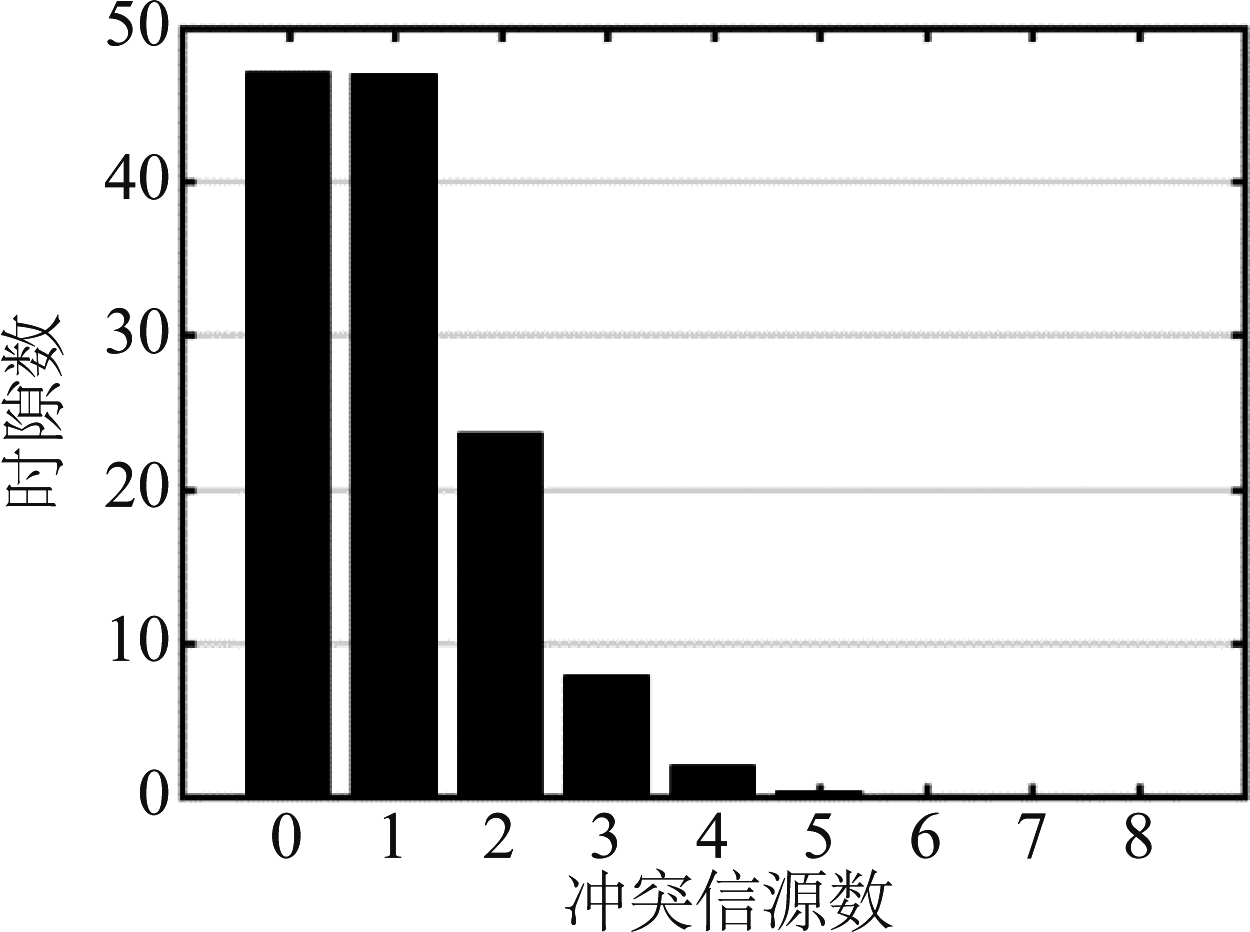
图14 帧长和冲突时隙均为128时,ALOHA系统中各冲突时隙数统计
Fig.14 The number of collision slots with 0 to 8 sources in ALOHA system where a frame length and collision time slot are both 128
7.2 实测数据
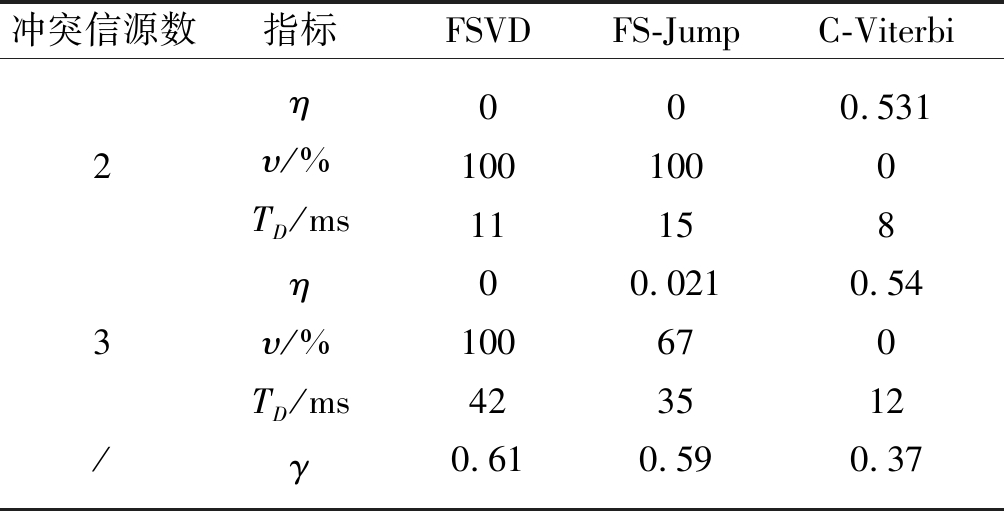
本部分的实测数据由USRP平台产生,图15给出了当阅读器与标签通信时,我们截取Collision Detected RN16一段作为冲突信号,图16给出了信源数分别为2、3的冲突信号图,其信号幅值为计算I路和Q路构成复数的模而来,然后对这些冲突信号进行解码得到表7的实验结果。注意到,由于实测数据中信道系数无法预先得到,因此未给出H-Viterbi的实验结果。从该表可以看到,FSVD的误码率、分离效率性能和吞吐量均为最好,而C-Viterbi由于未能正确解码冲突信号,因此其吞吐量只能接近纯ALOHA系统。然而,从表中也可以看到FSVD在解码2个和3个信源的算法时间分别约是C-Viterbi的3倍和5倍,另外值得注意的是,C-Viterbi算法在对实测冲突数据进行解码时,解码效率为0,其原因在于,当接收的冲突信号去除载波泄露后,所得到的信号衰落系数均为0.05以下,该结果如同图12所示类似,搜索的幸存路径失败。当然,我们可以增加信号发射功率或拉近标签与天线距离,但是增加发射功率会增加功耗,而拉近距离却不一定在任何应用场景下都能满足。
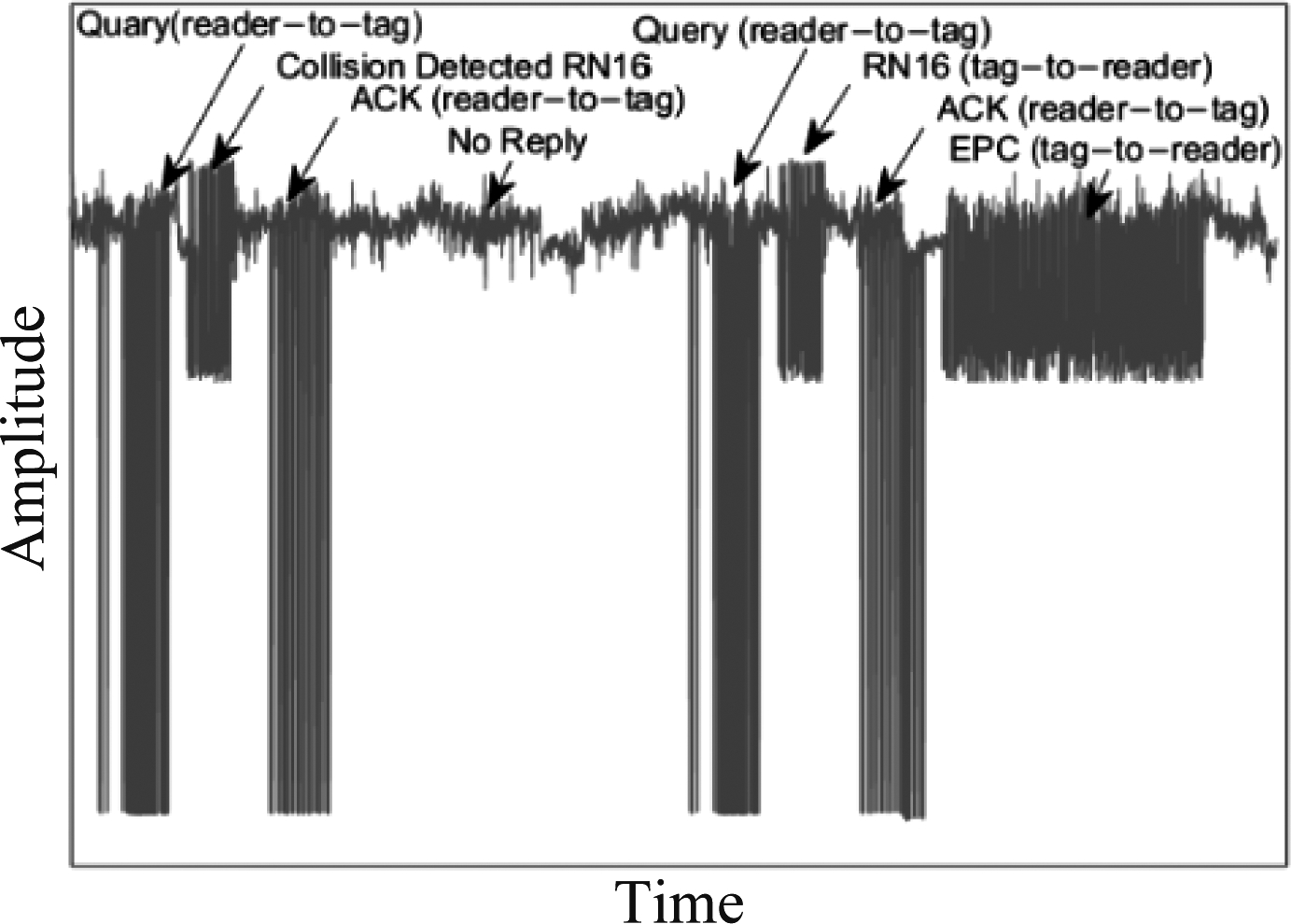
图15 双向通信下阅读器捕获的波形
Fig.15 Wave captured by USRP reader from EPC C1 Gen2
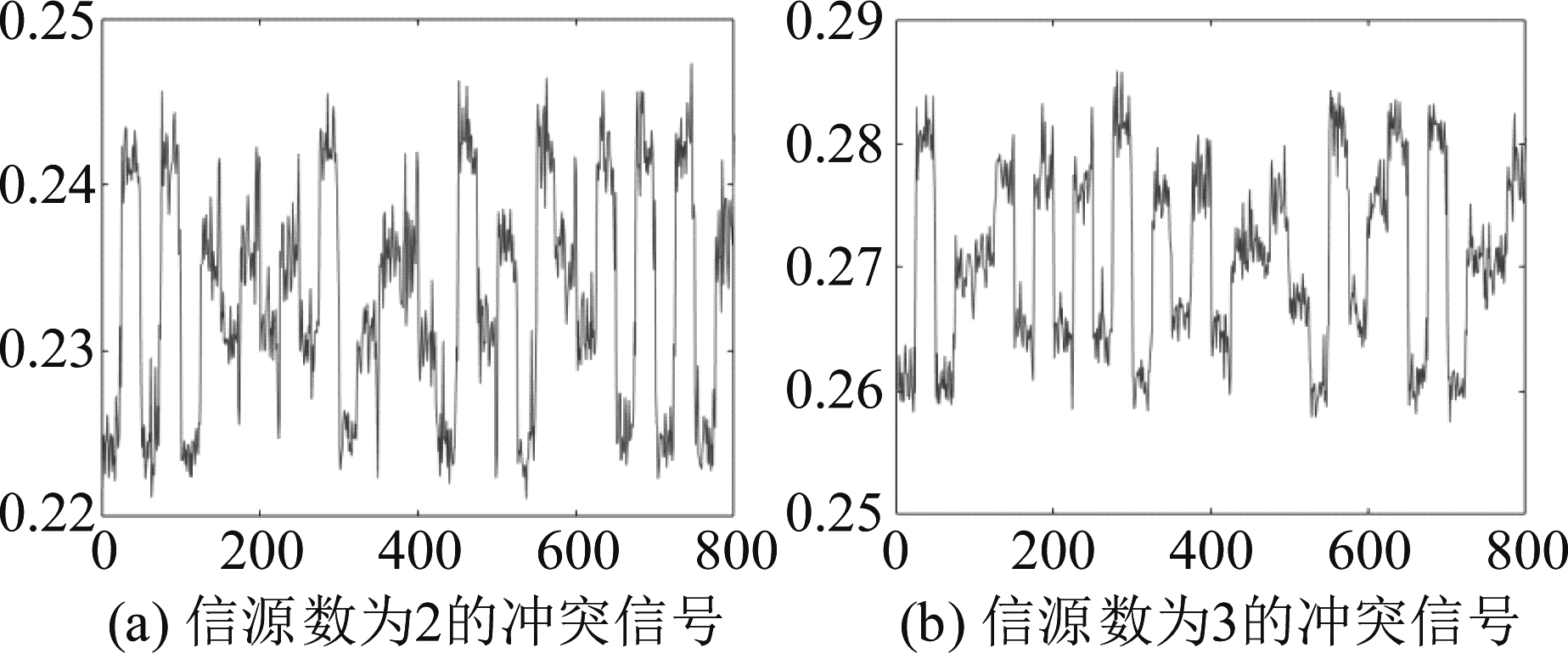
图16 实测数据下不同信源数叠加的冲突信号
Fig.16 Module of complex collision signal captured by USRP
表7 实测数据下各算法性能
Tab.7 Results of evaluated algorithms for measured data
冲突信源数指标FSVDFS-JumpC-Viterbi23/ηυ/%TD/msηυ/%TD/msγ0100110100420.610100150.02167350.590.531080.540120.37
8 结论
本文针对近场无线通信系统并结合ALOHA随机多址网络,利用分离型的冲突分解方法对冲突信号进行分离解码,以此提高网络的吞吐量。在ALOHA网络的仿真实验中,本文提出的FSVD算法的吞吐量在信噪比15 dB时约0.62,而信道已知的H-Viterbi算法的吞吐量约0.63,两者仅差0.01,但FSVD并不需要估计信道。另外一方面,传统的C-Viterbi算法在一些信道系数下会导致幸存路径误判,本仿真实验中C-Viterbi的吞吐量与纯ALOHA相比并未得到很大提升。本文还利用软件无线电平台,根据EPC C1 Gen2标准构建了一个ALOHA近场通信网络,对该平台所得到的数据进行处理后,本文FSVD吞吐量达到了0.61,相比传统的ALOHA系统,吞吐量提高了约0.25。
FSVD方法通过无监督聚类和有限符号集的优化方法来分离冲突信号,从而无需信道信息,但完成聚类和优化算法需要花费较多的时间,注意到在一个高效率的ALOHA网络中,帧长与信号源数目相等时,发生4个信号源冲突的概率约为1%,为节省时间可不分离该冲突时隙,而主要分离冲突信号源为2或3的冲突时隙。
本算法复杂度并不低,特别相比MAC协议,但是它确实提供了另外一种去提高系统吞吐量的技术路线,另外,在本文的实测数据实验中,我们将由软件无线电得到的数据中送至MatLab软件中进行处理,以得到各算法的性能指标。更完整的测试应该是将算法嵌入至软件无线电平台中,然后据此测试算法性能,因此在将来的工作中,我们将完成各算法的相关软件无线电代码,从而得到更全面的实验结果。
附录
由(4)可得
H=D†C
(附-1)
将(附-1)代入(4)中有
C=DD†C
(附-2)
令
是字典矩阵D的一个估计值,则当误差平方和
(附-3)
为最小时,所求为最优估计,表示为
(附- 4)
对(附- 4)中的符号进行简化,令
代入(附- 4)得到式(7)。
[1] BANSAL B, RANA S. Internet of Things: Vision, Applications and Challenges[J]. International Journal of Engineering Trends and Technology, 2017, 47(7): 380-384. DOI: 10.14445/22315381/IJETT-V47P263.
[2] MAKHDOOM I, ABOLHASAN M, ABBAS H, et al. Blockchain’s Adoption in IoT: The Challenges, and A Way Forward[J]. Journal of Network and Computer Applications, 2018, 125: 251-279. DOI: 10.1016/j.jnca.2018.10.019.
[3] COSKUN V, OZDENIZCI B, OK K. A Survey on Near Field Communication (NFC)[J]. Wireless Personal Communications, 2013, 71(3): 2259-2294. DOI: 10.1007/s11277-012-0935-5.
[4] ALI S, HOSSAIN E, KIM D I. LTE/LTE-A Random Access for Massive Machine-Type Communications in Smart Cities[J]. IEEE Communications Magazine, 2017, 55(1): 76- 83. DOI: 10.1109/MCOM.2017.1600215CM.
[5] TUNG D, WONG C, CHEN Q. Multi-Channel Pure Collective Aloha MAC Protocol with Decollision Algorithm for Satellite Uplink[C]∥2018 IEEE 4th World Forum Internet Things, 2018: 251-256. DOI: 10.1109/WF-IoT.2018.8355107.
[6] CHAE S, KANG K, CHO Y. A randomized adaptive neighbor discovery for wireless networks with multi-packet reception capability[J]. Journal of Parallel and Distributed Computing, 2018, 131: 235-244. DOI: 10.1016/j.jpdc.2018.11.010.
[7] ARUN I B, VENKATESH T G. Design and Performance Analysis of a MAC protocol for wireless LANs supporting Multipacket Reception[J]. Journal of Network and Computer Applications, 2017, 87: 223-236. DOI: 10.1016/j.jnca.2017.03.010.
[8] BELTRAMELLI L, MAHMOOD A, OSTERBERG P, et al. LoRa beyond ALOHA: An Investigation of Alternative Random Access Protocols[J]. IEEE Transactions on Industrial Informatics. 2020, 3203: 1-11. DOI: 10.1109/TII.2020.2977046.
[9] VAZQUEZ-GALLEGO F, MEMBER S. Goodbye, ALOHA![J]. IEEE Access, 2016, 4: 2029-2044. DOI: 10.1109/ACCESS.2016.2557758.
[10] OPERATOR-BASED C D, GUO B, PENG S, et al. Complex-valued Differential Operator-based Method for Multi-component Signal Separation[J]. Signal Processing, 2016, 132: 66-76. DOI: 10.1016/j.sigpro.2016.09.015.
[11] HUANG Z, SU J, WEN G, et al. A Physical Layer Algorithm for Estimation of Number of Tags in UHF RFID Anti-Collision Design[J]. Computers, Materials & Continua, 2019, 61(1): 399- 408. DOI: 10.32604/cmc.2019.05876.
[12] KIM Y G, MEMBER S,VINCK A J H. Anti-Collision Algorithms for FM0 Code and Miller Subcarrier Sequence in RFID Applications[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 5168-5173. DOI: 10.1109/TVT.2018.2817587.
[13] LI J, WU H, ZENG Y. Recovery of collided RFID tags with frequency drift on physical layer[J]. IEEE/CAA Journal of Automatica Sinica, 2019, PP: 1-11. DOI: 10.1109/JAS.2019.1911720.
[14] SHEN D, WOO G, REED D P, et al. Separation of multiple passive RFID signals using software defined radio[C]∥2009 IEEE International Conference on RFID, 2009: 139-146. DOI: 10.1109/RFID.2009.4911203.
[15] NGUYEN B, DE BAETS B. Kernel-Based Distance Metric Learning for Supervised-Means Clustering[J]. IEEE Transactions on Neural Networks and Learning Systems, 2019, 30(10): 3084-3095. DOI: 10.1109/TNNLS.2018.2890021.
[16] CHEN W C, CHUNG C D. Spectrally Efficient OFDM Pilot Waveform for Channel Estimation[J]. IEEE Trans. Communications, 2017, 65(1): 387- 402. DOI: 10.1109/TCOMM.2016.2616859.
[17] ZHANG Q, et al. Algorithms for Blind Separation and Estimation of Transmitter and Receiver IQ Imbalances[J]. Journal of Lightwave Technology, 2019, 37(10): 2201-2208. DOI: 10.1109/JLT.2019.2899833.
[18] KIM T, CHAE S H. A Channel Estimator via Non-Orthogonal Pilot Signals for Uplink Cellular IoT[J]. IEEE Access, 2019, 7: 53419-53428. DOI: 10.1109/ACCESS.2019.2912446.
[19] SCAGLIONE A, LARSEN T, MEMBER S. Multipacket Reception of Passive UHF RFID Tags: A Communication Theoretic Approach[J]. IEEE Trans. SIGNAL Process., 2011, 59(9): 4225- 4237.
[20] HOU Y, OU J, ZHENG Y, et al. PLACE: Physical layer cardinality estimation for large-scale RFID systems[J]. IEEE/ACM Transactions on Networking, 2016, 24(5): 2702-2714. DOI: 10.1109/TNET.2015.2481999.
[21] EPCTM Radio-Frequency Identity Protocols Class-1 Generation-2 UHF RFID Protocol for Communications at 860 MHz～960 MHz Version 2.0.1[M]. EPCglobal, G.S. (2015). Inc., Brussels, BE, 2015: 11-147.
[22] KARGAS N, MAVROMATIS F, BLETSAS A. Fully-Coherent reader with commodity SDR for Gen2 FM0 and computational RFID[J]. IEEE Wireless Communications Letters, 2015, 4(6): 617- 620. DOI: 10.1109/LWC.2015.2475749.
[23] ANGERER C, LANGWIESER R, RUPP M. RFID Reader Receivers for Physical Layer Collision Recovery[J]. in IEEE Transactions on Communications, 2010, 58(12): 3526-3537. DOI: 10.1109/TCOMM.2010.101910.100004.
