1 引言
由于无线信道的广播特性,使得基于无线通信的数据传输存在安全隐患。然而经过时间反演(Time Reversal, TR)技术处理后的信号不仅能够适应各种介质环境,而且TR技术的空时聚焦性[1]使保密信号只能在固定的时间和空间中检测,超出固定范围很难被检测,能够实现保密传输,这一特性,使得TR技术成为物理层安全研究的一个热点[2-3]。
在基于时间反演的物理层安全研究中,为了提高系统的安全性,已经提出了以下几种信号处理方法:发端天线选择[4](Transmit Antenna Selection, TAS)技术、发端波束成形[5](Transmit Beam Forming, TBF)技术、发端人工噪声[6-10](Transmit Artificial Noise, TAN)技术和接收端人工噪声[11-12](Receive Artificial Noise, RAN)技术。其中,TAS技术和TBF技术是通过提高主信道的质量来提高系统的安全性,而TAN技术和RAN技术是通过恶化窃听信道的方式提高系统的安全性。TAS技术主要是利用多天线系统空间分集的优点,发射端选择合法接收端信噪比相对大的一些天线发送信息,该技术还减少了用于发射的射频链路,降低了硬件成本和复杂度。TBF技术通过调整控制各阵元信号的幅度和相位,使天线发射的信号在指定方向上增强,使合法用户的接收信噪比增大,从而提高系统的安全性。TAN技术是由发送端发送人工噪声(Artificial Noise, AN)干扰窃听用户,对于发端具有多根天线的TR系统,则是利用系统空间分集发送AN[10],然而对于发端仅有一根天线的TR系统,则利用TR系统的时间分集发送AN[6-9]。现有RAN技术都是合法接收端配备两根天线,一根天线用于接收保密信息,另一根天线用于发送AN恶化窃听信道,AN对合法用户的干扰采用自干扰消除技术或者全双工无线技术消除[13]。
目前TR系统的物理层安全研究还存在一些局限性:首先,主要针对单个窃听者的系统模型,难以解决多个窃听者随机分布下的物理层安全问题;其次,大多数仅考虑了小尺度衰落,忽略了大尺度衰落引起的路径损耗对安全性的影响;此外,AN辅助TR的系统中引入功率分配因子时,缺少对功率分配因子的优化。
为此,考虑在多个窃听者随机分布的场景下,同时考虑路径损耗和小尺度衰落的影响,以AN辅助TR的多输入单输出(Multiple Input Single Output, MISO)传输为基础,提出一种物理层安全吞吐量优化方案,主要工作包括:
(1)为了对抗多个随机分布的窃听者且尽可能的减少合法者受到AN的影响,将AN置于等效合法信道主径零空间内。
(2)在多个窃听者随机分布的场景下考虑路径损耗,利用随机几何理论,推导了连接中断概率(Connection Outage Probability, COP)和安全中断概率(Security Outage Probability, SOP)的闭合表达式分别表征系统的可靠性和安全性,并通过蒙特卡洛仿真验证了推导的正确性。
(3)基于上述(2)中推导的COP和SOP的闭合表达式,综合考虑系统的可靠性和安全性,提出基于最优功率分配因子的安全吞吐量优化方案。
2 系统模型
系统框图如图1所示,该模型包括一个配备M根天线的发射端,一个合法接收端,多个窃听者,窃听者的窃听方式为被动窃听。假设多个窃听者的位置和数量未知,各个窃听者之间独立的接收和解码保密信息。由于均匀泊松点过程[14](Homogenous Poisson Point Process, HPPP)可以模拟点与点之间的独立随机分布特性,故采用HPPP模型模拟多个窃听者的分布,即在无线区域内窃听者的位置服从均匀分布,窃听者的数量服从密度为λe的泊松分布,用Φ表示。假设所有无线信道中的噪声为均值为0,方差为σ2的加性高斯白噪声(Additive White Gaussian Noise, AWGN)。
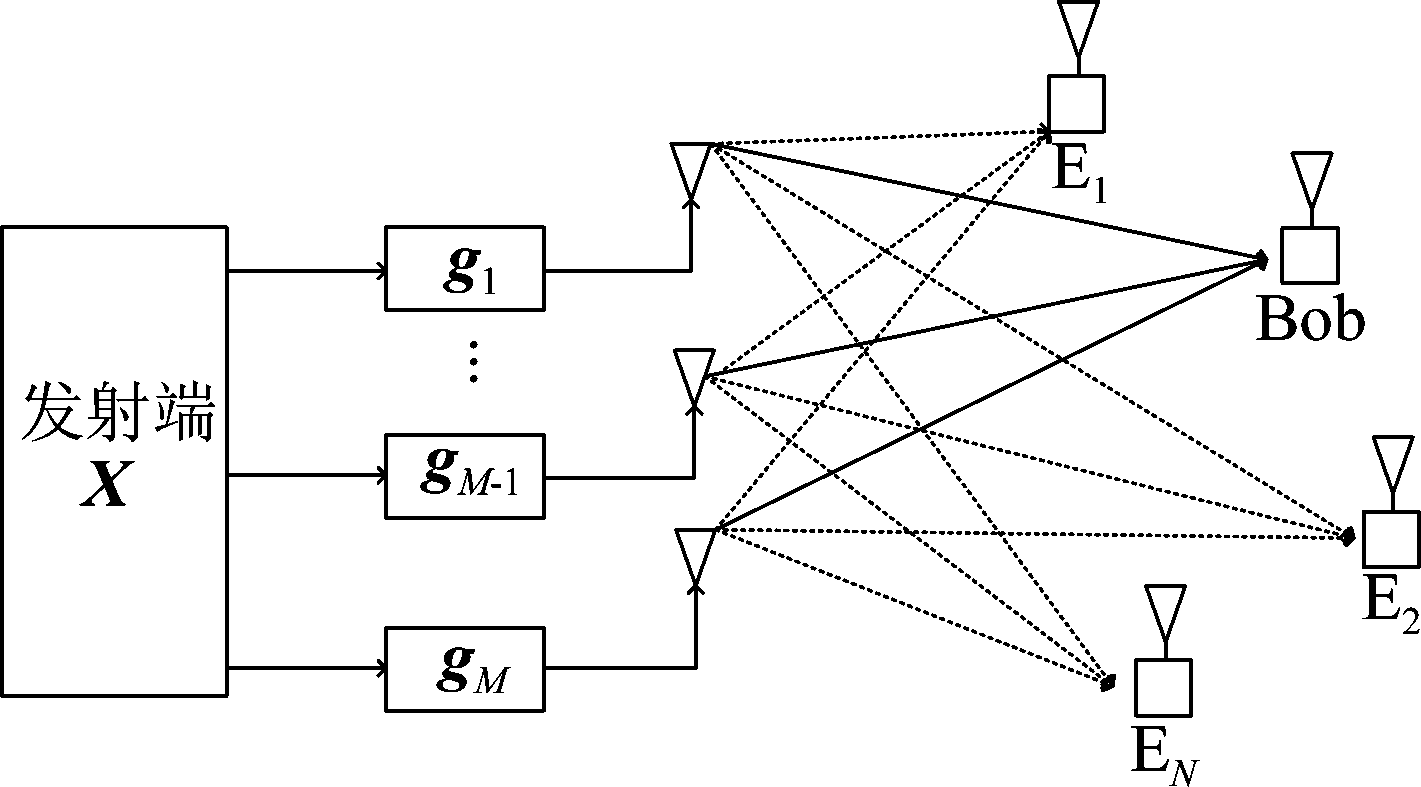
图1 窃听者呈HPPP分布的MISO系统模型
Fig.1 MISO system model with HPPP distribution for eavesdropper
发射天线m(0<m≤M)和用户n之间的信道冲激响应(Channel Impulse Response, CIR)可以表示为
(1)
其中,L为多径总数,αmn,l和τmn,l分别为第l条多径的幅度和时延,n∈{r,x},r表示合法者,x表示第x个窃听者。CIR在时域上离散化为矩阵hmn∈CL×1,每条链路hmn[l]都是循环对称复高斯(Circular Symmetric Complex Gaussian, CSCG)变量,其均值为0,方差为![]() 其中,Ts为系统采样周期,σT为信道均方延迟扩展。
其中,Ts为系统采样周期,σT为信道均方延迟扩展。
为了对抗多个窃听者,首先,在发射端设置功率分配因子ρ,将发射端的一部分功率用来发送人工噪声。假设系统总的发送功率为PX,保密信息向量为S=[S1[k],S2[k],…,SM[k]]T,人工噪声向量为W=[W1[k],W2[k],…,WM[k]]T。其中,Sm[k]和Wm[k]分别代表第m根天线所发送的保密信息和人工噪声,E[SHS]=PS,E[WHW]=PW,满足PX=(1-ρ)PS+ρPW=P。因此,发射端最终发送的信号为
(2)
然后,将发送信号注入时间反演腔内,第m根天线对应的时间反演腔向量gmr∈CL×1,其中,每个分量为
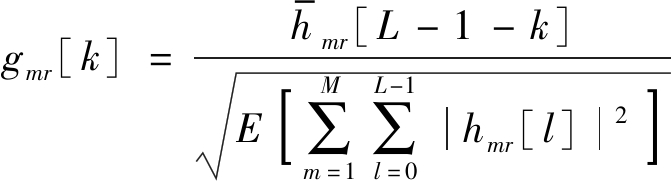
(3)
其中,![]() 代表hmn取共轭。在此时间反演腔是对合法者的CIR在时域上取逆,为了防止时间反演腔引入功率增益再对其进行归一化处理。
代表hmn取共轭。在此时间反演腔是对合法者的CIR在时域上取逆,为了防止时间反演腔引入功率增益再对其进行归一化处理。
由于TR技术的聚焦特性,多径信道的各条路径的能量向经过TR技术处理后的合法等效信道的主径聚焦,使得合法接收端的信号增强,从而增大合法者的信干噪比(Signal to Interference and Noise Ratio, SINR)。为了尽可能的减少AN对合法者的干扰,又由于窃听者信道状态信息、数量、位置都未知,且AN只能与其中的一条路径相正交。故设计AN均匀分布在合法等效信道主径的零空间中,即
(4)
其中,*表示卷积,(hmr*gmr)[L-1]表示合法等效信道的主径。最后,经过多径信道后合法者和第x个窃听者接收的信号分别为
![]()
![]()
![]()
![]()
+n[k] (AWGN)
(5)
![]()
![]()
![]()
![]()
![]()
+n[k] (AWGN)
(6)
其中,n为信道中的AWGN,dmr代表发射端到合法者之间的距离,dmx代表发射端到第x个窃听者之间的距离,α是路径损耗因子。由公式(5)和(6)可知,合法者和第x个窃听者接收到的信号由期望信号(Signal)、符号间干扰(Inter Symbol Interference, ISI)、AN和AWGN这四部分组成。其中,窃听者接收信号中的ISI是由期望信号和AN引起的ISI两部分组成。
从公式(5)可以看出,合法者也会受到AN的干扰,由于TR的聚焦特性,大部分能量都集中到合法者等效信道的主径上,同时也为了方便公式的推导,根据文献[3]和[15]可将AN和ISI对合法者的影响忽略不计。合法者SINR可表示为
(7)
同理,忽略ISI对第x个窃听者的影响,由公式(6)可得第x个窃听者SINR可表示为
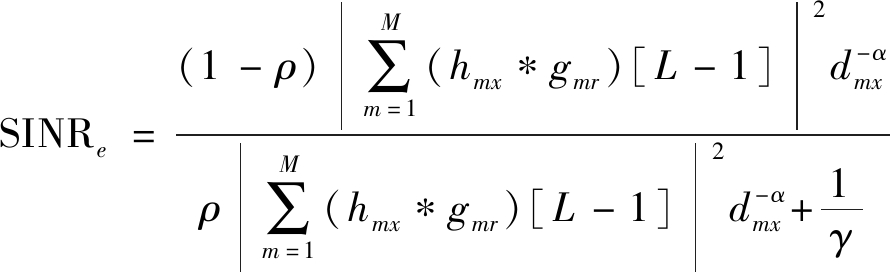
(8)
公式(7)和(8)中,γ表示发射信噪比。
3 连接中断概率和安全中断概率
使用COP和SOP分别表征系统的可靠性和安全性[16],本节中利用随机几何等相关理论推导出COP和SOP的闭合表达式,下一节中将基于这两个闭合表达式提出安全吞吐量优化方案。
3.1 连接中断概率
使用Wyner编码方案[17]进行保密信息传输,其中,速率参数有传输码字速率Rb、安全速率Rs以及冗余速率Re Rb-Rs。冗余速率可理解为是为了防止窃听者窃听所付出的代价。当合法信道容量Cb小于码字传输速率Rb时,合法者不能够实现正确的解码所接收到的码字。故将COP定义为合法者的信道容量Cb小于码字传输速率Rb的概率,即
Rb-Rs。冗余速率可理解为是为了防止窃听者窃听所付出的代价。当合法信道容量Cb小于码字传输速率Rb时,合法者不能够实现正确的解码所接收到的码字。故将COP定义为合法者的信道容量Cb小于码字传输速率Rb的概率,即
Pcop P(log2(1+SINRb)<Rb)=FSINRb(2Rb-1)
P(log2(1+SINRb)<Rb)=FSINRb(2Rb-1)
(9)
其中,FSINRb(y)表示合法信道SINR的累积分布函数(Cumulative Distribution Function, CDF)。
定理1 令公式(7)中![]() 合法信道SINR可表示为
合法信道SINR可表示为![]() 该系统的COP为
该系统的COP为
(10)
证明 该证明过程分为以下3步:
(1)证明A服从指数分布
由于每条链路hmn[l]都是CSCG变量,即该变量是实部和虚部均服从高斯分布且均值为0,方差相等的复变量。公式(3)中![]() 是一个常数,所以gmr[l]也是一个CSCG变量。根据CSCG变量的定义可证明(hmr*gmr)[L-1]是一个CSCG变量。
是一个常数,所以gmr[l]也是一个CSCG变量。根据CSCG变量的定义可证明(hmr*gmr)[L-1]是一个CSCG变量。![]() 表示有限多个CSCG变量相加,显然,仍然是一个CSCG变量。又因为CSCG变量模的平方服从指数分布,所以A服从指数分布。
表示有限多个CSCG变量相加,显然,仍然是一个CSCG变量。又因为CSCG变量模的平方服从指数分布,所以A服从指数分布。
(2)计算E[A]

(11)
为了计算公式(11)中后半部分的均值,需要使用类似于公式(12)和(13)形式的公式。
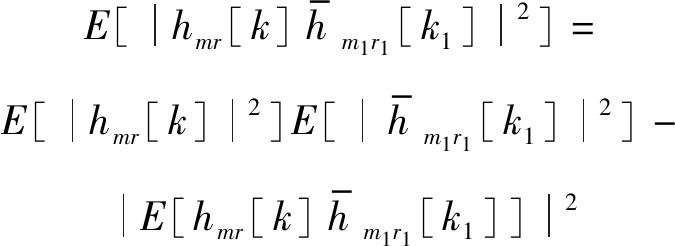
(12)
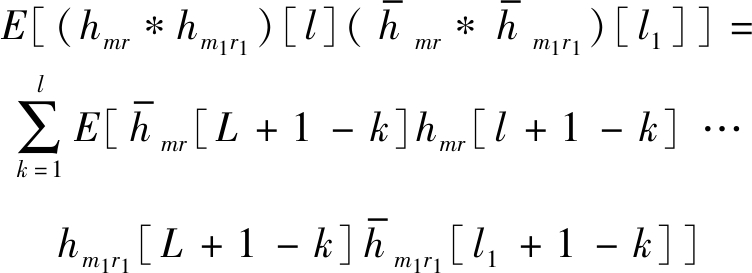
(13)
四个联合高斯变量乘积的均值为[18]
E[X1X2X3X4]=E[X1X2]E[X3X4]+E[X1X3]E[X2X3]+
E[X1X4]E[X2X3]-2E[X1]E[X2]E[X3]E[X4]
(14)
由公式(12)~(14)可得公式(15)和(16)
E[|(hmr*gmr)[L-1]|2]=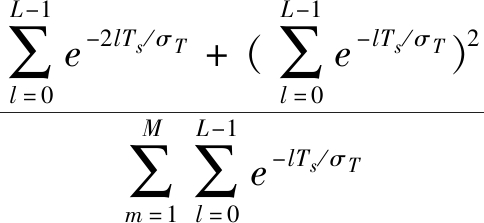
(15)
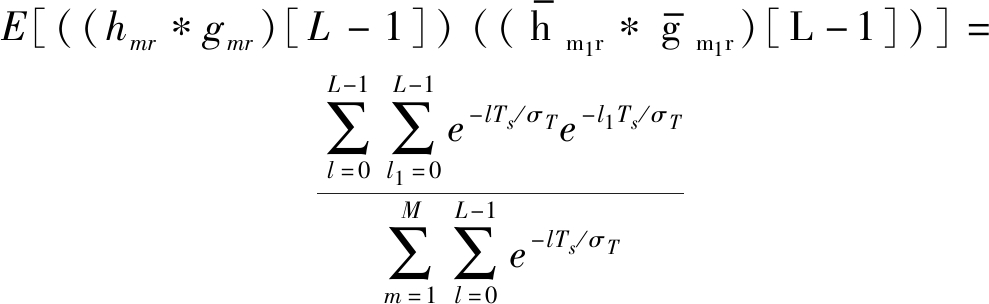
(16)
将(15)和(16)代入公式(11)得
(17)
(3)计算累积分布函数
①由(1)知A服从指数分布,且(2)中求出了E[A]的闭合表达式,则A是服从参数为1/E[A]的指数分布。
②![]() 中A为变量,其他参数为常数,则SINRb也服从指数分布且
中A为变量,其他参数为常数,则SINRb也服从指数分布且![]() 故SINRb是服从参数为
故SINRb是服从参数为![]() 的指数分布。
的指数分布。
③根据指数分布CDF的定义可知,合法信道SINR的CDF为
(18)
将(18)代入公式(9)可得公式(10)。
证毕。
3.2 安全中断概率
当窃听信道容量Ce大于冗余速率Re,保密信息不能保证一定的安全性。故将SOP定义为窃听信道容量Ce大于冗余速率Re的概率,即
Psop P(log2(1+SINRe)>Re)=1-FSINRe(2Re-1)
P(log2(1+SINRe)>Re)=1-FSINRe(2Re-1)
(19)
其中,FSINRe(x)表示窃听信道SINR的CDF。
定理2 令公式(8)中![]() 第x个窃听者的SINR可表示为
第x个窃听者的SINR可表示为![]() 该系统的SOP为
该系统的SOP为
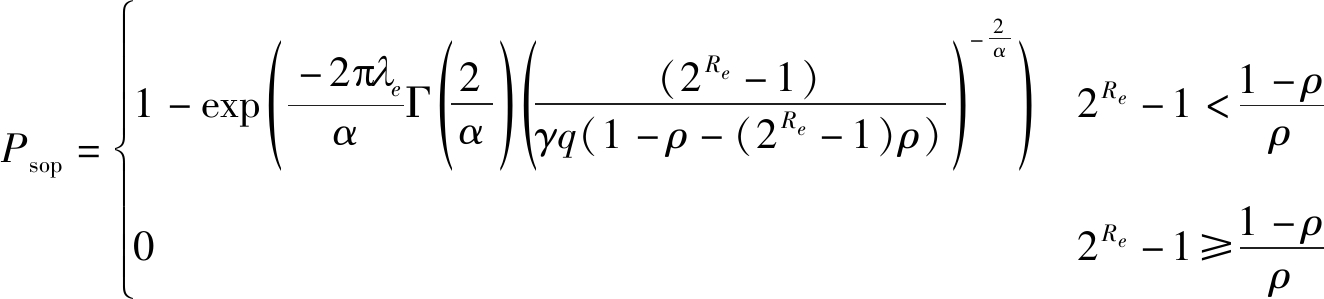
(20)
证明 考虑多个窃听者独立地接收和解码信息,故窃听信道SINR取决于所有窃听者中最大的窃听者的SINR,即窃听信道SINR为
SINRe=maxex∈ΦSINRx
(21)
窃听信道SINR的CDF可以表示为
FSINRe(t)=Pr{SINRe<t}=Pr{maxex∈ΦSINRx<t}=![]()
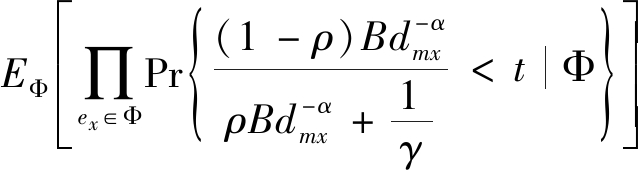
![]()
(22)
①当t<(1-ρ)/ρ时
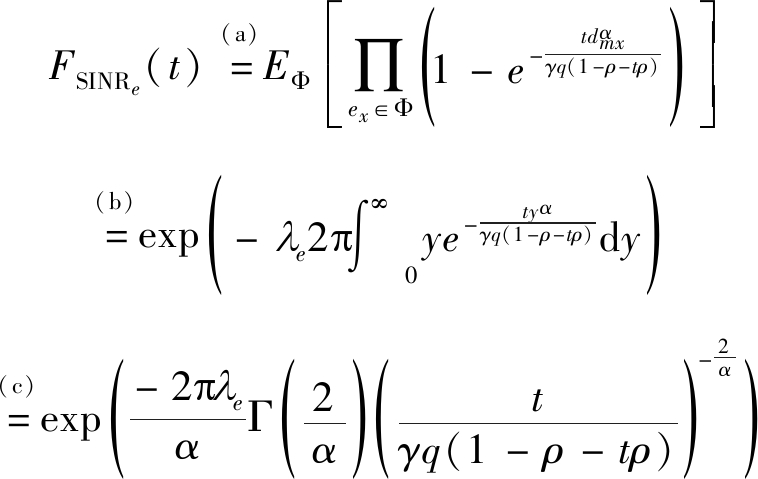
(23)
(a)与定理1同理可证明B服从指数分布,且![]()
(b)根据HPPP分布的概率生成函数定理(Probability Generating Functional Lemma, PGFL)。
(c) ![]() 其中
其中![]()
②当t≥(1-ρ)/ρ时
FSINRe(t)=1
(24)
将公式(23)和(24)代入公式(19)可得公式(20)。
证毕。
在3.1节和3.2节中,系统的COP和SOP都是在固定系统参数(ρ,Rb,Re)条件下进行推导的。通过分析3.1节的定理1和3.2节的定理2可知:
(1)当功率分配因子ρ取值较大时,发射端将有较少的功率发送保密信息,导致合法接收端的信噪比减小,系统的可靠性下降,但此时发射端将有较多的功率发送AN干扰随机分布的窃听者,窃听信道SINR降低,系统的安全性增大;
(2)当Wyner编码方案速率参数(Rb,Re)的取值较大时,只有合法信道的信道容量足够大,才能保证合法用户正确的解码信息,系统的可靠性降低,与此同时将有更大的速率用来防止窃听者的窃听,系统的安全性提高;
(3)若系统参数(ρ,Rb,Re)取值较小时,则与(1)和(2)相反。
由上述分析可知,系统参数(ρ,Rb,Re)的取值对该系统的可靠性和安全性存在一定的折中关系。因此在系统设计时,应综合考虑系统的可靠性和安全性,设置系统参数(ρ,Rb,Re)使整体的性能达到最优。
4 安全吞吐量的优化
基于上节推导的COP和SOP的闭合表达式,综合考虑系统的可靠性和安全性,提出在SOP小于安全性能下界的前提下,最大化安全吞吐量的优化方案。
按照文献[19]的方式定义安全吞吐量可表示为
ψ (1-Pcop)Rs
(1-Pcop)Rs
(25)
由于安全速率Rs=Rb-Re,该优化问题可以表示为
(26)
s.t Psop≤φ,0≤Re≤Rb,0≤ρ≤1
(27)
其中,φ表示系统安全性能下界。
下面对上述优化问题进行求解,过程如下:
将COP的闭合表达式(10)代入优化目标(26)中,上述问题可表示为:
(28)
s.t Psop≤φ,0≤Re≤Rb,0≤ρ≤1
(29)
其中,![]()
由SOP的闭合表达式(20)可以看出,Psop只与Re和ρ有关,将Psop对Re求一阶偏导可知,一阶偏导小于0。从公式(28)中可以看出,安全吞吐量ψ是关于Re的递减函数,因此,安全吞吐量最大时,Re最小,Psop越大,即对于固定的ρ,满足![]() 化简可得最优冗余速率为
化简可得最优冗余速率为
(30)
其中,
由公式ηb=2Rb-1可得码字传输速率为
Rb=log2(1+ηb)
(31)
将最优的冗余速率的闭合表达式(30)和码字传输速率式(31)代入公式(26)和(27)中,优化问题可表示为
(32)
(33)
令(32)为
(34)
将ψ(ηb,ρ)对ηb求一阶偏导,并使一阶导数等于0,可得
(35)
将ψ(ηb,ρ)对求ρ一阶偏导,并使一阶导数等于0,可得
(36)
结合公式(35)和(36)可得
(37)
将公式(37)代入(31)可得最优码字传输速率为
(38)
将最优的冗余速率的闭合表达式(30)和最优码字传输速率的闭合表达式(38)代入式(28)和(29),优化问题最终转化为
(39)
(40)
由公式(39)可知,ψ关于ρ的一阶导数和二阶导数比较难计算,最优功率分配因子ρ*的闭合表达式不易求出。通过观察ψ随着ρ变化的曲线图可知,ψ是关于ρ的先增后减的单峰函数。黄金分割法是一种常用的求解单峰函数极值的方法,具有最优性,该方法随着搜索次数的增加,趋于最优值,仿真图4验证了该理论。因此ρ*可采用黄金分割法在区间[(t-1)/2t,1]寻找最优值。由公式(30)和(38)可知,![]() 和
和![]() 的值与ρ*有关。故求出ρ*即可求得最大的安全吞吐量ψ*和最优的系统参数
的值与ρ*有关。故求出ρ*即可求得最大的安全吞吐量ψ*和最优的系统参数![]()
利用基于黄金分割法,对式(39)和(40)所表述的优化问题进行求解得到最优的功率分配因子,具体过程见表1。
表1 最优的功率分配因子求解算法
Tab.1 Optimal power allocation factor solution algorithm

5 仿真分析
对系统的COP和SOP的闭合表达式、最优功率分配因子和安全吞吐量进行了仿真。仿真参数设置如表2所示。
5.1 连接中断概率和安全中断概率的仿真
首先,分析了码字传输速率Rb和冗余速率Re不同取值条件下发射信噪比对系统安全性和可靠性的影响。图2给出了连接中断概率Pcop和安全中断概率Psop随发射信噪比变化的曲线图。从图中可以看出理论推导结果与仿真基本吻合,Pcop随着发射信噪比的增大而减小,说明了增大发射信噪比也是提高系统可靠性的一种有效途径。Psop随着发射信噪比的增大而增大,因为更大的发射信噪比将使得各个窃听者的接收信噪比增大,系统的安全性降低。另外也可以发现Pcop随着Rb的增大而增大,Psop随着Re的增大而减小,是因为合法信道容量小于Rb或窃听信道容量大于Re时中断事件发生。
表2 仿真参数
Tab.2 Simulation parameters
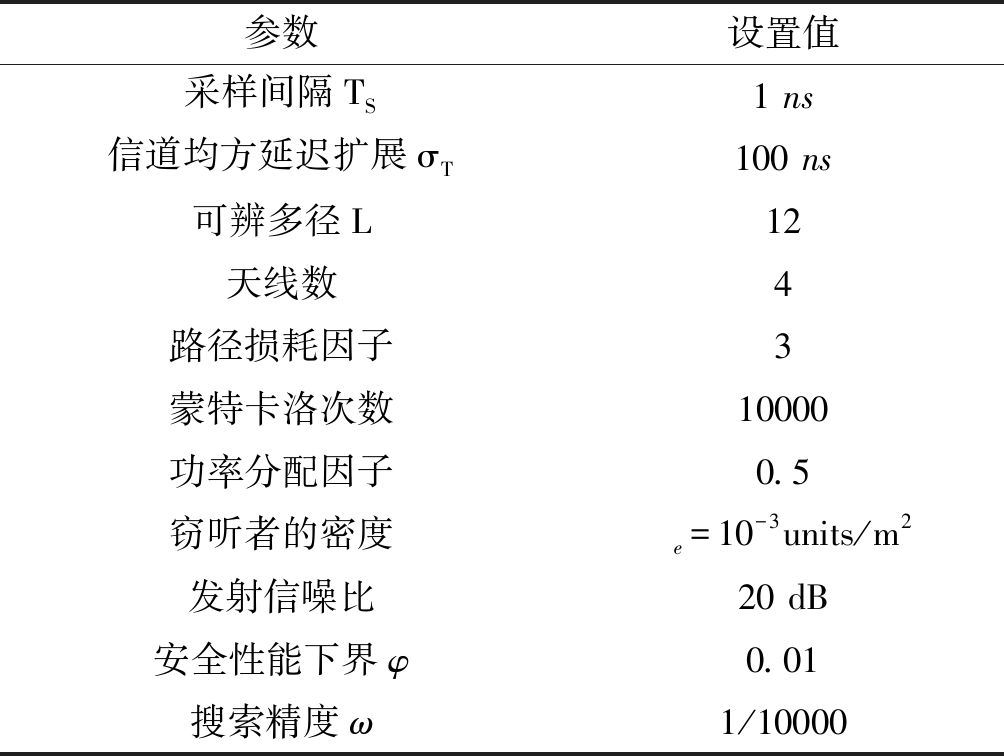
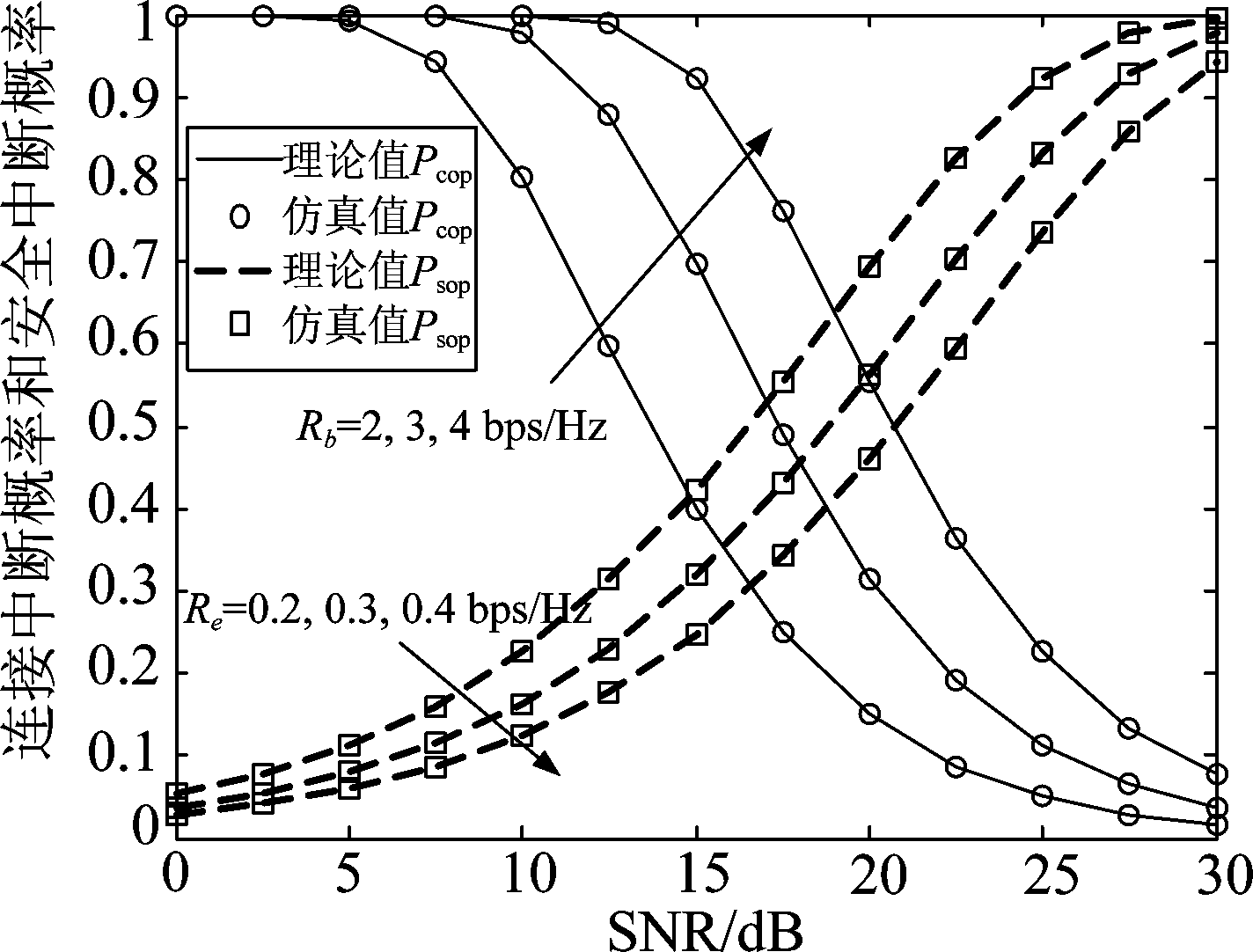
图2 Pcop、Psop与发射信噪比的关系图
Fig.2 Diagram of Pcop and Psop in relation to the transmitting signal ratio
连接中断概率Pcop和安全中断概率Psop随功率分配因子的变化如图3所示。从图中可知,Pcop随着功率分配因子的增大而增大,这是因为更少的功率用来发送保密信息。Psop随着功率分配因子的增大而减小,是因为更多的功率用来发送AN恶化窃听信道。同时,这也表明了功率分配因子引起了系统可靠性和安全性的折中。
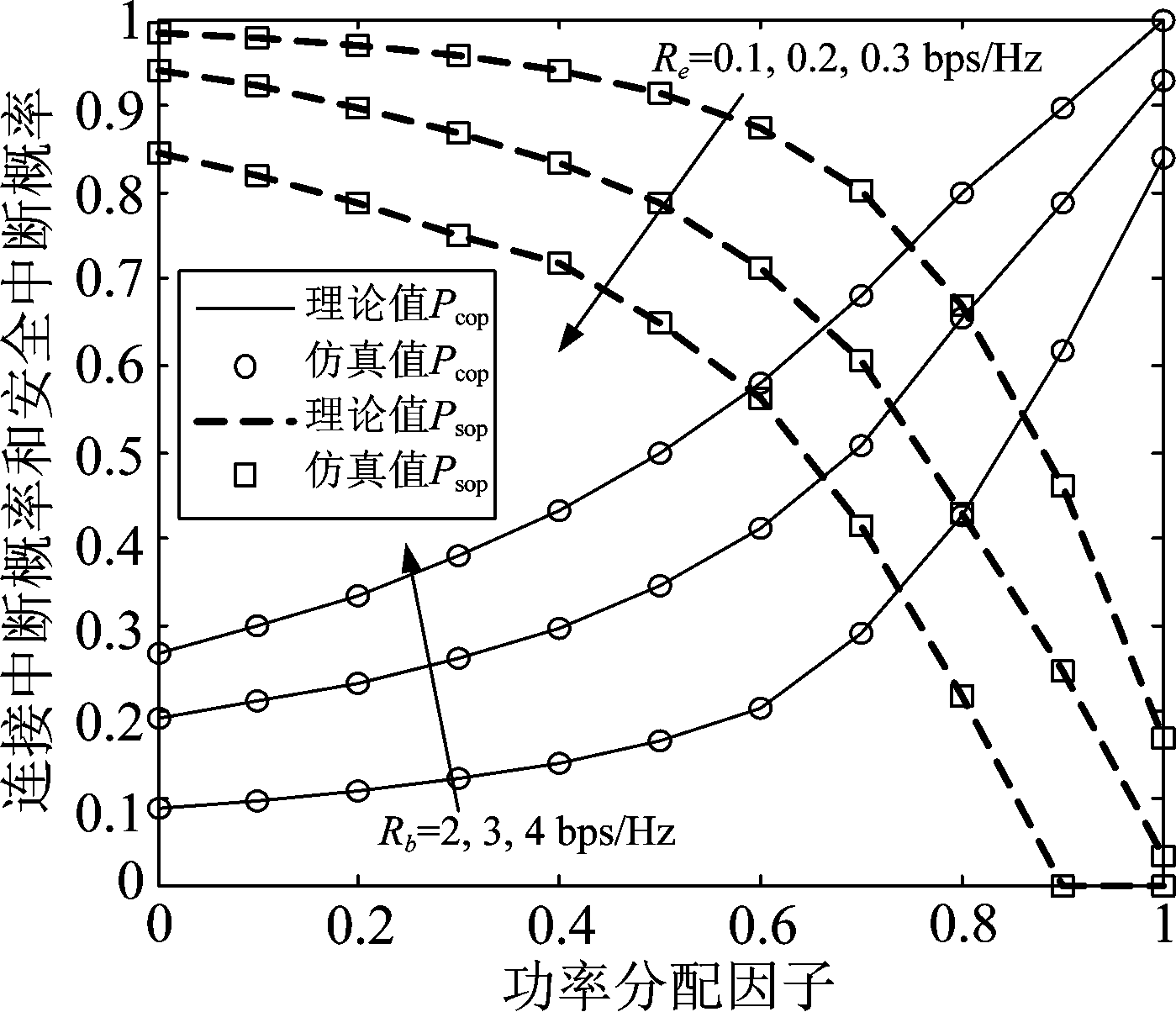
图3 Pcop、Psop与功率分配因子的关系图
Fig.3 Diagram of Pcop and Psop and power allocation factor
5.2 最优功率分配因子的仿真
图4和图5分别是不同搜索次数下最优功率分配因子和安全吞吐量的仿真曲线图。从仿真结果可知,当搜索次数越多,即搜索步长越小时,得到的最优功率分配因子及其所对应的最大安全吞吐量越准确。当搜索次数到达10次以上时,该系统的安全吞吐量已接近最大值,最优功率分配因子趋于平缓。当搜索次数大于15时,安全吞吐量和最优的功率分配因子基本上不再随着搜索次数的增加而变化。再后续的仿真中搜索次数设为20,即搜索步长为0.05。
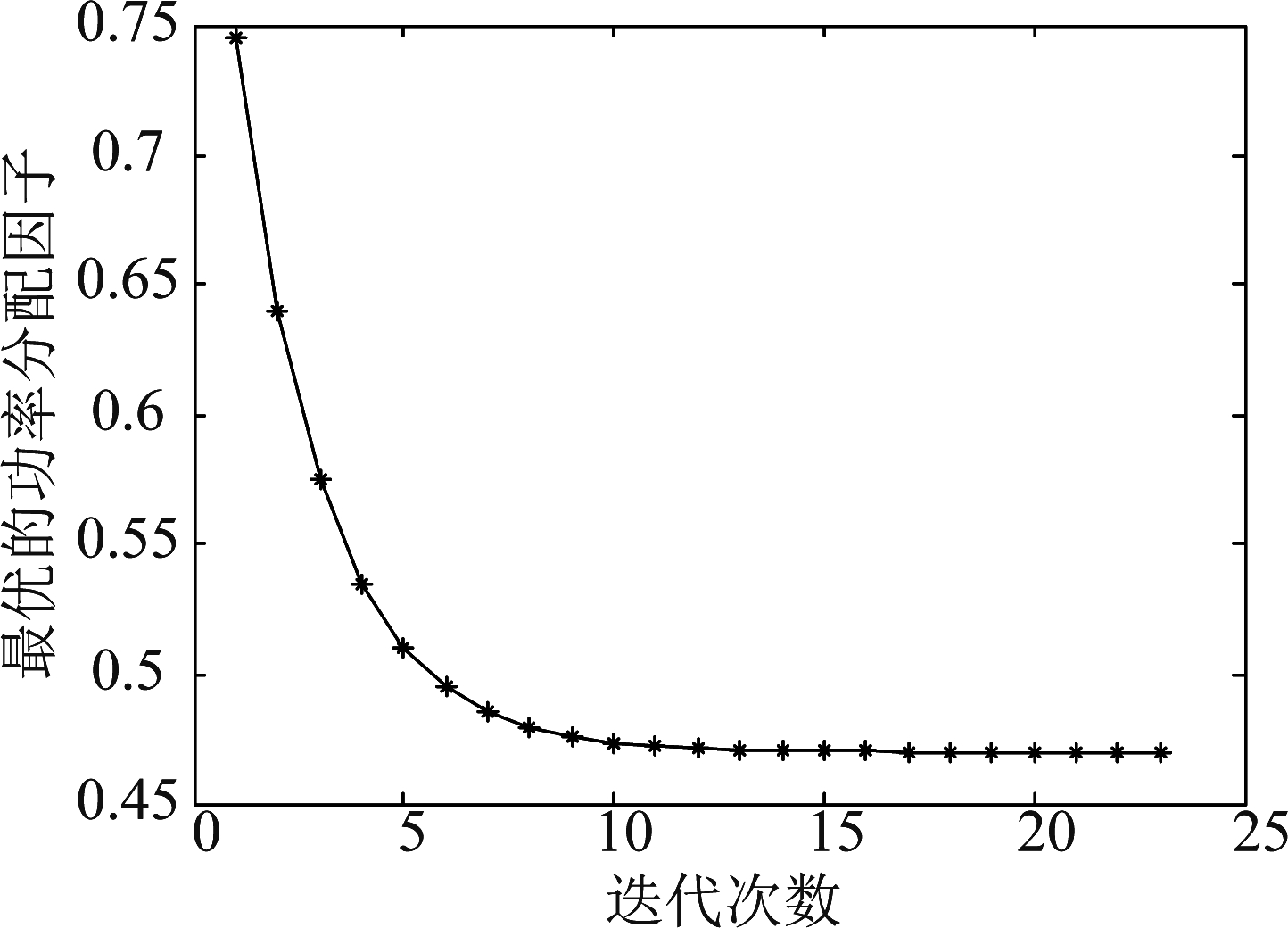
图4 迭代次数对最优功率分配因子的影响
Fig.4 Influence of search times on optimal power allocation factor
窃听者密度λe、合法者与发射端之间的距离dmr不同时,最优功率分配因子与安全性能下界φ的关系如图6所示。当dmr和λe一定时,最优的功率分配因子随着φ的增大而减小,此结果表明,当保密要求降低时,需要更少的人工噪声;当dmr和φ一定时,λe越大,最优的功率分配因子越大,即当被窃听的风险增大时,需要更多的人工噪声;当λe和φ一定时,dmr越大,最优的功率分配因子越大,是因为dmr越大时,AN在传输的过程中损耗越严重,需要更多的AN。
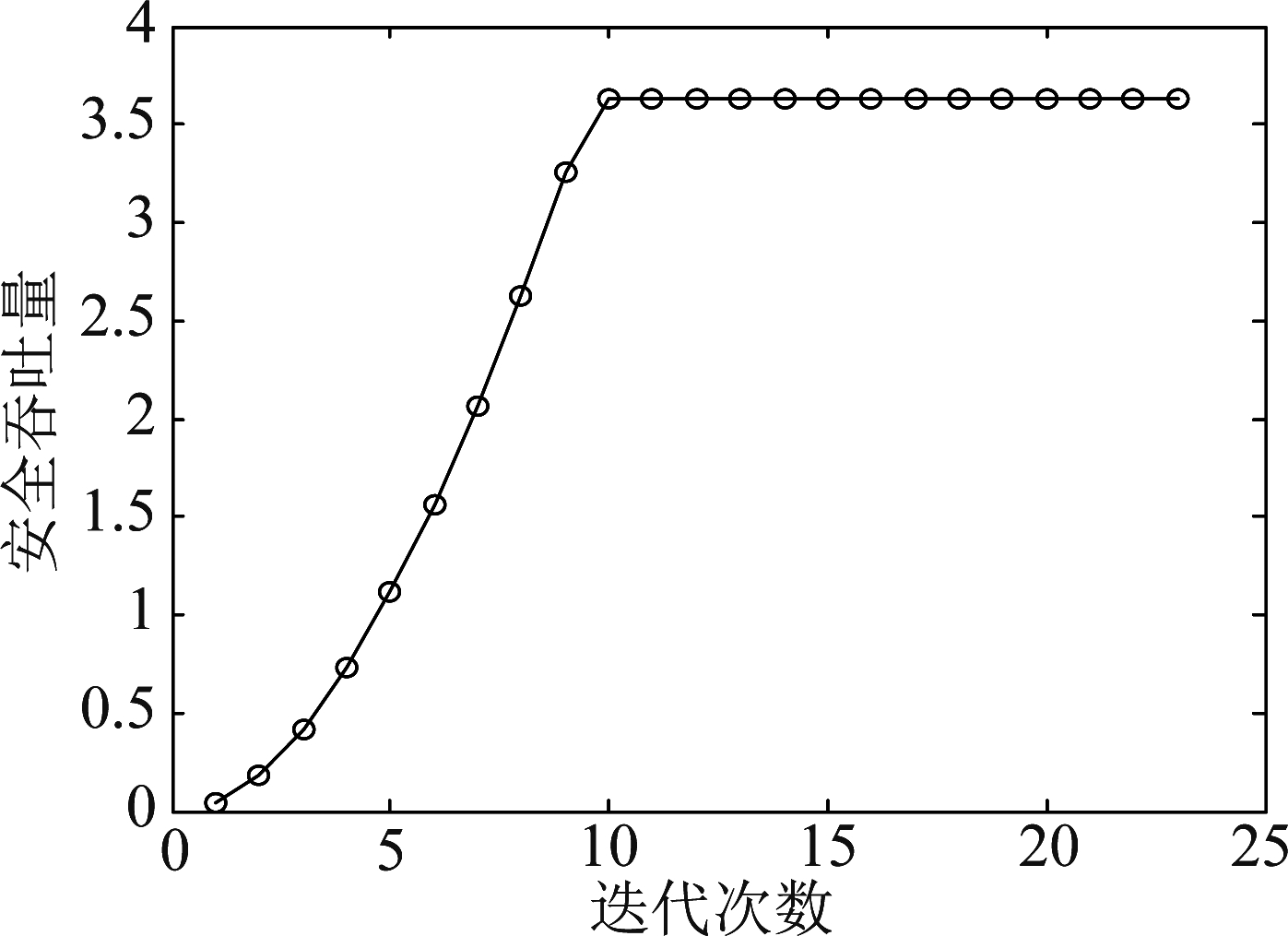
图5 迭代次数对安全吞吐量的影响
Fig.5 Influence of search times on security throughput
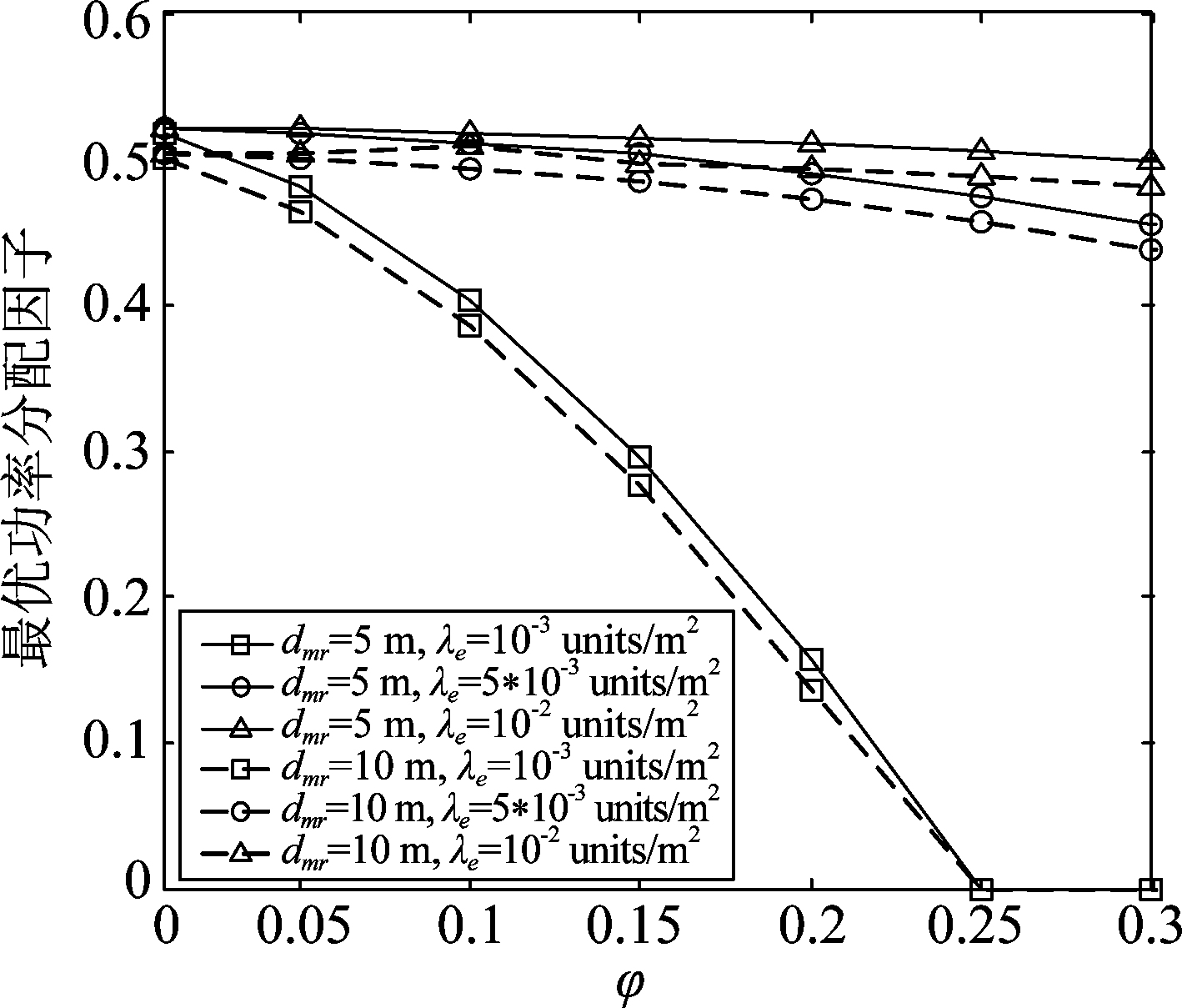
图6 最优功率分配因子与SOP下界的关系图
Fig.6 Diagram of optimal power distribution factor and lower bound of SOP
5.3 安全吞吐量的仿真
将本文所提方案与以下两种方案进行对比:
方案1 发射端发送人工噪声,但不进行时间反演操作[20];
方案2 发射端不发送人工噪声,只进行时间反演操作[3]。
图7是发射端与合法者之间的距离dmr不同时,安全吞吐量与发射信噪比的关系图。从图中可以看出,在相同参数下,所提方案明显优于另外两种方法。这三种方案都表明当dmr一定时,随着发射信噪比的增大,安全吞吐量增大。对于所提方案来说,当发射信噪比增大时,发射端将有更大的功率发送保密信息,合法用户接收信号强度增大。由于时间反演的聚焦特性,与方案1中不进行时间反演操作相比,本方案中的合法用户接收信号的强度将更大,同时,发射端将发送更大的人工噪声恶化窃听信道,与方案2发射端不发送人工噪声相比,本文方案的窃听信道更差。此外,当dmr越小,安全吞吐量越大,是由于信号在传播过程中的损耗减小了。
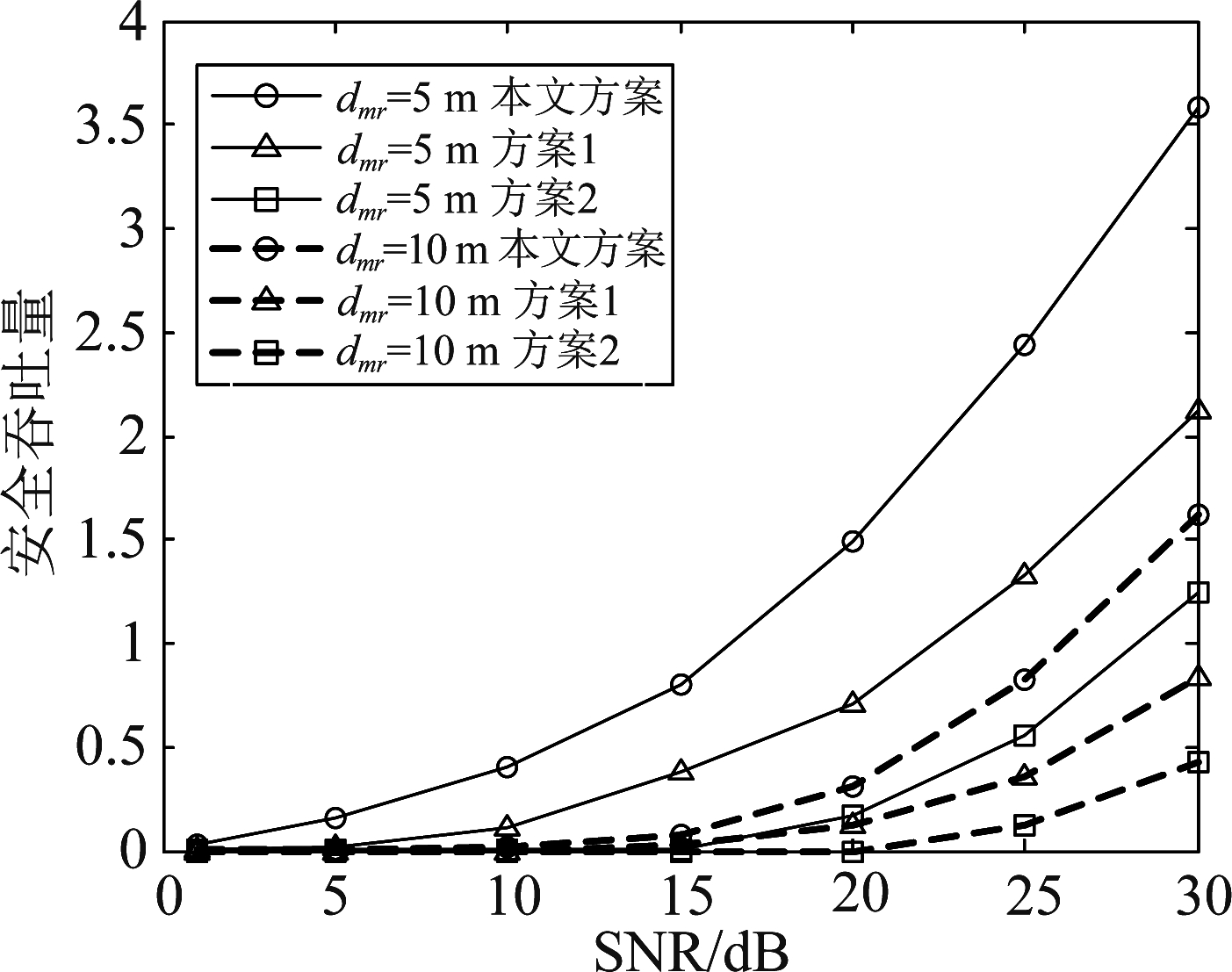
图7 安全吞吐量与发射信噪比的关系图
Fig.7 Diagram of security throughput and transmitted SNR
图8是安全吞吐量与窃听者密度的关系图。由仿真图可知,随着窃听者密度的增大,即当保密信息被窃听的风险增大时,安全吞吐量减小,本文方案优于其他两种方案,主要是因为在时间反演系统中加入人工噪声,用于干扰随机分布的窃听者,且优化了功率分配因子。
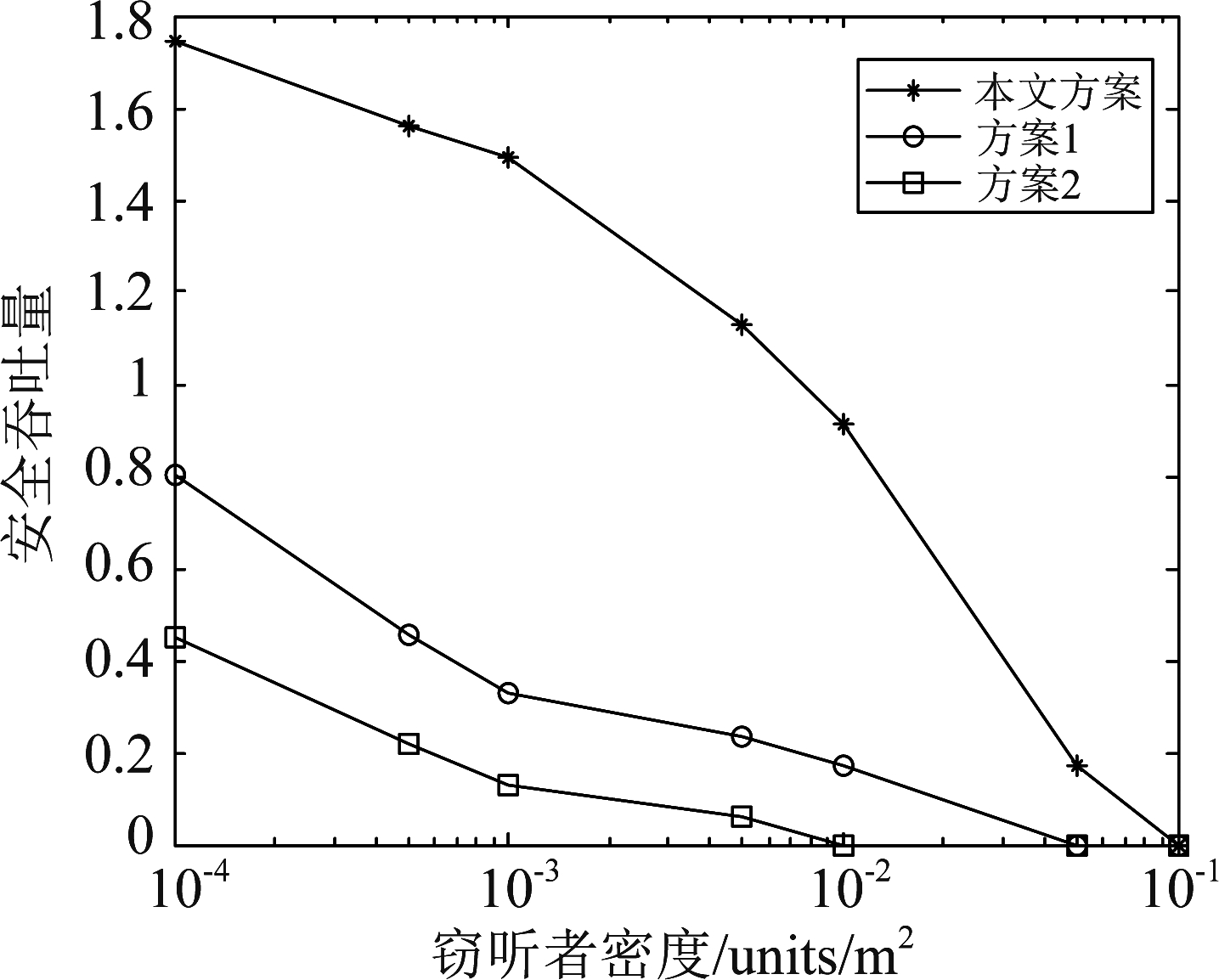
图8 安全吞吐量与窃听者密度的关系图
Fig.8 Diagram of security throughput and eavesdropper density
6 结论
针对TR系统中,存在多个窃听用户随机分布的物理层安全传输问题,提出一种人工噪声辅助时间反演的MISO物理层安全吞吐量优化方案。利用HPPP模拟多个随机分布的窃听者,为了对抗窃听者,在发送端设置功率分配因子,通过求解最优的功率分配因子实现安全吞吐量的最大化。仿真结果表明,该方案能够显著提高系统的安全吞吐量,使系统拥有更好的防窃听能力。需要指出的是,以上研究假设多个随机分布的窃听者独立的接收和解码信息,时间反演系统中,存在多个窃听用户共谋的物理层安全研究将作为后续工作。
[1] CHEN Y, WANG B, HAN Y, et al. Why Time Reversal for Future 5G Wireless?[J]. IEEE Signal Processing Magazine, 2016, 33(2): 17-26.
[2] GOLSTEIN S, NGUYEN T, HORLIN F, et al. Physical Layer Security in Frequency-Domain Time-Reversal SISO OFDM Communication[C]∥International Conference on Computing, Networking and Communications (ICNC), 2020: 222-227.
[3] LEI W J, YANG M M, LI Yao, et al. Physical layer security performance analysis of the time reversal transmission system[J]. IET Communications, 2020, 14(4): 635- 645.
[4] NGUYEN H, ZHENG F, KAISER T. Antenna Selection for Time Reversal MIMO UWB Systems[C]∥VTC Spring 2009-IEEE 69th Vehicular Technology Conference, 2009: 1-5.
[5] 李方伟, 汪苹, 张海波, 等. 基于时间反演的多用户下行安全传输技术[J]. 电波科学学报, 2019, 34(2): 18-24.
LI Fangwei, WANG Ping, ZHANG Haibo, et al. The secure transmission technology based on time reversal for multiuser downlink system[J]. Chinese Journal of Radio Science, 2019, 34(2): 18-24.(in Chinese)
[6] LI S, LI N, LIU Z, et al. Artificial noise aided path selection for secure TR communications[C]∥2017 IEEE/CIC International Conference on Communications in China (ICCC). IEEE, 2017: 1- 6.
[7] LI S, LI N, TAO X, et al. Artificial noise inserted secure communication in time-reversal systems[C]∥2018 IEEE Wireless Communications and Networking Conference (WCNC). IEEE, 2018: 1- 6.
[8] XV Q, REN P, DU Q, et al. Security-aware waveform and artificial noise design for time-reversal-based transmission[J]. IEEE Transactions on Vehicular Technology, 2018, 67(6): 5486-5490.
[9] XV Q, REN P, XU D. Combating Unknown Eavesdroppers by using Multipath Wireless Receptions[C]∥ICC 2019-2019 IEEE International Conference on Communications (ICC). IEEE, 2019: 1- 6.
[10] 朱江, 王雁, 杨甜, 等. 无线多径信道中基于时间反演的物理层安全传输机制[J]. 物理学报, 2018, 67(5): 7-17.
ZHU Jiang, WANG Yan, YANG Tian, et al. Physical layer security transmission mechanism based on time inversion in wireless multipath channel[J]. Acta Phys. Sin, 2018, 67(5): 7-17.(in Chinese)
[11] 朱江, 汪智豪. 基于李雅普洛夫优化的TRAN-SWIPT能效安全传输方案[J]. 系统工程与电子技术, 2019, 41(483): 216-221.
ZHU Jiang, WANG Zhihao. TRAN-SWIPT energy efficiency secure transmission scheme based on Lyapulov optimization[J]. Systems Engineering and Electronics, 2019, 41(483): 216-221.(in Chinese)
[12] 朱江, 汪智豪. 时间反演联合接收端人工噪声的安全传输方案[J]. 系统工程与电子技术, 2020, 42(10): 232-238.
ZHU Jiang, WANG Zhihao. Secure transmission scheme based on time-reversal combined with artificial noise at receiver[J]. Systems Engineering and Electronics, 2020, 42(10): 232-238.(in Chinese)
[13] 李为, 陈彬, 魏急波, 等. 基于接收机人工噪声的物理层安全技术及保密区域分析[J]. 信号处理, 2012, 28(9): 1314-1320.
LI W, CHEN B, WEI J B, et al. Secure Communications via Sending Artificial Noise by the Receiver: Ergodic Secure Region Analysis[J]. Signal Processing, 2012, 28(9): 1314-1320.(in Chinese)
[14] HAENGGI M, ANDREWS J, BACCELLI F, et al. Stochastic geometry and random graphs for the analysis and design of wireless networks[J]. IEEE J. Sel. Areas Commun, 2009, 27(7): 1029-1046.
[15] WANG L, LI R, CAO C, et al. SNR Analysis of Time Reversal Signaling on Target and Unintended Receivers in Distributed Transmission[J]. IEEE Transactions on Communications, 2016, 64(5): 2176-2191.
[16] 于宝泉, 蔡跃明, 胡健伟, 等. 认知无线电非正交多址接入随机网络物理层安全性能分析[J]. 电子与信息学报, 2020, 42(4): 950-956.
YU Baoquan, CAI Yueming, HU Jianwei, et al. Performance analysis of physical layer security for cognitive radio non-orthogonal multiple access random network[J]. Journal of Electronics & Information Technology, 2020, 42(4): 950-956.(in Chinese)
[17] SHAFIE A E, MABROUK A, TOURKI K, et al. Efficient AN-Aided Scheme to Power RF-EH Source Nodes and Secure Their Transmissions[J]. IEEE Wireless Communication Letters, 2017, 6(5): 670- 673.
[18] TRAN H, TRAN H, KADDOUM G, et al. Effective secrecy-SINR analysis of time reversal-employed systems over correlated multi-path channel[C]∥Wireless and Mobile Computing, Networking and Communications, 2015: 527-532.
[19] ZHOU X, MCKAY M R, MAHAM B, et al. Rethinking the Secrecy Outage Formulation: A Secure Transmission Design Perspective[J]. IEEE Communications Letters, 2011, 15(3): 302-304.
[20] 邓浩, 王慧明. 人工噪声策略的临界信噪比和功率分配研究[J]. 通信学报, 2019, 40(6): 66-73.
DENG Hao, WANG Huiming. Research on critical SNR and power allocation of artificial noise assisted secure transmission[J]. Journal on Communications, 2019, 40(6): 66-73.(in Chinese)

