1 引言
作为航空气象学领域内的一种灾难性大气现象,低空风切变具有尺度小、强度大、破坏力强、不易检测等特点,出现高度一般为 600 m以下[1]。飞机起飞和降落阶段都将经历这一高度,若此时遭遇低空风切变,将会由于缺乏足够的时间和空间予以应对而给航空安全带来严重威胁。所以,低空风切变的检测和预警技术一直都是国内外民航领域的研究热点[2],而风切变风速估计是整个检测流程的基础,直接影响着后续检测的准确程度。
机载气象雷达是用于对飞机前方航路上的危险气象区域进行实时探测,保障飞行安全的重要航空电子设备,可用于监测降水、风切变、湍流等情况[3]。目前,机载气象雷达大多发射厘米波,与之相比,毫米波波长短、频带宽、波束窄、便于小型化生产[4]。机载气象雷达使用毫米波,可以在降低天线尺寸的同时保证更加精确的目标位置和速度信息,为目标检测和跟踪提供更高的分辨率和精度[5]。此外,随着电子信息设备使用数量的激增,雷达工作的电磁环境日益复杂,电磁信号在时域上突发多变、空域上纵横交错、频域上拥堵重叠,导致机载气象雷达不得不应对各式各样的干扰,从而使目标的识别和检测更加困难。捷变频作为雷达抗干扰的一种重要手段,在增强雷达对抗干扰能力的同时还可提高目标截面测量精度从而改善雷达对目标的分辨能力[6]。将捷变频技术与机载气象雷达相结合,无疑会大大增强雷达抗干扰能力,改善对低空风切变的检测性能。
在探测低空风切变过程中,机载气象雷达会接收到强地杂波回波,造成低空风切变信号被淹没。因此削减地杂波的影响是进行风切变风速估计的基础。当前得到广泛使用的空时自适应处理(Space-Time Adaptive Processing,STAP)技术可以依据回波空时耦合性进行杂波抑制、信号匹配[7]。基于此,目前已有基于空时最优的低空风切变风速估计方法[8]、基于多通道联合的低空风切变风速估计方法[9]、基于广义相邻多波束的低空风切变风速估计方法[10]等,但这些方法均没有考虑存在速度模糊的情况。毫米波雷达信号波长很短,系统可测的不模糊速度范围非常有限,极易发生测速模糊,这无疑会降低低空风切变的检测性能,使民航飞机的飞行安全受到威胁,因此必须考虑解模糊问题。目前,主流的解模糊方法是基于多频参差的,主要有剩余定理(孙子定理)法[11]、余差查表法[12]、一维集算法[13]等,这些算法已在解模糊领域得到了广泛的应用。但上述算法普遍运算量大、对测量精度要求较高,且它们均未考虑捷变频体制下由于发射信号载频捷变而导致的多重频下目标真实多普勒频率不再固定的问题,因此必须寻求捷变频下的解模糊方法。
基于此,本文提出了毫米波捷变频体制下的低空风切变风速估计方法。该方法中,载频捷变方式采用脉组间捷变,首先在每个脉组内采用TDPC级联CMCAP估计出风场模糊多普勒值;之后将每个脉组内的估计结果从多普勒频率域转换到速度域,再采用错位差分查表的方式恢复出风场的真实速度值。
2 信号模型
图1所示的是机载前视阵雷达模型,天线为均匀面阵,通常将其进行微波合成等效为一个阵元数为N的等距均匀线阵。载频跳变方式采用脉组间捷变,在一次相干处理时间(Coherent Processing Interval,CPI)内共K个脉冲,将一个完整的CPI均匀划分为两组,每组各有K/2个脉冲,且这两组的载频分别为
相应的阵元间距分别为
其中,c为光速,V为载机飞行速度, fr为脉冲重复频率,H为载机高度,杂波块的俯仰角和方位角分别为φ、θ,风切变信号的俯仰角和方位角分别为φl、θ0。
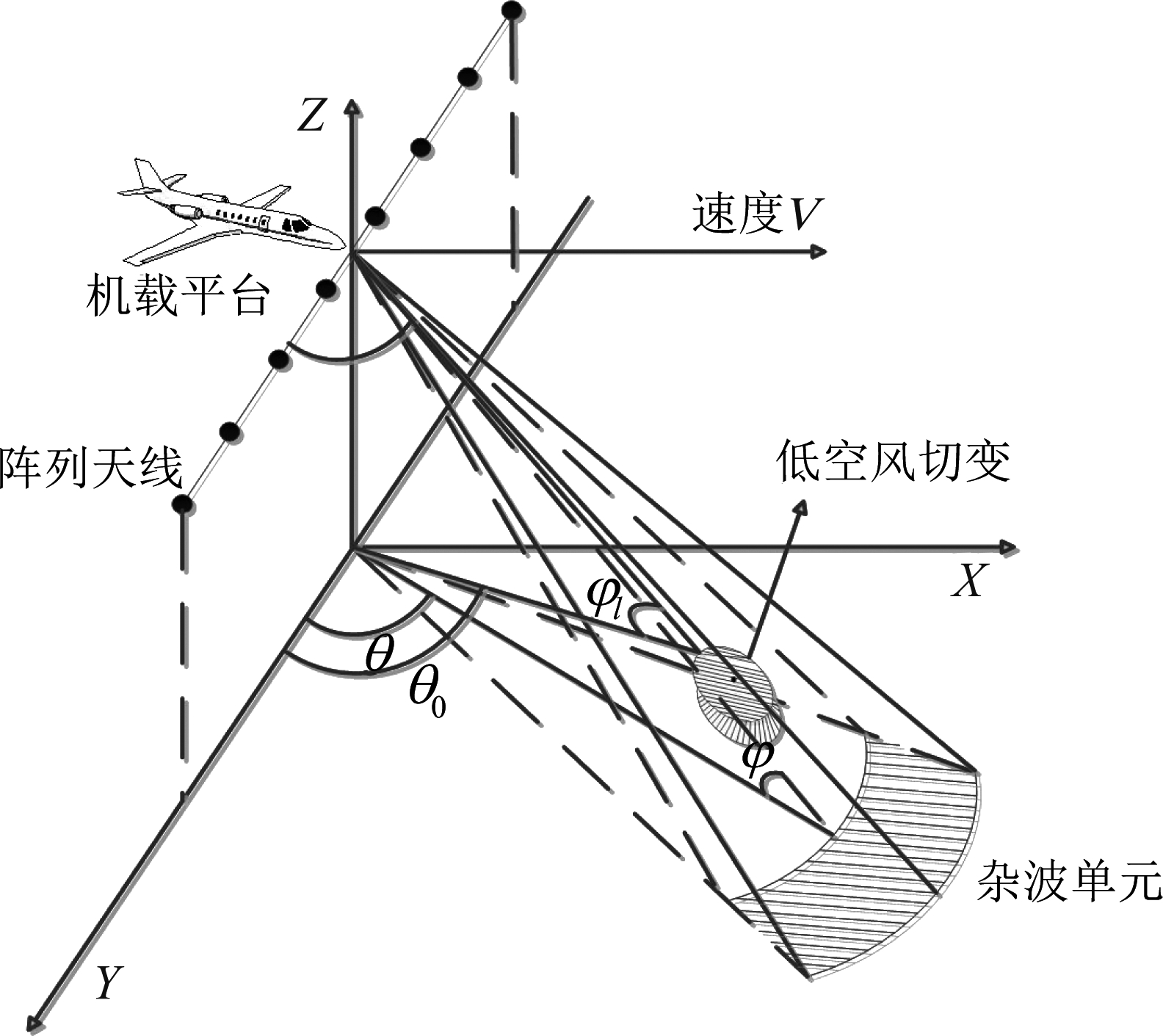
图1 机载前视阵示意图
Fig.1 Geometry of the airborne forward-looking radar
假设机载气象雷达在其工作范围内有L个距离单元,在第i个脉组(i=1,2)内,第l个距离单元的空时二维快拍数据为
zi(l)=ξlyi,l(ψ0,fl)+c(l)+n
(1)
式中:c(l)是第l个距离单元的地杂波,n为高斯白噪声,ξl为该距离单元的风场回波复幅度,yi,l(ψ0, fl)为该距离单元的风场空时导向矢量,ψ0为风场信号空间锥角,且有cos ψ0=cos θ0cos φl, fl为该距离单元内风场目标回波的多普勒中心频率。yi,l(ψ0, fl)可表示为
yi,l(ψ0, fl)=yi,t(fl)⊗yi,s(ψ0)
(2)
式中:⊗为Kronecker积,yi,t(fl)为第i个脉组对应的风场时域导向矢量,yi,s(ψ0)则为空域导向矢量。yi,t(fl)和yi,s(ψ0)可以分别表示为:
yi,t(fl)=ai,t(fl)⊙gi(σf)
(3)
yi,s(ψ0)=ai,s(ψ0)⊙gi(ψ0)
(4)
式中:ai,t(fl)=[ejπ(K(i-1)/2)fl ejπ(K(i-1)/2+1)fl … ejπ(Ki/2-1)fl]T表示第i个脉组对应的该距离单元中多普勒中心频率为fl的点目标的时域导向矢量,gi(σf)=
表示频率扩展函数,⊙为Hadamard积,ai,s(ψ0)=[1 ej2πdifi0cos ψ0/c … ej2π(N-1)difi0cos ψ0/c]T表示第i个脉组对应的该距离单元风场中心上点目标的空域导向矢量,gi(ψ0)=[1 e(2πdifi0/c)2Δ/2 … e(2π(N-1)difi0/c)2Δ/2]T为风场信号的角度扩展函数,
表示θ方向的角度扩展,σφ表示φl方向上的角度扩展。
3 基于TDPC-CMCAP的多普勒估计方法
基于TDPC-CMCAP的多普勒估计方法首先需要构造TDPC预滤波器来沿着杂波轨迹形成凹口抑制杂波,削减杂波功率,接着再构造CMCAP降维处理器,对待检测距离单元预滤波之后的雷达回波数据进行降维以及自适应滤波,进而在减小运算量的同时有效抑制剩余杂波,并匹配目标信号得到风场多普勒估计。下面对TDPC滤波器、CMCAP降维处理器、低空风切变多普勒估计进行详细描述。
3.1 TDPC滤波器设计
假设地面各个杂波散射单元的回波统计独立,根据地杂波Ward模型,在第i个脉组内,第l个距离单元第k个脉冲的杂波回波数据可以写为
ci,k(l)=ZDka
(5)
式中:Z、Dk、a分别表示第l个距离单元内,雷达系统在第k个脉冲内接收的杂波回波的空域相位、多普勒相位以及复幅度。它们可分别表示为:
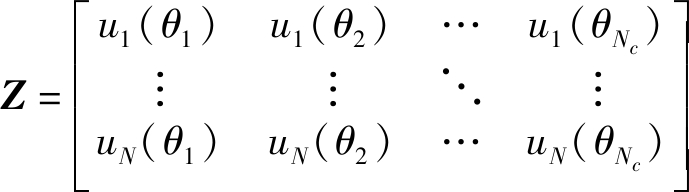
(6)
Dk=diag([ωk(θ1),ωk(θ2),…,ωk(θNc)])
(7)
a=[a(θ1),a(θ2),…,a(θNc)]T
(8)
式中:un(θm)、ωk(θm)、a(θm)(m=1,2,…,Nc)分别代表第l个距离单元内第m个杂波散射单元的空域相位、多普勒相位、回波复幅度,Nc为一个距离单元内杂波散射单元的个数。它们可分别表示如下:
un(θm)=ej2π(n-1)ωs(θm,φl)
(9)
ωk(θm)=ej2π(k-1)ωt(θm,φl)
(10)
(11)
式中:ρm为与杂波所属环境有关的反射系数,F(θm,φl)为接收方向图,Rl为第l个距离单元与雷达的斜距,
为空间角频率,
为时间角频率。
在忽略相邻两个脉冲间杂波回波复幅度的变化时,可认为第i个脉组内,第l个距离单元第k+1个脉冲的杂波回波数据仅需在式(5)中增加一个多普勒相位[14],相应的可以表示为
(12)
式中,
=ej2πωt(θm,φl)。
因此,可以设计滤波系数矩阵Qi,使得杂波对消后剩余杂波能量最小,即
(13)
利用Cauthy-Schwartz不等式可以得到式(13)的闭式解为
(14)
进而,由杂波对消系数矩阵构造出TDPC预滤波矩阵
为
(15)
式中,IN∈CN×N为单位矩阵。
3.2 构造组合空时主通道降维联合空时变换矩阵
CMCAP结构实现图如图2所示。
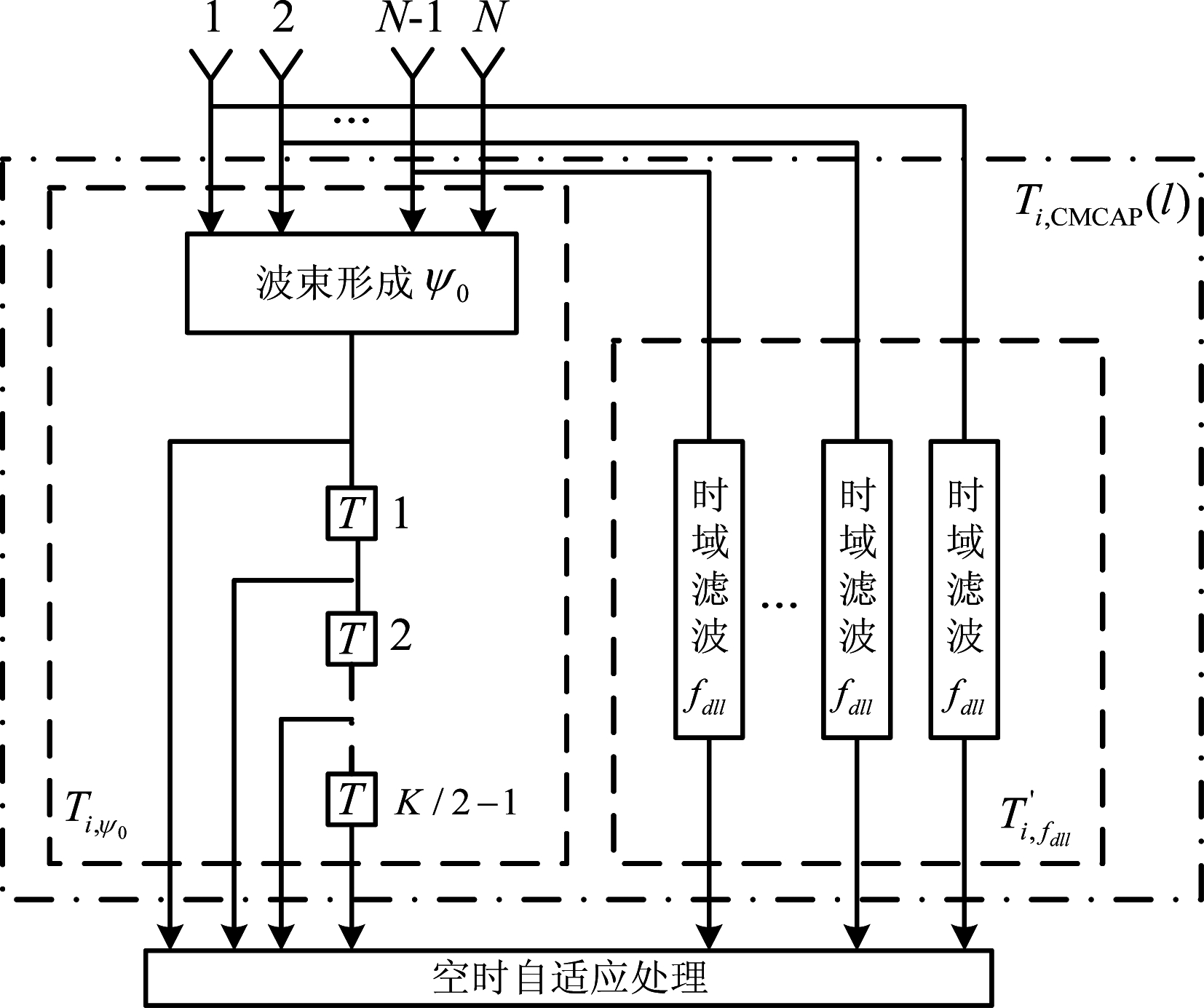
图2 组合空时主通道自适应降维处理器结构实现图
Fig.2 Architecture implementation diagram of the CMCAP dimension-reduced adaptive processor
本文所提方法用天线波束对雷达方位向进行扫描,之后把每个方位向扫描所得的回波数据分别应用CMCAP方法进行处理,则在处理某个方位的回波数据时,认为该数据的方位信息是已知的。假设在第i个脉组内第l个距离单元风切变信号的空时导向矢量为yi,l(ψ0, fdll),其中,ψ0表示风场的空间锥角, fdll表示当前距离单元风场的归一化多普勒频率。采用切比雪夫权对导向矢量进行加权可以保证后续处理时杂波仅在ψ=ψ0和f=fdll两条通带内。定义两个二维导向矢量集合:
(16)
其中Λi,ψ为ψ=ψ0通带内的所有导向矢量集合,Λi, f为f=fdll通带内所有导向矢量集合,ψ为风切变信号占据的空间锥角范围, f为风切变信号所处的归一化多普勒频率范围,Bi(ψ0, f)以及Bi(ψ, fdll)可以表示为:
Bi(ψ0, f)=Bi,t( f )⊗Bi,s(ψ0)=
(IK/2-1⊗Bi,s(ψ0))Bi,t( f )=Ti,ψ0Bi,t( f )
(17)
Bi(ψ, fdll)=Bi,t(fdll)⊗Bi,s(ψ)=
(Bi,t(fdll)⊗IN)Bi,s(ψ)=Ti, fdllBi,s(ψ)
(18)
式中:Bi,t( f )={yi,t( f ), f∈[-1 1]}为风切变信号所处归一化多普勒频域内全部的时域导向矢量集合,Bi,s(ψ)={yi,s(ψ),ψ∈[0 π]}为风切变信号空域范围内全部空域导向矢量集合。IK/2-1和IN分别为(K/2-1)×(K/2-1)和N×N的单位阵。Bi,s(ψ0)为空间锥角在ψ0方向上的空域导向矢量,Bi,t(fdll)为归一化多普勒频率为fdll的时域导向矢量,分别可以表示为:
Bi,s(ψ0)=ξs⊙yi,s(ψ0)=ξs⊙ai,s(ψ0)⊙gi(ψ0)
(19)
Bi,t(fdll)=ξt⊙yi,t(fdll)=ξt⊙ai,t(fdll)⊙gi(σf)
(20)
式中,ξs=[qs1 qs2 … qsN]T和ξt=[qt1 qt2 … qtK/2-1]T分别为空域和时域的切比雪夫加权矢量。Ti,ψ0=IK/2-1⊗Bi,s(ψ0)∈CN(K/2-1)×(K/2-1)和Ti, fdll=Bi,t(fdll)⊗IN∈CN(K/2-1)×N的列矢量分别代表ψ=ψ0和f=fdll通道中所有导向矢量的一组基。由文献[15]可知,Ti,ψ0和Ti, fdll构成的矩阵[Ti,ψ0 Ti, fdll]N(K/2-1)×(N+K/2-1)的秩为N+K/2-2,也即矩阵[Ti,ψ0 Ti, fdll]N(K/2-1)×(N+K/2-1)中任意N+K/2-2个列向量相互独立。基于此,可以构造组合空时主通道降维联合空时变换矩阵:
(21)
其中,
由Ti, fdll的前N-1列组成。
3.3 低空风切变多普勒估计
根据线性约束最小方差准则,在第i个脉组内,第l个距离单元的CMCAP降维处理器可以表示为式(22)所示数学优化问题:
(22)
式中:
为降维后的杂波协方差矩阵,
ri(j)
(j)为第l个距离单元的估计协方差矩阵,其中ri(j)=Pj,lzi(j),(1≤j≤L, j≠l)为第j号参考距离单元矫正后的数据,zi(j)为该参考单元雷达接收数据,Pj,l为多普勒频移补偿矩阵。Bi,T(l)为第l个距离单元降维后的低空风切变信号空时导向矢量,可以表示为:
(23)
ωi,T(l)为处理器的最优权矢量,可以表示为:
(24)
利用求解的最优权矢量构造得到式(25)所示代价函数,以此来估计第l个待测单元中低空风切变信号的多普勒频率
(25)
当代价函数为最大值时,即得到参数估计结果。其中,
为第l个距离单元的降维后数据,
对所有距离单元重复上述计算过程即可得到整个风场的多普勒估计。注意到,由于毫米波信号波长很短,故求得的风场多普勒估计结果存在模糊问题。
4 基于错位差分查表法的速度解模糊
对于一般的脉冲多普勒雷达,可以直接在多普勒域完成速度解模糊。假设雷达以双重频fr1和fr2交替发射脉冲,测得目标的视在多普勒频率分别为fd1、 fd2,设真实多普勒频率为fd,则可通过求解如下方程组来实现解模糊
(26)
其中n1、n2均为未知数。从工程实现上来说,运算量较大,尤其是对于高速目标而言,需要搜索的次数更多,运算量相应的也就更大。
对于频率捷变体制的雷达而言,解模糊时每种重频下所使用的载频不同,而对于一个径向速度为V的目标来说,它在每种重频下产生的视在多普勒频率fdi是与载频
有关的[16],具体关系为:
(27)
式中,mod(·)为求余运算。因此,即便没有发生模糊,同一目标在不同重频下得到的视在多普勒频率也是不一样的,则捷变频下无法在多普勒域解模糊。然而,目标真实速度不会因载频不同而改变,因此本文把视在多普勒值转换为视在速度值,然后在速度域实现解模糊,转换公式为:
fdiλi/2+nifriλi/2=fdλi/2=Vdi+niVri=Vd
(28)
式中:λi是第i个载频对应的波长,Vdi表示第i重频下目标的视在速度值,Vd表示真实速度。
在实际工程实现时,多普勒滤波器分辨力会因可用脉冲数量有限而受到限制,进而视在速度值的测量会存在较大的量化误差,造成上述方程组求解误差较大[17]。考虑采用错位差分查表方式进行解模糊,以两重频解速度模糊为例,错位差分查表法步骤为:
1)计算两重频下的模糊速度Vd1=fd1λ1/2,Vd2=fd2λ2/2;
2) 构建如表1所示的速度模糊表格。其中,V1(n)=nλ1/(2T1)+Vd1,V2(n)=nλ2/(2T2)+Vd2,Ti为第i个脉冲重复周期,n=-N′,…,N′,N′值应满足最大测速范围;
3) 查找相差最小的两个速度值。对表1的第1行和第2行分别进行重组得到两个新的向量Va=[V1(2:2N′+1)V1(1:2N′)V1(2:2N′+1)]、Vb=[V2(1:2N′)V2(2:2N′+1)V2(2:2N′+1)],差分搜索最小值所在位置
4) 求目标的不模糊真实速度V=(Va(diff_m)+Vb(diff_m))/2。
表1 速度模糊表
Tab.1 Speed ambiguity table
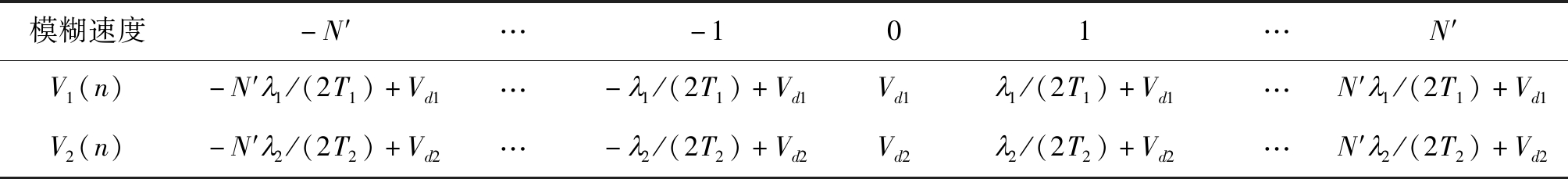
模糊速度-N′…-101…N′V1(n)-N1/(2T1)+Vd1…1/(2T1)+Vd1Vd1/(2T1)+Vd1…N1/(2T1)+Vd1V2(n)-N2/(2T2)+Vd2…2/(2T2)+Vd2Vd2/(2T2)+Vd2…N2/(2T2)+Vd2
5 算法流程
毫米波捷变频体制下低空风切变风速估计方法流程图如图3所示。
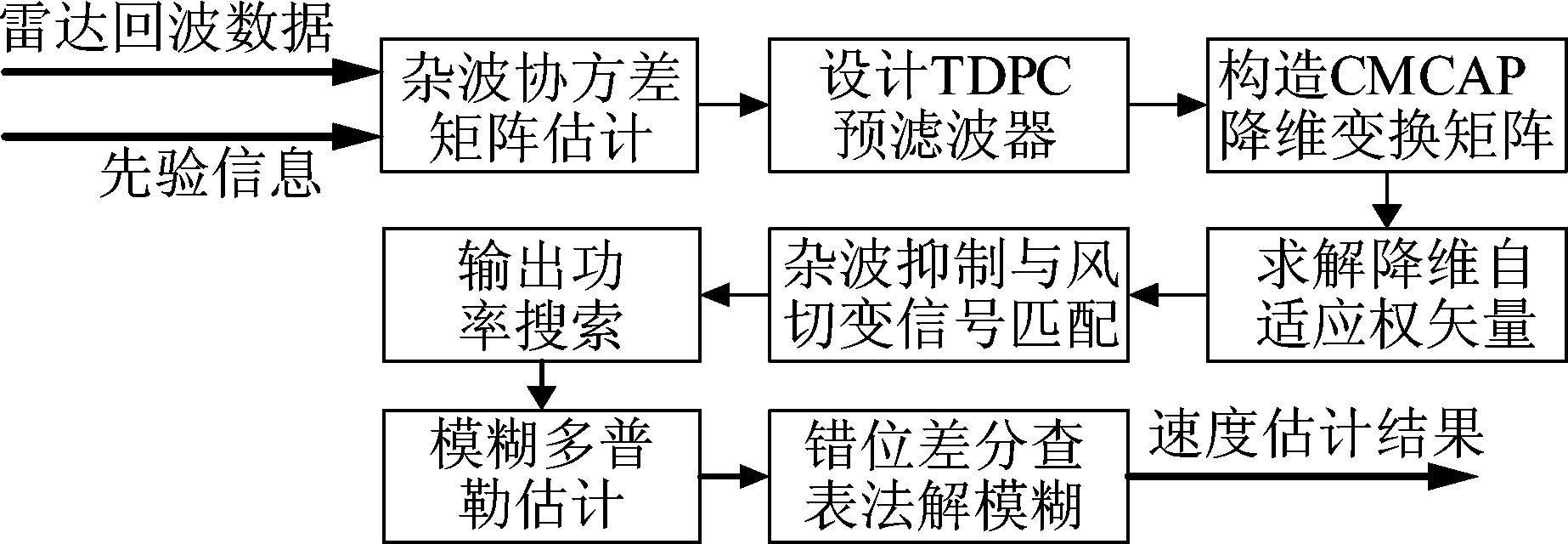
图3 毫米波捷变频体制下低空风切变风速估计方法流程图
Fig.3 Flow chart of low-altitude wind-shear wind speed estimation under millimeter wave frequency agile system
6 仿真结果及分析
6.1 仿真条件
表2所示为仿真时系统主要参数值。
表2 系统仿真参数表
Tab.2 System simulation parameter table
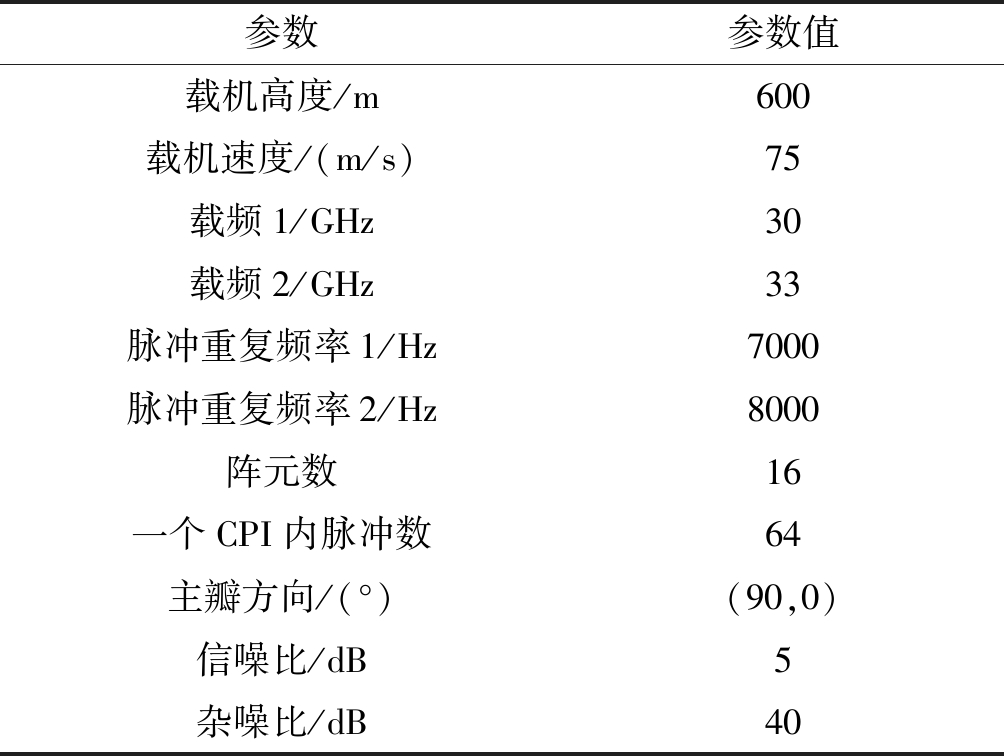
参数参数值载机高度/m600载机速度/(m/s)75载频1/GHz30载频2/GHz33脉冲重复频率1/Hz7000脉冲重复频率2/Hz8000阵元数16一个CPI内脉冲数64主瓣方向/(°)(90,0)信噪比/dB5杂噪比/dB40
6.2 仿真结果分析
图4仿真了脉冲重复频率为7000 Hz,载波频率为30 GHz时毫米波捷变频雷达回波信号的功率谱。经观察可以发现,当雷达工作于前视模式时,地杂波的功率谱呈椭圆形分布,其中主瓣杂波的功率最大,且杂波在空时二维平面上沿多普勒维出现了折叠现象。风切变回波信号的空时二维谱是一条窄带。而且地杂波的回波功率明显高于风切变场的回波功率,这将导致微弱的风切变信号被淹没,给雷达的检测带来困难。
图4 雷达回波信号的功率谱(PRF=7000 Hz, f0=30 GHz)
Fig.4 Power spectrum of radar echo signal (PRF=7000 Hz, f0=30 GHz)
图5是以第60号距离单元为例,当脉冲重复频率为7000 Hz,载波频率为30 GHz时,地杂波信号在预滤波前后的功率谱对比图。其中,图5(a)为预滤波之前的地杂波信号功率谱,可以看出,旁瓣杂波在空时二维平面上出现了折叠现象,此时STAP技术难以沿着杂波迹形成凹口去滤除杂波,进而会影响目标检测效果。图5(b)为使用TDPC预滤波矩阵对杂波进行预滤波之后的功率谱,从图中可知,TDPC预滤波器能够沿着杂波轨迹形成一道较深的凹口来抑制杂波,从而提高后续STAP处理的目标检测性能。
图6为在毫米波捷变频雷达体制下,采用本文方法得到的解模糊前后风场速度估计结果对比图。载频跳变方式选用脉组间捷变,即将一个完整的CPI分为两组,每组各32个脉冲,分别以脉冲重复频率为7000 Hz、载频为30 GHz以及脉冲重复频率为8000 Hz、载频为33 GHz进行脉冲的发射。图6(a)为重频7000 Hz、载频30 GHz时得到的风场速度估计结果,此时系统可测的最大不模糊速度为17.5 m/s。因此,在地杂波被有效抑制后,风速的估计结果在±17.5 m/s的范围之内与原始风速非常吻合,但在该范围之外,风速估计结果出现了跳变,即出现了速度模糊。图6(b)为重频8000 Hz、载频33 GHz时得到的风场速度估计结果,此时系统可测的最大不模糊速度为18.2 m/s,因此风场速度的估计值在超过±18.2 m/s时也发生了跳变,出现了模糊现象。图6(c)为采用错位差分查表法解模糊后得到的风速估计结果,可以看出估计的风场速度与原始风场速度分布非常吻合,且风场速度随距离呈现反“S”形分布的特点,经计算,风速估计的均方根误差为2.2037 m/s,由此可以说明本文所提方法能够较好地抑制地杂波干扰并解决风场速度的模糊问题,从而得到低空风切变风速的有效估计。
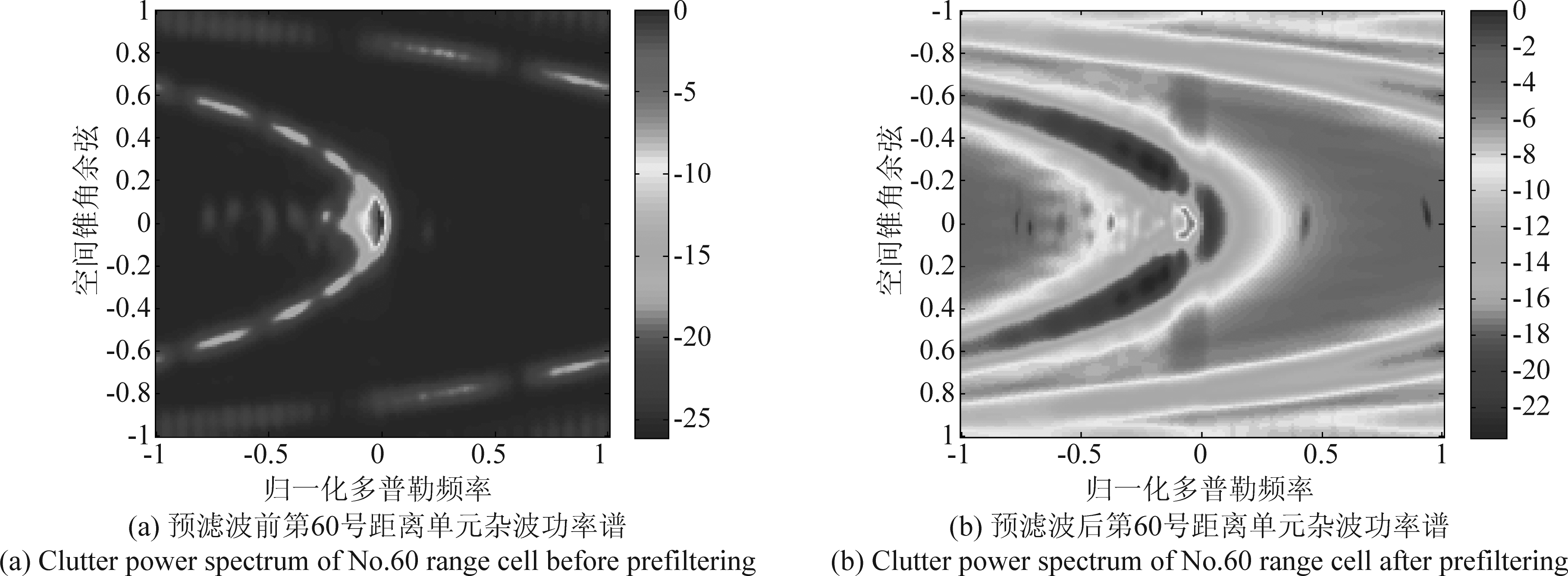
图5 预滤波前后第60号距离单元杂波功率谱对比图
Fig.5 Clutter power spectrum comparison of No.60 range cell before and after prefiltering
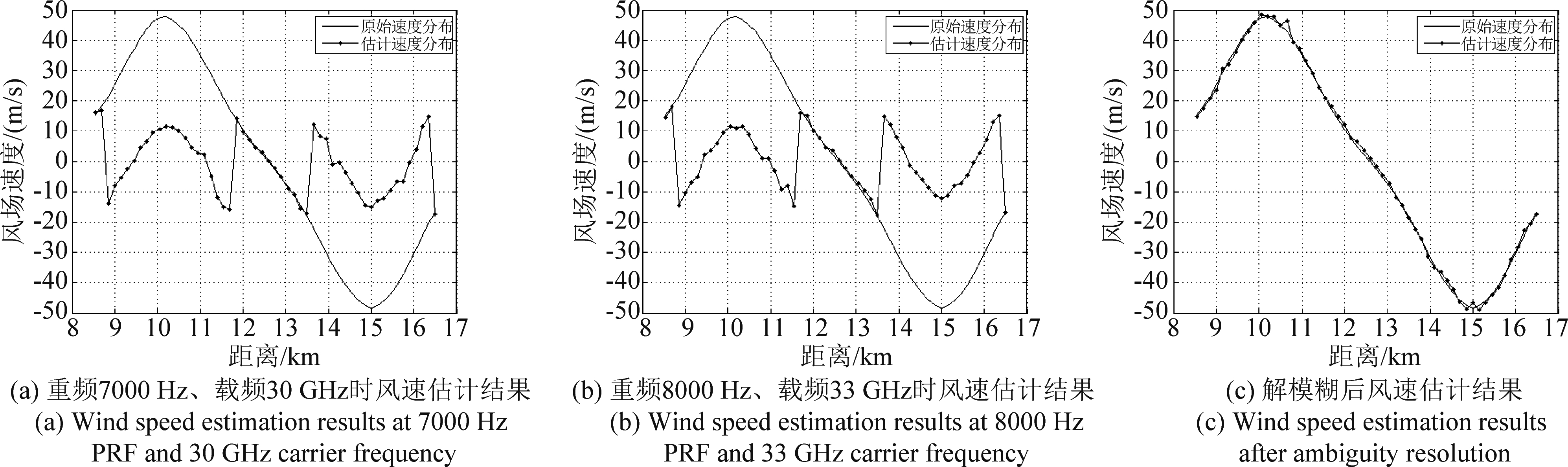
图6 解模糊前后风速估计结果比较
Fig.6 Comparison of wind speed estimation results before and after ambiguity resolution
图7为对厘米波段信号采用本文方法得到的解模糊前后风场速度估计结果对比图。对表2中仿真参数进行修改,载频采用6 GHz、9.3 GHz,相应的脉冲重复频率分别为2000 Hz、3000 Hz,其他参数保持不变。图7(a)为重频2000 Hz、载频6 GHz时得到的风场速度估计结果,此时系统可测的最大不模糊速度为25 m/s,因此,风速的估计结果在±25 m/s的范围之外出现了跳变,即出现了速度模糊。图7(b)为重频3000 Hz、载频9.3 GHz时得到的风场速度估计结果,此时系统可测的最大不模糊速度为24 m/s,则风场速度的估计值在超过±24 m/s时也发生了跳变,出现了模糊现象。图7(c)为采用错位差分查表法解模糊后得到的风速估计结果,可以看出估计的风场速度很好的逼近了原始风场速度分布,计算得到风速估计的均方根误差为2.4516 m/s。由此可以说明本文所提方法不仅适用于毫米波段,对其他微波频段同样适用。
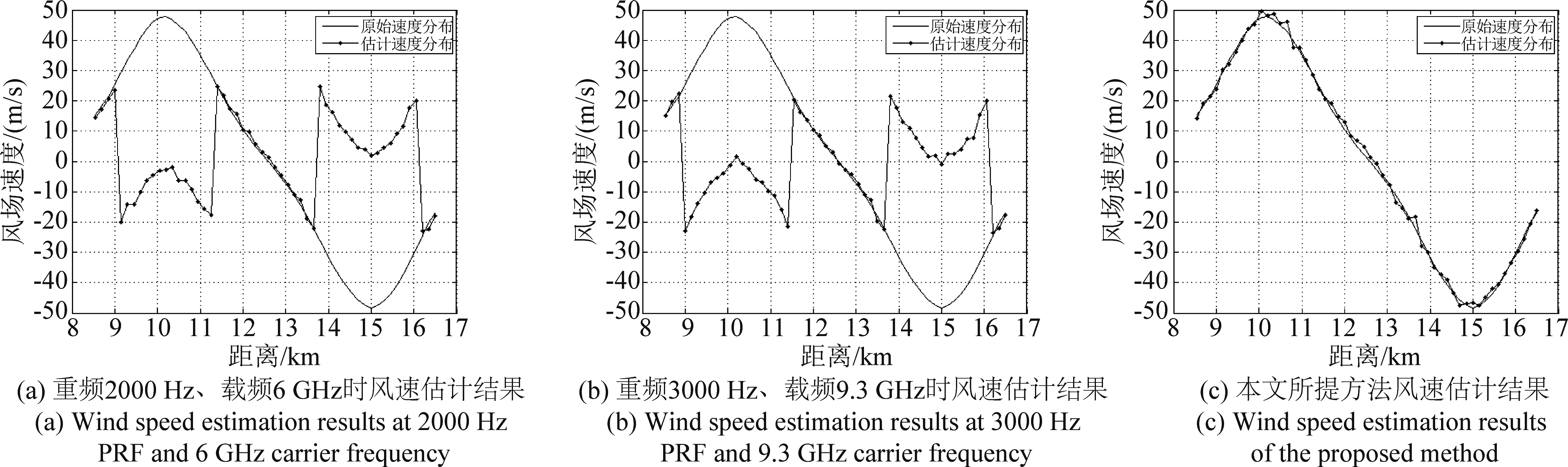
图7 厘米波段信号解模糊前后风速估计结果比较
Fig.7 Comparison of wind speed estimation results before and after ambiguity resolution of centimeter wave signal
图8为不同方法下解速度模糊估计结果对比图。经计算可得采用孙子定理法得到的风速估计均方根误差为2.9774 m/s,采用一维集算法得到的风速估计均方根误差为2.3102 m/s,而本文所提方法的均方根误差为2.2037 m/s,小于其他两种方法。从算法计算量来看,以两重频为例,孙子定理法需要将其中一重频下的每个速度可能值与另一重频的所有速度可能值进行减法运算,计算量较大;一维集算法首先需要将两重频下的所有速度可能值从小到大进行排序,之后以每两个频率值为一组计算方差和均值,计算量更大;而本文所提方法建立速度模糊表,采用错位差分的方式进行搜索,减法计算的次数小于孙子定理法,且不需要像一维集算法那样计算方差,因而更适合实时处理。
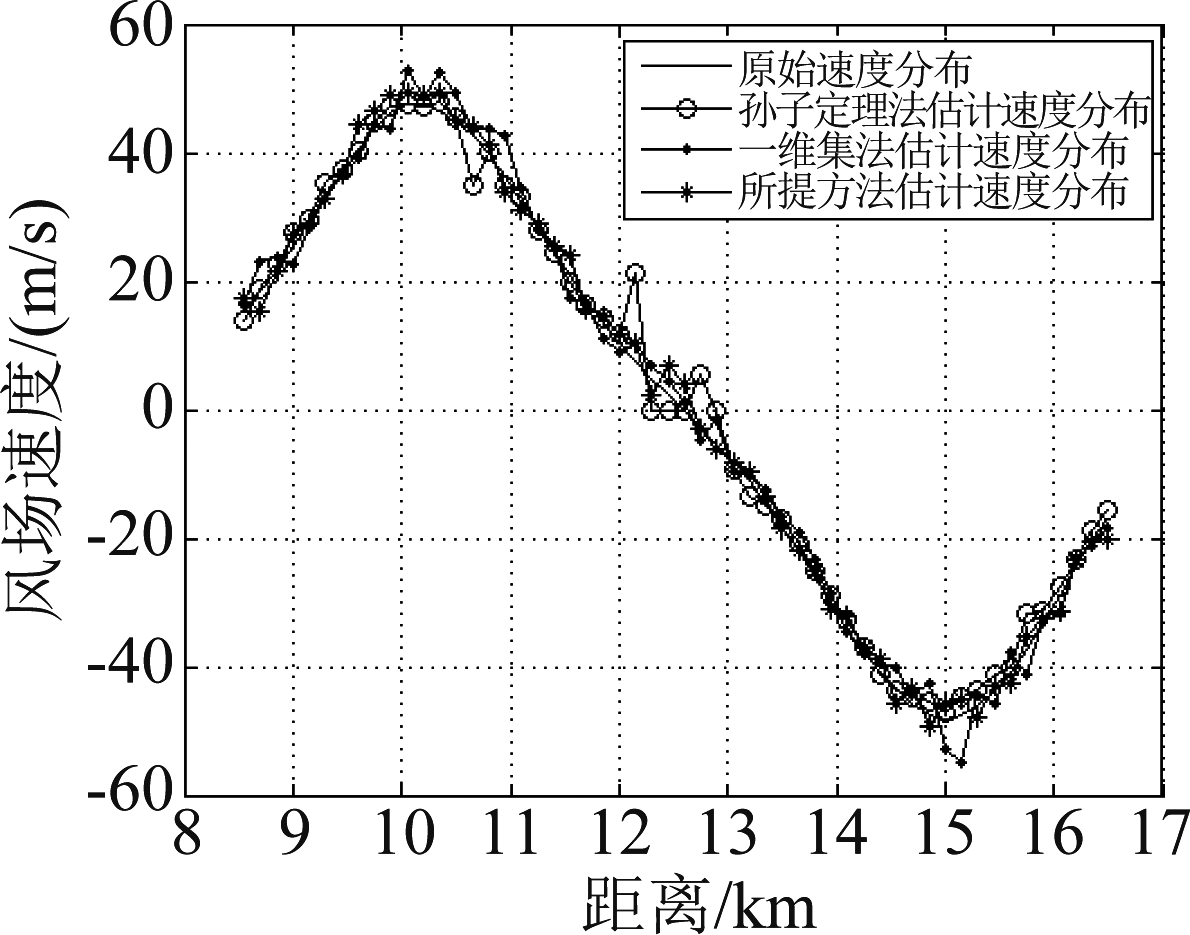
图8 不同方法下解速度模糊结果对比
Fig.8 Comparison of the results of solving speed ambiguity with different methods
7 结论
针对机载气象雷达下视探测低空风切变时,强烈的电磁干扰以及地杂波会降低其对目标检测性能,导致风场速度估计不准的问题,本文提出一种毫米波捷变频体制下的低空风切变风速估计方法。该方法首先在每个脉组内利用系统工作参数等先验信息构造TDPC预滤波器对雷达回波进行预滤波;然后构造组合空时主通道降维联合空时变换处理器对回波数据进行空时二维滤波,得到风切变信号的模糊多普勒估计值;最后将每个脉组的估计结果从多普勒频率域转换到速度域,采用错位差分查表的方式求解风场的真实速度值。仿真结果表明,所提方法可以有效的实现低空风切变的风速估计。
[1] LI Hai, ZHOU Meng, GUO Qinghua, et al. Compressive sensing-based wind speed estimation for low-altitude wind-shear with airborne phased array radar[J]. Multidimensional Systems and Signal Processing, 2016, 29(7): 1-14.
[2] FALCONI M T, MARZANO F S. Weather Radar Data Processing and Atmospheric Applications: An overview of tools for Monitoring Clouds and Detecting Wind Shear[J]. IEEE Signal Processing Magazine, 2019, 36(4): 85-97.
[3] BARBER S, PARAMORE S, WOODELL D L. Airborne Weather Radar System and Radar Display[P]. US patent: 7109913B1, 2006-09-19.
[4] 汪洋. 毫米波雷达目标检测及恒虚警处理研究[D]. 广州: 广东工业大学, 2019.
WANG Yang. Research on Target Detection and Constant False Alarm Processing of Millimeter Wave Radar[D]. Guangzhou: Guangdong University of Technology, 2019.(in Chinese)
[5] 王瑞昕. 基于毫米波雷达的多目标检测与跟踪技术研究[D]. 西安: 西安电子科技大学, 2019.
WANG Ruixin. Research on Multi-target Detection and Tracking Based on Millimeter Wave Radar[D]. Xi’an: Xi’an University of Electronic Science and Technology, 2019.(in Chinese)
[6] 余正冬. W波段捷变频雷达频率源相参测试技术研究[D]. 成都: 电子科技大学, 2010.
YU Zhengdong. Research on coherent measurement technology of frequency source of W-band frequency agile radar[D]. Chengdu: University of Electronic Science and Technology, 2010.(in Chinese)
[7] 王永良, 彭应宁. 空时自适应处理[M]. 北京: 清华大学出版社, 2000: 46.
WANG Yongliang, PENG Yingning. Space time adaptive processing[M]. Beijing: Tsinghua University Press, 2000: 46.(in Chinese)
[8] 吴仁彪, 张彪, 李海, 等. 基于空时自适应处理的低空风切变风速估计方法[J]. 电子与信息学报, 2015, 37(3): 631- 636.
WU Renbiao, ZHANG Biao, LI Hai, et al. Wind speed estimation method of low-altitude wind-shear based on space-time adaptive processing[J]. Journal of Electronics and Information, 2015, 37(3): 631- 636.(in Chinese)
[9] LI Hai, ZHOU Meng, WU Renbiao, et al. Wind Speed Estimation of Low-Altitude Wind-Shear Based on Multiple Doppler Channels Joint Adaptive Processing[C]∥IEEE International Conference on Acoustics, Speech and Signal Processing. Shanghai: IEEE, 2016: 3116-3120.
[10] LI Yijing, LI Hai, WU Renbiao. Wind Speed Estimation of Low-altitude Wind-Shear Based on Generalized Adjacent Multi-Beam Space-Time Adaptive Processing under Aircraft Yawing[C]∥IEEE International Conference on Speech and Signal Processing. Beijing: IEEE, 2018: 220-223.
[11] 崔伟芳. 高速目标解模糊方法及机载雷达演示系统[D]. 西安: 西安电子科技大学, 2014.
CUI Weifang. Ambiguity Resolution of High Speed Target and Demonstration System of Airborne Radar[D]. Xi’an: Xi’an University of Electronic Science and Technology, 2014.(in Chinese)
[12] 刘志英. 基于剩余定理和一维集法的PD雷达解模糊处理[J]. 现代电子技术, 2012, 35(9): 28-30.
LIU Zhiying. Ambiguity resolution for PD radar with remainder theorem and one-dimensional set algorithm[J]. Modern Electronic Technology, 2012, 35(9): 28-30.(in Chinese)
[13] 马超, 王丹, 李毓琦. 一维集筛选法解高速运动目标距离模糊[J]. 制导与引信, 2012, 33(2): 1-5.
MA Chao, WANG Dan, LI Yuqi. The One-Dimensional Algorithm Applied on Resolving Range Ambiguity in High-speed Target[J]. Guidance and Fuze, 2012, 33(2): 1-5.(in Chinese)
[14] 曹杨, 冯大政, 水鹏朗, 等. 机载多输入多输出雷达脉冲相消杂波抑制方法[J]. 电子与信息学报, 2013, 35(3): 595- 600.
CAO Yang, FENG Dazheng, SHUI Penglang, et al. Clutter Suppression of Pulse-to-Pulse Canceller in Airborne MIMO Radar[J]. Journal of Electronics and Information, 2013, 35(3): 595- 600.(in Chinese)
[15] GUERCI J R. Space-time adaptive processing for radar[M]. Norwood, MA: Artech House Press, 2003: 3-55.
[16] 张森. 一种用于PD体制频率捷变雷达的解模糊方法[J]. 科技资讯, 2015, 13(6): 4-5.
ZHANG Sen. A method of ambiguity resolution for PD frequency agile radar[J]. Technology Information, 2015, 13(6): 4-5.(in Chinese)
[17] 陈亚方, 柴晋飞, 徐晓天, 等. 捷变频脉冲雷达解速度模糊算法研究[J]. 空军雷达学院学报, 2012, 26(6): 409- 411.
CHEN Yafang, CHAI Jinfei, XU Xiaotian, et al. Algorithm for Resolving Velocity Ambiguity of Frequency-agile Pulse Radar[J]. Journal of Air Force Radar Institute, 2012, 26(6): 409- 411.(in Chinese)
