1 引言
高光谱图像解混(Hyperspectral Unmixing,HU)是对高光谱图像预处理和分析的一种技术,是许多遥感和地球观测应用的基础和核心[1]。由于高光谱成像仪设备空间分辨率有限,在自然场景中通常存在混合像元[2]。混合像元由不同纯物质(端元)的光谱[3]以相应的组成分量(丰度系数)混合而成,而HU就是从混合像元中提取端元并计算各个端元在混合像元中所占的比例[4]。
稀疏解混(Sparse Unmixing,SU)技术[7]是在提取端元时,将观察到的图像建模为具有先验估计的大型线性端元库[5],然后采用稀疏回归[6]方法来估计端元丰度的技术,代表性的研究有:Iordache等人提出了基于增广拉格朗日稀疏回归模型的光谱解混(Sparse Unmixing via Variable Splitting and Augmented Lagrangian,SUnSAL)算法[8],由于该算法仅考虑了l2,1稀疏性,解混结果不够准确。进而,2012年Iordache等人又提出了总变差空间正则化的稀疏解混[9](Total Variation Spatial Regularization for Sparse Hyperspectral Unmixing,SUnSAL_TV)算法,基于丰度矩阵的行向量,在不损害相邻像素之间尖锐性的同时也表示出了某物质丰度图的分段平滑性,从而提高了解混效果。2014年Iordache等人又提出了基于协同稀疏回归的高光谱解混(Collaborative SUnSAL,CLSUnSAL)算法[10],利用丰度系数的行稀疏特性进一步提高了解混精度。尽管标准的稀疏解混方法在高光谱图像解混方面取得了成功,但是大型频谱库的使用会导致解混问题变得复杂,并且对存在的噪声和异常值非常敏感。针对异常值问题,2015年Xu等人提出了采用l2,1范数的鲁棒稀疏解混(Robust Sparse Hyperspectral Unmixing With l2,1Norm,RSU)算法[11],虽然一定程度上可以抵抗噪声和离群值敏感性,提高了解混的鲁棒性,但是由于该算法忽略了像素之间的空间关系,解混精度并没有提高。因此,2019年Li等人基于RSU算法提出了保持局部像素相似性(Local Spectral Similarity Preserving, LSSP)的方法[12],利用像素级差异指导丰度级差异,极大地提高了解混精度,但也忽略了局部像素的光谱相似性对高光谱解混的影响。
此外,也有许多研究引入了超像素分割的方法将相似的局部像素分割成多个有意义的同质区域,从而获取到更精细的图像空间信息。在众多超像素分割算法中,简单线性迭代聚类(Simple Linear Iterative Clustering,SLIC)算法[13]在计算速度和存储效率方面具有更好的分割性能,因此在高光谱图像解混中得到了广泛应用[14]。2018年Ricardo等人提出了多尺度稀疏解混(A Fast Multiscale Spatial Regularization for Sparse Hyperspectral Unmixing,MSU)算法[15],先将高光谱图像分割成超像素进行粗域解混,再利用粗域解混结果指导原始域解混。该算法缩短了解混时间,但是解混精度和鲁棒性均较低。2019年Zhang等人提出了超像素指导的稀疏解混(Superpixel-Guided Sparse Unmixing,SPGSU)算法[16],该算法利用了光谱空间信息的SU框架,结合光谱和空间双重加权因子[17]对超像素内的像素进行加权以增强解混结果的稀疏性,从而提高了解混精度,但是忽略了超像素之间的空间信息对解混结果的影响并且算法复杂性较高。
综上,现有的结合空间信息的高光谱图像稀疏解混方法大多忽略了局部像素的光谱相似性[18],或者引入超像素分割算法来提高解混精度,但解混复杂度也随之提高。针对上述问题,本文提出了一种多尺度光谱相似性指导的高光谱解混算法。首先,使用SLIC算法将高光谱图像中相似像素分割成超像素来表征光谱图像的空间信息;然后,提出一种稀疏矩阵来表示相邻超像素的空间关系,并作为近似域的约束进行近似域解混来提高解混精度;最后,将近似域的解混结果转换到原始域并结合实际像素光谱进行原始域的逐像素精确解混。另外,在本文中还引入了l2,1范数来加强丰度矩阵的稀疏性,以考查不同约束对所提算法结果的影响。实验结果表明,相比于其他算法,本文提出的算法所得的丰度图与真实的丰度图更相似,解混精度更高,解混复杂度也明显低于SPGSU算法。
本文的其余部分安排如下:第2节详细描述了本文总体框架、所提算法思路和具体实现步骤;第3节对合成的模拟数据集和真实高光谱图像数据进行了本文所提算法与比较算法的解混实验;最后第4节给出结论。
2 多尺度光谱相似性指导的高光谱解混算法
2.1 高光谱图像稀疏解混
在高光谱图像中,假设观测数据的光谱特征可以表示为纯光谱特征的线性组合[19],使用频谱库可以将线性光谱解混(Linear Spectral Unmixing,LSU)模型扩展到以下SU模型:
Y=AX+E
(1)
其中,Y∈RL×N表示高光谱图像(L为波段数,N为每个波段图像中的像素总数);A∈RL×P,P为光谱库中地物光谱数目;X∈RP×N为光谱库A对应的丰度系数矩阵,E∈RL×N是系统噪声。根据基于光谱库的高光谱混合像元解混机理[20],A中的光谱数远大于实际的端元个数,即X中非零系数的个数小于等于P,X的每一列x是一个稀疏向量。这种稀疏性能够提高高光谱混合像元解混的准确性,因此将解混问题公式化为l0优化问题。
(2)
其中,第一项为重构误差项,第二项为稀疏性约束项;![]() 为Frobenius范数;||X||0是X的l0范数,计算X中非零元素的个数;X≥0表示X中每个元素均非负,满足“非负性”约束(Abundance non-negativity constraint,ANC);1TX=1表示X每一列满足“和为一”约束(Abundance sum-to-one constraint, ASC),1T∈RP×1且各元素全为1;λ是正则化参数。
为Frobenius范数;||X||0是X的l0范数,计算X中非零元素的个数;X≥0表示X中每个元素均非负,满足“非负性”约束(Abundance non-negativity constraint,ANC);1TX=1表示X每一列满足“和为一”约束(Abundance sum-to-one constraint, ASC),1T∈RP×1且各元素全为1;λ是正则化参数。
然而,根据稀疏表示理论,l0范数求解困难。因此,使用l1范数代替l0范数放松约束的稀疏度,所得目标函数为:
(3)
其中,![]() 代表X的第k行)表示矩阵元素之和。
代表X的第k行)表示矩阵元素之和。
2.2 本文算法总体框图与具体步骤
2.2.1 本文算法总体框图
图1为本文算法的框架图,本文将解混问题分解为两个简单步骤:第一步在近似图像域中利用相邻超像素之间差异性的稀疏矩阵作为近似域的解混约束进行近似域解混,第二步在原始图像域中结合实际像素光谱作为原始域的约束进行逐像素解混。
2.2.2 多尺度光谱相似性指导的高光谱解混模型
实际情况中,高光谱图像的空间分辨率较低,无法精确表示空间结构,而采用超像素分割的方法将高光谱图像分割为近似域图像进行处理,再转换到原始域以获取到更精细的图像空间信息,可以提高解混的准确性。因此,本文引用多尺度的高光谱解混方法。
设线性算子W∈RN×n来实现原始域到近似域的空间变换[15],并计算YW得到每个超像素内部所有像素矢量的平均值,从而捕获空间相关性并减少噪声的影响。
YC=YW,XC=XW
(4)
其中,YC∈RL×n为超像素分割后的近似域光谱图像,XC∈RP×n为分割后的丰度近似矩阵。
高光谱图像采用超像素分割时,同种地物可能被分割为多个超像素表示,导致相邻超像素之间存在光谱相似性,利用相邻超像素的这种相关性,可以有效提高解混的准确性。进一步分析相邻超像素间的空间相关性,可以发现这种相关性与像元间空间相关性类似,丰度系数矩阵都具有稀疏性。由此提出一种稀疏矩阵表示相邻超像素之间的空间关系,更能有效的刻画近似域丰度系数的稀疏模式,具有更强的稀疏性。

图1 多尺度光谱相似性指导的高光谱解混算法框图
Fig.1 The process of hyperspectral sparse unmixing based on multi-scale spectral similarity guidance
本文所提出的近似域稀疏解混模型可表示如下:
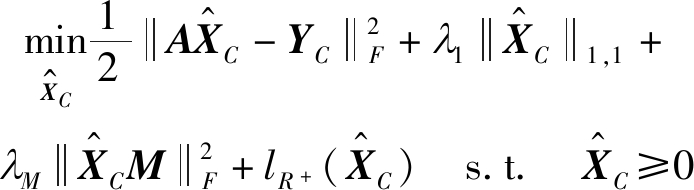
(5)
其中,![]() 表示近似域解混后的丰度矩阵;M∈Rn×n表示计算相邻超像素空间关系的稀疏矩阵,近似域空间关系表示为
表示近似域解混后的丰度矩阵;M∈Rn×n表示计算相邻超像素空间关系的稀疏矩阵,近似域空间关系表示为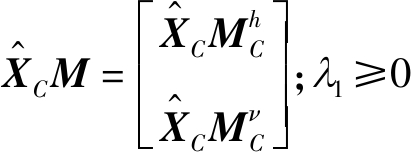 和λM≥0分别为l1,1稀疏约束项和近似域丰度系数矩阵稀疏正则项的正则化参数;lR+(X)表示“非负性”约束,
和λM≥0分别为l1,1稀疏约束项和近似域丰度系数矩阵稀疏正则项的正则化参数;lR+(X)表示“非负性”约束,![]() 表示X的第i行、第j列元素,当Xi, j为非负时lR+(Xi, j)=0,当Xi, j为负数时lR+(Xi, j)=+∞。
表示X的第i行、第j列元素,当Xi, j为非负时lR+(Xi, j)=0,当Xi, j为负数时lR+(Xi, j)=+∞。
M的具体定义为:![]() 为相邻超像素之间水平差的线性算子,则超像素水平方向上的空间关系为
为相邻超像素之间水平差的线性算子,则超像素水平方向上的空间关系为![]() 其中
其中![]() 和ih表示某一超像素及其水平相邻超像素的索引值;
和ih表示某一超像素及其水平相邻超像素的索引值;![]() 为相邻超像素之间垂直差的线性算子,则超像素垂直方向上的空间关系为
为相邻超像素之间垂直差的线性算子,则超像素垂直方向上的空间关系为![]() 其中
其中![]() 和iν表示像素及其垂直相邻像素的索引值。
和iν表示像素及其垂直相邻像素的索引值。
原始域解混时,由于在实际情况中,两个相邻像素的端元相似度越高,相应的丰度系数的相似度也越高。因此,本文使用像素级差异来加权丰度级差异的空间约束,从而提高原始域的解混的精确度。
本文所提出的原始域逐像素解混模型如下:
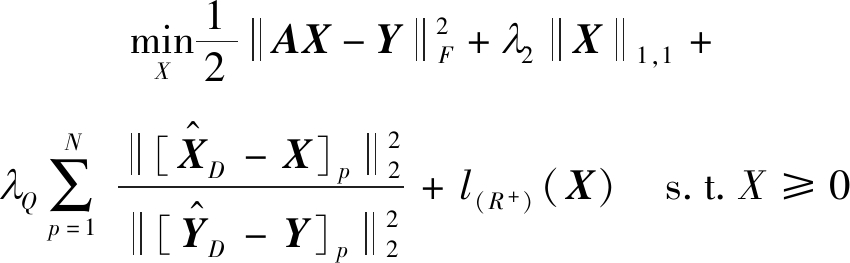
(6)
其中,![]() 是原始域的近似丰度矩阵;
是原始域的近似丰度矩阵;![]() 是超像素转换到原始域后的估计像素矩阵;
是超像素转换到原始域后的估计像素矩阵;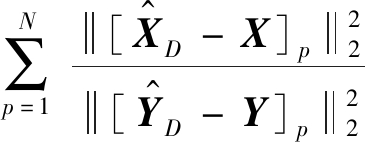 表示近似域解混结果结合实际像素光谱对原始域进行逐像素的解混,
表示近似域解混结果结合实际像素光谱对原始域进行逐像素的解混,![]() 表示近似图像与原始图像之间像素级别的差异;
表示近似图像与原始图像之间像素级别的差异;![]() 表示近似域丰度系数与原始丰度系数的差异,[a]p表示逐像素,p=1,2,…,N,λ2≥0和λQ≥0分别为l1,1稀疏约束项和原始域约束正则项的正则化参数。
表示近似域丰度系数与原始丰度系数的差异,[a]p表示逐像素,p=1,2,…,N,λ2≥0和λQ≥0分别为l1,1稀疏约束项和原始域约束正则项的正则化参数。
为进一步加强稀疏性的讨论,本文还采用l2,1范数对解混模型中的丰度矩阵X进行约束求解,l2,1范数[11]的计算公式为:
(7)
由公式可以看出l2,1范数实际是求X每一行的l2范数,然后再求l1范数,即l2,1范数更要求行稀疏性。因此,本文将传统稀疏解混模型中对丰度矩阵的l1,1约束替换为l2,1约束,下文分别用Proposed1和Proposed2表示l1,1约束和l2,1约束的实验结果。
近似域解混模型:
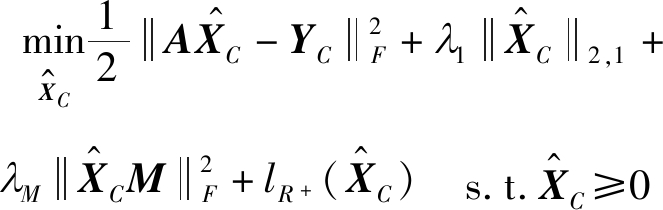
(8)
原始域解混模型:
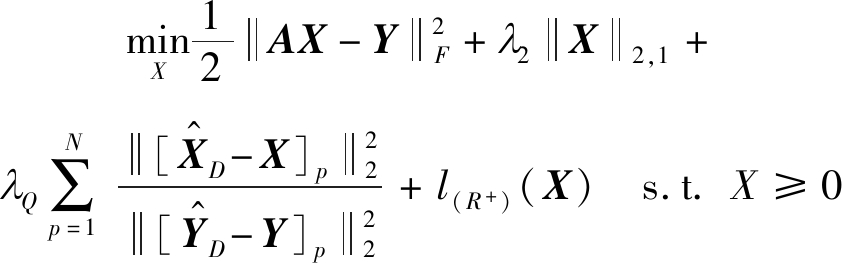
(9)
2.3 模型求解
对于式(5)和式(6)的求解,本文采用交替方向乘子法[21](Alternating Direction Method of Multipliers,ADMM)进行优化。
2.3.1 近似域解混求解过程
首先,通过添加辅助矩阵P1、W1、R和U1来表示式(5),再进行ADMM优化:
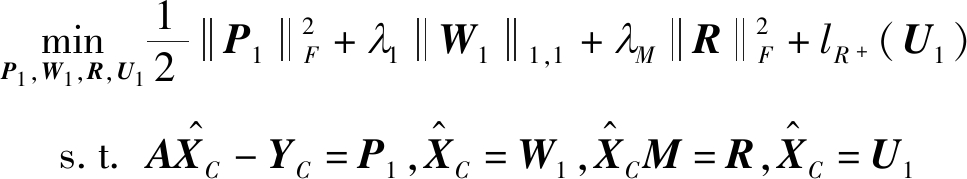
(10)
式(10)中引入辅助变量,降低求解问题的复杂性,并用符号E(U1,V)表示如下:
![]()
![]()
(11)
则最优化问题(10)为约束最小化问题,其增广拉格朗日方程为:
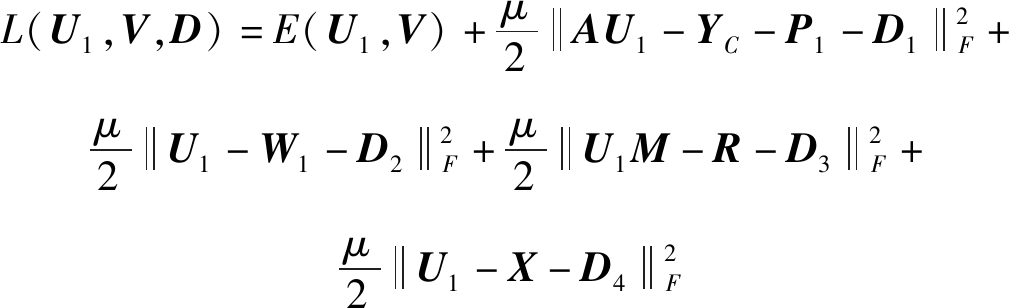
(12)
迭代参数的具体更新过程如下:
1)更新P1时,可以忽略与式(12)中P1无关的项,其相应的优化问题变为:
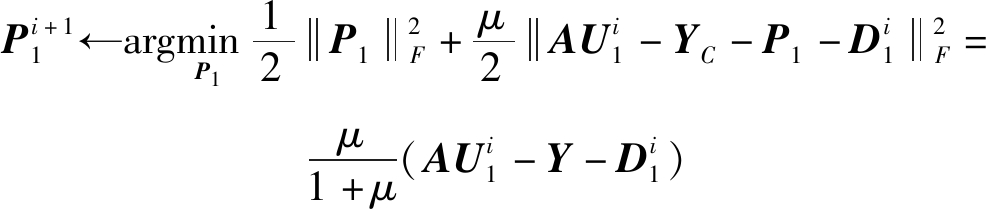
(13)
2)更新W1时,其优化问题变为:
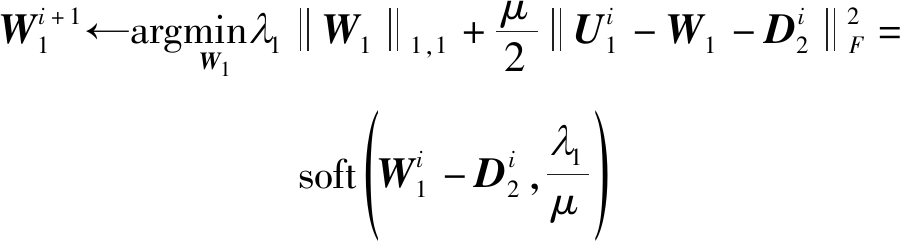
(14)
其中![]()
3)更新R时,其优化问题变为:
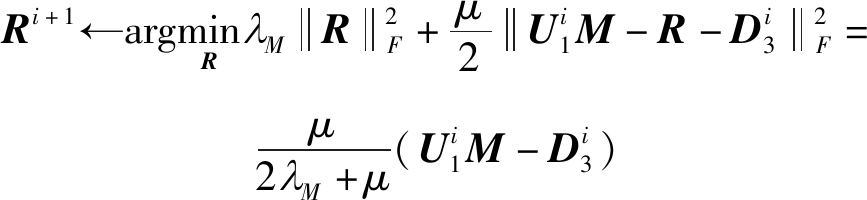
(15)
4)X的更新公式为:
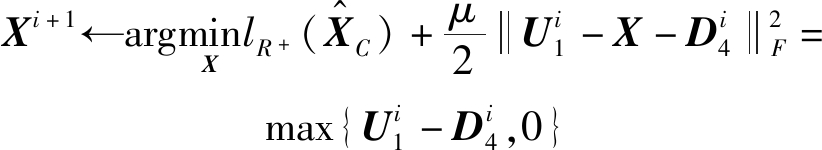
(16)
5)U1优化问题的解决方法为:
![]()
![]()
![]()
![]()
(17)
其中,Dk表示拉格朗日乘数。
表1 算法1 ADMM求解过程
Tab.1 Algorithm 1 ADMM solution process

2.3.2 原始域解混求解过程
同理,通过添加辅助矩阵P2、W2、Q、B和U2来表示式(6),并进行ADMM优化,将优化问题表示为:
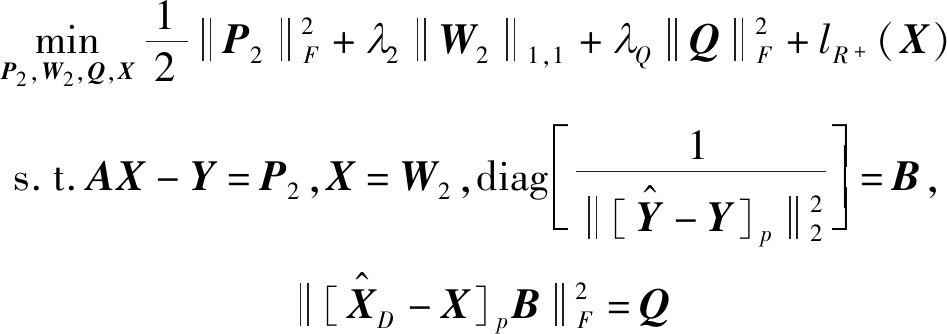
(18)
![]()
s.t. V≡(P2,W2,Q,X)
(19)
则最优化问题(6)的增广拉格朗日方程为:
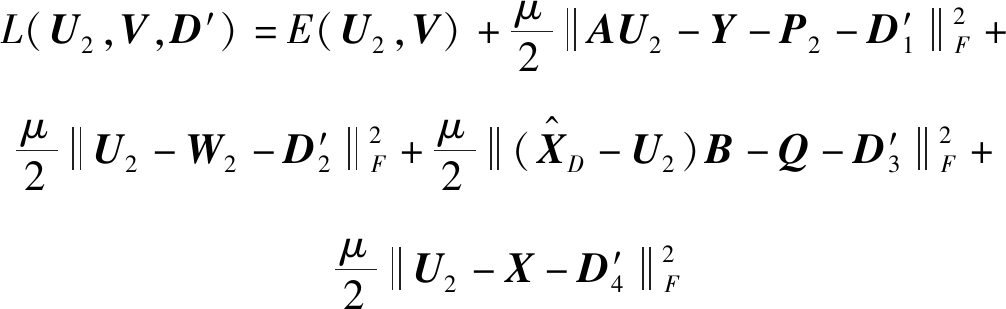
(20)
式(20)中迭代参数的具体更新过程如表2。
表2 算法2 ADMM求解过程
Tab.2 Algorithm 2 ADMM solution process

该算法近似域的停止准则为||AU1+2U1+U1M-YC-P1-W1-R-X![]() ≤σ1,原始域的停止准则为||AU2
≤σ1,原始域的停止准则为||AU2![]() 其中σ1、σ2≥0表示误差容忍度。当达到最大迭代次数或满足上述停止准则时,则停止迭代。在ADMM计算过程中阈值参数μ对最终收敛速度有较大影响,在迭代中不断地更新μ值,可以使原始残差和对偶残差之间的比率保持在一定范围内。
其中σ1、σ2≥0表示误差容忍度。当达到最大迭代次数或满足上述停止准则时,则停止迭代。在ADMM计算过程中阈值参数μ对最终收敛速度有较大影响,在迭代中不断地更新μ值,可以使原始残差和对偶残差之间的比率保持在一定范围内。
3 实验与分析
为验证本文算法的有效性,分别采用模拟数据和真实数据进行了实验。在这些实验中,将本文算法与其他几种解混算法进行比较,分别为SUnSAL[8]、SUnSAL_TV[9]、MSU中的SLIC_spreg[15]、S2WSU[22]、RSU[11]和SPGSU[16],其中SLIC_spreg和SPGSU都采用超像素分割来表示空间信息;SUnSAL_TV和S2WSU则是采用简单结构表示空间信息。
1)本文的模拟高光谱数据集与SUnSAL_TV[9]中采用的模拟数据集为相同的合成方式,它包含224个光谱,每个光谱包含75×75个像素。图2显示了DC1数据集的5个端元分别对应的丰度图,分别用不同的颜色表示。
2)本文真实数据集采用Samson数据集[15]和Cuprite数据集[9],Samson数据集是通过高光谱Samson传感器获得的,该数据集的光谱分辨率为3.2 nm,其大小为95×95×156,光谱范围为400~900 nm,具有三个主要成分,即土壤、树木和水。Cuprite数据集已经被广泛用于高光谱图像解混的研究中,在本实验中选择了该数据集190×140的像素子集,以及0.4~2.5 μm之间的224个光谱带。

图2 DC1模拟数据5个端元的真实丰度图
Fig.2 The true abundance graph of the 5 terminal elements of DC1 simulation data
3.1 实验结果衡量指标与数据设置
3.1.1 实验结果衡量指标
对于模拟数据集,本文采用信号重建误差[5](Signal-to-Reconstruction Error,SRE)进行定量评估算法性能,具体定义为:
(21)
其中,x为真实丰度矢量,![]() 解混算法重建的丰度矢量,SRE值越大,丰度估计结果越准确。
解混算法重建的丰度矢量,SRE值越大,丰度估计结果越准确。
由于真实数据集没有真实丰度数据用于计算SRE值,所以通常采用均方根误差[5](Root Mean Square Error,RMSE)来定量评估真实高光谱图像的解混结果。高光谱图像的RMSE值可以通过如下公式计算:
(22)
其中,![]() 为解混后重建的光谱图像
为解混后重建的光谱图像![]() 值越小表示解混后的重构精度越好。
值越小表示解混后的重构精度越好。
3.1.2 实验数据设置
1)对于模拟数据集,本文在三种不同级别的信噪比(Signal-to Noise Ratio,SNR)下进行解混实验,即20 dB、30 dB和40 dB。表3为本文在不同信噪比下设置的正则项参数。
表3 不同SNR对应的参数值
Tab.3 Parameter values corresponding to different SNRs

表4为DC1数据集在不同信噪比下采用不同超像素分割尺寸的实验结果,当SLIC分割尺寸设置为6像素时,解混效果达到最好,此时该数据集被分割成169个超像素。
2)对于Samson数据集,如图3所示本文在多次实验得到分割尺寸为10像素时,解混效果最好。图4为本文算法四种正则化参数λ1、λ2、λM和λR的不同取值对算法性能的影响,由图中可见四种参数分别取3e-3、3e- 4、1e-3和3e-3时,得到较好的解混结果。
表4 不同SLIC分割尺寸在不同SNR下的解混结果
Tab.4 Unmixing results of different SLIC_size under different SNR
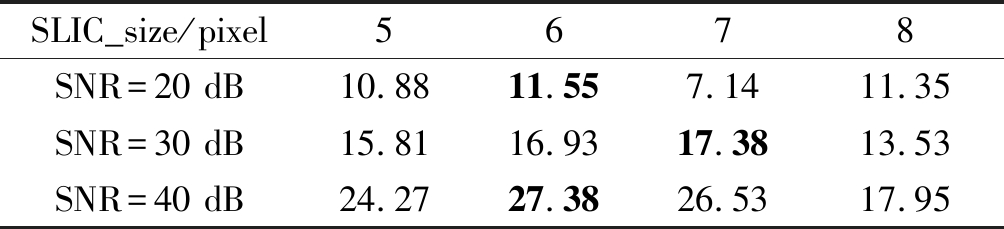
SLIC_size/pixel5678SNR=20 dB10.8811.557.1411.35SNR=30 dB15.8116.9317.3813.53SNR=40 dB24.2727.3826.5317.95
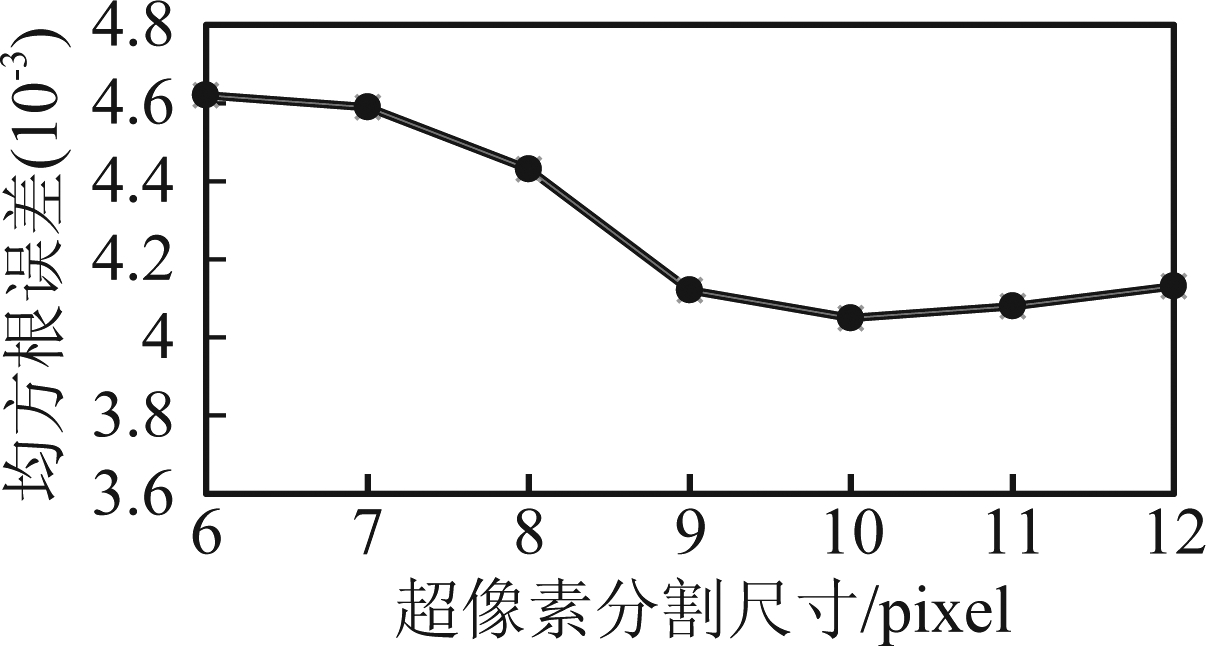
图3 不同超像素分割尺寸得到的RMSE值
Fig.3 RMSE obtained by different SLIC_size
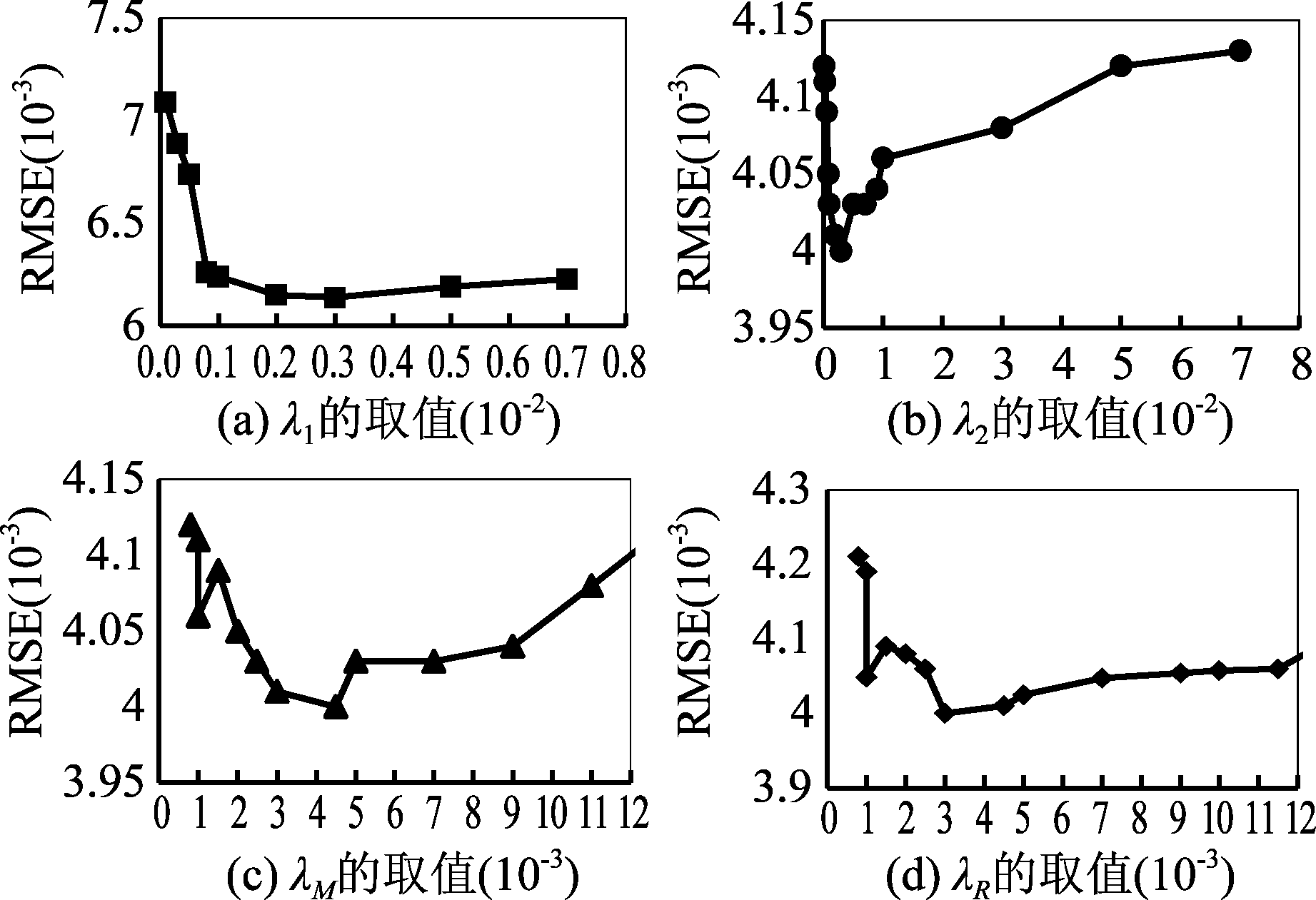
图4 四种正则化参数的不同取值对应的实验结果
Fig.4 Experimental results corresponding to different values of the four regularization parameters
本文对比算法的正则化参数采用原文献中推荐的参数设置,则λ在SUnSAL、S2WSU、SPGSU和RSU中分别设置为1e-3、2e-3、2e-3和1e-2,SUnSAL-TV中的参数λ和λTV分别设置为5e- 4和3e-3。本文算法的参数λ1、λ2、λM和λR分别设置为5e- 4、5e- 4、4.5e-3和3e-3。此外,拉格朗日乘数正则化参数μ、最大迭代次数和容错值分别设置为1e- 4、2e3和1e- 6。为提高实验结果的可靠性,每组数据重复进行20次,取其平均值为最终结果。
3.2 模拟数据集实验结果分析
1)近似域解混结果分析
图5为DC1数据集的真实丰度和近似域解混得到的估计丰度,图中X0为原始数据集的丰度,Spreg_X0和Proposed_X0分别为SLIC_spreg和本文算法在SNR=30 dB时得到的近似域解混丰度。由图中可见本文采用相邻超像素空间信息约束得到的丰度更接近X0,证实了本文在近似域采用相邻超像素空间信息作为约束解混的必要性。
表5 各算法在不同SNR下得到的SRE (dB)值(Proposed1为l1,1范数,Proposed2为l2,1范数)
Tab.5 SRE (dB) obtained by different algorithms under different SNR (Proposed1 is l1,1-norm, Proposed2 is l2,1-norm)

SNR/dBSUnSALSUnSAL_TVS2WSURSUSLIC_spregSPGSUProposed1Proposed220dB1.2169.4237.6974.5455.3387.104511.551812.84030dB7.00314.44015.4864.88316.11414.23116.932522.85940dB11.09822.09025.4618.06923.06024.56127.385124.005
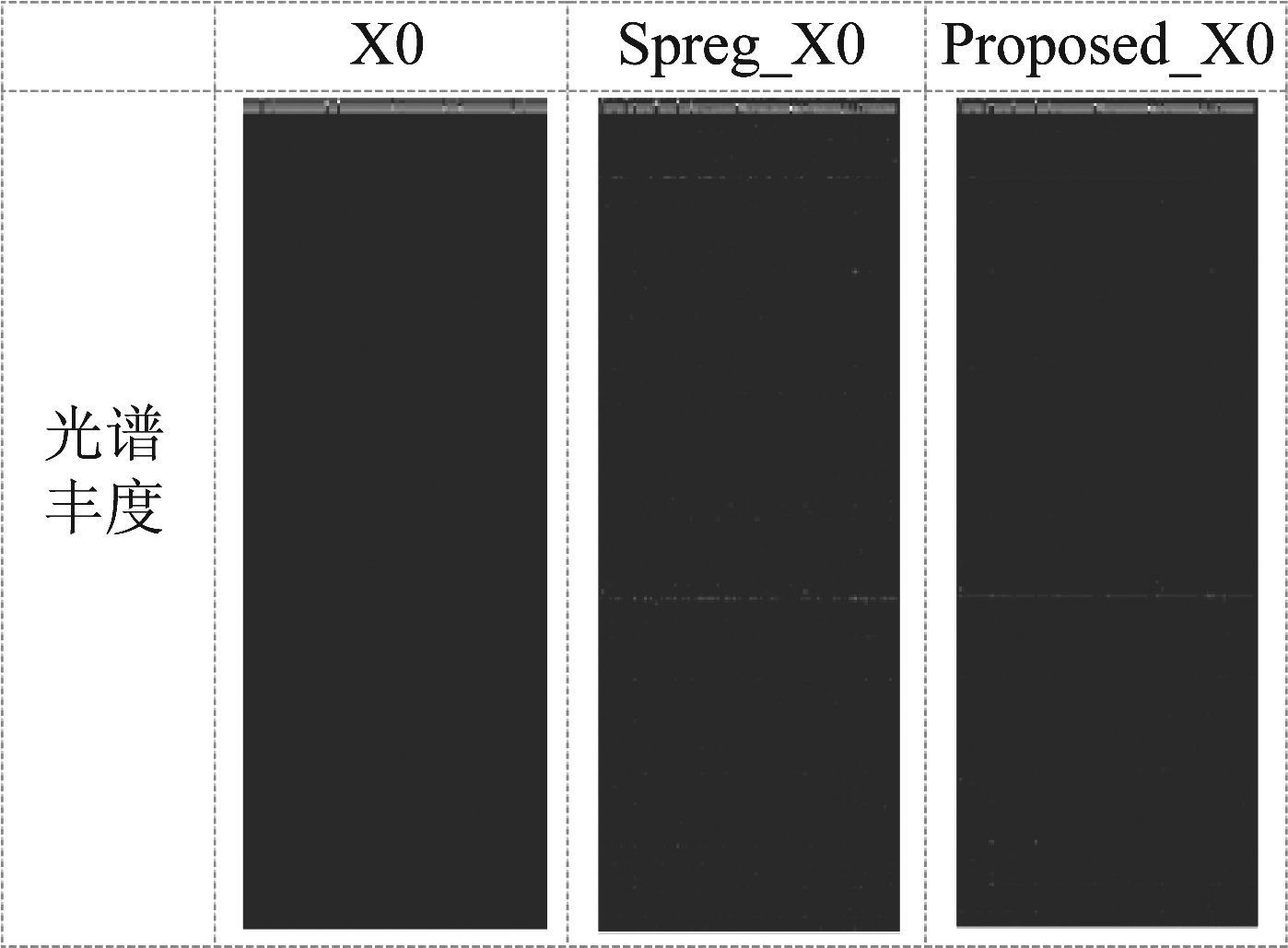
图5 DC1数据集的真实丰度和近似域解混得到的估计丰度
Fig.5 Ground-truth and estimated abundances obtained by unmixing the approximate domain of the DC1
2)原始域解混结果分析
为了更直观地显示解混的效果,图6为本文提出的算法在近似域和原始域是否添加了约束条件时的解混结果对比,图中(a)为近似域与原始域都未加约束的实验结果,(b)为近似域加了空间相关性约束而原始域未加约束的实验结果,(c)为近似域未加约束而原始域加了像元指导的约束实验结果,(d)为近似域与原始域都加了约束的实验结果,由图中四种情况下实验结果的端元丰度图和SRE值可知,本文在近似域添加空间约束并同时在原始域添加相似性指导约束具有更优的解混性能。表5中可见,本文所提算法在各信噪比情况下都具有更高的SRE值,且在低信噪比时,采用l2,1范数约束的结果比l1,1范数约束的结果更优。

图6 DC1数据在不同约束条件下解混的结果对比(SNR=30 dB)
Fig.6 Comparison of unmixing results of different constraints of DC1 data (SNR=30 dB)
为了进一步验证本文算法的优越性,我们将表5中各类算法得到的估计丰度矩阵进行可视化,并在图7中给出了第二个端元的丰度图。图中可见,本文算法与其他算法得到的丰度图相比更清晰,且背景噪声更少。由此表明,本文所提的多尺度光谱相似性指导的高光谱解混算法对高光谱图像有更好地解混性能,并且对高光谱图像存在的噪声具有更好地鲁棒性。

图7 数据集DC1在不同解混算法下得到的第二个端元的估计丰度图
Fig.7 Abundance maps obtained by different unmixing methods for endmember #2 in DC1
3.3 真实数据集实验结果分析
3.3.1 Samson数据集实验
1)近似域解混结果分析
图8为各端元估计丰度矩阵可视化后的估计丰度图,若无特别说明Proposed表示采用l1,1约束的Proposed1,由图中可见本文算法近似域解混后的估计丰度图较于SLIC_spreg算法端元边缘结构更清晰。

图8 近似域解混各端元的估计丰度图
Fig.8 Abundance map of each endmember obtained by unmixing the approximate domain
2)原始域解混结果分析
图9为本文提出的算法在Samson数据集的近似域和原始域解混时,是否添加了约束条件结果的对比,图中(a)、(b)、(c)、(d)添加的约束关系与图4相同,由图中四种实验结果的端元丰度图和RMSE值可知,本文算法的端元丰度图的结构最清晰,RMSE的值最小,具有更优的解混性能。图10显示了Samson数据集在不同解混算法下得到的估计丰度图,图中可见,本文算法相比于其他算法解混后的端元丰度图的结构更清晰,背景噪声更小。表6中,从各算法的RMSE值可见,本文算法最佳均方误差值最小。从算法的运行时间可见,本文算法与当前较好的解混方法SPGSU相比,运行时间更少,这表明本文算法在时间上有一定的优越性。

图9 不同约束条件下解混的结果对比
Fig.9 Comparison of unmixing results under different constraints
3.3.2 Cuprite数据集实验
图11给出了本文不同稀疏解混算法得到的Cuprite数据集的估计丰度图,其中本文算法相比于其他算法解混得到的端元丰度图更加均匀,并且清楚地描绘出了各端元材料的轮廓。表7给出了Cuprite数据集在不同解混算法下得到的RMSE值和运行时间。由表7中可见,本文算法的RMSE值小于其他几种算法,运行时间低于SPGSU算法。因此,本文算法能够使光谱库较好地适应实际场景,具有较好的解混性能。
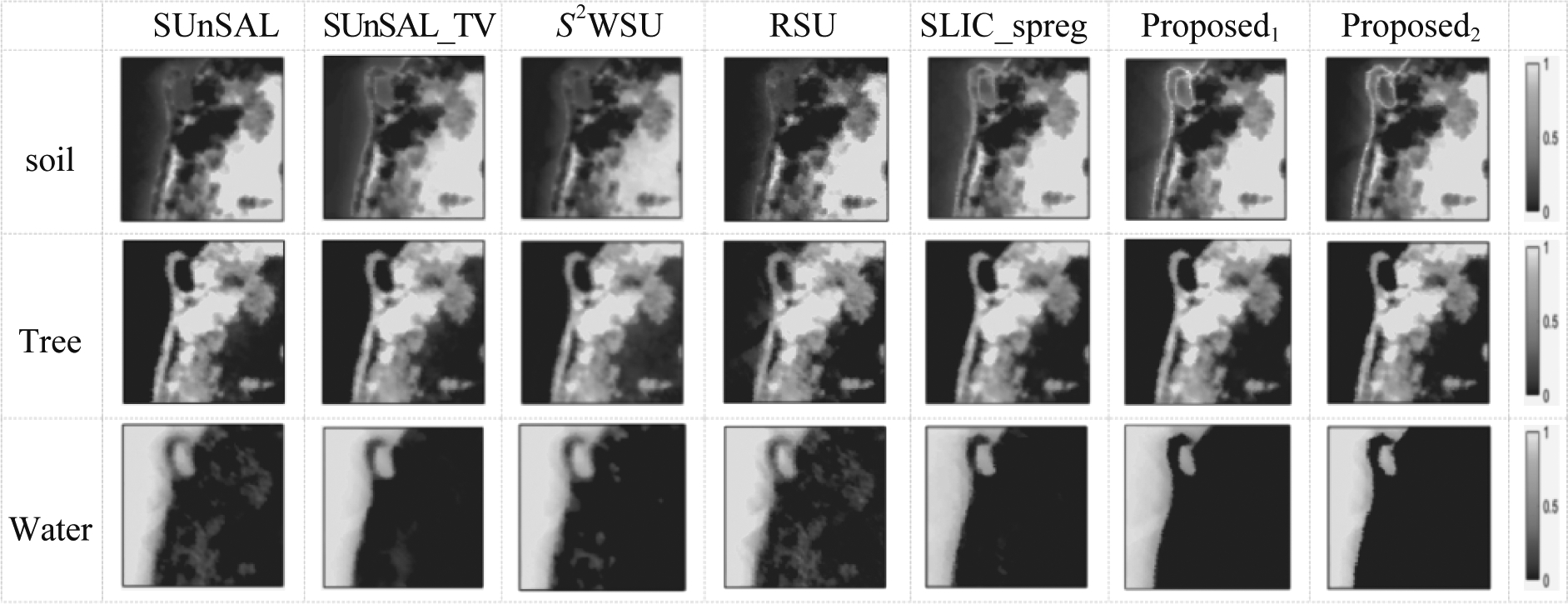
图10 Samson数据集在不同算法下得到的估计丰度图
Fig.10 Fractional abundance maps estimated for the Samson image
表6 Samson数据集在不同算法下的RMSE和运行时间
Tab.6 RMSE and Time of Samson dataset under different algorithms
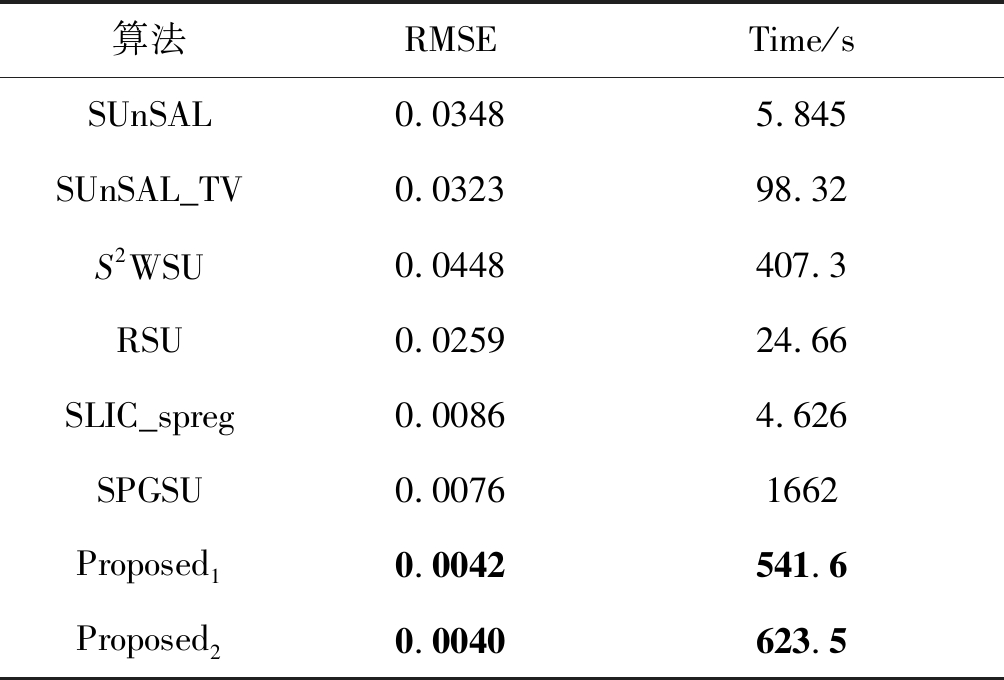
算法RMSETime/sSUnSAL0.03485.845SUnSAL_TV0.032398.32S2WSU0.0448407.3RSU0.025924.66SLIC_spreg0.00864.626SPGSU0.00761662Proposed10.0042541.6Proposed20.0040623.5
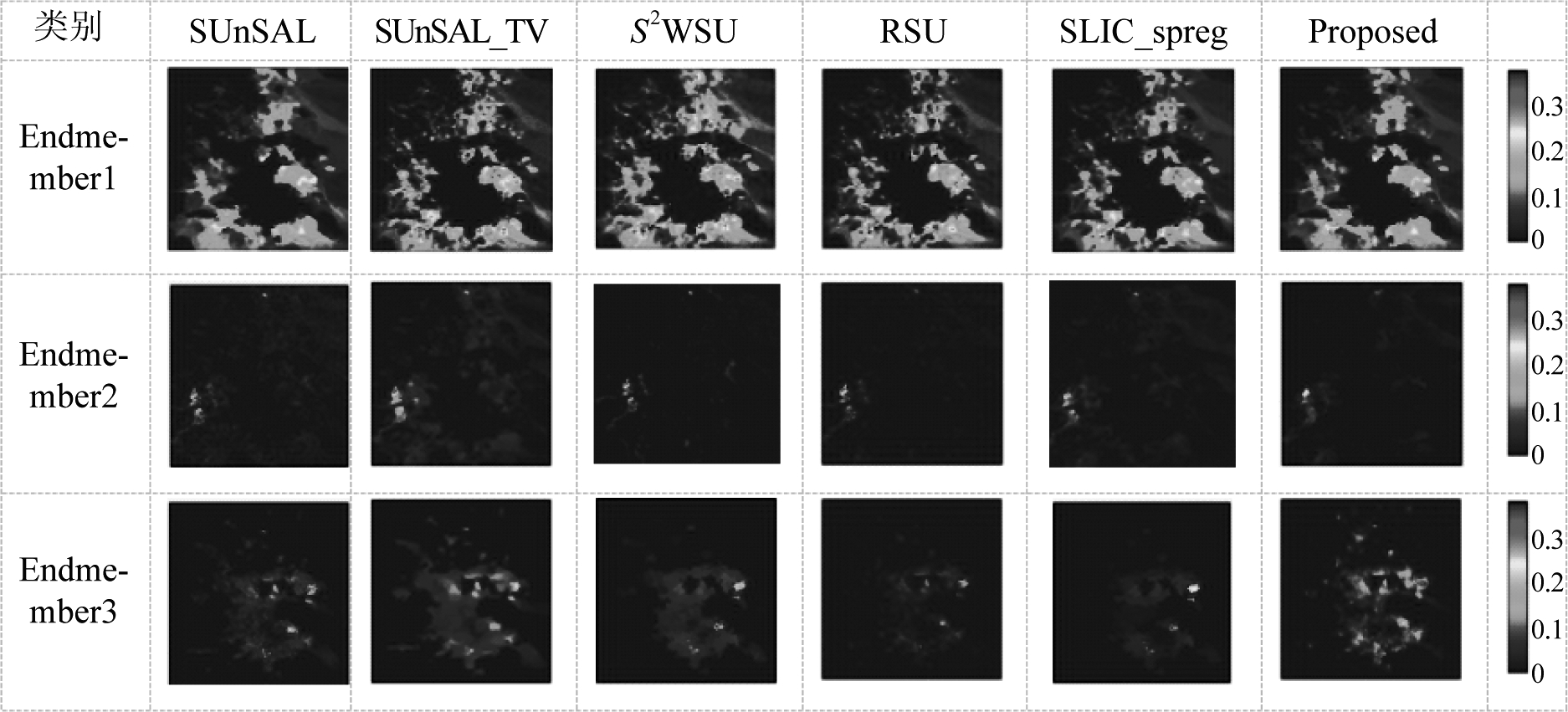
图11 Cuprite图像的估计丰度图(从上到下分别是明矾石、水铵长石和玉髓)
Fig.11 Fractional abundance maps estimated for the Cuprite image (Top to Bottom are Alunite, Buddingtonite and Chalcedony)
表7 各算法所得的RMSE和运行时间
Tab.7 RMSE and Time obtained by each algorithm
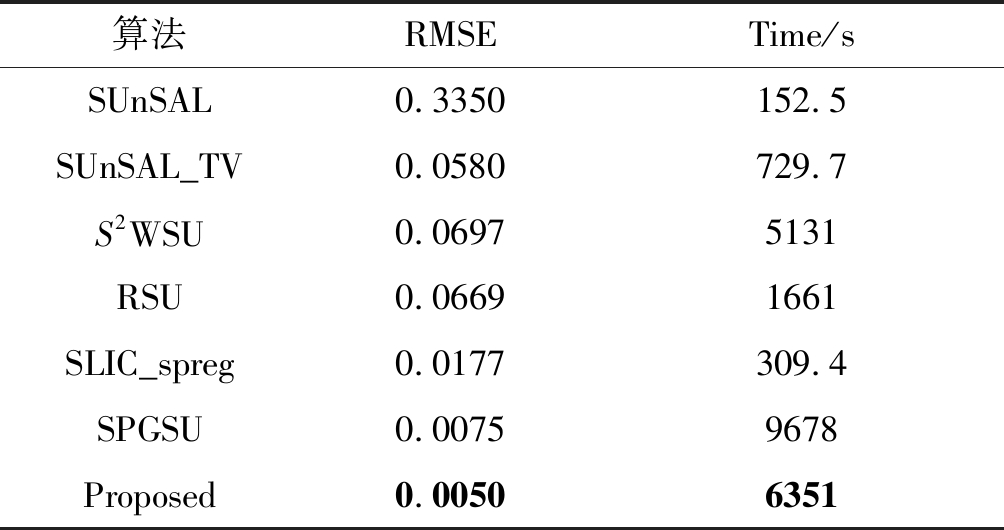
算法RMSETime/sSUnSAL0.3350152.5SUnSAL_TV0.0580729.7S2WSU0.06975131RSU0.06691661SLIC_spreg0.0177309.4SPGSU0.00759678Proposed0.00506351
4 结论
本文提出了一种多尺度光谱相似性指导的高光谱稀疏解混算法,该算法将高光谱图像分割成超像素表示的近似域图像,同时利用超像素之间的空间信息进行近似域解混;然后,将近似域解混后得到的估计丰度矩阵结合像元指导进行原始域解混计算。此外,本文还提出采用了l2,1范数来加强丰度矩阵的稀疏性。通过模拟和真实数据的实验结果表明,本算法相比于其他算法,在模拟数据集上具有更好的SRE值,在真实数据集上具有更低的RMSE值,而且解混后的估计丰度图边缘结构更加清晰,验证了本文解混算法的精确性。
[1] BIOUCAS-DIAS J M, PLAZA A, DOBIGEON N, et al. Hyperspectral Unmixing Overview: Geometrical, Statistical, and Sparse Regression-Based Approaches[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2012, 5(2): 354-379.
[2] 袁静, 章毓晋, 高方平. 线性高光谱解混模型综述[J]. 红外与毫米波学报, 2018, 37(5): 43- 61.
YUAN Jing, ZHANG Yujin, GAO Fangping. An Overview on Linear Hyperspectral Unmixing[J]. Journal of Infrared and Millimeter Waves, 2018, 37(5): 43- 61.(in Chinese)
[3] 袁宗泽, 孙浩, 计科峰, 等. 局部非负稀疏编码的高光谱目标检测方法研究[J]. 信号处理, 2014, 30(5): 561-568.
YUAN Zongze, SUN Hao, JI Kefeng, et al. Hyperspectral Image Target Detection Approach Based on Local Non-Negative Sparse Coding[J]. Signal Processing, 2014, 30(5): 561-568.(in Chinese)
[4] IMBIRIBA T, BERMUDEZ J C M, RICHARD C, et al. Nonparametric Detection of Nonlinearly Mixed Pixels and Endmember Estimation in Hyperspectral Images[J]. IEEE Transactions on Image Processing, 2016, 25(3): 1136-1151.
[5] 陈允杰, 葛魏东, 孙乐. 一种基于协同稀疏和全变差的高光谱线性解混方法[J]. 自动化学报, 2018, 44(1): 116-128.
CHEN Yunjie, GE Weidong, SUN Le. A Novel Linear Hyperspectral Unmixing Method Based on Collaborative Sparsity and Total Variation[J]. Acta Automatica Sinica, 2018, 44(1): 116-128.(in Chinese)
[6] ZHENG C Y, LI H, WANG Q, et al. Reweighted Sparse Regression for Hyperspectral Unmixing[J]. IEEE Transactions on Geoscience & Remote Sensing, 2016, 54(1): 479- 488.
[7] SUN L, WU Z, XIAO L, et al. A Novel l1/2 Sparse Regression Method for Hyperspectral Unmixing[J]. International Journal of Remote Sensing, 2013, 34(20): 6983-7001.
[8] BIOUCAS-DIAS J M, FIGUEIREDO M A T. Alternating Direction Algorithms for Constrained Sparse Regression: Application to Hyperspectral Unmixing[C]∥IEEE 2010 2nd Workshop on Hyperspectral Image and Signal Processing: Evolution in Remote Sensing (WHISPERS), Reykjavik, 2010: 1- 4.
[9] IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Total Variation Spatial Regularization for Sparse Hyperspectral Unmixing[J]. IEEE Transactions on Geoscience & Remote Sensing, 2012, 50(11): 4484- 4502.
[10] IORDACHE M D, BIOUCAS-DIAS J M, PLAZA A. Collaborative Sparse Regression for Hyperspectral Unmixing[J]. IEEE Transactions on Geoscience & Remote Sensing, 2014, 52(1): 341-354.
[11] XU Y, FANG F, ZHANG G. Similarity-Guided and lp Regularized Sparse Unmixing of Hyperspectral Data[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(11): 2311-2315.
[12] LI J, LI Y, SONG R, et al. Local Spectral Similarity Preserving Regularized Robust Sparse Hyperspectral Unmixing[J]. In IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(10): 7756-7769.
[13] ACHANTA R, SHAJI A, SMITH K, et al. Slic Superpixels Compared to State-of-the-Art Superpixel Methods[J]. IEEE Transactions on Pattern Analysis & Machine Intelligence, 2012, 34(11): 2274-2282.
[14] ZHANG S, LI J, LI H C, et al. Spectral-Spatial Weighted Sparse Regression for Hyperspectral Image Unmixing[J]. IEEE Transactions on Geoscience & Remote Sensing, 2018, 56(6): 3265-3276.
[15] BORSOI R A, IMBIRIBA T, BERMUDEZ J C M, et al. A Fast Multiscale Spatial Regularization for Sparse Hyperspectral Unmixing[J]. In IEEE Geoscience and Remote Sensing Letters, 2019, 16(4): 598- 602.
[16] ZHANG S, DENG C Z, et al. Superpixel-Guided Sparse Unmixing for Remotely Sensed Hyperspectral Imagery[C]∥IGARSS 2019 IEEE International Geoscience and Remote Sensing Symposium, Yokohama, Japan, 2019: 2155-2158.
[17] WANG R, LI H C, PIZURICA A, et al. Hyperspectral Unmixing Using Double Reweighted Sparse Regression and Total Variation[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(7): 1146-1150.
[18] ZHONG Y, FENG R, ZHANG L. Non-local Sparse Unmixing for Hyperspectral Remote Sensing Imagery[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2014, 7(6): 1889-1909.
[19] 张兵. 高光谱图像处理与信息提取前沿[J]. 遥感学报, 2016, 20(5): 1062-1090.
ZHANG Bing. Advancement of Hyperspectral Image Processing and Information Extraction[J]. Journal of Remote Sensing, 2016, 20(5): 1062-1090.(in Chinese)
[20] SHRIVASTAVA P, SINGH U P. Noise Removal Using First Order Neighborhood Mean Filter[C]∥2014 Conference on IT in Business, Industry and Government (CSIBIG), Indore, 2014: 1- 6.
[21] LIU Q, SHEN X, GU Y. Linearized ADMM for Nonconvex Nonsmooth Optimization with Convergence Analysis[J]. IEEE Access, 2019, 7: 76131-76144.




