1 引言
无线电频谱资源是国家重要的战略资源、无线通信技术发展的核心资源,高效利用频谱资源是未来无线通信的必要条件,而认知无线电可以动态利用频谱,使系统具有感知和评估可用资源的能力,降低了频谱损耗。其中,频谱感知作为实现认知无线电的关键技术,成为研究热点[1]。
传统频谱感知算法主要包括能量检测算法、匹配滤波器检测算法、循环平稳特征检测算法等[2-3]。凭借复杂度低和无需先验信息等优点,能量检测算法成为目前通用的感知算法。然而,由于检测受噪声影响较大,该算法的感知性能在低信噪比下不够理想[4-5]。为此,研究者提出一些新的频谱感知算法,其中文献[6-7]引入群智感知的激励机制,将其与协作频谱感知有效结合,提出了两种基于多任务学习的频谱感知算法。文献[8]结合压缩采样和特征学习,将学习到的特征通过一般似然比检验进行检测。文献[9]在已知接收信号与噪声统计协方差条件下分别提出了基于二项分布的检测算法和基于Wilcoxon符号秩的检测算法。通过LDLT对接收信号进行矩阵分解,文献[10]分别提出了基于OR准则和AND准则的最大最小特征值检测算法,并利用硬判决提升了判决阈值的准确率。尽管文献[6-10]中的算法在一定程度上提升了检测性能,但需要对判决阈值进行准确估计,而阈值的精度严重影响着频谱感知的效果。因此,不少学者提出了基于机器学习、深度学习的频谱感知算法[11-14]。
文献[11]将自动编码器和支持向量机相结合,利用自动编码器提取信号特征并通过支持向量机对所获取的特征进行分类从而得到检测结果。文献[12]对接收的信号矩阵进行了重组与分解,并利用构造的特征向量训练K均值聚类分类器。文献[13]利用完整的接收信号序列训练LSTM,最大程度保留原接收信号的结构信息,并利用该网络对新的信号序列进行检测。文献[14]采用纯数据驱动卷积神经网络来做感知,存在网络复杂、训练困难等问题。文献[11-14]表明,与传统感知算法相比,基于机器学习、深度学习的频谱感知算法不仅可以避免预设阈值问题而且能够极大提升检测性能。尽管如此,基于机器学习、深度学习的感知算法同样也面临着诸多挑战,例如:网络模型复杂、训练复杂度高等问题。
受上述启发,本文对接收信号进行多点均值计算处理,构造新的特征向量,搭建基于均值辅助的LSTM网络。该网络尽可能在保留原接收信号结构信息的基础上降低网络的训练复杂度,在训练复杂度和保留原接收信号结构信息之间达到一个平衡。通过仿真验证,所提算法检测性能优于对比算法,在与文献[13]相同的检测性能下,网络复杂度大大降低。
本文其他部分组织如下:第2节介绍了LSTM网络;第3节给出了所提算法的详细过程;第4节进行了算法性能对比和复杂度分析;最后给出了结论。
2 LSTM网络
神经网络已经在图像和自然语言处理等领域取得突破性进展,其中循环神经网(Recurrent Neural Network, RNN)因其可以学习到数据前后时间的关联信息,而被广泛使用在处理和预测时间序列问题上。LSTM作为RNN的一种重要变体,针对经典RNN中存在的长期依赖问题,LSTM在结构设计上使用三个“门”来控制隐藏层状态,可以保留每个时刻有用的信息,在很多任务上,采用LSTM比经典的RNN表现更好。
经典的RNN结构如图1所示,在每一个时刻t,RNN都会根据当前时刻的输入和当前的模型状态产生输出,进而更新模型状态。网络的输入包括来自输入层的xt和来自上一时刻隐藏层的ht-1两部分。在接收到输入后,模块S会得到新的隐藏层状态ht,并产生当前时刻的输出ot。由于RNN存在权值共享的特点,也就是在不同时间步位置共享参数,故RNN可看作是同一单元结构的无限复制,如图2所示。
图1 RNN经典结构图
Fig.1 The structure diagram of RNN
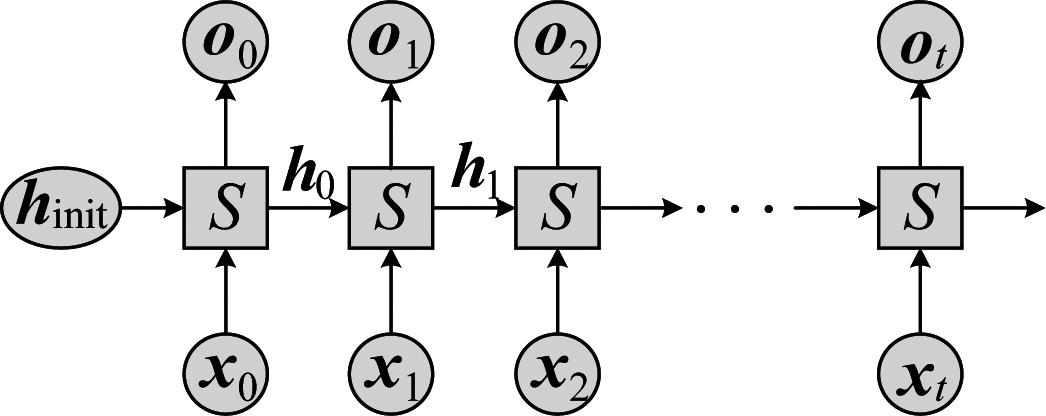
图2 RNN经典结构展开图
Fig.2 The extended structure diagram of RNN
从RNN到LSTM本质上是单元结构模块S的变化,RNN的单元结构模块如图3所示,其前向传播计算公式可表示为
ht=tanh(Wh[ht-1,xt])+bh
(1)
ot=Woht+bo
(2)
其中,ht和ht-1分别为t时刻和t-1时刻的隐藏层状态,Wh和Wo分别为隐藏层和输出层的权重矩阵,xt为t时刻的输入,bh和bo分别为隐藏层和输出层的偏置,ot为t时刻的输出。
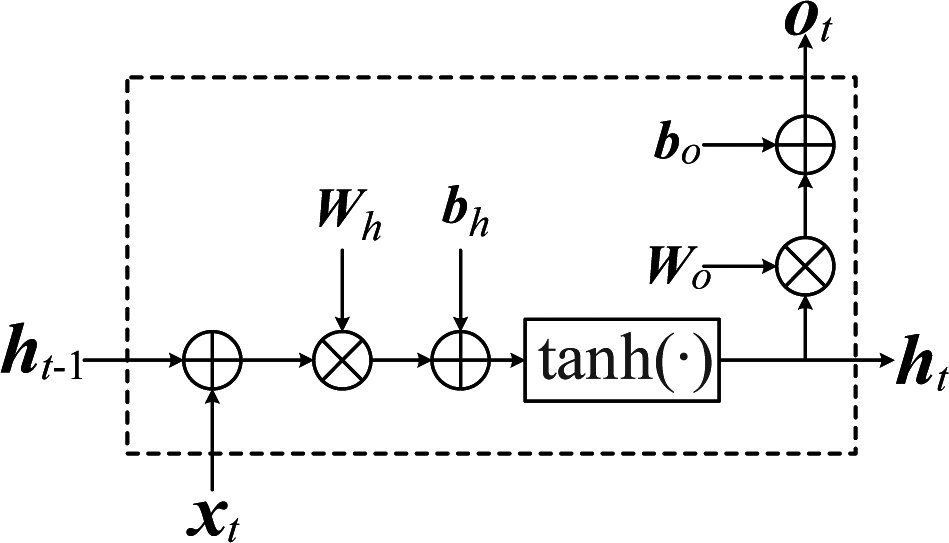
图3 RNN单元结构模块图
Fig.3 The unit structure module diagram of RNN
LSTM单元结构模块如图4所示,与RNN单元结构模块相比,LSTM单元结构模块更为复杂,有更多的参数,其前向传播计算公式如下:
z=tanh(Wz[ht-1,xt])(输入值) (3)i=sigmoid(Wi[ht-1,xt])(输入门) (4)f=sigmoid(Wf[ht-1,xt])(遗忘门) (5)o=sigmoid(Wo[ht-1,xt])(输出门) (6)ct=f·ct-1+i·z(新状态) (7)ht=o·tanhct(隐藏层输出) (8)
其中xt是t时刻的输入,Wz、Wi、Wf、Wo分别为输入、输入门、遗忘门、输出门的权重矩阵,ht和ht-1为t和t-1时刻的隐藏层状态,ct和ct-1为t和t-1时刻的细胞状态。
图4 LSTM单元结构模块图
Fig.4 The unit structure module diagram of LSTM
“门”的含义是控制有多少信息量可以通过,三个“门”都使用sigmoid激活函数将输出映射到[0,1]区间内。当数值为1时,表示全部信息都可以通过,当数值为0时,表示没有信息通过。其中输入门、遗忘门和输出门接收到的信息都是xt和ht-1,输入门决定哪些信息加入到ct-1来更新ct,遗忘门则是让网络忘记那些没有用的信息,输出门和ct-1共同决定t时刻的输出ht。ct-1到ct是记忆细胞的更新,也是解决长期依赖问题的关键,记忆细胞存储着各个时刻的有用信息,并不断通过遗忘门摒弃无用消息,通过输入门接收新信息,从而实现对细胞状态的更新。通过使用记忆细胞,LSTM可以捕捉到时间序列中前后信息之间的关联性。
3 基于均值辅助的LSTM频谱感知算法
3.1 频谱感知模型
将频谱感知建模为一个二分类问题,即:当检验统计量大于检测门限时,判定为H1,认为主用户(Primary User, PU)存在;当检验统计量小于检测门限时,判定为H0,认为PU不存在。接收信号r(n)可表示如下:
(9)
其中w(n)、h(n)、s(n)分别为噪声、信道增益、主用户信号。
3.2 算法流程
算法流程如图5所示,对接收信号进行M次顺序采样,依次得到长度为N的接收序列ri(n)(i=1,2,...,M;n=1,2,...,N),于是第i个接收序列可表示为ri(n)=[ri(1),ri(2),...,ri(N)],相应地,得到样本集
同时对样本分别进行标注,标签为0或者1,分别代表PU不存在H0和PU存在H1,得到的标签集
每次在样本集中随机抽取第i个样本ri(n)输入到均值处理模块中,均值处理模块根据均值步长L(假定N/L是整数)对样本进行处理,处理规则为:
图5 算法流程图
Fig.5 The flow chart of algorithm
(10)
经过处理后的均值样本集为
其规模为原数据规模的L分之一。然后,对均值样本集按照比例7∶2∶1划分为训练集、验证集和测试集。在训练集中每次拿出K条均值样本作为一个batch,对网络进行训练。第i条训练样本xi=[xi(1),xi(2),...,xi(N/L)]将通过LSTM,最终由softmax层得出两个在[0,1]区间内的输出P1和P0,分别为此条样本为正样本H1的概率和为负样本H0的概率。整个网络从输入到输出的映射关系可以表示如下:
(Pi1,Pi0)=fW,b(xi)
(11)
其中W和b为整个网络的权重矩阵和偏置,(Pi1,Pi0)为经过LSTM网络和softmax层映射后的分类概率。
网络采用Adam优化器,取一个batch的样本进行训练,并使用网络预测结果和数据标签构建交叉熵作为误差损失函数,表达式如下:
(12)
其中K为一个batch的样本数量,yi是第i条样本的标签,Pi1是第i条样本为正样本的概率。
在训练过程中,需要根据损失曲线和验证集准确率不断调整网络的超参数来降低Loss值,使模型性能达到最优。所提算法如下:
算法:基于均值辅助的LSTM频谱感知算法1.对接收序列进行L点均值计算,并将新的均值数据集进行划分。2.设定LSTM网络结构,并初始化权重矩阵和偏置。3.将训练集样本输入LSTM网络,前向传播后计算Loss值。4.使用梯度下降法更新网络权重矩阵和偏置,不断迭代至设置轮数。5.对损失曲线和验证集准确率进行分析,若损失曲线不收敛,则适当调整超参数(主要为学习率)后回到步骤2,若损失曲线收敛,则保存Loss最小的模型后进行下一步。6.重载Loss最小的模型,输入测试集样本,得到测试集准确率。7.回到步骤2,更改网络结构参数,重新设定网络结构,重复步骤2～6。8.得到测试集准确率最优的网络结构模型。
4 实验分析及对比
4.1 实验数据及仿真平台
文中实验数据同文献[12-13]为Matlab仿真生成的幅度调制信号,其参数见表1。结果均在CPU为Inter(R) Core(R)i7- 4790 CPU of 3.60 GHz,内存16 GB的计算机上运行得到。
表1 仿真数据集参数
Tab.1 The parameters of simulation data set
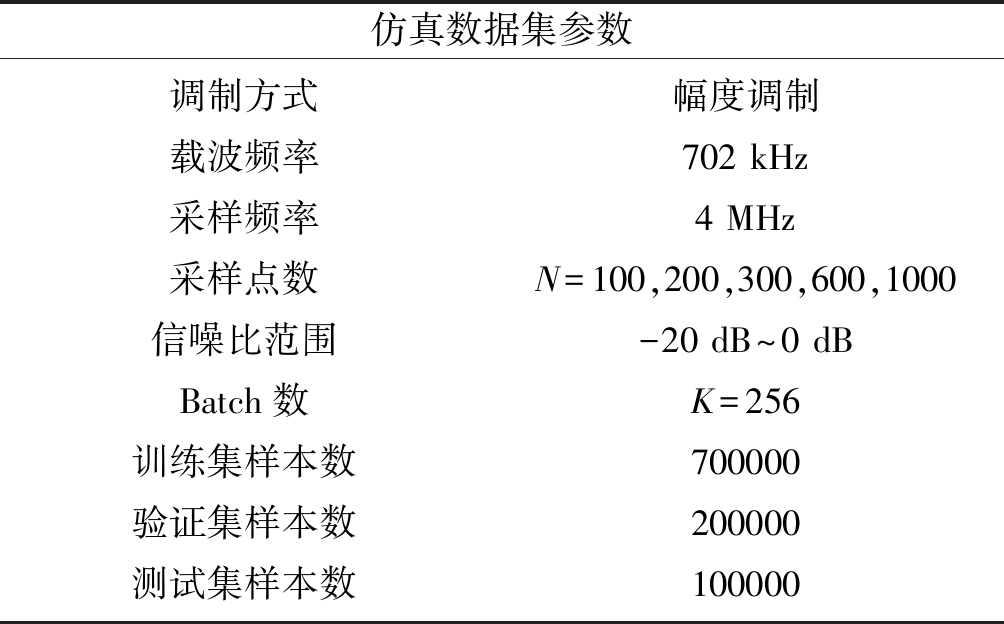
仿真数据集参数调制方式载波频率采样频率采样点数信噪比范围Batch数训练集样本数验证集样本数测试集样本数幅度调制702 kHz4 MHzN=100,200,300,600,1000-20 dB～0 dBK=256700000200000100000
4.2 算法性能及分析
算法实现基于Python3.7版本语言和Tensorflow2.0开源框架,网络调参策略同文献[13]。均值步长L是影响准确率和网络复杂度的关键因素,为了得到合适的L,探究不同采样点下L对测试集结果的影响是否一致,图6给出采样点N为300和600时不同L的测试集准确率对比。在L=5和L=10时,300采样点的测试集准确率为0.8920和0.8990,在L=15时,300采样点的测试集准确率为0.8586。结果表明随着L的增大,300采样点和600采样点测试集准确率逐步降低。但是在L取5和10时测试集的准确率没有明显的下降,L大于20时下降加快,这是因为L较小时均值数据较好的保留了原始数据的结构信息。综合考虑算法性能和复杂度,在之后的算法性能对比中L均取10。
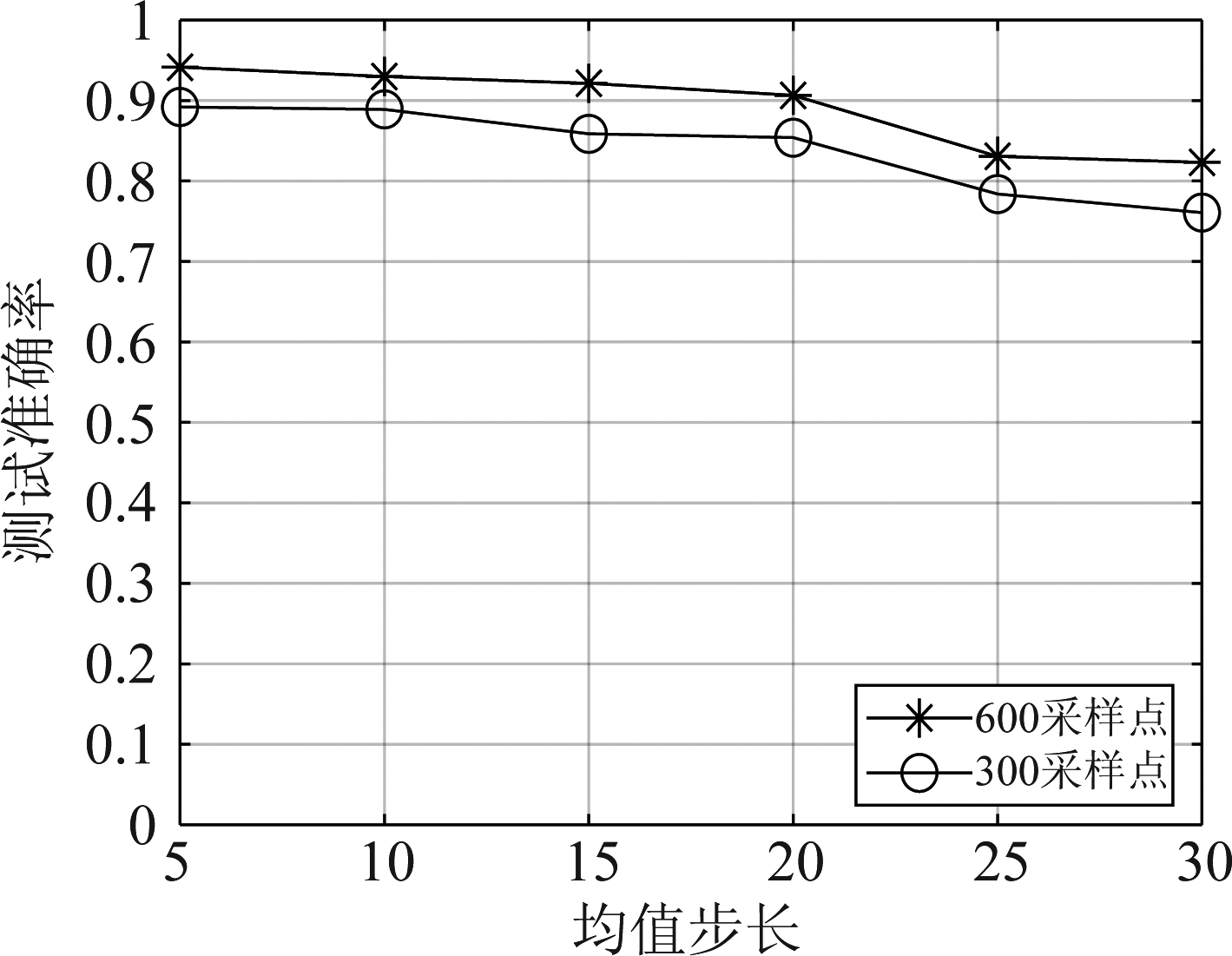
图6 采样点N=300、600时不同均值步长L的测试准确率(SNR=-13 dB)
Fig.6 Test accuracy of different average step size L when sampling point N=300 and 600 (SNR=-13 dB)
采样点数是观测时间的直接表现,在给定采样频率的条件下采样点数越多,观测时间越长,LSTM网络就可以学习到更长时间数据前后之间的联系,为了验证这一观点,本文对算法性能与采样点数的关系进行仿真分析。表2展示了所提算法在L=10时不同采样点数N的准确率,N从100到1000时,测试集准确率从0.5812到0.9252,N=600时的测试集准确率为0.9298。结果表明验证集和测试集的准确率随着N的增加而提升,但是当N达到600时提升的趋势已经不明显,这是因为此时数据前后之间的关联性已经非常微弱,网络难以学习到有用的关联信息。
表2 均值步长L=10时不同采样点N的准确率
Tab.2 The accuracy of the different sampling point N when the average step length L=10
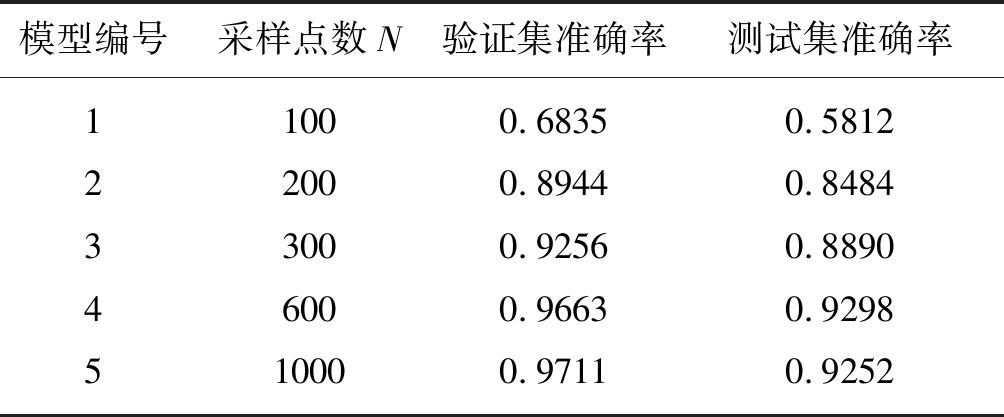
模型编号采样点数N验证集准确率测试集准确率1234510020030060010000.68350.89440.92560.96630.97110.58120.84840.88900.92980.9252
4.3 算法性能对比
为了进一步体现所提算法的性能优势,本文与传统能量检测(Energy Detection, ED)算法、BP神经网络(Back Propagation Neural Network, BPNN)、文献[12]和文献[13]的人工智能算法进行了对比。在ED算法和文献[12]的算法中,主用户采用1000采样点,所提算法、BPNN算法和文献[13]算法主用户采样点数为300。其次,所提算法均值步长设置为10,网络隐藏层数为1,隐藏层节点数为16。
图7为SNR=-11 dB时各算法的受试者工作特性曲线(Receiver Operating Characteristic, ROC),可以直观的看出所提算法ROC曲线下方的面积(Area Under Curve, AUC)均大于对比算法。由于检测概率Pd和虚警概率Pf同增同减的特性,这里重点关注虚警概率Pf小于0.2的区域,当Pf=0.2时ED算法的Pd为0.6352,BPNN为0.8810,文献[12]算法四种情况中最高的可达到0.9540,而所提算法的Pd为0.9916,均优于对比算法。
图7 算法ROC曲线(SNR=-11 dB)
Fig.7 Algorithm ROC curve (SNR=-11 dB)
图8展示了SNR=-13 dB时各算法的ROC曲线对比,在信噪比降低的时候,所提算法的性能与对比算法的AUC差距在变大,在Pf=0.2时,ED算法的Pd为0.5560,BPNN为0.7280,文献[12]算法四种情况中最高的可达到为0.7250,所提算法的Pd可以达到0.9379,结果充分说明了所提算法在低信噪比时也能保持较好的性能。
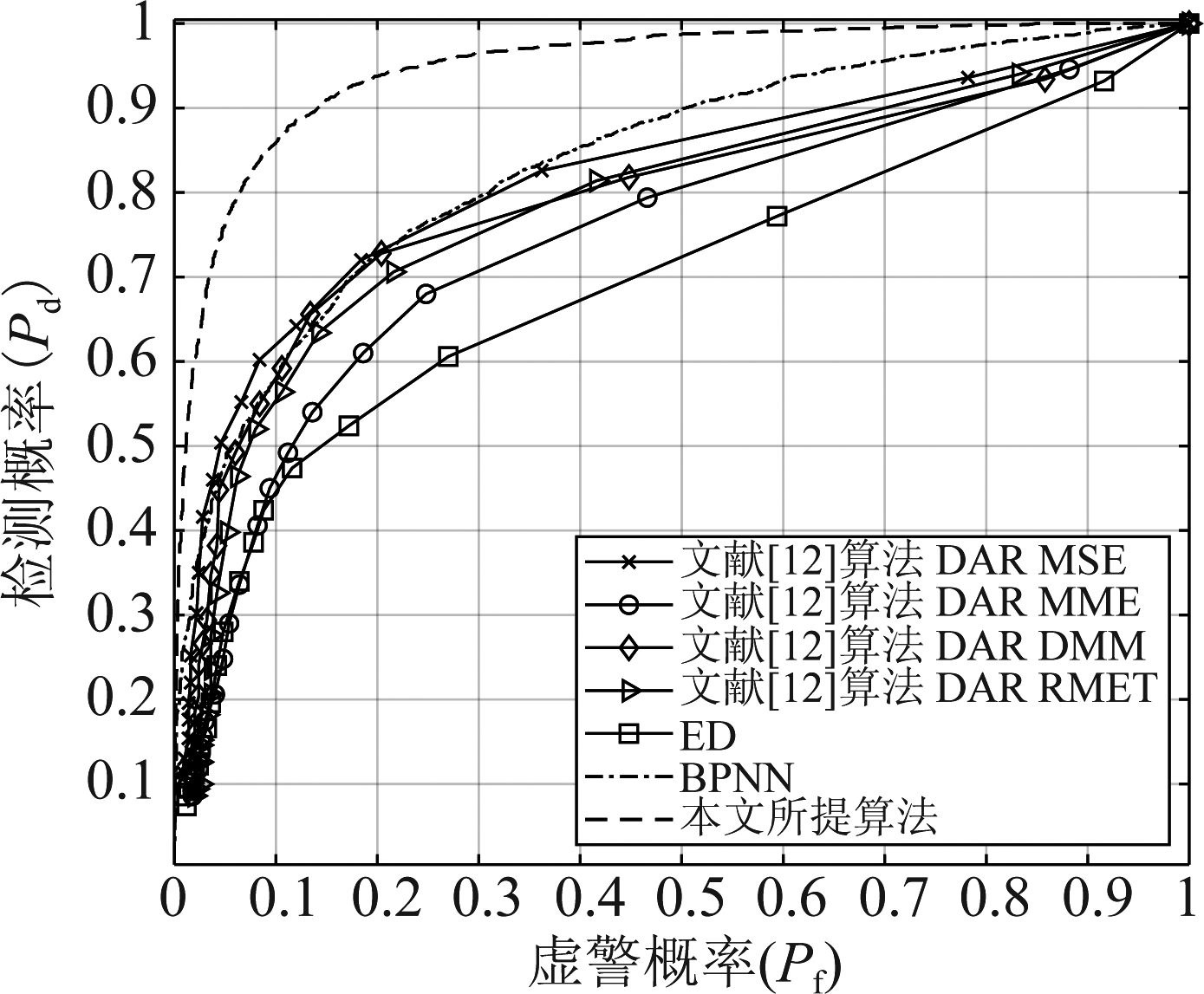
图8 算法ROC曲线(SNR=-13 dB)
Fig.8 Algorithm ROC curve (SNR=-13 dB)
为了探究所提算法在降低复杂度时所付出的代价,图9给出了在SNR=-11 dB和SNR=-13 dB时,所提算法与同样采用LSTM网络的文献[13]算法ROC曲线对比,两种算法使用相同的接收信号序列作为训练数据,文献[13]算法直接使用接收信号序列对网络进行训练,而所提算法则采用均值辅助构造出新的均值特征向量来训练网络,相比于原始接收信号序列,均值特征向量在尽可能保留接收序列结构信息的基础上降低了网络的复杂度,训练数据量大幅减少。在SNR=-11 dB,Pf=0.1时,两种算法Pd的差距不超过一个百分点。在SNR=-13 dB,Pf=0.1时,两种算法Pd的差距不超过两个百分点。如果将L从10调整为5或者2,那么两种算法的差距会进一步缩小甚至消失,只需要付出一些网络复杂度作为代价,但所提算法的复杂度仍远远小于文献[13],具体的复杂度对比分析见4.4小节。
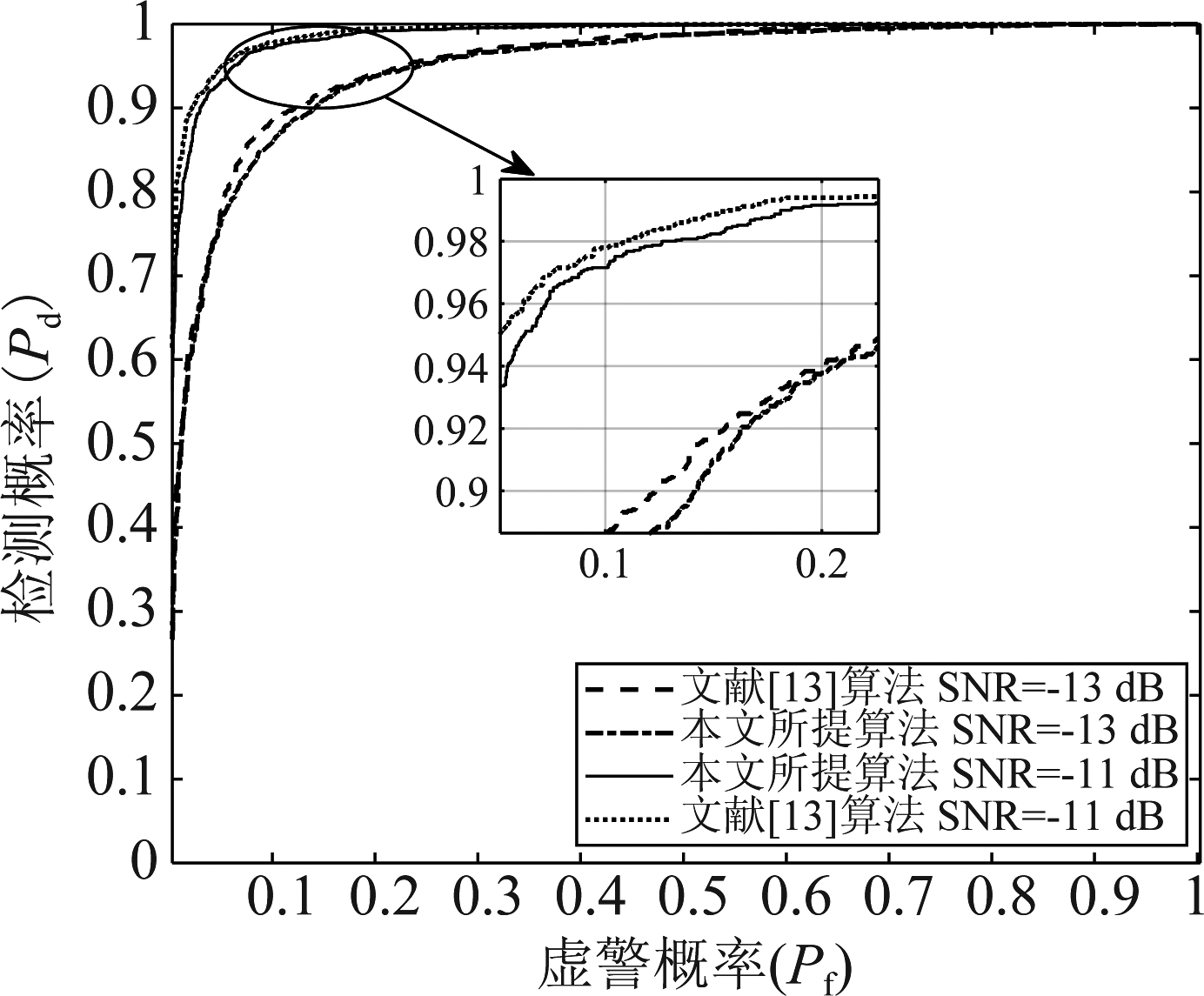
图9 算法ROC曲线(SNR=-11 dB,SNR=-13 dB)
Fig.9 Algorithm ROC curve (SNR=-11 dB,SNR=-13 dB)
为了探究所提算法在衰落信道下的感知性能,在每条样本内衰落不变的情况下,图10给出了在SNR=-13 dB时所提算法在瑞利信道和莱斯信道下的ROC曲线对比,在Pf=0.05时,瑞利信道下的Pd=0.722,莱斯因子K=-40、K=0、K=15的莱斯信道的Pd都可以达到0.81左右,在Pf大于0.2时,四种不同信道情况下的检测概率几乎没有差别。结果表明了所提算法具有良好的对抗衰落能力且对不同衰落信道具有较强的鲁棒性。
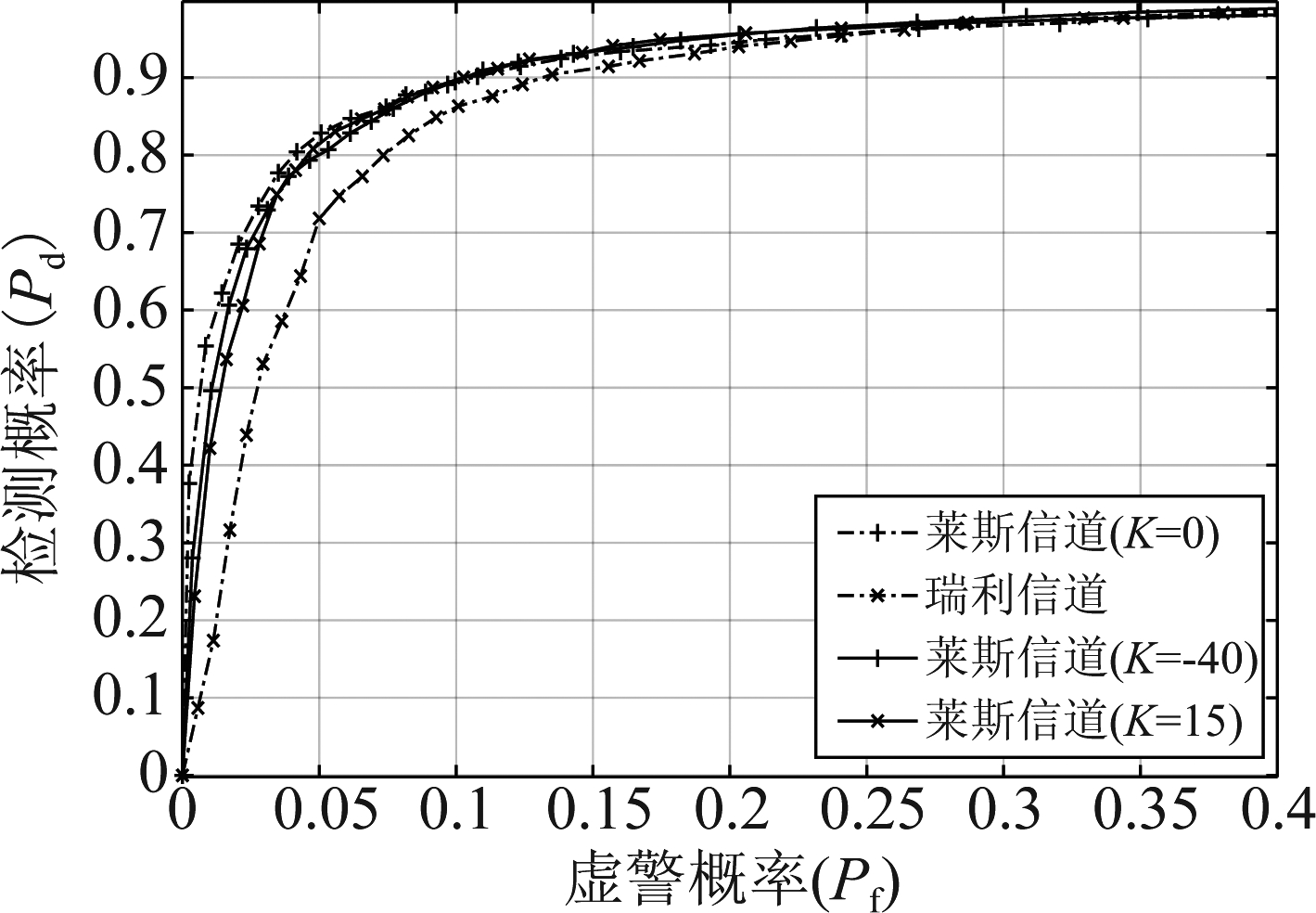
图10 衰落信道下的算法ROC曲线(SNR=-13 dB)
Fig.10 Algorithm ROC curve under fading channel (SNR=-13 dB)
4.4 算法复杂度分析及对比
为了探究使用神经网络所带来的训练时间长、网络复杂度高的问题,本文从训练时间、网络参数量两方面进行分析,并和同样采用LSTM网络的文献[13]进行对比。训练的迭代轮数都设置为5000以保证网络模型训练充分,并且选择测试结果最好模型的网络结构参数(见表3)。由于测试时间在整个神经网络调试中占比很小,且LSTM具有权值共享的特点,故本文只比较训练时间和一个LSTM单元中的参数数量。
图11给出了两种算法的训练时间对比柱状图,在N为300时,文献[13]的训练时间为3776 s;而所提算法L等于5时训练时间为610 s,L等于10时为383 s,N为600时训练时间仍远远小于文献[13]。结果表明所提算法可以在保持高性能的同时大幅减少训练时间,为神经网络算法的实现降低了复杂度。
表3 网络结构参数
Tab.3 The parameters of Network structure
采样点算法300文献[13]算法本文算法L=5本文算法L=10600文献[13]算法本文算法L=5本文算法L=10输入层节点数300603060012060隐藏层节点数12832163247232隐藏层数111111输出节点数222222
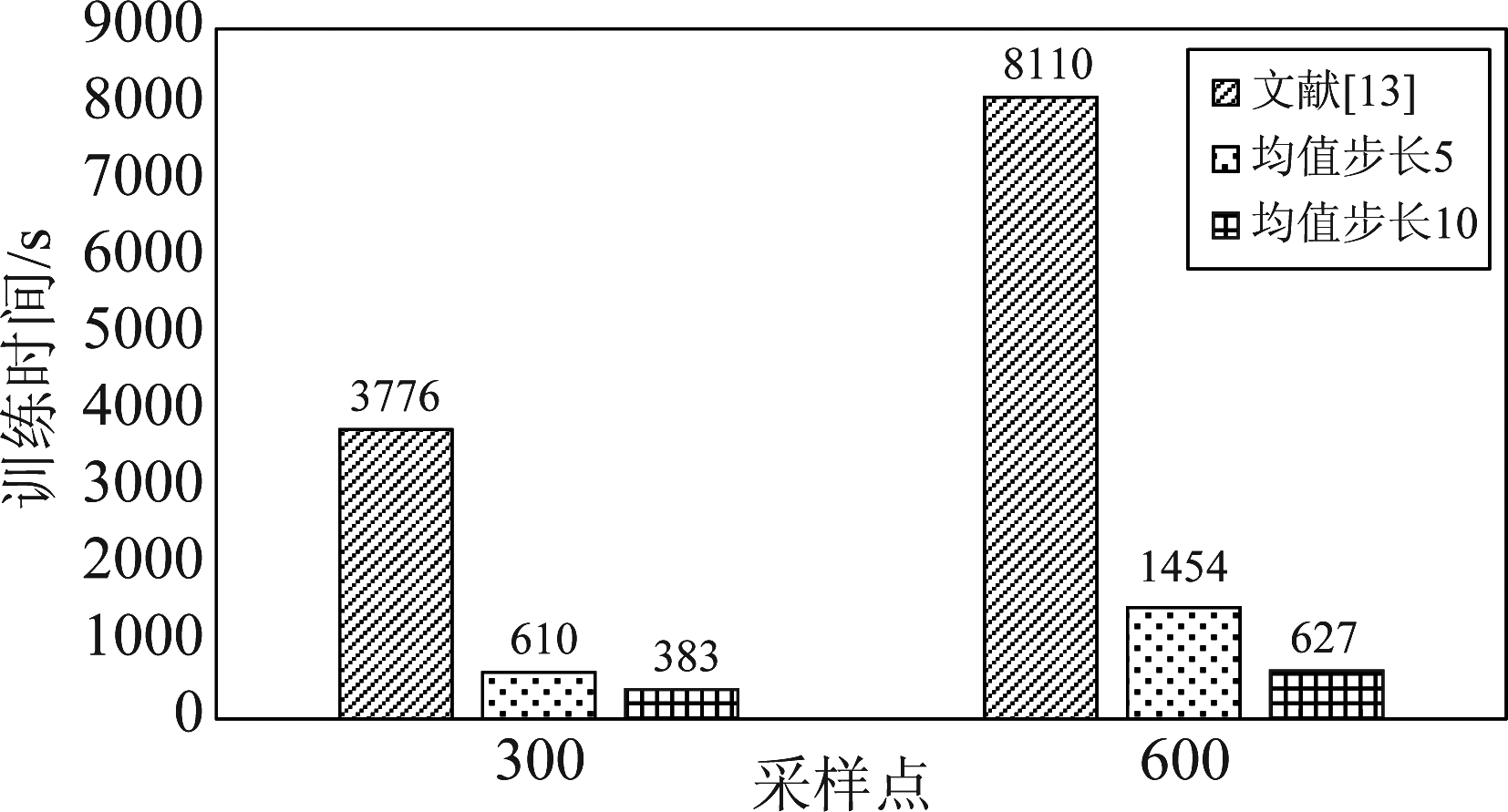
图11 训练时间对比
Fig.11 The comparison of training time
参数数量是分析复杂度的另一个角度,在LSTM中,每个单元的参数量越大,运算也就越复杂,耗费时间和资源也就越多。首先给出LSTM网络中每个单元的参数量计算公式:
Nopara=(hs·(hs+xd)+hs)·4
(13)
其中hs为隐藏层节点数,xd为每个时间步输入LSTM单元的数据维数。图12给出了所提算法和文献[13]算法单个LSTM单元中所含参数量的对比,在N等于300时,文献[13]每个LSTM单元的参数量为66560,所提算法在L为5和10时为4352和1152,在N为600时,文献[13]更是达到了422496,而所提算法在L为5和10时只有21312和4352。结果进一步表明了所提算法在降低网络参数量,减少复杂度方面的优势。
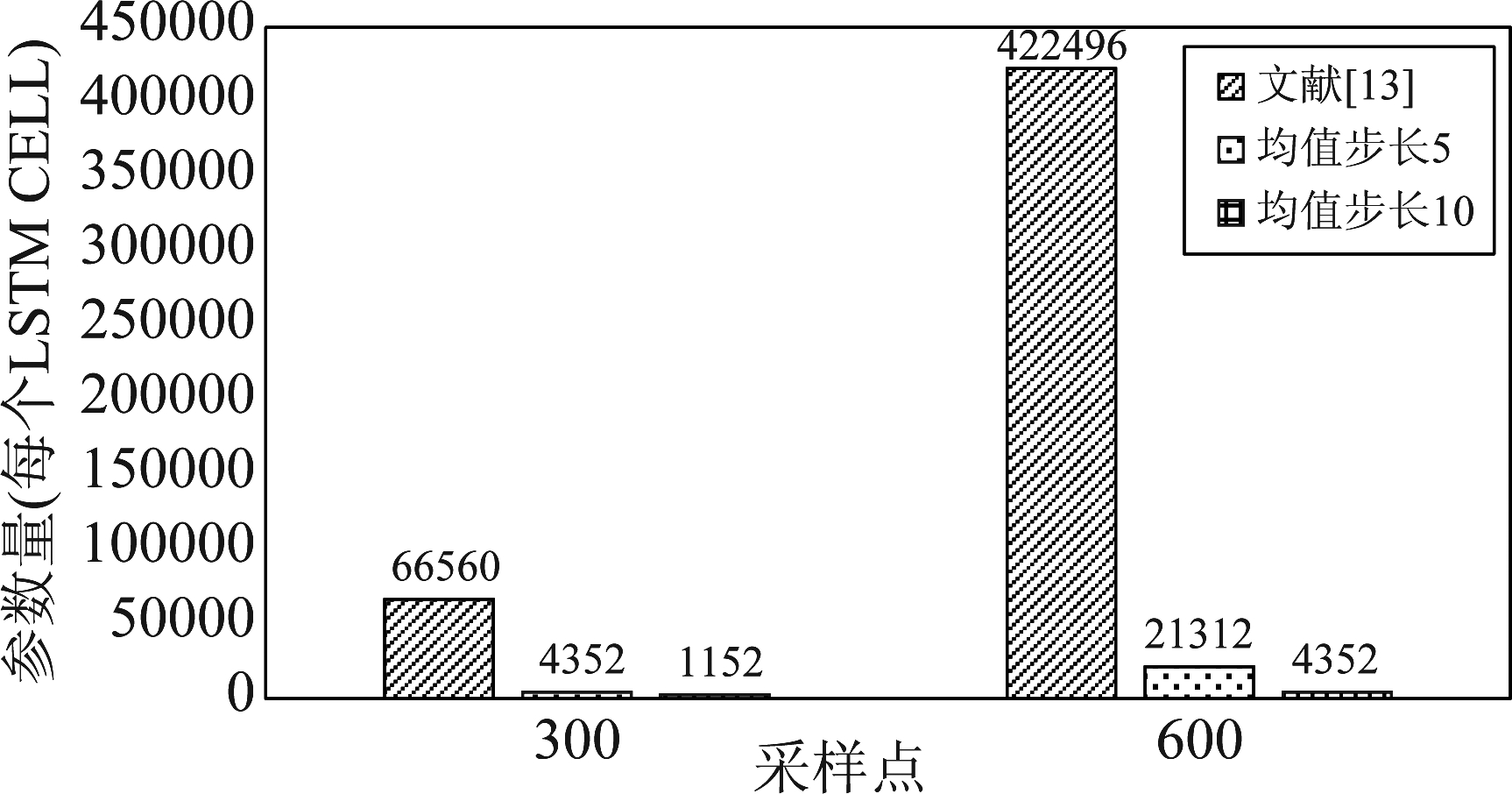
图12 单个LSTM单元参数量对比
Fig.12 The comparison of parameters of a single LSTM unit
5 结论
本文在探究如何将先验知识及数据统计特征和神经网络融合的过程中提出基于均值辅助的LSTM网络频谱感知算法,首先通过对接收信号进行多点均值计算构造出均值特征向量,然后使用均值向量训练LSTM网络得到二分类模型,最后使用训练好的模型进行频谱感知。仿真结果表明所提算法在保证较高检测率的同时可以将网络的复杂度大大降低。
[1] ZHOU Xiangwei, SUN Mingxuan, LI Ye, et al. Intelligent wireless communications enabled by cognitive radio and machine learning[J]. China Communications, 2018, 15 (12): 16- 48.
[2] ALOM M Z, GODDER T K, MORSHED M N. A survey of spectrum sensing techniques in cognitive radio network[C]∥Proc of 3rd International Conference on Advances in Electrical Engineering. Piscataway, NJ: IEEE Press, 2015: 161-164.
[3] YUCEK T, ARSLAN H. A survey of spectrum sensing algorithms for cognitive radio applications[J]. IEEE Communications Surveys and Tutorials, 2009, 11(1): 116-130.
[4] ALOM M Z, GODDER T K, MORSHED M N, et al. Enhanced spectrum sensing based on Energy detection in cognitive radio network using adaptive threshold[C]∥4th International Conference on Networking, Systems and Security. Piscataway, NJ: IEEE Press, 2017: 138-143.
[5] ZHU J, XU Z, WANG F, et al. Double Threshold Energy Detection of Cooperative Spectrum Sensing in Cognitive Radio[C]∥International Conference on Cognitive Radio Oriented Wireless Networks and Communications. Piscataway, NJ: IEEE Press, 2008: 1-5.
[6] 张小盈, 朱琦. 基于Stackelberg博弈的多任务协作频谱感知算法[J]. 信号处理, 2020, 36(1): 77- 83.
ZHANG Xiaoying, ZHU Qi. A Multi-task Cooperative Spectrum Sensing Algorithm Based on Stackelberg Game[J]. Journal of Signal Processing, 2020, 36(1): 77- 83.(in Chinese)
[7] 吕鑫鑫, 朱琦. 多任务群智频谱感知算法[J]. 信号处理, 2018, 34(4): 487- 493.
LÜ XinXin, ZHU Qi. A Multi-Task Crowd Cooperative Spectrum Sensing Algorithm[J]. Journal of Signal Processing, 2018, 34(4): 487- 493.(in Chinese)
[8] CHEN H, VUN C H. An efficient compressive spectrum sensing technique for cognitive radio system[C]∥IEEE Region 10 Conference. Piscataway, NJ: IEEE Press, 2016: 1105-1110.
[9] LU G, XU C, YE Y. Multiantenna Based Blind Spectrum Sensing via Nonparametric Test[C]∥International Conference on Communications & Networking in China. Switzerland: Springer, Cham, 2016: 165-174.
[10] LU G, LI Y, YE Y, et al. LDLT Decomposition Based Spectrum Sensing in Cognitive Radio Using Hard Decision Criterion[C]∥Vehicular Technology Conference. Piscataway, NJ: IEEE Press, 2017: 1-5.
[11] SUBEKTI A, PARDEDE H F, SUSTIKA R, et al. Spectrum Sensing for Cognitive Radio using Deep Autoencoder Neural Network and SVM[C]∥IEEE International Radar Conference. Piscataway, NJ: IEEE Press, 2018: 81- 85.
[12] WANG Y, ZHANG Y, ZHANG S, et al. A Cooperative Spectrum Sensing Method Based on a Feature and Clustering Algorithm[C]∥Proc of IEEE CAC 2018. Piscataway, NJ: IEEE Press, 2018: 1029-1033.
[13] 卢光跃, 施聪, 吕少卿, 等. 基于LSTM神经网络的频谱感知算法[J]. 信号处理, 2019, 35(12): 2070-2076.
LU Guangyue, SHI Cong, LÜ Shaoqing, et al. A Spectrum Sensing Algorithm Based on LSTM Neural Network[J]. Journal of Signal Processing, 2019, 35(12): 2070-2076.(in Chinese)
[14] XIE J, LIU C, LIANG Y, et al. Activity Pattern Aware Spectrum Sensing: A CNN-Based Deep Learning Approach[J]. IEEE Communications Letters, 2019, 23(6): 1025-1028.
