1 引言
近年来,由于无人机具有易操纵、体积小、成本低等优点[1],使得无人机产业飞速发展,为军用和民用领域提供了极大便利。但是,无人机的快速发展也带来了隐患,尤其是小型旋翼无人机对一些特殊环境的威胁,例如在机场环境下,“黑飞”状态的小型旋翼无人机影响民航飞机的正常起飞和着陆,甚至有与飞机相撞的隐患,严重影响到民航飞机的安全飞行,因此对小型旋翼无人机的监视与识别意义重大。微多普勒特征是目标识别与分类的关键,代表目标微动的微多普勒特征,如无人机叶片的旋转、鸟类翅膀的振动、人体走动时手和腿的摆动[2],已被广泛用于目标的分类与识别。微动特征分析与提取已经成为雷达目标分类、识别与检测中一个研究热点。
在微动特征分析方法方面,通常在时频域分析目标的微动特性,短时傅里叶变换(Short Time Fourier Transform,STFT)计算简单且无交叉项,但不能兼顾时间分辨率和频率分辨率[3- 4]。Wigner-Ville分布(Wigner-Ville Distribution,WVD)时频分辨率得到提升,但同时会出现交叉项的影响[5]。平滑伪Wigner-Ville分布(Smoothed Pseudo Wigner-Ville Distribution,SPWVD)抑制了交叉项的干扰,但其计算量较大且时频分辨率在一定程度上会有所下降。近年来,一些学者对传统时频分析方法做了改进,Whitelonis N等人提出了一种基于压缩感知的时频分析方法,明显抑制了交叉项,相比STFT提供了更好的时频定位,但对多分量信号进行谱图分析时易丢失目标信息,分析效果并不理想[6]。Ram S S等人将重排谱图(Reassigned Spectrogram,RSP)用于人体不同部位的微多普勒特征分析,在取得良好分辨率的同时有效抑制了交叉项的干扰,更加精准的识别了人体不同部位的微动特征[7]。本文将此方法应用到旋翼无人机微动特征分析中,在一定程度上提升了弱微动特征的时频分辨率。
时频分析获取了微多普勒信号在时频域的能量分布,但要得到微动目标动力学参数,还需要在特征分析的基础上对其进行特征提取。对于微动特征提取方法,Harmanny R I A等人利用倒谱提取无人机旋翼的闪烁周期,此方法容易受到噪声的干扰[8-9]。也有学者通过自相关函数法、奇异值分解(Singular Value Decomposition,SVD)以及经验模式分解(Empirical Mode Decomposition,EMD)的方法提取目标的微动频率,但对于多分量信号而言提取效果并不理想[10-13]。Zhang Wenyu等人在STFT的基础上沿着时间轴作FFT形成CFD(Cadence Frequency Diagram)谱图,通过在CFD谱图中选取峰值点对不同类型的无人机分类[14]。Ren Jianfeng等人设计了一种鸟类与无人机自动分类系统,提出正则化二维复对数谱方法,对于无人机特征提取来说,该方法虽可以提取旋翼无人机的微动参数,但相比CFD方法运算复杂并且提取效果并无优势[15]。
旋翼无人机自身的弱散射特性和各个旋翼初始相位的随机性加大了微动特征提取的难度。本文针对小型旋翼无人机的微动特征提取,利用RSP方法对无人机进行微动特征分析,在保证较好时频分辨率的前提下,利用CFD方法实现旋翼无人机微动特征的提取。最后通过极大值法能够准确地估计出旋翼无人机的旋翼转速和叶片长度。
2 旋翼无人机微动特征分析
无人机是低慢小飞行目标,其雷达回波较为微弱,尤其在分析多旋翼无人机时,由于旋翼转速和初始相位的不同,使得频率分量在时频平面上严重交叠,因此在不丢失目标特征的基础上拥有好的时频分辨率对无人机的微动特征分析是至关重要的。本文以四旋翼无人机和小型无人直升机为实验对象,两架无人机的运动状态都为悬停状态,四旋翼无人机在飞行时每个旋翼都要提供升力,并且对角旋翼旋转方向相同,而相邻旋翼旋转方向相反。本文仿真实验中采用C波段线性调频脉冲体制雷达,雷达及无人机相关参数如表1~表2所示(无人机参数设定参考大疆精灵3S和Mikado logo400se[12,16])。
表1 雷达工作参数
Tab.1 Radar operating parameters

参数数值工作频率5.5 GHzPRI60 μs快时间采样率80 MHz带宽20 MHz观测时间192 ms
表2 无人机参数
Tab.2 UAV parameters
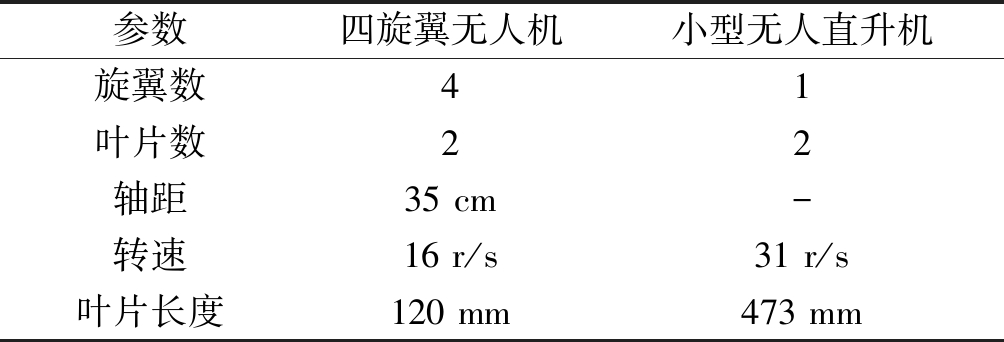
参数四旋翼无人机小型无人直升机旋翼数41叶片数22轴距35 cm-转速16 r/s31 r/s叶片长度120 mm473 mm
2.1 旋翼无人机微动特征分析方法
对旋翼无人机微动特征分析时,为了解决交叉项的影响和分辨率不足的问题,可以对时频分布特征进行重排,即利用RSP方法分析其微动特征。基于时频谱图进行谱重排,其对应的谱图可以看做信号的WVD分布和窗函数的WVD分布之间的卷积,其表达式为[17]
(1)
其中,h为对信号x进行时频分析时所用的窗函数,Wx是x的WVD分布,Wh是h的WVD分布。
RSP方法将时频谱中的点重新分配到信号的重心位置,从而达到防止能量扩散的目的。将时频谱中点(t, f)处的能量值分配到信号能量的重心位置![]() 即[18]
即[18]
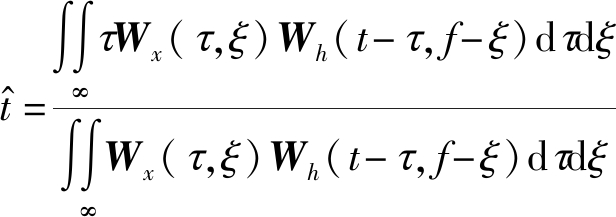
(2)
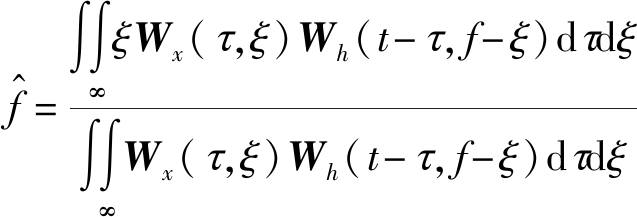
(3)
重排后的谱图可以写为[18]
(4)
在时频域对旋翼无人机进行微动特征分析时,其微多普勒受到旋翼转速、初始相位等多个参数的影响,所以拥有好的时频分辨率对无人机微动特征分析是至关重要的。对于主流的时频分析方法,窗函数的存在虽有效抑制了交叉项,但对信号的分析长度有限,使得时频分辨率下降。而RSP方法将时频谱中的点重新分配到更接近于信号的真实坐标位置,这样不仅抑制了交叉项的干扰,而且时频聚集性得到提高。
2.2 时频分析方法性能比较
对于无人机旋翼叶片的雷达回波仿真,可以认为叶片为多个散射点的线性叠加;对无人机机身来说,由于机身的RCS远大于旋翼叶片,可以将机身看作点目标。基于RSP对两种不同类型的无人机微多普勒特征进行分析,并与目前主流时频分析方法性能进行对比分析。无人机与雷达参数如表1~表2所示,无人机距地面的高度为80 m,与雷达之间的地距为4000 m,方位角为0°,四旋翼无人机旋翼初始相位服从[-π,π]的均匀分布。
由于无人机的类型不同,它们的微多普勒特征也是不同的,小型无人直升机和四旋翼无人机的微动特征分析如图1和图2所示,为同时兼顾时间分辨率与频率分辨率,使时频图呈现较好的分析效果,文中时频分析方法均采用高斯窗为滑动窗,设置窗长为128,滑动步长为1。考虑机身的散射,小型无人直升机叶片闪烁呈周期型分布,只有唯一的叶片闪烁周期。而四旋翼无人机的四个旋翼初始相位角随机,导致出现不同时刻的叶片闪烁,所以在谱图中的叶片闪烁较为混乱。对于不同的分析方法中,STFT方法的时频分辨率最低。WVD方法中时频分辨率虽达到最佳,但时频域中产生了严重的交叉项。SPWVD方法虽有效抑制了交叉项的影响,但分辨率低于WVD和RSP方法。RSP方法展示了几乎与WVD相近的时频分辨率,并且抑制了交叉项的干扰。具体的比较结果如表3所示。
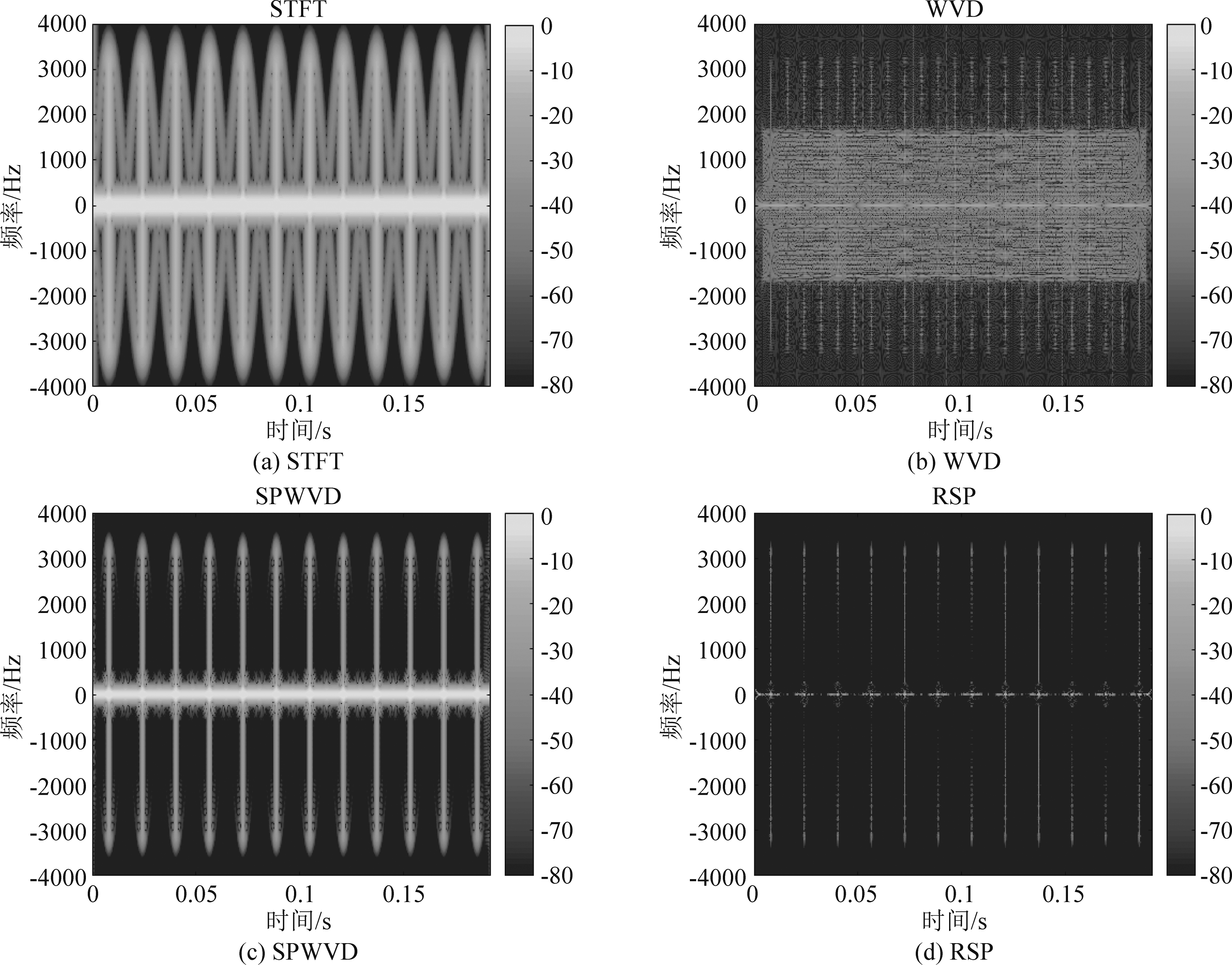
图1 小型无人直升机微多普勒特征分析
Fig.1 Micro-Doppler analysis of small unmanned helicopter
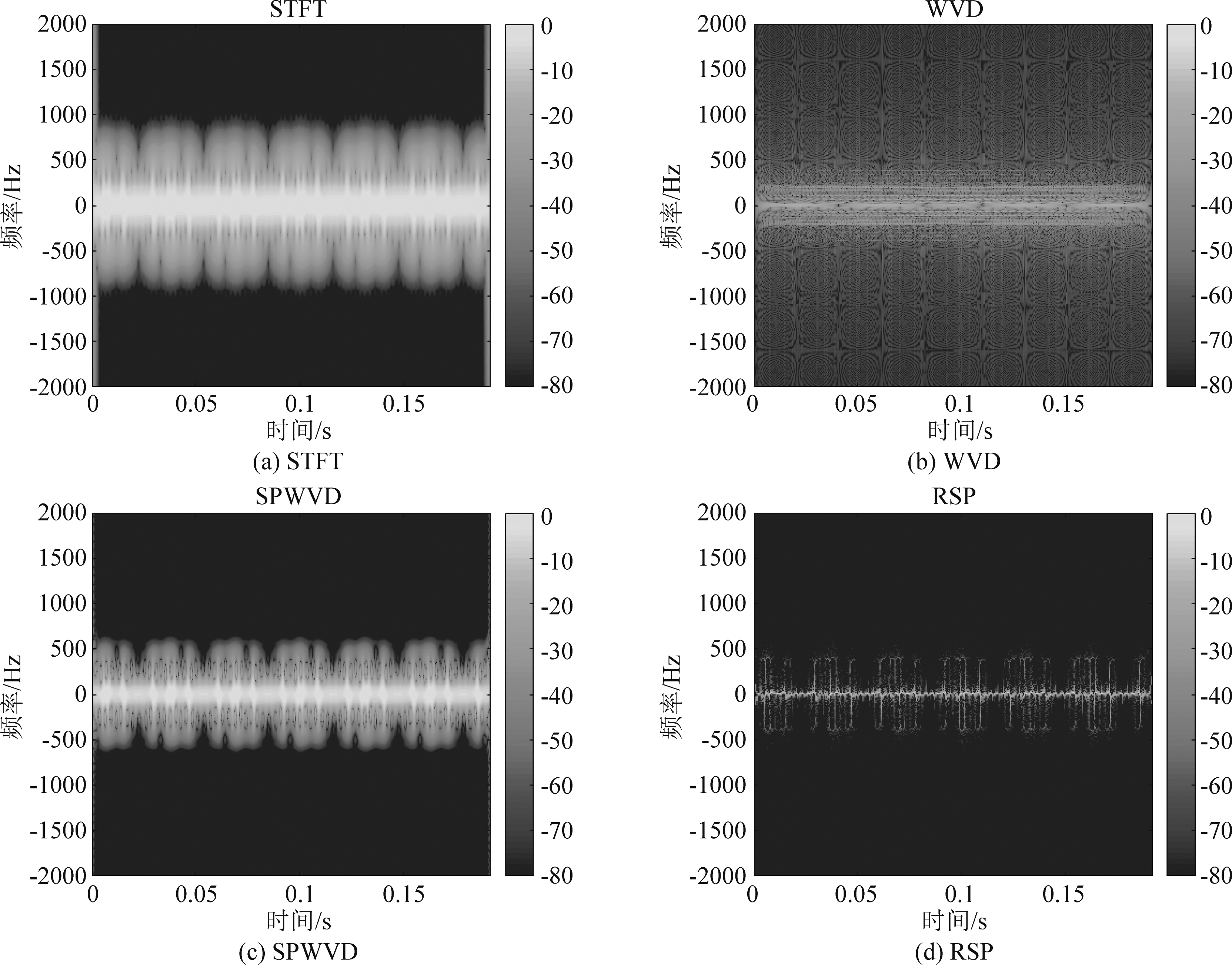
图2 四旋翼无人机微多普勒特征分析
Fig.2 Micro-Doppler analysis of quadrotor UAV
时频分析方法获取了无人机信号在时频域的能量分布,显示了旋翼叶片的闪烁特性,若要精确的估计微动参数进行旋翼无人机分类,还需在无人机微动特征分析的基础上进行微多普勒特征提取。
表3 对时频分析方法的评价
Tab.3 Evaluation of time-frequency analysis methods

方法评价STFT能够识别无人机旋翼的旋转特性,但受到时间分辨率和频率分辨率的折中。WVD时频分辨率达到最佳,但交叉项干扰严重,无法识别无人机信号。SPWVD抑制了交叉项的干扰,但由于窗函数的影响时频分辨率相比WVD有明显退化。RSP明显抑制了交叉项,分辨率得到有效提升,对无人机的分析结果相较于以上三种方法达到最佳。
3 旋翼无人机微动特征提取
对于传统的特征提取算法,如:EMD、SVD方法,对多分量信号而言提取效果欠佳,并且小型无人机的雷达回波较为微弱,同时多旋翼无人机不同旋翼初始相位的随机性,加大了识别目标的难度。在综合分析传统微动特征提取方法的基础上,本节引入CFD方法实现旋翼无人机微动特征的提取。
3.1 CFD方法
获得无人机雷达回波之后,用长度为N的窗函数对信号沿着时间维度滑动,被分成M个数据帧{x0,x1,...xM-1},得到一个N×M的数据矩阵S,第i个窗口xi的离散傅里叶变换为
Xi=miexp{jθi}
(5)
对时频图进行重排后得到数据矩阵RSP,通过对时频图沿着时间轴进行FFT得到CFD谱图,即[15]
CFD=Ft{RSP}
(6)
Ft表示对时频图沿着时间轴进行FFT。
由2.2节对旋翼无人机微动特征分析结果可知,CFD方法相当于对时频图中一系列周期性的脉冲串进行傅里叶变换,时频图中的多普勒信息维不变,而时间信息转变为Cadence frequency信息,它表示每个多普勒频率分量的重复频率,所以CFD谱图中提供了时频图中各个多普勒分量的频率、形状和大小信息。
3.2 旋翼无人机微动参数估计
对于多分量信号而言,峰值位置估计方法已无法准确估计信号的微动参数,在此基础上引入了极大值估计法[19]。此方法能够获取时频域中信号的瞬时能量,通过求得局部最值实现对多分量信号的精确估计。
对于旋翼无人机,当雷达波束垂直照射叶片时,叶片叶尖的径向速度最大,此时多普勒频率达到最大,则最大多普勒频率为
(7)
其中,λ为雷达波长,β为雷达相对于无人机质点中心的俯仰角,L为叶片长度, frot为转速。本文直接在RSP时频域中完成对fdmax的估计,无人机回波信号经时频变换后,各分量信号在时频域的局部峰值相当于在时频域的极大值。设RSP(n,m)为N×M的矩阵,为了减小噪声的影响,将时频矩阵通过设定的门限值,然后对时频矩阵的每列进行极大值搜索,即[19]
(8)
f1(∶,i)为第i列搜索到的极大值所在位置对应的多普勒频率,arg{·}为宗量运算,Peak[·]为求取极大值,因此f1中频率维所对应的多普勒展宽值为最大多普勒频率的估计值![]() 即
即
(9)
式(9), f1max与f1min分别对应f1中信号分量多普勒频率的最大值和最小值。
本文无人机每个旋翼的叶片个数为2,叶片闪烁频率为相邻闪烁所用时间的倒数。CFD谱图中Cadence frequency维代表了叶片闪烁频率信息,同理,对CFD矩阵每列进行极大值搜索,即
(10)
f2(∶, j)为第j列搜索到的极大值所在位置对应的多普勒频率, f2中在Cadence frequency维相邻分量的周期间隔为叶片闪烁频率![]() 因为叶片个数为2,则叶片闪烁频率为转速的2倍,即
因为叶片个数为2,则叶片闪烁频率为转速的2倍,即
(11)
得到转速![]() 和最大多普勒频率
和最大多普勒频率![]() 后,由此推导出叶片长度为
后,由此推导出叶片长度为
(12)
叶片长度主要与转速和最大多普勒频率有关,得到这两个参数之后,就可计算叶片长度。
实现旋翼无人机微动参数(转速、叶长等)的准确估计,对检测和识别无人机具有关键意义,同时也为无人机分类提供了重要的“线索”。
3.3 算法框图及实现步骤
基于RSP-CFD方法的旋翼无人机参数估计实现框图如图3所示,在获取无人机雷达回波数据之后,首先对回波信号在快时间维进行脉冲压缩,然后对信号进行时频分析获得时频数据矩阵,在时频图中获取最大多普勒频率信息,最后对时频矩阵沿着时间维作FFT提取无人机的叶片闪烁频率,进而实现转速和叶片长度的估计。
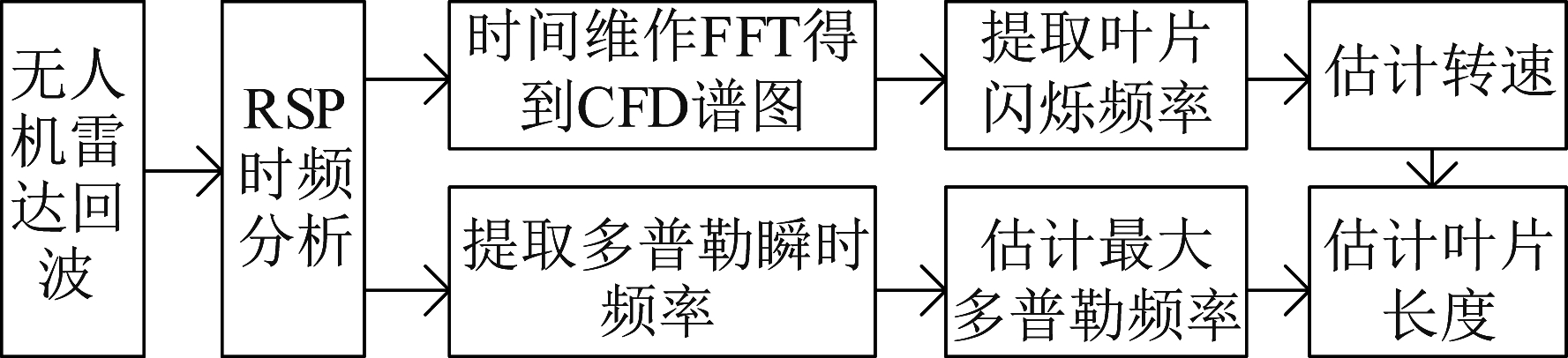
图3 RSP-CFD方法特征提取实现框图
Fig.3 Block diagram of RSP-CFD method feature extraction
对于传统的特征提取方法,具有“低慢小”特征的无人机容易受到噪声的干扰,再加上多旋翼无人机各个旋翼初始相位的随机性,导致不易提取无人机的微动特征。而本文方法在高分辨时频分析方法的基础上,利用CFD方法解决了无人机微动参数的难估计问题。
4 实验结果与分析
4.1 小型无人直升机微动参数估计
对于两个叶片的无人直升机,雷达参数和无人机参数不变(表1~表2所示),实验中均考虑无人机机身散射,设置信噪比为20 dB(无人机旋翼与噪声的实际信噪比为11 dB),图4为小型无人直升机微动参数估计结果。
对小型无人直升机的微动特征分析结果中,RSP方法展示了较高的分辨率,最大多普勒的理论值为3379.2 Hz,利用极大值法在时频谱图中得到的最大多普勒频率估计值为(3400-(-3384))/2=3392 Hz。CFD谱图中显示了时频图中频率分量的周期特性,叶片闪烁频率的理论值为 62 Hz,在图4(d)得到叶片闪烁频率的估计值为61.98 Hz。为验证此方法的性能,进行50次蒙特卡洛实验,计算结果如表4所示,转速和叶片长度的相对均方根误差分别为0.03%和0.49%,试验证明该算法能有效估计无人直升机的微动参数。
表4 无人直升机叶片长度和转速计算结果
Tab.4 Calculation results of blade length and speed of unmanned helicopter

真实值估计值相对均方根误差转速31 r/s30.99 r/s0.03%叶片长度473 mm473.09 mm0.49%
为分析不同信噪比本文方法对转速、叶片长度的估计精度,将信噪比设置为-8 dB,-5 dB,0 dB,5 dB,10 dB,15 dB,20 dB(此信噪比为无人机旋翼与噪声的实际信噪比),在每个信噪比进行50次蒙特卡洛实验,得到单旋翼无人机转速和叶长的相对均方根误差随信噪比的变化曲线如图5所示。
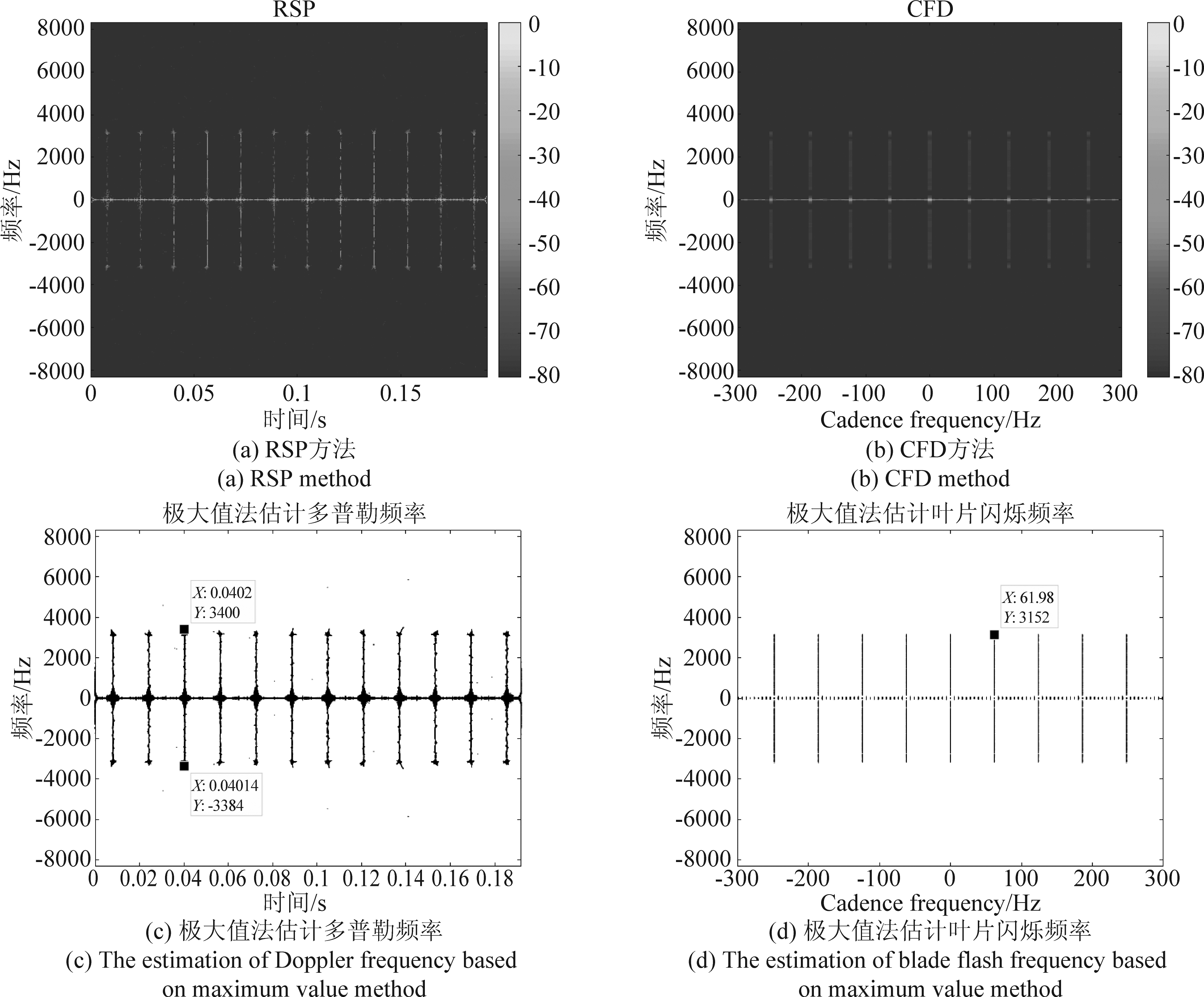
图4 小型无人直升机微动参数估计
Fig.4 Estimation of micro-motion parameters of small unmanned helicopter
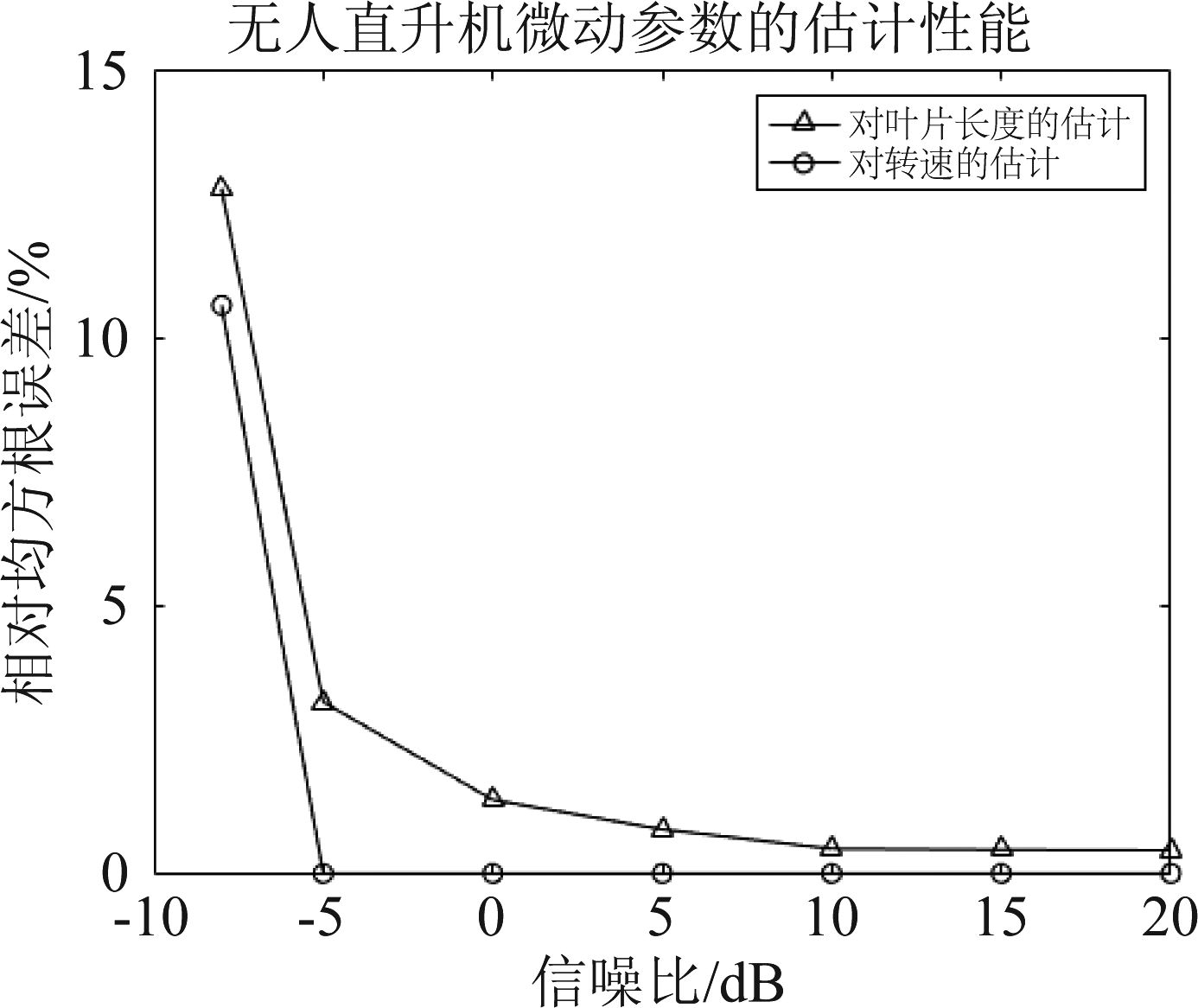
图5 小型无人直升机微动参数的估计性能曲线
Fig.5 The estimated performance curve of the micro-motion parameters of small unmanned helicopter
由图5可知,信噪比在-8 dB时转速和叶长的相对均方根误差分别达到10.61%和12.78%,估计精度会随着信噪比的增大而提升,当信噪比大于-5 dB时,两个微动参数的相对均方根误差均小于3.5%,当信噪比达到10 dB时,转速和叶长的相对均方根误差分别趋于0.03%和0.46%。因为叶片长度是由最大多普勒频率和转速决定的,对叶长的估计存在这两个参数的误差累积,所以转速的估计精度要比叶片长度估计精度高。
4.2 四旋翼悬停状态无人机微动参数估计
对空中悬停状态的无人机进行微动参数估计,雷达参数与无人机参数不变,四个旋翼的初始相位服从[-π,π]的均匀分布,设置信噪比为20 dB(无人机旋翼与噪声的实际信噪比为8 dB),图6为四旋翼无人机微动参数估计结果。
四旋翼无人机四个旋翼初始相位的随机性导致每个旋翼叶片出现的闪烁时刻有所不同,可能会出现交叠现象,但在RSP谱图中依然可以看到叶片的闪烁特性,最大多普勒的理论值为442.5 Hz,用极大值法得到的最大多普勒频率估计值为(441.6-(-429.4))/2=435.5 Hz。由于悬停状态四旋翼无人机每个旋翼的转速一致,因此具有唯一的闪烁频率,叶片闪烁频率的理论值为 32 Hz,在图6(d)得到叶片闪烁频率的估计值为32.03 Hz。进行50次蒙特卡洛实验,每次实验四个旋翼的初始相位随机,计算结果如表5所示,转速和叶片长度的相对均方根误差分别为0.09%和2.85%,结果表明该方法能够准确估计四旋翼无人机的微动参数。

图6 四旋翼无人机微动参数估计
Fig.6 Estimation of micro-motion parameters of quadrotor UAV
表5 四旋翼无人机叶片长度和转速计算结果
Tab.5 Calculation results of blade length and speed of quadrotor UAV

真实值估计值相对均方根误差转速16 r/s16.02 r/s0.09%叶片长度120 mm118.93 mm2.85%
同上,将信噪比设置为-8 dB,-5 dB,0 dB,5 dB,10 dB,15 dB,20 dB,在每个信噪比进行50次蒙特卡洛实验,每次实验保证四个旋翼初始相位的随机性,得到四旋翼无人机转速和叶长的相对均方根误差随信噪比的变化曲线如图7所示。
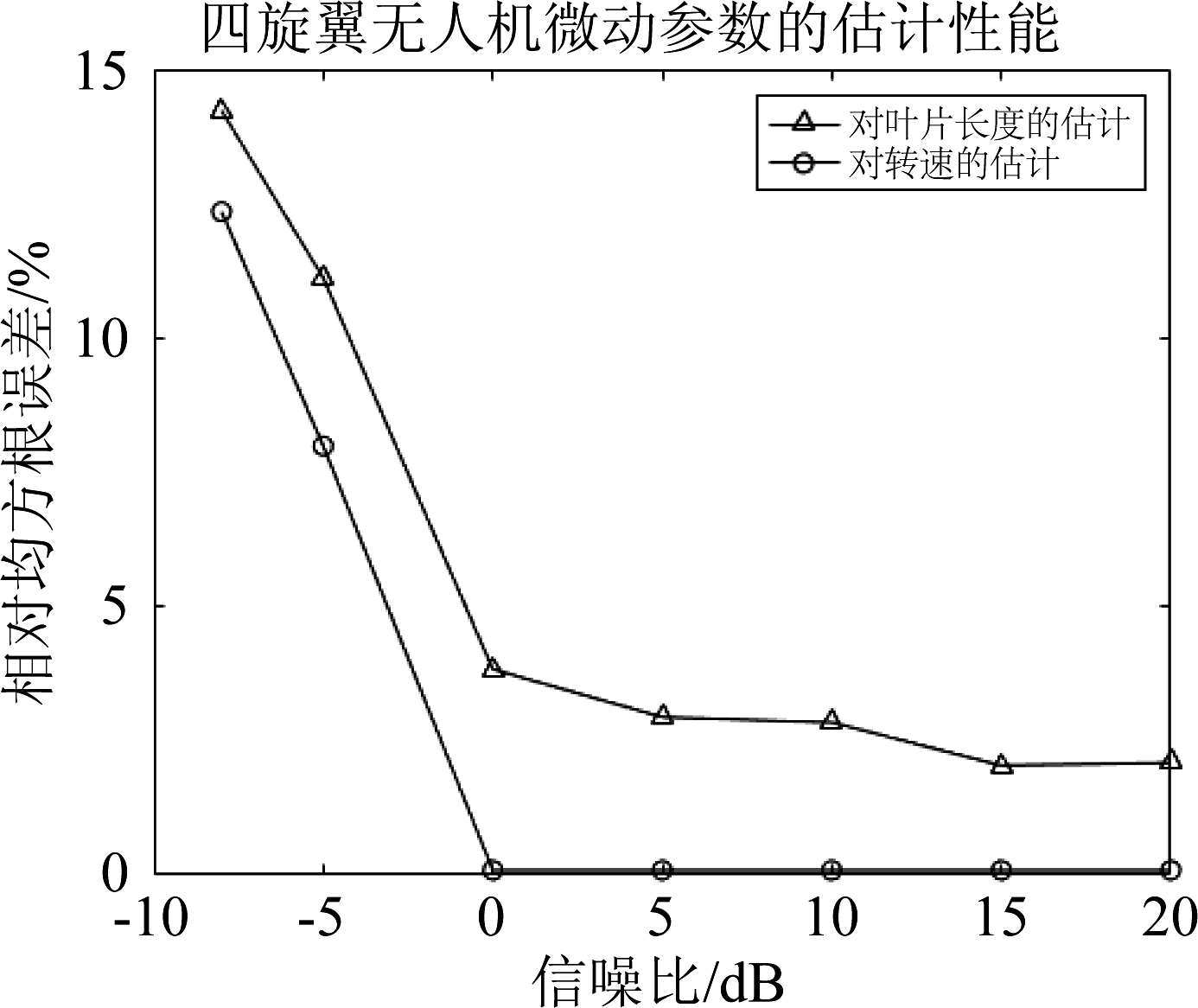
图7 四旋翼无人机微动参数的估计性能曲线
Fig.7 The estimated performance curve of the micro-motion parameters of quadrotor UAV
对四旋翼无人机而言,信噪比在-8 dB时转速和叶长的相对均方根误差分别达到12.35%和14.23%,当信噪比大于0 dB时,两个微动参数的相对均方根误差均小于4%,当信噪比达到15 dB时,转速和叶长的相对均方根误差分别趋于0.09%和2.09%。
4.3 本文方法参数估计性能分析
针对旋翼无人机微动参数估计,对RSP-CFD、STFT-CFD和正则化二维复对数谱的估计性能进行比较。首先在时频域中完成对旋翼无人机最大多普勒的估计,以四旋翼无人机为例,参数设置同4.2节(如表1~表2所示),图8(a)与(b)分别为RSP和STFT方法对四旋翼无人机的分析结果。
最大多普勒的理论值为442.5 Hz,结合极大值参数估计方法,RSP中得到的最大多普勒估计值为449.7 Hz,在STFT中得到的最大多普勒估计值为476.2 Hz, RSP的估计精度更高。由图8可知,RSP谱图重排方法有效抑制了交叉项,虽牺牲了分辨率,因为重排效应,RSP的时频分辨率相较于STFT要有优势,并且RSP对噪声并不敏感,所以在提取最大多普勒方面RSP方法要优于STFT方法。
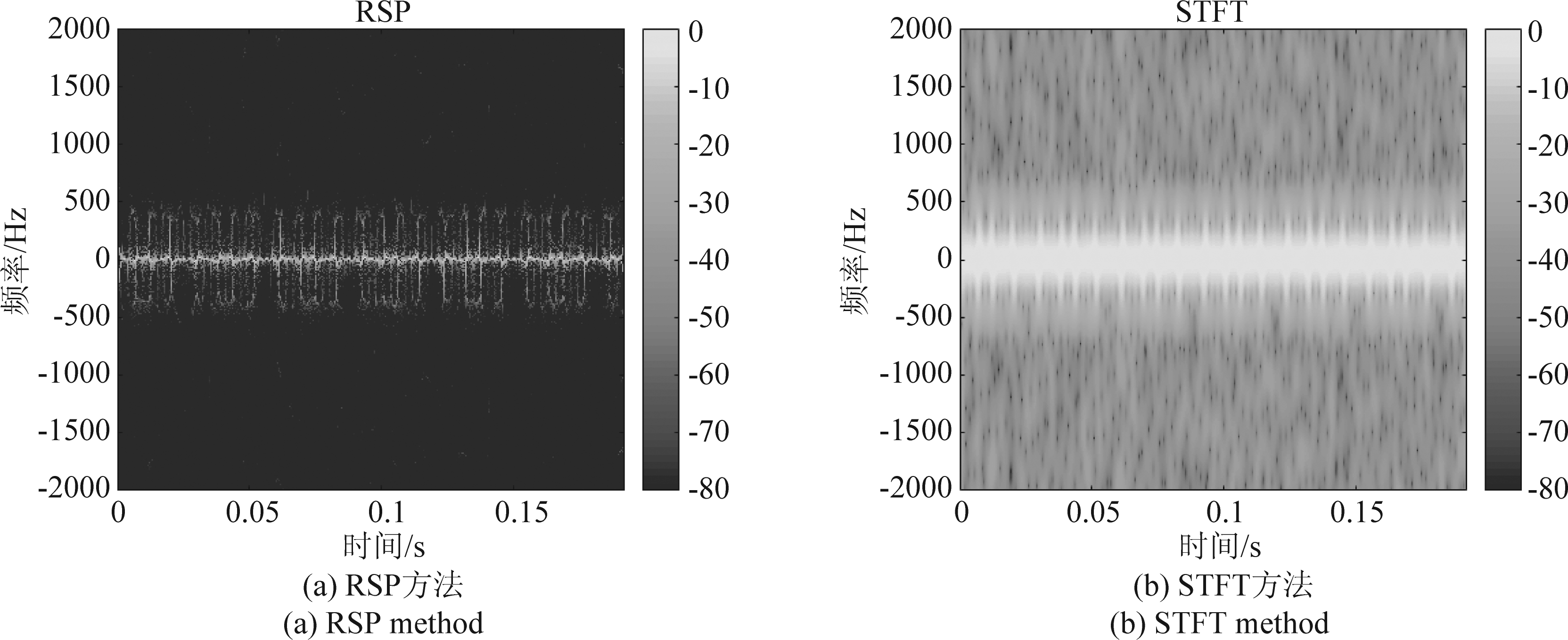
图8 四旋翼无人机微动特征分析
Fig.8 Micro-motion characteristics analysis of quadrotor UAV
在时频分析的基础上,对时频矩阵沿着时间轴进行FFT可以得到无人机的叶片闪烁频率,当对时频图进行CFD变换时,为减小由于FFT截断效应所导致的参数估计误差,先对时频图进行大约整数倍的周期截断,再进行CFD变换,减轻FFT带来的提取误差[20]。图9(a)、(b)和(c)分别为RSP-CFD、STFT-CFD和正则化二维复对数谱对四旋翼无人机特征提取的实验结果。
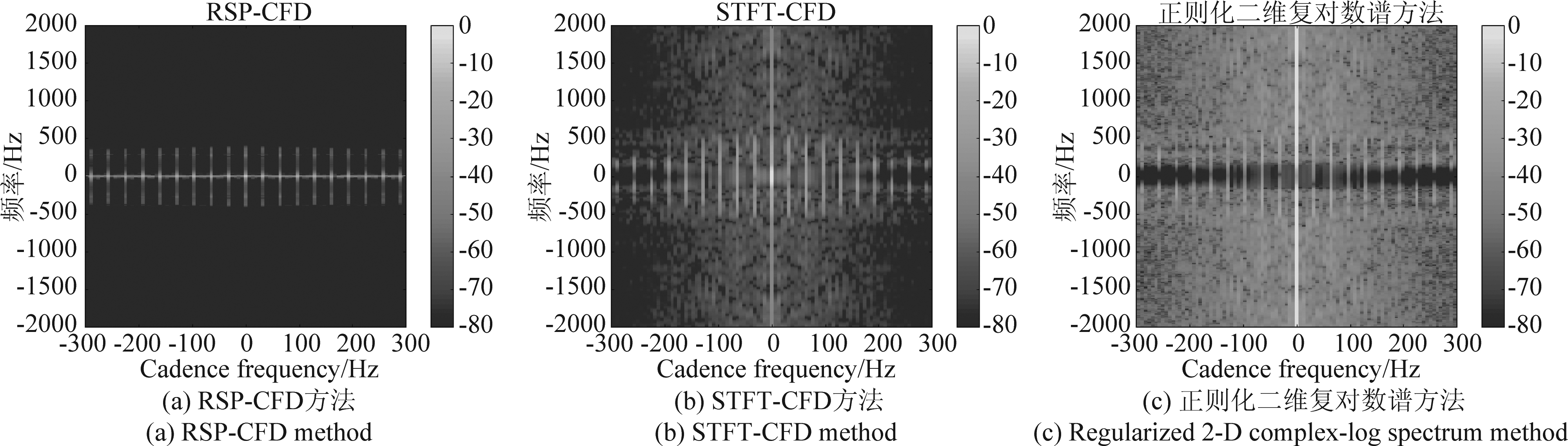
图9 四旋翼无人机微动特征提取
Fig.9 Micro-motion features extraction of quadrotor UAV
叶片闪烁频率的理论值为32 Hz,结合极大值参数估计方法,在RSP-CFD、STFT-CFD和正则化二维复对数谱中估计的叶片闪烁频率都为32.03 Hz。利用RSP方法对时频图进行重排时,其重排位置与信号的真实位置可能有微小的偏差,在此基础上进行CFD变换提取叶片闪烁频率,对其保留四位有效数字之后提取精度与STFT-CFD、正则化二维复对数谱方法一致,因此重排后的微小误差对闪烁频率的提取结果影响不大。正则化二维复对数谱方法增加了对时频矩阵取对数过程和正则化过程,且利用了时频谱的相位信息,能够提供更多的信息,对无人机分类方面有较好的效果,但对于无人机微动参数估计来说,相比RSP-CFD运算过程复杂,且提取效果并无优势。
5 结论
本文利用不同的时频分析方法对两种不同类型的无人机进行微多普勒特征分析,结果表明RSP方法的时频分辨率较高并明显抑制了交叉项,优于其他主流时频分析方法。针对旋翼无人机微动参数提取,在RSP特征分析方法的基础上,将CFD方法应用到无人机特征提取中,并进一步实现旋翼无人机转速、旋翼叶长等参数的估计,实验结果表明当信噪比大于0 dB时,该方法对悬停状态单旋翼和四旋翼无人机转速和叶长的相对均方根误差基本控制在4%以内。针对非悬停状态的四旋翼无人机,由于每个旋翼转速的不同和旋翼初始相位的随机性,时频谱图混叠严重,无法实现对转速和叶片长度的准确估计,在以后工作中会针对非悬停状态无人机微动参数估计进行研究。
[1] 张静, 张科, 王靖宇, 等. 低空反无人机技术现状与发展趋势[J]. 航空工程进展, 2018, 9(1): 1- 8.
ZHANG Jing, ZHANG Ke, WANG Jingyu, et al. A survey on anti-UAV technology and its future trend[J]. Advances in Aeronautical Science and Engineering, 2018, 9(1): 1- 8.(in Chinese)
[2] 袁延鑫, 孙莉, 张群. 基于卷积神经网络和微动特征的人体步态识别技术[J]. 信号处理, 2018, 34(5): 602- 609.
YUAN Yanxin, SUN Li, Zhang Qun. Human gait recognition based on convolution neural network and micro-motion feature[J]. Journal of Signal Processing, 2018, 34(5): 602- 609.(in Chinese)
[3] BJÖRKLUND S. Target detection and classification of small drones by boosting on radar micro-Doppler[C]∥2018 15th European Radar Conference (EuRAD). Madrid, Spain, 2018: 182-185.
[4] BOZDAG B O, ERER I. A comparative study on micro-Doppler signature generation methods for UAVs using rotor blade model[C]∥2019 International Conference on Electrical and Electronics Engineering (ICEEE). Istanbul, Turkey: IEEE, 2019: 298-301.
[5] KIM Y, NAZAROFF M, OH D. Extraction of micro-doppler characteristics of drones using high-resolution time-frequency transforms[J]. Microwave and Optical Technology Letters, 2018, 60(10): 2949-2954.
[6] WHITELONIS N, LING H. Radar signature analysis using a joint time-frequency distribution based on compressed sensing[J]. IEEE Transactions on Antennas and Propagation, 2014, 62(2): 755-763.
[7] RAM S S, LING H. Analysis of micro-Dopplers from human gait using reassigned joint time-frequency transform[J]. Electronics Letters, 2007, 43(23): 1309-1311.
[8] HARMANNY R I A, WIT J J M D, CABIC G P. Radar micro-Doppler feature extraction using the spectrogram and the cepstrogram[C]∥2014 11th European Radar Conference (EuRAD). Rome, Italy: IEEE, 2014: 165-168.
[9] HARMANNY R I A, WIT J J M D, CABIC G P. Radar micro-Doppler mini-UAV classification using spectrograms and cepstrograms[J]. International Journal of Microwave and Wireless Technologies, 2015, 7(3): 469- 477.
[10] 夏赛强, 朱名烁, 陈文峰, 等. 基于闪烁现象的旋翼微动特征提取方法[J]. 雷达科学与技术, 2019, 17(6): 671- 678.
XIA Saiqiang, ZHU Mingshuo, CHEN Wenfeng, et al. Feature extraction algorithm for micro-motion target based on flash phenomenon[J]. Radar Science and Technology, 2019, 17(6): 671- 678.(in Chinese)
[11] WIT J J M D, HARMANNY R I A, MOLCHANOV P. Radar micro-Doppler feature extraction using the singular value decomposition[C]∥2014 International Radar Conference. Lille, France: IEEE, 2014: 1- 6.
[12] OH B S, GUO Xin, WAN Fangyuan, et al. An EMD-based micro-Doppler signature analysis for mini-UAV blade flash reconstruction[C]∥2017 22nd International Conference on Digital Signal Processing (DSP). London, UK: IEEE, 2017.
[13] ZHAO Yichao, SU Yi. Sparse recovery on intrinsic mode functions for the micro-Doppler parameters estimation of small UAVs[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(9): 7182-7193.
[14] ZHANG Wenyu, LI Gang. Detection of multiple micro-drones via cadence velocity diagram analysis[J]. Electronics Letters, 2018, 54(7): 441- 443.
[15] REN Jianfeng, JIANG Xudong. Regularized 2-D complex-Log spectral analysis and subspace reliability analysis of micro-Doppler signature for UAV detection[J]. Pattern Recognition, 2017, 69: 225-237.
[16] 马娇, 董勇伟, 李原, 等. 多旋翼无人机微多普勒特性分析与特征提取[J]. 中国科学院研究生院学报, 2019, 36(2): 235-243.
MA Jiao, DONG Yongwei, LI Yuan, et al. Multi-rotor UAV’s micro-Doppler characteristic analysis and feature extraction[J]. Journal of University of Chinese Academy of Sciences, 2019, 36(2): 235-243.(in Chinese)
[17] 魏庆国, 吴建华. 非平稳信号时频分析的重排方法及其在语音信号处理中的应用[J]. 南昌大学学报(理科版), 2004, 28(2): 74-77.
WEI Qingguo, WU Jianhua. Reassignment-based nonstationary signal time-frequency analysis & its application in speech signal processing[J]. Journal of Nanchang University(Natural Science), 2004, 28(2): 74-77.(in Chinese)
[18] AUGER F, FLANDRIN P. Improving the readability of time-frequency and time-scale representations by the reassignment method[J]. IEEE Transactions on Signal Processing, 1995, 43(5): 1068-1089.
[19] 黄志星. 基于微多普勒的空间多目标特征提取与参数估计[D]. 成都: 电子科技大学, 2014.
HUANG Zhixing. Signatures extraction and parameters estimation of spatial multi-target based on micro-Doppler[D]. Chengdu: University of Electronic Science and Technology of China, 2014.(in Chinese)
[20] 王艳芬, 王刚, 张晓光, 等. 数字信号处理原理及实现[M]. 北京: 清华大学出版社, 2008: 96-108.
WANG Yanfen, WANG Gang, ZHANG Xiaoguang, et al. Digital signal processing principle and implementation[M]. Beijing: Tsinghua University Press, 2008: 96-108.(in Chinese)



