1 引言
用分布式多传感器网络跟踪多个目标,相对于用集中式多传感器跟踪多个目标,有着不依赖任意网络节点、增加/删除节点灵活、鲁棒性强等方面的优势[1-3]。因此,用分布式传感器网络跟踪多个目标运动是如今的研究热点。
在分布式传感器网络中,每个传感器都有信息感知、计算和信息传递的功能。在每个时刻,每个传感器生成一组量测信息(包括目标的量测和杂波),并迭代的向其邻居传感器传递并共享信息,该信息可能是量测信息[4-5]、目标的先验/后验密度信息[6-10]、目标的估计或航迹[11-13]。在达到最大的迭代次数后,所有的传感器达成共识,即便经过更多次迭代,分布式网络上的各个传感器的量测信息不再变化。
现有的多传感器多目标跟踪算法,大多是基于马尔科夫-贝叶斯模型,如分布式PHD滤波器[14-16],这些滤波器的跟踪性能依赖先验信息与实际场景的一致程度,在实际应用中存在以下问题:
(1)需要诸如目标的数目、出现和消失的时间、运动模型等先验信息,而这些先验信息在实际目标运动场景中可能因环境噪声过大而不准确并造成目标跟踪精度下降。
(2)运行比较复杂,这意味着当传感器的功率受限时,运行复杂的滤波器不能对目标实时跟踪。
为了解决上述问题,文献[17]提出了一种仅依赖传感器量测的数据驱动算法,泛洪聚类(flooding then clustering,FTC)算法,FTC算法通过泛洪(Flooding)[18]共识算法,将共享的量测集通过DBSCAN算法[19]和k-means算法[20]进行聚类,聚类得到的簇的中心即估计的目标的位置,簇的个数为目标的个数。相对于分布式PHD算法,FTC算法在计算速度和跟踪精度上均取得了较好的效果[17]。但是,FTC算法依赖DBSCAN算法的聚类效果。分布式传感器在不同的迭代次数,共享的量测数据点的局部密度变化较大,用同样的参数,DBSCAN算法的聚类性能会有所下降,而DBSCAN算法的参数推断是DBSCAN算法的一个固有难题。当传感器的量测为非线性时下降更为严重,参考文献[17]第5节。为了改善以上问题,本文提出了一种改进的密度峰值聚类[21](Improved density peaks clustering, IDPC)算法,如3.2节所示,改进后的算法更加高效。本文提出的算法包括以下三个步骤:
(1)通过分布式泛洪共识算法[18]在每个传感器之间迭代的传递、共享量测数据。
(2)每个传感器将共享的量测数据转换为二维笛卡尔坐标系中的点。
(3)将这些数据点的集合用IDPC算法进行聚类,聚类得到的每个簇为某个目标的观测集,簇的个数即为目标的个数、聚类中心即为目标的位置。
本文提出的算法在三种场景中与迭代校正PHD(iterated corrector PHD, IC-PHD)滤波器[15],FTC算法[17],算术平均PHD(arithmetic average PHD, AA-PHD)滤波器[22-23]进行对比,对于AA-PHD滤波器和IC-PHD滤波器,提供了满足其最佳性能所需的先验信息。相反,IDPC算法和FTC算法不需要上述先验信息,仅仅通过各个传感器的量测即可检测和估计各个目标。
2 问题描述
2.1 符号与假设
分布式传感器网络可以用图的形式来表示,该图由传感器的集合S={1,2,…,s}和边的集合ε⊆S×S组成。边是由两个有序的传感器对(i, j)∈ε组成的,传感器j可以直接连接传感器i,其中传感器j是传感器i的外邻居(out-neighbor)传感器,传感器i是传感器j的内邻居(in-neighbor)传感器。我们定义内邻居传感器的量测集Nj,Nj
{i∈S|(i, j)∈ε,i≠j}。此外,传感器j的第
次迭代构成的传感器的集合表示为
则Nj(1)=Nj,Nj(0)=j。
如果分布式传感器网络中任意一个传感器经过有限次的迭代,可以到达传感器网络中的另一个传感器,则称该传感器网络构成的图为强连接(strong connected,SC)网络。两个传感器之间的最大距离Dm称为图的直径。
对于存在漏检和虚警情况下的多目标跟踪问题,我们有以下假设:
(1)在任意时刻,目标的数目Nk和状态Xk均是随机的;
(2)每个目标只产生一个量测数据,各个传感器的量测数据相互独立;
(3)每一时刻每个传感器的杂波个数由泊松率控制,随机产生且杂波的密度远小于目标的量测的密度。
2.2 分布式传感器网络及泛洪共识算法
在本文中,我们采用分布式泛洪算法[18]在传感器网络上传递各自的量测数据,通过该方法,所有传感器都将信息同步的传递到相邻的传感器。假设网络是SC网络,则分布式传感器网络中的每个传感器能够在Dm次迭代之后达成共识(即每一个传感器具有完全相同的量测集)。尽管泛洪共识算法对本地传感器的存储和通信能力提出了很大的挑战,但在传感器具有足够的存储和通信能力的某些应用中,有收敛速度快的优点。
简而言之,每个传感器都存储了当前所有已知传感器的初始数据表(每个传感器的id)。在第t∈{1,2,…}次通信迭代时,分布式传感器网络上的每个传感器向其第t个互连的邻居传感器更新数据表的内容,并传递/共享数据表中传感器的量测数据集。具体而言,每个具有Zi={z1,z2,…},i∈S的传感器的量测集将在第
次迭代更新为Zi(t)。我们使用Zi(0)=Zi表示在传感器i∈S的初始测量值[18]。
当t=1时,每个传感器从其内邻传感器接受量测集。
(1)
当t≥2时,每个传感器收集其内邻居传感器在先前迭代中已收到的新的量测集。
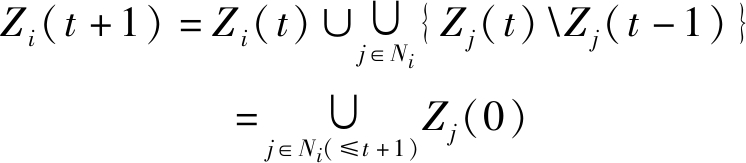
(2)
其中,A\B代表集合A和B的集合差,即属于A而不属于B的所有元素的集合。
当t≥Dm时,分布式传感器网络中每一个传感器中的量测数据将全部相同。
(3)
2.3 基于量测数据的推断
我们将分布式多目标跟踪问题定义为通过量测数据来估计目标的位置和个数。为了简化问题,我们将研究重点放在两种类型的传感器上:线性传感器和非线性传感器,这两种类型的传感器的量测数据均被投影在二维平面上,并进行聚类[24]。
线性位置量测模型如下
(4)
其中,[px,k,py,k]T是目标的位置,νk,1和νk,2是相互独立的量测噪声。
线性量测在状态空间的无偏估计如下
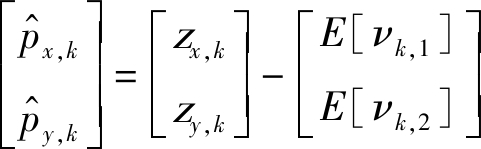
(5)
其中,E[νk,1]和E[νk,2]为量测噪声νk,1和νk,2的平均值。非线性量测模型如下
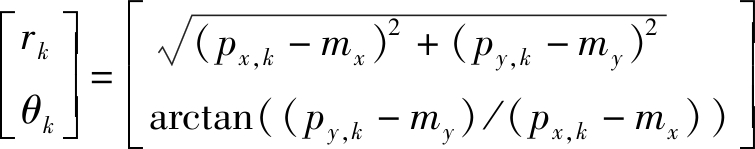
(6)
其中,[mx,my]T是传感器的位置,νrk和νθk是影响范围和角度的噪声。
非线性量测在二维空间的投影如下:
(7)
其中,
和
依赖目标在传感器感应范围的象限[17,24]。
2.4 聚类约束
经过tmax次量测数据迭代传输后,每个传感器汇总的量测集(杂波和目标的量测)将达成共识。将汇总的量测集投影到二维空间,可以发现:目标的量测集聚集的地方,局部密度较高;杂波的局部密度较低。则可以通过一种密度聚类算法对量测集进行聚类,滤除杂波,从而筛选出目标的量测形成的簇,簇的中心即目标的状态、簇的个数即为目标的个数。为了得到更准确的聚类结果,需要遵守以下几个约束条件。
(1)聚类得到的每一个簇Ci,其期望的大小E[|Ci|]应该在⎣NS(≤tmax)/2」和|NS(≤tmax)|之间,在已知迭代次数和给定传感器目标检测概率的情况下,可以认定E[|Ci|]=r,r为一个常数。
(2)重叠簇是指相互靠近的两个或者更多个目标的量测相互重叠,造成簇的大小特别大,需要将其划分为满足约束(1)的子簇。
(3)聚类后目标的量测形成的簇,来自每个传感器的量测数据点应该小于等于1。
3 本文提出的算法
3.1 密度峰值聚类算法
2014年,密度峰值聚类算法[21](density peaks clustering, DPC)发表在《科学》杂志上。DPC算法属于密度聚类算法范畴,其核心思想是聚类中心具有较高的局部密度和相对较远的距离。截断距离dc是唯一需要的参数,可以通过用户自定义或者在线学习来计算得到。DPC算法需要计算两个量:局部密度ρi和距离δi。局部密度ρi定义为:
(8)
其中dij是数据点的距离矩阵,χ(x)是一个分段函数,当x<0时,χ(x)=1;当x≥0时,χ(x)=0。dc是截断距离,可以通过预定义或从数据集中学习[17,21]。ρi在数值上等于数据点截断距离内的点的个数。ρi越大,表明数据点i的局部密度越大,其是目标的量测的可能性越大。
DPC算法定义δi为数据点i与局部密度更高的数据点j的最小距离
(9)
自DPC算法发表以来,诸多学者提出了基于DPC算法的改进算法,如:边缘检测密度峰值[25](boundary detection density peaks clustering, BDDPC)和密度峰值k最近邻[26](density peaks clustering k nearest neighbor, DPC-KNN)。纵观这些改进的算法可以发现,这些算法基本都是在DPC算法上做“加法”,如BDDPC算法将DPC算法与不对称度量相结合;DPC-KNN算法将DPC算法与KNN算法相结合。以上这些改进算法无疑又增加了DPC算法的运算耗时。分析DPC算法,其运算耗时主要是局部密度ρi和距离δi的计算耗时。根据文献[21]的数据集,经过计算我们发现:计算变量ρi的耗时tρ与计算变量δi的耗时tδ二者的关系为:tδ≈0.562tρ。如何在不降低跟踪效率的情况下减少tρ和tδ,是加速DPC算法的关键。
3.2 本文所提出的算法
本文提出一种改进的DPC算法(improved density peaks clustering, IDPC),该算法仅仅通过局部密度ρi即可求得多个传感器量测数据的聚类中心,与原始的DPC算法相比,在保证聚类精度的同时,节省了计算距离δi的时间。在二维空间中,目标的量测围绕在目标真实位置周围,而杂波服从泊松分布,随机分散在空间中,多个传感器的量测叠加,会造成目标的量测局部密度较大,而杂波的局部密度较小。我们可以设定阈值,当量测数据点的局部密度大于阈值时,判定其为目标的量测,当量测数据点的局部密度小于阈值时,则判定其为杂波。在给定传感器检测概率的情况下,目标的量测的集合可以定义为:
(10)
其中CT是目标的量测集,n是传感器的数目,l是一个常数,l∈[0.2,0.4]。l的选取依赖目标生成的量测数据点的局部密度,在非线性传感器组成的分布式传感器网络中,目标生成的量测数据点在空间上更为分散,导致截断距离内的数据点的个数较少,即ρi相对较小,l∈[0.2,0.3];在线性传感器网络中,目标的量测数据点在空间上较为集中,导致截断距离内的数据点相对较多,ρi相对较大,l∈[0.3,0.4]。ρi≥l×n是指数据点i截断距离内的数据点的数目必须大于阈值l×n。
在求得CT的情况下,可以通过公式(11)来求得目标的个数,目标的个数正确与否直接关系着聚类的精度和准确度。
(11)
对于任意一个目标生成的量测数据点形成的簇,其目标的个数为
(12)
在给定CT和∑ki条件下,通常情况下优先考虑用k-means算法[20]进行聚类,但在实验的过程中,我们发现,在数据集中有重叠簇的情况下,k-means算法得到的聚类结果往往不满足CL约束。为了解决这个问题,文献[27]提出了多源密度峰值聚类(multi-source density peaks clustering,MSDPC)算法,MSDPC算法首先判断CT中有无重叠簇,然后根据有重叠簇和无重叠簇两种情况分别进行处理:在数据集中无重叠簇的时候,通过k-means算法对CT进行聚类,k可以通过公式(11)计算得到;在数据集中有重叠簇的情况下,要先计算ρi和δi来确定初始聚类中心,再对重叠簇进行二次聚类,详细过程参考文献[27]第3节。MSDPC算法的不足之处是:k-means算法是一个多次迭代的过程,比较耗时,且在同样的参数CT和∑ki条件下,多次聚类其聚类结果可能有差异;其次,当数据集中有重叠簇时,需要计算δi,增加了耗时。IDPC算法可以有效解决MSDPC算法的上述问题。
在本文中,在得到CT和∑ki的情况下,根据这样一个先验规律:CT中ρi最大的数据点max(ρi)为局部密度最大的点,也是当前局部密度最大的某个簇的中心。通过迭代的查找CT中局部密度最大的数据点max(ρi)及其截断距离内的数据点的集合,即可将CT中的数据点分配给多个簇,根据每个簇的数据点的数目,判断该簇是否为重叠簇。对于非重叠簇,每个簇的数据点的坐标平均值即为估计的目标的位置;对于有重叠簇的情况,通过k-means算法对重叠簇进行二次聚类。IDPC算法的具体步骤如下所示。
IDPC算法输入:CT和∑ki。输出:簇Ci及其聚类中心z^i, i∈{1,2,…,k}。1. 查找CT中的局部密度最大的点ρj,并求点j的截断距离dc′内的点集Cj,dc′=mdc,m∈[1.1,1.5]。CT=CT\Cj。2. 重复步骤1,直到CT=。检查簇Cj与其他簇Ce有无交集,j,e∈[1,2,…,k],j≠e。如果Cj∩Ce≠,则Cj=Cj∪Ce,Ce=。3. 根据每个簇Cj的大小,如果Cj为重叠簇,则用k-means算法求子簇及其聚类中心,如果Ci为非重叠簇,则簇Ci的聚类中心为各个点的横纵坐标平均值。
4 实验对比
本节的主要目的是将IDPC算法与FTC算法[17]、分布式PHD算法[15,22-23]在三个不同场景进行对比,来证明IDPC算法的有效性和可靠性。目标运行的区域范围为[-1000,1000]×[-1000,1000](m),实验所用到的目标模型、参数、实验场景以及传感器拓扑和文献[17]一致。考虑了具有不同网络拓扑和目标轨迹的两种情况。实验一和实验二的分布式传感器网络是由20个具有线性或非线性测量模型的传感器(Dm=4)组成,如图1所示,实验三的分布式传感器网络是由18个传感器(线性和非线性传感器各占一半,Dm=5)组成,如图4所示。
新生目标的状态
其高斯分量分别为:m1=[-100,10,-800,30]T,m2=[-800,20,-500,0]T,m3=[0,0,950,-30]T,Qr=diag([100,25,100,25]T)。Qr为其方差。每一个目标的生存概率均为0.98,且每一个目标有一个恒定的速度,其值与文献[17]相同。状态转移噪声为
以上有关目标的统计信息是提供给PHD滤波器的,以获得最佳性能,FTC算法和IDPC算法仅仅需要各个传感器的量测集,截断距离可以实现给定或从传感器的量测中学习得到[28]。每个场景均使用随机生成的量测数据但目标轨迹相同,进行了100次蒙特卡洛实验。每次运行包含60个时刻。我们用最佳子模式分配(optimal sub-pattern assignment, OSPA)度量[29]用于评估位置估计精度,其中截止参数c=1000,顺序参数p=2。此外,我们将网络OSPA定义为分布式网络中所有传感器在每个采样步骤获得的OSPA的平均值,而时间平均网络OSPA则定义为所有过滤步骤中网络OSPA的平均值[22-23]。
为了评估通信成本,一个高斯分量由权重参数(1个元组),4维矢量均值(4个元组)和4×4对称矩阵协方差(10个元组),共15个元组组成。目标个数参数为1个元组,每个加权粒子取5个元组(状态向量为4个元组,权重为1个元组)。
4.1 线性传感器网络
图1给出了传感器网络拓扑和目标的轨迹,每个传感器运行一个线性量测模型,其中
我们假设每个传感器的目标检测概率为pD(xk)=0.95,对于PHD滤波器来说,权重小于10-4的高斯分量被裁剪掉,马氏距离小于4的两个高斯分量参与融合,最大的高斯分量数目为100。分布式PHD滤波器在每次迭代过程中按照部分共识传递部分权重较大的高斯分量[22],融合后权重大于0.1的高斯分量在相邻的传感器之间互相传递。
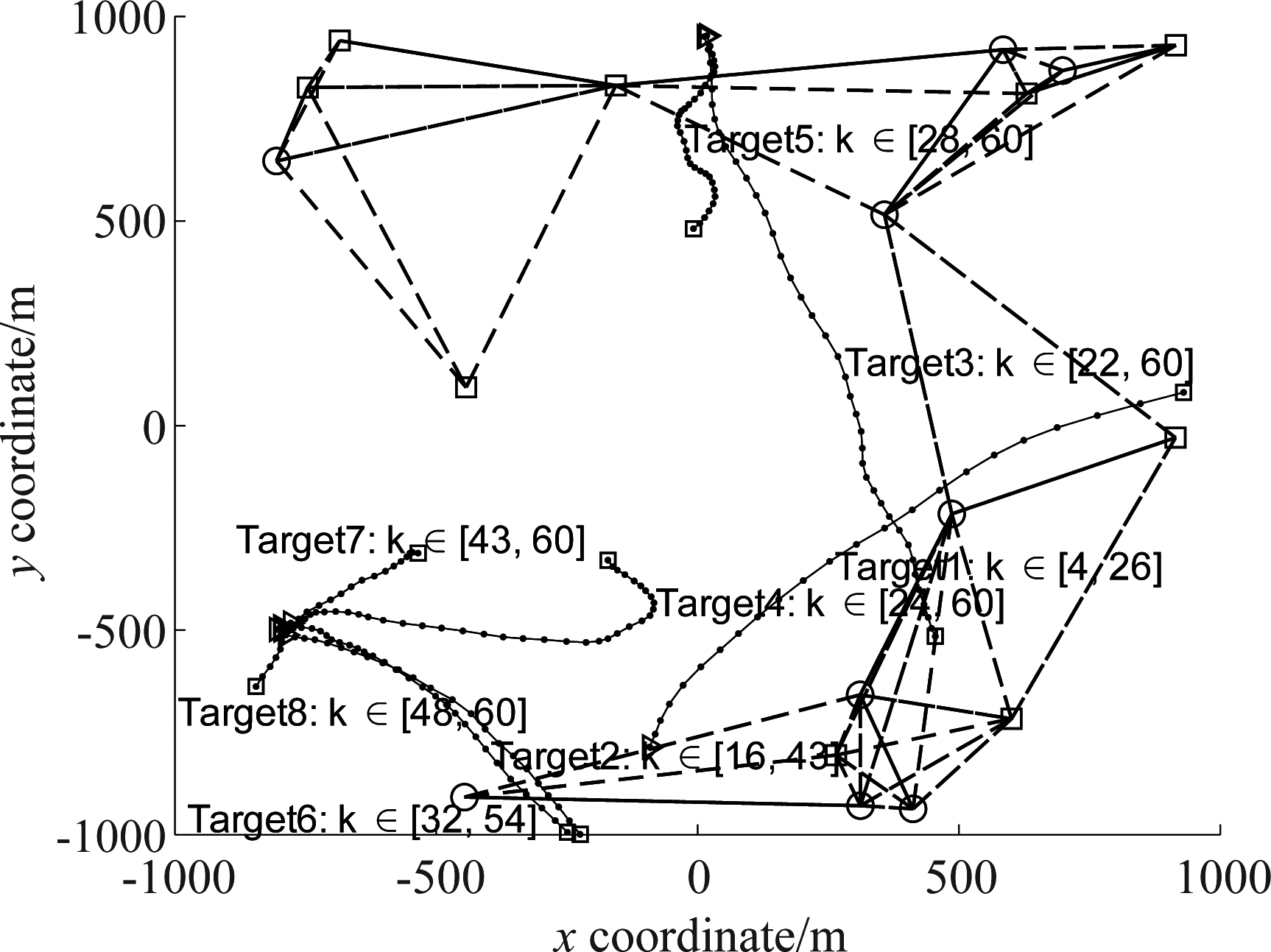
图1 场景1:每个目标从“△”位置开始运动并终止运动于“□”位置,分布式传感器网络用虚线相连
Fig.1 Scenario 1: each target starts at ‘△’and ends at ‘□’and links between neighbor sensors are given in dash lines
当迭代次数为4的时候,传感器网络的OSPA,平均目标数目估计和每次迭代步骤的平均计算时间在图2第一行中分别给出。不同迭代次数(从t=0到t=4),时间平均网络OSPA和不同方法的网络通信成本在图2第二行中给出,图3和图5第一行与第二行与图2类似。不同算法的比较结果为:
(1)滤波精度方面
随着泛洪迭代次数的增加,四个算法的OSPA均相应的减少,但通信代价随之增大。算术平均融合方法明显优于对传感器顺序敏感的IC-GM-PHD滤波器[20]。我们注意到,这个问题可以在近似乘积的多传感器PHD滤波器中得到缓解[4],但是其运算比较耗时,并导致了一个比例失衡[30]的新问题,并且随着传感器数量的增加,问题变得更加严重。
当t=0时,IDPC算法和FTC方法的性能较差,因为单个传感器的量测数据中,杂波和目标的量测的局部密度相同,无法通过聚类对其进行区分。当t≥1(即相邻传感器进行通信),IDPC和FTC算法其性能优于IC GM-PHD滤波器。
当t≥2时,IDPC算法和FTC算法表现优异,且优于其他的算法,且IDPC算法和FTC算法的通信成本和耗时优于其他两种算法,IDPC算法的耗时最低。IPDC和FTC算法在滤波精度上有优势的主要原因为:给定的噪声是零均值噪声,聚类算法可以得到比基于模型的方法更无偏的估计值。
(2)通信方面:IDPC,FTC和IC-GM-PHD算法通信成本相同,且远低于AA-GM-PHD算法。
(3)计算耗时:IDPC算法的计算速度最快,FTC算法的计算速度第二,IC-GM-PHD算法最为耗时。多传感器IC-GM-PHD滤波器需要迭代更新步骤,并且计算成本最高。
4.2 非线性传感器网络
在本实验中,传感器网络拓扑结构以及目标轨迹和场景1完全相同,其区别为该实验用到的传感器为非线性传感器,每个非线性传感器的检测范围是一个围绕每个传感器位置的半径为3000 m的圆形区域。传感器的量测模型如公式(6)所示,其中
其中σr=10 m,σθ=π/90 rad/s。传感器的位置为[ma,x,ma,y],其目标检测概率为pD(xk)=0.95。杂波均匀分布在视场区域,杂波率为10。
图2 线性传感器网络:不同算法性能对比和不同t的平均性能
Fig.2 Linear sensor network: average performance of different approaches over the filtering time and against different t
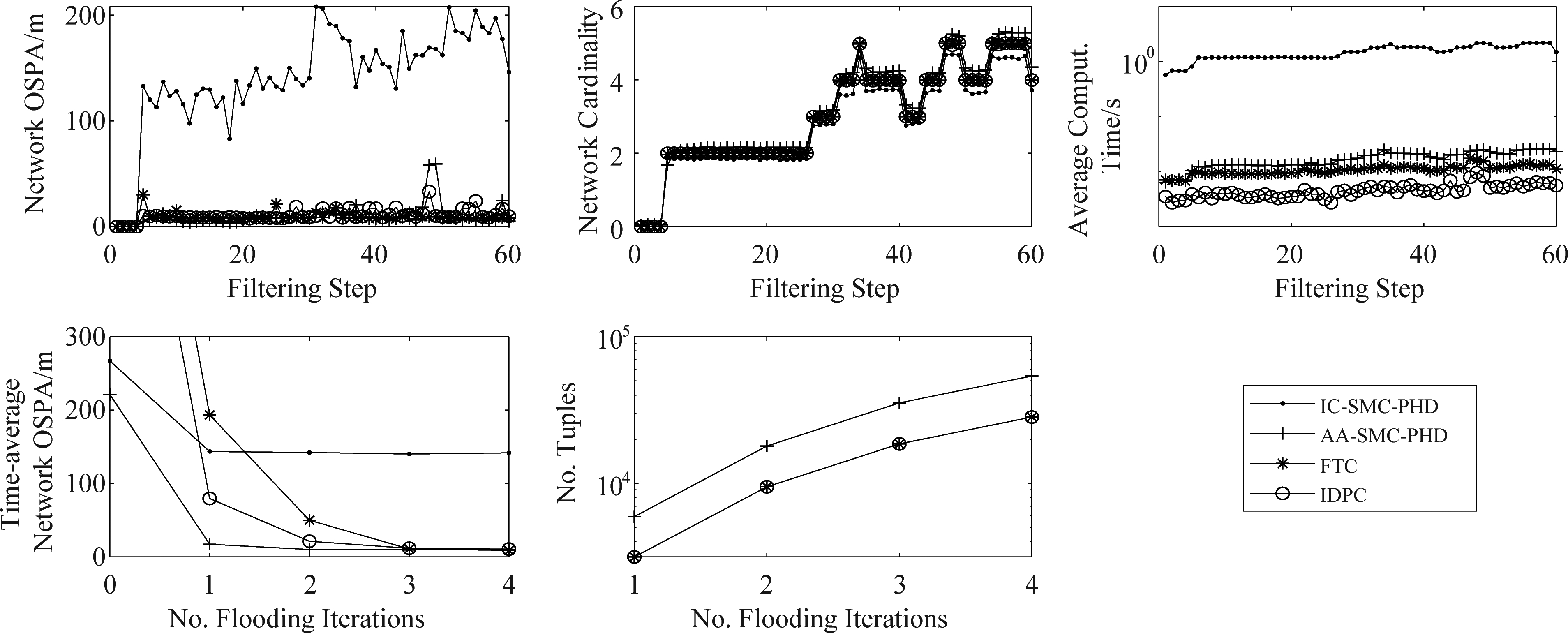
图3 非线性分布式传感器网络:不同算法性能对比和不同t的平均性能
Fig.3 Nonlinear sensor network: average performance of different approaches against the filtering time and against different t
以上这些参数是为AA-SMC-PHD算法[23]和IC-SMC-PHD算法[15]提供的。AA-SMC-PHD算法的计算流程,参考文献[23]第4节的内容。由于在非线性场景中,目标产生的量测较为分散,IDPC算法采用高斯核函数来计算ρi,比较耗时,但是有不错的估计精度。对于IC-SMC-PHD滤波器,我们采用k-means聚类应用于粒子集以进行估计[31],但是该策略表明,目标检测精度较低。仿真结果如图3所示,相对于图2的实验结果,两次实验结果基本一致,除了以下区别:
(1)IDPC算法和FTC算法在非线性模型的情况下,相对于线性模型,其计算时间有所增加,主要原因是公式(7)的非线性转换的耗时。
(2)随着迭代次数t的增加,IDPC算法、FTC算法的平均OSPA和AA-SMC-PHD滤波器收敛到几乎相同的水平,IDPC算法相对于FTC算法,收敛速度更快,但是Dm=4时,其OSPA误差稍大。
(3)当t=0时,IC-SMC-PHD的性能比其他AA-SMC-PHD滤波器差,这是因为用于估计的粒子上的k-means聚类较差。
4.3 混合传感器网络
在本实验中,传感器网络同时包含线性传感器和非线性传感器,网络拓扑最大迭代次数为Dm=5,分布式网络和目标运动轨迹如图4所示。FTC算法和IDPC算法将两种传感器的量测数据投影到空间坐标系,作为对比,线性传感器运行GM-PHD滤波器、非线性传感器运行SMC-PHD滤波器,传感器之间传递高斯分量,并进行融合。
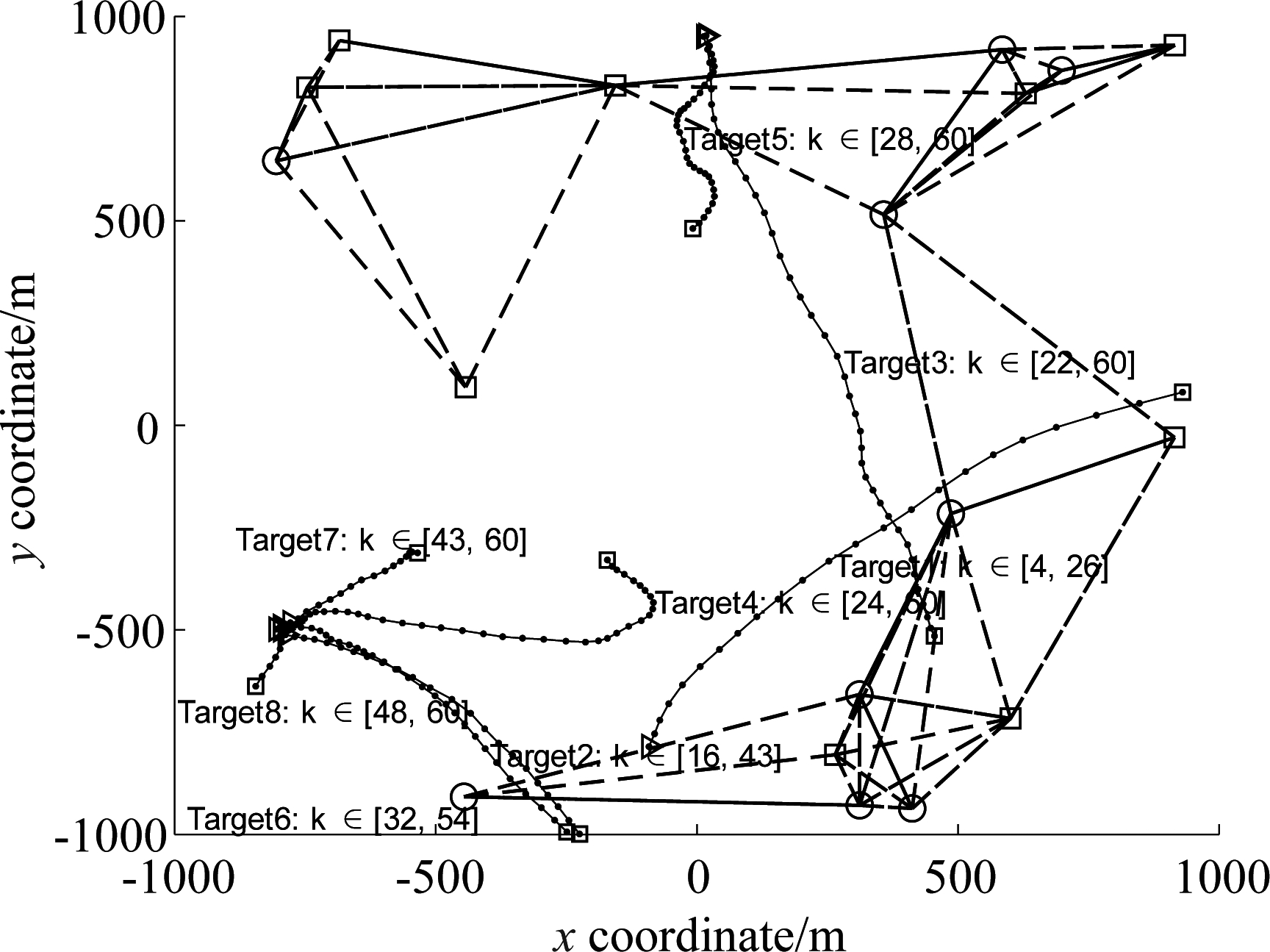
图4 场景2:包括8个目标和18个传感器
Fig.4 Scenario 2 consisting 8 targets and 18 sensors
实验结果对比在图5中给出。IDPC算法和FTC算法均有较低的运算量和较高的融合精度,并且不需要任何先验信息。我们可以看到,基于模型的PHD滤波器,其精度并不能随着传感器数量的增多而提高。FTC算法比IDPC算法精度要高,但是在运算时间上,IDPC算法运行时间要小于FTC算法。
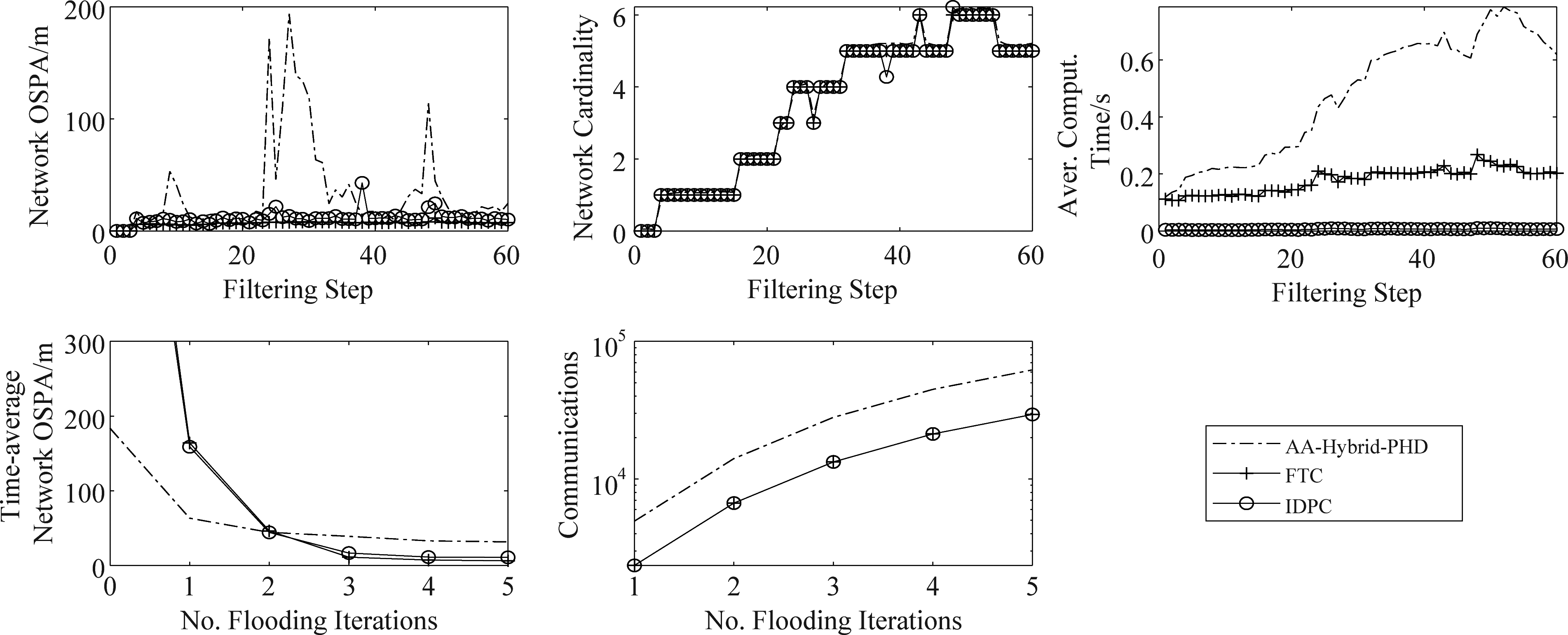
图5 混合传感器网络:不同算法性能对比和不同t的平均性能
Fig.5 Hybrid sensor network: average performance of different approaches over the filtering time and against different t
5 结论
我们提出了一个高效的分布式多传感器聚类算法,该算法通过一个改进的密度峰值聚类算法,将分布式传感器上的量测集进行聚类,聚类得到的簇的个数即为目标的个数,簇的中心即估计的目标的位置。相对于基于模型的分布式传感器跟踪算法,本文提出的算法不需要诸如运动模型、噪声参数、目标个数和状态等先验信息,且在跟踪精度、通信成本、运算时间上都有较大的优势。
[1] CHONG C Y, KUMAR S P. Sensor networks: evolution, opportunities, and challenges[J]. Proceedings of the IEEE. Aug 2003, 91(8): 1247-1256.
[2] OLFATI-SABER R, FAX J A, MURRAY R M. Consensus and Cooperation in Networked Multi-Agent Systems[J]. Proceedings of the IEEE, 2007, 95(1): 215-233.
[3] SAYED, ALI H. Adaptive Networks[J]. Proceedings of the IEEE, 2014, 102(4): 460- 497.
[4] MAHLER R. Approximate multisensor CPHD and PHD filters[C]∥International Conference on Information Fusion, 2010: 1- 8.
[5] KHALEGHI B, KHAMIS A, KARRAY F O, et al. Multisensor data fusion: A review of the state-of-the-art[J]. Information Fusion, 2013, 14(1): 28- 44.
[6] CLARK D, JULIER S, MAHLER R, et al. Robust multi-object sensor fusion with unknown correlations[C]∥Sensor Signal Processing for Defence (SSPD 2010). 2010: 1-5.
[7] CHANG K C, CHONG C, MORI S, et al. Analytical and Computational Evaluation of Scalable Distributed Fusion Algorithms[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(4): 2022-2034.
[8] UNEY M, CLARK D E, JULIER S J. Distributed Fusion of PHD Filters Via Exponential Mixture Densities[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 521-531.
[9] BATTISTELLI G, CHISCI L, FANTACCI C, et al. Consensus CPHD Filter for Distributed Multitarget Tracking[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(3): 508-520.
[10] MEYER F, BRACA P, WILLETT P, et al. A Scalable Algorithm for Tracking an Unknown Number of Targets Using Multiple Sensors[J]. IEEE Transactions on Signal Processing, 2017, 65(13): 3478-3493.
[11] MORI S, CHANG K C, CHONG C Y. Comparison of track fusion rules and track association metrics[C]∥International Conference on Information Fusion, 2012: 1996-2003.
[12] NOACK B, REINHARDT M, HANEBECK U D. On nonlinear track-totrack fusion with Gaussian mixtures[C]∥International Conference on Information Fusion, (FUSION), 2014: 1- 8.
[13] ZHU H, WANG M, YUEN K, et al. Track-to-Track Association by Coherent Point Drift[J]. IEEE Signal Processing Letters, 2017, 24(5): 643- 647.
[14] MAHLER R P S. Multitarget Bayes filtering via first-order multitarget moments[J]. IEEE Transactions on Aerospace & Electronic Systems, 2004, 39(4): 1152-1178.
[15] RONALD Mahler. The multisensor PHD filter: II. Erroneous solution via Poisson magic[J]. Proceedings of SPIEN. 2009, 7336: 7336-12.
[16] STREIT R L. Multisensor multitarget intensity filter[C]∥International Conference on Information Fusion, 2008: 1- 8.
[17] LI T, CORCHADO J M, CHEN H. Distributed Flooding-then-Clustering: A Lazy Networking Approach for Distributed Multiple Target Tracking[C]∥2018 International Conference on Information Fusion (FUSION), 2018: 2415-2422.
[18] LI T, CORCHADO J M, PRIETO J. Convergence of Distributed Flooding and Its Application for Distributed Bayesian Filtering[J]. Signal and Information Processing over Networks, IEEE Transactions on, 2017, 3(3): 580-591.
[19] ESTER M, KRIEGEL H, SANDER J, et al. A density-based algorithm for discovering clusters in large spatial Databases with Noise[C]∥Knowledge discovery and data mining, 1996: 226-231.
[20] JAIN A K.Data clustering: 50 years beyond K-means[C]∥International Conference on Pattern Recognition, 2010, 31(8): 651- 666.
[21] RODRIGUEZ A, LAIO A. Clustering by fast search and find of density peaks[J]. Science, 2014, 344: 1492-1496.
[22] LI T, CORCHADO J M, SUN S, et al. Partial Consensus and Conservative Fusion of Gaussian Mixtures for Distributed PHD Fusion[J]. IEEE Transactions on Aerospace and Electronic Systems, 2019, 55(5): 2150-2163.
[23] LI T. Distributed SMC-PHD fusion for partial arithmetic average consensus. arXiv: 1712.06128, 2017.
[24] LI T, CORCHADO J M, SUN S, et al. Clustering for filtering: Multi-object detection and estimation using multiple /massive sensors[J]. Information Sciences, 2017, 388-389: 172-190.
[25] QIAO D, LIANG Y, JIAO L. Boundary Detection-Based Density Peaks Clustering[J]. IEEE Access, 2019, 19: 755-765.
[26] JIANG J, CHEN Y, MENG X, et al. A novel density peaks clustering algorithm based on k nearest neighbors for improving assignment process[J]. Physica A: Statistical Mechanics and its Applications, 2019, 523: 702-713.
[27] FAN J, XIE W, DU H, et al. A Robust Multi-Sensor Data Fusion Clustering Algorithm Based on Density Peaks[J]. Sensors, 2019, 20(1): 1-14.
[28] LI T, PINTADO F D L P, CORCHADO J M, et al. Multi-source Homogeneous Data Clustering for Multi-target Detection from Cluttered Background with Misdetection[J]. Applied Soft Computing, 2017, 60: 436- 446.
[29] SCHUHMACHER D, VO B T, VO B N. A Consistent Metric for Performance Evaluation of Multi-Object Filters[J]. IEEE Transactions on Signal Processing, 2008, 56(8): 3447-3457.
[30] OUYANG C, JI H. Scale unbalance problem in product multisensor PHD filter[J]. Electronics Letters, 2011, 47(22): 1247-1249.
[31] VO B N, SINGH S, DOUCET A. Sequential Monte Carlo methods for multi-target filtering with random finite sets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2005, 41(4): 1224-1245.
