1 引言
针对高机动目标及低可观测目标,必须采用长时间相参积累的技术提高信噪比,从而使雷达在足够远的距离检测到雷达的横截面积(RCS:Radar Cross Section)较小的高速目标,为相应军事行动提供充足的时间。传统的动目标检测(MTD:Moving Target Detection)方法已经广泛的应用于现代雷达体系[1-2],但是MTD在单个距离单元的目标驻留时间受限,为此,MTD很难改善低信噪比或高速运动目标的探测能力[3- 4]。为此许稼等提出了Radon-Fourier Transform (RFT)算法以及generalized Radon-Fourier transform(GRFT)算法[5-7],通过搜索目标的运动参数,完成脉冲间的相位对准,从而实现相参积累。但是,GRFT算法通过联合搜索目标的速度、加速度、加加速度这些运动参数来完成各回波相位之间的对准,这无疑会带来巨大的运算量。因此这种多维搜索在传统的CPU上难以短时间内完成,不利于雷达对目标的实时检测。而且,搜索运动参数的过程中,每次搜索之间没有先后的顺序,这为并行计算提供了有利的条件。
针对上述问题,本文提出一种基于图形处理器的并行化算法,并采用通用并行架构CUDA完成GRFT算法的具体化实现。近年来,图形处理器(Graphic Processing Unit, GPU)由专用图形处理器发展成处理密集型及并行计算的平台。相对于其他并行处理工具,如FPGA(Field Programmable Gate Array),本身具有一定的优势。不过,FPGA的并行处理具有很强的实时性和灵活性,实时性体现在其数据并行时延迟低、处理速度快,灵活性体现在其功能可以随时改变。但是,FPGA芯片的成本高,开发难度大。而GPU具有多核处理器,开发成本低,使用SIMD(Single Instruction Multiple Data)架构即只需一条指令可以平行处理大量数据,适用于大数据量的并行处理。因此,GPU在各个领域中得以迅猛发展,如GPU已应用于合成孔径雷达(SAR)[8-10]、生物医学成像[11]等领域。商哲然等[12]提出了基于GPU的RFT算法并行化,在一定程度上实现了目标的实时检测,但该种方法并没有考虑目标的高阶运动,无法有效的检测具有高阶运动的飞行目标。而对于高速运动的目标而言,其运动方式是复杂多变的,这种运动方式在径向距离之间的投影通常是一个高阶运动。即使目标在匀速运动,但是目标的飞行方向和径向之间的夹角也会发生改变,这在径向的方向的运动形式仍旧是高阶运动形式。为了实时准确的远距离检测到高机动目标,本文采用GPU用来提高计算密集型应用程序中并行段的执行速度,采用CPU负责管理设备端上的资源。使用CUDA编程在功能强大的GPU硬件平台上充分挖掘GRFT算法的并行性,使GRFT的搜索运动目标参数这个计算密集型过程并行实行。
2 GRFT算法
假设目标相对雷达的运动可用一个三阶模型来近似:
Rm=R0+νmTr+a(mTr)2+aa(mTr)3
(1)
其中:R0是m=0时雷达与目标的初始距离,ν代表目标相对雷达的径向速度,a代表目标相对雷达的径向加速度,aa代表目标相对雷达的径向加加速度,m是非负整数,Tr是雷达的脉冲重复间隔。则回波信号的形式可以写为:
smn(φ)=![]()
![]()
![]()
(2)
其中:A是回波的相位,p(·)是发射的基带信号,在本文中是一个线性调频信号。φ是发射信号的初始相位。通过参考文献[3]结合目标的高阶运动运动形式,可以得到GRFT检测的频率域方法的公式为:
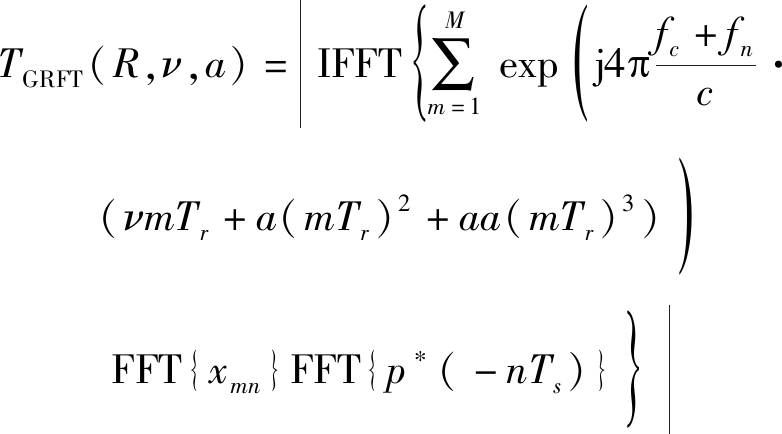
(3)
其中:fc是载频,fn是基带波形p(t)的频率,m代表第m个回波信号,c是光速。
xmn=smn+wmn,smn是回波信号中的信号部分,wmn是高斯白噪声,它的分布服从N(0,σ2)。
通过式(3)可以看到频率域RFT(FBRFT),在距离频率脉冲维实现了匹配滤波和脉冲积累,将一个二维信号通过一维的傅里叶变换和一维的傅里叶逆变换完成相参积累,通过这个过程使信噪比在脉冲压缩处理完成后增加时宽带宽积倍,又通过相参积累使信噪比增大了M倍。可以使检测的信噪比满足探测远距离高机动隐形目标的需求。
3 长时间相参积累的CUDA实现
3.1 并行化GRFT算法
并行实现GRFT算法的目的是获得较高的加速比,从而在较短的时间内完成能量聚焦,实时检测出目标。GRFT算法实现的主要步骤是通过搜索运动参数,在频率域完成脉冲压缩和脉冲积累。在进行脉冲积累时,需要通过所搜索的运动参数构建补偿项。然后频域回波信号,频域匹配响应与补偿项进行相应的点乘运算完成不同信号间的相位对准,再将同一距离单元的数据进行相加,完成脉冲积累。最后对完成积累的信号进行逆快速傅里叶变换。在这一过程中补偿项的构建,点乘,叠加运算所需的计算量很大,因此采用并行计算来实现。并行化GRFT算法流程如图1所示。
本文利用NVIDIA 的CUFFT函数库中的cufftPlanMany函数完成时频域的转换,cufftPlanMany函数为GPU提供了高度并行化的FFT/IFFT操作。先将回波信号数据传输到设备端,通过配置函数的相应参数来批量的进行傅里叶变换,将原始回波信号转换为快时间频域信号。也可以通过配置该函数参数,对积累后的脉冲进行逆傅里叶变换,再将所得的数据结果从设备端传输到主机端。
本文采用快速傅里叶变换法将回波信号和匹配滤波函数转换到频域,并将结果数据继续存储在设备端,然后通过调用第一个Kernel函数完成补偿项的构建,第二个kernel函数完成点乘运算,第三个kernel函数完成累加运算。最后将结果传输回主机端。
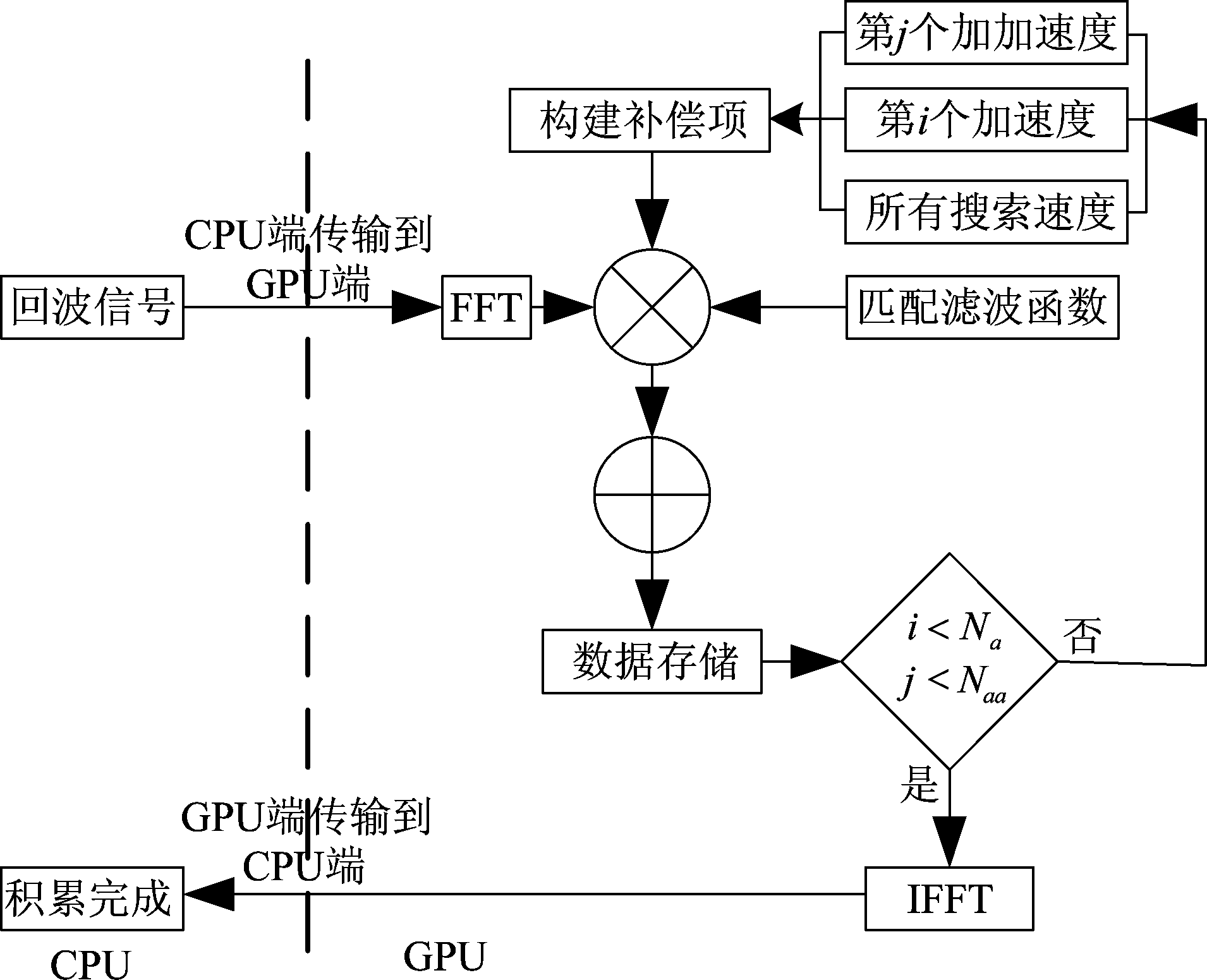
图1 并行化GRFT算法流程
Fig.1 Parallel GRFT algorithm flow
3.2 并行化GRFT算法的实现
本文结合并行计算和CUDA架构的特点,主要介绍GRFT算法中补偿项的构建,点乘和累加的并行实现。在整个长时间相参积累的过程中,共积累M个脉冲,每一个脉冲的采样点数为Nn,每一个脉冲的频域采样点数也为Nn,所搜索的速度的个数为Nν,搜索的加速度的个数为Na,搜索的加加速度的个数为Naa。将回波信号通过快速傅里叶变换转换到快时间频域,则其形成的矩阵的维度为:M×Nn,通过构建匹配滤波函数完成脉冲压缩,匹配滤波器的响应矩阵的维度为:1×Nn,根据所搜索的运动参数构建补偿项。每一组运动参数所构成的补偿项的矩阵维度为:M×Nn。一共会有Nν×Na×Naa组M×Nn维度的矩阵。
(1)线程网格和线程块维度的设计
CUDA程序将线程网格中的线程块分配到GPU端来执行并行操作。当在主机端启动一个核函数时,它会根据网格和块的划分进行线程的索引,在设备端进行执行,此时设备中会产生大量的线程并且每个线程都会执行核函数中的特定语句。本文通过三维块维度的不同索引,来读取对应的内存数据从而完成补偿项的构建,点乘和累加的并行计算。
(2)并行化的实现
本文通过三维块和三维网格来实现,每一个三维的块都由x,y,z三个方向组成,所有的三维块构建成一个三维的网格。在三维网格中的x方向的每一个线程对应于距离采样数据的一个采样点,故x维度的大小是Nn。三维网格中的y方向的线程对应所积累的回波信号的个数,y方向的大小是M。三维网格中的z方向处理的是所要搜索的运动参数,因此z方向的大小是Nν×Na×Naa。这样所构建补偿项需要的总的线程数为:M×Nn×Nν×Na×Naa。但是受到编程时,计算机申请的内存,网格各个方向上的最大值和显卡本身所拥有的线程总数等诸多方面的限制,无法同时产生这么大的计算量。因此将模型进行简化。x和y方向保持不变。在z的方向上仅处理速度这一个运动参数,故将z方向的大小简化为Nν。最终的实施方案为在CPU端采用搜索加速度参数和加加速度的参数两维循环来对加速度和加加速度的参数进行遍历。他们的循环体是由所有速度参数和其中的一个加速度参数,加加速度参数并行构建的补偿项语句,并行点乘语句,并行累加语句,和累加结果存储语句。补偿项最终产生的形式如图2(a)所示。
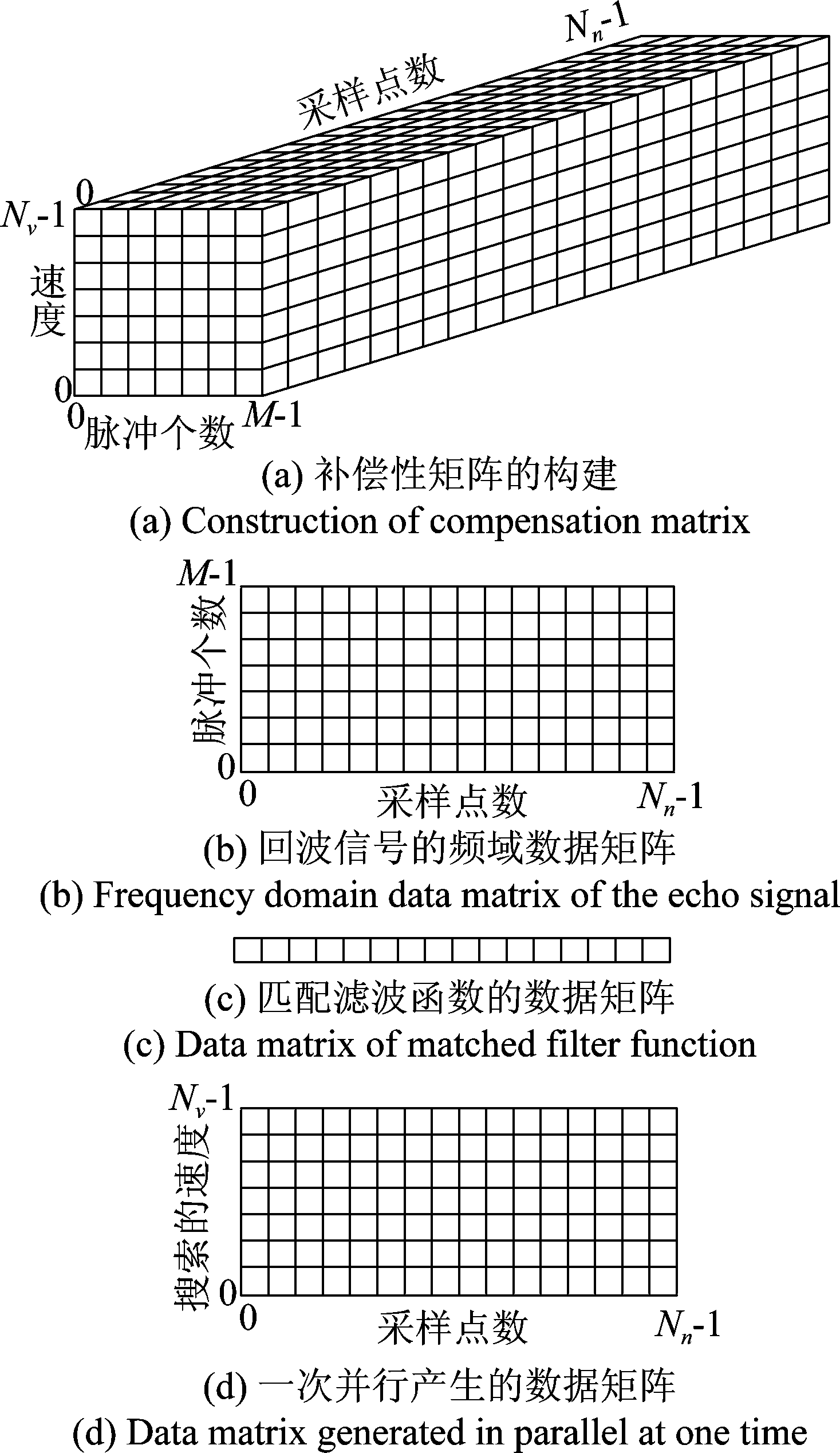
图2 数据的存储形式
Fig.2 Data storage format
并行计算的核函数通过x方向的线程来索引补偿性的采样点数,回波信号的采样点数和匹配滤波函数的数据,通过y方向的线程索引补偿项和回波信号的脉冲数,通过z方向索引不同的速度参数。最终完成点乘运算,最终形成的结果数据和图2(a)中的矩阵结构维度相同。在通过这样的一次索引完成各个脉冲之间的数据叠加。形成一次循环后的结果数据,将数据传回到CPU端进行存储。在进行加速度和加加速度的循环,直到遍历完所有搜索的运动参数。完成长时间相参积累。本文一共需要在CPU端进行Na×Naa次循环,循环体主要的作用是:并行产生图2(a)的补偿项矩阵,并行点乘,将图2(b)中的每一行和图2(c)中的数据对应点乘,产生的结果和图2(b)的矩阵维度相同,再将该结果与图2(a)中的每一个垂直于速度方向的平面进行对应点乘,最终形成如图2(a)中的数据维度。然后进行脉冲积累,将点乘结果沿垂直于脉冲方向的所有平面的数据进行对应点数相加。最终产生图2(d)中的数据矩阵。注意:循环体的每次执行就是一次并行运行,图2(d)就是一次循环体产生的结果,还需对加速度,加加速度进行二次循环遍历,最终产生Na×Naa个图2(d)形式的数据矩阵。从而完成整个过程。
4 仿真结果与分析
本文使用C语言和CUDA来实现GRFT算法。为验证基于GPU的GRFT算法的并行方案,采用计时函数cudaEventRecord函数, 统计并行过程的运行时间,并与CPU上的运行时间相比较。本文仿真的平台数据如下:CPU的处理器为 i7-9700k CPU@3.60 GHz, 内存32 GB。GPU平台为INVDIA GeForce RTX 2080Ti,具有11.0 GB的专用GPU内存。假设雷达探测一个空中运动目标,目标相对雷达的径向距离为400 km,径向速度、径向加速度、径向加加速度分别是:403 m/s、0.19 m/s2、-0.0034 m/s3。雷达的工作参数如下:载频2 GHz,脉冲宽度100 μs,带宽40 MHz,采样率60 MHz,脉冲重复周期为1 ms。并行化参数为:线程块的维度是block(32, 8, 4),线程网格的维度为:
grid((Nn+block.x-1)/block.x,(M+block.y-1)/block.y,(Nν+block.z-1)/block.z)
采用ix=threadIdx.x+blockIdx.x·blockDim.x,来索引x方向上的数据;
采用iy=threadIdx.y+blockIdx.y·blockDim.y,来索引y方向上的数据;
采用iz=threadIdx.z+blockIdx.z·blockDim.z,来索引z方向上的数据。
则GRFT并行算法的整体运行时间为:一次并行运行时间乘以Na×Naa。注意:一次并行运行时间不仅包括并行代码执行时间,而且还包括主机端和设备端的数据传输时间。
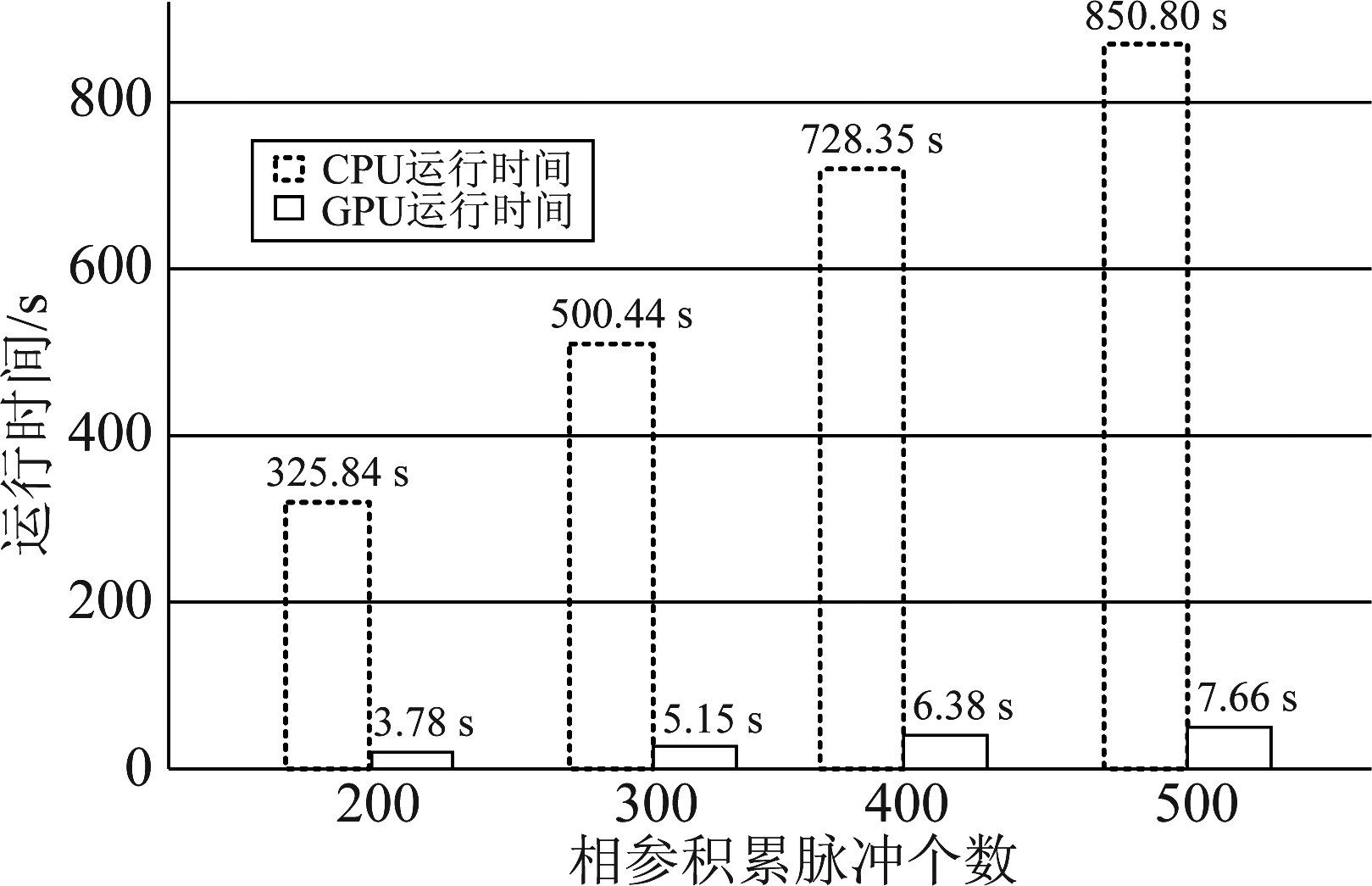
图3 积累脉冲个数的时间对比
Fig.3 Time comparison of the number of accumulated pulses
图3是在运动搜索参数一定的情况下,随着相参积累的脉冲数的变化,所带来的GRFT算法在GPU上和CPU上运行的时间的对比。上图橙色的柱状图代表在GPU上运行的时间,蓝色的柱状图代表在CPU上运行的时间,根据整体的运行时间为:一次并行运行时间乘以Na×Naa的理论分析。脉冲积累数量已经集成到并行计算里面,改变脉冲的积累数量, GRFT在GPU上的耗时基本保持稳定,主要的时间来自于将数据从CPU拷贝到GPU上进行运算,再从GPU上将运行结果传输到CPU上进行存储这个数据传输过程。图4是搜索速度参数个数不同的情况下,所统计的在CPU和GPU两种平台下的运行时间,整体的运行时间为:一次并行运行时间乘以Na×Naa,搜索速度个数的不同带来的改变也是一次并行运行的时间,GRFT在GPU上的耗时基本保持稳定,其主要运行时间的损耗也主要来自于数据传输的过程。随着速度搜索参数的变大,一次并行产生的数据量也会线性增大,造成在GPU上运行时间的增加。
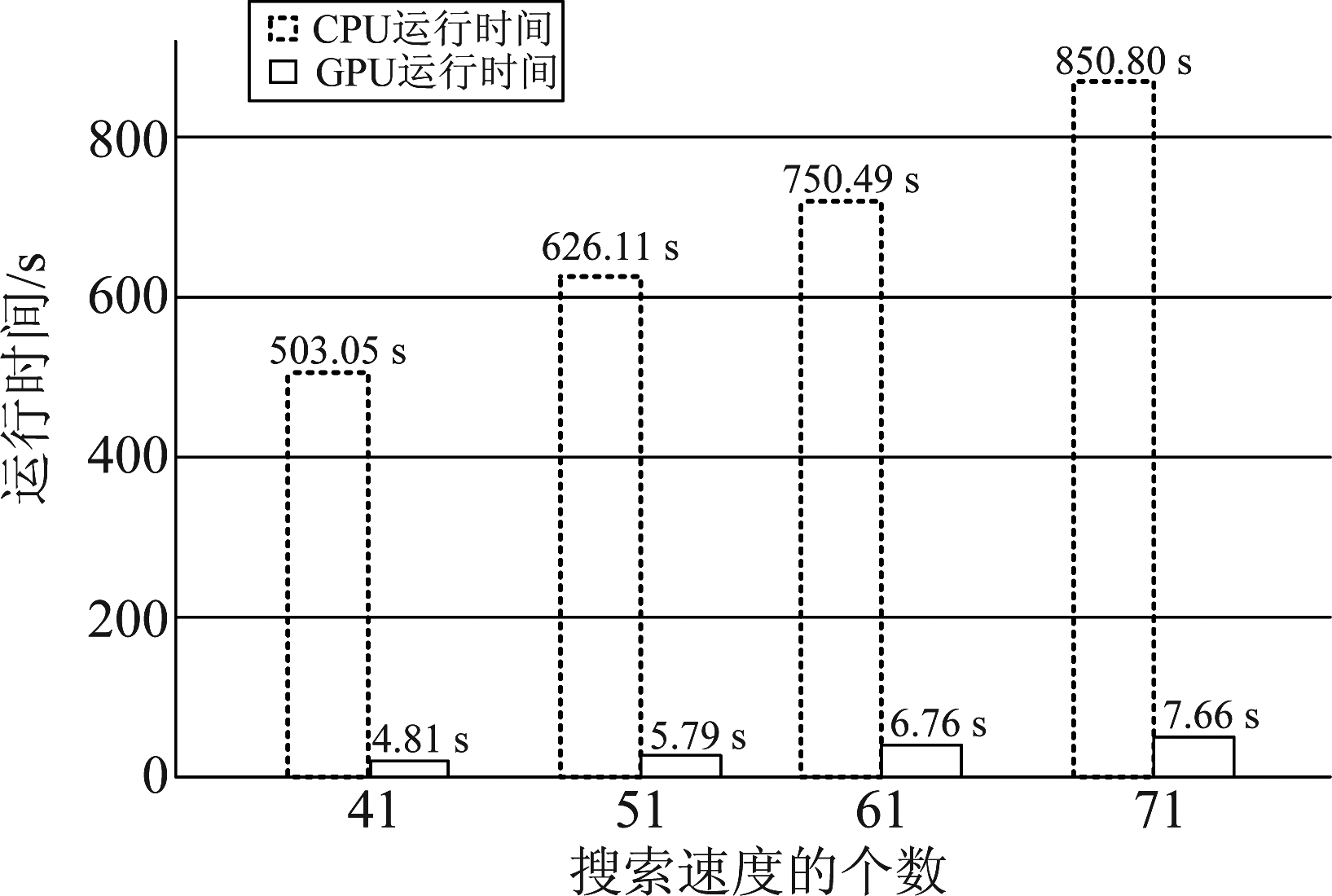
图4 搜索速度的时间对比
Fig.4 Time comparison of search speed
对于本文所采用的算法,见图1并行化GRFT算法流程,因为硬件条件的限制,在仿真时将加速度和加加速度的搜索放在了CPU端,计时方式的计算方式为:一次并行运行时间乘以Na×Naa,随着加速度和加加速度的搜索个数的增加,其耗时是线性增加的。在加上主机端和设备端数据传输的损耗,其整体在GPU上的耗时时间是显著增加的。所以这两个参数计算出的加速比受脉冲个数影响和速度搜索个数影响的加速比要低很多。图5和图6分别对应不同的加速度搜索个数和加加速度搜索个数的情况下,在两种平台下所运行的时间。
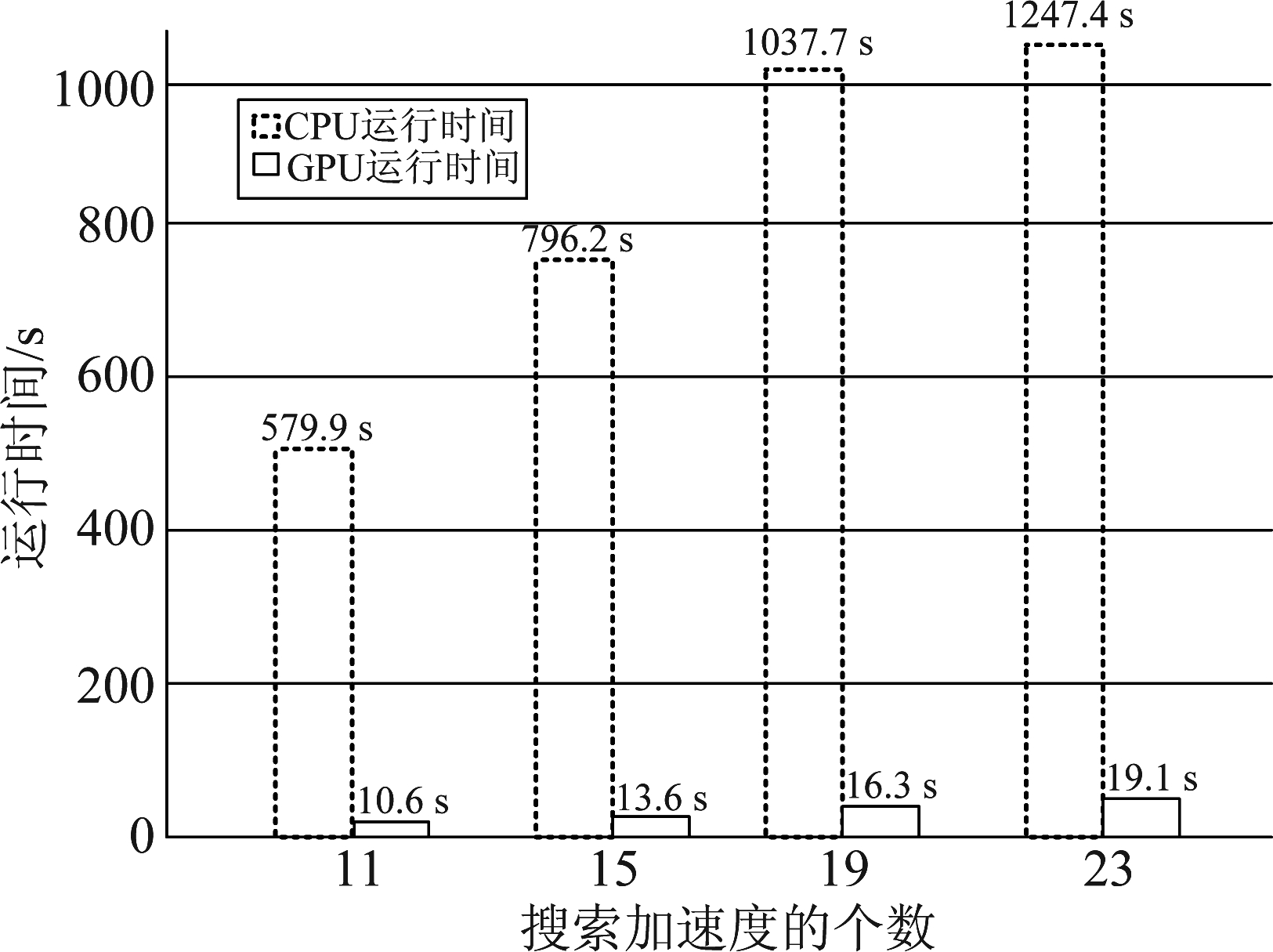
图5 搜索加速度的时间对比
Fig.5 Search acceleration time comparison
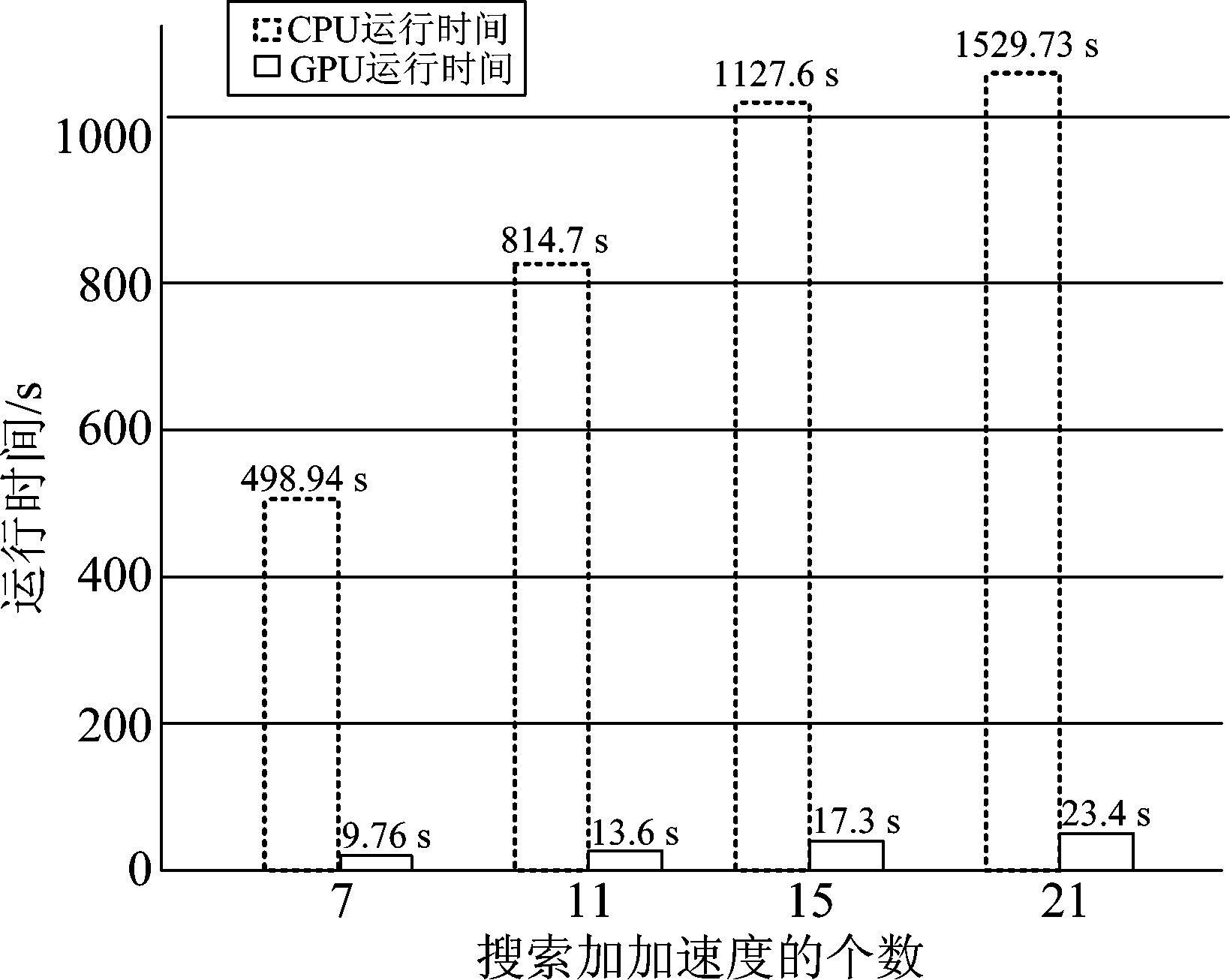
图6 搜索加加速度的时间对比
Fig.6 Search jerk time comparison
本文的加速比是GRFT算法在CPU端串行执行的时间和在GPU端并行执行的时间的比率。加速比的获得除与GRFT算法的并行化策略有关外,还与主机端和设备的数据量的传输有关,使得并行方案设计的加速比很难进行计算。只能通过仿真实验来统计GRFT并行化算法的加速比。表1是不同积累脉冲个数的情况下所形成的加速比,表2是不同搜索加速度个数所形成的加速比。积累的脉冲数和搜索的加速度的个数最大的不同在于,在有限的硬件条件下,积累的脉冲数集成到了并行处理中,而搜索的加速度是在CPU端串行执行。在表1中,随着积累的脉冲数增大,在CPU中的耗时是线性增长,但在GPU中会调用更多的线程来处理脉冲数,其耗时的增加主要受主机端和设备端数据传输的影响。所以随着脉冲数的增多其加速比是逐渐增大的。但是随着脉冲数积累到一定程度,传输数据的耗时影响会越来越大,造成加速比趋于稳定。 同理,积累的速度参数的加速比也有类似的现象。在表2中,搜索的加速度也是在CPU端,随着加速度搜索个数的增多,在CPU端的耗时是线性增长。在GPU端的耗时大致可以表示为:一次并行运行时间乘以Na×Naa,这也是线性增长。因此随着搜索加速度个数的变化,其加速比一直是趋于稳定。同理,搜索的加加速度也有类似情况。因为积累的脉冲数集成到了并行处理中,而搜索的加速度是在CPU端串行执行。这也造成了并行化处理的脉冲个数积累和搜索的速度比串行搜索的加速度和加加速度的加速比要高。
表1 不同脉冲积累个数的加速比
Tab.1 Acceleration ratio of different pulse accumulation

脉冲个数加速比20086.230097.17400114.6500111.1
表2 不同搜索加速度个数的加速比
Tab.2 Speedup ratio of different search acceleration numbers

搜索加速度的个数加速比1154.71558.541963.662365.28
为了使仿真的加速比最大化,在硬件受限的并行编程中,要对比所积累的脉冲,搜索的速度的个数,加速度的个数,加加速度的个数,数值最大的参数将其并行在线程块的y方向,将次最大的参数并行在线程块的z方向。这样才会达到最大的加速比。剩余两个参数在CPU端通过循环的形式串行实现。如果显卡的版本足够高,将所有的搜索参数放在线程块的某一方向上,在进行并行编程可以达到最佳的加速比,此时搜索参数的变化造成数据传输数据量的变换,使得在GPU上运行时间的改变将只会受到从主机端和设备端进行数据传输的影响。
5 结论
仿真实验表明:GRFT算法通过搜索目标的速度、加速度、加加速度等运动参数完成长时间相参积累,使得雷达可以探测远距离高机动目标。但是搜索目标运动参数的过程产生了大量的计算量,传统的串行处理很难在较短的时间内处理。基于GPU的GRFT算法通过并行化的手段让GRFT算法获得较高的加速比使得长时间相参积累能够在较短的时间内完成。但由于加速度和加加速度这两维运动参数仍采用串行的方式进行搜索,造成了一定的加速比损失。另外,提出的算法只采用单个GPU进行处理,如何利用多GPU实现算法的并行化是今后研究的一个方向。
[1] BARTON D K. Radar system analysis and modeling[J]. IEEE Aerospace & Electronic Systems Magazine, 2005, 20(4): 23-25.
[2] MERRILIVANSKOLNIK. Introduction to Radar System[M]. MCGRAW-HILL, 1962.
[3] SKOLNIK M, LINDE G, MEADS K. Senrad: an advanced wideband air-surveillance radar[J]. Aerospace & Electronic Systems IEEE Transactions on, 2001, 37(4): 1163-1175.
[4] LOOMIS J M. Army Radar Requirements for the 21st Century[C]∥Radar Conference, 2007 IEEE. IEEE, 2007.
[5] XU J, YU J, PENG Y N, et al. Radon-Fourier Transform for Radar Target Detection, I: Generalized Doppler Filter Bank[J]. IEEE Transactions on Aerospace & Electronic Systems, 2011, 47(2): 1186-1202.
[6] XU J, YU J, PENG Y N, et al. Radon-Fourier Transform for Radar Target Detection (II): Blind Speed Sidelobe Suppression[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2473-2489.
[7] YU J, XU J, PENG Y N, et al. Radon-Fourier Transform for Radar Target Detection (III): Optimality and Fast Implementations[J]. IEEE Transactions on Aerospace & Electronic Systems, 2012, 48(2): 991-1004.
[8] ROMANO D, MELE V, LAPEGNA M. The Challenge of Onboard SAR Processing: A GPU Opportunity[M]. Computational Science-ICCS 2020, 2020.
[9] ROMANO D, LAPEGNA M, MELE V, et al. Designing a GPU-parallel algorithm for raw SAR data compression: A focus on parallel performance estimation[J]. Future Generation Computer Systems, 2020, 112: 695-708.
[10] WIJAYASIRI A, BANERJEE T, RANKA S, et al. Multiobjective Optimization of SAR Reconstruction on Hybrid Multicore Systems[J]. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 2020, 13: 4674- 4688.
[11] 朱珊珊, 高万荣, 史伟松. 基于图形处理器的人体皮肤组织实时成像谱域相干光断层成像系统[J]. 激光与光电子学进展, 2018, 55(4): 309-316.
ZHU Shanshan, GAO Wanrong, SHI Weisong. GPU-Based Fourier Domain Optical Coherence Tomography System for Real Time Imaging of Human Skin[J]. Progress in Laser and Optoelectronics, 2018, 55(4): 309-316.(in Chinese)
[12] 商哲然, 谭贤四, 曲智国, 等. 基于GPU的RFT算法并行化[J]. 雷达科学与技术, 2016, 14(5): 505-516.
SHANG Zheran, TAN Xiansi, QU Zhiguo, et al. Parallelization of RFT algorithm based on GPU[J]. Radar Science and Technology, 2016, 14(5): 505-516.(in Chinese)

