1 引言
第五代(5th-generation, 5G)与超5G移动通信系统将面向两大机器类应用场景:大规模机器类通信和超可靠低时延通信(Ultra-Reliable Low-Latency Communication, URLLC)[1]。其中,URLLC旨在满足延迟敏感性服务,如触觉互联网、车对车通信、自动驾驶和远程控制等[2]。与4G追求无线通信系统高容量指标不同,URLLC主要面向系统的可靠性与低延迟性,被认为是5G通信中最具有创新性的无线连接技术[3]。如何设计信号传输方案来同时满足两大性能指标“超可靠性”与“低时延性”也已吸引了研究人员的广泛关注。
由于对时延的严格要求,URLLC物理层数据传输的主要特征是进行短包传输(Short Packet Transmissions)[4],这需要对当前物理层传输方案进行再思考:一方面,当尝试最小化时延时,使用短包通信导致信道编码增益严重下降。另一方面,为提高系统可靠性传统技术(例如:奇偶校验,冗余和重新传输)将占用更多的资源[5]。因此,如何在时延约束条件下,设计物理层信号编码与调制方案,来实现短包超可靠传输是5G实现URLLC亟待解决的关键问题。
为实现较高可靠性,大规模多输入多输出(Multiple-Input Multiple-Output, MIMO)系统是依赖于较为准确的信道状态信息(Channel State Information, CSI)。然而,在短包传输过程中,信道使用次数有限,基于有限长训练序列估计的CSI精度有限。Bana等人[6]针对该问题,在URLLC背景下采用一种双阶段序贯非相干和相干检测策略,其中接收器首先执行非相干能量检测,以缩小可能的接收符号范围,然后使用CSI相干地检测确切的符号,证明了低信噪比下非相干检测的误差性能要优于使用相干检测器的系统误差性能[7]。然而,该方案仅局限于4-QAM星座,可扩展性不足。通过使用基于能量检测的单时隙非相干脉冲幅度调制(Pulse Amplitude Modulation, PAM)星座,Chowdhury等人证实了幅度调制在低信噪比(Signal-to-Noise Ratio, SNR)时,具有较好的误差性能[8],然而该方案仅在幅度维度上面实现信息的调制,随着调制阶数的增加,其可达误差性能将受到限制。另外,在MIMO通信系统中,酉星座[9]在高SNR中被认为是最优的非相干星座结构,但其在低SNR中的误差性能效果较差,难以确保系统在功率受限场景下的可靠性。基于以上背景,Li等人[10]研究了一种基于黎曼距离(Riemann distance, RD)的大规模单入多出(Single-Input Multiple-Output, SIMO)系统的大规模唯一可分解星座(Massive Uniquely Factorable Constellation, MUFC)设计方案;通过联合开发调制空间的幅度、相位与角度参数,提出了连续空间中的参数化编码方案,该方案在低SNR大天线数下具有较好的误差性能,能够适用于URLLC场景下对能耗和可靠性具有严格要求的5G服务类别。然而,该方案并未给出MUFC的具体星座映射方案,也并未探讨其编码调制模块的联合优化问题,这也限制了该方案误差性能的进一步提升。
本文根据多级编码调制的思想[11],在闭式大规模MUFC基础上[10],结合外层卷积编码模块,研究内层星座映射方案设计工作。具体地,本文的主要贡献可以总结为以下两点:
1)基于黎曼测度准则,在大规模SIMO基站端建立了软判决MUFC符号序列检测方法,并建立了面向符号序列的信号优化目标函数。
2)基于上述信号优化目标函数,以最大最小化符号序列间的黎曼距离为目标,设计具体的星座映射方案,旨在优化系统误差性能。
本文中CM×N表示M×N复空间,A*,AT,AH分别表示矩阵A的共轭,转置和共轭转置。||.||和E{·}表示欧几里得范数和期望运算,tr(·)代表矩阵求迹。Z+代表正整数集,C代表复数集,R{·}代表实部。
2 系统模型
本部分首先介绍本文考虑的大规模SIMO上行链路系统物理层联合编码调制模块,然后介绍大规模非相干唯一可分解星座(Uniquely Factorable Constellation, UFC)的构造方法与基于RD测度准则的多符号解调方法。
2.1 大规模SIMO上行链路系统非相干编码调制模块
本文是在国际电信联盟5G NR Node B协议下,对信号的编码调制方案进行研究[4]。具体来讲,5G NR Node B协议标准定义了包含有2个正交频分复用(Orthogonal Frequency Division Multiplexing, OFDM)符号的微时隙(mini-slot)信号帧结构。在相同子载波上,本文首先在连续两个符号周期上进行信号的编码调制(如图1),产生出符号序列s0,s1,...,sn-1。然后经过K个符号周期,再进行下轮数据的传输。
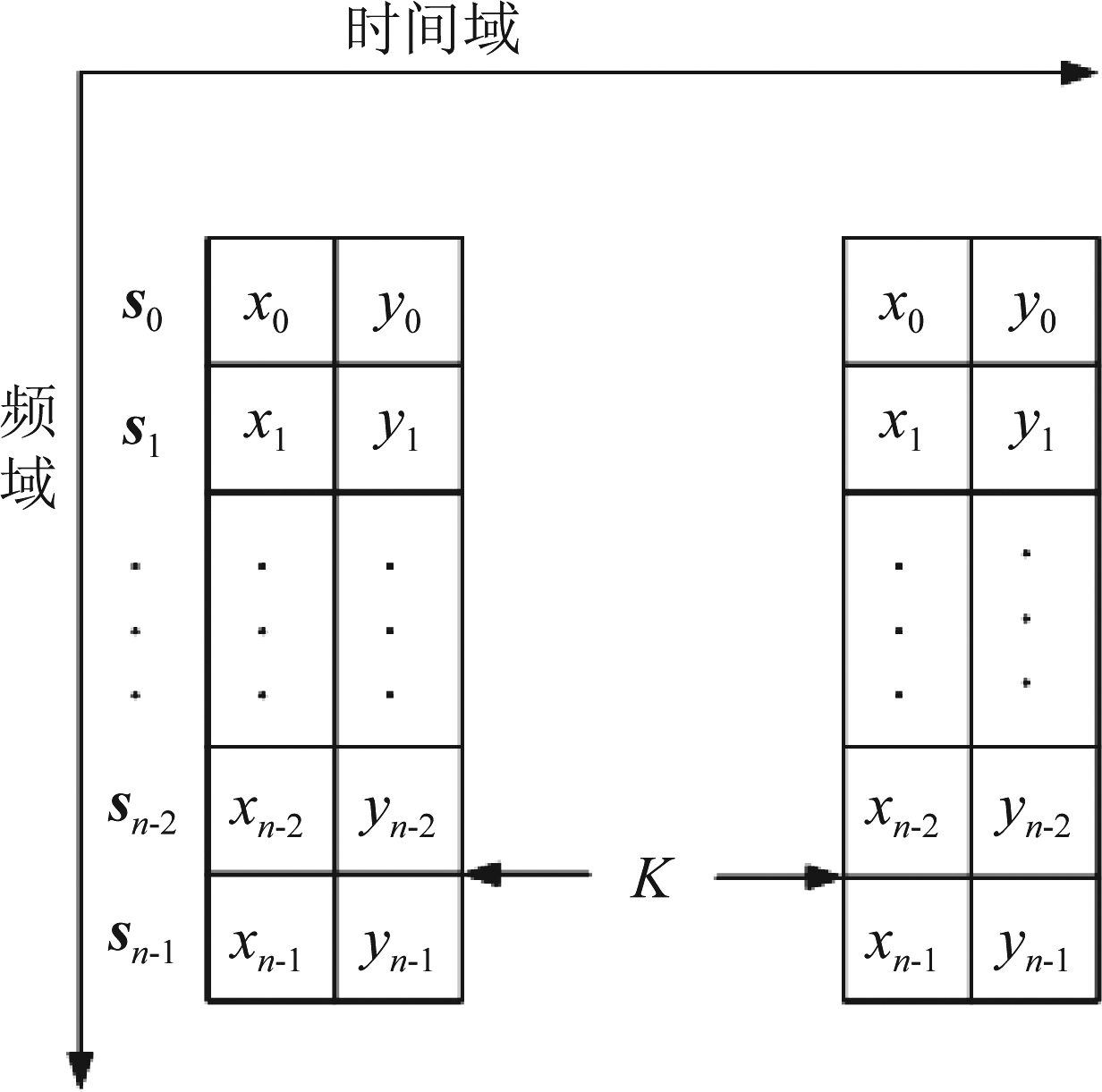
图1 NR中mini-slot两个符号传输结构图
Fig.1 Transmission structure diagram of two mini-slot symbols in NR
在URLLC场景中,系统时延主要包括传输时延、传播等待时延、编码和解码的处理时间和重新传输的时间[12]。其中,信号的传输时延占主要部分。5G NR协议规定子载波间隔可设为15 kHz、30 kHz、60 kHz、120 kHz。当子载波间隔为15 kHz时,传输两个OFDM符号所需的信号传输时延约为0.143 ms,而URLLC场景下的最大容忍时延则规定为1 ms。因此,利用上述信号帧结构,可以很大程度上减少传输延迟。
针对图1中的数据帧结构,本文将进一步利用大规模SIMO系统空间分集来提高系统的可靠性,最终实现信号的超可靠低时延传输。具体建模过程如下:在该系统中,发射端具有单根发射天线,接收端具有M根接收天线(M≥1),信道矢量h=[h1,h2,…,hM]T∈CM×1为发射端到接收端之间的M×1信道矢量,其中h对于发射端与接收端都是未知的,具体概率密度分布f(h)未知,接收端R有信道的二阶统计信息hHh,且h每两个符号周期变化一次。标记s为发射端在单个时隙内的发送符号,在第一个时隙内,发送信号s=x;在第二个时隙中s=y,则接收端的信号表达式为:
R=hsT+N
(1)
其中s=(x,y)T∈C2×1,在第一个时隙中s=x作为发送信号,则r1=hx+n1,同理第二个时隙的发送信号为s=y,则r2=hy+n2所以有R=(r1,r2)∈CM×2,s=(x,y)T∈C2×1,N=(n1,n2)∈CM×2,其中N中元素服从独立同分布的复高斯分布,其均值为零且方差为![]() 针对式(1)中的接收信号模型,本文采用文献[10]中提出的MUFC在连续的两个符号周期中对发送信号进行调制。标记
针对式(1)中的接收信号模型,本文采用文献[10]中提出的MUFC在连续的两个符号周期中对发送信号进行调制。标记![]() 为s的集合,它的具体形式如式(2)所示。
为s的集合,它的具体形式如式(2)所示。
(2)
其中,Qα,Qθ,Qφ代表参数α,θ,φ的三个子星座。标记三个子星座的调制阶级数分别为kα,kθ与kφ,即|Qα|=2kα,|Qθ|=2kθ,|Qφ|=2kφ,其中|Q|代表星座Q的星座点的个数。三个子星座的最优结构可由命题1确定。
命题![]() 的阶级数目是固定值且满足
的阶级数目是固定值且满足![]() 为
为![]() 星座点上的比特位数目。三个子星座调制阶级在满足kα+kθ+kφ=R和平均传输功率的约束下,找到三个非负的整数kα,kθ和kφ,即满足kα,kθ,kφ∈{0}∪Z+。以及调制阶级数分别满足|Qα|=2kα,|Qθ|=2kθ和|Qφ|=2kφ的三个子星座参数Qα,Qθ和Qφ。则最优星座解的结构可表示为:
星座点上的比特位数目。三个子星座调制阶级在满足kα+kθ+kφ=R和平均传输功率的约束下,找到三个非负的整数kα,kθ和kφ,即满足kα,kθ,kφ∈{0}∪Z+。以及调制阶级数分别满足|Qα|=2kα,|Qθ|=2kθ和|Qφ|=2kφ的三个子星座参数Qα,Qθ和Qφ。则最优星座解的结构可表示为:![]() 可以看出为Qα与Qθ为实数等差序列,Qφ服从标准的PSK星座,其中α0,d,Δθ等的具体数值可参照文献[10]。
可以看出为Qα与Qθ为实数等差序列,Qφ服从标准的PSK星座,其中α0,d,Δθ等的具体数值可参照文献[10]。
命题1中的星座参数设计确保了单符号间的最小黎曼距离最大化,从而实现了非相干黎曼检测器的最优误差性能。然而,当使用黎曼距离检测器对符号序列进行联合检测时,检测器的误差性能将取决于符号序列间的最小RD之和,这将在2.2节进行详细探讨。
由于h概率密度分布未知,基于最小二乘准则联合发射信号检测和信道估计建立目标函数为[10]:
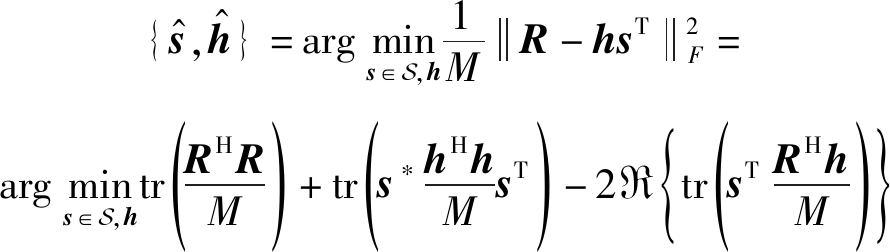
(3)
其中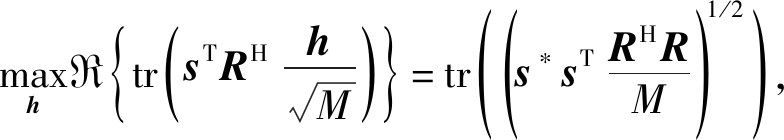 利用此等式,式(3)可等效转换为s的非相干检测器:
利用此等式,式(3)可等效转换为s的非相干检测器:
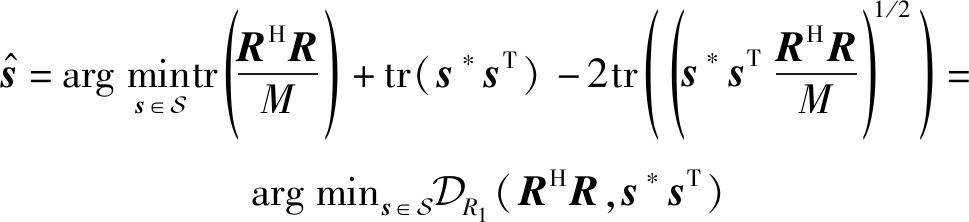
(4)
其中![]() 表示距离度量。可以观察到,该检测器本质上就是寻找与
表示距离度量。可以观察到,该检测器本质上就是寻找与![]() 之间的第一类RD最小的矩阵s*sT。
之间的第一类RD最小的矩阵s*sT。
通过上述推理过程,可以看出式(4)检测器仅与输入和接收信号有关。在无线通信系统,常用的信号优化准则是系统的误差概率或成对差错概率,但在本文中,由于未知随机信道的具体概率密度分布,无法确定系统的具体误差概率。考虑这一点,本文拟以最小距离准则来简化信号的优化设计问题。由此基于最小距离准则,文献[10]指出影响其误差性能的决定因素可由式(5)决定:
(5)
其中![]() 是用来衡量两个信号点之间的RD,在式(5)中
是用来衡量两个信号点之间的RD,在式(5)中![]() 其中s*sT代表序列中的正确信号,
其中s*sT代表序列中的正确信号,![]() 代表已通过信道模型的调制信号。在文献[13]中可以知道实际的第一类RD公式为:
代表已通过信道模型的调制信号。在文献[13]中可以知道实际的第一类RD公式为:
(6)
其中,Pm和Pn是两个功率谱密度矩阵,因为本文中s*sT和RHR都是半定矩阵,所以利用式(6)作为信号点间的测度准则比欧氏距离更为合适,式(5)是由式(6)推理演变而来。
由于5G通信中URLLC场景对低延迟的严格要求,具有最佳误码性能的信道编码方案可能并不是最佳选择。例如,Mahyar等人[12]指出在URLLC背景下,Turbo码与LDPC码应用在短至中等长度数据包传输时的误差性能不佳,而卷积编码由于编译码操作简单,可作为URLLC场景下的信道编码方案。Mehmet等人[14]指出卷积编码能够极大降低信号传输时延,并提出了自适应SNR的卷积编码OSTBC系统。因此本文针对URLLC的短包传输利用![]() 根据多级信道编码的思想,在系统编码调制模块外层使用线性卷积编码,内层使用MUFC。具体来讲,信息比特流在外层通过卷积编码(编码速率假设为k/n),然后经过调制模块产生调制符号序列s1 s2 s3…,经过无线信道达到接收端。接收端根据相应的接收信号矢量R1 R2 R3…,依次根据RD检测器(7)解调出
根据多级信道编码的思想,在系统编码调制模块外层使用线性卷积编码,内层使用MUFC。具体来讲,信息比特流在外层通过卷积编码(编码速率假设为k/n),然后经过调制模块产生调制符号序列s1 s2 s3…,经过无线信道达到接收端。接收端根据相应的接收信号矢量R1 R2 R3…,依次根据RD检测器(7)解调出![]() 并通过逆映射译码输出信息比特流。
并通过逆映射译码输出信息比特流。
2.2 软判决符号序列检测方法
利用式(4),当调制信道输入端是信号序列时,可建立多个符号周期内的联合信号检测器:
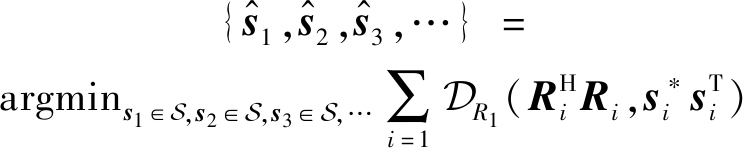
(7)
其中,在联合检测中可知![]() 为解调信号,si为输入信号,S为所有星座集合,
为解调信号,si为输入信号,S为所有星座集合,![]() 计算调制输出信号与原信号之间的RD之和。
计算调制输出信号与原信号之间的RD之和。
根据在文献[10]中的表述基于RD的检测器式(4)的误差性能取决于信号点间的最小RD,所以作者基于最小RD最大化准则设计出了闭合的最优MUFC,但该文献并未考虑外层信道编码与内层信号调制之间的联合优化问题。为进一步提高系统可靠性,本文将对编码和调制模块进行联合优化,优化后的误差性能是由基于式(5)信号序列之间的![]() 之和所决定。其中联合信号检测器式(7)的优化准则是由式(8)所决定的,旨在最大化信号序列之间的最小RD之和,即
之和所决定。其中联合信号检测器式(7)的优化准则是由式(8)所决定的,旨在最大化信号序列之间的最小RD之和,即
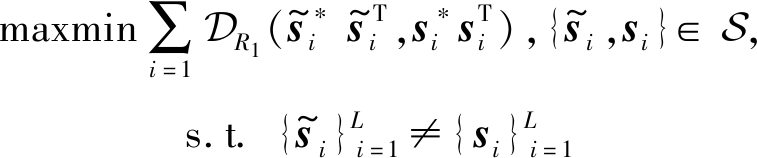
(8)
其中,L为符号序列长度,在优化准则中si与![]() 都是星座
都是星座![]() 子集但
子集但![]() 是计算不同序列中信号之间的RD之和。虽然本文所提方案聚焦于大规模SIMO系统,但需要指出的是,其扩展到MIMO系统中也是适用的[15]。例如,在点对点MIMO系统中,可以考虑的是使用发射天线选择技术,利用单天线来应用MUFC方案;对于多用户MIMO系统,则可以采用OFDMA技术,将不同的子载波分配给不同的用户,从而在不同的子载波上实现MUFC调制。
是计算不同序列中信号之间的RD之和。虽然本文所提方案聚焦于大规模SIMO系统,但需要指出的是,其扩展到MIMO系统中也是适用的[15]。例如,在点对点MIMO系统中,可以考虑的是使用发射天线选择技术,利用单天线来应用MUFC方案;对于多用户MIMO系统,则可以采用OFDMA技术,将不同的子载波分配给不同的用户,从而在不同的子载波上实现MUFC调制。
另外,本文与文献[10]中工作主要差别在于本文考虑的是内外层调制之间联合优化问题,是基于多符号之间的最小RD之和来建立联合信号检测器;并以最大最小化符号序列间的黎曼距离为目标,来设计具体的星座映射方案。
3 基于最大化最小RD的星座映射方法
在2.2节给出的MUFC调制符号联合检测器的误差性能取决于符号序列间的最小RD之和的结论基础上,本节拟结合外层的信道卷积编码方案来优化调制符号序列输出,在低时延的前提下提高系统的误差性能。具体方案包括两种,即基于格雷(Gray)编码的星座映射方法和基于格状编码调制(Trellis Code Modulation, TCM)的星座映射方法。
3.1 基于格雷编码的星座映射
格雷是一种绝对编码方式,在传统星座(例如QAM星座,QPSK星座等)中, 格雷编码的特点是在星座点与其有最小欧氏距离的星座点之间的编码仅有一位比特的不同。这主要是因为,欧氏距离较小的星座点更加容易引起误判,因此该编码方案能够降低误比特率的大小,提高系统的可靠性。然而,在MUFC中,星座点的距离是按照RD测度准则来进行优化的。是否存在类似的映射方案,以及编码后的编码增益如何衡量,这是本小节探讨的主要内容。
由命题1可知,最优![]() 可由三个子星座表征,而三个子星座的结构是具有规律性的。因此,
可由三个子星座表征,而三个子星座的结构是具有规律性的。因此,![]() 的星座点格雷编码映射准则,可在三个子星座空间中展开。主要思想就是:由于Qα与Qθ是实数等差序列,因此可采用类似传统幅度调制(PAM)星座对其进行格雷编码映射,Qφ是标准的PSK序列,同理可对该子星座点也进行格雷编码映射,三个子星座分别的格雷编码映射即组成一个整体星座信号点的映射。
的星座点格雷编码映射准则,可在三个子星座空间中展开。主要思想就是:由于Qα与Qθ是实数等差序列,因此可采用类似传统幅度调制(PAM)星座对其进行格雷编码映射,Qφ是标准的PSK序列,同理可对该子星座点也进行格雷编码映射,三个子星座分别的格雷编码映射即组成一个整体星座信号点的映射。
格雷编码映射主要针对的是单个符号的之间最小RD距离最大化,但在本文2.2中检测方法是以多个符号周期内的联合信号检测器进行检测,此时多个符号之间的最小RD距离和不满足最大化这个优化准则,所以此方案在多个符号周期内传输时性能并没有改善。
3.2 基于TCM星座映射
TCM的核心思想就是把信道编码和调制有机结合起来的一项技术,可以在不增加信道频带宽度的基础上提高信息传输系统的有效性和可靠性[16]。基本原理就是通过集分割的方法将通过卷积编码器的信息比特的编码转化为对星座上信号点的编码,即将外层的信道编码与内层的系统信号组成的星座看成是一个整体来进行设计,以达到有效性和可靠性的相对统一。
具体来讲,输入端的信息比特流,经过串并转换,由一路比特流分成两路比特流,其中一路不经过任何编码进入TCM,另一路经过卷积编码器输出多路的比特流进入TCM,根据信号点间按照RD测度准则进行星座分割,再通过信道模型后根据逆映射译码规则思想进行译码,并串转化后形成一串比特流输出,图2为系统模型的框架。因此,为了改善误码的性能,本文利用卷积编码比率为:R=m/m+1(此时的卷积编码状态数目较少,而且译码路径相对简单,可以减少译码的复杂程度与时延,适用于URLLC通信场景),输入的总的比特流为n,则m比特流进入卷积编码器。
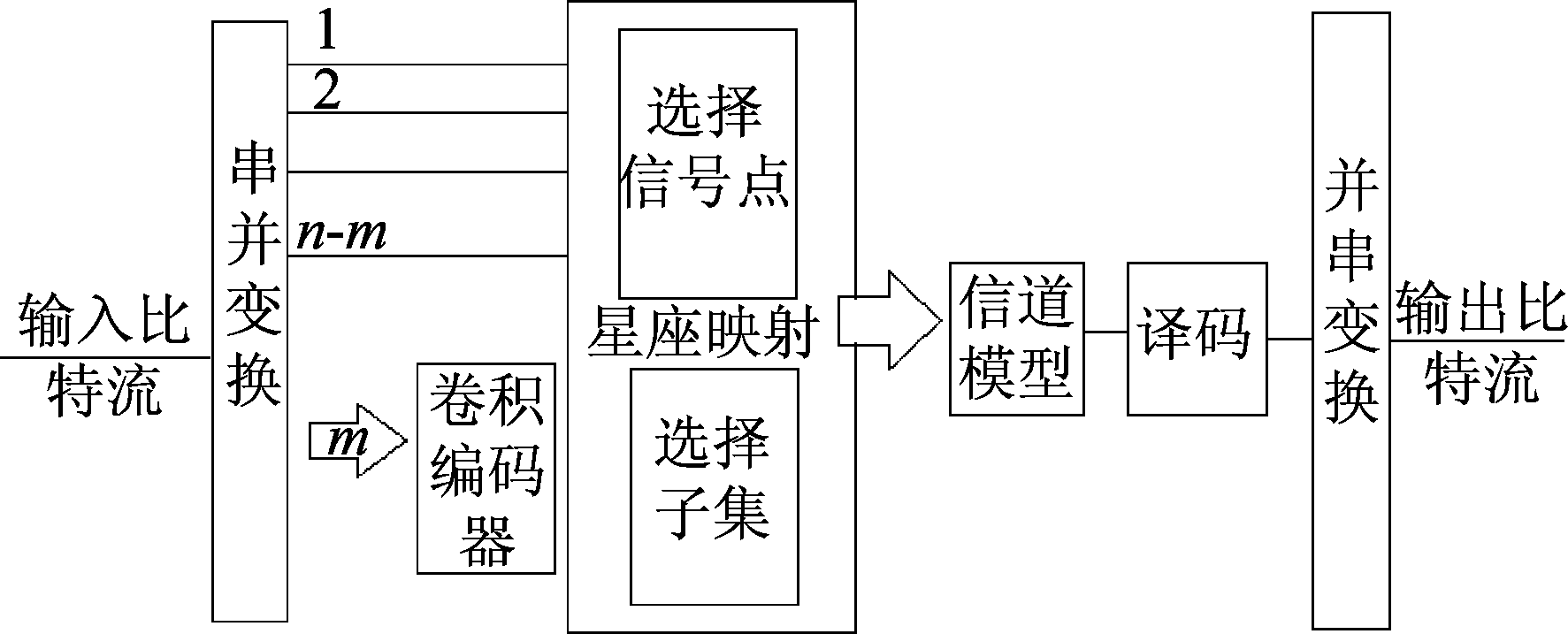
图2 系统模型图
Fig.2 System model diagram
分割集是TCM的核心内容,把一个空间中全部信号点按照最小RD最大化规则依次分割,并且每次分割后的RD依次增加。每次分割都是把一个较大的信号集分割成较小的两个子集,每一次分割就意味着,子集数目是前一次的2倍,同时子集内的RD亦增大。在本文中集分割是通过对已知具有最低编码译码复杂度的唯一可分解星座进行分割。
通过卷积编码器后的信号在每个分支经过星座映射,使得每条信号路径之间有最大的RD,此时的星座分割生成的编码为最优码。星座的最佳分割方案同时也满足TCM最优码的分配通道信号规则:
(1)星座上的信号点都应以相等的概率出现,并具有相当数量的规则性和对称性[17],在本文中3.3是以调制阶级数目8为例;
(2)同状态的转移,信号是从第一次分割的子集B0或B1中选择,也就是处于相同状态的转移时,信号是来自子集B0 B1[17]。
(3)并行转移分支如何分配是基于间隔距离为最大的RD,同时信号点应取自子集C0C1C2C3中。
尽管在星座基于TCM映射情况中单个符号间的最小RD不能够保证是最大化,但是本文在2.2中所使用的软判决符号序列检测方法是计算多个符号序列之间最小RD之和,此时由于星座映射是利用TCM方案,所以可以使信号序列之间的最小RD之和最大化。这样基于TCM星座映射的最小RD之和与基于Gray星座映射的最小RD之和相比距离要更大,因此基于TCM星座映射要比基于Gray星座映射的通信性能要好。
3.3 两种星座映射方案的性能分析
本部分根据3.1与3.2中介绍的两种不同的适用于一般阶级数目星座映射方法,本节以阶级数目8星座为例进行详细的星座映射方案叙述。
根据3.2中的想法构成了两状态卷积编码器的调制输出如图3所示,其中未编码的比特为1位也就是m=1,剩余的一位经过卷积编码器编码率为R=1/2,增加冗余共组成一位3比特的码组,最高位比特为未编码比特。
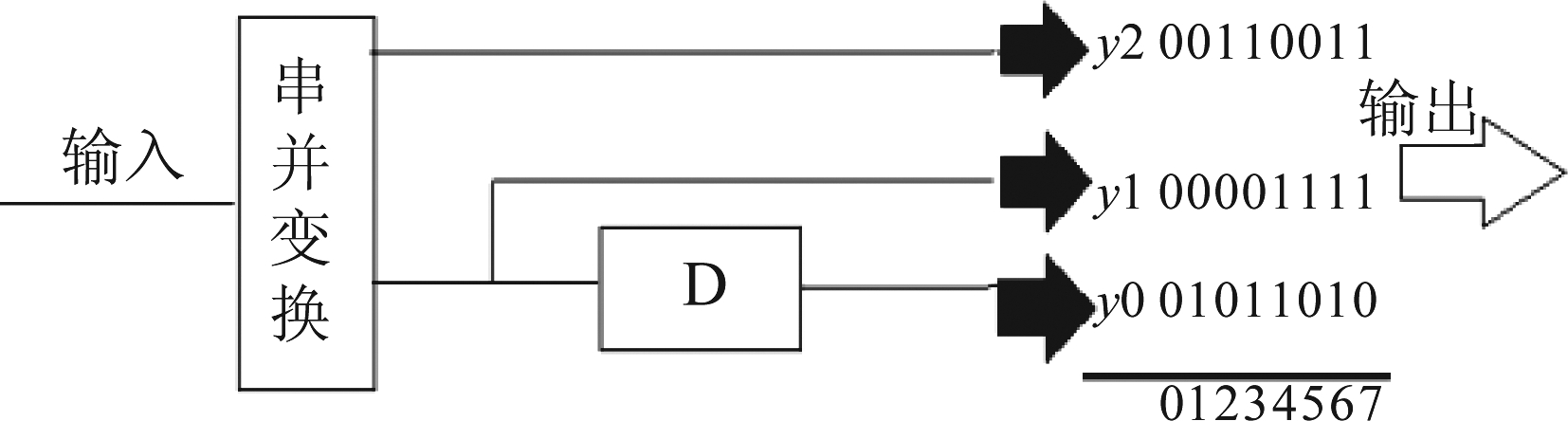
图3 两状态的(2,1,3)卷积编码器TCM调制输出
Fig.3 Two-state (2,1,3) convolutional encoder
在阶级数目为8时基于3.1所叙述普遍的格雷映射方案下,进行具体的分配。此时的R为3,三个子星座参数Qα,Qθ,Qφ分别是PAM和PSK结构的格雷映射,具体映射规则在表1中表述。
根据上文3.2中的普遍适用的TCM星座映射方案,此时调制阶数为23的星座,初始信号点之间的最小RD为:![]() 经过依次的分割之后会产生
经过依次的分割之后会产生![]() 该RD在软判决检测模型中起到关键性作用。
该RD在软判决检测模型中起到关键性作用。
最优比特调制阶数为8的所有信号点组成一个星座集合,通过上文TCM分割方案把8个信号点分割成两个子集B0和B1,子集中最小的RD为![]() 再将子集B0和B1分别分割,即四个子集C0C1C2C3,且B0=C0UC2 B1=C1UC3,最小的RD增加到
再将子集B0和B1分别分割,即四个子集C0C1C2C3,且B0=C0UC2 B1=C1UC3,最小的RD增加到![]() 继续分割,四个子集再次分割可以得到8个子集。图4为调制阶级数目8的具体分割情况:对于下图来说从半径较小的左上角开始逆时针旋转直至半径较大的一圈结束。
继续分割,四个子集再次分割可以得到8个子集。图4为调制阶级数目8的具体分割情况:对于下图来说从半径较小的左上角开始逆时针旋转直至半径较大的一圈结束。
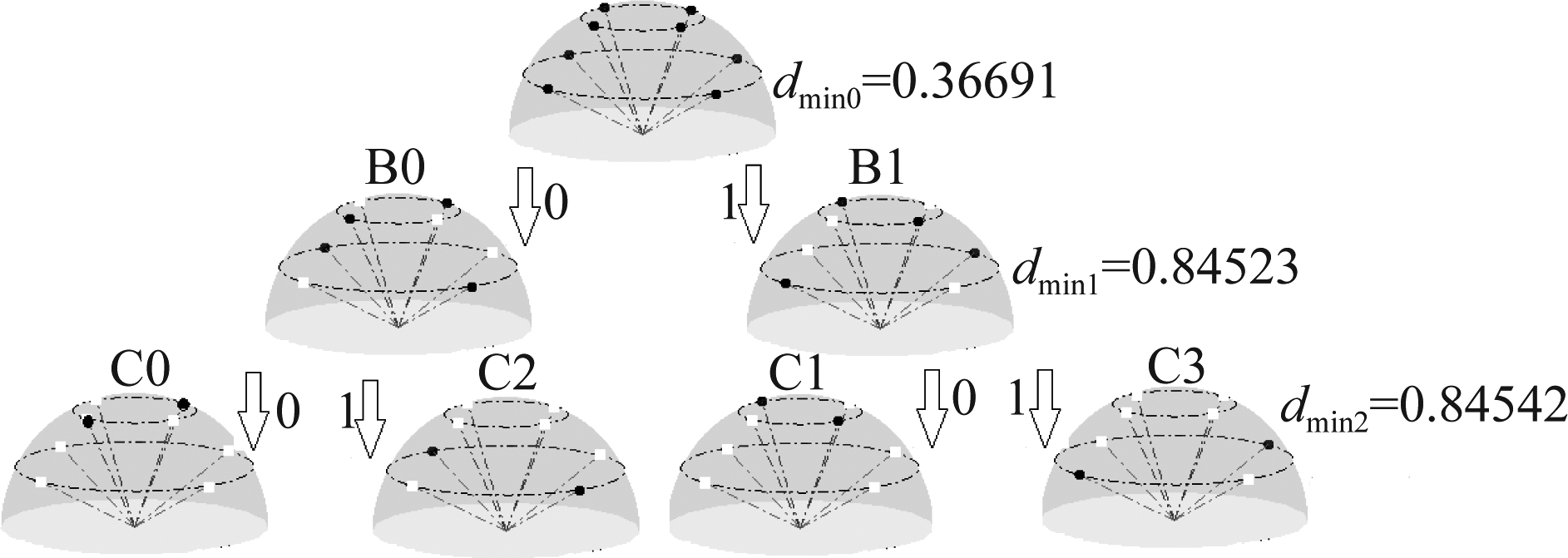
图4 调制阶数为8的星座集分割
Fig.4 Constellation set division with modulation order 8
根据图4下面具体解释基于RD的TCM分割后输出的3比特码组如何一一对应星座图上的信号点,本文设置(2,1,3)卷积编码器,其输出2比特码组为y1y0,即是属于C0C1C2C3中的子集。当y1y0=00时,选择子集中的C0;当y1y0=01时选择子集C2;当y1y0=10时选择子集C1;当y1y0=11时选择子集C3。则未编码比特映射到y2(最高位),在选定其子集Ci后,由最高位来随机选择子集中两个星座点之中的一个。
在星座映射后的软判决检测机制中所用的是(3,2,3)两状态的状态转移图,具体格状转移图如图5所示。
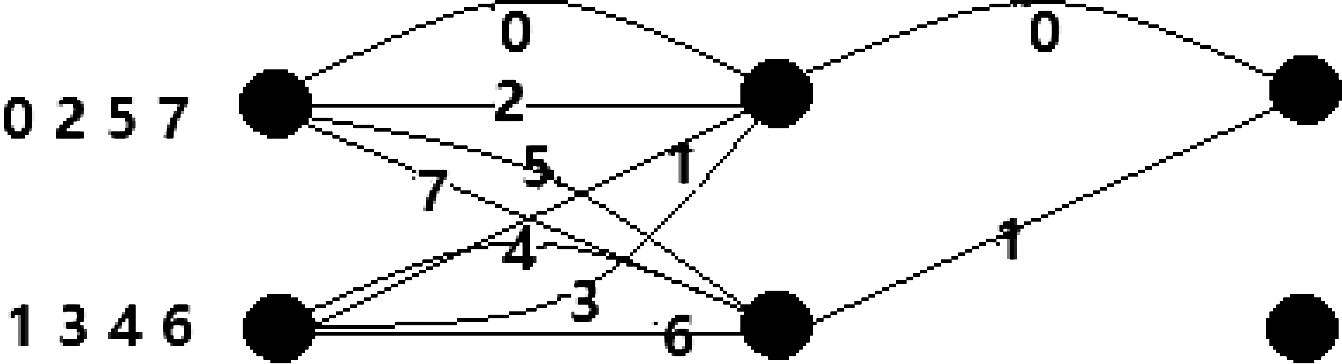
图5 两状态的TCM状态转移图[16]
Fig.5 Two state TCM state transition diagram[16]
由两状态的卷积编码器可知,从一个状态到下一个状态有两条路径,这两条路径是可以到达同一个状态的不同的编码比特,可以称之为并行距离[16]。假设第2个时刻接收到的信号为r2,从开始进入到下一个状态利用RD联合信号检测器式(8)计算出所有分支距离值的可能,其次通过式(7)选出此时的RD之和为最小值时的![]() 得到与之相对应的编码输入值,作为逆映射译码结果。
得到与之相对应的编码输入值,作为逆映射译码结果。
在表1中表示了调制阶级数目为8的TCM映射方案与Gray映射方案规则,则在表2中根据表中不同的阶级数目与映射方案计算出两信号点之间的最小RD值,可以明确的看出TCM星座映射方案的优势。
表1 TCM映射方案与Gray映射方案规则
Tab.1 TCM mapping scheme and Gray mapping scheme rules
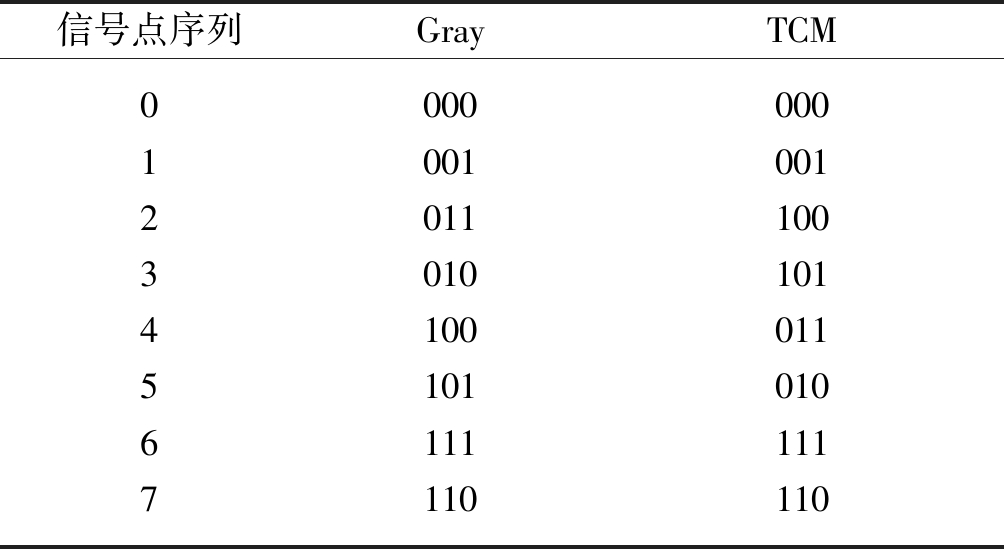
信号点序列GrayTCM01234567000001011010100101111110000001100101011010111110
表2 最小黎曼距离比较
Tab.2 Comparison of minimum Riemann distance

星座阶级数目基于Gray星座映射信号点间最小黎曼距离基于TCM星座映射信号点间最小黎曼距离48160.58580.36690.20512.00000.84540.5345
4 仿真结果图分析
本节通过计算机仿真来检查所提出的编码方案的错误性能。具体来说,就是根据上文所描述的两个基于Gray和TCM的不同的星座映射规则,在大规模SIMO系统下对其错误性能进行分析。基于两种不同的映射方案来说,在理论上TCM方案相比较来说性能比较好,也就是说TCM的错误性能较小。对于这两个方案比较要尽可能的公平,所以输入的比特数目是固定的,但是具体比特是随机的同时他们的信道系数是相同的。并且这两种方案在外层使用的卷积编码器的配置相同,在内层信号的星座集合是一致的,最后都是经过软判决译码方式输出。所以本文将基于TCM星座映射与基于Gray星座映射和文献[10]中的调制阶级数目为4的星座进行比较。其仿真参数设置如表3:其中模拟仿真次数106。
表3 仿真参数设置
Tab.3 Simulation parameter setting

参数数值kα,kθ,kϕ0,1,2d,Δθ0,0.6154α0,θ01,0.4777m1
在图6中显示天线数目M=64时的误比特率(Bit Error Rate, BER)与SNR之间的关系。![]() 其中k为星座符号携带的比特数)。可以看出所提出基于TCM星座映射方案性能优于参考的两个方案,此时基于Gray星座映射方案最差,其次是调制阶级数目为4的星座。图7显示了M=64与M=128的系统中BER与SNR之间的关系,其中虚线为M=128。可以观察到,当SNR=-10 dB时,三种方案的BER彼此相当。然而,随着SNR的增大,基于TCM星座映射方案的误差性能优势越来越明显;而且,在SNR=-2 dB时,其BER即可达到10-6。
其中k为星座符号携带的比特数)。可以看出所提出基于TCM星座映射方案性能优于参考的两个方案,此时基于Gray星座映射方案最差,其次是调制阶级数目为4的星座。图7显示了M=64与M=128的系统中BER与SNR之间的关系,其中虚线为M=128。可以观察到,当SNR=-10 dB时,三种方案的BER彼此相当。然而,随着SNR的增大,基于TCM星座映射方案的误差性能优势越来越明显;而且,在SNR=-2 dB时,其BER即可达到10-6。
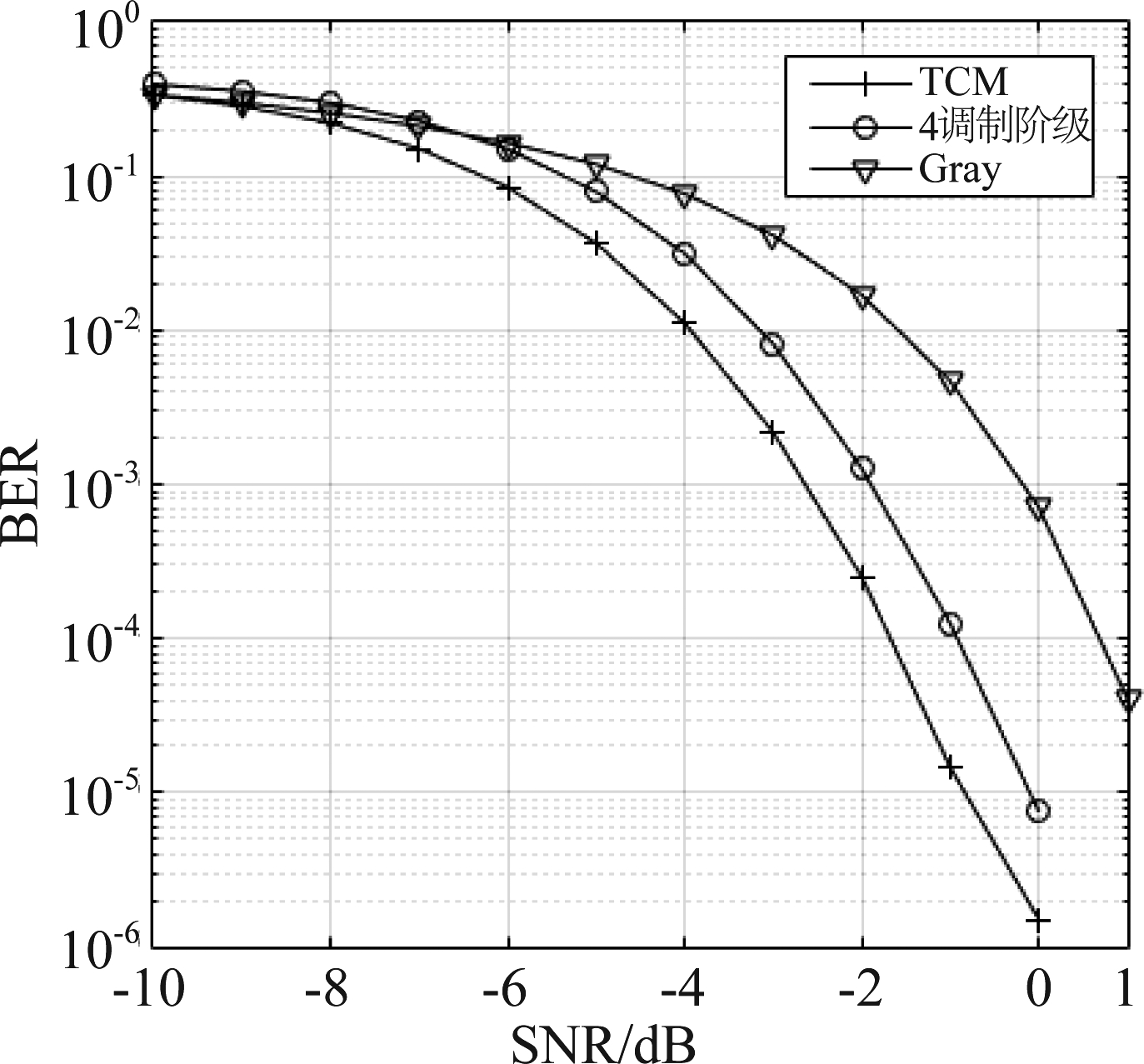
图6 M=64的BER和SNR关系图
Fig.6 BER vs. SNR with M=64
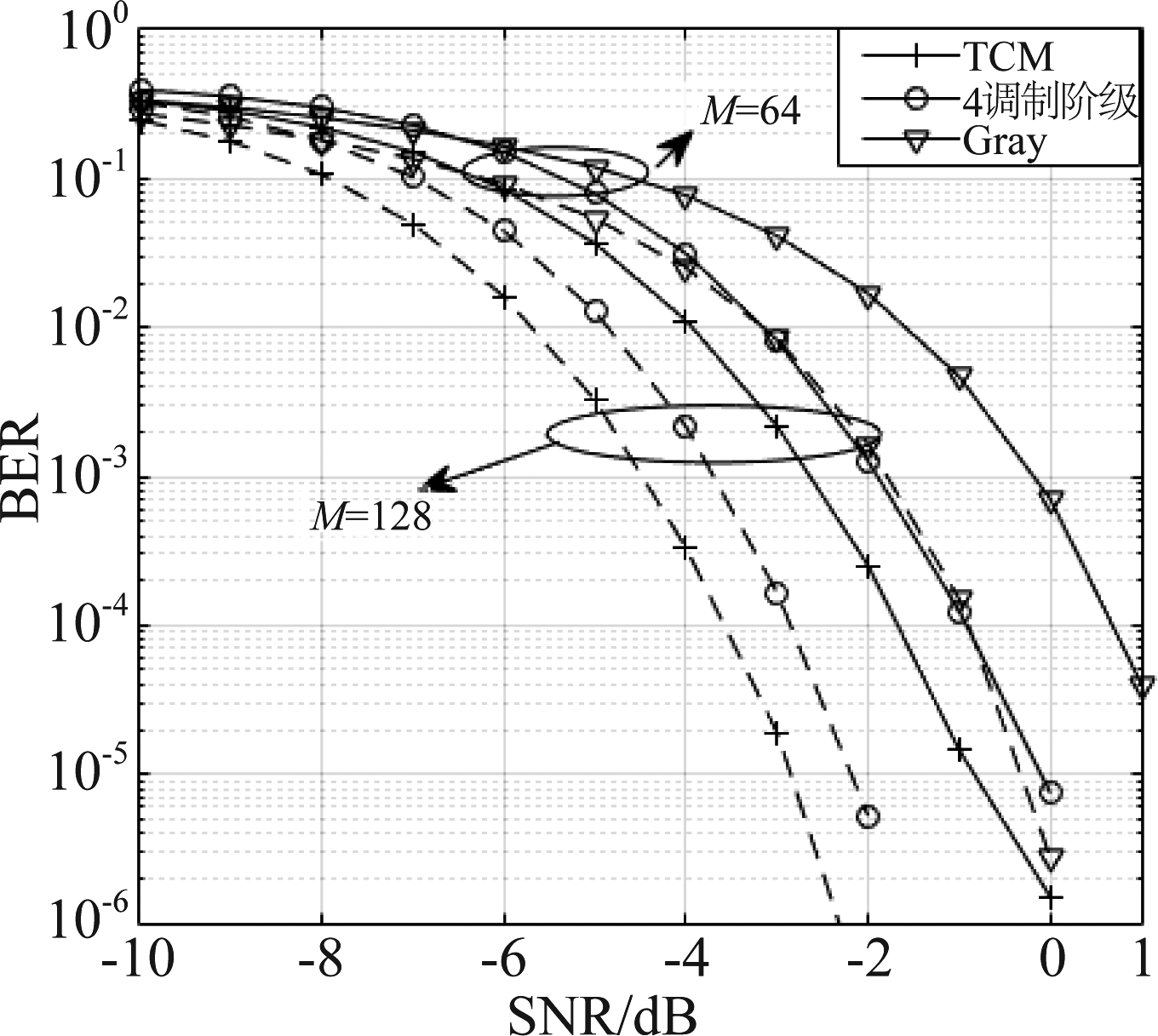
图7 M=64和M=128的BER和SNR关系图
Fig.7 BER vs. SNR with M=64 and M=128
对于固定SNR来说,接收器天线的数量越大,误差性能差距也越大。在图8中,本文研究比较了根据不同的天线数目,固定其SNR值,SNR的值分别是-5 dB和-10 dB,可以看出三个方案的BER走向,天线数目M越大,BER性能越好,同时基于TCM星座映射方案始终优越于其他两个方案。在图9中,研究了在莱斯信道模型下,当SNR的值为-5 dB时,莱斯因子K=0和K=10时,其中K=0时信道模型为瑞利信道。从仿真图可以看出随着莱斯因子的增大,本文提出的两个星座映射方案性能会提高且基于TCM星座映射方案优于基于Gray星座映射方案。
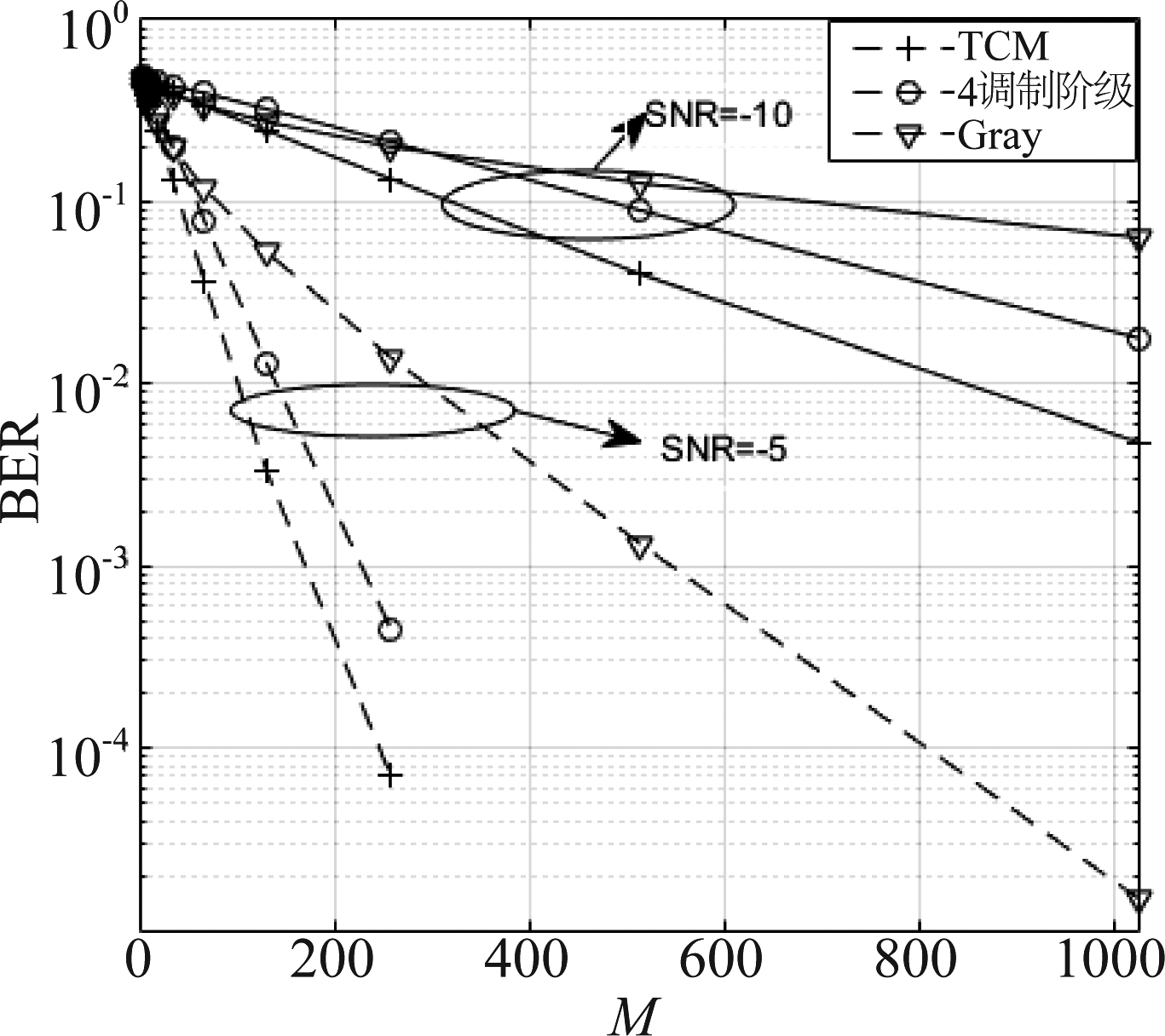
图8 SNR=-5 dB和SNR=-10 dB的M和BER关系
Fig.8 BER vs. M when SNR=-5 dB and SNR=-10 dB
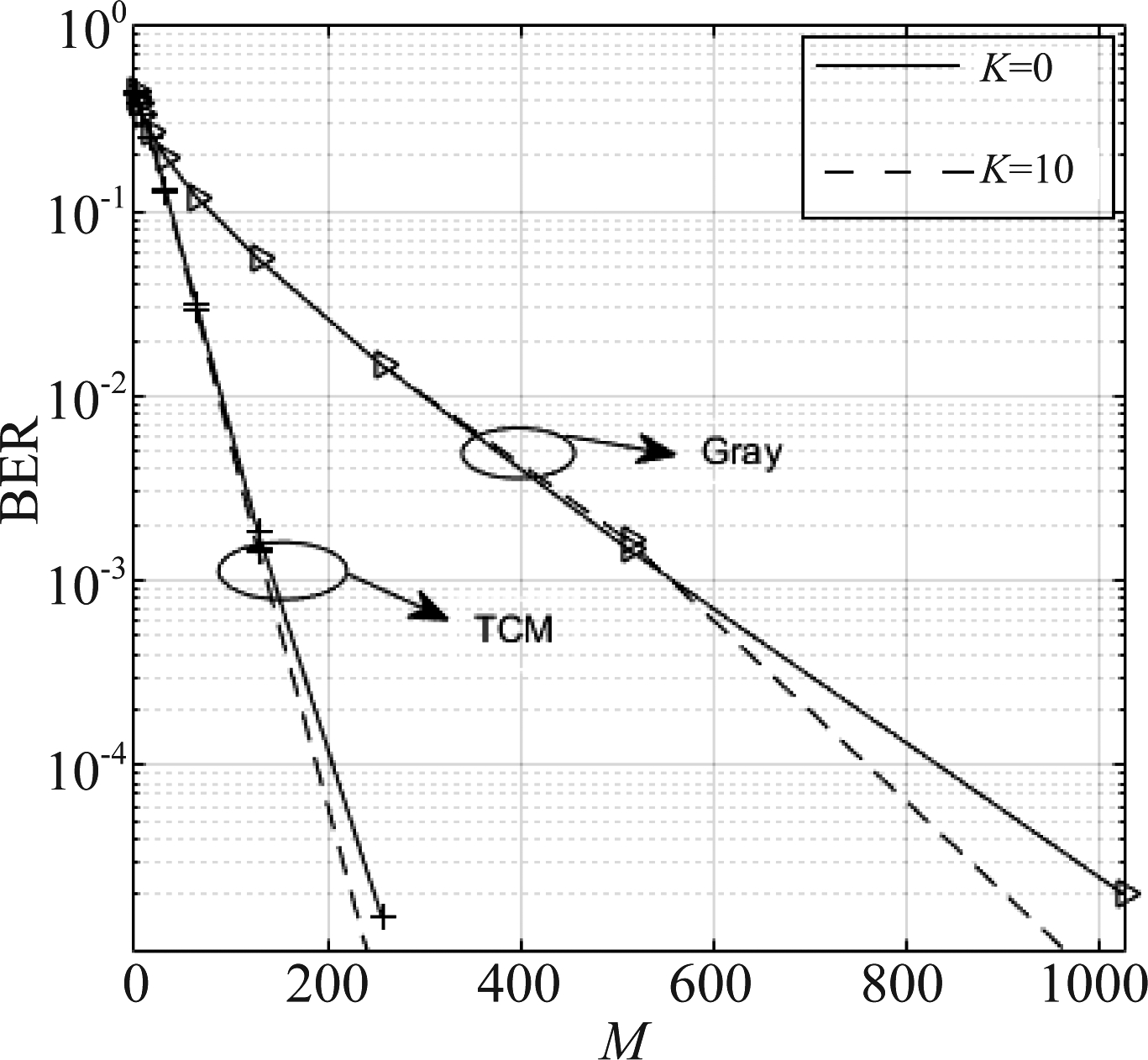
图9 莱斯信道SNR=-5 dB时M和BER关系
Fig.9 BER vs. M when SNR=-5 dB under Rice channel
5 结论
本文研究了一种大规模SIMO系统性能的非相干信号低时延高可靠传输模型,其中单天线的发射端使用级联的信道卷积编码方案与MUFC调制模块对发送信号进行处理。在该系统中,信道系数每两个符号周期变化一次。针对该系统模型,提出了一种基于RD的符号序列检测器,并建立基于符号序列编码优化准则。而且,通过利用格状编码思想,建立了旨在提高系统误差性能的星座映射方案。最后,理论和仿真结果验证了所提方案的有效性。
[1] 陆忠梅, 陈巍, 魏杰, 等. 车联网极低时延与高可靠通信: 现状与展望[J]. 信号处理, 2019, 35(11): 1773-1783.
LU Zhongmei, CHEN Wei, WEI Jie, et al. Current situation and prospect of V2X with ultra-reliable and low-latency[J]. Journal of Signal Processing, 2019, 35(11): 1773-1783.`(in Chinese)
[2] SHIOMITSU Y, OKAMOTO E, MIKAMI M, et al. Effective frame configuration of 5G URLLC using open-loop HARQ for autonomous driving[C]∥IEEE Vehicular Networking Conference (VNC). IEEE, 2019.
[3] NOURI P, ALVES H, UUSITALO M A, et al. Machine-type wireless communications enablers for beyond 5G: enabling URLLC via diversity under hard deadlines[J]. Computer Networks, 2020, 174.
[4] SACHS J, WIKSTROM G, DUDDA T. 5G radio network design for ultra-reliable low-latency communication[J]. IEEE Network, 2018, 32(2): 24-31.
[5] CHEN R, LI C, YAN S, et al. Physical layer security for ultra-reliable and low-latency communications[J]. IEEE Wireless Communications, 2019, 26(5): 6-11.
[6] BANA A S, ANGJELICHINOSKI M, CARVALHO E D, et al. Massive MIMO for ultra-reliable communications with constellations for dual coherent-noncoherent detection[C]∥WSA 2018; 22nd International ITG Workshop on Smart Antennas. VDE, 2018: 1- 4.
[7] POPOVSKI P, STEFANOVI E, NIELSEN J J, et al. Wireless access in ultra-reliable low-latency communication(URLLC)[J]. IEEE Transactions on Communications, 2019, 67(8): 5783-5801.
[8] CHOWDHURY M, MANOLAKOS A, GOLDSMITH A. Scaling laws for noncoherent energy-based communications in the SIMO mac[J]. IEEE Transactions on Information Theory, 2016, 62(4): 1980-1992.
[9] HOCHWALD B M, MARZETTA T L. Unitary space-time modulation for multiple-antenna communications in Rayleigh flat fading[J]. IEEE Transactions on Information Theory, 2002, 46(2): 543-564.
[10] LI S, ZHANG J K, MU X. Design of optimal noncoherent constellations for SIMO systems[J]. IEEE Transactions on Communications, 2019, 67(8): 5706-5720.
[11] YODA D, OCHIAI H. Multilevel coded modulation with reduced latency decoding based on novel set partitioning for APSK[J]. IEEE Transactions on Broadcasting, 2015, 61(4): 674- 684.
[12] SHIRVANIMOGHADDAM M, MOHAMMADI M S, ABBAS R, et al. Short block-length codes for ultra-reliable low-latency communications[J]. IEEE Communications Magazine, 2018: 1- 8.
[13] LI Y, WONG K M. Riemannian distances for signal classification by power spectral density[J]. IEEE Journal of Selected Topics in Signal Processing, 2013, 7(4): 655- 669.
[14] CAGRI ILTER M, WICHMAN R, HAMALAINEN J, et al. A convolutionally encoded OSTBC system with SNR-adaptive constellations for low-latency and low-complexity communications[C]∥2018 IEEE 19th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC). Kalamata, 2018: 1-5.
[15] 王海荣, 俞菲, 黄永明, 等. 大规模MIMO多小区TDD系统中的预编码策略和导频调度[J]. 信号处理, 2013, 29(8): 915-924.
WANG Hairong, YU Fei, HUANG Yongming, et al. Precoding and pilot scheduling in very large MIMO multi-cell TDD systems[J]. Journal of Signal Processing, 2013, 29(8): 915-924.(in Chinese)
[16] 刘煜, 傅必亮. 编码与调制相结合的技术(TCM)及其应用[J]. 电子技术, 2016, 45(6): 59- 62.
LIU Yu, FU Biliang. The technology of trellis coded modulation and how to use[J]. Electronic Technology, 2016, 45(6): 59- 62.(in Chinese)
[17] UNGERBOECK G. Channel coding with multilevel/phase signals[J]. IEEE Transactions on Information Theory, 1982, 28(1): 55- 67.



