1 引言
正交波形被广泛应用于多输入多输出(Multiple Input Multiple Output,MIMO)雷达系统[1-2]和抗欺骗干扰技术[3]。正交波形设计的核心是保证较低的信号自模糊函数副瓣,同时尽可能降低信号互模糊函数电平,以获得较好的波形分集增益与波形隔离度。PC信号因其分辨率、测量精度较高的优点被广泛研究,但是运用在高速运动平台和高速目标探测中存在多普勒敏感问题,并且形式简单,抗干扰能力较差,制约了其在正交波形中的应用。基于LFM信号和PC信号复合调制的LFM-PC信号[4],兼顾了LFM信号和PC信号的优点,具有较高的分辨率、测量精度,同时扩展了PC信号的多普勒容限,还可以提高信号的复杂程度,从而提高雷达系统的抗干扰能力。
为了获得较好的波形分集增益与波形隔离度,国内外学者利用多种优化算法对PC信号进行正交波形优化设计,启发式算法主要包括:模拟退火算法[5]、离散粒子群滤波算法[6]、遗传算法[7]、基于飞蛾扑火的改进优化算法[8]。除了上述启发式算法以外,序列二次规划方法(Sequential Quadratic Programming,SQP)也被运用到波形设计中,文献[9]以最小化峰值相关旁瓣为优化准则,采用约束非线性规划设计MIMO雷达的正交波形。Li等人[10]提出了用于设计正交波形的Multi-CAN算法。该算法根据帕塞瓦尔准则将目标函数转化为频域上的逼近问题,经过循环迭代可获得最优解。此外该方法利用FFT优化计算量,具有占用内存空间更少,运算速度更快的优点。Kerahroodi[11-12]等人将坐标下降法(Coordinates Down, CD)应用到PC信号优化设计中,CD算法在当前点处沿一个坐标方向进行一维搜索以求得目标函数的局部最优解,在整个过程中循环使用不同的坐标方向以求得目标函数的全局最优解。以上文献均未考虑到当平台或目标快速移动时,信号的主副瓣比会急剧恶化。为了解决此问题,Khan[13]、Huang[14]等人在设计正交波形时考虑多普勒频率的影响,Huang提出了一种叫做序列锥规划的算法,算法的核心在于每次迭代中利用一阶泰勒展开式来近似估计约束条件。但是上述两篇文献依然无法克服PC信号多普勒容限过窄的问题。
传统的LFM-PC复合调制信号在脉间实现相位编码调制,脉内实现线性频率调制。本文研究的LFM-PC信号在脉内实现线性频率和相位编码复合调制。对该种复合调制信号的优化设计还处于起步研究阶段,Majumder等人[15]利用Walsh正交码实现脉内相位编码调制。吴悦[4]利用SQP算法优化设计LFM-PC信号正交波形,每次迭代中通过求解一个二次规划子问题来确定下降方向,以减少价值函数来搜索步长,通过多次迭代求得优化问题的解。但是其研究的调制相位为连续相位,对离散相位调制缺少研究。
在高速运动平台和高速目标探测运用的多普勒敏感问题,制约了PC信号在正交波形中的应用。本文研究了一种宽多普勒容限的LFM-PC复合调制信号,首先简单介绍了信号形式并给出了其模糊函数、主峰幅度;其次,在多普勒容限内基于模糊函数建立优化设计模型,将基于ADMM的低复杂度信号优化方法用于求解优化模型。仿真结果表明,此方法相比GA算法能更快速,更有效地对LFM-PC进行正交波形设计。优化之后的LFM-PC信号在多普勒容限内具有更低的自模糊函数旁瓣与互模糊函数。
2 信号模型
2.1 时域波形
雷达发射一组共M个脉冲信号,可表示为:
(1)
式(1)中,ui(t)表示第i个LFM-PC复合调制脉冲信号
(2)
式(2)中,μ表示调频斜率,N表示码长,
表示第i个脉冲的编码序列,ki(n)∈[0,1,…,K-1],K表示调制相位数,
表示M个脉冲信号的编码序列,pn(t)为宽度TP为理想矩形脉冲,可表示为:
式中,
表示码元宽度。
2.2 模糊函数
模糊函数定义为
(3)
式(3)中,τ表示延时, f表示多普勒频移。当i=j时,式(3)表示单脉冲信号si(t)的自模糊函数;当i≠j,式(3)表示脉间信号si(t)、sj(t)的互模糊函数,互模糊函数无法同自模糊函数一样形成主峰。
当i=j时,将式(2)代入模糊函数定义式(3),则其自模糊函数可写为
(4)
为了推导单脉冲信号的自模糊函数主峰幅度,取f=μτ(τ>0),则式(4)在较小的时延范围内可近似改写为
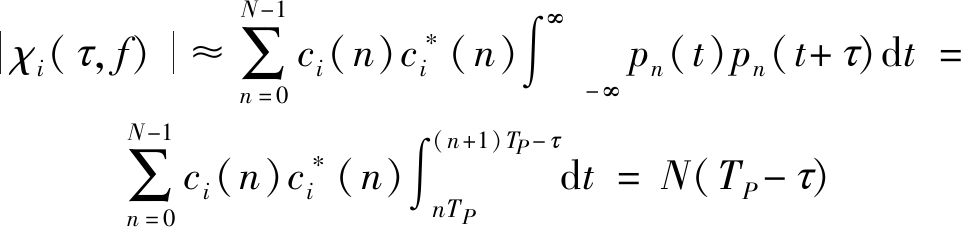
(5)
因此,单脉冲信号的自模糊函数的归一化主峰幅度可表示为
(6)
当多普勒频移f确定时,|χi(τ0, f)|为一定值。定义主峰幅度下降3 dB的多普勒频移范围为多普勒容限(Doppler Tolerance, DT),则LFM-PC信号的多普勒容限为
fDT=0.293μTP
(7)
设一个码元内采样NS点,则采样周期为
一个脉冲内总采样点数N′=N·NS。将式(2)重写为
(8)
其中,
表示采样后的第i个脉冲的编码序列,
表示宽度为TS的理想矩形脉冲。
将脉间信号ui(t),uj(t)代入式(3)
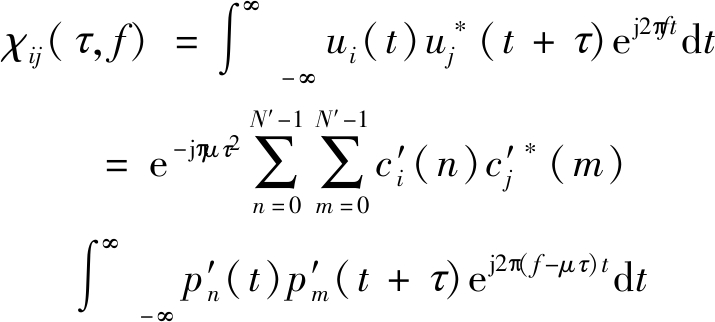
(9)
取τ=kTS,-(N′-1)≤k≤N′-1,
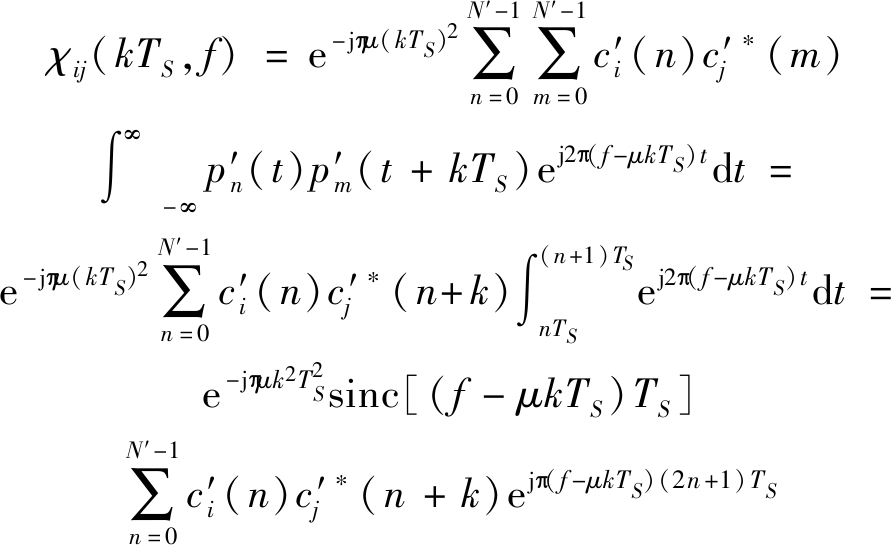
(10)
取f=μpTS,-(N′-1)≤p≤N′-1,
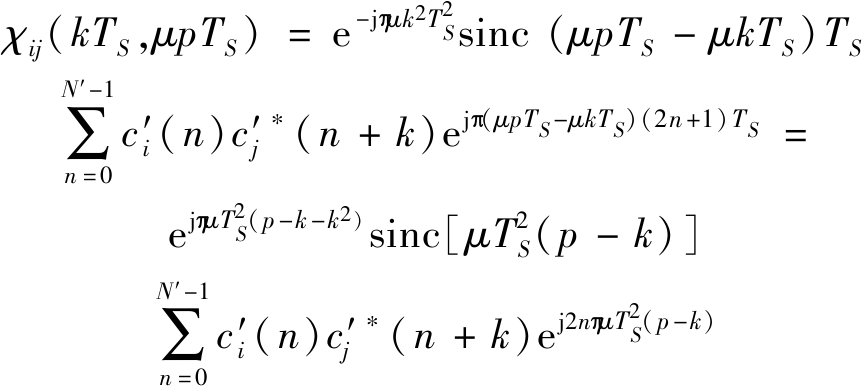
(11)
那么χij(kTS,μpTS)可简写为,
(12)
其中
H(k,p)=ςk,pJkDk,p
Jk表示转移矩阵
其中,
表示克罗内克函数。
当i=j时,式(12)转化为自模糊函数
(13)
3 模糊函数优化
3.1 优化方法
ADMM算法[16]是一种求解优化问题的计算框架,适用于求解具有分布式结构的凸优化问题。ADMM通过分解协调过程,将大的全局问题分解为多个较小、较容易解决的局部子问题,并通过协调子问题的解而得到大的全局问题的解。
ADMM求解问题的表达式
min f(x)+g(z)
s.t. Ax+Bz=c
(14)
ρ为惩罚项,对应的扩展拉格朗日为:
Lρ(x,z,λ)=f(x)+g(z)+
(15)
设
则求解步骤可表示为:
u(t+1)=u(t)+Ax(t+1)+Bz(t+1)-c
(16)
3.2 优化模型
单脉冲信号自模糊函数主峰幅度已由式(6)表示,离散形式可表示为:
(17)
则,多普勒容限内归一化自模糊函数表示
-NDT≤p≤NDT
(18)
式(18)中,
为多普勒容限(fDT=0.293μTP)对应的范围。⎣·」表示四舍五入。
正交波形设计要求脉间信号的自模糊函数旁瓣和互模糊函数都逼近为零;同时,为了提高多普勒失谐时自模糊函数的主副瓣比,将归一化后的自模糊函数加入优化模型。因此优化模型可描述为:在多普勒容限范围内,以脉间信号的归一化自模糊函数副瓣、互模糊函数之和最小化为准则,对LFM-PC信号进行正交波形设计优化。目标函数可表示为
(19)
式(19)中,Ψ=[(k,p)|NS≤|k|≤N′-1,0≤|p|≤NDT]表示自模糊函数在多普勒容限内的副瓣范围,Φ=[(k,p)|0≤|k|≤N′-1,0≤|p|≤NDT]表示互模糊函数在多普勒容限内的范围。
3.3 优化过程
利用ADMM架构嵌套拟牛顿法优化LFM-PC信号的归一化自模糊函数、互模糊函数,使两者之和最小化。优化问题为
i=0,1,…,M-1;kn∈[0,1,…,K-1]
(20)
式(20)可转换为
i=0,1,…,M-1;kn∈[0,1,…,K-1]
(21)
在问题(21)转中引入辅助变量z和约束化c=z,即:
s.t. c=z
i=0,1,…,M-1;kn∈[0,1,…,K-1]
(22)
问题(21)和问题(22)等价。根据式(22)写出增广拉格朗日方程:
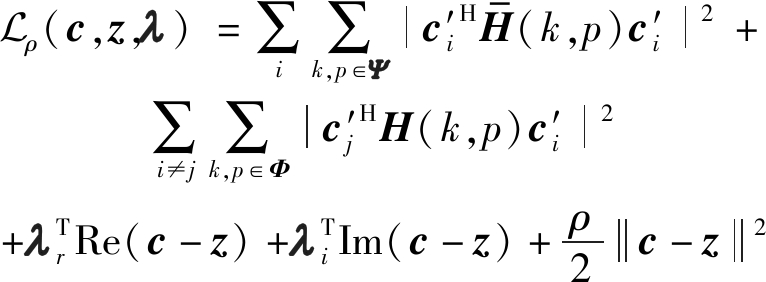
(23)
记u=(λr+jλi)/ρ,则式(23)可写为:
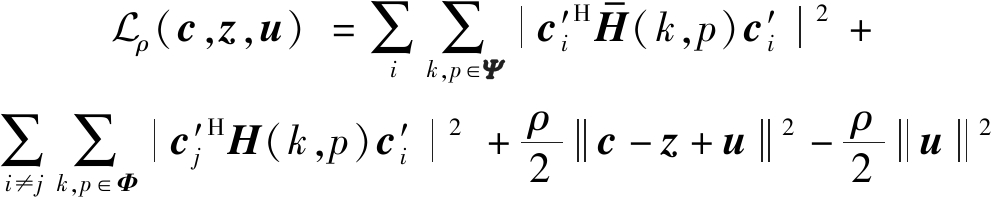
(24)
记c(t)为第t次ADMM迭代后的c值(z和u相应的记为z(t),u(t)),给定初值c(0),z(0),u(0)则该问题的求解可按照如下步骤进行:
1)更新c,此时z(t),u(t)看作已知量:
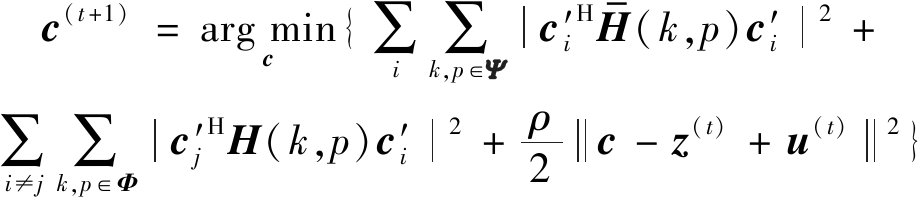
(25)
该问题为无约束最优化问题,可使用拟牛顿法求解,首先需将复数形式的目标函数转化为实数形式:设
则
可转化为:
(26)
转化为:
(27)
在后续计算中,要将实向量转化为
还原成复向量
2)更新z,此时c(t+1),u(t)看作已知量:
i=0,1,…,M-1;kn∈[0,1,…,K-1]
(28)
上式可转化为:
i=0,1,…,M-1;kn∈[0,1,…,K-1]
(29)
由于(29)是一个线性问题,且z中的元素彼此独立,则可将其分解为若干个子问题,子问题可表述为:
(30)
若将复数
看成复平面上的向量,则(30)中目标函数可表示成:
(31)
忽略常值部分,则(30)转化为:
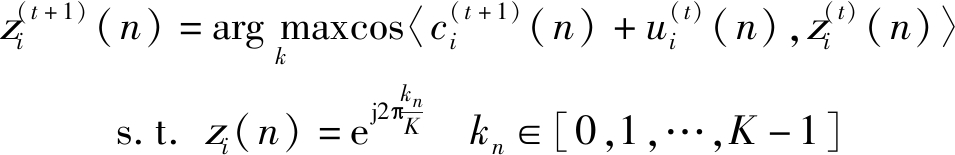
(32)
即求整数k(0≤k<K),使复平面上的向量
和
的夹角最小,k的解为:
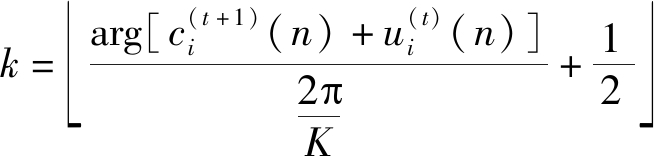
(33)
则(28)的解为:
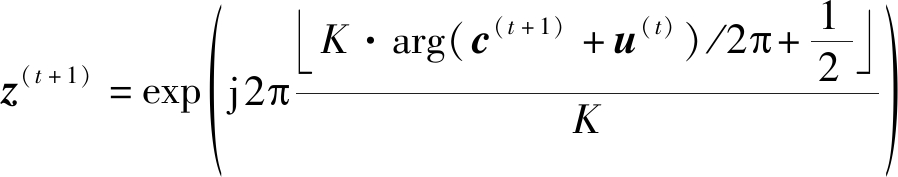
(34)
3)更新u:
u(t+1)=u(t)+c(t+1)-z(t+1)
(35)
由此,ADMM算法的基本思路:初始化变量c(0),z(0),u(0),接着重复步骤1)到步骤3)直至满足迭代停止条件,迭代停止条件包括:迭代次数达到上限,或者|Δ(t+1)-Δ(t)|≤ε,ε为一个较小的正数,作为收敛门限。以上,输出优化后的结果。
下表1给出利用交替方向乘子法求解优化模型的步骤。
表1 ADMM步骤
Tab.1 ADMM procedure
4 仿真及结果分析
根据优化模型(19)中的前后两项,分别定义自相关-平均副瓣(Auto Correlation Average Side Lobe, AC-ASL)、互相关-平均电平(Cross Correlation Average Level, CC-AL)
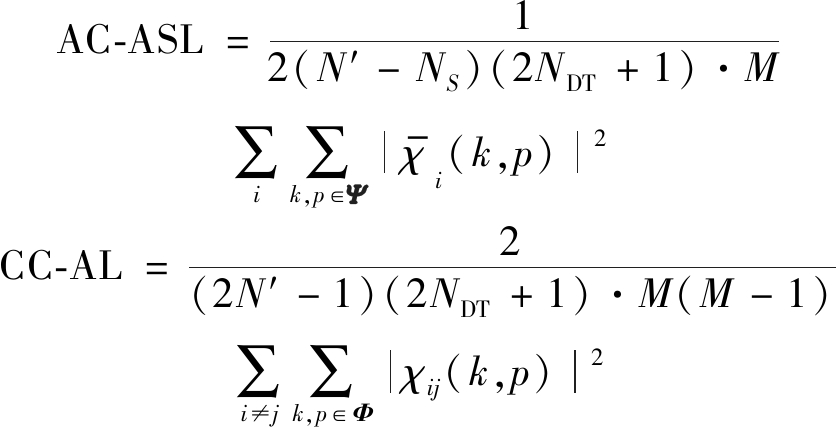
(36)
式中,Ψ=[(k,p)|NS≤|k|≤N′-1,0≤|p|≤NDT]表示自模糊函数在多普勒容限内的副瓣范围,Φ=[(k,p)|0≤|k|≤N′-1,0≤|p|≤NDT]表示互模糊函数在多普勒容限内的范围。
设置码长N=60,脉冲数M=3,调制相位数K=2/4/8,迭代次数上限50次,分别用上述ADMM算法以及GA算法对相同的初始波形进行优化。图1表示K=8时优化前后的一组自模糊函数示意图以及一组互模糊函数示意图,图中颜色越深说明优化效果越好,经过ADMM方法优化的效果比GA算法更好。
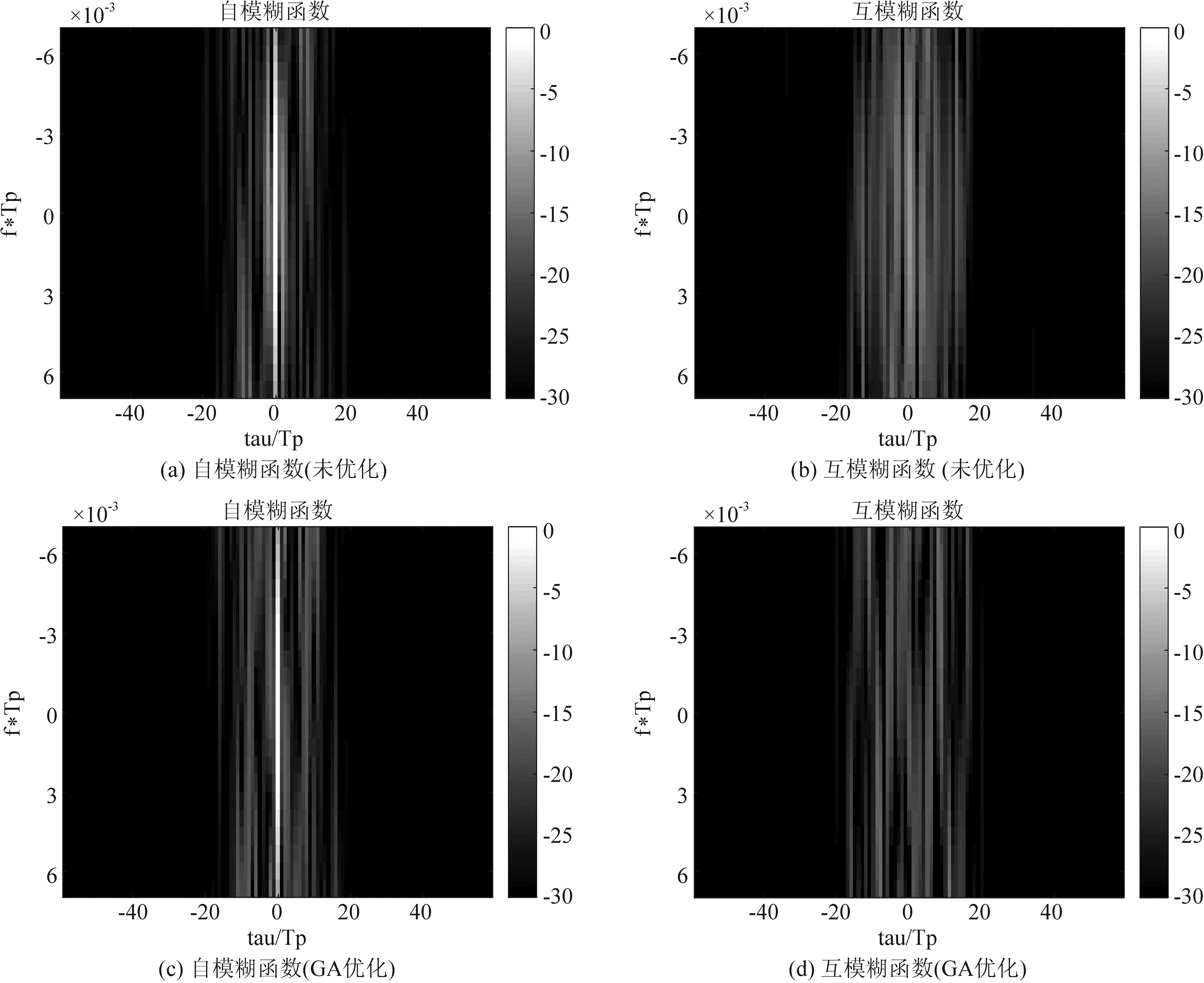
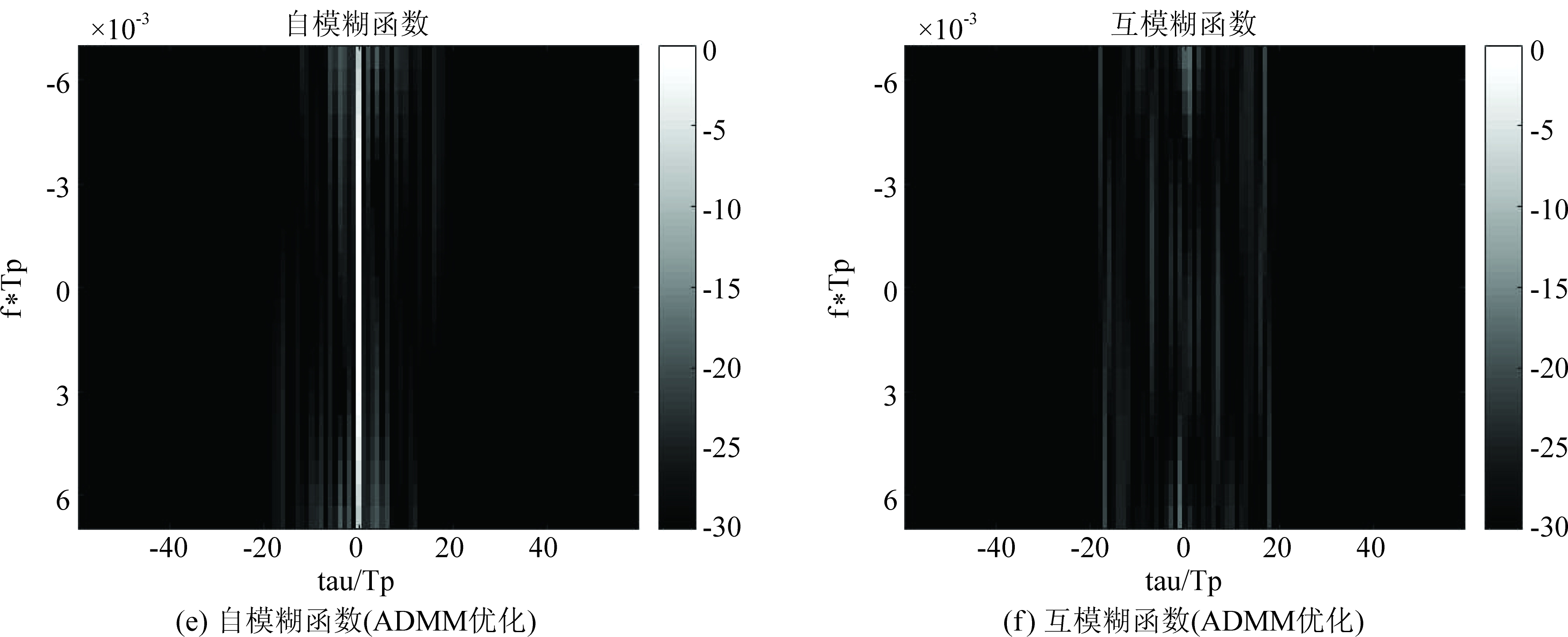
图1 优化前后模糊函数示意图
Fig.1 Diagram of ambiguity function before and after optimization
初始波形AC-ASL=-24.8040 dB,CC-AL=-25.0624 dB。优化仿真数据如表2所示。从表2可以看出,利用ADMM算法优化的波形相比于未优化的波形,AC-ASL、CC-AL下降明显,并且随着相位数的增加,优化效果愈发显著。作为对比的GA算法,优化效果一般,并且随着相位数的增加,优化效果反而下降。因此,经过ADMM算法优化的LFM-PC信号具有更好的波形分集增益和波形隔离度。
观察图2的优化算法迭代收敛曲线以及表3的优化算法时间对比,我们可以发现ADMM算法相比于GA算法迭代次数更少、收敛时间更快、优化效果更好。
表2 仿真数据(dB)
Tab.2 Simulation data(dB)
K=2AC-ASLCC-ALK=4AC-ASLCC-ALK=8AC-ASLCC-ALGA-28.0128-26.8928-26.6000-26.0746-26.8713-26.3941ADMM-28.7169-27.6719-29.0256-29.9253-31.1796-30.8433差值-0.7041-0.7791-2.4256-3.8507-4.3083-4.4492
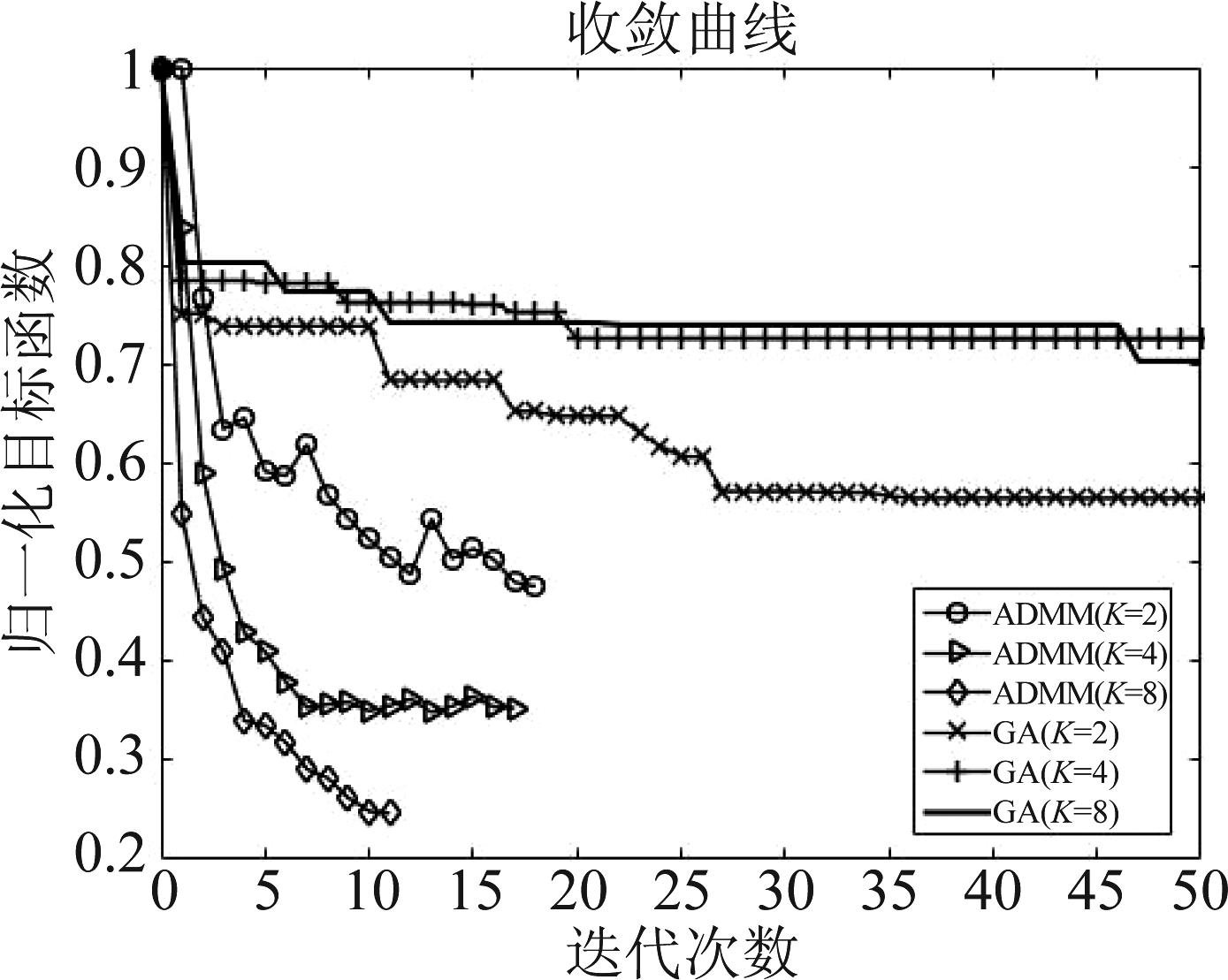
图2 ADMM与GA收敛曲线对比
Fig.2 Comparison of convergence curve between ADMM and GA
表3 ADMM与GA优化时间对比
Tab.3 Comparison of optimization time between ADMM and GA
K=2K=4K=8GA41 min 04 s38 min 25 s45 min 02 sADMM10 min 23 s12 min 45 s13 min 30 s倍数3.9553.0133.336
5 结论
本文基于宽多普勒容限的LFM-PC复合调制信号,在多普勒容限内以最小归一化自模糊函数旁瓣、互模糊函数之和为准则建立优化模型,利用ADMM算法设计正交波形。仿真结果表明,ADMM算法相比GA算法能更快速、更有效地在多普勒容限内优化波形自模糊函数以及互模糊函数。经过优化的LFM-PC信号具有更好的波形分集增益与波形隔离度。
[1] 李旭, 安涛, 刘金鹏. 一种优化MIMO雷达波形设计的算法[J]. 舰船电子对抗, 2019, 42(4): 66-70.
LI X, AN T, LIU J P. An Algorithm Optimizing MIMO Radar Waveform Design[J]. Shipboard Electronic Countermeasure, 2019, 42(4): 66-70.(in Chinese)
[2] TANG B, ZHANG Y, TANG J. An Efficient Minorization Maximization Approach for MIMO Radar Waveform Optimization via Relative Entropy[J]. IEEE Transactions on Signal Processing, 2018, 66(2): 400- 411.
[3] 靳若安. 雷达抗干扰波形优化设计算法研究[D]. 西安: 西安电子科技大学, 2015.
JIN R A. A study of the optimization design of radar anti-jamming waveform[D]. Xi’an: Xidian University, 2015.(in Chinese)
[4] 吴悦. 基于自适应捷变波形的认知雷达干扰对抗技术[D]. 南京: 南京航空航天大学, 2018.
WU Y. Anti-Jamming Technology of Cognitive Radar Based on Adaptive Agile Waveform[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018.(in Chinese)
[5] DENG H. Polyphase Code Design for Orthogonal Netted Radar Systems[J]. IEEE Transactions on Signal Processing, 2004, 52(11): 3126-3135.
[6] REDDY B R, KUMARI M U. Polyphase Orthogonal Waveform Using Modified Particle Swarm Optimization Algorithm for MIMO Radar[C]∥2012 IEEE International Conference on Signal Processing, Computing and Control. Waknaghat Solan: IEEE, 2012: 1- 6.
[7] 黎薇萍, 陶海红, 廖桂生, 等. 抗干扰多波形优化设计技术[J]. 电波科学学报, 2010, 25(5): 940-946.
LI W P, TAO H H, LIAO G S, et al. Multi-Waveform Optimal Design Technique Against Repeat Radar Jammers[J]. Chinese Journal of Radio Science, 2010, 25(5): 940-946.(in Chinese)
[8] 王娇, 李琦, 高军萍, 等. 基于改进飞蛾扑火优化算法的MIMO雷达相位编码信号集设计[J]. 信息与控制, 2019, 48(3): 279-284.
WANG J, LI Q, GAO J P, et al. Phase-Coded Signal Design of MIMO Radar Based on Modified Moth-Flame Optimization Algorithm[J]. Information and Control, 2019, 48(3): 279-284.(in Chinese)
[9] 胡亮兵, 刘宏伟, 吴顺君. 基于约束非线性规划的MIMO雷达正交波形设计[J]. 系统工程与电子技术, 2011, 33(1): 64- 68.
HU L B, LIU H W, WU S J. Orthogonal Waveform Design for MIMO Radar via Constrained Nonlinear Programming[J]. Systems Engineering and Electronics, 2011, 33(1): 64- 68.(in Chinese)
[10] LI J, STOICA P, HE H. Waveform Design for Active Sensing Systems: a Computational Approach[M]. Cambridge: Cambridge University Press, 2012: 31- 65.
[11] KERAHROODI M A, MISHRA K V, SHANKAR M R, et al. Discrete-Phase Sequence Design for Coexistence of MIMO Radar and MIMO Communications[C]∥2019 IEEE 20th International Workshop on Signal Processing Advances in Wireless Communications (SPAWC). Cannes France: IEEE, 2019: 1-5.
[12] KERAHROODI M A, SHANKAR M R, MISHRA K V, et al. Meeting the Lower Bound on Designing Set of Unimodular Sequences with Small Aperiodic/Periodic ISL[C]∥2019 20th International Radar Symposium (IRS). Ulm Germany: IEEE, 2019: 1-13.
[13] KHAN H, EDWARDS D. Doppler problems in orthogonal MIMO radars[C]∥2006 IEEE Conference on Radar. NY, USA: IEEE, 2006: 4.
[14] HUANG Z, TANG B, ZHANG S. Sequential optimisation of orthogonal waveforms for MIMO radar[J]. The Journal of Engineering, 2019, 2019(21): 7912-7917.
[15] MAJUMDER U, BELL M R, RANGASWAMY M. Design and Analysis of Radar Waveforms Achieving Transmit and Receive Orthogonality[J]. IEEE Transactions on Aerospace and Electronic Systems, 2016, 52(3): 1056-1066.
[16] BOYD Stephen, et al. Distributed Optimization and Statistical Learning via the Alternating Direction Method of Multipliers[M]. Oxford: Oxford Univ Press, 2010.
