1 引言
阵列信号处理技术是实现空时域信号处理的一个重要方式,经过若干年的发展,其已经被广泛应用于通信、航海、定位等众多领域[1]。在阵列信号处理理论中,若干个分布在不同位置上的传感器可以对某一来波方向的信号进行数据采集,所得数据通过空域滤波、谱值分析、特征值分解等操作,可以最大限度抑制干扰,得到所需有用信息。阵列信号处理的应用场景主要集中在波束形成、空间谱估计、信源分离、定位等相关领域。其中,波束形成技术是近年来研究的热点之一,其主要包括波达方向估计[2]、自适应波束形成器以及宽带波束形成器等研究领域。在波束形成技术中,不同的阵列流形具有不同的波束特性。以均匀圆阵为例,当俯仰角从0°变化到90°时,其主瓣的宽度会逐渐变宽,使得在不同的俯仰角下,波束形成器的空域滤波的特性会受到很大的影响。因此,在均匀圆阵中,为了确保波束形成的性能在不同俯仰角方向上不发生太大的变化,需要将主瓣的宽度在一定俯仰角范围内保持不变。基于此,方向不变波束形成(Steering Invariant Beamforming,SIB)算法被提出,该方法可以在一定程度上保证波束形成器在不同角度时,其主瓣宽度保持恒定不变。
波束形成从机理上可以分为自适应波束形成和固定波束形成两类。其中恒定束宽波束形成属于固定波束形成范畴,方向不变与频率不变波束形成则属于恒定束宽波束形成。近年来,针对宽带频率不变波束形成的研究日益深入[3- 4],但恒定束宽方向不变波束形成的研究则屈指可数。文献[5]提出的方向不变波束形成只适用于均匀线阵,无法适用于任意型阵列。文献[6]中,幸高翔等人引入了基于二阶锥约束的方向不变恒定束宽波束形成。上面所提到的方向不变波束形成技术,当阵列孔径固定时,波束形成器的性能也将固定。相关研究表明,波束的旁瓣水平与阵列个数呈现负相关性,即波束旁瓣水平会随着阵元个数的减少而变高,这将导致波束形成器性能的恶化。目前,针对方向不变波束旁瓣水平优化的研究还不是很多。因此,本文结合压缩感知理论,提出了可以对波束主瓣与旁瓣水平进行优化的方向不变波束形成方法,即基于压缩感知的方向不变波束形成(CSSIB)。
压缩感知(Compressed Sensing,CS)是一种完全不同于以往的采样定理[7]。CS理论指出,通过利用信号的稀疏性,可以在远小于奈奎斯特采样率的条件下实现信号的采样,并通过稀疏重构算法将其恢复出来[8]。压缩感知理论自提出以来,就一直受到各个领域的关注,目前基于压缩感知这一理论在图像处理[9]、医学影像[10]和信号处理方面[11]都有比较深入的应用。文献[12]表明压缩感知在时域和空域情形下,具有降低信号采样率,压缩阵元的作用。
当信号满足稀疏性时,引入压缩感知方法,可以将信号通过压缩采样的形式,使其映射到一个更低维度的空间中,然后通过稀疏重构算法将其恢复到和原始信号一样的水准。因此,本文引入压缩感知理论,并将M个实际稀疏阵元扩展为N个阵元(M<N)。经由压缩感知处理完后,阵元个数变多,阵列的孔径变大,从而提升了波束形成器的性能,使得其旁瓣水平更低。通过实验仿真,在相同的阵元个数的前提下,基于本文提出的CSSIB方法比传统的SIB方法,其旁瓣水平更低,主瓣宽度更窄。波束形成器的性能得到明显改善。
2 压缩感知理论
2.1 均匀圆阵阵列信号模型
所选阵列为均匀圆阵,入射信号的波长为λ,阵元间距为半波长λ/2。现在有L个远场窄带信号入射到该圆阵上,其与均匀圆阵Z轴的正方向的夹角记为俯仰角θsl,与X轴正方向的夹角记为方位角φ、信号幅度为sl(t)(l=1,2,...,L)。其中只有一个信号为期望信号,其余都为干扰信号。假设当前均匀圆阵的阵元数为M,则阵列接收到的信号,可以表示为X=[x1(t),x2(t),...,xM(t)]T。理想情况下,不考虑接收机噪声和其他干扰的情况下,有
(1)
其中,X是M×Q维矩阵;Q为快拍数;a(θsl,φ)表示阵列在俯仰角为θsl、方位角为φ时的导向矢量[13]。其可以表示为
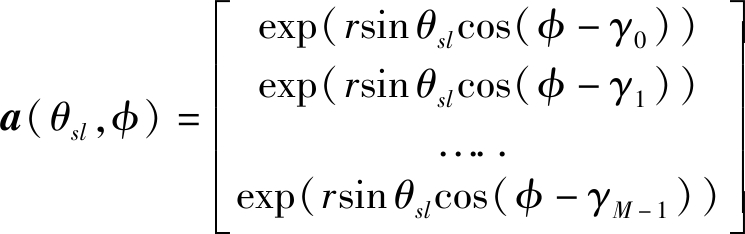
(2)
其中,r=j 2πR/λ,R为阵元半径,γm=2πm/M,m=0,1,...,M-1,其表示为M个阵元相对于X轴正方向基准阵元的角度。
式(1)可简写为:
X=AS
(3)
A为M×L维由导向矢量构成的矩阵;S为L×Q维由信号向量构成的矩阵。
2.2 压缩感知理论
稀疏基与测量矩阵的选取,是决定压缩感知能否成功实现的重要准则。已知一长度为N 的离散信号X,记为x(n),n=1,2,...,N。由信号处理基础理论可知,假定我们此时选择的一组基为Ψ,其中ΨT=[ψ1,ψ2,...,ψn,...,ψN]。那么,信号X就可以由Ψ的线性组合来表示,其形式如下所示
(4)
式(4)中,A与X为N×1维矩阵,Ψ是N×N维矩阵,αn=〈X, ψn〉为X映射到Ψ上的系数。一般将A中非零元素的个数我们称为稀疏度K。那么当K≪N时,表明该信号具有稀疏性,此时称矩阵Ψ为信号X的稀疏基,即该稀疏基满足压缩感知理论。如果不满足,表明该信号不是稀疏的,即压缩感知理论并不适用于该信号。
选定好稀疏基Ψ后,直接对信号X进行编码测量是不可行的。压缩感知理论指出,我们需要将信号X向某一向量空间进行映射,这个被映射的向量空间就是我们所指的测量矩阵,即Φ=[φ1,φ2,...,φm,...,φM],通过投影,将信号X映射到该向量空间中,可以得到与之相关的测量值,即![]() 可写为:
可写为:
y=ΦX
(5)
其中,Φ是M×N维的测量矩阵;y是M×1维的测量值矩阵。代入公式(4),可得
y=ΦX=ΦΨΑ=ΘΑ
(6)
式中,Θ=ΦΨ为M×N维的传感矩阵。
式(6)中,M≪N,由线性代数理论可知,方程组的数量远小于变量的数量,如果对式(6)进行矩阵求解,其会有无穷多解,因而从y的N个测量值中通过求解多元方程组的形式来得到信号X是不可行的。有鉴于此,Candes等人指出,式(6)中传感矩阵Θ必须满足受限等距特性(Restricted Isometry Property, RIP)准则[14]。严格在定义上满足RIP准则基本不可能实现,所以一种和RIP准则等价的准则就被提出来,该准则表示只要稀疏矩阵Ψ和测量矩阵Φ之间不相关,就可以得到恢复的信号。
2.3 确定传感矩阵
在均匀圆阵中,信号的入射角度分为方位角与俯仰角,其中方位角是各向同性的,所以本文选择固定方位角为φ,并将俯仰角范围等分为N份,得到θ1,θ2,...,θN。通过这N个俯仰角得到N维导向矢量,记为Ψ:
Ψ=[a(θ1,φ),a(θ2,φ),...,a(θN,φ)]
(7)
由阵列信号处理知识可得,我们可以将信号X表示为导向矢量Ψ的线性组合,即
X=Ψ S
(8)
式(8)中S为X映射到Ψ上的一组系数,相关研究表明其与Ψ满足线性关系,且该线性组合系数S中非零系数的个数为K,则可以将式(8)写为X=〈S,a(θsk,φ)〉的形式,θsk(k=1,2,...,K)均为θ1,θ2,θ3,...,θN中之一。因此S可以表示为[0,0,...,s1(t),0,...,0,...,sK(t),0,...,0]的形式,使得非零值sk(t)均匀散布在N-K个0当中。此时,当K满足K≪N时,我们认为我们可以按照压缩感知的理论,将Ψ视为稀疏基,将S视为稀疏系数,相应的K即为稀疏度。
经研究表明,当稀疏基确定后,可以选择M×N维随机矩阵作为测量矩阵Φ。经由式(6)可以得到相应的稀疏测量值y,接着,将稀疏测量值y代入式(5),此时可以采用正交匹配追踪算法(OMP)恢复出N个阵元采集的信号,从而达到减少阵元数量的目的。
2.4 OMP恢复算法
压缩感知的恢复算法有很多,常用的有子空间追踪法(SP)、正交匹配追踪法(OMP)、压缩采样追踪法(CoSaMP)等[15]。OMP算法具有运算速度快、容易实现、且恢复信号准确度高等特点[16]。由于篇幅所限,因此本文在此只简要介绍正交匹配追踪法。
OMP算法可以视为向量的求解问题,即不断逼近原始的稀疏向量问题[17]。由公式(8)可知,由于线性组合系数S中只存在有限的小部分非零值,假设其个数为K。由式(6)可知,我们可以证明实际测量得到的观测矩阵y可以由稀疏基Ψ的K个列向量线性表示出来。当知道了稀疏基Ψ中那些可以线性表示y的列后,就可以确定出稀疏系数S。因此,在每次迭代中,通过遍历Ψ中的所有列,搜索出和y最相关的列,然后将其去掉,再从剩下的部分中找到和y最相关的列,重复进行,直到没有和y相关的列时,程序结束。
3 基于均匀圆阵的CSSIB方法
3.1 方法原理
对于一个包含M个实际阵元的均匀圆阵,其阵元间距为λ/2,我们可以将该阵列进行虚拟扩展。扩展后所形成的虚拟阵列包括M个实际阵元和N-M个虚拟阵元。当某一方向的窄带信号通过该N元虚拟阵列时,可以得到M个采样值的稀疏阵列样本。此时,采用压缩感知恢复算法对采集到的信号进行恢复,并用该恢复的信号实现方向不变波束形成。压缩感知理论指出,M和N的关系满足式(9)[18],其中K为稀疏度。
(9)
对于均匀圆阵来说,当阵元间距为λ/2时,其半径定义如下:
R=λ/4sin(π/arrNum)
(10)
式(10)中,arrNum表示阵元数。在对阵列进行虚拟扩展时,阵元的间距保持不变,仍保持为半波长λ/2。在经过阵列的虚拟扩展后,arrNum变大,从而导致π/arrNum变小。由于正弦函数在[0,π/2]区间内是单调递增的,因此,半径R的分母变小。在分子不变的情况下,使得R变大。由阵列孔径的定义指出,均匀圆阵的孔径可以表示为该阵列直径的大小。因此,本文所提出的阵列虚拟扩展的方法,可以在较少阵元的情形下虚拟出较大的阵列孔径,从而进一步提升波束形成器的性能。
3.2 阵列的虚拟扩展
对于均匀连续圆阵来讲,在方位角方向上,各阵元是严格对称的,是满足各向同性的。而对于均匀非连续圆阵,其阵元可近似认为满足该性质。所以,假设一个实际阵元数为N的均匀圆阵,从中随机抽取M个阵元,作为压缩采样阵元,即实际情况中M个阵元的分布位置。抽取M个阵元的方式为:在[1,N]区间内随机生成M个随机数,如果有重复出现的,就重复抽取,直到抽到的M个数各不相同。
3.3 使用压缩感知恢复信号
在均匀圆阵中,当来波信号以角度θ入射到虚拟阵列时,由于经过虚拟扩展的阵列其实际阵元只有M个,所以其接收到的信号实际上是缺失了部分信息的不完整信号。由2.2节压缩感知理论可知,当前所接收到的部分信号可视为入射信号X的稀疏测量值。通过采用压缩重构算法对其进行恢复,可以得到对应于N元虚拟阵列的虚拟加权值。具体计算过程为:
已知阵元数为N的虚拟阵列,其虚拟接收信号可表示为:
Xvirtual(n)=[x1(n),x2(n),...,xN(n)]T
(11)
Xvirtual(n)为N×1维。由于该虚拟阵元中实际阵元数为M个,其余的N-M个都是虚拟阵元,其值都为零。所以,将Xvirtual(n)中M个非零项提取出来,设为ycompressed(n),表示为:
ycompressed(n)=[y1(n),y2(n),...,yM(n)]T
(12)
ycompressed(n)就是2.2节压缩感知理论中提到的稀疏测量值。基于2.4节的正交匹配追踪算法,来恢复信号,其表达式如式(7),其中![]() 为相应的恢复信号:
为相应的恢复信号:
(13)
基于恢复信号Xrecovery(n),我们可以计算出经过虚拟扩展后的加权矢量Wrecovery。阵列虚拟扩展的目的就是使用数量较少的阵元来实现较多阵元的波束形成,所以阵元数为N的虚拟阵元所得到的波束图与实际阵元数为N的波束图应该是一致的。因此,将阵元数为N的实际均匀圆阵所形成的波束作为参考,来进行N维虚拟权值的计算。
我们采用基于SOCP的稳健旁瓣控制高增益波束设计方法,对一个实际阵元数为N的均匀圆阵进行权值设计,得到N×1维的权值向量Woptimal。阵列信号的输出可表示为如下形式:
Z(n)=WHX(n)
(14)
这里我们用Zoptimal(n)来表示此时的信号输出,则其可写为
(15)
以此输出信号为参考,我们可以得到这样的表达式。
(16)
线性代数相关理论指出,式(16)是一个欠定方程,我们无法对其进行直接求解。在这里采用凸优化领域的内点法来得到相应的权值向量的最优数值解Wrecovery,之后可以进一步结合方向不变波束形成方法,来实现基于压缩感知的方向不变波束形成方法(CSSIB)。
3.4 方向不变波束形成
对于均匀线阵来讲,其只能探测到信号入射的方位角,而无法探测到信号的俯仰角。实际应用中,来波信号所含空域信息不仅包含方位角上的信息,更需要包含俯仰角上的信息。因此,本文所选阵列为具有各向同性的均匀圆阵。由于均匀圆阵在方位角上是完全对称的,因此其在方位角上基本上是方向不变的。但是,均匀圆阵在俯仰角上并不对称,其主瓣宽度会随着俯仰角的变大而逐渐变大。因而,为了保证波束形成器的性能,需要使得各个指向角上的波束的主瓣的差异尽可能小,同时还必须保证旁瓣水平尽可能低。方向不变波束形成实现原理如下:
以基于文献[6]中的二阶锥规划方法实现的恒定束宽波束形成作为参考波束。参考波束的旁瓣水平设为HSL(dB),参考波束的方位角设为固定值φ,参考波束的俯仰角定义为θr。定义相应的参考波束图为Pr(φ,θ),其中Prml(φ,θ)为由旁瓣级束宽切割的参考波束主瓣。通过将Prml(φ,θ)在期望的波束指向区间进行左右平移,可以得到在不同指向角下对应的参考波束主瓣,平移的角度为|θd-θr|,其中θd为设计的期望波束指向角。
阵列的法线方向对应的俯仰角设为0°,均匀圆阵的俯仰角范围为[θL,θR]。选取[θL,θR]范围内的N个离散值作为主瓣指向角,即θs1,θs2,…,θsi,…,θsN,θsi∈[θL,θR]。基于上述条件,该波束的优化约束形式为:
![]()
s.t. wHa(φ,θsi)=1![]() θiq∈[θL,θR]i
θiq∈[θL,θR]i
(17)
上式中,θsi为给定俯仰角范围内的主瓣指向角,相应的,该主瓣指向角所对应的旁瓣范围为ΘiSL。a(φ,θsi)为均匀圆阵的导向矢量,Pd(φ,θiq)为波束指向角θsi对应的波束主瓣的第q个值,![]() 为θsi经过平移后的波束指向角
为θsi经过平移后的波束指向角![]() 对应的波束主瓣的第q个值。[θL,θR]i为波束指向角θsi时对应的主瓣区域(由旁瓣级束宽决定),ε为所设的最小均方误差的上界。此时,当俯仰角θsi指向不同角度时,其主瓣宽度都会保持恒定,且旁瓣区域会尽可能的调整到约束条件下的最小值。此时,所形成的波束图就是恒定束宽方向不变的。基于式(17)的约束优化方程,将其改写为凸优化的形式,利用Matlab中的sedumi函数可以求解出相应权值。
对应的波束主瓣的第q个值。[θL,θR]i为波束指向角θsi时对应的主瓣区域(由旁瓣级束宽决定),ε为所设的最小均方误差的上界。此时,当俯仰角θsi指向不同角度时,其主瓣宽度都会保持恒定,且旁瓣区域会尽可能的调整到约束条件下的最小值。此时,所形成的波束图就是恒定束宽方向不变的。基于式(17)的约束优化方程,将其改写为凸优化的形式,利用Matlab中的sedumi函数可以求解出相应权值。
4 仿真分析
仿真条件:所选阵列为均匀圆阵,均匀圆阵中相邻阵元之间的间距满足阵列信号采样定理,即间距为半波长λ/2。入射信号为频率为f0=20000 Hz,采样频率为fs=40000 Hz的正弦信号。信号稀疏度为K=4。基于SOCP方法的波束形成的阵元数为M=10。提出方法使用的实际阵元数为M=10(压缩测量值个数),虚拟扩展后得到阵元数为N=30(原始数据长度)。参考波束设计指标为:主瓣宽度为28°(旁瓣级束宽),旁瓣水平设为-20 dB,波束主瓣指向角为0°。对比两种方法在实际阵元个数相同时的性能指标参数。仿真实验结果如下所示。
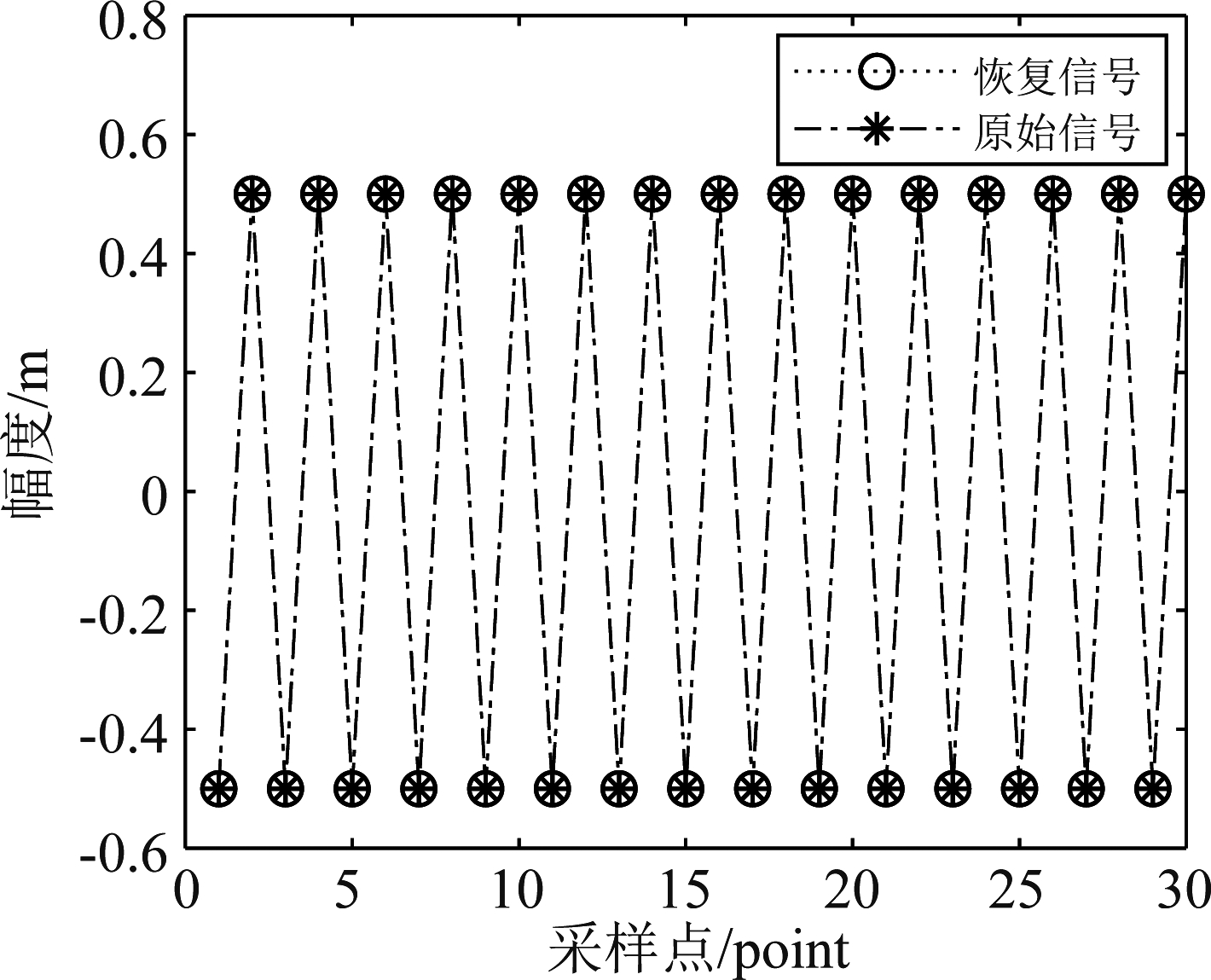
图1 CS恢复信号与原始信号
Fig.1 CS recovery signal and original signal
图1表示采用CS理论所得到的恢复信号与原始信号的对比图。图1表明,实际阵元为30个阵元采集得到的信号与采用CS理论对10个实际阵元的信号进行稀疏重构与恢复后所得到的信号之间的差距很小。实验表明CS理论可以大概率将信号恢复出来。
图2、图3和图4分别表示:阵元数为10,采用原始SIB方法的方向不变波束图;阵元数为10,采用提出CSSIB方法的方向不变波束图;阵元数为30,采用原始SIB方法的方向不变波束图。图2、图3、图4的子图(a)、(b)、(c)分别表示方向不变波束图的正视图、侧视图和俯视图。从图2、图3、图4分析可知,图2的波束图的方向不变性并不佳,远差于图3和图4。图3和图4的性能几乎一样,这表明采用图3中提出的CSSIB方法能在实际阵元数为10个时实现实际阵元数为30的性能,同时比图2具有更低的旁瓣水平和更窄的主瓣。

图2 10阵元、采用原始SIB方法时的方向不变波束图
Fig.2 Steering invariant beam pattern with 10 elements and original SIB method
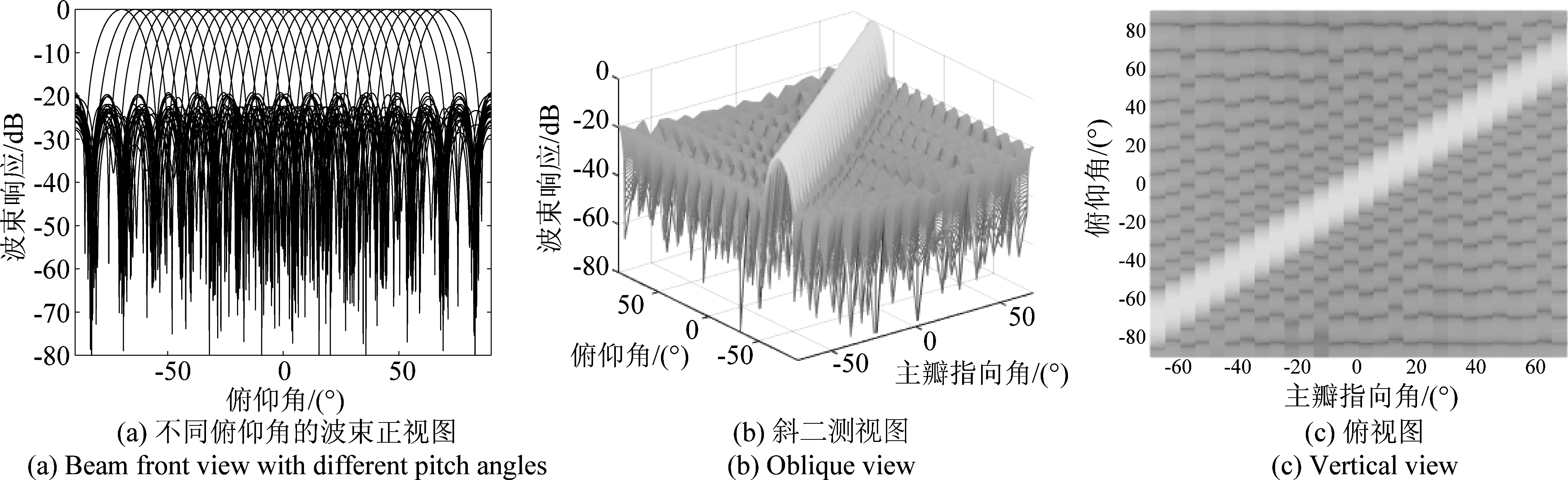
图3 10阵元、采用提出CSSIB方法时的方向不变波束图
Fig.3 Steering invariant beam pattern with 10 elements and proposed CSSIB method
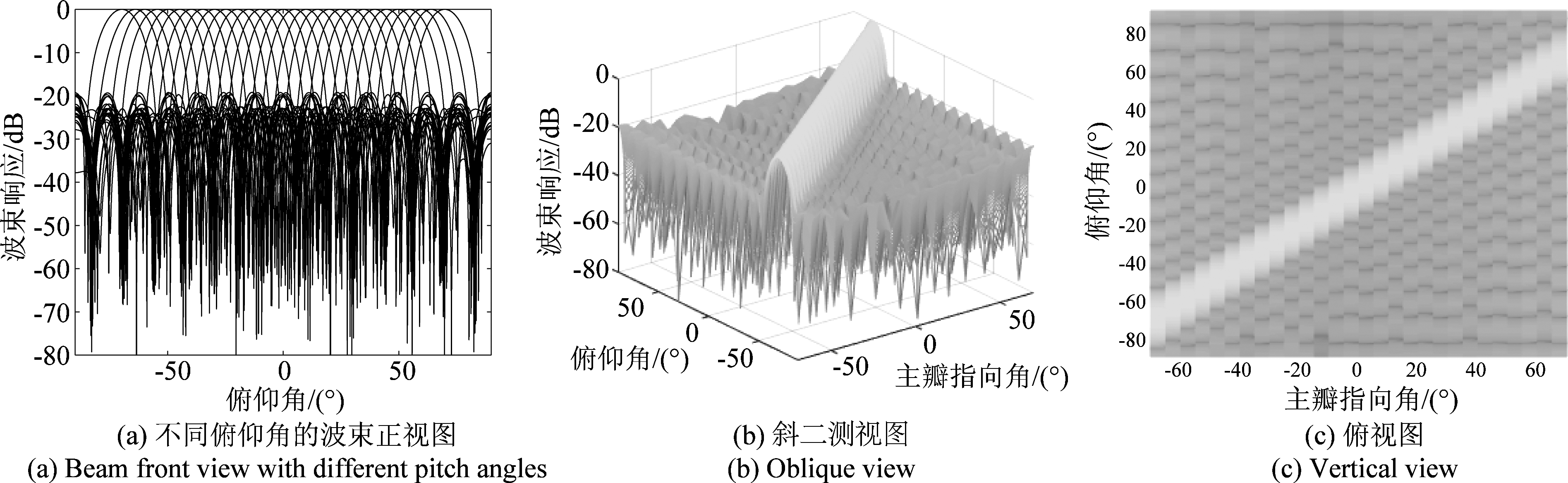
图4 30阵元、采用原始SIB方法时的方向不变波束图
Fig.4 Steering invariant beam pattern with 30 elements and original SIB method
图5和图6分别表示采用原始SIB和采用提出的CSSIB方法的波束的主瓣宽度和旁瓣水平。从中可以清晰看出,采用提出的CSSIB方法具有更低的旁瓣水平和更窄的主瓣,其主瓣宽度和旁瓣水平与实际阵元为30阵元时几乎一致。实际阵元为10个时所提出CSSIB方法,其旁瓣水平比实际阵元数为10个的原始SIB方法低15 dB,主瓣宽度比原始方法少7°。
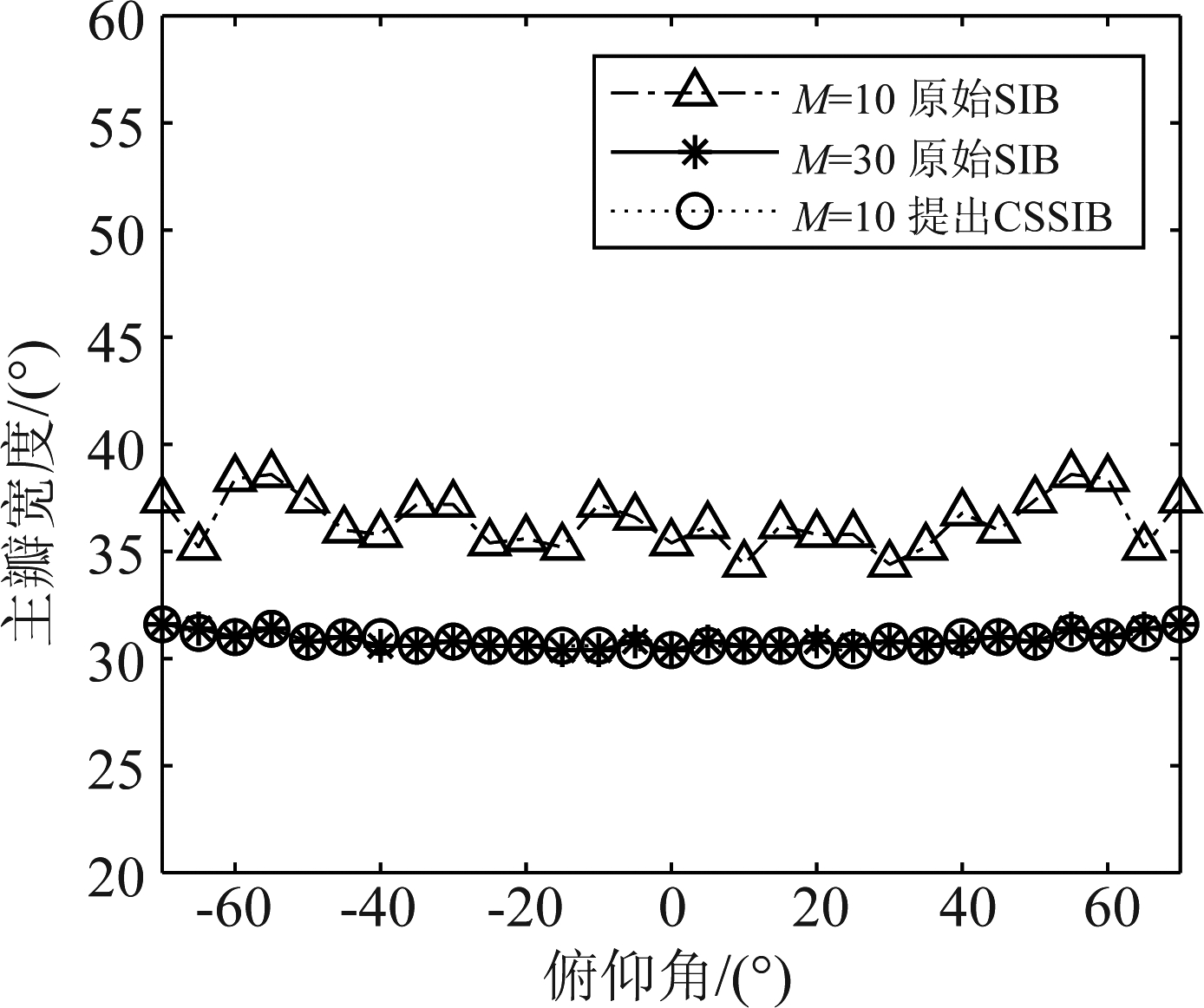
图5 不同方法对应的波束主瓣宽度对比
Fig.5 Comparison of beam main lobe width corresponding to different methods
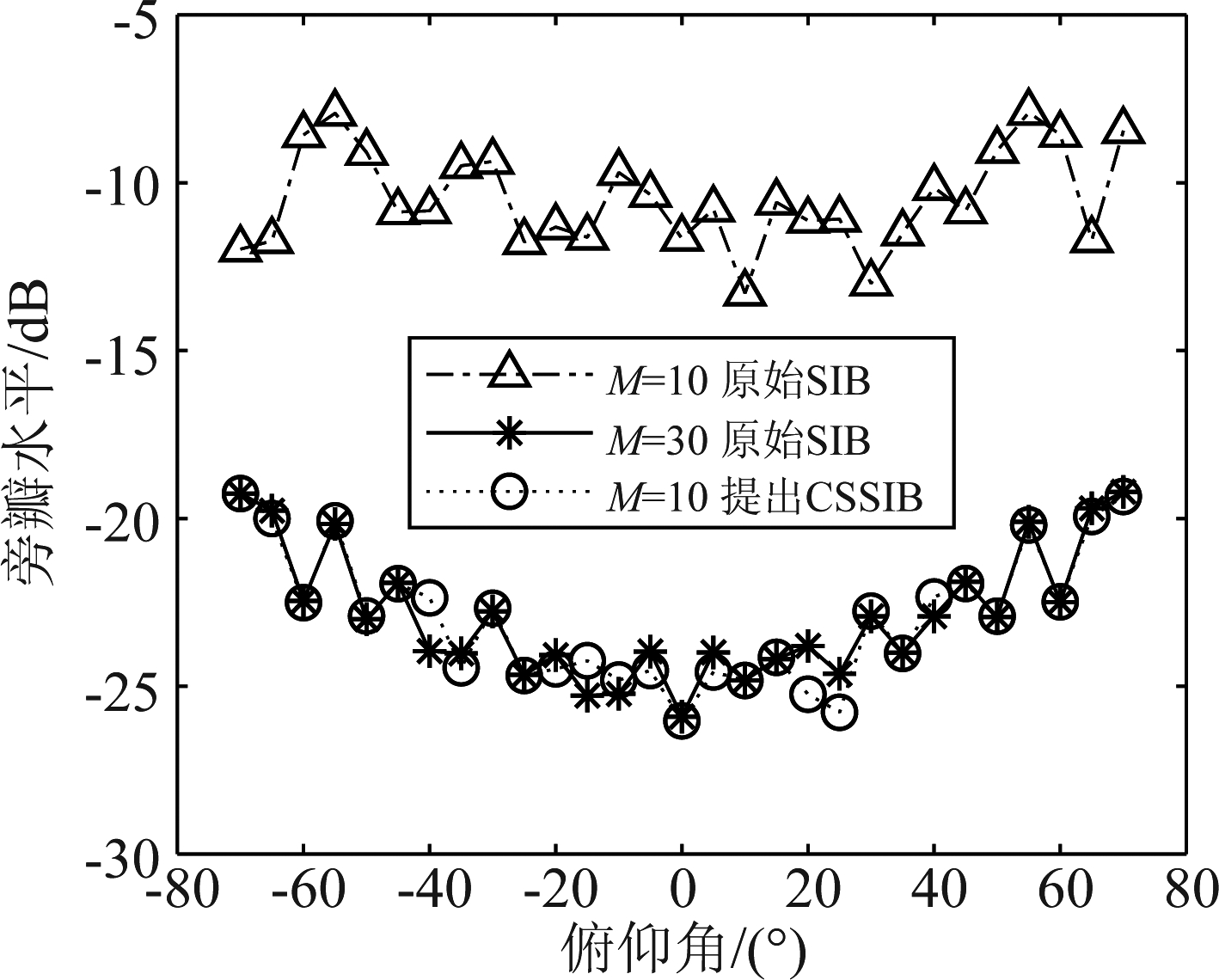
图6 不同方法对应的波束旁瓣水平对比
Fig.6 Comparison of beam sidelobe levels corresponding to different methods
上述实验结果表明,本文提出的基于压缩感知的方向不变波束优化方法(CSSIB),通过引入压缩感知理论,可以对实际阵列进行虚拟扩展,阵列经过虚拟扩展后,增大了阵列的孔径,所形成的波束自然要比采用原始SIB方法所形成的波束具有更窄的主瓣宽度和更低的旁瓣水平,进而对方向不变波束形成的性能有了进一步提升。
5 结论
本文所提出的压缩感知方向不变波束形成(CSSIB)方法是针对均匀圆阵,结合压缩感知和方向不变波束形成理论,通过对实际阵列孔径进行虚拟扩展来实现方向不变波束形成的性能提升。实验结果也表明,本文所提CSSIB方法能够在一定程度上优化主瓣宽度和旁瓣水平,在阵列信号处理领域具有一定的理论意义。
[1] KRIM H, VIBERG M. Two decades of array signal processing research: The parametric approach[J]. IEEE Signal Proc Mag, 1996, 13(4): 67-94.
[2] MINH T H, VIBERG M, PESAVENTO M. Partial relaxation approach: An eigenvalue-based DOA estimator framework[J]. IEEE Transactions on Signal Processing, 2018, 66(23): 6190- 6203.
[3] LIU W, WEISS S. Design of frequency invariant beamformers for broadband arrays[J]. IEEE Trans Signal Proc, 2008, 56(2): 855- 860.
[4] WANG Yong, YANG Yixin, HE Zhengyao, et al. Robust superdirective Frequency-Invariant Beamforming for circular sensor arrays[J]. IEEE Signal Processing Letters, 2017, 24(8): 1193-1197.
[5] ANH P, THUYEN H D, KINH D D. A numerical pattern synthesis algorithm for arbitrary arrays[C]∥6th International Symposium on Antennas, China, Beijing, 2003: 210-213.
[6] 幸高翔, 蔡志明. 旁瓣约束方向不变恒定束宽波束自适应综合[J]. 声学技术, 2009, 28(2): 172-175.
XING Gaoxiang, CAI Zhiming. Synthesis of adaptive steering invariant constant beamwidth pattern with sidelobe constraints[J]. Technical Acoustics, 2009, 28(2): 172-175.(in Chinese)
[7] AMENI Mejri, MOUFIDA Hajjaj, SALEM Hasnaoui. Structured analysis/synthesis compressive sensing-based channel estimation in wideband mmWave large scale multiple input multiple output systems[J]. Transactions on Emerging Telecommunications Technologies, 2020, 31(7): 131-136.
[8] LI Lizhao, SONG Xiao, ZHAO Yimin. Joint group and residual sparse coding for image compressive sensing[J]. Neurocomputing, 2020, 405(2020): 72- 84.
[9] CHEN Wen, CHEN Xudong. Object authentication in computational ghost imaging with the realizations less than 5%of Nyquist Limit[J]. Optics Letters, 2013, 38(4): 546-548.
[10] ZONG Xiaopeng, LEE Juyoung, ALEXANDER John Poplawsky, et al. Compressed sensing FMRI using gradient-recalled echo and EPI sequences[J]. NeuroImage, 2014, 92(5): 312-221.
[11] 姜义. 基于压缩感知的雷达侦察信号处理技术研究[D]. 西安: 西安电子科技大学, 2018.
JIANG Yi. Research on signal processing technology of radar reconnaissance based on compressed sensing[D]. Xi’an: Xidian University, 2018.(in Chinese)
[12] SATHEESH B A, DEEPA B, BHAI S, et al. Compressive sensing for array signal processing[C]∥Proceedings of the India Conference(INDICON), India, Kochi, 2012: 555-560.
[13] ZHANG Yuanrui, WOODS R, MARSHALL, et al. Security optimization of exposure region-based beamforming with a uniform circular array[J]. IEEE Transactions on Communications, 2018, 66(6): 2630-2641.
[14] CAND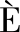 S E, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans Inform Theory, 2006, 52(2): 489-509.
S E, ROMBERG J, TAO T. Robust uncertainty principles: Exact signal reconstruction from highly incomplete frequency information[J]. IEEE Trans Inform Theory, 2006, 52(2): 489-509.
[15] 孙会. 基于压缩感知理论的重建算法研究[D]. 合肥: 中国科学技术大学, 2014.
SUN Hui. Research on reconstruction algorithm based on compressed sensing theory[D]. Hefei: University of Science and Technology of China, 2014.(in Chinese)
[16] 高悦, 陈砚圃, 闵刚, 等. 基于线性预测分析和差分变换的语音信号压缩感知[J]. 电子与信息学报, 2012, 34(6): 1408-1413.
GAO Yue, CHEN Yanpu, MIN Gang, et al. Compressed sensing of speech signals based on linear prediction coefficients and difference transformation[J]. Journal of Electronics and Information, 2012, 34(6): 1408-1413.(in Chinese)
[17] 曾爽. 基于空域稀疏表示的单站无源定位技术研究[D]. 西安: 西安电子科技大学, 2018.
ZENG Shuang. Research on single station passive location technology based on spatial sparse representation[D]. Xi’an: Xidian University, 2018.(in Chinese)
[18] DONOHO D L. Compressed sensing[J]. IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.



