1 引言
最小频移键控(Minimum Shift Keying,MSK)信号因其相位连续,频带利用率较高,已被广泛应用于军事无线通信系统中,例如在美军和北约广泛使用的保密性高抗干扰能力强的Link 16战术数据链传输波形采用的是MSK调制方式[1],美军最新的敌我识别系统MarkXIIA模式5在询问链路和应答链路也采用的是MSK调制波形[2]。
MSK信号检测分为相干和非相干两种方案。相干检测需要精确的信道估计,因此其复杂度较高;非相干检测的性能略差于相干检测,但其不需要信道估计,易于实现,因而得到了更加广泛的应用。在文献[3]中,Osborne和Luntz提出了一种多符号非相干检测(Multi-Symbol Noncoherent Detection,MSNCD)算法,该算法通过对2a+1个比特区间进行观察以检测中间比特,a越大,该算法的检测性能越好,但是当a较大时,该算法的计算复杂度较高;文献[4]提出了一种1比特差分检测算法,该算法计算复杂度低,但检测性能较差;在文献[5]中,周世阳等提出了一种最大似然非相干检测(Maximum Likelihood Noncoherent Detection,MLNCD)算法,通过利用CPM信号的Laurent表示,MLNCD可以在保持和MSNCD相同检测性能的同时降低计算复杂度;文献[6]提出了一种基于差分复合网络的非相干检测算法,该算法具有较好的抗多普勒频移性能;Wu等在文献[7]中提出了一种简化的多符号检测算法,通过结合1比特差分检测算法和MSNCD,该算法实现了计算复杂度和检测性能的折衷。
窄带干扰可以严重恶化MSK非相干检测的误码率(Bit Error Rate,BER)性能,因此MSK非相干接收机一般首先对接收信号进行干扰抑制,然后进行非相干检测。针对窄带干扰,通常采用的抑制算法为重叠加窗干扰抑制算法[2],然而,在干扰抑制的过程中,干扰带宽内的MSK频域信号也会被抑制,因此MSK时域信号会产生一定的畸变,而现有MSK非相干检测算法都未考虑这种畸变,这制约了窄带干扰下非相干检测的MSK通信系统的BER性能。
近年来,深度学习已经展示出了其联合优化通信物理层模块的能力。在文献[9]中,Ye等设计了一种用于正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)系统信道估计和信号检测的深度神经网络; Lin等在文献[10]中提出了一种用于多输入多输出非正交多址接入(Multiple-input Multiple-output Non-orthogonal Multiple Access,MIMO-NOMA)下行链路信号检测的深度神经网络;文献[11]设计了一种用于滤波器组多载波(Filter Bank Multicarrier,FBMC)通信系统信道估计和均衡的深度神经网络;通过联合优化,这些深度神经网络都实现了比传统算法更优的性能。
为了联合优化干扰抑制与MSK非相干检测,本文提出了一种基于深度学习的MSK非相干接收机(Deep Learning-Based MSK Noncoherent Receiver,DL-MSKNCR),该接收机由一个干扰抑制子网络和一个MSK非相干检测子网络构成,仿真结果表明,通过联合优化,干扰抑制子网络可以完成对窄带干扰的抑制,且MSK非相干检测子网络可以有效地应对干扰抑制对MSK信号造成的畸变,并显著地提高窄带干扰下非相干检测的MSK通信系统的BER性能。本文内容安排如下:第2节描述窄带干扰下非相干检测的MSK通信系统模型;第3节详细阐述了所提出的DL-MSKNCR;第4节对DL-MSKNCR进行性能仿真分析,并与现有MSK非相干检测算法进行性能对比;最后总结全文。
2 系统模型
窄带干扰下非相干检测的MSK通信系统如图1所示,发信机对信源比特进行MSK调制,接收机首先对接收信号进行干扰检测和干扰抑制,然后进行MSK非相干检测。MSK信号的等效低通表达式为
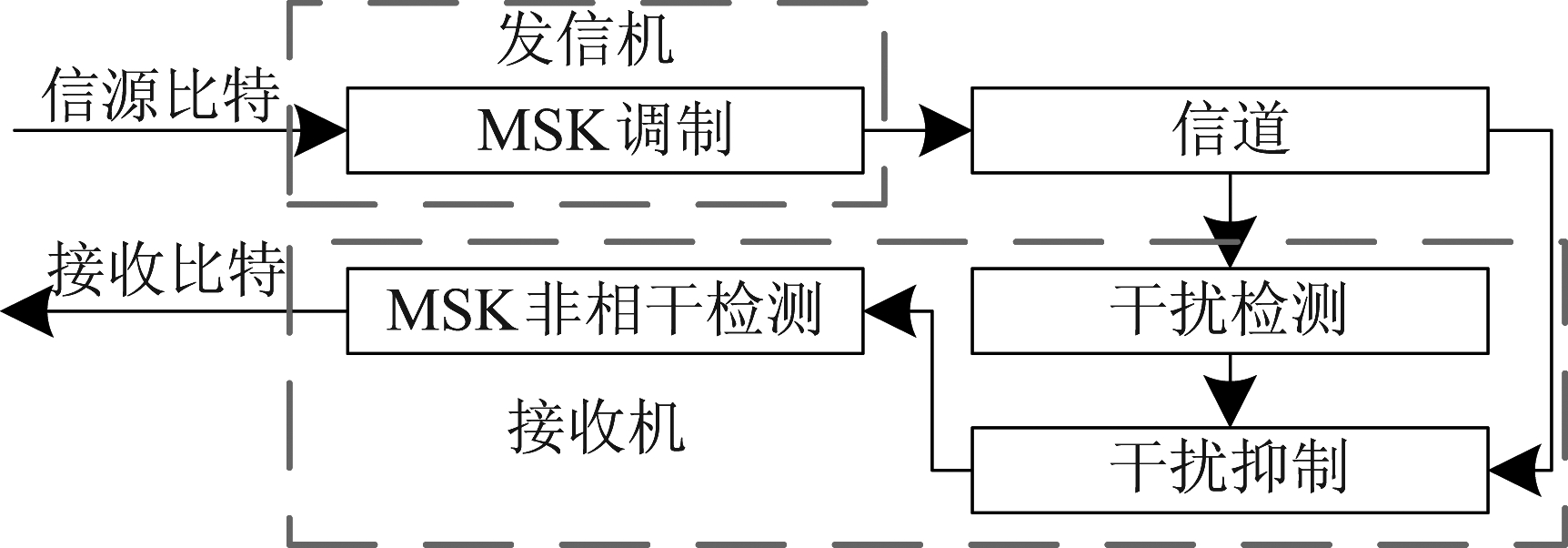
图1 窄带干扰下非相干检测的MSK通信系统
Fig.1 MSK communication system with noncoherent detection under narrowband interference
![]()
(1)
其中A为幅度,ui为iT≤t<(i+1)T时间内的码元符号且ui=2bi-1,bi为信源比特,T为一个码元的持续时间,φi是第i个码元的起始相位且满足
(2)
在加性高斯白噪声(Additive White Gaussian Noise,AWGN)信道和单径莱斯衰落信道下,接收信号可以表示为
r(t)=h(t)s(t)+x(t)+w(t)
(3)
其中h(t)为信道衰落系数,x(t)为窄带干扰,w(t)为噪声且w(t)~CN(0,2σ2)。
设系统采样率为fs且满足fs=M/T,其中M为上采倍数,则离散的MSK接收信号可以表示为
(4)
其中n=0,1,…,N-1,N=BM,B为一帧数据所包含的比特数。
一般地,窄带干扰x[n]可以被建模为[2]
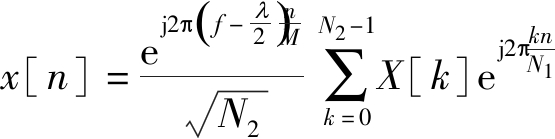
(5)
其中N1为一个远大于N的整数,![]() 为干扰因子且λ=BI/Rb,BI为干扰带宽,Rb为数据速率且Rb=1/T, f为归一化的干扰中心频率且f=fI/Rb, fI为干扰中心频率。
为干扰因子且λ=BI/Rb,BI为干扰带宽,Rb为数据速率且Rb=1/T, f为归一化的干扰中心频率且f=fI/Rb, fI为干扰中心频率。
由于干扰频带与MSK信号频带重叠,因而在对接收信号进行干扰抑制时干扰频带内的MSK频域信号也会被抑制,这会导致MSK时域信号出现畸变。现有MSK非相干检测算法都无法避免这种畸变对检测性能的影响,这制约了窄带干扰下非相干检测的MSK通信系统的BER性能。
3 本文提出的DL-MSKNCR
为了提高窄带干扰下非相干检测的MSK通信系统的BER性能,本文提出了一种基于深度学习的抗窄带干扰MSK非相干检测接收机,该接收机由一维卷积神经(1-dimensional convolutional,Conv1D)层构成,包含一个干扰抑制子网络和一个MSK非相干检测子网络,如图2所示。
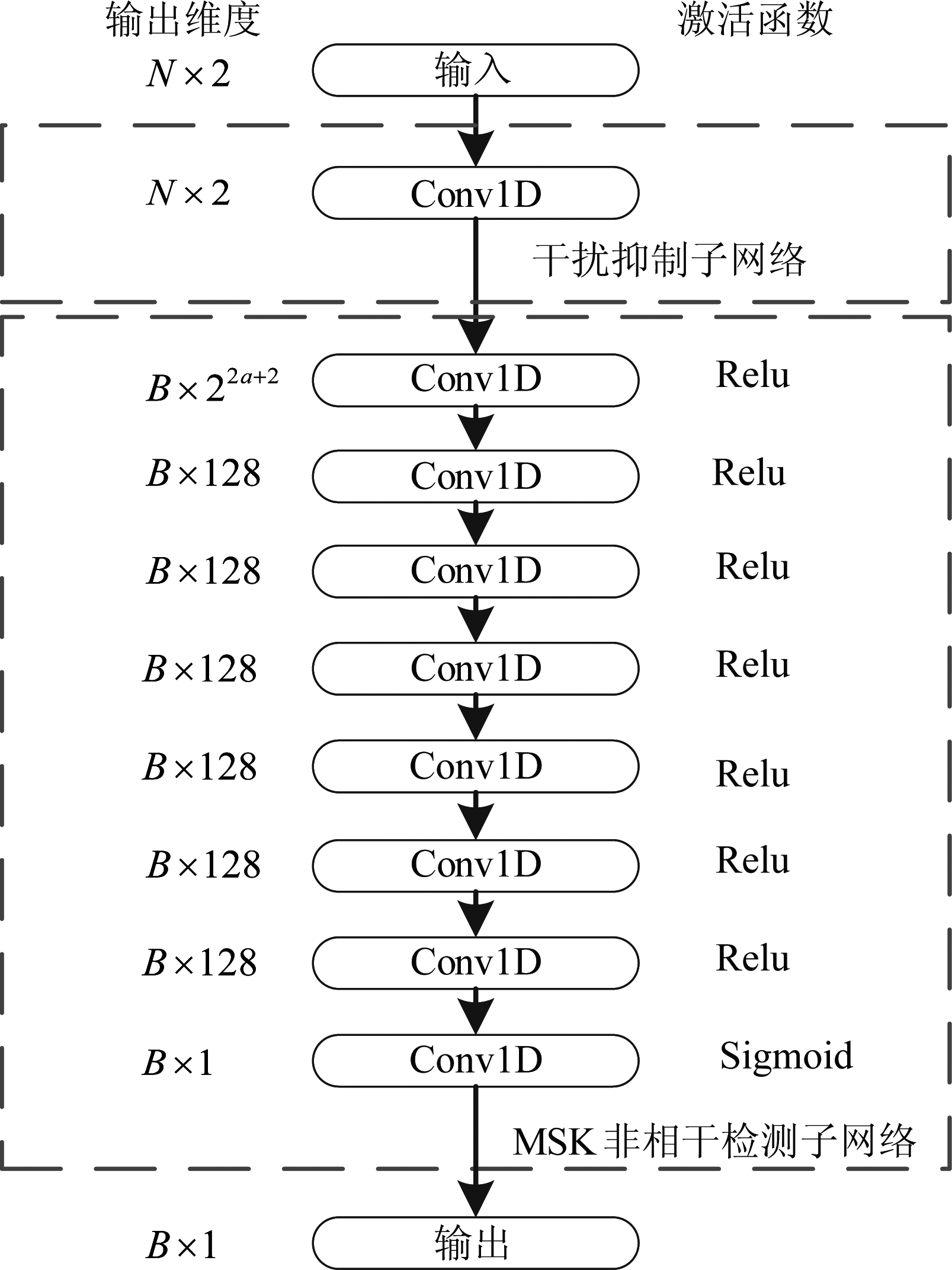
图2 DL-MSKNCR的结构
Fig.2 The structure of DL-MSKNCR
设Conv1D层的输入为dl,ν,其中l=0,1,…,L-1,ν=0,1,…,V-1,L为输入长度,V为输入通道数,则Conv1D层的输出可以表示为
(6)
其中l′=0,1,…,L′-1,L′=(L+2η-α+β)/β,α为卷积核大小,β为步长,η为填充长度,ν′=0,1,…,V′-1,V′为输出通道数, fy,ν,ν′为卷积核权重,gν′为卷积核偏置;α、 β、η和V′为Conv1D层的超参数, fy,ν,ν′和gν′为Conv1D层的可学习参数。
因为卷积神经网络采用实数运算,所以DL-MSKNCR的输入为![]() ,其中
,其中
r=[r[0],r[1],…,r[N-1]]T
(7)
干扰抑制可由滤波实现,因此干扰抑制子网络仅包含1个Conv1D层,在这一层中,α=73,β=1,η=36,V′=2,因此有L′=N。
MSK非相干检测子网络包含8个Conv1D层,在第1个Conv1D层中,α=(2a+1)M,β=M,η=aM,V′=22a+2,因此有L′=B;在第2到第7个Conv1D层中,α=1,β=1,η=0,V′=128;在最后一个Conv1D层中,α=1,β=1,η=0,V′=1。
DL-MSKNCR采用的损失函数为多标签二元交叉熵[12],即
(8)
其中qi为Sigmoid激活函数的输出,设Sigmoid激活函数的输入为pi,则qi可以表示为
(9)
根据式(8)可知,当网络训练完成后,DL-MSKNCR的输出比特可以表示为
(10)
根据DL-MSKNCR的超参数可知,MSK非相干检测子网络与MSNCD和MLNCD相似,都通过对2a+1个比特区间进行观察以检测中间比特,不同之处在于该子网络可以根据干扰抑制子网络对MSK信号造成的畸变来调整可学习参数,因此,通过联合训练与优化,MSK非相干检测子网络可以有效地应对干扰抑制子网络对MSK波形造成的畸变,此外,因为DL-MSKNCR由Conv1D层构成,所以其支持包含任意比特长度的输入,为了降低网络训练所需的数据集大小,可在训练阶段将B设置为一个较小的值,在测试阶段,再根据实际需求重新设置B的大小。
4 性能仿真分析
本节首先在无干扰的条件下,仿真对比本文所提的DL-MSKNCR、MLNCD以及1比特差分的BER性能,然后在有窄带干扰的条件下,仿真对比DL-MSKNCR以及采用重叠加窗干扰抑制与MLNCD的MSK接收机的BER性能。
仿真参数如下:采样率fs=106 Hz,上采倍数M=8,数据速率Rb=125 kbps,衰落信道为单径莱斯衰落信道,莱斯因子为20,最大多普勒频移为400 Hz,优化器为Adam,初始学习率为0.001,训练周期为96,学习率下降周期为32,学习率下降因子为0.1,在训练阶段,B被设置为15,训练数据集包含32768个不同的MSK信号帧,小批量(mini-batch)大小为1024,在测试阶段,B被设置为480。
在训练阶段,当a=4且B=15时,网络的计算量约为10.9MFLOPs,访存量约为0.4 MB;在测试阶段,当a=4且B=480时,网络的计算量约为348.4MFLOPs,访存量约为1.2 MB。仿真采用的软件平台为MATLAB 2019b,CPU为i7- 8700K,GPU为NVIDIA GeForce GTX 1660 Ti,在此平台上,DL-MSKNCR的训练时间约为210 s。
4.1 无干扰
在无干扰时,DL-MSKNCR固定在Eb/N0=5 dB下训练。
图3给出了无干扰时DL-MSKNCR与其他MSK非相干检测算法的BER性能;可以看出,DL-MSKNCR的BER性能优于1比特差分,且a越大,其性能越好;因为DL-MSKNCR和MLNCD都通过观察2a+1个比特区间以判决中间比特,所以在无干扰时他们具有相同的BER性能。
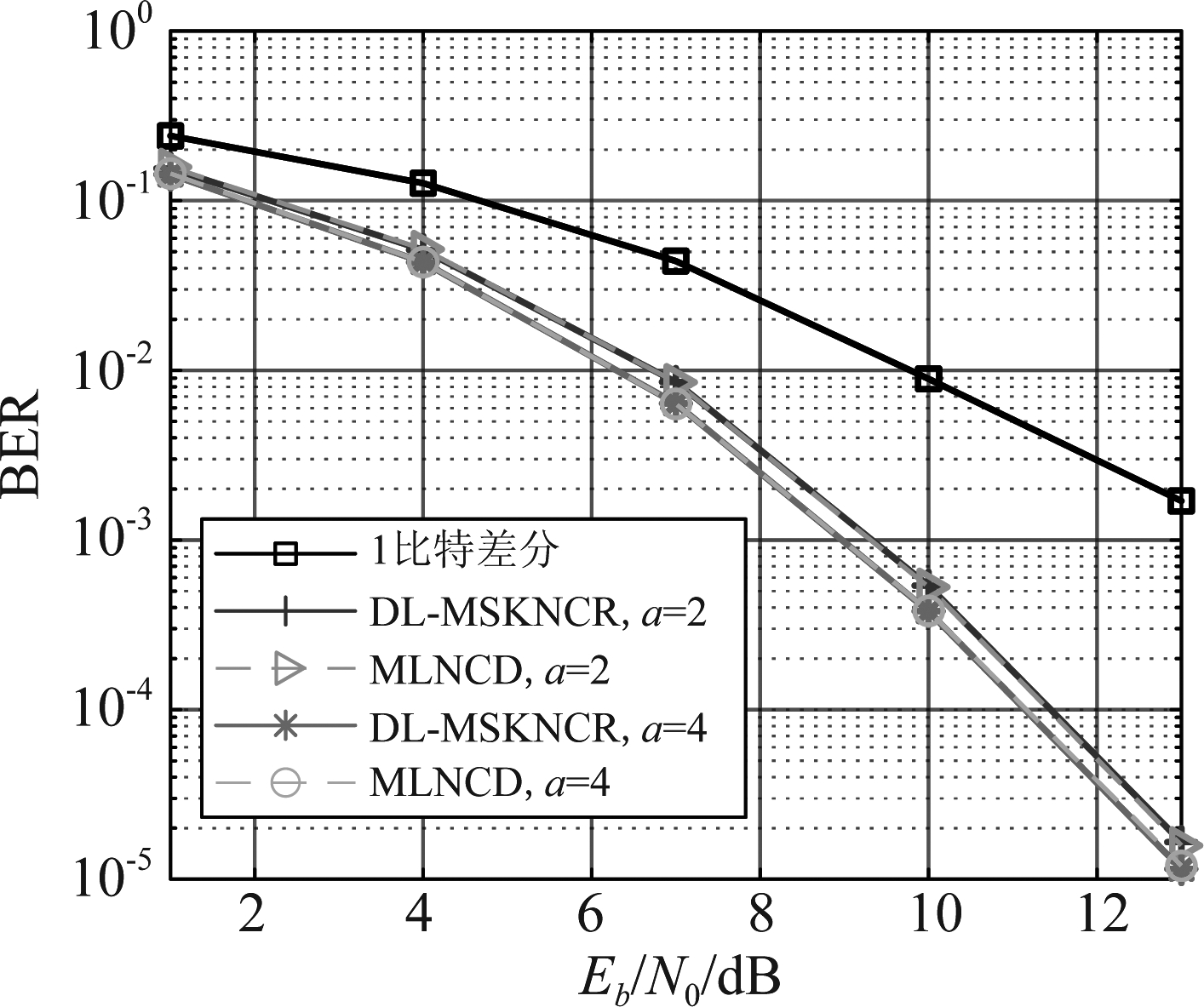
图3 无干扰时DL-MSKNCR与现有MSK非相干检测算法BER性能
Fig.3 BER performance of DL-MSKNCR and existing MSK noncoherent detection algorithms when there is no interference
4.2 窄带干扰
在有窄带干扰时,DL-MSKNCR固定在Eb/N0=12 dB,λ=0.1, f=0且干信比(Interference-to-Signal Ratio,ISR)为10 dB下训练。在本小节中,a被设置为4。
图4展示了ISR=10 dB、λ=0.1、 f=0且无噪声时,接收信号与干扰抑制后信号的功率谱密度(Power Spectral Density,PSD);重叠加窗干扰抑制算法采用汉明窗、理想的干扰检测以及512点的离散傅里叶变换(Discrete Fourier Transform,DFT);从图4中可以看出,重叠加窗干扰抑制算法和DL-MSKNCR的干扰抑制子网络都可以有效地对窄带干扰进行抑制;因为干扰抑制子网络采用时域滤波,所以干扰抑制后信号主瓣外的谱线与MSK信号的有一定的差异。
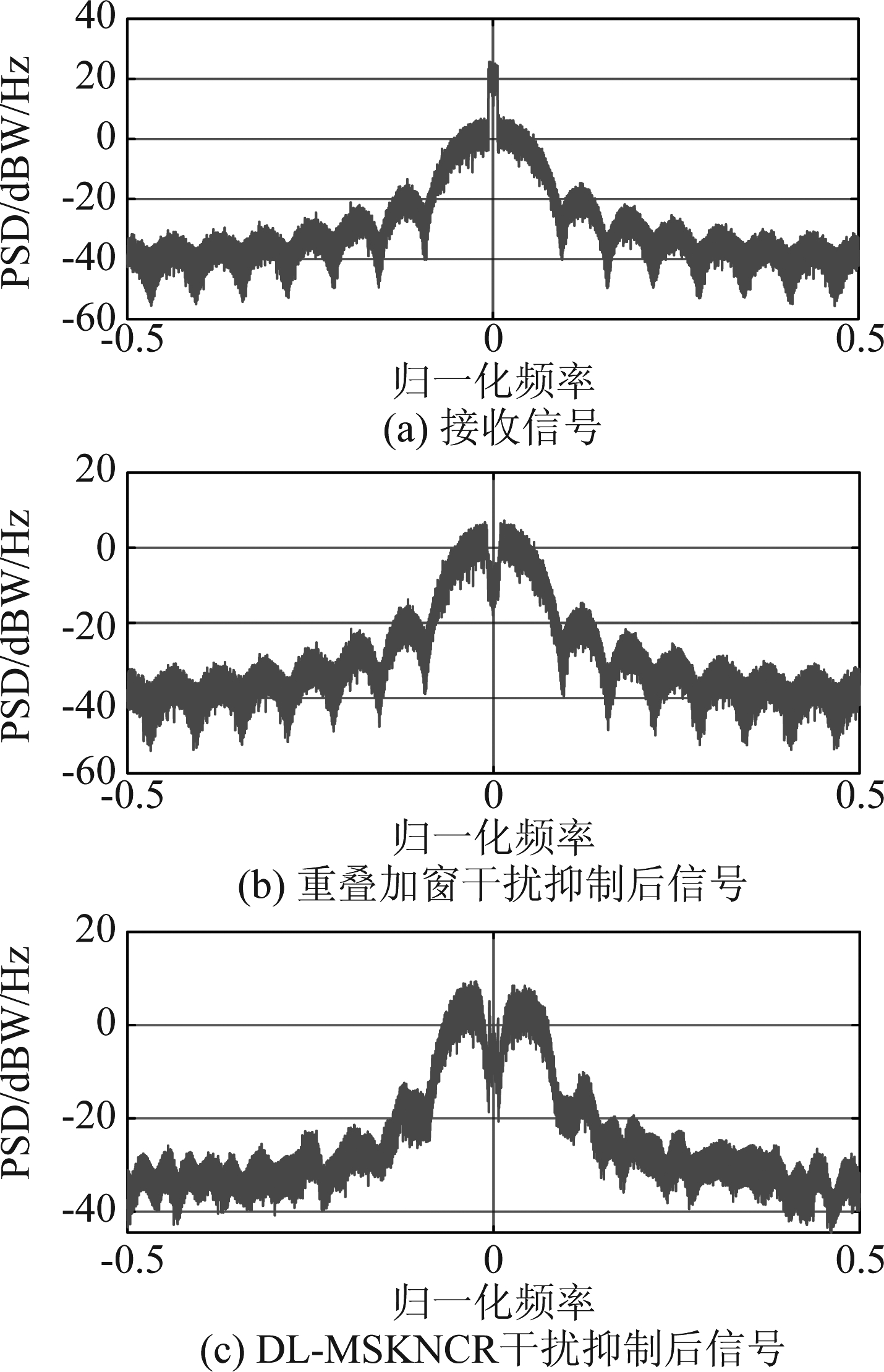
图4 ISR=10 dB、λ=0.1、 f=0且无噪声时接收信号与干扰抑制后信号的PSD
Fig.4 PSD of the received signal and the signal after interference suppression when ISR=10 dB,λ=0.1, f=0 and there is no noise
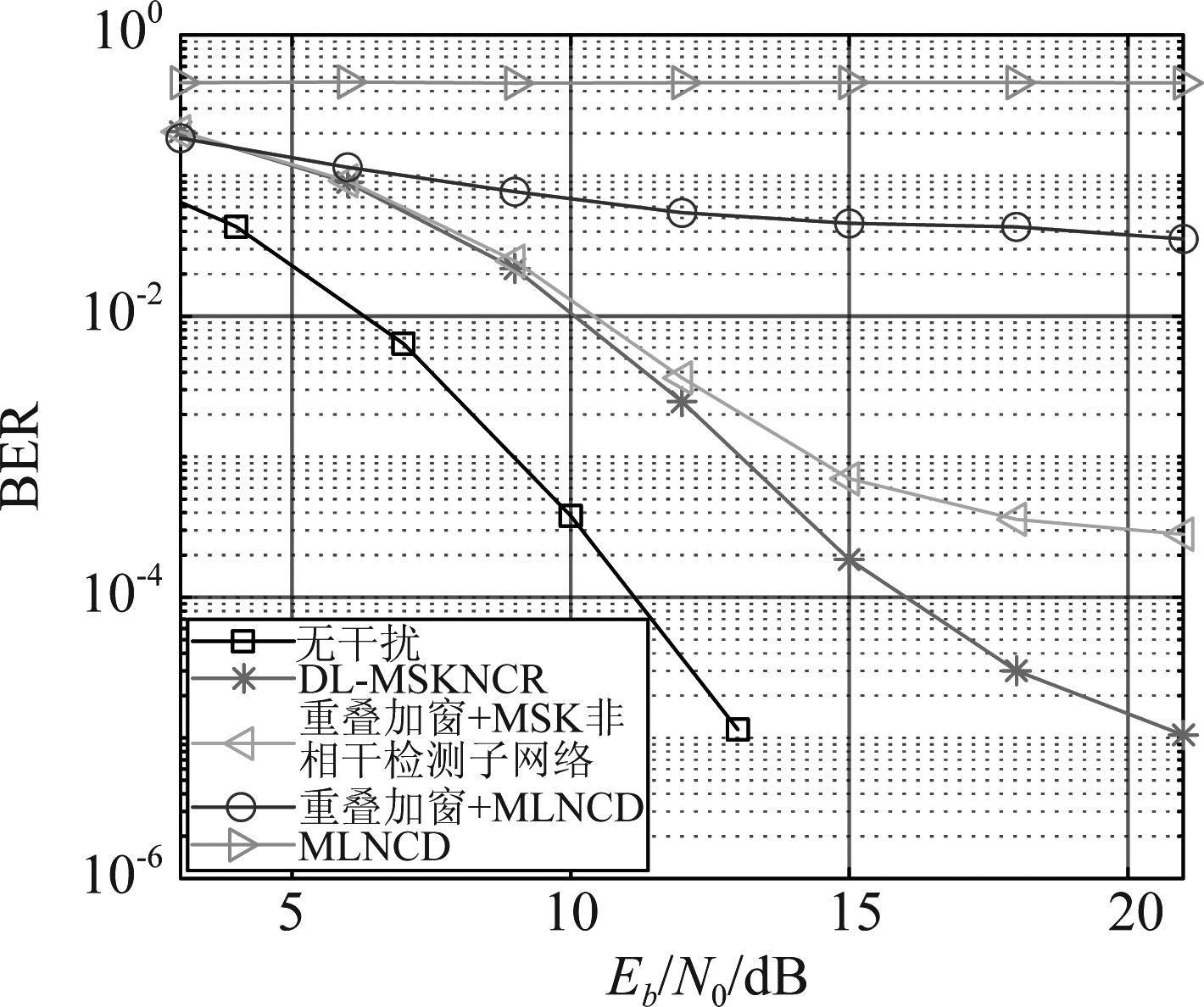
图5 ISR=10 dB、λ=0.1且f=0时各MSK非相干接收机的BER性能
Fig.5 BER performance of different MSK noncoherent receivers when ISR=10 dB, λ=0.1 and f=0
图5给出了ISR=10 dB、λ=0.1且f=0时各MSK非相干接收机的BER性能;可以看出,重叠加窗干扰抑制可以改善MLNCD的检测性能,然而当Eb/N0>18 dB时,‘重叠加窗+MLNCD’的BER仍然大于10-2,这是因为干扰抑制对MSK信号造成的畸变制约了MLNCD的检测性能;‘重叠加窗+MSK非相干检测子网络’的BER性能优于‘重叠加窗+MLNCD’,这说明MSK非相干检测子网络可以有效地应对重叠加窗干扰抑制对MSK信号造成的畸变;DL-MSKNCR的BER性能优于‘重叠加窗+MLNCD’和‘重叠加窗+MSK非相干检测子网络’,当Eb/N0=21 dB时,其BER约为10-5,这是因为通过联合优化,干扰抑制子网络可以在完成干扰抑制的同时,使MSK信号产生的畸变更容易被MSK非相干检测子网络处理。
需要注意的是,因为已训练的DL-MSKNCR中的干扰抑制子网络和MSK非相干检测子网络会根据彼此的特性调整参数,所以不能直接将这两个子网络与传统算法结合;为了得到‘重叠加窗+MSK非相干检测子网络’的性能,首先对接收信号进行重叠加窗干扰抑制,然后用干扰抑制后的信号训练MSK非相干检测子网络;因为MLNCD不能产生反馈误差,所以本节未给出‘干扰抑制子网络+MLNCD’的BER性能。

图6 当Eb/N0=15 dB、λ=0.1且f=0时各MSK非相干接收机的BER性能
Fig.6 BER performance of different MSK noncoherent receivers when Eb/N0=15 dB, λ=0.1 and f=0
图6为Eb/N0=15 dB、λ=0.1且f=0时各MSK非相干接收机的BER性能;可以看出,MLNCD算法因为没有进行干扰抑制,所以其BER性能很差,当ISR≥4 dB时,其BER就达到了0.5;对于‘重叠加窗+MLNCD’、‘重叠加窗+MSK非相干检测子网络’和DL-MSKNCR,由于首先对接收信号进行了干扰抑制,所以有效地抑制了大部分干扰,但抑制干扰的同时也会抑制一些有效的MSK信号,导致MSK信号产生畸变,其中MLNCD算法无法应对这些畸变,畸变对其造成的影响较大,误码率性能不理想,在ISR为10 dB时,误码率约为4×10-2,而且随着ISR的增大,误码率逐渐增大;MSK非相干检测子网络通过训练和学习,对被抑制的MSK信号畸变有一定的补偿能力,相比MLNCD,大大提高了检测性能,在ISR为10 dB时,误码率约为8×10-4,但随着ISR的增大,畸变造成的影响逐渐增大,当ISR为19 dB时,误码率增大到4×10-3;DL-MSKNCR基于深度学习,联合优化了干扰抑制和非相干检测,相比前面两种算法,进一步提升了检测性能,在ISR为10 dB时,误码率为2×10-4,在ISR为19 dB时,误码率为2×10-3。
图7给出了不同λ下各MSK非相干接收机的BER性能;在图7中,Eb/N0=15 dB,ISR=10 dB且f=0;随着λ的增大,‘重叠加窗+MLNCD’的BER也逐渐增大,这是因为干扰带宽越大,干扰抑制对MSK波形造成的畸变也越大;当λ<0.1时,DL-MSKNCR的BER性能比较稳定,且优于‘重叠加窗+MLNCD’和‘重叠加窗+MSK非相干检测子网络’,当λ>0.1时,DL-MSKNCR的BER迅速增大,且当λ>0.16时,DL-MSKNCR的BER超过了‘重叠加窗+MSK非相干检测子网络’的BER,这是因为在训练DL-MSKNCR时λ被固定为0.1,所以当λ>0.1时干扰带宽超过了干扰抑制子网络的有效抑制带宽,而重叠加窗干扰抑制采用了理想的干扰检测,其可以对干扰进行精确的抑制,如图8所示。
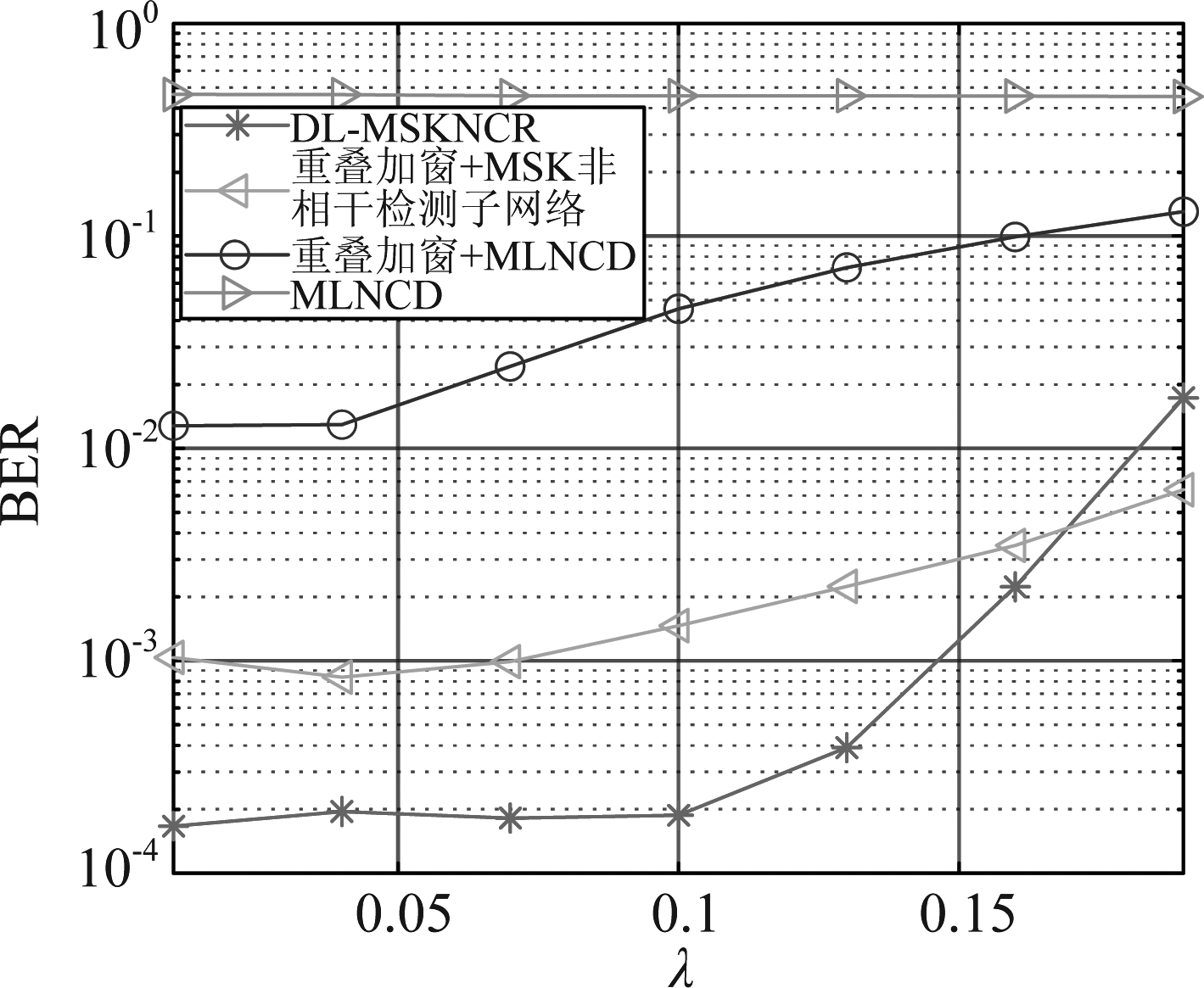
图7 不同干扰因子下各MSK非相干接收机BER的性能
Fig.7 BER performance of different MSK noncoherent receivers under different interference factors
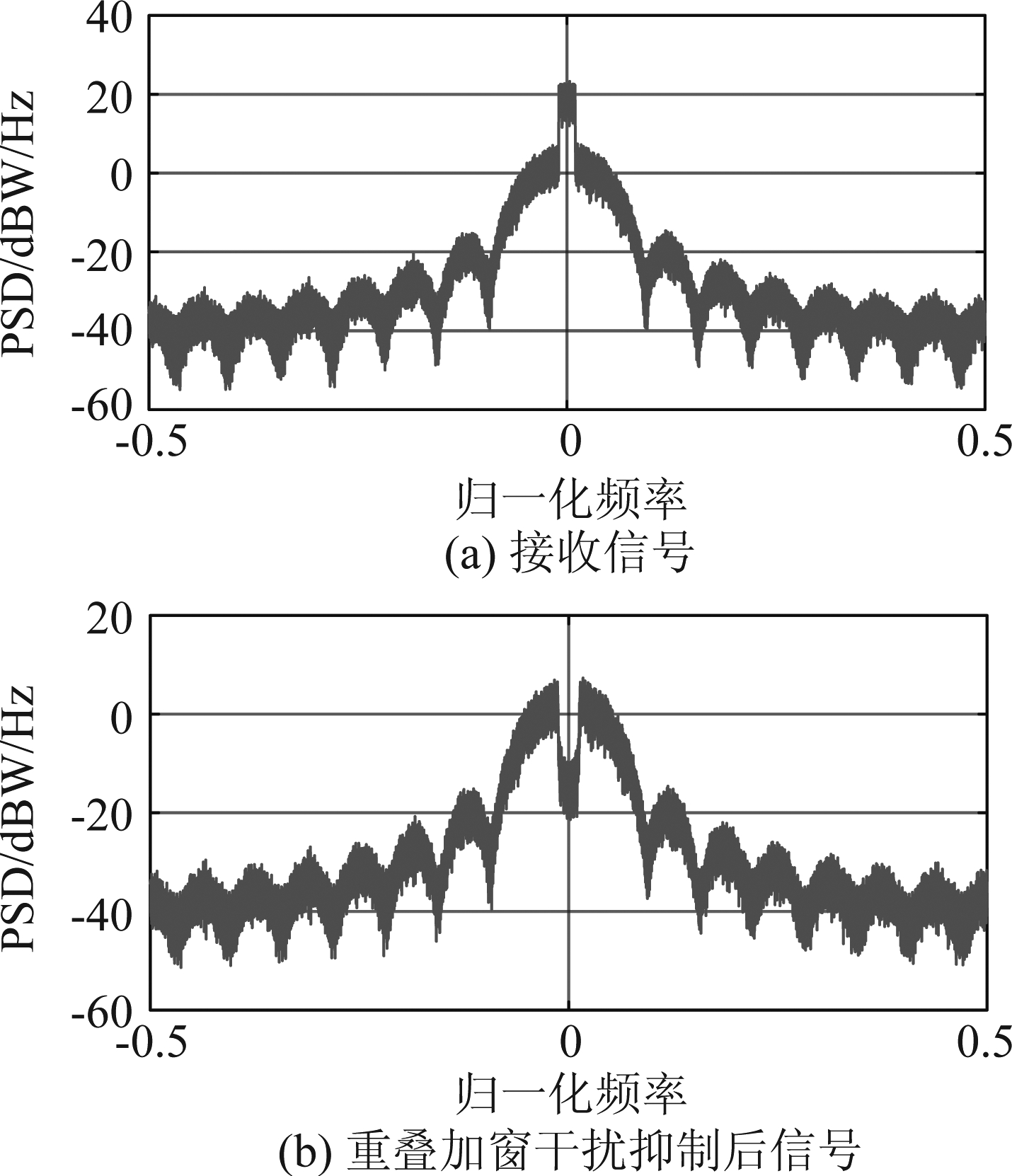
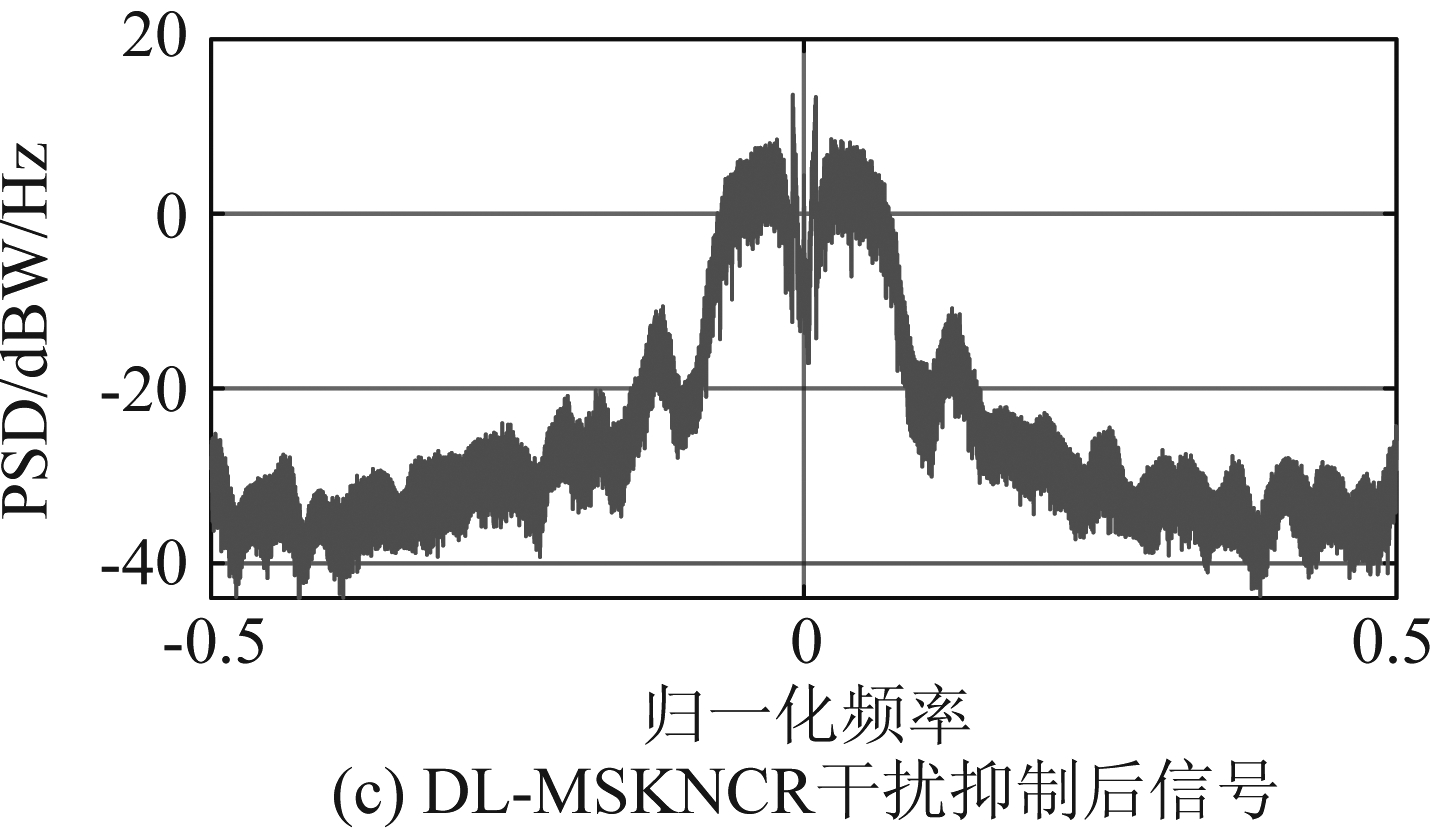
图8 ISR=10 dB、λ=0.16、 f=0且无噪声时
接收信号与干扰抑制后信号的PSD
Fig.8 PSD of the received signal and the signal after interference suppression when ISR=10 dB, λ=0.16, f=0 and there is no noise
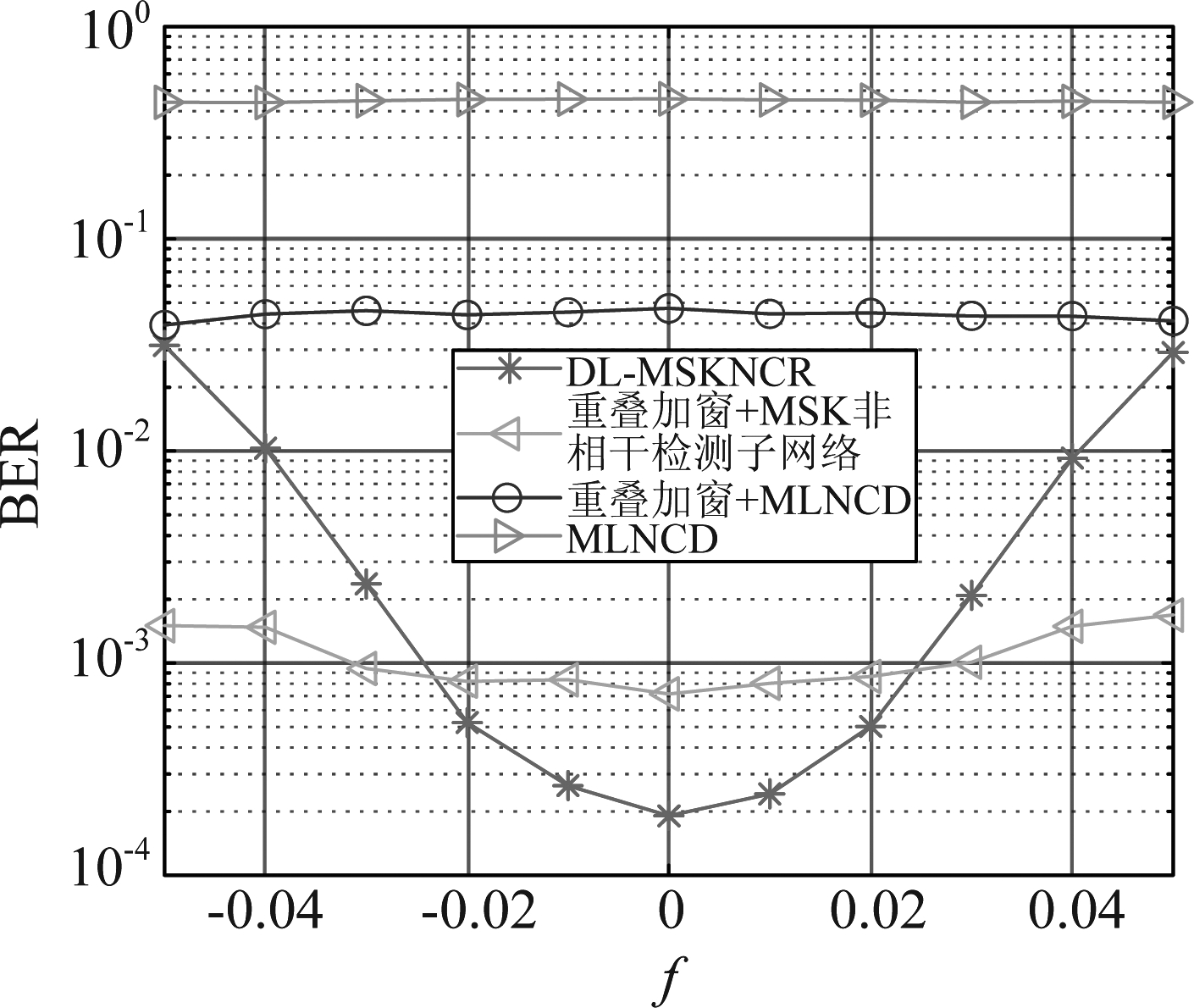
图9 不同干扰中心频率下各MSK非相干接收机的BER性能
Fig.9 BER performance of different MSK noncoherent receivers under different interference center frequencies
图9给出了不同干扰中心频率下各MSK接收机的性能。ISR=10 dB、Eb/N0=15 dB且λ=0.1。当归一化干扰中心频率满足|f|<0.023时,DL-MSKNCR具有最优的BER性能,当|f|>0.023时,‘重叠加窗+MSK非相干检测子网络’的BER性能优于DL-MSKNCR,这是因为在训练DL-MSKNCR时f被固定为0,所以当f≠0时,网络训练时的干扰带宽和测试时的干扰带宽不再相同,‘重叠加窗+MSK非相干检测子网络’采用了理想的干扰检测,其可以对干扰进行有效地抑制,而DL-MSKNCR的干扰抑制子网络则不能将干扰完全抑制,如图10所示。
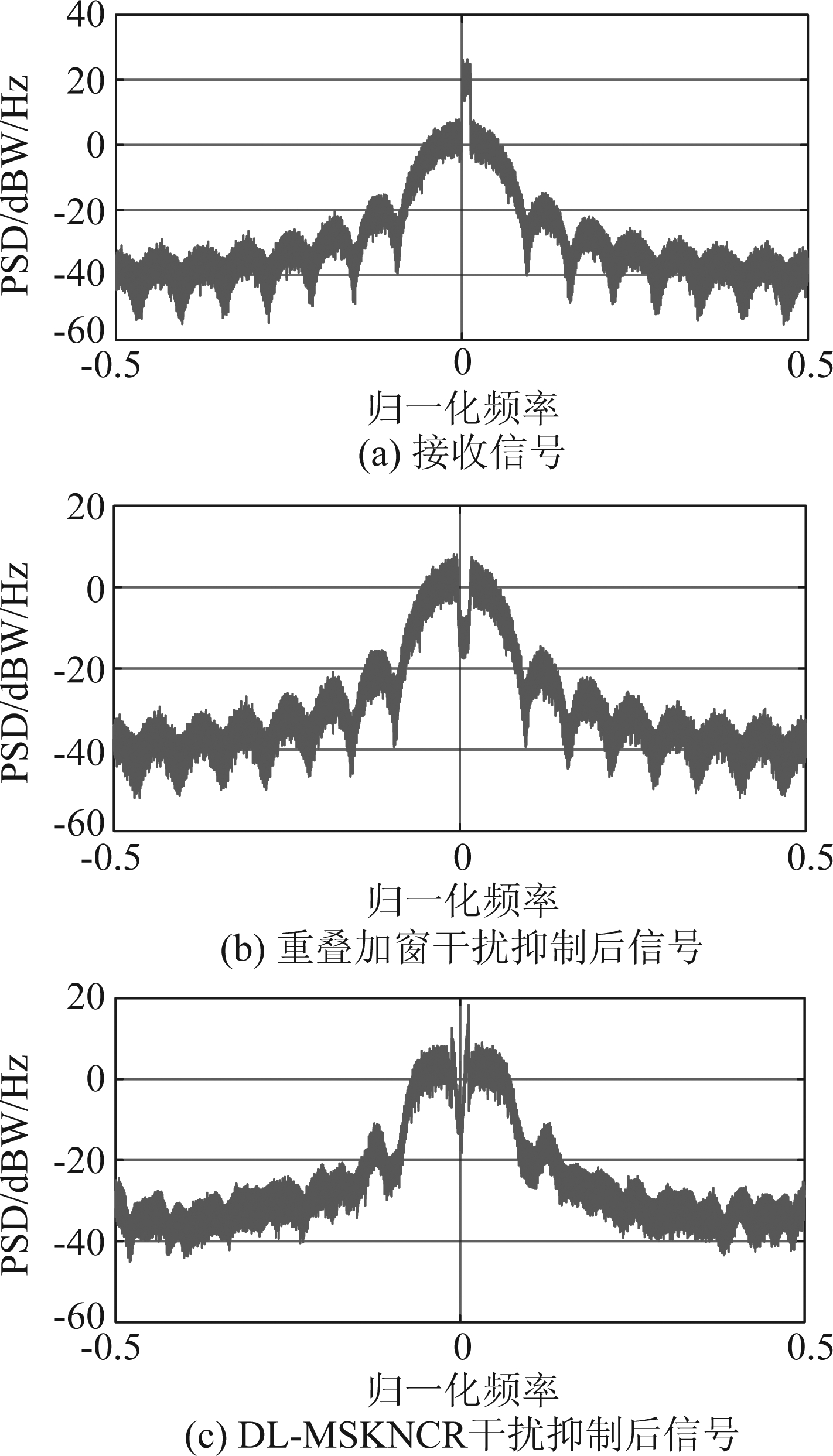
图10 ISR=10 dB、λ=0.1、 f=0.05且无噪声时
接收信号与干扰抑制后信号的PSD
Fig.10 PSD of the received signal and the signal after interference suppression when ISR=10 dB, λ=0.1, f=0.05 and there is no noise
虽然DL-MSKNCR缺乏对干扰位置的泛化能力,但是可以通过如下方法解决:当网络训练时间小于干扰位置变化周期时,接收机可以根据干扰检测得到的干扰位置信息自行产生测试数据并开启网络训练,当训练完成后将接收信号送入该网络进行处理;当网络训练时间大于干扰位置变化周期时,接收机可预先对常见的干扰位置进行训练,并将已训练的网络存入网络库,在工作阶段,接收机首先检测干扰位置,然后判断当前干扰位置是否有对应的已训练网络,若有,则将接收信号送入该网络进行处理,否则利用传统算法处理接收数据,同时开启对该干扰位置的网络训练,训练完成后更新网络库。
图11给出了当网络训练时间小于干扰位置变化周期时不同干扰中心频率下各MSK非相干接收机的BER性能。在图11中,ISR=10 dB、Eb/N0=15 dB且λ=0.1。因为网络训练时间小于干扰位置变化时间,所以f每改变一次,网络就根据新的f重新训练一次。从图11中可以看出,通过追踪干扰位置并重新训练网络,DL-MSKNCR在各干扰中心频率下都实现了优于其他MSK非相干接收机的BER性能。
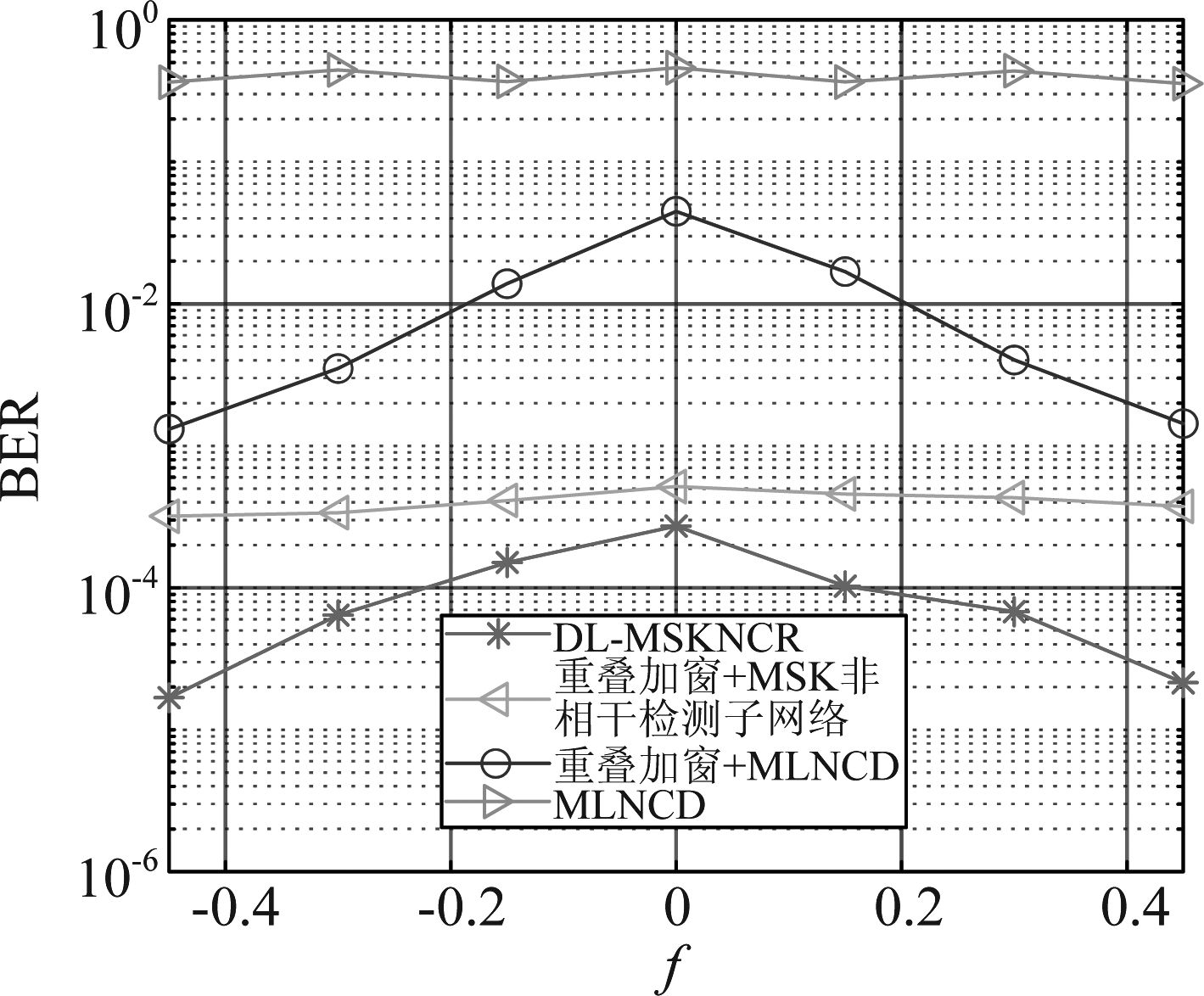
图11 网络训练时间小于干扰位置变化周期时不同干扰中心频率下各MSK非相干接收机的BER性能
Fig.11 BER performance of different MSK noncoherent receivers under different interference center frequencies when the network training time is less than the interference position change period

图12 MSK非相干检测子网络包含不同数量的Conv1D层时DL-MSKNCR的BER性能
Fig.12 BER performance of DL-MSKNCR when MSK noncoherent detection subnetwork has different number of Conv1D layers
图12对比了MSK非相干检测子网络包含不同数量的Conv1D层时DL-MSKNCR的BER性能;在图12中,ISR=10 dB,λ=0.1, f=0;可以看出,当层数不大于8时,层数越多,DL-MSKNCR的BER性能越好,当层数大于8时,DL-MSKNCR的BER性能几乎不再提升,因此在DL-MSKNCR中,MSK非相干检测子网络的Conv1D层数被设置为8。
5 结论
本文提出了一种基于深度学习的抗窄带干扰MSK非相干接收机,通过联合优化干扰抑制和MSK非相干检测,所提接收机显著提高了窄带干扰下非相干检测的MSK通信系统的BER性能。
[1] 白晓东. Link 16数据链传输波形关键技术研究与验证[D]. 成都: 电子科技大学, 2018.
BAI Xiaodong. Key Technology Research and Verification of Link16 Data Link Transmission Wareform[D]. Chengdu: University of Electronic Science and Technology of China, 2018.(in Chinese)
[2] 陈海霞. Mark XIIA Mode5系统链路仿真及其干扰抑制技术研究[D]. 成都: 电子科技大学, 2019.
CHEN Haixia. Mark XIIA Mode5 System Link Simulation and Research on Interference Suppression Technology[D]. Chengdu: University of Electronic Science and Technology of China, 2019.(in Chinese)
[3] OSBORNE W, LUNTZ M. Coherent and Noncoherent Detection CPFSK[J]. IEEE Transactions on Communications, 1974, 22(8): 1023-1036.
[4] SIMON M K, WANG C C. Differential detection of Gaussian MSK in a mobile radio environment[J]. IEEE Transactions on Vehicular Technology, 1984, 33(4): 307-320.
[5] 周世阳, 王赏, 程郁凡, 等. MSK信号的最大似然非相干检测算法研究[J]. 信号处理, 2016, 32(7): 866- 871.
ZHOU Shiyang, WANG Shang, CHENG Yufan, et al. The Research of MSK Maximum Likelihood Noncoherent Detection Algorithm[J]. Journal of Signal Processing, 2016, 32(7): 866- 871.(in Chinese)
[6] 田文飚, 王鹏, 芮国胜, 等. 基于差分复合网格的MSK非相干解调算法[J]. 通信学报, 2018, 39(12): 160-166.
TIAN Wenbiao, WANG Peng, RUI Guosheng, et al. Non-coherent Demodulation Algorithm of MSK Based on Differential Composite[J]. Journal on Communications, 2018, 39(12): 160-166.(in Chinese)
[7] WU C, WANG S, ZHAO Y. A Low Complexity Multi-symbol Non-coherent MSK Receiver[C]∥IEEE International Conference on Communication Software and Networks, Chongqing, China, 2019: 133-139.
[8] 邹宁, 徐松涛, 刘明园, 等. 一种重叠加窗频域抑制窄带干扰算法及研究[J]. 现代防御技术, 2010, 38(3): 120-125, 152.
ZOU Ning, XU Songtao, LIU Mingyuan, et al. An Overlap Window-Based Frequency-Domain Narrowband Interference Suppression Algorithm and Its Analysis[J]. Modern Defence Technology, 2010, 38(3): 120-125, 152.(in Chinese)
[9] YE H, LI G Y, JUANG B. Power of Deep Learning for Channel Estimation and Signal Detection in OFDM Systems[J]. IEEE Wireless Communications Letters, 2018, 7(1): 114-117.
[10] LIN C, CHANG Q, LI X. A Deep Learning Approach for MIMO-NOMA Downlink Signal Detection[J]. Sensors, 2019, 19(11): 1-22.
[11] CHENG X, LIU D, WANG C, et al. Deep Learning-Based Channel Estimation and Equalization Scheme for FBMC/OQAM Systems[J]. IEEE Wireless Communications Letters, 2019, 8(3): 881- 884.
[12] CAMMERER S, AOUDIA F A, DORNER S, et al. Trainable Communication Systems: Concepts and Prototype[J]. IEEE Transactions on Communications, 2020, 68(9): 5489-5503.


