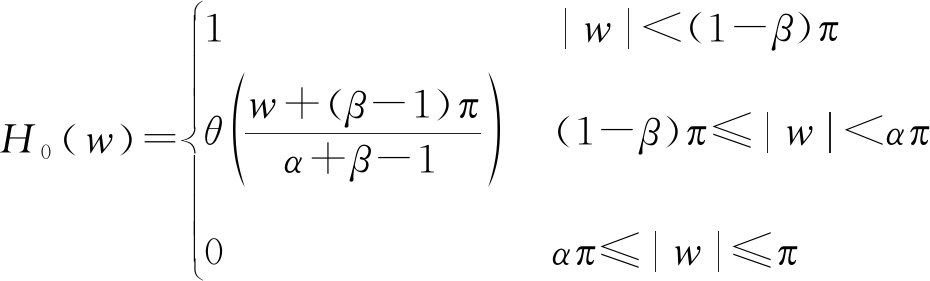
Reference format: FENG Yun, ZONG Zhulin, LI Siqi. Based on Adaptive Tunable Q-factor Wavelet Transform Target Detection Technology under Sea Clutter Background[J]. Journal of Signal Processing, 2021, 37(2): 304-316. DOI: 10.16798/j.issn.1003- 0530.2021.02.016.
海杂波是指雷达接收到的海表面的后向散射回波，它受多种因素的影响，如海洋环境参数(风速、风向、涌浪、洋流等)和雷达设备参数(擦地角、波长、极化方式等)[1- 4]。这些因素的共同作用导致海杂波的物理机制极其复杂，现有的研究虽然对海杂波的特性有了比较深入的认识，但是仍然存在盲区；并且已有的海杂波模型也存在局限，不能很好的描述各种情况下海杂波的特性。
经典的杂波抑制和动目标检测方法的理论依据是目标和杂波有不同径向速度，根据多普勒效应可推知它们的多普勒频移也不同，因此可通过窄带多普勒滤波器组来将杂波和目标进行分离，从而实现从杂波中检测出动目标的目的[5- 6]。但是在强海杂波环境下，海浪的运动会导致海杂波的多普勒谱展宽[2]，慢速运动的目标易落入海杂波的多普勒通道中，且目标的多普勒谱会和海杂波多普勒谱重叠[7]，此时采用经典的MTI和MTD技术不能有效检测出强海杂波背景下的微弱动目标。
陈小龙等人[8]将稀疏表示理论引入到海杂波抑制和微动目标检测中，提出一种基于形态成分分析(MCA)的海杂波抑制与微动目标检测方法。于晓涵等人[9]提出了一种自适应双阈值稀疏傅里叶变换算法，从信号的稀疏性角度去区分海杂波和目标，拓展了传统的基于变换域的动目标检测技术。Selesnick等人[10]提出了一种可调品质因子Q的小波变换(Tunable Q-factor Wavelet Transform，TQWT)，从频域上构造过完备小波变换，通过品质因子(Q)、冗余度(r)以及分解层数(J)三个关键的TQWT参数，使可调品质因子小波对具有特定振荡行为的特征信号成分实现最优匹配。随后，Farshchian M等人[11]利用双可调Q小波变换对海面回波进行处理，成功地将处于弱杂波区的鸟群和刚性充气小船分离，有效的检测出小船。Nguyen N等人[12]提出了一种基于可调Q小波变换的海杂波抑制方法，并在实测数据集上进行了验证。随后潘美艳等人[13]提出了一种基于能量选择的改进TQWT海杂波抑制算法，实现了海杂波与目标的分离；但是该文提出的算法，对可调Q小波变换的关键参数组合(Q,r,J)的选择依赖于目标和杂波的先验信息，不能对目标进行自适应的检测。
本文针对文献[13]的不足作出改进，提出一种基于A-TQWT的海杂波背景下的目标检测技术,对可调Q小波变换的关键参数组合(Q,r,J)进行约束和自适应计算，以选择最能匹配目标振荡特性的参数组合，用于对目标进行稀疏表示和重构，提高海杂波抑制效果，改善目标的信杂比，提高检测性能。通过在实测海杂波数据集中添加仿真的微弱运动目标验证了本文提出的方法的有效性。
TQWT是一种Q因子可调的离散时间小波变换，它通过三元参数组合(Q,r,J)来参数化。其中Q代表品质因子，影响小波的振荡行为；r代表冗余度，是指当分解层数J为无穷大时小波变换所有子带的总的过采样率；J代表分解层数，是双通道分解/重构滤波器组的数目。
图1表示了层数为J时的TQWT的分解和重构滤波器组的结构框图，其中LPS α和HPS β分别表示尺度参数为α的低通滤波器及尺度参数为β的高通滤波器。从图1可知，TQWT由两个通道分解/重构滤波器组的级联构成，每个滤波器组的低通输出作为下一个分解/重构滤波器组的输入。这样通过将上一个滤波器组的低通输出迭代地用于下一个滤波器组的输入，TQWT可以产生J+1个子带的小波系数。低通滤波器和高通滤波器的频率响应H0(w)、H1(w)如下所示。
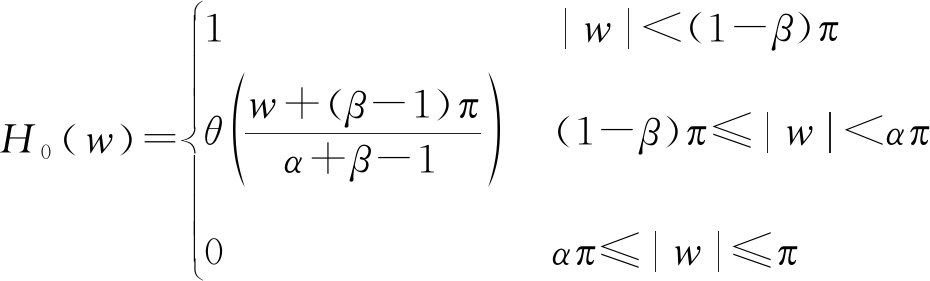
(1)
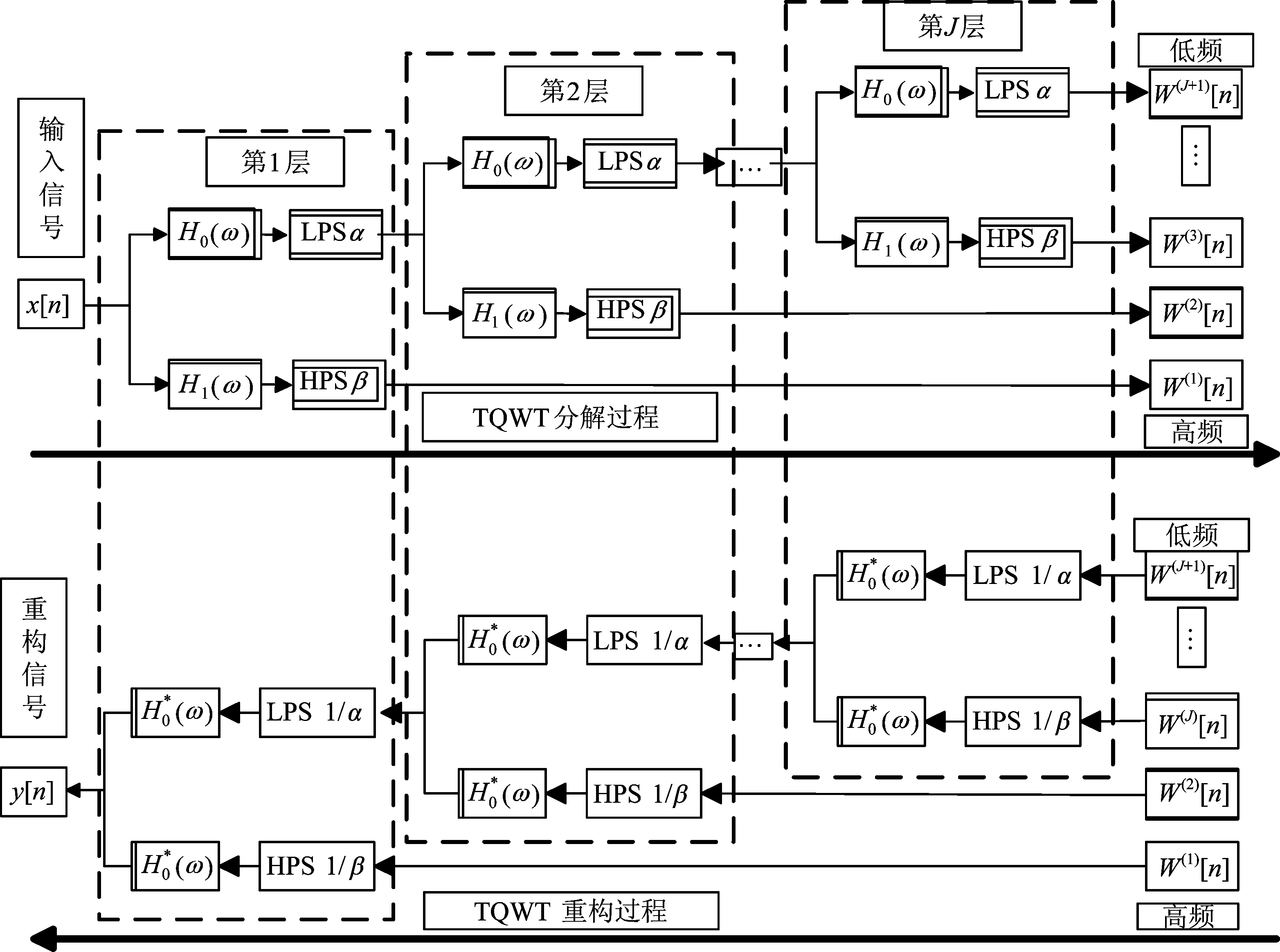
图1 TQWT信号分解与重构过程
Fig.1 Signal decomposition and reconstruction process of TQWT
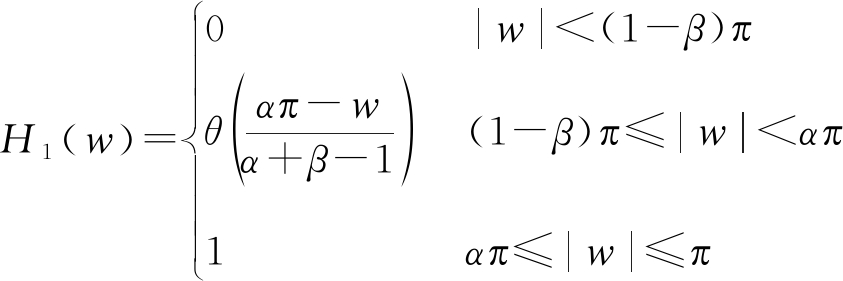
(2)
式中：α、β分别为低通、高通滤波器的尺度变换参数，为保证TQWT不会过度冗余，保留完美重构的性质，α、β以及低、高通滤波器频响函数H0(w)、H1(w)在各自的通带以及过渡带上均要满足以下条件：
(3)
(4)
此外，θ(w)为具有二阶消失矩的德比契斯(Daubechies)频率响应，其满足以2π为周期的功率互补特性，可以表示为:
θ2(ω)+θ2(π-ω)=1
(5)
(6)
TQWT信号重构过程是分解过程的逆过程，只需按图1所示，将每一层低通、高通滤波器输出的小波系数作为当前层的输入，进行多层重构，就可得到原始信号的重构信号。
在海杂波抑制中，高海况条件下，海杂波受风浪等因素的影响，多普勒谱会展宽，而目标的频谱相对较窄，使得海杂波相对目标来说具有较小的品质因子Q，振荡特性也较低。品质因子定义为信号的中心频率fc与带宽BW的比值，并且Q可以通过式(7)来确定高通滤波器的尺度参数β；冗余度r与α和β的关系如式(8)所示。
Q=fc/BW=(2-β)/β
(7)
r=β/(1-α)
(8)
由于高通滤波器带宽的限制，文献[10]中指出，对于给定的品质因子Q与冗余度r，最大的分解层数为：
(9)
式中: ⎣*」表示向下取整。由上述公式可知，对于TQWT的确定参数组合(Q，r)，高通、低通滤波器组的尺度变换参数可由式(10)得出。
β=2/(Q-1),α=1-β/r=1-2/[(Q+1)r]
(10)
由此，当确定三元参数组合(Q,r,J)后，就可确定TQWT小波基函数及其频率响应。
不考虑其他干扰信号，对海雷达的回波主要是目标回波与海杂波的混合信号。将海面回波信号y表示为目标回波xt和海杂波xc的叠加，即：
y=xt+xc
(11)
文献[13]指出目标和海杂波的频谱特性及振荡特性各有不同。运动的目标相对雷达而言有确定的径向速度，因而由式(7)可知其品质因子Q值大，振荡属性高; 而海杂波由于海浪的运动会导致其频谱扩展，其品质因子Q值小，振荡属性低; 因此，可采用形态分量分析法(MCA)建立优化模型，利用TQWT将目标在高Q因子对应的小波基函数上进行稀疏表示，将海杂波在低Q因子对应的小波基函数上进行稀疏表示，通过求解约束优化问题，实现目标与海杂波的分离，达到抑制杂波的目的[13]。
假设TQWTt和TQWT c分别对应匹配目标和海杂波振荡特性的可调Q小波变换；
和
分别为其逆变换。因此分解可以通过求解以下优化问题得到。
(12)
由于海面回波中，微弱目标的信杂比较低，回波中海杂波能量占优，在式(12)中通过在优化问题中引入参数θ(0<θ<1)来调节目标和海杂波之间的相对权重，参数λt和λc可以通过求解相应小波子带的2-范数得到。通过设置合适的θ和迭代步长、次数，运用分裂增广拉格朗日收缩算法(Split Augmented Lagrangian Shrinkage Algorithm, SALSA)求解式(12)的优化问题，可以得到对应于xt和xc的稀疏小波系数Wt和Wc。再根据目标所对应的小波系数Wt各小波子带占总能量的比重，选取合适的门限确定重构小波系数集进行重构，就可得到目标的重构信号，从而将目标和海杂波分离，达到抑制海杂波的目的。
TQWT主要取决于三元参数：品质因子(Q)、冗余度(r)和分解层数(J)的选择。分解层数过大时不仅可能导致信号的过度分解或冗余分解,还会降低算法的硬件可实现性。由于海面慢速微弱动目标的多普勒谱往往和海杂波的多普勒谱重叠，因此合理的分解层数既要保证足够宽的频域范围来覆盖目标或杂波的频域信息，同时又不能过大而导致计算复杂度过大。
对于给定品质因子Q与冗余度r，分解层数存在最大值Jmax，以保证Jmax尺度下的小波持续时间长度不超过所分析信号的时域范围。
文献[14]研究了TQWT多尺度分解下的等效滤波器，提出基于中心频率比(CFR)的合理分解层数确定准则[14]，中心频率比定义如下所示。
(13)
式中：
为分解层数为J时第J层的等效高通滤波器中心频率，fs为输入信号的采样频率。根据中心频率比确定最优分解层数(Jopt)的方法可以通过如下优化问题解决：
(14)
η为合理的CFR阈值，选择范围为0.02～0.05。Jmax为给定(Q，r)参数后的得出的最大分解层数。
Q因子的选取视为选取最能代表分析信号的小波基，即母小波的选取。文献[15]指出在已有的小波选择方法中，能量与香农熵的比值是一种强有力的选择标准，因为它既通过最大化小波能量来最大化表示能力，又通过最小化香农熵来使信号分解的复杂度最小[15]。因此，本文采用基于能量-香农熵比准则的信号自适应Q因子选择方法，来确定适合形态分量分析(MCA)分离的Q因子。对于一个固定的三元参数组合(Q,r,Jmax)确定的能量熵比RQ(Q,r,Jmax)定义如下：
(15)
(16)
(17)
式中：Nj为第j层小波系数的个数，为了降低计算量Nj通常取2的整数次幂；
为第j层小波系数的第i个元素，
为第j层小波系数Wj的能量；
为第j层小波能量概率密度分布，并且满足概率归一化定律，即
为第j层小波系数的香农熵，Rj(Q,r,Jmax)为第j层小波系数的能量-香农熵比，对于一个固定的三元参数组合(Q,r,Jmax)，其能量-香农熵比为(Jopt+1)层小波系数的能量-香农熵比Rj(Q,r,Jopt)的最大值，如式(17)所示。
对于(Qmin,ΔQ,Qmax)之间的一系列可能的Q值，选取合适的参数r，计算每一组(Q,r)参数所对应的最大分解层数Jmax。以三元参数组合(Q,r,Jmax)分别计算RQ(Q,r,Jmax)值，从中选取RQ(Q,r,Jmax)最大值所对应的一组参数作为最优三元参数(Qopt,r,Jmax)，以该组参数作为信号TQWT分解的参数，可以得到信号的最优分解,该过程可用式(18)所示的优化问题描述。
(18)
但是，当分解层数为Jmax时，会导致计算量过大，因此在是实际中，确定最优参数(Q,r)后，可以应用式(13)、(14)对式(18)进行修正为如下形式：
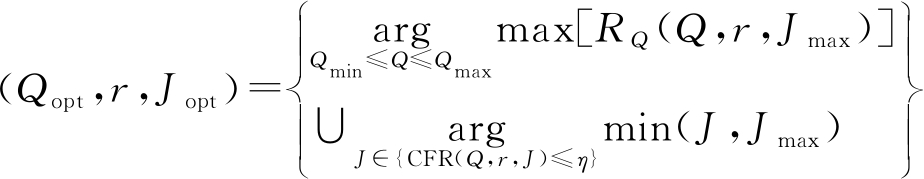
(19)
综上，针对三元参数(Q,r,J)特定的参数组合，构造自适应可调Q小波变换(A-TQWT)海杂波背景下的目标检测算法的步骤为：
1)设定一维Q参数空间{Q|Q∈(Qmin∶ΔQ∶Qmax)}，在该参数空间中，迭代计算、寻找最优的Q参数。式中Qmin、Qmax为搜索起始值和终止值，ΔQ为搜索步长。根据已有文献和实验对冗余度参数r进行约束，分别选取低振荡特性TQWT的冗余度参数rL和高振荡特性TQWT的冗余度参数rH。
2)在1)的基础上，确定所有可能的TQWT的三元参数组合(Q,rH,Jmax)构成的参数空间Ω；选择冗余度参数为rH是为了搜索出的最优品质因子Qopt时可以更好的匹配目标的振荡特性。
3)选取Ω中的每一组(Q,rH,Jmax)，以此作为TQWT的输入参数，用于对海面回波信号进行多尺度分解，并计算每一组参数(Q,rH,Jmax)所对应的能量-香农熵比RQ(Q,rH,Jmax)。
4)根据能量-香农熵比RQ(Q,rH,Jmax)的变化趋势，确定低振荡特性Q参数集合QL和高振荡特性Q参数集合QH的边界。
5)确定最优分解层数Jopt；根据式(20)、(21)分别在QL、QH中确定低振荡特性TQWT的最优参数(QL_opt,rL,Jopt)和高振荡特性TQWT的最优参数(QH_opt,rL,Jopt)。
(QL_opt,rL,Jopt)=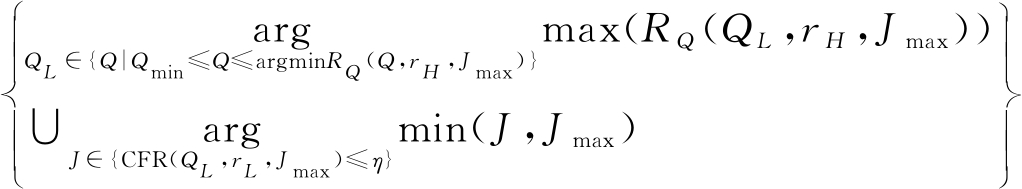
(20)
(QH_opt,rH,Jopt)=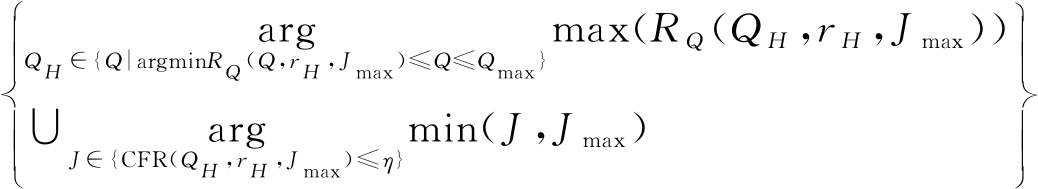
(21)
6)利用形态分量分析法(MCA)建立如式(12)所示的优化模型，选取目标分量和杂波分量的相对权重参数θ(本文设置为0.3进行仿真)，确定迭代计算的次数和步长(本文设置迭代步长为2，迭代次数为100进行仿真)，利用分裂增广拉格朗日收缩算法(Split Augmented Lagrangian Shrinkage Algorithm, SALSA)求解该约束问题，用已确定的最优参数组合(QL_opt,rL,Jopt)、(QH_opt,rL,Jopt)对海面回波信号进行形态分量分析，得到目标的最优稀疏小波系数。
7)以目标分量各小波子带占总能量的比重为重构准则，确定门限，选取合适的重构小波系数集通过可调Q因子小波逆变换(TQWT-1)对目标回波信号进行重构，实现杂波与目标的分离，达到抑制海杂波的目的。
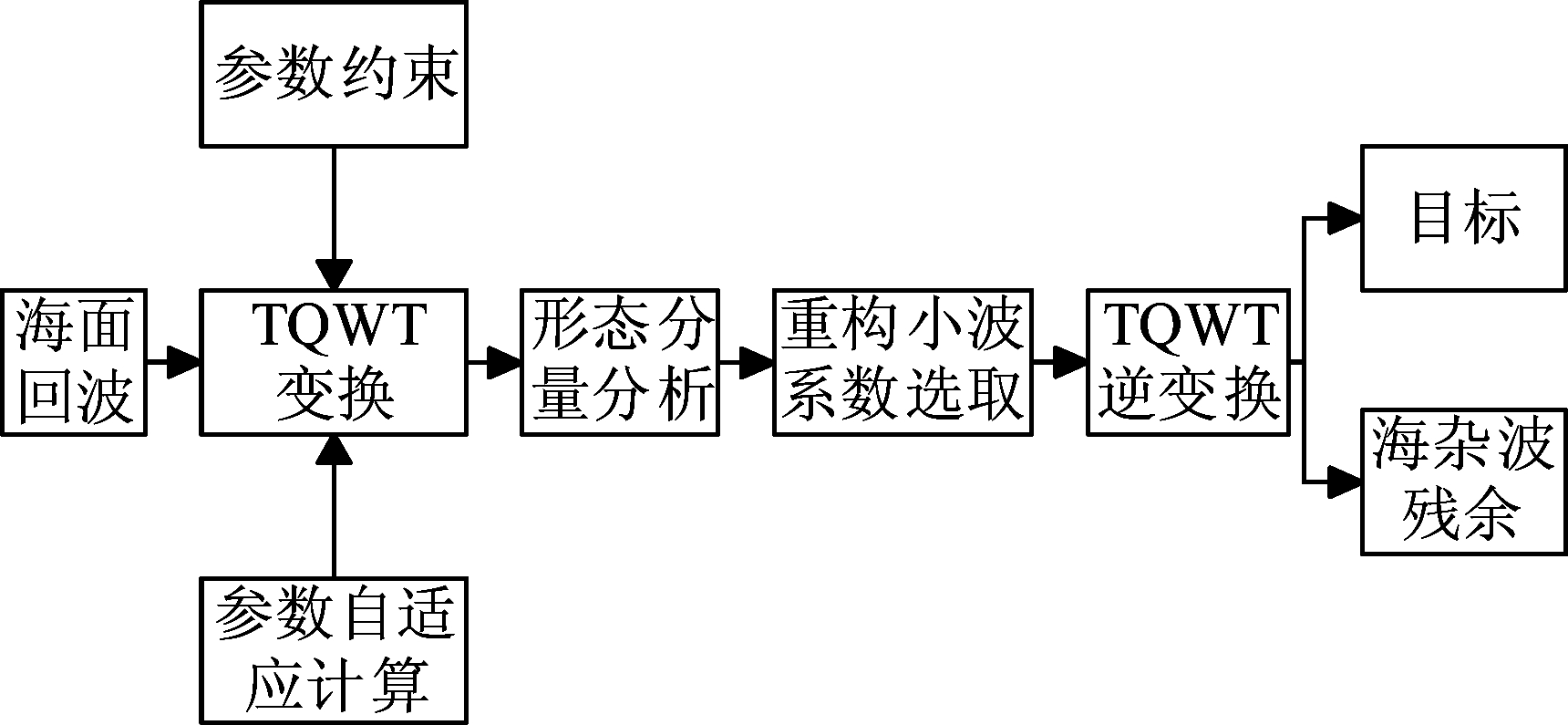
图2 算法实现框图
Fig.2 Block diagram of algorithm implementation
由于本文提出的算法的核心部分是可调Q因子小波变换(TQWT)，其也是计算量最大的部分。为了降低算法的计算成本，在做TQWT时，使所有的离散傅里叶变换(DFT)长度均为2的幂，并且为了便于快速实现，对DFT采用了FFT算法进行快速实现。根据TQWT基本理论分析，基2-TQWT的计算量主要在于基2-FFT运算及分解/重构滤波器组的运算。
对于一个N点的基2-FFT运算，复数乘法的计算量为
复数加法的计算量为
而单层分析/重构滤波器组的计算量为O(N(j))。因此对于一个分解层数为J的基2-TQWT，FFT的总的计算量为K次复乘运算和复加运算；分解/重构滤波器组总的计算量为2rN[10]。K的表达式及其上界如式(22)所示。
(22)
综上，基2-TQWT FFT运算的总的计算量为
远远大于所有层的分解/重构滤波器组总的计算量。因此，考虑算法的最大计算量，总的计算量为其中N为输入信号的长度，r为冗余度参数。
为验证本文提出的算法，采用来自加拿大McMaster大学的IPIX雷达数据库网站的实测海杂波数据[16]。该数据集采集于1993年，采用X波段全相参雷达进行测量，雷达工作频率为9.39 GHz，脉冲宽度为200 ns，脉冲重复频率为1000 Hz，脉冲个数为131072。分别选取高、低海况条件下测量的海杂波数据进行验证。数据的相关信息如表1所示。
表1 海杂波实测数据信息
Tab.1 Information about sea clutter measured data
数据编号浪高/m海浪级别海况分区海况级别距离单元数距离分辨率/m172.1大浪4级高海况1430400.9轻浪2级低海况1430
将给定信杂比SCR(Signal-to-Clutter Ratio)和多普勒频率fd的单频仿真目标信号加入第5个纯海杂波距离单元上；仿真目标[17-18]、目标的多普勒导向矢量及目标与海杂波的信杂比的形式如下式(23)、(24)、(25)所示。
s(n)=AΩ
(23)
Ω=[1,exp(j(2πfdTr)),…,
exp(j(2π(Pulse_num-1)fdTr))]T
(24)
SCR=10log10(A2/Pc)
(25)
其中fd为目标的多普勒频率，Tr=1/PRF为脉冲重复周期，幅度A用于调节信杂比(SCR)，Pulse_num为一个相干处理时间(CPI)内雷达发射的脉冲个数，Pc为海杂波的平均功率。
将仿真的运动目标分别添加到IPIX实测数据集的第#17数据和第#40数据的第5个距离单元中。目标的信杂比分别为-10 dB、0 dB、10 dB；多普勒频率为30 Hz、60 Hz,由多普勒频率公式fd=2vf0/c可知目标的多普勒速度分别约为0.5 m/s、1 m/s，目标的多普勒谱与海杂波的多普勒谱相混叠，目标位于强海杂波区域，且位于负频率轴。
4.2.1 高海况条件下不同信杂比，不同多普勒频率的目标的检测
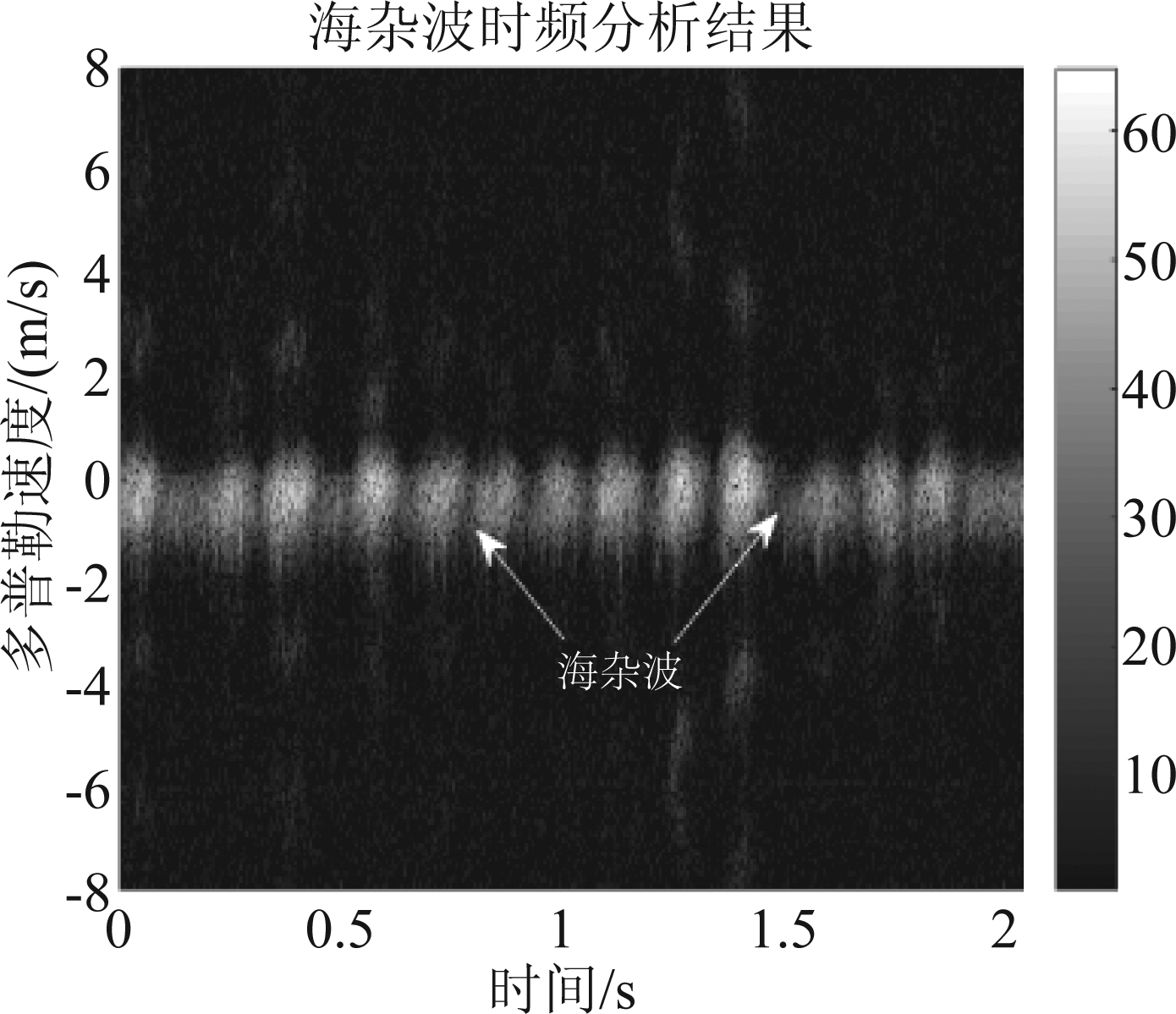
图3 海杂波时频分析结果(#17)
Fig.3 Time-frequency analysis results of sea Clutter (#17)
在IPIX数据集#17号数据中添加目标多普勒频率为30 Hz的微弱运动目标，从图3～图4可以看出目标的中心频率和海杂波的中心频率相重叠，目标落入海杂波的多普勒谱通道中，当目标的信杂比较低时，目标被强海杂波所淹没，传统的基于频域滤波的方法不能有效检测出目标。对海面回波信号应用本文提出的算法，海杂波抑制后的时频分析和频谱分析结果如下图5和图6所示，从中可以看出，在低信杂比条件下(-10 dB)，本文提出的算法能有效地抑制强海杂波，改善信杂比，提升雷达对微弱目标的检测能力。并且随着目标的信杂比增高，本文提出的算法的杂波抑制效果也随着增高，在后续的处理中可以很容易的将目标提取出来。
图4 海面回波时频分析结果(#17, 多普勒频率：30 Hz)
Fig.4 Time-frequency analysis results of sea surface echo (#17, Doppler frequency:30 Hz)
为了验证本文提出的算法对不同多普勒频率的目标的检测能力，在上述步骤中将仿真目标的多普勒频率设定为60 Hz，重新应用本文提出的算法对海面回波信号进行处理，结果如下图7～图9所示。可以发现，本文提出的算法对落入海杂波多普勒谱中的具有不同多普勒频率的微弱目标也具有良好的杂波抑制和目标检测效果。
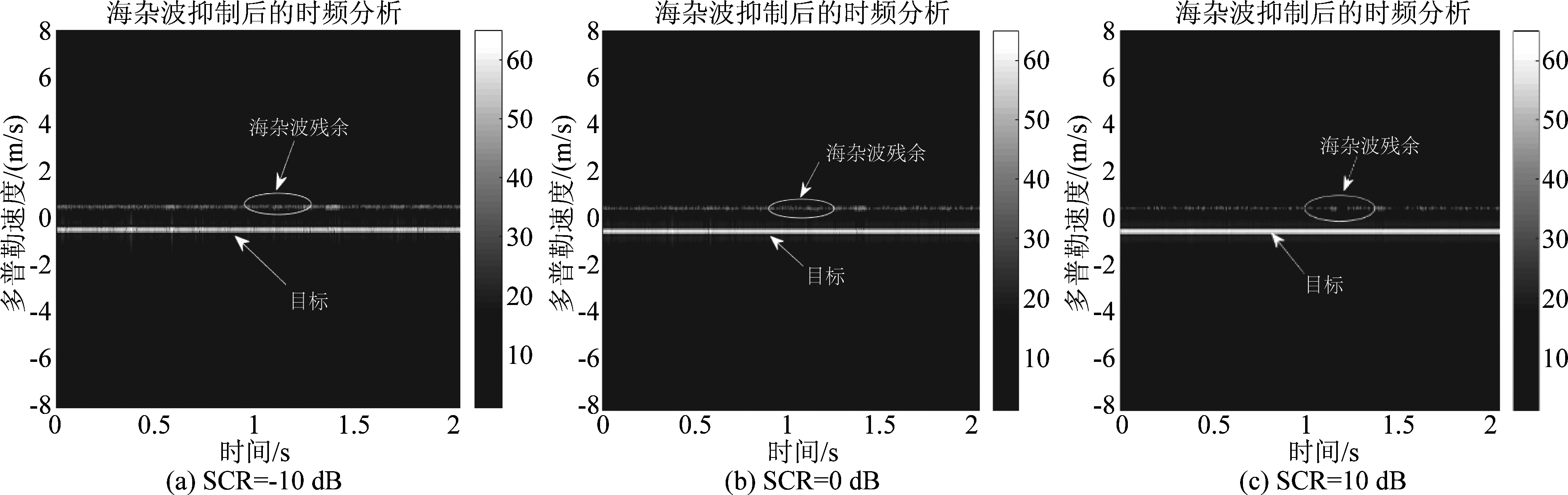
图5 海杂波抑制后的时频分析结果(#17, 多普勒频率：30 Hz)
Fig.5 Time-frequency analysis results after sea clutter suppression (#17, Doppler frequency:30 Hz)
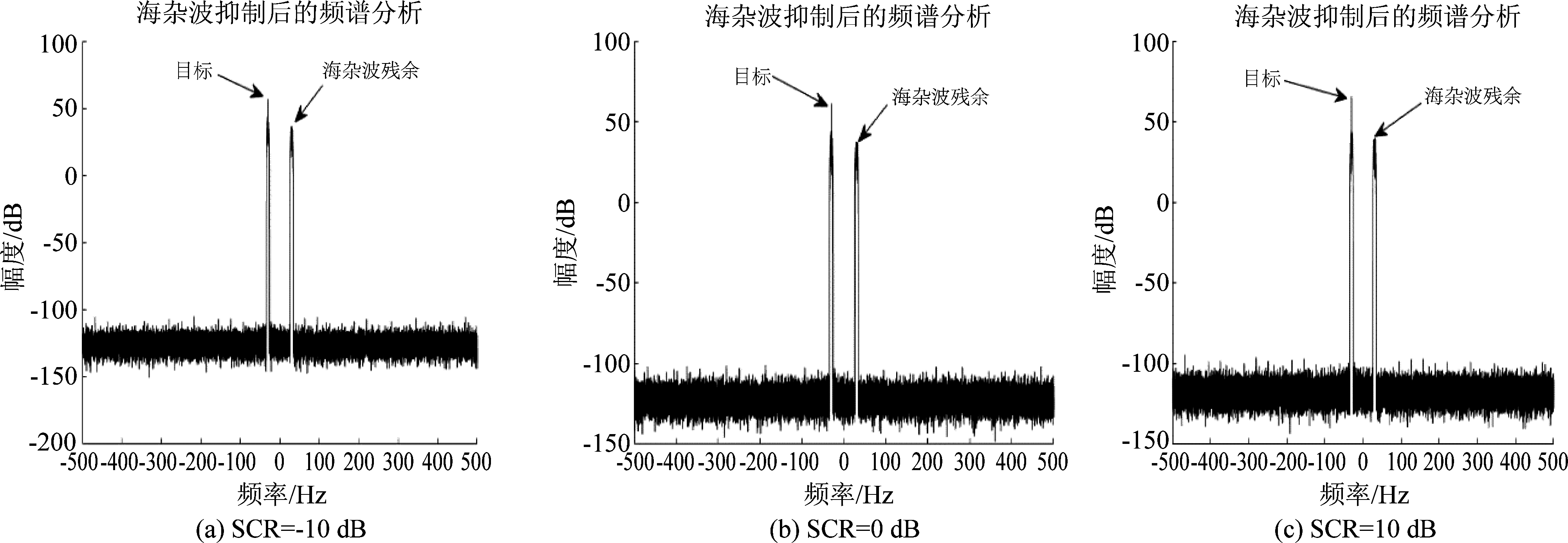
图6 海杂波抑制后的频谱分析结果(#17, 多普勒频率：30 Hz)
Fig.6 Spectral analysis results after sea clutter suppression (#17, Doppler frequency:30 Hz)
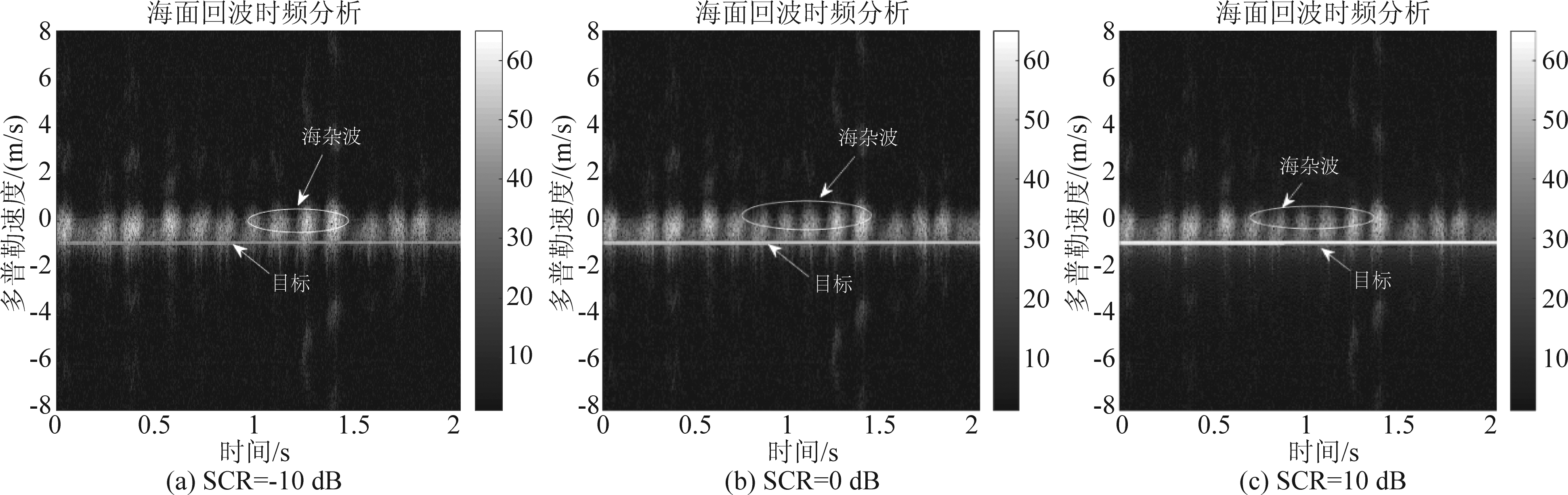
图7 海面回波时频分析结果(#17, 多普勒频率：60 Hz)
Fig.7 Time-frequency analysis results of sea surface echo (#17, Doppler frequency:60 Hz)
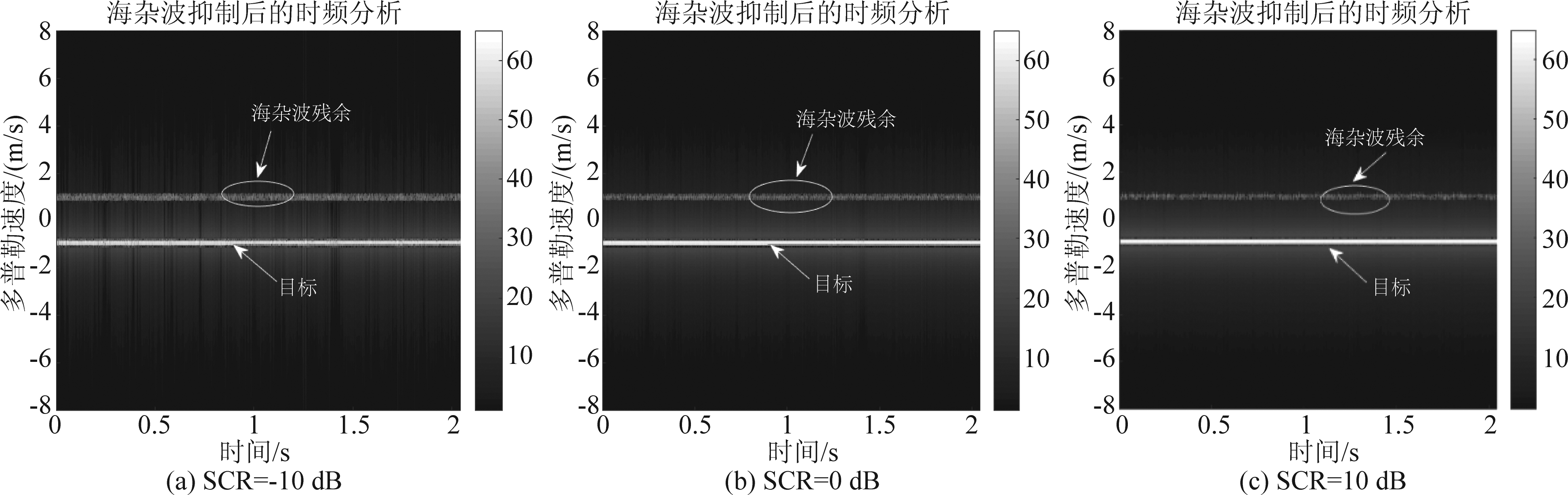
图8 海杂波抑制后的时频分析结果(#17, 多普勒频率：60 Hz)
Fig.8 Time-frequency analysis results after sea clutter suppression (#17, Doppler frequency:60 Hz)
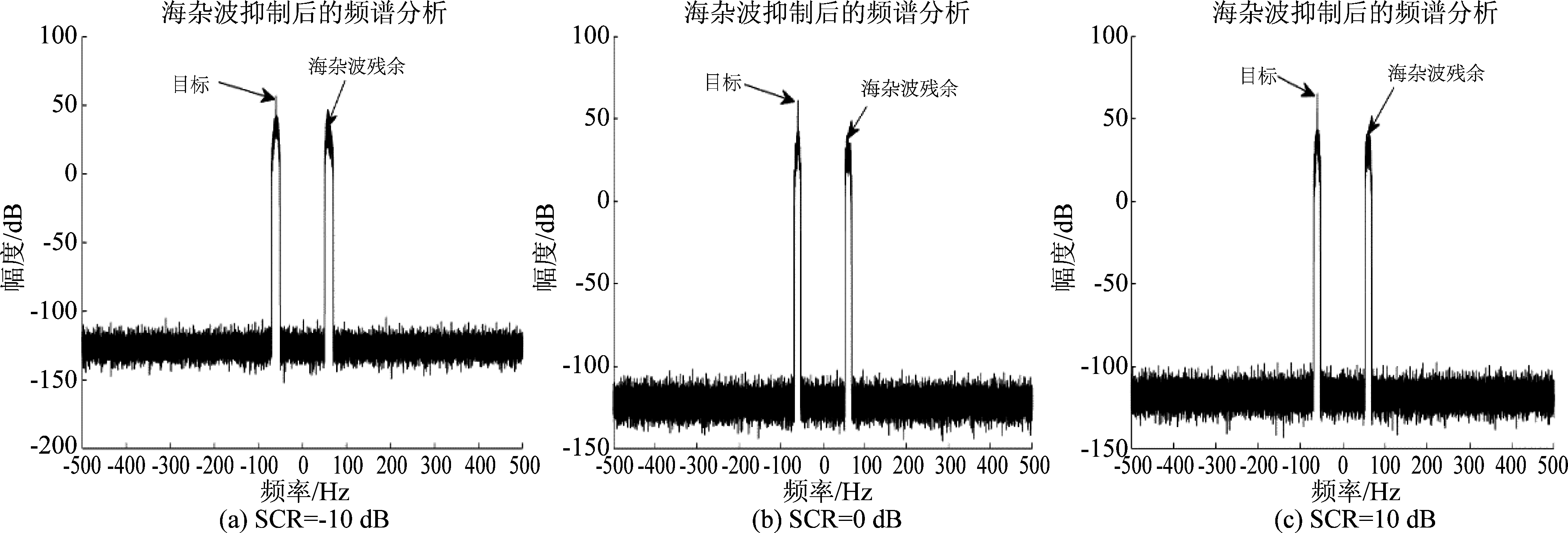
图9 海杂波抑制后的频谱分析结果(#17, 多普勒频率：60 Hz)
Fig.9 Spectral analysis results after sea clutter suppression (#17, Doppler frequency:60 Hz)
综合以上结果分析，本文提出的算法在高海况条件下能有效地对强海杂波进行抑制，改善微弱运动目标的信杂比，有效检测出位于海杂波多普勒通道中的微弱运动目标，并且杂波抑制是自适应的，不需要任何目标和杂波的先验信息。
4.2.2 低海况条件下不同信杂比，不同多普勒频率的目标的检测
在IPIX数据集第#40号数据中添加目标多普勒频率为30 Hz、60 Hz的具有不同信杂比的微弱运动目标，验证在低海况条件下，本文提出的算法的海杂波抑制和目标检测效果，结果如下图10～图16所示。仿真结果表明在低海况条件下，本文提出的算法也能有效地对强海杂波进行抑制，检测出落入海杂波多普勒通道中的具有不同多普勒频率的微弱运动目标。
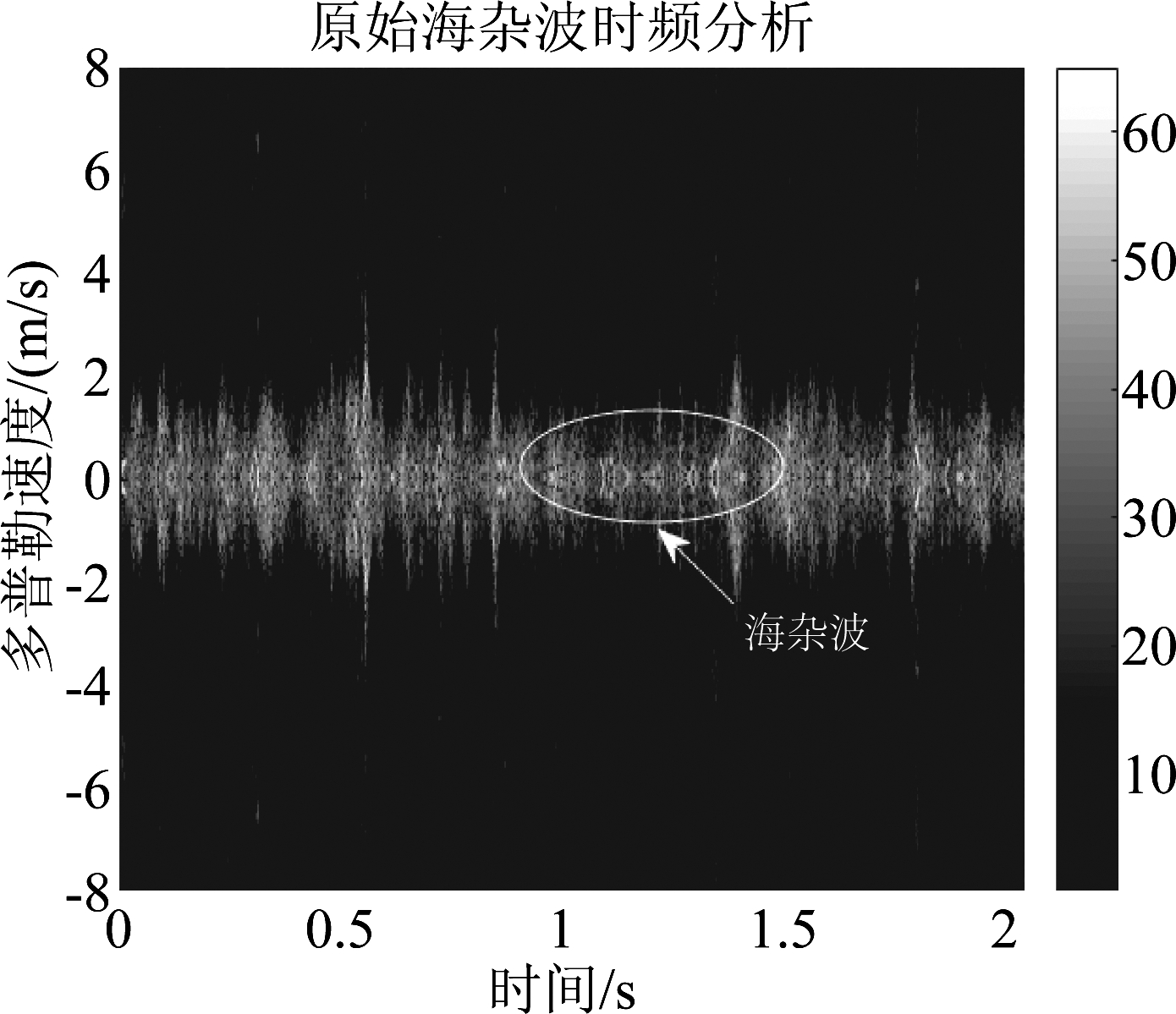
图10 海杂波时频分析结果(#40)
Fig.10 Time-frequency analysis results of sea Clutter (#40)
最后，本文提出的算法在对目标信号进行重构时，由于实验发现对信号作J层TQWT分解后，最后一层的小波系数蕴含了大量海杂波能量，重构时予以了去除。以子带能量占总能量的百分比为重构小波子带的选择标准，设定阈值对目标信号进行重构。为了验证在大信杂比条件下，重构准则不会误把杂波当成目标或者把目标当成杂波，特选择在#17(高海况)、#40(低海况)号数据中，信杂比SCR=40 dB、多普勒频率为30 Hz条件下进行实验验证，结果如下图17～图18所示，结果表明在大信杂比条件下，本文提出的算法的目标信号的重构准则不会对目标或杂波造成误判。
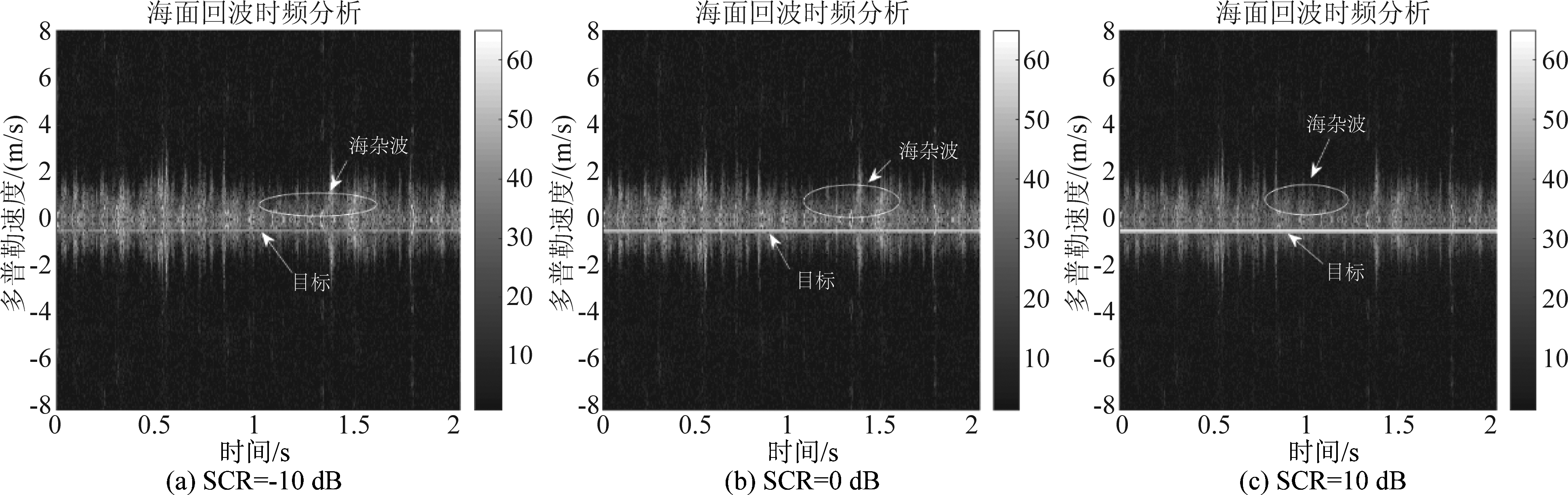
图11 海面回波时频分析结果(#40, 多普勒频率：30 Hz)
Fig.11 Time-frequency analysis results of sea surface echo (#40, Doppler frequency:30 Hz)
图12 海杂波抑制后的时频分析结果(#40, 多普勒频率：30 Hz)
Fig.12 Time-frequency analysis results after sea clutter suppression (#40, Doppler frequency:30 Hz)
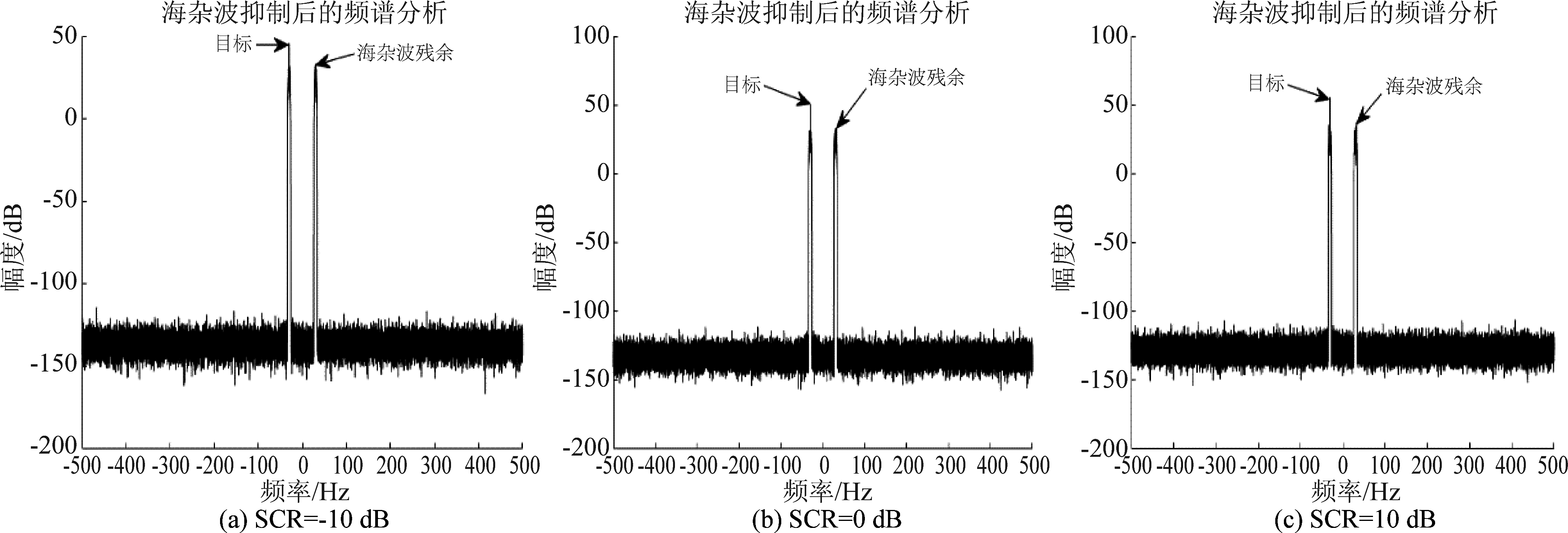
图13 海杂波抑制后的频谱分析结果(#40, 多普勒频率：30 Hz)
Fig.13 Spectral analysis results after sea clutter suppression (#40, Doppler frequency:30 Hz)
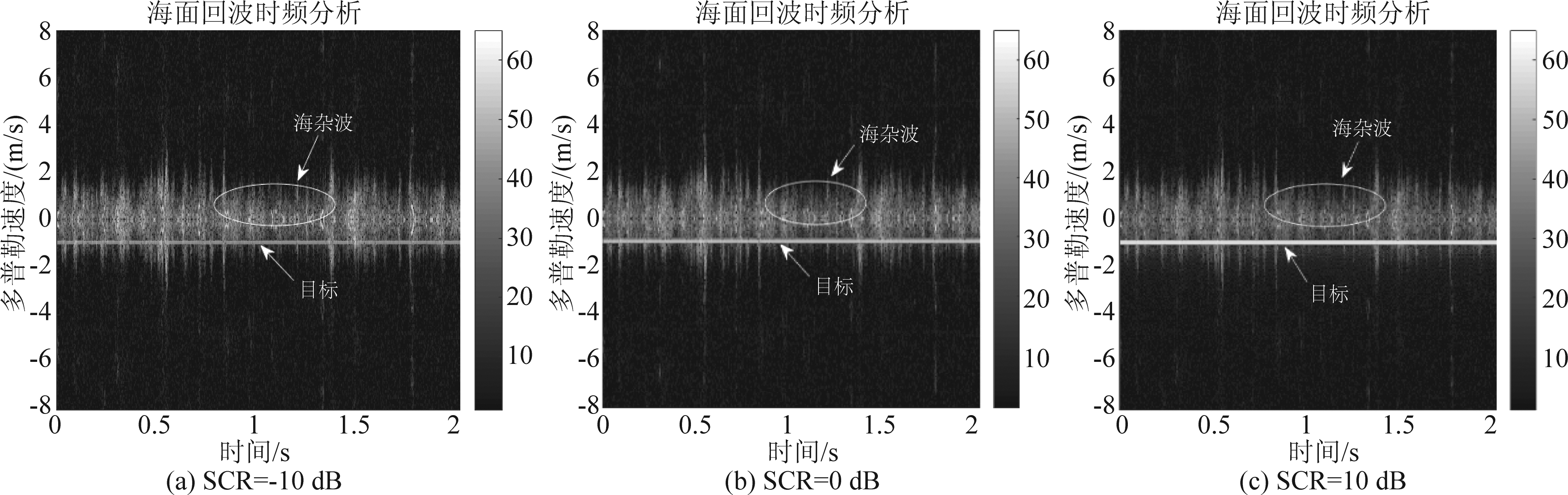
图14 海面回波时频分析结果(#40, 多普勒频率：60 Hz)
Fig.14 Time-frequency analysis results of sea surface echo (#40, Doppler frequency:60 Hz)
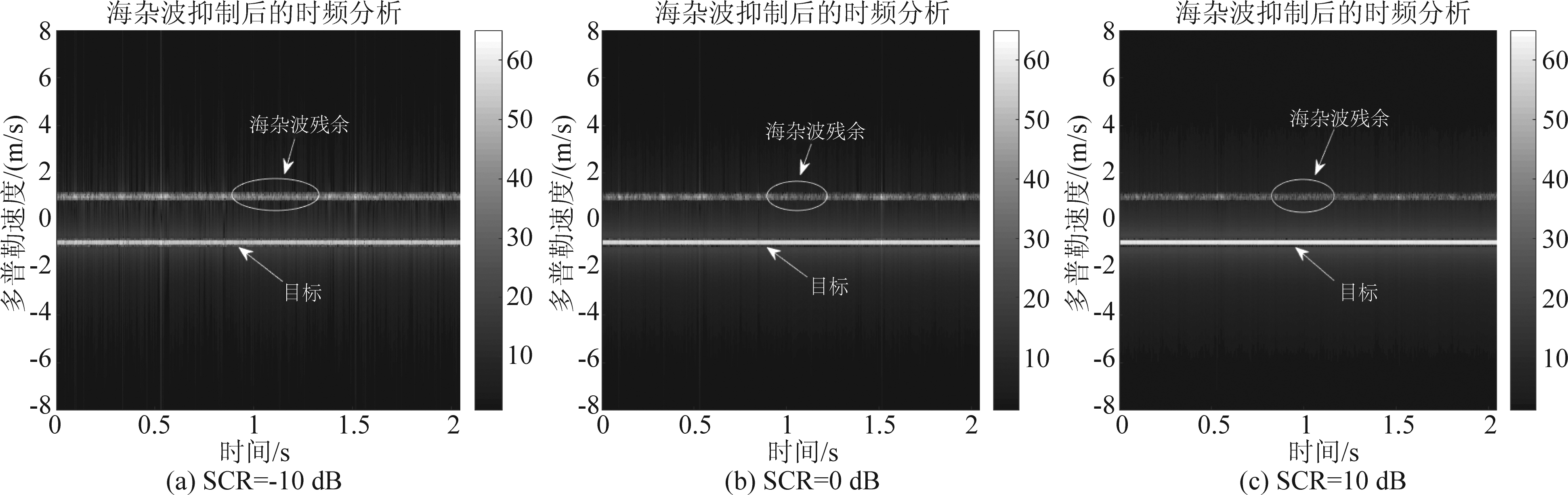
图15 海杂波抑制后的时频分析结果(#40, 多普勒频率：60 Hz)
Fig.15 Time-frequency analysis results after sea clutter suppression (#40, Doppler frequency:60 Hz)
为了进一步说明本文提出的算法的有效性和优势，将本文提出的算法同文献[13]提出的算法进行对比分析。文献[13]提出的算法在输入SCR=-8 dB条件下，输出信杂比约为13 dB[13]，并且对TQWT的关键参数组合(Q, r , J)的选择依赖于目标和杂波的先验信息；而本文提出的方法在高海况、低信杂比(4级海况，SCR=-8 dB)的条件下输出信杂比也约为13 dB，取得良好的海杂波抑制效果的同时，算法所需要的关键参数可以做到自适应地计算，不再需要任何目标和杂波的先验信息，海杂波的抑制是自适应的，具有很好的工程实用价值，这相比于文献[13]提出的算法有明显优势。并且为了定量说明本文提出的算法对海杂波的抑制能力，在仿真时设置不同输入信杂比条件，计算应用本文提出的算法对海杂波抑制后的输出信杂比，结果如下图19所示，结果表明，不论是在高海况条件(#17号数据)，还是在低海况条件(#40号数据)，本文提出的算法在低输入信杂比(-15 dB)的条件下，信杂比改善约为25 dB，具有良好的海杂波抑制能力。
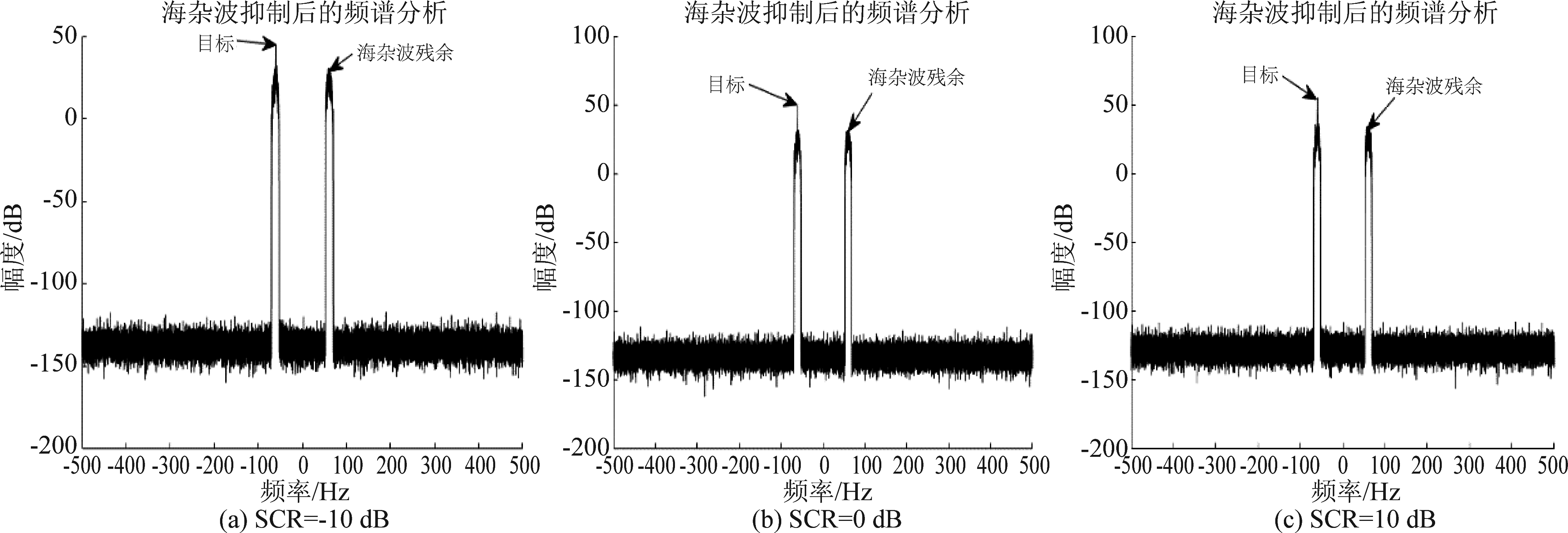
图16 海杂波抑制后的频谱分析结果(#40, 多普勒频率：60 Hz)
Fig.16 Spectral analysis results after sea clutter suppression (#40, Doppler frequency:60 Hz)
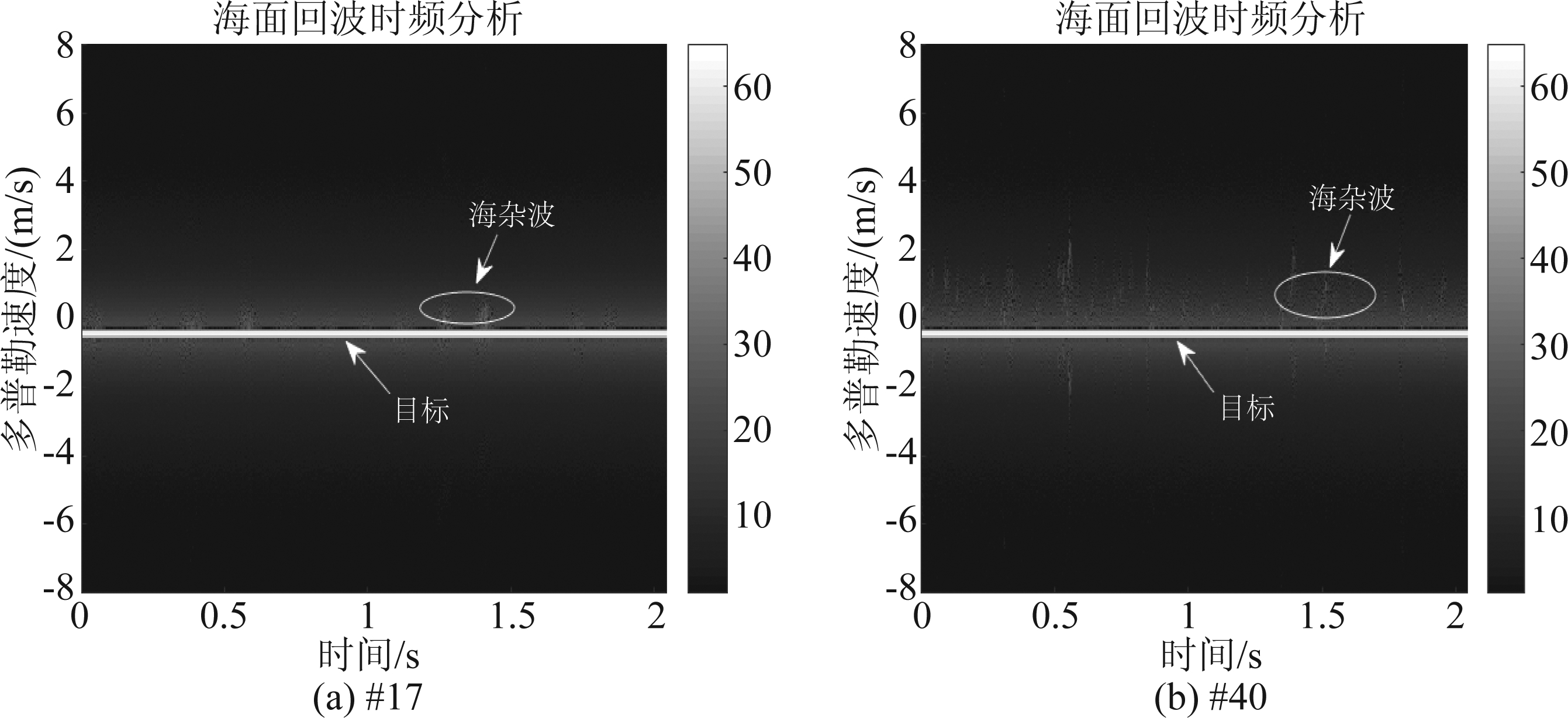
图17 海面回波时频分析结果(SCR=40 dB, 多普勒频率：30 Hz)
Fig.17 Time-frequency analysis results of sea surface echo (SCR=40 dB, Doppler frequency:30 Hz)
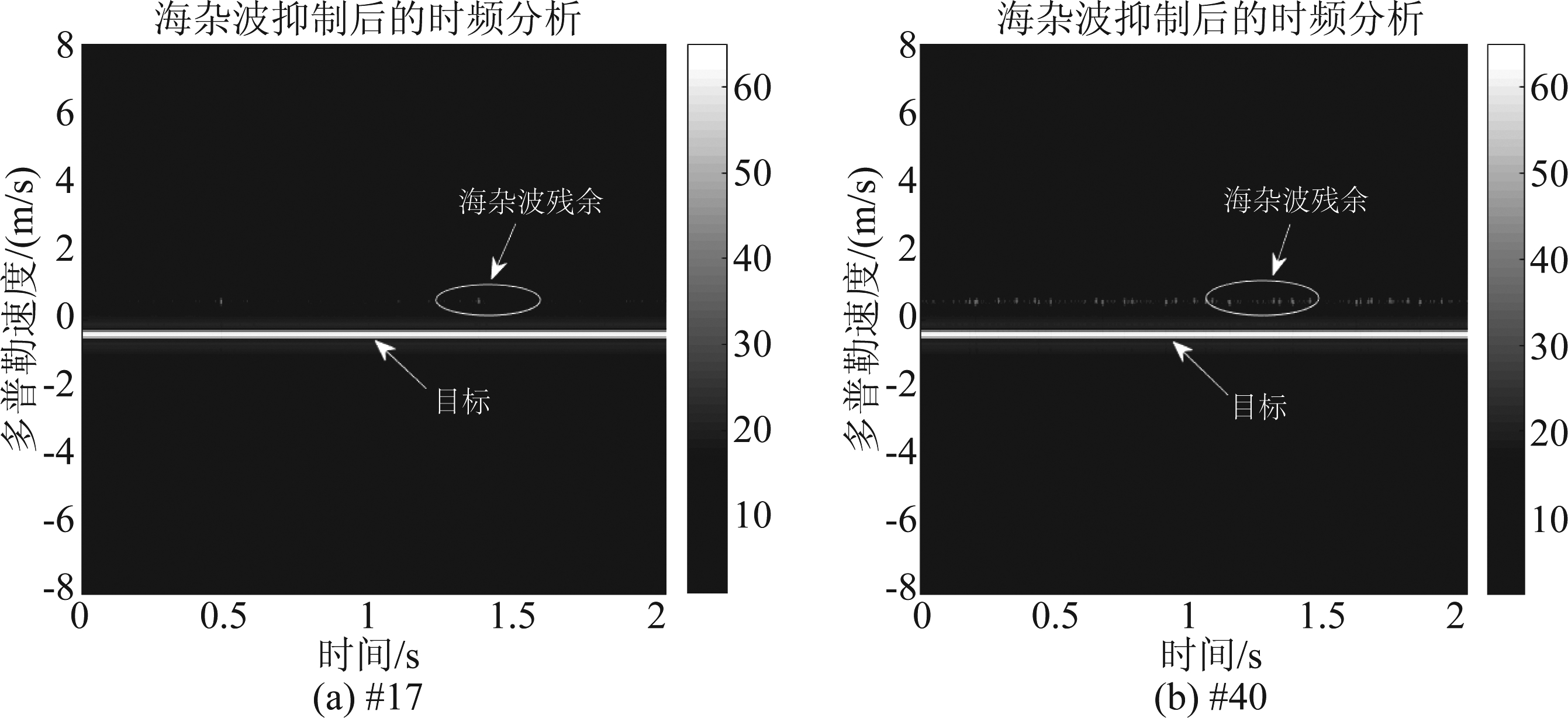
图18 海杂波抑制后的时频分析结果(SCR=40 dB, 多普勒频率：30 Hz)
Fig.18 Time-frequency analysis results after sea clutter suppression (SCR=40 dB, Doppler frequency:30 Hz)
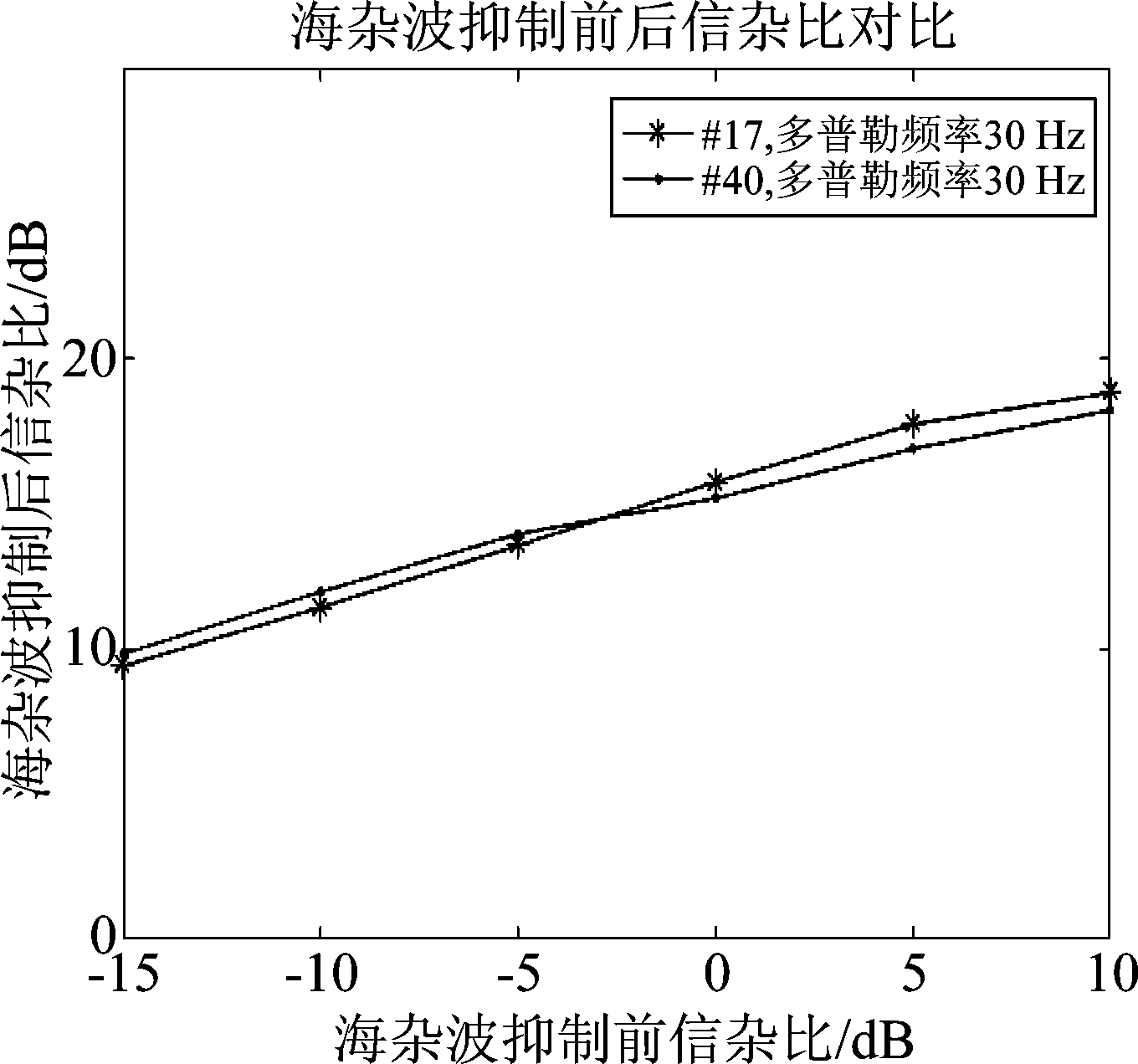
图19 海杂波抑制前后信杂比对比(多普勒频率：30 Hz)
Fig.19 SCR comparison before and after sea clutter suppression (Doppler frequency: 30 Hz)
本文针对海杂波背景下慢速微弱运动目标的检测问题提出了一种基于自适应可调Q因子小波变换(A-TQWT)的海杂波背景下的微弱目标检测算法，其根据海杂波和目标的振荡特性差异，迭代计算、搜索、约束最能匹配海杂波和目标振荡特性的TQWT三元参数组合(Q,r,J)，运用形态分量分析法(MCA)对海面回波进行分析，得到目标回波信号的稀疏表示，再根据目标分量各小波子带占总能量的比重，确定门限，选取合适的小波系数集对目标信号进行重构，从而实现了目标和海杂波的有效分离，达到目标检测的目的。仿真结果表明，本文提出的算法能够有效检测出落入海杂波多普勒通道中的慢速微弱目标，且不需要任何目标和杂波的先验信息。
[1] 施赛楠. 海面弱目标最优相干和联合特征检测方法研究[D]. 西安：西安电子科技大学, 2018.
SHI Sainan. Study on optimal coherence and Joint feature detection for weak surface targets[D]. Xi’an: Xidian University, 2018.(in Chinese)
[2] WARD K D, TOUGH R J A, WSTTS S. Sea clutter scattering: the K-Distribution and radr performance[M]. London, UK: The Institution of Engineering and Technology, 2013: 19-23.
[3] 朱雪瑗, 杨勇虎, 李颖. 一种经验模式分解下的海杂波小目标检测方法[J]. 电讯技术, 2018, 58(3): 251-256.
ZHU Xueyuan, YANG Yonghu, LI Ying. A novel small target detection method in sea clutter after empirical mode decomposition[J]. Telecommunication Engineering, 2018, 58(3): 251-256.(in Chinese)
[4] 左磊, 产秀秀, 禄晓飞, 等. 时频域分解海面回波及慢速微弱目标检测[J]. 西安电子科技大学学报, 2019, 46(5): 84-90.
ZUO Lei, CHAN Xiuxiu, LU Xiaofei, et al. Detection of slow and weak target in time-frequency domain decomposition surface echo wave[J]. Journal of Xidian University, 2019, 46(5): 84-90.(in Chinese)
[5] 陈小龙, 关键, 何友, 等. 高分辨稀疏表示及其在雷达动目标检测中的应用[J]. 雷达学报, 2017, 6(3): 239-251.
CHEN Xiaolong, GUAN Jian, HE You, et al. High resolution sparse representation and its application in radar moving target detection[J]. Journal of Radars, 2017, 6(3): 239-251.(in Chinese)
[6] 陈小龙, 关键, 于晓涵, 等. 基于短时稀疏时频分布的雷达目标微动特征提取及检测方法[J]. 电子与信息学报, 2017, 39(5): 1017-1023.
CHEN Xiaolong, GUAN Jian, YU Xiaohan, et al. Radar micro-Doppler signature extraction and detection via short-time sparse time-frequency distribution[J]. Journal of Electronics and Information Technology, 2017, 39(5): 1017-1023.(in Chinese)
[7] 李庆忠, 周祥振, 黎明, 等. 基于时频分析的海杂波背景下舰船目标检测[J]. 计算机应用研究, 2018, 35(1): 52-55, 61.
LI Qingzhong, ZHOU Xiangzhen, LI Ming, et al. Ship target detection under sea clutter background based on time-frequency analysis[J]. Application Research of Computers, 2008, 35(1): 52-55, 61.(in Chinese)
[8] 陈小龙, 关键, 董云龙, 等. 稀疏域海杂波抑制与微动目标检测方法[J]. 电子学报, 2016, 44(4): 860- 867.
CHEN Xiaolong, GUAN Jian, DONG Yunlong, et al. Sea clutter suppression and fretting target detection in sparse domain[J]. Acta Electronica Sinica, 2016, 44(4): 860- 867.(in Chinese)
[9] YU Xiaohan, CHEN Xiaolong, HUANG Yong, et al. Radar moving target detection in clutter background via adaptive dual-Threshold sparse fourier transform[J]. IEEE Access, 2019, 7: 58200-58211.
[10] SELESNICK I. Wavelet transform with tunable Q-factor[J]. IEEE Transactions on Signal Processing, 2011, 59(8): 3560-3575.
[11] FAR SHCNIAN M, SELESNICK T. Application of a sparse time-frequency technique for target with oscill-atory fluctuations[C]∥International Waveform Diversity and Design Conference. Kauai, Hawaii, USA: IEEE Press, 2015: 191-196.
[12] NGUYEN S, AL-ASHWAL W. Sea clutter mitigation using resonance-based signal decomposition[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(11): 2257-2261.
[13] 潘美艳, 杨予昊, 李大圣, 等. 一种基于能量选择的改进TQWT海杂波抑制算法[J]. 现代雷达, 2018, 40(10): 32-37.
PAN Meiyan, YANG Yuhao, LI Dasheng, et al. An improved TQWT sea clutter suppression algorithm based on energy selection[J]. Modern Radar, 2008, 40(10): 32-37.(in Chinese)
[14] 孔运, 王天杨, 褚福磊. 自适应TQWT滤波器算法及其在冲击特征提取中的应用[J]. 振动与冲击, 2019, 38(11): 9-16, 23.
KONG Yun, WANG Tianyang, CHU Fulei. Adaptive TQWT filter algorithm and its application in shock feature extraction[J]. Journal of Vibration and Shock, 2019, 38(11): 9-16, 23.(in Chinese)
[15] OZKURT N. Signal adaptive Q factor selection for resonance based signal separation using tunable-Q wavelet transform[C]∥2018 41st International Conference on Telecommunications and Signal Processing (TSP), Athens, 2018: 1- 4.
[16] http:∥soma.ece.mcmaster.ca/ipix/dartmouth/index.html.
[17] HUA Xiaoqiang, SHI Yifei, ZENG Yang, et al. A divergence mean-based geometric detector with a pre-processing procedure[J]. Measurement, 2019, 131: 640- 646.
[18] 时艳玲, 林毓峰, 宛汀. 部分均匀海杂波中雷达目标的平滑自适应检测[J]. 系统工程与电子技术, 2016, 38(12): 2745-2751.
SHI Yanling, LIN Yufeng, WAN Ting. Smooth adaptive detection of radar targets in partially uniform sea clutter[J]. Systems Engineering and Electronics, 2016, 38(12): 2745-2751.(in Chinese)
冯 云 男， 1989年生， 四川人。电子科技大学电子科学技术研究院硕士研究生， 主要研究方向为海杂波背景下的目标检测技术。
E-mail： 625354149@qq.com
宗竹林 男， 1983年生， 江西人。博士， 电子科技大学电子科学技术研究院副研究员， 主要研究方向为雷达信号处理、相控阵雷达系统、频控阵雷达系统。
E-mail： zongzhulin@uestc.edu.cn
李思琦 女， 1996年生， 四川人。电子科技大学电子科学技术研究院硕士研究生， 主要研究方向为频控阵雷达抗干扰。
E-mail： 18708215826@163.com