
图1 无人机坐标系及操控示意图
Fig.1 The drone coordinate system and the control schematic
Reference format: WANG Xiaoliang, WANG Chengxiang, HE Weikun. Radar Echoes Simulation of the Quadrotor Drone Utilizing Flight Control Characteristics[J]. Journal of Signal Processing, 2021, 37(2): 292-303. DOI: 10.16798/j.issn.1003- 0530.2021.02.015.
近年来,全球无人机产业飞速发展,随着消费级无人机的日益普及,无人机也给国家安全和公众安全带来了潜在威胁,在机场、核电站等重要设施和重要活动场所,需要对无人机进行有效的探测与识别。雷达是探测和识别无人机的重要技术手段,虽然已有专门针对无人机监视的雷达面世,但这些产品在复杂环境下探测和识别无人机的性能仍有望进一步提高。消费级无人机由于其“低小慢”的特点,检测难度大,且不易与鸟、风吹动的树等易混淆目标相区分。由于多旋翼无人机旋翼的转动与鸟的振翅运动、树的运动有所不同,能够反映目标内部局部运动特点的微多普勒特征已成为雷达检测无人机以及分辨无人机与其他易混淆目标的重要技术手段。雷达对无人机检测和分类的研究需要较多的测试数据,特别对于分类的研究往往需要大量数据对分类器进行训练,但实测数据能够涵盖的各种不同的无人机机型、各种不同的无人机运动变化状态有限,且实测数据对于一些参数不易控制。而无人机雷达回波信号仿真是开展无人机雷达探测和识别研究的重要技术手段。
近年来国内外学者已在旋翼无人机雷达回波仿真方面开展了一些研究工作。旋转叶片是无人机一个显著特征,对于旋转叶片雷达回波的仿真,Victor Chen教授针对直升机雷达回波的仿真,将直升机旋翼叶片等效为刚性均匀的线条,采用各散射点回波积分的方法,建立了旋转叶片的雷达回波模型[1]。针对包含旋转叶片的风力发电机雷达回波的仿真,本课题组和其他一些学者也做了不少工作[2- 4]。在单个叶片雷达回波模型的基础上,学者们建立了多旋翼无人机雷达回波的仿真模型。这些模型一般分别计算无人机每个旋翼中每个叶片的雷达回波,再进行叠加[5-7]。有些多旋翼无人机雷达回波模型没有考虑多旋翼无人机相对雷达波束的方位角,文献[8]的无人机回波模型引入了方位角参数。文献[9]与[10]进一步给出了FMCW雷达的旋翼无人机回波模型。多数仿真模型将无人机叶片和机身的散射强度简化为一个特定的系数,文献[11]与[12]还用电磁计算方法对无人机叶片和机身的RCS进行了进一步分析,并在此基础上建立了雷达回波仿真模型。此外文献[9]在无人机雷达回波的分析中还考虑了旋翼转速的变化。
多旋翼无人机的运动状态由各旋翼的转速决定,无人机的速度与旋翼转速有密切联系。然而,现有无人机雷达回波仿真模型将旋转叶片和机身分别建模再叠加,没有考虑机身速度与旋翼转速间的相关性,与实际情况有不一致之处,也无法充分体现旋翼无人机运动的特点。为此,针对最常见的四旋翼无人机,本文提出了一种将机身运动与旋翼转速相结合的四旋翼无人机雷达回波仿真方法。该方法可以为无人机监视雷达的研究与测试、特别是雷达对无人机检测与分类的研究提供微多普勒特征更准确的、参数可控的、数量丰富的测试数据源。获得的仿真数据可以弥补实测数据的不足,解决无人机识别中实测数据训练样本对于无人机的机型、各种变化状态覆盖率低的问题。
该方法首先针对雷达回波仿真的需求根据多旋翼无人机飞控原理给出了一种机身速度与旋翼转速关联的简化运动模型,其次推导并给出了线性调频体制雷达考虑旋翼倾转的四旋翼无人机雷达回波信号模型,最后利用坐标系转换将无人机简化运动模型与雷达回波信号模型相结合进行雷达回波仿真。
四旋翼无人机的布局通常有“十”型和“X”型两种,“十”型布局前飞时只有单个旋翼在最前方,而“X”形布局前飞时则为两个相邻的旋翼同时在最前方。这两种布局控制方式类似,下面以消费级无人机中更为常见的“X”形布局进行分析。
四旋翼无人机对角线上的旋翼旋转方向相同,而相邻的旋翼旋转方向相反,以抵消旋翼旋转的反扭矩。悬停状态时,四个旋翼转速相同,操控无人机时,通过改变四个旋翼的转速来改变无人机的运动状态。如图1,通过四个旋翼转速同时增减来改变升力控制升降,通过控制旋翼1、2的转速大于旋翼3、4的转速,使无人机俯仰角变化,进而产生向前的力而前进,俯仰角越大,向前的力越大。类似的可控制无人机向后和向左右平飞。通过控制对角线旋翼1、3的转速大于或小于另一对角线旋翼2、4的转速控制无人机向左或向右旋转。

图1 无人机坐标系及操控示意图
Fig.1 The drone coordinate system and the control schematic
目前市场上的四旋翼无人机都有系统的飞行控制算法保持无人机运动状态的稳定。四旋翼无人机遥控器的左右两个摇杆分别控制无人机的升降、自身旋转(即偏航运动)、前后运动(即俯仰运动)和左右运动(即横滚运动),即有4个通道的控制。利用遥控器控制无人机飞行的常见飞行控制过程为[13-14]:(1)利用遥控器控制无人机期望状态(期望总拉力、期望俯仰角、期望横滚角、期望偏航角速度);(2)由期望状态利用飞控算法解算期望总拉力和控制姿态的期望力矩;(3)由期望总拉力和期望力矩通过控制分配得到各旋翼转速;(4)根据各旋翼转速解算期望电机油门指令;(5)由期望电机油门指令控制旋翼实际转速;(6)由旋翼实际转速控制实际总拉力和力矩;(7)由实际总拉力和力矩控制加速度、速度、角加速度、角速度;(8)由加速度、速度、角加速度、角速度得到无人机的位置与姿态。
由上述控制过程可以看出,旋翼转速为无人机飞行控制的直接输出量,影响无人机机体运动状态的速度、加速度等参量与旋翼转速紧密相联系。
针对无人机雷达回波仿真的目标,对上述控制过程进行简化建模,可以作如下假设:(1)由于四旋翼无人机姿态变化完成的时间很短,因此忽略四旋翼控制器控制姿态变化的过程,即假设无人机的姿态根据遥控器指令瞬间达到期望俯仰角、横滚角和偏航角速度,且姿态保持稳定。(2)忽略飞行过程中因为阵风等环境因素产生的扰动、忽略飞控系统因为扰动因素进行的旋翼转速的微调。(3)假设实际无人机俯仰角、横滚角和偏航角速度、总拉力、力矩、各旋翼转速与期望值相同。这样可以直接用遥控器指令的期望值进行无人机动力学模型建模。(4)影响四旋翼姿态的力矩主要包括旋翼力矩、陀螺力矩、诱导阻力力矩、扰动力矩等,假设姿态达到稳态时无人机所受合力矩为0,飞行控制参量三轴的旋翼力矩分别与遥控器指令,即期望俯仰角、横滚角和偏航角速度成正比。于是得到将旋翼转速与无人机机体运动状态相关联,用于雷达回波仿真无人机运动模型如图2所示。
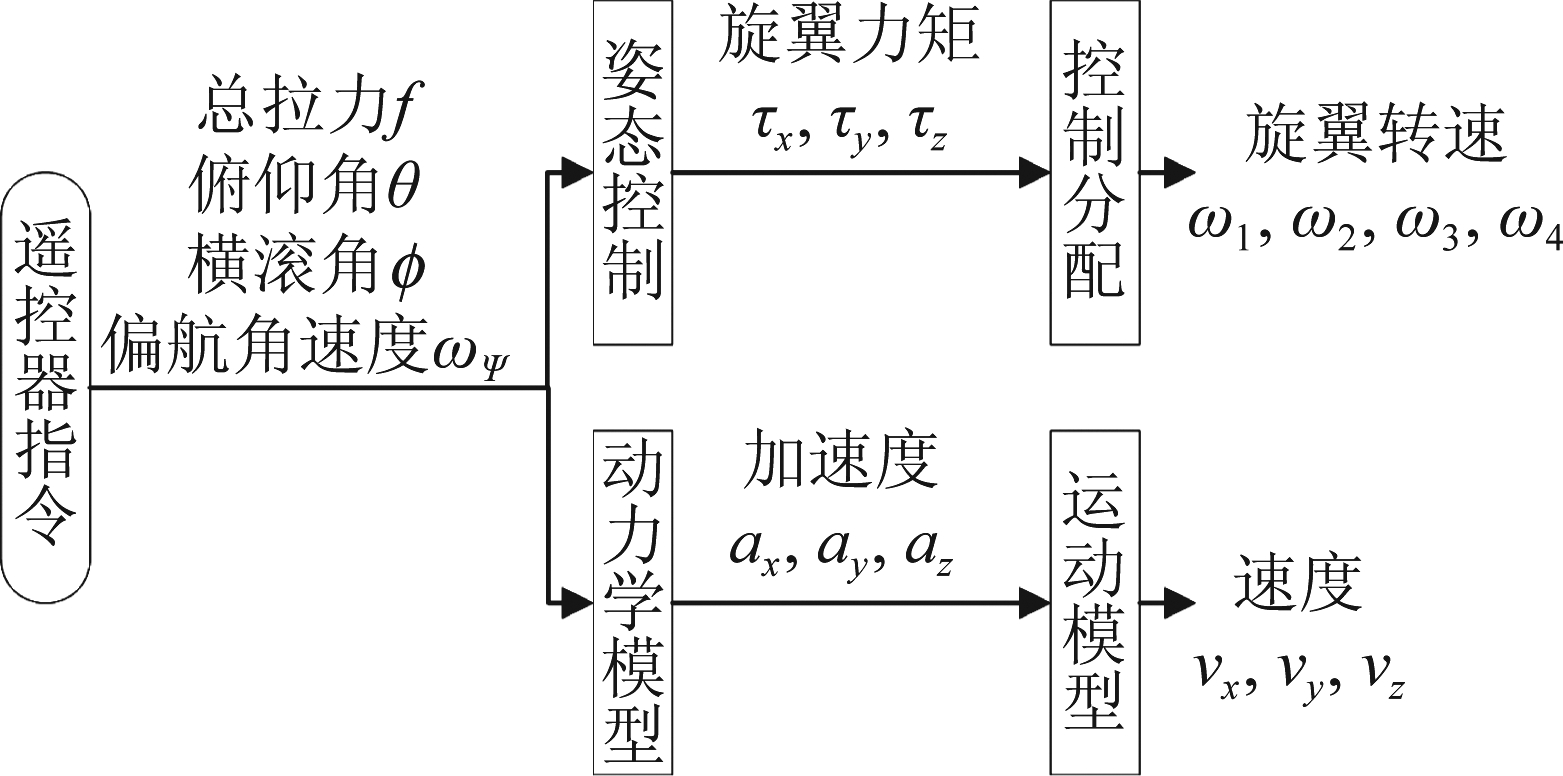
图2 运动状态与旋翼转速相关联的简化无人机运动模型
Fig.2 The simplified drone motion model with motion state associated with rotors rotation speed
建立如图1所示的坐标系,根据前述假设,姿态控制模型可简化为
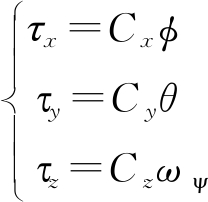
(1)
式中φ,θ,ωψ分别为无人机期望的横滚角、俯仰角和偏航角速度,τx,τy,τz分别对应沿横滚、俯仰和偏航方向转动的旋翼力矩,Cx,Cy,Cz为比例系数。
四旋翼无人机旋翼总拉力f和旋翼力矩τx,τy,τz与各旋翼转速ω1,ω2,ω3,ω4的关系为[15]
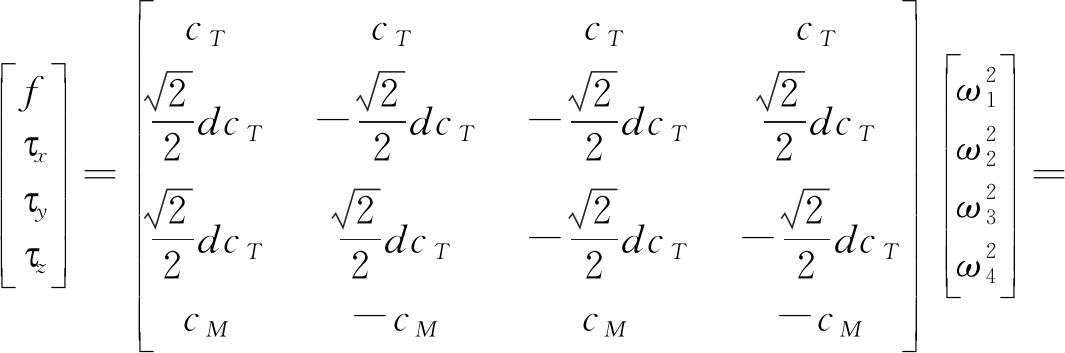
![]()
(2)
式中cT,cM分别为与旋翼拉力和旋翼力矩相关的常数,部分机型的cT,cM可以查到,cT还可以通过悬停时的旋翼转速和受力平衡推算。d为旋翼中心到机体中心的距离,对于“X”型无人机,旋翼产生的机体的转动力臂正好为![]() 由上式易解得控制分配模型为
由上式易解得控制分配模型为
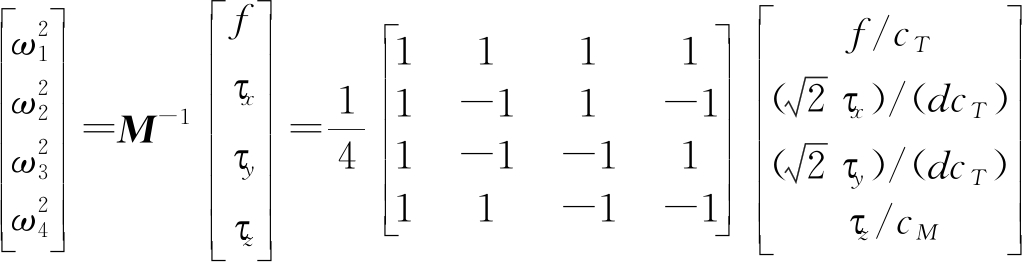
(3)
由于仿真中假设无人机姿态的变化瞬间完成,姿态变化后姿态保持稳定,所以动力学模型仅考虑机体的平动,不考虑机体自身转动引起的姿态变化。于是可得其动力学模型为
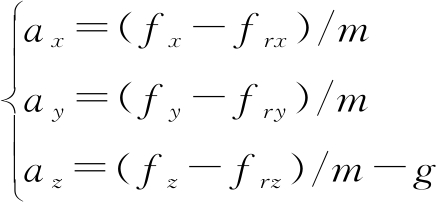
(4)
式中ax,ay,az为地面坐标系下沿三个坐标轴方向的加速度, fx, fy, fz为旋翼升力在三个轴向的分量, frx, fry, frz为空气阻力在三个轴向的分量,m为无人机质量,g为重力加速度。根据机体坐标系到地面坐标系的转换矩阵,可得[16]
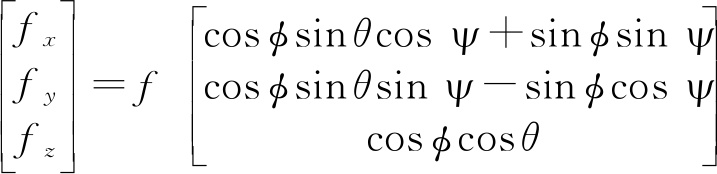
(5)
根据加速度即容易算得无人机任意时刻t的速度,再利用积分即可得t时刻的位置。为方便雷达回波仿真,仅利用该模型计算速度,位置待将坐标转换到雷达坐标系后再进行计算。
对于无人机一般的运动,需要对时间进行采样,分别计算各采样时刻的旋翼力矩和加速度,并根据各采样时刻的旋翼总拉力和旋翼力矩计算该采样时刻的各旋翼转速,根据各采样时刻的加速度计算下一采样时刻的机身速度。对于无人机飞行中常见的向前后或左右沿直线平飞,以及沿直线斜向上或斜向下飞的情况,上述模型可进一步简化。
遥控器俯仰和横滚摇杆控制无人机向前后或左右平飞,因为向各方向飞行类似,下面以前飞为例进行分析。无人机前飞时,可令横滚角φ=0,偏航角ψ=0,前飞时仅在前进方向即X方向受到空气阻力,在X方向空气阻力分量即为总的空气阻力fr,于是动力学模型式(4)简化为
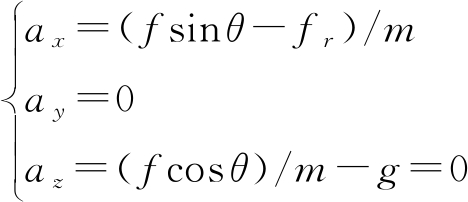
(6)
式中f为旋翼总拉力。
向前平飞时机体向前倾斜,旋翼总拉力在竖直方向上的分量与重力平衡。其中空气阻力fr可表示为[17]
fr=Kν2
(7)
式中ν为无人机平飞速度,K为空气阻力比例系数,空气阻力随速度变化,于是可得前进方向的加速度为
(8)
解微分方程,得到在0时刻速度为ν0时,任意时刻t的速度为

(9)
式中tanh(·)为双曲正切函数,ar tanh(·)为反双曲正切函数。当向前的拉力与空气阻力相等时,无人机达到最大速度,在俯仰角θ下,能够达到的最大速度为
(10)
式(7)中的空气阻力比例系数K可由空气阻力计算公式计算,也可根据式(10)利用无人机手册与资料给出的最大速度与俯仰角的对应关系计算。
以向前斜向上或斜向下飞为例,此时竖直方向的受力平衡不再成立。这里仅考虑从悬停状态开始斜向上或斜向下飞的情况,这种情况下ν0=0,起始时空气阻力为0,速度方向与加速度方向相同。此时加速度方向相对水平方向的仰角[18]
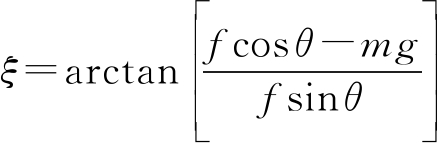
(11)
在该方向加速度的大小为
(12)
式中F为无人机除空气阻力外所受的合力的大小,具体为![]()
与前面类似解微分方程,可得从悬停状态开始斜向上或斜向下飞,任意时刻t的速度为
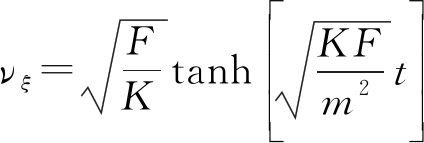
(13)
最大速度为
(14)
若发射信号为单频脉冲信号,发射信号第m个脉冲可表示为
(15)
式中T为脉冲宽度, fc为信号载频,![]() 为快时间变量,
为快时间变量,
(16)
则按照“走-停”模型,对于散射点P,其第m个脉冲的回波为
(17)
式中tm=mTPRI为第m个脉冲对应的慢时间,其中TPRI为脉冲重复间隔,σP为散射系数,RP(tm)为tm时刻散射点P到雷达的距离。
以雷达为坐标系原点建立雷达坐标系如图3所示,坐标系X轴正方向为t=0时刻雷达波束中心指向。将叶片上各散射点的回波累加,积分后可得单个旋转叶片的回波。根据文献[8]给出的结果,第m个脉冲单个叶片回波信号去载波后的基带信号为
![]()
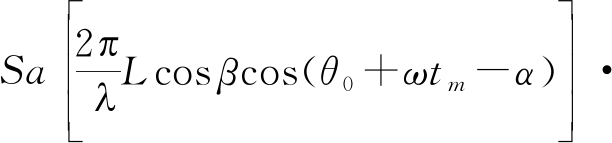
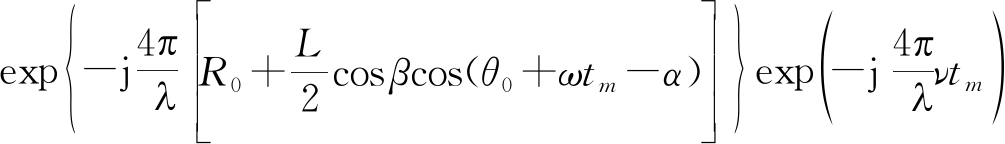
(18)
式中Sa(x)=sin x/x,σ为叶片散射系数,R0为叶片旋转轴心到雷达的距离,c为光速,L为叶片长度,λ为发射信号的波长,ω为叶片转速,β、α分别为叶片旋转轴心相对雷达的俯仰角和方位角,方位角为0时叶片旋转轴心位于坐标系X轴正方向,θ0为t=0叶片的初始相位,叶片指向X轴正方向θ0=0,ν为无人机机身运动相对雷达的径向速度,远离雷达方向为正。若旋翼旋转平面相对水平面存在倾斜,只需对β、α进行修正即可。设在以叶片旋转轴心为原点,旋翼旋转平面为XOY平面的坐标系下,雷达相对叶片旋转轴心的俯仰角和方位角分别β′、α′,则需要将β、α修正为β=-β′、α=α′-180°。
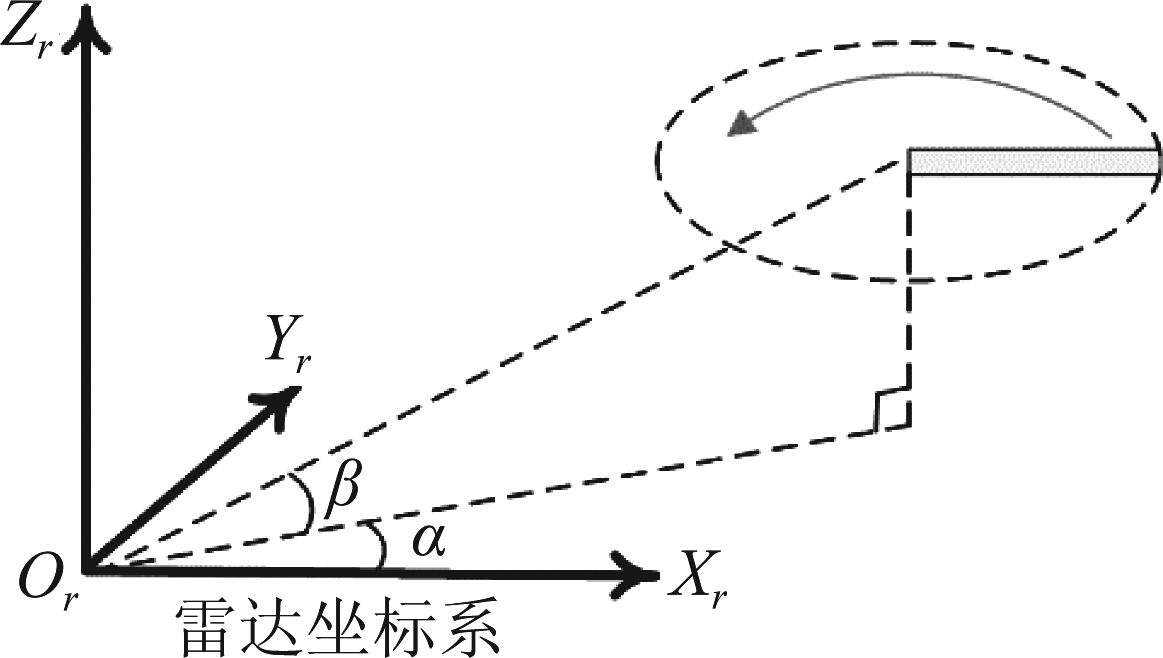
图3 雷达与目标的几何关系
Fig.3 The geometric relationship between
the radar and the target
为提高目标距离向分辨率,现有脉冲体制无人机监视雷达发射信号多采用线性调频信号,此时发射信号第m个脉冲可表示为
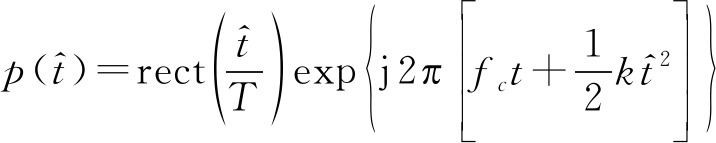
(19)
式中k为信号线性调频率。按照“走-停”模型,对于散射点P,其第m个脉冲的回波去载波后经匹配滤波处理得到
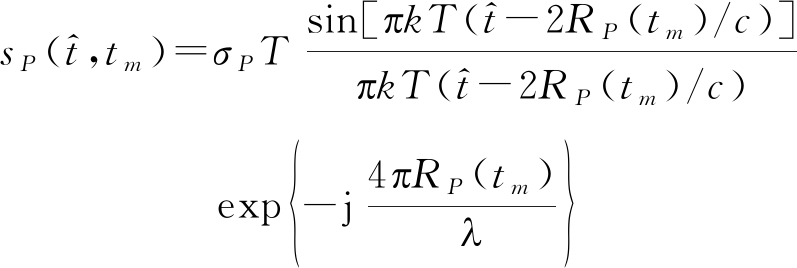
(20)
与式(17)相比幅度项略有不同。对叶片上各散射点的回波进行累加时,由于各散射点到雷达的距离不同,导致式(20)中各散射点雷达回波的幅度项不同,给积分带来了难题。
仍然令R0为叶片旋转轴心到雷达的距离,令散射点P到雷达的距离RP(tm)=R0+ΔR(tm),利用麦克劳林级数,在![]() 附近,即在距离为R0的散射点的回波峰值附近,式(20)中随RP(tm)变化的幅度项可近似为
附近,即在距离为R0的散射点的回波峰值附近,式(20)中随RP(tm)变化的幅度项可近似为
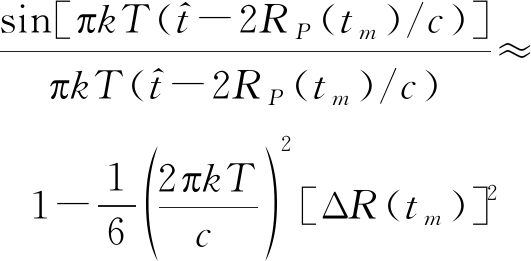
(21)
可以看到幅度的变化量与射频带宽(信号射频带宽为|k|T)与叶片上散射点到旋转轴心的距离有关。由于无人机叶片长度很小,当kT=20 MHz,ΔR=0.5 m时,变化的幅度项由峰值1衰减到0.9927。因此对于旋翼无人机的分析,可以认为随RP(tm)变化的幅度项近似为常数。
于是利用叶片上各散射点回波的累加,可得发射信号为线性调频信号时,第m个脉冲单个叶片回波信号去载波并经匹配滤波后的信号为
![]()
![]()
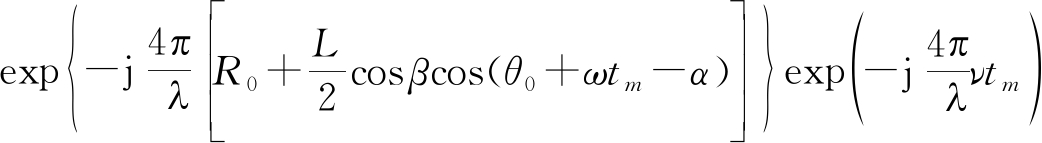
(22)
若单个旋翼的叶片数为N,其中一个叶片的初始相位为θ0,则各个叶片的初始旋转相位分别为:
θ0=θ0+2nπ/N (n=0,1,2,...,N-1)
(23)
单个旋翼的回波为各叶片回波的和,目前四旋翼无人机每个旋翼多为两个叶片,初始相位分别为θ0,θ0+π,对两个叶片的回波求和得到

(24)
式中cosh(·)为双曲余弦函数。
令四旋翼无人机各旋翼的转速、其中一个叶片的初始相位、旋翼旋转轴心到雷达的距离分别为ωi,θi,Ri,i=1,2,3,4,令四旋翼无人机中心点在旋翼所在平面内的投影点O到雷达的距离为Rd。由于各旋翼旋转轴心相对雷达的距离、俯仰角、方位角与中心点投影点O相对雷达的距离、俯仰角、方位角偏差很小,因此回波仿真中可以忽略各旋翼旋转轴心与中心点投影点O的位置偏差[5]。将无人机机身建模为固定散射强度的点目标,整个无人机的回波为机身回波与四个旋翼回波的叠加,于是得到四旋翼无人机的回波信号为
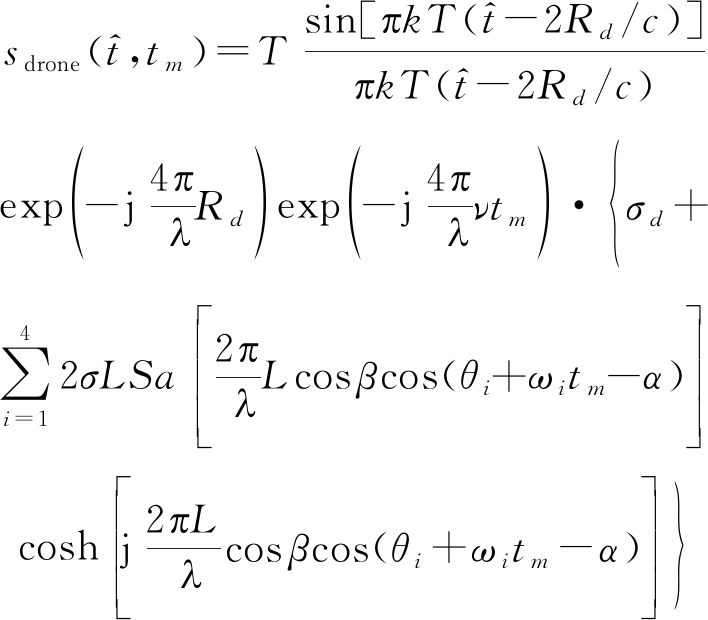
(25)
式中σd为机身散射系数,β、α分别为无人机中心点投影点O相对雷达的俯仰角和方位角。若旋翼旋转平面相对水平面存在倾斜,则用前文所述方法进行修正。
雷达坐标系与无人机运动模型中的地面坐标系在方位向相差一个偏转角,设雷达坐标系相对地面坐标系的水平方向偏转角为γ,则无人机速度从地面坐标系转换到雷达坐标系的转换公式为
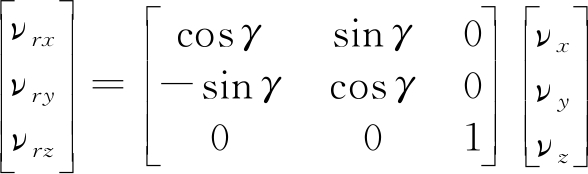
(26)
式中![]() 为雷达坐标系下速度,径向速度为
为雷达坐标系下速度,径向速度为
ν=νrxcos βcos α+νyxcos βsin α+νzxsin β
(27)
径向速度远离雷达为正。
实验中,四旋翼无人机的相关参数参考大疆精灵4 Pro无人机,具体参数如表1,表中升力系数cT由悬停时的转速60 rps根据平衡关系反推得到,空气阻力比例系数K根据最大速度与俯仰角的对应关系由式(10)计算得到。机身散射系数σd根据文献[19]的结果按照单个叶片的峰值功率比机身低10 dB设定。雷达参数参考某无人机监视雷达参数,该雷达采用线性调频脉冲体制,具体参数如表2。
表1 四旋翼无人机参数
Tab.1 Parameters of the quadrotor drone
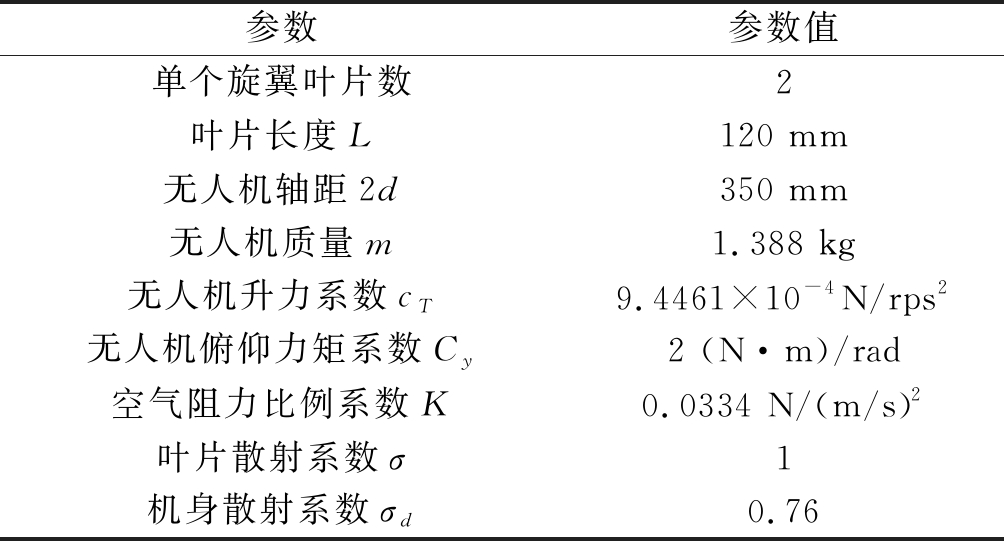
参数参数值单个旋翼叶片数2叶片长度L120 mm无人机轴距2d350 mm无人机质量m1.388 kg无人机升力系数cT9.4461×10-4N/rps2无人机俯仰力矩系数Cy2 (N·m)/rad空气阻力比例系数K0.0334 N/(m/s)2叶片散射系数σ1机身散射系数σd0.76
表2 无人机监视雷达参数
Tab.2 Parameters of the UAV surveillance radar

参数参数值射频频率5.5 GHz带宽20 MHz采样率80 MHz脉冲宽度20 μs脉冲重复间隔60 μs相干脉冲间隔192 ms
设无人机初始时在雷达坐标系(4000,0,100)m位置处于悬停状态,沿雷达坐标系X轴远离雷达平飞,在0~5 s,5~10 s,10~15 s的俯仰角分别为10°,30°,20°。根据本文方法可以得到飞行过程中运动参数的变化如图4,相对应的旋翼转速的变化如图5。可以看到无人机的运动状态随俯仰角的不同呈现不同的变化。
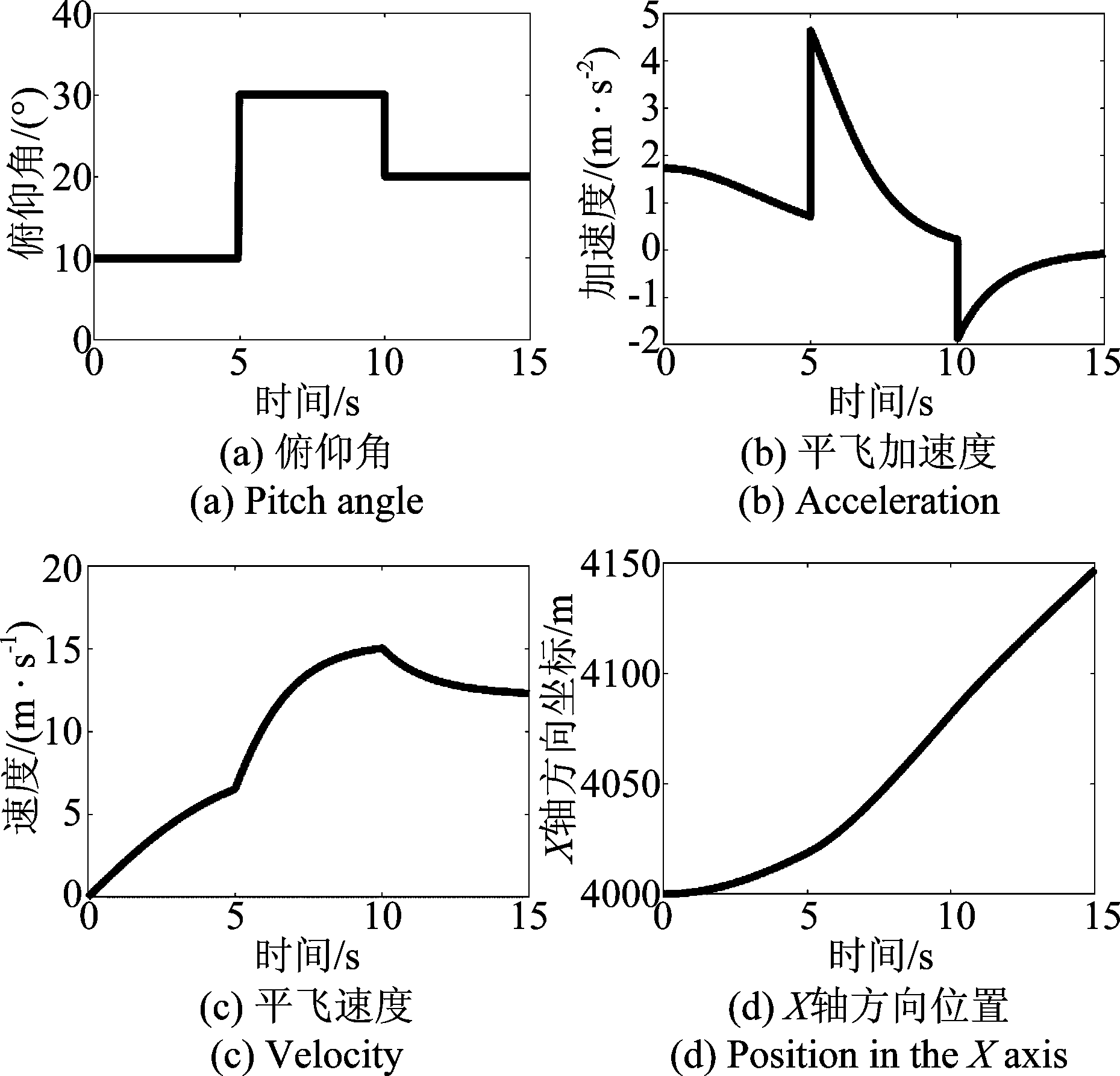
图4 平飞过程运动参数变化
Fig.4 Motion parameters variation during a level flight
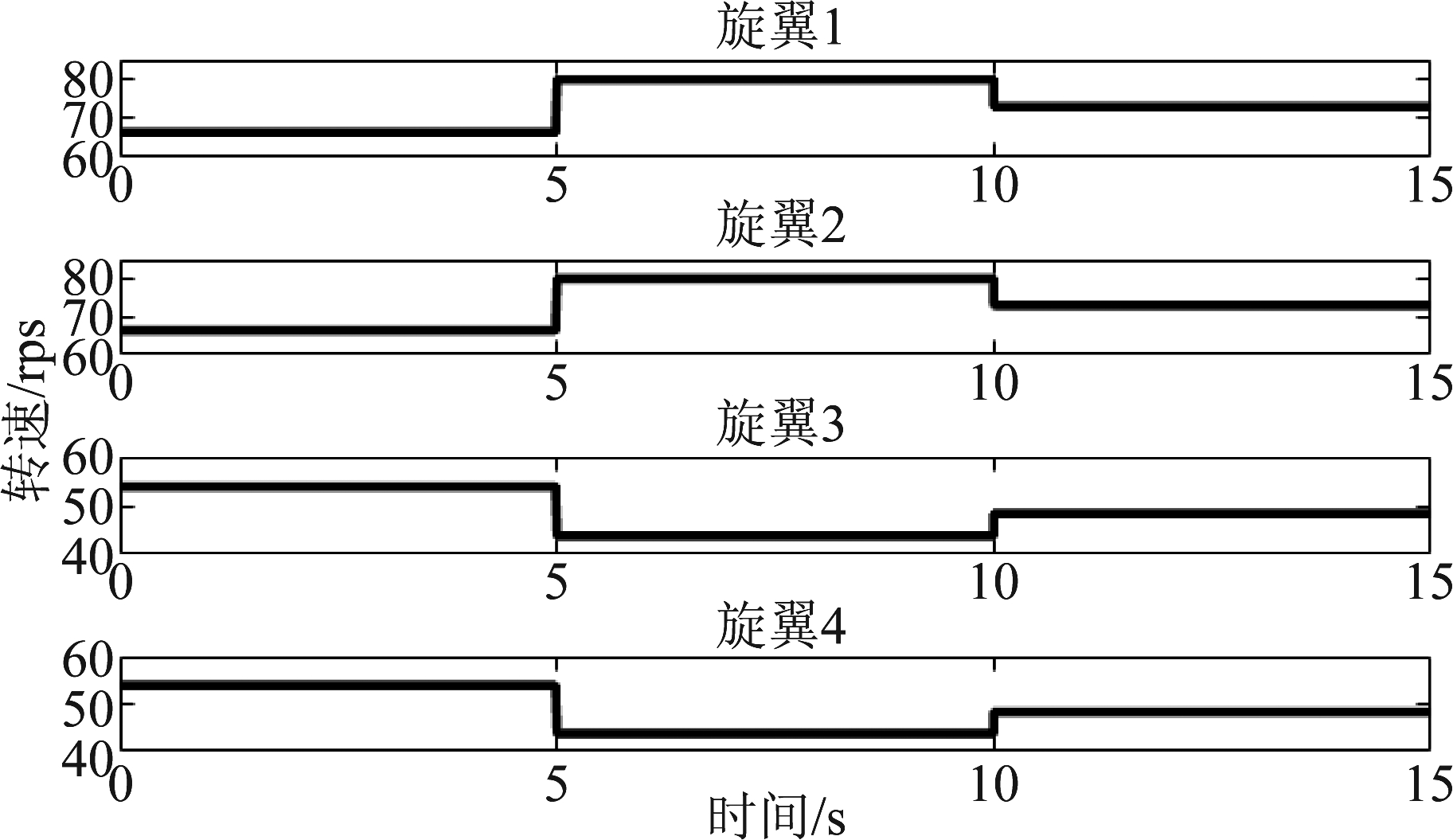
图5 平飞过程旋翼转速变化
Fig.5 The rotation speed variation of rotors during a level flight
根据平飞过程运动参数和旋翼转速的变化仿真雷达回波数据。目标除质心平动以外的目标内部的转动、振动等局部运动常称为微动[20]。不同类型的目标由于其内部局部运动的不同,在雷达回波中会产生不同的微多普勒特征。时频分析是分析目标微多普勒特征的一种重要技术手段。旋翼无人机由于其旋翼的转动,具有独特的微多普勒特征,利用时频分析获得目标的微多普勒特征已成为雷达对无人机进行检测与识别中区分无人机与其他易混淆目标的重要技术手段。消费级无人机往往尺寸很小,整个无人机在雷达回波中往往表现为一个点目标,无法直接在距离维分辨无人机不同的旋翼等不同的组成部分。然而,却有可能通过对无人机所在距离单元进行时频分析,通过目标微多普勒特征区分出不同旋翼对应的微多普勒特征。当无人机某个旋翼的叶片与雷达波束垂直时,会得到较宽的多普勒谱,在时频分析图中表现为一条较亮的竖线,这一竖线通常称为时频闪烁。由于不同旋翼的叶片与雷达波束垂直的时刻不同,因此旋翼无人机上不同叶片对应的时频闪烁的时刻也不同。因此,我们通过时频分析进一步分析仿真雷达回波的特征。
实验中无人机四个旋翼叶片的初始相位服从[-π,π]的均匀分布。分别分析第0 s、2.5 s、5 s、7.5 s、10 s、12.5 s附近的回波数据。时频分析采用短时傅里叶变换(STFT)方法,为进一步提高时间分辨力,还采用了重排谱图(Reassigned Spectrogram,RSP)[21]方法进行时频分析。其结果如图6。

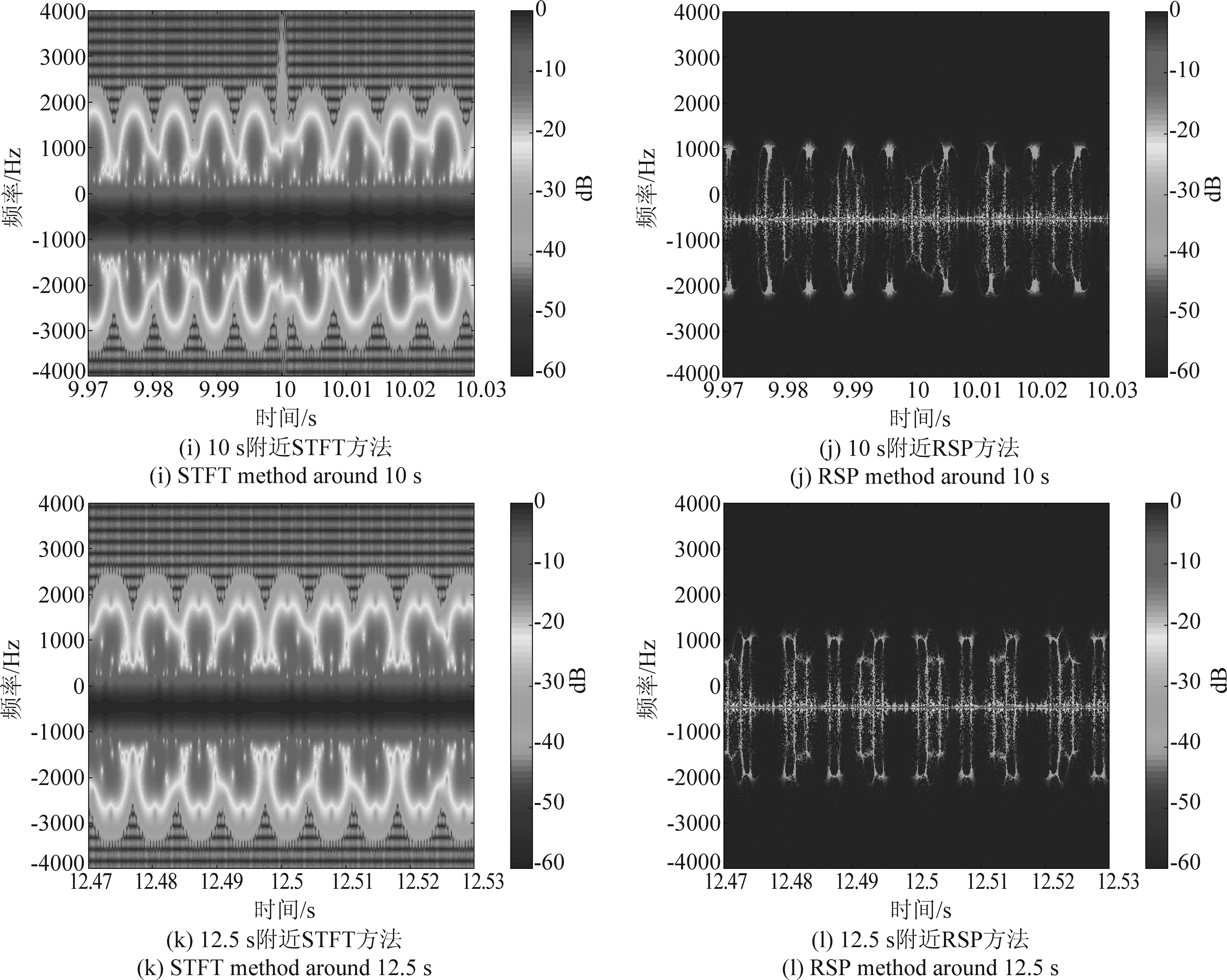
图6 平飞仿真雷达回波数据时频分析结果
Fig.6 Time frequency analysis results of simulated radar echoes in a level flight
时频分析结果中可以看出两组最大多普勒频率不同的闪烁(图中竖线),对应两组不同转速的旋翼,两组多普勒闪烁的重复周期也因为旋翼转速的不同有所差异。无人机在第5 s和第10 s运动状态发生改变,旋翼转速发生变化。在第5 s,旋翼1与旋翼2的转速由66.35 rps变化为79.96 rps,叶片叶尖对应的最大多普勒频率由1799 Hz变化为1888 Hz,旋翼3与旋翼4的转速由53.94 rps变化为43.78 rps,叶片叶尖对应的最大多普勒频率由1463 Hz变化为1034 Hz。在第10 s,旋翼1与旋翼2的转速由79.96 rps变化为72.97 rps,叶片叶尖对应的最大多普勒频率由1888 Hz变化为1879 Hz,旋翼3与旋翼4的转速由43.78 rps变化为48.35 rps,叶片叶尖对应的最大多普勒频率由1034 Hz变化为1245 Hz。在第5 s和第10 s的时频分析结果图中能够清晰地看到运动状态转换前后两组旋翼对应的最大多普勒频率的变化。
时频分析结果中较强的横线对应无人机机身的散射。不同时刻横线的位置不同,即相应的多普勒频率不同,对应于不同时刻机身不同的速度。
从实验结果可以看出,同样是平飞过程,但不同时间其时频分析结果表现出明显的差异。时频分析结果中间亮线的位置差异明显,呈周期性的多普勒闪烁也因为旋翼转速的差别存在明显差异。
从实验结果还可看出,无人机前飞的俯仰角与无人机的运动状态和旋翼转速密切相关。与前述实验一致,无人机在0时刻处于悬停状态,从0时刻开始以一个固定的俯仰角向前平飞。分析在第2.5 s时无人机的旋翼转速、机身速度、旋翼最大微多普勒频率与前飞俯仰角的关系,分析结果如图7所示。由于大疆精灵4 Pro无人机的最大前飞俯仰角为42°[14],因此仅分析俯仰角从0°到42°的变化情况。从图中可以看出平飞过程中各相关参数随俯仰角的变化情况。
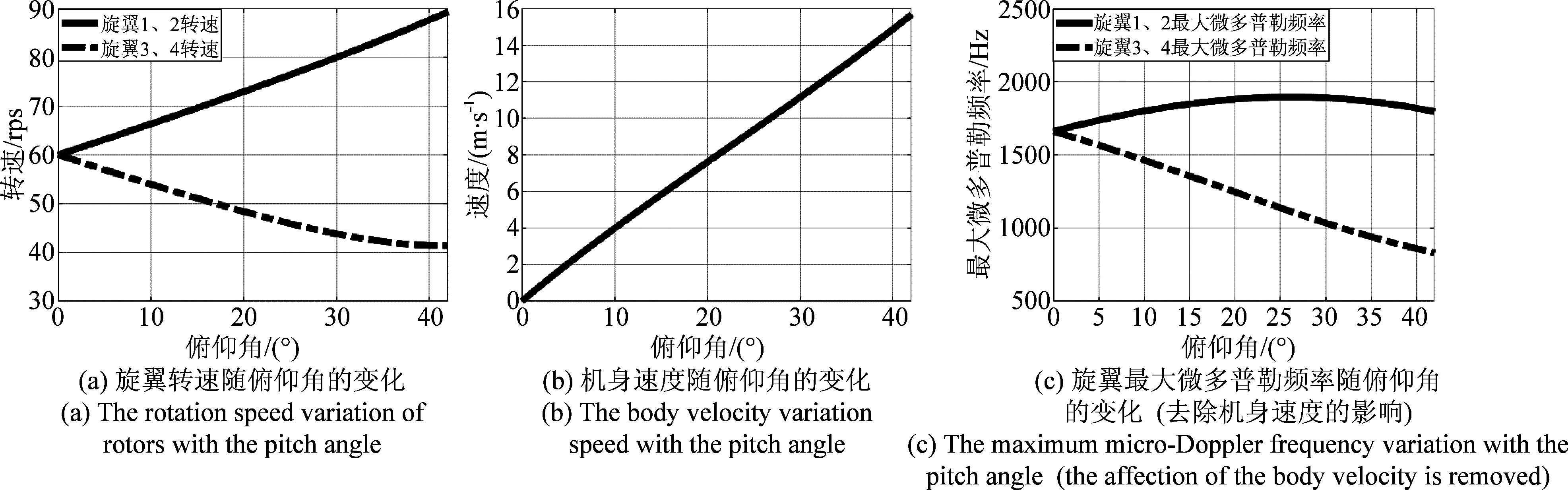
图7 平飞过程运动参数随平飞俯仰角的变化
Fig.7 Motion parameters variation with the pitch angle during a level flight
雷达的工作频率同样会对无人机的微多普勒特征产生影响,雷达工作频率主要影响无人机微多普勒特征的最大微多普勒频率。与前述实验一致,分析第2.5 s无人机在不同雷达工作频率下旋翼的最大微多普勒频率,其分析结果如图8所示。最大微多普勒频率随雷达工作频率的升高线性增大,但无人机旋翼的转速不同,线性增大的斜率不同。
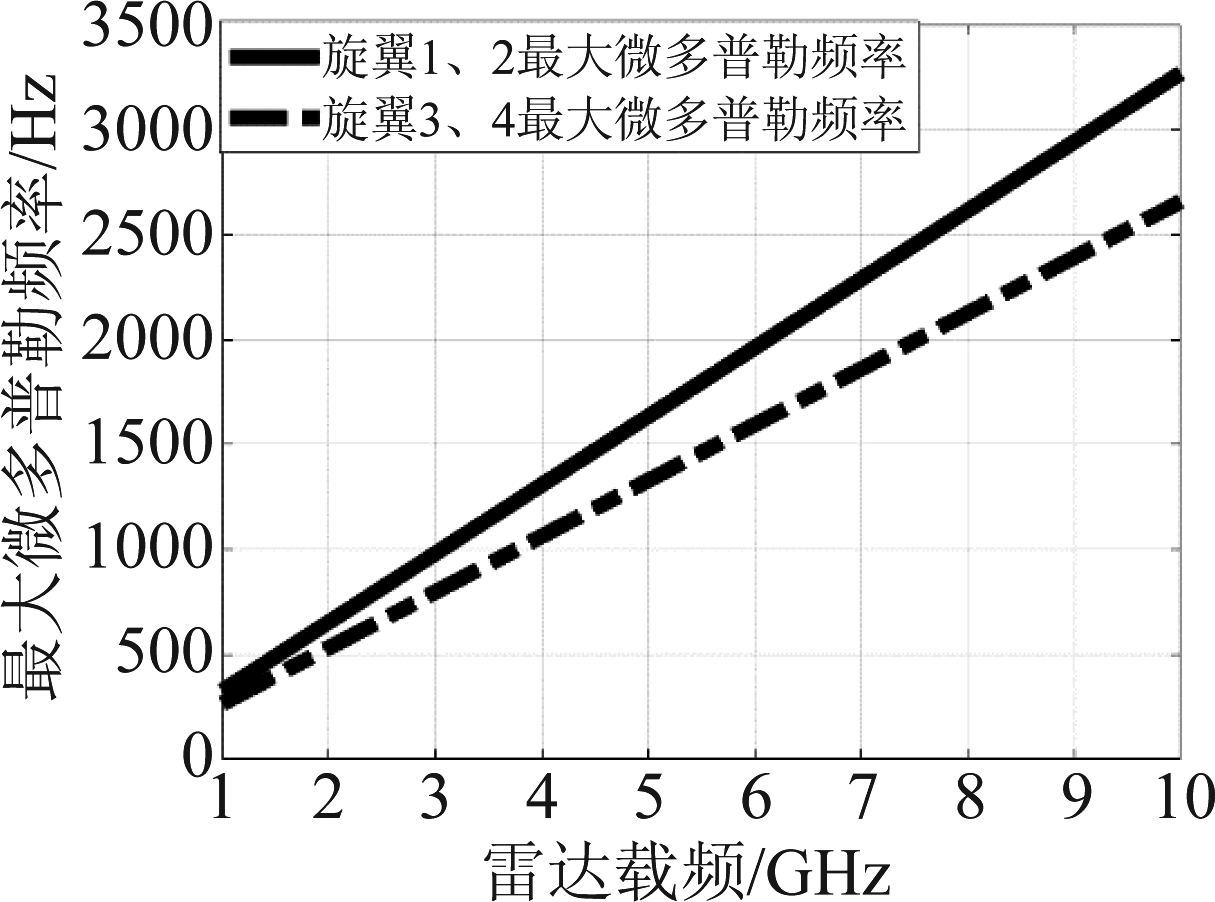
图8 旋翼最大微多普勒频率随雷达工作频率的变化(去除机身速度的影响)
Fig.8 The maximum micro-Doppler frequency variation with the radar working frequency (the affection of the body velocity is removed)
设无人机初始时在雷达坐标系(4000, 0, 100)m位置处于悬停状态,沿雷达坐标系X轴远离雷达以相对水平方向的仰角ξ=35°斜向上飞行。在0~5 s,5~10 s,10~15 s机身的俯仰角与平飞实验类似同样分别为10°,30°,20°。其第5 s、7.5 s附近回波数据时频分析的结果如图9。
从实验结果可以看出,斜飞的时频分析结果与平飞类似,但因为斜向上飞行时需要更大的旋翼拉力,所以斜飞的时频分析结果,与平飞相比多普勒闪烁的最大多普勒频率更大,重复周期更短。在第5 s,旋翼1与旋翼2的转速由70.12 rps变化为96.01 rps,叶片叶尖对应的最大多普勒频率由1901 Hz变化为2263 Hz,旋翼3与旋翼4的转速由58.51 rps变化为68.83 rps,叶片叶尖对应的最大多普勒频率由1586 Hz变化为1622 Hz。在第7.5 s,虽然叶片转速与第5 s无人机运动状态变化后相同,但由于无人机相对雷达的俯仰角发生了一定变化,因此叶片叶尖对应的两组最大多普勒频率略有变化变为2257 Hz、1618 Hz。
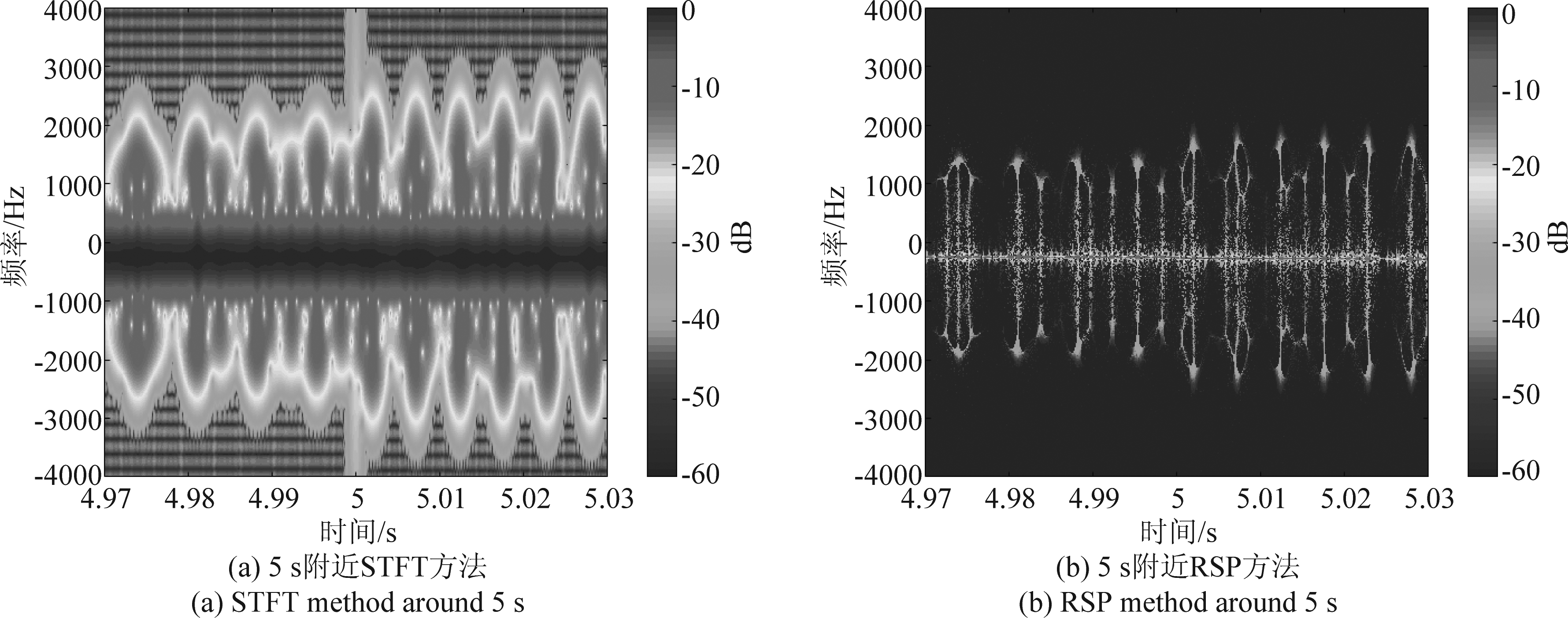
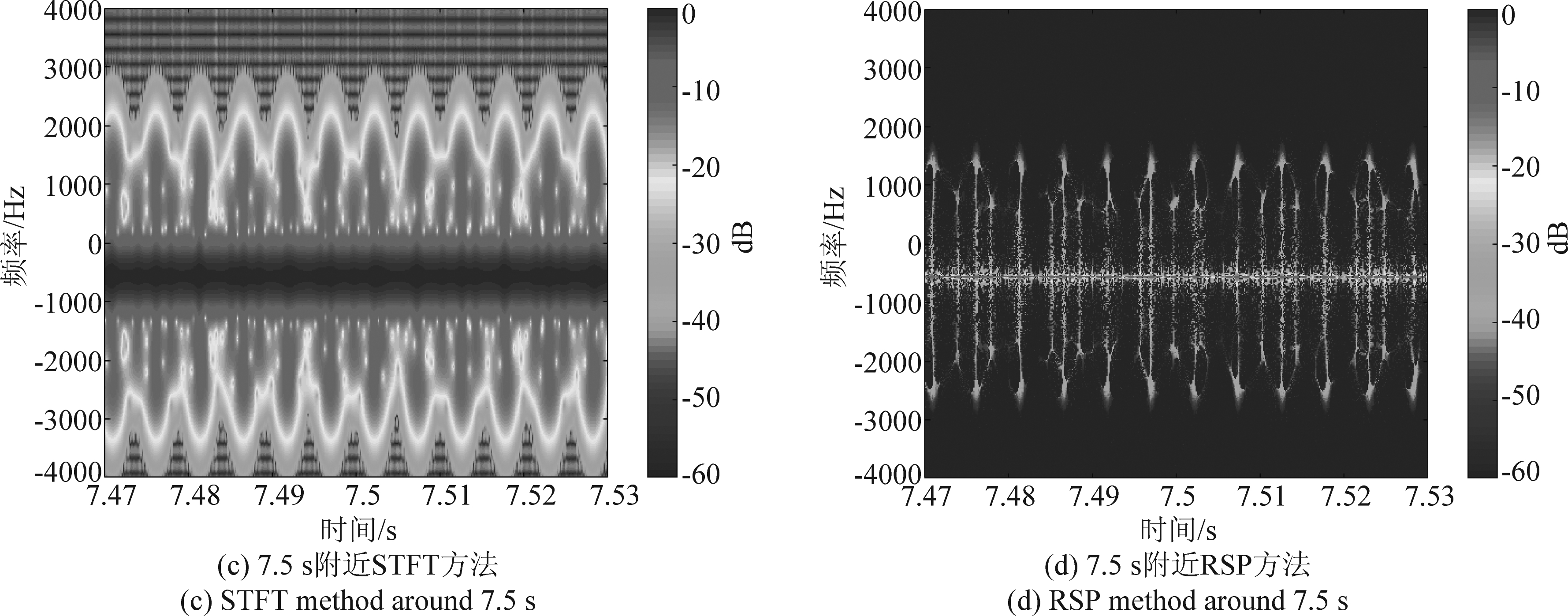
图9 斜飞仿真雷达回波数据时频分析结果
Fig.9 Time frequency analysis results of simulated radar echoes in an oblique flight
四旋翼无人机的运动状态与各旋翼的转速密切相关,本文给出的利用飞控特征的四旋翼无人机雷达回波仿真方法能够有效体现无人机机身速度、倾角等运动状态与各旋翼转速的相关性。旋翼无人机雷达回波的时频分析结果能够体现机身速度和旋翼转速相关联的微多普勒特征。无人机飞行过程中,不同的飞行状态可能造成其微多普勒特征产生显著差异。即使是单一的向前平飞运动,也会因为无人机操控的原因,使无人机的运动状态和微多普勒特征产生显著差异。对于无人机运动状态变化的情况,其雷达回波仿真有必要利用机身速度与各旋翼转速的相关性将二者联合考虑。
[1] CHEN V. The micro-Doppler effect in radar[M]. Norwood, MA, USA: Artech House, 2011: 92-109.
[2] 何炜琨, 孙鹏涛, 刘昂. 风轮机叶片电磁散射特性的占比分析与解析模型的建立[J]. 信号处理, 2020, 36(3): 337-344.
HE Weikun, SUN Pengtao, LIU Ang. The proportion analysis of the electromagnetic scattering characteristics and the construction of analytical model for wind turbine blades[J]. Journal of Signal Processing, 2020, 36(3): 337-344.(in Chinese)
[3] 何炜琨, 石玉洛, 郭双双, 等. 风轮机雷达散射特性仿真及微多普勒特征分析[J]. 电波科学学报, 2017, 32(1): 103-111.
HE Weikun, SHI Yuluo, GUO Shuangshuang, et al. Simulation on wind turbine radar scattering characteristics and its micro-Doppler analysis[J]. Chinese Journal of Radio Science, 2017, 32(1): 103-111.(in Chinese)
[4] ROBERT M, BEAUCHAMP, CHANDRASEKAR V. Characterization and modeling of the wind turbine radar signature using turbine state telemetry[J]. IEEE Transactions on Geoscience and Remote Sensing, 2017, 55(9): 5134-5147.
[5] 马娇, 董勇伟, 李原, 等. 多旋翼无人机微多普勒特性分析与特征提取[J]. 中国科学院研究生院学报, 2019, 36(2): 235-243.
MA Jiao, DONG Yongwei, LI Yuan, et al. Multi-rotor UAV’s micro-Doppler characteristic analysis and feature extraction[J]. Journal of University of Chinese Academy of Sciences, 2019, 36(2): 235-243.(in Chinese)
[6] MARK A. Micro-Doppler signal decomposition of small commercial drones[C]∥2017 IEEE Radar Conference. Seattle: WA, 2017: 0425-0429.
[7] CAI Yefeng, KRASNOV O, YAROVOY A. Simulation of radar micro-Doppler patterns for multi-propeller drones[C]∥2019 International Radar Conference. Toulon: France, 2019: 1-5.
[8] 王宝帅. 基于微多普勒效应的空中飞机目标分类研究[D]. 西安: 西安电子科技大学, 2015.
WANG Baoshuai. Study on classification of airplane targets based on micro-Doppler effect[D]. Xi’an: Xidian University, 2015.(in Chinese)
[9] 宋晨, 周良将, 吴一戎, 等. 基于自相关-倒谱联合分析的无人机旋翼转动频率估计方法[J]. 电子与信息学报, 2019, 41(2): 255-261.
SONG Chen, ZHOU Liangjiang, WU Yirong, et al. An estimation method of rotation frequency of unmanned aerial vehicle based on auto-correlation and cepstrum[J]. Journal of Electronics and Information Technology, 2019, 41(2): 255-261.(in Chinese)
[10] 卜子容. 基于微多普勒特性的无人机目标检测与参数估计方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2019.
BU Zirong. Research on target detection and parameter estimation of UAV based on micro-Doppler signatures[D]. Harbin: Harbin Institute of Technology, 2019.(in Chinese)
[11] SHRÖDER A, AULENBACHER U, RENKER M, et al. Numerical RCS and micro-Doppler investigations of a consumer UAV[C]∥Society of Photo-Optical Instrumentation Engineers Conference. Series, 2016.
[12] PETER J, SHRÖDER A, RENKER M, et al. Comparisons between simulated and measured x-band signatures of quad-, hexa-and octocopters[C]∥2018 15th European Radar Conference. Madrid, 2018: 325-328.
[13] 全权. 多旋翼飞行器设计与控制[M]. 北京: 电子工业出版社, 2018: 6-9.
QUAN Quan. Introduction to multicopter design and control[M]. Beijing: Publishing House of Electronics Industry, 2018: 6-9.(in Chinese)
[14] 大疆创新公司. Phanton4 pro/pro+用户手册[EB/OL]. https:∥dl.djicdn.com/downloads/phantom_4_pro/20171017/Phantom_4_Pro_Pro_Plus_User_Manual-CN. pdf, (2017-10)[2020-08].
DJI Innovation. Phanton4 pro/pro+user manual[EB/OL]. https:∥dl.djicdn.com/downloads/phantom_4_pro/20171017/Phantom_4_Pro_Pro_Plus_User_Manual-CN. pdf, (2017-10)[2020-08].(in Chinese)
[15] 符长青. 多旋翼无人机技术基础[M]. 北京: 清华大学出版社, 2017: 236-237.
FU Changqing. Fundamentals of multi-rotor unmanned aerial vehicle[M]. Beijing: Tsinghua University Press, 2017: 236-237.(in Chinese)
[16] 魏丽文. 四旋翼飞行器控制系统设计[D]. 哈尔滨: 哈尔滨工业大学, 2010.
WEI Liwen. Design of four-rotor aircraft control system[D]. Harbin: Harbin Institute of Technology, 2010.(in Chinese)
[17] ORSAG M, BOGDAN S. Influence of forward and descent flight on quadrotor dynamics[M]. Recent Advances in Aircraft Technology, 2012: 141-156.
[18] 张洪涛. 四旋翼微型飞行器位姿及控制策略的研究[D]. 哈尔滨: 哈尔滨工业大学, 2014.
ZHANG Hongtao. Study on pose and control strategy of quad-rotor micro air vehicles[D]. Harbin: Harbin Institute of Technology, 2014.(in Chinese)
[19] RITCHIE M, FIORANELLI F, GRIFFITHS H, et al. Monostatic and bistatic radar measurements of birds and micro-drone[C]∥2016 IEEE Radar Conference, Philadelphia, PA, 2016: 1-5.
[20] 庄钊文, 刘永祥, 黎湘. 目标微动特性研究进展[J]. 电子学报, 2007, 35(3): 520-525.
ZHUANG Zhaowen, LIU Yongxiang, LI Xiang. The achievements of target characteristic with micro-motion[J]. Acta Electronica Sinica, 2007, 35(3): 520-525.(in Chinese)
[21] RAM S, LING H. Analysis of micro-Dopplers from human gait using reassigned joint time-frequency transform[J]. Electronics Letters, 2007, 43(23): 1309-1311.
王晓亮 男, 1982年生, 甘肃兰州人。中国民航大学天津市智能信号与图像处理重点实验室, 副教授, 博士, 主要研究方向为雷达信号处理、图像处理与识别。
E-mail: wxl_ee@126.com
王承祥 男, 1995年生, 山东菏泽人。中国民航大学天津市智能信号与图像处理重点实验室, 硕士研究生, 主要研究方向为旋翼无人机雷达回波建模。
E-mail: 1440950490@qq.com
何炜琨 女, 1977年生, 黑龙江龙江人。中国民航大学天津市智能信号与图像处理重点实验室, 教授, 博士, 主要研究方向为雷达信号处理, 风电场杂波抑制。
E-mail: hwkcauc@126.com