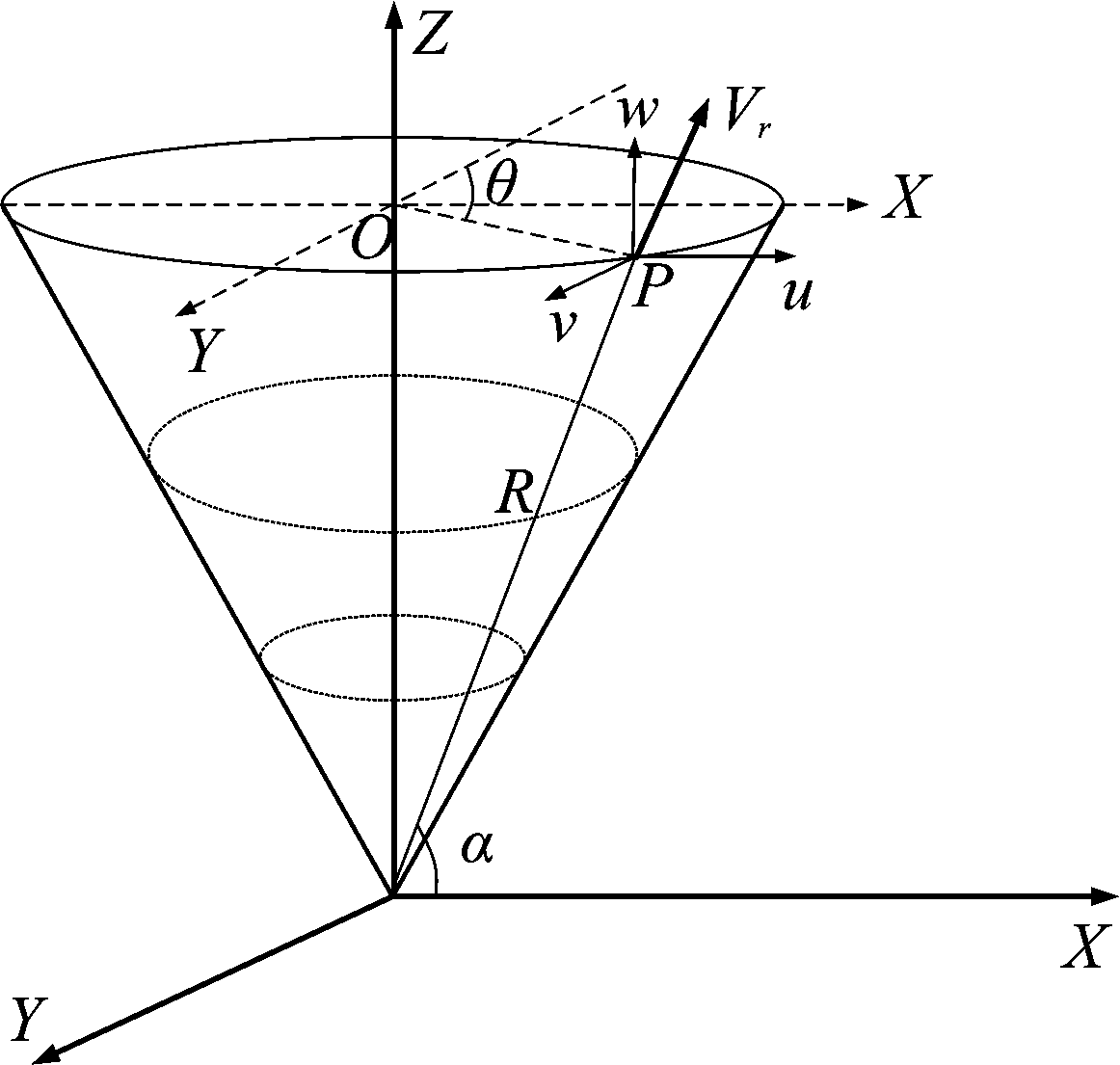
图1 传统VAD技术几何关系
Fig.1 The geometry of traditional VAD method
Reference format: HU Jiaqi, DONG Xichao, HU Cheng. Research on Nonlinear Wind Field Retrieval Method Based on Modified VAD Analysis[J]. Journal of Signal Processing, 2021, 37(2): 284-291. DOI: 10.16798/j.issn.1003- 0530.2021.02.014.
对流风暴的新生和发展演变与三维风场存在密切联系,三维风场可以指示风暴发生前环境的辐合、形变、风切变等动力特征,一定程度上决定了风暴及其所产生的强对流天气类型。因此,如何获取高时空分辨率的三维风场,来研究其精细化特征,对于中小尺度大气信息和台风、龙卷等强对流天气过程的临近预报、预警就显得尤为重要。多普勒天气雷达可利用多普勒效应获取径向多普勒速度资料,及时地反映风场信息。
一般来说三维风场分量的反演需要三部或三部以上的雷达通过合理的布局同时对探测区域进行测量,然而采用多部雷达探测气象目标时,不能保证对空间同一个点同时进行采样,严重影响反演的准确性,对于快速发展的强对流天气尤为突出,且雷达造价昂贵,因此通常不采用多部雷达来反演三维风场。为了克服这一困难,早在1968年Atlas等人[1]提出了采用多基地多普勒雷达探测大气三维结构,后续又发展了多基地多普勒雷达网络,并进行了大气三维风场的反演[2];国内吴彬等人[3]提出了基于三维变分的双基地雷达的风场反演系统,验证了双基地多普勒雷达反演风场的可行性。该系统的缺点是被动接收天线对旁瓣效应和二次回波过于敏感,导致反演的风场较常规雷达反演的误差要大。
速度方位显示(VAD)技术是目前应用最广泛的使用单部多普勒雷达反演三维风场的方法。VAD技术最早是在1961年由Lhermitte和Atlas[4]提出,假设水平风场呈空间均匀分布,利用雷达波束以某一固定仰角实现360°的全方位圆周扫描,获得等方位间隔的径向多普勒速度资料,反演出水平面上的平均风向风速;后来Browning等人[5]在此基础上,假设水平风场呈空间线性分布,进一步反演出水平风场的平均散度、形变等信息。目前,VAD技术也已直接应用于机载多普勒天气雷达,可准确高效地反演机下空域三维风场[6]。此外,1985年Srivastava和Matejka[7]提出了扩展VAD(EVAD)技术,解决了大仰角情况下反演误差大的问题; 2001年Tarary等[8]提出梯度VAD技术(GVAD),利用径向速度方位梯度反演风场信息,解决了传统VAD技术受速度模糊影响较大的问题,2018年李瑞义等人[9]进一步研究了GVAD技术在新一代天气雷达中的应用,该方法也应用于单多普勒激光雷达的风场探测中[10-11];2015年刘红艳等人[12]通过VAD技术进行了雷达回波的外推预报。上述VAD技术均是基于水平风场的空间线性分布假设,并利用等方位间隔的径向多普勒速度资料完成三维风场的反演。
然而,对于台风、龙卷等强对流天气系统,其内部风场空间分布复杂,线性风场假设不成立,导致基于线性风场分布假设的VAD技术反演性能下降。例如,1992年D.Caya等人对非线性风场的VAD技术进行了研究讨论,指出对于某些线性假设不成立的风场,利用VAD技术进行反演会得出与实际风场情况完全不同的结果[13];国内万蓉等人对风场的非线性程度进行了估计,并从非线性风场中提取风场信息[14]。此外,对于机动平台,如临近空间飞艇,平台自身的运动速度会对风场反演造成影响,且由于平台抖动等外部因素导致数据缺测,或出现数据异常点需要剔除,无法保证获取等方位间隔的均匀采样,也会严重影响三维风场的反演精度。
因此,本文提出了一种基于修正VAD技术的非线性风场三维反演方法,通过建立机动平台下视圆锥扫描几何关系以及复杂风场的非线性空间分布模型,利用全方位非均匀采样的径向多普勒速度数据,实现对复杂三维风场的精确反演。其中,非线性风场假设更能表示真实的复杂风场结构,利用非均匀采样的径向多普勒速度进行反演风场的方法更适用于平台抖动、数据出现异常点等外部扰动条件存在时的情况。因此本文提出的修正的VAD技术相对于要求线性风场假设以及等方位间隔均匀采样的传统VAD技术,具有更好的反演效果。
传统地基雷达VAD技术利用雷达在某一固定仰角上做360°的全方位圆周扫描所获得的不同方位上的Vr来求得扫描区域的风场特征量,其几何关系如图1所示。
图1 传统VAD技术几何关系
Fig.1 The geometry of traditional VAD method
建立如图1所示的坐标系,X轴指向东,Y轴指向北,Z轴向上。Vr为径向多普勒速度,θ为方位角, α为仰角,R为雷达与目标之间的径向距离。则径向速度与三维速度分量的关系为:
Vr(θ)=νcos θcos α+usin θcos α+wsin α
(1)
其中u、ν和w分别为X、Y和Z方向风场分量。
假定风场是线性的且垂直风场为常量,则将u,ν在扫描中心点O处一阶泰勒展开:
u=u0+ux·x+uy·y
ν=ν0+νx·x+νy·y
(2)
根据坐标转换关系:
x=Rcos αsin θ
y=Rcos αcos θ
z=Rsin α
(3)
将(3)代入(2)再代入(1),即可得到径向多普勒速度Vr随方位角θ变化的傅里叶展开形式:
Vr(θ)=a0+a1cos θ+a2sin θ+a3cos 2θ+a4sin 2θ
(4)
其中:
a1=ν0cos α
a2=u0cos α
(5)
对于实际观测资料,若雷达按等间隔方位角测量一个Vrk(θk)的方式进行全方位扫描,扫描一周后有M个Vrk(θk)的值。对于均匀分布的观测值,傅里叶系数可由下式确定[5]:
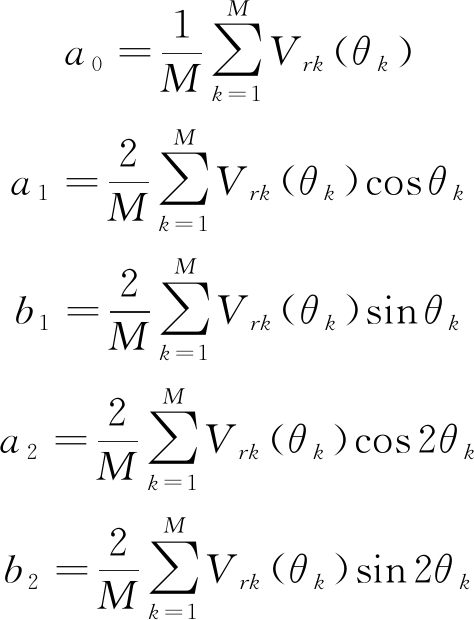
(6)
因此,由(5)和(6)即可得到水平平均风速的表达式:
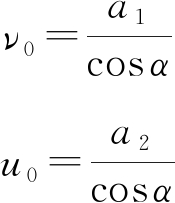
(7)
在飞机、飞艇等机动平台上搭载多普勒雷达,对台风等强对流天气进行连续观测和持续跟踪,获取目标内部气象参数,实现对强对流天气的预警与预报。然而,强对流天气系统的内部风场空间分布复杂,传统VAD技术中线性风场假设不成立;此外,机动平台自身的运动速度会对风场反演造成影响,且平台抖动等外部因素会导致数据缺测,或出现数据异常点需要剔除,无法保证获取等方位间隔的均匀采样。因此,需要针对这两个问题对传统VAD技术进行修正。
如图2为机动平台下视圆锥扫描几何关系和三维坐标系,雷达波束以某一固定下视角做360°的全方位圆周扫描获得不同方位角上的径向多普勒速度,考虑平台的运动速度,可得到所述径向多普勒速度与三维风速之间的关系。
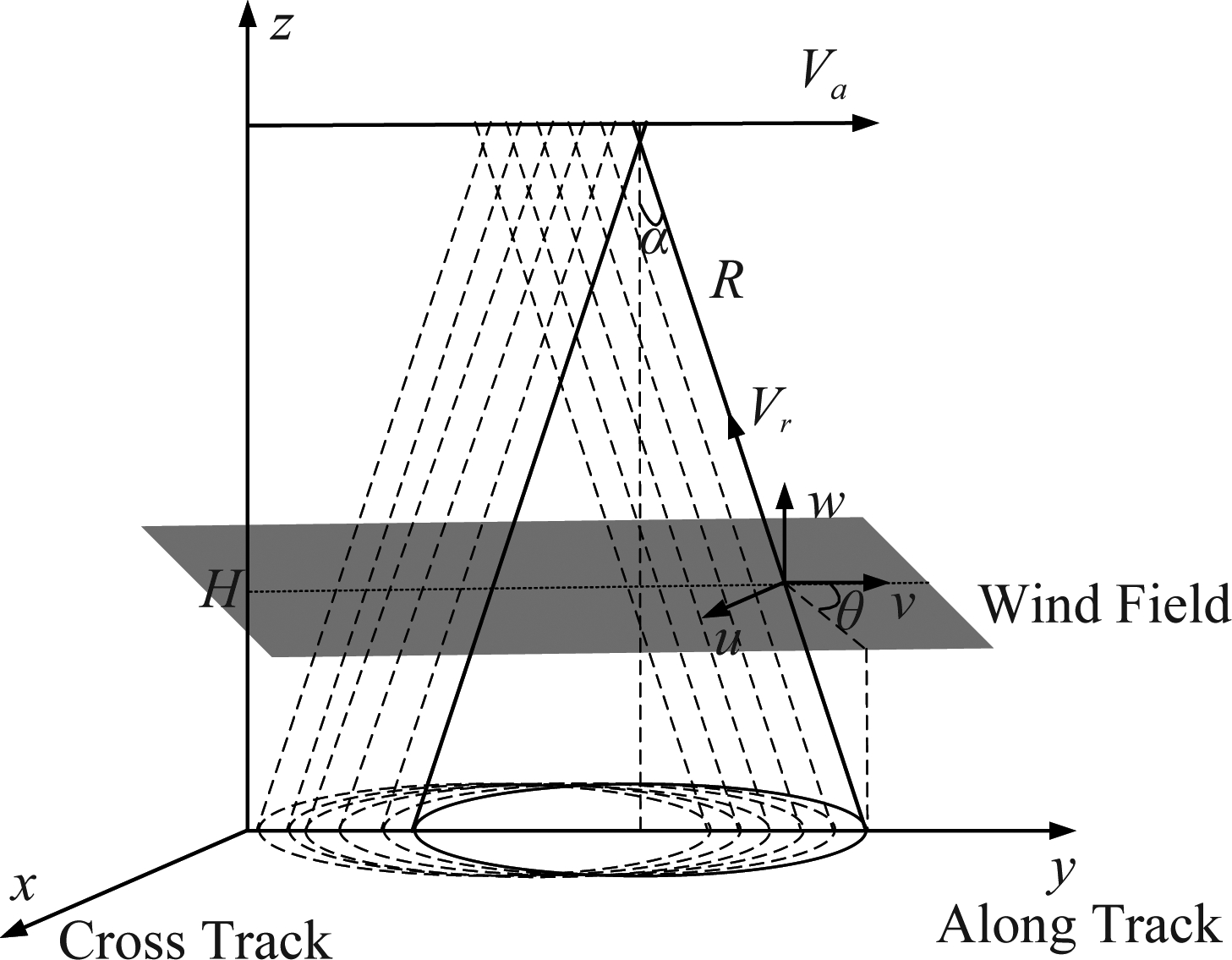
图2 修正VAD技术几何关系
Fig.2 The geometry of modified VAD method
机动平台以速度Va沿固定方向运动,以机动平台运动方向为y轴,交轨方向为x轴,垂直地面方向为z轴,建立三维坐标系,三轴与径向距离的关系如式(8)所示,其中α为下视角,θ为方位角,R为径向距离,T为波束扫描周期。
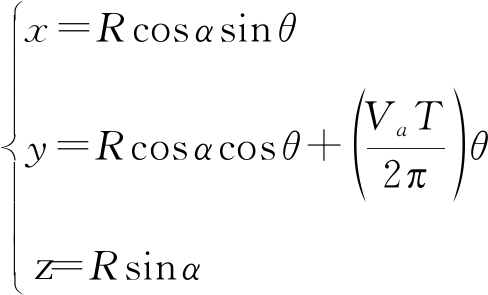
(8)
雷达波束以固定下视角α进行下视圆锥扫描,获取任意方位角θ方向上的径向多普勒速度Vr(θ);通过下视角α和方位角θ得到径向多普勒速度与三维风速之间的关系,如式(9)所示,其中下视角α在一个扫描周期内不变,u、ν和w分别为x、y和z方向的风场分量。
Vr(θ)=νcos θcos α+usin θcos α+wsin α
(9)
将径向多普勒速度写为多阶傅里叶谐波展开的形式为:
(10)
其中N是截断阶数,径向多普勒速度的谐波展开系数an和bn包含了风场信息,C是与平台运动有关的项。对于本文中的三维风场反演需求,只有包含水平平均风速的一阶谐波系数a1和b1是求解重点,而其他阶谐波系数的含义将在后续的研究中进行进一步分析,因此,如何求解a1和b1是接下来需要研究的问题。
当雷达以任意方位角获取多普勒速度,即全方位非均匀采样,且每个扫描周期采样M个数据时,可通过Thomas算法进行傅里叶系数的计算[15],在Thomas算法中,在进行傅里叶系数计算之前,利用经初步VAD分析得到的径向速度V′r(θj)与实际采样的径向速度Vr(θj)进行方差计算,即
若该方差超过了某个阈值,则作为奇异点或野点剔除,而其余的非奇异点用于傅里叶系数的求解,而这些径向速度采样值所在的采样范围将决定了是否能够准确求解傅里叶系数,并对风场反演产生影响。万蓉等人利用山东省滨州市气象局S波段全相干气象雷达的非全方位采样资料,对Thomas算法的适用采样范围进行了分析,他们的分析资料表明,利用Thomas算法进行非均匀采样处理时,要求方位向数据范围在275°以上[16]。此外,天线扫描直径也会影响风场反演的精度,一般情况下天线扫描直径不超过30 km,可以保证VAD技术的反演效果。
定义基函数f(θ):
f(θ)=[1 cos θ sin θ cos 2θ sin 2θ …]=
[f0 f1(θ) f2(θ) f3(θ) f4(θ) …]
(11)
则傅里叶系数an和bn可通过式(12)求解,a1和b1即包含了VAD圆心位置的平均水平风速信息,其中F-1(θ)为基函数f(θ)的协方差矩阵的逆矩阵,
[a0 a1 b1 a2 b2 …]T=F-1(θ)q
(12)
在水平风场呈非线性空间分布,且垂直风场呈空间均匀分布的假设下,将水平方向两个风场分量u,ν以平台位置(0,0)为中心进行二阶泰勒展开:
w=w0
(13)
将(8)代入(13)后再代入(9),与(10)对比即可得到傅里叶系数a1和b1如下:
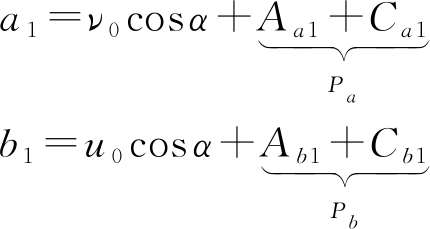
(14)
其中
和
是与径向探测距离R有关的项,
和
是与平台运动有关的项;Pa和Pb是风场非线性项;a1和b1可通过式(12)得到。
假设圆心位置处的平均风速u0和ν0、风场非线性项Pa和Pb不变,以雷达位置为圆心,在不改变探测高度的情况下改变下视角α,获取n组多普勒速度数据,并通过式(12)进行拟合,得到n组a1和b1,再采用如下所述的最小二乘法求解出u0和ν0;垂直速度w0可通过质量连续方程积分获得。
式(14)的矩阵形式可写为:
ya=ν0x+PaI=Xca
yb=u0x+PbI=Xcb
(15)
其中:
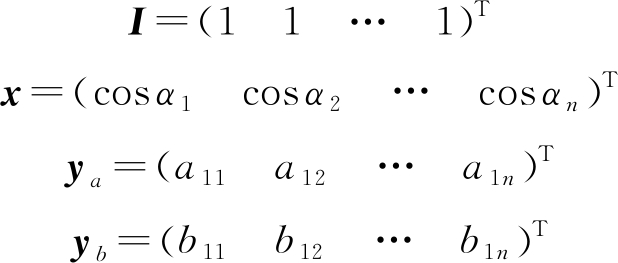
(16)
X=[x,I]
ca=(ν0,Pa)T
cb=(u0,Pb)T
(17)
则式(15)的最小二乘解为:
ca=(XTX)-1XTya=(ν0,Pa)T
cb=(XTX)-1XTyb=(u0,Pb)T
(18)
因此,修正VAD技术的计算流程可总结如下:
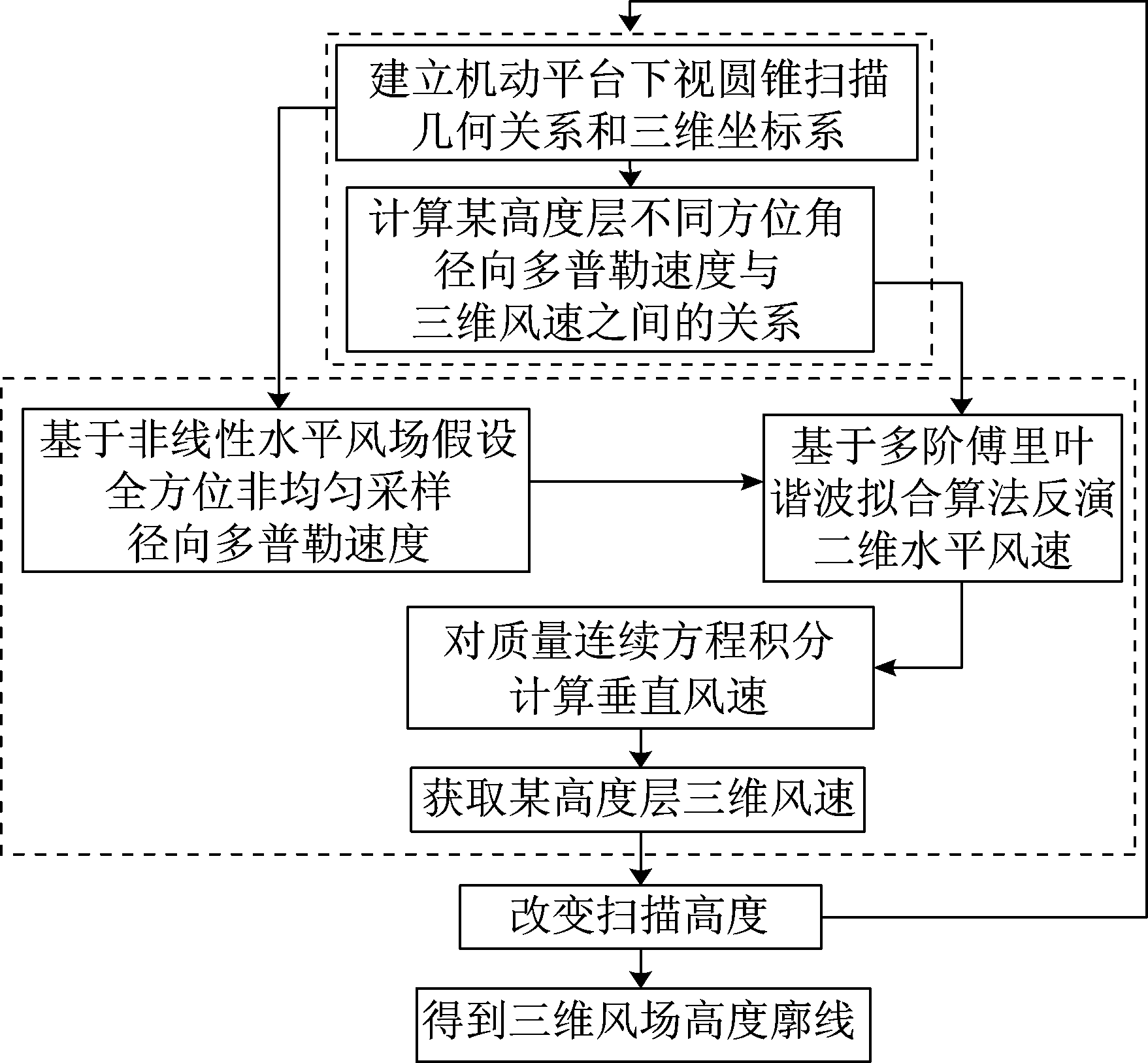
图3 修正VAD技术反演三维风场流程图
Fig.3 The flow chart of modified VAD technology
本节以临近空间飞艇平台为例,利用气象研究与预报模式(WRF)数值模拟仿真三维台风气象场景,获取台风降水的微物理特性,得到的台风眼处的三维风场数据,验证本文提出的修正VAD技术的三维风场反演效果。获得三维风场数据后,选取合适的天线扫描半径(一般不超过15 km),对在VAD圆上的速度值进行采样,并利用式(9)将三维风场投影到径向方向,作为VAD技术的输入,即径向多普勒速度采样数据。飞艇运动参数与台风数据信息如表1所示。
表1 飞艇运动参数与台风数据信息
Tab.1 Airship motion parameters and typhoon data information
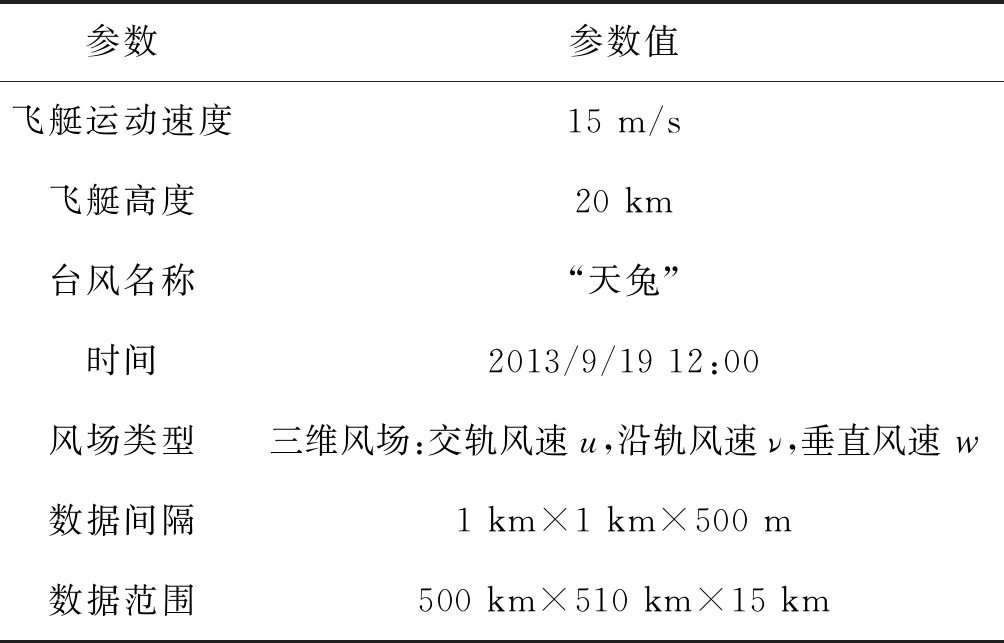
参数参数值飞艇运动速度15 m/s飞艇高度20 km台风名称“天兔”时间2013/9/19 12:00风场类型三维风场:交轨风速u,沿轨风速ν,垂直风速w数据间隔1 km×1 km×500 m数据范围500 km×510 km×15 km
对于每个VAD圆上的每个径向多普勒采样值都需要一次矩阵求逆的运算来得到基函数协方差矩阵的逆,用于后续的风场反演,此时矩阵求逆的病态问题是需要考虑的因素。矩阵病态问题可以通过调整VAD圆的半径来预防,对于求解结果中出现的少数奇异值,由于小场景内风场变化可认为是连续的,因此可利用中值滤波进行平滑处理。此外,径向速度采样值所在的采样范围也将决定是否能够准确求解傅里叶系数,因此,仿真中保证径向速度采样值所在的方位向数据采样范围在275°以上。
获取径向多普勒速度的采样数据后,利用图3所示的VAD技术流程进行三维风场的反演,并将反演结果与WRF数值模拟得到的仿真结果进行对比,即可对VAD技术的反演效果进行评估。利用WRF数值模拟得到的实际风场的沿轨风速ν、交轨风速u和垂直风速w以及利用传统VAD技术和修正VAD技术得到的沿轨风速ν0 、交轨风速u0和垂直风速w0随飞行方向变化的垂直截面分布图分别如图4、图5和图6所示。
从仿真结果可以看出,采用本文提出的修正VAD技术的三维风场反演结果更符合实际风场的分布,尤其是台风眼处等风场变化较大的位置,利用修正VAD反演效果的更好。
图7为利用传统VAD技术和修正VAD技术反演的沿轨风速ν0 和交轨风速u0的最小均方误差(RMSE)垂直廓线分布结果,可以看出,对于台风这种强对流天气,传统的基于线性风场假设的VAD方法反演误差较大,尤其是交轨分量u0,这一点也可以从图5和图6中看出;而本文中采用非线性风场假设和非均匀采样的修正VAD方法,与传统VAD方法相比具有更好的反演效果,最小均方误差RMSE一般情况下小于2 m/s。
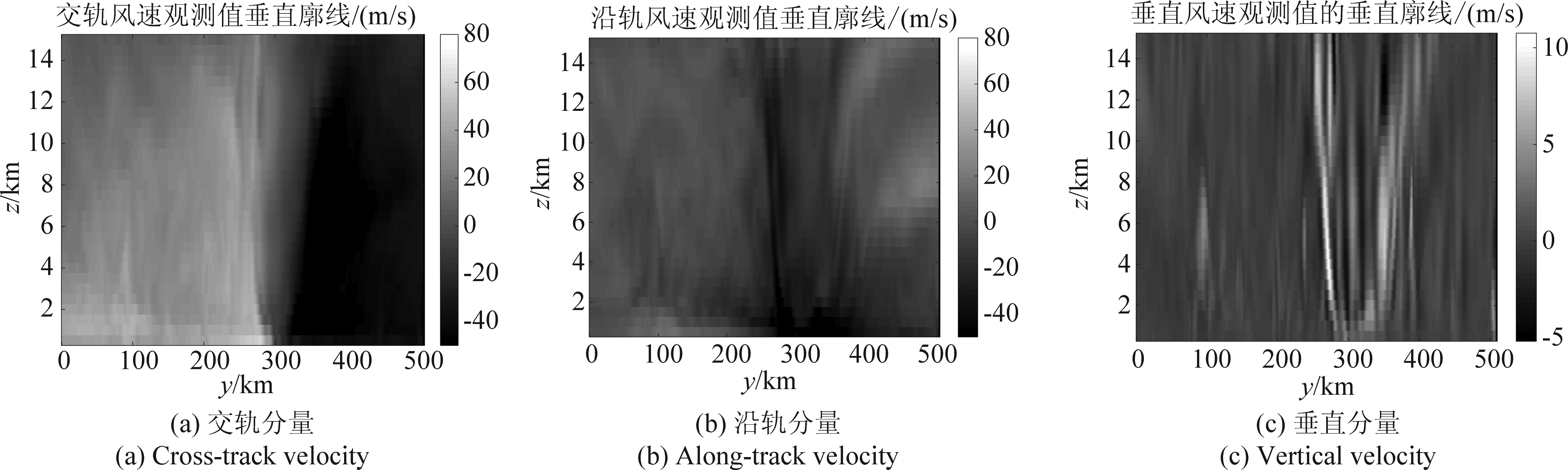
图4 实际三维风场垂直截面
Fig.4 The vertical profile of the actual three-dimensional wind field
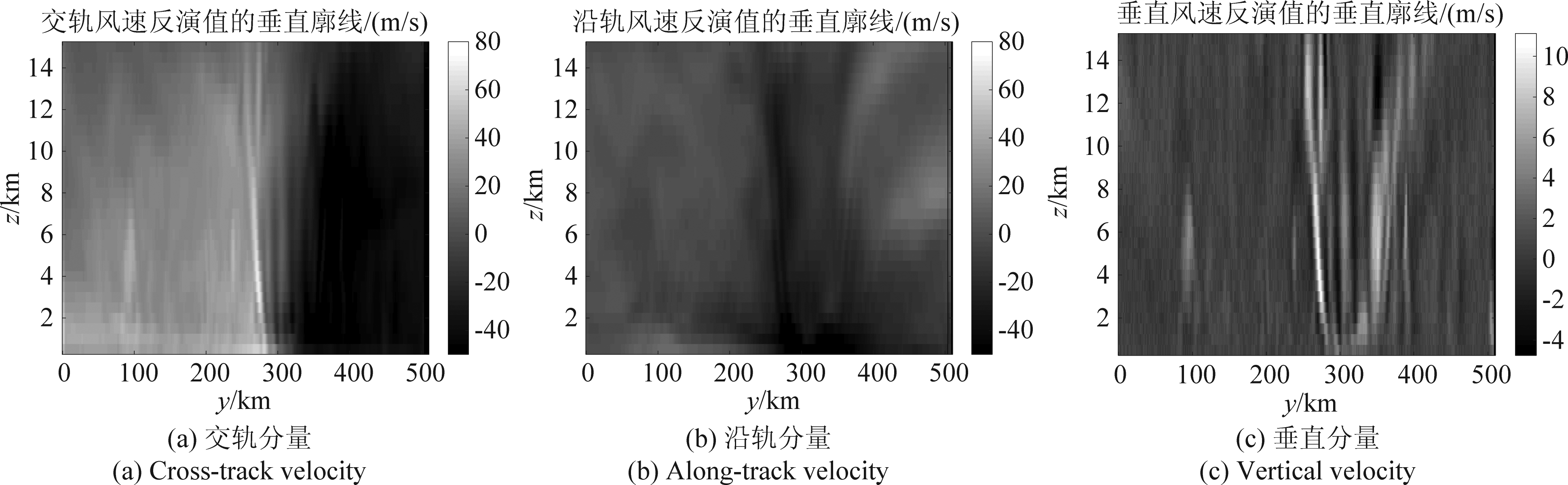
图5 传统VAD技术三维风场反演结果
Fig.5 The vertical profile of the three-dimensional wind field from traditional VAD method
图6 修正VAD技术三维风场反演结果
Fig.6 The vertical profile of the three-dimensional wind field from modified VAD method
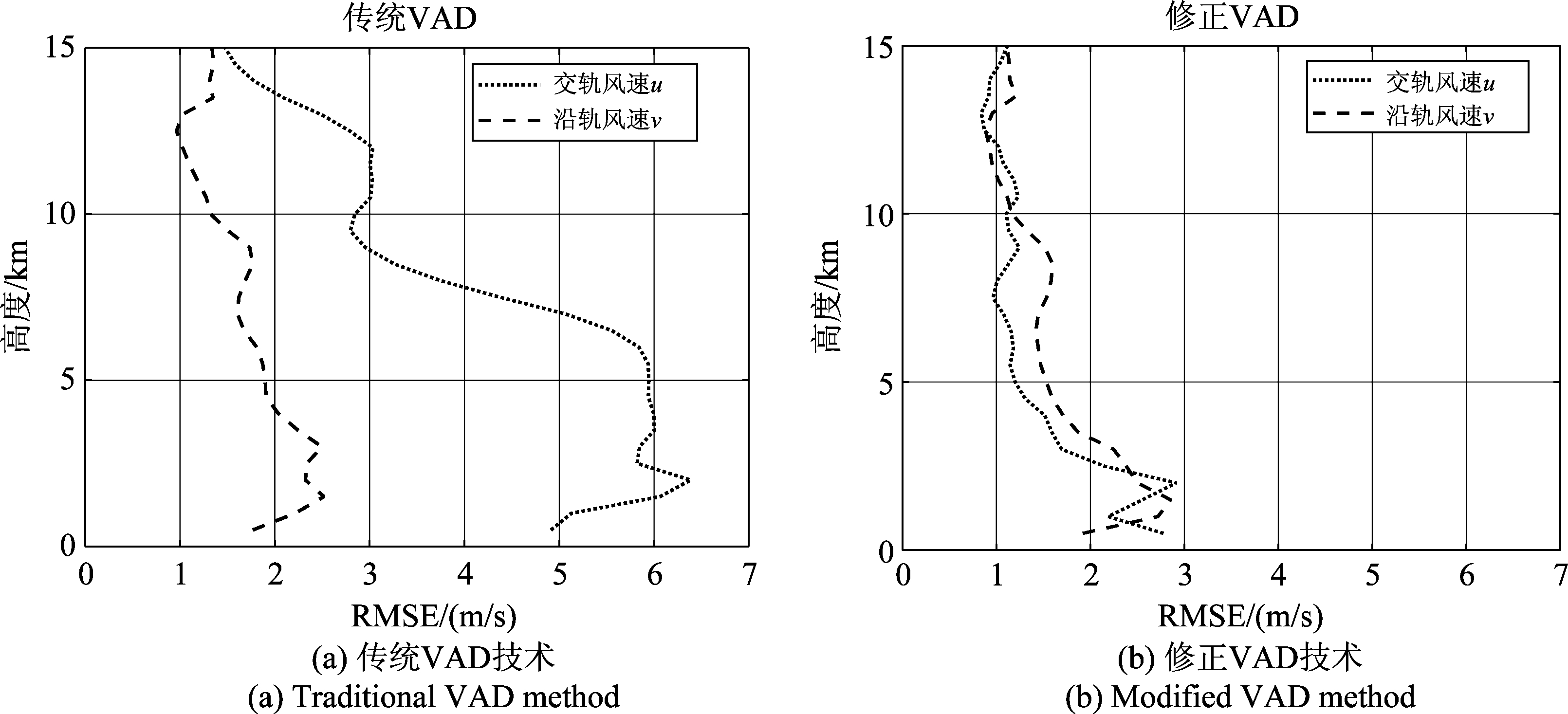
图7 沿轨风速和交轨风速的最小均方误差(RMSE)垂直廓线分布
Fig.7 The vertical profile of the RMSE of along-track and cross-track velocity
本文提出了一种基于非线性水平风场假设和非均匀采样的修正VAD技术的三维风场反演方法,建立了复杂风场的非线性水平空间分布模型用于表示真实的复杂风场结构,且利用全方位非均匀采样的径向多普勒速度数据反演风场的方法更适用于平台抖动、数据出现异常点等外部扰动条件存在时的情况。仿真表明,本文提出的修正VAD技术相对于要求线性风场假设以及等方位间隔均匀采样的传统VAD技术,具有更好的反演效果。
[1] ATLAS D, NAITO K, CARBONE R E. Bistatic Microwave Probing of a Refractively Perturbed Clear Atmosphere[J]. Journal of the Atmospheric Sciences, 2010, 25(2): 257-268.
[2] WURMAN J, HECKMAN S, BOCCIPPIO D. A Bistatic Multiple-Doppler Radar Network[J]. Journal of Applied Meteorology, 1993, 32(12): 1802-1814.
[3] 吴彬, 黄琳玲, 陈卫峰, 等. 双基地多普勒天气雷达三维变分风场反演及格点化研究[C]∥ 气象综合探测技术研讨会, 2011.
WU Bin, HUANG Linling, CHEN Weifeng, et al. Research on Retrieval and Grid Retrieval of Three-Dimensional Variational Wind Field of Bistatic Doppler Weather Radar[C]∥Comprehensive Meteorological Detection Technology Seminar, 2011.(in Chinese)
[4] LHERMITTE R M, ATLAS D. Precipitation motion by pulse Doppler[C]∥ Preprints Ninth Weather Radar Conference. Amer Meteor Soc, 1961: 218-223.
[5] BROWNING K A, WEXLER R. The determination of kinematic properties of a wind field using Doppler radar[J]. Applied Meteorology., 1968, 7(1): 105-113.
[6] LIN Tian, HEYMSFIELD G M, DIDLAKE A C, et al. Velocity-Azimuth Display Analysis of Doppler Velocity for HIWRAP[J]. Journal of Applied Meteorology and Climatology, 2015, 54(8): 150713095729000.
[7] MATEJKA T, SRIVASTAVA R C. An Improved Version of the Extended Velocity-Azimuth Display Analysis of Single-Doppler Radar Data[J]. Journal of Atmospheric and Oceanic Technology, 1991, 8(4): 453- 466.
[8] TABARY P, SCIALOM G, GERMANN U. Real-Time Retrieval of the Wind from Aliased Velocities Measured by Doppler Radars[J]. Journal of Atmospheric and Oceanic Technology, 2001, 18(6): 875- 882.
[9] 李瑞义, 杨洪平, 赵坤, 等. GVAD技术及其在新一代天气雷达中的应用[J]. 气象, 2018, 44(4): 511- 517.
LI Ruiyi, YANG Hongping, ZHAO Kun, et al. GVAD Technology and Its Application in CINRAD[J]. Meteorological Monthly, 2018, 44(4): 511-517.(in Chinese)
[10] 冯长中, 吴松华, 黄海广,等. 梯度下降VAD方法的单多普勒激光雷达风场探测技术[J]. 红外与激光工程, 2018, 47(11):58-66.
FENG Changzhong, WU Songhua, HUANG Haiguang, et al. The Single Doppler Laser Radar Wind Field Detection Technique Based on the Gradient Descent VAD Method[J]. Infrared and Laser Engineering, 2018, 47(11): 58- 66.(in Chinese)
[11] 王贵宁, 刘秉义, 冯长中,等. 相干测风激光雷达VAD风场反演的数据质量控制方法[J]. 红外与激光工程, 2018,47(2):147-154.
WANG Guining, LIU Bingyi, FENG Changzhong, et al. Data quality control method for VAD wind field retrieval based on coherent wind lidar[J]. Infrared and Laser Engineering, 2018, 47(2): 147-154.(in Chinese)
[12] 刘红艳, 魏鸣, 管理. 多普勒雷达风场资料在临近预报中的应用[J]. 大气科学学报, 2015, 38(4):483- 491.
LIU Hongyan, WEI Ming, GUAN Li. Application of Doppler radar radial velocity data to nowcasting[J]. Transactions of Atmospheric Sciences, 2015, 38(4): 483- 491.(in Chinese)
[13] CAYA, D. VAD analysis of no-linear wind fields[J]. Atmos. Oceanic Technol, 1992, 9.
[14] 万蓉, 汤达章, 张鹏,等. 非线性风场的VAD分析初探[J].气象科学,2003,23(3):314-324.
WAN Rong, TANG Dazhang, ZHANG Peng, et al. Preliminary Study on VAD Analysis of Nonlinear Wind Field[J]. Meteorological Science, 2003, 23(3): 314-324.(in Chinese)
[15] MATEJKA T, SRIVASTAVA R C. An Improved Version of the Extended Velocity-Azimuth Display Analysis of Single-Doppler Radar Data[J]. Journal of Atmospheric & Oceanic Technology, 1991, 8(4): 453- 466.
[16] WAN Rong, TANG Dazhang, ZHANG Peng, et al. Comparison and Application of Two VAD Algorithms[J]. Journal of Atmospheric Sciences, 2002, 25(5): 648- 655.
胡佳琪 女, 1995年生, 河南济源人。北京理工大学, 博士生, 主要研究方向为气象雷达回波信号处理及三维风场反演研究。
E-mail: katherinehu1995@foxmail.com
董锡超 男, 1986年生, 山东潍坊人。博士, 北京理工大学信息与电子学院副研究员, 博士生导师, 主要研究方向为新体制SAR系统分析与成像、气象雷达系统及信号处理。
E-mail: xcdong@bit.edu.cn
胡 程 男, 1981年生, 湖南岳阳人。博士, 北京理工大学信息与电子学院研究员, 博士生导师, 主要研究方向为新体制合成孔径雷达系统与信号处理、生物探测雷达系统与信息处理技术等。
E-mail: hucheng.bit@gmail.com