图1 距离门拖引干扰场景示意图
Fig.1 Schematic diagram of range gate pull-off jamming scene
Reference format: JIA Rui, ZHANG Tianxian, WANG Yuanhang, et al. An Intelligent Generation Method of Range Gate Pull-off (RGPO) Jamming Strategy[J]. Journal of Signal Processing, 2021, 37(2): 276-283. DOI: 10.16798/j.issn.1003- 0530.2021.02.013.
近年来,随着电子技术和军事智能化的发展,电子对抗在现代战争中占据了越来越重要的地位[1- 4]。距离门拖引干扰作为对雷达距离信息欺骗的一种有效技术手段,由于具有干扰功率低、灵活性强等优点,近年来已成为一大研究热点。文献[5]梳理了距离门拖引干扰的工作机理,分析了基于数字射频存储器延迟量化对干扰信号的影响。文献[6]推导了线性和抛物线性距离门拖引干扰信号的时域及频域解析表达式。文献[7]提出了一种双向假目标的距离门拖引干扰方法,该方法可以有效对抗雷达脉冲前沿跟踪和脉冲后沿跟踪技术。然而,上述文献对距离门拖引干扰的研究主要集中于干扰信号层面的波形设计和生成,拖引策略较为单一,其主要以匀速和匀加速拖引为主,远远没有充分挖掘拖引策略的效能。
在实际应用中,距离门拖引干扰分为捕获期、拖引期和关闭期[8]。拖引期并非一个探测(扫描)帧内拖引完成,而是多个探测帧共同作用的结果。在这种情况下,多帧拖引策略的联合优化对距离门拖引干扰的效果是至关重要的。众所周知,距离门拖引干扰效果通常严重依赖专家经验。但不准确的专家经验会造成干扰性能的下降甚至导致干扰失败。例如,拖引前期拖引速度过快,敌方雷达的跟踪系统可能无法及时响应,进而导致拖引干扰失败;拖引太慢则干扰方很容易被敌方火控雷达锁定,这也会致使拖引干扰失败。因此,一个优效的多帧联合拖引策略对于自卫干扰是必须的。然而,据本文作者所知,对距离门拖引干扰策略的多帧联合优化问题尚未被研究。
本文研究距离门拖引干扰的策略优化问题,首先,为了衡量距离门拖引干扰的效果,选择平均波门偏移距离作为目标函数,并介绍了问题研究背景及距离门拖引干扰的多帧优化模型;然后,为了解决目标函数解析表达式难以获取以及优化维度过高等问题,分别提出了结合奖励机制的蒙特卡洛目标函数拟合方法和基于粒子群算法的策略优化方法;最后,通过数值仿真的方式验证了所提算法的有效性。
距离门拖引干扰是干扰机通过发送虚假距离信息引导敌方雷达对干扰信号进行跟踪,从而保护真目标的一种技术手段。典型的距离门拖引干扰分为以下三步[9]:
(1)捕获期:干扰机收到雷达发射信号后,以最小的延迟时间转发一个干扰信号。通常要求干扰信号的幅度要大于目标雷达回波信号,且保持一段时间,目的是让干扰信号与目标回波信号同时作用在距离波门上。
(2)拖引期:当距离波门跟踪到干扰信号以后,干扰机每截获一个雷达照射信号,就逐步增加转发延迟时间,使距离波门随干扰信号移动而逐渐离开目标回波,直到距离波门偏离目标回波预定距离为止。
(3)关闭期:当干扰信号把距离波门从真目标上拖开足够的距离以后,干扰机关闭。这时,距离波门内既无干扰信号也没有目标回波信号,雷达转入搜索状态。
等雷达再次捕获到目标时,周期性重复执行以上三个步骤。
如图1所示,假设雷达工作在跟踪模式,干扰方为了摆脱雷达的跟踪而采用距离门拖引干扰。
图1 距离门拖引干扰场景示意图
Fig.1 Schematic diagram of range gate pull-off jamming scene
假设在时间T内拖引的总帧数为N,第i帧的干扰信号转发延时为
则第i帧的拖引距离Ri为
(1)
其中c表示光速,Δri为第i帧拖引增量,其定义为第i帧比第i-1帧多拖引的距离。记第i帧真目标的位置为
为直角坐标系中真目标的横坐标,y(i)为纵坐标,则第i帧形成的假目标位置
为
(2)
设第i帧r(i)与x方向夹角为θi,则假目标的横坐标位置
和纵坐标位置
可分别表示为
(3)
在现代复杂电磁环境下,跟踪方为了解决杂波、虚假目标对单个目标跟踪的影响问题,一般情况下只对落入波门内的信号进行处理。雷达跟踪的为波门内信号的合成质心位置。则在不考虑杂波的情况下跟踪方将可能出现四类状态:真假目标同时处于一个距离波门内、假目标在距离波门内,真目标在距离波门外、真目标在距离波门内,假目标在距离波门外以及真假目标都在波门外。四种不同的状态下对应的量测值各不相同,用数学公式表示为
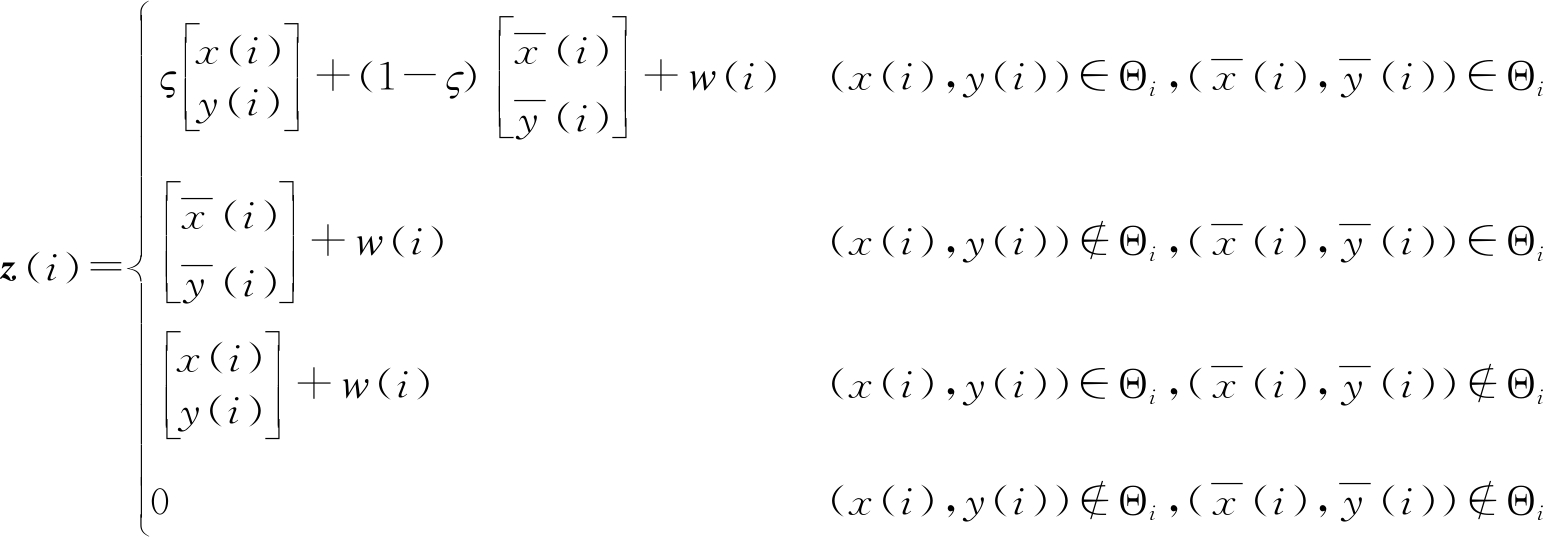
(4)
其中ς是一个与干信比J/S有关的系数,ς=1/(1+J/S),Θi属于第i帧预测的波门范围,其由第i帧距离波门中心的预测值、波门类型以及波门宽度共同决定。
第i帧距离波门中心的预测值可由前i-1帧递推求得。不失一般性,假设跟踪方采用线性卡尔曼滤波器[10]进行目标跟踪,则求解第i帧距离波门中心预测值的过程如下:
设第i-1帧距离波门中心x方向的一步预测为
第i-1帧距离波门中心y方向的一步预测为
为
的一阶导,
为
的一阶导,则第i-1帧距离波门中心的一步预测位置
(5)
第i-1帧距离波门状态的一步预测
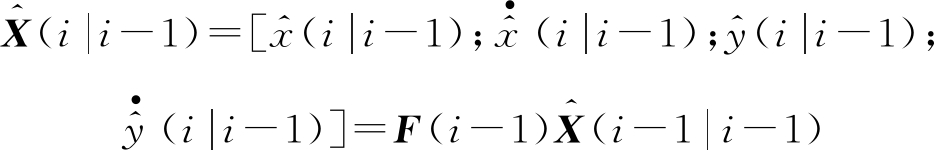
(6)
其中,F(i-1)为第i-1帧的目标运动状态转移矩阵,记第i帧和第i-1帧的重访时间间隔为Ti,则F(i-1)可表示为
(7)
为第i-1帧的波门状态估计,其可以表示为
(8)
其中v(i-1)为第i-1帧的新息,即跟踪方实际量测与对目标量测的预测值之差,可以表示为:
(9)
其中H(i-1)代表量测矩阵
(10)
式(8)中K(i-1)为第i-1帧卡尔曼滤波器增益
K(i-1)=P(i-1|i-2)H(i-1)TS-1(i-1)
(11)
其中,P(i-1|i-2)是第i-1帧状态估计误差协方差矩阵的预测值,其计算公式为:
P(i-1|i-2)=F(i-2)P(i-2|i-2)
F(i-2)T+Γ(i-2)q(i-2)Γ′(i-2)
(12)
其中,P(i-2|i-2)是第i-2帧状态估计误差协方差矩阵的修正值,Γ(i-2)为第i-2帧的过程噪声分布矩阵,q(i-2)是过程噪声的协方差矩阵。
式(11)中的S(i-1)是第i-1帧的新息协方差矩阵,其可以表示为:
S(i-1)=H(i-1)P(i-1|i-2)H(i-1)T+R(i-1)
(13)
其中,R(i-1)是第i-1帧的量测噪声协方差矩阵。最后状态估计误差协方差矩阵的更新公式为:
P(i-1|i-1)=P(i-1|i-2)-K(i-1)S(i-1)KT(i-1)
(14)
在距离波门拖引过程中,干扰机关闭前的波门偏移距离是影响雷达重新捕获目标的一个重要因素,因此我们选其作为距离门拖引干扰效果的评价指标。不难发现为了干扰成功,波门偏移距离越大,对于干扰方就越有利,越能降低被敌方武器摧毁的概率。对于干扰方而言,量测噪声、真假目标在同一距离波门中假目标被识别的概率等因素无法准确获知,因此为了更加准确地评价拖引策略的性能,在此取数学期望,称为平均波门偏移距离。将上述距离门拖引策略问题建模为优化问题可表述为
s.t. 0≤Δri≤Δrmax
(15)
其中E(·)代表数学期望,Δrmax为单帧的最大拖引距离。
综上所述,不难发现在解决距离门拖引干扰策略问题时存在以下两个难点:(1)对于干扰方而言真目标位置以及波门中心预测位置难以准确获知,换句话说目标函数的解析表达式难以获取;(2)当拖引总帧数N增加时,优化问题的维度过高。因此传统的优化算法不能直接用于解决此问题。基于此,本文提出了一种基于改进粒子群算法(Improved particle swarm optimization, IPSO)的策略优化方案。
粒子群算法(Particle swarm optimization,PSO)是一种受鸟类觅食行为启发的群体智能算法[11-12]。由于其简单性,可行性和快速收敛特性,PSO被广泛用于解决各种优化维度过高的问题。PSO在解决优化问题时,通常粒子的适应度值(目标函数)是确知的。然而对于距离门拖引干扰策略优化问题,目标函数难以准确获知,因此文章首先提出了结合奖励机制的蒙特卡洛目标函数拟合方法,然后在进行PSO的优化求解。为了与传统PSO进行区分,本文所提方法记为IPSO。
当使用IPSO优化距离门拖引干扰策略时,每个粒子的位置代表候选距离门拖引干扰策略。以第j个粒子为例,其位置的数学表达式为
(16)
其适应度函数的计算过程如下所述:
由于波门偏移距离对于干扰方不可确知,因此,引入奖励机制对其进行优化。设其奖励函数为reward=RN*ξ(ξ∈[0,1]),其中RN为第N帧的拖引距离,ξ为奖励因子,其中ξ不一定特别精确,只需要通过认知确定干扰是否起作用(比如观察敌方雷达工作模式是否发生改变)[13-15],如果干扰起作用ξ=1,否则ξ=0。为了减轻过程噪声以及雷达量测噪声等因素对于优化结果的影响,通过使用蒙特卡洛法[16]求取均值,然后对求取均值后的结果进行优化。基于改进粒子群算法的策略优化方案的具体步骤如下:
第一步 确定粒子数M,在N维的0≤Δrk≤Δrmax(1≤k≤N)变量空间中随机初始化粒子群的位置和速度,利用结合奖励机制的蒙特卡洛目标函数拟合方法计算每个粒子当前位置的适应度值;
第二步 确定每个粒子的个体最优位置
(下标0代表第0代)和全局最优位置gbest0(粒子适应度值最大的粒子位置),算法进入第1轮迭代即i=1;
第三步 更新种群中所有粒子的位置和速度,更新公式如下[17](以第i次迭代的第j个粒子为例)
(17)
其中v代表粒子的速度,w是动态常数,其控制着粒子前一时刻速度对当前时刻速度的影响,当取值很大的时候,粒子的全局搜索能力强;c1和c2代表学习因子,通常情况下用来调整学习的步长,c1调整他们飞向自身最好的位置,c2调整粒子飞向全局最好的位置;r1和r2是服从0～1均匀分布且相互独立的随机数。为了避免粒子群算法早熟或者在全局最优解附近震荡,动态常数w随迭代次数线性依次减少,其数学表达式为
(18)
其中wmax和wmin分别代表w的最大值和最小值。imax代表最大迭代次数,通常情况下wmax=0.9,wmin=0.5。
第四步 利用结合奖励机制的蒙特卡洛目标函数拟合方法计算粒子新位置的适应度值,更新所有粒子的个体最优和全局最优,更新公式如下
(19)
(20)
第五步 判断是否达到最大预先定义的迭代次数imax。如果i<imax,i=i+1,算法返回第三步,否则迭代终止,输出优效拖引策略η*
η*=gbestimax
(21)
在本节,将用一些仿真结果来验证基于IPSO的距离门拖引干扰策略性能。为了接下来更好的对比验证,先介绍RGPO干扰的传统拖引方式——匀速拖引和匀加速拖引。匀速拖引的第i帧拖引距离可表示为
(22)
其中
代表匀速拖引的速度。匀加速拖引的第i帧拖引距离可表示为
(23)
其中ν0代表匀加速拖引的初速度,a代表匀加速拖引的加速度。
假设目标在二维空间中运动,它从初始位置
出发,在x方向以-200 m/s做近似匀速直线运动,其运动的x方向和y方向过程噪声均服从均值为零,方差为25 m2的高斯分布。干扰方的拖引总帧数N=10,单帧的最大拖引增量Δrmax=250 m;跟踪方采用卡尔曼滤波器进行跟踪,其x方向量测噪声服从均值为0,方差为1 m2的高斯分布,y方向量测噪声服从均值为0,方差为0.25 m2的高斯分布,第i帧重访时间Ti等于0.5 s,跟踪方采用矩形波门进行跟踪,x方向距离波门宽度Lx=150 m,跟踪方y方向的距离波门宽度Ly=150 m,真假目标处于同一距离波门时假目标被跟踪方识别的概率为0.8,与干信比相关的系数
蒙特卡洛次数为20000次;对于PSO而言,粒子数N=50,常数c1=c2=2,惯性系数的最大值wmax=0.9,惯性系数的最小值wmin=0.5,PSO算法的最大迭代次数imax=800。
图2(a)、(b)分别显示了基于IPSO算法的拖引策略与匀速拖引、匀加速拖引的性能对比曲线,其中,点A表示匀速拖引的性能最高点,点B表示匀加速拖引的性能最高点(x坐标为加速度,y坐标初速度);图2(c)、(d)分别显示了图2(b)沿点B的x方向和y方向的切面图。从图2可知,在当前参数条件下,当拖引速度取154 m/s时,匀速拖引的最后一帧平均波门偏移距离达到最大值532.5 m;当拖引初速度为86 m/s,加速度为64 m/s时,匀加速拖引的最后一帧平均波门偏移距离达到最大值860.6 m。而基于IPSO的拖引方式的最后一帧平均波门偏移距离为1274 m。因此基于IPSO算法拖引策略的性能明显优于匀速和匀加速拖引策略。IPSO、匀速拖引的A点和匀加速拖引B点的拖引策略图3所示。
图2 IPSO与传统拖引策略的最后一帧性能对比曲线
Fig.2 The last frame performance comparison curve of IPSO and traditional pull-off strategy
从图3可知,IPSO算法可以通过调整不同探测帧数的拖引距离,实现探测帧与帧之间的相互配合,从而把真目标尽快移到距离波门外;其次,当真目标移除距离波门外后,通过快速的增加当前探测帧的拖引距离,以便尽快将距离波门拖远。而匀速拖引、匀加速拖引的灵活性则较低。图4(a)、(b)中匀速拖引、匀加速拖引的部分策略以及基于IPSO拖引策略在整个探测帧的拖引情况如图4所示。
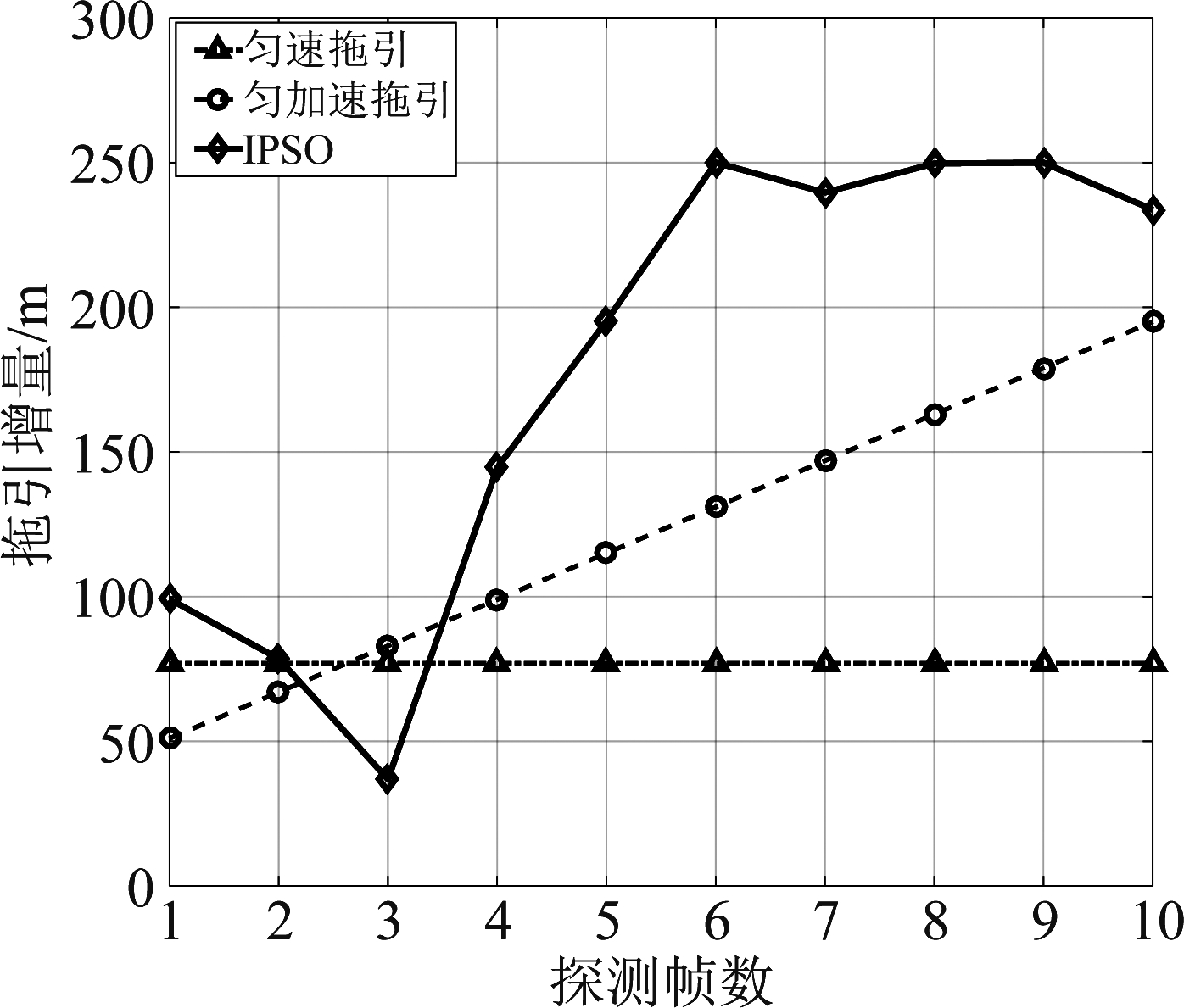
图3 不同拖引方法的拖引策略
Fig.3 Pull-off strategies for different pull-off methods
从图4可知,基于IPSO算法的拖引策略在每个探测帧的平均波门偏移距离几乎都大于匀速拖引和匀加速拖引策略。基于IPSO算法的拖引策略在拖引期的初期,雷达跟踪的为真假目标的合成位置,拖引速度适中,此时平均波门偏移距离较小(如上图中第1和第2帧所示);在拖引的中后期,一个较快的拖引速度则可以很快将距离波门拖远,此时平均波门偏移距离增大。而对于匀速拖引来说,拖引速度较小,则真假目标长时间处于同一个距离波门内,此时导致最后一帧平均波门偏移距离较小;随着初速度的增加,最后一帧平均波门偏移距离逐渐增加;当拖引速度过大时,则雷达不能及时响应这种突然变化,导致最后一帧平均波门偏移距离反而减小。对于匀加速拖引,当初速度较小时,随着加速度的增加,最后一帧的平均波门偏移距离呈上升在下降趋势;当初速度过大时,随着加速度的增加,最后一帧的平均波门偏移距离呈下降趋势(如(d)图所示)。
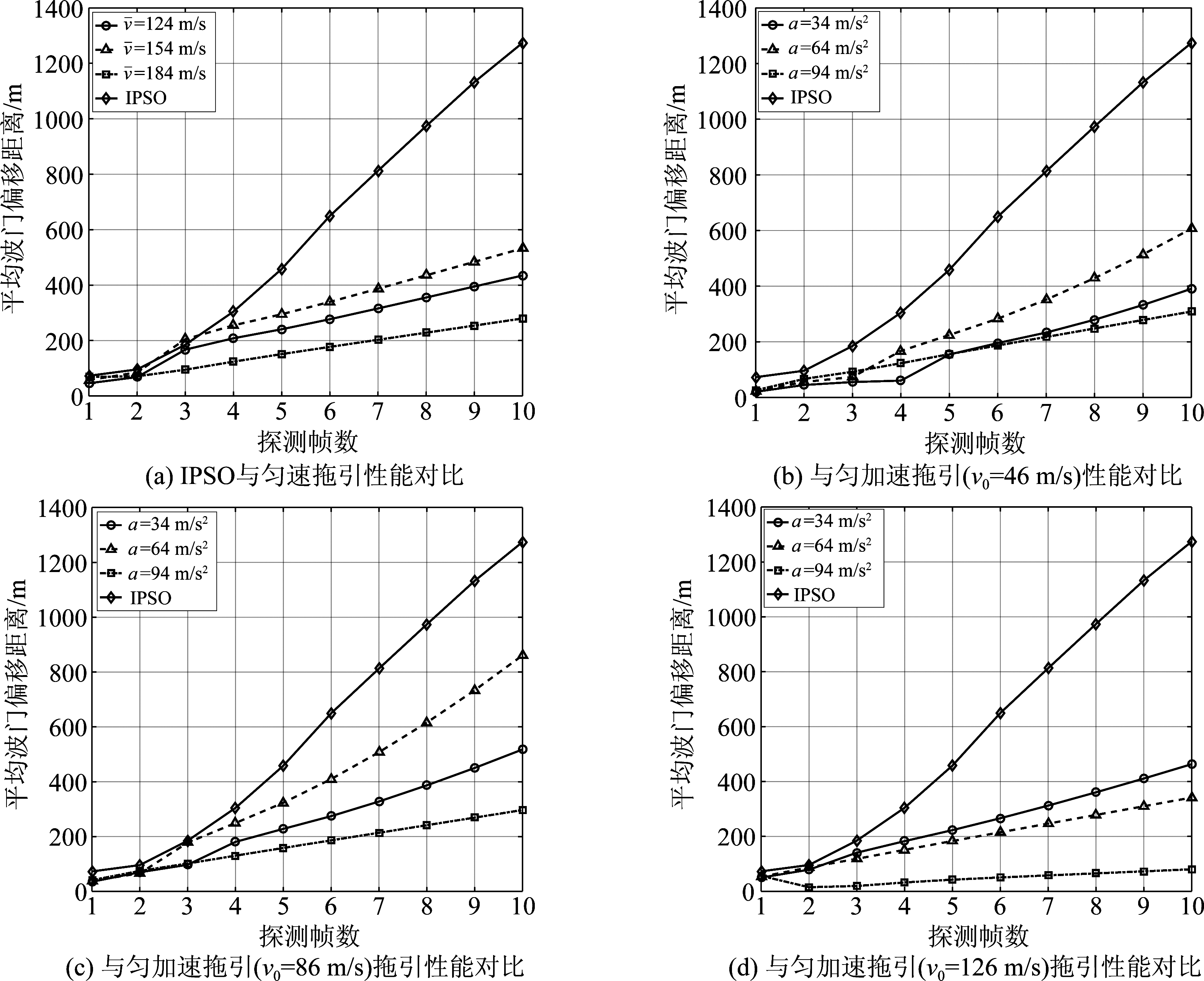
图4 不同探测帧的IPSO与传统拖引性能对比曲线
Fig.4 Comparison curve of IPSO and traditional pull-off performance for different detection frames
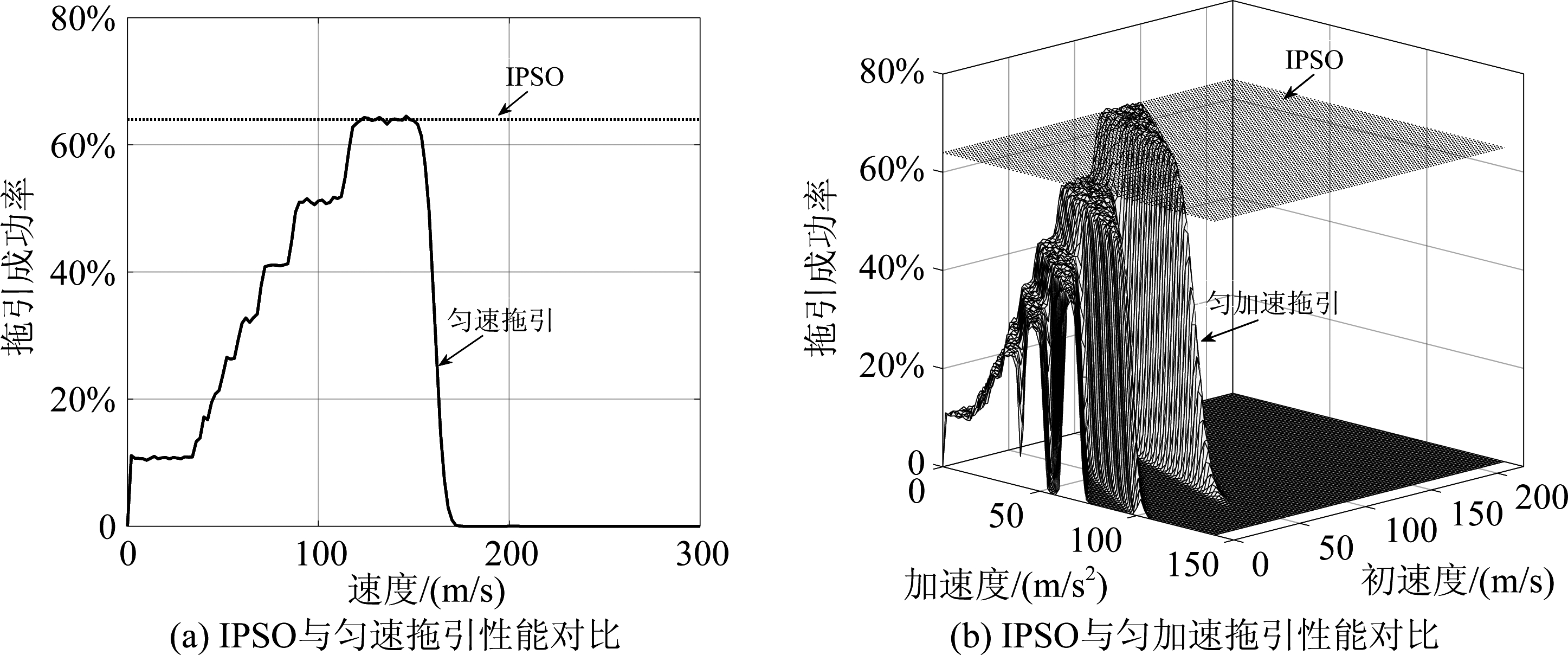
图5 不同拖引策略下的拖引成功率对比曲线
Fig.5 Comparison curve of the pull-off success rate of different towing strategies
另外,实际应用中,拖引成功率也是评价距离门拖引干扰的重要评价指标。拖引成功率不仅与雷达探测/跟踪的系统性能相关,还与武器系统的作战效果相关。本文仅考虑雷达探测/跟踪的系统性能,其拖引成功率与真假目标在同一距离波门内的帧数以及假目标被识别的概率等因素相关,仿真结果如图5所示。
从图5可以看出,基于IPSO算法的拖引成功率仍然高于匀速拖引和匀加速拖引方法,对于匀速和匀加速拖引策略虽然在某个确定参数下,拖引成功率与基于IPSO拖引策略的成功率近似相等,但是由图2可知平均波门偏移距离小于基于IPSO的拖引策略。
综上所述,基于本文所提算法的拖引策略性能优于匀速和匀加速拖引策略。
本文针对未知环境模型下的多帧距离门拖引干扰的策略优化问题,提出了基于改进粒子群算法的策略优化方法。首先,通过平均波门偏移距离作为目标函数,构造了距离门拖引干扰的多帧联合优化模型;然后为了提升干扰性能,提出了结合奖励机制的蒙特卡洛目标函数拟合方法以及基于粒子群算法的策略优化方法;最后,仿真实验结果表明,相比传统的匀速和匀加速距离门拖引干扰方法,本文提出的拖引干扰方法显著提升了距离门拖引干扰的性能。
[1] SCHROER R. Electronic warfare. [A century of powered flight: 19032003][J]. IEEE Aerospace and Electronic Systems Magazine, 2003, 18(7): 49-54.
[2] 吴晓芳, 代大海, 王雪松, 等. 合成孔径雷达电子对抗技术综述[J]. 信号处理, 2010, 26(3): 424- 435.
WU Xiaofang, DAI Dahai, WANG Xuesong, et al. Review of Synthetic Aperture Radar Electronic Countermeasures[J]. Signal Processing, 2010, 26(3): 424- 435.(in Chinese)
[3] LAZAROV L. Perspectives and Trends for the Development of Electronic Warfare Systems[C]∥2019 International Conference on Creative Business for Smart and Sustainable Growth (CREBUS), Okayama, Sandanski, Bulgaria, 2019: 1-3.
[4] TAN Q J O, ROMERO R A. Jammer-Nulling Transmit-Adaptive Radar Against Knowledge-Based Jammers in Electronic Warfare[J]. in IEEE Access, 2019, 7: 181899-181915.
[5] GRECO M, GINI F, FARINA A, et al. Effect of phase and range gate pull-off delay quantisation on jammer signal[J]. IEE Proceedings-Radar, Sonar and Navigation, 2006, 153(5): 454- 459.
[6] ÖZTÜRK M T, DALVEREN Y, KARA A. Spectrum analysis of parabolic range gate pull-off (RGPO) signals[C]∥2015 23nd Signal Processing and Communications Applications Conference (SIU), Malatya, 2015: 1026-1029.
[7] XIE Min, LIU Longlong, ZHANG Chengyan, et al. Bidirectional false targets RGPO jamming[C]∥2018 13th IEEE Conference on Industrial Electronics and Applications (ICIEA), Wuhan, 2018: 2345-2348.
[8] LI Wei, LIU Wei, GUO Liyong, et al. Joint slow/fast-time pulse diversity method for countering range gate pull off jamming[C]∥IET International Radar Conference 2015, Hangzhou, 2015: 1- 4.
[9] BLAIR W D, WATSON G A. Benchmark for radar allocation and tracking in ECM[J]. IEEE Transactions on Aerospace and Electronic Systems, 1998, 34(4): 1097-1114.
[10] SLOCUMB B J, WEST P D, SHIREY T N, et al. Tracking a maneuvering target in the presence of false returns and ECM using a variable state dimension Kalman filter[C]∥Proceedings of 1995 American Control Conference-ACC’95, Seattle, WA, USA, 1995: 2611-2615.
[11] AZIZ N A B A, MOHEMMED A W, ALIAS M Y. A wireless sensor network coverage optimization algorithm based on particle swarm optimization and Voronoi diagram[C]∥2009 International Conference on Networking, Sensing and Control, Okayama, 2009: 602- 607.
[12] 陈江琦, 马尽文. 基于改进粒子群算法的压缩感知[J]. 信号处理, 2017, 33(4): 488- 495.
CHEN Jiangqi, MA Jinwen. The Improved Particle Swarm Optimization Algorithm Based Compressive Sensing[J]. Journal of Signal Processing, 2017, 33(4): 488- 495.(in Chinese)
[13] XING Qiang, ZHU Weigang, JIA Xin. Intelligent countermeasure design of radar working-modes unknown[C]∥2017 IEEE International Conference on Signal Processing, Communications and Computing (ICSPCC), Xiamen, 2017: 1-5.
[14] WANG Wei, WANG Yubing. A Parameter-Optimized SLS-TSVM Method for Working Modes Recognition of Airborne Fire Control Radar[C]∥2020 IEEE 4th Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chongqing, 2020: 948-953.
[15] 王沙飞. 认知电子战原理与技术/现代电子战技术丛书[M]. 国防工业出版社, 2018: 1-195.
WANG Shafei. Principle and Technology of Cognitive Electronic Warfare[M]. National Defence Industrial Press, 2018: 1-195.(in Chinese)
[16] RAMANI S, BLU T, UNSER M. Monte-Carlo Sure: A Black-Box Optimization of Regularization Parameters for General Denoising Algorithms[J]. IEEE Transactions on Image Processing, 2008, 17(9): 1540-1554.
[17] KENNEDY J, EBERHART R. Particle swarm optimization[C]∥Proc. IEEE International Conference Neural Networks, 1995: 1942-1948.
贾 瑞 男, 1994年生, 甘肃人。电子科技大学信息与通信工程学院硕士研究生, 研究方向包括: 雷达信号处理、雷达干扰博弈进化技术等。
E-mail: jerry@std.uestc.edu.cn
张天贤 男, 1985年生, 广东人。电子科技大学信息与通信工程学院, 副教授, 研究方向包括: 雷达干扰博弈进化技术、探通一体资源管控技术、微弱目标探测技术、多功能波形设计等。
E-mail: txzhang@uestc.edu.cn
王远航 男, 1994年生, 辽宁人。电子科技大学信息与通信工程学院博士生, 研究方向包括: 雷达信号处理、雷达干扰博弈进化技术等。
E-mail: 201721020436@std.uestc.edu.cn
邓艳红 女, 1995年生, 湖南人。电子科技大学信息与通信工程学院硕士研究生, 研究方向包括: 雷达信号处理、探通一体资源管控技术等。
E-mail: 201821010938@std.uestc.edu.cn
孔令讲 男, 1974年生, 河南南阳人。电子科技大学信息与通信工程学院, 教授、博士生导师、佛罗里达大学访问学者、科技部中青年科技创新领军人才、四川省学术和技术带头人、教育部新世纪优秀人才支持计划获得者、长江学者, 研究方向包括: 隐蔽目标探测技术、雷达干扰博弈进化技术、弱目标检测跟踪技术、图像处理技术等。
E-mail: ljkong@uestc.edu.cn