u(t′)dt′+φ)Reference format: MAO Jiaqi, LUO Feng, WEI Jingxin. Strong Mainlobe Interference Suppression Method Based on Eigen-Subspace[J]. Journal of Signal Processing, 2021, 37(2): 268-275. DOI: 10.16798/j.issn.1003- 0530.2021.02.012.
相控阵雷达在执行远程精密目标探测时,敌方施放于目标周围的干扰将主要落入天线主瓣。主瓣干扰受天线主瓣调制的影响,通常功率更大且与目标在空域内具有更强相关性,因而成为了影响相控阵雷达生存能力的重要威胁。当施放的干扰形式为有源压制式干扰[1]时,大功率的噪声或类噪声形式的干扰信号将会抬高目标检测门限,从而覆盖并淹没弱目标,并降低雷达的目标捕获概率,因而对抗主瓣有源压制式干扰显得尤为重要。然而,在对抗主瓣干扰时,传统自适应波束形成方法[2-5]所产生的凹口位于主波束内,这会使得主波束严重变形,原有指向处的能量发生衰减,旁瓣电平也随即升高。除此之外,对后续的信号处理环节也会产生一定的影响,具体包括虚警概率上升、测向精度下降等[6]。
近年来,主瓣干扰抑制作为空域对抗领域新的研究方向,持续引发了各方的广泛聚焦与深入研究。文献[7]在特征子空间的理论基础上,首先推导出基于特征投影预处理(Eigen-projection Matrix Preprocessing,EMP)的主瓣干扰抑制方法[8],该方法将接收数据投影到主瓣干扰的正交子空间中,这一过程无需估计主瓣干扰角度并且没有阵列自由度的损失,但存在方向图主瓣峰值偏移以及低快拍下输出SINR较低等问题[9]。文献[10]提出了基于特征投影与协方差矩阵重构(Eigen-Projection and Covariance Matrix Reconstruction,EP-CMR)的主瓣干扰抑制方法,该方法通过重构措施修正了噪声特征值中的微小量,并消除了主瓣干扰对自适应权矢量的影响,因而能够避免期望方向的功率损失,并实现主瓣偏移的有效改善。文献[11]在EP-CMR方法的基础上,利用矩阵滤波估计及相关性判别分离出多个主瓣干扰的特征矢量,实现了空间内多个主瓣干扰的共同抑制。然而,EMP及EP-CMR类方法均对干扰信号的强度变化十分敏感,当主、旁瓣范围同时存在干扰时,旁瓣干扰处的对消凹口会随着主瓣干扰功率的增加而迅速变浅,因而在一定程度上损失了算法的干扰对抗效能[12]。文献[13]在干扰相关的条件下,提出了基于迭代自适应(Iterative Adaptive Approach,IAA)空间谱估计和干扰加噪声协方差矩阵(Interference-plus-Noise Covariance Matrix,INCM)重构[14]的主瓣干扰抑制方法;文献[15]提出基于特征投影与协方差矩阵积分重构(Eigen-Projection and Covariance Matrix Integral Reconstruction,EP-CMIR)的方法。两种方法均利用谱估计提取干扰信息,所获得的重构INCM也仅包含旁瓣干扰及噪声分量,因而在一定程度上保证了自适应滤波凹口的稳定性,但谱估计法存在能量泄露和易受噪声扰动的问题,重构的INCM与真实值间存在误差,因而难以达到最优的干扰抑制效果。
针对上述问题,本文以相控阵雷达对抗强主瓣干扰为目标,首先联合AIC准则与相关性判别对干扰的特征信息进行分类,构造出更为准确的特征投影矩阵;然后定义双重约束条件,即主瓣子空间投影恒定及旁瓣干扰增益置零,求解自适应权矢量,所得权可同时实现主瓣保形与旁瓣凹口置零;最后通过特征投影与自适应加权,剔除回波中的主、旁瓣干扰成分。所提方法不受主瓣干扰功率变化的影响,所得方向图在旁瓣干扰处零陷更深,系统输出的SINR亦更为稳定。
在主瓣有源压制式干扰环境下,假设单个主瓣干扰和P个旁瓣干扰入射到由M(P+1<M)个阵元组成的雷达接收阵面。由于利用噪声信号对射频信号的幅度、频率或相位进行调制,可产生不同类型的压制式干扰。因而本文仅选择其中具有宽动态范围、高发射功率优势的噪声调频式干扰作为模型,所建立的干扰时域波形为:
si(t)=Uiexp(ωit+2πKFMu(t′)dt′+φ)
(1)
其中,Ui为幅度,φ为在[0,2π)内均匀分布的随机变量,ωi为中心频率,KFM为调频斜率,u(t)为调制噪声,且服从零均值、方差为
的高斯分布,i=1,2,…,P+1。调制噪声u(t)的功率谱密度函数为:
(2)
其中,Δfn为调制噪声带宽。根据式(2)可定义有效调频指数
当mfe≪1时为瞄频式干扰,当mfe≫1时为阻塞式干扰。因而,k时刻雷达接收的干扰加噪声数据可表示为:
(3)
其中,sP+1(k)和si(k)(i=1,2,…,P)分别为主瓣干扰及旁瓣干扰的离散采样,θi为第i个干扰的入射角度,a(θi)为其对应的导向矢量,n(k)为零均值的高斯白噪声信号,N为回波采样数。此时,回波的协方差矩阵可表示为:
(4)
其中,pi为第i个干扰的功率,N为噪声协方差矩阵。由于式(4)无法准确获得,因而训练过程中使用采样协方差矩阵作其估计:
(5)
其中,Xd=[x1,x2,…,xNd]为训练数据,Nd为训练样本数,n=1,2,…,Nd。对上式进行特征分解:
(6)
其中,λm为特征值且存在关系λ1≥λ2≥…≥λm≥…≥λM,与其对应的um则为特征矢量,m=1,2,…,M。由于干扰功率大于噪声功率,因而P+1个大特征值组成的对角矩阵Λs=diag(λ1,λ2,…,λP+1)为干扰信号的特征值矩阵,对应Us=[u1,u2,…,uP+1]为干扰信号的特征矢量矩阵。其余则组成噪声的特征值矩阵Λn=diag(λP+2,λP+3,…,λM),对应Un=[uP+2,uP+3,…,uM]为噪声的特征矢量矩阵。
1)AIC准则下干扰数量估计
在理想情况下(信号协方差矩阵精确已知,或训练样本数足够大且干噪比较高),训练信号的特征值排布会呈现出显著的阶梯型规律。但在回波的采样点数有限或干噪比较低的情况下,将无法直观的按照其分布特性判定大特征值个数。因此我们以AIC准则为依据,估计回波中的主瓣及旁瓣干扰的数量总和。
AIC准则是以熵为基础、衡量统计模型拟合性能的一种标准,文献[16]首先将其应用于信号源的数量估计。通过最小化式(3)所建回波训练模型的AIC值,即可获得干扰特征模型的最优化匹配。根据式(6)的特征分解结果,AIC曲线可由下式给出:
AIC(p)=-2L[Φ(p)]+2p(2M-p)
(7)
其中,Φ(p)为包含干扰特征信息的参数向量,p(p=0,1,…,M-1)为可能干扰数。且:
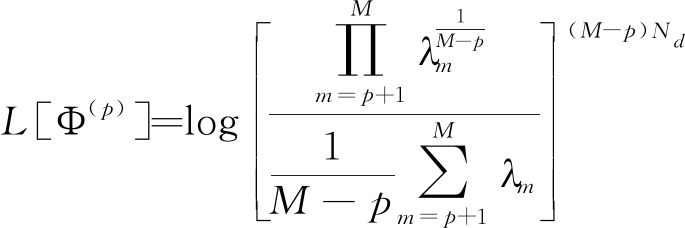
(8)
式(7)中第一项表示所建模型与真实分布的偏差,第二项为防止过估计而增加的罚函数。AIC值越小,模型的契合程度越高。因而对式(7)中的p值在0～M-1范围内进行寻优,式(7)值最小时的p值即为大特征值数量的估计:
(9)
2)相关性判别
在这Q个干扰中,由于主瓣干扰最靠近波束指向θ0,因而主瓣干扰的特征矢量与波束指向θ0方向的导向矢量相关性最大,可通过下式计算:
(10)
则u1、u2、…、uQ中其余Q-1个特征矢量则对应于旁瓣干扰,即Uside=[u1,u2,…,uq-1,uq+1,…,uQ]。由此将特征矢量按照所属类型完成了准确的分类。
根据特征子空间理论,构造特征投影矩阵:
(11)
将特征投影矩阵B与训练数据Xd相乘,消除主瓣干扰分量:
Xb=BXd=[xb(1),xb(2),…,xb(Nd)]
(12)
自适应权矢量直接决定方向图的形状,为了保证主波束不发生偏移,可以通过主瓣子空间约束自适应权矢量的求解,以保证权矢量中影响方向图主瓣波束形状的部分不发生改变。在构造静态方向图的主瓣子空间前,首先在主瓣区域内对导向矢量的自相关函数进行积分,以构造主瓣协方差矩阵[17]:
(13)
其中,BW0为波束主瓣的零点范围。由于式(13)的协方差矩阵无法准确获得,因而按照角度间隔Δθ依次选取K个角度θ1、θ2、…、θK,获得Rθ3 dB的采样估计结果:
(14)
其中,l=1,2,…,K。对式(14)进行特征分解,得到如下表达式:
(15)
其中,
为矩阵
特征值,且
为特征矢量,m=1,2,…,M。按照式(7)及式(9)估计出其中大值个数R,权矢量v1,v2,…,vR则为主瓣子空间的一组基。因而可将M维空间进行划分,获得静态方向图的主瓣子空间及其正交子空间的投影矩阵,分别为:
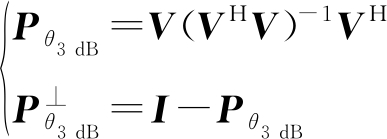
(16)
其中,V=[v1,v2,…,vR]为主瓣子空间的特征矢量矩阵。因而自适应权矢量w可分解为:
(17)
其中,wmain为权矢量中影响主瓣特性的成分,wside为权矢量中影响旁瓣特性的成分。
首先若令w与静态权矢量在主瓣子空间内的投影分量重合:
Pθ3 dBw=Pθ3 dBwstatic
(18)
其中,wstatic=a(θ0)。将式(18)代入式(17),整理可得:
w=Pθ3 dBwstatic+wside
(19)
从式(19)可知,当权矢量发生变化时,其中决定主瓣形状的分量将保持恒定,即可实现主瓣保形,因而式(18)可作为自适应权矢量求解的约束条件之一。
另外,为保证算法在主瓣干扰功率较大时依然能够有效抑制旁瓣干扰,在求解自适应权矢量时可对旁瓣干扰进行约束。由文献[10]可知,自适应阵列方向图与特征值及特征矢量有关:
(20)
其中,
为最小特征值,Fq(θ)=a(θ0)Ha(θ0)为静态方向图,
为干扰对应的特征波束,其特点是在第m个干扰方向的增益最大,而在其余位置则增益较小。因而可利用旁瓣干扰特征矢量估计其所在角度:
i=1,2,…,q-1,q+1,…,Q
(21)
其中,寻优范围Θ∉(θ0-BW0,θ0+BW0)。因而对旁瓣干扰方向的权矢量响应做出如下约束:
(22)
其中,
综合式(18)与式(22)两个约束条件,以输出功率最小为准则,按照下式计算最优权矢量:
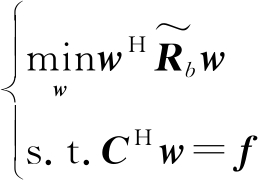
(23)
其中,
求解式(23)可得:
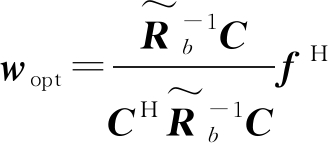
(24)
利用式(11)所得特征投影矩阵对回波信号进行预处理:
Xband=BX=[Bx(1),Bx(2),…,Bx(N)]
(25)
此时回波信号中的主瓣分量已被消除,然后利用式(24)得到的自适应权,对预处理输出进行加权:
(26)
此时,回波信号中的旁瓣干扰分量被准确剔除,同时在自适应权矢量的作用下,波束的指向得到矫正,波束的主瓣形状得到保型。算法流程如图1所示。
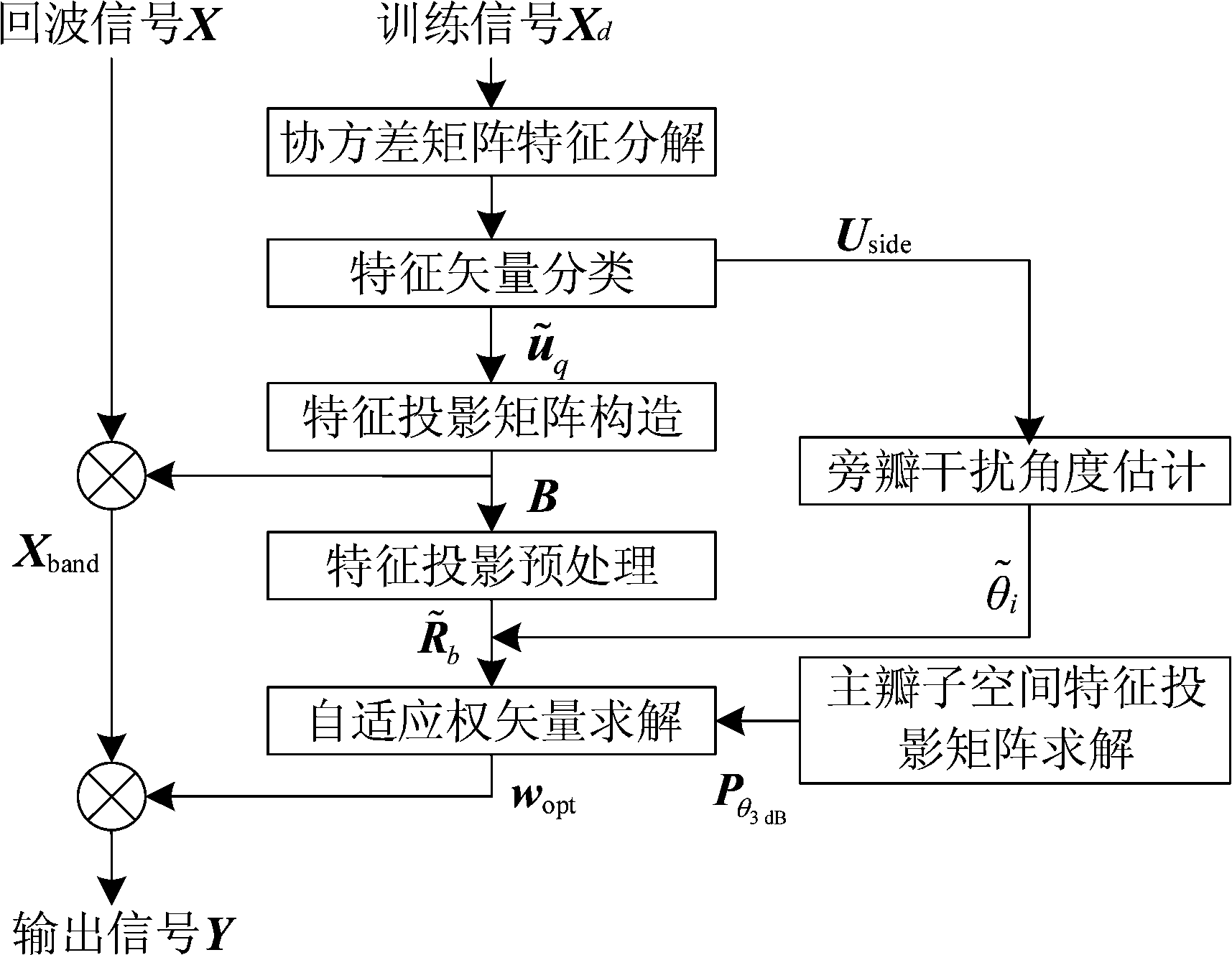
图1 算法流程
Fig.1 Flow diagram of the proposed algorithm
为验证本文方法的干扰对抗有效性,将毫米波相控阵雷达作为实验模型,仿真设置的雷达主要参数如表1所示。除此之外,对接收阵列作出假设,假设接收阵列由12个均匀排布的各向同性的阵列单元组成,阵元间距为波长的一半。空间中存在一静止目标,所在距离为18800 m,入射角度为0°,信噪比为0 dB。主瓣及旁瓣干扰信号均为噪声调频式的瞄频干扰,假设干扰频段中心对准雷达信号中心,干扰带宽为20 MHz,有效调制系数为3.2×10- 8。干扰信号分别从2°、-20°和50°进入天线阵,位于2°的主瓣干扰干噪比(Interference to Noise Ratio,INR)为5 dB或30 dB,位于-20°和50°的旁瓣干扰INR为35 dB和30 dB。在仿真时,考虑下变频后回波数据的处理,所取训练样本的快拍数为500。
表1 雷达主要参数
Tab.1 Simulation parameters of radar
参数参数值信号波长/mm8重频周期/μs200脉冲宽度/μs20信号带宽/MHz5脉冲个数64
图2(a)和图2(b)分别比较了EMP方法、EP-CMR方法和本文方法(IMPROVED)在主瓣干扰的INR分别为5 dB和30 dB时的天线方向图,并与静态方向图(QUI)进行对比。由图2(a)可知,当主瓣干扰的入射功率较小时三种方法均能有效抑制主瓣干扰,但EMP方法所形成的主瓣峰值产生了一定程度的偏移,本文方法在实现最为理想的主瓣保型效果的同时,具有最深的旁瓣干扰抑制凹口。由图2(b)可知,当主瓣干扰的入射功率接近于旁瓣干扰时,本文方法依然能够保持稳定的干扰抑制能力和良好的自适应波束保形能力,其在旁瓣范围内形成的抑制凹口依然超过-90 dB,但EMP方法和EP-CMR方法的对抗效果则急剧变差,在旁瓣干扰处形成的凹口则几乎完全消失。
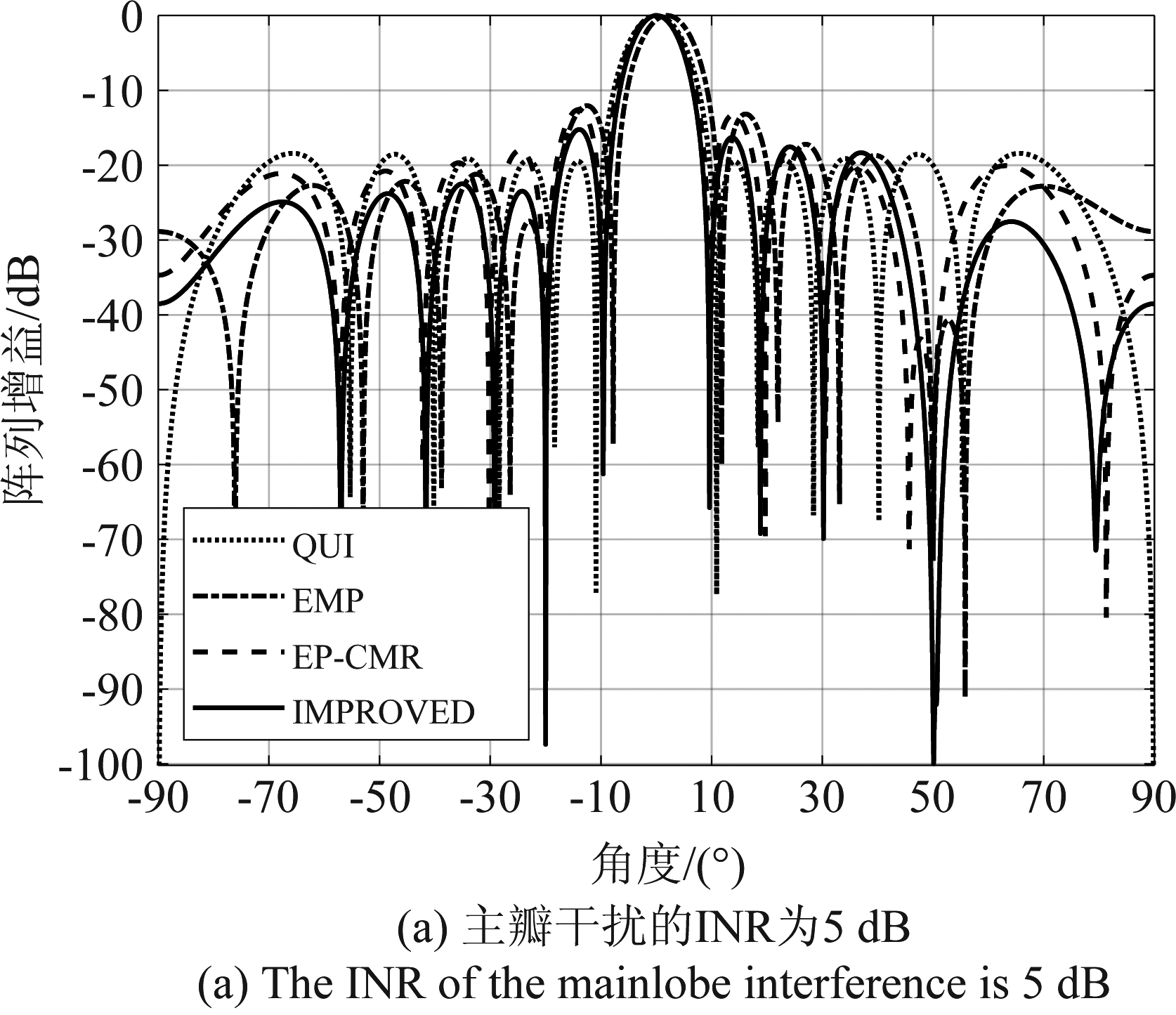
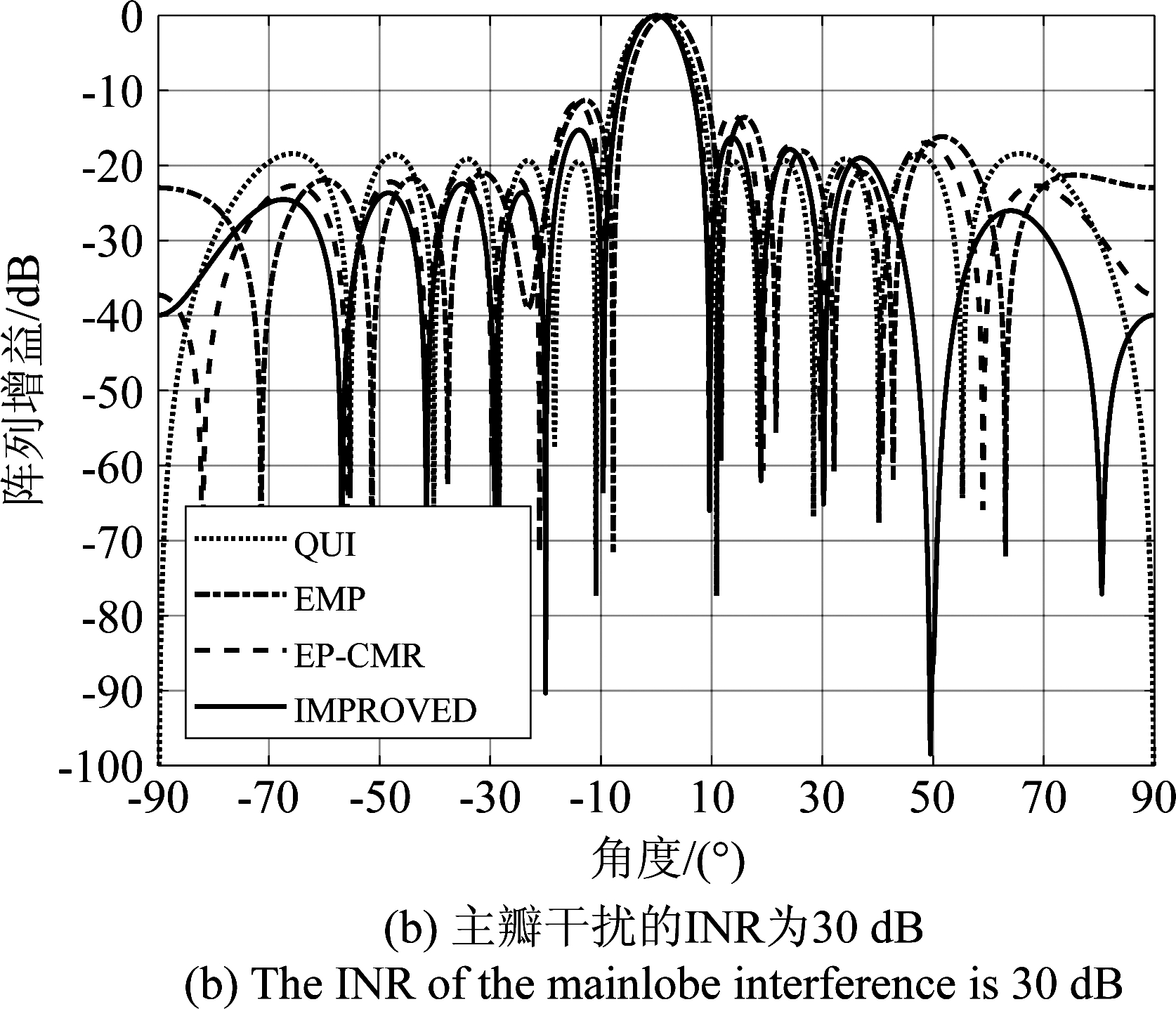
图2 方向图对比
Fig.2 Pattern comparison
图3(a)、图3(b)分别为本文方法与EMP方法及EP-CMR方法在干扰抑制后的归一化目标检测对比,此时主瓣干扰的INR为30 dB。分析图3(a)及图3(b)可知,本文方法通过干扰抑制有效地提高了目标的SINR,从而使得目标能量能够在距离维正确积累,因而更有利于目标的精密检测。但EMP方法及EP-CMR方法的系统输出中残留大量旁瓣干扰分量,因而使得目标淹没在干扰及噪声当中。
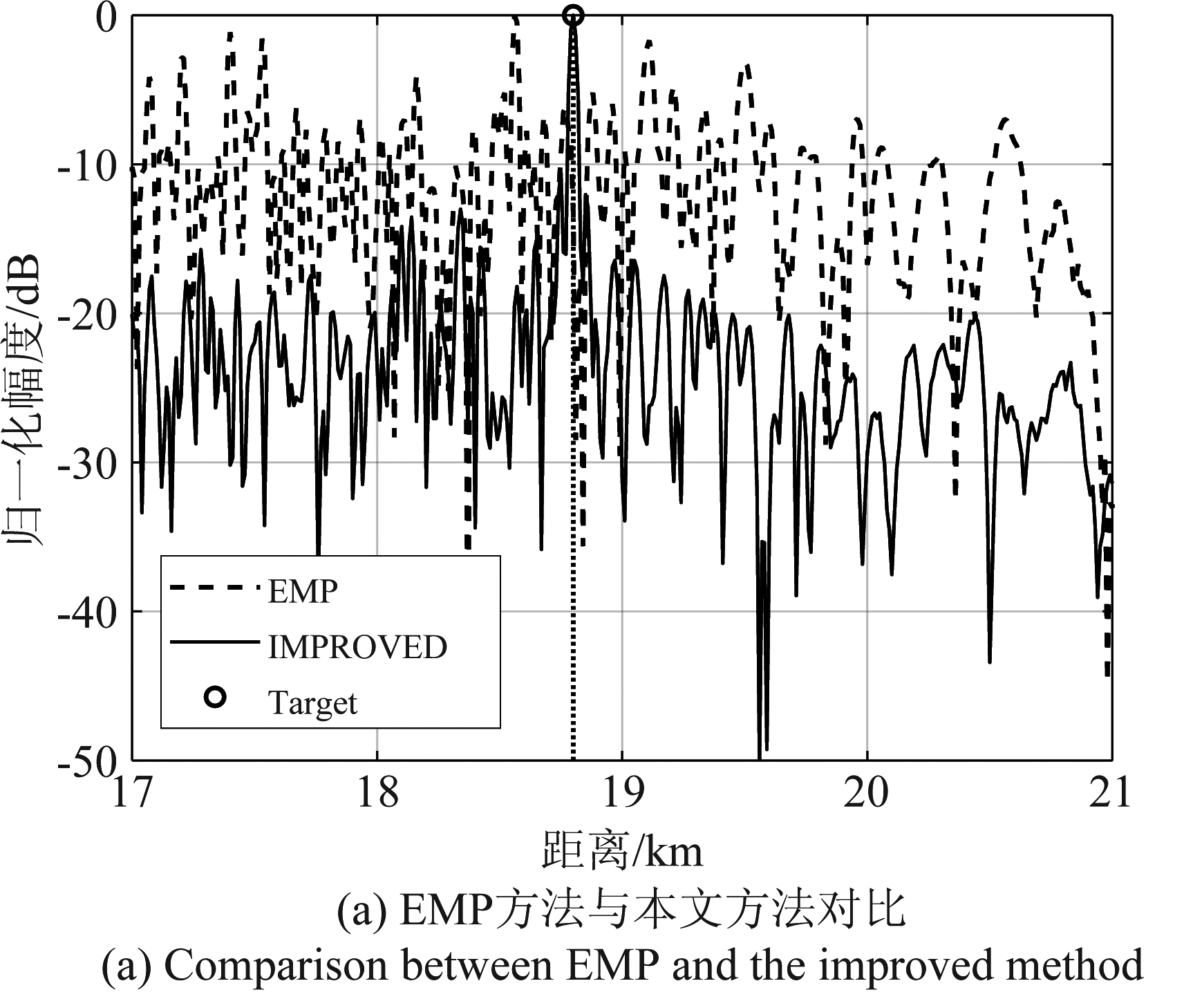
图3 目标检测对比
Fig.3 Target detection comparison
图4为EMP方法、EP-CMR方法和本文方法在不同主瓣干扰INR下的输出SINR变化曲线,可知本文方法与其余两种方法相比,在相同输入下能够获得更高的输出SINR,并且随着主瓣干扰INR的增加,曲线具有更为缓慢的下降趋势。而EMP及EP-CMR方法在横坐标达到15 dB左右开始迅速下降,算法性能持续变差。这说明本文方法受主瓣干扰强度的影响较小,其干扰抑制能力得到大幅度提升。
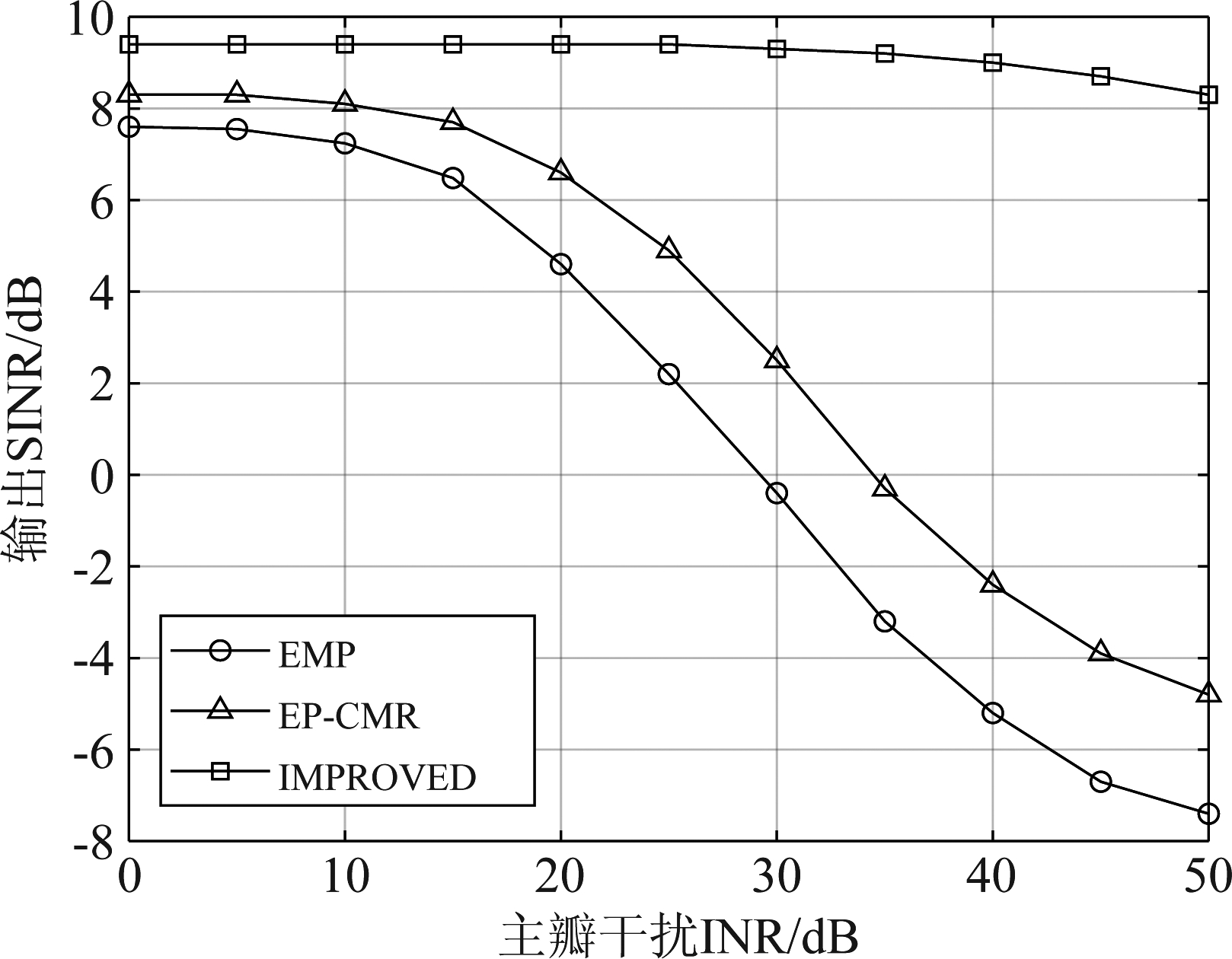
图4 不同主瓣干扰INR下的输出SINR
Fig.4 Output SINR with different mainlobe interference INR
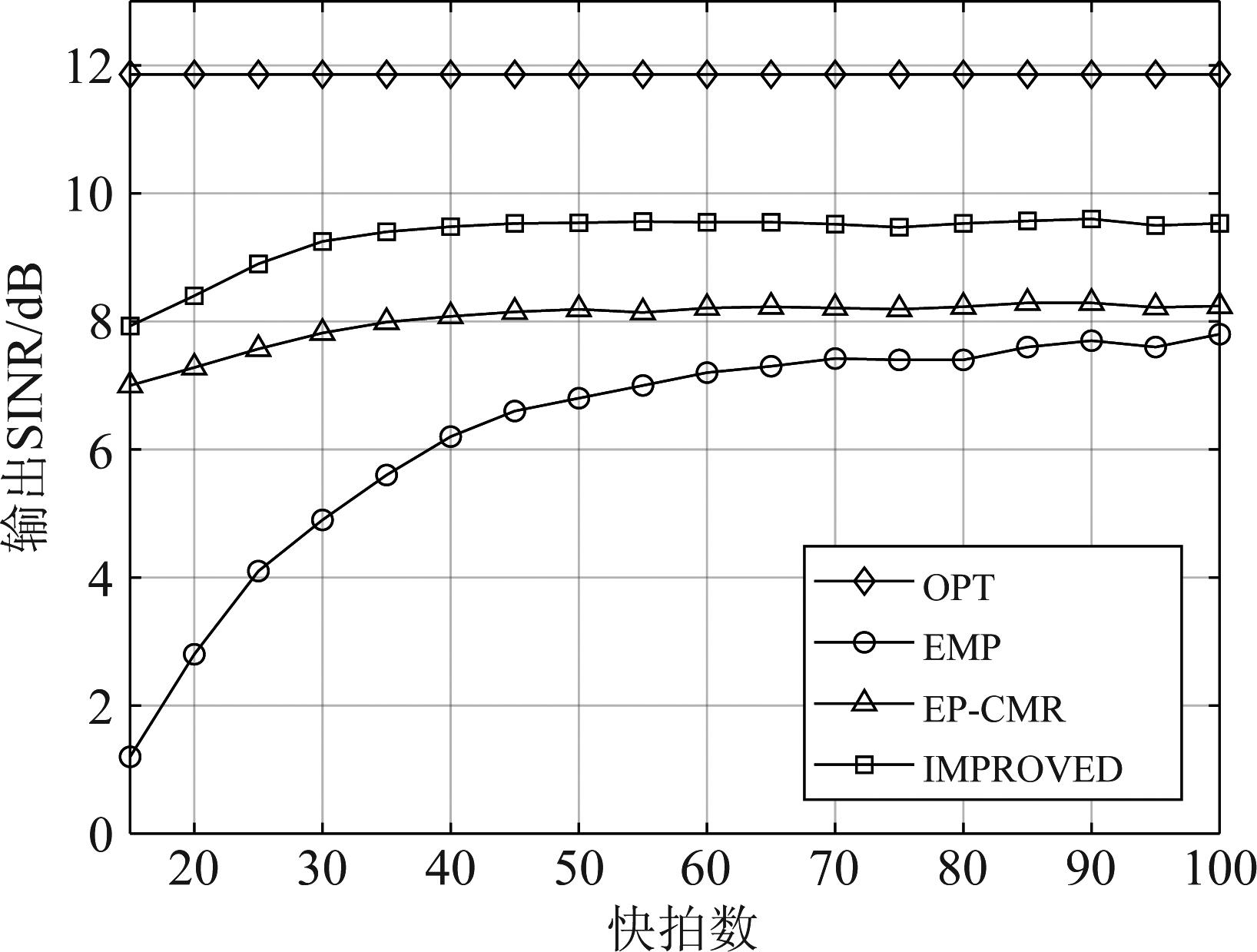
图5 不同快拍数下的输出SINR
Fig.5 Output SINR with different snapshot
图5为主瓣干扰的INR为5 dB时,测试EMP方法,EP-CMR方法和本文方法随快拍数增加而获得的SINR变化趋势,并与最优(OPT)的输出情况进行比较。实验中设置快拍的递增范围为15～100,单次独立实验的递增步长为5,蒙特卡洛实验总数为200。由图可知,与EMP、EP-CMR方法相比,本文方法具有最优的输出效果和收敛性能,能够在快拍数递增到30时开始收敛,收敛速度快,并且达到的输出SINR最高,并且在低快拍时也拥有稳定的SINR输出。
利用某相控阵雷达所获实测数据对算法性能进行验证。该雷达的阵面天线由均匀排成两排的20个接收阵元组成,本文仅利用其中单排的接收数据进行干扰对抗。实验场景如图6所示,天线保持静止且对准模拟目标源方向,信源与干扰均设置在固定位置。雷达工作频率为400 MHz,数据速率为3 Mbps。模拟目标源以中频注入的形式产生单个目标回波,信号形式为线性调频信号,带宽为2 MHz,脉宽为200 μs,距离雷达约50 m。干扰机在开机后自动发射带宽为100 MHz的噪声调频式阻塞干扰,并将主瓣及旁瓣干扰源的初始方位标定为2°和27°,两干扰的INR均为30 dB。接收数据共为10路,取每路波门内2000点数据进行干扰对抗。
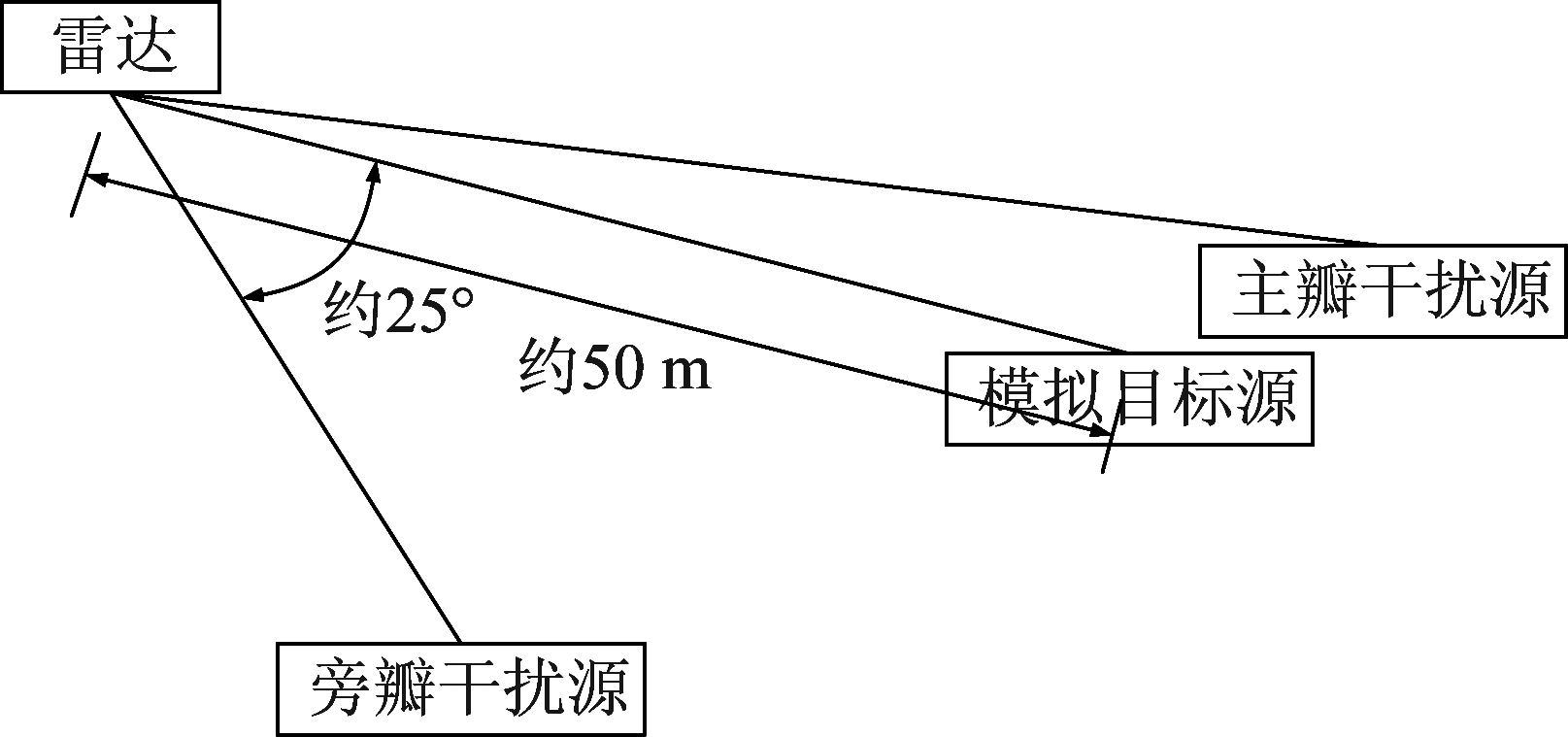
图6 实验场景
Fig.6 Experimental scene
图7(a)、图7(b)分别为通道1的实测采样回波数据及利用本文方法对抗干扰后的目标检测结果。结合两图分析可知,在干扰抑制前,大功率的有源压制式干扰完全淹没了弱目标回波,此时模拟目标源在时域上不可分辨。而在干扰抑制后,实验环境中的主瓣及旁瓣干扰信号均被有效对抗,从而使得目标源被正确检测。
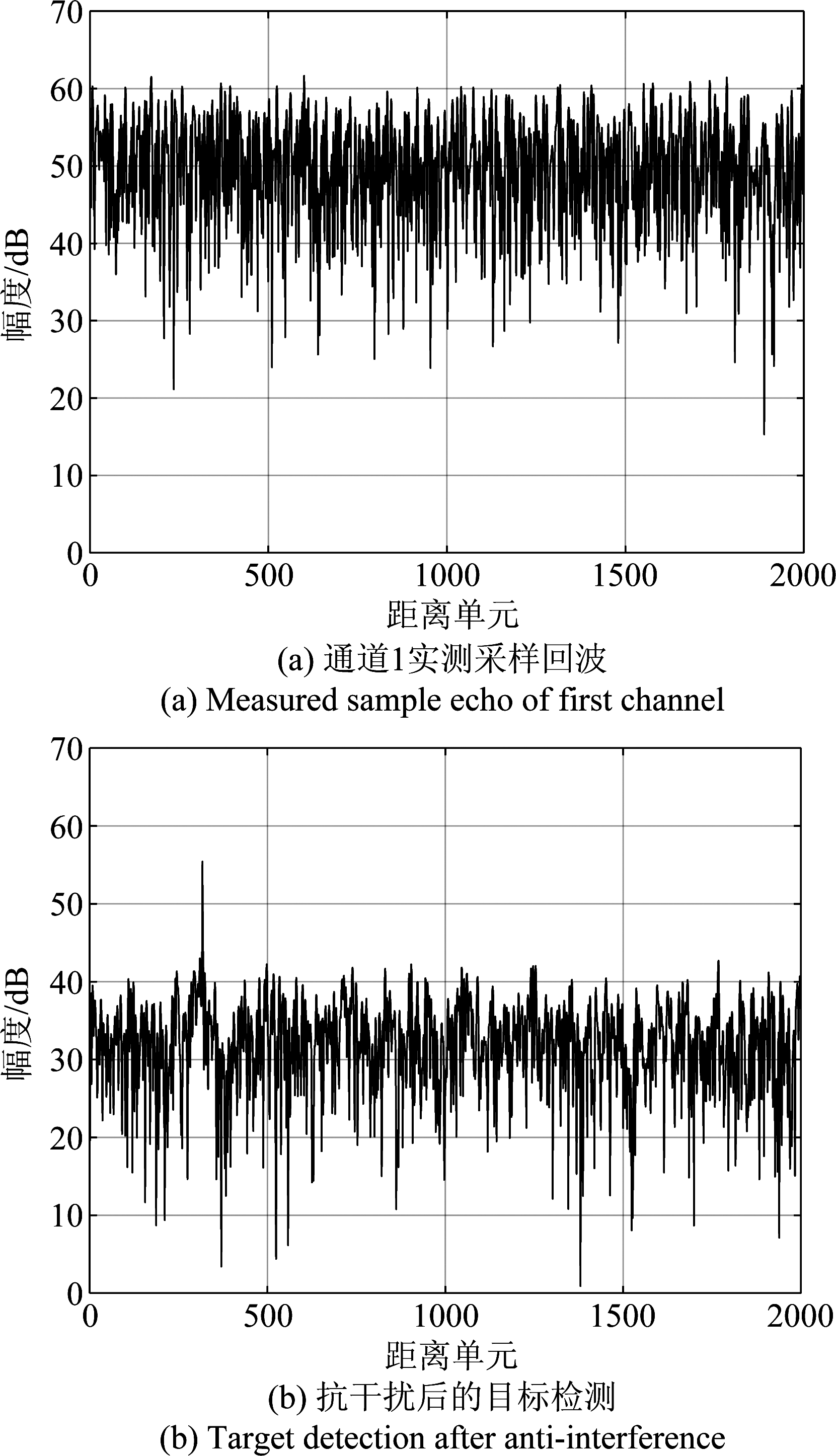
图7 实测回波与抗干扰结果
Fig.7 Measured echo and anti-interference result
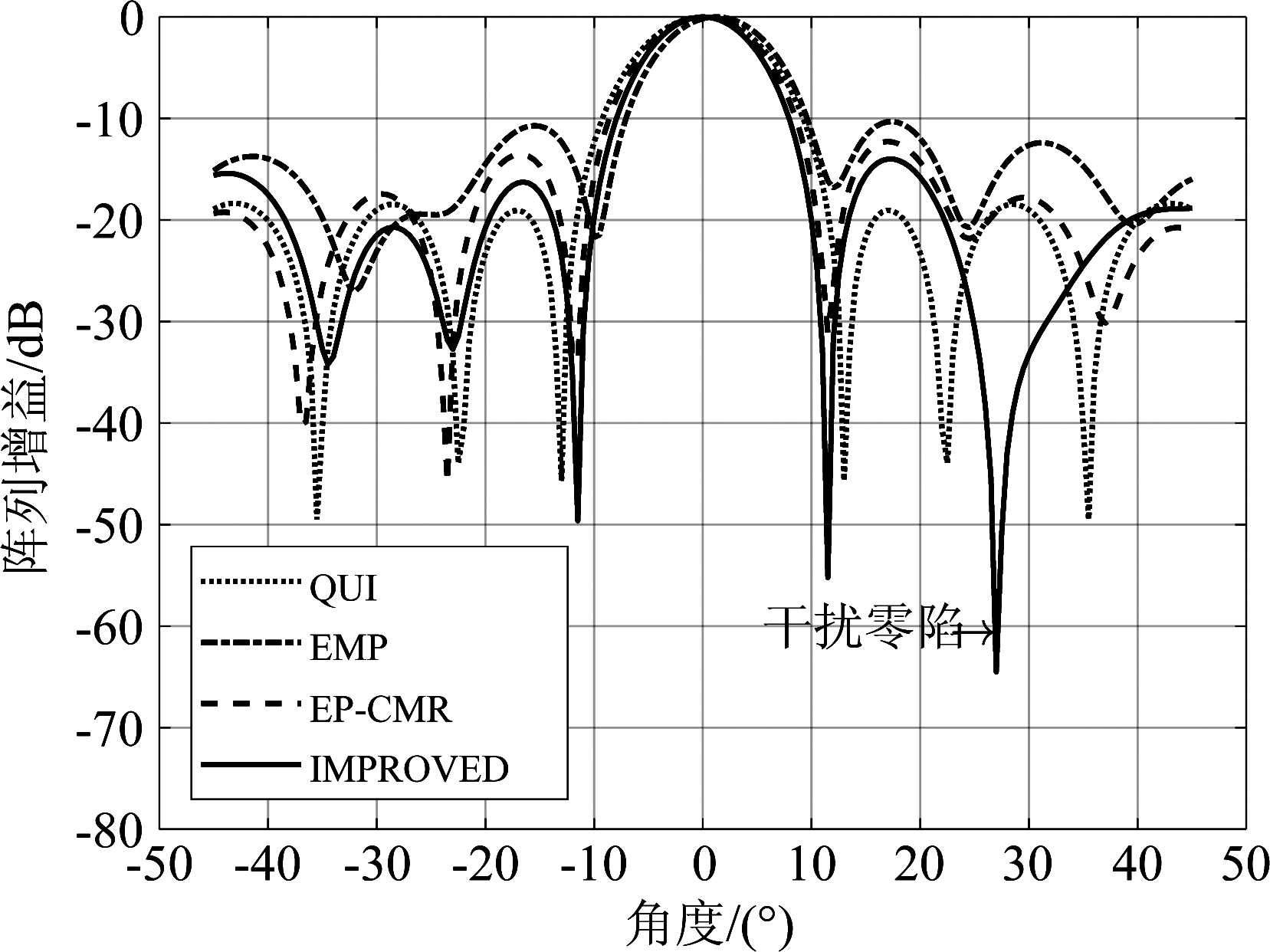
图8 实测方向图
Fig.8 Measured pattern
图8比较了利用EMP方法、EP-CMR方法和本文方法处理该组测试数据所获得的天线方向图,并与静态方向图进行对比。可知EMP方法所形成的方向图主瓣指向偏移了1.5°左右,且与EP-CMR方法均在旁瓣内失去干扰抑制的能力,非感兴趣角度范围内的电平被整体抬高。然而,本文方法所形成的方向图在主瓣范围内维持了稳定保型,同时在标定的旁瓣干扰方向形成了超过-60 dB的零陷,与理论一致。
图9为EMP方法、EP-CMR方法和本文方法在不同主瓣干扰角度下的输出SINR。通过调整主瓣干扰源所在位置,使得主瓣干扰回波的入射角度在0°至6°间按照间隔0.5°逐次完成测试,旁瓣干扰源则保持不变。通过对比三条输出SINR曲线可知,当主瓣干扰的角度逼近目标所在角度时,三种方法输出的SINR均迅速下降。但与其他两条曲线相比,本文方法在目标角度处形成的凹口最窄,收敛时所获得的输出SINR更小,意味着其在主瓣范围内的干扰抑制性能更为稳定。
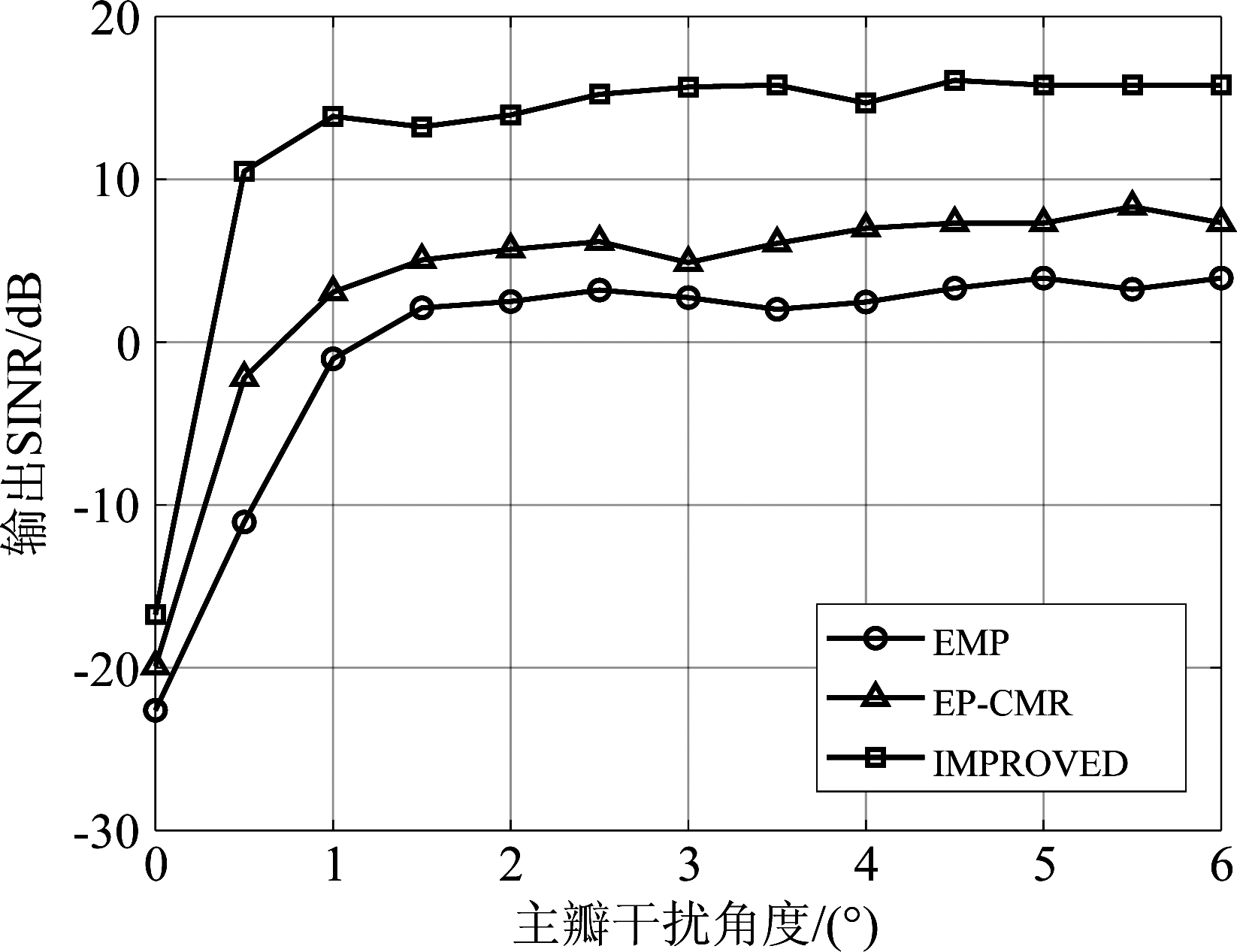
图9 不同主瓣干扰角度下的输出SINR
Fig.9 Output SINR with different mainlobe interference angle
从雷达的实际作战环境出发,本文综合利用了主瓣干扰、旁瓣干扰与静态主瓣子空间的特征信息,提出一种能够对抗空间内强主瓣干扰的新方法,极大地提高了相控阵雷达在高主瓣干扰功率及低快拍等极端条件下的生存能力,更有利于其对弱目标信号的检测。仿真实验证明了该方法的优越性,实测数据的检验亦佐证了该方法的有效性。
[1] 孔文青, 宋万杰, 胡敏, 等. 相控阵雷达抗混合干扰算法研究[J]. 信号处理, 2017, 33(12): 1625-1630.
KONG Wenqing, SONG Wanjie, HU Min, et al. Study of Mixed Jamming Suppression Algorithm for Phased Array Radar[J]. Journal of Signal Processing, 2017, 33(12): 1625-1630.(in Chinese)
[2] 焦亚萌, 武岳, 崔琳, 等. 均匀先验分布Bayesian自适应波束形成方法[J]. 信号处理, 2020, 36(5): 717-722.
JIAO Yamen, WU Yue, CUI Lin, et al. Uniformly Priorized Bayesian Adaptive Beamforming Method[J]. Journal of Signal Processing, 2020, 36(5): 717-722.(in Chinese)
[3] ZHOU Miao, MA Xiaofeng, SHEN Peng, et al. Weighted Subspace-Constrained Adaptive Beamforming for Sidelobe Control[J]. IEEE Communications Letters, 2019, 23(3): 458- 461.
[4] HUANG Junsheng, SU Hongtao, YANG Yang. Robust Adaptive Beamforming Method Based on Desired Signal Steering Vector Estimation and Interference-plus-Noise Covariance Matrix Reconstruction[J]. IEEE Communications Letters, 2019, 2019(21): 7683-7686.
[5] AI Xiaoyu, GAN Lu. Robust Adaptive Beamforming with Subspace Projection and Covariance Matrix Reconstruction[J]. IEEE Access, 2019, 7(7): 102149-102159.
[6] CHEN Xinzhu, SHU Ting, YU K B, et al. Joint Adaptive Beamforming Techniques for Distributed Array Radars in Multiple Mainlobe and Sidelobe Jammings[J]. IEEE Antennas and Wireless Propagation Letters, 2020, 19(2): 248-252.
[7] 李荣锋, 王永良, 万山虎. 主瓣干扰下自适应方向图保形方法的研究[J]. 现代雷达, 2002, 24(3): 50-55.
LI Rongfeng, WANG Yongliang, WAN Shanhu. Research of Reshaping Adapted Pattern under Mainlobe Interference Conditions[J]. Modern Radar, 2002, 24(3): 50-55.(in Chinese)
[8] 陈静, 李晗, 张洪纲, 等. 分布式雷达主瓣间歇采样转发干扰抑制方法[J]. 信号处理, 2018, 34(11): 1368-1376.
CHEN Jing, LI Han, ZHANG Honggang, et al. Main-Lobe Interrupted Sampling Repeater Jamming Suppression Method in Distributed Radar[J]. Journal of Signal Processing, 2018, 34(11): 1368-1376.(in Chinese)
[9] PAN Shuai, ZHANG Yongshun, GE Qichao, et al. Multi-mainlobe Interferences Suppression Based on Interference Covariance Matrix Reconstruction[C]∥International Seminar on Computer Science and Engineering Technology. Shanghai: Yanshan Univ, 2018: 1-5.
[10] YANG Xiaopeng, ZHANG Zongao, ZENG Tao, et al. Mainlobe Interference Suppression Based on Eigen-Projection Procession and Covariance Matrix Reconstruction[J]. IEEE Antennas & Wireless Propagation Letters, 2014, 13(6): 1369-1372.
[11] WANG Yasen, BAO Qinglong, CHEN Zengping. Multiple Mainlobe Interferences Suppression Based on Subspace Matrix Filtering and Covariance Matrix Reconstruction[J]. Journal of Applied Remote Sensing, 2016, 10(3): 1- 8.
[12] LU Liujian, LIAO Yanping. Improved Algorithm of Mainlobe Interference Suppression Based on Eigen-Subspace[C]∥International Conference on Communication and Signal Processing. Melmaruvathur: IEEE, 2016: 133-137.
[13] WANG Yasen, BAO Qinglong, CHEN Zengping. Robust Mainlobe Interference Suppression for Coherent Interference Environment[J]. Eurasip Journal on Advances in Signal Processing, 2016, 2016(1): 135-141.
[14] WANG Yasen, BAO Qinglong, CHEN Zengping. Robust Adaptive Beamforming Using IAA Interference-plus-Noise Covariance Based Matrix Reconstruction[J]. Electronics Letters, 2016, 52(13): 1185-1186.
[15] LUO Zhangkai, WANG Huali, LV Wanghan, et al. Mainlobe Anti-Jamming via Eigen-Projection Processing and Covariance Matrix Reconstruction[J]. Ieice Transactions on Fundamentals of Electronics Communications & Computer Sciences, 2017, E100-A(4): 1055-1059.
[16] WAX Mati, KAILATH Thomas. Detection of Signals by Information Theoretic Criteria[J]. IEEE Transactions on Acoustics, Speech, and Signal Processing, 1985, 33(2): 387-392.
[17] MA Xiaofeng, LU Le, SHENG Weixing, et al. Adaptive Interference Nulling with Pattern Maintaining under Mainlobe Subspace and Quadratic Constraints[J]. IET Microwaves, Antennas & Propagation, 2018, 12(1): 40- 48.
毛家琪 女, 1995年生, 陕西西安人。西安导航技术研究所, 助理工程师, 硕士, 主要研究方向为阵列信号处理、火控雷达系统设计、自适应干扰抑制。
E-mail: mjq2020xidian@163.com
罗 丰 男, 1971年生, 湖南新化人。西安电子科技大学雷达信号处理国家重点实验室, 教授, 博士, 主要研究方向为雷达系统设计、雷达信号与信息处理、高速实时信号处理。
E-mail: luofeng@xidian.edu.cn
韦婧歆 女, 1995年生, 陕西西安人。西安电子科技大学雷达信号处理国家重点实验室, 博士研究生, 主要研究方向为雷达信号处理、阵列信号处理、自适应信号处理。
E-mail: jingxinwei@stu.xidian.edu.cn