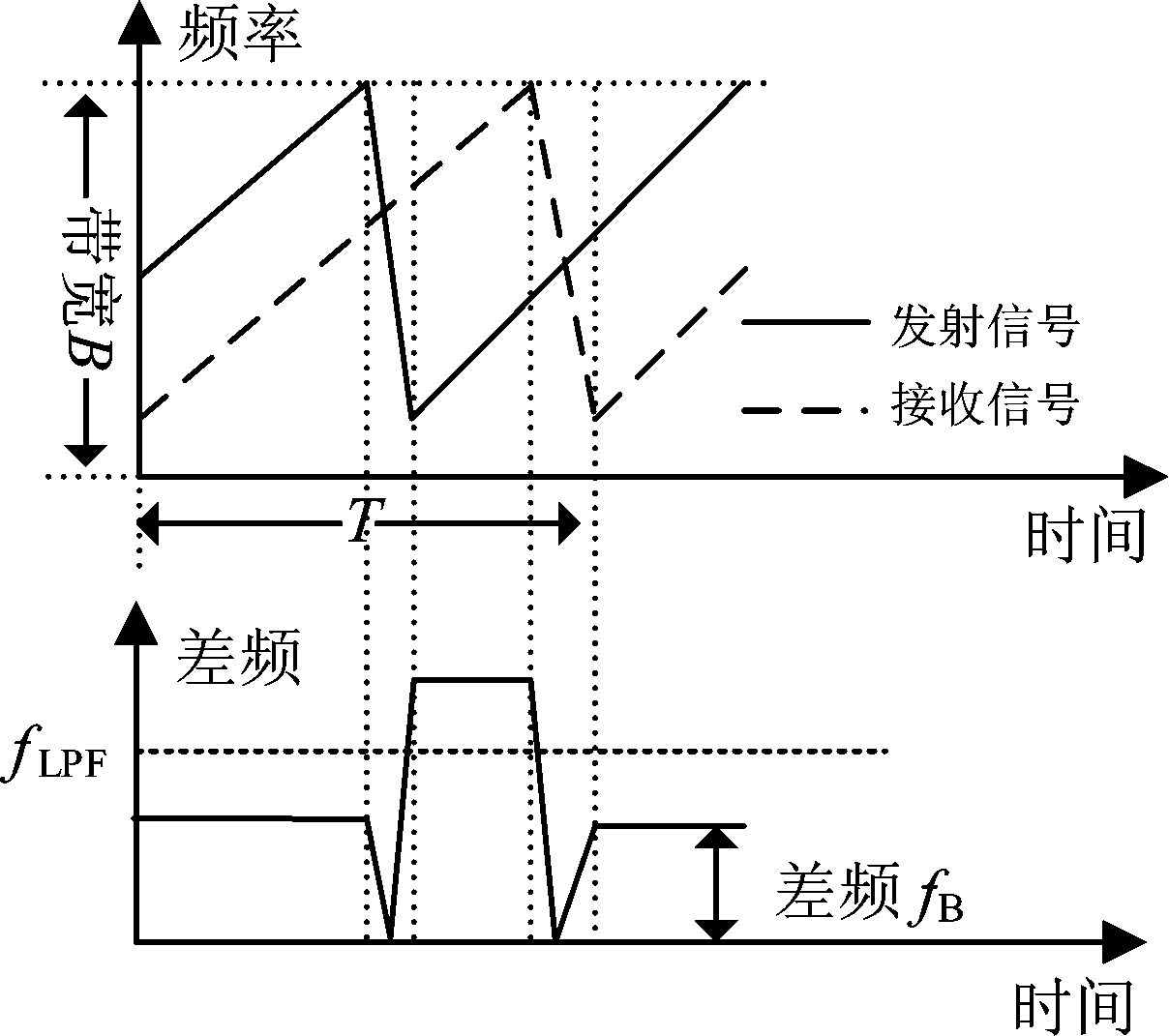
图1 FMCW雷达锯齿波调制波形
Fig.1 FMCW radar sawtooth modulation waveform
Reference format: LI Yang, WANG Chuyuan, CHEN Qiao, et al. Mutual Interference Suppression Method for FMCW Automotive Radar[J]. Journal of Signal Processing, 2021, 37(2): 258-267. DOI: 10.16798/j.issn.1003- 0530.2021.02.011.
随着车载雷达的广泛应用,雷达相互干扰问题不容忽视。与其他探测雷达相比,调频连续波(Frequency Modulated Continuous Wave, FMCW)雷达结构简单、易于调制、成本低,已成为车载雷达的主流波形。因此FMCW车载雷达及其抗干扰技术的研究,对于提高汽车智能化程度和交通安全性有着重要意义。
国内外就车载雷达互干扰现象及抗干扰技术进行了一系列研究 [1- 2]。当前车载雷达的抗干扰技术就应用层面可分为时域、频域、编码域、空间域、极化域、策略类等六类[3]。时域抗干扰方法主要通过采用调制、波形参数随机化等方法,降低与其他波形的时间重叠度。频域抗干扰的主要思路是避免其他雷达处于工作雷达的接收带宽,利用带通滤波器滤除干扰。编码主要指通过雷达波形调制,使不同设备具备不同信号特征。空间域干扰抑制主要有两种方法,一是采用机械或电子波束扫描降低干扰概率,多应用于路边固定雷达,在车载雷达中应用较少,二是自适应波束形成方法,较为复杂。极化抗干扰需要考虑发射信号在当前极化方式下衰减,受限较多。策略类方法通常是建立控制中心对雷达进行参数协调。
就抗干扰的位置而言,抗干扰技术又可分为发射端抗干扰和接收端抗干扰。雷达发射端主要包括波形调制、信号编码、频带协同、发射窄波束、随机生成波形参数等,目的主要是降低干扰与发射波形在时间和频带上重叠的概率[4]。波形设计及优化是发射端常用的雷达干扰抑制方法。文献[5]提出了一种TDM MIMO雷达的多载频随机发射调频序列波形和相应的信号处理方法,实验结果表明该方案显著降低了相邻雷达系统间的干扰。文献[6]通过编码增加雷达波形脉冲的伪随机性,降低雷达回波与间歇采样干扰的相关性,能够有效抑制假目标。文献[7]中利用遗传算法进行波形优化,以最大化各类目标之间的匹配距离的最小值作为优化准则,通过遗传算法求解得到优化波形信号,但是遗传算法的计算量较大,限制了波形优化的实时性。文献[8]提出利用量子遗传算法进行MIMO雷达正交波形设计,降低了不同目标回波之间的相互干扰。接收端主要通过各类信号处理方法来检测、消除干扰,降低干扰的影响。其中自适应滤波自1975年被B. Widrow[9]首次提出以来,被广泛用于从附加干扰中检测目标信号。但是当前对于FMCW雷达干扰抑制的自适应滤波的研究较少。专利[10]中将自适应线性增强器引入调相连续波 (Phase Modulated Continuous Wave, PMCW)雷达系统,以减轻FMCW雷达的干扰,但该方法不适用于FMCW雷达间的相互干扰。文献[11]中提出采用自适应消除方法,即构建维纳滤波器作为自适应噪声消除器处理FMCW雷达之间的干扰,该文认为各厂商不同,调频斜率近似的概率较低,因此可通过自适应干扰消除方法消除干扰。文献[12]表明,当工作雷达与干扰雷达的调频斜率相似时,雷达间干扰变得显着,但此时其混频结果无法满足维纳滤波方法所需的平稳特性,该情况下文献[11]所提方法的抗干扰效果下降。
本文提出了一种基于粒子群优化和自适应对消的FMCW雷达干扰抑制方法,该方法将发射端波形参数优化和接收端自适应滤波相结合,进行时频域联合抗干扰,进一步提高干扰抑制效果。首先在部分参数约束范围内,通过粒子群算法优化波形,使工作波形与干扰波形相关度最低。然后利用正交接收机内干扰的正负频谱共轭相关的特性,通过最小均方(Least Mean Square, LMS)迭代得到最优滤波器,实现自适应干扰对消。最后,仿真结果表明该方法对多干扰有良好的抑制效果。
FMCW雷达常用调制波形包括三角波调制和锯齿波调制。其中锯齿波调制使用上/下线性调频,具有短线性调频周期的快速线性调频有利于多目标检测[10],且具有更好的抗干扰能力[13]。本文主要就锯齿波调制FMCW信号展开分析和研究。图1展示了使用上线性调频的锯齿波调制波形和差频。

图1 FMCW雷达锯齿波调制波形
Fig.1 FMCW radar sawtooth modulation waveform
考虑到未来汽车FMCW雷达将被密集部署,雷达间干扰可能是一个严重的问题。雷达干扰会导致底噪抬升,某些情况下会产生假目标,而工作雷达和干扰雷达的调频斜率是否相同对干扰结果有较大影响。
当干扰雷达与工作雷达的调频斜率不同时,会在时域产生脉冲状的干扰信号[12]。由于脉冲信号的频谱在整个频率范围内是平坦的,因此在接收信号的频谱中底噪会增加,对应于频谱中目标所在位置处信噪比(Signal to Noise Ratio, SNR)会降低,可能导致目标漏检。
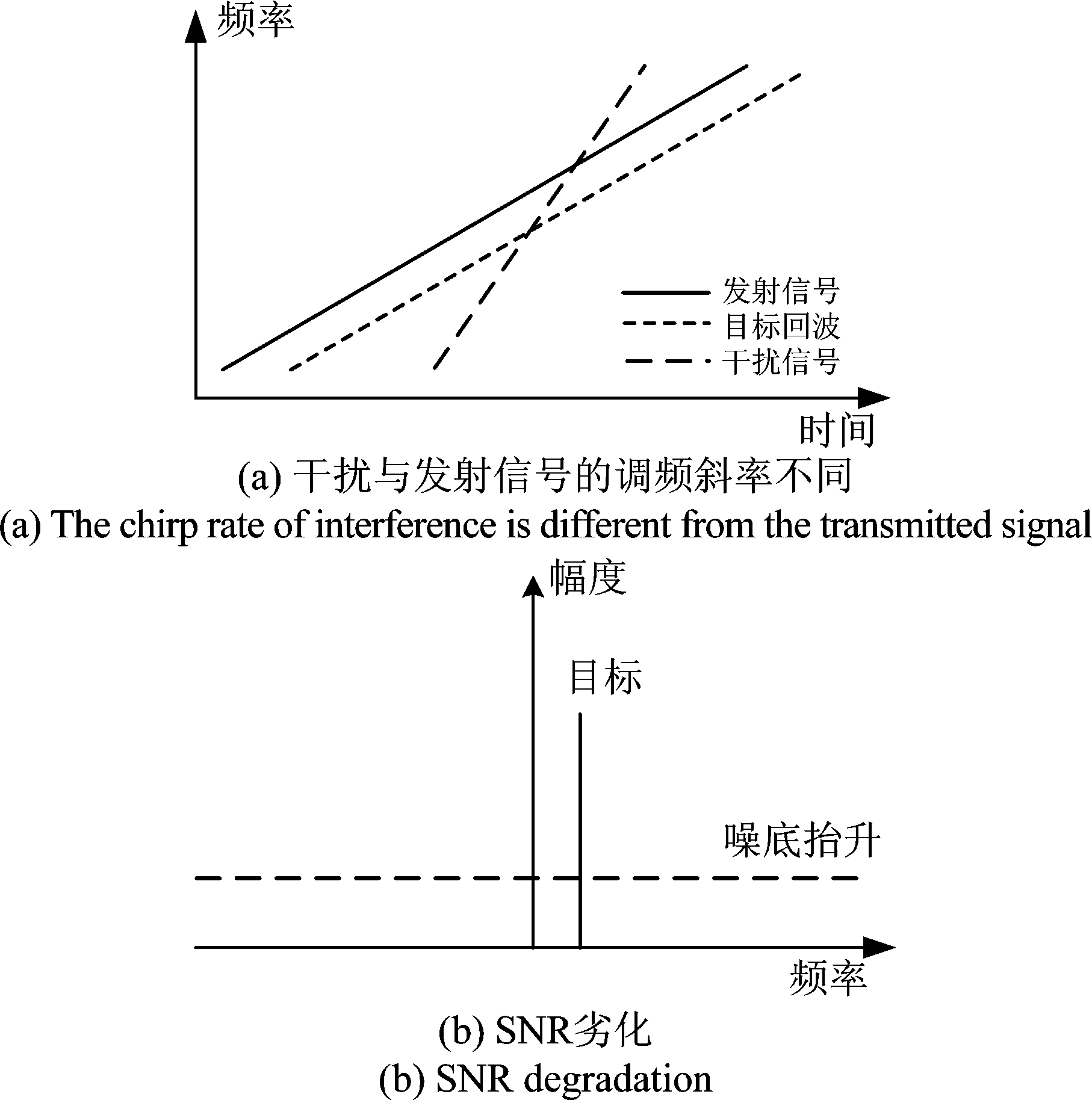
图2 不同调频斜率干扰示意图
Fig.2 Schematic diagram of interference with different chirp rate
当干扰雷达与工作雷达的调频斜率相同,且干扰信号与工作信号的差频位于抗混叠滤波器的带宽内时,干扰与参考信号的混频结果会在频谱呈现一个尖峰,可能被错误地检测为目标[12],即为假目标。
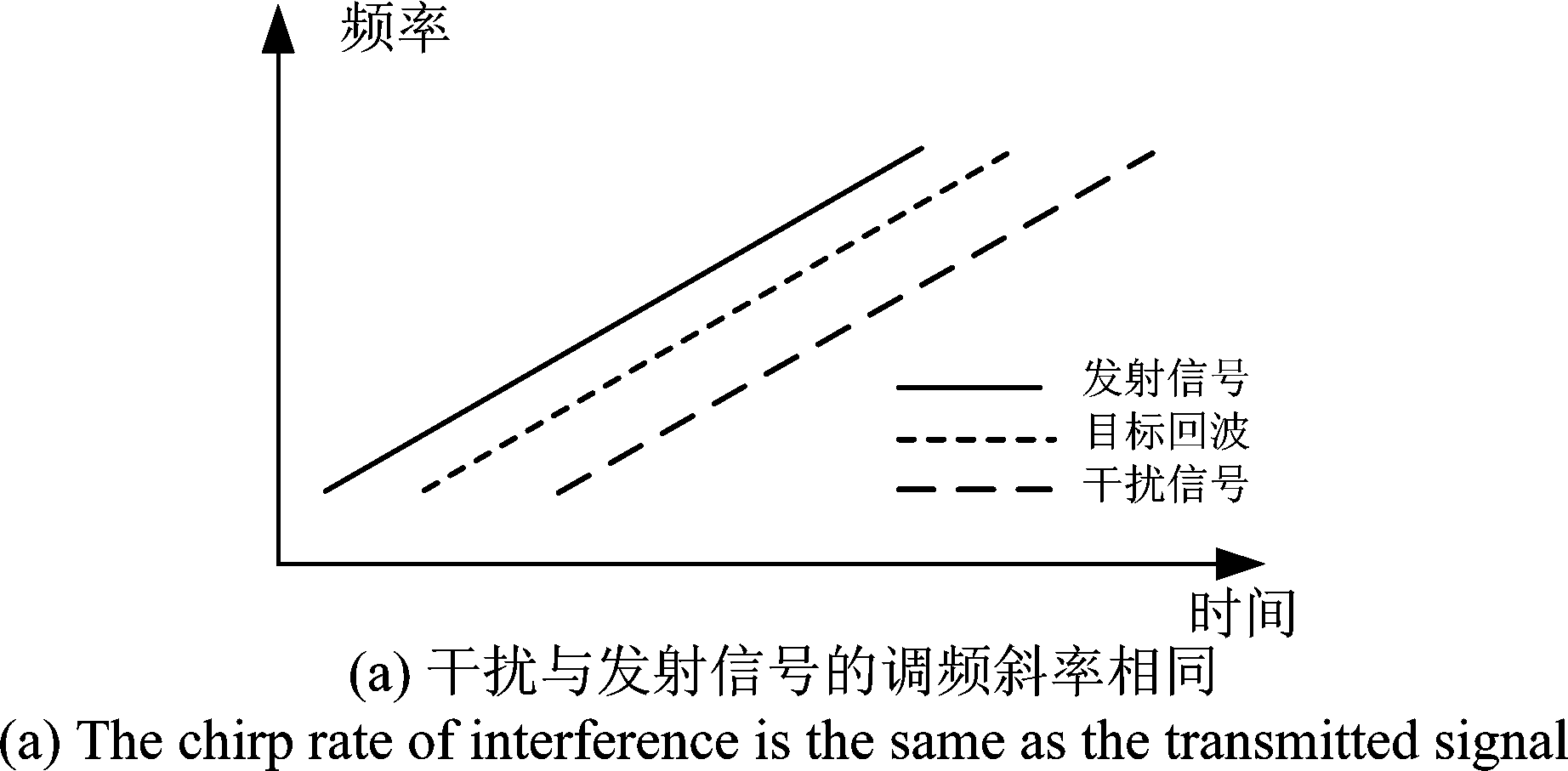
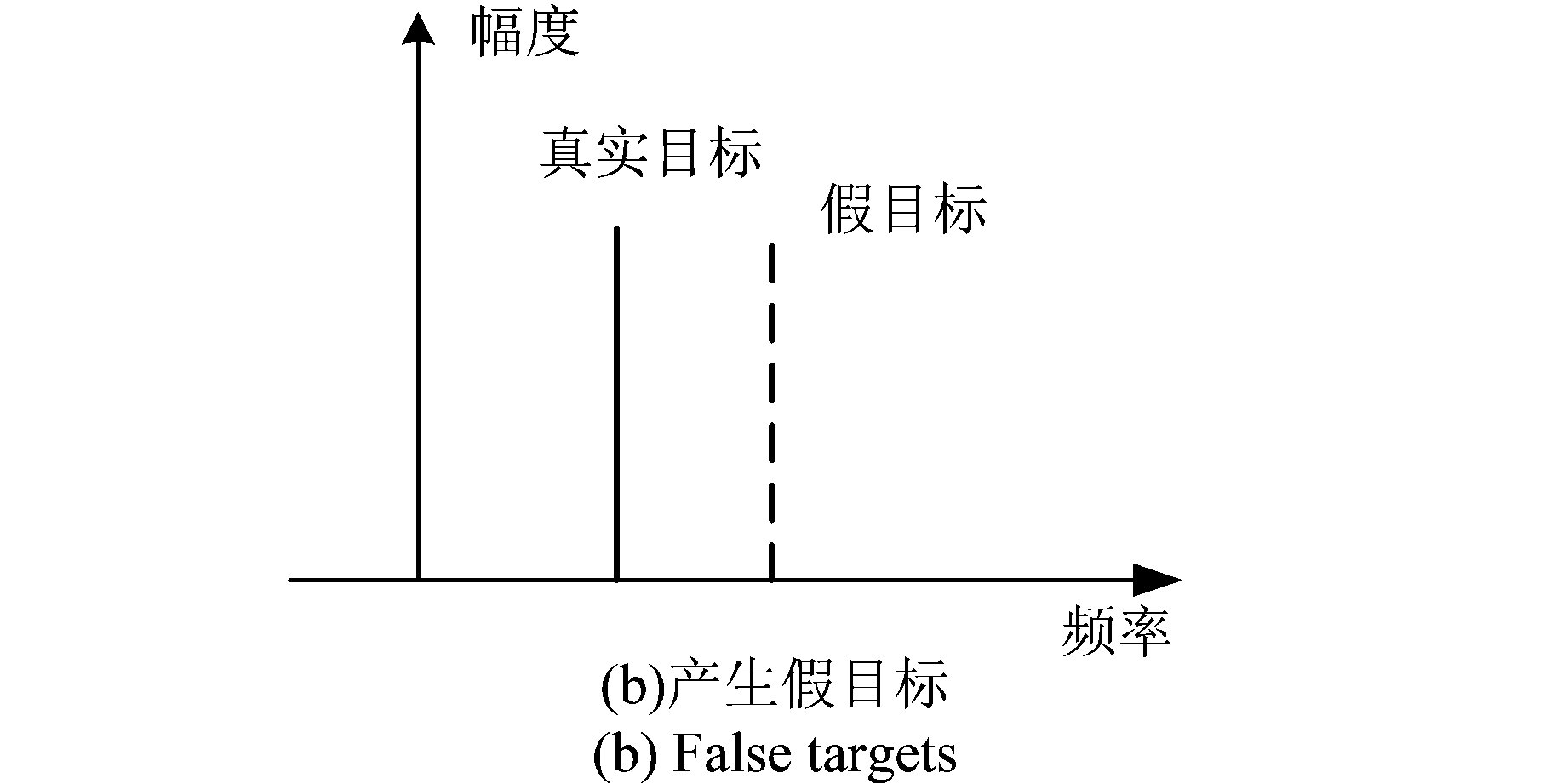
图3 相同调频斜率干扰示意图
Fig.3 Schematic diagram of interference with the same chirp rate
根据干扰分析,本文提出一种基于粒子群优化和自适应对消的干扰抑制方法。首先通过粒子群算法搜索与干扰波形相关度最低的波形参数,生成最优工作波形。再利用正交接收机内干扰的正负频谱共轭相关的特性,通过最小均方迭代得到最优滤波器,进一步实现干扰对消。该方法的示意图如图4所示。
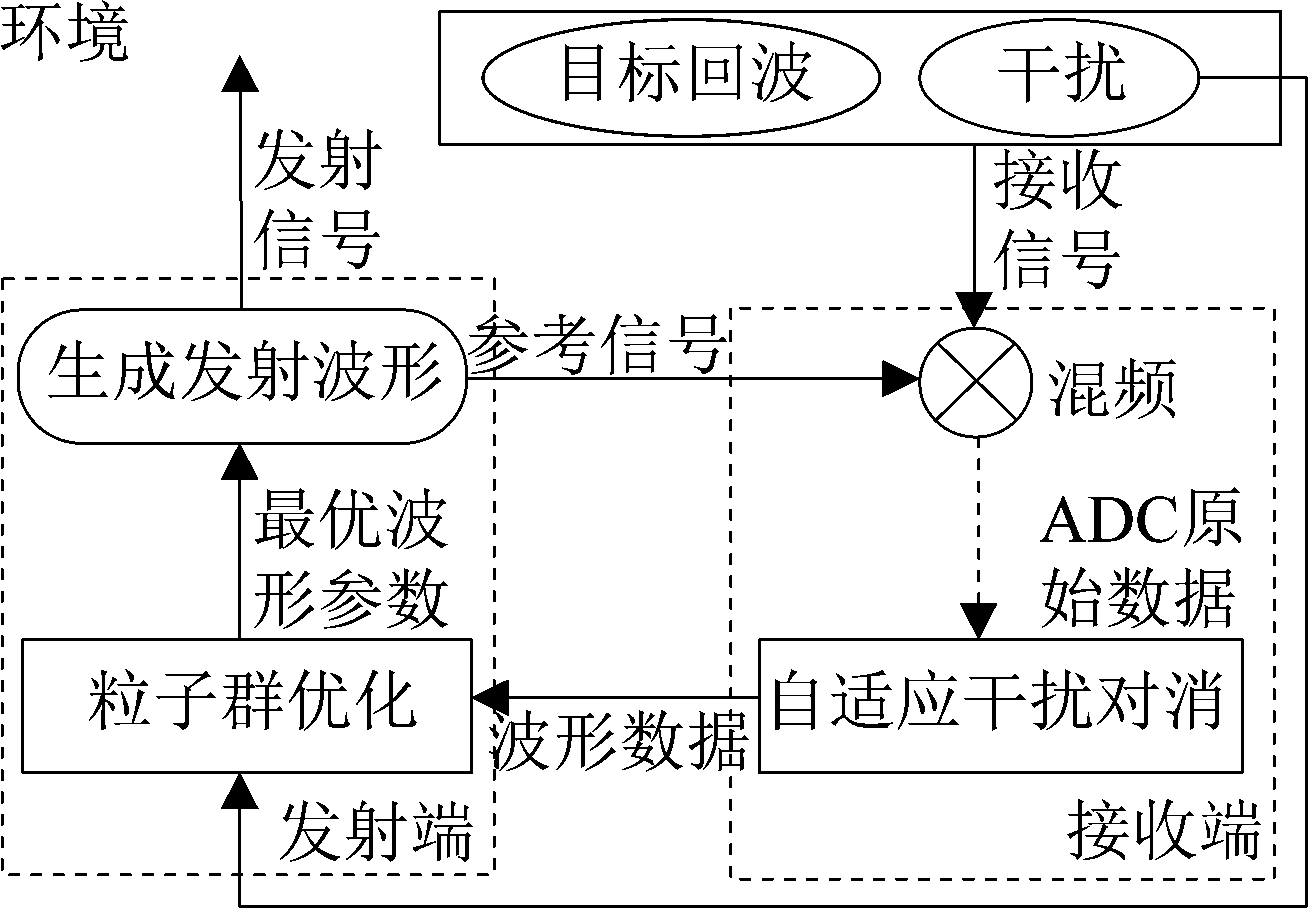
图4 所提方法示意图
Fig.4 Schematic diagram of the proposed method
本文波形优化的基本思路是在不改变调制方式的条件下,调整波形参数(主要是调频斜率和载频),使得雷达工作波形与干扰信号尽可能非相关、混频结果趋于平稳,从而结合后续干扰对消方法实现更好的干扰抑制效果。
图5为通过调整波形参数对信号进行优化的例子。图5(a)调整载频,使得信号与干扰在同一时刻的频率不重叠。在可用频段允许的情况下,可分到不同频段,通过信号处理前端的低通滤波彻底消除。图5(b)调整调频斜率,调频斜率差距增大,波形间的相关性减少,混频结果趋于平稳,可通过去噪方法进行干扰消除。
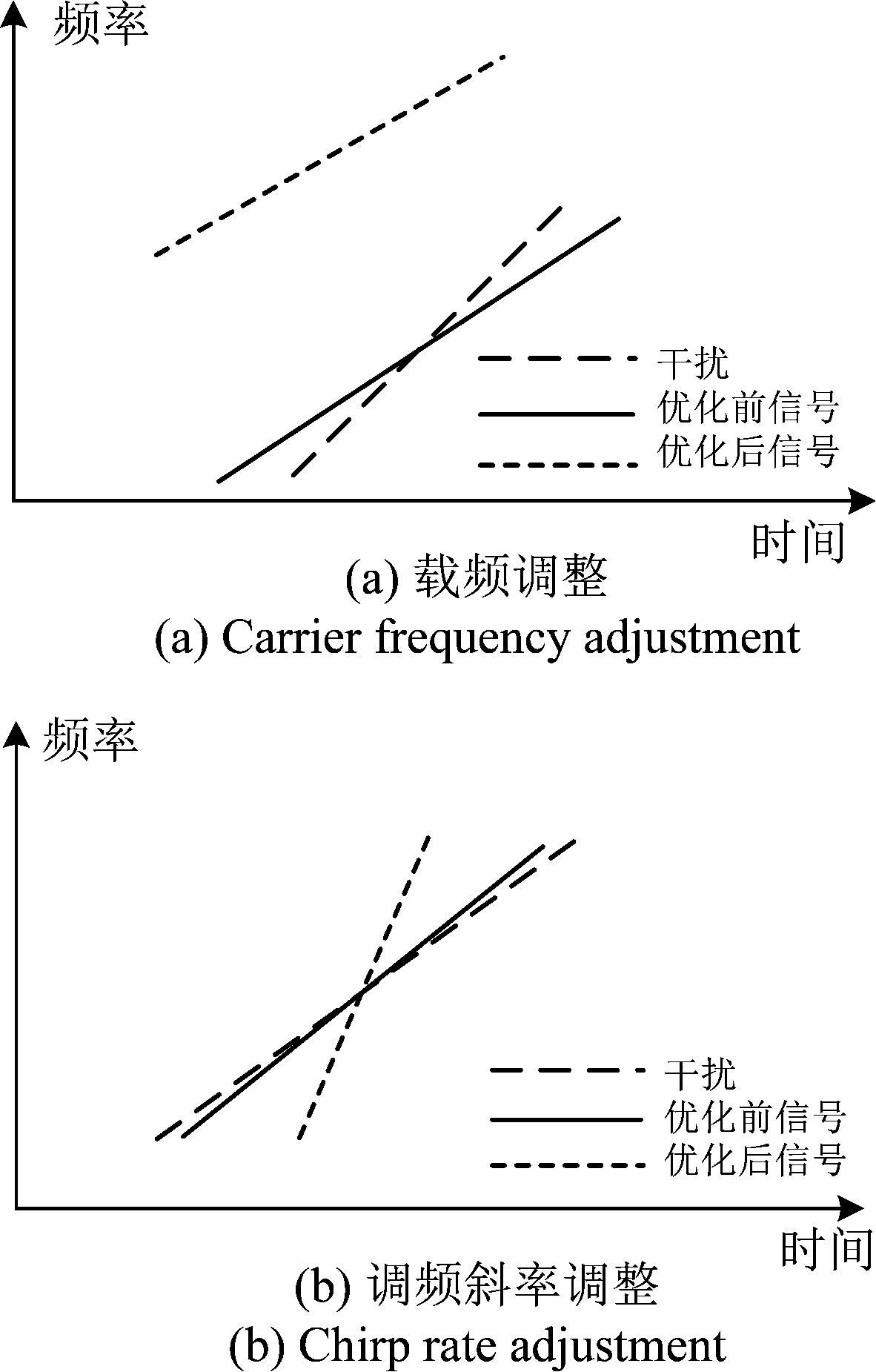
图5 波形参数优化示例
Fig.5 Example of waveform parameter optimization
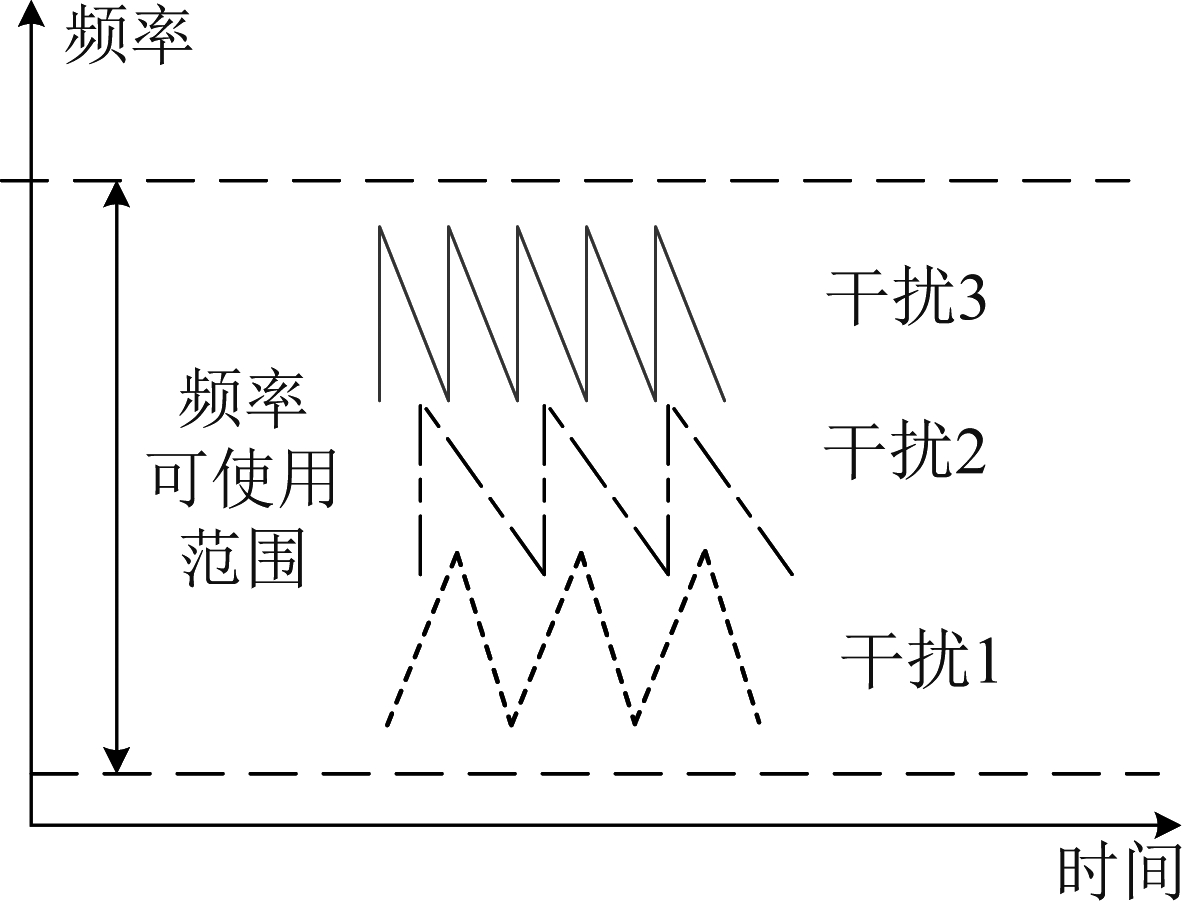
图6 多干扰情况下时频示意图
Fig.6 Time-frequency diagram in the case of multiple interference
上述干扰分析主要就FMCW雷达干扰信号展开,但波形相关性与干扰结果的联系可延展适用于其他多种干扰波形。在实际应用情况中,由于各雷达产品性能、厂商等不同,雷达干扰信号的形式较为多样,面对多数量、多种类干扰,无法通过上述的简单策略完成波形优化。智能优化算法如粒子群(Particle Swarm Optimization, PSO)算法、遗传算法(Genetic Algorithm, GA)等可以用于求解最优问题,文献[14]提出了利用粒子群算法解决大型阵列的子阵划分问题,以差波束最大副瓣电平以及权矢量逼近误差两项性能指标作为适应度函数,对比其他的常规方法,证明了粒子群算法可以收敛到最优的子阵结构。文献[15]提出一种改进的带调整参数小波阈值函数,采用粒子群优化算法寻找改进阈值函数在某一背景噪声环境中的最优参数值。因此本文中考虑采用最优化搜索方法进行波形优化。相对于GA,PSO算法的收敛速度快[16],更适应于运算性能有限、对运算实时性要求高的车载毫米波平台。故可采用PSO作为搜索算法,进行波形的最优化处理。
粒子群优化算法通过粒子之间共享信息以迭代方式得到最优解[17]。通过粒子群算法,搜索可变化范围内所有波形参数(主要对调频斜率和载频参数作约束)的最优解,即与当前干扰波形相关性最低的结果作为当前电磁环境下的最优波形。干扰获取主要参考“说前听”策略[3],在发射信号之前的短时间内仅接受外部干扰信号,通过选择与干扰相关度最低的波形参数自适应生成发射波形。利用粒子群算法进行波形参数优化的步骤如下:
STEP 1 初始化波形。根据波形优化思路,对工作波形的载频和调频斜率参数等进行最优选择。线性调频斜率由信号带宽和脉冲宽度决定,而带宽决定测量的分辨率,通常设置为固定值,故本文通过改变脉宽来改变信号调频斜率。设定自变量为脉宽和载频(考虑实际频带占用情况,以脉宽调节为主),设定约束条件为最大的搜索空间,即脉宽和载频的变化范围(其中载频变化范围设为±2%,调频斜率范围为±50%),设定最大迭代数为300。检测当前波形功率是否达到干扰抑制阈值。
STEP 2 初始化粒子群算法,设定粒子群粒子个数n为100,设定粒子初始随机位置分别为X1,X2,…,X100,设定粒子最大速度Vmax,初始化时每个粒子的初始速度都是由Vmax乘以一个取值为-1~1的随机数生成。
STEP 3 根据干扰分析确定信号波形的评价准则为工作波形和干扰波形的相关性,确定目标函数为发射信号和干扰信号的互相关函数,即
(1)
其中s(t)为工作信号,i(t)为干扰信号。将粒子位置代入目标函数,以在约束条件内使目标函数最小的自变量取值作为最优解,求个体最优解Pn和全局最优解G,更新粒子速度。
STEP 4 判断是否达到粒子群算法最大迭代次数,若不满足则更新粒子位置,并返回STEP 3继续搜索最优值;若满足输出全局最优值。
STEP 5 将全局最优的参数作为下一帧工作波形参数。
在正交接收机中,回波频谱(归一化频率)正半部分的干扰与负半部分的干扰相关,理想条件下为共轭对称。而实际目标回波仅存在于频谱的正半部分。因此,可在距离维快速傅里叶变换后,得到距离维频谱。将频谱负半部分作为滤波器功率估计的参考,正半部分和负半部分分别馈入自适应干扰消除器的主信道和参考信道,通过最小均方误差方法迭代逼近最优滤波器。
如图7所示,主输入信号d[n]包含目标回波s[n]和干扰信号i[n],参考输入i′[n]是与i[n]相关的信号。调节滤波器抽头wo,得到滤波器输出y[n],y[n]是i[n]的最佳估计,i[n]和i′[n]是宽平稳信号且与s[n]不相关。误差值e[n]是目标回波s[n]的最佳估计。在n时刻,自适应干扰对消系统的输出为
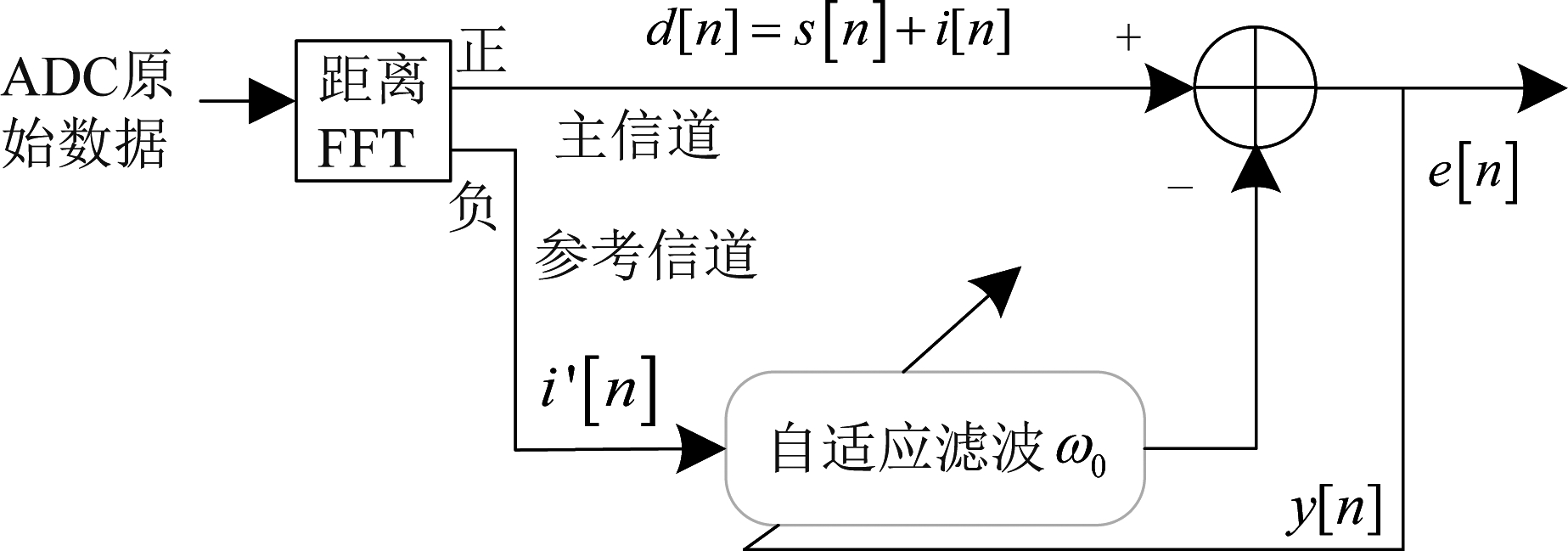
图7 自适应干扰对消示意图
Fig.7 Schematic diagram of adaptive interference canceller
![]()
(2)
进行移位和取平方、期望后,得到
min{E[(e-s)2]}=min{E[(i-y)2]}
(3)
E[s2]与滤波器的调节无关,当E[e2]最小时E[(e-s)2]最小,此时e[n]是s[n]的最小均方误差估计。最小均方(LMS)方法将过滤器的权向量w以Δw逐步迭代,得到最佳值wo。Δw控制自适应滤波器的收敛速度和稳定性。最常用的迭代最优算法是最陡下降算法,可通过下式计算权更新,
(4)
其中,▽J(n)为梯度表达式,
▽J(n)=-ri′d+2Ri′w(n)
(5)
由于最陡下降法迭代过程中需要先验的自相关矩阵和互相关向量,在实际中难以实现,因为对最陡下降法的梯度式进行估计,令
(6)
(7)
可得
(8)
将式(8)代入式(4),得到权向量更新计算如下:
w(n+1)=w(n)+Δw·i′[n]e*[n]
(9)
故采用LMS算法的自适应干扰消除器可归纳如下[18]:
滤波器输出:
y[n]=wT[n]i′[n]
(10)
代价函数:
e[n]=s[n]+i[n]-y[n]
(11)
权系数更新:
w(n+1)=w(n)+Δw·i′[n]e*[n]
(12)
通过干扰分析可知,当不同雷达的调频斜率区别度较大时,其混频结果逐渐平缓,可视为平稳。而当干扰波形调频斜率与工作波形接近时,容易产生假目标,此时的信号由于尖峰的出现无法视为平稳,但可以通过检测干扰,改变信号发射波形以增加信号与干扰间的不相关度及噪底平稳度,进而满足信号零均值广义平稳假设。表明对信号波形进行适当的优化能够更有效地利用滤波方法进行干扰抑制。文献[19]基于距离维和速度维的二维傅里叶变换技术,研究了密集地物杂波条件下LFMCW对低小慢目标的检测性能,研究表明,对于强杂波背景下的低小慢目标检测,速度维的检测至关重要。后续仿真中目标检测主要基于距离维和速度维信息展开。
仿真多部雷达场景,如图8所示。设置两个与自车同向行驶的目标和三部与自车相向行驶的干扰雷达。其中,自车雷达波形和干扰雷达1、3波形均为FMCW锯齿波调制波形,干扰雷达2为调频三角波,干扰雷达1的调频斜率与自车雷达的调频斜率相同。
雷达仿真参数配置如表1所示。
表1 仿真配置
Tab.1 Simulation configuration

类型参数(单位)值本车雷达(FMCW)fc/GHzB/MHzT/μsfs/MHzP /dBmEIRP /dBm(x0,y0)/m(νx,νy)/(m·s-1)N772005040012350,030,0256干扰1(FMCW)fc/GHzB/MHzT/μs(x0,y0)/m(νx,νy)/(m·s-1)7720050100,-2.6-25,0干扰2(调频三角波)fc/GHz77B/MHz300T/μs80(x0,y0)/m80,-3.2(νx,νy)/(m·s-1)-25,0干扰3(FMCW)fc/GHz76.8B/MHz1000T/μs20(x0,y0)/m60,-3.7(νx,νy)/(m·s-1)-30,0目标1(x0,y0)/m50,0(νx,νy)/(m·s-1)25,0目标2(x0,y0)/m70,3.1(νx,νy)/(m·s-1)35,0
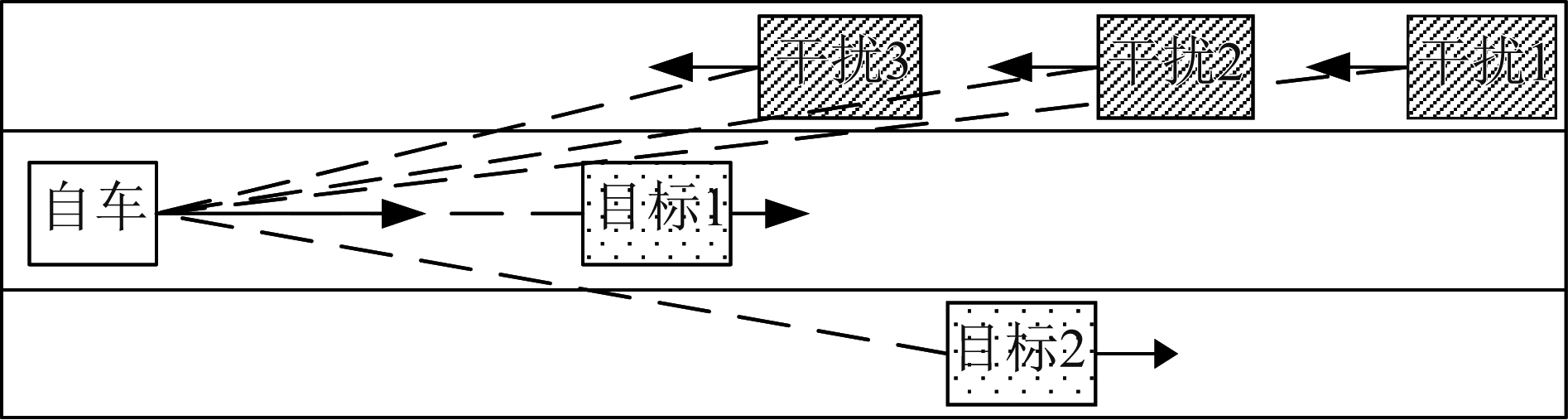
图8 仿真场景示意图
Fig.8 Schematic diagram of simulation scene
其中, fc为载频,B为带宽,T为脉宽, fs为采样率,P为发射功率,EIRP(Effective Isotropic Radiated Power)为各向有效同性辐射功率,N为相干积累个数,(x0,y0)为位置坐标,(νx,νy)为速度。
仿真得到无干扰和有干扰条件下的距离-多普勒二维和三维结果,分别如图9和图10所示。
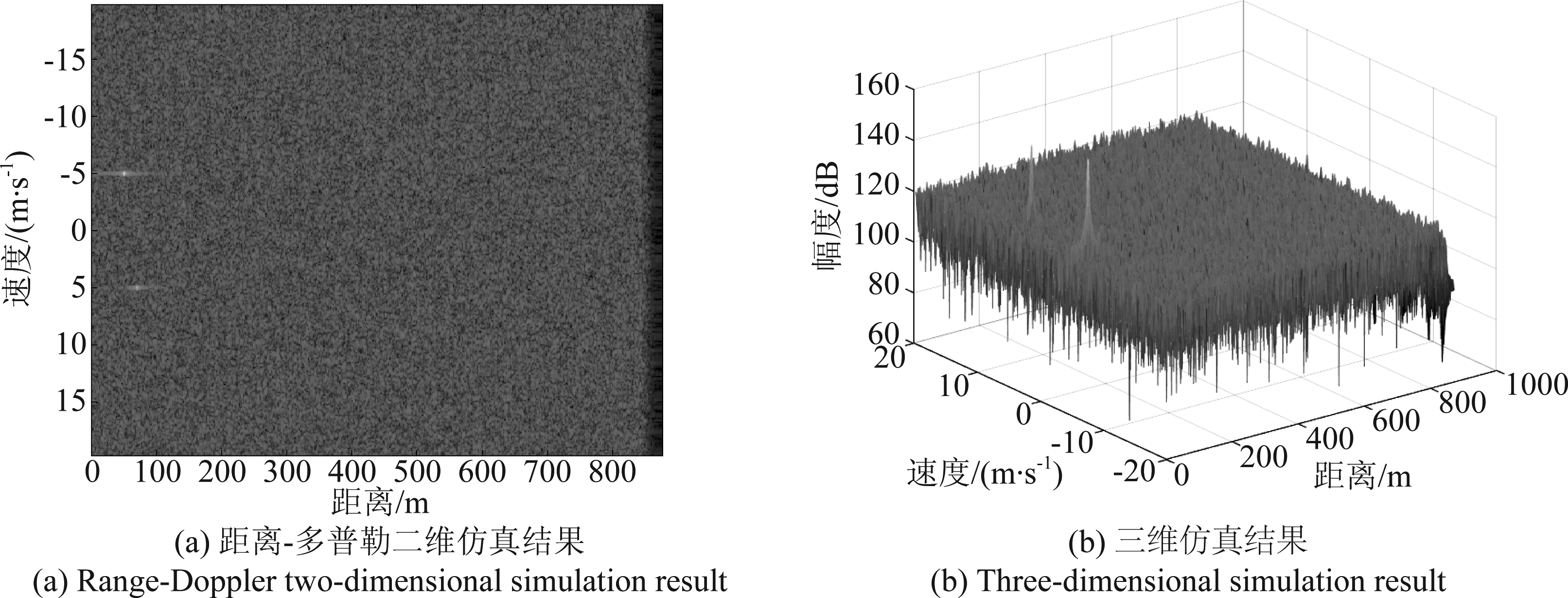
图9 无干扰时仿真结果
Fig.9 Simulation results without interference
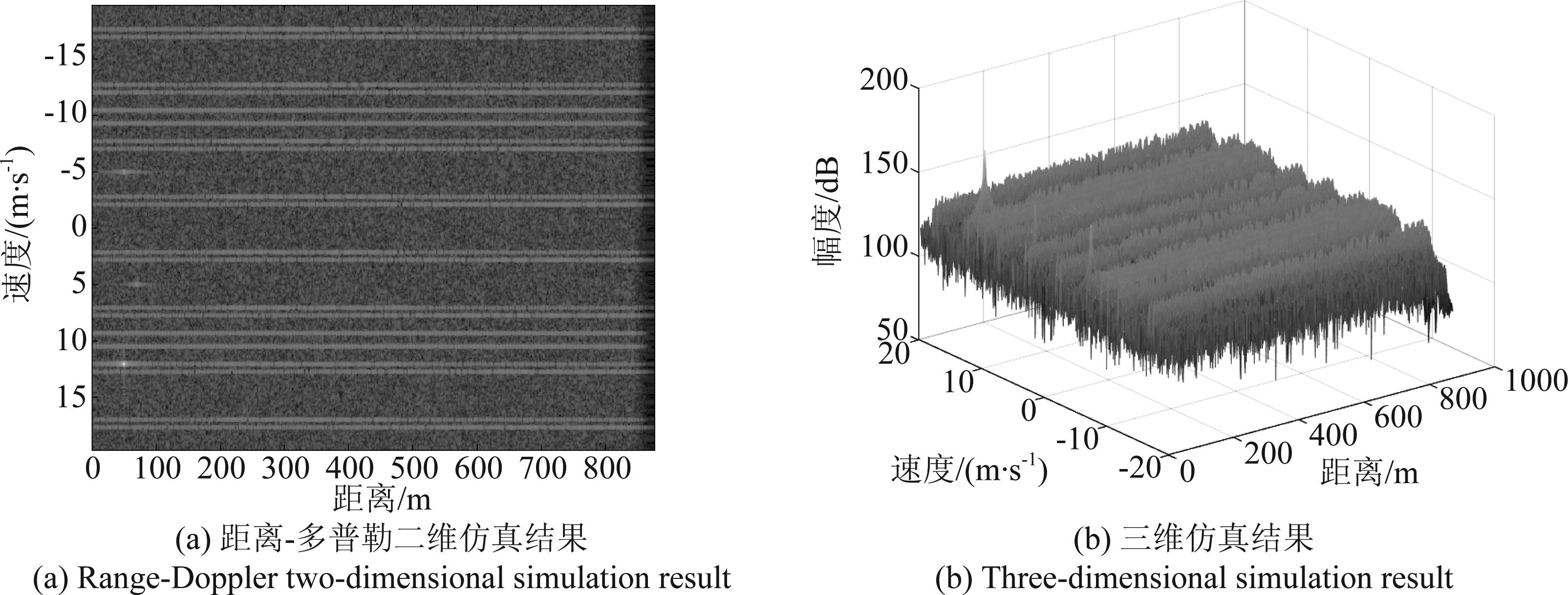
图10 有干扰时仿真结果
Fig.10 Simulation results with interference
从图10可以看出,干扰抑制前,速度单元多处有明显干扰条带,对各速度单元上的检测造成影响,此时弱目标容易被干扰信号淹没。此外,由于存在与本车雷达信号的调频斜率一致的干扰信号,仿真结果中距离本车49 m处出现了假目标。假目标的距离及速度一维像如图11所示。
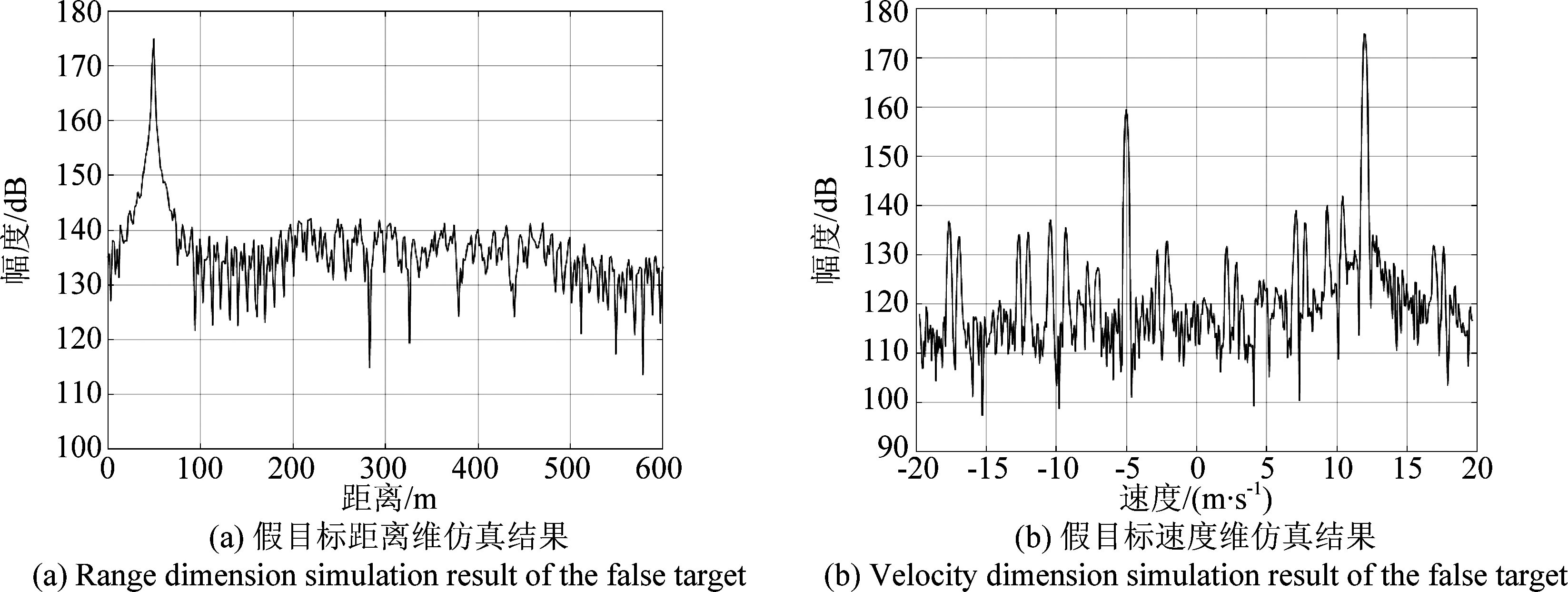
图11 假目标的距离和速度信息
Fig.11 Range and velocity information of the false target
进行滤波处理,结果如图12所示。
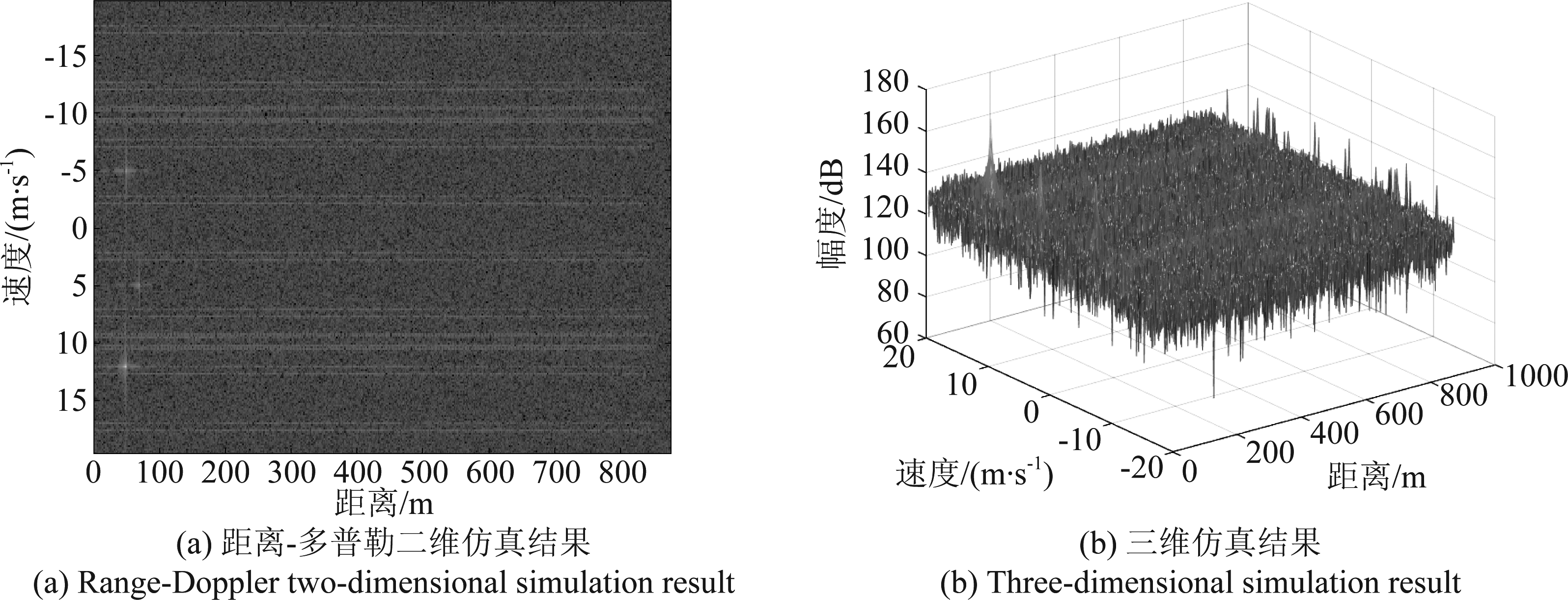
图12 滤波后仿真结果
Fig.12 Simulation results after filtering
可以看出,干扰抑制后各速度单元上的条带状干扰得到抑制,信噪比有所改善,但是假目标仍然存在,影响检测效果。故而对本车雷达发射信号进行粒子群优化,改变波形的脉宽和载频,降低发射波形同干扰波形的相关度,获得可变范围内最优解,波形优化后的二维仿真结果和原假目标位置处的信息如图13所示。
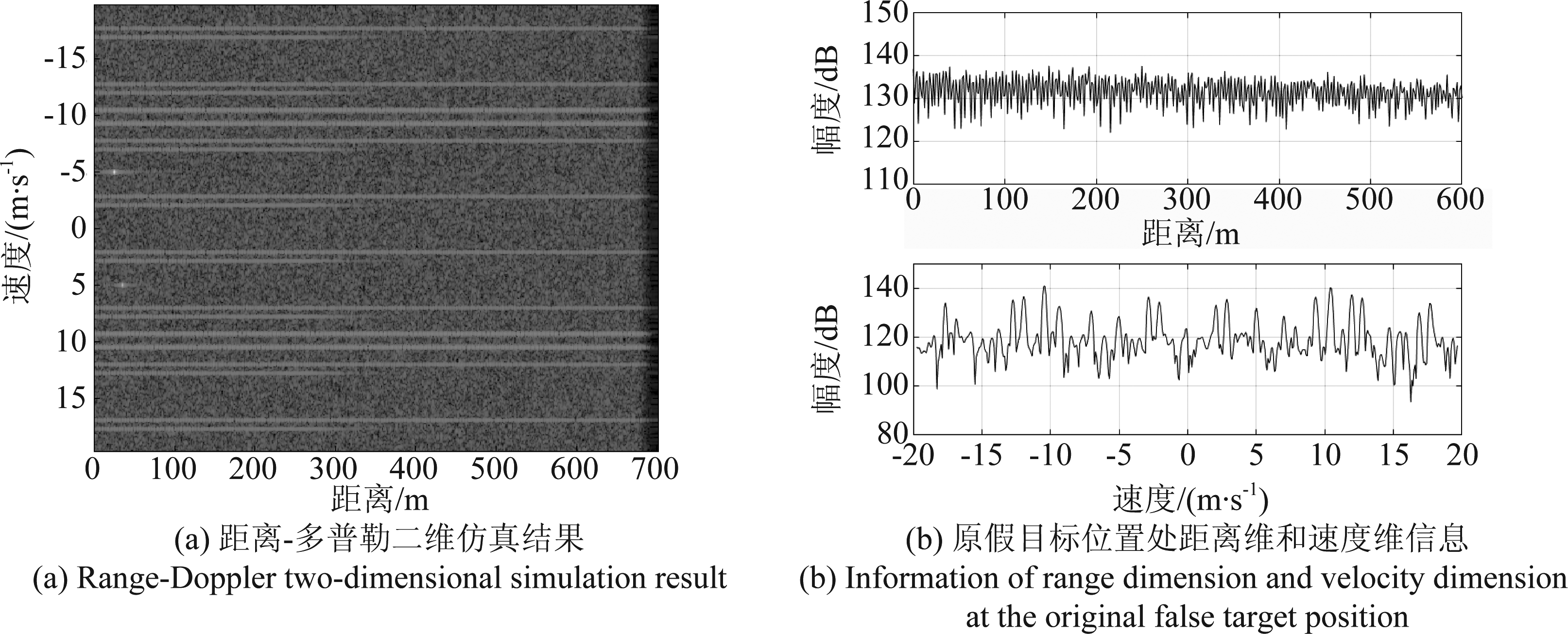
图13 波形优化后仿真结果
Fig.13 Simulation results after waveform optimization
由仿真结果可知,波形优化后,假目标位置处峰值大幅降低,假目标“消失”。此时,优化后发射波形相关参数为fc=77.02 GHz,T=32 μs。
联合波形优化和自适应对消方法进行干扰抑制,仿真结果如图14所示。
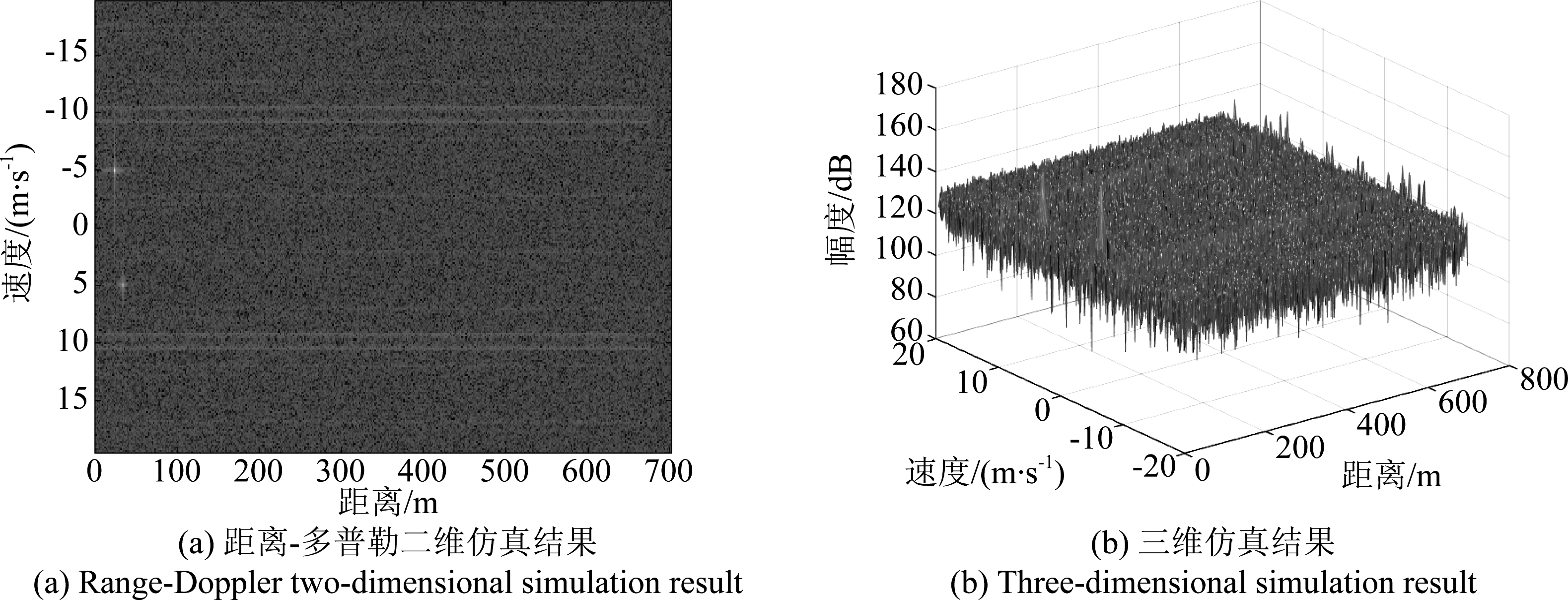
图14 应用所提算法后仿真结果
Fig.14 Simulation results after applying the proposed algorithm
由仿真结果可以看出,波形优化有利于改善假目标情况,且自适应干扰对消后信噪比改善,有利于目标检测。在此通过比较信噪比改善量来评估干扰抑制性能。对干扰抑制前、粒子群优化、使用[9]中维纳滤波方法进行干扰抑制和基于波形优化进行干扰对消四种情况进行信噪比统计,结果如表2所示。
表2 信噪比统计情况
Tab.2 Statistics of signal-to-noise ratio
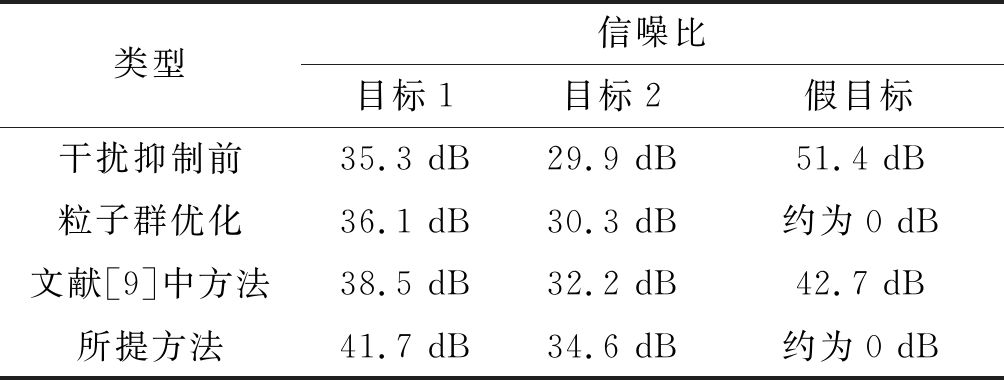
类型信噪比目标1目标2假目标干扰抑制前35.3 dB29.9 dB51.4 dB粒子群优化36.1 dB30.3 dB约为0 dB文献[9]中方法38.5 dB32.2 dB42.7 dB所提方法41.7 dB34.6 dB约为0 dB
由统计结果可以看出,文献[9]中所提维纳滤波方法可以改善信噪比,但不能完全消除假目标,粒子群优化能有效缓解虚警问题。与传统的滤波方法相比,本文所提方法能有效抑制假目标,提高信噪比。
分别使用粒子群算法和遗传算法对目标函数进行最大搜索范围内最优解求取,对算法参数进行调整达到最优状态。
表3 优化算法仿真参数
Tab.3 Optimization algorithm simulation parameters
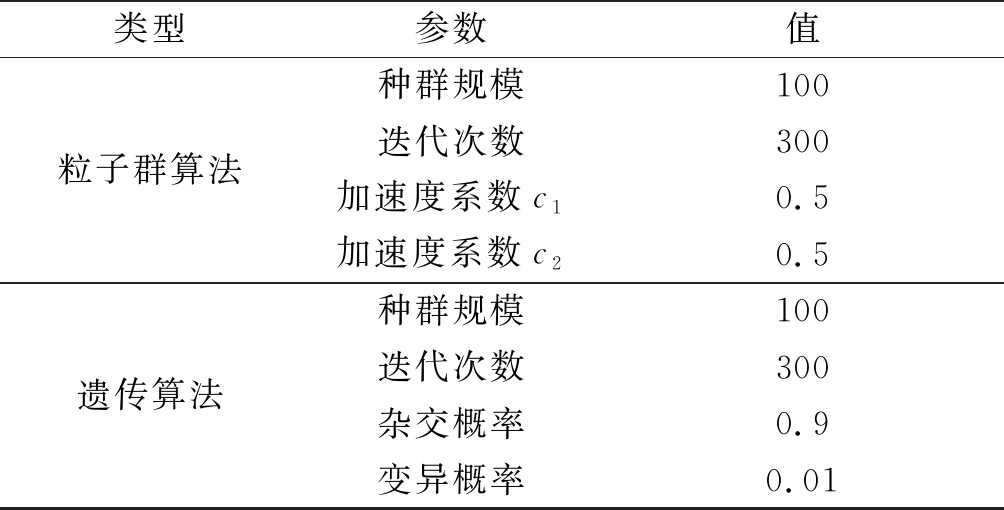
类型参数值粒子群算法种群规模迭代次数加速度系数c1加速度系数c21003000.50.5遗传算法种群规模100迭代次数300杂交概率0.9变异概率0.01
得到其收敛时间的仿真结果如图15。
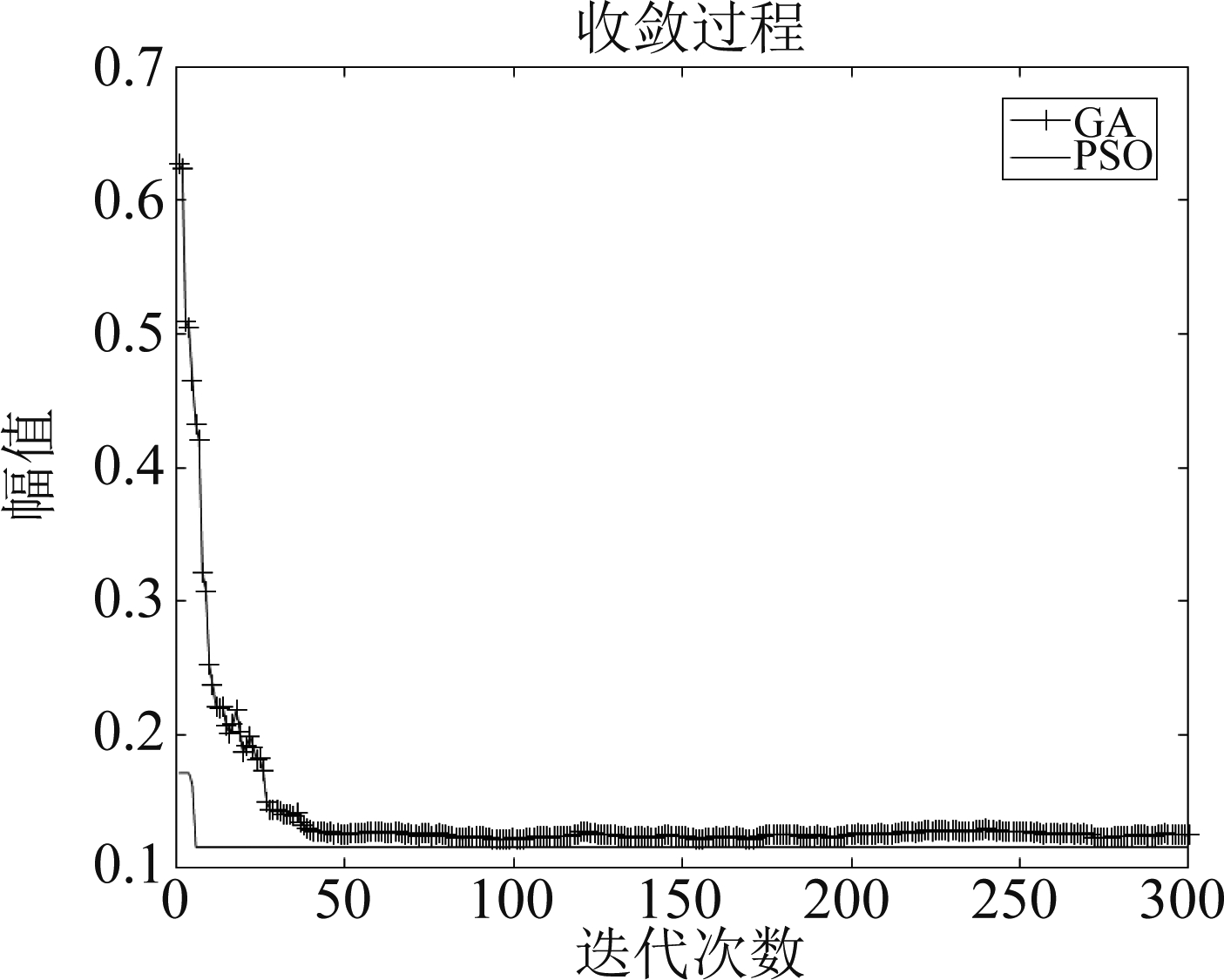
图15 优化算法收敛时间比较
Fig.15 Comparison of optimization algorithm convergence time
由仿真结果可知,使用两种算法使得相应的目标函数收敛到最优解,粒子群算法收敛的最优解略小于遗传算法。粒子群算法在迭代7次后达到最优解,而遗传算法迭代了46次后达到最优解,可以看出,粒子群算法的收敛时间比遗传算法更短,更有利于进行实时处理。
本文针对FMCW车载雷达干扰问题,提出了基于粒子群优化和自适应干扰对消的干扰抑制方法,该方法将发射端波形优化和接收端自适应滤波相结合,进行时频域联合抗干扰,进一步提高干扰抑制效果。利用粒子群算法在约束范围内得到最优波形参数,使发射波形与干扰波形的相关度最低。通过最小均方方法构建最优滤波器,根据干扰在正负频谱共轭相关的特点实现干扰对消。仿真结果表明,与传统抗干扰方法相比,本文提出的方法更适用于密集多干扰交通环境,并且可以更好地进行实时处理和实现雷达间相互干扰抑制,有效缓解假目标问题。
[1] 贺利良. 77 GHz车载雷达系统防干扰技术及专利申请分布研究[J]. 科学与信息化, 2018(30): 44- 44.
HE Liliang. Research on anti-interference technology and patent application distribution of 77 GHz vehicle radar system[J]. Science and Information Technology, 2018(30): 44- 44.(in Chinese)
[2] BROOKER G M. Mutual interference of millimeter-wave radar systems[J]. IEEE Transactions on Electromagnetic Compatibility, 2007, 49(1): 170-181.
[3] MARTIN KUNERT. The EU project MOSARIM: A general overview of project objectives and conducted work[C]∥2012 9th European Radar Conference (EuRAD). 2012(01): 1-5.
[4] SEFA Tanis. 汽车雷达传感器和拥挤不堪的无线电频谱: 潜在的城市电子战场[J]. 微波杂志, 2019, 3/4: 46-54.
SEFA Tanis. Automotive Radar Sensors and Congested Radio Spectrum: An Urban Electronic Battle field[J]. Microwave Journal China, 2019, 3/4: 46-54.(in Chinese)
[5] HU Xueyao, LI Yang, LU Man, et al. A Multi-Carrier-Frequency Random-Transmission Chirp Sequence for TDM MIMO Automotive Radar[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3672-3685.
[6] 李骥, 段杏燕, 王威, 等. 载波编码多载波相位编码雷达信号抗间歇采样干扰研究[J]. 信号处理, 2020, 36(7): 1166-1174.
LI Ji, DUAN Xingyan, WANG Wei, et al. Research on Anti-Interrupted Sampling Repeater Jamming Based on CC-MCPC Radar Signal[J]. Journal of Signal Processing, 2020, 36(7): 1166-1174.(in Chinese)
[7] 纠博, 刘宏伟, 胡利平, 等. 针对目标识别的波形优化设计方法[J]. 电子与信息学报, 2009, 31(11): 2585-2590.
JIU Bo, LIU Hongwei, HU Liping, et al. Waveform optimization design method for target recognition[J]. Journal of Electronics and Information, 2009, 31(11): 2585-2590.(in Chinese)
[8] 郝昭昕, 孙进平. 基于量子遗传算法的MIMO雷达正交信号波形设计[J]. 信号处理, 2019, 35(6): 1064-1071.
HAO Zhaoxin, SUN Jinping. MIMO Radar Orthogonal Waveform Design Based on Quantum Genetic Algorithm[J]. Journal of Signal Processing, 2019, 35(6): 1064-1071.(in Chinese)
[9] WIDROW B, GLOVER J R, MCCOOL J M, et al. Adaptive noise cancelling: Principles and applications[J]. Proceedings of the IEEE, 1975, 63(12): 1692-1716.
[10] HARRIS F, TRAGER D, DAVIS C, et al. Adaptive filtering for FMCW interference mitigation in PMCW radar systems[P]. U.S.: 9791564, 2017.10.17.
[11] JIN F, CAO S. Automotive radar interference mitigation using adaptive noise canceller[J]. IEEE Transactions on Vehicular Technology, 2019, 68(4): 3747-3754.
[12] MAKINO Y, NOZAWA T, UMEHIRA M, et al. Inter-radar interference analysis of FMCW radars with different chirp rates[J]. The Journal of Engineering, 2019, 2019(19): 5634-5638.
[13] KIM G, MUN J, LEE J. A peer-to-peer interference analysis for automotive chirp sequence radars[J]. IEEE Transactions on Vehicular Technology, 2018, 67(9): 8110- 8117.
[14] 胡尚坤, 孙雨泽, 杨小鹏, 等. 一种基于粒子群算法的多目标子阵划分优化方法[J]. 信号处理, 2017, 33(8): 1132-1137.
HU Shangkun, SUN Yuze, YANG Xiaopeng, et al. A Multi-Objective Optimization Subarray Partition Method Based On Particle Swarm Optimization[J]. Journal of Signal Processing, 2017, 33(8): 1132-1137.(in Chinese)
[15] 唐鹏, 郭宝平. 改进型阈值函数寻优法的小波去噪分析[J]. 信号处理, 2017, 33(1): 102-110.
TANG Peng, GUO Baoping. Wavelet Denoising Based on Modified Threshold Function Optimization Method[J]. Journal of Signal Processing, 2017, 33(1): 102-110.(in Chinese)
[16] 沈艳, 郭兵, 古天祥. 粒子群优化算法及其与遗传算法的比较[J]. 电子科技大学学报, 2005(5): 696- 699.
SHEN Yan, GUO Bin, GU Tianxiang. Particle swarm optimization algorithm and its comparison with genetic algorithm[J]. Journal of University of Electronic Science and Technology of China, 2005(5): 696- 699.(in Chinese)
[17] BAI Q. Analysis of particle swarm optimization algorithm[J]. Computer and Information Science, 2010, 3(1): 180.
[18] HAYKIN S S. Adaptive filter theory[M]. Pearson Education India, 2008.
[19] 余启, 饶彬, 罗鹏飞. 线性调频连续波雷达对低小慢目标检测及性能分析[J]. 信号处理, 2019, 35(1): 1-7.
YU Qi, RAO Bin, LUO Pengfei. Detection Performance Analysis of Low Slow and Small Target Based on LFMCW Radar[J]. Journal of Signal Processing, 2019, 35(1): 1-7.(in Chinese)
李 阳 男, 1979年生, 辽宁人。北京理工大学信息与电子学院副研究员, 主要研究方向为宽带雷达系统、雷达信号处理。
E-mail: bit_liyang@bit.edu.cn
王楚媛 女, 1996年生, 云南人。北京理工大学信息与电子学院硕士研究生, 主要研究方向为雷达抗干扰技术。
E-mail: trulyw919@163.com
陈 桥 男,1987年生,山东人。北京理工睿行电子科技有限公司雷达系统工程师,硕士,主要研究方向为雷达信号处理。
E-mail: chenqiao@racodf.com
李 枫(通信作者) 男, 1979年生, 吉林人。北京理工大学信息与电子学院讲师, 主要研究方向为雷达抗干扰技术、SAR成像算法、雷达系统。
E-mail: karl1820@bit.edu.cn
胡 程 男, 1981年生, 湖南人。北京理工大学信息与电子学院教授, 主要研究方向为新体制雷达、雷达信号处理。
E-mail: cchchb@bit.edu.cn