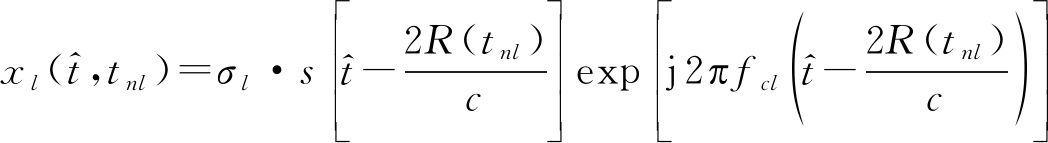
Reference format: WANG Ning, MENG Jinli, LIU Guoqing, et al. Airborne Radar Weak Target Interframe Noncoherent Integration and Detection Method[J]. Journal of Signal Processing, 2021, 37(2): 248-257. DOI: 10.16798/j.issn.1003- 0530.2021.02.010.
机载雷达具有探测范围广、部署机动灵活等优势,在现代战争中具有非常重要的军事意义。现代战争中隐身飞机、无人飞机、巡航导弹等低雷达横截面积(RCS)目标的广泛应用,使得微弱目标探测成为雷达的重要需求。虽然进行雷达系统设计时,可以通过提高发射机功率和效率、降低接收机噪声系数和系统损耗、增大天线阵面孔径等措施,可以提升雷达的探测威力。但是这些措施会受限于价格、功耗、体积等因素,尤其是机载平台条件更加严苛。在优化系统设计的基础上,通过实现灵活和低费效比的信号处理手段来进行微弱目标检测,一直以来都是雷达技术研究中重点关注的发展方向。
雷达对微弱目标的探测,主要通过以下两类技术路线来实现:第一类技术路线是增加目标探测时波束驻留时间的长时间相参积累技术,通过在单帧数据中对目标进行长时间观测,提升雷达的探测性能。但是,运动目标在雷达观测过程中由于距离和速度变化,可能会存在“三跨问题”,即跨距离单元、跨多普勒单元和跨波束等问题。研究人员针对目标的长时间积累技术开展了广泛研究,提出了一系列应用于不同场景的有效方法。Keystone变换[1]可以实现径向速度近似匀速的目标距离单元走动补偿,改进目标的长时间积累性能。Radon-Fourier变换(RFT)方法[2- 6]根据目标的运动参数进行距离-速度二维搜索,以实现目标的长时间积累。匀加速模型也是一种常用的目标运动模型,即假设目标具有近似恒定的径向加速度,此时目标回波在脉冲间的表现为线性调频信号。为了实现这种模型下目标的长时间积累,研究人员提出了Radon-Wigner变换[7- 8]、Wigner-Hough变换[9-10]、分数阶傅里叶变换[11]等方法。第二类技术路线是检测前跟踪(TBD)技术,通过多帧数据的联合处理,提升微弱目标的检测性能。TBD的思想是,降低单帧检测门限提高微弱目标的检测概率,但检测的虚警概率也被指数级提高。此时需要借助跟踪算法来抑制虚警,同时对可能的目标运动轨迹进行能量积累,最后根据目标运动轨迹做出检测判决。典型的TBD算法包括基于Hough变换、基于动态规划和基于粒子滤波的TBD算法[12-23]等。近年来,为了实现更优的弱目标检测,研究人员还提出了对多帧数据进行相参积累的相参TBD算法[24-25]。相参TBD算法一般假设多帧之间的工作参数保持不变,且帧间回波仍能保证相参性。这些假设在工程实现上往往受到一定的限制。
机载雷达采用脉冲多普勒(PD)技术分离静止杂波与运动目标,以实现强杂波下的目标探测。机载雷达采用PD体制进行目标探测时,发射一组具有相同脉冲重复间隔(PRI)的脉冲,所获得的回波信号称为一帧数据。机载雷达的PD工作模式,脉冲间PRI一般较小,目标存在距离模糊问题。为了解决目标距离模糊问题,需要同一个波束指向采用多组不同PRI进行探测,利用不同帧间的PRI参差实现距离解模糊。同时,为了避免发射信号被有意或无意辐射源干扰,不同帧之间往往采用不同载频。机载雷达的广域探测需求,使得单帧数据的积累时间长度受限。多帧之间载频和/或PRI的改变,使得目标在不同帧间的多普勒单元不同,同时雷达载机和目标的相对速度较大,目标在多帧之间还存在目标跨距离单元的问题。而且,由于需要帧间解距离模糊,若采用较低的门限进行目标检测,大量的虚警点不仅会大幅提升帧间数据关联和跟踪算法的处理复杂度,还极易形成虚假航迹。因此常规的长时间积累和TBD算法的应用均存在一定的局限性。针对机载雷达进行微弱目标探测时面临的以上问题,提出了一种应用于匀速运动目标的帧间非相参积累和目标检测方法,通过对不同帧间目标的多普勒校正和距离补偿,实现帧间目标的非相参积累,提升微弱目标的检测性能。
假设某机载雷达一帧数据中发射N个脉冲,一个波束指向内发射L帧不同参数的波形进行目标探测,其中第l帧的载频为fcl,发射PRI为Trl,l=1,…,L。假设每帧数据的发射脉冲数N保持不变,并且脉冲采用相同的调制方式,信号带宽为B,信号的脉冲宽度为T。
假设一个相对于雷达径向速度为匀速运动的目标,在雷达某个探测波位中,目标与雷达的相对运动速度为ν=νt+νa,其中νt和νa分别为目标径向速度和雷达载机径向速度,初始距离为R0。对于绝大多数目标而言,满足ν≪c的条件(c是电磁波传播速度),雷达一帧回波信号的目标模型可以采用“stop-go”模型[26]。若雷达每帧数据都以它的第一个脉冲的起始作为初始时刻,则第n(n=1,…,N)个脉冲的发射时刻为tnl=(n-1)Trl,其目标回波信号可以表示为:
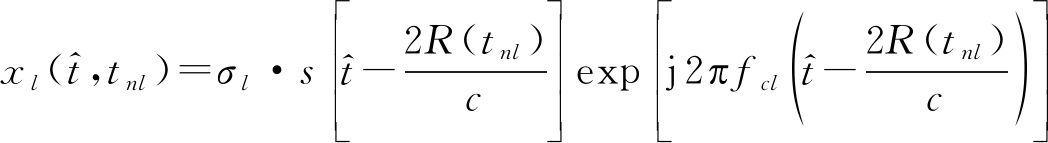
(1)
其中,σl表示第l帧数据中目标回波的幅度和相位,一般情况下假设在一帧数据中该值为常数。s(t)为基带信号。上式中,雷达时间
其中,
为距离维脉内采样时间,即快时间;tnl为脉冲维脉间时间,即慢时间。R(tnl)=R0-ν·tnl表示第n个脉冲时目标和雷达之间的径向距离。
对于机载雷达而言,进行目标探测时大多采用窄带信号,因此可以假设目标在一帧数据的探测时间内不存在距离走动问题,也不会出现跨波束问题。但是由于同一个波位需要进行多帧探测,多帧的总时间长度内目标距离走动问题不可忽略,但一般而言仍然不存在目标跨波束问题。假设对于某个波束指向第l帧数据的积累时间为TCl。以第一帧数据的第一个发射脉冲的起始作为初始时刻,则第l帧数据的起始时刻可以表示为
对于一个匀速运动目标,其在第l帧的第n个脉冲时与雷达的距离表示为:
Rl(tnl)=R0-ν·[TFramel+tnl]
(2)
则第l帧的第n个脉冲的回波信号可以重新表示为:
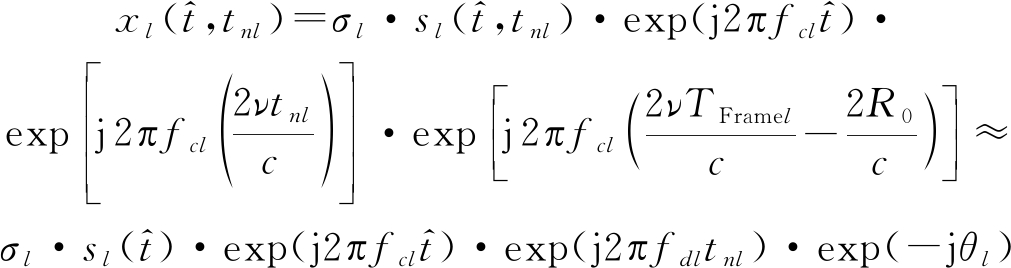
(3)
其中, fdl=2νfcl/c为第l帧数据的目标多普勒频率,θl=4πfcl(R0-νTFramel)/c表示第l帧的目标相位,
表示第l帧数据内的目标基带回波信号。由于可以忽略目标在一帧时间内的距离走动,而只需考虑目标在不同帧间的距离变化,则
Rl(tnl)≈Rl0=R0-νTFramel
(4)
因此,可以认为
公式(3)进行下变频和数字AD转换后的基带数字信号可写成:
xl(m,n)=σl·sl(m)·exp(j2πfdl·nTrl)·exp(-jθl)
(5)
其中,m和n表示第n个脉冲的第m个采样点。ts为快时间采样间隔, fs=1/ts为快时间采样率。为了保证回波信号的无失真采样,采样率需要满足fs≥B。不失一般性的,假设fs=B。
获取的接收信号xl(m,n)需要先对每个脉冲进行脉冲压缩,然后对每个距离单元进行脉冲间PD相参积累。公式(5)中的接收基带波形sl(m)经过脉冲压缩后,积累的目标能量位于目标延时对应的采样单元,因此我们可以将σl重新表示为目标经过脉压后的回波幅度,则第l帧数据的信号可以表示为:
xl(m,n)=[σl·exp(-jθl)]·exp(j2πfdl·nTrl)=
alexp(j2πfdl·nTrl)
(6)
其中,al=[σl·exp(-jθl)]为一复常数,包含了目标的反射系数、回波初始相位等信息。由于需要对每个距离单元逐一进行PD处理,为了表示方便将采样距离单元的标识m省略。
根据上一节构建的机载雷达信号模型,同一个波束指向的L帧数据中,信号的带宽和脉宽相同,但是载频和/或PRI不同。直接进行多帧数据的非相参积累存在以下几个问题:
1)每帧数据采用的载频和/或PRI不同时,相同速度的匀速运动目标,所在的多普勒频率单元不同。
2)同一个波束指向多帧数据的总时间长度较长,运动目标在多帧数据中存在距离单元走动。
3)每帧数据采用不同PRI,意味着每帧的最大模糊距离不同。远距离目标存在距离模糊,会造成目标在多帧数据之间的距离单元不同。
针对上述问题,为了提升微弱目标的检测性能,提出了一种帧间多普勒频率校正方法,然后进行目标距离走动补偿,以及模糊距离扩展,实现帧间的目标积累,并解决目标的距离模糊问题。
由于载机速度νa已知,可以先对载机速度引起的多普勒频率进行补偿,在公式(6)中的目标回波信号变为:
alexp(j2πftl·nTrl)
(7)
其中, ftl=2νt fcl/c为第l帧数据中目标径向速度引起的多普勒频率。
对公式(7)的yl(n)进行PD处理,其本质是进行傅里叶变换,可得:
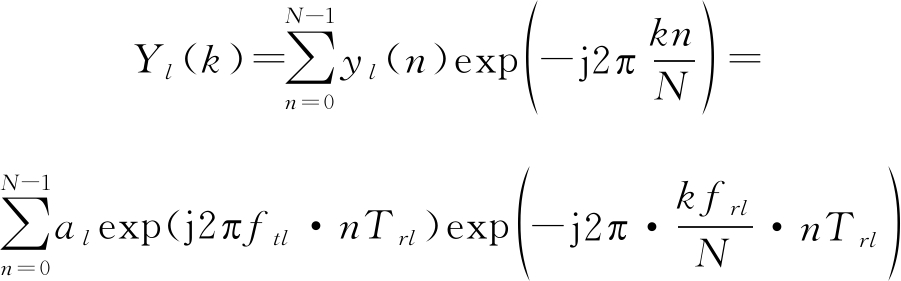
(8)
其中, frl为第l帧数据的脉冲重复频率(PRF),即
表示第k个多普勒单元。
显然,当帧间的载频不同、PRI不同时,同一速度的目标会出现在不同多普勒单元。可以通过如下的伸缩变换使得目标在不同参数的数据中,出现在相同的多普勒单元:
(9)
其中, fc0和Tr0为参考载频和参考PRI。γl=γflγTl称为第l帧数据的变换系数,
为载频变换系数,
为PRI的变换系数。速度为νt的目标在参考载频下的多普勒都变为
机载雷达MPRF工作模式具有更好的场景适应性,可以用于探测迎头、尾追等各种场景下的高速或慢速目标,后续分析中重点基于MPRF工作模式展开。MPRF模式下,目标可能同时存在距离模糊和速度模糊。为了使得目标在不同参数的数据中出现在相同的多普勒单元,进行公式(8)中的伸缩变换,并考虑到MPRF模式下运动目标的速度模糊,需要进行如下变换:
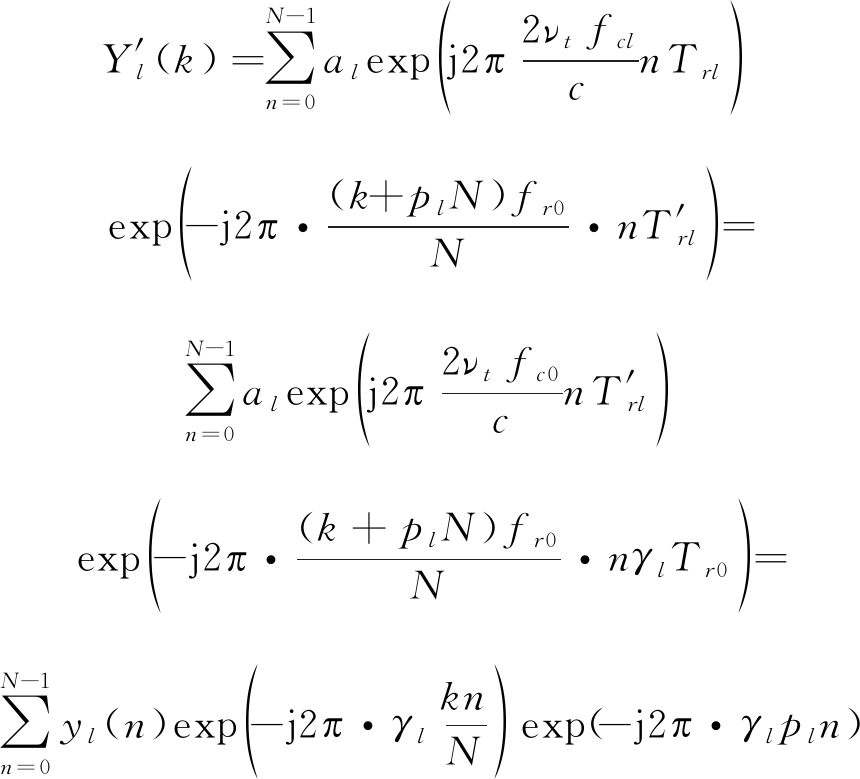
(10)
其中,pl=fix(2νt fcl/frl)为第l帧数据中的目标速度模糊数, fix(·)为向零取整操作。上述运算可以利用CZT(Chirp Z Transform)来快速实现[27]。
需要说明的是,此处的信号模型以及后续提出的算法,考虑了最复杂的场景,即,距离模糊、速度模糊、距离走动同时存在的情况。这是为了说明本文提出算法具有应用于不同场景的普适性。实际应用场景中,距离模糊和距离走动情况的现象较为常见,而速度模糊问题在不同系统中可能存在不同的情况。通过公式(10)可知,不同速度模糊数的目标需要进行不同处理。这与传统机载雷达的PD处理方式相比,可能会带来计算量成倍的增加。但是,对于工作在较低频率的机载预警雷达而言,以美军E2-D预警机为例,其AN/APY-1雷达工作频段为UHF,300 m/s速度的目标在300 MHz载频时对应的多普勒频率为600 Hz,远小于雷达MPRF模式下采用的PRF,即可以不考虑目标的速度模糊问题,将p取值为1。
同时,考虑到机载雷达探测时受到强地理杂波的影响,PD处理时需要进行多普勒维加窗以降低杂波副瓣的影响。假设加窗的窗函数为w(n),n=1,…N,则公式(10)可重新表示为:
exp(-j2π·γlpn)
(11)
经过帧间多普勒频率校正处理后,匀速运动目标在不同帧间都处于相同的多普勒单元。但是,考虑到多帧探测时间较长,目标与雷达之间的相对径向速度会引起目标在不同帧间的距离单元走动。
公式(11)获得的距离-多普勒二维数据,不同多普勒单元对应不同的目标速度。由于多普勒维共K个多普勒单元,每个多普勒单元的频率分辨率为Δf=fr0/K,对应的速度分辨率为Δν=cfr0/2Kfc0。考虑到可能存在的速度模糊情况,第k个多普勒单元的目标速度估计值为:
(12)
其中,p0=fix(2νt fc0Tr0)为目标在参考载频和参考PRI时的速度模糊数。可以基于
对不同帧间的目标进行距离走动补偿,第l帧数据第k个多普勒单元的距离补偿值为:
(13)
根据距离走动的估计值,对不同帧不同多普勒单元进行距离走动补偿,可以采用频域时延补偿等方法。经过上述处理后的结果表示为Zl(m,k)。
通过以上处理,目标被校正到相同的多普勒单元,目标的帧间距离走动被补偿。但是目标在MPRF工作模式下存在距离模糊,无法直接进行非相参积累,需要通过距离扩展来解距离模糊。如图1所示,两个不同距离的目标,它们在不同PRI数据中的模糊距离不同。对于多普勒校正和距离补偿后的数据Zl(ml,k),其模糊距离为Rml=mlΔR,则其可能的距离为:
Rtl=mlΔR+qlRul, ql=0,1,…,Ql
(14)
其中,ΔR=c/2B为距离单元分辨率,Rul=Trlc/2为第l个PRI对应的最大模糊距离。ml、ql和Ql分别为第l帧数据中目标的距离单元、距离模糊数以及最大距离模糊数。对Zl(ml,k)进行周期扩展得到Zcl(m,k),只有当目标位于其真实距离处时,多帧之间的目标才处于同一距离单元。图1中当目标1的q1=q2=0,目标2的q1=q2=1时,目标位于各自的真实距离处。
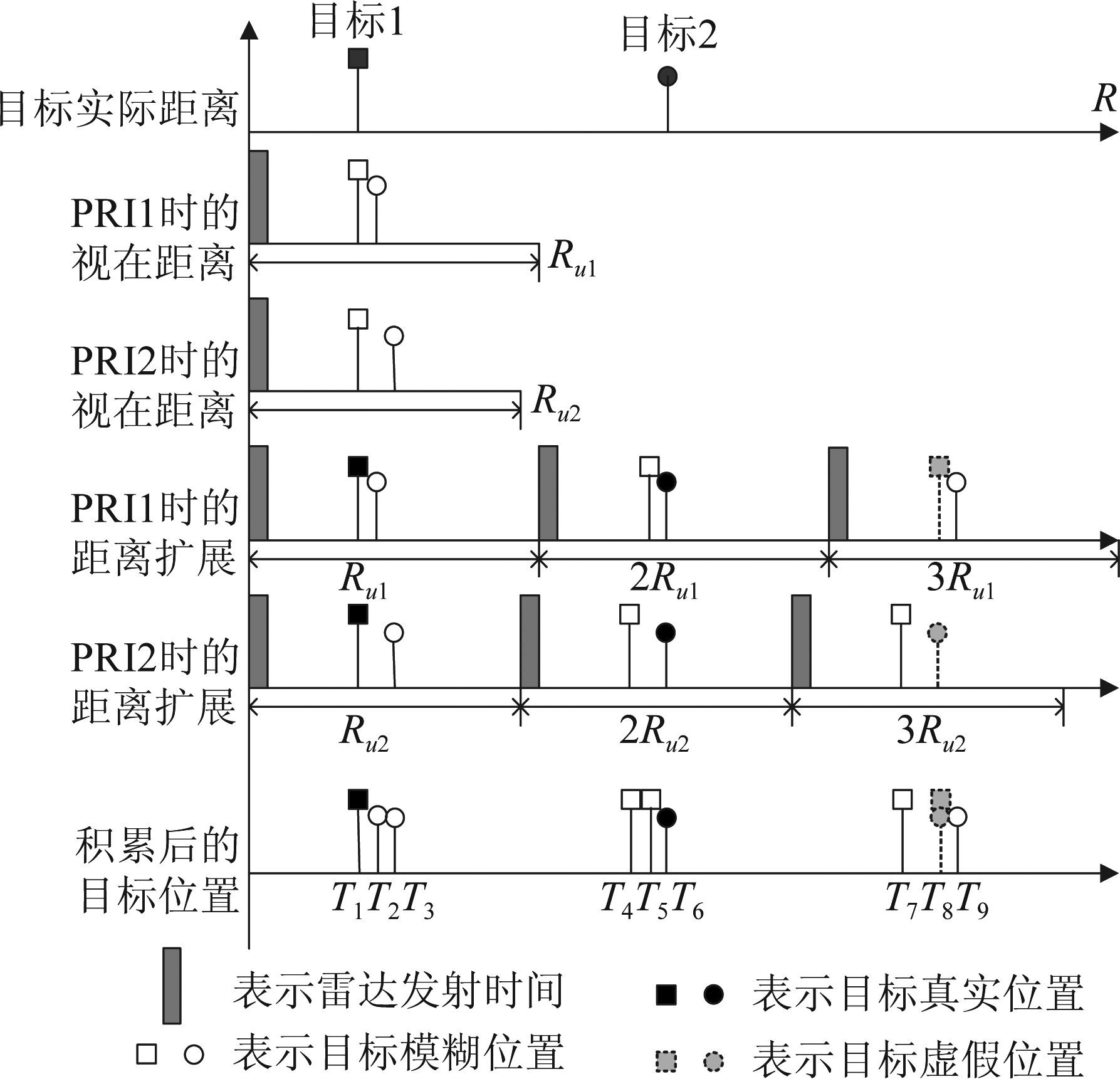
图1 距离周期扩展解距离模糊
Fig.1 Range ambiguity resolving by range cycle expansion
直接对距离周期扩展后的结果Zcl(m,k)进行非相参积累,即取模后帧间求均值,可能使得强目标引入虚假目标,如图2所示。以目标1为例,由于其目标回波幅度较强,经过距离周期扩展后的帧间幅度平均结果,仍然会超过检测门限,从而形成多个虚假目标,造成虚警率抬升以及虚假航迹。因此,可以采用较高的检测门限ThStrong对未进行距离周期扩展结果Zl(m,k)进行强目标检测和剔除,从而消除强目标对检测结果影响。强目标仍然按照传统的解距离模糊方法,例如中华余数定理等进行解距离模糊处理。将
和
分别表示为经过大目标检测和剔除后的距离-多普勒校正结果和距离周期扩展结果。
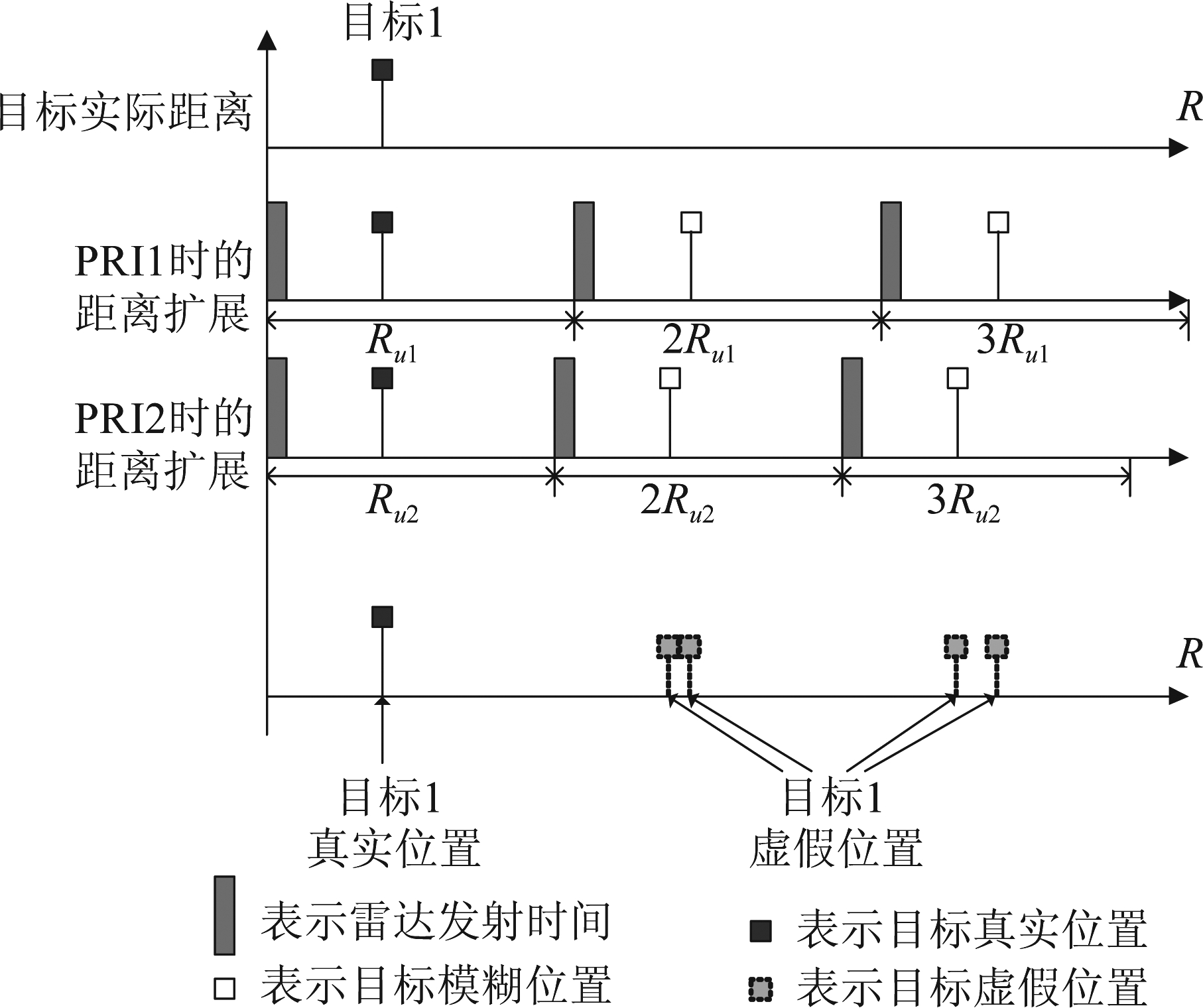
图2 强目标非相参积累后引入虚假目标
Fig.2 False target introduced by the strong target noncoherent integration
经过上述处理后,最终的非相参积累结果可以表示为:
(15)
对Z(m,k)采用更低的检测门限ThWeak进行恒虚警(CFAR)检测,将超过门限的检测单元成为待定检测单元(md,kd)。为了进一步抑制非相参积累后的虚假目标,定义该检测单元帧间熵为:
(16)
其中,pl为该检测单元的帧间归一化幅度概率:
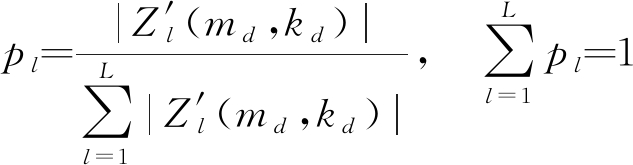
(17)
帧间熵表示该检测单元在不同帧之间的幅度起伏情况。若目标幅度保持不变,则熵值较大;反之,若目标幅度起伏较大,则熵值较少。设置帧间熵的门限ThE,用于判别该检测单元是否为目标:帧间熵低于门限判别为虚警,帧间熵超过门限判别为弱目标。
文中设置了强目标检测门限ThStrong、帧间熵门限ThE,以及帧间非相参积累后的弱目标检测门限ThWeak。为了保证强弱目标的检测性能,尽量减少强目标引入的虚警,以及弱目标的漏检,需根据系统要求的检测概率、虚警概率、积累帧数等参数进行联合优化设计。
最后,将强弱目标的检测结果进行融合,输出最终的目标检测结果。
需要说明的是,在距离模糊情况下,经距离周期扩展后,某一距离单元积累的不同帧的回波不一定属于同一个目标。如图1所示,积累后的目标包括T1～T9共9个可能的位置,其中T1和T6为两个目标的真实位置,而T8为两个不同的目标经过周期扩展后重合的距离单元,此时可能会引入虚警。但是,文中提出的处理流程尽可能降低出现这一问题的概率:首先,剔除了大目标之后,重叠位置的目标强度受到约束;其次,通过帧间熵值的计算,即使多帧非相参积累出现了不同目标解模糊形成的虚警,由于其帧间起伏较大,也会被当成虚警被抑制;同时,考虑到实际工程应用中,会采用不同PRI进行帧间解模糊处理,即使在某一组PRI参数下目标解模糊后形成了少量的虚警点,但是采用多组不同PRI参数时其形成虚假航迹的可能性会大大降低。多普勒模糊的情况下也会存在同样类似的结果。
针对机载雷达的微弱目标探测问题,提出了一种帧间非相参积累与检测方法。该方法的处理流程如图3所示,具体处理过程如下:
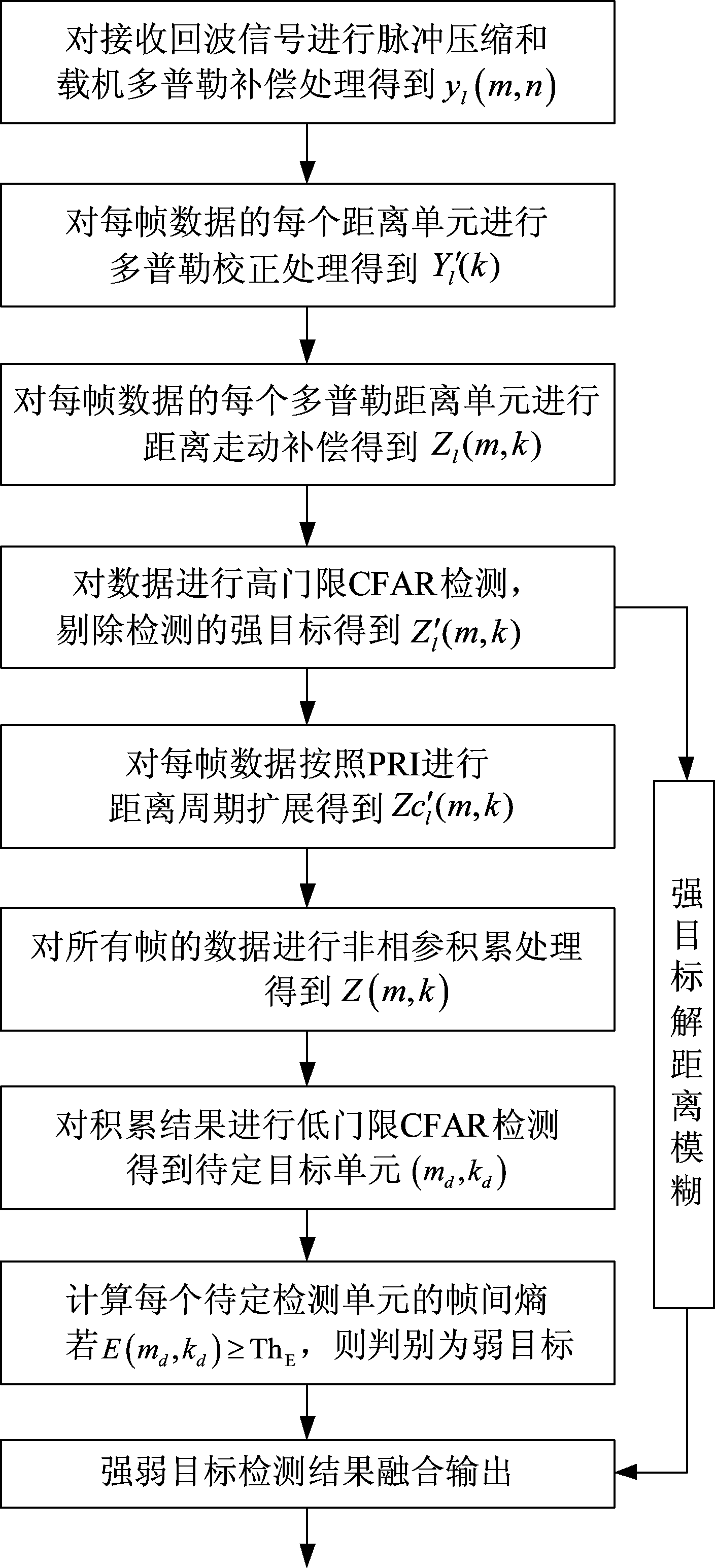
图3 提出方法的处理流程
Fig.3 The process flow of the proposed method
1)对接收回波的每个脉冲进行脉冲压缩和载机多普勒补偿;
2)对每帧数据的每个距离单元,进行不同载频、不同PRI的多普勒校正;
3)对每帧多普勒校正数据的每个多普勒距离单元,进行距离走动补偿;
4)对距离-多普勒校正结果进行强目标检测和剔除,并对强目标进行传统解距离模糊处理;
5)对剔除强目标后的每帧数据,进行距离周期扩展;
6)对距离周期扩展后的数据,进行非相参积累处理;
7)对积累结果进行低门限CFAR检测得到待定目标单元;
8)计算待定检测单元的帧间熵,并与门限ThE比较,进行虚警剔除;
9)对检测得到的强弱目标进行结果融合,输出最终的检测结果。
假设雷达在一个波束指向发射L=4帧不同参数的信号进行探测。其中,载频分别为[300,305,310,315] MHz,PRI分别为[331,317,307,293] μs。假设每帧数据中的脉冲采用相同带宽和脉宽参数,且采用相同的积累脉冲数N=256,距离单元分辨率为50 m。假设有3个目标起始距离分别为[125,65,160] km,每帧数据中目标的信噪比(SNR)保持不变分别为[20,15,10] dB,目标速度分别为[200,-300,500] m/s,载机飞行速度为200 m/s。由于机载雷达杂波的多普勒均处于0附近,且分布在全部距离单元上。提出的方法对杂波的影响可以忽略,因此仿真中不考虑机载杂波。
采用上述参数开展仿真试验,常规处理方法为文献[28]中介绍的脉冲压缩、脉冲多普勒处理的机载雷达信号处理流程。回波信号经过常规方法和提出算法处理后的结果如图4所示。
图4 提出方法校正前后的处理结果对比
Fig.4 The result comparison before and after processing by the proposed method
表1 经过提出方法处理前后的目标距离多普勒单元位置
Tab.1 The range Doppler cell of targets before and after the processing by the proposed method
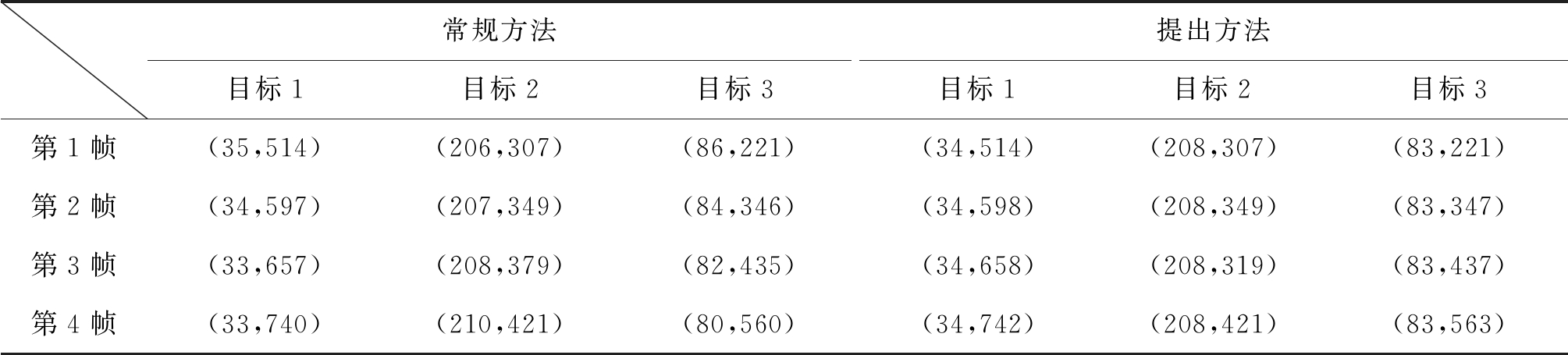
常规方法目标1目标2目标3提出方法目标1目标2目标3第1帧(35,514)(206,307)(86,221)(34,514)(208,307)(83,221)第2帧(34,597)(207,349)(84,346)(34,598)(208,349)(83,347)第3帧(33,657)(208,379)(82,435)(34,658)(208,319)(83,437)第4帧(33,740)(210,421)(80,560)(34,742)(208,421)(83,563)
仿真的3个不同目标在距离多普勒二维图中检测单元的位置变化,如表1所示。可见,不同载频和不同PRI参数回波中的目标,经过提出方法处理后均处于被校正到相同的多普勒单元。同时,可以观测到目标所在的距离单元不同,这是由于目标在不同PRI时的模糊距离不同,需要进行距离解模糊。
各帧数据进行距离周期扩展和非相参积累后,目标1(强目标)和目标3(弱目标)所在多普勒单元的距离维结果分别如图5所示。目标1单帧SNR为20 dB,经过处理后位于第34个多普勒单元,其距离维信号如图5(a)所示,真实位置125 km处所有帧数据中的目标实现了非相参积累。同时,在30、80、170 km处存在多组目标,这是由于目标SNR较强,经过距离周期扩展和非相参积累后形成了如图2所示的虚假目标。利用高检测门限ThStrong在Zl(m,k)中进行行强目标检测和剔除,就是为了消
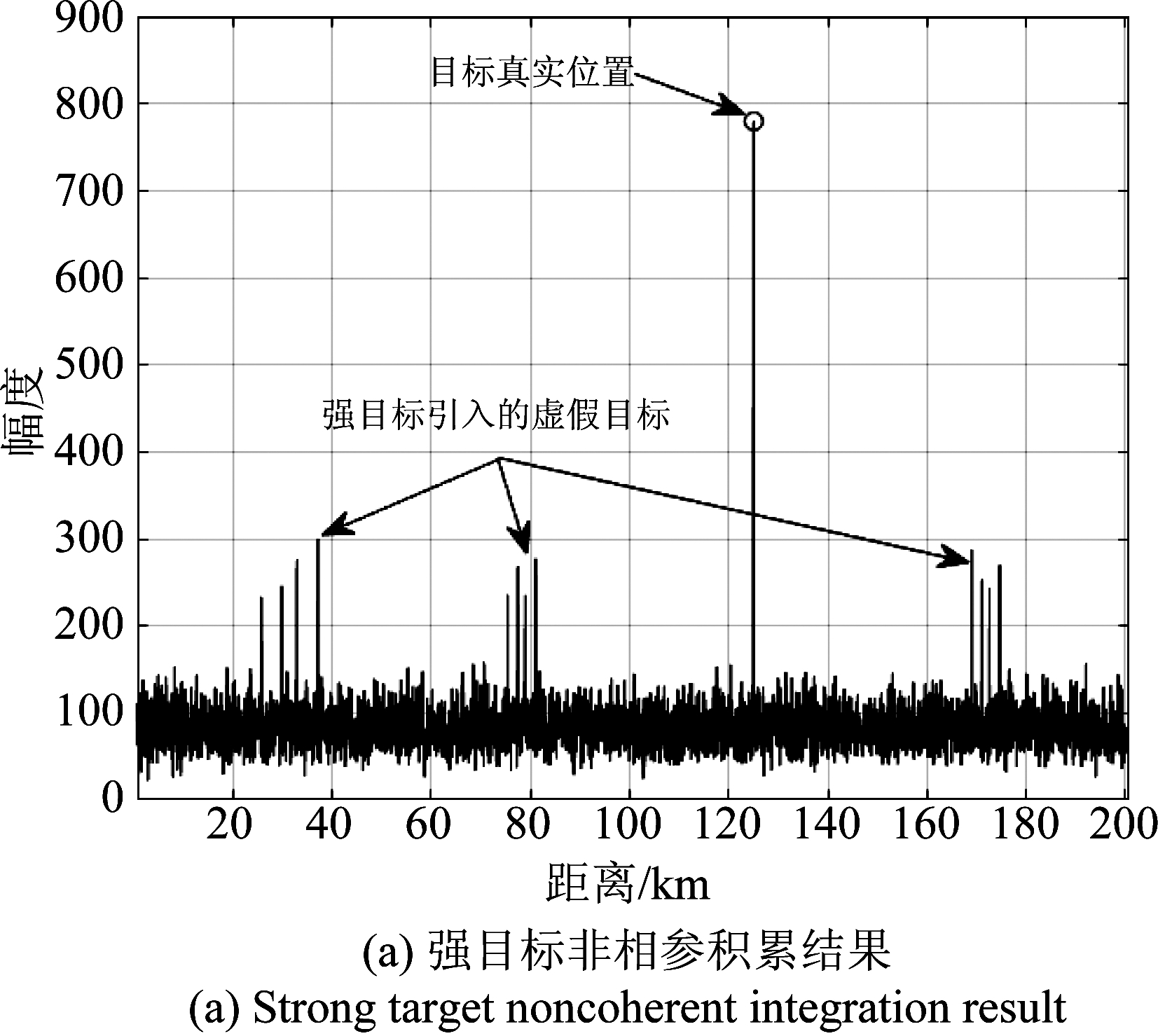
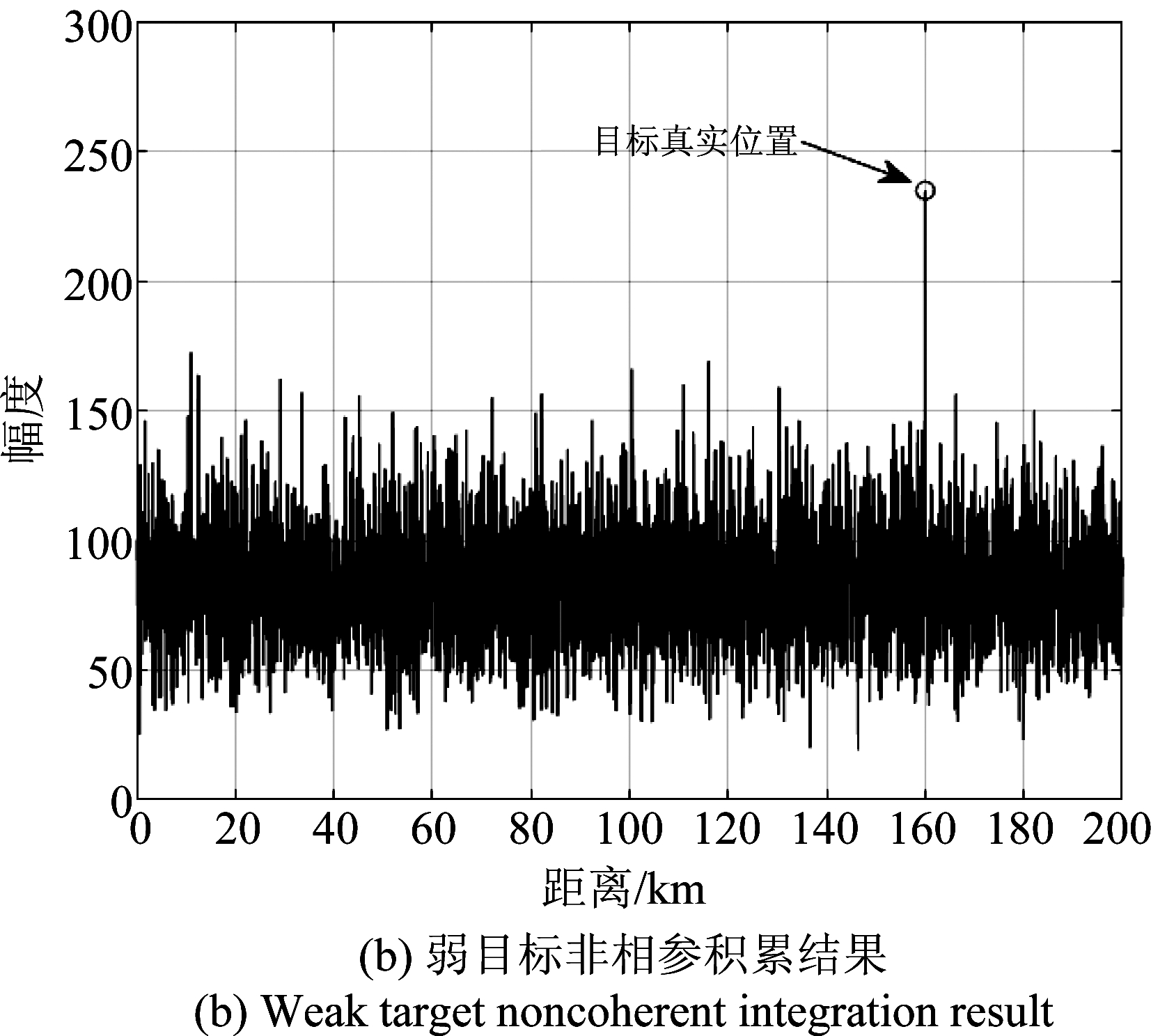
图5 非相参积累后目标所在多普勒单元的距离维结果
Fig.5 The range result of target Doppler cell after noncoherent integration
除这一现象。目标3单帧SNR为10 dB,经过处理后位于第83个多普勒单元,其距离维信号如图5(b)所示,真实位置160 km处所有帧数据中的目标实现了非相参积累。由于目标SNR较弱,经过处理后无明显虚假目标。
同一个波束指向的多帧数据具有不同的PRI,这就意味着各帧的距离盲区不同。当进行非相参积累处理时可能存在如图6所示的多种情况。图中非相参积累结果的放大部分显示,同一个距离单元非相参积累的帧数可能取不同的值Lnonin≤L。其中Lnonin=0时意味着此处距离为所有帧的探测距离盲区。
下面对Lnonin取不同值时目标的检测性能进行仿真实验分析。假设目标为Swerling 0型即非起伏目标,改变目标在单帧数据中的SNR,并将各种场景下的目标检测虚警概率统一设置为10-6,结果如图7所示。仿真结果证明,与常规进行单帧检测相比,经过提出方法处理后的目标检测性能得到较大提升。
图6 多帧数据非相参积累时的不同情况
Fig.6 The different condition of multiple frame noncoherent integration
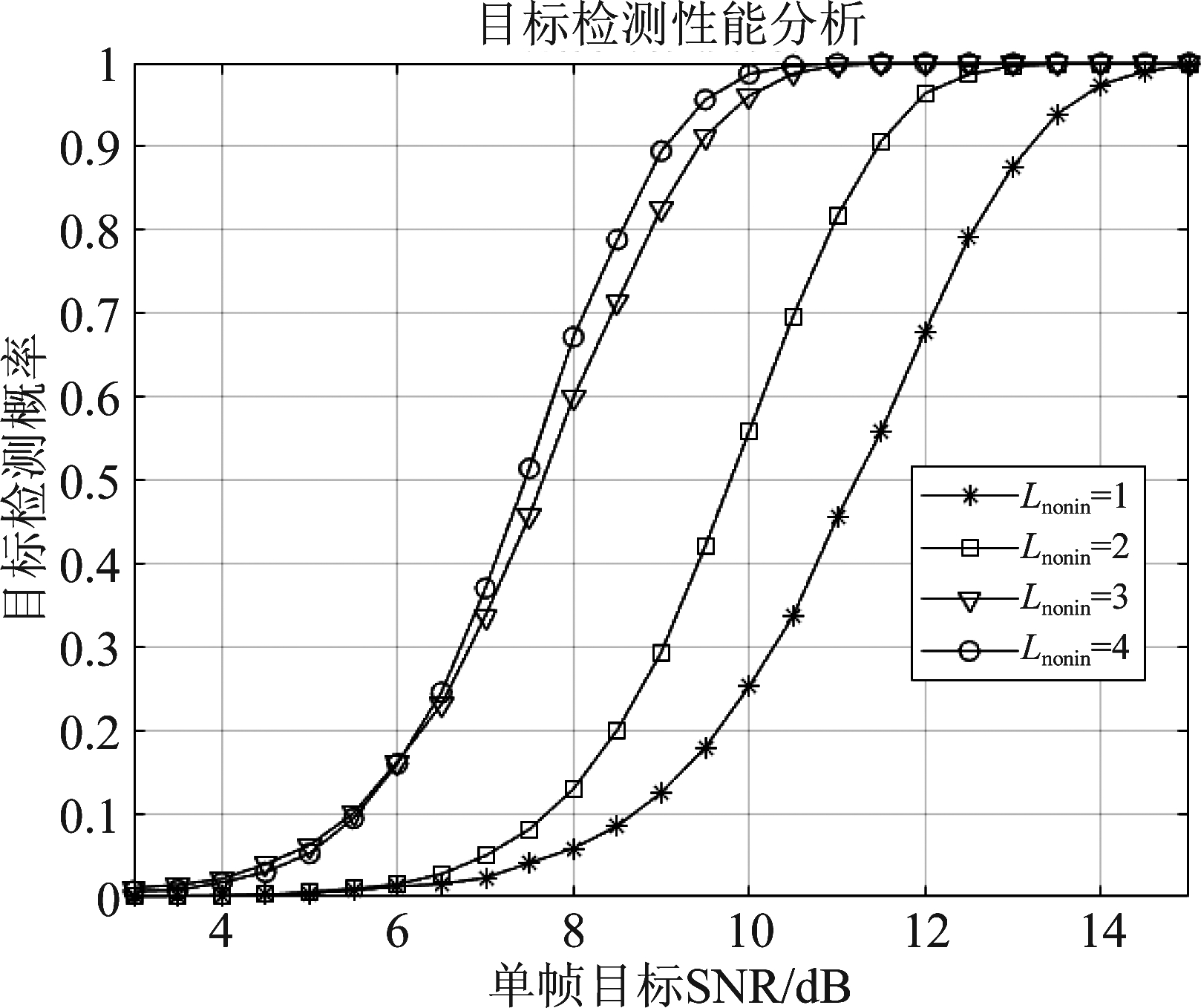
图7 目标检测性能分析
Fig.7 The analysis of target detection performance
文章提出的算法利用基于CZT变换的帧间多普勒校正方法、目标距离走动补偿方法,解决了多帧数据中不同载频、不同PRI引起的目标多普勒单元不同、目标距离单元走动等问题,避免了现有算法进行多帧检测结果融合时,目标多普勒-距离单位无法精确对齐等问题。提出算法提升了多帧间的弱目标检测性能,避免了现有算法进行弱目标检测时,单帧数据采用低门限引入的大量虚警,以及由此造成的多帧检测结果融合时的复杂处理流程和虚假点迹的问题。这也降低了多帧检测结果融合时所需要的计算资源。但是,由于文章所提算法的CFAR检测处理,是在解模糊和非相参积累处理后进行的,因此与传统算法相比计算复杂度会有所增加。不过现有的CFAR检测流程可以采用快速实现方法,其计算复杂度的增加不会造成太大的计算资源压力。
针对机载雷达微弱目标帧间非相参积累和检测技术开展了研究。首先,分析了同一波束的多帧数据采用不同载频和脉冲重复周期场景下的回波信号模型。然后,基于该信号模型提出了帧间非相参积累技术,通过CZT变换实现了目标的帧间多普勒单元校正,并对不同多普勒单元对应的速度进行目标距离走动补偿。为了避免强目标引入虚警,先进行强目标高门限检测和剔除,然后通过距离周期扩展和非相参积累实现弱目标检测性能的提升。最后,结合仿真试验对提出算法的有效性进行了验证。
[1] 张顺生, 曾涛. 基于keystone变换的微弱目标检测[J]. 电子学报, 2005, 33(9): 1675-1678.
ZHANG Shunsheng, ZENG Tao. Weak target detection based on Keystone transform[J]. Acta Electronica Sinica, 2005, 33(9): 1675-1678.(in Chinese)
[2] XU J, YU J, PENG Y N, et al. Radon-Fourier transform for radar target detection I: generalized Doppler filter bank[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(2): 1183-1202.
[3] XU J, YU J, PENG Y N, et al. Radon-Fourier transform for radar target detection II: blind speed sidelobe suppression[J]. IEEE Transactions on Aerospace and Electronic Systems, 2011, 47(4): 2473-2489.
[4] XU J, YU J, PENG Y N, et al. Radon-Fourier transform for radar target detection III: optimality and fast Implementations[J]. IEEE Transactions on Aerospace and Electronic Systems, 2012, 48(2): 991-1004.
[5] XU J, YAN L, LONG T, et al. Adaptive Radon-Fourier transform for weak radar target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(4): 1641-1663.
[6] 周煦, 许稼, 钱李昌, 等. 雷达高机动目标长时间混合积累快速算法[J]. 信号处理, 2015, 31(12): 1547-1553.
ZHOU X, XU J, QIAN L C, et al. Fast algorithm of long-time hybrid integration for highly maneuvering radar target detection[J]. Journal of Signal Processing, 2015, 31(12): 1547-1553.(in Chinese)
[7] WOOD J C, BARRY D T. Linear signal synthesis using the Radon-Wigner transform[J]. IEEE Transaction on Signal Processing, 1994, 42(8): 2105-2111.
[8] WOOD J C, BARRY D T. Radon transformation of time-frequency distributions for analysis of multicomponent signals[J]. IEEE Transaction on Signal Processing, 1994, 42(11): 3166-3177.
[9] SUN Y, WILLETT O. Hough transform for long Chirp detection[J]. IEEE Transaction on Aerospace and Electronic Systems, 2002, 38(2): 553-569.
[10] LIU W F, ZHANG Z Q, CHEN X H, et al. Dictionary learning based Hough transform for road detection in multispectral image[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(12): 2330-2334.
[11] 张南, 陶然, 王越. 基于变标处理和分数阶傅里叶变换的运动目标检测算法[J]. 电子学报, 2010, 38(3): 683- 688.
ZHANG N, TAO R, WANG Y. A target detection algorithm based on scaling processing and fractional Fourier transform[J]. Acta Electronica Sinica, 2010, 38(3): 683- 688.(in Chinese)
[12] CARLSON B D, EVANS E D, WILSON S L. Search radar detection and track with the Hough transform[J]. IEEE Transactions on Aerospace and Electronic Systems, 1994, 30(1): 102-125.
[13] FAN L, ZHANG X, WEI L. TBD algorithm based on improved Randomized Hough Transform for dim target detection[J]. Progress In Electromagnetices Research C, 2012, 31: 271-285.
[14] BARNIV Y. Dynamic programming solution for detecting dim moving targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 1985, 21(1): 144-156.
[15] RUTTEN M G, RISTIC B, GORDON N J. A comparison of particle filters for recursive track-before-detect[C]∥ 2005 7th International Conference on Information Fusion. Philadelphia, PA, USA, 2005: 169-175.
[16] ZHENG D K, WANG S Y, MENG Q W. Dynamic programming track-before-detect algorithm for radar target detection based on polynomial time series prediction[J]. IET Radar, Sonar & Navigation, 2016, 10(8): 1327-1336.
[17] YAN B, XU L P, LI M Q, et al. Track-before-detect algorithm based on dynamic programming for multi-extended-targets detection[J]. IET Signal Processing, 2017, 11(6): 674- 686.
[18] LUIS 
M. Adaptive auxiliary particle filter for track-before-detect with multiple targets[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 53(5): 2317-2330.
[19] WANG J H, YI W, KIRUBARAJAN T, et al. An efficient recursive multiframe track-before-detect algorithm[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(1): 190-204.
[20] WANG H. Greedy algorithm-based track-before-detect in radar systems[J]. IEEE Sensors Journal, 2018, 18(17): 7158-7165.
[21] GARCIA F J, MANDAL P K, BOCQUEL M, et al. Riemann-Langevin particle filtering in track-before-detect[J]. IEEE Signal Processing Letters, 2018, 25(7): 1039-1043.
[22] ZHANG X W, SUN J P, ZHANG Y X, et al. H-PMHT track-before-detect processing with DP-based track initiation and termination[J]. IET Signal Processing, 2016, 10(9): 1118-1125.
[23] WU W, WANG G H, SUN J P. Polynomial radon-polynomial Fourier transform for near space hypersonic maneuvering target detection[J]. IEEE Transactions on Aerospace and Electronic Systems, 2018, 54(3): 1306-1322.
[24] 蒋千. 高速目标雷达信号长时间积累技术研究[D]. 成都: 电子科技大学, 2013.
JIANG Q. Research of Long-Time Integration Algorithm for High Speed Radar Target Detection[D]. Chengdu: University of Electronic Science and Technology of China, 2013.(in Chinese)
[25] 李海, 马頔, 卢晓光. 利用改进频域补偿和分数阶Fourier变换的多帧相参TBD方法[J]. 信号处理, 2015, 31(11): 1510-1517.
LI Hai, MA Di , LU Xiaoguang. Multi-Frame Coherent Integration Track-Before-Detect Algorithm Based on Modified Range-Frequency Compensation and Fractional Fourier Transform[J]. Journal of Signal Processing, 2015, 31(11): 1510-1517.(in Chinese)
[26] 鞠佩恒. 合成孔径雷达Chirp Z-Transform成像算法研究[D]. 北京: 中国科学院电子研究所, 2004.
JU P H. A Study of Chirp Z-Transform Algorithm for Synthetic Aperture Radar[D]. Beijing: Institute of Electronics of CAS, 2004.(in Chinese)
[27] 樊玲. 微弱目标检测前跟踪算法研究[D]. 成都: 电子科技大学, 2013.
FAN L. Research on track-before-detection algorithms for weak targets[D]. Chengdu: University of Electronic Science and Technology of China, 2013.(in Chinese)
[28] GEORGE W S, HUGH D G, CHRIS J B, et al. Introduction to Airborne Radar[M]. 3rd Edition. Edison, NJ, SciTech Publishing, 2014.
王 宁 男,1986年生, 山东聊城人。南京电子技术研究所, 高级工程师, 博士, 主要研究方向为雷达信号处理与目标检测。
E-mail: wangning11@cetc.com.cn
孟晋丽 女, 1976年生, 山西忻州人。南京电子技术研究所, 研究员, 博士, 主要研究方向为雷达信号处理与目标检测。
E-mail: mengjinli@cetc.com.cn
刘国庆 男, 1987年生, 山东潍坊人。南京电子技术研究所, 高级工程师, 博士。研究方向为雷达信号处理与目标检测。
E-mail: liuguoqing3@cetc.com.cn
杨予昊 男, 1984年生, 江苏南通人。南京电子技术研究所, 高级工程师, 博士。研究方向为雷达信号处理与目标识别。
E-mail: yangyuhao@cetc.com.cn
孙 俊 男, 1974年生, 云南昆明人。南京电子技术研究所, 研究员, 博士。研究方向为雷达信号处理与目标识别。
E-mail: sunjun1@cetc.com.cn