Reference format: ZHANG Yule, HU Guoping, ZHOU Hao, et al. Three-level Nested Array: Optimization for Degree of Freedom and Mutual Coupling[J]. Journal of Signal Processing, 2021, 37(2): 234-241. DOI: 10.16798/j.issn.1003- 0530.2021.02.008.
传统波达方向(Direction of Arrival,DOA)估计通常采用均匀线阵(Uniform Linear Array, ULA)[1- 2],其阵元间距相等且不大于半波长,由此带来以下问题:信号频率过高时,较小的阵元间距使得物理布阵难以实现,且会产生较大的阵元互耦[3];高分辨率意味着较大的阵列孔径,更多的物理阵元会进一步增大系统成本和复杂度。稀疏阵列(如最小冗余阵[4]、嵌套阵[5]、互质阵[6])能够克服阵元间距的限制条件而得到了巨大发展和广泛应用。相比于均匀线阵,稀疏阵列在提高估计精度、增强角度分辨力和降低物理成本等方面具有较大优势:较大的阵元间距能够进一步扩展虚拟孔径,进而增大可检测信源个数和角度分辨力;阵元间距的增大也能够有效抑制阵元互耦效应,进而提高估计精度。
文献[7]深入分析了互耦对稀疏阵列DOA估计的影响,通过对比证明最小冗余阵列受互耦影响最小,但其一般采用穷举法或循环搜索确定物理阵元位置,难以确定自由度的有效闭式解,且随着物理阵元个数增加,其计算量将急剧上升,进而增大了阵列结构的设计难度。
嵌套阵由于简单的阵列结构和高自由度特征取得了巨大发展,但存在密布子阵而具有较大的阵列互耦。文献[8]对嵌套阵的第二层子阵的前两个阵元间距进行调整后得到了更高自由度的优化嵌套结构。文献[9]通过引入附加阵元建立了改进嵌套阵结构,具有自由度闭式解,且其“差联合阵列”为无孔的均匀虚拟线阵,较二阶嵌套阵具有更高自由度,同时,第二层阵元间距增大降低了阵元间互耦。文献[10]基于二阶嵌套阵的思想,在一个单独阵元的两端分别布置一个不同阵元间距的ULA结构,该结构较二阶嵌套阵具有更高的自由度和更低的阵元互耦,进而在角度分辨和参数估计方面具有更高的性能。文献[11-12]通过设计特定系统程序确定物理阵元位置,建立超级嵌套阵结构,该结构具有传统嵌套阵的所有优势,且由于邻近阵元更少而具有较低的阵元互耦。
互质阵是由两个阵元间距互质的稀疏ULA交替构成,因较低的阵元互耦和较大的自由度而受到广泛关注。与嵌套阵不同的是,其“差联合阵列”形成的虚拟线阵中存在离散虚拟阵元,传统的DOA估计算法只能通过选取连续虚拟阵元部分,进行目标角度估计,但离散部分虚拟阵元的舍弃会造成有效信息的损失,导致估计性能下降。为此,文献[13]根据互质阵“差联合阵列”形成的虚拟阵列中孔洞位置关系,内插少量天线,在不扩展原始虚拟阵列孔径的情况下增加阵列自由度。文献[14]基于原子范数最小化理论,建立了内插虚拟阵列协方差矩阵的无网格化重建问题,实现了DOA的精确估计。但上述两种方法均需采用空间平滑技术或Toeplitz矩阵重构法克服向量化协方差矩阵造成的单快拍影响,会损失一半的自由度。文献[15]研究了压缩感知(Compressed Sensing, CS)在互质阵DOA估计中的应用,充分利用信源空域的稀疏特征克服了单快拍影响,具有较高的角度估计性能。
为进一步提高角度估计性能,本文基于自由度和互耦联合优化的思想,设计了一个采用三级ULA结构级联的三阶嵌套阵,并结合CS算法进行DOA估计。该结构的“差联合阵列”是一个无孔的均匀虚拟阵列,且具有自由度的闭式解,较现有的稀疏阵列结构具有更高的自由度和较低的阵元互耦,在角度估计中具有更优越的性能。
假设空间中有K个远场窄带非相干目标入射到阵元数为G的稀疏非均匀线阵中,信源方向为θ={θk,k=1,2,…,K}。则阵列回波信号矢量为:
y(t)=As(t)+n(t)
(1)
式中,A=[a(θ1),a(θ2),…,a(θK)],且a(θk)=[1,e-j2πd2dsinθk/λ,…,e-j2πdGdsinθk/λ]T为第k个信源的导向矢量;d为单位阵元间距,(通常取d=λ/2,λ为信号波长),di为第i个阵元与第1个阵元的阵元间距,d1=0;(·)T为矩阵的转置运算;s(t)=[s1(t),s2(t),…,sK(t)]T,sk(t)为第k个信源的基带波形;n(t)为加性高斯白噪声。
根据文献[11],引入互耦矩阵C可得互耦条件下的回波信号模型为:
x(t)=CAs(t)+n(t)
(2)
式中,矩阵C的元素受天线类型、雷达工作模式、天线阵元间距、阻抗等因素影响,其闭式解非常复杂。本文只针对线阵模型,则矩阵的元素可近似为B带对称的Toeplitz矩阵结构。
(3)
式中,Cij为矩阵C第i行第j列元素,1=c0>|c1|…>|cB|>|cB+1|=0。
为便于衡量互耦影响程度,对于给定的非均匀线阵可定义互耦率Ω为:
(4)
式中,[diag(C)]ij=Cijδij,δij为狄利克雷函数,||·||F为矩阵的范数运算。由式(4)可知,Ω越小,互耦影响越弱。
由式(2)可计算互耦条件下回波信号协方差矩阵为:
(5)
式中,
为信源协方差矩阵,
为第k个信源的信号能量,
为噪声能量,E[·]表示数学期望,(·)H为矩阵复共轭转置运算,IG为G×G维单位矩阵,diag(·)为矩阵对角运算。实际应用中,通常可由采样快拍数L估计求解,即:
(6)
式中,
为估计值。
对式(5)中协方差矩阵R向量化可得:
(7)
式中,C0=C*⊗C,A*⊙A=[a*(θ1)⊗ a(θ1),a*(θ2)⊗a(θ2),…,a*(θK)⊗a(θK)]为单快拍测量的r虚拟阵列流型矩阵,
表示矩阵向量化运算,(·)*表示矩阵复共轭运算,⊙和⊗分别表示Khatri-Rao积和Kronecker积,由上述分析可知,矩阵A*⊙A的虚拟阵元位置由实际物理阵元位置的“差联合阵列“组成。
嵌套阵是通过给子阵设置不同阵元间距实现自由度增加和互耦降低。因此,本文采用ULA进行级联,建立三阶嵌套阵结构如图1所示。
则天线阵元位置可表示为:
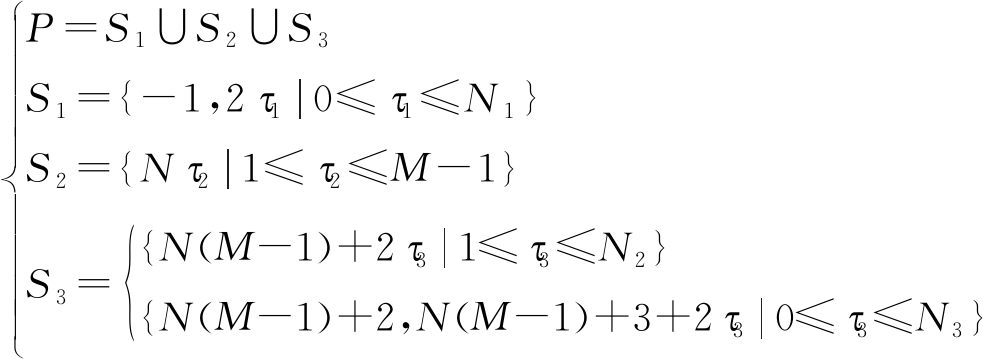
(8)
其中,
N2=(N-1)/2, N为奇数;N3=(N-4)/2, N为偶数。
结合图1和式(8)可定义三阶嵌套阵的“差联合阵列”如下:
Sd={sd|sd=di-dj,di∈P,dj∈P}
(9)
定理 三阶嵌套阵具有以下特征:
(1)集合Sd中连续虚拟阵元范围可表示为[-MN,MN];
(2)集合Sd的自由度等于2g+1,其中g=MN。
证明:
可以用一个通用表达式来描述sd:
sd=Nγ+τ
(10)
式中,-(M-1)≤γ≤M-1,-N≤τ≤N。并且可以在集合S1,S2和S3中找到对应元素使得sd为一个连续的整数。当γ=M-1,τ=N时,maxsd=MN。
证毕
图1 三阶嵌套阵结构
Fig.1 Three-level nested array structure
当阵元总数一定时(G=(M-1)+N),可通过优化自由度求解最佳的阵元配置结构,具体见表1。
表1 物理阵元最佳配置结构
Tab.1 Optimal configuration structure for physical array
GM-1N最优(M-1),N自由度奇数奇数偶数偶数奇数M-1=(G-1)/2,N=(G+1)/2(G2+3)/2+G偶数奇数偶数奇数偶数M-1=N=G/2(G2+2)/2+G
压缩感知技术具体由信号稀疏表示、测量矩阵构建和信号稀疏重构三部分组成。结合信源方向稀疏性,将压缩感知技术应用于信源DOA估计能够很好地解决向量化协方差矩阵造成的单快拍影响。根据式(7),可建立如下凸优化问题:
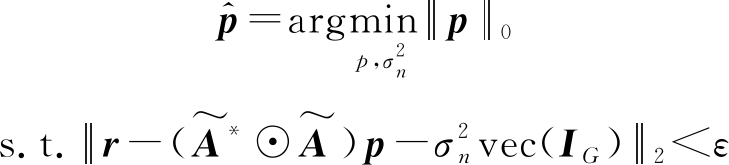
(11)
式中,ε为误差门限值,
表示p的估计值,
是由搜索方向矢量构成的感知矩阵,||·||0和||·||2分别表示矢量l0范数和l2范数。
假设
(12)
则式(11)可重新表示为:
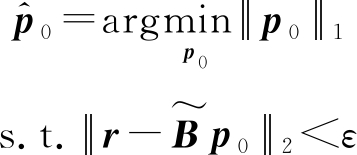
(13)
然而式(13)中优化问题属于NP难问题。因此,引入l1范数可重构上述问题。文献[16]提出一种基于LASSO优化的空间信号恢复方法,具体为:
(14)
式中,l2范数表示最小平方代价函数,l1范数为空间约束,λt为用于平衡估计中非零点最小平方误差的惩罚参数。上述目标函数可以采用CVX工具箱进行优化。
设置物理阵元总数为10,即M=6,N=5;互耦矩阵C中的元素满足c0=1,c1=0.5ejπ/4,c2=0.5ej0.7π/2,c3=0.5ej0.7π/3,c4=0.5ej0.7π/4,B=4。以嵌套阵、文献[7]阵列、文献[8]阵列、互质阵和文献[9]阵列为比较对象,采用4节所提CS算法进行DOA估计。角度估计的均方误差的计算公式为:
(15)
式中,ξ为蒙特卡洛实验次数,
为第i次实验中θk的估计值。
表2给出了互耦条件下不同阵列结构间物理阵元位置和自由度及互耦率的对比关系。
由表2可以看出,嵌套阵由于存在密布子阵而具有最大的互耦率;互质阵需要满足阵元数互质关系而具有较低的自由度;文献[8]阵列和文献[9]阵列虽然比嵌套阵的自由度高,但仍存在较高互耦率;本文阵列较嵌套阵和互质阵实现了自由度的提升,较所对比的五种阵列结构均实现了互耦的优化。因此,本文阵列可通过改善阵元间距降低互耦率进而实现角度估计性能提升。
表2 不同阵列结构自由度和互耦率对比
Tab.2 Degree of freedom and mutual coupling of different array structures
阵列结构物理阵元位置自由度互耦率嵌套阵{1,2,3,4,5,6,12,18,24,30}590.6657文献[7]阵列{1,2,3,4,5,6,13,19,25,31}610.6657文献[8]阵列{1,2,3,4,5,11,17,23,29,34}670.6329互质阵{0,3,6,9,12,5,10,15,20,25}430.4628文献[9]阵列{1,2,3,4,8,16,24,32,40,49}730.5762本文阵列{-1,0,2,5,10,15,20,25,27,29}610.4373
图2给出了不同阵列结构的“差联合阵列”位置与权重(指“差联合阵列”中虚拟阵元出现的次数)的变化关系。
可以看出,嵌套阵、文献[7]阵列、文献[8]阵列和本文阵列均可以获得连续的虚拟阵元,互质阵和文献[9]阵列存在离散阵元。需要指出的是,本文阵列由于阵元间距较大,0位置附近的虚拟阵元数较少,因此互耦率最小。嵌套阵和文献[7]阵列的0位置附近阵元较多且权重较大,因此互耦率最大。
图2 不同阵列结构“差联合阵列”位置
Fig.2 “Difference co-array” of different array structures
为进一步说明本文阵列的估计性能,图3给出了不同阵列结构的CS谱。其中,信噪比SNR=0 dB,快拍数为100,11个非相干的远场窄带目标分别位于[-25°∶5°∶25°],点划线表示真实的角度方向。
由图3可知,互质阵由于自由度较小而估计性能最弱,嵌套阵,文献[7]阵列,文献[8]阵列和文献[9]阵列不能估计出所有目标,本文阵列能够识别所有目标,具有更好的空间谱。因此,本文阵列通过优化自由度和互耦率可获得比传统稀疏阵列更好的角度估计性能。
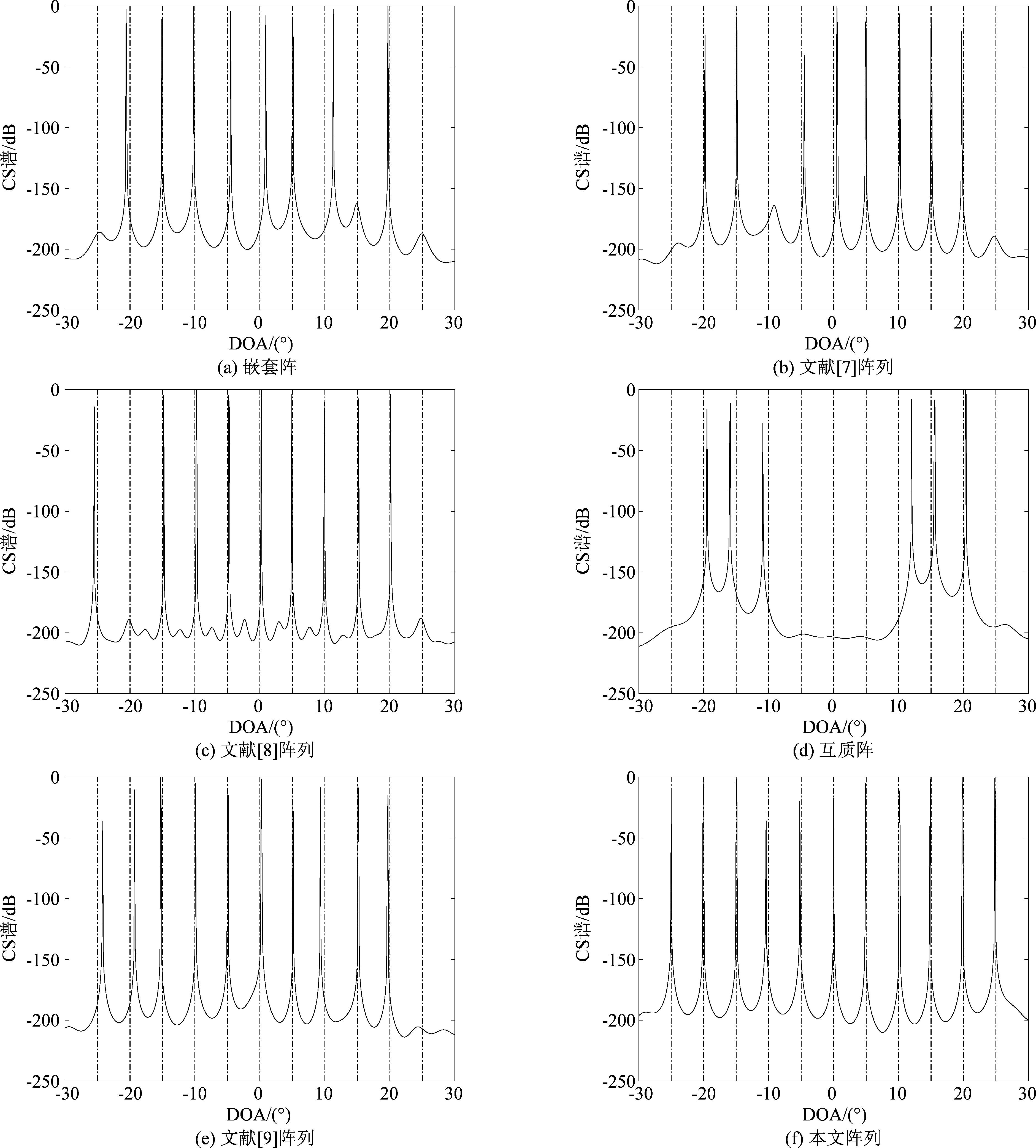
图3 不同阵列结构CS谱
Fig.3 CS spectrum of different array structures
图4(a)描述了角度估计的均方误差随信噪比的变化关系,其中快拍数为200;图4(b)描述了角度估计的均方误差随快拍数的变化关系,其中信噪比SNR=0 dB;信源方向为15°和20°。
由图4可知,随着信噪比和快拍数的增大,各阵列结构估计性能逐步提升,本文阵列通过降低阵元互耦而具有最优的估计性能。并且,尽管互质阵的自由度较低,由于互耦率更小,互质阵比嵌套阵具有更好的估计性能。因此,降低阵列互耦对提高阵列估计性能具有重要意义。
图4 不同阵列结构估计性能
Fig.4 RMSE of different array structures
图5描述了不同阵列结构的邻近目标分辨性能。假设两个邻近目标分布在4°和6°,信噪比SNR=0 dB,快拍数为100,搜索范围为[0°,10°],步长为0.01°。
由图5可以看出,互质阵仅能估计出一个目标,且空间谱明显偏离真实角度;本文阵列和其余阵列可以分辨上述两个目标,但本文阵列比其余阵列具有更高精度的CS谱。
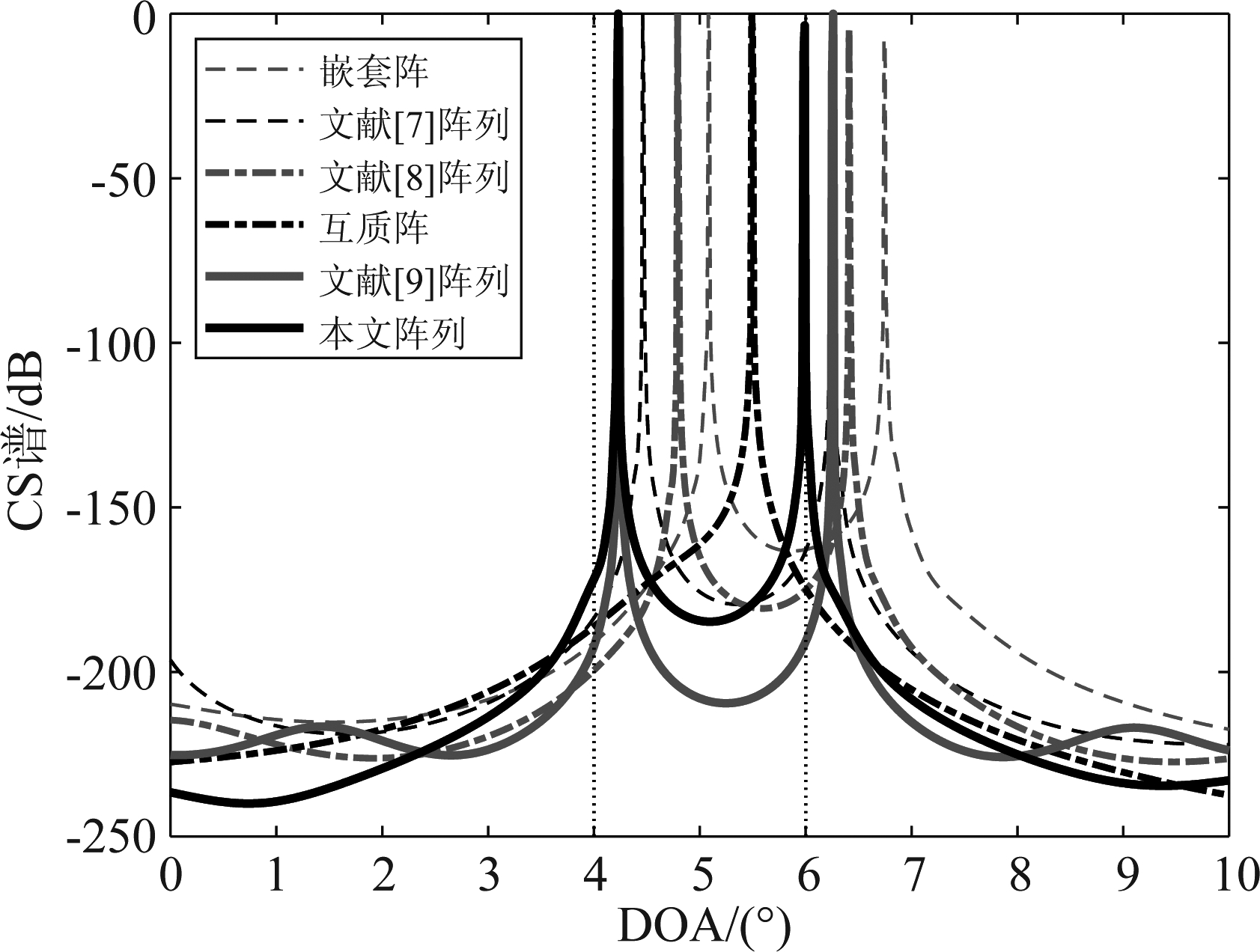
图5 不同阵列结构邻近目标CS谱
Fig.5 CS spectrum of two closely targets of different array structures
本文提出了一种三阶嵌套阵列结构,通过调整阵元间距,该结构可以实现自由度和互耦联合优化,具有物理阵元位置和自由度的闭式解,且其“差联合阵列”是一个无孔的虚拟均匀线阵。仿真实验表明,较低的阵元互耦使其在CS谱和测向精度方面较现有稀疏阵列结构具有显著的优势。
[1] WANG Yuexian, WANG Lin, XIE Jian, et al. DOA estimation under mutual coupling of uniform linear arrays using sparse reconstruction[J]. IEEE Wireless Communications Letters, 2019, 8(4): 1- 4.
[2] 陈宝欣, 黄勇, 陈小龙, 等. 基于迭代超分辨的单快拍DOA估计[J]. 信号处理, 2019, 35(5): 775-780.
CHEN Baoxin, HUANG Yong, CHEN Xiaolong, et al. Single Snapshot DOA Estimation Method Based on Reiterative Super-resolution[J]. Journal of Signal Processing, 2019, 35(5): 775-780.(in Chinese)
[3] WEN Fangqing, ZHANG Zijing, WANG Ke, et al. Angle estimation and mutual coupling self-calibrztion for ULA-based bistatic MIMO radar[J]. Signal Processing, 2018, 144(2): 61- 67.
[4] MOFFET A. Minimum-redundancy linear arrays[J]. IEEE Transactions on Antennas and Propagation, 1968, 16(3): 172-175.
[5] PAL P, VAIDYANATHAN P P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom[J]. IEEE Transactions on Signal Processing, 2010, 58(8): 4167- 4181.
[6] VAIDYANATHAN P P, PAL P. Sparse sensing with co-prime samplers and arrays[J]. IEEE Transactions on Signal Processing, 2011, 59(2): 573-586.
[7] BOUDAHER E, AHAMD F, AMIN M, et al. Mutual coupling effect and compensation in non-uniform arrays for direction-of-arrival estimation[J]. Digital Signal Processing, 2017, 61(1): 3-14.
[8] IIZUKA Y, ICHIGE K. Extension of two-level nested array with larger aperture and more degrees of freedom[C]∥Proceedings of International Symposium on Antennas and Propagation. Okinawa, Japan: IEEE, 2016: 442- 443.
[9] YANG Minglei, SUN Lei, YUAN Xin, et al. Improved nested array with hole-free DCA and more degrees of freedom[J]. Electronics Letters, 2016, 52(25): 2068-2070.
[10] HUANG Huiping, LIAO Bin, WANG Xiaoye, et al. A New Nested Array Configuration with Increased Degrees of Freedom[J]. IEEE Access, 2018, 6(1): 1490-1497.
[11] LIU Chunlin, VAIDYANATHAN P P. Super nested arrays: Linear sparse arrays with reduced mutual coupling-Part I: Fundamentals[J]. IEEE Transactions on Signal Processing, 2016, 64(15): 3997- 4012.
[12] LIU Chunlin, VAIDYANATHAN P P. Super nested arrays: Linear sparse arrays with reduced mutual coupling-Part II: High-order extensions[J]. IEEE Transactions on Signal Processing, 2016, 64(16): 4203- 4217.
[13] 艾明, 虞贵财, 王志强. 互质阵列空洞中内插阵元的DOA估计算法[J]. 南昌大学学报(工科版), 2019, 41(4): 398- 403.
AI Ming, YU Guicai, WANG Zhiqiang. DOA estimation algorithm with interpolated array elements for coprime array holes[J]. Journal of Nanchang University (Engineering and Technology), 2019, 41(4): 398- 403.(in Chinese)
[14] ZHOU Chengwei, GU Yujie, FAN Xing, et al. Direction-of-arrival estimation for coprime array via virtual array interpolation[J]. IEEE Transactions on Signal Processing, 2018, 66(22): 5956-5971.
[15] JIA Tianyi, WANG Haiyan, SHEN Xiaohong, et al. Direction of arrival estimation with co-prime arrays via compressed sensing methods[C]∥IEEE Oceans, shanghai, 2016: 1-5.
[16] TIBSHIRANI R. Regression shrinkage and selection via the LASSO[J]. Journal of the Royal Statistical Society, Series B, 1996, 58(1): 267-288.
张宇乐 男, 1997年生, 陕西咸阳人。空军工程大学防空反导学院, 硕士研究生, 主要研究方向为阵列信号处理、稀疏阵列MIMO雷达测向研究。
E-mail: 874474324@qq.com
胡国平 男, 1964年生, 江西南昌人。空军工程大学防空反导学院, 教授, 博士, 主要研究方向为雷达信号处理、雷达反隐身技术、无线通信技术和图像处理。
E-mail: hgp6068@163.com
周 豪 男, 1990年生, 河南南阳人。空军工程大学防空反导学院, 讲师, 博士, 主要研究方向为低空目标探测技术。
E-mail: 17792611529@qq.com
赵飞龙 男, 1982年生, 陕西咸阳人。空军工程大学防空反导学院，硕士,中国人民解放军93951部队, 主要研究方向为雷达信号处理。
E-mail: 35656635@qq.com