图1 含旋转部件的目标转台模型
Fig.1 Rotation model of targets with rotational components
Reference format: CHEN Xuebin, YE Chunmao, ZHANG Yan, et al. Separately Imaging for ISAR Target with Rotational Components[J]. Journal of Signal Processing, 2021, 37(2): 209-221. DOI: 10.16798/j.issn.1003- 0530.2021.02.006.
随着雷达技术的发展,雷达成像的质量也不断走向清晰化、细致化、精确化。伴随着横、纵向距离分辨能力的提升,传统逆合成孔径雷达成像方法已不足以满足当今的精细化成像需求。一方面,ISAR成像的实现建立在目标小角度转动的转台模型上,而随着距离-多普勒二维分辨力的增加,由目标转台运动所导致的纵向距离单元迁徙、多普勒谱展宽现象变得不可忽略[1-2]。另一方面,由于逆合成孔径雷达针对飞机、舰船等扩展目标进行成像,该类目标上的螺旋桨、涡轮、机翼等部件会出现转动、振动等运动方式,而由此产生的部件回波同样影响到扩展目标的整体成像质量[3- 4],需要将其单独提取并独立地分析成像。
针对距离-多普勒二维高分辨下转台转动补偿,叶春茂等人提出了通过Keystone变换补偿一阶距离走动、再采用匹配处理补偿一阶多普勒走动的方法[5],实现了转台目标的聚焦成像,但该方法并不适用于含有旋转部件的扩展目标;针对旋转部件回波,现有的研究多采用逆Radon变换(inverse radon transform,IRT)方法来进行处理[6-7],通过对具备正弦类曲线图像的线积分处理,该方法可估计出转动部件的转动半径、转动周期等参数,但旋转部件的回波经常在距离-多普勒域与刚体的回波混叠,刚体强散射点的回波会影响IRT方法的估计精度;为此,需要考虑将来自刚体和部件的回波进行分离。针对旋转部件回波的分离提取,Thayaparan T等人提出了基于小波变换的分解方法[8],而基于复值经验模态分解的方法也被证明是一种有效的手段[9];此外,Zhou Wei等人提出了一种基于稳健主成分分析的回波分离方法[10],通过把回波矩阵分解成低秩阵和稀疏阵的相加,来完成对刚体与游离部件回波的精确分离;Li Bin等人则使用基于Chirplet分解的方法进行刚体回波的分离提取[11];白雪茹等人则在使用低调频率匹配滤波方法分离回波后,对转动部件回波进行了分析与运动参数估计[12];袁斌等人则研究了基于复数局部均值分解的微多普勒分离方法,通过分析各分量的多普勒差异,来实现微多普勒信号分离[13];张馨元等人采用自适应小波变换来分离活动部件与目标,以剔除活动部件的影响[14];张群等人引入压缩感知理论,利用多重测量矢量模型进行信号重建来获得目标的主体ISAR像,并用逆Radon变换获得旋转部件的ISAR像[15]。然而上述文章在论述分离后的刚体、部件回波处理时,并未提及到扩展目标本身的转台运动加成在转动部件上的影响:实际上,目标转台运动带来的一阶、二阶的二维距离走动同样会影响到IRT、匹配滤波式搜索等转动分析方法的估计精度。
为克服目标转台运动给旋转部件回波分析带来的影响,并实现含旋转部件的扩展目标的精细化成像,本文在上述研究成果的基础上,提出了一种基于回波分离、参数估计方式的含旋转部件分量的ISAR回波处理流程,来完成对转台影响的补偿以及目标物刚体、旋转部件的成像。本文的内容安排如下:第2章节介绍本文所基于的目标回波模型;第3章节介绍本文所提出的回波分离式处理流程;第4、5章节则分别用仿真和实测数据检验了该流程处理的有效性。
本文所建立的回波模型基于如下两个假设:1.扩展目标由散射点/散射中心组成,且散射点/散射中心固定不变;2.扩展目标的平动运动已经被完全补偿,可视作目标在转台上进行成像。
图1 含旋转部件的目标转台模型
Fig.1 Rotation model of targets with rotational components
如图1所示,坐标系XOY可表示ISAR成像平面,坐标系原点与转台中心重合。某扩展目标绕着转台中心点O以转速度ωB作匀速转动,其上有两个散射点目标P1与P2。其中,点目标P1为刚体散射点,其运动方式与扩展目标整体保持一致;点目标P2为旋转部件散射点,除了作转台运动外,该点还相对于扩展目标本身作以O′为圆心、rP为半径、φP为初始相位的匀速转动。
由图1可推导出点目标P1与P2在纵向距离上的距离变化轨迹:
P1∶ RP1(t)=r0+R1·cos(ωB·t+θ1)
(1)
P2∶ RP2(t)=r0+R2·cos(ωB·t+θ2)+
rP·cos(ωP·t+φP)
(2)
其中,r0表示雷达到转台中心O的距离。由于ISAR成像建立在小角度转动的转台模型上,故当目标在处理时间段内转动的角度足够小时,以上两式可近似表示为:
(3)
P2∶ RP2(t)≈r0+x2-(ωB·y2)·
(4)
其中,xi=Ricos(θi);yi=Risin(θi)。由式(3)与式(4)可看出刚体散射点的纵向距离变化轨迹由转台模型决定,而旋转部件散射点的轨迹则在转台运动变化轨迹的基础上叠加上部件自身的旋转轨迹。
现假设某散射点Pi的雷达回波经下变频、脉压后可表达为:
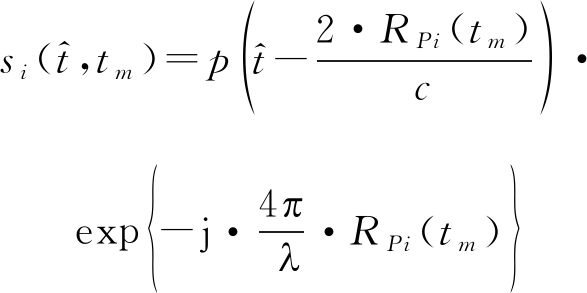
(5)
其中,p表示回波包络项;c为光速;λ表示波长。将式(3)、式(4)代入式(5),并计算其多普勒频率表达式,可得:
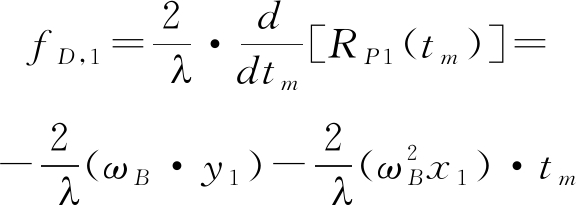
(6)
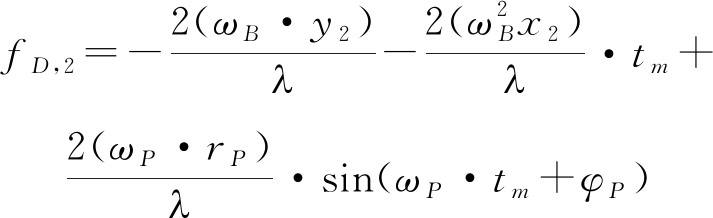
(7)
由式(5)与式(6)可见,转台模型所产生的关于慢时间的一阶、二阶距离走动会反映在回波中:一阶距离走动会使包络峰值发生偏移,导致纵向图像散焦;二阶距离走动则同时影响距离-多普勒维度的散射点聚焦。而由(7)可看出,旋转部件的成像除了受到转台模型的影响外,还会受到自身转动的影响,正弦类包络偏移项、相位项的引入使得成像图在横、纵向上的能量更加发散。
由上述分析可知,要完成刚体目标的成像聚焦,就需要对转台运动的一阶、二阶纵向距离走动逐项进行补偿;而对旋转部件而言,则应在转台转动补偿完成的基础上,再消除正弦类纵向距离走动的影响。考虑到刚体、部件的回波经常在距离-多普勒域混叠,就需要先将其分离,再各自独立进行相关处理。
对于在成像域混叠的刚体、旋转部件回波,本文使用基于时频分布图能量积累的Radon-Wigner变换(Radon-Wigner transform,RWT)方法,通过对慢时间信号的Wigner-Ville分布(Wigner-Ville Distribution,WVD)图进行直线线积分,来判断某散射点属于刚体还是游离部件。RWT的表达式为:
(8)
式中, f0表示初始频率,γ表示调频率;WVD的表达式[16]则为:
(9)
其中,s(tm)表示某个距离单元上的慢时间回波。
由式(6)可知,刚体散射点的相位回波可等效为一种线性调频信号,而用WVD对线性调频信号做时频分析的分辨率是最高的[17]。另一方面,Radon变换本质为一种沿给定路径进行积分投影的变换,其通过对图像中的直线进行线性积分,来将其从图像中的一条直线转化成参数域的一个点,从而实现图中直线参数的提取[18]。因此,线性调频信号在WVD中的直线分布特性便使得RWT方法得以适用。而对于式(7),其时频分布图则是绕着某一直线进行上下浮动,故用式(8)和式(9)对图进行能量线积分时,其所得值远小于刚体散射点的所得值。因此,通过设立阈值,将RWT后所积累能量超过阈值的线性调频分量提取出来,将其视为刚体散射点的回波,而未超过阈值的回波部分则可视为旋转部件的回波,从而完成刚体-旋转部件的回波分离。
然而,需要注意的是,WVD在面对回波中含有多个线性调频分量时,其所得的时频分布图中会出现交叉项成分。当所含线性调频分量的数量较多时,交叉项在图中的混叠会掩盖已有的线性调频分量的分布或形成一条虚假线性能量分布,使得依靠线积分操作的RWT方法做出错误的估计与判决,影响回波分离的精确性。为此,本文并不是在一次RWT操作后便将超过阈值的分量全部提取而出,而是引入CLEAN技术[19],通过定位积累能量最大分量、获取调频参数估计、重建单分量信号、更新残余信号的方式迭代提取回波中的各线性调频分量,从而有效抑制了WVD中交叉项成分对RWT的影响。图2展示了CLEAN技术用于RWT处理的具体操作流程。
对于用RWT分离出的刚体回波,由式(6)可知,其多普勒频率表达式含有一个会使成像点横向散焦的调频率项。要使成像点横向聚焦并完成刚体回波的成像后定标,便需要对转台模型的等效旋转速度进行估计。应注意到,在式(6)中调频率γ与转速度ωB之间存在着以下的关系:
(10)
其中,x1表示某刚体散射点到转台中心的相对纵向距离,r1则表示该散射点到雷达处的纵向距离。因此,只要能获得刚体中各散射点目标的纵向距离以及该点回波的调频率值,便可使用一次二项式拟合的方式,估计出拟合直线的斜率,计算出等效转速度ωB与等效转动中心位置r0的估计值。
由于本文在分离回波时,已使用RWT方法估计出了各距离单元上的刚体散射点回波的调频率值,此处可直接使用最小二乘法对这些值进行线性拟合,并估计出等效转速度的模值。这也是选用RWT分离刚体回波的一个优势所在。
在使用估计的转速度值进行定标前需要对二阶距离走动进行补偿。由于二阶距离走动对包络偏移的影响不可忽略,本文采用空时域分析(space-time analysis,STA)的表达形式,对包络-相位进行联合补偿。现将式(5)对快时间
进行傅里叶变换,得到STA下的回波表达式[20]:
si(fb,tm)=P(fb)·
(11)
式中,P(fb)表示
的频谱, fc表示载频。将RPi(tm)中表示二阶距离走动的项代入,得到:
si(fb,tm)=P(fb)·
(12)
上式便为二阶距离走动在空-时域中的表示,若需要将其补偿,只需要将上式中的相位项消去。由于ωB与x1都已被估计得出,故可构造补偿相位项:
(13)
其中,
与
为估计值。将该补偿相位项与式(11)所示回波相乘,再对频域fb进行反傅里叶变换,即可完成补偿。
应注意的是,基于STA的补偿项应不仅用于刚体回波的处理,由式(4)、式(7)可知,旋转部件的回波同样需要对二阶距离走动进行补偿。而在二阶距离走动补偿后,可使用Keystone变换对刚体回波进行包络项的一阶距离走动补偿[5],使刚体目标像在纵向距离维度上达到聚焦的效果。
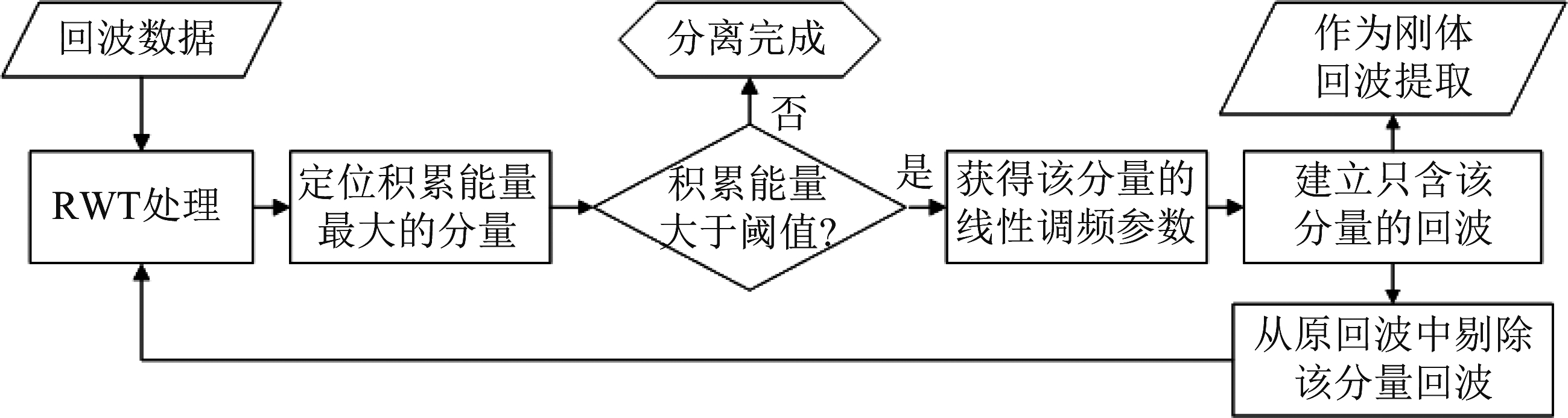
图2 使用CLEAN的RWT处理流程
Fig.2 The flow of RWT processing by using CLEAN
由式(4)、式(7)的表达式可看出,无论是包络偏移的余弦函数项,还是多普勒展宽的正弦函数项,都符合正弦类函数的基本特征,即具备三个自由度变量:幅度、频率、初始相位。换言之,只要能获得这三个参数的估计值,就可以计算出部件点目标具备的旋转运动参数值,从而实现补偿及精细成像。
对于正弦类曲线,IRT方法具备十分良好的分析效果,因此被本文采用。该方法的本质同样在于对某图形的能量分布以线积分形式进行积累,而此时的线L则对应不同参数值的正弦曲线。若假设该正弦曲线在一幅灰度图(u,ν)上的表示为:
L∶ R(u,ν)=δ[ν-Asin(u+φ)]
(14)
则对该图的IRT处理表达式[21]可写为:
exp{j 2π(kxx+kyy)}dudkxdky=
δ(x-Asin φ)·δ(y-Acos φ)
(15)
其中,
可以看出,对于任意一条正弦曲线ν=Asin(u+φ),IRT都可将其聚焦到灰度图(x,y)上的一个点,且从该点的坐标(x0,y0)能获得该曲线两个参数的估计值:
(16)
(17)
事实上,针对旋转目标的回波,有两种正弦曲线图可用:一是在纵向分辨能力足够大时直接取包络走动曲线图作为待处理灰度图;二是在频谱折叠次数不多时,对慢时间回波进行时频分析所得的时频分布图。
当使用时频分布图时,式(14)中的灰度图(u,ν)等效于(ωtm, f)。由于慢时间tm的取值固定,角频率ω可视作一种尺度因子,只有当其数值等于图中所含正弦曲线的频点时,IRT结果图(x,y)中才会出现一个高度聚焦的点,因此可将聚焦效果评价作为角频率ω估计的目标函数进行搜索,获得估计值
本文所使用的评价标准是将灰度图(ωtm, f)进行IRT处理后所得的图像的最大幅度值,其表达式为:
(18)
但需要注意的是,在上一节中本文已经补偿了部件回波中的二阶距离走动,但回波中仍含有一阶距离走动项,该项使得时频图中的正弦曲线向上/下发生了移动,即曲线表达式由式(14)变为:
L∶ R(ωtm, f)=δ[f-Asin(ωtm+φ)+fshift]
(19)
这会导致聚焦点的再次散焦,需要将其平移回时频图的中间位置。而根据一阶距离走动像对多普勒的影响:
fshift=-2(ωB·y2)/λ
(20)
可以从平移补偿的频率长度
反向估算出该部件的转动中心的横向距离位置
获得了正弦曲线三个参数的估计值后,便可将其转化为旋转运动参数用于部件成像。由于一阶、二阶距离走动皆已补偿,式(7)可化为:
(21)
将式(21)与式(14)相对比,可获得旋转半径的估计表达式:
(22)
而由图1可知,旋转点目标的初始位置坐标则为:
(23)
其中,对旋转部件转动中心的纵向距离位置
可从对部件回波的包络的几何中心进行估计来获得。
当时频分布图发生折叠时,若折叠数较少,正弦曲线特征仍存在,则可以使用频谱拼接的方式进行处理[21];但当折叠数大、时频图上已经看不出正弦曲线的轮廓时,则应选择包络走动曲线图进行IRT处理。此时,灰度图(u,ν)等效于
为相对纵向距离。应注意的是,当纵向距离分辨力足够大时,一阶距离走动同样会影响包络走动曲线,需将其进行初速度估计、补偿以避免IRT结果图散焦。初速度的估计值同样可用作转动中心的横向距离位置估计,即依照转台模型有以下关系:
νshift=ωB·y2
(24)
其中,νshift表示包络走动的初速度值。
值得一提的是,由于此时所处理的灰度图已含纵向距离参数
其IRT结果图I(x,y)实际上即为以部件旋转中心为原点的横、纵向成像图,无需再进行正弦-旋转参数的转化。
为保证上述各步骤处理之间互不影响、确保估计补偿的精度,本文设计了对含旋转部件的扩展目标成像的处理流程,如图3所示。
图3中,含旋转部件的扩展目标的ISAR回波经脉冲压缩后先进行平动补偿的处理,以使该目标的运动符合转台模型;再对补偿后的目标回波用RWT方法将其分离成刚体回波和旋转部件回波,以便后续的分别处理;由于转台转动同时作用于刚体和旋转部件,为实现精细成像应先基于STA方法对二者回波中存在的由转台转动引起的二阶距离走动项进行参数化补偿。
对于补偿后的刚体回波,则应再使用Keystone方法将转台转动引起的一阶距离走动的影响消除,使刚体所成像在横、纵向上得以聚焦,完成刚体目标成像。而对于补偿后的旋转部件回波则应根据其频谱折叠程度,分情形进行相应处理:当折叠程度不大,慢时间回波的时频分布图具备正弦特征时,则应选用时频分布图进行IRT处理;当频谱折叠次数过多,时频分布图中已看不出正弦曲线形状时,则应选用回波的包络进行IRT处理。无论是哪种情形,在IRT操作完成后,可利用包络的走动、几何信息估计出该部件的旋转中心所处的位置,从而完成旋转部件成像。
需要注意的是,本文所提的流程适用于目标物平稳运动时的小角度转动成像;当目标物做高机动运动时,转动的不均匀或转过的角度大皆会使式(1)～(4)所示的距离轨迹变化模型不再适用。另一方面,若旋转部件散射点的回波,不仅频谱折叠次数过多,而且包络中的正弦函数形走动也不明显时,本文所提的流程同样不适用;但随着雷达器件技术的发展,更大带宽的使用将带来纵向距离分辨力的不断提升,旋转散射点的正弦包络也将愈发明显,从而满足本文所提流程的使用条件。因此,本文所提流程在未来的ISAR精细化成像处理中依然具备潜力。
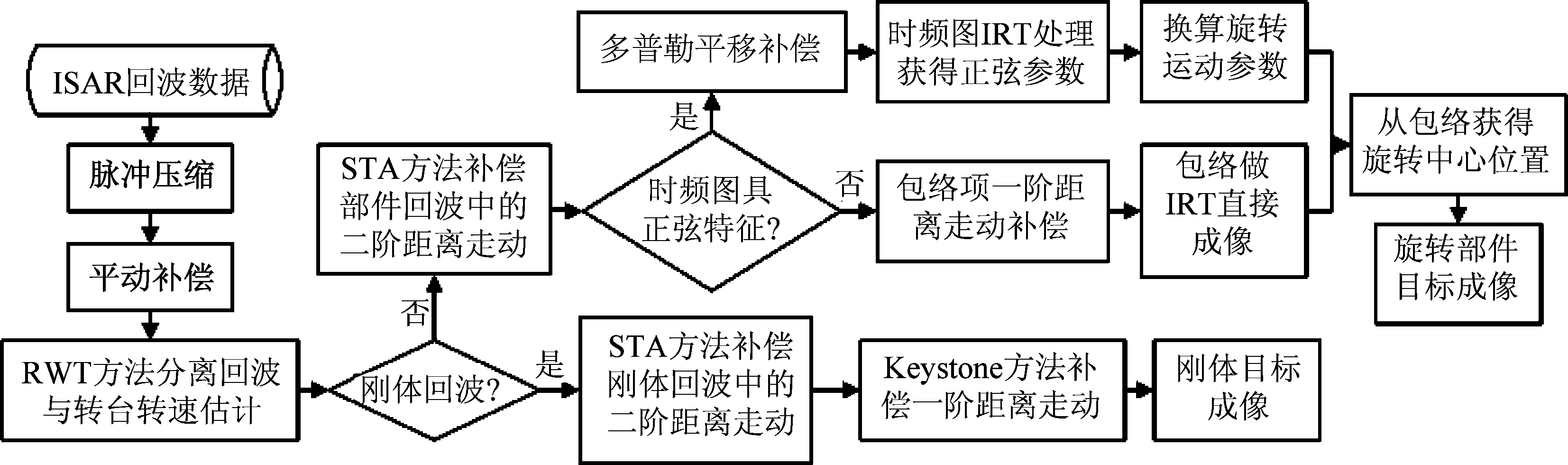
图3 含旋转部件的目标回波处理流程
Fig.3 Processing flow of target echo with rotational components
现采用仿真数据来检验本文所提出的流程有效性。仿真数据的回波参数如下:雷达载频fc为5.5 GHz,信号带宽B为1 GHz,脉冲重复频率PRF为500 Hz,回波脉压前的信噪比(signal-to-noise ratio, SNR)为20 dB。散射点在成像平面上的初始分布如图4(a)所示。
图4(a)中,转台的转动中心设在坐标(0,0)处,转台以0.08 rad/s进行转动。刚体散射点用“*”表示,两类旋转部件散射点分别用“○”与“◇”进行标注。其中,6个“○”分布在纵向距离-10 m、10 m附近,分别绕着坐标(-9,6)、(9,6)作半径0.24 m、转速度4π rad/s的匀速转动;3个“◇”分布在纵向距离0 m附近,绕着坐标(0,-9)作半径1.92 m、转速度40π rad/s的匀速转动。仿真数据不含平动分量,其慢时间处理用脉冲数为512,图4(b)展示了对该回波直接进行RD成像所得结果图。
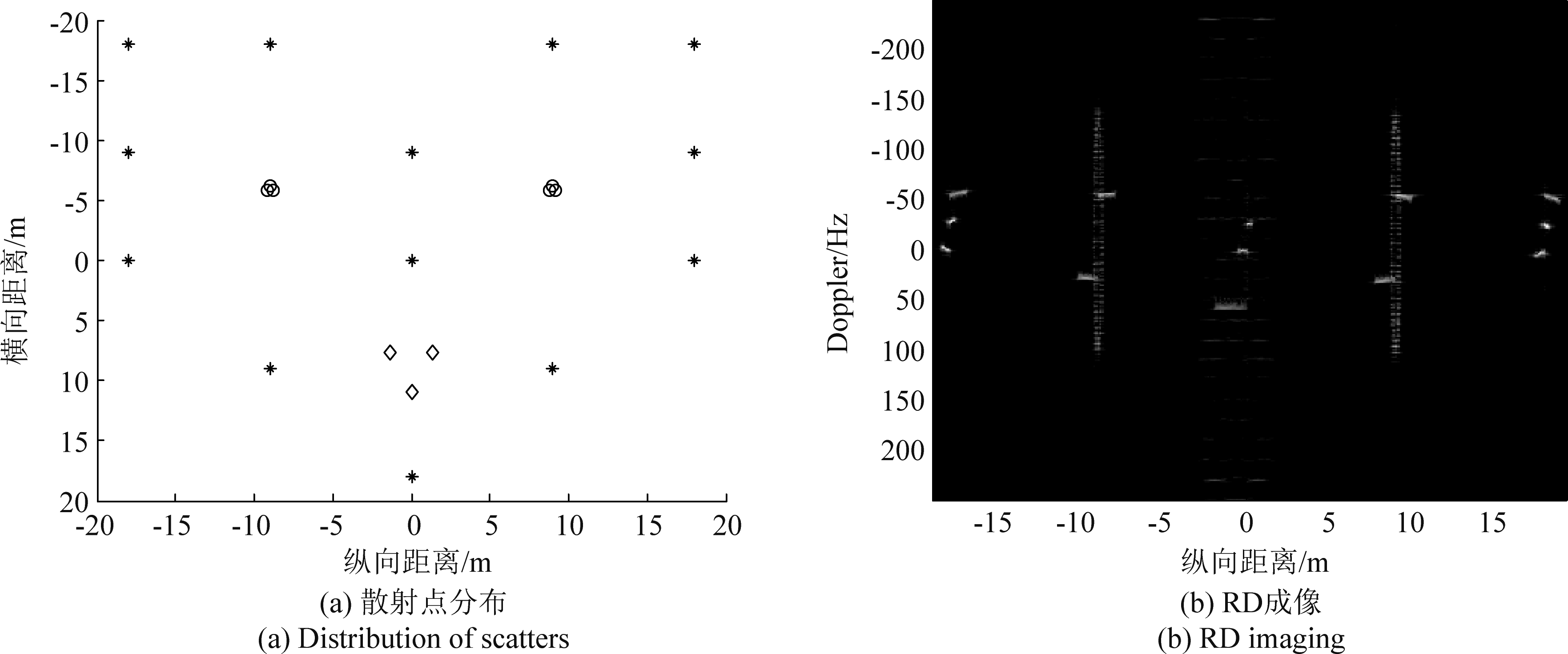
图4 仿真点目标分布与RD成像图
Fig.4 Distribution of scatters and RD imaging of simulation
从图4(b)可看出,由于转动分量的存在,无论是刚体还是旋转部件的成像,都出现了距离-多普勒二维的散焦。现以本文所设计的处理流程对该回波进行处理。如图5所示,本文对经过脉压后的仿真回波逐距离单元地进行RWT处理,使得刚体回波得到分离,再进行RD成像来展示回波分离情况。图5重点展示了在距离-多普勒域混叠的刚体、部件回波的分离情况,可以看到分离的效果显著。
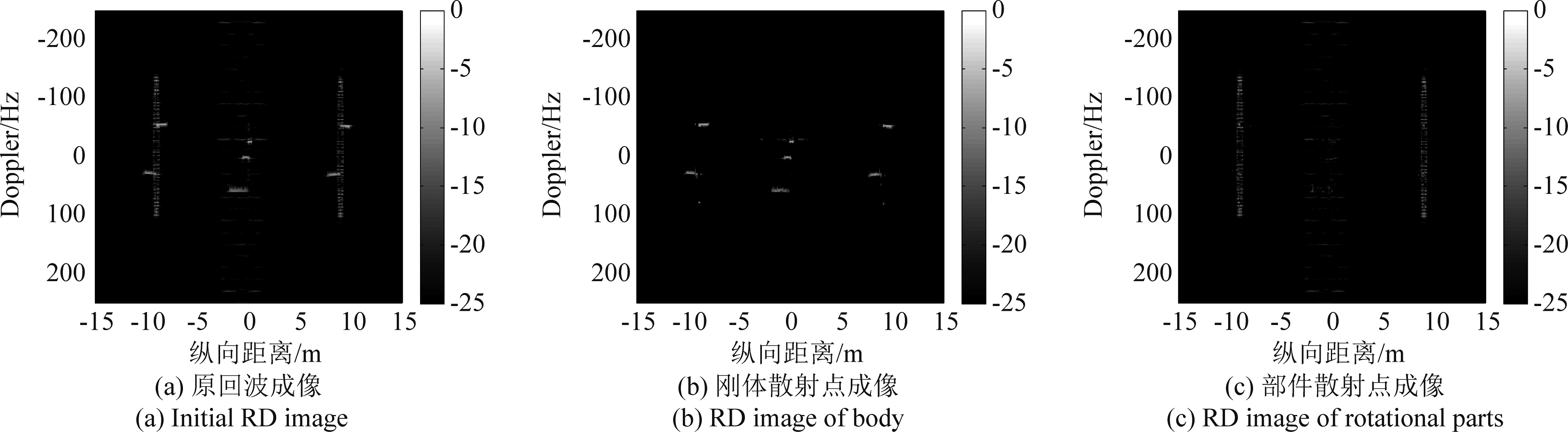
图5 混叠部分刚体、旋转部件回波的分离成像图(dB)
Fig.5 RD imaging of body and rotational scatters after echo separation (in dB)
同时,本文也利用RWT估算出转台的转速度约为0.0833 rad/s,根据上文所述的STA方法,对刚体、部件回波进行二阶距离走动补偿,再对刚体回波进行Keystone变换校正一阶距离走动。图6展示了两次补偿前后的刚体散射点目标的成像图。图6(a)中的散射点在横、纵向二维发散展宽;经STA补偿后散射点在横向上已经聚焦,横向上离转动中心越远的散射点在纵向越散焦;而在Keystone变换后,各散射点在纵向上也得到聚焦,形成十分明亮的点迹。
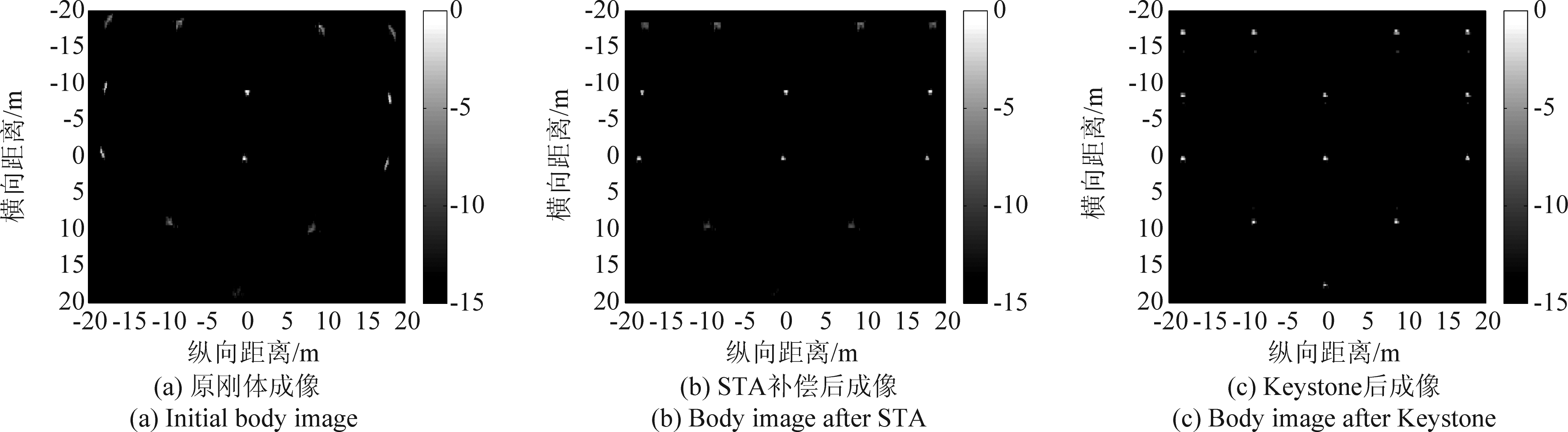
图6 刚体回波两次补偿前后的成像图(dB)
Fig.6 Imaging of body echo before and after twice compensation (in dB)
刚体散射点成像之后,现对纵向距离-10 m附近的旋转点“○”的回波进行处理。由图5(c)可知该区域的回波频谱未发生折叠,故可用时频分布图进行IRT处理。由于图5(c)所示的部件回波分布在多个距离单元内,本文根据傅里叶变换是线性算子这一特性,将-10 m附近的距离单元上的慢时间回波进行叠加,再对叠加后的回波进行短时傅里叶变换(Short-time Fourier transform,STFT)。虽损失了纵向距离信息,但保证了IRT的估计精度。STFT分析结果如图7(a)所示,可看到整个频谱由于一阶距离走动的影响,正弦曲线向上偏移了一段。而根据偏移的频率量,可粗略估计出转动中心的横向位置。
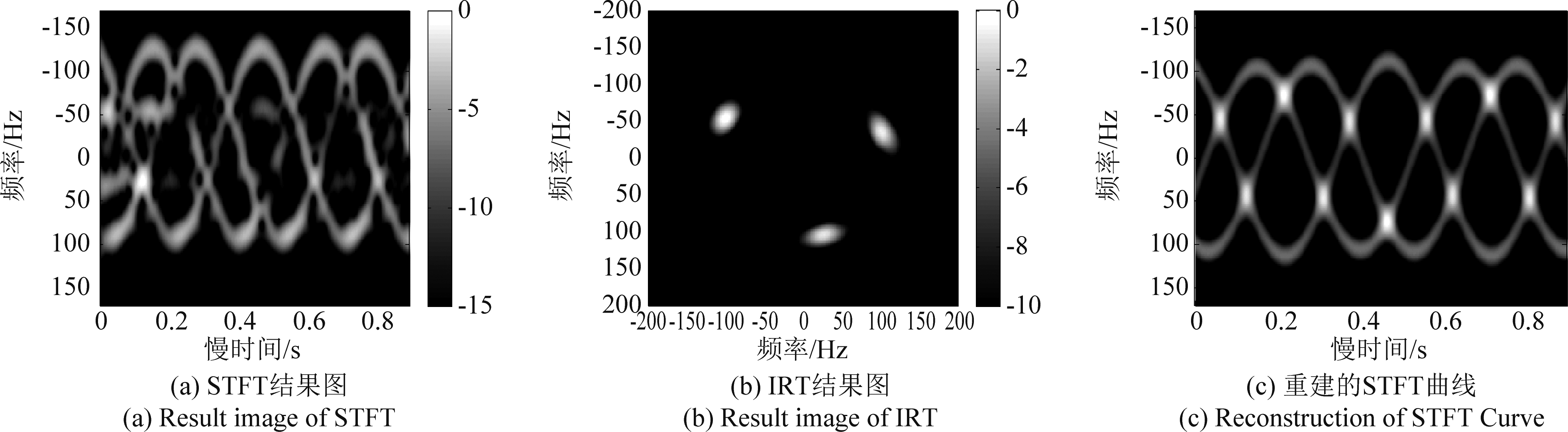
图7 对旋转部件回波的处理结果(dB)
Fig.7 Results of processing for rotational component echo (in dB)
图7(a)中除了正弦成分外,还有刚体回波剥离后所残留的一些频率分量,但在IRT的线积分中,这些残余能量积累远小于正弦曲线的能量积累,因此并不影响图7(b)所示的IRT结果图。
表1 旋转运动参数估计与真值对比
Tab.1 Rotation parameters estimate and their true value
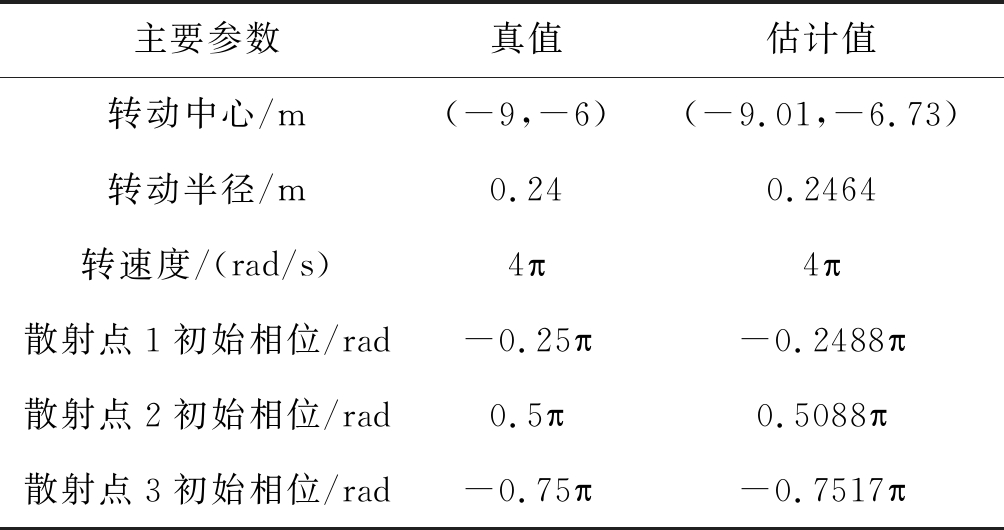
主要参数真值估计值转动中心/m(-9,-6)(-9.01,-6.73)转动半径/m0.240.2464转速度/(rad/s)4葩4葩散射点1初始相位/rad-0.25葩-0.2488葩散射点2初始相位/rad0.5葩0.5088葩散射点3初始相位/rad-0.75葩-0.7517葩
由式(16)到式(23),可对图7(b)进行参数估计,重构部件回波所得的STFT图如图7(c)所示。对比7(a)、7(c)两图,可知重构是有效的。相关正弦参数值可转化为旋转参数,如表1所示。
而对纵向距离10 m附近的三个“○”散射点,可做同样的处理。再根据所得的估计值,将散射点标注在刚体散射点的成像图中,得到图8。通过图8中(a)与(b)、(c)与(d)、(e)与( f )的对比可以看出,虽然对部件转动中心的横向位置的估计产生了一定误差,但各散射点之间的相对距离与其真实值保持一致。这说明该旋转部件的结构特征并未被破坏,IRT处理时频分布图来获得旋转部件散射点成像是有效的。而由式(20)可知,横向位置的估计误差的产生应归因于两点:一、是在将时频图中的正弦曲线平移回中间位置时,由于STFT所获正弦曲线的线条较粗,校正偏移量时对偏移频率量的估计精度不足,产生了约3 Hz的绝对误差;二、是使用RWT方法估计转台转速度值时,产生的约0.0033 rad/s的误差。二者共同导致了对转动中心横向位置估计的误差的产生。
再考虑“◇”散射点的处理,由图5(c)可知,该旋转部件回波的频谱发生了多次折叠,其时频分布图中已看不出正弦曲线的形状特征,因此应换成对包络进行IRT处理,得到图9。
如图9(a)所示,由于部件回波中的由转台运动所致的一阶距离走动并未消除,回波包络出现一阶距离走动,为能使用IRT,应对其进行走动补偿。本文使用包络对齐与线性函数拟合相结合的方式,来进行走动补偿的操作。先用相邻相关法进行包络对齐,再将对齐所得的各脉冲平移距离值用最小二乘法进行线性函数拟合,得到初速度的估计值。依据所得估计值补偿距离走动后,本文先对其某一单元慢回波做包络自相关计算来获得转动频率估计[22],可得该部件转动周期为0.05 s,即转动频率为20 Hz、转动速度为40π rad/s。再对包络进行IRT处理,平移到所估计的转动中心,便获得如图9(b)所示的成像图。对比图9(b)与图8(a),可以发现除了转动中心的横向位置依然存在误差外,散射点的相对位置同样与真实值基本一致,说明对包络做IRT处理进行旋转部件成像同样有效。而由式(24)可知,此时横向位置的估计误差的产生则应归因于初速度的估计精度以及RWT估计转台转速的误差。
下面讨论噪声对本文所提流程的影响。将仿真回波的信噪比SNR调整为0 dB时,该流程对刚体、部件的成像处理依然有效,如图10(a)～10(c)所示;而当回波信噪比为-10 dB时,如图10(d)所示,虽然刚体成像依然聚焦良好,但噪声对旋转部件的运动参数估计与成像处理却造成了严重影响。
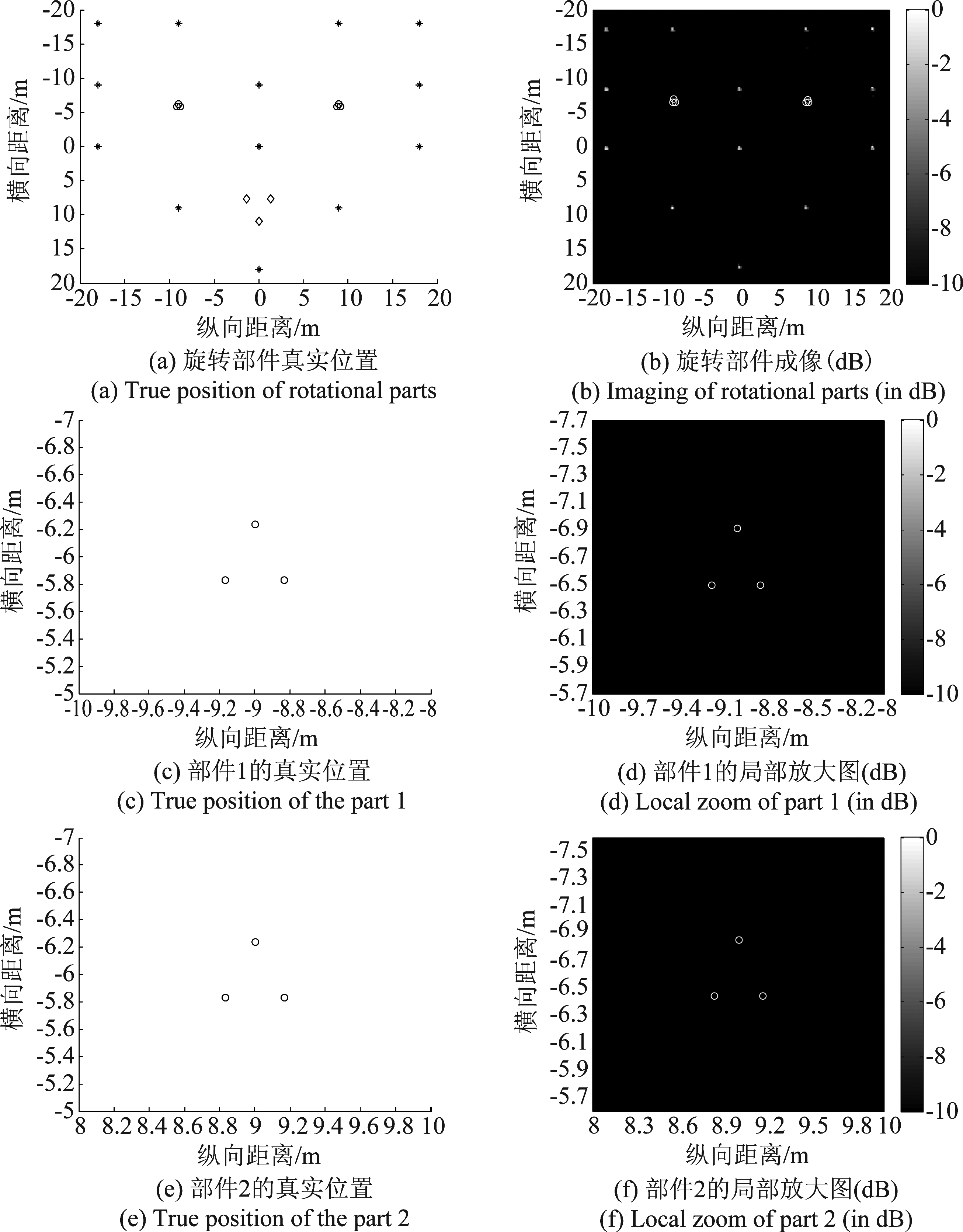
图8 旋转部件的成像与真值对比
Fig.8 Imaging of rotational parts and comparison with true position
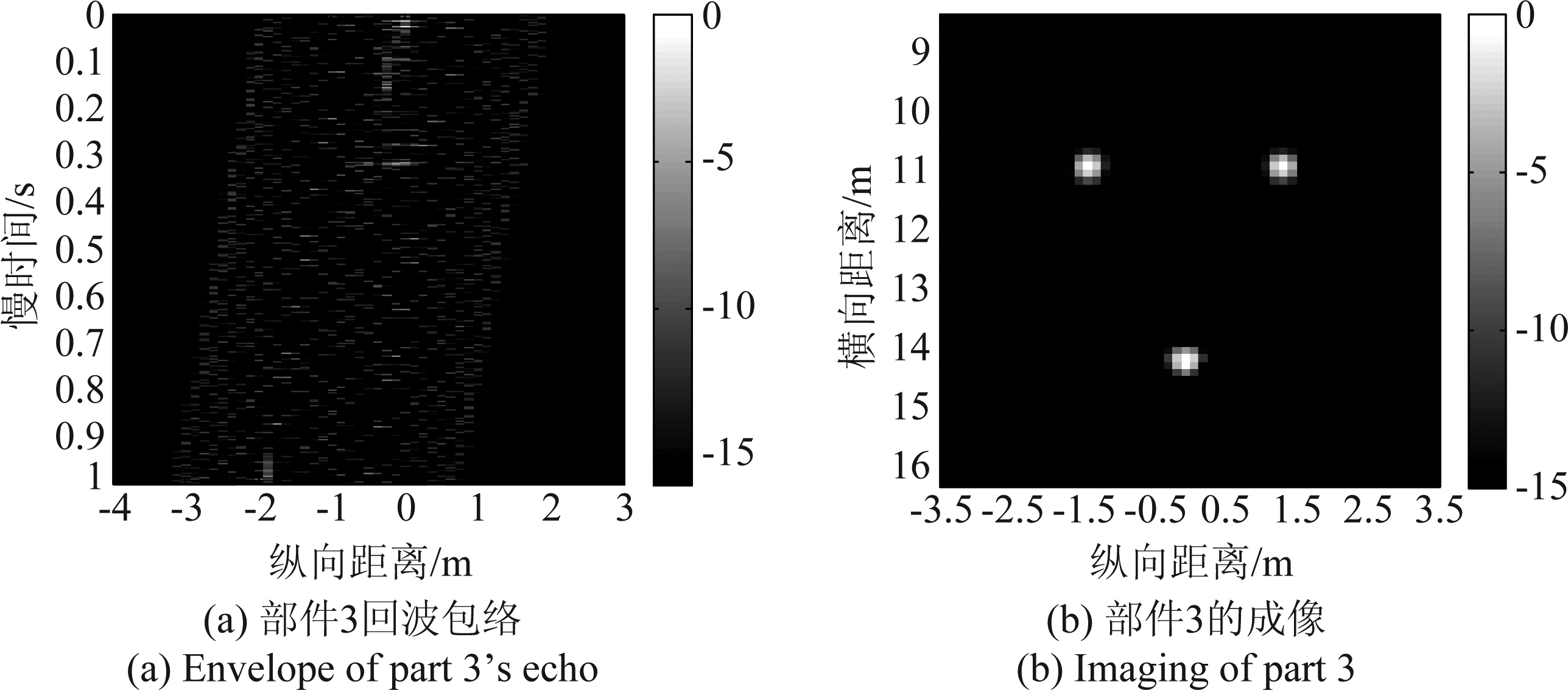
图9 对包络进行IRT处理的结果图(dB)
Fig.9 Results of IRT processing using echo’s envelope (in dB)
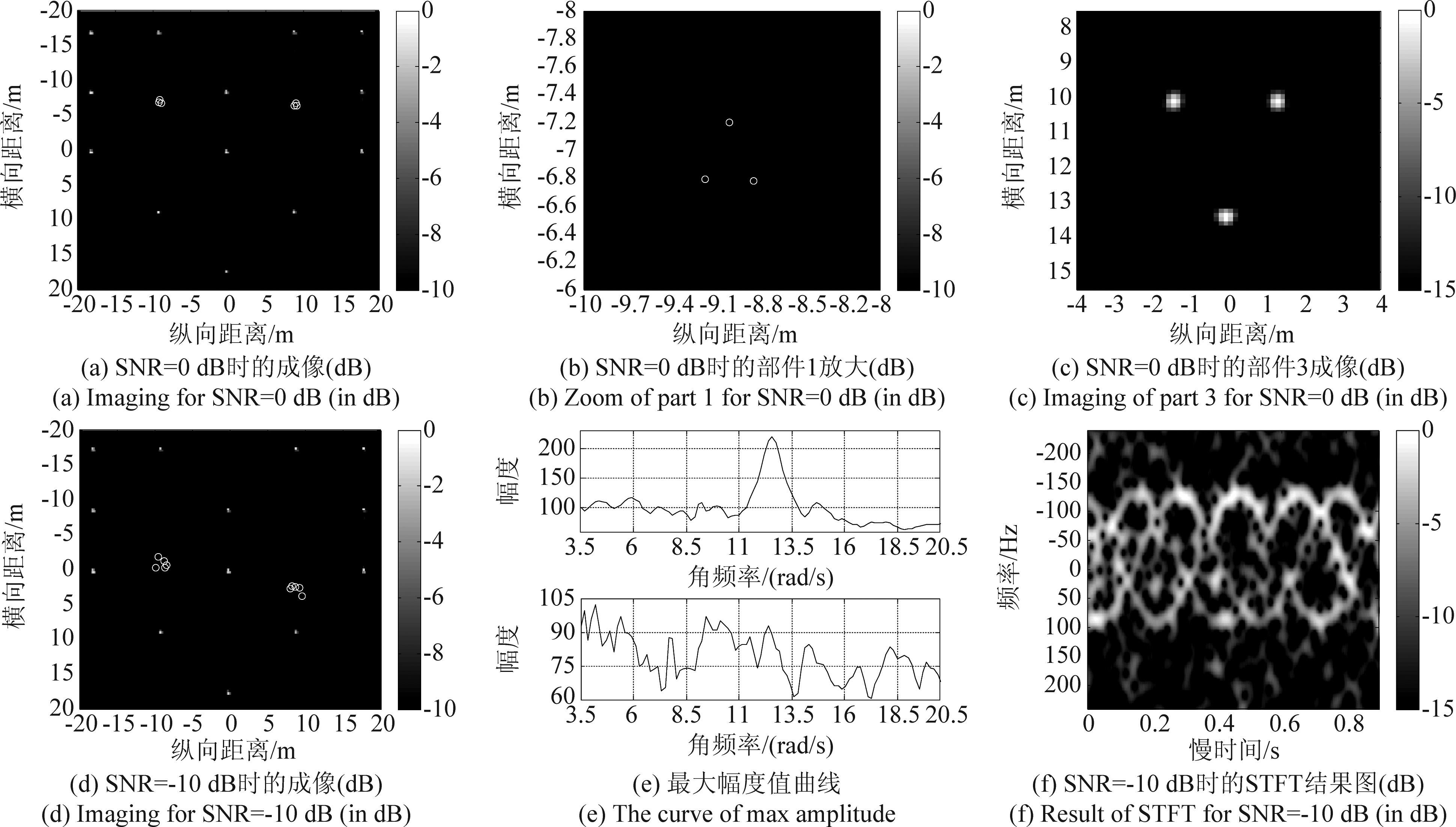
图10 对不同信噪比条件下所提流程的成像效果的分析
Fig.10 Analysis of the effect of imaging using proposed flow under different kinds of SNR conditions
由图10(d)可看出,在SNR为-10 dB情况下,噪声对旋转部件的成像影响很大,这种影响来源于IRT处理对噪声比较敏感。举例来说,3.3节提到,在IRT处理中含有对角频率ω进行一维搜索估计的步骤,而该搜索又以IRT处理结果图中的最大幅度值作为评价指标,搜索估计方式如式(18)所示。图10(e)展示了SNR取0 dB(上图)和SNR取-10 dB(下图)时, IRT处理结果图中最大幅度值随角频率ω变化的曲线。可见,在信噪比较高时,变化曲线在ω取4π rad/s处存在一个显著突出的峰值;而在信噪比低时,变化曲线在搜索范围内存在着诸多峰值,4π处的峰值被埋没其中难以辨认,这就导致了对ω值的错误估计。图10( f )则展示了SNR取-10 dB时对部件1回波的STFT处理图,与图7(a)相比较可见,在噪声的影响下,用于IRT处理的时频分布图中产生了大量的噪点,同时图中正弦曲线的能量也出现分散,从而在进行线积分时产生了图10(e)的下图所示的多峰值曲线。
因此,鉴于IRT处理对噪声的敏感性,本文所提流程适用于较高信噪比条件下的回波处理。
现使用An-26飞机的C波段ISAR实测数据对本文所提流程进行验证。该雷达数据的带宽为400 MHz,脉冲重复频率为400 Hz。图11(a)展示了在对该回波进行平动补偿后所得的RD成像图。可以看到,飞机上的两个螺旋桨部件所产生的回波能量扩展到了整个频谱。使用RWT法分离回波后,所得刚体、部件的回波的RD成像分别如图11(b)、11(c)所示,分离效果显著。
图12则展示了对分离后回波的处理结果。其中图12(a)到图12(c)展示的是本文流程对飞机刚体目标回波的处理结果。
观察图12可知,经过STA方法补偿的图12(b)在横向距离向上更加聚焦;而经过Keystone变换补偿的图12(c)在纵向距离上聚焦程度更高。为更好评价聚焦程度,本文计算了该三幅图的图像熵。图12(a)的图像熵值为1.3943,图12(b)的熵值为1.3900,图12(c)的熵值为1.3869。熵值越低,图像聚焦程度越高。
刚体成像后,需对两个螺旋桨的回波进行成像。由图11(c)可看出,该回波同样属于频谱多次折叠的情况,其时频分布图中正弦曲线的形状已不可分辨。故本文选择对其包络进行IRT处理。处理前,先对其回波的某单元包络进行自相关计算,获得其旋转周期约为0.0475 s,即旋转频率约为21.05 Hz。
图11 RWT分离回波前后的RD成像图(dB)
Fig.11 RD Imaging before and after echo separation by RWT (in dB)
图12 刚体与部件回波的处理与成像(dB)
Fig.12 Processing and imaging of body’s and parts’ echoes (in dB)
事实上,由于受到该实测数据的纵向距离分辨力的限制,一阶纵向距离走动在该包络中并不体现。由实测数据的带宽参数以及纵向距离分辨率的表达式:
(25)
可得最小可分辨距离ΔR为0.3747 m。其中,C表示光速。而由RWT所估计的转台转速度ωB约为0.0474 rad/s,相干积累时间Tobs为0.64 s,若假设转动中心的横向距离yC为10 m,则可以由下式
Rshift=νshift·Tobs=ωB·yC·Tobs
(26)
计算得该段时间内包络的一阶纵向距离走动距离Rshift为0.3034 m,小于纵向最小可分辨距离0.3747 m。而根据图12可知,由于螺旋桨依附在飞机刚体上,其转动中心必然与机体重合,因此横向距离也小于10 m,故实际的包络一阶纵向距离走动必小于最小可分辨距离。因此,该走动在包络上不体现,进而难以获得旋转中心的横向位置估计。因此,图12(d)与图12(e)展示的是相对于旋转中心的两个螺旋桨的IRT成像图。
针对含旋转部件的扩展目标回波,本文提出了一种基于分离信号、参数估计方式的回波处理与成像流程。该流程先使用RWT方法将目标刚体与旋转部件的回波进行分离,并从刚体的回波中估计出目标转台运动的等效转速度;再基于STA方法对刚体与旋转部件的回波同时进行二阶的二维距离走动补偿;然后,采用Keystone变换、IRT方法分别对刚体、旋转部件回波进行一阶距离走动的处理;最后,通过补偿、参数估计等方式完成整个扩展目标的精细化成像。仿真和实测数据处理结果证明了该流程处理的有效性。
值得一提的是,本文中用正弦包络曲线做IRT处理的方法随着雷达技术的发展、纵向距离分辨能力的提升,相信其所成像的精确程度会在未来能够满足ISAR精细化成像的需求。同时,如何提高对旋转部件旋转中心横向位置的估计精度,也是对旋转部件精细化成像的下一步研究方向。
[1] 刘鑫阁, 邢孟道, 孙光才. 一种高精度的ISAR转动补偿和方位定标方法[J]. 电子与信息学报, 2018, 40 (9): 2250-2257.
LIU Xinge, XING Mengdao, SUN Guangcai. A High-precision Method of the Rotation Compensation and Cross-range Scaling for ISAR Imaging[J]. Journal of E1ectronics & Information Technology, 2018, 40(9): 2250-2257.(in Chinese)
[2] 杨利超, 邢孟道, 孙光才, 等. 一种微波光子雷达ISAR成像新方法[J]. 电子与信息学报, 2019, 41(6): 1271-1279.
YANG Lichao, XING Mengdao, SUN Guangcai, et al. A Novel ISAR Imaging Algorithm for Microwave Photonics Radar[J]. Journal of Electronics & Information Technology, 2019, 41(6): 1271-1279.(in Chinese)
[3] 符吉祥, 刑孟道, 徐丹, 等. 一种基于微波光子超高分辨雷达机翼振动参数估计方法[J]. 雷达学报, 2019, 8(2): 232-242.
FU Jixiang, XING Mengdao, XU Dan, et al. Vibration-parameters Estimation Method for Airplane Wings Based on Microwave-photonics Ultrahigh-resolution Radar[J]. Journal of Radars, 2019, 8(2): 232-242.(in Chinese)
[4] ZHANG Qun, YEO T S, TAN H S, et al. Imaging of a Moving Target With Rotating Parts Based on the Hough Transform[J]. IEEE Transactions on Geoscience and Remote Sensing, 2008, 46(1): 291-299.
[5] 叶春茂, 鲁耀兵, 宋建社, 等. 一种ISAR目标转动补偿及图像尺寸标定方法[J]. 电子学报, 2014, 42(3): 611- 615.
YE Chunmao, LU Yaobing, SONG Jianshe, et al. A Rotation Compensation and Image Scaling Method for ISAR Targets[J]. Acta Electronica Sinica, 2014, 42(3): 611- 615.(in Chinese)
[6] 周阳, 毕大平, 沈爱国. 基于IRT的大动态反射系数微动目标检测算法[J]. 系统工程与电子技术, 2020, 42(9): 1935-1944.
ZHOU Yang, BI Daping, SHEN Aiguo. Micro-motion target detection algorithm of IRT based large dynamic reflection coefficient[J]. Systems Engineering and Electronics, 2020, 42(9): 1935-1944.(in Chinese)
[7] STANKOVIC L, DJUROVIC I, THAYAPARAN T. Separation of Target Rigid Body and Micro-Doppler Effects in ISAR Imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(4): 1496-1506.
[8] THAYAPARAN T, ABROL S, RISEBOROUGH E, et al. Analysis of Radar Micro-Doppler Signatures from Experimental Helicopter and Human Data[J]. IET Radar, Sonar & Navigation, 2007, 1(4): 289-299.
[9] BAI Xueru, XING Mengdao, ZHOU Feng, et al. Imaging of Micromotion Targets With Rotating Parts Based on Empirical-Mode Decomposition[J]. IEEE Transactions on Geoscience & Remote Sensing, 2008, 46(11): 3514-3523.
[10] ZHOU Wei, YEH Chunmao, JIN Ruijin, et al. ISAR Imaging of Targets with Rotating Parts Based on Robust Principal Component Analysis[J]. IET Radar, Sonar & Navigation, 2017, 11(4): 563-569. .
[11] LI Bin, WAN Jianwei, YAO Kangze, et al. ISAR Based on Micro-Doppler Analysis and Chirplet Parameter Separation[C]∥Proc. of 1st Asian and Pacific Conference on Synthetic Aperture Radar, 2007: 379-384.
[12] 白雪茹. 空天目标逆合孔径雷达成像新方法研究[D]. 西安: 西安电子科技大学, 2011.
BAI Xueru. Research on new methods of ISAR imaging for space targets[D]. Xi’an: Xidian University, 2011.(in Chinese)
[13] 袁斌, 徐世友, 陈曾平. 基于复数局部均值分解的含旋转部件目标微多普勒分离技术[J]. 电子与信息学报, 2012, 34(12): 2927-2933.
YUAN Bin, XU Shiyou, CHEN Zengping. Micro-Doppler separation from targets with rotating parts based on complex local mean decomposition[J]. Journal of Electronics & Information Technology, 2012, 34(12): 2927-2933.(in Chinese)
[14] 张馨元, 齐玉涛, 林刚. 含旋转部件的动态目标特征提取方法研究[J]. 电波科学学报, 2019, 34(1): 65- 69.
ZHANG Xinyuan, QI Yutao, LIN Gang. Dynamic object feature extraction with rotating parts[J]. Chinese Journal of Radio Science, 2019, 34(1): 65- 69.(in Chinese)
[15] 张群, 蒋国建, 康乐, 等. 基于多重测量矢量的含旋转部件目标ISAR成像方法[J]. 空军工程大学学报(自然科学版), 2020, 21(4): 36- 42.
ZHANG Qun, JIANG Guojian, KANG Le, et al. An ISAR imaging algorithm for targets with rotating parts based on multiple measurement vectors[J]. Journal of Air Force Engineering University (Natural Science Edition), 2020, 21(4): 36- 42.(in Chinese)
[16] CHEN V C, LI F, HO S S, et al. Micro-Doppler Effect in Radar: Phenomenon, Model, and Simulation Study[J]. IEEE Transactions on Aerospace and Electronic Systems, 2006, 42(1): 2-21.
[17] 保铮, 邢孟道, 王彤. 雷达成像技术[M]. 北京: 电子工业出版社, 2005: 263-269.
BAO Zheng, XING Mengdao, WANG Tong. Radar Imaging Technique[M]. Beijing: Publishing House of Electronics Industry, 2005: 263-269.(in Chinese)
[18] 胡程, 张天然, 王锐. 基于Radon变换的昆虫上升下降率提取算法及实验验证[J]. 信号处理, 2019, 35(6): 1072-1078.
HU Cheng, ZHANG Tianran, WANG Rui. Ascent and descent rate extraction algorithm and experimental verification based on Radon transform[J]. Journal of Signal Processing, 2019, 35(6): 1072-1078.(in Chinese)
[19] 贾琼琼, 李海, 吴仁彪. 基于STAP的高速空中微弱多目标检测[J]. 信号处理, 2011, 27(10): 1531-1535.
JIA Qiongqiong, LI Hai, WU Renbiao. Multiple fast moving air dim targets detection via STAP[J]. Signal Processing, 2011, 27(10): 1531-1535.(in Chinese)
[20] YEH Chunmao, YANG Jian, PENG Yingning, et al. Rotation Estimation for ISAR Targets With a Space-Time Analysis Technique[J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(5): 899-903.
[21] YANG Qi, DENG Bin, WANG Hongqiang, et al. Doppler Aliasing Free Micro-Motion Parameter Estimation Algorithm Based on the Spliced Time-Frequency Image and Inverse Radon Transform [C]∥Proc. of the International Conference on Information and Communications Technologies, 2014.
[22] SUN Zhaoqiang, LI Baozhu, LU Yaobing. Research on micro-motion and micro-Doppler of ballistic targets[C]∥Proc. of 2009 IET International Radar Conference, 2009.
陈学斌 男, 1995年生, 福建福州人。北京无线电测量研究所, 博士研究生, 主要研究方向为雷达成像技术。
E-mail: cxb1995xx@126.com
叶春茂(通信作者) 男, 1981年生, 湖北咸宁人。北京无线电测量研究所, 研究员, 博士, 主要研究方向为雷达系统总体技术、雷达成像与识别。
E-mail: danielgodman@163.com
张 彦 男, 1993年生, 安徽黄山人。北京无线电测量研究所, 博士研究生, 主要研究方向为雷达波形设计与识别。
E-mail: zoo1881@163.com
胡庆荣 男, 1974年生, 河北人。北京无线电测量研究所, 研究员, 博士, 主要研究方向为雷达总体技术、雷达成像。
E-mail: 328298074@163.com