
图1 全极化昆虫雷达
Fig.1 The fully polarimetric radar
Reference format: WANG Rui, LI Weidong, HU Cheng, et al. Insect Biological Parameters Estimation Method and Field Quantitative Experiment Verification for Fully Polarimetric Entomological Radar[J]. Journal of Signal Processing, 2021, 37(2): 199-208. DOI: 10.16798/j.issn.1003- 0530.2021.02.005.
昆虫迁飞是陆地上最重要的动物迁徙行为[1]。每年,不计其数的昆虫进行长距离季节性迁飞,庞大数量的迁飞昆虫影响着生态系统的功能[2]。昆虫对生态过程至关重要,它们分解有机物、调节害虫、为农作物授粉、是许多脊椎动物的重要食物来源[3]。而迁飞昆虫是不同生态系统的沟通纽带,促进了生态系统之间能量、营养物质、繁殖体(如花粉)、病原体和寄生虫的传输,并通过构建捕食与被捕食的关系来影响生态相互作用[1,4]。然而,对于迁飞昆虫在空中生态系统中的生态学意义以及昆虫迁飞机理还有很多未解之谜。例如,“空中昆虫群落结构和种群数量的季节性/年际性波动规律、昆虫种内/种间的物种关系、害虫与天敌的协同进化关系”等空中生态系统问题,以及“昆虫由‘居留型’转变为‘迁飞型’的诱导原因”、“远距离迁飞对昆虫种群的生态学意义”、“昆虫迁飞收益与迁飞风险权衡策略”等迁飞机理问题。若要研究迁飞昆虫在空中生态系统中的生态学意义以及昆虫迁飞机理,前提是能对迁飞昆虫进行有效监测。
传统的昆虫迁飞观测手段包括网捕、诱虫灯诱捕、标记重捕等,均是间接的研究手段,并且这些方法会干扰昆虫的迁飞行为,从而使得对昆虫迁飞行为的解译变得困难[5-6]。基于传统观测手段的迁飞昆虫研究进展缓慢,而将雷达用于迁飞昆虫研究彻底地改变了这一现状。雷达具有全天时、全天候、探测距离远的特性,可以在不干扰昆虫飞行的情况下,观测昆虫飞行,测量目标的高度、数量、密度、位移方向、速度、体轴朝向等行为信息,以及体重、振翅频率等生物学参数[7-8]。昆虫雷达的这些测量能力,使得人们首次具备了深入研究昆虫迁飞行为的能力,并先后发现了昆虫迁飞时的共同定向、高度聚集成层等震撼人心的现象,大大提高了人们对于昆虫迁飞的认识[9]。
昆虫雷达最早出现在20世纪60年代。最开始的昆虫雷达为非相参扫描体制,探测到的目标回波强度显示在PPI显示屏上,通过拍照等方式记录目标回波。扫描雷达仅能观测昆虫的数量、密度以及群体的共同定向,无法测量个体昆虫的参数,并且雷达数据的保存和分析费时费力,使用成本很高,仅适于短期的昆虫迁飞观测研究,难以实现长期观测[10]。20世纪90年代出现的垂直雷达(称为VLR,Vertical-looking radar)实现了长期全自动化观测,促进了昆虫雷达的推广应用。VLR为波束章动的旋转线极化体制。其天线垂直对天,波束偏离垂直轴一个很小的角度,并以垂直轴为中心高速旋转。波束的旋转使得线极化方向跟着360°旋转,可测量目标腹部在不同极化方向的回波,这使得VLR具备了测量昆虫体轴朝向的能力;波束章动对目标回波的调制使得VLR可测量目标在波束中的位置,从而具备了对个体目标RCS的测量能力,进而根据昆虫体重与RCS的映射观测,可估计昆虫的体重;此外,根据昆虫飞行时振翅对回波的微多普勒调制,通过频谱分析,可得到目标的振翅频率[8]。对个体昆虫体轴朝向、体重和振翅频率的测量,提升了昆虫雷达的测量能力,帮助人们发现了迁飞昆虫复杂的朝向和高度选择策略等行为,极大地促进了迁飞昆虫学的发展[9]。然而,VLR为单极化、非相参体制,仅能测量目标幅度信息,无法测量目标相位和完整的极化信息,由于获取的信息维度少,VLR在测量目标生物参数时存在朝向90°误差难辨别、体重反演误差大、无法反演体长等问题[11-12]。
为了解决当前VLR在测量生物参数时存在的问题,本团队开发了相参体制全极化昆虫雷达。全极化雷达通过发射一组极化正交的脉冲可直接测量目标的散射矩阵(SM,Scattering matrix),SM中不仅包含了VLR测量的不同极化方向的目标幅度信息,还包含了目标相位和完整的极化信息。研究表明,基于昆虫SM中包含的幅度、极化和相位等更多维的目标信息,能较大提升全极化昆虫雷达对昆虫生物参数的测量能力,解决传统VLR测量生物参数的难题。例如,基于SM相对特征相位,可实现“平行”和“垂直”昆虫辨别,解决传统体轴朝向测量存在的谐振区大昆虫90°朝向错误难辨别问题[11];基于SM主特征向量,可实现更高精度的体轴朝向反演[13];基于SM极化不变量,可实现昆虫体长反演并提高昆虫体重反演精度[12]。以上研究均基于在微波暗室中,利用矢量网络分析仪搭建的全极化设备测量的昆虫全极化数据开展,并基于微波暗室实测数据验证方法的有效性。然而,这些方法还没有经历实际全极化雷达系统的应用检验,能否实际应用还需要开展进一步的定量试验验证。
定量试验验证就是利用实际全极化雷达测量体轴朝向、体重和体长已知的昆虫样本,对比雷达反演值与真值的差别,评估测量精度是否满足实际应用的需求。定量试验的难点在于实现很困难。昆虫的体型小(体长几毫米到几厘米),RCS微弱(低至约-70 dBsm),极易受杂波影响;昆虫生物参数反演均是基于昆虫平飞、雷达垂直向上照射的情景下实现,试验测量时需要确保昆虫腹部正对雷达波束;若要验证体轴朝向测量方法,需精确控制昆虫的体轴朝向;昆虫雷达通常是脉冲雷达体制,存在较大的盲距,雷达很难对准目标。以本团队开发的全极化昆虫雷达为例,该雷达盲距为150 m,在150 m外将雷达波束对准昆虫,并调整昆虫的姿态,满足腹部正对雷达以及不同体轴朝向的测量需求,同时还要防止环境杂波干扰,极难实现。最简单的测量方案是在150 m之外,竖立2根高杆,将昆虫粘在细鱼线上,并将细鱼线系在杆上,通过调整两个杆上鱼线系的高度,调整昆虫体轴朝向。该方案的问题在于,地杂波和杆子引入的杂波将非常强,昆虫微弱的回波将被杂波淹没,另外,很难控制昆虫的身体姿态使其腹部正对着雷达并准确调整昆虫体轴朝向(由于重力作用,昆虫身体很难与鱼线平行)。
本文将首先介绍全极化昆虫雷达生物参数反演方法,然后基于团队开发的全极化昆虫雷达,采用基于双无人机协同飞行悬吊昆虫的试验方案解决定量试验的难题,并开展定量试验验证生物参数反演方法在外场全极化昆虫雷达的应用。
本文的安排如下:第2章介绍本团队全极化昆虫雷达系统和基于全极化的昆虫体轴朝向、体重和体长等生物参数反演方法;第3章介绍基于全极化昆虫雷达的外场定量试验,并基于试验数据验证生物参数反演方法在全极化雷达的实际应用情况,分析测量精度。
关于本团队开发的全极化昆虫雷达的详细信息可参考文献[14-16],这里仅给出该雷达的简单介绍。雷达如图1所示,工作在Ku波段,中心频率16.2 GHz,距离分辨率0.2 m。雷达为相参体制,采用同时全极化技术通过同时发射水平(H,Horizontal)和垂直(V,Vertical)线极化雷达波,实现全极化测量,获取目标的SM。雷达盲距150 m。天线为直径1 m的双极化抛物面天线,波束宽度约为1.5°。雷达配备二维转台伺服,可在方位(0~360°)和俯仰(0~90°)二维转动。

图1 全极化昆虫雷达
Fig.1 The fully polarimetric radar
传统昆虫雷达为非相参、单极化雷达,对应的生物参数反演方法均为非相参、单极化的处理。全极化昆虫雷达直接测量昆虫的SM,可获取目标的极化、幅度和相位等更多维度的信息。为了充分发挥全极化雷达的测量优势,需采用全新的基于目标SM的生物参数反演方法。下面将介绍面向全极化雷达提出的基于目标SM的体轴朝向、体重和体长等生物反演方法[11-13]。相对于传统VLR采用的生物参数反演方法,这些方法可解决体轴朝向90°错误难辨别问题,并提高体轴朝向、体重和体长的反演精度。
(1)体轴朝向反演
传统昆虫体轴朝向反演是基于当雷达极化方向平行于体轴时回波RCS最大的假设,然而,该假设仅对瑞利区昆虫有效,对于谐振区昆虫会存在最大RCS出现在极化垂直于体轴朝向的情况。我们将满足该假设的昆虫称为“平行(PA,parallel)”昆虫,而最大RCS出现在极化垂直于体轴朝向的昆虫称为“垂直(PE,perpendicular)”昆虫。对于PE昆虫,传统VLR是没有能力辨别的,因此,传统体轴朝向反演存在90°朝向反演错误难辨别问题。若要正确反演昆虫体轴朝向,首先需要辨别昆虫的类型(PA/PE),然后提取最大RCS的方向,获得体轴朝向。基于SM的相对特征相位和主特征向量可分别实现PA和PE昆虫辨别,并提高体轴朝向反演精度[11,13]。
假设雷达测量的目标SM为
(1)
其中,s11、s12、s21和s22分别定义为HH、HV、VH和VV极化RCS(单位:m2)的平方根;β、β′和γ为对应的相位。
对S进行特征值分解,可得到散射矩阵的2个特征值:
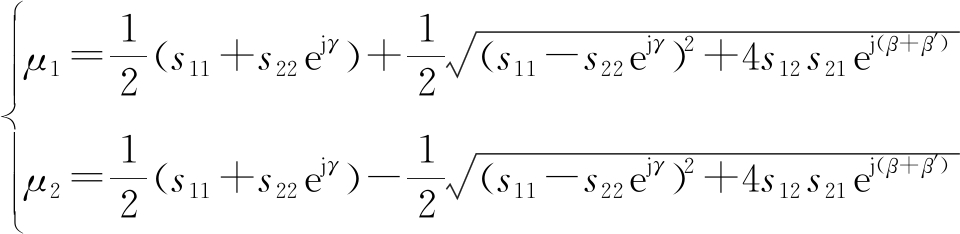
(2)
其中,|μ1|≥|μ2|。
相对特征相位定义为:
(3)
其中,arg(·)表示取相位运算。
基于微波暗室实测不同体型昆虫数据的研究发现,对于PA昆虫,Δφ恒小于0;而对于PE昆虫,Δφ恒大于0。由该发现可得到昆虫类型辨别方法:
昆虫类型![]()
(4)
辨别昆虫的类型后,提取出昆虫最大RCS对应的极化方向即可得到昆虫体轴朝向。根据极化理论,当雷达的极化方式为目标散射矩阵主特征向量时,回波功率最大,即目标RCS最大。此时极化的方向就是最大RCS对应的极化方向。散射矩阵主特征向量可表示为
(5)
其中,
(6)
将主特征向量写为雷达极化方式的极化椭圆表示式:
(7)
其中,αm为最大RCS对应的极化方向,τm为椭圆率。
另式(5)与式(7)相等,可得到昆虫最大RCS对应的极化方向的表达式:
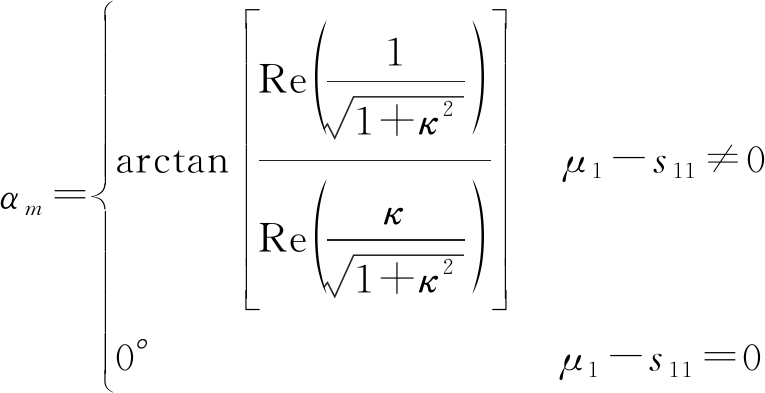
(8)
因而,昆虫体轴朝向表达式为
(9)
(2)体重/体长反演
基于昆虫实测数据的研究发现,昆虫SM的两个极化不变量ν和d与体重、体长有很强的单调映射关系,通过多项式拟合可得到体重/体长与极化不变量的关系式,用于体重/体长反演[12]。ν表示极化方向与昆虫体轴垂直时的RCS;d表示极化方向与昆虫体轴平行和垂直时的RCS乘积。2个极化不变量ν和d的表达式分别为:
(10)
(11)
其中,
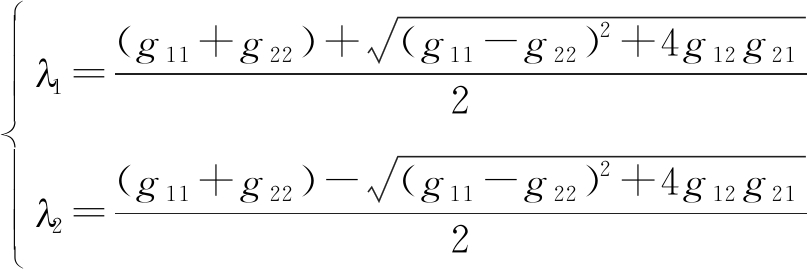
(12)
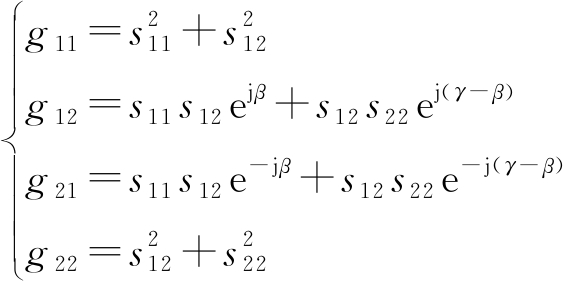
(13)
两种体重反演经验公式分别为:
Mυ=100.07(lgυ)2+1.13·lgυ+5.51,lgυ∈[-5.7,-3.4]
(14)
Md(mg)=100.1296(lgd)2+1.9455·lgd+7.8014,
lgd∈[-5.1,-3.6]
(15)
两种体长反演经验公式分别为:
Lυ=1.82(lgυ)3+26.72(lgυ)2+
134.31·lgυ+243.78,
lgυ∈[-5.7,-3.4]
(16)
Ld(mm)=-0.9498(lgd)3-7.6202(lgd)2-
4.0505·lgd+62.8207,lgd∈[-5.1,-3.6]
(17)
为避免杂波干扰、便于昆虫体轴朝向调整,提出了基于双无人机协同飞行悬吊昆虫的测量试验方案。试验测量示意如图2(a)所示,实际测量场景如图2(b)所示。两架无人机(大疆经纬M600 Pro)相距120 m,中间悬挂一根120 m 长0.1 mm直径的细鱼线,昆虫位于两个无人机中间,背部中央粘在鱼线上,体轴与鱼线平行,鱼线拉直后,昆虫为平飞姿态。雷达垂直对天观测,无人机协同飞行至200 m高度悬停,将昆虫悬吊在雷达正上方。在无人机起飞前,调整昆虫的位置,使其位于雷达正上方;调整雷达方位角,使得雷达水平极化方向与昆虫体轴朝向(鱼线)平行,此时测量的体轴朝向真值为0°;无人机升空后保持悬停,通过旋转雷达极化方向调整昆虫体轴朝向(雷达测量的体轴朝向为昆虫体轴朝向与H极化的夹角)。综上所述,该试验方案通过雷达垂直对天、双无人机协同悬吊昆虫的方式,解决地面杂波干扰强、难探测问题,两架无人机间隔120 m、悬吊昆虫的鱼线直径仅0.1 mm,均不会引入杂波;通过昆虫背部粘在水平拉直的细鱼线的方式,解决昆虫姿态难控制问题;通过昆虫朝向不变、雷达极化方向旋转的方式调整雷达测量的昆虫朝向,解决昆虫体轴朝向难精确调整的问题;通过先将昆虫位置调整在雷达正上方再起飞的方式,避免雷达远距离难对准问题。
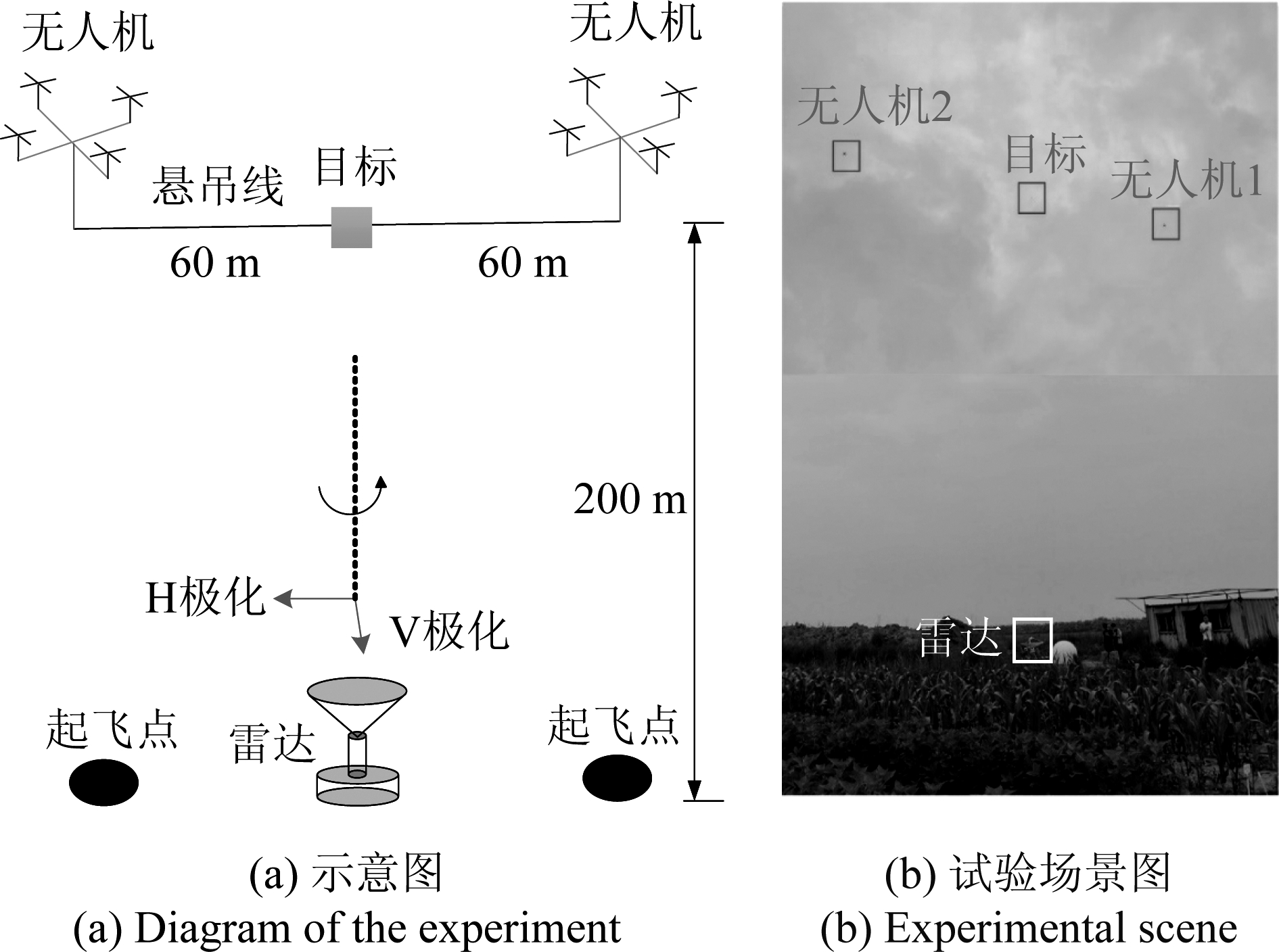
图2 双无人机协同吊飞昆虫测量试验场景
Fig.2 Experimental scene of measuring insect lifted by two cooperative flight UAVs
所测量的昆虫样本是在试验的前一晚用探照灯诱捕得到。共测量了44只昆虫样本,包括棉铃虫、小地老虎、甘蓝夜蛾、粘虫、玉米螟等种类,样本的体重范围19.8~274.1 mg、体长范围8.5~22.1 mm,所有昆虫的体型分布如图3所示。对于每只昆虫样本,分别测量了体轴朝向为0°、30°、45°、60°、90°等情况的昆虫数据。在试验中,同时测量了直径13 cm的金属球,用于极化和RCS定标[14]。
(1)体轴朝向反演
根据前面的介绍,为了避免90°错误,体轴朝向反演首先要根据相对特征相位Δφ的符号辨别昆虫的类型(PA或者PE),若Δφ<0,则昆虫是PA昆虫,其最大RCS出现的极化方向就在体轴朝向;若Δφ>0,则昆虫为PE昆虫,其最大RCS出现的极化方向与体轴朝向垂直。图4给出了测量的44只昆虫样本在不同体轴朝向下的Δφ,每个图的横轴表示昆虫编号(按照体重由小到大顺序),纵轴表示Δφ,中间的实线指示了Δφ=0的位置,圆点表示PA昆虫,方框表示PE昆虫。每个图的右面给出了测量时昆虫体轴朝向。根据判别准则,圆点(PA昆虫)应位于实线之下(Δφ<0);方框(PE昆虫)应在实线之上(Δφ>0)。不满足以上规则的昆虫会被错误判别为相反的类型。从图4可以看到,在0°体轴朝向下,2只PA昆虫的Δφ大于0,会被错误判别为PA昆虫,因而在0°体轴朝向的判别正确率为95.45%;在30°、45°和60°体轴朝向下,所有昆虫的Δφ均满足判别准则,正确率100%;在90°体轴朝向下,4只PA昆虫的Δφ大于0、1只PE昆虫Δφ小于0,均会发生判别错误,因而在90°体轴朝向的判别正确率为88.64%。若将昆虫在所有朝向下的判别结果一起统计,则PA和PE昆虫判别正确率为96.82%。因此,PA和PE昆虫辨别方法在全极化雷达实际应用时,正确率较高,可较好地用于90°朝向错误的辨别。

图3 昆虫样本体型分布
Fig.3 Body size of measured insect specimens
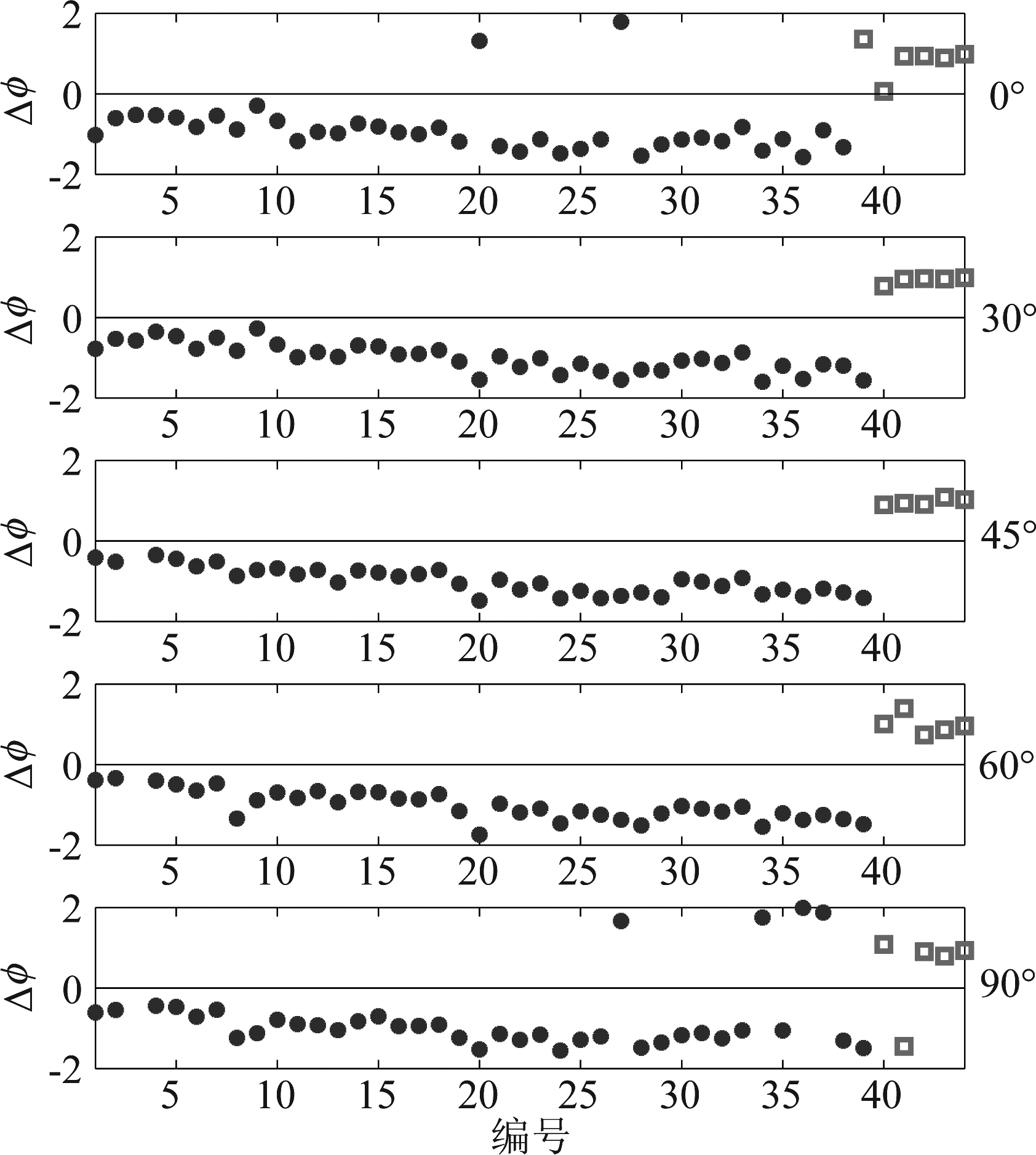
图4 昆虫相对特征相位
Fig.4 Insect relative phase of eigenvalues
在PA和PE辨别的基础上,根据式(9)可反演昆虫的体轴朝向。由于上面已分析过PA和PE昆虫辨别的情况,下面将不再考虑PA和PE昆虫辨别,默认所有昆虫都能正确辨别类型,仅考虑体轴朝向反演的精度。
在试验中,昆虫体轴朝向的调整通过旋转雷达天线改变H极化方向与体轴的夹角实现的,而初始的0°朝向是通过肉眼观察,将H极化方向调整至与体轴平行,会存在一定的偏差。对同一只昆虫,这个偏差在不同朝向下是固定的,因此,可以做统一的补偿。补偿的方法是,对每一只昆虫,计算不同朝向下的朝向测量误差的均值作为该固定偏差,并对所有朝向的测量值均减去该均值。不同昆虫的测量偏差一般是不同的,因此,在补偿时对每一只昆虫单独补偿。统计的所有昆虫朝向测量固定偏差的散点图和直方图如图5所示。可以看到,朝向测量固定偏差分布在-10°~10°之间,固定偏差的分布基本符合正态分布。
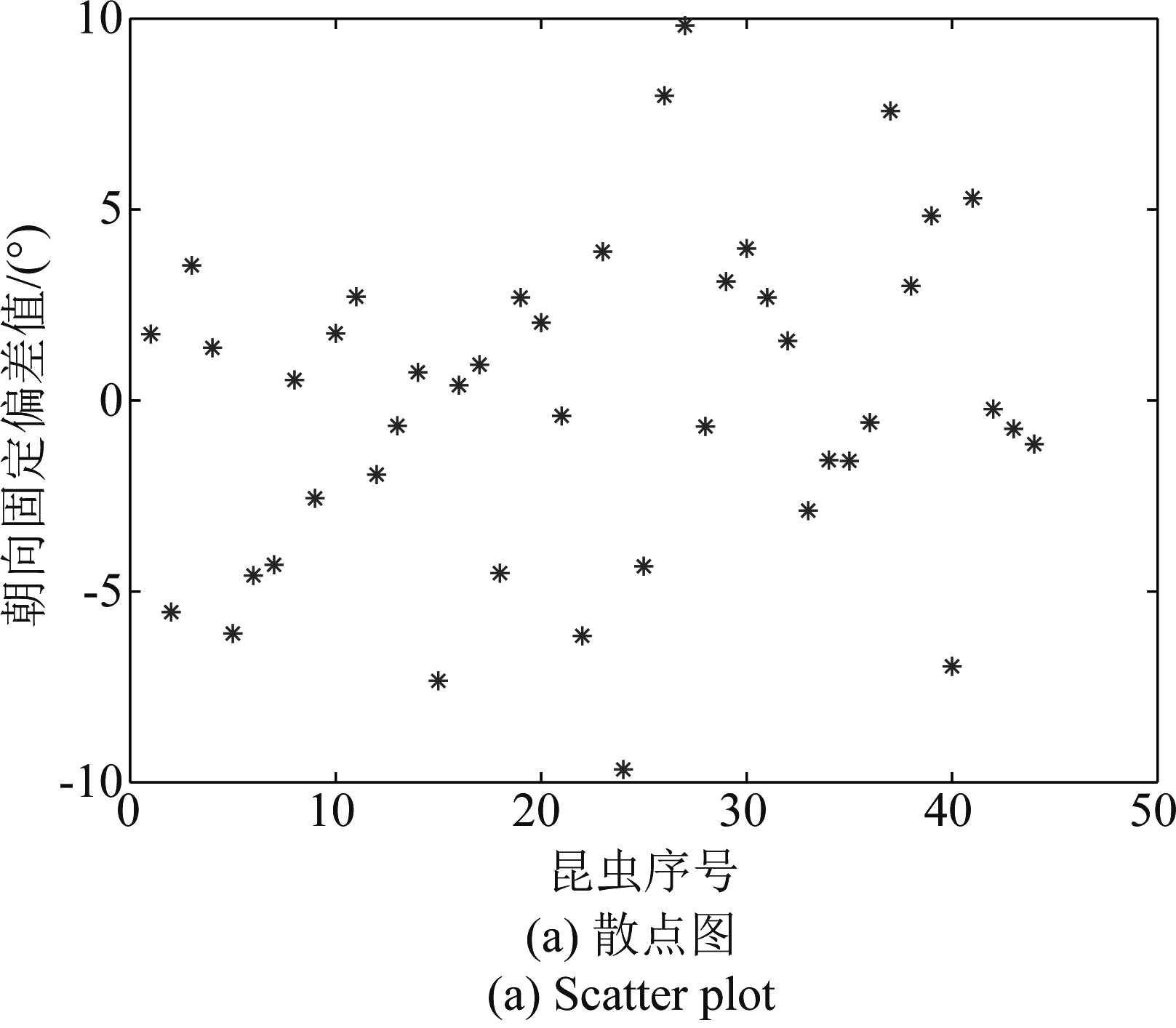
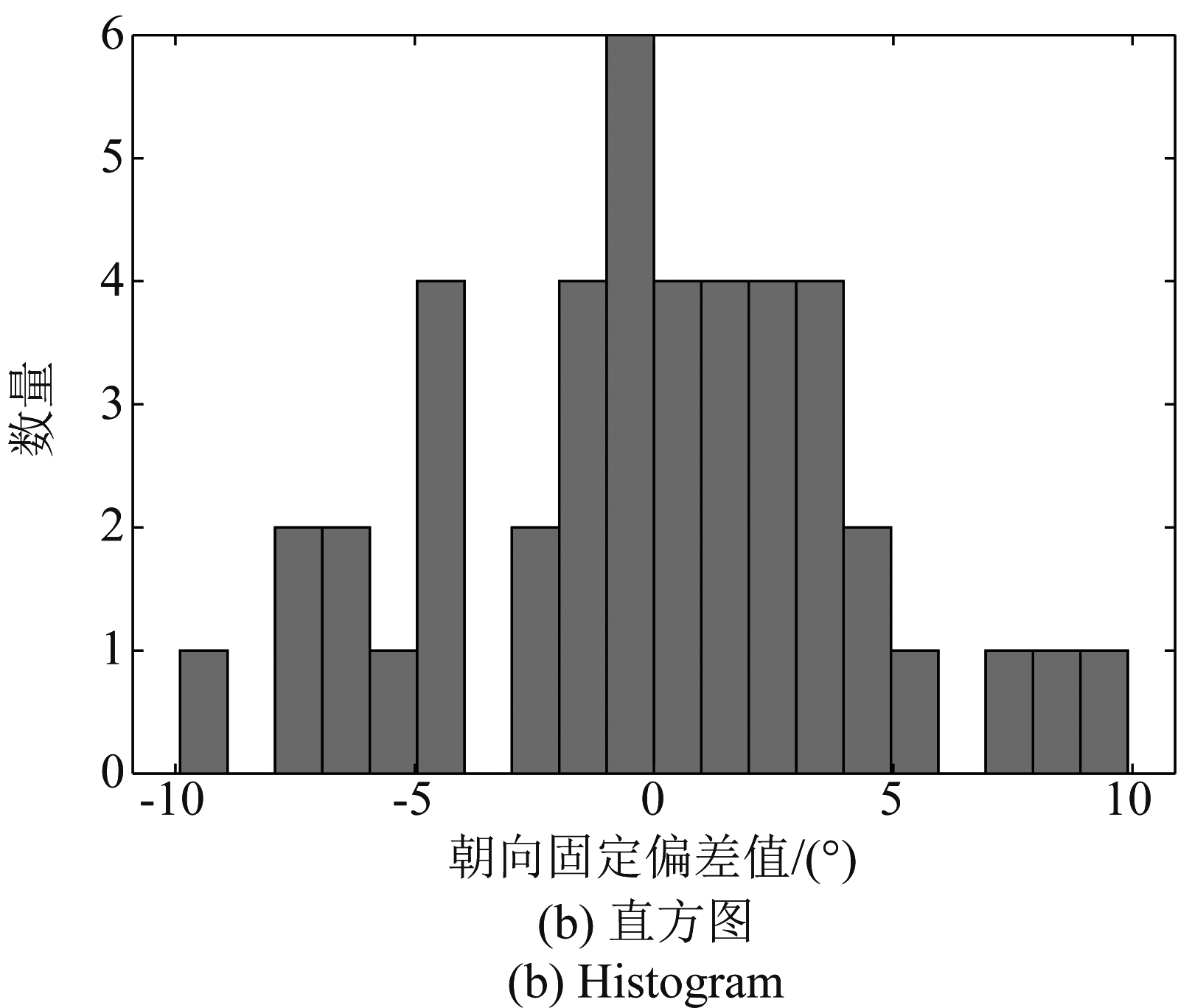
图5 昆虫朝向测量固定偏差
Fig.5 Fixed deviation of insect orientation measurement
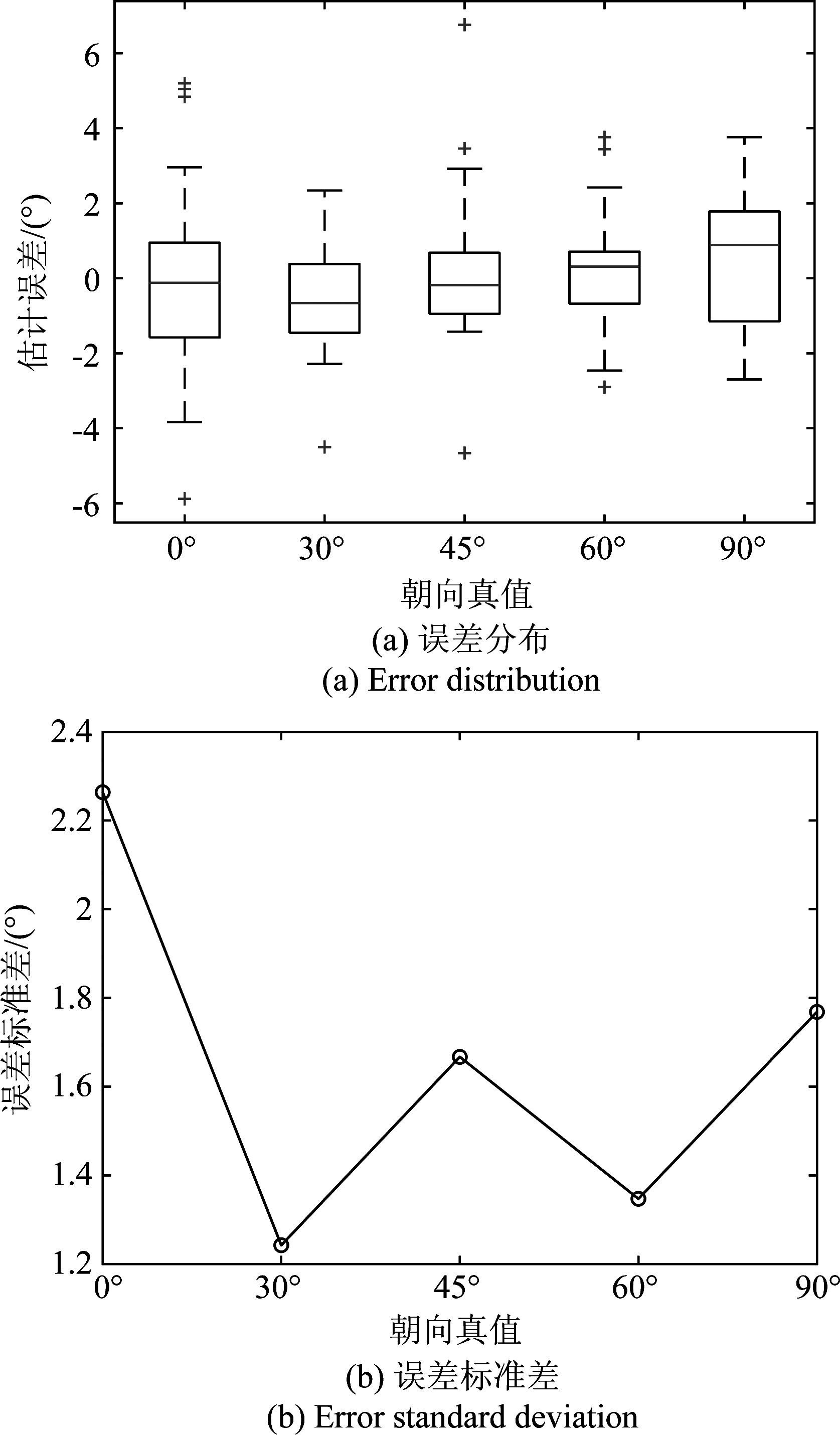
图6 昆虫朝向测量误差
Fig.6 Measurement error of insect orientation
图6给出了补偿固定偏差之后的朝向测量误差分布箱形图(图6(a))以及朝向误差标准差(图6(b))。从图6(a)可以看到,在所有朝向下,朝向误差中位数在-1°~1°之间分布,超过一半的昆虫,朝向误差在±2°以内,绝大多数昆虫的朝向误差不超过±3°。图6(b)给出了不同朝向下的朝向误差标准差,可以见到,朝向为0°时的误差标准差最大,约为2.3°;其余朝向下,误差标准差在1.2°~1.8°之间。所有昆虫总体朝向误差的标准差为1.7°。总体而言,朝向测量精度较高,可满足迁飞昆虫体轴朝向测量需求。
(2)体重反演
基于式(14)和式(15)表示的昆虫体重反演经验公式,反演了所测量昆虫的体重,并计算了体重反演的相对误差,相对误差定义为:
相对误差![]()
(18)
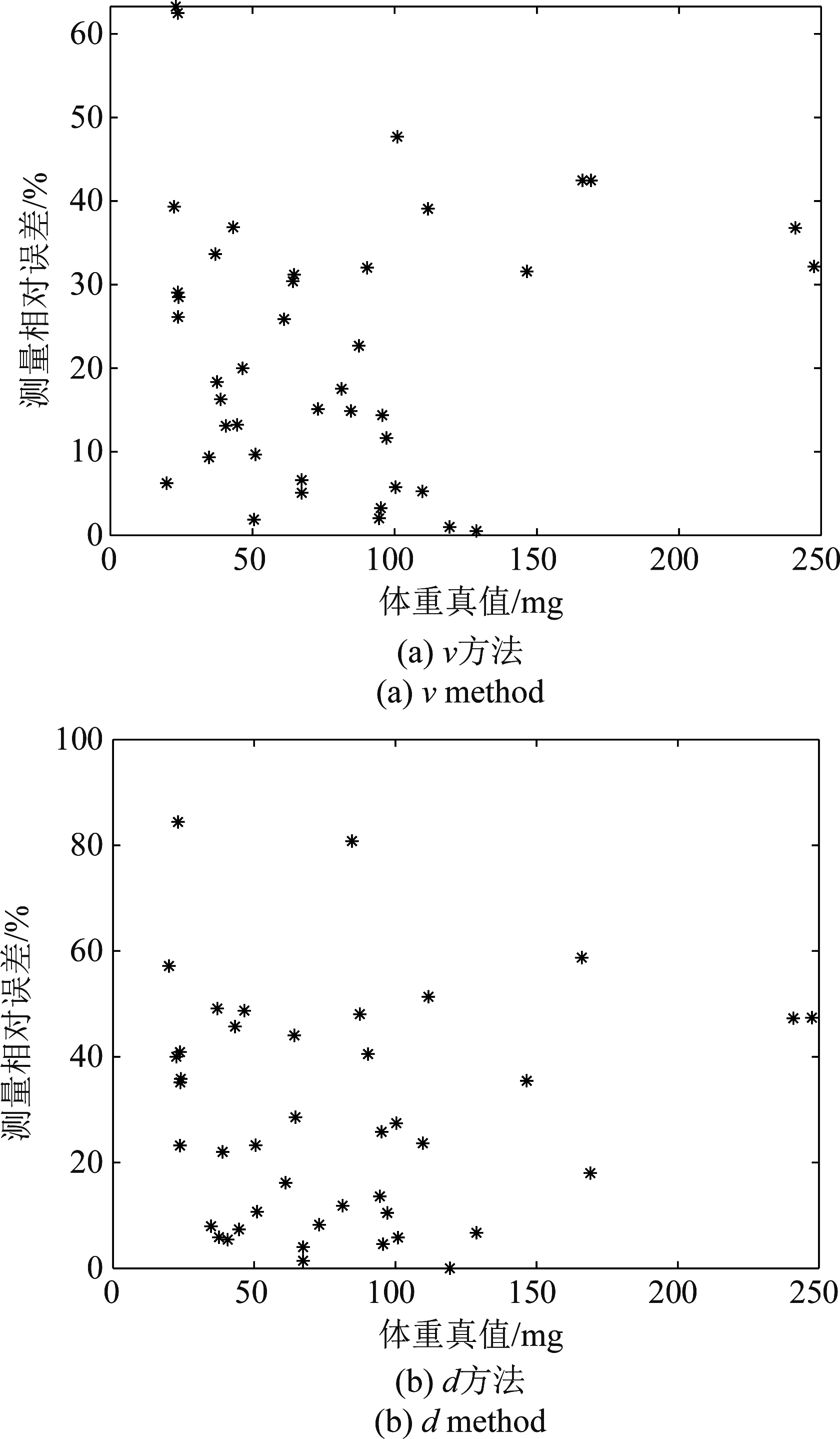
图7 昆虫体重反演误差
Fig.7 Insect mass estimation error
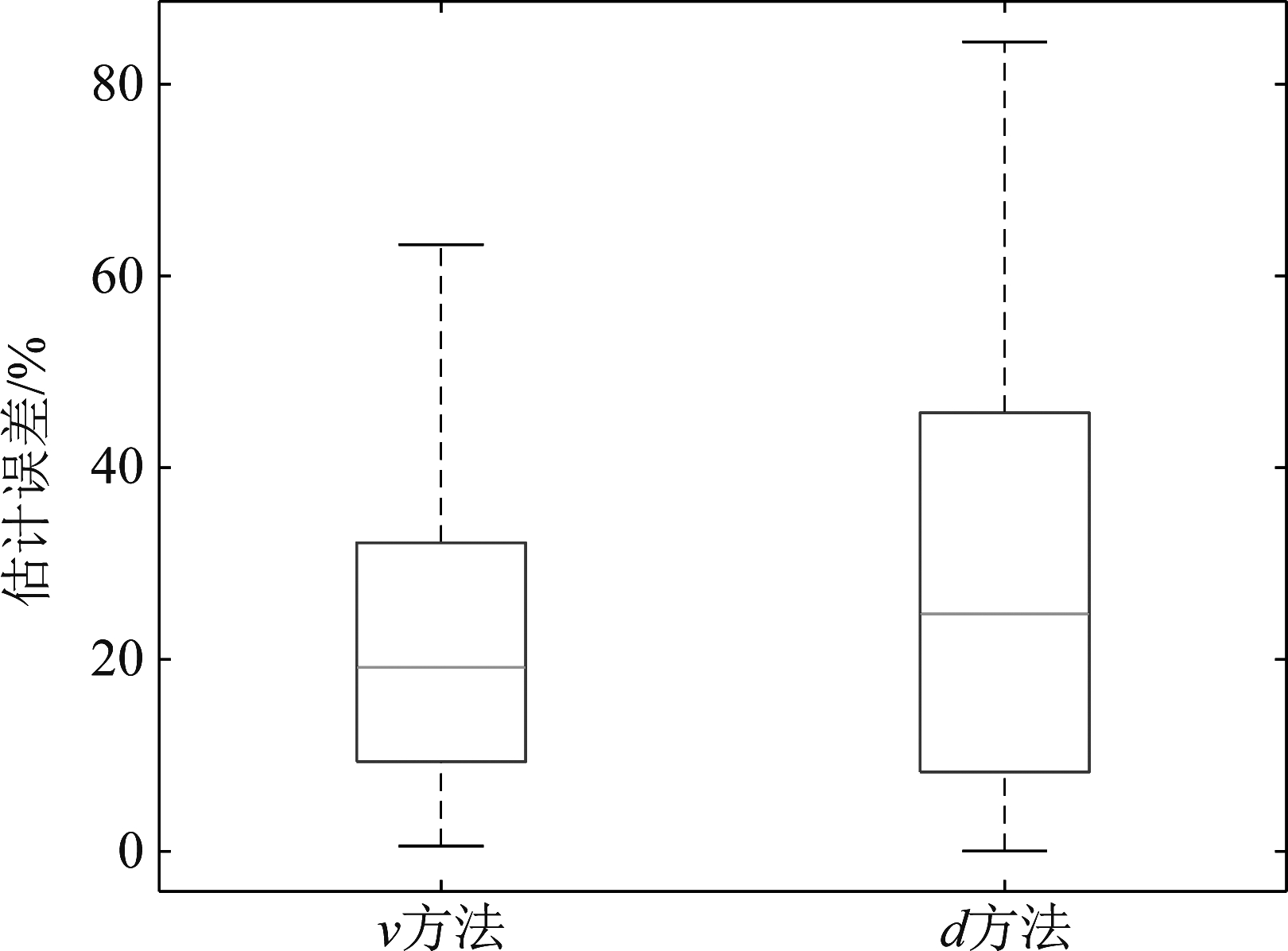
图8 昆虫体重反演误差箱形图
Fig.8 Boxplot of insect mass estimation error
两种方法对所有昆虫的体重测量相对误差如图7所示,可以看到,ν方法反演体重的相对误差基本在40%以下,均值为22.5%;而d方法的误差相对大一些,绝大多数在60%以下,均值为28.66%。图8给出了两种方法反演体重的相对误差箱形图,可以看到,ν方法相对误差的中位数为19.18%,有一半昆虫的体重测量相对误差分布在9.34%~32.17%之间,相对误差最小值为0.53%,最大值为63.27%;d方法相对误差的中位数为24.75%,有一半昆虫的体重测量相对误差分布在8.27%~45.73%之间,相对误差最小值为0.02%,最大值为84.42%。总体而言,ν方法反演精度高于d方法。然而,即使对于性能相对较好的ν方法,依然有部分昆虫体重反演误差高达40%~63%。造成较大误差的可能原因有2个:一方面,外场试验目标到雷达的距离远,可能存在波束中心未对准昆虫的情况,此时会造成反演值偏小;另一方面,体重反演公式所代表的体重与特征量(ν和d)的关系并不是绝对成立的,而是通过数据拟合得到经验公式,它能保证大多数昆虫的体重反演值误差不大,但是部分昆虫有较大误差是不可避免的。若要进一步降低体重反演误差,可行的方法是通过进一步研究寻找与体重的映射关系更强的特征量。
传统昆虫雷达体重反演的不确定度为50%(实验室环境测量),反演结果对于昆虫迁飞监测依然具有重要的指导意义。基于ν方法的全极化雷达外场测量的体重精度高于传统方法实验室测量精度,显然可以很好地用于迁飞昆虫观测。
(3)体长反演
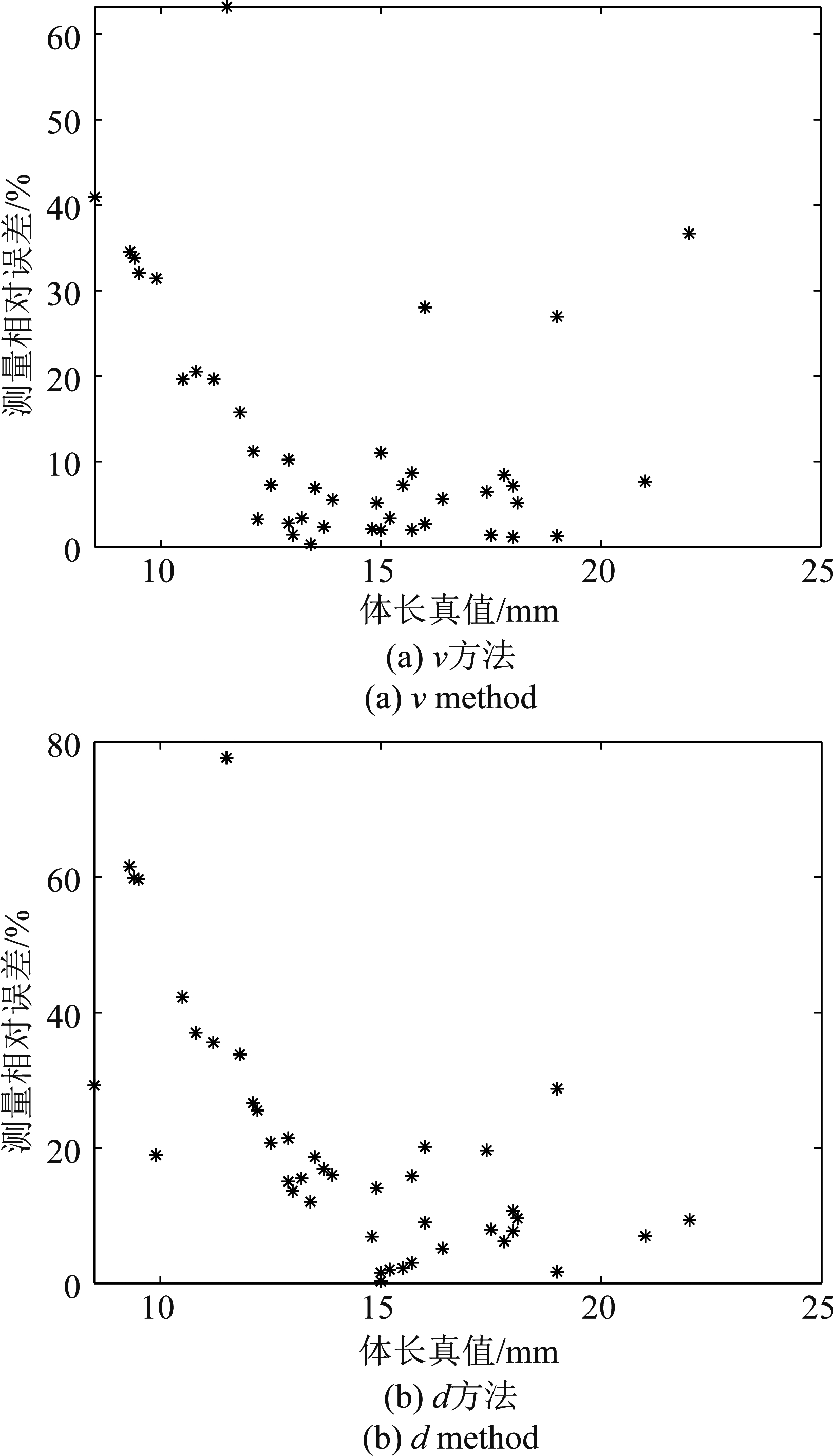
图9 昆虫体长反演误差
Fig.9 Insect body length estimation error

图10 昆虫体长反演误差箱形图
Fig.10 Boxplot of insect body length estimation error
基于式(16)和式(17)所表示的两种体长反演经验公式反演的体长相对误差如图9所示,可以看到,ν方法反演体长的相对误差大部分小于20%,相对误差均值为12.99%,体长12 mm以下昆虫的反演误差大于更大体长的昆虫;d方法大部分昆虫的反演误差小于30%,相对误差均值为20.18%,同样小昆虫的体长反演误差大于大昆虫的误差。体长反演相对误差的箱形图如图10所示,可以看到,ν方法反演体长相对误差的中位数为7.18%,一半昆虫的反演相对误差在2.76%~19.61%之间,相对误差上边界为40.93%,下边界(最小值)为0.33%;d方法反演体长相对误差的中位数为15.7%,一半昆虫的反演相对误差在7.72%~26.64%之间,相对误差上边界为42.31%,下边界(最小值)为0.32%。总体而言,ν方法体长反演精度高于d方法。
相对于体重反演而言,体长反演精度更高,因此,对迁飞昆虫监测更具指导意义。但是值得注意的是,两种体长反演方法均存在小昆虫反演误差更大的问题,这表明,两种体长反演方法还需要针对小昆虫进行进一步优化。
本文介绍了全极化昆虫雷达的生物参数反演方法,并开展了基于双无人机协同飞行悬吊昆虫的全极化雷达外场定量测量试验,成功验证了昆虫体轴朝向、体重和体长反演方法在实际全极化雷达的应用。结果显示,全极化雷达辨别平行和垂直昆虫的正确率为96.82%,朝向测量精度1.7°,体重和体长反演平均相对误差分别为22.5%和12.99%。朝向、体重和体长的测量精度均能较好地支撑全极化昆虫雷达迁飞昆虫观测。同时,本文也揭示了一些全极化雷达生物参数反演方法需要在未来进一步优化的地方,例如,在0°和90°朝向下,平行和垂直昆虫辨别正确率和朝向测量精度低于其他朝向的结果;12 mm以下小昆虫体长估计精度随着体长的减小而降低等。此外,当前测试的昆虫样本量还较少,未来可扩大样本量,开展更精细的分析,如针对不同种类昆虫进行试验归类分析等,以增强雷达测量能力,为农业生产提供更为针对性的监测预警信息。
[1] HU Gao, LIM K S, HORVITZ N, et al. Mass seasonal bioflows of high-flying insect migrants[J]. Science, 2016, 354(6319): 1584-1587.
[2] SATTERFIELD D A, SILLETT T S, CHAPMAN J W, et al. Seasonal insect migrations: massive, influential, and overlooked[J]. Frontiers in Ecology and the Environment, 2020.
[3] LOSEY J E, VAUGHAN M. The economic value of ecological services provided by insects[J]. Bioscience, 2006, 56(4): 311-323.
[4] BAUER S, CHAPMAN J W, REYNOLDS D R, et al. From agricultural benefits to aviation safety: realizing the potential of continent-wide radar networks[J]. BioScience, 2017, 67(10): 912-918.
[5] TOWNES H. A light-weight Malaise trap[J]. Entomological News, 1972, 83(9): 239-247.
[6] MACAULAY E D M, TATCHELL G M, TAYLOR L R. The Rothamsted Insect Survey ‘12-metre’suction trap[J]. Bulletin of Entomological Research, 1988, 78(1): 121-128.
[7] 曾涛, 卢峄灵, 向寅, 等. 一种强杂波环境下雷达目标微振动信号提取方法[J]. 信号处理, 2019, 35(6): 935-943.
ZENG Tao, LU Yiling, XIANG Yin, et al. A Micro-Oscillation Signal Extraction Method for Radar Target in Strong Clutter Environment[J]. Journal of Signal Processing, 2019, 35(6): 935-943.(in Chinese)
[8] DRAKE, V A, REYNOLDS, D R. Radar entomology: observing insect flight and migration[J]. Radar Entomology Observing Insect Flight & Migration, 2012: 282-311.
[9] CHAPMAN J W, DRAKE V A, REYNOLDS D R. Recent insights from radar studies of insect flight[J]. Annual Review of Entomology, 2011, 56: 337-356.
[10] 翟保平. 追踪天使——雷达昆虫学 30 年[J]. 昆虫学报, 1999, 42(3): 315-315.
ZHAI Baoping. Tracking angels: 30 years of radar entomology[J]. Acta Entomologica Sinica, 1999, 42(3): 315-315.(in Chinese)
[11] HU Cheng, LI Weidong, WANG Rui, et al. Discrimination of parallel and perpendicular insects based on relative phase of scattering matrix eigenvalues[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 3927-3940.
[12] HU Cheng, LI Weidong, WANG Rui, et al. Insect biological parameter estimation based on the invariant target parameters of the scattering matrix[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(8): 6212- 6225.
[13] HU Cheng, LI Weidong, WANG Rui, et al. Accurate insect orientation extraction based on polarization scattering matrix estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1755-1759.
[14] 胡程, 李卫东, 王锐. 基于全极化的相参雷达迁飞昆虫观测[J]. 信号处理, 2019, 35(6): 951-957.
HU Cheng, LI Weidong, WANG Rui. Fully Polarimetric Coherent Radar for Migratory Insect Observation[J]. Journal of Signal Processing, 2019, 35(6): 951-957.(in Chinese)
[15] 胡程, 张天然, 王锐. 基于 Radon 变换的昆虫上升下降率提取算法及实验验证[J]. 信号处理, 2019, 35(6): 1072-1078.
HU Cheng, ZHANG Tianran, WANG Rui. Ascent and Descent Rate Extraction Algorithm and Experimental Verification Based on Radon Transform[J]. Journal of Signal Processing, 2019, 35(6): 1072-1078.(in Chinese)
[16] HU Cheng, LI Wenqing, WANG Rui, et al. Insect flight speed estimation analysis based on a full-polarization radar[J]. Science China Information Sciences, 2018, 61(10): 109306.
王 锐 男, 1985年生, 山西太原人。北京理工大学信息与电子学院副教授, 主要研究方向为昆虫雷达信号处理。
E-mail: bit.wangrui@gmail.com
李卫东(通信作者) 男, 1991年生, 山东临沂人。北京理工大学信息与电子学院博士研究生, 主要研究方向为昆虫雷达极化信号处理。
E-mail: lwd0539@163.com
胡 程 男, 1981年生, 湖南岳阳人。北京理工大学信息与电子学院教授, 主要研究方向为昆虫雷达信号处理、GEO SAR成像处理、双基地SAR成像处理和前向散射雷达信号处理。
E-mail: hucheng.bit@gmail.com
李沐阳 男, 1996年生, 河南周口人。北京理工大学信息与电子学院博士研究生, 主要研究方向为雷达极化校准。
E-mail: muyangli_bit@163.com
毛华锋 男, 1995年生, 浙江绍兴人。北京理工大学信息与电子学院博士研究生, 主要研究方向为多传感数据融合和气象雷达生物探测。
E-mail: huafengmao@163.com