Reference format: WANG Pengzheng, LI Yang, ZHANG Ning. Environment Sensing Information Aided Waveform Parameters Intelligent Selection for Cognitive Radar[J]. Journal of Signal Processing, 2021, 37(2): 186-198. DOI: 10.16798/j.issn.1003- 0530.2021.02.004.
实时动态变化环境中的高效检测、跟踪和监视任务需求促进了现代雷达技术的不断发展和进步。基于知识的信号和数据处理、认知雷达、波形分集、分布式协同探测等概念和方法的提出对雷达智能化水平的提升提出了更高的技术要求[1]。实际工作场景中,雷达与环境的交互是一个动态过程,目标和环境特性是时变系统。如果仅针对静态环境设计检测跟踪算法,则会导致雷达在环境变化时性能下降。针对该问题,2006年加拿大McMaster大学Haykin S教授首次提出了认知雷达的概念,希望可以借鉴蝙蝠回声定位过程中的认知结构,将雷达的发射接收与环境建立起联系,从而构成一个闭环的回路,实现雷达自适应处理[2]。基于该闭环处理结构,认知雷达可以在与环境的交互中获取先验知识,对环境进行学习,从而适应环境变化,提高雷达系统性能[3]。
相对于发射与接收相互独立的传统雷达架构,认知雷达的优势在于其可以通过接收机获取环境的信息得到先验知识,结合该知识可以使雷达根据环境的变化自适应地调整发射波形参数,从而达到与环境的最优匹配,降低杂波和干扰的影响,提升有效信号的质量,实现最大信息获取,这个过程也被称为是波形优化[4]。Haykin S提出了一种认知雷达最优波形设计方法,该方法结合雷达检测和估计任务,设计了一种优化目标函数[5]。之后又在文献[6]中提出了感知-行动周期(Perception-Action Cycle),通过该结构详细阐释了认知雷达与环境交互的过程,使雷达能够利用先验信息和准则函数进行自适应地工作。文献[7]提出了一种利用先验信息的非均匀杂波环境感知方法,设计了可以抑制强杂波的相控阵波束,提高了回波信号的信杂噪比。文献[8]以雷达-通信一体化系统为平台,从波形设计角度出发,建立凸优化模型求解优化信号,提出了一种利用先验信息的波形设计方法,降低了运算次数。文献[9]提出了一种基于分数阶傅里叶变换的认知雷达波形优化方法,获得了更好的目标检测性能。文献[10]在机载雷达回波中的地物杂波建模的基础上研究了基于知识辅助的空时自适应处理技术,有效地提升了机载雷达在非均匀杂波场景中的杂波抑制性能。文献[11]构建了雷达环境知识库,基于知识库中杂波、电子干扰和环境频谱等先验知识实现波形设计,改善了雷达在复杂电磁环境下的检测性能。
在面向目标跟踪的波形优化研究方面,文献[12-13]基于信息熵准则,分别研究了基于检测门限跟踪的自适应波形调整算法和交互多模型的自适应模型转移概率调整算法。在波形参数选择方面,2018年俄亥俄州立大学Mitchell A E对当前主流的波形参数选择方法进行了整理[14]。文献[15]提出了一种用于目标检测和跟踪的认知雷达框架,并设计一种代价函数的通用模型,但并未给出具体实现方式。文献[16]应用神经网络方法训练了波形参数选择网。文献[17-18]在存在干扰的跟踪场景下设计了一种包含跟踪性能及量测代价的认知雷达准则函数。文献[19-20]根据杂波环境下目标估计的贝叶斯克拉美罗下界,研究了多目标跟踪时MIMO雷达多波束工作模式下的工作资源分配方案。在文献[21]中将全自适应雷达框架用于单目标跟踪,实时调整脉冲波形,从而提高单目标跟踪信噪比。文献[22]基于量测误差椭圆与目标状态预测误差椭圆正交理论,研究了基于基带脉冲波形模糊函数旋转波形库的自适应波形选择技术。Martone A F通过使用强化学习中Q学习算法调度雷达工作频谱实现了雷达通信系统的频谱共享[23],文献[24]在文献[23]的基础上进行了扩展,研究了深度Q学习网络(DQN)算法在雷达工作频谱调度上的效果,提高了学习效率,降低了雷达通信系统之间的冲突次数。
传统的波形优化算法通常获得的是当前时刻的最优解。如果仅考虑当下性能最优,则无法得到全局最优解。强化学习算法通常用于时序决策过程,在雷达跟踪过程中通过与环境的交互,不断地进行“探索和利用”,通过折扣因子,在进行奖励函数评估时,将后几个时刻的奖励反馈在当前时刻,从而获取整个过程的全局最优决策方案。
针对现有方法优化结构单一,难以适用多雷达任务的问题,本文在环境感知和杂波特征提取的基础上,设计了一种面向目标检测和跟踪优化的奖励函数结构;在最大信噪比准则和最小均方误差准则的基础上,根据雷达实际工作任务有针对性地优化检测与跟踪性能。进一步的,针对杂波环境和机动目标检测与跟踪性能优化问题,采用Q学习和DQN算法,通过Q值函数与多帧杂波特征先验信息的联合处理与应用,实现波形参数优化选择,提升检测和跟踪性能。
杂波的存在会影响目标检测与跟踪性能,可通过自适应调整雷达波形参数减少杂波影响,实现雷达检测和跟踪性能的提升。在目标检测过程中,波形参数的选择应适应环境中的杂波变化,故而需要对当前杂波进行特征提取和描述。提取后的特征值可生成当前环境状态S,并用于强化学习训练。
本文提出的背景分区算法首先使用K-L散度(Kullback-Leibler Divergence)对检测背景中的各分辨单元进行统计分析,再利用阈值分割算法实现对杂波背景分区,如大津法(OSTU)等。
固定平台下雷达回波中的地物杂波多是静态的,其多普勒分量常分布在零频附近。而机载脉冲多普勒雷达由于平台运动,检测背景中的地物回波相对于雷达有径向速度,因此在距离-多普勒谱中会发生一定程度的扩展。通常可将地物杂波分为以下三个部分[25]:
1)主瓣杂波:机载雷达的天线主瓣下视照射,投影在地面上形成多个同心圆环,这些圆环相对雷达具有不同的俯仰角,当地面与载机发生相对运动时,不同的环带区域相对雷达具有不同的径向速度,因此产生不同的多普勒频移,这些多普勒频移就构成了主瓣杂波。由于主瓣增益较高,因此主瓣杂波通常表现为强杂波。
2)旁瓣杂波:同主瓣杂波的生成原理,机载雷达天线旁瓣下视照射产生的杂波回波构成了旁瓣杂波。由于旁瓣的增益相对较低,因此旁瓣杂波频谱密度相对较小,但其频谱分布相对更广。
3)高度线杂波:机载雷达天线的部分旁瓣向载机的正下方照射,俯仰角度近似垂直于地面,形成高度线杂波。该照射区域相对雷达没有径向速度,其多普勒频移常分布于零频附近。由于电磁波的垂直反射最强且地面与载机间的相对距离最近,该杂波强度较强。
上述三种杂波是最基本也是最主要的地物杂波类型。本文将对这三种杂波进行仿真分析,通过杂波分区与特征提取获得杂波环境的先验信息,并将其用于辅助波形参数选择。
K-L散度能够度量两个模型P和Q之间的差异[26]。P表示真实分布,Q为P的近似分布,二者之间的K-L散度公式为
![]()
(1)
式中D(P‖Q)表示当用Q来近似P时的信息损失或从Q到P的“距离”,当D(P‖Q)数值越大,表示P和Q差异越大,当D(P‖Q)数值越小,表示Q越接近于P。
由于雷达检测背景中杂波和目标之间的分布不同,不同杂波类型间分布也有所差异,可以计算各个分辨单元与整个雷达检测平面间的K-L散度,从而区分不同类型的杂波和目标。假设某一检测分辨单元的概率密度分布函数为p1(x),而整个检测平面的概率分布函数为p2(x),它们之间的K-L散度可定义为
(2)
利用上式,可将两个分辨单元之间的K-L距离值转换为所有分辨单元分布与整个检测平面分布之间的K-L距离。实际处理过程中常选用当前分辨单元的滑窗平均作为该单元的分布代替。在此基础上,采用OSTU(大津法)[27]获取一个K-L散度分割阈值以区分不同的分布单元。通过多次使用阈值分割的方法可以分割出无杂波区、弱杂波区和强杂波区,进而实现杂波区域分割。
进一步的,从分割后的RD谱中可提取如下杂波区域特征,用于强化学习算法的状态标识。
Ct={c1,c2,...,ci,...,cn}
(3)
ci=[CNR, f1, f2,R1,R2,p],i=1,2,...,n
(4)
其中n为最终分出的杂波区个数,CNR为该区域杂波的平均杂噪比, f1, f2,R1,R2分别为分出的杂波区的多普勒距离上下限,p表示该区域中杂波的比例。
认知雷达系统主要由三部分组成:具有智能决策能力的执行器(发射机)、具有感知和估计能力的感知器(接收机)以及系统的外部环境[28],如图1所示。从图中可以看出,认知雷达通过发射机和接收机与其所处的电磁环境进行交互,构成闭环回路。这里发射机作为认知系统的执行器,与环境的交互体现在发射具有一定波形参数的电磁波;发射机发射的电磁波经过外部环境再返回到接收机;接收机在认知系统里扮演感知器角色,负责接收来自外界环境的反馈,在目标检测任务中表现为接收的回波信号RD谱和杂波信息,在目标跟踪过程中表现为量测信息。在雷达系统内部,通过接收机反馈计算奖励函数,进一步地形成决策方案,选择最优的波形参数,控制发射机自适应地发射雷达信号。
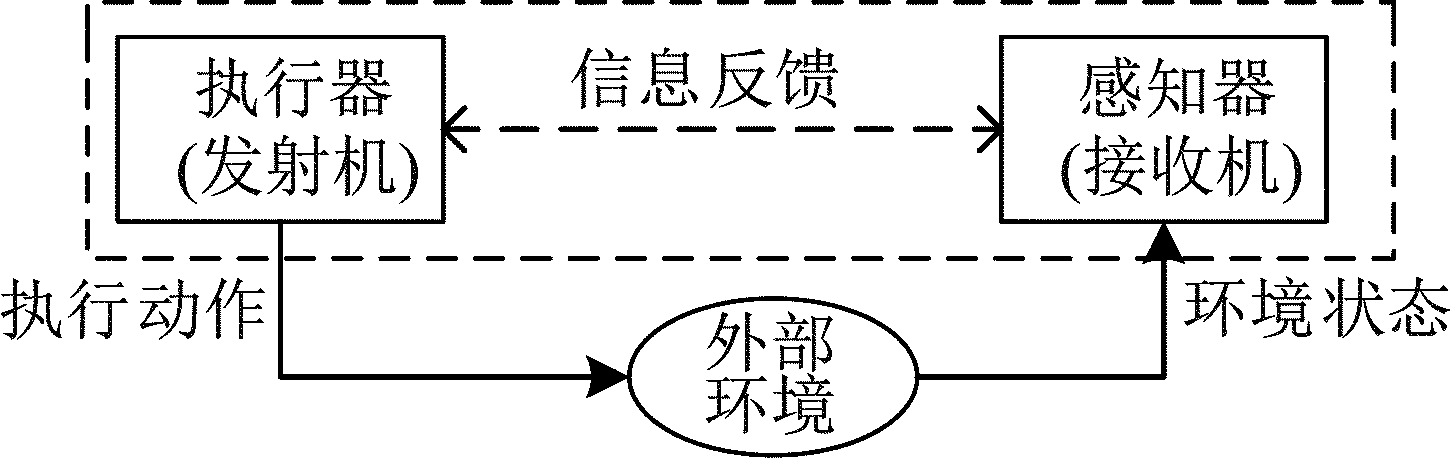
图1 认知雷达闭环回路
Fig.1 The closed loop of cognitive radar
不同形式、参数的雷达信号会与环境产生不同的交互,从而得到不同的回波信号。本文主要研究线性调频信号中脉冲重复频率(PRF)与积累脉冲个数(Np)对机载雷达任务的影响,并据此设计波形参数选择方案以提升雷达的检测跟踪性能。
3.1.1 对目标检测的影响
在目标检测过程中,由于机载雷达平台运动,在对地探测时,低PRF会导致主瓣杂波谱展宽,频率维高度模糊;而在距离维上,低PRF使脉冲间时延增加,无距离模糊。与之相对的是采用高PRF波形,回波信号将在距离维上严重模糊;在频率维上不折叠,最大可探测速度范围增加,可用于迎头目标的探测。而在对尾随目标探测时,由于其多普勒频移较小,目标往往被副瓣杂波遮盖。
距离与速度的耦合导致模糊现象不可回避,所以必须扩大不模糊测量范围以削弱模糊对目标检测的影响。因此,需要根据具体的目标运动情况、雷达探测任务和外界杂波干扰情况等自适应地调整PRF以实现目标检测性能优化。
根据脉冲体制雷达测距原理可知,脉冲雷达最大可探测距离(距离不模糊)为
(5)
最大不模糊速度为
(6)
对于相参积累来说,积累的脉冲数越多,回波信号的信噪比越大。但脉冲串越长,相参积累时间越长,对于高速机动目标,其距离速度在积累时间内均会发生变化,会导致目标在RD谱的距离多普勒轴上有一定的徙动,无法实现完全积累,而导致合成的信噪比损失较大,不利于目标的检测。只有在相参积累时间内,包络移动不超过一个距离分辨单元时,包络徙动的效应可以忽略,即满足
![]() ≤Δτ
≤Δτ
(7)
3.1.2 对目标跟踪的影响
对于已经检测到目标的情况下,克拉美罗下界可作为目标时延和多普勒测量误差估计中的重要依据。给出目标检测的费舍尔信息矩阵的表达式如下:
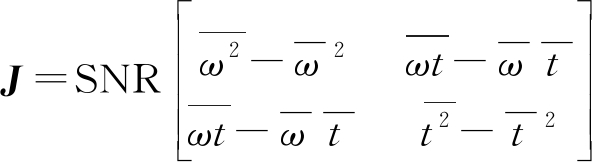
(8)
费舍尔信息矩阵的逆在量测误差协方差矩阵上是克拉美罗下界的无偏估计,因此表示如下:
Rτ-w=J(θ)-1
(9)
根据时延-多普勒转换为距离-速度的公式r=(τc)/2以及ν=-(cw)/(2wc),如果量测是距离和速度,则
(10)
T=diag[c/2,-c/2wc]是参数转换的Jacobian矩阵。那么
R=TJ-1TT
(11)
带入前述讨论选择的多脉冲矩形脉冲LFM信号表达式,得到其量测噪声协方差矩阵如下:
(12)
其中
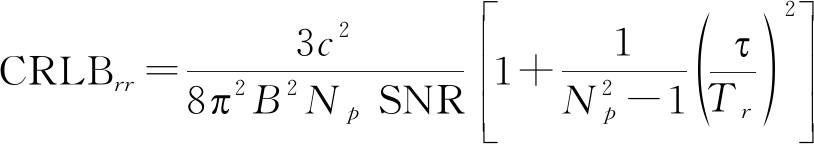
(13)
(14)
(15)
从上式可以知道,量测噪声协方差矩阵与信噪比SNR、带宽B、脉冲宽度τ和载频fc以及脉冲重复周期Tr、积累脉冲数Np有关。本文主要研究PRF和Np两个波形参数对目标跟踪的量测误差影响。
波形最优化要求在一定的系统限制条件下最大化系统性能。在波形最优化过程中根据系统性能的需求形成一定的性能准则,作为调整波形的依据。性能准则函数的选取根据雷达系统的任务和工作模式而定。在认知雷达闭环回路中,根据准则函数可以设计环境的反馈,即整个闭环回路的奖励函数(或称代价函数)。
3.2.1 准则函数
1)最大信噪比准则
在恒虚警检测过程中,目标的发现概率与目标回波的信噪比有关,SNR越大,发现概率越高,如下式所示
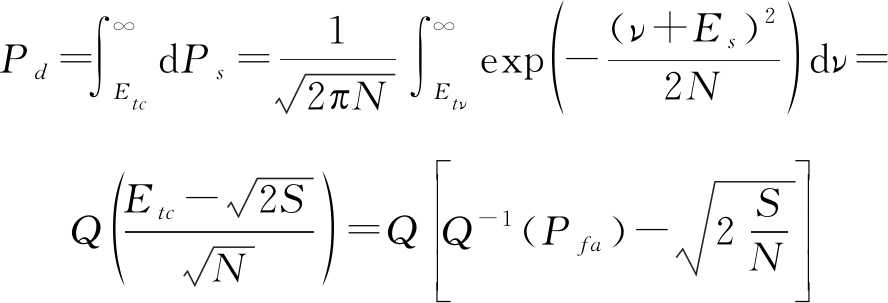
(16)
其中Q(E)为高斯分布积分及Q-1(P)为其逆:
(17)
Q-1(P)=E
(18)
故而在目标检测过程中往往采用最大信噪比准则来优化检测性能。
2)最小均方误差准则
均方误差可以表示目标跟踪的精度,均方误差越小表示跟踪效果越好。最小均方误差准则是使每个时刻目标状态估计误差最小化,为:
(19)
其中,||||表示的是欧几里得范数,![]() 表示在1到k+1时刻的量测集合。卡尔曼滤波算法的过程中,跟踪滤波误差协方差的计算如下:
表示在1到k+1时刻的量测集合。卡尔曼滤波算法的过程中,跟踪滤波误差协方差的计算如下:
P(k+1|k+1)=
E[εk+1|k+1(θk)εk+1|k+1(θk)T|Zk+1]
(20)
式中![]() 表示滤波估计的误差。两边同时取迹得到:
表示滤波估计的误差。两边同时取迹得到:
Tr(P(k+1|k+1))=![]()
(21)
因此,最小均方误差准则下的准则函数为[29]:
(22)
式中,Tr[]表示矩阵的迹,![]() 表示波形库,θk+1表示k+1时刻的波形参数。
表示波形库,θk+1表示k+1时刻的波形参数。
3)最大互信息准则
对于联合高斯随机变量x和z,其协方差矩阵为
(23)
x和z的互信息[30]可表达为
(24)
将目标跟踪过程的量测方程zk=Hxk|k-1+νk代入上式,可得一步状态预测值与量测值之间的互信息为
I(xk|k-1;zk)=![]()
![]()
![]()
![]()
![]()
(25)
I(xk|k-1;zk)表示在量测值zk的条件下,目标状态的一步状态预测值xk|k-1不确定性减小的大小。因此,发射波形应采取最大互信息准则,其最优波形参数为
![]()
![]()
(26)
这里滤波误差协方差矩阵Pk|k行列式的值为
(27)
上式中的det(Pk|k-1)与发射波形θk无关,故最优波形参数为
(28)
4)最小波门准则
最小波门准则即最小化确认门限体积准则,使当前时刻测量空间的体积最小,常用于杂波密度较大或噪声强度较大的跟踪场景。确认门限的体积正比于量测的新息协方差行列式的均方根,那么该最优化准则的表达式为[31]
(29)
3.2.2 奖励函数
结合上述准则函数,可以构建目标检测与机动目标跟踪的综合奖励函数表达式:
R=wδRδ+wmaxνRmaxν+wmaxrRmaxr+wtRCIT+
wSNRRSNR+wCRC+wtrackRtrack
(30)
其中Rδ,Rmaxν,Rmaxr,RCIT,分别表示距离速度分辨力,最大不模糊速度,最大不模糊距离,相参积累时间,由于这些参数对应的代价在实际目标检测过程中影响较小,故采取较小的权重;RSNR表示回波信噪比和当前波形参数带来的回波SNR,是影响目标检测的主要因素,故使用较大的权重;同时根据当前强杂波区域的特征和跟踪滤波的一步状态预测值,判断下一时刻目标点是否会因模糊折叠至强杂波区而被遮蔽,并将其结果生成奖励函数RC;Rtrack是由目标跟踪准则函数生成的奖励函数,对于目标跟踪任务来说,该项奖励的权重应为最大。表 1给出了一种较为合理的权重设计方案。
表1 一种可能的权重设计
Tab.1 A kind of possible weight design
类型RδRmaxνRmaxrRCITRSNRRCRtrack权重大小32238510
信噪比主要与目标信号是否处于杂波区域以及杂波区域的强度有关,而杂波和目标的RD谱是时刻变化的,很难用确定的关系来衡量。一种解决方法是针对当前信息和以往记忆信息(记忆库)对下一帧进行预测,并据此遍历波形库,计算每一种波形参数的奖励函数值,选取最优的波形参数组合。同样也可以采用强化学习的方式实现该决策过程。
基于强化学习的认知雷达波形选择算法实现流程如图2所示。环境的反馈、接收机、决策方案、发射机、波形参数调整五个部分构成了该认知雷达闭合回路。
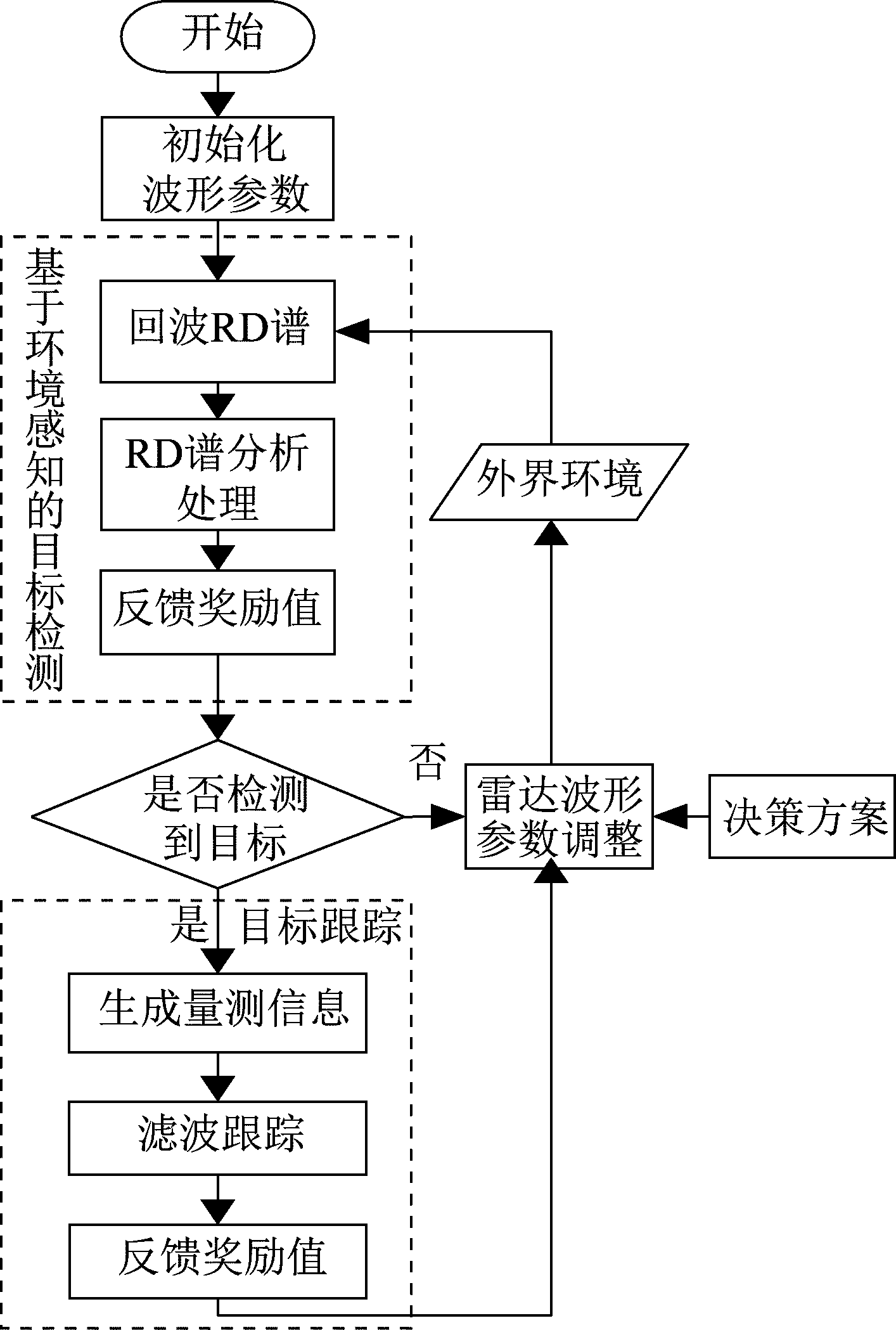
图2 认知雷达实现流程
Fig.2 Flowchart of cognitive radar
1)整个雷达任务反馈的奖励值分为两个部分:目标检测过程的奖励值和目标跟踪过程的奖励值。目标检测的奖励值主要来自于回波SNR(最大信噪比准则)和距离速度量测的分辨率、最大量测范围等,是通过对回波RD谱的分析处理和杂波特征提取过程获得的,如图3所示。若未检测到目标,则直接根据目标检测过程的奖励值进行波形调度;若检测到目标则计算相应奖励值,并进行目标跟踪。
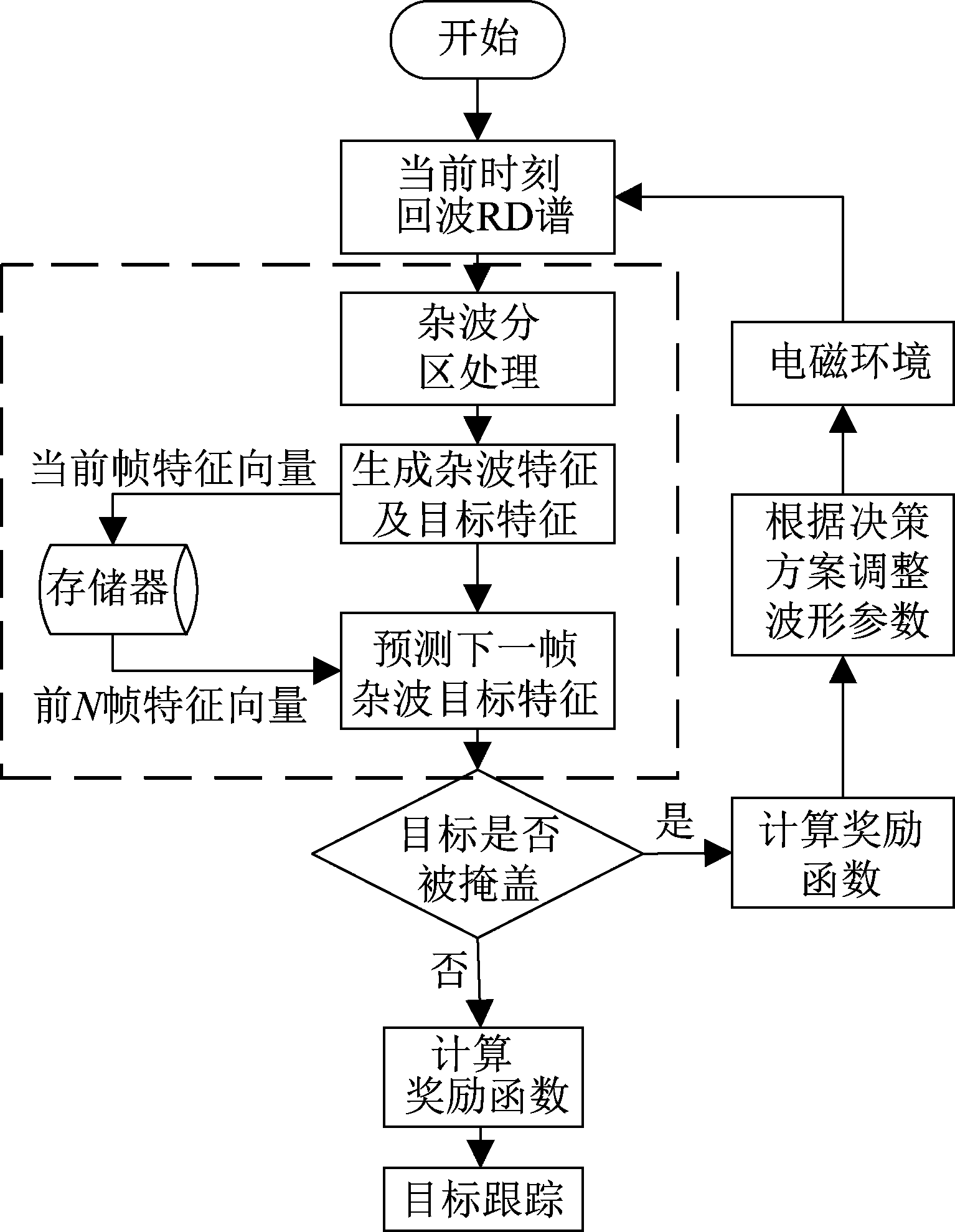
图3 目标检测的闭环回路
Fig.3 Closed-loop of targets detection
目标跟踪的波形参数选择闭环回路实现如图4所示,其奖励值主要来源于跟踪估计的精度,由当前时刻的估计结果和一步状态预测计算得到。该过程的奖励函数与目标检测过程的奖励函数进行一定加权,得到总的奖励函数,作为波形参数调度的依据。
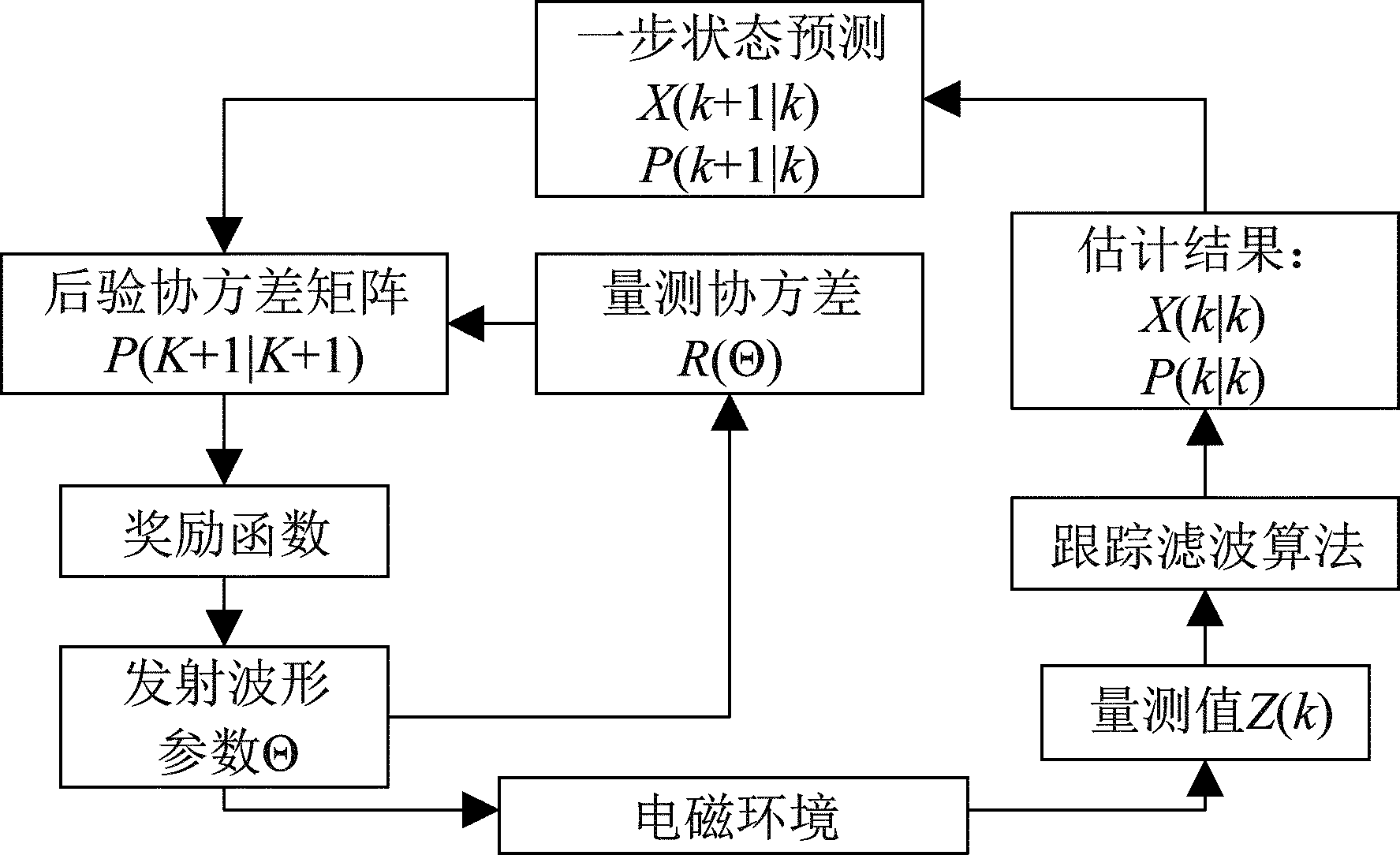
图4 目标跟踪的闭环回路
Fig.4 Closed-loop of targets tracking
2)决策方案是基于整个雷达系统的工作性能最大化实现的,表现为设计的奖励函数最大化(代价函数最小化)。可以通过遍历波形库的方式计算每种波形参数的奖励值,选取波形参数,也可利用强化学习算法,通过雷达与环境的交互,求得最佳的波形调度方案。
决策方案是连接奖励函数与执行动作的纽带。强化学习算法是一种时序决策过程的算法,相比传统算法,其可以通过折扣因子将后几个时刻的奖励反馈在当前状态的决策过程中,在多次的“探索与利用”中进行试错,迭代更新奖励值,从而获取全局的最优解。因此,本文利用强化学习算法,通过雷达与环境交互学习,迭代更新值函数,获得最佳的波形调度方案。
Q学习(Q-learning)是时序差分算法的一种,通过智能体与环境间的交互迭代更新每一个状态-动作的值函数,继而求得最优策略。它是一种无模型的强化学习算法,不知道也不需要状态转移概率矩阵,状态之间由动作进行关联。Q学习方法将每一个状态和该状态下采取的动作划分为一个单元,该单元的价值函数以Q因子的形式存储,用以评估当前策略对整个决策过程的影响,是一种近似动态规划的求解算法。
Q学习的理论基础是状态-动作值函数更新的贝尔曼方程。奖励r只存在于当前状态s和下一状态s′之间,下一状态s′及其之后的奖励完全反映在s′的Q值(状态-动作值函数)中。在Q学习中,通过贝尔曼方程,利用下一个状态的Q值可以计算出当前状态的Q值。计算得到的Q值与原来状态的Q值有一个差异,即增量,通过它就可以更新当前的Q值:
Q(s,a)=Q(s,a)+α[r+γQ(s′,a′)-Q(s,a)]
(31)
其中α是学习率,决定收敛快慢;γ是折现因子。
训练过程中,Q学习采取贪婪算法,以贪婪度ε的概率采取最大Q值对应的动作,以1-ε的概率随机探索新的动作可能,实现动作的“探索-利用”过程,防止陷入局部最优,同时提高学习效率。
Q学习算法是一步一更新的在线更新算法,在某一状态s决策完毕之后,即刻将参数(s,a,s′)对应的Q值存储到表格中,称之为Q表。通过有限次数的训练回合,不断更新迭代,最终所有的Q值均应收敛到一个固定值,也即该状态-动作组合的综合奖励。完成训练后,获得的最佳决策方案为:对于某一状态s,选择Q值最大的动作a,即
(32)
综上,得到Q学习算法实现流程如图5所示,目标检测和目标跟踪过程获取的相关信息分别组成Q学习部分的即刻奖励值r和状态s。
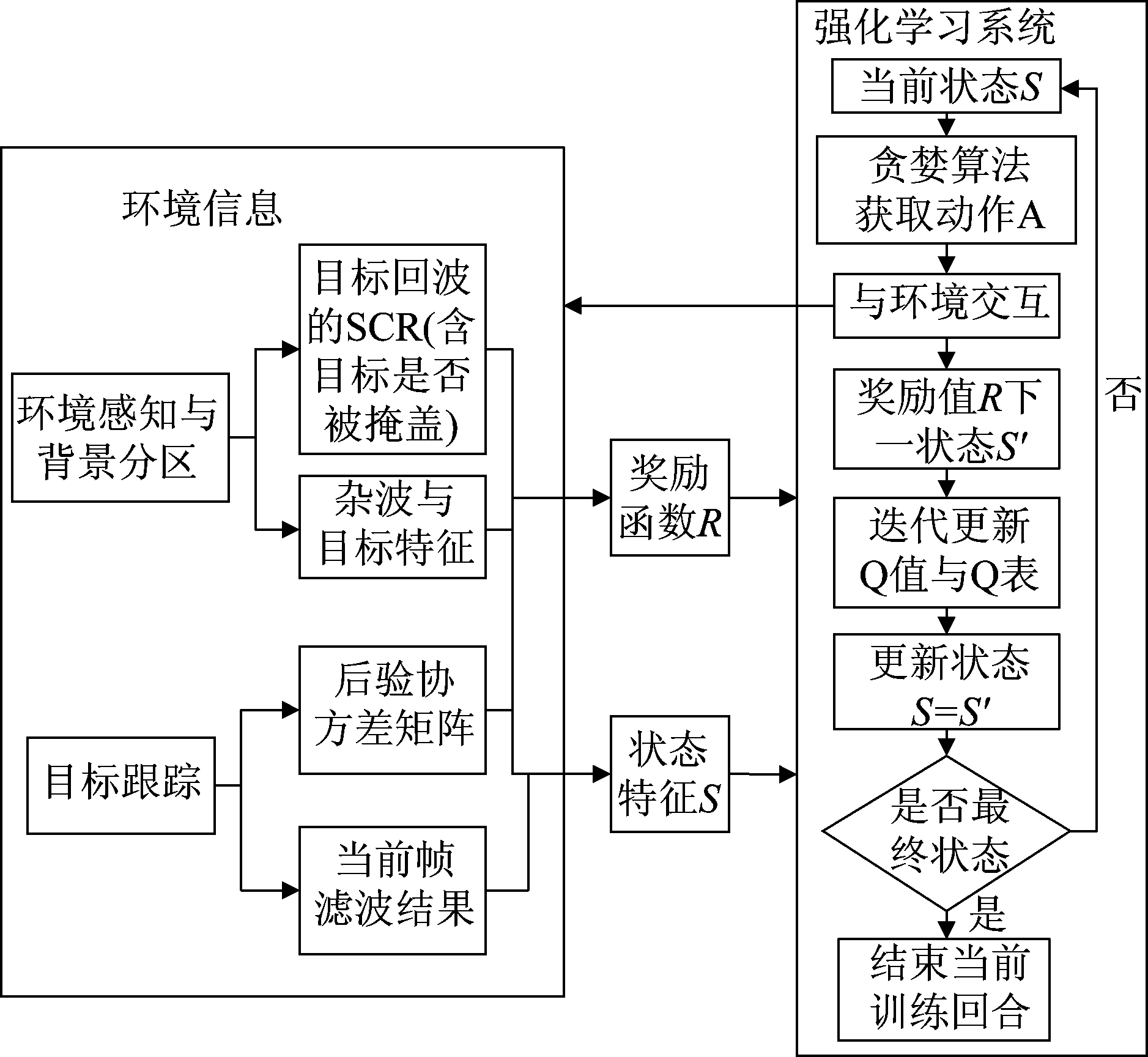
图5 Q学习单次训练流程
Fig.5 Single training process of the Q-learning
DQN(Deep Q-learning Network)是深度强化学习的一种,是Q学习算法的一种改进,在Q学习基础上加入神经网络,通过对状态-动作与Q值之间非线性拟合的方式代替Q表查询。
DQN中Q值计算方式与Q学习相同:
(33)
Qevaluate(s,a)=Qnet(s,a)
(34)
其中Qnet(s,a)是网络输出,Q值更新算法同上:
Q(s,a)←Qevaluate(s,a)+α[Qreal(s,a)-Qevaluate(s,a)]
(35)
对于神经网络的更新也就是损失函数为
(36)
若神经网络采用BP神经网络,梯度更新公式为
θi+1=θi+α▽θL(θi)
(37)
从公式中可以看出,通过神经网络预测Q值得到的是Qevaluate,类似于Q学习中原有Q表格中存储的Q值;Qreal是选择一个动作后得到的奖励值结合下一状态的Q值计算得到的,下一状态s′的Q值也是通过神经网络计算得到的,但是两个神经网络并不相同。通过构建两个结构相同,参数不同的神经网络,打乱两者之间的相关性:计算Qevaluate的网络NET1是实时更新的,每产生一组Qreal就进行网络训练,更新NET1,故而NET1拥有最新参数;而计算Qreal所用到的神经网络NET2的参数是NET1很久之前的旧参数,也即NET1每训练一段时间,就将其网络参数赋给NET2,实现流程如图6所示。
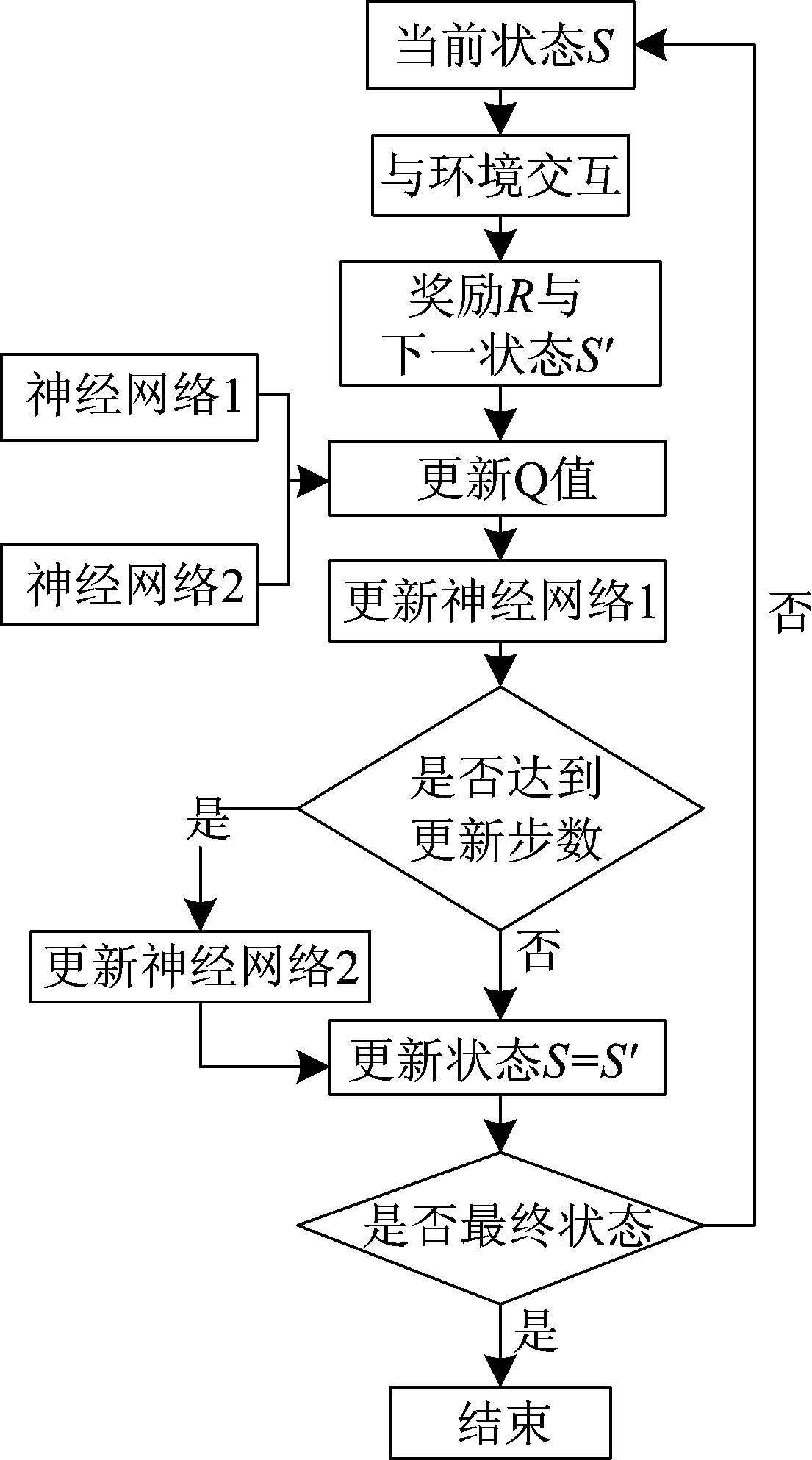
图6 DQN算法流程
Fig.6 Flowchart of DQN
该波形调度算法主要应用于机载雷达目标检测和跟踪任务。为验证上述算法的可行性和有效性,设计并进行了相关的仿真实验。仿真实验的运动物理模型侧视剖面图如图7所示。
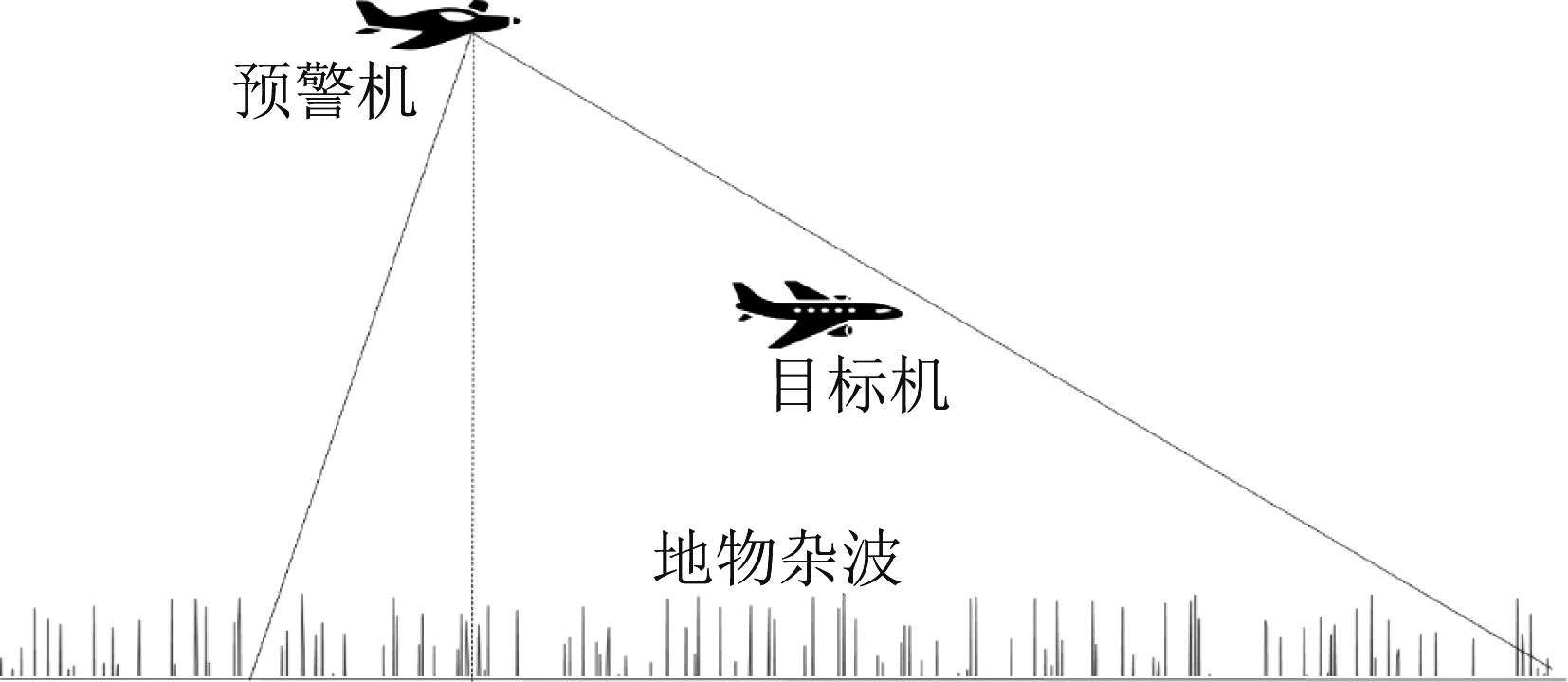
图7 物理模型侧视图
Fig.7 Side view of physical model
在仿真实验中,载机采取跑道型的复杂运动进行巡航,首先以200 m/s 的速度进行匀速直线运动,后速度不变地进行加速度为120 m/s2的匀速圆周运动,并以上述两个运动过程为周期形成跑道型运动,如图8所示(俯视图),物理模型参数见表 2。目标机为机动目标,考虑目标机的匀速运动CV,匀加速运动CA,匀速圆周运动CT三种运动模型,采用IMM-PDA-EKF算法进行杂波环境下的机动目标跟踪。目标机先进行速度为100 m/s的匀速直线运动;后被预警机(载机)发现,开始改变运动轨迹,调转方向,进行加速度为60 m/s2的匀速圆周运动;最后目标以40 m/s2的加速度逃离。
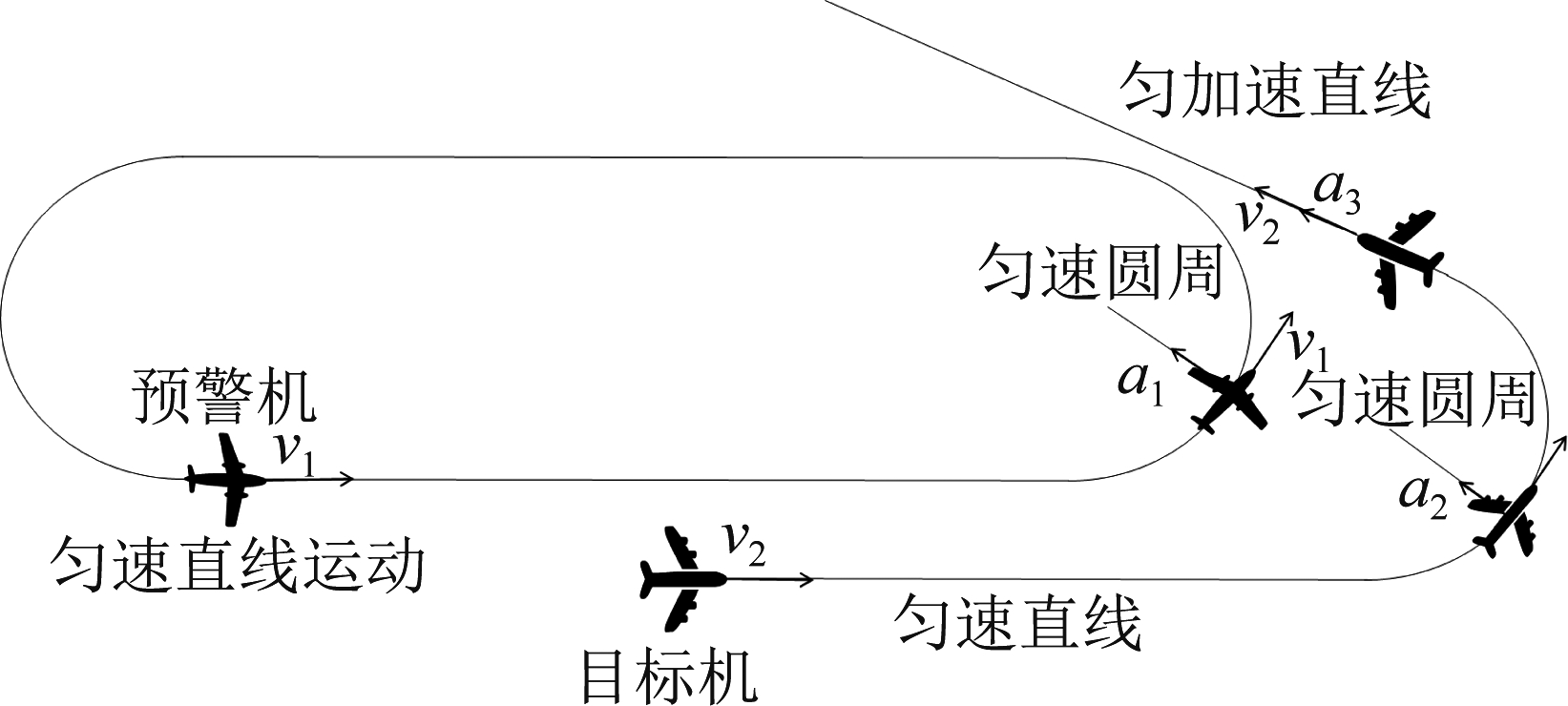
图8 物理模型的俯视图
Fig.8 Top view of physical model
仿真实验中,由于遍历式启发算法和Q学习算法只能处理离散有限个数的波形类型选择,故而脉冲多普勒雷达的波形参数PRF、Np波形库采用离散采样方式获取,雷达参数如表 3所示。
表2 运动模型参数
Tab.2 Motion model parameters
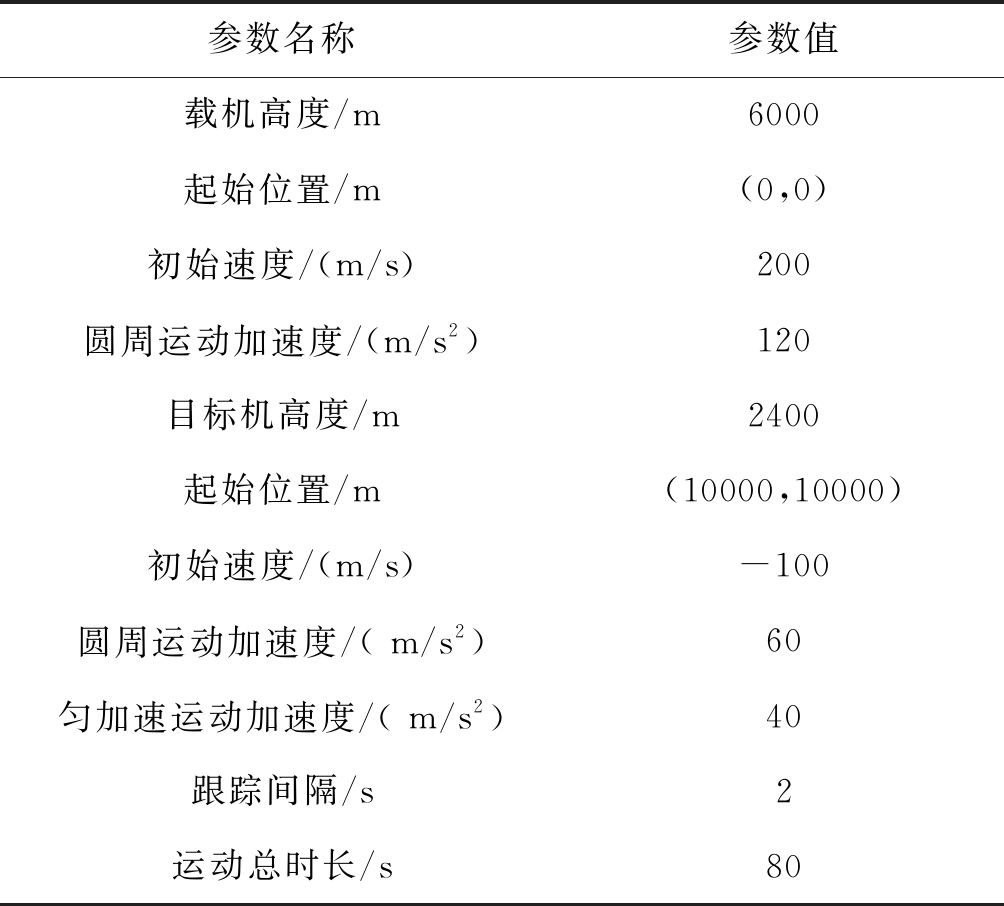
参数名称参数值载机高度/m6000起始位置/m(0,0)初始速度/(m/s)200圆周运动加速度/(m/s2)120目标机高度/m2400起始位置/m(10000,10000)初始速度/(m/s)-100圆周运动加速度/( m/s2)60匀加速运动加速度/( m/s2)40跟踪间隔/s2运动总时长/s80
表3 雷达系统参数
Tab.3 Radar system parameters
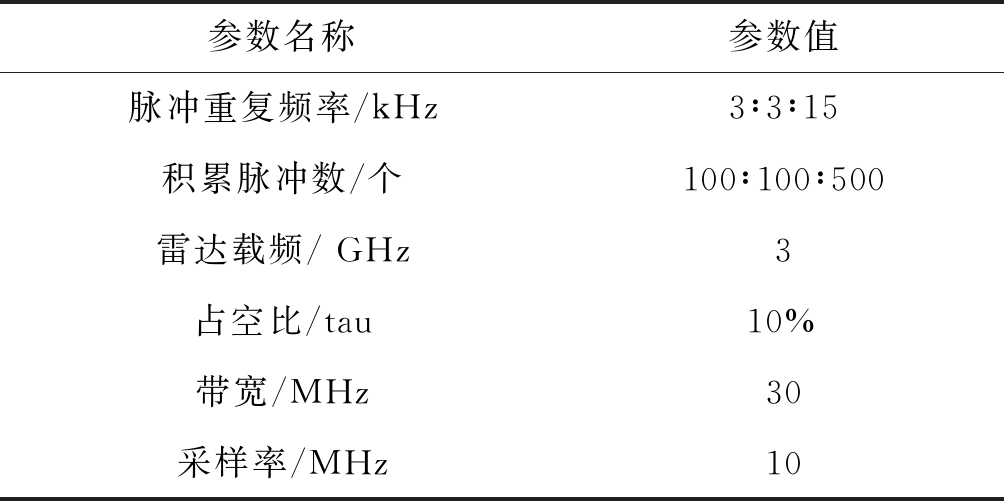
参数名称参数值脉冲重复频率/kHz3∶3∶15积累脉冲数/个100∶100∶500雷达载频/ GHz3占空比/tau10%带宽/MHz30采样率/MHz10
在进行强化学习的训练过程时,训练参数如表 4所示。
表4 强化学习训练参数
Tab.4 RL Training parameters
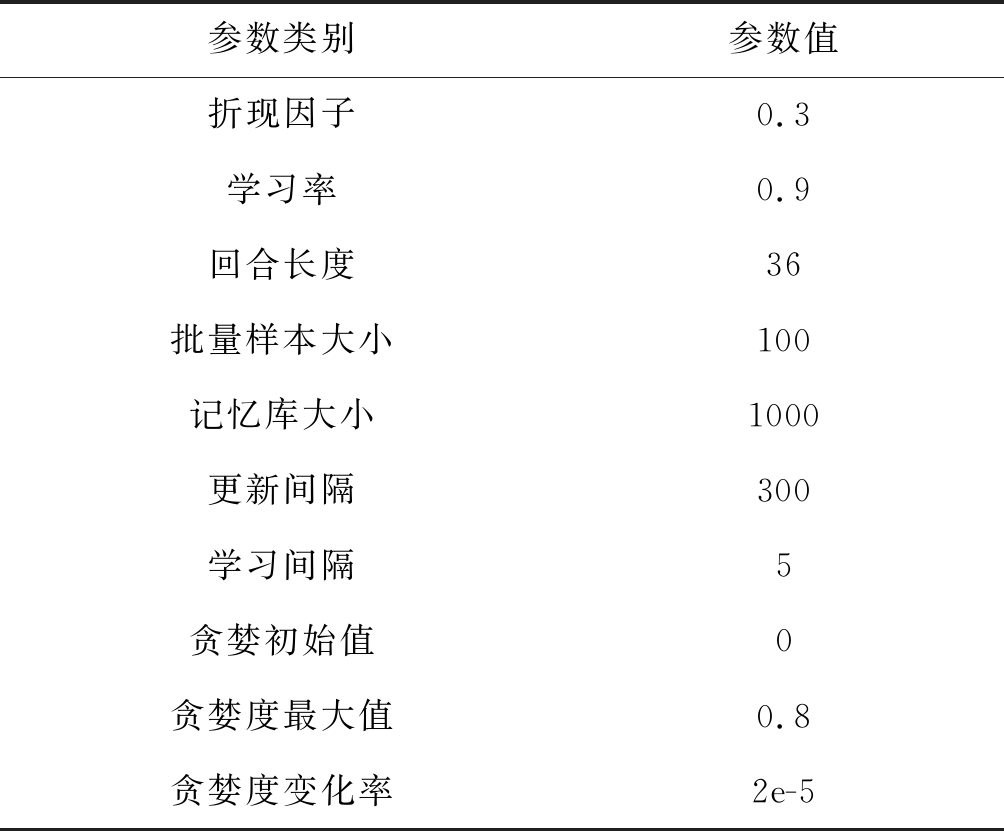
参数类别参数值折现因子0.3学习率0.9回合长度36批量样本大小100记忆库大小1000更新间隔300学习间隔5贪婪初始值0贪婪度最大值0.8贪婪度变化率2e-5
首先使用K-L散度和阈值分割算法对回波RD谱进行分割和特征提取,将杂波特征作为强化学习的状态输入。分割结果如图9所示。
图10给出几种准则函数下的波形参数选择结果。从图中可以看出,最大互信息准则和最小波门准则采取的波形参数选择方案是基本保持波形参数不变,在外界发生一定变化时再进行调整;而最小均方误差准则时刻调整自身波形参数以提高雷达的跟踪性能。
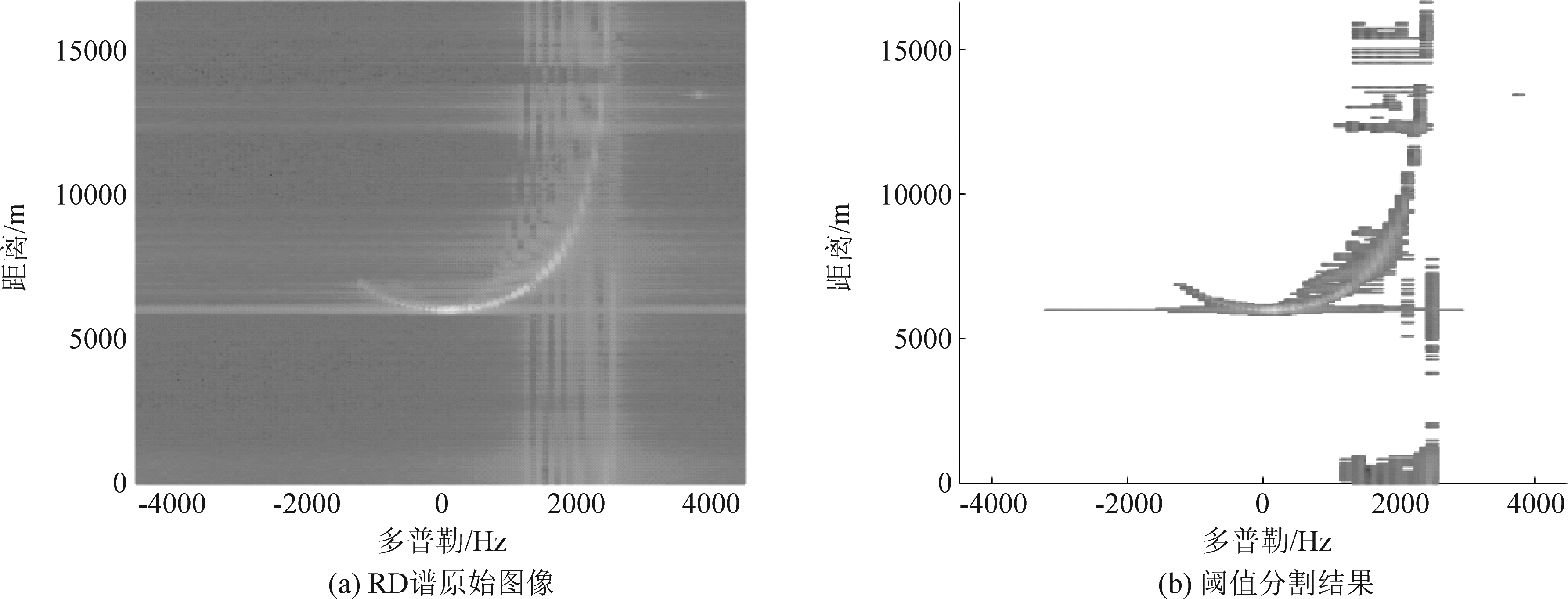
图9 阈值分割结果
Fig.9 Results of Optimum Thresholding
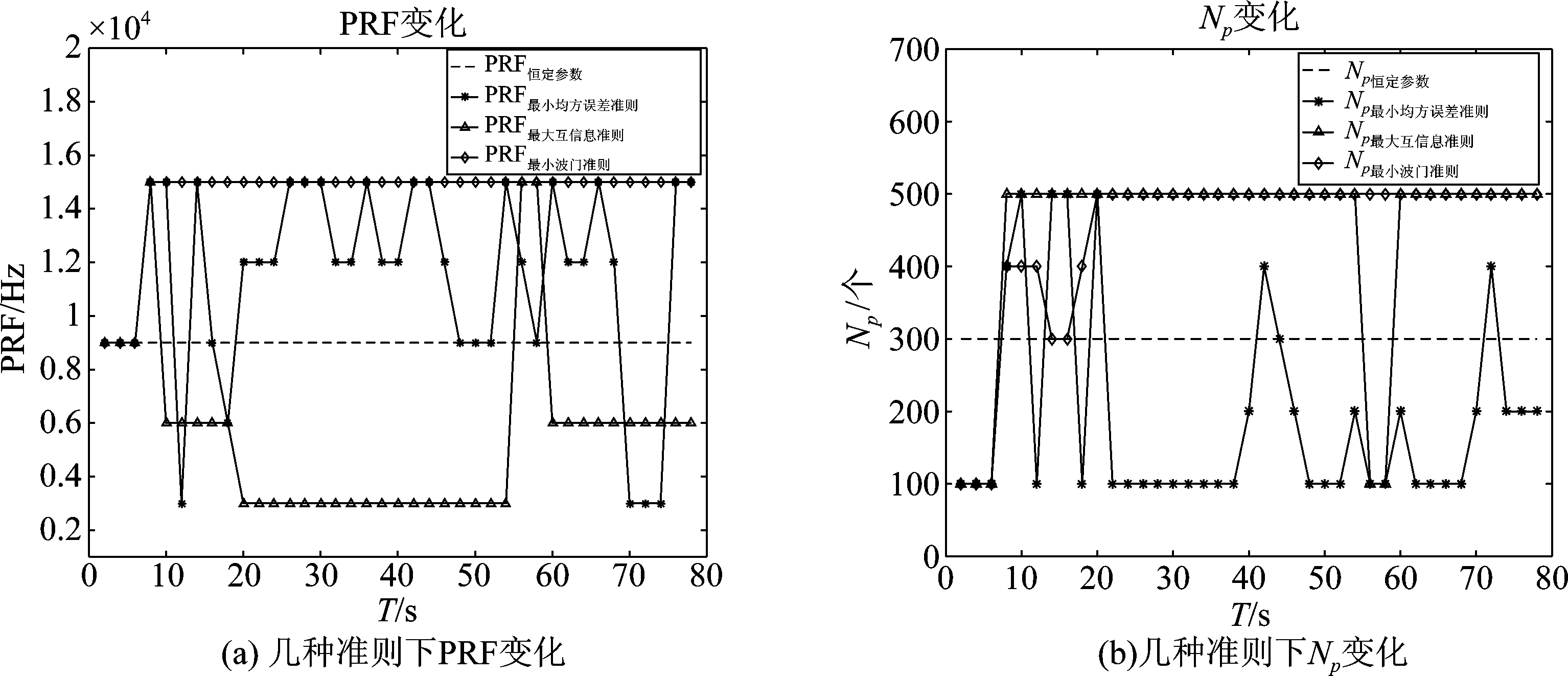
图10 几种准则函数下的波形参数变化
Fig.10 Waveform parameters change under several criterion functions
图11给出几种不同准则函数的回波SNR与跟踪估计误差。可以发现,在最大互信息准则和最小均方误差准则下进行波形参数优化后,回波的SNR均得到一定提升,最大互信息准则提升明显,最小波门准则的SNR与恒定波形参数的回波SNR基本持平。在目标跟踪的估计误差改善方面,最大互信息准则与最小波门准则对目标的距离速度估计得到一定改善优化,如下表 5。可见,在整个目标检测与跟踪任务中,最小均方误差准则表现更好。因此,本文后续的仿真和分析将主要研究基于最小均方误差准则的智能波形参数选择方法。
在基于最小均方误差准则的基础上,采用强化学习算法来实现波形参数的智能选择,图12给出了遍历波形库的启发式算法与强化学习算法的波形选择结果。可以看出,DQN更倾向于采用较为稳定的波形参数,Np通常采用最大值,PRF随目标和电磁环境的变化稳定在最大值或最小值;Q学习则更倾向于每个时刻都调整波形参数以适应不断变化的环境。
表5 几种准则函数的性能提升
Tab.5 Performance improvement of criterion functions
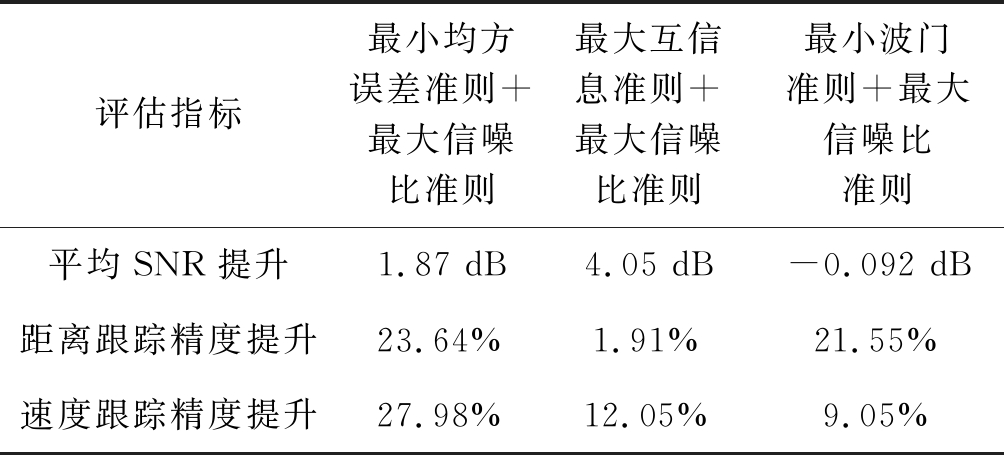
评估指标最小均方误差准则+最大信噪比准则最大互信息准则+最大信噪比准则最小波门准则+最大信噪比准则平均SNR提升1.87 dB4.05 dB-0.092 dB距离跟踪精度提升23.64%1.91%21.55%速度跟踪精度提升27.98%12.05%9.05%

图11 几种准则函数的性能改善
Fig.11 Performance improvement under several criterion functions
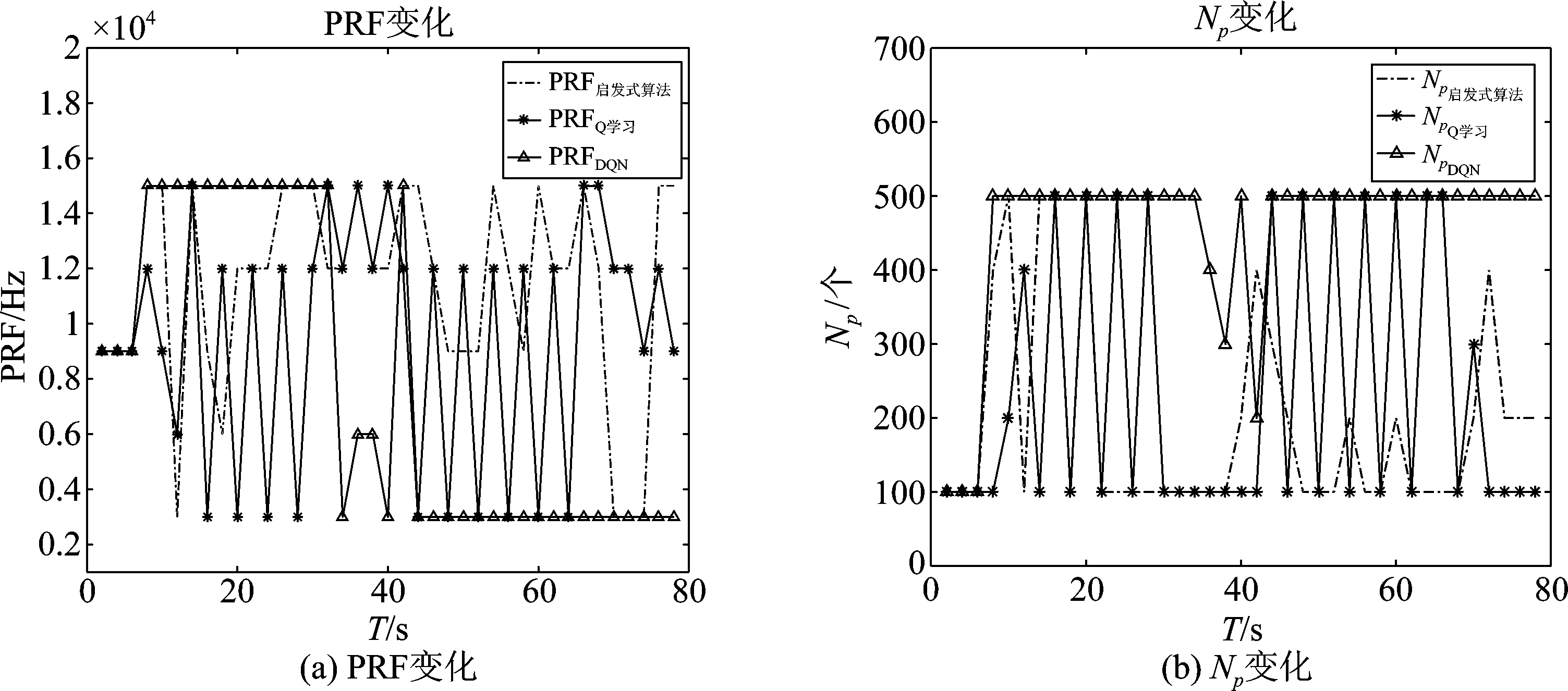
图12 强化学习算法与启发式算法的波形参数变化
Fig.12 Waveform parameters change of RL and heuristic algorithm
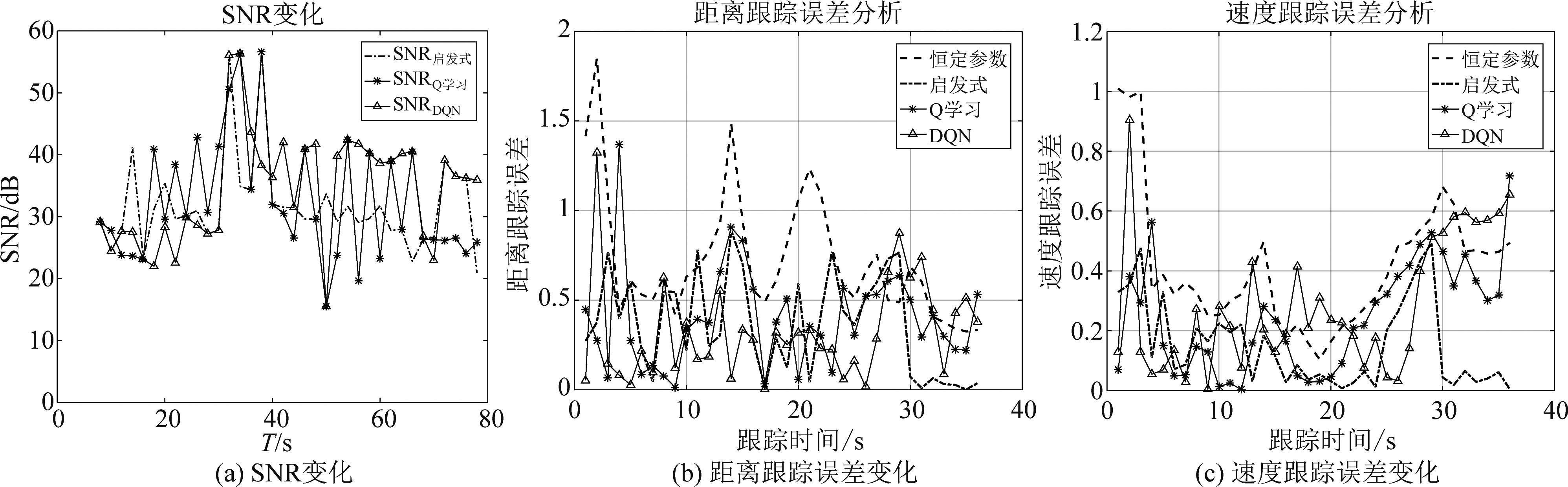
图13 几种波形选择算法的性能改善
Fig.13 Performance improvement of several waveform parameters changing algorithm
图13给出了几种波形选择算法的SNR变化和跟踪精度变化。可见,经过波形参数调整,回波信号的SNR均得到一定的提升。其中DQN算法的SNR提高幅度最大,目标检测性能提升效果最好,Q学习检测性能提升效果仅次于DQN,优于启发式算法,见表 6。在目标跟踪精度提升方面,DQN的距离估计误差大幅降低,优化效果最为明显,而速度估计误差略低于Q学习,但也优于启发式算法;Q学习的距离、速度估计精度提高水平都相对较好,远高于启发式算法。Q学习在跟踪的综合性能上提升效果较好,DQN在距离估计方面提升效果较好,均优于启发式算法。
表6 三种算法的性能提升
Tab.6 Performance improvement of the three algorithms

评估指标启发式算法Q学习DQN平均SNR提升1.87 dB2.50 dB4.57 dB距离跟踪精度提升23.64%84.1%125.51%速度跟踪精度提升27.98%70.64%45.67%
三种算法的决策时长见表 7。启发式算法需要遍历波形库,计算每种波形参数对应的奖励值,继而选取当前时刻最优的波形参数,故计算效率最低。在训练之后,Q学习以查表的形式进行波形参数选择的决策,计算量较小,通过查询找到最佳动作的速度较快,其决策过程比DQN快36.02%。然而,Q学习能够适用的状态数是有限且少量的。如果状态数较多,则表格内容的增加会占用大量内存空间,影响运算速度。此外,从表格中查询所需数据并重新写入也须耗费大量时间,波形选择的效率相对较低。在实际雷达工作环境中,状态往往无限多且通常是连续的,这种情况下采用Q表则无法实现。此时,神经网络是一种很好替代方式,可通过DQN算法实现波形参数的在线选择。
表7 波形选择算法时长
Tab.7 Waveform scheduling algorithm duration

类别平均时长启发式算法波形选择0.028636 sQ学习波形选择0.000075 sDQN波形选择0.018000 s
针对传统雷达波形参数固定、工作模式单一,难以适应复杂多变的战场环境的问题,本文在环境感知和杂波特征提取的基础上,面向目标检测与跟踪性能优化,提出了一种基于强化学习的认知雷达波形参数智能选择方法。根据波形参数对目标检测和机动目标跟踪的影响选取合适的准则函数并设计奖励函数,通过Q学习和DQN两种强化学习算法训练雷达行为,实现雷达自适应波形参数调整。在训练过程中,通过折扣因子将采取动作后未来几帧的奖励反馈到当前时刻的决策中,使雷达在整个过程的全局奖励值最大,从而实现整体性能提升。通过仿真实验验证了算法的有效性。结果表明,基于最大信噪比准则和最小均方误差准则的奖励函数可提升雷达在杂波环境下的目标检测和机动目标跟踪性能。相比于启发式算法,强化学习算法的决策时间大大降低,性能优化提升效果更好。进一步的,相比于Q学习,DQN可以更好的适用于状态和动作空间更大的复杂工作场景中。
[1] 王晓海. 认知雷达系统技术发展综述[J]. 数字通信世界, 2018(S1): 40- 43.
WANG Xiaohai. Overview of cognitive radar system technology development[J]. Digital Communication Word, 2018(S1): 40- 43.(in Chinese)
[2] HAYKIN S. Cognitive radar: a way of the future [J]. IEEE Signal Processing Magazine, 2006, 23(1): 30- 40.
[3] 黎湘, 范梅梅. 认知雷达及其关键技术研究进展[J]. 电子学报, 2012, 40(9): 1863-1870.
LI Xiang, FAN Meimei. Research Advance on Cognitive Radar and Its Key Technology [J]. Acta Electronic Sinica, 2012, 40(9): 1863-1870.(in Chinese)
[4] 袁赛柏, 金胜, 朱天林. 认知雷达技术与发展[J]. 现代雷达, 2016, 38(1): 1- 4.
YUAN Saibai, JIN Sheng, ZHU Tianlin. Cognitive radar technology and development [J]. Modern Radar, 2016, 38(1): 1- 4.(in Chinese)
[5] HAYKIN S, XUE Y B, DAVIDSON T. Optimal waveform design for cognitive radar [C]∥ Proc. 42nd Asilomar Confenence on Signals, Systems and Computers, Oct, 2008: 3-7.
[6] HAYKIN S. Cognitive Dynamic Systems: Radar, Control, and Radio, in Proceedings of the IEEE, 2012, 100(7): 2095-2103.
[7] 王涛, 陈剑, 赵婵娟. 基于杂波感知的认知雷达发射波形设计[J]. 无线电工程, 2018, 48(7): 565-568.
WANG Tao, CHEN Jian, ZHAO Chanjuan. Design on Transmit Waveform of Cognitive Radar Based on Clutter Sensing [J]. Radio Engineering, 2018, 48(7): 565-568.(in Chinese)
[8] 张令浩, 张剑云, 周青松. 雷达与通信共享频谱波形优化算法研究[J]. 信号处理, 2019, 35(11): 1861-1870.
ZHANG Linghao, ZHANG Jianyun, ZHOU Qingsong. Research on Waveform Optimization Algorithm of Radar and Communication Spectrum Sharing [J]. Journal of Signal Processing, 2019, 35(11): 1861-1870.(in Chinese)
[9] 张晓雯. 认知雷达波形优化设计研究[D]. 上海: 上海交通大学, 2019.
ZHANG Xiaowen. Cognitive Radar Waveform Optimization Design [D]. Shanghai: Shanghai Jiao Tong University, 2019.(in Chinese)
[10] 蒋峰. 机载阵列雷达认知信号处理与杂波抑制技术[D]. 成都: 电子科技大学, 2020.
JIANG Feng. Cognitive Signal Processing and Clutter Suppression Technology of Airborne Array Radar [D]. Chengdu: University of Electronic Science and Technology of China, 2020.(in Chinese)
[11] 卢术平. 基于知识的雷达目标检测与波形设计算法研究[D]. 成都: 电子科技大学, 2018.
LU Shuping. Knowledge-Based Radar Target Detection and Waveform Design Algorithms[D]. Chengdu: University of Electronic Science and Technology of China, 2018.(in Chinese)
[12] 王树亮, 毕大平, 张奎, 等. 认知雷达波形和检测门限自适应跟踪算法[J]. 西安交通大学学报, 2019, 53(4): 65-71.
WANG Shuliang, BI Daping, ZHANG Kui, et al. An Adaptive Tracking Algorithm Based on Waveform and Detection Threshold of Cognitive Radars [J]. Journal of Xi’an Jiaotong University, 2019, 53(4): 65-71.(in Chinese)
[13] 王树亮, 毕大平, 阮怀林, 等. 基于信息熵准则的认知雷达机动目标跟踪算法[J]. 电子学报, 2019, 47(6): 1277-1284.
WANG Shuliang, BI Daping, RUAN Huailin, et al. Cognitive Radar Maneuvering Target Tracking Algorithm Based on Information Entropy Criterion [J]. Acta Electronic Sinica, 2019, 47(6): 1277-1284.(in Chinese)
[14] MITCHELL A E, SMITH G E, BELL K L, et al. Fully adaptive radar cost function design[C]∥ 2018 IEEE Radar Conference, Oklahoma City, OK, 2018:1301-1306.
[15] BELL K L, BAKER C J, SMITH G E, et al. Cognitive Radar Framework for Target Detection and Tracking[J]. IEEE Journal of Selected Topics in Signal Processing, 2015, 9(8): 1427-1439.
[16] BAPTISTE P J, SMITH G E. Utilizing Neural Networks for Fully Adaptive Radar[C]∥ 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 2019:1- 6.
[17] OECHSLIN R, WELLIG P, HINRICHSEN S, et al. Aulenbacher and K. Rech, Cognitive radar parameter optimization in a congested spectrum environment[C]∥ 2018 IEEE Radar Conference, Oklahoma City, OK, 2018: 0218-0223.
[18] OECHSLIN R, WELLIG P, AULENBACHER U, et al. Cognitive Radar Performance Analysis with different Types of Targets[C]∥ 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 2019: 1- 6.
[19] YAN J, JIU B, LIU H, et al. Prior Knowledge-Based Simultaneous Multibeam Power Allocation Algorithm for Cognitive Multiple Targets Tracking in Clutter[J]. IEEE Transactions on Signal Processing, 2015,63(2): 512-527.
[20] YAN J, JIU B, LIU H, et al. Simultaneous Multibeam Resource Allocation Scheme for Multiple Target Tracking[J]. IEEE Transactions on Signal Processing, 2015,63(12): 3110-3122.
[21] MITCHELL A E, SMITH G E, BELL K L, et al. Single target tracking with distributed cognitive radar[C]∥ 2017 IEEE Radar Conference (RadarConf), Seattle, WA, 2017: 0285-0288.
[22] 王树亮, 毕大平, 刘宝, 等. 基于波形自适应的认知雷达机动目标跟踪算法[J]. 现代雷达, 2019, 41(1): 53-59.
WANG Shuliang, BI Daping, LIU Bao, et al. Cognitive Radar Maneuvering Target Tracking Algorithm Based on Waveform Adaption [J]. Modern Radar, 2019, 41(1): 53-59.(in Chinese)
[23] MARTONE A F, RANNEY K I, SHERBONDY K, et al. Spectrum Allocation for Noncooperative Radar Coexistence[J]. IEEE Transactions on Aerospace and Electronic Systems, 2017, 54(1): 90-105.
[24] THORNTON C E, BUEHRER R M, MARTONE A F, et al. Experimental Analysis of Reinforcement Learning Techniques for Spectrum Sharing Radar[C]∥ 2020 IEEE International Radar Conference (RADAR), Washington, DC, USA, 2020: 67-72.
[25] STIMSON G W. Introduction to Airborne Radar Second Edition [M]. SciTech Publishing, Inc, 1998: 581-599.
[26] KULLBACK S, LEIBLER R A. On Information and Sufficiency[M]. Annals of Mathematical Statistics, 1951: 79- 86.
[27] OSTU N. A threshold selection method from gray-level histogram[J]. IEEE Trans Systems Man Cybernetic, 1978(8): 62- 65.
[28] KIRK B H, GALLAGHER K A, OWEN J W, et al. Cognitive software defined radar: A reactive approach to RFI avoidance[C]∥ 2018 IEEE Radar Conference (RadarConf18), Oklahoma City, OK, 2018: 0630-0635.
[29] 夏洪恩. 基于目标跟踪的波形自适应选择技术[D]. 长沙: 国防科学技术大学, 2010.
XIA Hongen. Adaptive Waveform Selection Techniques for Target Tracking[D]. Changsha: National University of Defense Technology, 2010.(in Chinese)
[30] WILLIAMS J L. Information Theoretic Sensor Management [D].Massachusetts:Massachusetts Institute of Technology, 2007.
[31] 常俊杰. 认知雷达目标跟踪算法研究[D]. 成都: 电子科技大学, 2016.
CHANG Junjie. Research on Target Tracking Algorithm of Cognitive Radar[D]. Chengdu: University of Electronic Science and Technology of China, 2016.(in Chinese)
王鹏峥 男, 1998年生, 河南南阳人。哈尔滨工业大学电信学院电子工程技术研究所硕士研究生, 主要研究方向为认知雷达系统、雷达智能信号处理、波形设计。
E-mail: wangpengzheng@hotmail.com
李 杨 男, 1978年生, 黑龙江哈尔滨人。哈尔滨工业大学电信学院电子工程技术研究所教授、博士生导师, 主要研究方向为认知雷达系统、雷达智能信号处理、新体制雷达目标检测、识别与抗干扰。
E-mail: li.yang@hit.edu.cn
张 宁 男, 1957年生, 湖北宜昌人。哈尔滨工业大学电信学院电子工程技术研究所教授、博士生导师, 主要研究方向为弱信号检测与处理、信号处理及应用、并行信号处理。
E-mail: zhangn@hit.edu.cn