Reference format: LI Muyang, WANG Rui, YU Teng, et al. Influence of Channel Imbalance on Insect Orientation Estimation in Fully Polarimetric Radar[J]. Journal of Signal Processing, 2021, 37(2): 177-185. DOI: 10.16798/j.issn.1003- 0530.2021.02.003.
害虫预警和防控是农业生产中的重要组成部分[1]。相关的学者通过迁飞害虫轨迹分析对迁飞性虫害进行预警,并指导防控[2]。通常可以结合昆虫头部朝向和准确的风向判断昆虫迁飞方向[3],这是迁飞害虫轨迹分析的基础。研究发现,昆虫头部朝向并不是固定的,而是同时与风、季节等因素具有复杂的关系[4]。因此,为了获取准确的昆虫迁飞轨迹,我们需要实时并精确地测量出昆虫的头部朝向。
昆虫雷达凭借着探测距离远,探测范围广,全天候等特点,在高空昆虫迁飞监测方面发挥着重要的作用[5]。目前应用最广泛的垂直波束昆虫雷达(VLR)通过周期性旋转天线极化方向,获取波束中昆虫RCS最大值方向,并以此为根据估计昆虫朝向。国内外很多学者通过VLR开展了大量研究,发现了一系列极具价值的昆虫迁飞规律[6]。VLR需要目标在波束中稳定停留时间超过一个极化旋转周期才能完成对个体目标的测量,因此,其效率和朝向估计准确度通常不高。另外,VLR还存在着分辨率低,非相参等问题[7]。
为了解决VLR所面对的一系列问题,北京理工大学雷达技术研究所成功开发了一种Ku频段全极化相参雷达,并将其成功的应用于迁飞昆虫的飞行观测和参数提取[8-9]。该雷达采用同时全极化体制,通过H和V通道同时发射、同时接收两路时域正交信号,利用信号间的正交性分离出目标极化散射矩阵(PSM)中不同通道的元素,完成全极化测量[10]。同时全极化体制雷达能够获取包含动态目标的全极化相参信息的PSM[11],进而可以估计昆虫的朝向[12]。
全极化系统中的非理想因素会导致测量到的目标PSM出现误差[13],进而造成估计到的昆虫朝向出现偏差。发射过程中,基带信号需要分别经过射频和天线中互相独立的两个通道。这两个通道可以分别记为H和V。由于两通道物理结构上完全独立,通道间幅度和相位特性通常不会完全一致。另外,射频中有源器件传输特性会随环境温度变化,这会导致更加难以保证系统H和V通道传输特性相同。接收过程中也存在类似的问题。通道间幅相不一致会导致PSM各个通道的信号传输特性存在差异,这是造成昆虫朝向估计误差的主要原因。两通道间的交叉串扰同样会造成测量到的昆虫朝向出现误差,但是通常通道间交叉串扰的成分包含能量较小,对朝向测量结果的影响也较小。为了简化分析过程,本文将忽略通道间交叉串扰对朝向测量结果的影响。
为了分析系统幅相不一致性对朝向估计的影响机制,本文基于昆虫极化散射和全极化系统模型展开误差分析,并对通过实测昆虫PSM进行了验证。结果表明,昆虫朝向误差不仅与系统有关,还与昆虫散射特性和真实朝向有关。事实上,求解昆虫头部朝向的方法与极化合成孔径雷达中求解极化定向角的原理相同[14],相同的分析方法也能用于求解极化定向角的场景。
文章后续章节安排如下:第2节介绍了昆虫散射模型和头部朝向估计算法;第3节对全极化系统进行建模,并理论推导了头部朝向估计误差与不同影响因素间的关系;第4节利用真实的昆虫极化散射矩阵验证了系统误差对昆虫个体朝向误差和群体朝向分布的影响机制;第5节对全文进行总结。
很多研究表明,昆虫目标通常相对于体轴高度对称[15]。可以通过理论证明,如果在雷达视角下目标相对于H或V极化方向对称,则目标的PSM的交叉通道为0[16]。所以我们可以通过计算使目标PSM交叉通道最小的方向,估计目标朝向。
后向对准约定下,目标的PSM通常可以表示为:
(1)
其中sij(i, j=h,ν)表示j通道发射,i通道接收的目标回波。单站情况下,无源目标通常满足互易性[17],此时PSM中的元素满足:
shν=sνh
(2)
假设目标关于体轴完全对称,则H极化方向平行于体轴时目标的PSM为:
(3)
其中λh表示目标平行于H极化方向时的HH通道回波信号,λν表示目标平行于H极化方向时的VV通道回波信号。λh和λν还有一些等效形式的定义,这里不展开说明。定义雷达坐标系如图1。
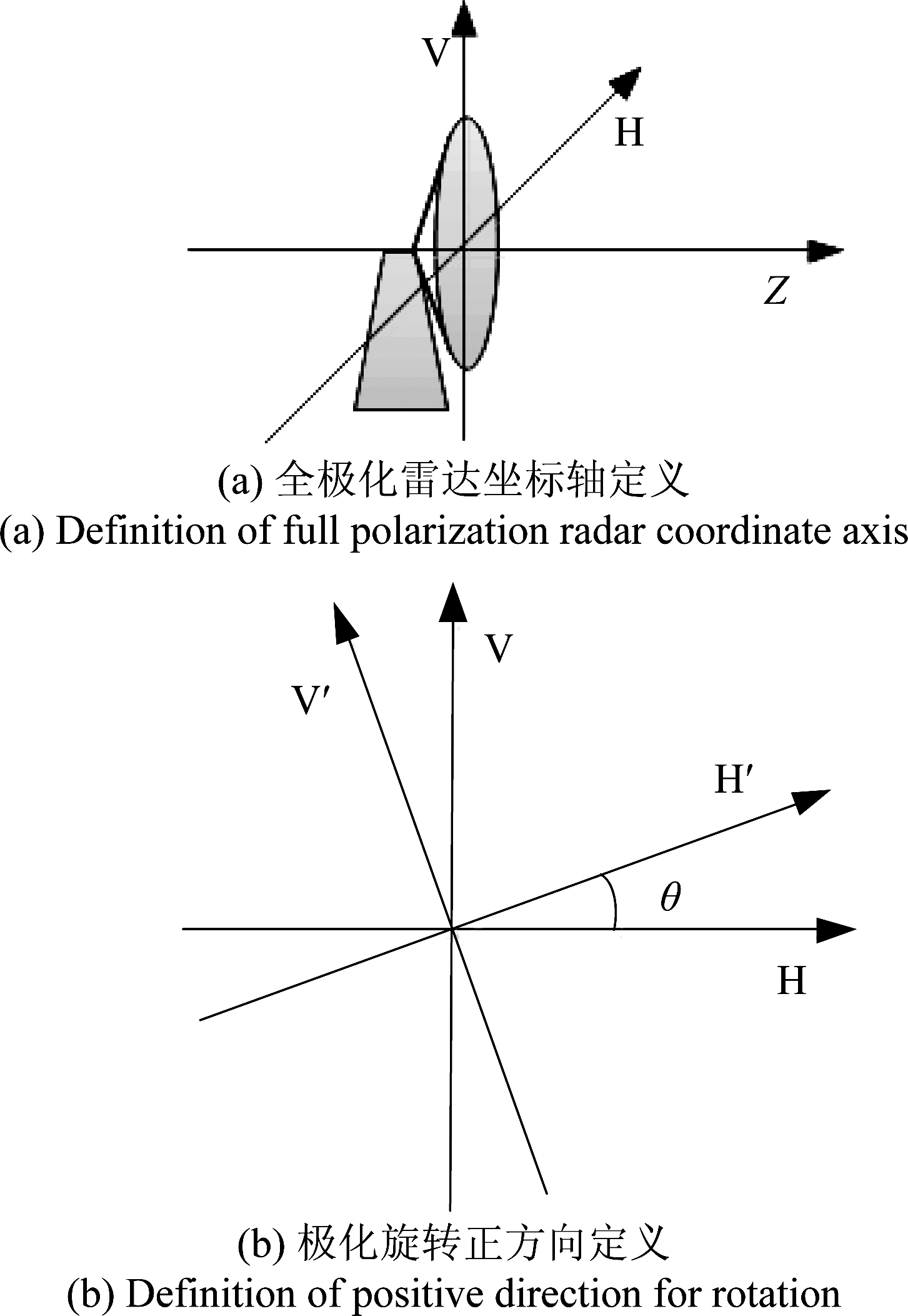
图1 坐标系和雷达旋转方向定义
Fig.1 The definition of coordinate system and positive rotation direction
图1(a)中H表示水平极化轴,V表示垂直极化轴,Z表示雷达发射信号的传播方向,H-V-Z正方向构成笛卡尔坐标系。图1(b)中H′表示旋转后的水平极化轴,V′表示旋转后的垂直极化方向,θ表示雷达旋转的角度。信号垂直于纸面向上传播,此时,逆时针方向定义为雷达旋转的正方向。
在规定雷达坐标系之后,可以得到雷达极化方向旋转任意θ角度后,目标的PSM:
(4)
其中,(·)T表示矩阵的转置。R表示旋转前后两坐标系中矢量间的变换关系,数学形式为:
(5)
θ表示雷达极化旋转的角度,范围是(-π/2,π/2)。可以将式(4)展开,得到θ角度时目标极化散射矩阵各个通道分量为:
shh=λhcos2θ+λνsin 2θ
shν=-λhcos θsin θ+λνcos θsin θ
sνh=shν
sνν=λνcos2θ+λhsin 2θ
(6)
可以通过PSM元素估计θ:
(7)
其中,θc∈(-π/4,π/4),sij(i, j=h,ν)为昆虫极化散射矩阵元素。实际情况下,真实昆虫目标的不可能完全关于体轴对称,求解出的θc通常也不是实数。需要通过对式(7)取实部排除非对称分量引入的虚部,得到目标对称分量的朝向。另外,我们可以注意到θc的取值范围比θ取值范围小,这意味着求解出的昆虫朝向发生了模糊。相关学者给出过解模糊的方法[18],这里不再详述。用θe表示取实部,解模糊之后的结果:
θe=sa(real(θc))
(8)
其中real (·)表示取实部,sa(·)表示根据PSM的一些特征对θc解模糊。
我们在推导的过程中,为了和传统定义方法保持一致,θe表示的是雷达相对于昆虫体轴转动的角度,而非昆虫角度相对于雷达的角度。因此,如果想求解出昆虫目标相对于H极化的角度,只需要取θe的相反数。用θt表示求解出的目标角度为:
θt=-θe
(9)
因为系统中非理想因素的存在,测量到的PSM会存在误差,求解出的昆虫头部朝向也会出现误差。由于朝向求解形式和系统模型的复杂性,系统对朝向的影响机制也是复杂而难解析的。下面我们将针对系统通道间幅相不一致对朝向估计的影响展开分析。
这里的通道间幅相不一致包括发射H和V通道间幅度不一致、发射H和V通道间相位不一致、接收H和V通道间幅度不一致、接收H和V通道间相位不一致。通过后续分析可以知道这些不理想因素可以归结为统一的形式中,因此我们将其统称为幅相不一致。通道间不一致的来源主要是射频传输链路中H和V通道之间的差异和双极化天线两通道之间的差异。全极化系统测量到的θ角度的昆虫PSM可以表示为[13]:
(10)
sij(i, j=h,ν)与式(6)中的定义相同,表示昆虫头部朝向为θ角度时PSM的极化散射矩阵元素;g表示系统信号传输过程中的衰减;rh、rν、th和tν分别表示H接收通道特性,V接收通道特性,H发射通道特性,V发射通道特性;Ci(i=1,2,3,4)表示发射和接收时H和V通道间的交叉串扰。Ci(i=1,2,3,4)的值通常较小,因此,后面的分析中我们忽略交叉串扰,假设Ci(i=1,2,3,4)=0。
在求解昆虫头部朝向的过程只利用的相对极化散射矩阵,因此,我们可以将式(10)进一步变化为:
(11)
其中g′=grhth,表示系统H通道传输特性,g′与极化散射矩阵元素间的相对大小无关;ar=rν/rh表示系统H和V接收通道间的幅相不一致性;at=tν/th表示系统H和V发射通道间的幅相不一致性。ai(i=h,ν)=1时,系统中信号传输通道特性理想。在忽略通道间交叉串扰之后,头部朝向估计误差只与ai(i=h,ν)有关。
用mij(i, j=h,ν)表示通过系统后的目标PSM元素:
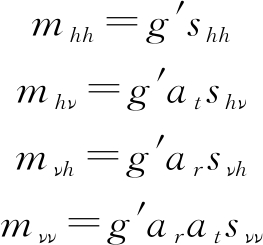
(12)
根据式(7),利用通过系统后的PSM元素求解朝向,可以得到解模糊前的朝向估计值为:
(13)
把mij(i, j=h,ν)的值带入式(13)可得:
(14)
把式(6)中的sij(i, j=h,ν)带入式(14),并在ai(i=h,ν)=1处进行一阶泰勒展开并化简可得:
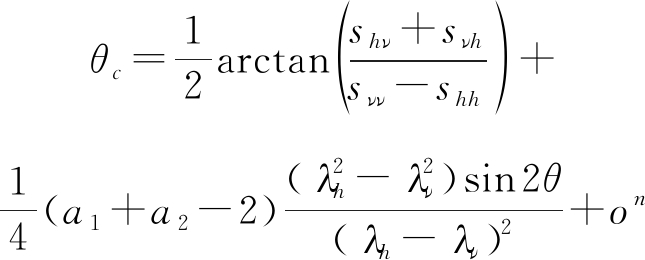
(15)
可以看出式(15)的前一项就是不存在误差解模糊前的θ。假设通道间幅相不一致性较小,不会导致解模糊操作出现错误。对式(15)取实部,解模糊,取相反数可得昆虫朝向估计值:
(16)
由于θ指的是雷达相对于昆虫旋转的方向,令θ′为昆虫相对于H极化的方向,则θ′=-θ。式(16)可以重新写为:
(17)
令:a1=A1ejφ1,a2=A2ejφ2。其中Ai(i=1,2)用来描述幅度不一致性,φi(i=1,2)用来描述相位不一致性。式(17)可以转化为:
θt=θ′+Δθmaxsin 2θ′+on
(18)
其中θ′表示昆虫角度,on表示高阶误差项。Δθmax表示一阶展开项带来的最大误差,与系统幅相不一致性和昆虫自身散射特性相关,可以表示为:
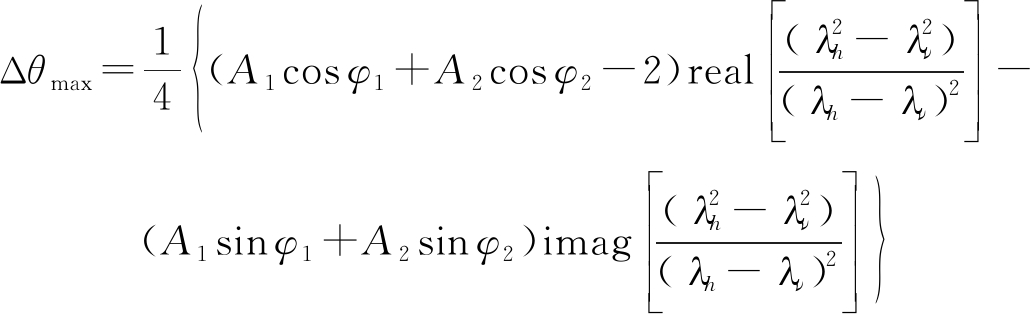
(19)
用式(18)减去真实的朝向得到朝向误差为:
Δθ=θt-θ′=Δθmaxsin 2θ′+on
(20)
可以看出朝向误差不仅与系统幅相不一致性相关,还与昆虫自身特性,昆虫真实角度相关。误差会随昆虫真实朝向以sin (2θ′)的形式变化,估计出的结果会在目标角度为π/8、3π/8、5π/8、7π/8的位置会误差最大,最大值的大小为|Δθmax|。如图2,当Δθmax>0,θ′属于(0,π/2) 区间时,sin 2θ′>0,则估计出来的角度都会比原始角度大,所有的角度都会往V极化方向偏;θ′属于(-π/2,0)区间时,sin 2θ′<0,则所有的角度都会比之前的小,同样会造成估计出来的角度偏向V极化方向;当θ′位于(π/2,π)和(-π,-π/2)区间时,获取到的回波与目标位于(-π/2,0)和(0,π/2)时的回波相同,得到的结论依旧是目标朝向会偏向V极化方向。如图3,Δθmax<0时,与前文类似的分析可以知道,估计出来的所有角度偏向H极化方向。
若系统相位不一致较小而幅度不一致较大,Δθmax趋近于![]() 在X频段大部分昆虫满足:
在X频段大部分昆虫满足:![]() 此时如果A1+A2-2>0则有Δθmax>0,得到的大部分昆虫朝向会往V极化方向靠拢;如果A1+A2-2<0,则有Δθmax<0,得到的大部分昆虫朝向会往H极化方向靠拢。
此时如果A1+A2-2>0则有Δθmax>0,得到的大部分昆虫朝向会往V极化方向靠拢;如果A1+A2-2<0,则有Δθmax<0,得到的大部分昆虫朝向会往H极化方向靠拢。
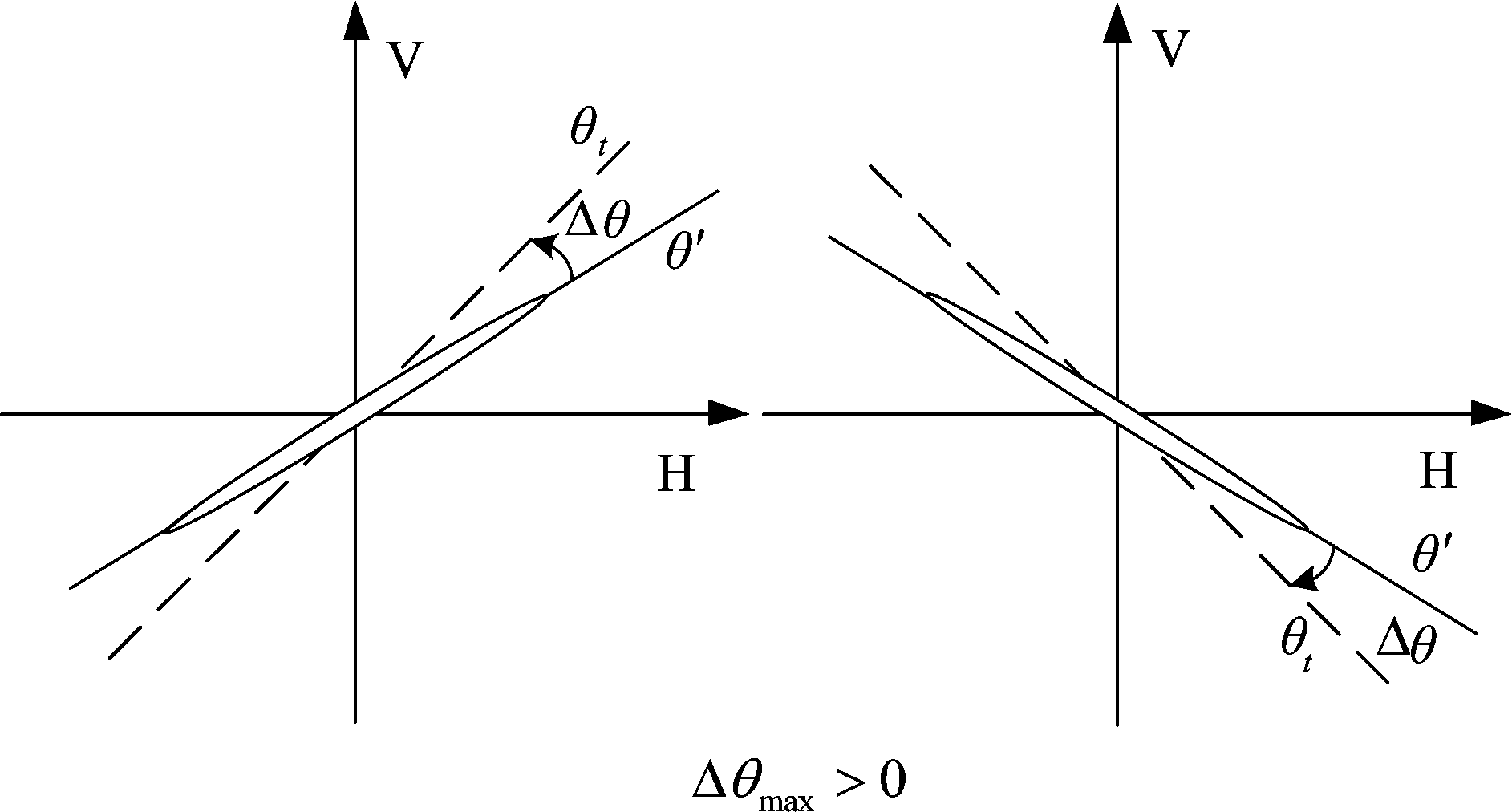
图2 Δθmax>0时系统对个体朝向测量的影响
Fig.2 The influence of system on individual orientation estimation when Δθmax>0
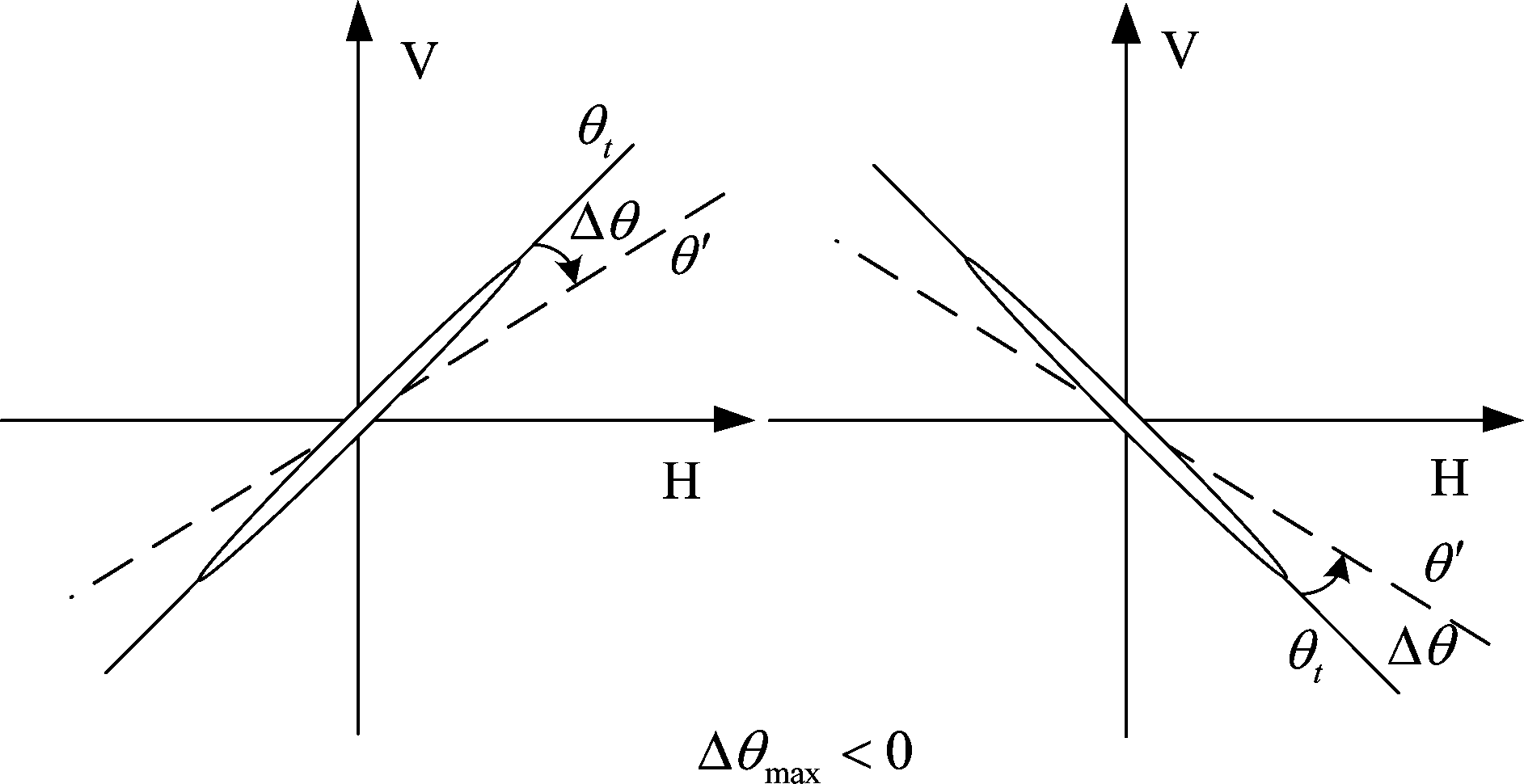
图3 Δθmax<0时系统对个体朝向测量的影响
Fig.3 The influence of system on individual orientation estimation when Δθmax<0
如果系统相位不一致较大而幅度不一致较小,Δθmax趋近于![]() 在X频段大部分昆虫满足:
在X频段大部分昆虫满足:![]() 此时如果φ1+φ2>0,则Δθmax<0,得到的大部分昆虫朝向会往H极化方向靠拢;如果φ1+φ2<0,则Δθmax>0,得到的大部分昆虫朝向会往V极化方向靠拢。
此时如果φ1+φ2>0,则Δθmax<0,得到的大部分昆虫朝向会往H极化方向靠拢;如果φ1+φ2<0,则Δθmax>0,得到的大部分昆虫朝向会往V极化方向靠拢。
为了说明上述结论的准确性,我们比较了上述理论分析与仿真的结果,并给出了高阶误差项的大小。仿真中使用的昆虫PSM数据集来自于我们在2018年9月在北京理工大学暗室中的实验,共包含12个种类,80只昆虫样本。样本体重范围是28~893 mg,体长范围是12~45 mm,更具体的信息可参见[18]。我们只使用了其中X波段9~10 GHz的测量结果。
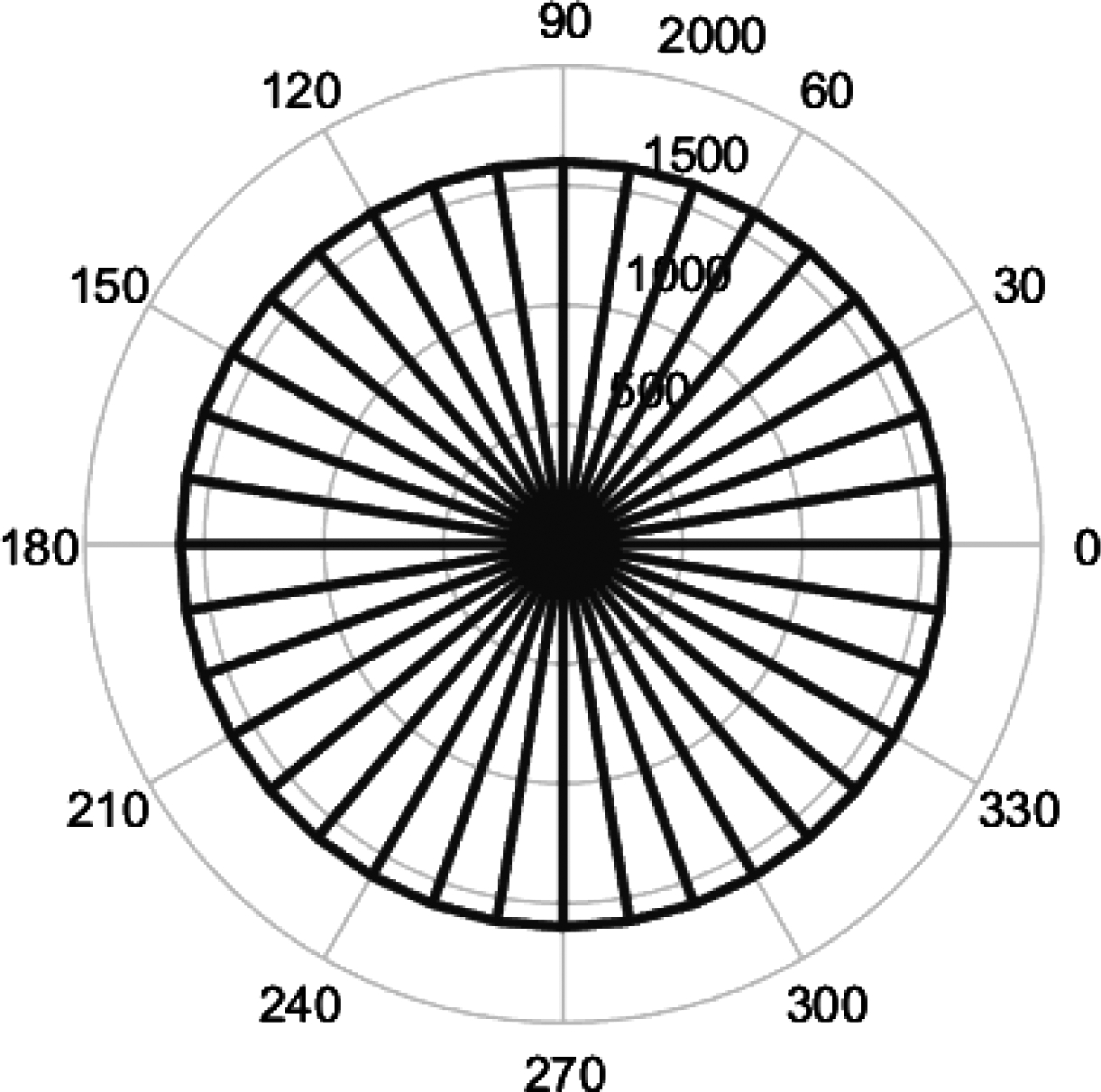
图4 原始朝向分布
Fig.4 The distribution of original orientation
数据集中只包含昆虫头部朝向接近于0度时的昆虫PSM,我们可以通过式(8)求解出昆虫准确的朝向,并在此基础上通过式(4)获得任意角度下昆虫的PSM。在仿真过程中,我们将所有昆虫PSM随机且均匀的旋转至0到360°的区间上,得到的虫群朝向分布如图4;然后根据需求设置不同的系统参数,并通过式(11)获取通过系统之后的昆虫PSM;最后重新估计昆虫朝向并统计结果。
为了直观的展示出仿真结果,绘图的过程中我们把弧度转换为了角度。
仿真中设置收通道和发通道幅度不一致的大小都是1.5 dB和-1.5 dB两种情况,忽略系统相位不一致性的影响。图5给出3头差异较大的昆虫的误差随朝向变化的情况,这三只昆虫的参数可参见表1。可以看出,估计误差随昆虫真实朝向近似以正弦函数的形式变化,正弦函数周期为π。当幅度不一致为1.5 dB时,Δθmax>0,最终所有估计出来的角度偏向V极化方向,虫群朝向分布如图6(a)。当幅度不一致为-1.5 dB时,Δθmax<0,最终所有估计出来的角度偏向H极化方向,虫群朝向分布如图6(b)。

图5 幅度不一致造成的朝向误差
Fig.5 Orientation error caused by amplitude inconsistency
表1 昆虫参数
Tab.1 Insect parameters
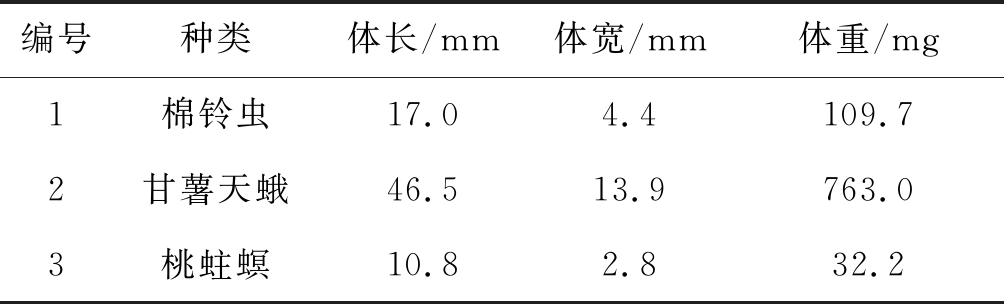
编号种类体长/mm体宽/mm体重/mg1棉铃虫17.04.4109.72甘薯天蛾46.513.9763.03桃蛀螟10.82.832.2
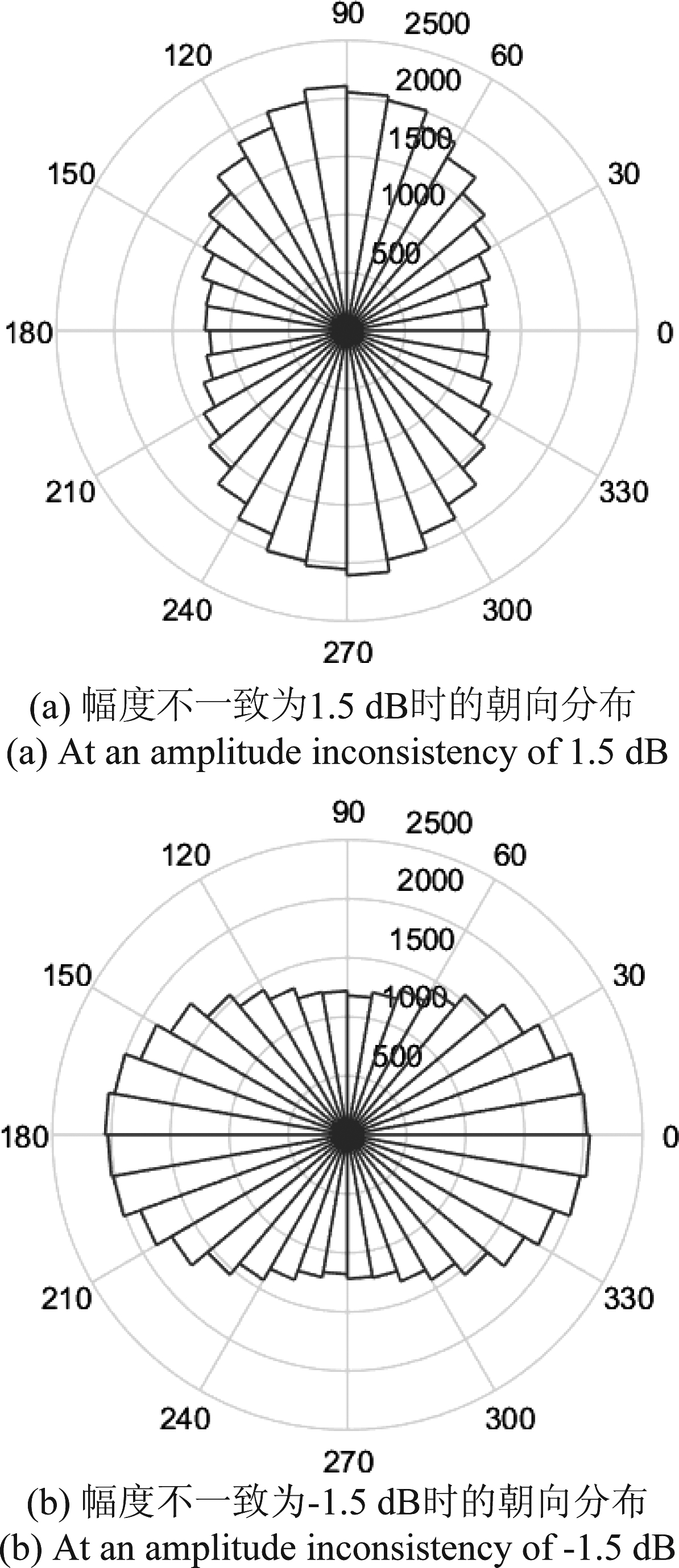
图6 幅度不一致对群体朝向分布的影响
Fig.6 Effect of amplitude inconsistency on orientation distribution of insect population
图7(a)给出了随机一只昆虫在幅度不一致为-1.5 dB时仿真得到的朝向误差结果和通过泰勒展开计算得到的朝向误差结果。通过图7(a)可以看出,仿真结果、一阶泰勒展开计算得到的朝向误差与二阶泰勒展开得到的朝向误差非常接近。图7(b)给出了泰勒一阶展开与泰勒二阶展开计算到的朝向误差与仿真得到的朝向误差的差值,我们称之为残留误差。残留误差可以反映出泰勒展开计算朝向误差的准确度,残留误差越小,估计得到的朝向误差越准确。可以看出,一阶泰勒展开与二阶泰勒展开残留误差比仿真得到的朝向误差小很多,这说明了泰勒展开的准确性。一阶泰勒展开残留误差与二阶泰勒展开残留误差大小在同一数量级,因此考虑到计算的复杂度,我们可以用一阶泰勒展开近似替代朝向误差。
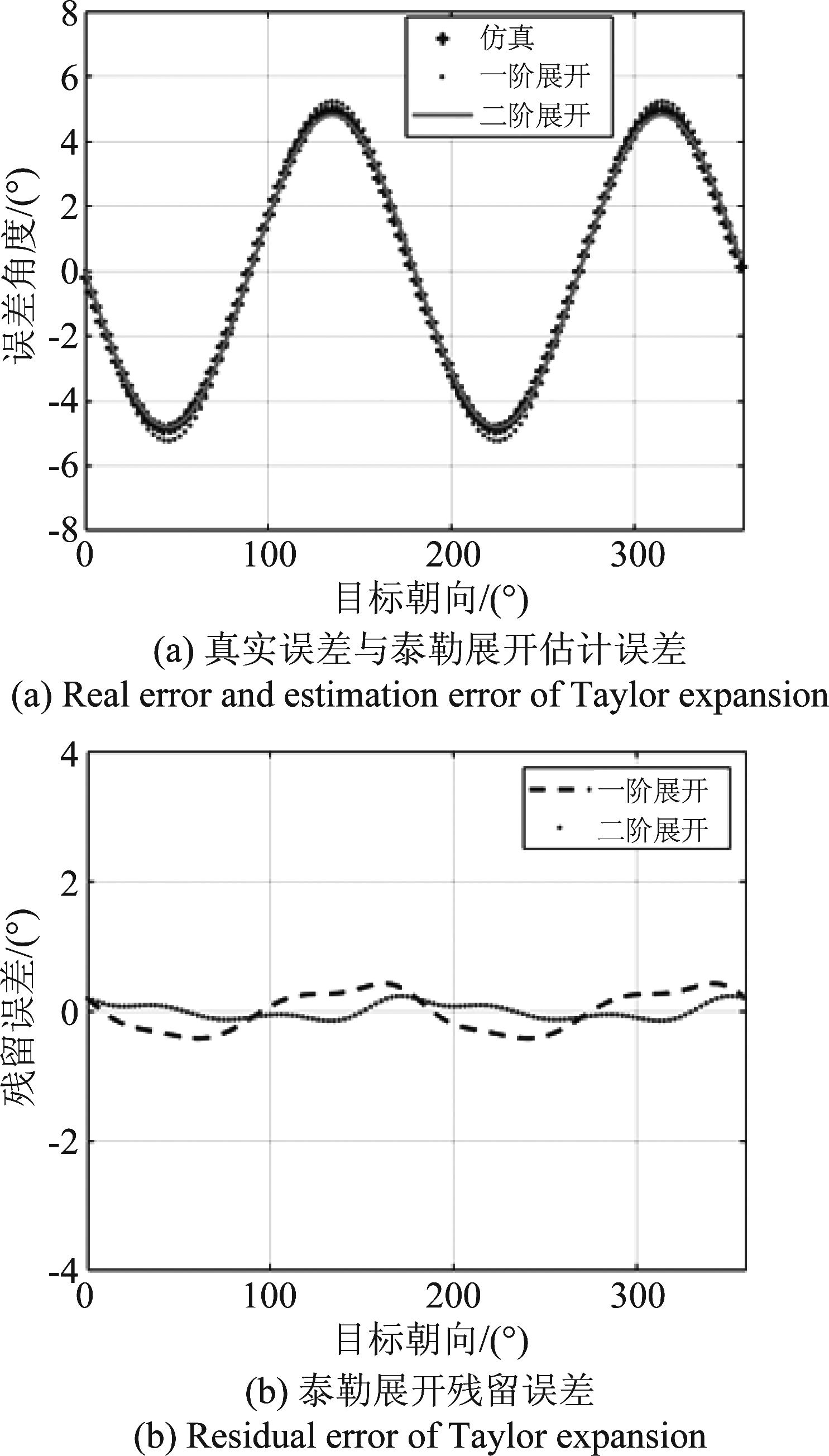
图7 存在幅度不一致时不同阶次泰勒展开结果
Fig.7 Results of different order Taylor expansion for amplitude inconsistency
仿真中设置收通道和发通道相位不一致的大小都是10°和-10°两种情况,忽略系幅度不一致性的影响。图8给出了表1中3头不同昆虫的误差随朝向变化的情况。从图8可以看出,估计误差随昆虫真实朝向近似以正弦函数的形式变化,正弦函数周期为π。当相位不一致为10°时,与4.1节分析类似所有估计出来的角度偏向H极化方向,虫群朝向分布如图9(a)。当相位不一致为-10°时,最终所有估计出来的角度偏向V极化方向,虫群朝向分布如图9(b)。结果与第3部分解析结果一致。
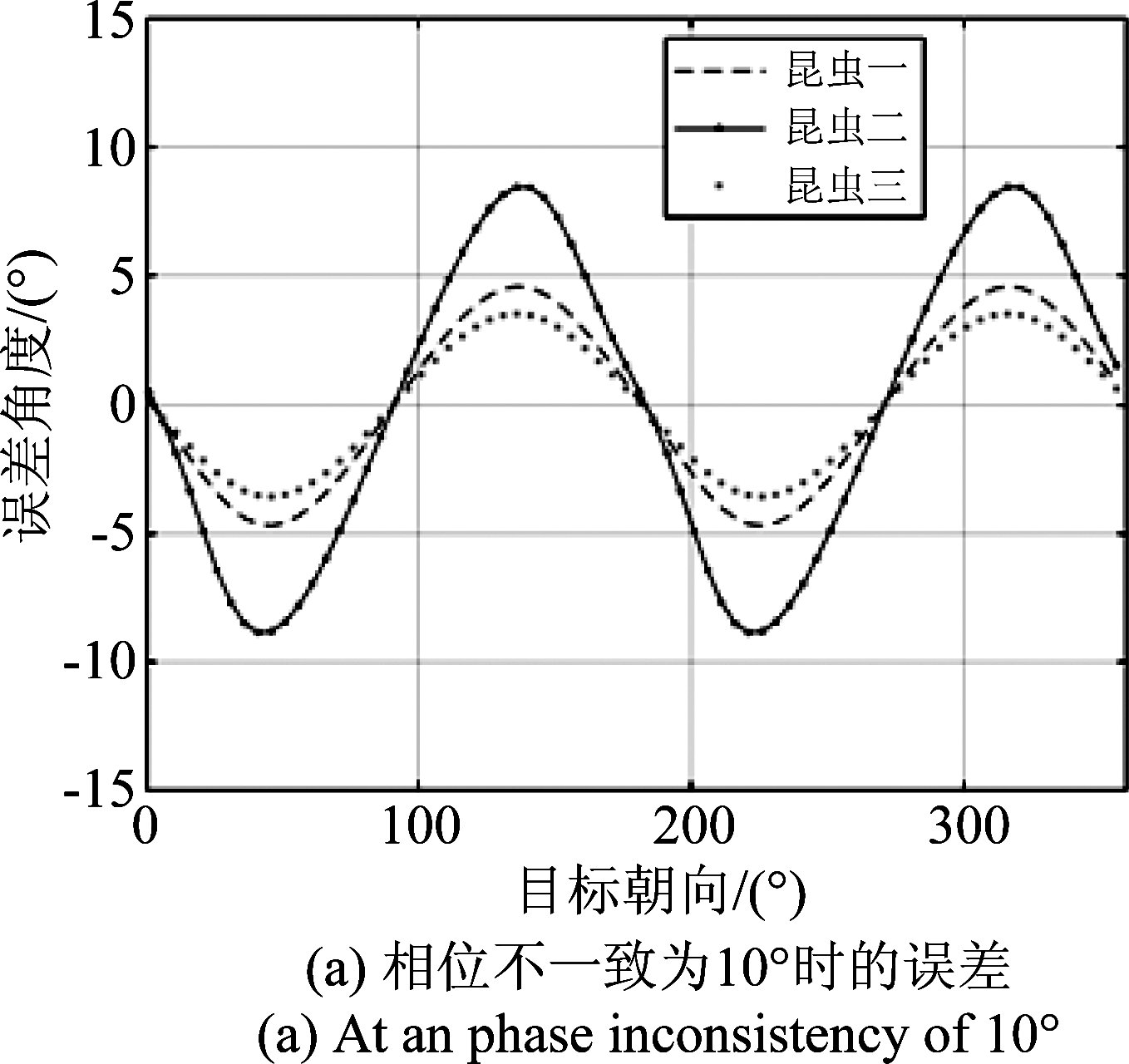
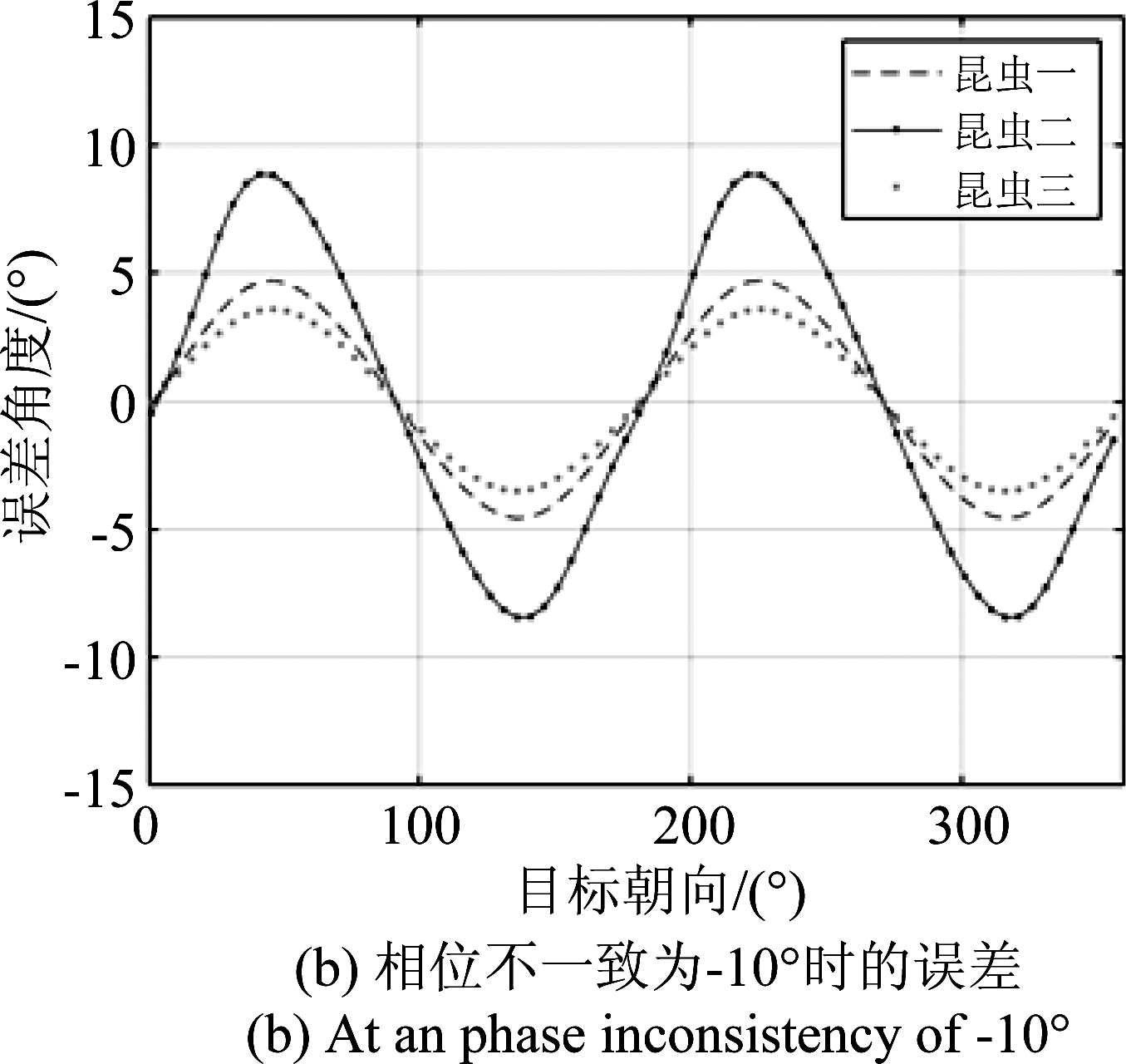
图8 相位不一致造成的朝向误差
Fig.8 Orientation error caused by phase inconsistency
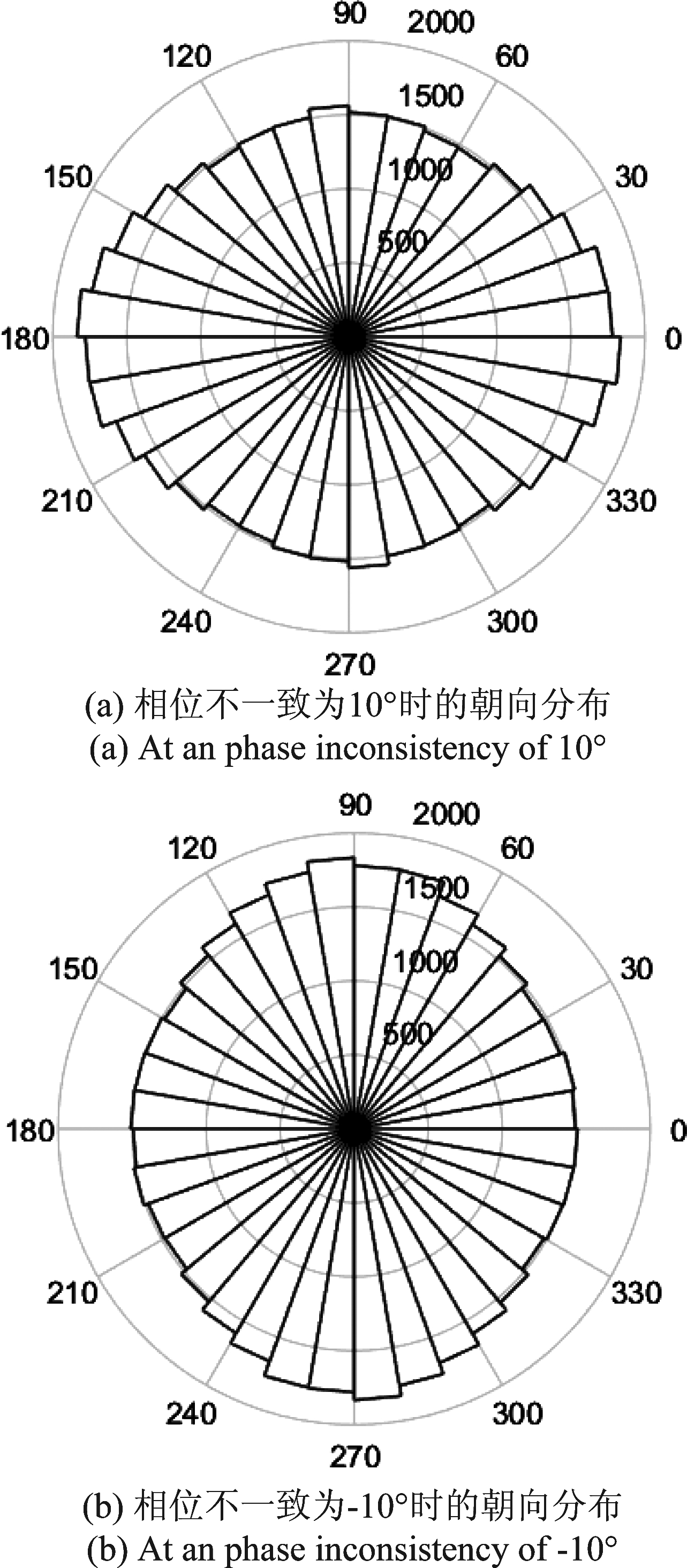
图9 相位不一致对群体朝向测量的影响
Fig.9 Effect of phase inconsistency on orientation distribution of insect population
图10(a)给出系统相位不一致为-10°时,昆虫一仿真得到的朝向误差结果和通过泰勒展开计算得到的朝向误差结果,图10(b)给出了泰勒一阶展开与泰勒二阶展开的残留误差。分析方法和结论与4.1类似,泰勒一阶展开残留误差比昆虫真实误差小了一个数量级,因此可以用泰勒一阶展开的结果近似表示朝向估计误差。
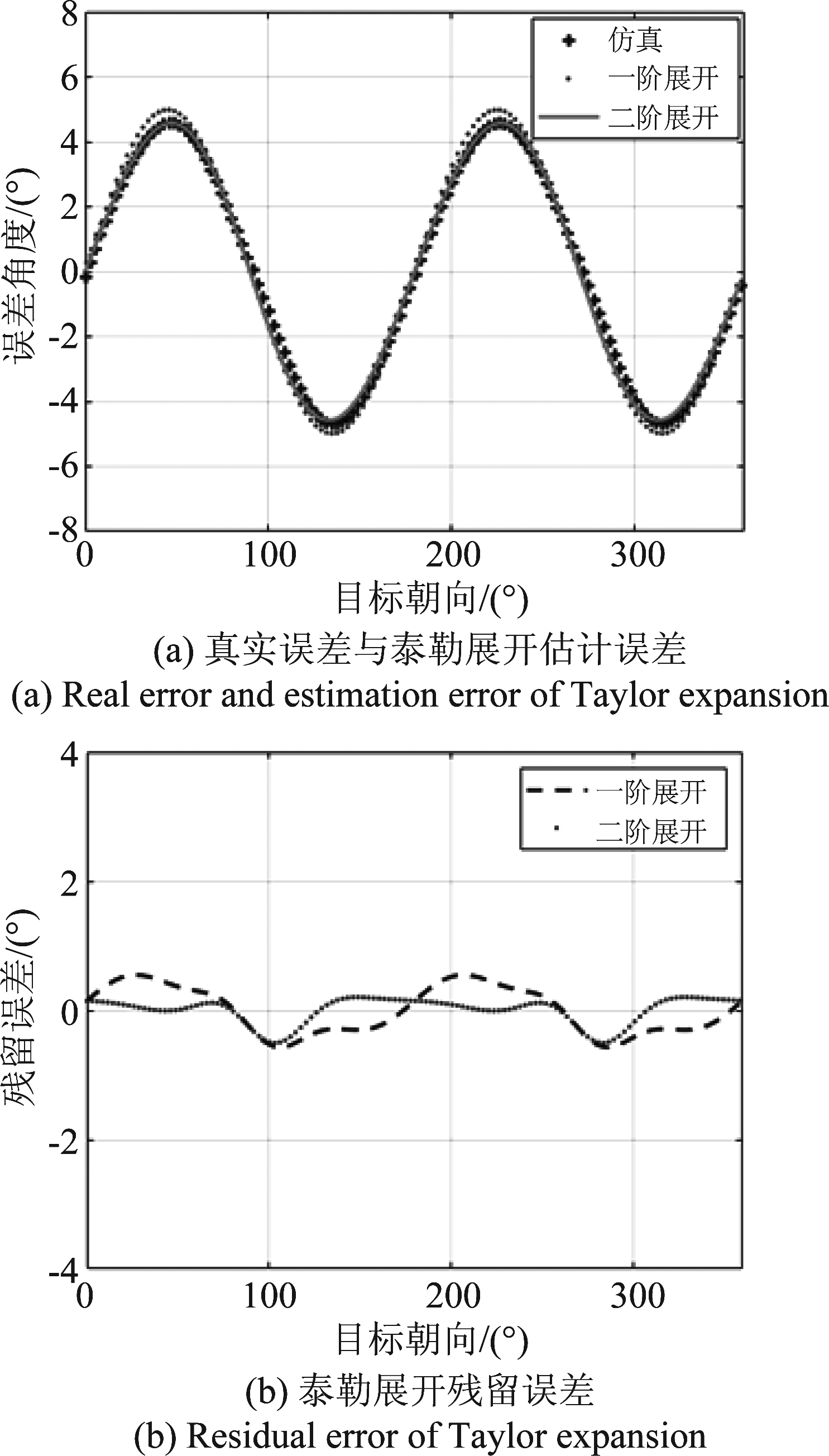
图10 不同阶次泰勒展开结果
Fig.10 Results of different order Taylor expansion for phase inconsistency
本文对全极化系统和昆虫极化散射特征进行了建模,通过泰勒展开分析了系统幅相不一致性对昆虫头部朝向估计的影响机制。通过对系统模型的分析发现系统H和V发射通道间的差异与系统H和V接收通道间的差异导致系统存在幅相不一致性。理想情况下,H和V通道完全相同,此时系统不存在幅相不一致性;实际情况下,H和V通道的幅度与相位不可能完全一致,这会导致系统测量昆虫PSM产生误差。进而导致朝向测量出现误差,因此我们针对系统幅相不一致对朝向测量的影响进行了理论分析和仿真。结果表明:昆虫个体头部朝向误差不仅与系统有关,还与昆虫个体散射特性以及昆虫真实朝向有关。对于已经确定的系统,幅相不一致会导致估计出的虫群朝向整体偏向H极化或V极化方向,仿真结果说明上述结论成立。另外,幅相不一致一阶泰勒展开估计结果与仿真结果误差较小。因此,可以用一阶泰勒展开得到的参数Δθmax近似表示系统造成的最大朝向误差。在系统设计时,可以根据期望朝向误差范围,设定系统最大误差角度Δθmax;然后结合昆虫PSM,快速求解出系统幅相不一致性,进而为全极化雷达系统设计和极化校准方案选择提供支持。
[1] 萧玉涛, 吴超, 吴孔明. 中国农业害虫防治科技70年的成就与展望[J]. 应用昆虫学报, 2019, 56(6): 1115-1124.
XIAO Yutao, WU Chao, WU Kongming. Agricultural pest control in China over the past 70 years: Achievements and future prospects[J]. Chinese Journal of Applied Entomology, 2019, 56(6): 1115-1124.(in Chinese)
[2] 吴秋琳, 姜玉英, 胡高, 等. 中国热带和南亚热带地区草地贪夜蛾春夏两季迁飞轨迹的分析[J]. 植物保护, 2019, 45(3): 1-9.
WU Qiulin, JIANG Yuying, HU Gao, et al. Analysis on spring and summer migration routes of fall armyworm(Spodoptera freguperda) from tropical and southern subtropical zones of China[J]. Plant Protection, 2019, 45(3): 1-9.(in Chinese)
[3] HAO Zhenhua, DRAKE V, TAYLOR John. Resolving the heading-direction ambiguity in vertical-beam radar observations of migrating insects[J]. Ecology and Evolution, 2019, 9(10): 1002.
[4] CHAPMAN J W, REYNOLDS D R, MOURITSEN H, et al. Wind selection and drift compensation optimize migratory pathways in a high-flying moth[J]. Current Biology, 2008, 18(7): 514-518.
[5] 张智, 张云慧, 姜玉英, 等. 我国昆虫雷达发展现状与应用展望[J]. 中国植保导刊, 2017, 37(4): 27-32.
ZHANG Zhi, ZHANG Yunhui, JIANG Yuying, et al. Research progress and application prospect of radar entomology[J]. China Plant Protection, 2017, 37(4): 27-32.(in Chinese)
[6] 翟保平. 追踪天使——雷达昆虫学30年[J]. 昆虫学报, 1999, 42(3): 315-326.
ZHAI Baoping. Tracking Angles: 30 Years of Radar Entomology[J]. Acta Entomologica Sinica, 1999, 42(3): 315-326.(in Chinese)
[7] LONG Teng, HU Cheng, WANG Rui, et al. Entomological Radar Overview: System and Signal Processing[J]. IEEE Aerospace and Electronic Systems Magazine, 2020, 35(1): 20-32.
[8] 胡程, 李卫东, 王锐. 基于全极化的相参雷达迁飞昆虫观测[J]. 信号处理, 2019, 35(6): 951-957.
HU Cheng, LI Weidong, WANG Rui. Fully Polarimetric Coherent Radar for Migratory Insect Observation[J]. Journal of Signal Processing, 2019, 35(6): 951-957.(in Chinese)
[9] 胡程, 张天然, 王锐. 基于Radon变换的昆虫上升下降率提取算法及实验验证[J]. 信号处理, 2019, 35(6): 1072-1078.
HU Cheng, ZHANG Tianran, WANG Rui. Ascent and Descent Rate Extraction Algorithm and Experimental Verification Based on Radon Transform[J]. Journal of Signal Processing, 2019, 35(6): 1072-1078.(in Chinese)
[10] 刘勇, 李永祯, 王雪松, 等. 基于正交互补序列的瞬时极化测量编码波形设计[J]. 信号处理, 2009, 25(9): 1353-1359.
LIU Yong, LI Yongzhen, WANG Xuesong, et al. The coding waveform design for instantaneous polarization measurement based on orthogonal complementary sequences[J]. Signal Processing, 2009, 25(9): 1353-1359.(in Chinese)
[11] 王雪松, 常宇亮, 李永祯, 等. 极化雷达的同时全极化测量与校准技术[J]. 科技导报, 2011, 29(26): 45-51.
WANG Xuesong, CHANG Yuliang, LI Yongzhen, et al. Polarization Measurement and calibration technologies of instantaneous polatimetric radar[J]. Science & Technology Review, 2011, 29(26): 45-51.(in Chinese)
[12] HU Cheng, LI Weidong, WANG Rui, et al. Accurate Insect Orientation Extraction Based on Polarization Scattering Matrix Estimation[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(10): 1-5.
[13] SARABANDI K, ULABY F T. A convenient technique for polarimetric calibration of single-antenna radar systems[J]. IEEE Transactions on Geoscience and Remote Sensing, 1990, 6(28): 1022-1033.
[14] ZHU Feiya, ZHANG Yunhua, DONG Li. A novel deorientation method in Pol-SAR data processing[J]. Remote Sensing Letters, 2016, 7(11): 1083-1092.
[15] RILEY J R. Radar cross section of insects[J]. Proceedings of the IEEE, 2005, 73(2): 228-232.
[16] HOBBS S E, ALDHOUS A C. Insect ventral radar cross-section polarisation dependence measurements for radar entomology[J]. IEE Proceedings-Radar, Sonar and Navigation, 2007, 153(6): 502-508.
[17] SAXON, DAVID S. Tensor Scattering Matrix for the Electromagnetic Field[J]. Physical Review, 1955, 100(6): 1771-1775.
[18] HU Cheng, LI Weidong, WANG Rui, et al, Discrimination of Parallel and Perpendicular Insects Based on Relative Phase of Scattering Matrix Eigenvalues[J]. IEEE Transactions on Geoscience and Remote Sensing, 2020, 58(6): 3927-3940.
李沐阳 男, 1996年生, 河南周口人。北京理工大学信息与电子学院博士研究生, 主要研究方向为极化校准。
E-mail: muyangli_bit@163.com
王 锐 男, 1985年生, 山西太原人。北京理工大学信息与电子学院副教授, 主要研究方向为昆虫雷达信号处理。
E-mail: bit.wangrui@gmail.com
于 腾 男, 1990年生, 江苏盐城人。北京理工大学信息与电子学院博士, 主要研究方向为昆虫雷达信号处理、全极化雷达系统设计。
E-mail: yuteng.008@163.com
胡 程 男, 1981年生, 湖南岳阳人。北京理工大学信息与电子学院教授, 主要研究方向为昆虫雷达信号处理、GEO SAR成像处理、双基地SAR成像处理和前向散射雷达信号处理。
E-mail: hucheng.bit@gmail.com