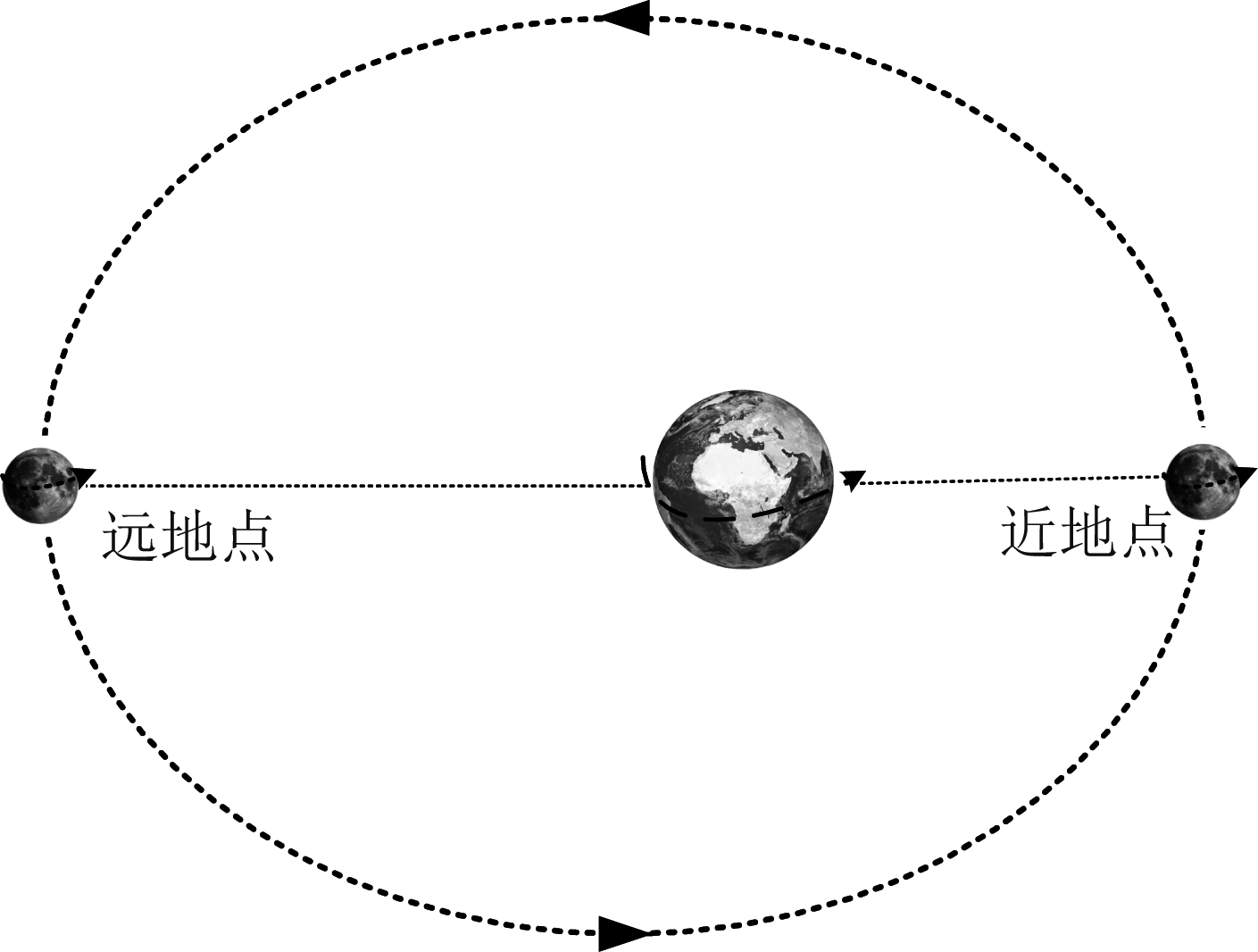
图1 地月运动几何模型
Fig.1 Geometric model of Earth Moon motion
Reference format: DING Zegang, ZHANG Guangwei, LIU Siyuan, et al. Earth-Based Radar Mapping Technology of the Moon Based on Parametric Motion Compensation[J]. Journal of Signal Processing, 2021, 37(2): 167-176. DOI: 10.16798/j.issn.1003- 0530.2021.02.002.
地基雷达是利用地面大口径天线发射电磁波并接收目标回波的雷达系统,具备全天时、全天候、高分辨的独特优势,可以获得天体的距离、形貌、电磁散射等信息,是开展深空探测的有效手段。地基雷达对月成像通过发射大带宽信号实现距离高分辨,利用地月之间的相对运动合成大孔径实现方位高分辨。
人类利用地基雷达开展对月球探测的历史可以追溯到二战后。1946年,美军利用雷达向月球发射电磁波并首次接收到了来自月球的回波,开启了人类利用雷达观测天体的先河[1]。此后随着雷达技术的发展,地基雷达越来越广泛的应用到月球的探测当中,以美国的Haystack雷达站、阿雷西博(Arecibo)射电望远镜和戈尔德斯顿太阳系雷达(Goldstone Solar System Radar,GSSR)为典型代表。自上世纪60年代起,美国麻省理工大学林肯实验室利用Haystack雷达对月球进行了观测,由于受到天线口径、功率、带宽等限制,Haystack对月球成像的分辨率仅为2 km[2]。Arecibo是世界上除FAST外的第二大单口径望远镜,早期实现了对月球的大面积测绘,其中在1966～1969年的观测中得到了分辨率为5～10 km的月球正面散射图[3]。GSSR对月球的探测主要是两极地形测量和水冰探测,2006年GSSR干涉测量获取了月球南极地形图[4],经过处理空间分辨率达到20 m,高程测量精度达到5 m;GSSR对月球南极永久阴影区的成像观测可用于确定水冰的分布范围,通过分析回波的圆极化率来确定是否存在水冰。近年来,美国宇航局利用月球勘测轨道飞行器搭载的微型射频仪器与Arecibo和GSSR的发射天线一起开展双基地雷达探测,研究了月球的雷达圆极化特性与观测几何的关系[5];此外,挪威特罗姆瑟大学Juha Vierinen等学者研究了6 m波长的对月成像结果,提出了长波有助于分析月球表面成分的结论[6]。总之,国外自上世纪六七十年代起就广泛开展了地基雷达对月球的探测,实现了对月二维高分辨成像,并获得了地形地貌及电磁散射等特征信息。
我国利用地基雷达对月球的探测处于起步阶段,中科院国家天文台、测量与地球物理研究所等单位已经开展了地基雷达对月探测的理论研究,文献[7]介绍了地基雷达的基本工作原理并给出了近年来地基雷达的发展情况和探测成果,文献[8]总结了国外地基雷达天体探测的成果和数据处理方法,并进行了仿真和实测数据处理工作,文献[9]介绍了GSSR在深空探测领域的最新应用进展,探讨了GSSR成像雷达对我国深空探测任务的启示。目前国家天文台与俄罗斯相关机构合作,实现了双基地雷达模式下月球回波信号的频谱测量[10],但在雷达天文成像方面尚属空白,我国具有广域分布、大口径、高灵敏度的射电望远镜,如果结合大口径、高发射功率的地基雷达,可以开展双站以及多站模式的天体成像试验,因此亟需研究地基雷达天文成像算法,为我国将来开展对月成像试验提供技术支撑。
本文结构安排如下:第2节基于地月运动几何模型分析了延迟多普勒算法的关键问题,包括成像原理、分辨率和模糊问题,第3节提出了一种参数化运动补偿算法,采用了基于图像熵值的布谷鸟搜索算法来加快参数搜索速度,第4节给出了点目标及面目标的仿真结果,最后一节对全文进行了总结。
地基雷达对月成像利用地月之间的相对运动合成大孔径,实现方位高分辨。地月之间的相对运动较为复杂,包含着地球自转、地球公转、月球自转、月球公转等多种形式。图1为地月运动几何模型,月球在白道面上绕地球自西向东公转,地球和月球本身也在由西向东自转。月球自转周期和公转周期几乎相同,约为27.32天,可以计算得到月球自转和公转角速度约为2.66e-6 rad/s,地球自转角速度约为7.27e-5 rad/s。因此,可以得出结论,地基雷达对月成像主要由地球自转合成大孔径,其相对转动角速度ω约为1.2e-6 rad/s。图2为月球表面坐标系下的地基雷达运行轨迹示意图,合成孔径时间为8 h,对应的合成孔径长度约6700 km。
图1 地月运动几何模型
Fig.1 Geometric model of Earth Moon motion
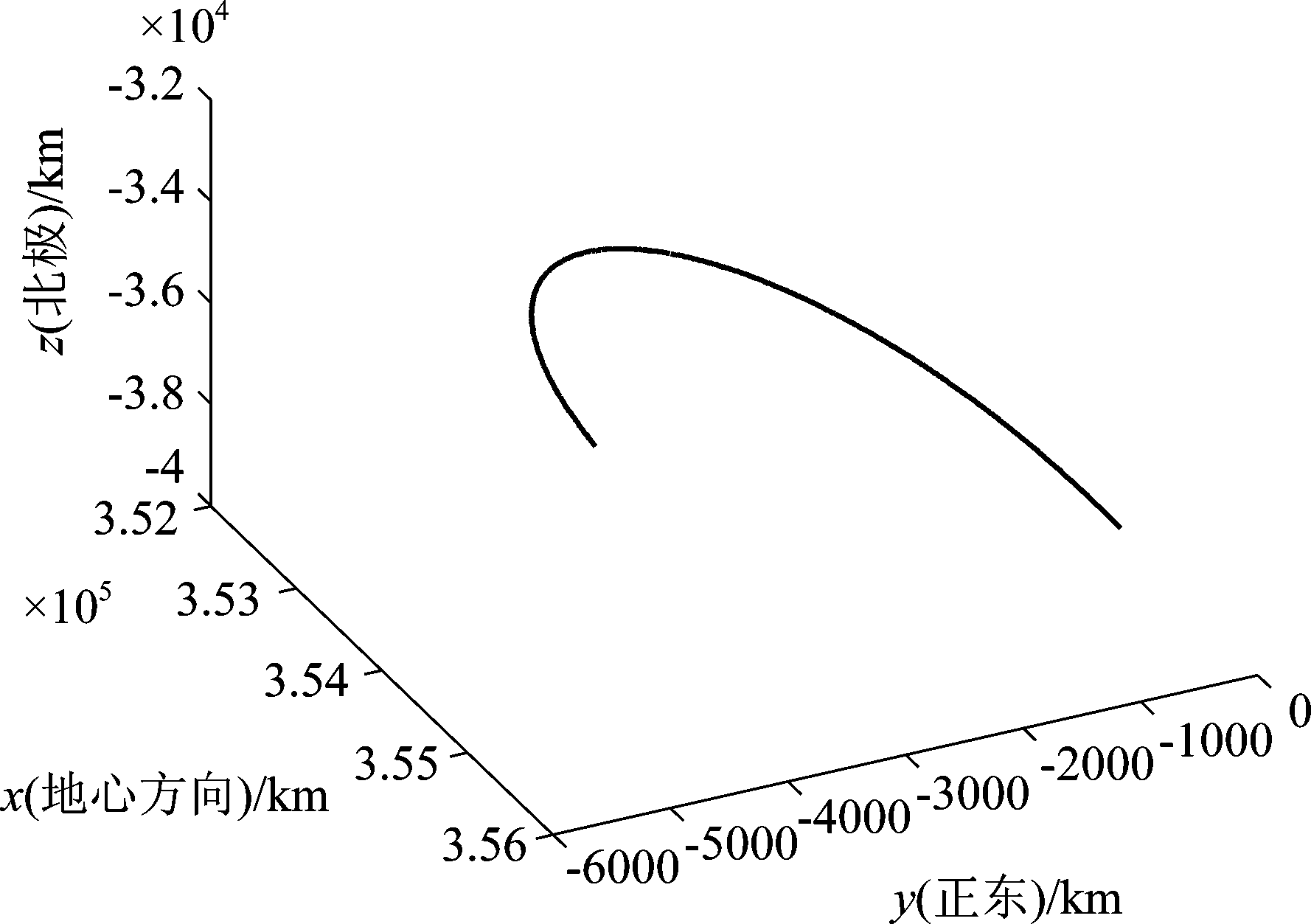
图2 地基雷达运行轨迹
Fig.2 Earth-based radar trajectory
地基雷达天文成像主要采用延迟多普勒技术,这种技术最早在1960年由Price和Green提出,首次应用于美国Millstone雷达对月球的探测中[11]。对月成像的延迟多普勒模型如图3所示[12],这种模型基于两个前提:一是假设月球是一个规则的球体,二是假设雷达视线是平行的。对于正视图来说,在与雷达视线垂直的方向上做切片,天体表面形成圆环,且圆上各点到雷达距离相同,即等延迟环。同理,在与雷达视线平行的方向上做切片,从侧面看也会形成一个圆环,且圆上各个点到雷达视线的垂直距离相同,也就是相对雷达的径向速度和多普勒频移相同,即等多普勒环。延迟多普勒算法的主要思想是通过脉压技术提取目标的时延信息,通过方位频谱分析提取多普勒频移信息,将目标区域划分为不同的延迟多普勒单元,从而得到月球的二维雷达图像。
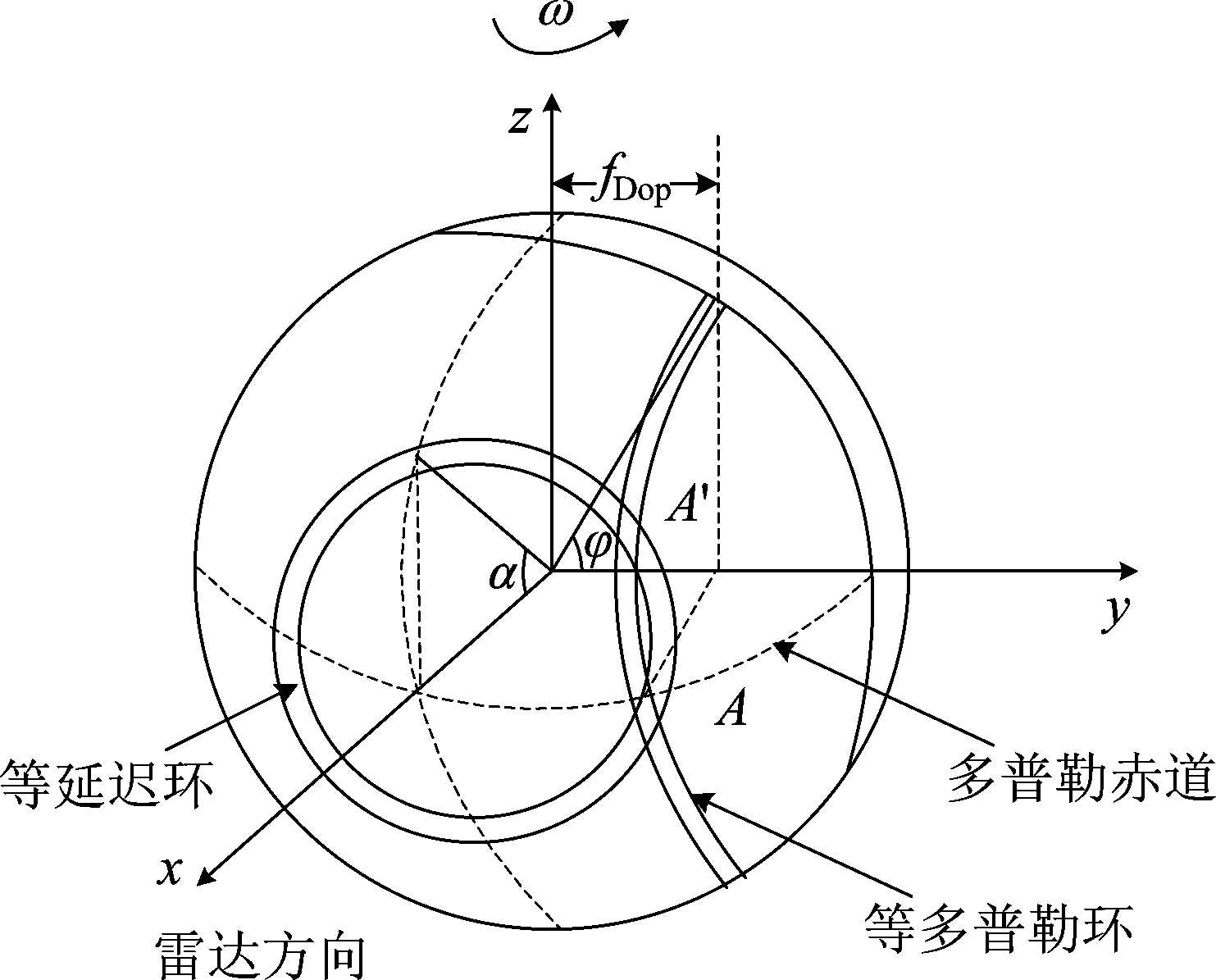
图3 延迟多普勒模型
Fig.3 Delay Doppler model
月球二维成像分辨率包括距离和方位分辨率。距离分辨率与信号带宽相关,主要通过发射大带宽的信号来实现距离高分辨;方位分辨率主要取决于积累时间,通过对连续的脉冲串进行脉间相参处理实现方位高分辨。
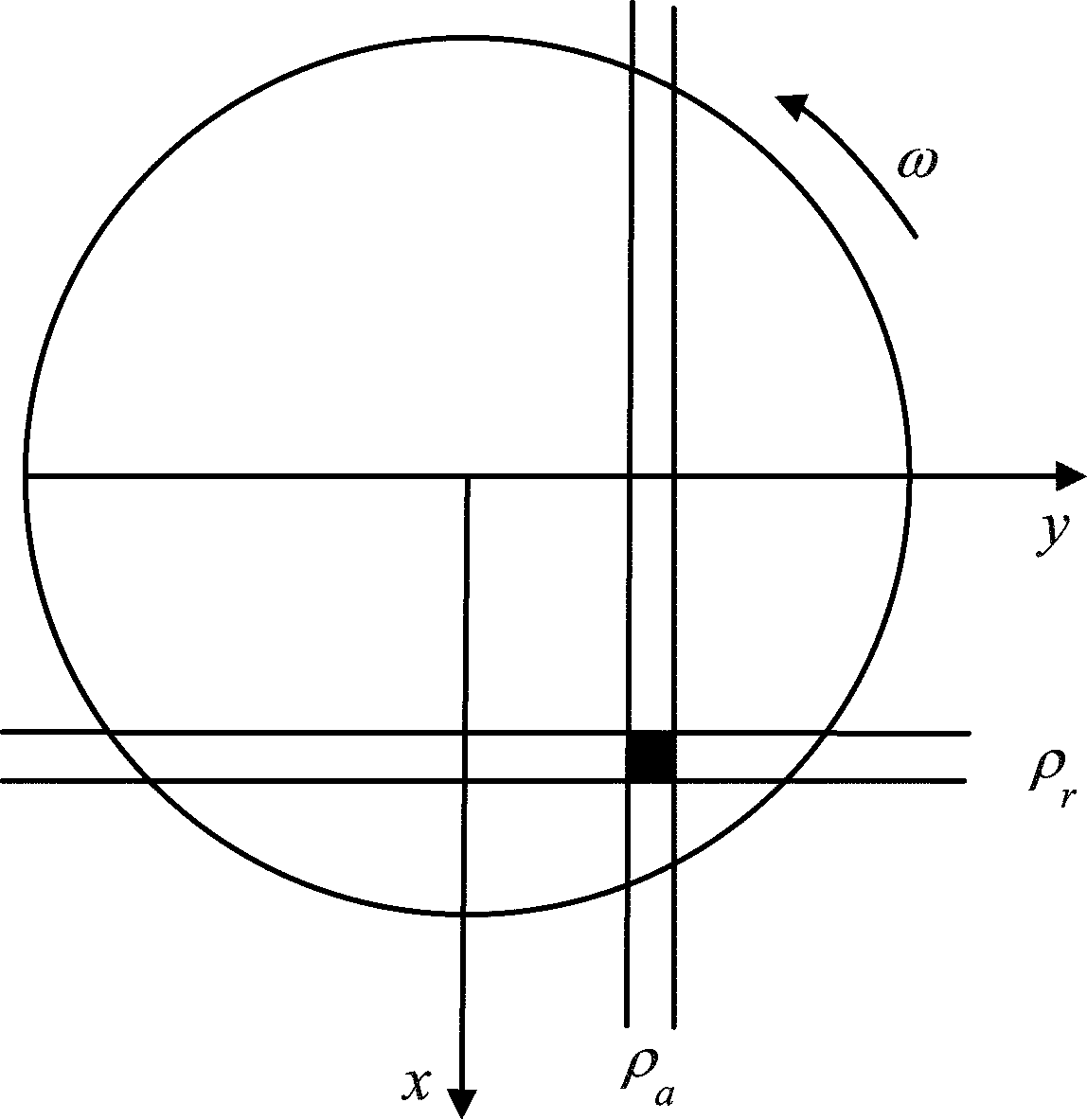
图4 延迟多普勒模型俯视图
Fig.4 Delay Doppler model top view
图4为延迟多普勒模型的俯视图,雷达视线方向可以划分为延迟分辨单元,距离分辨率[8]为:
(1)
其中,c为光速,B为信号带宽。
方位向可以划分为多普勒分辨单元,方位分辨率[8]为:
(2)
其中,Da为天体方位直径,Δf为多普勒分辨,是合成孔径时间Ta的倒数,BD为天体的多普勒带宽,λ为波长,ω为月球相对自转角速度,为1.2e-6 rad/s,θ为积累角,可见积累角越大,方位分辨率越高。
上述分辨率是月面在xoy平面的投影分辨率,而月球表面的地距分辨单元要大于投影分辨单元,地距分辨单元大小[13]为:
(3)
其中,投影因子Fproj表示为1/sin(lat),lat为延迟多普勒坐标系下的纬度值。由(3)可知月球表面分辨率具有空变性,纬度越低,分辨率越差,极端情况下多普勒赤道部分不具备二维分辨能力。
此外,延迟多普勒算法具有一定的局限性。当目标转角较小时,距离徙动小于一个距离分辨单元,聚焦效果良好,当目标转角较大时,目标会出现跨越距离单元徙动的情况,FFT图像重建会出现散焦情况,因此,利用FFT实现方位聚焦的条件[14]为:
<ρr
(4)
结合方位分辨率公式,有:
<ρrρa
(5)
从上述结论可知,若要实现高分辨率成像,目标极容易出现跨越距离单元的情况,需要研究大转角成像算法。
模糊性是评价延迟多普勒成像性能的重要指标。在对月成像中,延迟多普勒算法存在南北模糊和延迟多普勒模糊[12]。如图3所示,等延迟环和等多普勒环在南北半球相交,相交区域的延迟和多普勒频移相同,在雷达图像中无法区分,即南北模糊。解决南北模糊可以采用窄天线分别照射南北半球,这种技术仅仅限于直径较大的近距离目标,如月球;除此之外,还可以采用两个或者多个天线干涉处理的方法来解决[15]。延迟多普勒模糊是大型快速旋转目标普遍存在的,目标半径、旋转速度等参数决定了延迟深度以及多普勒带宽。在参数设计时,对于脉冲雷达体制来说,其模糊函数如图5所示,为了避免距离模糊,应设置脉冲重复间隔(PRT)大于延迟深度;为了避免多普勒模糊,应设置脉冲重复频率(PRF)大于最大多普勒频移。延迟深度和多普勒带宽的乘积定义为扩展因子F,当F小于1时,不存在模糊,此时采用延迟多普勒算法是可以的,对月成像即属于这种情况;当F大于1时,存在模糊,采用延迟多普勒算法无法避免模糊。
图5 脉冲体制的模糊函数
Fig.5 Ambiguity function of impulse system
运动补偿是延迟多普勒成像的关键。在对月成像中,由于天体回波的低信噪比特性,传统的包络补偿和自聚焦方法不再适应,需要采用参数化运动补偿方法。在参数化运动补偿中,包络补偿的精度需要达到距离单元尺度,自聚焦的精度需要达到波长级别。由于星历误差(亚米级精度)、大气延迟误差以及高程误差等非理想因素的影响,雷达与目标参考点之间存在运动误差,因此需要进行精确的参数化运动补偿。
参数化运动补偿算法的基本思路是将目标的运动建模为多项式模型,通过参数搜索算法精确估计运动参数。文献[16]提出的算法将平移运动建立为多项式模型,以图像熵、对比度和峰值作为运动参数搜索的评价指标,并采用粒子群(PSO)算法加快参数搜索过程,以实现运动的参数估计与补偿。文献[17]首次将广义瑞登傅里叶变换(GRFT)理论应用到成像中,实现了多分量回波信号的相干积分,然后采用恒虚警率(CFAR)检测获得强散射点的信息以重构多分量信号,最后获得高质量的成像结果。本文将采用参数化运动补偿理论以实现天体回波信号的距离对准及相位误差校正。
下面给出天体目标的参数化运动补偿过程。天体目标成像模型如图6所示,O为月心,r为地基雷达至月心的斜距,R为雷达至散射点k的距离。
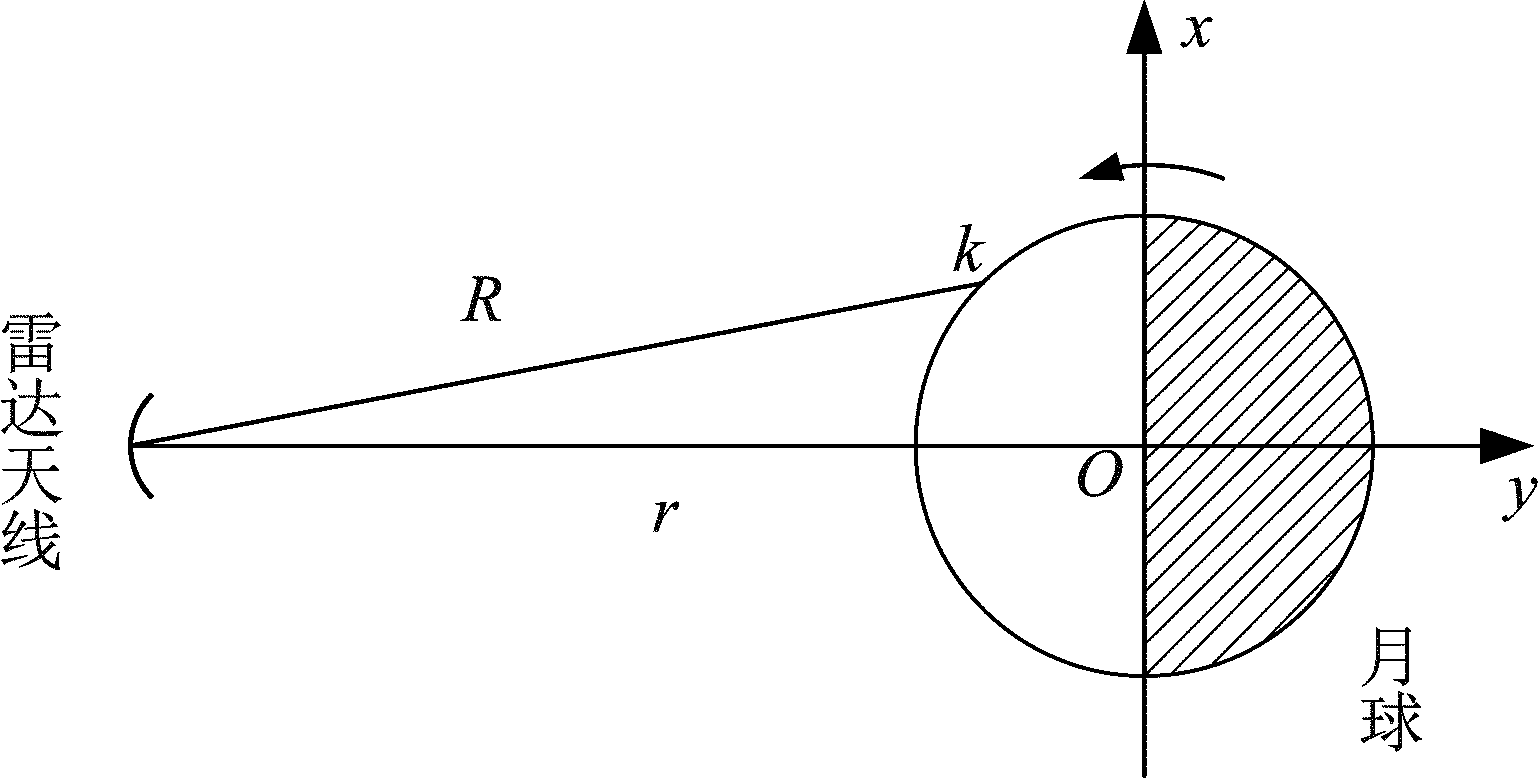
图6 天体目标成像模型
Fig.6 Mapping model of Celestial target
当雷达与目标距离远大于目标大小以及转角较小时,雷达至散射点k的斜距可表示为[16]:
(6)
其中,r(t)为目标参考点平移运动分量的泰勒展开式,N为多项式阶数,an为第n阶多项式系数,初始斜距为r0。
假设雷达发射线性调频信号,信号包络为p(τ),距离向快时间为τ,慢时间为t,则发射信号可以表示为:
(7)
其中,rect(τ/Tp)为窗函数, fc是载频,Tp是脉冲宽度。
目标的回波经过下变频后,可以表示为:
(8)
其中,σk是散射点k的散射系数。
首先对回波进行脉冲压缩,脉压后的信号时域表示如下:
(9)
其中,pc(τ)为脉压后的信号包络。
由于地月之间存在相对运动,需要进行运动补偿,首先建立地月运动的多项式模型,然后采用基于图像熵的参数搜索算法精确估计运动参数,最终估计的运动多项式模型表示为:
(10)
其中,
为估计的第n阶多项式参数,利用估计的运动多项式在距离频域对脉压信号进行包络和相位的联合补偿,忽略估计误差的影响,平动补偿过程如下所示:
(11)
其中, f为快时间频率,经过平动补偿后,可以利用目标的转动分量进行成像,方位FFT处理后信号变为:
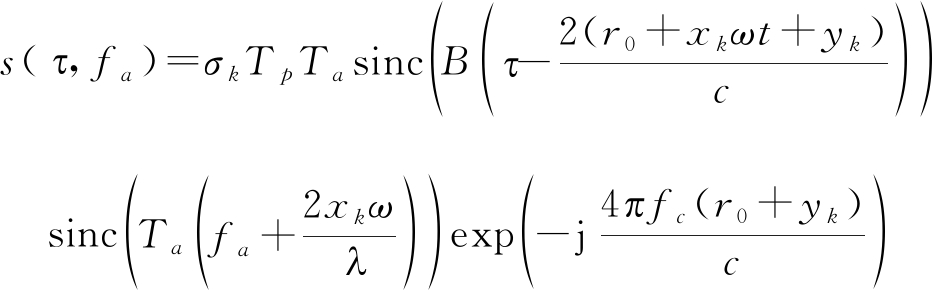
(12)
其中,距离向位置由目标时延参数确定,方位向位置由目标多普勒信息确定,最终得到延迟多普勒二维图像。
若要得到地理坐标系下的散射图需要进行地理编码。假设雷达至星下点的距离为rsrp,月球半径为rm,参考点的坐标为[x0,y0,z0],根据散射点的延迟多普勒参数(r, fa)可以得到三维坐标:
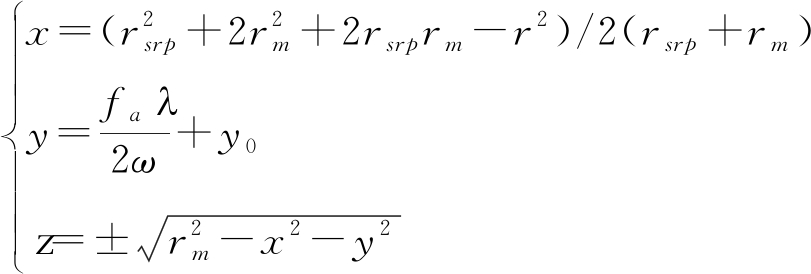
(13)
天体直角坐标系(X,Y,Z)经过两次旋转得到延迟多普勒坐标系(x,y,z),先沿Y轴、Z轴旋转θ、λ,得到坐标系(x′,y′,z′),其中x′轴指向雷达视线方向,然后沿x′轴旋转γ,得到延迟多普勒坐标系,其中z轴指向视旋转轴方向,因此从延迟多普勒坐标系到天体直角坐标系的转换关系[7]为:
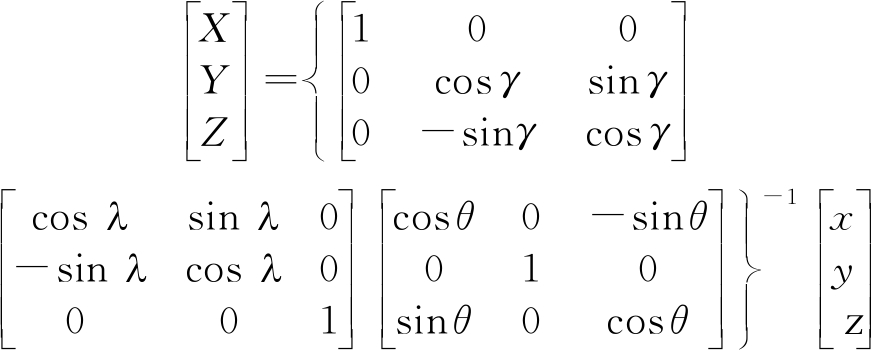
(14)
经过地理解码后,可以得到月球表面特定区域的散射图。为了获得月球正面大场景的散射图像,提高图像边缘的聚焦性能,可以采用子块算法[18],即将大场景划分成多个较小的场景,并对雷达和每个小场景中心之间的运动进行补偿,最后将形成的子图像集进行拼接处理,从而获得聚焦性能更优的大场景散射图像。
运动参数估计若采用遍历搜索的方法,运算量会随着参数空间的增多呈指数增长。为了加快参数搜索速度,通常与启发式寻优算法相结合,常用的启发式寻优算法有遗传算法、粒子群算法、萤火虫算法等。2009年,剑桥大学的学者提出了布谷鸟搜索(CS)算法[19],研究表明布谷鸟算法比遗传算法和粒子群算法具有更高的寻优性能,本文将采用布谷鸟搜索算法实现参数化运动补偿。
布谷鸟搜索算法是基于某些种类的布谷鸟的孵卵寄生行为并结合Levy飞行方式而开发的元启发式算法,可以寻找问题的最优解,从本质上来说,布谷鸟算法是全局随机游走和局部随机游走两种寻优机制的组合。
全局随机游走是由Levy飞行机制实现,Levy飞行是一种步长满足重尾分布的随机游走方式,其位置更新公式如下:
(15)
(16)
其中
为第i个鸟巢在第l次迭代的位置,α为步长控制系数,服从正态分布,L(s,λ)为Levy飞行路径,s为Levy步长,λ为Levy指数,Levy飞行的特点表现为经常性的小步长行走和偶尔的大步长行走,可以有效地去寻找全局最优解,避免过快地陷入局部最优解。
局部随机游走是由发现概率Pa控制的,主要是为了获得局部最优解,其位置更新公式如下:
(17)
其中H是阶跃函数,α是步长控制系数,可以控制局部寻优的范围,s是步长,ε是满足均匀分布的随机数,
和
是第l次迭代中随机选取的两个位置,可见,局部随机游走比较充分的利用了已有的位置信息。
这里给出布谷鸟算法的实现过程:
1)初始化:设置宿主巢规模、空间维数、最大迭代次数、搜索精度、发现概率等参数,随机生成一组宿主巢X=[X1,X2,…,Xn]。
2)选择适应度函数f(X),计算每个鸟巢位置的函数值,并得到当前最优函数值以及其对应的最优鸟巢位置。
3)采用Levy飞行机制更新除最优鸟巢外的其他鸟巢的位置,计算适应度函数值,选择每个鸟巢的较优函数值的对应位置。
4)在鸟巢位置更新后,对于每个鸟巢生成随机数r(r∈[0,1]),并与发现概率Pa进行比较,若r>Pa,随机更新对应的鸟巢位置,否则保持位置不变,选择每个鸟巢的较优函数值的对应位置。
5)若达到最大迭代次数或者搜索精度要求,输出全局最优鸟巢位置,否则返回步骤2)。
综上所述,采用布谷鸟算法进行参数搜索,选择图像熵值作为适应度函数,基于参数化运动补偿的延迟多普勒算法基本流程如图7所示。
下面以浮点运算量来评价所提算法的计算复杂度。由图7可知,算法主要的计算复杂度在参数估计部分的迭代运算,设最大迭代次数为jmax,鸟巢数为I,多项式阶数为N,脉冲数为Na,脉冲采样点数为Nr,在每次迭代中,平移运动的计算量为(2N-1)Na次,运动补偿的计算量为10NrNalog2(Nr)+6NaNr次,成像处理的计算量为5NrNalog2(Na)次,图像熵的计算量为7NrNa-1次,所以主要的计算复杂度为:
C=O(jmaxINaNr(log2(Nr)+log2(Na)))
(18)
因此,可以通过改变迭代次数和鸟巢数来调整算法的复杂度。
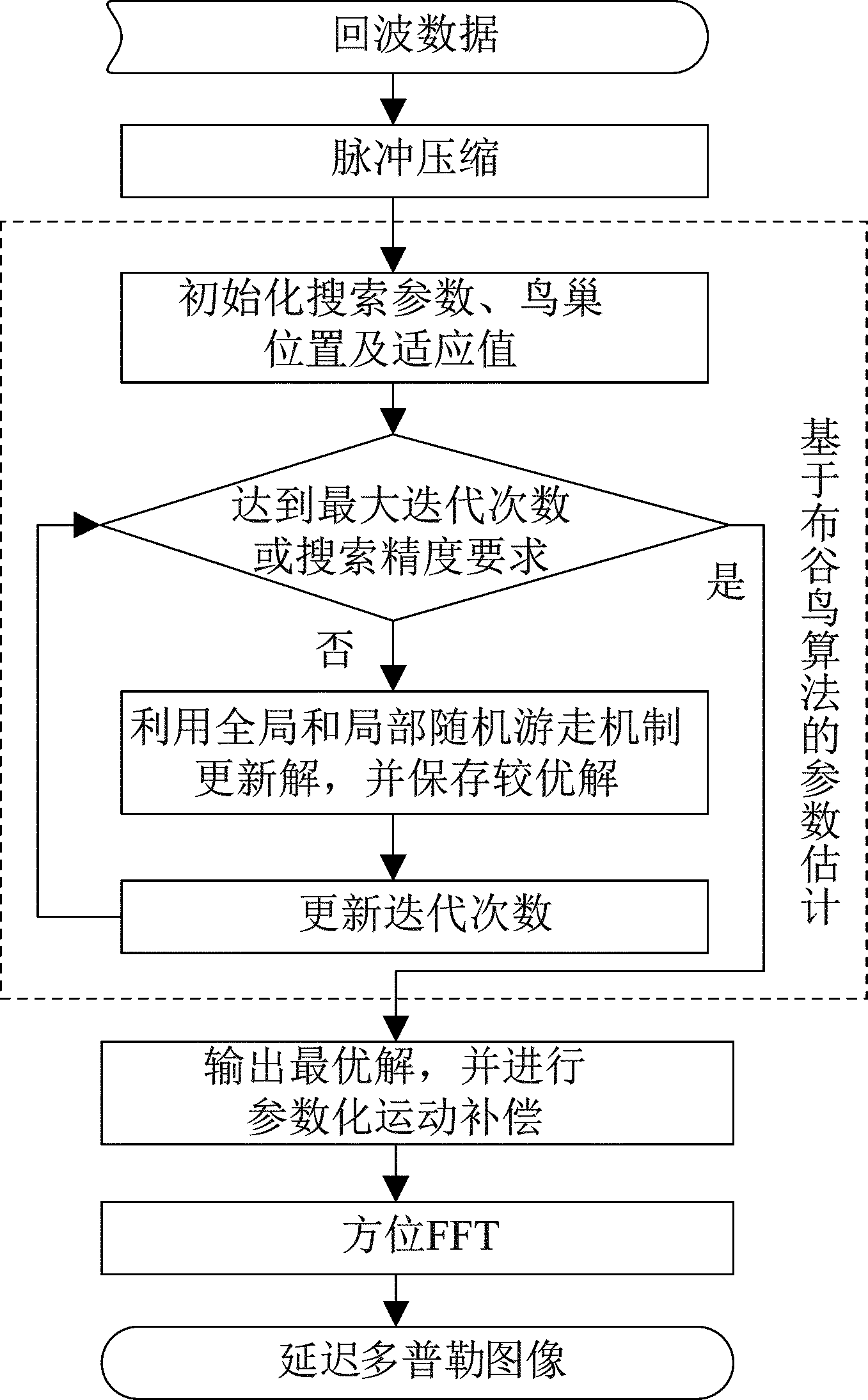
图7 基于参数化运动补偿的延迟多普勒算法流程图
Fig.7 Flow chart of delay Doppler algorithm based on parametric motion compensation
为了验证上述算法,本节开展点目标延迟多普勒成像仿真。点目标位置分布如图8所示。
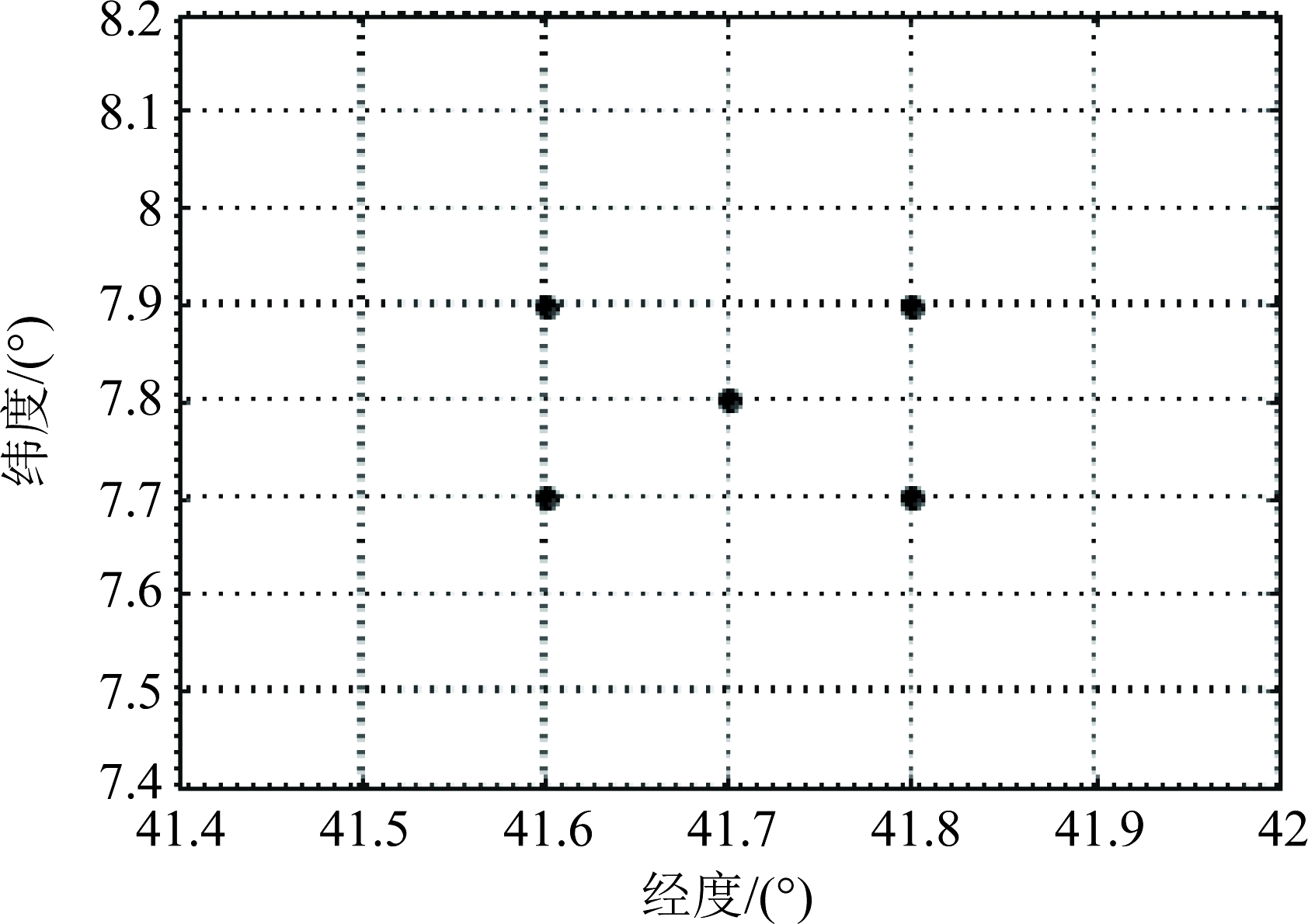
图8 点目标位置分布
Fig.8 Location distribution of point targets
在确定仿真场景后,需要进行系统参数设计。首先确定成像的分辨率指标,然后根据分辨率计算信号带宽和合成孔径时间,根据无模糊要求选择合适的脉冲重复频率,具体仿真参数如表1所示。场景的斜距历程从卫星工具箱(satellite tool kit,STK)中导出。
表1 仿真参数
Tab.1 Simulation parameters
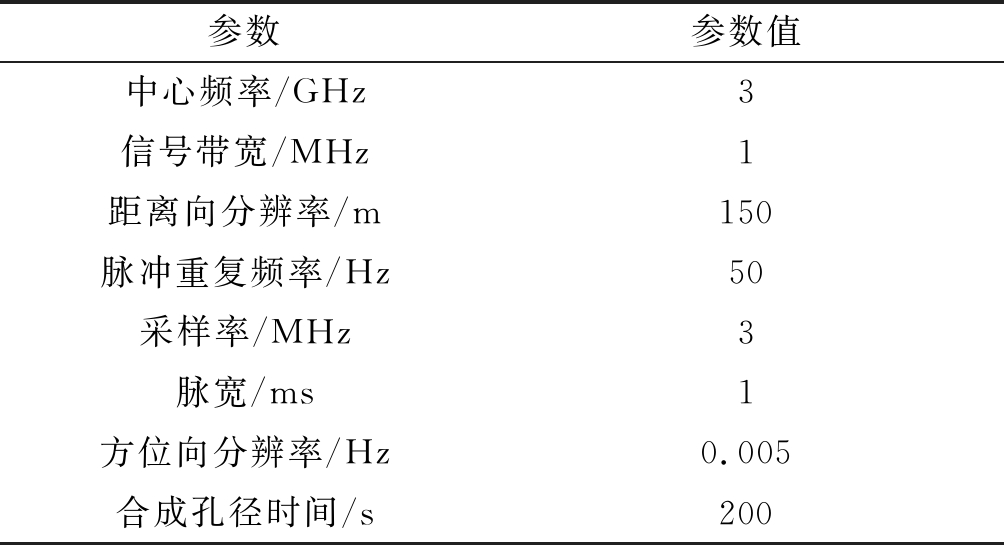
参数参数值中心频率/GHz3信号带宽/MHz1距离向分辨率/m150脉冲重复频率/Hz50采样率/MHz3脉宽/ms1方位向分辨率/Hz0.005合成孔径时间/s200
为了使仿真更加真实,需要考虑天体回波的信噪比,这里以GSSR的系统参数[20]为参考,具体参数如表2所示,经测算回波信噪比约为-30 dB。
表2 GSSR系统参数
Tab.2 GSSR system parameters
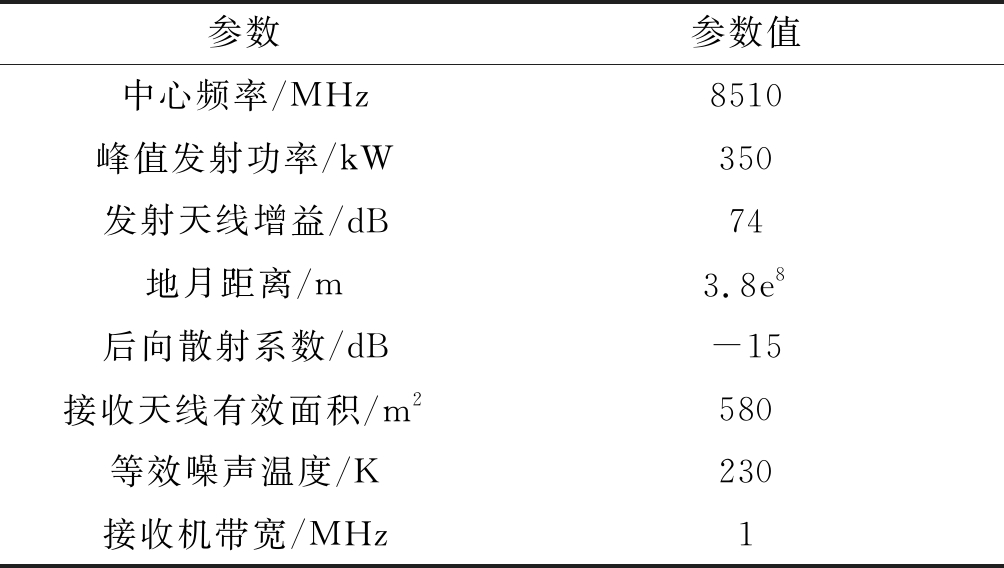
参数参数值中心频率/MHz8510峰值发射功率/kW350发射天线增益/dB74地月距离/m3.8e8后向散射系数/dB-15接收天线有效面积/m2580等效噪声温度/K230接收机带宽/MHz1
根据系统仿真参数开展点回波仿真,原始回波结果如图9(a)所示,天体散射信号已经被噪声淹没,经过脉冲压缩、运动补偿以及方位FFT后可以获得二维图像,如图9(b)所示,经测算图像信噪比可达40 dB。结果显示点目标聚焦效果良好,且各点具有不同的时延和多普勒频移信息。
为了评估所提算法的有效性,图10给出了参数化补偿前后中心点目标的脉冲响应,评估指标如表3所示。传统方法直接利用星历信息进行补偿,忽略了非理想因素带来的运动误差,从而导致点目标的分辨率、峰值旁瓣比和积分旁瓣比等指标在方位向上恶化。经过参数化运动补偿后,点目标聚焦效果明显改善,从而验证了所提算法的有效性。
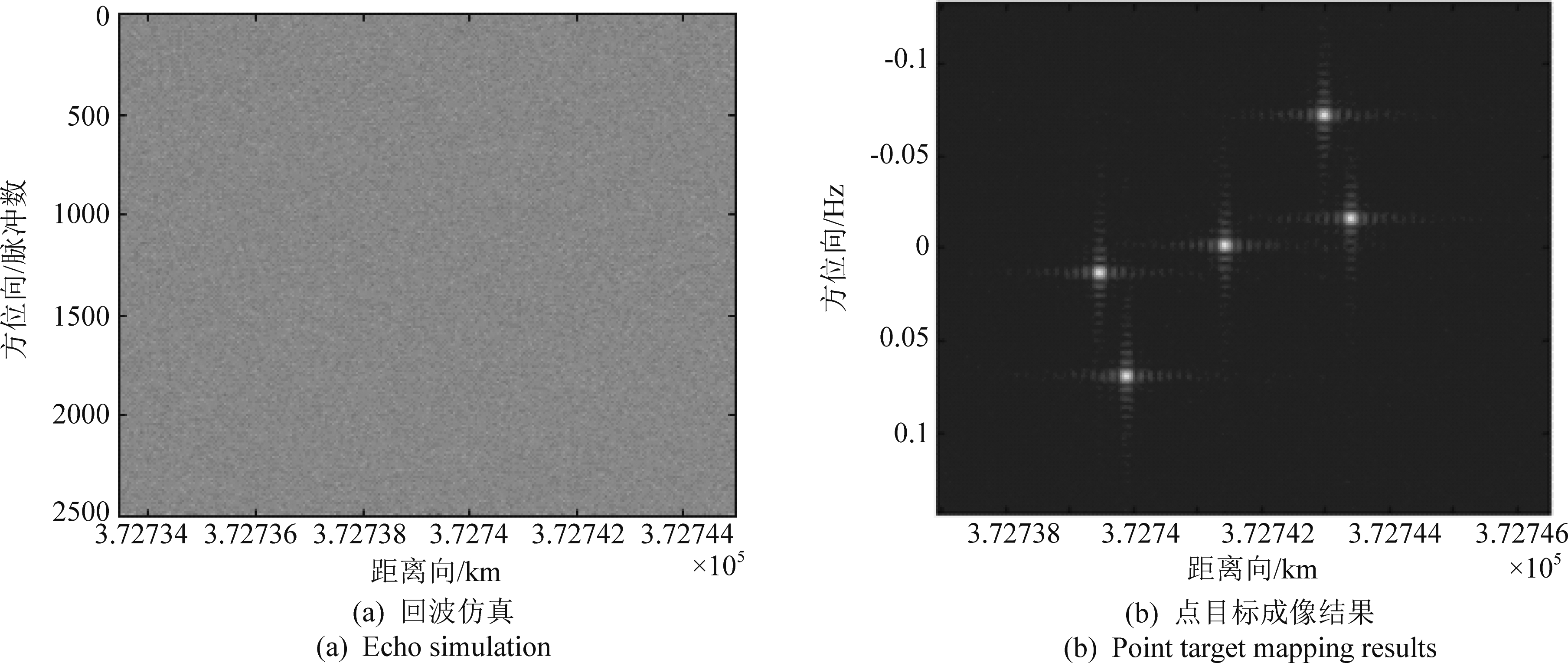
图9 延迟多普勒成像结果
Fig.9 Delay Doppler mapping results
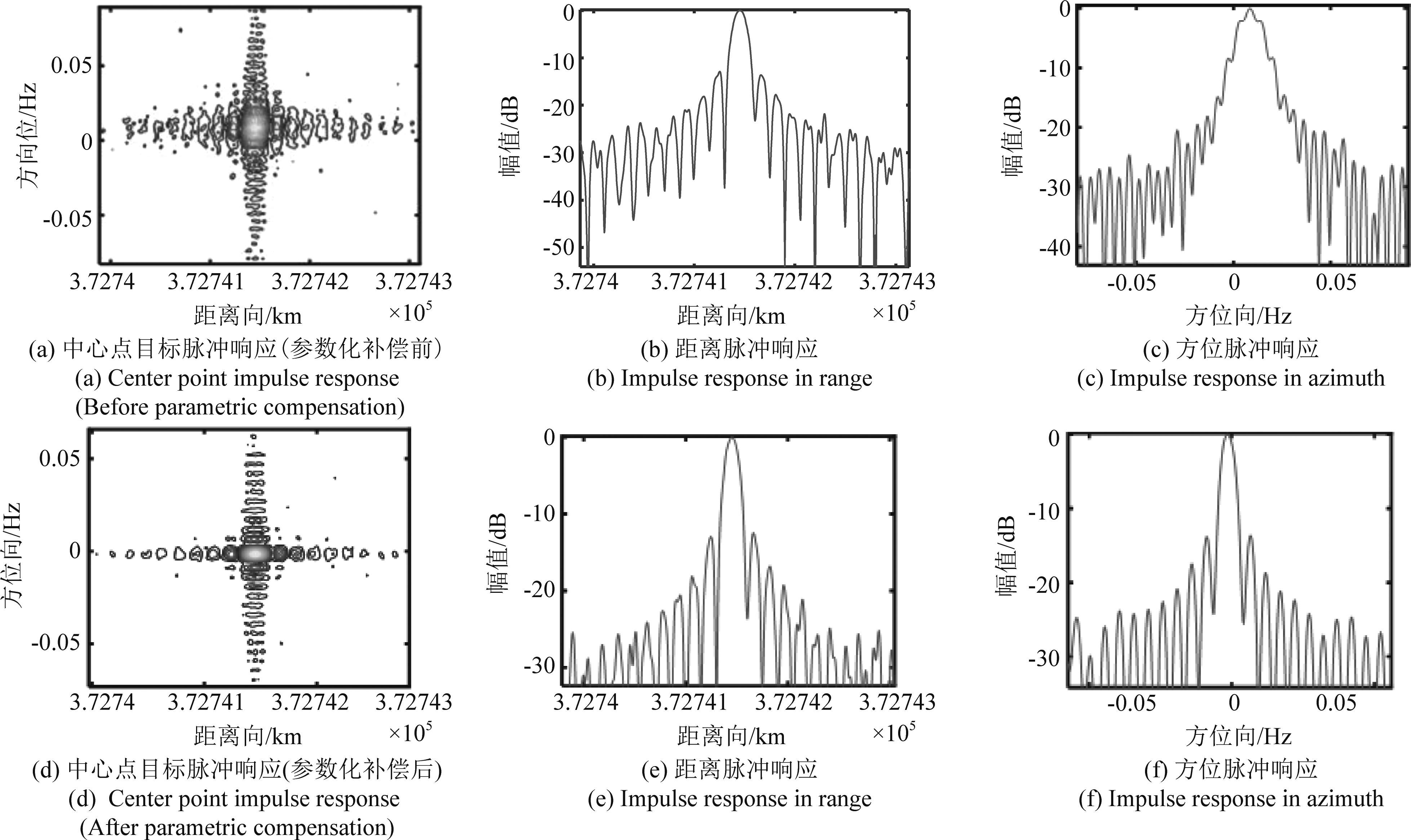
图10 中心点目标脉冲响应
Fig.10 Center point target impulse response
表3 中心点目标评估指标(未加窗)
Tab.3 Center point target evaluation index (without window)
分辨率距离/m方位/HzPSLR/dB距离方位ISLR/dB距离方位参数化补偿前1500.0143-12.86-8.39-9.690.02参数化补偿后1500.0049-13.63-13.27-9.80-9.27
为了评估算法的计算复杂度,表4给出了不同迭代次数和鸟巢数下的仿真结果,其中采样点数和脉冲数保持一致,结果显示,仿真运行时间和迭代次数以及鸟巢数成正比,与第3.2小节中的算法复杂度分析一致。
表4 计算复杂度评估
Tab.4 Computational complexity evaluation
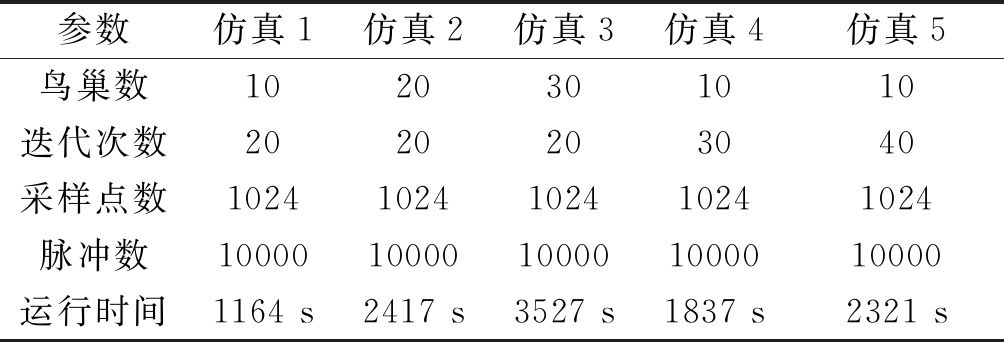
参数仿真1仿真2仿真3仿真4仿真5鸟巢数1020301010迭代次数2020203040采样点数10241024102410241024脉冲数1000010000100001000010000运行时间1164 s2417 s3527 s1837 s2321 s
为了进一步验证所提算法在地基雷达对月成像中的可行性,开展了月表的面目标成像仿真。场景选取月面的第谷陨石坑(西经6°～16°,南纬39°～47°),其高程模型如图11所示,陨石坑呈现出中间低、四周高的陡峭地形。
图11 面目标场景设置
Fig.11 Area target scene settings
图12 面目标成像结果
Fig.12 Area target mapping results
面目标仿真参数参照表1,面目标延迟多普勒成像结果如图12所示,显而易见,延迟多普勒成像的结果和第谷陨石坑的场景是匹配的。
本文针对地基雷达对月成像技术中的关键问题开展了研究。首先,基于地月运动几何模型分析了延迟多普勒技术的关键问题,包括成像原理、分辨率、模糊问题。其次,提出了一种参数化运动补偿算法,该方法基于图像最小熵与布谷鸟搜索算法,实现了对月成像中运动的快速参数搜索与补偿。最后,通过点目标和面目标的仿真结果,验证了所提算法的有效性,为后续开展试验验证奠定了基础。
[1] DEWITT J H, STODOLA E K. Detection of Radio Signals Reflected from the Moon[J]. Proceedings of the IRE, 1949, 37 (3): 229-242.
[2] ZISK S H, PETTENGILL G H, CATUNA G W. High-resolution radar maps of the lunar surface at 3.8-cm wavelength[J]. Moon, 1974, 10(1): 17-50.
[3] THOMPSON T W. Atlas of lunar radar maps at 70-cm wavelength[J]. Moon, 1974, 10(1): 51- 85.
[4] HENSLEY S, et al. An improved map of the lunar south pole with earth based radar interferometry[C]∥2008 IEEE Radar Conference, Rome, 2008: 1- 6.
[5] PATTERSON G W, STICKLE A M, TURNER F S, et al. Bistatic radar observations of the Moon using Mini-RF on LRO and the Arecibo Observatory[J]. Icarus, 2017, 283: 2-19.
[6] VIERINEN J, TVEITO T, GUSTAVSSON B, et al. Radar images of the Moon at 6-meter wavelength[J]. Icarus, 2017, 297: 179-188.
[7] 郑磊, 苏彦, 郑永春, 等. 地基雷达技术及其在太阳系天体探测中的应用[J]. 天文学进展, 2009, 27(4): 373-382.
ZHENG Lei, SU Yan, ZHENG Yongchun, et al. Earth-based radar technology and its application in the detection of celestial bodies in the solar system [J]. Progress in Astronomy, 2009, 27(4): 373-382.(in Chinese)
[8] 郑磊. 地基雷达对月成像数据处理方法研究[D]. 北京: 中国科学院, 2011.
ZHENG Lei. Research on processing method of earth-based radar mapping data for the moon [D]. Beijing: Chinese Academy of Sciences, 2011.(in Chinese)
[9] 李德伟, 江利明, 蒋厚军. GSSR成像雷达应用进展及其对我国深空探测的启示[J]. 遥感技术与应用, 2018, 33(3): 377-386.
LI Dewei, JIANG Liming, JIANG Houjun. Application progress of GSSR mapping radar and its enlightenment on deep space exploration in China [J]. Remote Sensing Technology and Application, 2018, 33(3): 377-386.(in Chinese)
[10] SUN Jing, PING Jinsong, BONDARENKO Y, et al. Promoting Earth-Based Radar Astronomical Observations of the Moon[J]. Sensors, 2020, 20(7): 1874.
[11] HARMON J K. Planetary delay-Doppler radar and the long-code method[J]. IEEE Transactions on Geoscience and Remote Sensing, 2002, 40(9): 1904-1916.
[12] STACY N J S. High-resolution synthetic aperture radar observations of the moon[D]. Ithaca: Cornell University, 1993.
[13] THOMPSON T W. A review of earth-based radar mapping of the moon[J]. Moon & the Planets, 1979, 20(2): 179-198.
[14] BROWN W M, FREDRICKS R J. Range-Doppler Imaging with Motion through Resolution Cells[J]. IEEE Transactions on Aerospace and Electronic Systems, 1969, 5(1): 98-102.
[15] THOMPSON T W. Map of lunar radar reflectivity at 7.5-m wavelength[J]. Icarus, 1970, 13(3): 363-370.
[16] LIU Lei, ZHOU Feng, TAO Mingliang, et al. Adaptive Translational Motion Compensation Method for ISAR Imaging Under Low SNR Based on Particle Swarm Optimization[J]. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2015, 8(11): 5146-5157.
[17] DING Zegang, ZHANG Tianyi, LI Yong, et al. A Ship ISAR Imaging Algorithm Based on Generalized Radon-Fourier Transform With Low SNR[J]. IEEE Transactions on Geoence and Remote Sensing, 2019, 57(9): 6385- 6396.
[18] AUSHERMAN D A, KOZMA A, WALKER J L, et al. Developments in Radar Imaging[J]. IEEE Transactions on Aerospace and Electronic Systems, 1984, 20(4): 363- 400.
[19] YANG X S, DEB S. Cuckoo Search via Lévy flights[C]∥2009 World Congress on Nature & Biologically Inspired Computing, Coimbatore, 2009: 210-214.
[20] MARGOT J L, CAMPBELL D B, JURGENS R F, et al. Digital elevation models of the Moon from Earth-based radar interferometry[J]. IEEE Transactions on Geoence & Remote Sensing, 2000, 38(2): 1122-1133.
丁泽刚 男, 1980年生, 河南信阳人。博士, 北京理工大学研究员、博士生导师, 主要研究方向为新体制雷达成像原理、成像处理和图像信息提取。
E-mail: z.ding@bit.edu.cn
张光伟 男, 1996年生, 山东青岛人。北京理工大学信息与电子学院硕士研究生, 主要研究方向为地基雷达天文成像。
E-mail: zhangguangwei@bit.edu.cn
刘思源 女, 1996年生, 北京人。北京理工大学信息与电子学院硕士研究生, 主要研究方向为微弱信号检测和ISAR成像。
E-mail: siyuanliu_bit@sina.com
李 根 男, 1993年生, 河北保定人。北京理工大学信息与电子学院博士研究生, 主要研究方向为机载干涉合成孔径雷达成像与地基雷达天文成像。
E-mail: Reagan0914@163.com
王 岩 男, 1989年生, 河北沧州人。博士, 北京理工大学副研究员、硕士生导师, 主要研究方向为新体制雷达系统、成像、干涉和极化应用。
E-mail: yan_wang@bit.edu.cn
曾 涛 男, 1971年生, 天津人。工学博士, 北京理工大学研究员, 博士生导师, 主要研究方向为雷达系统、雷达信号处理和新体制雷达。
E-mail: zengtao@bit.edu.cn
龙 腾 男, 1968年生, 湖北黄冈人。北京理工大学教授, 博士生导师, 现任雷达技术研究所所长。主要研究方向为新体制雷达和实时信息处理。
E-mail: longteng@bit.edu.cn