Reference format: LI Wenji, REN Lixiang, FAN Huayu, et al. A Phase-Derived Velocity Measurement Method for Variable Pulse Repetition Interval Waveform under Low SNR[J]. Journal of Signal Processing, 2021, 37(2): 159-166. DOI: 10.16798/j.issn.1003- 0530.2021.02.001.
提高雷达精确测速能力有助于目标的探测与识别,在空间监视和精确制导中有着重要的研究意义[1]。此外,精确测量目标的速度和距离等信息有助于提高雷达对目标精细运动的刻画能力,进而提取目标微动特征[2-3]。
相推测速利用相邻帧回波相位变化测量目标速度,可以实现半波长量级的测量精度。相推测速起源于美国在上个世纪七十年代提出的基于窄带回波相位的游标测距技术。随后,两篇专利[4-5]进一步论证了采用相推测距方法实现微动参数估计的可行性。相比于窄带方法来说,宽带雷达能够有效的区分目标各个散射点,提供目标更加精细的信息,更加容易实现对目标精细运动的刻画。文献[6]介绍了宽带雷达的相推测量方法,并将其应用于微动特征提取。
相推测速主要的研究难点包括提取回波相位和解相位模糊。文献[7]介绍了基于宽带脉冲多普勒雷达的相推测速方法。文献[8]和文献[9]研究了基于线性调频信号和基于调频步进信号的高速目标相推测速模型。文献[10-11]分别介绍了基于宽带线性调频信号的去斜处理和匹配脉压处理的相推测量模型,但是其主要分析的是静止目标,当目标有速度时,其方法要求较高的速度补偿精度。此外,该方法对信噪比的要求比较高,很难满足实际应用需求。文献[12]虽然对信噪比要求比较低,但是其方法要求相邻帧距离变化小于四分之一波长,实际中目标运动很难满足该要求。
由于相位变化的周期性,从回波中提取到的相位为模糊相位,需要对其进行解模糊处理后才能用于相推测速。常用的单帧解模糊的方法对信噪比要求较高。文献[13]介绍了基于宽带步进频信号的相推测距和测速技术,可以较好的适用于实际场景,并提出了联合多帧解相位模糊的方法,该方法联合多帧回波相位共同求解模糊数,能够显著降低相推测速对信噪比的要求。但是,该方法要求不同帧回波脉冲重复周期相同,不适用于脉冲重复周期渐变的波形。此外,当脉压后信噪比小于10 dB时,该方法会失效。本文进一步研究了更低信噪比下的解相位模糊方法,并针对实际中目标跟踪过程脉冲重复周期渐变的情形,推导了相推测速模型。
本文主要安排如下:首先,建立了脉冲重复周期渐变波形的回波模型。然后,基于包络粗测速结果,提出了采用最小二乘方法估计目标加速度,进而提高包络测速精度。接着,提出了低信噪比条件下的回波相位提取值修正以及相位模糊数修正方法,并给出了低信噪比下相推测速方法的处理流程图。最后,通过仿真实验验证了本文方法的有效性。
为简化起见,以线性调频信号为例进行回波建模,并提取回波相位,对于其他类型的信号,本文所提方法也同样适用。雷达发射的大带宽线性调频信号可以表示为:
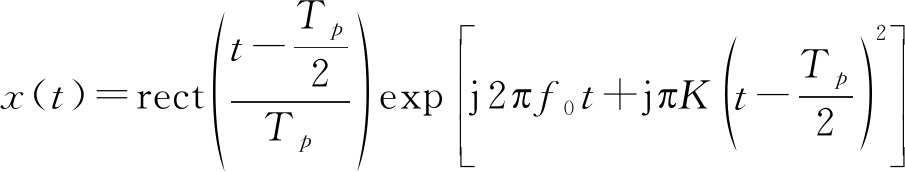
(1)
其中,
为脉冲宽度,K为线性调频信号的调频率,B=KTp为信号带宽, f0为载频。此外,考虑到发射信号的脉冲重复周期渐变,令Tn表示第n帧信号的脉冲重复周期。
假设目标沿着雷达视线方向运动,初始距离为R0,初始运动速度为ν0,远离雷达为正,靠近雷达为负。加速度为a,远离雷达为正,靠近雷达为负。忽略目标运动对回波信号脉内的影响,则对于第n帧信号目标相对雷达的距离和速度可以分别表示为:
(2)
(3)
忽略干扰和噪声的影响,雷达接收到的基带回波信号为:
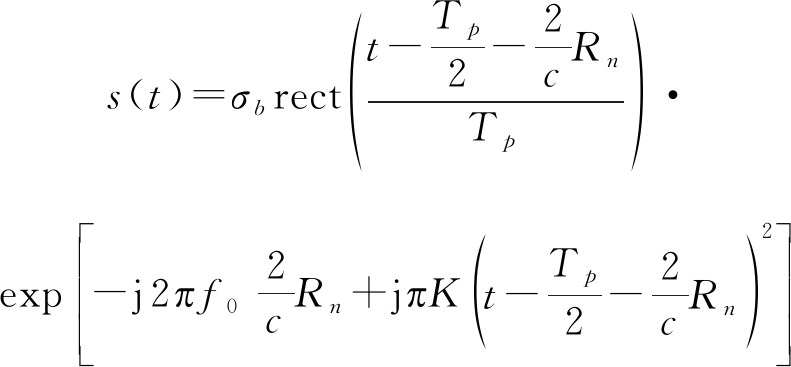
(4)
其中,σb为后向散射系数。
令σ′b表示脉压后的信号幅度,则匹配滤波处理后的脉压结果为:
(5)
假设目标具有单一强散射点,则可直接提取相邻帧高分辨一维距离像峰值点处的时延值。否则可参考文献[2]采用基于距离像互相关的相推测速方法。波形分析法利用回波脉冲波形的采样点幅度信息,通过求回波脉冲面积中心线的位置来精确测量目标的距离值[14-15]。根据式(5),利用波形分析法可得第n帧信号的峰值点处时延为:
(6)
对相邻帧回波时延相减,可得:
(7)
进一步计算化简如下:
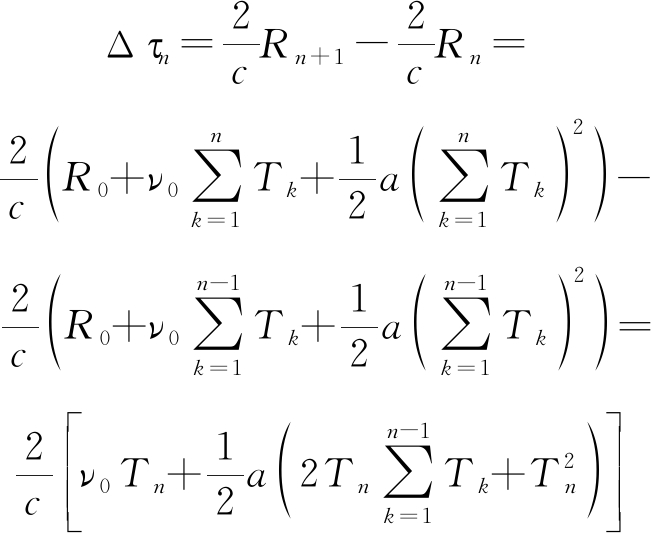
(8)
分析上式可以发现,相邻帧回波时延增量反映的是目标的距离增量信息。如果目标加速度为零时,可直接根据上式求解出目标的速度。当目标加速度不为零时,此时根据两帧的回波时延相减结果无法同时求解出速度和加速度。因此,此处提出了采用最小二乘估计方法结合多帧回波时延相减结果同时估计加速度和速度的方法。
假设总共有N帧回波,这样相邻帧回波时延相减可以得到N-1个时延增量的测量值,即可以测量得到Δτn,n=1,2,…,N-1。令
考虑如下最值问题:
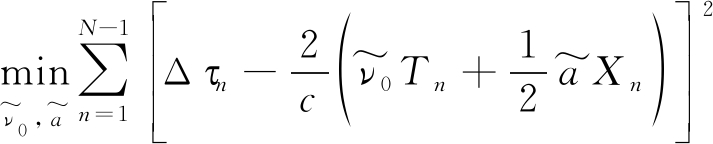
(9)
采用最小二乘估计的方法求解可得:
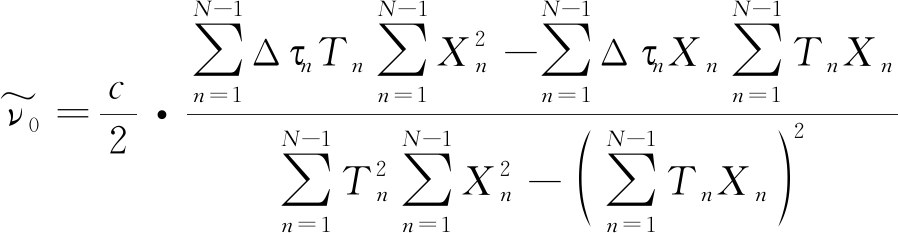
(10)
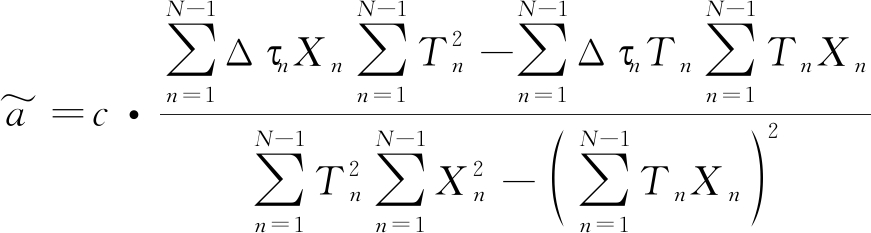
(11)
通过上面的方法即可得到目标初始运动速度和加速度的估计结果。
根据初始速度和加速度可以进一步得到发射不同帧回波时刻的目标速度精确测量结果。假设加速度粗测量结果用
表示,则可以得到不同帧的速度包络测量结果:
(12)
分析式(5)峰值点处的相位项:
(13)
同样,对相邻帧回波的相位相减,可得:
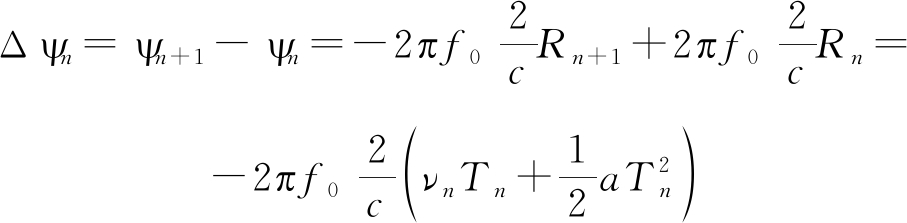
(14)
式(14)中,目标加速度值可使用包络测量的结果,这样根据式(14)便可以得到目标的相推测速结果:
(15)
需要指出的是,相推测速的关键是对相位解模糊。从一维距离像中直接提取出来的相位是模糊相位,不能直接用于求解目标速度。假设Δφ表示直接提取的模糊相位,Δψ表示经过解模糊后的精确相位,它们存在如下的制约关系:
Δψ=2πk+Δφ
(16)
其中,k代表模糊数。
由于提取到的模糊相位在-π rad到π rad之间,因此速度测量结果也会存在模糊,相应的模糊速度可以计算为:
(17)
常用的解相位模糊方法为单帧解模糊法。其实现方法如下:根据3.1节包络测量的速度结果,可以计算出相应地解模糊后的粗相位,表示为Δψ ′。模糊数可以按如下方式求得:
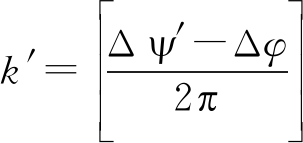
(18)
其中[·]表示取整运算。最终,解模糊后的相位可以按下式求出:
Δψ ″=2πk′+Δφ
(19)
根据文献[13],利用包络测量速度和利用相位测速的克拉美罗界(CRLB)可以表示如下:
(20)
(21)
其中,Tr表示脉冲重复周期,λ表示波长,β表示信号的均方根带宽,SNR表示的是一维高分辨距离像的信噪比。
采用包络测量的速度结果解相位模糊,该方法要求包络测量的速度转换为测相精度(1σ)后要小于π/3 rad,则测量误差(3σ)可以控制在π rad范围内。因此式(20)需满足:
(22)
即SNR需要满足:
(23)
由上式可知,相推测量对信噪比要求较高。对于低信噪比情况下,一般可以采用联合多帧解相位模糊的方法,该方法联合多帧回波相位共同求解模糊数,能够显著降低相推测速对信噪比的要求[13]。但是,该方法要求不同帧回波脉冲重复周期相同,不适用于脉冲重复周期渐变的波形。此外,当脉压后的信噪比小于10 dB时,该方法将不再适用。本文提出了更低信噪比下的解相位模糊的算法。
当信噪比比较低时,传统的相推方法测量精度将会严重恶化。低信噪比导致测量结果恶化的原因主要体现在两方面:一方面,低信噪比会导致回波峰值点处位置估计不准确,从而无法提取出回波相位;另一方面,低信噪比会导致包络测量结果变差,从而无法满足解相位模糊的精度要求。
针对回波峰值点处时延值估计和相位提取不准确问题,本文所提方法首先采用波形分析法得到峰值点处时延值,然后在剔除野值之后对时延值进行拟合,得到拟合的估计值。后续的包络测速和回波相位提取均可采用时延值的拟合结果。
针对包络测量结果无法满足解相位模糊精度要求的问题,本文提出逐帧遍历相位模糊数的方法。由文献[13],正确解模糊的条件要求平均包络测速误差小于νam/2。若允许模糊数求解结果出现±l的偏差,则会将正确解模糊的条件放宽为:平均包络测速误差小于νam/2+l·νam。在实际问题中,一般l取1或2即可。然后,可以根据均方根误差最小的原则,逐帧修正模糊数,进而得到相推测速结果。
假设基于包络测速解相推测速模糊的结果为
相位模糊数为
模糊数修正遍历的矩阵为L。一般情况下,包络测量结果恶化不是很严重,所以L可取值[-2, -1, 0, 1, 2]。假设目标处于被跟踪状态,且存在信噪比较高的部分数据,则可以将较高信噪比条件下的相推测速结果作为低信噪比数据的相位解模糊参考值。本文所提低信噪比条件下的相位模糊数修正方法如下:
1)对第m帧回波,提取到的模糊相位为Δφm,采用单帧解模糊得到的模糊数为
2)对L中的每个值进行遍历,假设修正值为l,则修正后的模糊数为
3)修正后的解模糊相位为:
由式(15)可以得到修正后的相推测速结果。
4)对前m帧的数据进行拟合,并计算出前m帧的相推测速均方根起伏误差。
5)重复第2步到第4步,遍历L中的每个值,得到不同修正值下的均方根起伏误差。
6)找出最小均方根起伏误差对应的模糊数,此即为相位模糊数修正值,记为l*。
7)经模糊数修正后的相位为:
由式(15)得到修正后的相推测速结果。
8)重复第1步到第7步,遍历所有的回波数据,即可得到对模糊数修正后的相推测速结果。
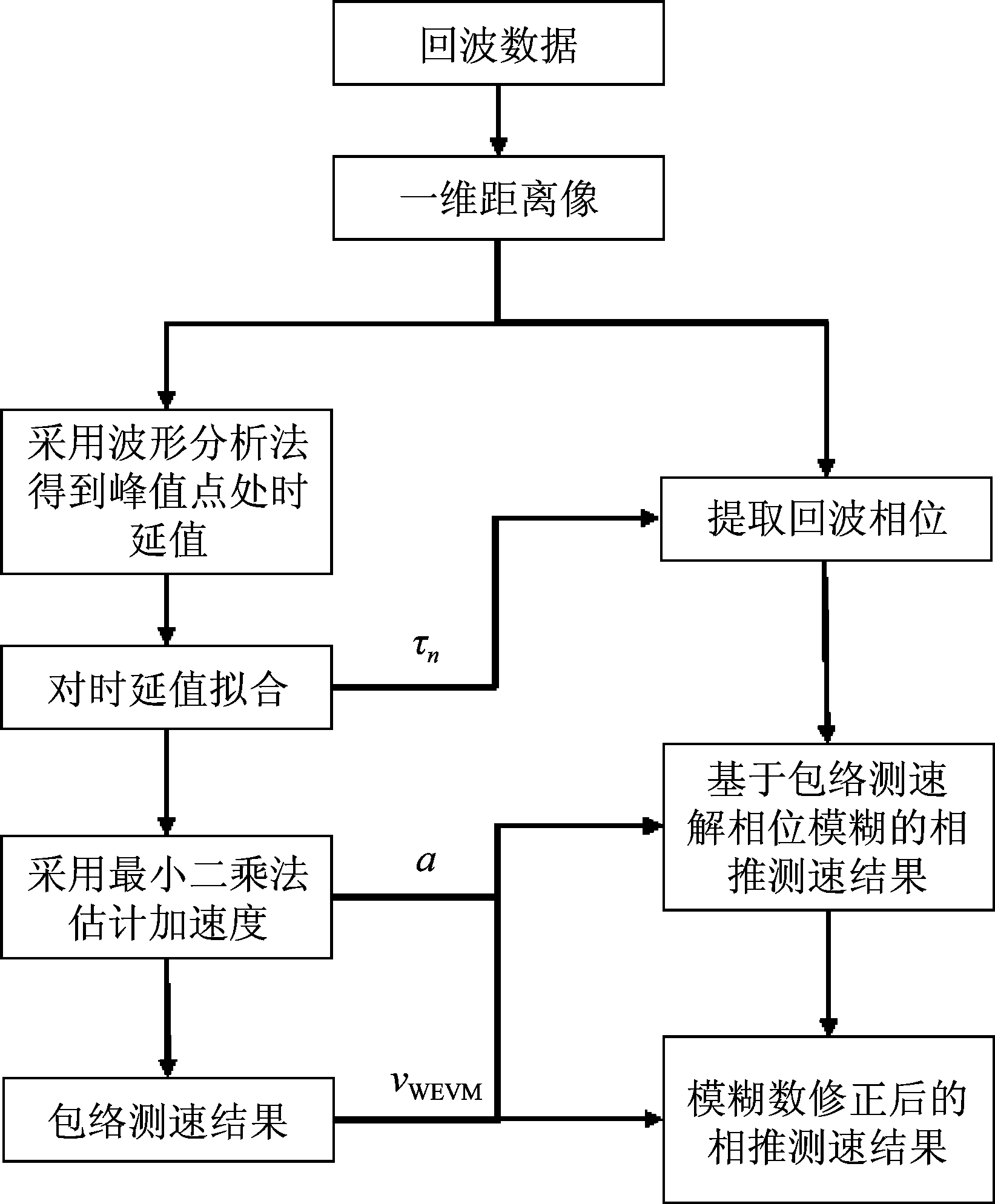
图1 低信噪比下的相推测速流程图
Fig.1 Flow chart of phase-derived velocity measurement method under low SNR
低信噪比条件下的相推测速实现方法流程图如图1所示。首先,在对回波数据脉压得到一维距离像之后,采用波形分析法得到时延估计值,并对时延估计结果进行拟合处理。拟合处理能够辅助剔除野值,并减小噪声对参数估计精度的影响,从而提高包络测速精度和回波相位提取准确度。然后,采用3.1节所述的最小二乘方法,可以获得高精度的加速度估计结果和包络测速结果。接着,利用加速度估计值和包络测速结果实现相推测速处理。最后,采用本文所提的相位模糊数修正方法,修正低信噪比条件下的相推测速结果。
下面通过仿真验证本文所提方法在低信噪比条件下的高精度测速性能。假设目标沿着雷达径向匀加速运动。目标初始距离为10 km,速度为100 m/s,加速度为50 m/s2。雷达参数如表1所示。
表1 雷达参数
Tab.1 Radar parameters
参数取值载频3 GHz带宽200 MHz采样频率300 MHz脉宽100 μs脉冲重复周期1～10帧 3 ms11～50帧 5 ms51～100帧 10 ms
考虑到目标运动越来越远,仿真中设置脉冲重复周期逐渐增加,同时信噪比逐渐减小。仿真产生100帧回波:第1～10帧脉冲重复周期为3 ms,其脉压后的信噪比为20 dB;第11～50帧脉冲重复周期为5 ms,其脉压后的信噪比为12 dB;第51～100帧脉冲重复周期为10 ms,其脉压后的信噪比为5 dB。
不同帧回波数据脉压后的结果如图2所示。由图可知,前面几帧信噪比比较高时,目标运动轨迹比较明显;而后面信噪比较低时,目标轨迹完全淹没在噪声里。但是可以根据前面高信噪比下的目标轨迹推测出后面低信噪比下的目标轨迹的大致位置。
图3给出了一维距离像峰值点处时延位置的提取结果。其中蓝色圆圈代表采用波形分析法得到的测量值,绿色点虚线代表剔除野值后的拟合值,红色实线代表真实值。由图3可知,高信噪比时测量值与真实值基本吻合,低信噪比时测量值存在很大的偏差。在低信噪比区域,剔除野值后对测量值进行拟合的结果可以很好的逼近真实值。将野值数据用拟合值代替,图4给出了平滑滤波后的峰值点位置。平滑滤波可以有效的提高提取的峰值点位置准确度,而准确的得到峰值点位置是后面包络测速和相推测速的前提条件。
图2 不同帧回波数据脉压结果
Fig.2 Results of echo data among different frames after pulse compression
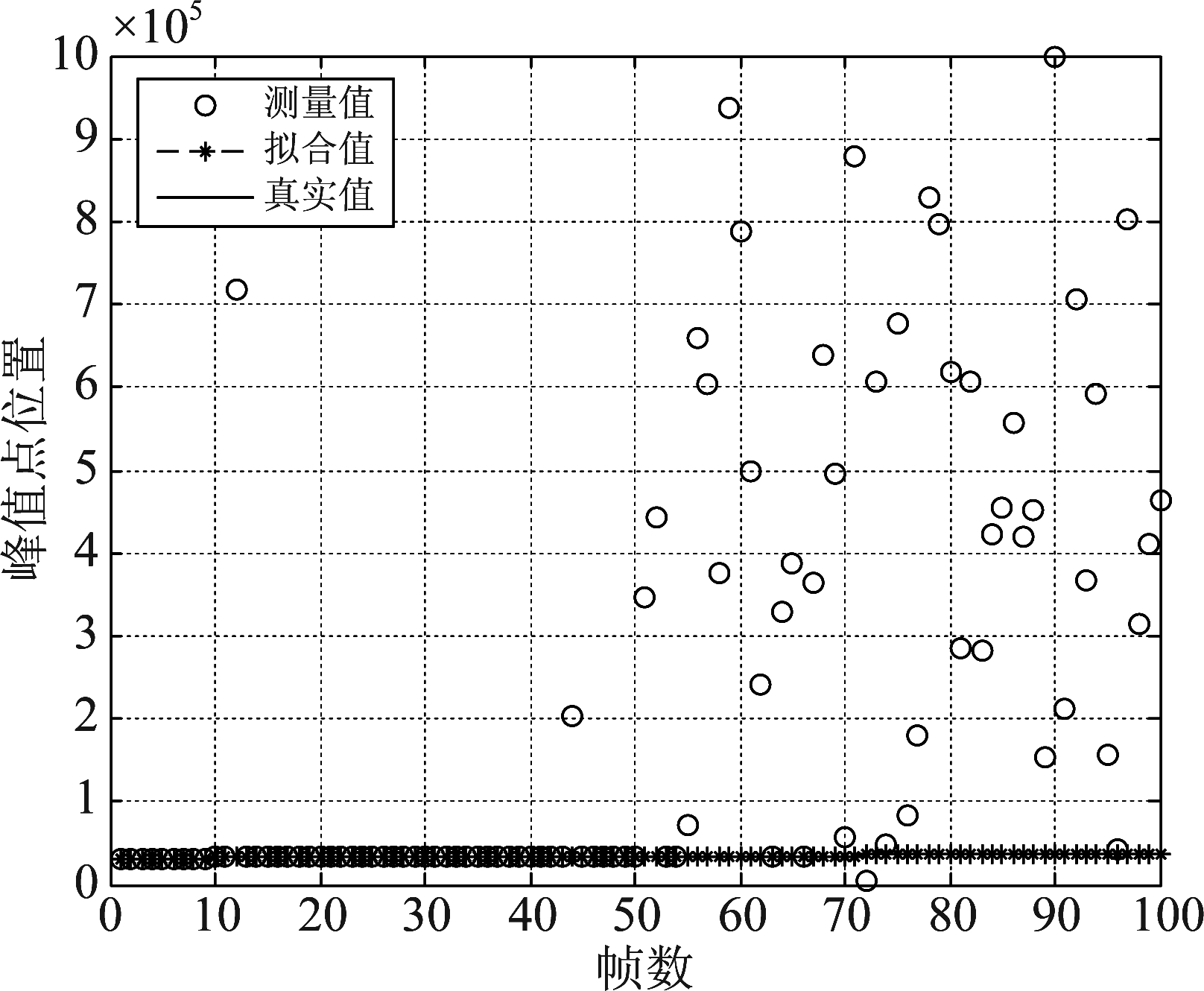
图3 一维距离像的峰值点位置
Fig.3 Peak positions of the one-dimensional range profile
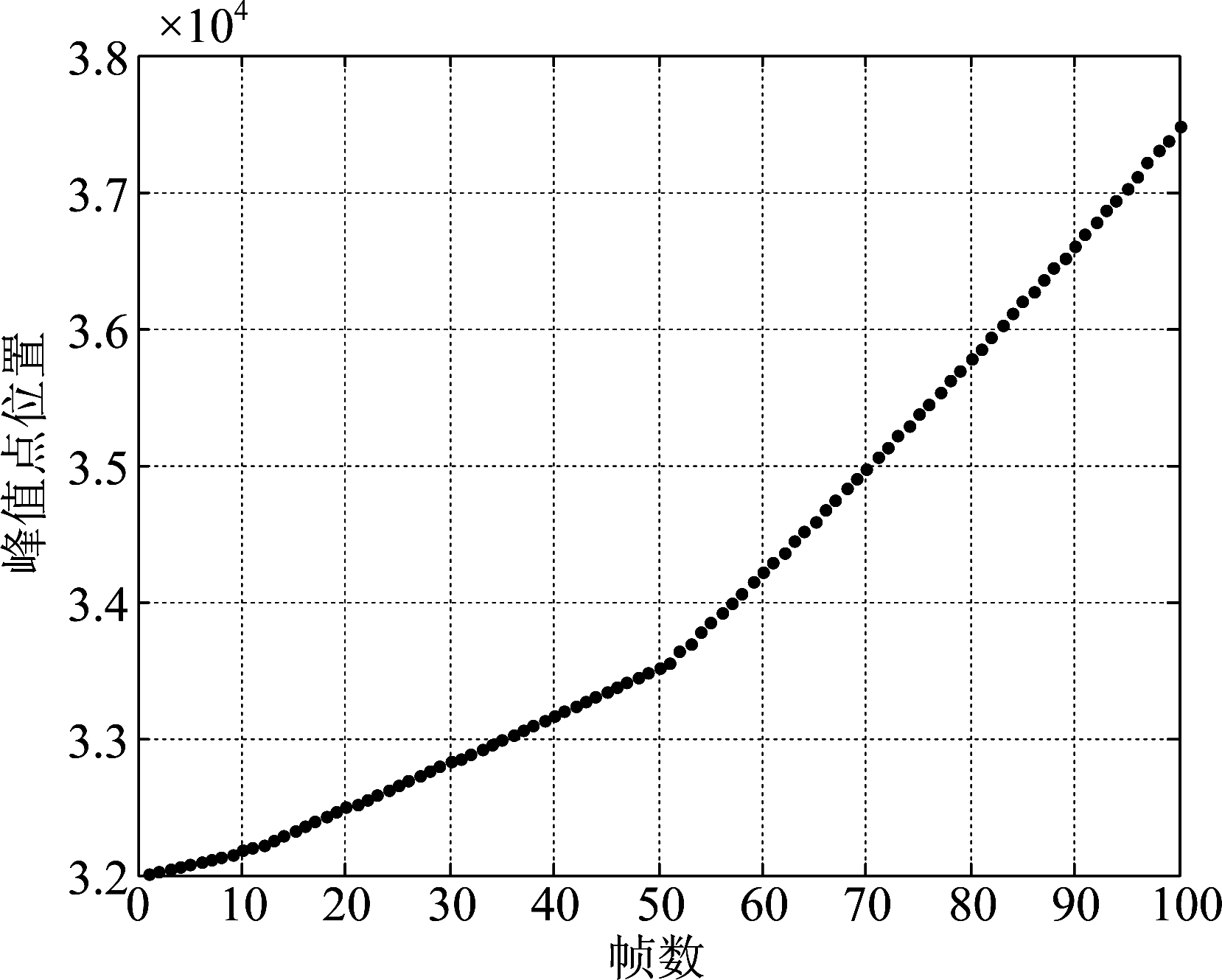
图4 平滑滤波后的峰值点位置
Fig.4 Peak positions after smooth filtering
根据求出的峰值点时延位置采用最小二乘法对初始速度和加速度进行粗估计。表2给出了估计结果,初始速度估计值为99.7253 m/s,加速度估计值为53.8393 m/s2,可知估计精度相对较高。因此加速度估计值可用于后续的包络测速和相推测速处理。
表2 最小二乘估计结果
Tab.2 The least square estimation results
初始速度加速度估计值99.7253 m/s53.8393 m/s2真实值100 m/s50 m/s2
图5和图6分别给出了包络测速结果和包络测速误差,其中图5的曲线含义同上,蓝色圆圈代表测量值,绿色点虚线代表拟合值,红色实线代表真实值。由图5可知,当信噪比较高时,包络测速结果相对准确,而当信噪比较低时,包络测速结果偏差较大。
图5 包络测速结果
Fig.5 Envelope velocity measurement result
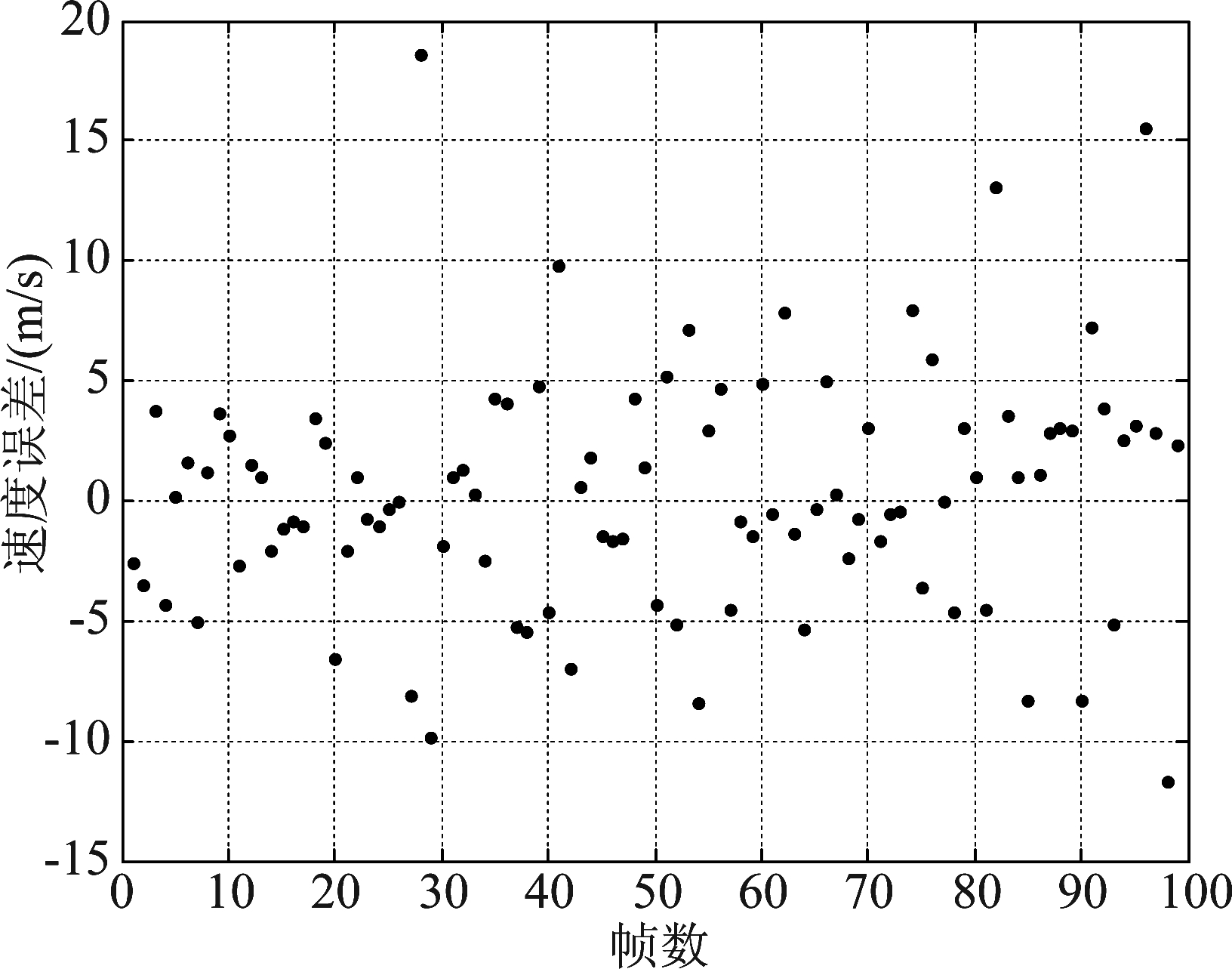
图6 包络测速误差
Fig.6 Envelope velocity measurement error
图7给出了采用包络测速解相位模糊时的相推测速误差。由于低信噪比时包络测速误差较大,导致相位解模糊出错,进而带来较大的相推测速误差。
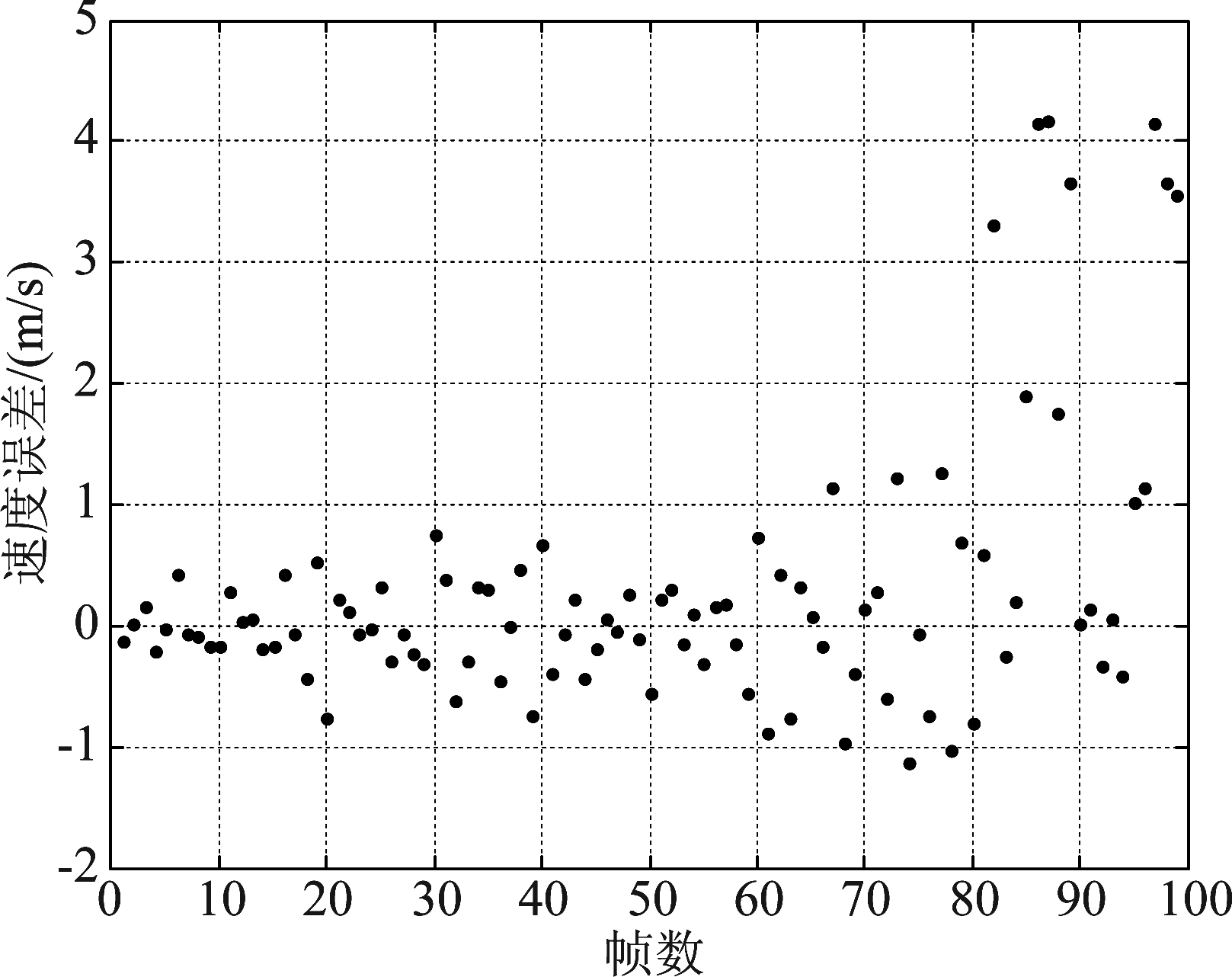
图7 相推测速误差
Fig.7 Phase-derived velocity measurement error
采用本文所提的相位模糊数修正方法之后,图8和图9分别给出了修正后的相推测速结果和相推测速误差。相比于图7,图9的相推测速误差变小,测量精度提高。表3分别给出了脉压后信噪比为
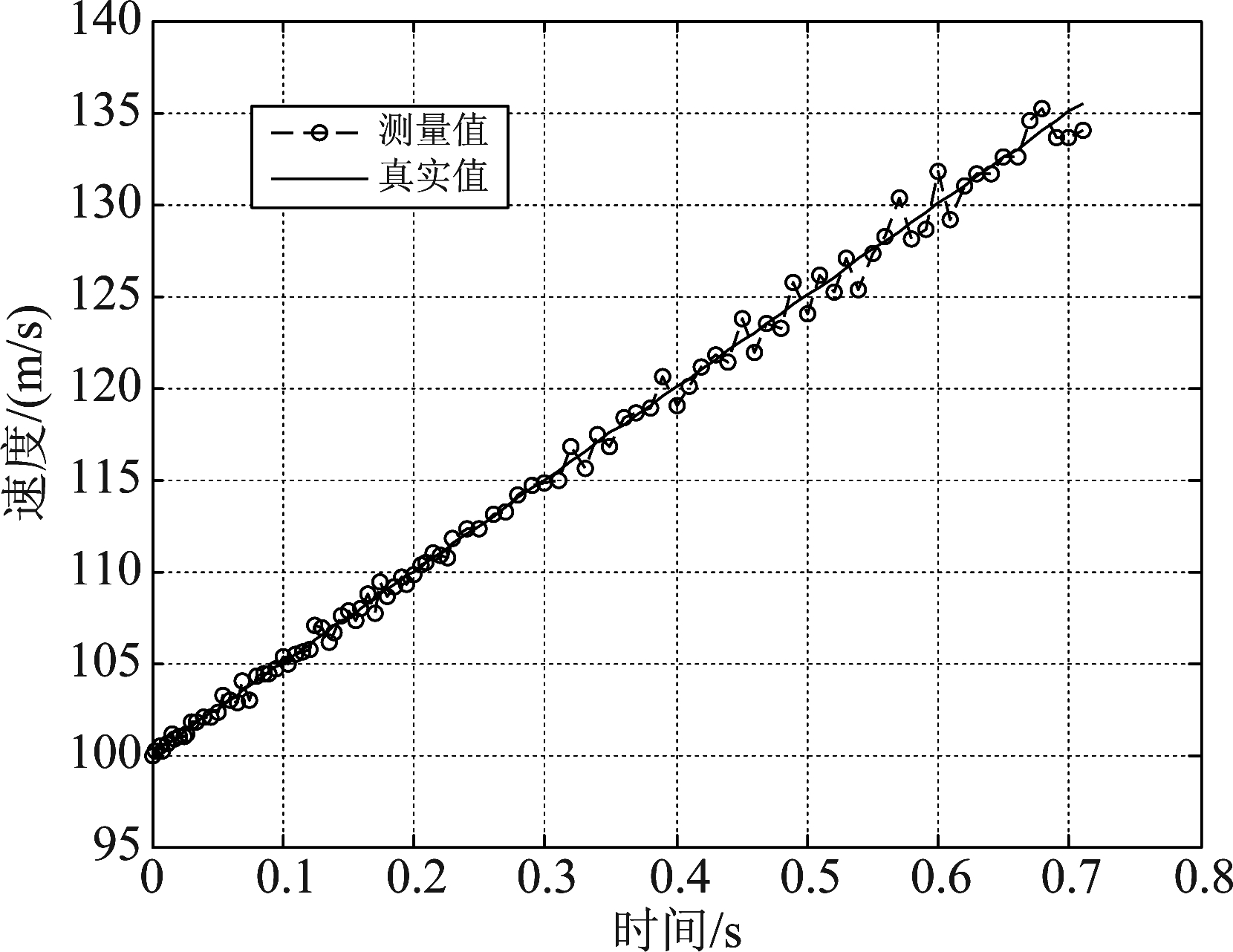
图8 模糊数修正后的相推测速结果
Fig.8 Phase-derived velocity measurement result after the ambiguity number correction
表3 相推测速结果
Tab.3 Phase-derived velocity measurement results
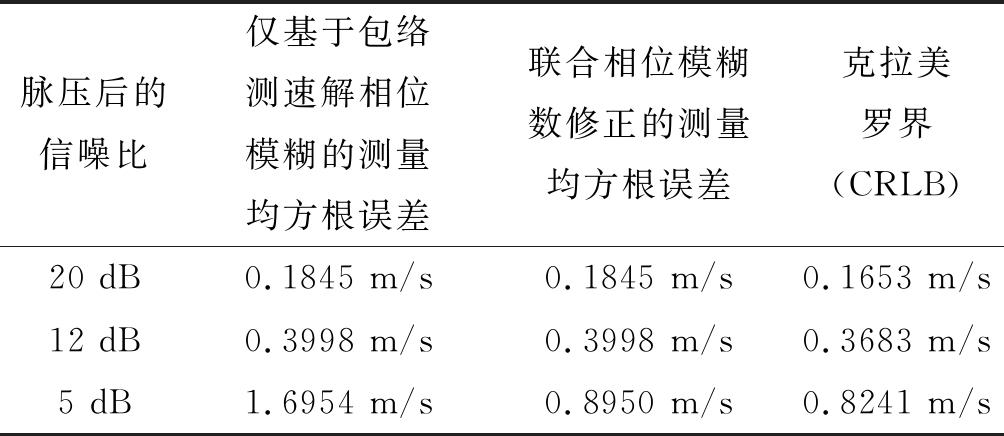
脉压后的信噪比仅基于包络测速解相位模糊的测量均方根误差联合相位模糊数修正的测量均方根误差克拉美罗界(CRLB)20 dB0.1845 m/s0.1845 m/s0.1653 m/s12 dB0.3998 m/s0.3998 m/s0.3683 m/s5 dB1.6954 m/s0.8950 m/s0.8241 m/s
20 dB、12 dB和5 dB时的测量结果的均方根误差和理论克拉美罗下界。其中克拉美罗界是根据式(21)计算得到。比较表中数据可知,测量结果与理论精度十分吻合,验证了本文所提方法在低信噪比下的高精度测速性能。
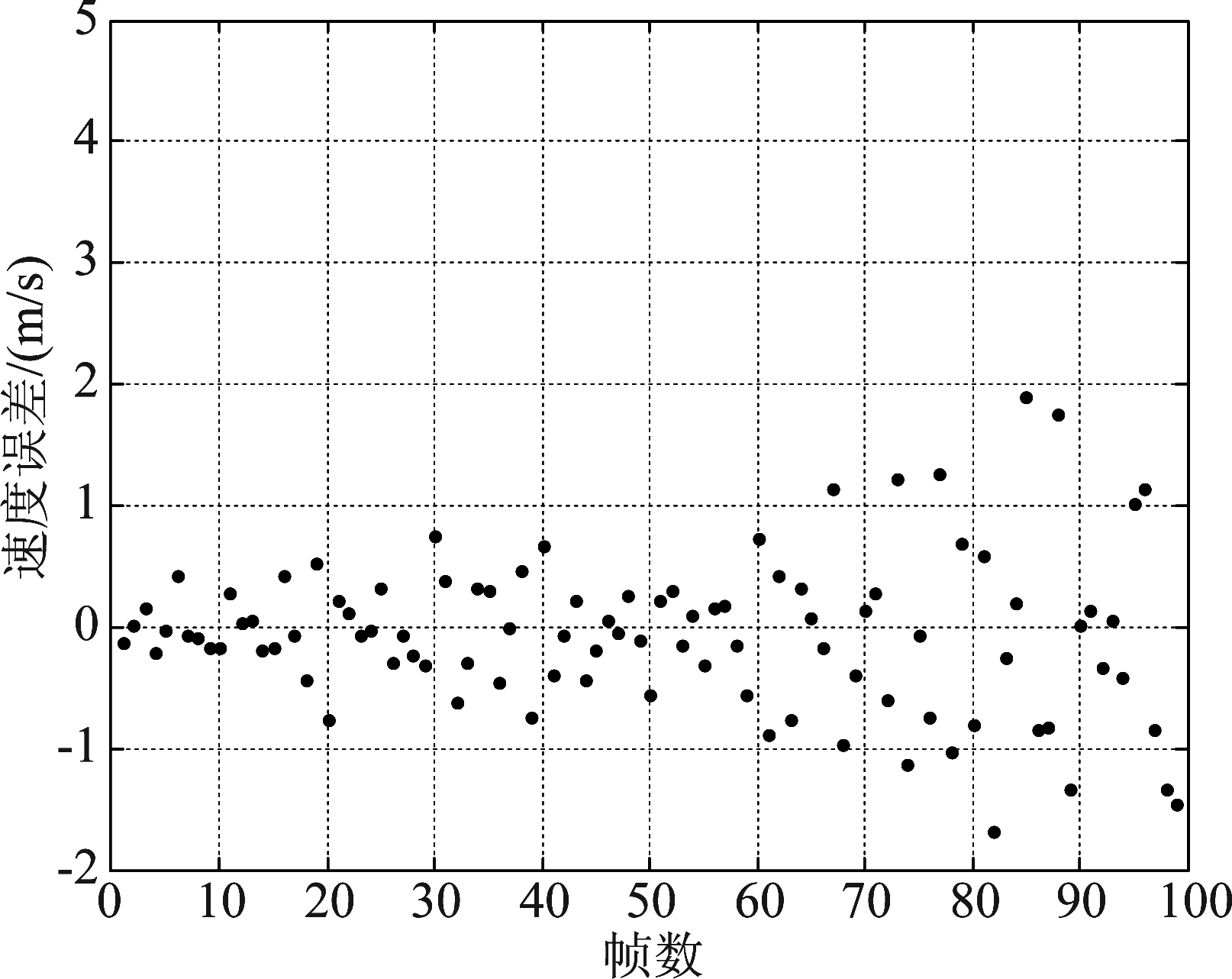
图9 模糊数修正后的相推测速误差
Fig.9 Phase-derived velocity measurement error after the ambiguity number correction
本文介绍了低信噪比条件下脉冲重复周期渐变波形的相推测速实现方法。首先,分析了脉冲重复周期渐变波形的回波相位,推导了相推测速模型;然后,针对相推测速在低信噪比条件下的相位解模糊难题,提出了回波相位提取值修正以及相位模糊数修正方法,所提方法综合利用了全部数据帧信息,因而能够有效降低相推测速对信噪比的要求。仿真结果表明,本文所提方法适用于部分数据信噪比低至5 dB的情况,验证了本文所提方法在低信噪比条件下的鲁棒性。
[1] LONG Teng, LIANG Zhennan, LIU Quanhua. Advanced technology of high-resolution radar: target detection, tracking, imaging, and recognition[J]. Science China Information Sciences, 2019, 62(4): 40301.
[2] LI Wenji, FAN Huayu, REN Lixiang, et al. Micromotion Feature Extraction Based on Phase-Derived Range and Velocity Measurement[J]. IEEE Access, 2019, 7: 114167-114182.
[3] 朱得糠, 刘永祥, 李康乐, 等. 基于雷达相位测距的微动特征获取[J]. 宇航学报, 2013, 34(4): 574-582.
ZHU Dekang, LIU Yongxiang, LI Kangle, et al. Feature Extraction for Target with Micro-Motion Based on Radar Phase Derived Range[J]. Journal of Astronautics, 2013, 34(4): 574-582.(in Chinese)
[4] STEUDEL F. An Improved Process for Phase-Derived-Range Measurements. World Intellectual Property Organization Patent, 1651978, 2005-2-24.
[5] STEUDEL F. Process for Phase-Derived-Range Measurements. U. S. Patent, 7046190, 2005-2-10.
[6] FAN Huayu, REN Lixiang, MAO Erke. A micro-motion measurement method based on wideband radar phase derived ranging[C]∥Proceedings of IET Radar Conference. Xi’an, China, 2013.
[7] FAN Huayu, REN Lixiang, LONG Teng, et al. A high-precision phase-derived range and velocity measurement method based on synthetic wideband pulse Doppler radar[J]. Sci China Inf Sci, 2017, 60(8): 082301.
[8] GUO Liyong, FAN Huayu, LIU Quanhua. A Novel High Accuracy Phase-derived Velocity Measurement Method for Fast Moving Space Target[J]. IEEE Geoscience and Remote Sensing Letters, 2019, 16(4): 529-533.
[9] LI Wenji, FAN Huayu, REN Lixiang, et al. A High-Accuracy Phase-Derived Velocity Measurement Method for High-Speed Spatial Targets Based on Stepped-Frequency Chirp Signals[J]. IEEE Transactions on Geoscience and Remote Sensing, to be published. DOI: 10.1109/TGRS.2020.3003039.
[10] LIU Yongxiang, ZHU Dekang, LI Xiang, et al. Micromotion Characteristic Acquisition Based on Wideband Radar Phase[J]. IEEE Transactions on Geoscience and Remote Sensing, 2014, 52(6): 3650-3657.
[11] ZHU Dekang, LIU Yongxiang, HUO Kai, et al. A Novel High-Precision Phase-Derived-Range Method for Direct Sampling LFM Radar[J]. IEEE Transactions on Geoscience and Remote Sensing, 2016, 54(2): 1131-1141.
[12] XIONG Xiangyu, DENG Zhenmiao, QI Wei, et al. A Novel High-Precision Range Estimation Method Based on Phase of Wideband Radar Echo[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(6): 3392-3403.
[13] FAN Huayu, REN Lixiang, MAO Erke, et al. A High-Precision Method of Phase-Derived Velocity Measurement and Its Application in Motion Compensation of ISAR Imaging[J]. IEEE Transactions on Geoscience and Remote Sensing, 2018, 56(1): 60-77.
[14] 田黎育, 高梅国. 距离-速度二维波形分析跟踪[J]. 现代雷达, 2002, 24(6): 39- 42.
TIAN Liyu, GAO Meiguo. A method for digital moving target tracking based on distance-speed two dimensions waveform analysis[J]. Modern Radar, 2002, 24(6): 39- 42.(in Chinese)
[15] 高梅国, 周冬友, 毛二可. 波形分析数字动目标跟踪技术[J]. 电子学报, 1998(12): 3-5.
GAO Meiguo, ZHOU Dongyou, MAO Erke. A method for digital moving target track based on waveform analysis[J]. Acta Electron. Sinica, 1998(12): 3-5.(in Chinese)
李文吉 男, 1996年生, 陕西西安人。北京理工大学雷达技术研究所博士研究生, 主要研究方向为宽带雷达信号处理、微动测量等。
E-mail: cubeescape@foxmail.com
任丽香(通信作者) 女, 1971年生, 河南焦作人。北京理工大学雷达技术研究所讲师, 主要研究方位为实时信号处理系统设计、宽带雷达信号处理等。
E-mail: lixiangr@bit.edu.cn
范花玉 女, 1989年生, 湖南邵阳人。北京理工大学雷达技术研究所预聘助理教授, 主要研究方向为宽带波形设计、宽带雷达信号处理、ISAR成像、微动测量等。
E-mail: fanhuayu@bit.edu.cn
毛二可 男, 1934年生, 内蒙古赤峰人。中国工程院院士, 北京理工大学雷达技术研究所教授, 博士研究生导师, 主要研究方向为雷达系统、数字信号处理等。
E-mail: maoerke@bit.edu.cn