1 引言
随着手机、数码相机等数字产品的日益普及，人们获取图像的手段越来越多样化。互联网的迅速发展，更加速了数字图像的广泛应用。人们可以非常方便地利用这些设备进行拍照，并且将其上传到微信空间、个人微博等。但同时我们也应该看到，随着计算机软件技术的迅速发展，图像编辑软件如Photoshop、ACDSee等的功能也日益强大，数字图像的篡改变得越来越容易。篡改图像若被用于新闻报导、科学研究、军事观察、以及法庭取证等领域，将会带来非常严重的后果，对经济文化的发展和社会稳定造成恶劣影响。
近年来，国内外在新闻、军事和科学等领域出现了一系列由于篡改图像而引发的恶劣事件。如在新闻领域，曾经入选影响2006年CCTV年度十大新闻图片的《藏羚羊生命中的十道难关——铁路关》摄影作品是被篡改过的假照片。该照片作者刘为强在事后接受媒体采访时承认照片中羚羊照片、火车照片是在同一地点但不同时刻拍摄的，为了追求“更具感染力”而将其合成在一起。在军事情报领域，伊朗革命卫队2008年网站发布了“导弹齐射”的图片。但之后《纽约时报》记者发现照片中同时发射升空的四枚导弹中，其中一枚为其他导弹复制粘贴而来。实际情况是有一枚导弹发射失败了，伊朗军方为掩饰事实对图片进行了修改。另外在科学研究领域，2005年韩国科学家Hwang Woo-Suk等人在著名的国际期刊《Science》发表了2篇关于干细胞的研究论文，其论文成果因具有开创性意义而引起了巨大轰动。但紧接着在2006年，作者Hwang Woo-Suk承认论文中展示的结果经过了人为篡改，并不是真实图像。此次事件给学术界带来了不小冲击，引发了人们对学术不端行为的深入探讨。
类似的图像篡改事件层出不穷，渗透到我们日常生活中的各个领域。在这种背景下，诞生了一门新的学科——数字图像取证。其基本思想是通过一定的技术手段对数字图像的来源及所可能经过的处理操作进行分析，以保证数据来源的真实性、可靠性和完整性。JPEG(Joint Photographic Experts Group)[1]是目前互联网上运用最为广泛的图像格式，在我们日常生活中具有非常重要的应用。当前无论是手机还是数码相机采集的图像，大部分是以JPEG格式存储的。因此，对JPEG图像进行分析和取证无疑具有非常重要的意义。已有的案例表明，许多篡改操作都发生在JPEG图像上，其操作基本流程是首先对JPEG文件进行解压，在空域进行篡改，篡改完成后再将篡改后的图片保存为JPEG格式，这样篡改后的图片就可能会被两次甚至多次JPEG压缩。因此，对于JPEG重压缩的检测可以作为判断图像是否经过篡改的重要依据，是当前数字图像篡改检测领域的一个重要分支。
本文主要报道JPEG图像重压缩检测领域在近年来取得的一系列成果，具体安排如下：首先对JPEG格式进行一个简单介绍，接下来详细阐述了两次量化表不一致情况下的重压缩检测、两次量化表一致情况下的重压缩检测算法和思路，并简要进行了性能分析和评价，最后分析了JPEG图像重压缩检测现存的问题，并对未来的发展方向进行展望。
2 JPEG重压缩检测现状
2.1 JPEG压缩图像编解码流程
JPEG(Joint Photographic Experts Group)即联合图像专家组，其标准由国际标准化组织(ISO)制订，是用于连续色调静态图像压缩的一种标准。它可以用有损压缩方式去除冗余的图像数据，是目前最常用的图像文件格式。JPEG压缩和解压缩的步骤如下图1所示。压缩过程主要包括色彩空间转换、分块DCT(Discrete Cosine Transform)变换、量化、熵编码几个步骤；解压缩过程与之对应，包括熵解码、反量化、分块DCT逆变换、色彩空间逆变换几个步骤。
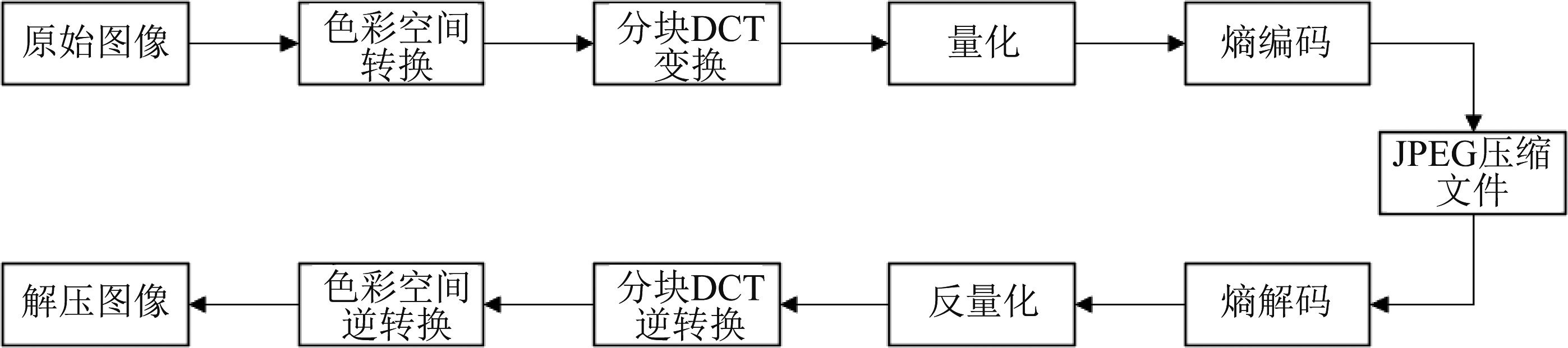
图1 JPEG图像编解码流程
Fig.1 The process of JPEG image encoding and decoding
2.2 JPEG重压缩模型
由上图1可见，JPEG图像是以压缩文件形式存储的。对JPEG图像进行篡改时，首先需要将压缩文件解压到空域，然后在空域完成篡改操作，操作完成后再以JPEG文件格式存储，具体可参见下图2。当JPEG图像被篡改并再次保存为JPEG格式时，会经历JPEG二次压缩，即JPEG重压缩过程。JPEG重压缩检测的分类如图3所示，根据第二次压缩的量化表是否与第一次相同，JPEG重压缩检测又可分为量化表相同情况下的二次压缩检测，和量化表不同情况下的二次压缩检测，下文将分别对这几方面的工作进行介绍。
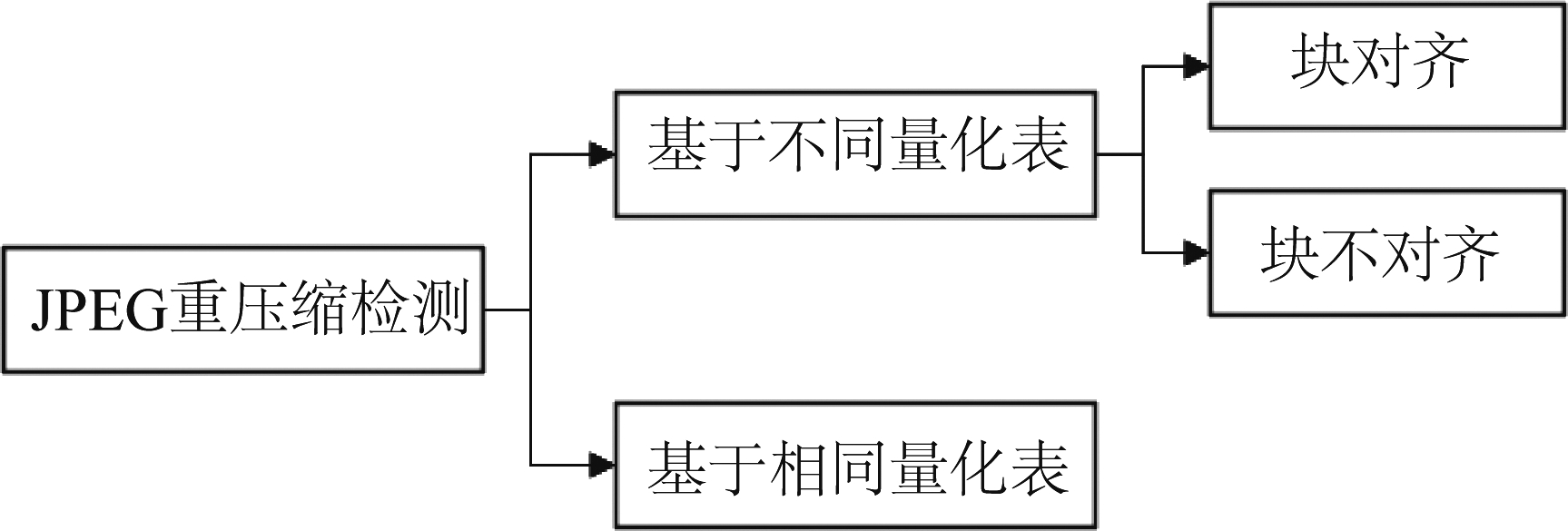
图3 JPEG重压缩检测的分类
Fig.3 Classification of JPEG recompression detection
图2 JPEG图像篡改操作流程
Fig.2 The process of JPEG image forensics
2.3 量化表不一致情况下的重压缩检测
由上文图1可知，在JPEG图像标准压缩流程中存在一个量化过程。根据JPEG图像压缩比不同，可以选择不同的量化表。通常而言，量化表中所对应的量化步长越大，JPEG图像的压缩比越高；反之量化步长越小，JPEG图像的压缩比越低。图4所示为对应于质量因子(QF, quality factor)为75和85的标准JPEG压缩量化表。由量化表可见，质量因子不同，在不同频段所对应的量化步长也不一样。根据第二次压缩过程中8×8网格与第一次压缩过程中的8×8网格是否对齐，又可以将JPEG重压缩检测分为对齐和非对齐重压缩检测两个方面。
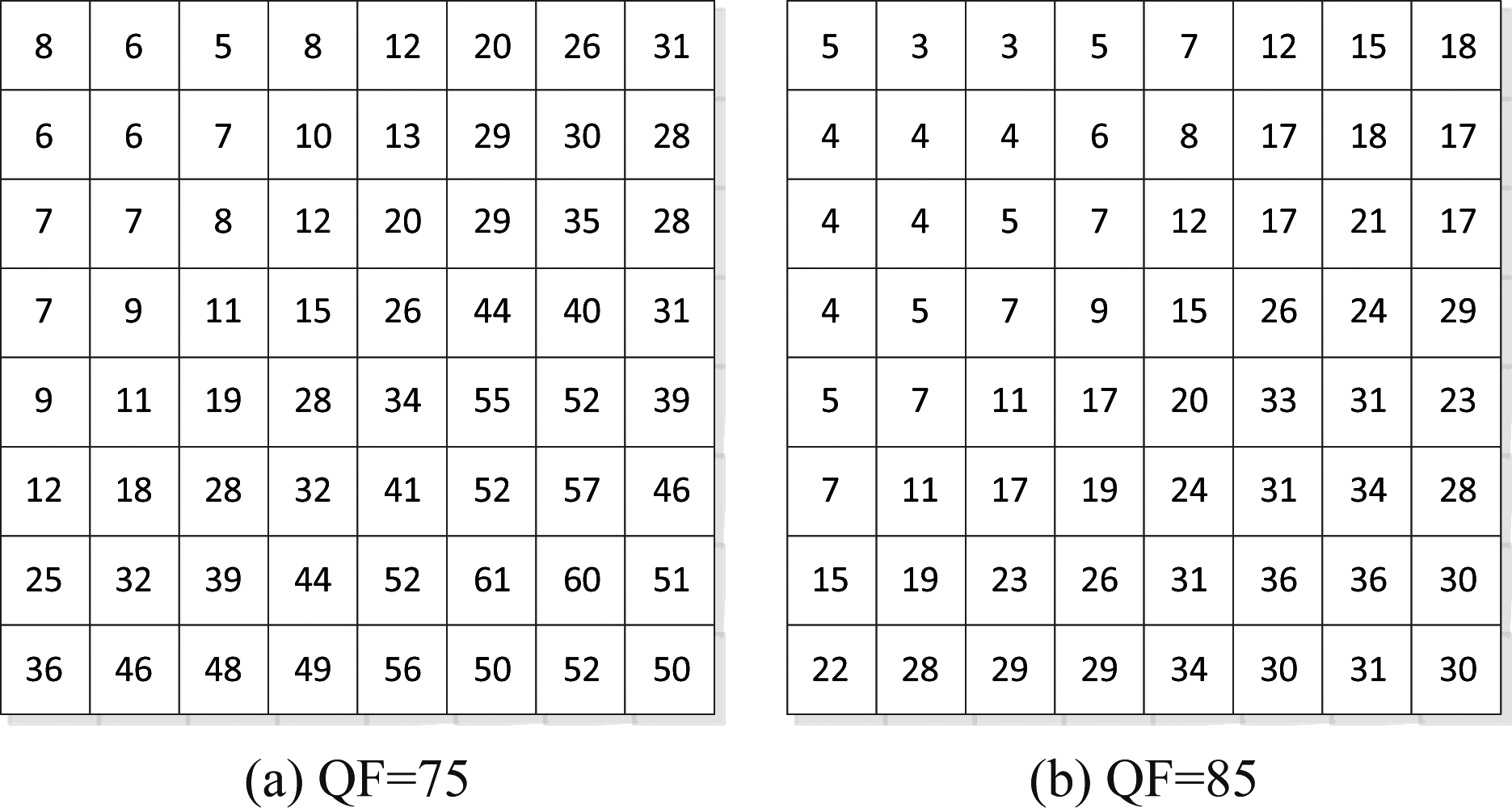
图4 质量因子为75和85时的标准量化表
Fig.4 Standard quantification table with different QFs
2.3.1 对齐情况下的重压缩检测
根据上文的介绍可知，JPEG压缩过程首先是进行分块DCT变换，然后再对分块后的DCT系数进行量化取整操作。在单次JPEG压缩图像中(设量化矩阵为Q1)，对8×8子块中任意频率(i, j)(0≤i, j≤7)所对应的系数进行量化后得到的量化DCT系数
直方图通常可用一个广义高斯分布来拟合[2]，其中N表示图像中所有8×8子块个数。当一个单次JPEG压缩图像(量化矩阵为Q1)被解压到空间域然后用另一量化矩阵Q2(Q2≠Q1)再次压缩，所得到的量化后DCT系数的直方图通常将不再服从广义高斯分布。
Fridrich等人[3- 4]较早对JPEG图像重压缩问题进行了研究，并指出如果在第一次压缩和第二次压缩过程中采用了不同的量化表，会在两次JPEG压缩图像的量化DCT系数直方图中出现明显的“零点”和“双峰”等异常特性。如图5所示为经过两次JPEG压缩后在频率(0, 1)处所对应的量化DCT系数直方图，其中横向表示量化后DCT系数值，纵向表示该系数出现的频次。由图5可见：当两次JPEG压缩选择的量化步长一致时，DCT系数直方图并没有明显的变化，如图5(a)所示；当第一次压缩的量化步长为8，而第二次选择得量化步长为4时，奇数DCT系数(如1、3、5等)在两次压缩的JPEG图像中出现的频次将为零，如图5(b)所示；第一次的量化步长为6，第二次压缩步长为4时，直方图中将在系数对1↔2,4↔5,7↔8等对应的位置出现局部双峰值现象，如图5(c)所示；第一次的量化步长为3，第二次压缩步长为4时，直方图与原始直方图会有明显不同，但局部双峰等现象并不十分明显，如图5(d)所示。图5表明，当两次量化步长选取不同组合时，会在两次JPEG压缩图像的DCT系数直方图中留下不同的痕迹，这一观察成为后续对该问题进行检测的主要思路。
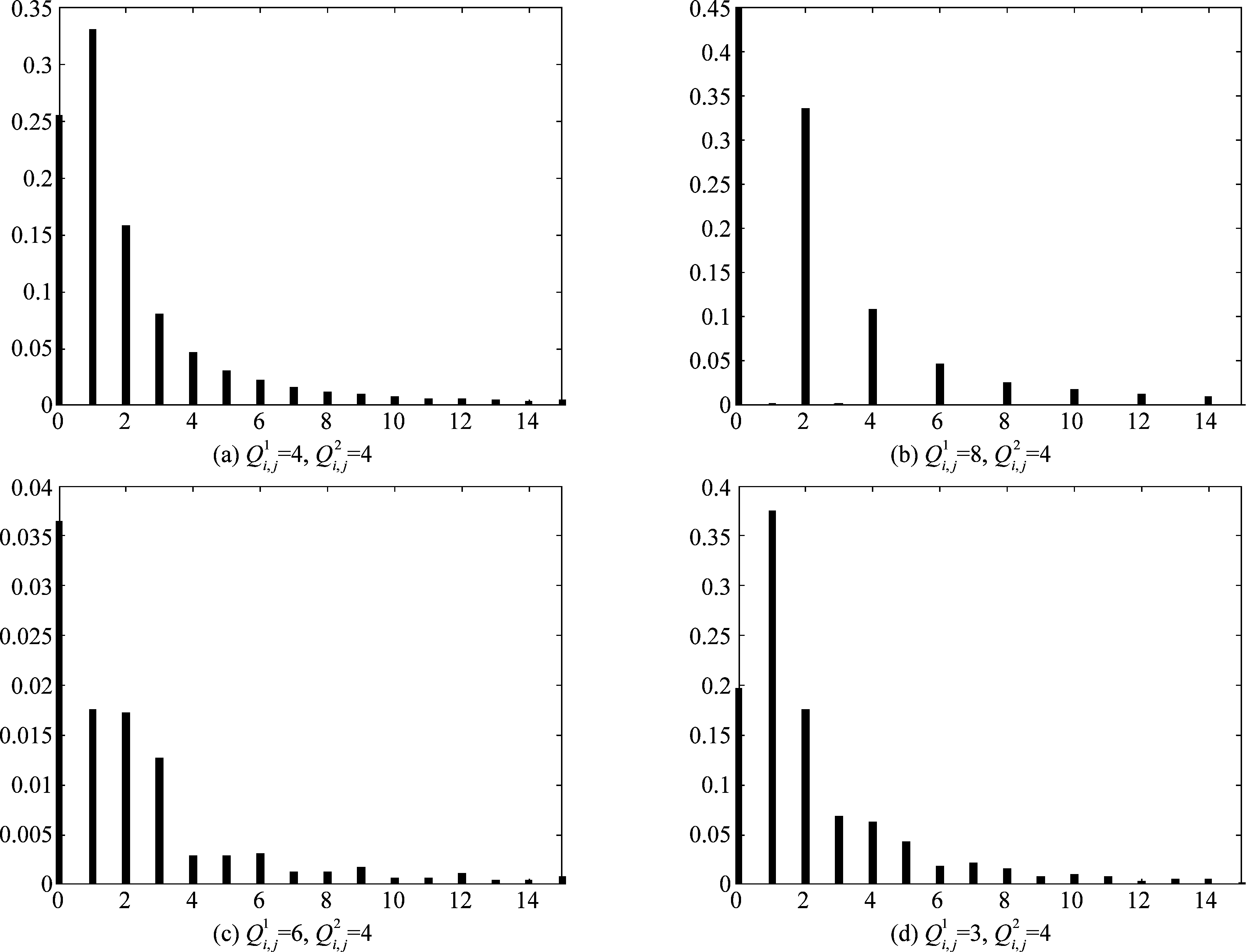
图5 两次压缩后JPEG图像频率(i, j)=(0,1)处量化DCT系数直方图
Fig.5 Histogram of quantized DCT coefficients at frequency (i, j)=(0,1) of doubly compressed JPEG image
与此同时，Popescu和Farid[5]指出，第一次压缩和第二次压缩如果采用了不同的量化步长，会在一些特定频率的DCT系数直方图中引入异常模式，将其进行傅里叶变换后会呈现某些周期特性，从而可以对JPEG图像重压缩进行有效检测。Feng等人[6]亦指出可以利用重压缩过程可能引入的周期效应、直方图不连续性等特征来对两次JPEG压缩进行检测。在文献[7]中，Fu等人指出单次JPEG压缩图像DCT系数的首位数字分布满足广义Benford法则[8]，而两次JPEG压缩图像由于引入了人为的扰动，其DCT系数的首位有效数字不再满足广义Benford法则。2008年，Li等人[9]指出可以通过使用广义Benford定律来对某些特定频率交流DCT系数首位数字的分布进行拟合，从而可进一步提高对两次JPEG压缩的检测性能。Dong等人[10]还提出可以用马尔可夫转移概率矩阵对DCT系数首位数字的分布进行建模，对两次JPEG压缩进行检测，实验结果亦表明了该方法的有效性。Chen等人[11]提出了一种基于机器学习的方案，通过在给定JPEG图像中提取了一个由马尔可夫转移概率组成的324维特征集，用于描述DCT系数块内和块间相关性的特征，并借助于支持向量机(SVM, Support Vector Machine)，可以有效地区分单次JPEG压缩的图像和两次JPEG压缩的图像。2011年，Liu等人[12]进一步对DCT系数块内和块间相关性进行了研究，通过在DCT系数上提取相邻联合密度特征和边缘密度特征，然后借助于SVM对这些特征进行分类，实现JPEG重压缩检测，性能比Chen等人[12]的方法有所提高。2016年，Shang等人[13]在Chen等人[11]方法的基础上，提出将图像分为纹理复杂区域和平滑区域，借助于高阶Markov转移概率矩阵来对DCT系数的块内和块间相关性进行描述，可进一步提高算法的性能。为了有效地捕捉JPEG图像DCT系数的块内和块间相关性，Li等人[14]提出可以先对DCT系数进行Zigzag排序，再按照特定的顺序进行行扫描和列扫描，结合Markov转移概率矩阵，性能取得了更进一步的提升。最近，Taimori等人[15]对具有不同量化因子的单压缩和双压缩JPEG图像进行统计分析，发现不同JPEG编码器设置下的单压缩和双压缩数据在特征空间中表示为有限数量的相干簇，并提出了针对性学习策略，通过分类器可对JPEG重压缩进行检测,该方法在具有较低的复杂度同时还具有较好的检测性能。考虑到在图像篡改过程中，如原始图像为JPEG图像，在篡改过程中需要先对其进行解压，然后对其中的部分区域进行篡改，图像篡改结束后再进行第二次压缩。显然，非篡改区域经历了两次压缩，因此在该部分区域的DCT系数直方图中会存在 “零值”和“双峰”效应。而如果篡改区域来源于非压缩图像(或者该部分区域来源于JPEG图像，但在将该区域粘贴到原始图像的过程中该部分区域的8×8网格没有和原始图像的8×8网格对齐)，则在该区域不存在“零值”和“双峰”效应。利用这种特性，可以完成对图像篡改区域的检测和定位。如在文献[16]中，He等人通过利用这种特性来对JPEG图像是否为篡改图像进行检测，并进一步定位篡改区域。
2.3.2 非对齐情况下的重压缩检测
如上所述，在实际篡改过程中，由于所选择的篡改区域的限制，通常会导致篡改区域并不能与原始图像的8×8分块网格严格对齐。如对原始JPEG图像篡改后，后期可能需要一些裁剪操作，对裁剪后的图像再进行压缩，这时候篡改后图像在进行JPEG压缩过程中所采取的8×8分块网格与原始载体的8×8分块网格之间可能存在没有对齐的情况。
非对齐情况下的JPEG重压缩检测研究，一个重要的出发点就在于JPEG图像是分块压缩，通常而言JPEG图像中会存在明显的块效应，特别是在JPEG图像质量因子较低的情况下。Fan等人[17]较早对JPEG图像中的块效应问题进行了研究。如下图6所示，粗体黑线表示对应的8×8分块网格，A、B、C、D代表位于子块内的四个像素，而E、F、G、H代表位于子块边缘的四个像素。通过比较Z′=|A-B-C+D|以及Z″=|E-F-G+H|之间的差异，可以有效地对原始图像是否经过JPEG压缩进行判别。
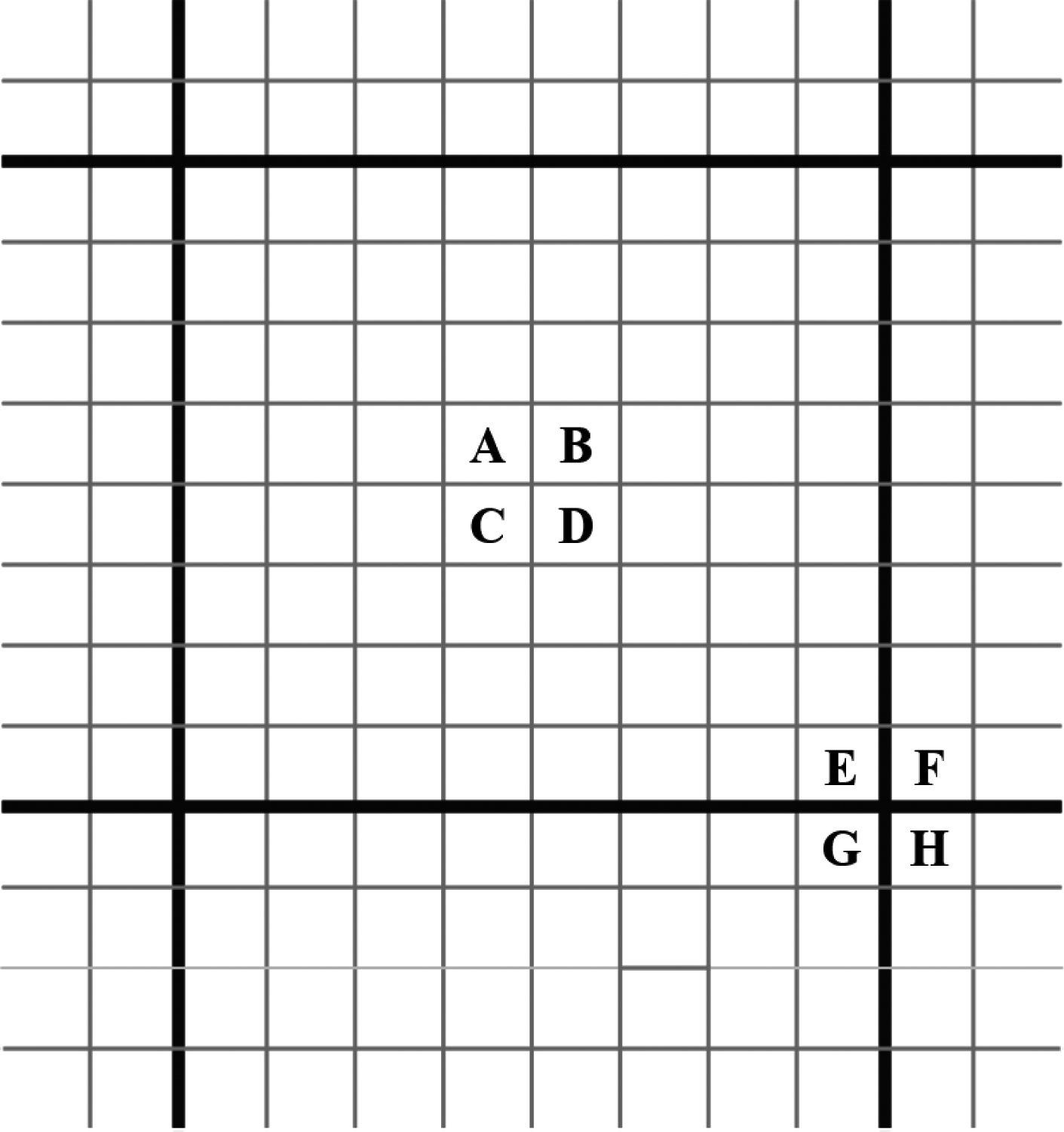
图6 JPEG压缩块效应模型
Fig.6 Block effect of JPEG compression
Luo等人[18]在此基础上，提出了块效应特征矩阵(BACM, blocking artifact characteristics matrix)。根据观察，BACM在单次压缩的JPEG图像中是对称的，而在非对齐JPEG重压缩后的图像中是不对称的，从而可以用其来对篡改图像中篡改区域大于500×500的重压缩块进行有效检测。Chen等人[19]提出首先在空间域中计算整个图像的块周期，然后将周期模型转换到频域，并从频率能量分布中提取统计特征，借助于支持向量机对两次JPEG压缩进行检测。文献[20]中，作者假设所有的源图像都是JPEG格式，在空间域和变换域中分别对JPEG图像中可能存在的周期性特性进行建模，并在此基础上设计了一种鲁棒的检测方法，能够对对齐或非对齐的两次JPEG压缩进行检测。Tralic等人[21]亦指出由于在复制粘贴操作后，得到的图像中会存在分块痕迹，通过提取块效应网格(BAGs, blocking artifact grids)痕迹，可以对两次JPEG压缩后的图像进行有效检测。Yang等人[22]提出用精细强度差(RID, refined intensity difference)来度量JPEG压缩图像中存在的块效应。为了避免图像纹理对块效应度量的影响，作者还提出了一种新的校准策略，可有效去除图像纹理对块效应度量方案的影响。针对彩色图像特征信息缺失以及块效应检测问题，Wang等人[23-24]提出了基于四元数离散余弦变换(QDCT, quaternion discrete cosine transform)域精细马尔可夫链的非对齐JPEG重压缩检测算法。文献[25]中，作者还提出了一种基于JPEG图像双重压缩偏移量估计的篡改区域自动检测定位方法，该方法首先利用尺度不变特征变换(SIFT, scale invariant features transform)提取图像的特征点和相应的特征向量，并采用最近邻算法对提取的特征向量进行初步匹配。对于彩色信息不一致引发的误匹配，作者引入色调饱和度(HIS, hue saturation intensity)彩色特征对其进行优化。然后，通过随机样本一致性(RANSAC, random sample consensus)算法对匹配对之间的仿射变换参数进行估计并消除错配，确定完整的复制粘贴区域。最后，根据各区域不同的重压缩偏移量来对复制区域和篡改区域进行判定和区分。实验结果表明该方法可以有效定位JPEG图像的复制篡改区域，对复制区域的几何变换以及常见的后处理操作具有较强的鲁棒性。
另外，考虑到非对齐JPEG重压缩虽然在量化后DCT系数直方图中不存在对齐情况下明显的双峰和零值效应，重压缩的过程仍然会在量化后的DCT系数直方图中留下痕迹。部分学者也提出了基于DCT系数特性的检测方案。如Qu等人[26]指出非对齐JPEG重压缩会破坏基于分块DCT系数独立值图(IVM, independent value map)的对称性，从而从盲源分离的角度提取了13个特征对非对齐的JPEG重压缩进行检测。Bianchi等人[27-28]发现在对齐情况下重压缩时，DCT系数会呈现明显的周期性，可以通过整数周期映射(IPM, integer periodicity map)的非均匀性特点来对两次压缩过程中存在的8×8网络偏移进行检测。但是，在随后的研究中表明这种基于IPM的检测方法可以很容易地被误导。2019年，Mandal等人[29]发现在不影响图像的视觉质量前提下，IPM可以很容易地修改，并提出了一种反检测方法，通过单压缩JPEG图像的直流系数(DC, direct current)的统计模型生成估计图像(该图像不受IPM中存在的量化伪影影响)，然后对估计的图像进行非对齐JPEG重压缩，可以误导Bianchi等人[27-28]提出的JPEG双压缩检测方法。
最近，Wang等人[30]提出一种基于卷积神经网络(CNN, convolutional neural network)的JPEG双压缩检测算法。考虑到JPEG压缩后DCT系数直方图在单压缩区域和双压缩区域之间存在差异，作者使用图像的DCT系数直方图作为输入，实现对非对齐两次JPEG压缩的有效检测。实验结果表明，该算法在第一次压缩质量因子高于第二次压缩质量因子的情况下具有良好的性能。Barni等人[31]分别使用手工提取的特征、原始图像和去噪后的图像作为CNN的输入对齐进行训练，研究表明基于手工特征的CNN能够在对齐JPEG重压缩的情况下达到更好的精度，而对于非对齐JPEG重压缩的检测，基于图像噪声的残差的CNN更具有优势。Li等人[32]提出了一种基于双域CNN(DD-CNN, double domain CNN)的非对齐JPEG双压缩检测算法，采用JPEG的DCT系数和解压缩图像的像素作为网络的输入，其中DCT域CNN用于从DCT子带间和DCT子带内提取特征，空域CNN用于从JPEG的8×8网格内和网格间提取特征。Verma等人[33]提出了一种基于DCT域的深度卷积神经网络，从图像中提取基于直方图的特征作为网络的输入进行训练，可以有效地对JPEG重压缩进行分类。Li等人[34]提出了一种基于多分支CNN的JPEG双压缩进行检测方案，该网络以JPEG图像的原始DCT系数作为输入，无需采用直方图提取特征或手工预处理操作。2019年，Zeng等人[35]提出了一种改进的DenseNet(densely connected convolutional network)用于检测给定图像的压缩历史记录，网络前端使用了一个特殊的滤波层，帮助后面的网络更容易地识别图像。该方法在质量因子较低的图像中，可以达到较高的性能。Alipour等人[36]提出通过训练一个深度卷积神经网络来分割JPEG块的边界，可准确地检测出与各种JPEG压缩相关的块边界。Niu等人[37]提出了一种端到端系统，该系统根据估计的原始量化矩阵对图像块进行聚类，并通过形态重建的方法对结果进行细化。所提出的方法可以在多种设置下得到较好的性能，包括对齐和非对齐的JPEG重压缩检测。
2.4 量化表相同情况下的重压缩检测
由JPEG压缩和解压缩过程可知，如果在两次压缩过程中采用相同的量化表，且保持两次压缩之间的8×8子块对齐，理论上讲第二次压缩的图像和原始JPEG图像之间应该没有区别。在JPEG重压缩问题被提出来后，相当长一段时间内，大部分研究者均认为，如果第二次压缩和第一次压缩采用相同的量化表，并且保持8×8的分块网格严格对齐，这种情况下两次压缩图像和一次压缩图像是相同的，无法有效检测。但我们知道，JPEG压缩是一种有损压缩方法。在压缩和解压缩过程中存在三种不同的误差。一是压缩过程中存在的量化误差，DCT系数在量化前是浮点数，量化后一般是四舍五入取整，这种DCT系数量化前后的差一般称为量化误差。第二类和第三类误差都存在于解压过程中。将逆DCT(IDCT, inverse DCT)应用于反量化后的DCT系数，得到空域一系列浮点数。为了在空域重建图像数据，小于0的值将被截断为0，而大于255的值将被截断为255，这种操作导致的误差称为截断误差。另外，在空间域重建图像时，需要将所属的浮点数四舍五入到最接近的整数，舍入过程中存在的误差称为舍入误差。
Huang等人[38]较早对量化表保持不变的问题进行了研究。指出由于上述三种误差，即量化误差、截断误差和舍入误差，即使使用与单压缩图像相同的量化矩阵对图像进行二次压缩，二次压缩后的图像与原始单压缩图像也会存在差异。如图7所示是在UCID数据库[39]上的实验结果，横坐标表示压缩次数，纵坐标表示量化表相同情况下前后两次压缩得到的JPEG文件之间不同DCT系数个数Dn，如横坐标2对应的是第二次JPEG压缩图像和第一次压缩图像之间不同DCT系数个数。由图7可见，连续两次压缩之间的DCT系数变化的数目随着压缩次数的增加会单调减少。基于这种观察，Huang等人[38]提出了一种对量化后DCT系数随机扰动的方法，可以有效解决量化表保持不变且8×8分块网格保持对齐情况下的重压缩检测问题。
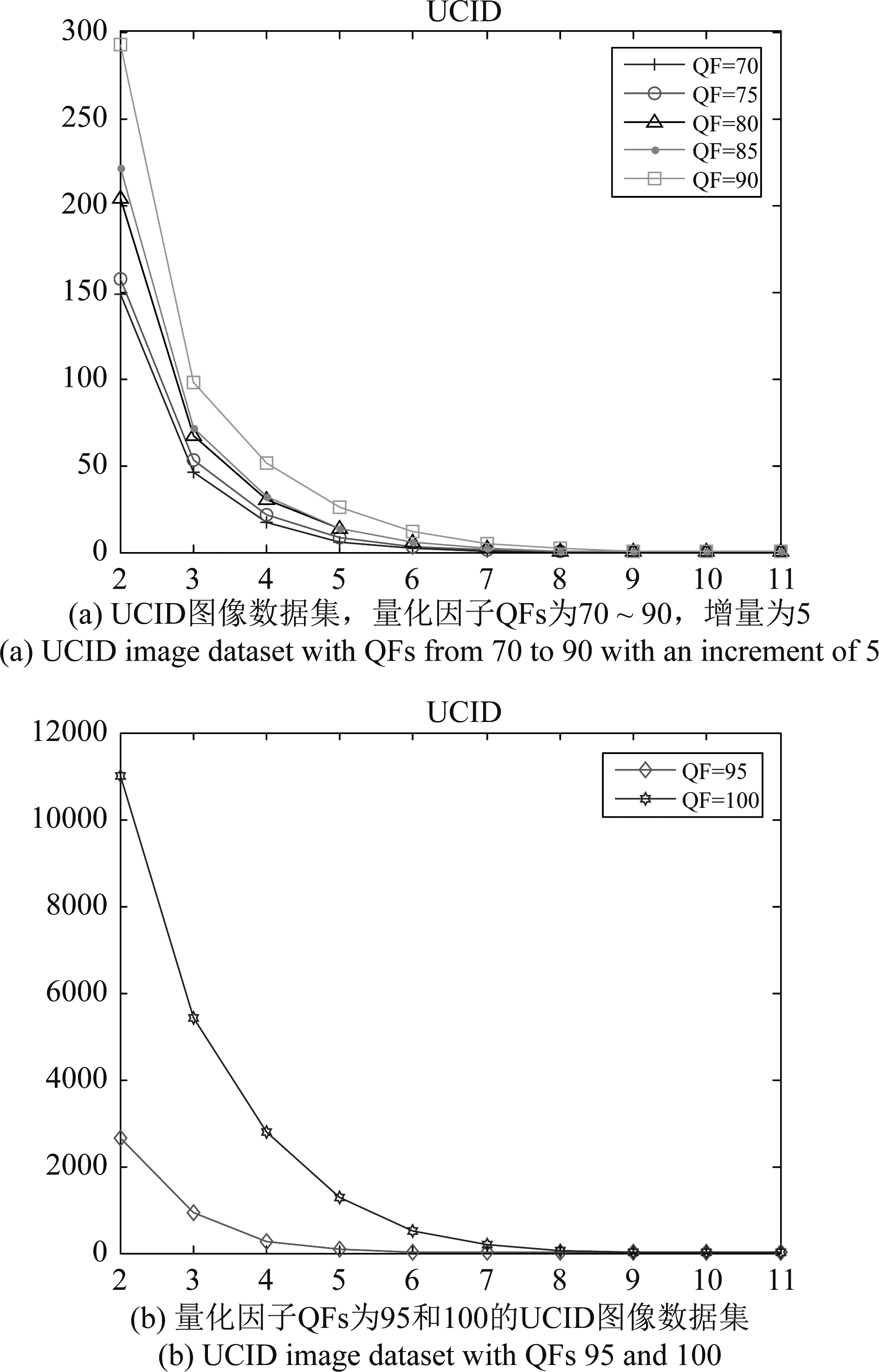
图7 不同图像量化因子QFs下Dn(n=1,2,…，10) 平均值的变化趋势
Fig.7 Variation tendency about the average values of Dn(n=1,2,…，10) for different image QFs
2019年，Niu等人[40]指出只针对值为±1的量化后DCT系数进行扰动，可以更进一步提高Huang等人算法[38]的检测效果。Lai和Böhme[41]提出了一种新的块收敛分析的方法，能检测质量因子为100的JPEG重压缩图像，并可以较为准确地估计重压缩的次数。Yang等人[42]通过计算IDCT后得到的值和重建图像中像素值之间的差值，得到误差图像(这个误差图像主要包含截断误差和舍入误差)，进而提出了一组特征来表征单次和两次JPEG压缩后得到的误差图像之间的统计差异，借助于SVM来识别给定的JPEG图像是否经过了双重压缩，该方法在实验中取得了较好的效果。针对现有算法在低质量因子情况下检测准确率不高的问题，Wang等人[43]提出了一种基于球坐标的检测算法，通过分析JPEG压缩对于颜色空间转换的影响提出转换误差，对截断误差和舍入误差在像素级上进行分类后投影到球坐标上，在避免混合误差的同时获取了更加明显的特征。实验结果表明在UCID数据库[39]中，该方法在质量因子小于80的情况下的检测准确率比Yang等人[42]的方法平均提高了5%，并且在质量因子为80和85的情况下，准确率亦有明显提高。总体而言，上述方法在大尺寸图像中具有较好的效果，但是对于尺寸较小和质量因子较低的JPEG图像，检测效果一般并不理想。Deshpande等人[44]基于在后续压缩阶段改变的量化DCT系数的个数，提出了一种可用于描述量化DCT系数差异的特征，并将其与Yang等人[42]提出的特征相结合，利用多层感知器(MLP, multi-layer perceptron)对单次JPEG压缩和两次JPEG压缩图像进行分类，该方法对于较小的图像尺寸和较低的质量因子，可以达到较好的性能。
随着深度学习在图像处理领域取得不俗的性能，近年来一些学者也将深度学习方法引入到量化表相同情况下的两次JPEG重压缩检测领域。不同于传统方法只提取某一具体类型特征，基于深度学习的算法可以通过网络训练提取JPEG重压缩特征。Huang等人[45]利用误差图像在JPEG重压缩检测方面的优势，将通过预处理获取的误差图像作为卷积神经网络(CNN)的输入。为了克服梯度消失的影响，在每层之间引入了密集连接，并提出了一个由八个卷积层组成的CNN体系结构来对JPEG重压缩图像进行检测。Peng等人[46]为了验证预处理对于实验性能影响，提出了将图像多次压缩获取的误差图像作为输入，构造了一个简单的CNN网络架构对JPEG重压缩图像进行检测。此外，针对三次或更高次数压缩的JPEG图像，Bakas等人[47]提出了一种深卷积神经网络模型，它能对两次甚至多次JPEG压缩的图像进行检测。
3 结论
JPEG是目前在互联网上运用最为广泛的图像格式。JPEG图像的重压缩检测在图像篡改取证领域具有非常重要的意义。本文主要从量化表是否保持不变的角度出发，对近年来JPEG重压缩检测领域的文献进行了一个回顾，介绍了该领域一些代表性的方法。总体而言，目前在JPEG重压缩领域已取得了一系列有意义的成果，但现有的绝大部分算法目前还主要处于理论研究阶段，缺乏在具体的工程实践中的应用。具体表现在：1)如现有方法大部分针对的是灰度图像重压缩检测，对于彩色JPEG图像重压缩检测较少考虑到彩色图像中各通道的特征；2)现有的算法一般针对具体的图像库具有较好的性能，但将训练好的模型或参数用于跨数据库测试性能一般会下降，算法的泛化性能还有待于进一步提高；3)针对具体的篡改问题，利用JPEG重压缩来进行篡改取证的成功案例较少，特别是篡改区域较小时，无法准确检测；4)现阶段的JPEG重压缩检测领域缺乏统一、权威的图像库和评价标准。
此外，由于信息与计算机等领域研究的飞速发展，一些与重压缩取证研究相关的领域也在不断的创新。如目前发展迅猛的深度学习为JPEG图像重压缩检测研究提供一系列新的检测手段。但深度学习领域在取得巨大突破的同时，也带来了许多潜在的安全隐患。当前越来越多的基于深度伪造的篡改图片出现在人们的生活中，这些也必将会对JPEG图像重压缩检测领域提出更大的挑战。如何设计新的更高效检测算法，并建立统一、权威的数据库和评价标准是JPEG重压缩检测领域亟待解决的问题。只有真正解决这些问题，才有可能将JPEG重压缩检测领域所取得的一系列成果推向实际的工程应用。
[1] WALLACE G K. The JPEG still picture compression standard[J]. IEEE Transactions on Consumer Electronics, 1992, 38(1): xviii-xxxiv.
[2] REININGER R C, GIBSON J D. Distributions of the Two-Dimensional DCT Coefficients for Images[J]. IEEE Transactions on Communications, 1983, 31(6): 835- 839.
[3] LUK
J, FRIDRICH J. Estimation of primary quantization matrix in double compressed JPEG images[C]∥Proc Digital Forensic Research Workshop, Cleveland, Ohio, USA, 2003.
T, FRIDRICH J. Detection of Double-Compression in JPEG Images for Applications in Steganography[J]. IEEE Transactions on Information Forensics and Security, 2008, 3(2):247-258.
[5] POPESCU A C, FARID H. Statistical Tools for Digital Forensics[M]∥Information Hiding. Berlin, Heidelberg: Springer Berlin Heidelberg, 2004: 128-147.
[6] FENG X, 
G. JPEG recompression detection[C]∥Proc SPIE 7541, Media Forensics and Security II. International Society for Optics and Photonics, 2010, 7541: 75410J.
[7] FU Dongdong, SHI Y Q, SU Wei. A generalized Benford's law for JPEG coefficients and its applications in image forensics[C]∥Proc SPIE 6505, Security, Steganography, and Watermarking of Multimedia Contents IX, 2007, 6505: 65051L.
[8] NEWCOMB S. Note on the frequency of use of the different digits in natural numbers[J]. American Journal of Mathematics, 1881, 4(1/4): 39- 40.
[9] LI B, SHI Y Q, HUANG Jiwu. Detecting doubly compressed JPEG images by using Mode Based First Digit Features[C]∥2008 IEEE 10th Workshop on Multimedia Signal Processing. Cairns, QLD, Australia. IEEE, 2008: 730-735.
[10]DONG Lisha, KONG Xiangwei, WANG Bo, et al. Double compression detection based on Markov model of the first digits of DCT coefficients[C]∥2011 Sixth International Conference on Image and Graphics. Hefei, China. IEEE, 2011: 234-237.
[11]CHEN Chunhua, SHI Y Q, SU Wei. A machine learning based scheme for double JPEG compression detection[C]∥2008 19th International Conference on Pattern Recognition. Tampa, FL, USA. IEEE, 2008: 1- 4.
[12]LIU Qingzhong, SUNG A H, QIAO Mengyu. A method to detect JPEG-based double compression[M]∥Advances in Neural Networks - ISNN 2011. Berlin, Heidelberg: Springer Berlin Heidelberg, 2011: 466- 476.
[13]SHANG Shumei, ZHAO Yao, NI Rongrong. Double JPEG detection using high order statistic features[C]∥2016 IEEE International Conference on Digital Signal Processing (DSP). Beijing, China. IEEE, 2016: 550-554.
[14]LI Jixian, LU Wei, WENG Jian, et al. Double JPEG compression detection based on block statistics[J]. Multimedia Tools and Applications, 2018, 77(24): 31895-31910.
[15]TAIMORI A, RAZZAZI F, BEHRAD A, et al. A part-level learning strategy for JPEG image recompression detection[J]. Multimedia Tools and Applications, 2021, 80(8): 12235-12247.
[16]HE Junfeng, LIN Zhouchen, WANG Lifeng, et al. Detecting doctored JPEG images via DCT coefficient analysis[C]∥European Conference on Computer Vision. Springer, Berlin, Heidelberg, 2006: 423- 435.
[17]FAN Zhigang, DE QUEIROZ R L. Identification of bitmap compression history: JPEG detection and quantizer estimation[J]. IEEE Transactions on Image Processing, 2003, 12(2): 230-235.
[18]LUO Weiqi, QU Zhenhua, HUANG Jiwu, et al. A novel method for detecting cropped and recompressed image block[C]∥2007 IEEE International Conference on Acoustics, Speech and Signal Processing. Honolulu, HI, USA. IEEE, 2007: II-217.
[19]CHEN Yilei, HSU C T. Image tampering detection by blocking periodicity analysis in JPEG compressed images[C]∥2008 IEEE 10th Workshop on Multimedia Signal Processing. Cairns, QLD, Australia. IEEE, 2008: 803- 808.
[20]CHEN Yilei, HSU C T. Detecting recompression of JPEG images via periodicity analysis of compression artifacts for tampering detection[J]. IEEE Transactions on Information Forensics and Security, 2011, 6(2): 396- 406.
[21]TRALIC D, PETROVIC J, GRGIC S. JPEG image tampering detection using blocking artifacts[C]∥2012 19th International Conference on Systems, Signals and Image Processing (IWSSIP). Vienna, Austria. IEEE, 2012: 5- 8.
[22]YANG Jianquan, ZHU Guopu, WANG Junlong, et al. Detecting non-aligned double JPEG compression based on refined intensity difference and calibration[C]∥Lecture Notes in Computer Science, 2014: 169-179.
[23]WANG Jinwei, HUANG Wei, LUO Xiangyang, et al. Double JPEG compression detection based on Markov model[M]∥Digital Forensics and Watermarking. Cham: Springer International Publishing, 2020: 141-149.
[24]WANG Jinwei, HUANG Wei, LUO Xiangyang, et al. Non-aligned double JPEG compression detection based on refined Markov features in QDCT domain[J]. Journal of Real-Time Image Processing, 2020, 17(1): 7-16.
[25]赵洁, 郭继昌, 张艳, 等. JPEG图像双重压缩偏移量估计的篡改区域自动检测定位[J]. 中国图象图形学报, 2015, 20(10): 1304-1312.
ZHAO Jie, GUO Jichang, ZHANG Yan, et al. Automatic detection and localization of image forgery regions based on offset estimation of double JPEG compression[J]. Journal of Image and Graphics, 2015, 20(10): 1304-1312. (in Chinese)
[26]QU Zhenhua, LUO Weiqi, HUANG Jiwu. A convolutive mixing model for shifted double JPEG compression with application to passive image authentication[C]∥2008 IEEE International Conference on Acoustics, Speech and Signal Processing. Las Vegas, NV, USA. IEEE, 2008: 1661-1664.
[27]BIANCHI T, PIVA A. Analysis of non-aligned double JPEG artifacts for the localization of image forgeries[C]∥2011 IEEE International Workshop on Information Forensics and Security. Iguacu Falls, Brazil. IEEE, 2011: 1- 6.
[28]BIANCHI T, PIVA A. Detection of nonaligned double JPEG compression based on integer periodicity maps[J]. IEEE Transactions on Information Forensics and Security, 2012, 7(2): 842- 848.
[29]MANDAL A B, DAS T K. Anti-forensics of a NAD-JPEG Detection Scheme Using Estimation of DC Coefficients[M]∥Information Systems Security. Cham: Springer International Publishing, 2019: 307-323.
[30]WANG Qing, ZHANG Rong. Double JPEG compression forensics based on a convolutional neural network[J]. EURASIP Journal on Information Security, 2016, 2016(1): 1-12.
[31]BARNI M, BONDI L, BONETTINI N, et al. Aligned and non-aligned double JPEG detection using convolutional neural networks[J]. Journal of Visual Communication and Image Representation, 2017, 49: 153-163.
[32]LI Bin, ZHANG Haoxi, LUO Hu, et al. Detecting double JPEG compression and its related anti-forensic operations with CNN[J]. Multimedia Tools and Applications, 2019, 78: 8577- 8601.
[33]VERMA V, AGARWAL N, KHANNA N. DCT-domain deep convolutional neural networks for multiple JPEG compression classification[J]. Signal Processing: Image Communication, 2018, 67: 22-33.
[34]LI Bin, LUO Hu, ZHANG Haoxi, et al. A multi-branch convolutional neural network for detecting double JPEG compression[EB/OL]. [2017-10-16]. https:∥arxiv.org/abs/1710.05477v1.
[35]ZENG Ximei, FENG Guorui, ZHANG Xinpeng. Detection of double JPEG compression using modified DenseNet model[J]. Multimedia Tools and Applications, 2019, 78(7): 8183- 8196.
[36]ALIPOUR N, BEHRAD A. Semantic segmentation of JPEG blocks using a deep CNN for non-aligned JPEG forgery detection and localization[J]. Multimedia Tools and Applications, 2020, 79(11/12): 8249- 8265.
[37]NIU Yakun, TONDI B, ZHAO Yao, et al. Image splicing detection, localization and attribution via JPEG primary quantization matrix estimation and clustering[EB/OL]. [2021-02-02]. https:∥arxiv.org/abs/2102.01439.
[38]HUANG Fangjun, HUANG Jiwu, SHI Yunqing. Detecting double JPEG compression with the same quantization matrix[J]. IEEE Transactions on Information Forensics and Security, 2010, 5(4): 848- 856.
[39]SCHAEFER G, STICH M. UCID: An uncompressed color image database[C]∥Proc SPIE 5307, Storage and Retrieval Methods and Applications for Multimedia 2004. 2003, 5307: 472- 480.
[40]NIU Yakun, LI Xiaolong, ZHAO Yao, et al. An enhanced approach for detecting double JPEG compression with the same quantization matrix[J]. Signal Processing: Image Communication, 2019, 76: 89-96.
[41]LAI Shiyue, BÖHME R. Block convergence in repeated transform coding: JPEG-100 forensics, carbon dating, and tamper detection[C]∥2013 IEEE International Conference on Acoustics, Speech and Signal Processing. Vancouver, BC, Canada. IEEE, 2013: 3028-3032.
[42]YANG Jianquan, XIE Jin, ZHU Guopu, et al. An effective method for detecting double JPEG compression with the same quantization matrix[J]. IEEE Transactions on Information Forensics and Security, 2014, 9(11): 1933-1942.
[43]WANG Jinwei, WANG Hao, LI Jian, et al. Detecting double JPEG compressed color images with the same quantization matrix in spherical coordinates[J]. IEEE Transactions on Circuits and Systems for Video Technology, 2020, 30(8): 2736-2749.
[44]DESHPANDE A U, HARISH A N, SINGH S, et al. Neural network based block-level detection of same quality factor double JPEG compression[C]∥2020 7th International Conference on Signal Processing and Integrated Networks (SPIN). Noida, India. IEEE, 2020: 828- 833.
[45]HUANG Xiaosa, WANG Shilin, LIU Gongshen. Detecting double JPEG compression with same quantization matrix based on dense CNN feature[C]∥2018 25th IEEE International Conference on Image Processing (ICIP). Athens, Greece. IEEE, 2018: 3813-3817.
[46]PENG Peng, SUN Tanfeng, JIANG Xinghao, et al. Detection of double JPEG compression with the same quantization matrix based on convolutional neural networks[C]∥2018 Asia-Pacific Signal and Information Processing Association Annual Summit and Conference (APSIPA ASC). Honolulu, HI, USA. IEEE, 2018: 717-721.
[47]BAKAS J, RAMACHANDRA S, NASKAR R. Double and triple compression-based forgery detection in JPEG images using deep convolutional neural network[J]. Journal of Electronic Imaging, 2020, 29(2): 023006.
