1 引言
空时自适应处理(Space-Time Adaptive Processing, STAP)技术可以实现机载雷达在强杂波背景下运动目标的检测[1-2]。STAP滤波器的性能取决于被测单元中杂波加噪声协方差矩阵(Clutter-plus-noise Covariance Matrix, CNCM)的估计精度。通常使用与被测距离单元相邻的训练样本来估计CNCM。根据RMB(Reed-Mallett-Brennan)准则,需要至少为2倍系统自由度的独立同分布训练样本,才能保持小于3 dB的输出信杂噪比损耗(Signal to Cutter plus Noise Ratio Loss, SCNRloss)[3]。因此,传统的STAP算法通常需要足够多来自同质杂波环境的训练样本。但是,雷达的工作环境复杂、多变,传统的STAP方法在非均匀杂波环境中会有明显的性能损失[4-5]。
研究者以减少STAP算法所需的训练样本数为目的,提出了降维STAP、降秩STAP、模型参数化STAP以及平滑STAP等方法[6]。降维STAP方法使用与杂波数据无关的线性变换,缩减了训练样本数量,但是降维STAP方法存在系统自由度缺失,导致杂波抑制能力降低、最小可检测速度增大、系统误差容忍变差等问题[7]。降秩方法的性能通常依赖于秩的大小,实际环境中杂波秩缺少明确解析表达式而难以确定,且降秩方法的计算复杂度不一定会减少,导致其应用受到了限制[8]。模型参数化STAP方法将杂波的空间时间二维分布模拟成多通道矢量自回归(Auto-Regressive, AR)模型,首先使用训练样本对AR模型参数进行估计,然后通过估计的AR模型参数建立STAP滤波器的权矢量,实现杂波抑制,该类算法所需的训练样本数量可以减少到AR模型阶数的2倍,但是算法中涉及的模型参数选择、计算复杂度等问题仍需要深入研究[8]。平滑STAP方法使用平滑处理,增加了降低维度的协方差矩阵估计的稳定度,但是这类方法无法避免由系统自由度损失而带来的杂波抑制性能的降低。
近年来,稀疏恢复(Sparse Recovery, SR)理论被应用到STAP中,形成了SR-STAP算法,仅需要少量训练样本就可以对杂波功率谱精确恢复[9-11],其理论恢复精度主要取决于空时导向矢量构成的字典以及稀疏恢复的具体方法。通常的SR-STAP算法中,字典是通过空时平面均匀离散化构成的,可能存在模型不匹配的问题,即真实杂波脊不在所构造字典的采样网格点上,称为离网问题[12],发生离网时,CNCM的估计精度会下降[13]。
针对SR-STAP中离网问题,相关学者提出一些解决措施。在文献[14]中,提出了基于知识辅助的网格校准方法,但该方法依赖于载机速度和偏航角度等先验知识的准确性。在文献[15]中,提出了基于正交匹配追踪的方法,通过梯度下降方法寻找与真实模型匹配的字典向量来解决字典失配问题,但正交匹配追踪方法的性能取决于参数,在非理想环境中参数的盲目性会导致STAP滤波器的性能下降[12]。目前,具有字典校正功能的稀疏恢复STAP算法依赖机载平台获得的准确先验知识,或者算法的性能对参数选择比较敏感,本文提出的基于迭代自适应(Iterative Adaptive Approach, IAA)[16-17]的字典校正空时自适应处理算法不依赖确切的环境先验知识,且算法性能对参数选择不敏感,仅需很少的训练样本就能精确地估计CNCM。为了克服离网问题带来的影响,首先基于IAA算法找到每个量化空间频率最大功率对应的原子,将选定原子附近的多普勒频率均匀离散成一个集合,然后通过最大化联合似然函数在局域中搜索最优原子,并将选定原子替换为最优原子,最后通过IAA算法的全局迭代,选择与杂波脊匹配的原子形成新的空时导向字典。实验证明,该方法能有效地减轻离网效应引起的杂波脊扩展[18],杂波抑制性能优于现有的空时导向字典均匀离散化的IAA-STAP方法。
本文的其余部分安排如下:第2节介绍了机载雷达的STAP信号模型;第3节讨论了SR-STAP模型、原理和相关的离网问题;第4节介绍了所提出的IAA-STAP离网校正方法;第5节进行算法的实验分析;第6节总结全文。
2 机载雷达的STAP信号模型
机载雷达阵列为均匀线性阵列,阵元个数为N,工作在正侧视模式下,在相干处理间隔(Coherent Processing Interval, CPI)内以恒定的脉冲重复频率发送M个脉冲。对于均匀线性阵列,接收信号的空时导向矢量可表示为
v(fs, fd)=vd(fd)⊗vs(fs)
(1)
其中,vs(fs)=[1,ej 2πfs,…,ej 2π(N-1)fs]T是空间导向矢量,vd(fd)=[1,ej 2πfd,…,ej2π(M-1)fd]T是时间导向矢量, fs和fd分别是归一化空间频率和多普勒频率,⊗表示Kronecker积。
雷达接收的信号为
x=xt+xc+n
(2)
其中,
为目标信号,在没有目标的情况下为0,a为复振幅,
是目标的空时导向矢量,
和
分别是目标的空间频率和多普勒频率;杂波信号
可以看成是多个杂波散射体反射信号的叠加,Nc为单个距离环中杂波散射体的个数,ak和
分别是第k个杂波散射体的复振幅和空时导向矢量,
和
分别是第k个杂波散射体的空间频率和多普勒频率;n∈CNM×1是零均值高斯白噪声矢量。
杂波协方差矩阵定义为
Rc=E[xcxcH]
(3)
通常,假设杂波和噪声分量是独立的,则杂波加噪声协方差矩阵可以表示为
(4)
σn2表示噪声的功率,INM为单位矩阵。
STAP的最优滤波权可通过解如下优化问题得到。
(5)
其中vt是目标导向矢量。计算得到最优滤波权矢量w为
(6)
Rc+n是检测距离单元的杂波统计特性,通常是未知的,可以利用均匀样本进行估计。传统采样矩阵求逆算法(Sample Matrix Inversion, SMI)[19]估计
计算量大,并且训练样本数量L≥2NM时才能保持小于3 dB的输出SCNRloss。在异构环境中,足够的独立同分布条件的训练样本很难得到,因此本文提出小样本、非均匀、非稳定条件下,获得高分辨率杂波空时功率谱的算法。
3 SR-STAP算法
3.1 SR-STAP模型及原理
SR-STAP方法利用角度-多普勒平面中杂波固有的稀疏性,在固定的冗余空时导向字典下利用SR算法恢复杂波。与传统的降维/降秩方法相比,SR-STAP方法可以提供高分辨率的杂波功率谱估计,仅需要少量的训练样本实现CNCM的精确估计。此类方法首先将角度-多普勒平面均匀划分成Ns×Nd网格,其中Ns=ρsN,Nd=ρdM,且ρs,ρd>1,它们分别是沿角度和多普勒轴的分辨率标度。所有网格点的空时导向矢量组成的空时导向字典Φ∈CNM×NsNd表示为
Φ=[v(fs,1, fd,1),v(fs,1, fd,2),…,v(fs,Ns, fd,Nd)]
(7)
其中, fs,i(i=1,2,…,Ns)和fd, j(j=1,2,…,Nd)分别表示在量化的角度-多普勒平面上第i个空间频率和第j个多普勒频率。
多快拍均匀样本数据的稀疏恢复模型可以表示为
X=ΦA+N
(8)
其中,X=[x1,x2,…,xL]∈CNM×L是L个距离单元的训练样本,A=[a1,a2,…,aL]∈CNsNd×L是稀疏系数矩阵,列矢量al(l=1,2,…,L)表示xl的稀疏系数向量,al中的非零元素表示相对应的杂波元素,N=[n1,n2,…,nL]∈CNM×L是高斯白噪声矩阵。
稀疏系数矩阵可以通过解下列最优化问题得到。
min||A||2,0 s.t. ||X-ΦA
≤ε
(9)
其中,||||2,0是一种混合范数,定义为由每行向量的l2范数构成向量的l0范数,||||F是矩阵的Frobenius范数,ε是噪声允许误差水平。通过求解稀疏系数矩阵,可以获得杂波的协方差矩阵为
Rc=Φdiag(p1,p2,…,pNsNd)ΦH
(10)
其中,
是Φ中第i个原子的功率。相关研究已经证明式(9)最优化问题的求解是NP难解的。通常可将l0范数非凸优化问题等效为l1范数凸优化问题来解决,即
min||A||2,1 s.t. ||X-ΦA≤ε 或min{||X-ΦA+k||A||2,1}
(11)
其中,||||2,1是一种混合范数,定义为由每行向量的l2范数构成的向量的l1范数。但在l1范数优化框架,SR-STAP滤波器对正则化参数k或者噪声的允许误差水平ε敏感。在非理想环境下,正则化参数设置不合理会导致STAP滤波器性能显著降低。IAA类方法是一种非参数化方法,对稀疏度不敏感,可以避免凸优化稀疏恢复类算法中涉及的正则化参数设置难的问题[8]。
3.2 SR-STAP中的离网问题
对于正侧视均匀线性阵列,角度-多普勒平面上杂波脊的斜率等于每个杂波斑块的空间频率和多普勒频率的比值。现有的稀疏恢复STAP都是假设杂波脊正好落在采样网格上,但是只有当Ns和Nd的比值等于杂波脊斜率的整数倍时,杂波脊才能精确地落在采样网格上。而实际情况下无法准确知道杂波脊斜率,因此无法构造使杂波脊精确落在采样网格上的空时导向字典,极易导致离网问题。离网一旦发生,杂波脊就会变宽和变低,从而降低了CNCM的估计精度。将空间频率和多普勒频率离散的间隔减小,可以在一定程度上减轻离网问题的影响[20],但是空时导向字典的列相关性会增强,并且大大增加了计算量[21]。
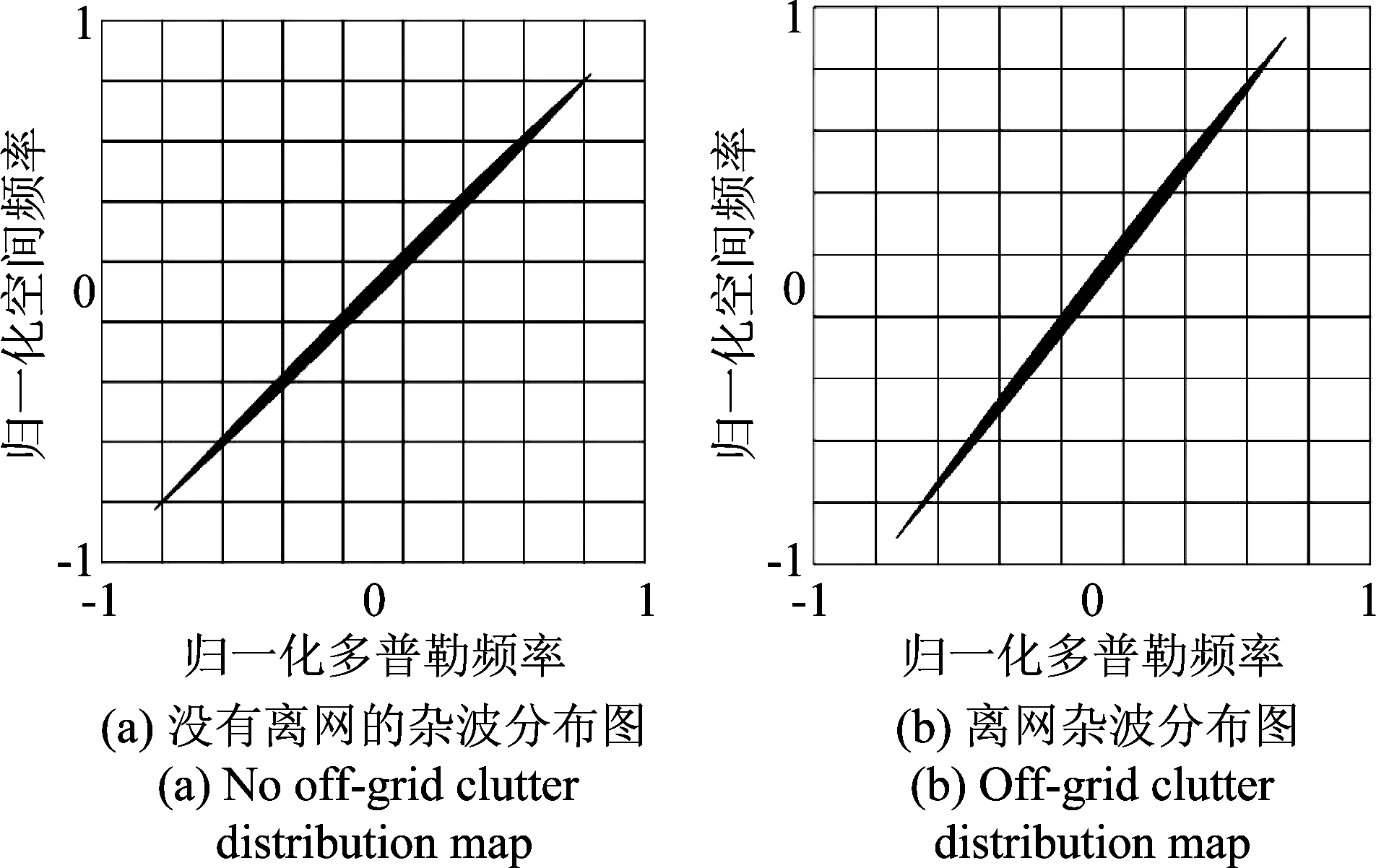
图1 空时二维平面上杂波分布图
Fig.1 Clutter distribution map on a two-dimensional space-time plane
图1为空时二维平面上杂波分布。图1(a)为没有发生离网的杂波分布,图1(b)为离网情况下杂波分布。
4 IAA-STAP字典校正方法
图2为字典校准方法示意图。假设在空间域中没有离网,从多普勒轴来看,杂波块的真多普勒频率不在均匀离散的多普勒网格上。首先在IAA的每次迭代中,找到原始空时导向字典中每个量化空间频率最大功率对应的原子,如图2蓝色圆点;其次围绕选定的原子局部网格划分并通过最大化联合似然函数在局域中搜索真杂波多普勒频率,以匹配真实杂波点,如图2红色圆点;然后将选定的原子替换成真杂波多普勒频率构成的原子,即图2蓝色点换成红色点;最后通过IAA算法的全局迭代选择与杂波脊匹配的原子形成新的空时导向字典。当某些量化的空间频率的杂波斑块发生离网时,新的空时导向字典的原子可以自适应地收敛到杂波脊。
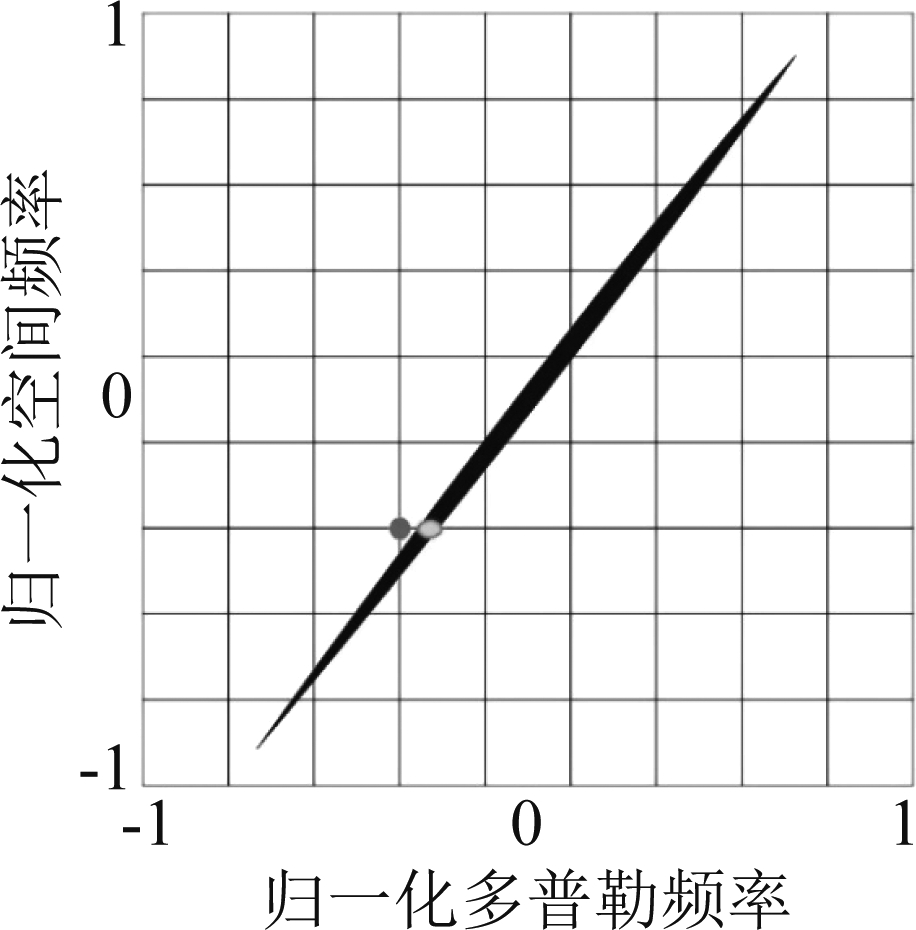
图2 字典校准方法示意图
Fig.2 Schematic diagram of dictionary calibration method
基于IAA-STAP离网校正流程图如图3所示。
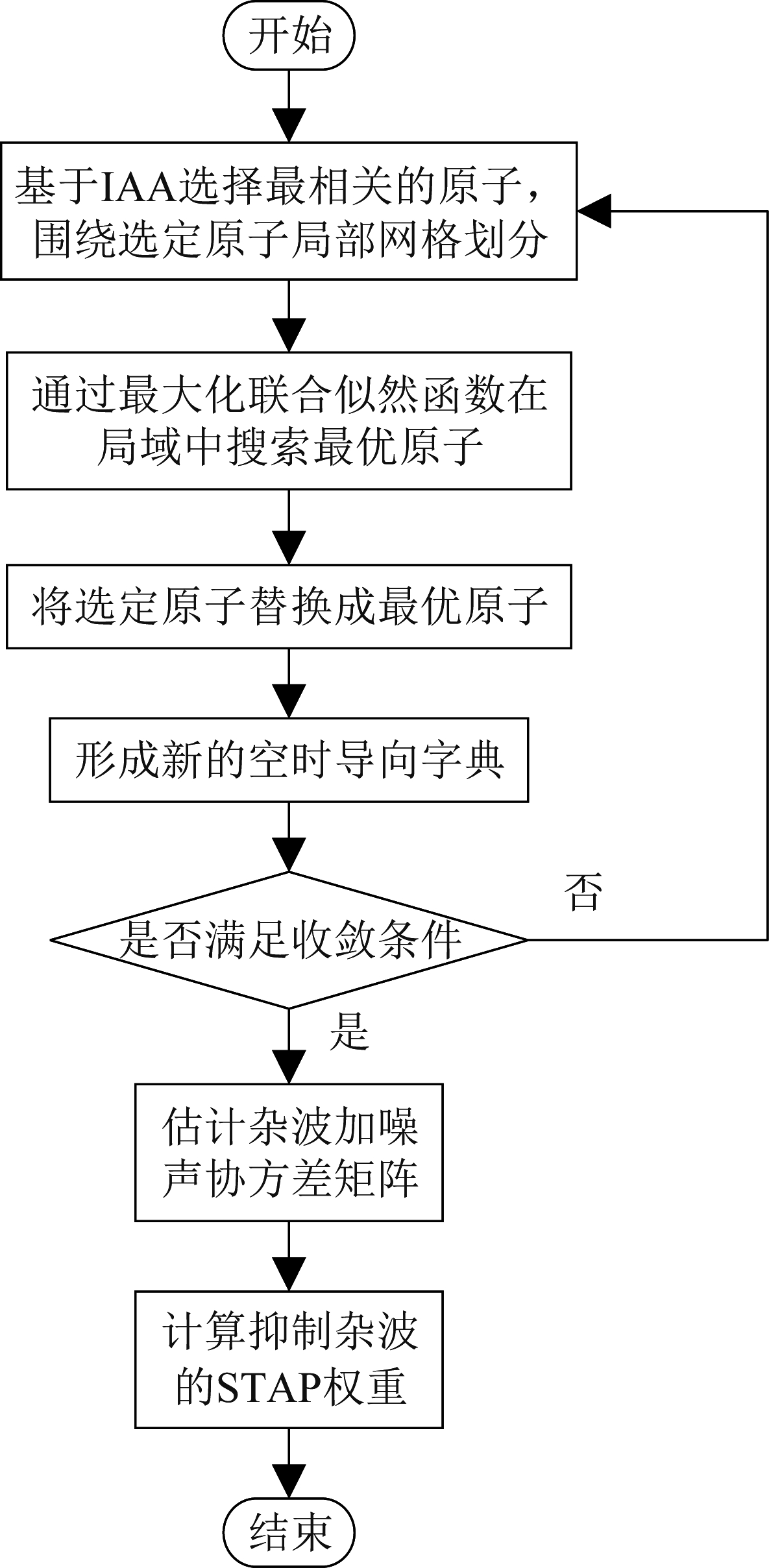
图3 IAA-STAP离网校正流程图
Fig.3 IAA-STAP off-grid calibration flow chart
4.1 IAA-STAP原理
IAA算法的基本思想就是求解下列加权最小二乘的优化问题[22]:
(12)
其中,
表示杂波(除了空间频率和多普勒频率为(fs,i, fd, j)信号分量之外的所有信号成分)的协方差矩阵,具体写为
Qi, j=R-pi, jv(fs,i, fd, j)v(fs,i, fd, j)H
(13)
其中,pi, j=|ai, j|2表示在点为(fs,i, fd, j)的信号功率,R=Φdiag(p1,1,p1,2,…,pNs,Nd)ΦH为空时协方差矩阵。通过求解式(12)的最优化问题,参数pi, j可以估计为
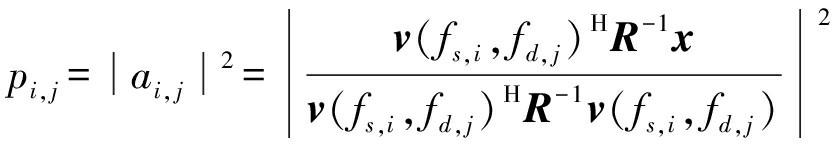
(14)
IAA-STAP算法步骤如表1所示[23],其中上标(k)代表第k次迭代,上标(k+1)代表第k+1次迭代。
4.2 字典校正过程
首先在IAA算法每次迭代中,估计原始空时导向字典上所有原子的功率,找到每个量化空间频率最大功率对应的原子,该原子就是与真实杂波导向矢量最相关的原子。设原始字典Φ的空间频率为fs,i(i=1,2,…,Ns),多普勒频率为fd, j(j=1,2,…,Nd),组成的原子功率为
每个量化空间频率最大功率对应的原子在多普勒轴上的多普勒频率f 0表示如下:
f 0=fd,pos
(15)
其次,围绕选定的原子局部网格划分并通过最大化联合似然函数在局域中搜索真杂波多普勒频率。在角度多普勒平面上,给定方向或者空间频率的杂波斑块在整个归一化多普勒范围内都是稀疏的,其多普勒频率始终位于功率最大的位置。假设杂波的空间频率为fs,i,对应的真多普勒频率为
通过最大化联合似然函数估计
的推导如下。
表1 IAA-STAP算法
Tab.1 IAA-STAP algorithm
初始化:p(0)i,j=1L∑Ll=1v(fs,i,fd,j)Hxlv(fs,i,fd,j)Hv(fs,i,fd,j)2,i=1,2,…,Ns,j=1,2,…,Nd估计R 重复迭代: 1.R(k+1)=Φdiag(p(k)1,1,p(k)1,2,…,p(k)Ns,Nd)ΦH2.for i=1:Nsfor j=1:Nda(k+1)l(i,j)=v(fs,i,fd,j)H(R(k+1))-1xlv(fs,i,fd,j)H(R(k+1))-1v(fs,i,fd,j)p(k+1)i,j=1L∑Ll=1a(k+1)l(i,j)2endend直到满足收敛条件,迭代停止计算STAP滤波器最优权矢量w=(R(k+1))-1vtvtH(R(k+1))-1vt
假设L个空时快拍样本xl (l=1,2,…,L)满足统计独立多维复数高斯分布,其均值为零,方差为矩阵R,单个空时快拍样本xl的似然函数为[8]
(16)
其中|R|表示矩阵R的行列式。L个空时快拍样本的联合似然函数为
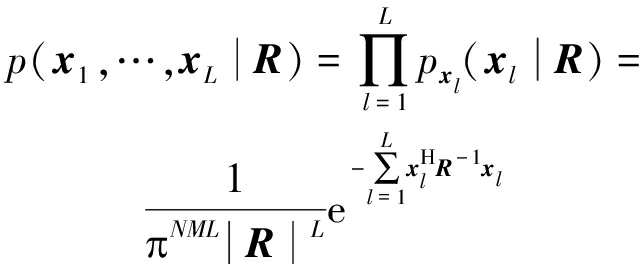
(17)
记X=[x1,…,xL]∈CNM×L,则式(17 )可重写为
(18)
其中Tr(·)是方阵的迹。
定义杂波(除了杂波
信号分量之外的所有信号成分)的协方差矩阵,具体写为
(19)
其中pi是杂波斑块
的功率。参数pi的最大似然估计(MLE)可以通过最大化联合似然函数求得:
arg min(Lln|R|+Tr(XHR-1X))
(20)
由上式(19)可知:
则R的行列式表示为
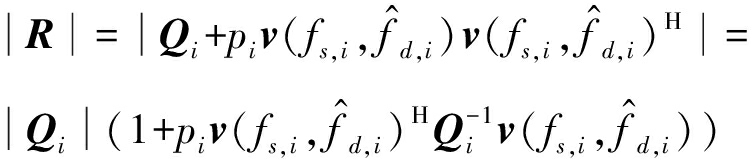
(21)
利用矩阵求逆引理,R-1表示为
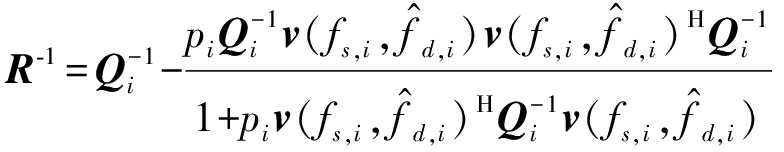
(22)
将式(21)和式(22)代入到式(20)中,式(20)重新写为
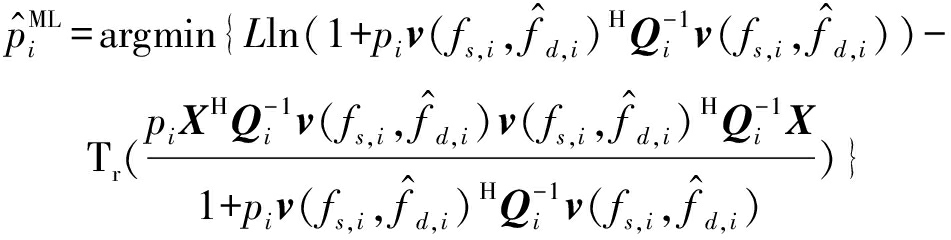
(23)
通过求解最优化问题式(23),参数pi的最大似然估计为
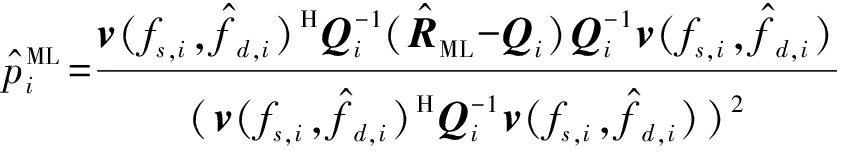
(24)
其中
使用式(19)和矩阵求逆定理,式(24)可以简化为如下表达式:
(25)
其中
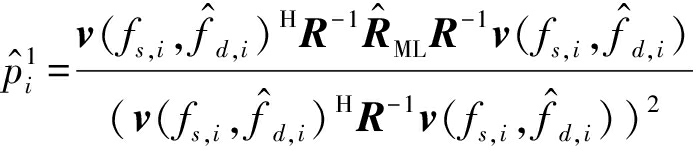
(26)
(27)
通常pi与
的值近似相等,则式(25)简化为
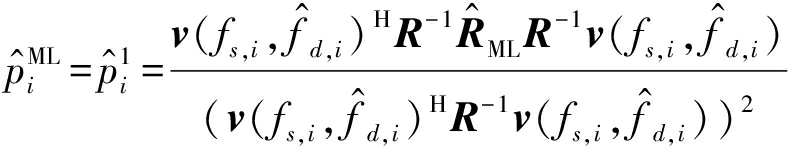
(28)
杂波的功率计算公式如式(28)所示,则估计为
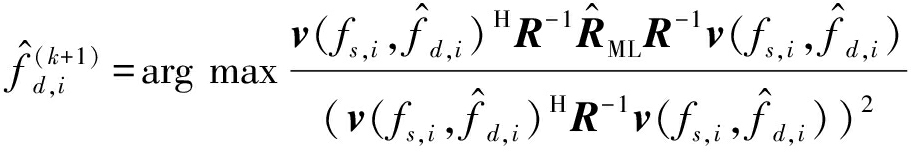
(29)
将
约束在局域
其中
通过式(29)在局域Ωi中搜索得到最优解
将函数(29)重写成局域搜索的形式:
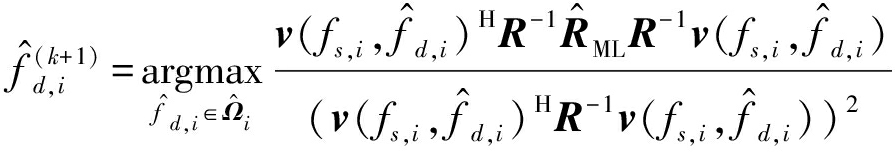
(30)
其中
为Ωi均匀离散化后形成的离散集合。
然后将原始空时导向字典中每个量化空间频率最大功率对应的原子在多普勒轴上的多普勒频率fd,pos替换成真杂波多普勒频率
(31)
最后通过选择与杂波脊匹配的原子形成新的空时导向字典Θ(k+1)。
当IAA算法的全局迭代达到规定的迭代次数时,迭代停止。基于字典校正的IAA-STAP算法步骤见表2。
表2 基于字典校正的IAA-STAP算法
Tab.2 IAA-STAP algorithm based on dictionary calibration
初始化:Θ(0)=Φpi(0)=1L∑Ll=1v(fs,i,fd,i)Hxlv(fs,i,fd,i)Hv(fs,i,fd,i)2,i=1,2,…,NsNd估计R 重复迭代: 1.R(k+1)=Θ(k)diag(p1(k),p2(k),…,p(k)NsNd)(Θ(k))H2.for i=1:NsNdal(i)(k+1)=v(fs,i,fd,i)H(R(k+1))-1xlv(fs,i,fd,i)H(R(k+1))-1v(fs,i,fd,i)pi(k+1)=1L∑Ll=1al(i)(k+1)2end3.字典校正过程R^ML=1LXXHfori=1:Nspos=argmaxj∈{1,2,…,Nd}p(k+1)(i-1)×Nd+jf0=fd,posΩi=éëêêf0-Δf2,f0+Δf2ùûúú,Δf=1ρdM将Ωi均匀离散化为Ω^if^(k+1)d,i=argmaxf^d,i∈Ω^iv(fs,i,f^d,i)H(R(k+1))-1R^ML(R(k+1))-1v(fs,i,f^d,i)(v(fs,i,f^d,i)H(R(k+1))-1v(fs,i,f^d,i))2 fd,pos=f^(k+1)d,iend4.构成新的空时导向字典Θ(k+1)直到满足收敛条件,迭代停止计算STAP滤波器最优权矢量w=(R(k+1))-1vtvtH(R(k+1))-1vt
5 算法仿真与分析
本节通过实验评估所提出的基于迭代自适应的字典校正STAP算法的性能,采用训练样本数为10,分别仿真离网发生时,相关算法的杂波功率谱和输出SCNRloss曲线。本节还对相关算法的计算复杂度进行分析。机载正侧视脉冲多普勒雷达系统的参数见表3。
表3 机载雷达系统参数
Tab.3 Parameters of airborne radar system
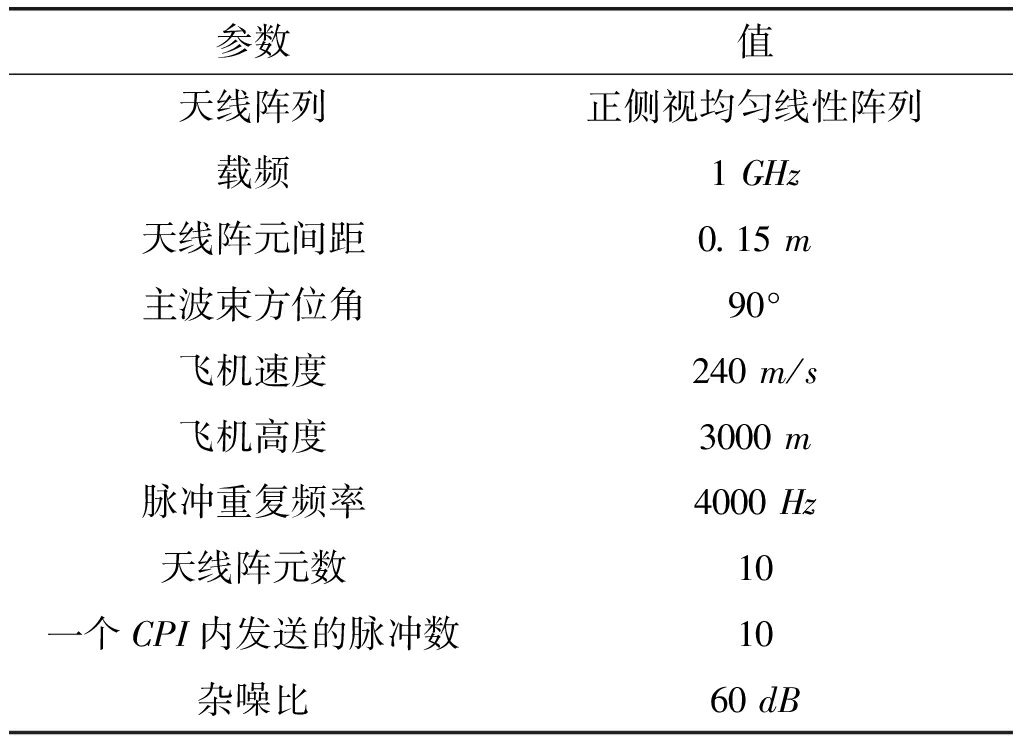
参数值天线阵列正侧视均匀线性阵列载频1 GHz天线阵元间距0.15 m主波束方位角90°飞机速度240 m/s飞机高度3000 m脉冲重复频率4000 Hz天线阵元数10一个CPI内发送的脉冲数10杂噪比60 dB
根据公式计算杂波脊的斜率
本文分别设置分辨率标度ρs=6和ρd=6,即Ns=60和Nd=60,Ns和Nd的比值不等于杂波脊斜率的整数倍,此时发生离网。
5.1 杂波功率谱分析
第一个实验比较SMI算法、传统IAA-STAP算法、基于文献[13]的IAA-STAP算法、基于稀疏贝叶斯学习(Sparse Bayesian Learning, SBL)的字典校正STAP算法[13]以及本文方法在发生离网的情况下杂波的Capon谱。Capon谱是STAP中用于分析杂波空时分布的一种高分辨率谱,杂波的Capon谱定义为
(32)
图4为发生离网时,不同算法的杂波功率谱估计结果。图4(a)为SMI算法的Capon谱,其估计精度较低,能量分布比较分散。图4(b)为传统IAA-STAP算法估计的Capon谱。图4(c)为基于文献[13]的IAA-STAP方法估计的Capon谱,文献[13]是基于稀疏贝叶斯学习方法估计杂波协方差矩阵,图4(c)是通过基于IAA方法估计杂波协方差矩阵,在此基础上增加文献[13]的字典校正过程得到的结果。图4(d)和图4(e)分别为文献[13]的SBL-STAP字典校正算法和本文方法估计的Capon谱。
图4 离网情况下杂波Capon谱估计
Fig.4 Clutter Capon spectrum estimation under off-grid conditions
传统的IAA-STAP由于离网效应的影响,杂波脊有一定展宽,频谱展宽会导致STAP滤波器的杂波抑制不充分,低速动目标检测性能变差。在少样本的条件下,基于文献[13]的IAA-STAP方法、SBL-STAP字典校正算法、本文方法形成的杂波谱均集中在杂波脊上,缓解了离网引起的杂波脊展宽。相较而言,本文方法估计的杂波功率谱更加准确。
5.2 输出信杂噪比损失分析
本文采用输出SCNRloss作为杂波抑制性能的评价指标,对比了在离网发生时,本文所提算法、传统IAA-STAP算法、基于文献[13]的 IAA-STAP算法、SBL-STAP字典校正算法的SCNRloss曲线。相关算法的SCNRloss曲线见图5。
由图5(a)可知,传统IAA-STAP方法的性能严重损失,是由于该方法的主瓣性能损失严重,旁瓣过高。相比而言,本文所提方法利用10个样本形成的滤波权得到的SCNRloss效果较好,体现了所提算法在小样本条件下的优势。本文所提具有离网校正功能的IAA-STAP方法的杂波抑制能力优于传统IAA-STAP方法和基于文献[13]的IAA-STAP方法。由图5(b)可知,文献[13]SBL-STAP字典校正方法和本文方法的杂波抑制性能都较好,但是文献[13]方法SCNRloss的凹口较宽,最小检测速度较大,导致低速动目标检测性能变差。
5.3 计算复杂度分析
本小节分析了传统IAA-STAP算法,采用文献[13]字典校正过程的IAA-STAP算法,文献[13]SBL-STAP字典校正算法,以及本文方法的计算复杂度。相关算法的单个样本的平均计算复杂度见表4,其中
传统IAA-STAP算法的计算复杂度较低,由5.1和5.2小节可知,传统IAA-STAP算法的性能也较差。传统IAA-STAP算法采用文献[13]的字典校正过程形成基于文献[13]的IAA-STAP算法,该算法的计算复杂度远高于传统IAA-STAP算法,是由于该算法采用互补字典校正原始空时导向字典。文献[13]是基于稀疏贝叶斯学习的字典校正STAP算法,该算法的计算复杂度远高于其他3个算法。
图5 离网情况下SCNRloss与归一化多普勒频率的关系
Fig.5 Relationship between SCNRloss and normalized Doppler frequency when off-grid appears
表4 单个样本的平均计算复杂度比较
Tab.4 Comparison of average computational complexity of a single sample
算法名称复数乘法数复数加法数传统IAA-STAP算法(2J2+5J+4)J～+J3(2J2+3J-4)J～+J3-J2基于文献[13]的IAA-STAP算法(2J2+5J+4)(J～+Ns)+J3+(2J2+4J+1)Ns(2J2+3J-4)(J～+Ns)+J3-J2+(2J2+J-3)Ns文献[13]所提算法(3J2+5J+4)(J～+Ns)+J3+(2J2+4J+1)Ns(3J2+1)(J～+Ns)+J3-J2-J+3+(2J2+J-3)Ns本文所提算法(2J2+5J+4)J～+J3+(2J2+4J+1)Ns(2J2+3J-4)J～+J3-J2+(2J2+J-3)Ns
与基于文献[13]的IAA-STAP算法相比,本文所提算法的复乘数比其少(2J2+5J+4)Ns,复加数比其少(2J2+3J-4)Ns。与文献[13]SBL-STAP字典校正算法相比,本文所提算法的复乘数比其少
复加数比其少
通过对比分析相关算法的杂波功率谱、输出SCNRloss曲线、计算复杂度可知,本文所提算法的杂波抑制性能优于传统IAA-STAP算法、采用文献[13]字典校正过程的IAA-STAP算法;计算复杂度低于基于文献[13]的IAA-STAP算法、文献[13]SBL-STAP字典校正算法。因此,本文所提算法在提高了STAP性能的基础上降低了计算量,改善了算法的实时性。
6 结论
基于稀疏恢复的空时自适应处理由于字典设置不合适或系统参数误差等因素,极易发生离网问题,导致明显的性能损失。为解决离网问题,本文提出了基于迭代自适应的字典校正稀疏STAP算法。首先基于IAA算法选择与杂波点最相关的原子,然后围绕选定的原子进行局部网格分割,并通过最大化联合似然函数在局域中搜索真杂波多普勒频率,其次将选定的原子替换成频率为真杂波多普勒频率的原子,最后通过IAA算法的全局迭代,选择与杂波脊匹配的原子形成新的空时导向字典,当发生离网时,新的空时导向字典的原子可以自适应地收敛到杂波脊,保证杂波脊准确落在采样网格上。实验结果表明,与现有算法相比,所提算法明显缓解了由离网引起的杂波脊扩展,提高了杂波抑制性能。
[1] 谢文冲, 段克清, 王永良. 机载雷达空时自适应处理技术研究综述[J]. 雷达学报, 2017, 6(6): 575-586.
XIE Wenchong, DUAN Keqing, WANG Yongliang. Space time adaptive processing technique for airborne radar: An overview of its development and prospects[J]. Journal of Radars, 2017, 6(6): 575-586.(in Chinese)
[2] KLEMM R. Introduction to space-time adaptive processing[J]. Electronics & Communication Engineering Journal, 1999, 11(1): 5-12.
[3] 张天祥. 基于稀疏恢复的机载MIMO雷达杂波抑制[D]. 南京: 南京航空航天大学, 2018.
ZHANG Tianxiang. Airborne MIMO radar clutter suppression based on sparse recovery[D]. Nanjing: Nanjing University of Aeronautics and Astronautics, 2018. (in Chinese)
[4] MELVIN W L. Space-time adaptive radar performance in heterogeneous clutter[J]. IEEE Transactions on Aerospace and Electronic Systems, 2000, 36(2): 621- 633.
[5] WU Yifeng, WANG Tong, WU Jianxin, et al. Training sample selection for space-time adaptive processing in heterogeneous environments[J]. IEEE Geoscience and Remote Sensing Letters, 2015, 12(4): 691- 695.
[6] 阳召成, 黎湘, 王宏强. 基于空时功率谱稀疏性的空时自适应处理技术研究进展[J]. 电子学报, 2014, 42(6): 1194-1204.
YANG Zhaocheng, LI Xiang, WANG Hongqiang. An overview of space-time adaptive processing technology based on sparsity of space-time power spectrum[J]. Acta Electronica Sinica, 2014, 42(6): 1194-1204.(in Chinese)
[7] 高志奇. 机载雷达的稳健稀疏空时自适应处理方法研究[D]. 西安: 西安电子科技大学, 2016.
GAO Zhiqi. Robust sparseness space-time adaptive processing algorithms for airborne radar[D]. Xi’an:Xidian University, 2016. (in Chinese)
[8] 阳召成. 基于稀疏性的空时自适应处理理论和方法[D]. 长沙: 国防科学技术大学, 2013.
YANG Zhaocheng. Theory and methods of sparsity-based space-time adaptive processing[D]. Changsha: National University of Defense Technology, 2013. (in Chinese)
[9] DONOHO D L, ELAD M, TEMLYAKOV V N. Stable recovery of sparse overcomplete representations in the presence of noise[J]. IEEE Transactions on Information Theory, 2006, 52(1): 6-18.
[10] DUAN Keqing, WANG Zetao, XIE Wenchong, et al. Sparsity-based STAP algorithm with multiple measurement vectors via sparse Bayesian learning strategy for airborne radar[J]. IET Signal Processing, 2017, 11(5): 544-553.
[11] 李志汇, 张永顺, 高乾, 等. 基于局部搜索OMP的网格失配STAP算法[J]. 系统工程与电子技术, 2018, 40(6): 1221-1226.
LI Zhihui, ZHANG Yongshun, GAO Qian, et al. Off-grid STAP algorithm based on local search orthogonal matching pursuit[J]. Systems Engineering and Electronics, 2018, 40(6): 1221-1226.(in Chinese)
[12] 章涛, 钟伦珑, 来燃, 等. 基于稀疏贝叶斯学习的字典失配杂波空时谱估计算法[J].航空学报,2021,42(5):324592.
ZHANG Tao, ZHONG Lunlong, LAI Ran, et al. Sparse Bayesian learning method for eliminating dictionary mismatch in clutter spectrum estimation [J]. Acta Aeronautica et Aeronautica Sinica, 2021,42(5): 324592. (in Chinese)
[13] YUAN Huadong, XU Hong, DUAN Keqing, et al. Sparse Bayesian learning-based space-time adaptive processing with off-grid self-calibration for airborne radar[J]. IEEE Access, 2018, 6: 47296- 47307.
[14] DUAN Keqing, LIU Weijian, DUAN Guangqing, et al. Off-grid effects mitigation exploiting knowledge of the clutter ridge for sparse recovery STAP[J]. IET Radar, Sonar & Navigation, 2018, 12(5): 557-564.
[15] BAI Gatai, TAO Ran, ZHAO Juan, et al. Parameter-searched OMP method for eliminating basis mismatch in space-time spectrum estimation[J]. Signal Processing, 2017, 138: 11-15.
[16] YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al. Adaptive clutter suppression based on iterative adaptive approach for airborne radar[J]. Signal Processing, 2013, 93(12): 3567-3577.
[17] FENG Weike, GUO Yiduo, HE Xingyu, et al. Jointly iterative adaptive approach based space time adaptive processing using MIMO radar[J]. IEEE Access, 2018, 6: 26605-26616.
[18] YANG Pengcheng, LYU Xiaode, CHAI Zhihai, et al. Clutter cancellation along the clutter ridge for airborne passive radar[J]. IEEE Geoscience and Remote Sensing Letters, 2017, 14(6): 951-955.
[19] KLEMM R. Applications of space-time adaptive processing[M]. The Institution of Engineering and Technology, Michael Faraday House, Six Hills Way,Stevenage SG1 2AY, UK: IET, 2004.
[20] YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al. Knowledge-aided STAP with sparse-recovery by exploiting spatio-temporal sparsity[J]. IET Signal Processing, 2016, 10(2): 150-161.
[21] CANDES E J, WAKIN M B. An introduction to compressive sampling[J]. IEEE Signal Processing Magazine, 2008, 25(2): 21-30.
[22] YARDIBI T, LI Jian, STOICA P, et al. Source localization and sensing: A nonparametric iterative adaptive approach based on weighted least squares[J]. IEEE Transactions on Aerospace and Electronic Systems, 2010, 46(1): 425- 443.
[23] YANG Zhaocheng, LI Xiang, WANG Hongqiang, et al. Adaptive clutter suppression based on iterative adaptive approach for airborne radar[J]. Signal Processing, 2013, 93(12): 3567-3577.
