1 引言
信道编码是现代通信中用来提高信道可靠度的一种泛用技术,发送端通过对原数据添加与其相关的冗余信息,再在接收端根据这种相关性来检测和纠正传输过程产生的差错从而减少传输过程的干扰。在非合作通信中,接收方需在信道编码参数未知的情况下对接收到的码字进行盲识别处理,即信道编码识别也成为了一个非常重要的问题[1]。文献[2]针对线性分组码参数盲识别容错性能较差的问题,提出了一种基于二元高斯列消元法的分组码参数盲识别方法;文献[3]针对BCH码提出一种改进的盲识别算法,提升了算法的容错性;文献[4]对码重分析法进行改进,通过计算码重分布的信息熵来识别线性分组码参数。
Turbo码因具有优秀的纠错能力而被广泛运用于现代数字通信系统中[5],它的分量编码器主要为递归系统卷积码(Recursive System Code,RSC),在非合作通信中,对RSC码的盲识别是Turbo码识别的基础,具有重要意义[6]。目前有大量针对RSC码盲识别方法的研究,文献[7]定义了双曲正切符合度并以此提出了能适应低信噪比条件的RSC码快速迭代识别算法;文献[8]对经典欧几里德算法的识别方法进行了改进;文献[9]针对RSC码提出了一种基于对数符合度下的识别新算法;文献[10]通过对RSC编码器参数进行遍历估计并与原来的输出序列进行对比来完成RSC编码参数的识别。而对Turbo码的识别主要包括码块长度、码字起点、分量编码器和交织器的识别[11],文献[12]通过定义差分似然差的概念提出一种低信噪比(SNR)下基于差分似然差(DLD)的低复杂度识别算法;文献[13]提出了一种新的基于奇偶校验方程符合度的估计算法,通过对列向量比较的方法来识别交织;文献[14]提出一种基于RSC编码器系数的最优余弦代价函数算法,在降低计算复杂度的同时提升了识别性能;文献[15]针对多维Turbo码提出了一种基于编码器结构分解的盲识别算法,能完成对分量编码器、交织等参数的识别;文献[16]提出了一种基于矩阵模型列相关性的识别方法,能有效识别出Turbo码的各项参数。
以上都是针对非删余型Turbo码的盲识别算法,而为了使Turbo码更加灵活与高效,通常会采用删余的模式来减小信息的冗余度,从而提高编码效率。针对删余型Turbo码文献[17]提到通过穷举遍历删余模式的方法来识别分量编码器参数,确实能识别一定参数但是计算量比较大;文献[18]通过使用传统线性矩阵分析法来对删余型Turbo码分量编码器参数进行盲识别,其所需要的先验信息量较大。由于部分校验位的缺失,删余型Turbo码的盲识别难度更高但更加高效与实用,对它的参数盲识别非常具有研究价值。
2 删余Turbo码简介
2.1 RSC码编码原理
RSC码因其具有系统码特性且译码快速简单的特点而被广泛作为Turbo码的分量编码器使用,对Turbo码分量编码器的识别本质上就是对RSC码的识别。一般RSC码的码率为1/2,图1为生成多项式八进制表示为(37,21)的RSC码编码结构图。
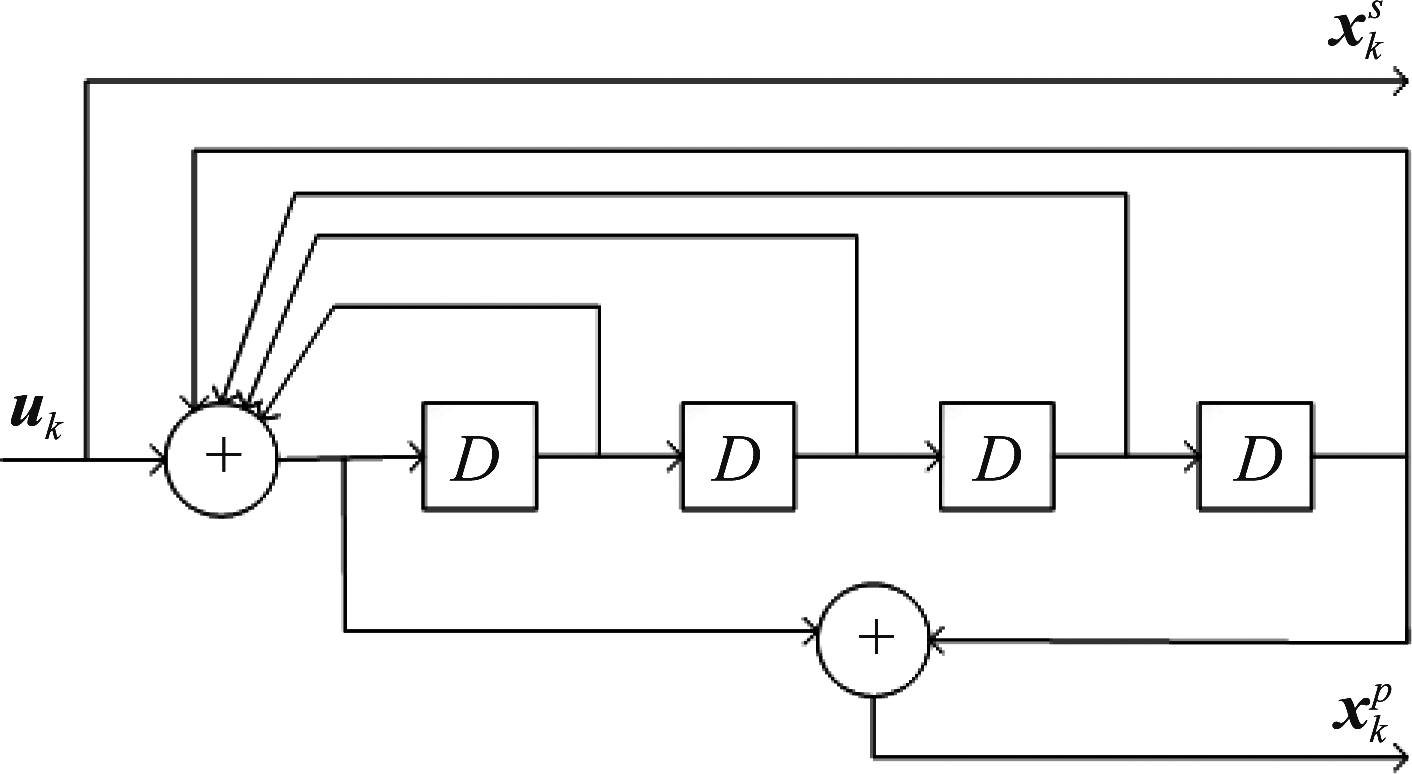
图1 (37,21)RSC码编码结构
Fig.1 (37, 21) RSC code encoding structure
码率为1/n的RSC码编码多项式C(D)可表示为
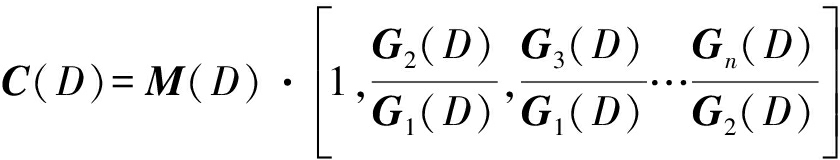
(1)
其中M(D)为信息码元多项式,Gi(D)表示每列输出对应的生成矩阵多项式。
2.2 RSC码的监督矩阵
对于任意参数的RSC码,都存在半无限生成矩阵G使c=m·G,其中m为信息序列,c为RSC码编码后的码字。每种生成矩阵G都有与之相对应的监督矩阵H使G·H=0,则有c·H=0,该关系是本文识别算法的理论基础。
RSC码可由非系统卷积码(Non System Convolutional,NSC)将生成多项式的各项都除以首项而得到,两种码的监督矩阵之间也存在对应的推导关系。RSC码的生成矩阵GR可由NSC码的生成矩阵GN经过初等列变换使每组多项式第一位所在列变为单位阵得到。值得注意的是对于RSC码该校验关系只满足于前信息位长度列,例如输入信息序列长度为100的RSC码与H相乘后只能保证前100项固定为0,而非整个半无限矩阵。
2.3 删余型Turbo码编码原理
码率为1/2的典型删余Turbo码编码器是由两个RSC码编码器通过一个随机交织器并行连接组成的,如图2所示。
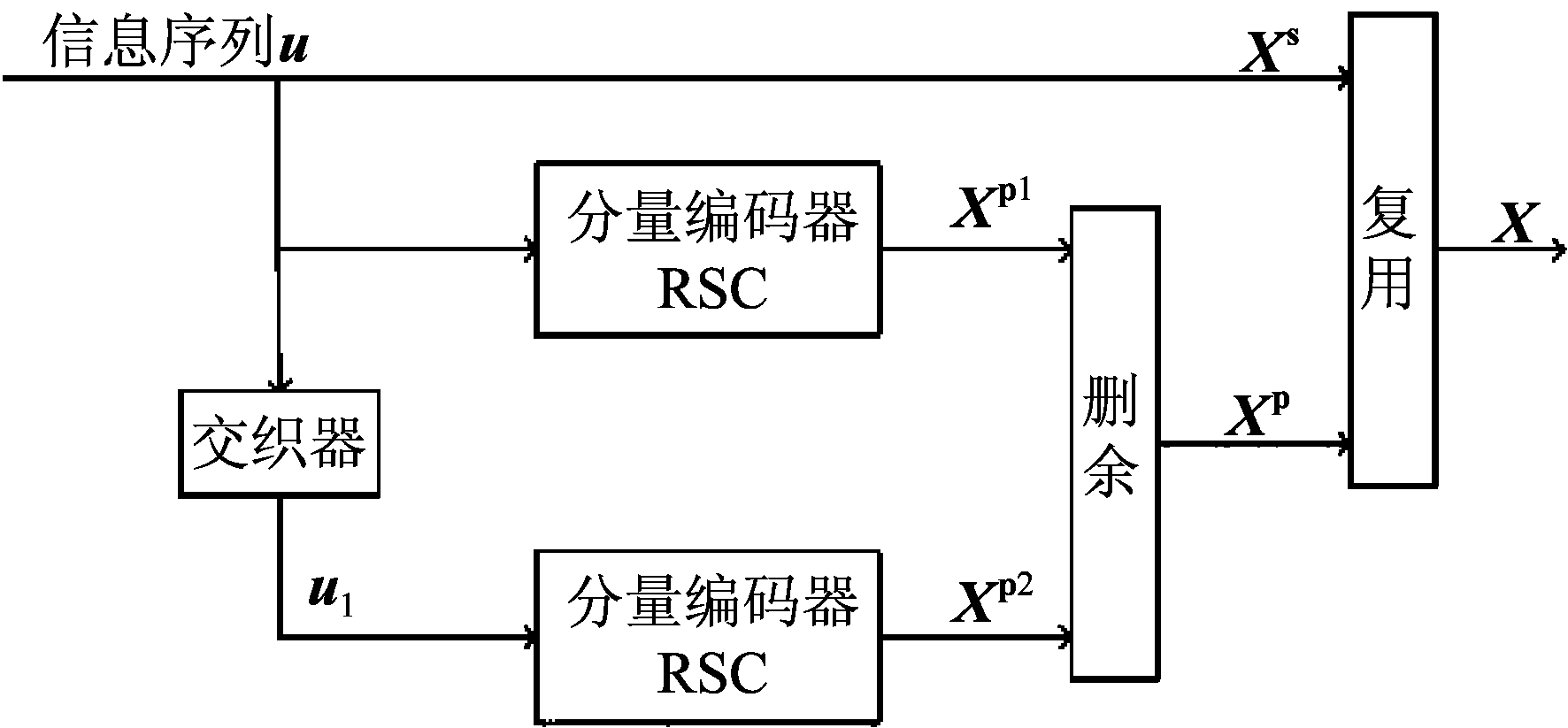
图2 删余型Turbo码编码器结构框图
Fig.2 Block diagram of punctured Turbo encoder
其中信息序列u经过交织器形成一个比特位置互换的新序列u1,u和u1分别经过RSC码编码器进行编码输出形成两个校验序列Xp1和Xp2,然后通过删余从这两个序列中周期性地删除一半校验位形成校验序列Xp,原信息序列Xs与Xp经过复用调制后形成删余型Turbo码序列X。
3 删余型Turbo码盲识别原理及方法
3.1 码长及起始点位置识别
识模型取最常用的1/3码率Turbo码,通过删余矩阵
得到码率为1/2的典型删余型Turbo码C′,其分量编码器为生成多项式
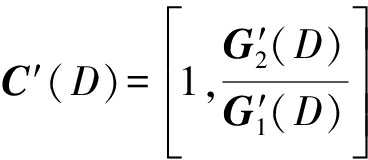的(2,1)RSC码编码器。截获若干条完整码字组成的比特流信息,非合作方需要从该截获比特流中识别出Turbo码的各项完整参数。
典型删余型Turbo码的编码方式可用矩阵形式表示为
C′=m[j1,0, j2,0, j3…]+ mG[0, j2,0,0,0, j6,0,0,0, j10…]+ 
(2)
其中m表示信息序列,G表示对应的RSC码生成矩阵,
表示经过交织后的信息序列, ji表示第i行为1其余为0的列向量。由于(2,1)RSC码是一种系统码,其编码方式按照类似的矩阵形式可拆分表示为
CRSC=mG=m[j1,0, j2,0, j3…]+ mG[0, j2,0, j4,0, j6…]
(3)
对比两种码的编码方式可知,典型删余型Turbo码与对应的RSC码只在编码序列中4的整数倍位(第4、8、16…4n位)上有所差异,前者在该位上是原码先经过交织再通过RSC编码后的校验位,而后者在该位上是原码经过RSC编码后的校验位,将这些位置称作为删余位。可以看出该删余型Turbo码与相应的RSC码在构造上具有一定的相似性,且由于交织只改变信息序列的位置关系,则Turbo码的各个码字之间也存在线性关系。于是同一般线性分组码一样可以使用线性矩阵分析法[18]来识别Turbo码码长及起点位置,将码字有序排列成p×q(p>q)的矩阵形式,其中p和q分别表示矩阵的行数和列数。则当q刚好等于码长或码长的倍数时矩阵列不满秩,且矩阵起点位置与码字位置重合时矩阵的秩最小,具体识别步骤如下:
①将接收到的码字有序排列为p×q的分析矩阵形式,并求出该矩阵的秩r,并定义秩信息熵h,如公式(5)所示
(4)
②遍历列数q的大小同时重复步骤①求出不同q下分析矩阵的秩信息熵,找到各个极大值点,所有极大值点所对应q的最大公约数就是该码字的码长n。
③求得码长n后将分析矩阵的列数调整为2n,然后遍历分析矩阵的起始点位置并计算出矩阵的秩,当分析矩阵的秩最小的时候该矩阵起点位置即为码字的起点位置。
3.2 分量编码器识别原理
对于分量编码器的参数识别主要是针对RSC码的生成矩阵G或生成多项式G(D)的识别,该参数是完成译码所必要的条件。对于非删余型Turbo码,由于不存在删余操作,接受到的码字中包含了完整的RSC码,于是其参数的识别就等价于RSC码的盲识别,所以本文针对删余型Turbo码分量编码器参数进行盲识别研究,更具有研究性和实用性。
文献[19]给出了约束长度7以内的RSC码生成多项式的八进制表达式,根据该表达式可以建立不同参数RSC码所对应生成矩阵的数据库。根据公式(2)可知,编码后的RSC码字cRSC与其对应的监督矩阵H之间存在以下关系
cRSC·H=0
(5)
也就是说H中的每一列都是RSC码字的零空间向量,而Turbo码在构造上又与RSC码存在一定相似性。在二元域中将接收到的码字与各个参数的校验矩阵按码长n进行迭代相乘,统计乘积结果向量中‘0’的个数作为衡量码字与该参数下校验矩阵的匹配度。由公式c·H=0可知,当选用的校验矩阵参数与实际参数值达到一致时,码字与它乘积结果中‘0’所占比例最大且远超其他错误参数构造下的校验矩阵,在无误码情况下能够达到百分之百。于是该匹配度能作为衡量校验矩阵参数是否与实际参数一致的指标,匹配度最大值所对应的校验矩阵参数即为所求,再根据校验矩阵计算出对应的生成矩阵则可完成对分量编码器的参数识别。
以上方法虽然能完成分量编码器的参数识别,但主要有以下缺点:①完成识别需要多段完整码字,对接收信息的总量有要求;②识别分量编码器参数前必须先完成对码长n的识别,若代入码长非真实码长则会对识别结果有所影响;③Turbo码经过删余操作后不包含完整的RSC码码字,它的码字不能用RSC码的生成矩阵来线性表示。为解决以上问题,本文针对删余型Turbo码对分量编码器的识别方法进行改进。
设x1和x2分别是长度为l1和l2的比特序列(l1<l2),且x1是与x2的前l1位相同的子序列。将x1和x2经过同一RSC码编码后生成码字c1和c2,则c1是与c2的前2l1位相同的子码,如下式所示
x1·Gl1=c1∈c2=x2·Gl2
(6)
于是在进行序列与监督矩阵匹配时,可从头截取非固定长度li的序列进行匹配,这样做一方面可以进行多次不同长度的序列匹配来提高识别率,另一方面是在码长N未知的情况下依然可以对生成多项式C(D)进行盲识别。
截取序列长度li的选择不能过长否则会包含大量误比特而影响识别率,过短则所包含的信息量过少而难以识别。且由于码率为1/2的删余型Turbo码输出具有周期为4的排列周期性,即按原码u、校验序列Xp1、原码u、校验序列Xp2的顺序周期性输出,如图3所示。
图3 删余Turbo码结构
Fig.3 Structure of punctured Turbo Codes
则li的取值尽量选择偶数且li之间的间隔不小于4,一般情况下li以不小于4的周期在70至100的范围内选取,具体选取情况在第4节中介绍。
除此之外,删余型Turbo码可看作在删余位上0和1出现概率均接近1/2的RSC码。从概率统计学的角度上来讲,可将删余位看作1的出现概率P=1/2的二项分布,此时分布是对称的。为使接收码字更加近似于对应的RSC码,可将码字删余位的比特进行归零处理,同时在构造监督矩阵数据库时,首先将RSC码生成矩阵中删余位所对应的整列取零,然后将这些矩阵在二元域中的零空间矩阵作为监督矩阵,这样能使监督矩阵与码字之间的契合度更高,从而提高识别率。
3.3 分量编码器识别步骤
根据3.2节中的分析与算法改进,针对删余型Turbo码分量编码器参数的具体的盲识别步骤如下:
①若接收端截获到足够多的L段码字且已经识别出真实码长n。
步骤1 把每段完整码字c1,c2,…,cL中的删余位比特归零构造出识别序列
步骤2 将不同参数生成矩阵中删余位对应的整列归零,求出它们二元域中的各个零空间向量。
步骤3 将各段识别序列
以码长n的长度与各参数下的零空间向量迭代相乘,分别统计它们乘积结果中‘0’的个数并取均值,该值越大则代表该校验矩阵参数与实际值越相近,它的最大值所对应的生成矩阵参数即为所求。
②若接收端截获到的码字较短且无法判断该码码长以及该码字是否完整。
步骤1 把接收到的整个码字序列c中的删余位比特归零,从码字起点位置开始分别以不同的合适长度li对序列进行截取来构造识别序列
步骤2 分别以各li作为码长来构建不同参数下的生成矩阵并将矩阵中删余位对应的整列归零,求出它们二元域中的各个零空间矩阵作为监督矩阵H的数据库使用。
步骤3 将每一组识别序列
与其长度一致的监督矩阵
相乘,统计不同生成多项式C(D)下乘积结果中‘0’出现的次数为
求出对应的匹配度
(7)
该参数如3.2节中所述能反映码字与监督矩阵之间的对应情况,当选取的检验矩阵参数与码字参数达到一致时,它们之间乘积结果中‘0’所占比例就达到最大值,于是该参数可以作为衡量指标使用。
步骤4 当同一生成多项式Cj(D)对应的匹配度在多个不同长度li下都为整个数据库中的最大值,则判断Cj(D)即为所求生成多项式C′(D)。如果匹配度最大值对应的生成多项式没有一个统一的量,则适当调整截取长度li返回步骤2,直到不同li下匹配度最大值对应生成多项式能够达到一定程度的统一。
4 仿真验证和性能分析
4.1 参数识别仿真
首先是码长的识别,假设接收端接收到若干组码长为128的典型删余型Turbo码序列,将码字按序排列为矩阵形式,分析矩阵行数p取600,计算出其列数q在60至520的秩信息熵分布如图4所示。
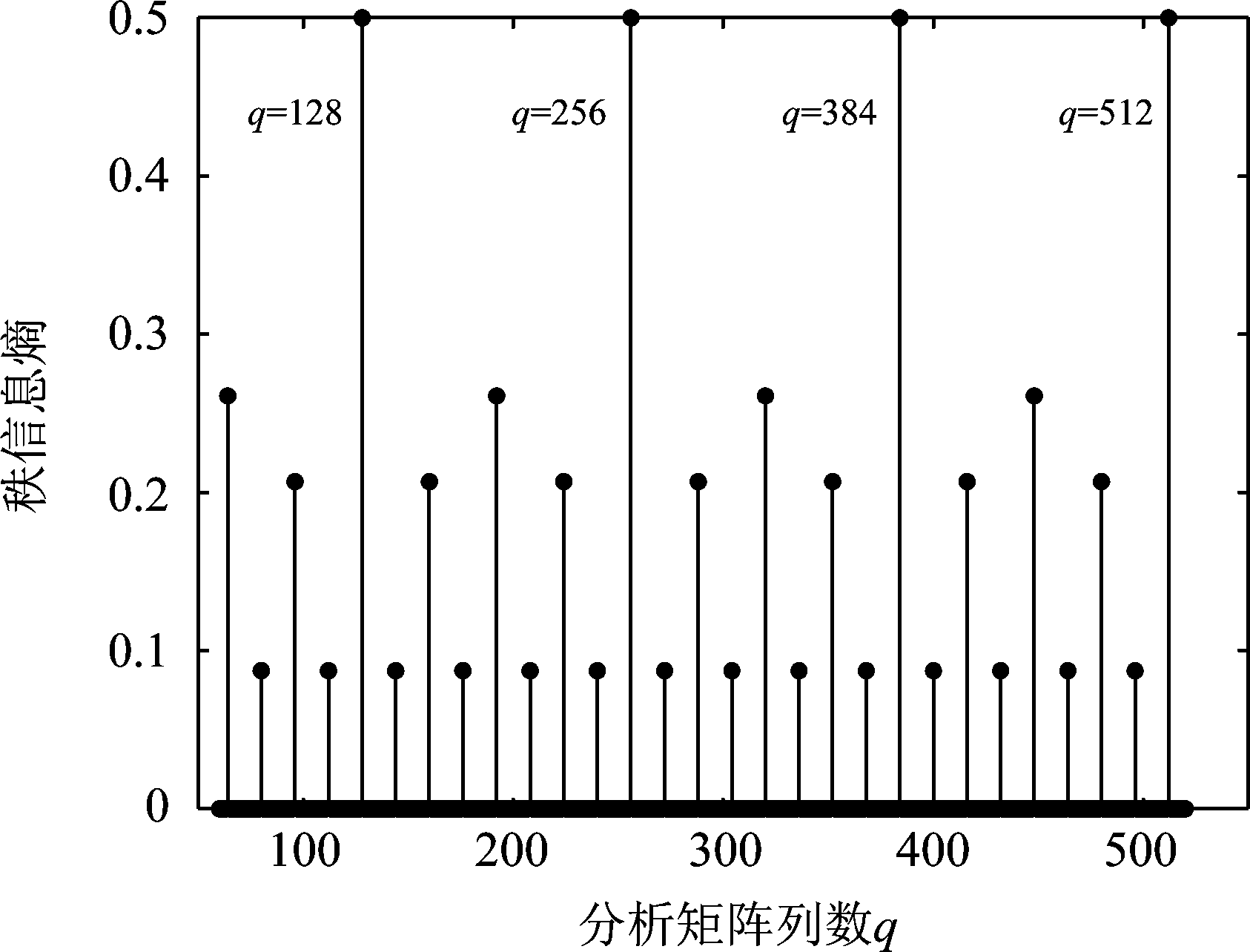
图4 秩信息熵分布情况
Fig.4 Information entropy distribution
根据图中秩信息熵的分布极大值的分布情况就可以识别出该码字的码长为128。
进一步规定该典型删余型Turbo码的分量RSC编码器生成多项式的八进制表示为(141,155),在约束长度7以内的RSC码生成多项式数据库中索引号为577。将接受到的码字按3.3节中情况①的方法进行分析与计算,图5为其乘积结果中‘0’出现次数均值的统计情况。
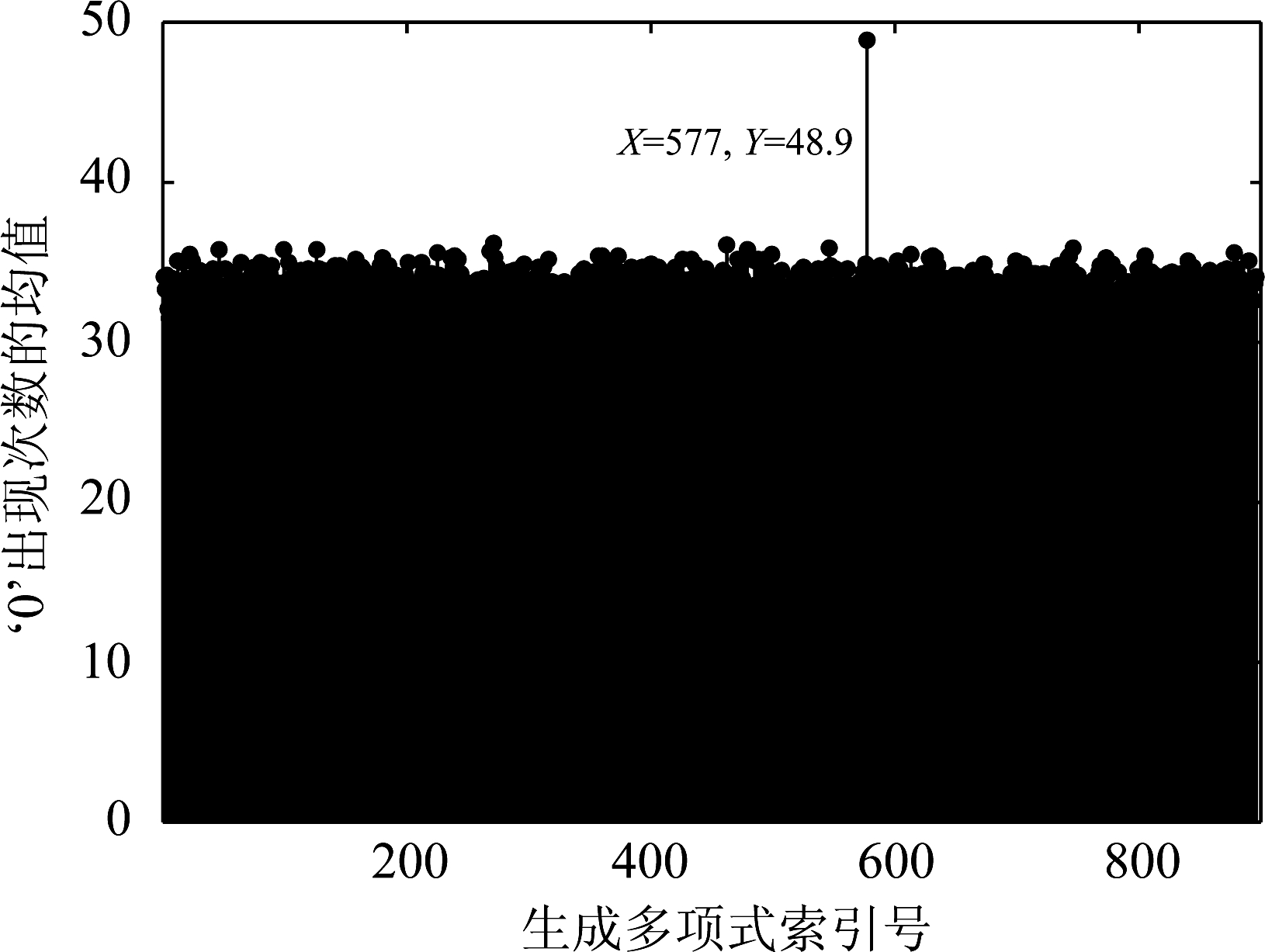
图5 分量编码器参数识别
Fig.5 Parameter recognition of component encoder
由图5可以看出,当生成多项式索引号为577时,该统计量有最大值48.9,而在取其他生成多项式参数时该值仅能达到35左右,由此就可以成功识别出该Turbo码分量编码器的生成多项式为所求的(141,155)。
假设接收端截获到的码字较少甚至没有一段完整的码字,且码长也是未知的情况下,则改为情况②中的算法步骤。在截取长度li分别取l1=80,l2=100,l3=120时,其匹配度计算的结果分布如图6所示。
由图6可知,截取序列长度li取不同值时匹配度最大值均为1,且其所对应的生成多项式索引号均为577,则以此盲识别出该RSC码的生成多项式八进制表示为(141,155),可见该算法在已知信息非常少的情况下也能对删余型Turbo码分量编码器参数进行有效识别。
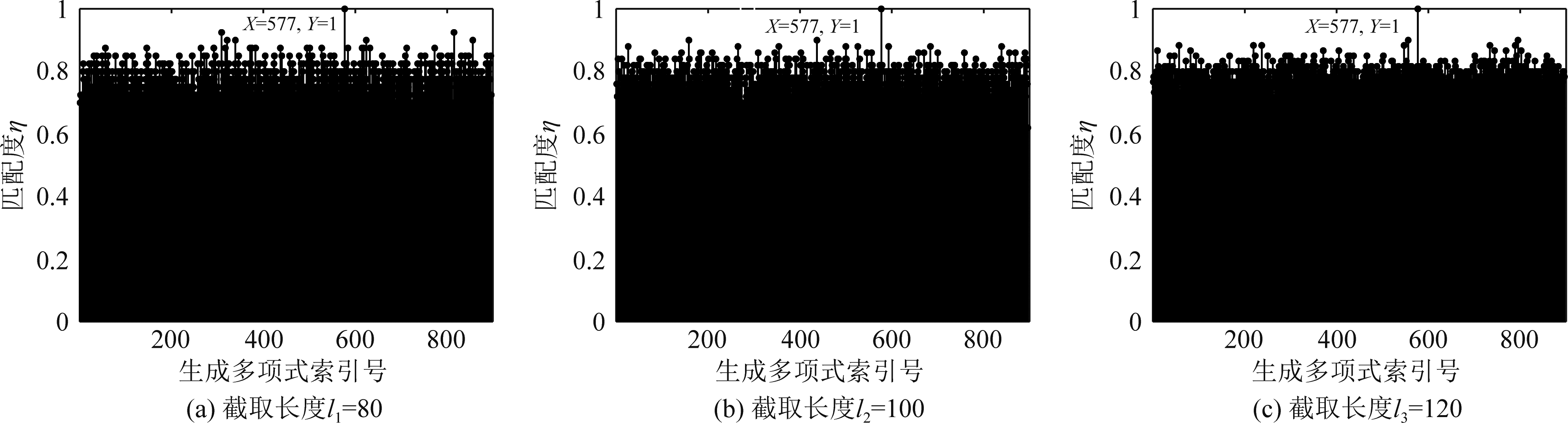
图6 不同截取序列长度li下匹配度分布情况
Fig.6 Distribution of matching degree under different length of intercepted sequence li
4.2 不同截取长度li下的最大匹配度分析
在3.3节中介绍了截取长度li的选择问题,本节则对不同截取长度li下的匹配度分布情况进行分析。假设截获信号的实际码长为200,在截取长度比较小取l4=50的情况下,其匹配度分布情况如图7所示。
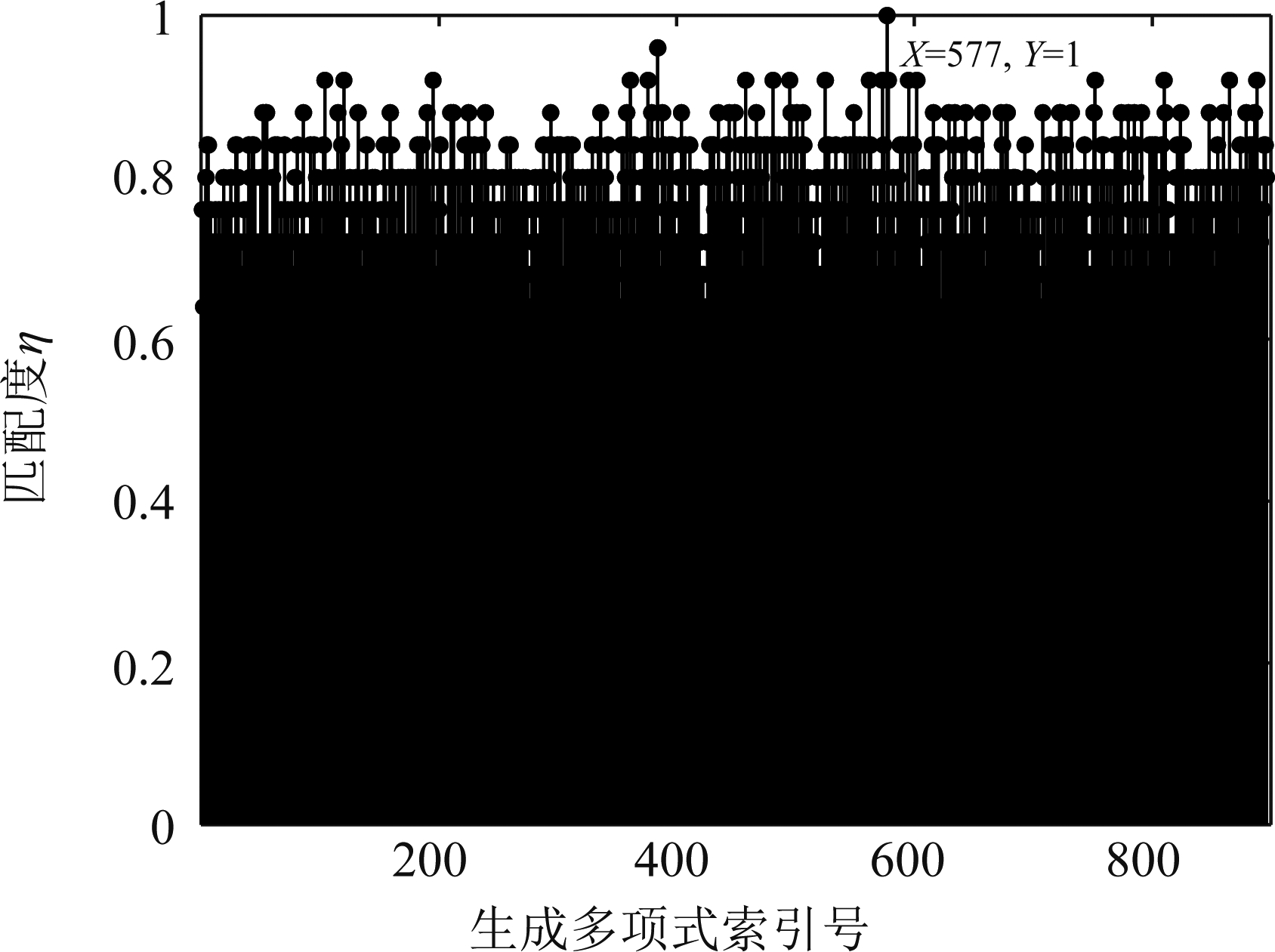
图7 截取序列长度较小时匹配度分布情况
Fig.7 The matching degree distribution of interception sequence with small length
从图7中可以看出虽然匹配度最大值所对应的生成多项式依然是(141,155),但该最大值与其他较大值之间的差距明显减小,这就容易使识别结果出错的现象出现,于是截取序列长度的选择一定不能过小。在识别过程中默认码长N是未知的,考虑截取长度li超过码长N的情况,假设码长为200的典型删余型Turbo码后面全是与其无关的随机序列,截取长度分别取l5=300和l6=400时的匹配度分布情况如图8所示。
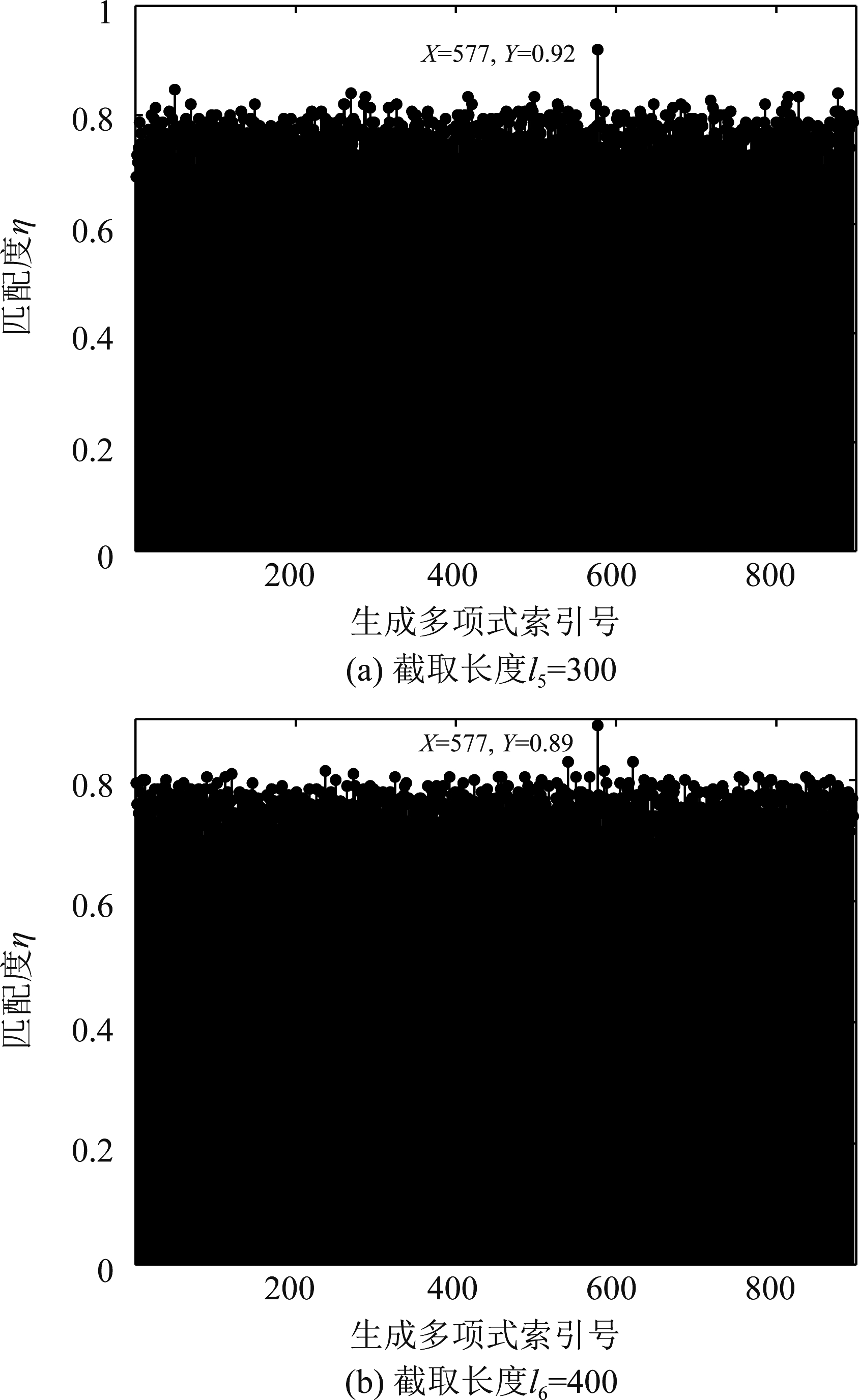
图8 截取序列长度较大时匹配度分布情况
Fig.8 The matching degree distribution of interception sequence with large length
从图8(a)中可以看出当截取长度超过了实际码长的情况下,虽然匹配度最大值减小至0.92,但其与其他匹配度的差值依然明显,此情况下仍可以正确识别出Turbo码的生成多项式。而图8(b)中当截取长度是实际码长两倍的情况下,由于包含了大量不相关的码字,其匹配度最大值降至0.89且与其他匹配度的差值较小,但其对应的生成多项式依然与实际值一致。以上现象说明该算法在截取长度超过实际码长的情况下依然能完成Turbo码生成多项式的盲识别,具有很好的容错率。
4.3 性能分析
若接收端分别接收到十组码长为256、512、900的典型删余型Turbo码,图9是对使用本文算法进行多次蒙特卡洛仿真的结果。其中横坐标为误比特率,取值范围为0到0.1,纵坐标为Turbo码分量编码器识别率。
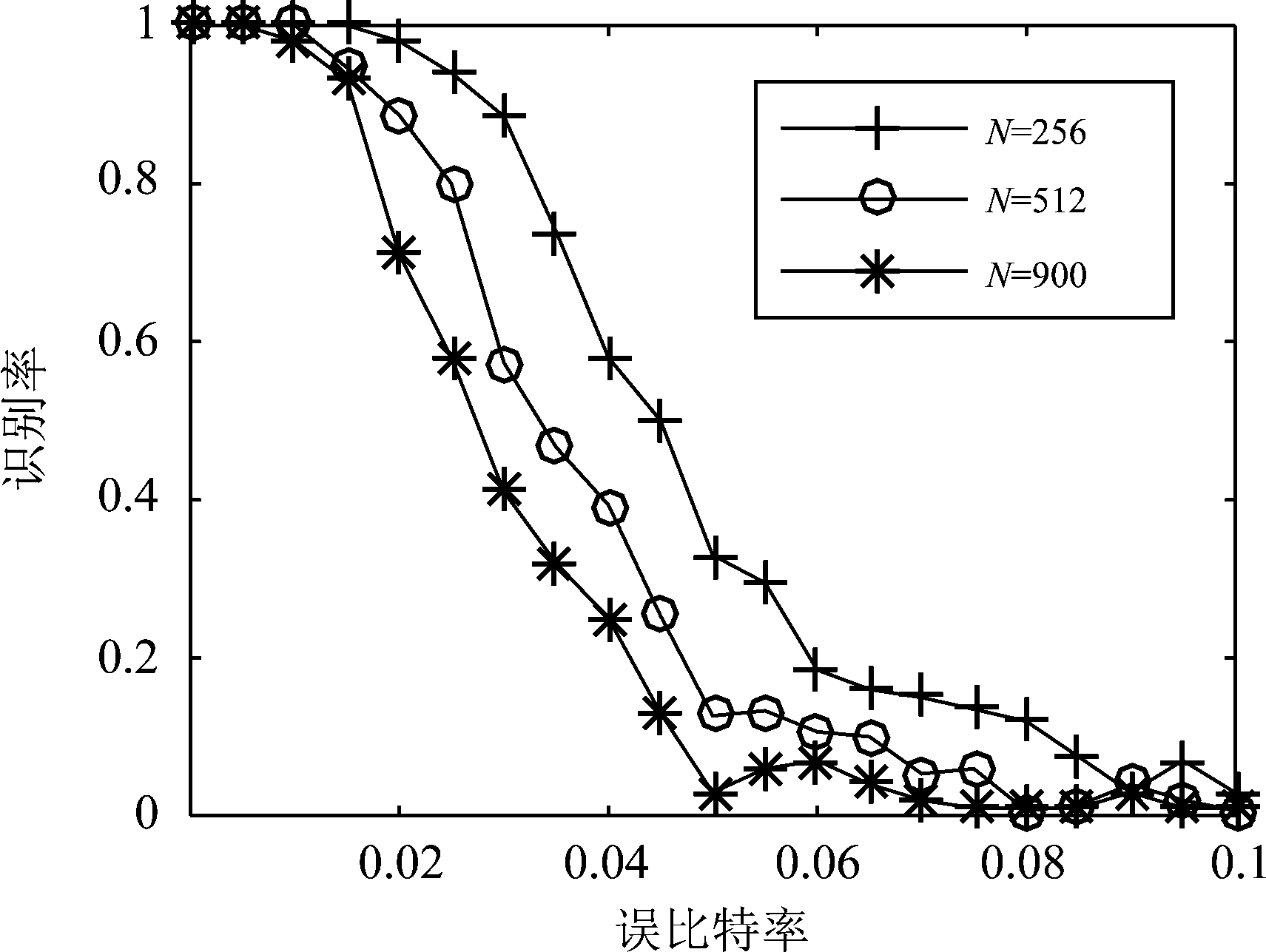
图9 对不同码长删余型Turbo码盲识别的性能仿真图
Fig.9 Performance simulation of blind recognition of punctured Turbo codes with different code lengths
由图9可以看出对删余型Turbo码分量编码器的参数盲识别,码长较短的码字比码长较长的码字有更好的识别效果,且它们的识别率随着误比特率的增大而以相似的速度减小,码长为256、512、900的删余型Turbo码识别率达到80%以上则分别要求最大误比特率不超过0.033、0.025、0.017左右。
在码长未知的情况下,对实际码长为256的单个同一典型删余型Turbo码选用不同截取长度的匹配序列进行分量编码器盲识别,截取长度li分别取32、64、92、156、320,超出码长的部分由无关的随机0,1序列组成,其500次蒙特卡洛仿真结果如图10所示,其中横坐标为误比特率,取值范围为0到0.05,纵坐标为Turbo码分量编码器识别率。
由图10可知,识别序列截取长度li的选择对识别率也有一定的影响,当截取长度选取过小,如当l=32的时候,在无误码的情况下基本上也不能识别出正确的分量编码器参数。当选取的截取长度增大到l=64的时候就能在一定程度内正确识别出分量编码器参数,但在无误码的情况下识别率也不能保持100%。截取长度取到l=92时,无误码状态下能达到100%的识别率且在误比特率不超过0.01的时候识别率能保持在80%以上。当截取长度进一步增加的,如l=156时可以看出虽然在低误码状态下能够正确识别出分量编码器参数,但随着误比特率的增大其识别率的下降速度明显加快。而当截取长度超过码字长度l=320时,仍能正确识别出分量编码器参数,但其识别率更容易受到误码的影响而快速下降。
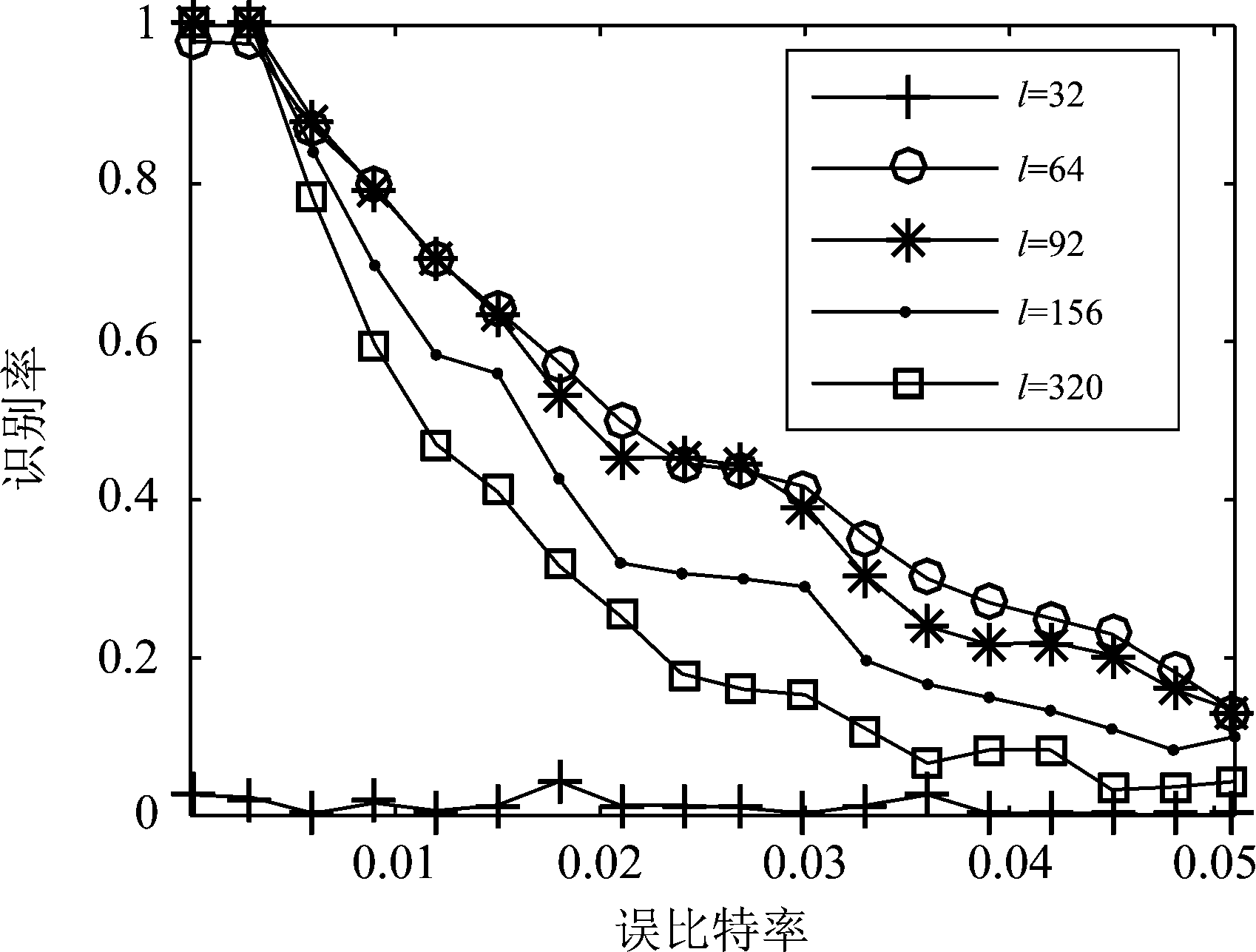
图10 选用不同截取长度对盲识别性能影响仿真图
Fig.10 Performance simulation of blind recognition of punctured turbo codes with different interception lengths
同样取l=92的截取长度对分量编码器参数进行识别,对比删余位不归零的传统校验矩阵匹配法与删余位归零的本文算法的性能差异,其仿真结果如图11所示。
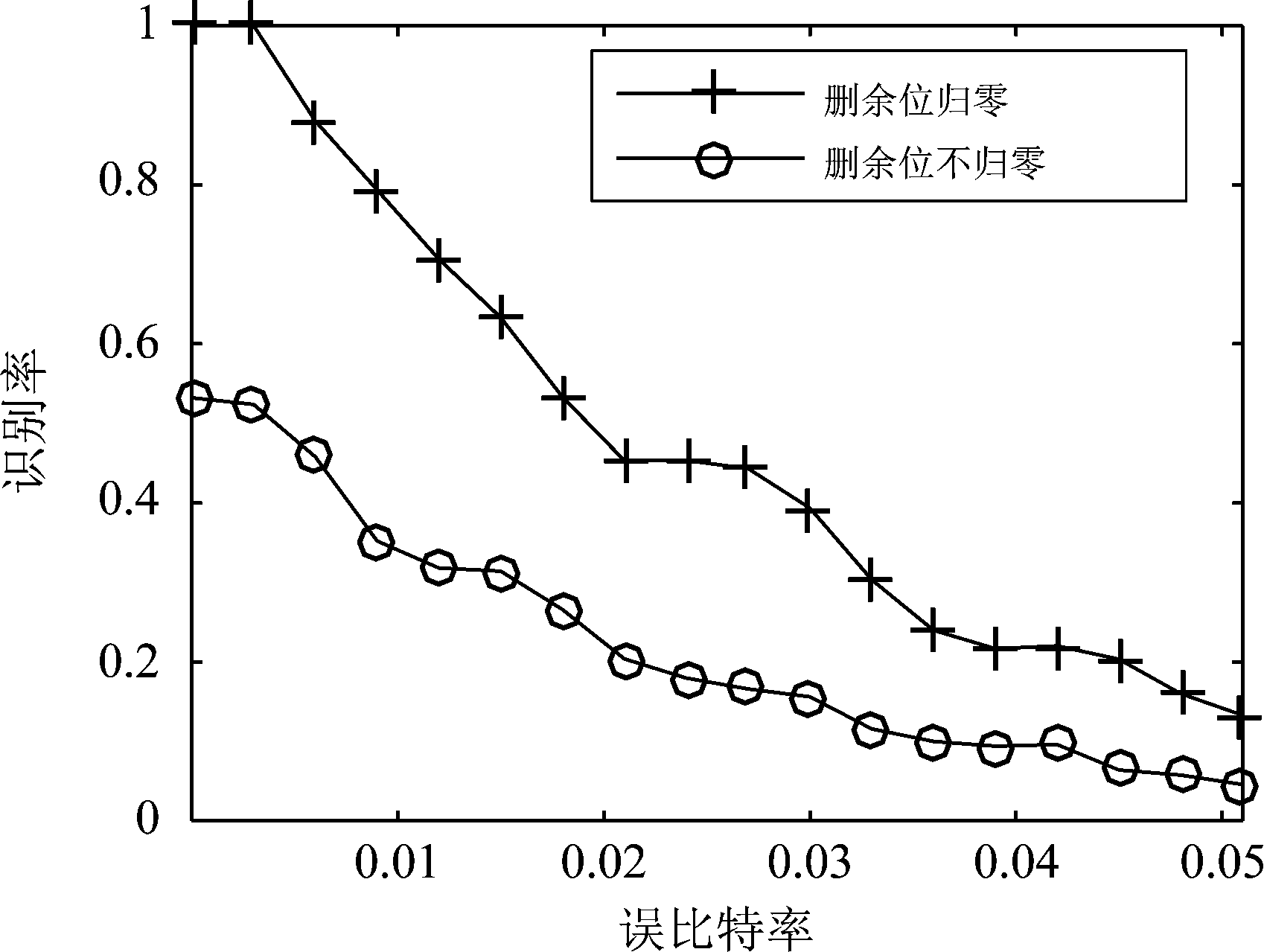
图11 两种算法的性能对比图
Fig.11 Performance comparison chart of two algorithms
从图11中可以看出对于删余位不归零的传统识别方法,由于删余位等价于错误概率为1/2的误码存在,其识别率在自然误比特率为0的情况下也只能达到50%左右,证明本文改进后的算法在性能上有较大的提升。
5 结论
本文重点提出了针对删余型Turbo码分量编码器参数的基于监督矩阵匹配的盲识别算法,首先根据原码的删余特性对删余位进行归零操作,然后截取合适的长度作为校验序列进行匹配度分布计算,最后根据匹配度大小对分量RSC码参数进行盲识别。由于在识别过程中对删余型Turbo码和传统RSC码进行差异化识别,该算法同样也适用于多个分量编码器不同的Turbo码,且对不同删余模式的Turbo码只需改变归零的删余位位置即可完成识别,具有一定泛用性。仿真结果表明该算法在码长和交织情况未知且存在一定误码的情况下也能完成识别,则该算法具备良好的容错性,以上结果表明其具备一定的实际应用的价值。
[1] 王丹, 李雨朦, 刘强, 等. 基于最大似然译码的快速信道编码盲识别算法[J]. 信号处理, 2018, 34(5): 620- 628.
WANG Dan, LI Yumeng, LIU Qiang, et al. Fast blind recognition scheme of channel codes based on maximum likelihood decoding[J]. Journal of Signal Processing, 2018, 34(5): 620- 628.(in Chinese)
[2] 张天骐, 易琛, 张刚, 等. 基于高斯列消元法的线性分组码参数盲识别[J]. 系统工程与电子技术, 2013, 35(7): 1514-1519.
ZHANG Tianqi, YI Chen, ZHANG Gang, et al. Blind identification of parameters of linear block codes based on columns Gaussian elimination[J]. Systems Engineering and Electronics, 2013, 35(7): 1514-1519.(in Chinese)
[3] 吴刚, 张邦宁, 郭道省. 非理想同步下BCH码盲识别的改进算法[J]. 信号处理, 2016, 32(6): 746-754.
WU Gang, ZHANG Bangning, GUO Daoxing. Improved algorithm for blind recognition of BCH codes under imperfect synchronization[J]. Journal of Signal Processing, 2016, 32(6): 746-754.(in Chinese)
[4] 陈金杰, 杨俊安. 基于码重分布信息熵的线性分组码盲识别方法[J]. 通信技术, 2018, 51(7): 1553-1560.
CHEN Jinjie, Yang Jun’an. Linear-block-code blind recognition based on code-weight-distribution information entropy[J]. Communications Technology, 2018, 51(7): 1553-1560.(in Chinese)
[5] BERROU C, GLAVIEUX A, THITIMAJSHIMA P. Near Shannon limit error-correcting coding and decoding: Turbo-codes. 1[C]∥Proceedings of ICC′93-IEEE International Conference on Communications. Geneva, Switzerland. IEEE, 1993: 1064-1070.
[6] 刘骏, 李静, 彭华. 基于校验方程平均符合度的Turbo码交织器估计[J]. 电子学报,2016,44(5):1213-1218.
LIU Jun, LI Jing, PENG Hua. Estimation of Turbo-code interleaver based on average conformity of parity-check equation[J]. Acta Electronica Sinica, 2016, 44(5): 1213-1218.(in Chinese)
[7] 吴昭军, 张立民, 钟兆根, 等. 低信噪比下RSC码快速迭代寻优识别算法[J]. 电子学报, 2019, 47(7): 1566-1574.
WU Zhaojun, ZHANG Limin, ZHONG Zhaogen, et al. Fast iterative recognition of RSC encoder at low SNR[J]. Acta Electronica Sinica, 2019, 47(7): 1566-1574.(in Chinese)
[8] 刘建成, 杨晓静. (n,1,m)RSC码的盲识别[J]. 电路与系统学报, 2012, 17(6): 84- 88.
LIU Jiancheng, YANG Xiaojing. Blind recognition of (n, 1, m) RSC code[J]. Journal of Circuits and Systems, 2012, 17(6): 84- 88.(in Chinese)
[9] 钟兆根, 吴昭军, 张立民, 等. 基于对数符合度下的RSC码识别[J]. 通信学报, 2018, 39(10): 79- 86.
ZHONG Zhaogen, WU Zhaojun, ZHANG Limin, et al. Blind recognition of RSC based on logarithmic conformity[J]. Journal on Communications, 2018, 39(10): 79- 86.(in Chinese)
[10] 彭贻云, 张玉, 杨晓静. 基于反向验证的RSC码编码参数盲识别[J]. 火力与指挥控制, 2017, 42(3): 29-31,35.
PENG Yiyun, ZHANG Yu, YANG Xiaojing. Blind recognition of RSC code encoding parameters based on reverse verification[J]. Fire Control & Command Control, 2017, 42(3): 29-31,35.(in Chinese)
[11] 武恒州, 罗霄斌, 刘杰. Turbo码盲识别方法研究[J]. 无线电工程, 2015, 45(5): 24-27.
WU Hengzhou, LUO Xiaobin, LIU Jie. Research on blind recognition of Turbo codes[J]. Radio Engineering, 2015, 45(5): 24-27.(in Chinese)
[12] 吴昭军, 张立民, 钟兆根, 等. 低信噪比下归零Turbo码码长及其帧同步识别[J]. 电子与信息学报, 2019, 41(9): 2063-2070.
WU Zhaojun, ZHANG Limin, ZHONG Zhaogen, et al. Blind recognition of code length and synchronization of Turbo codes on trellis termination at low SNR[J]. Journal of Electronics & Information Technology, 2019, 41(9): 2063-2070.(in Chinese)
[13] TAO Jinghe, DIAO Ming, CHEN Zengmao. An interleaver estimation algorithm for Turbo-code based on conformity of parity-check equation[C]∥2018 IEEE Asia-Pacific Conference on Antennas and Propagation (APCAP), Auckland,2018:336-340,doi:10.1109/APCAP.2018. 8538311.
[14] WU Zhaojun, ZHANG Limin, ZHONG Zhaogen. A maximum cosinoidal cost function method for parameter estimation of RSC turbo codes[C]∥IEEE Communications Letters. IEEE, 2019: 390-393.
[15] 范雪林, 鲁战锋, 胥桓. 一种多维Turbo码盲识别方法[J]. 通信技术, 2019, 52(4): 817- 822.
FAN Xuelin, LU Zhanfeng, XU Huan. Blind recognition method for multidimensional Turbo coding parameter[J]. Communications Technology, 2019, 52(4): 817- 822.(in Chinese)
[16] 钟兆根, 吴昭军, 刘杰, 等. 高误码率下归零Turbo码帧结构识别[J]. 电子学报, 2019, 47(10): 2089-2097.
ZHONG Zhaogen, WU Zhaojun, LIU Jie, et al. Blind identification of frame structure of Turbo codes on trellis termination at high bit error[J]. Acta Electronica Sinica, 2019, 47(10): 2089-2097.(in Chinese)
[17] 王艳涛. Turbo码编码参数盲识别研究[D]. 西安: 西安电子科技大学, 2018.
WANG Yantao. The research on the blind recognition for Turbo coding parameters[D]. Xi’an: Xidian University, 2018.(in Chinese)
[18] 张永光, 楼才义. 信道编码及其识别分析[M]. 北京: 电子工业出版社, 2010: 151-157.
ZHANG Yongguang, LOU Caiyi. Channel coding and the recognition analysis[M]. Beijing: Beijing Publishing House of Electronics Industry, 2010: 151-157.(in Chinese)
[19] 东阳. Turbo码盲识别技术研究与实现[D]. 成都: 电子科技大学, 2015.
DONG Yang. Research and implementationon of the recognizition of Turbo code[D]. Chengdu: University of Electronic Science and Technology of China, 2015.(in Chinese)
