1 引言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)作为多载波的调制方式,因具有良好的频谱选择特性和抗衰落性被广泛应用于无线通信系统[1]。然而,OFDM无线通信系统受复杂射频环境的影响,因此信道估计对OFDM系统尤为重要,往往决定了无线通信系统的性能。传统的信道估计最常用的方法为基于导频序列的插值方法,即根据在发送的有用数据中插入的已知导频符号,而由此获得的导频信道估计,并通过一定的插值算法进而获得未知的有用数据的信道估计。这类方法较为简单,代表性方法有最小二乘(Least Square,LS)[2]和最小均方误差(Mini-Mean Squared Error,MMSE)[3]:基于LS的估计算法通过最小化误差的平方和来获取信道估计,方法复杂度较低、实时性较好,但忽略了信道的时频相关性且未充分考虑噪声对信道的影响,使得估计算法的性能受到较大限制;而基于MMSE的信道估计算法通过利用信道和噪声方差的统计特性以减小接收信号与估计信号之间的误差,在信道估计性能方面优于LS估计算法,其复杂度也相应提高。这类传统算法按照一定的准则确定了待估信道参数且算法复杂度较低, 但算法缺少一定的智能性难以应对复杂的射频环境,在复杂无线通信环境中算法估计准确度下降、系统性能退化。
近年来,深度学习因其强大的特征学习能力在通信系统中得到广泛关注,不少学者将深度学习应用于信道反馈[4],信道编码[5]和信道估计[6- 8]等方面。2018年Ye等人将多维信道状态信息视为图像,借鉴源自图像恢复的神经网络来学习迭代中的参数和相应函数,从而有效地恢复原始信道[6]。这种将信道估计视为图像恢复过程的方式为基于深度学习的信道估计开辟了新的研究路径,相关学者也纷纷展开了基于图像处理的无线信道估计研究。2019年Soltani等人通过将导频信道矩阵看作二维图像,运用超分辨卷积网络和去噪卷积网络来提取时间—频率相关性等特征,进而重构原始信道[8]。同年Chen等人在Soltani的工作基础上,提出了一种非线性多项式图像超分辨方法,将非线性多项式应用于低分辨率信道图像中来学习信道特征,从而实现了从导频信号到完整信道的估计[9]。这些基于深度学习的方法,通过卷积神经网络(Convolution Neural Network)在信道估计上取得了较好的性能,但这些模型通常需要先通过插值方法将输入数据放大到与输出数据相同尺寸,再输入深度神经网络进行处理,数据的插值放大将导致后续卷积计算复杂度增大,网络参数量增加。近年来,研究人员发现反卷积神经网络(Deconvolution Neural Network)在图像恢复等处理中较卷积神经网络具有较大的优势,不同于卷积神经网络反卷积网络的反卷积操作可以逐步实现数据扩张,反卷积网络可以通过少数几层反卷积层在逐步实现同尺寸放大的同时实现图像恢复,在较少的网络参数量下达到更好的重构性能[10]。此外,为了进一步改善重构图像的质量,相关学者也开始借鉴深度学习的方法来对重构图像进行进一步抑噪。如Wang等人利用扩张卷积神经网络(Dilated Convolution Neural Network)来学习隐藏的高阶图像特征,以较低的计算复杂度实现了图像的进一步去噪，达到了较好的去噪性能[11]。
基于上述分析,本文将导频信道信息视为已知的低分辨率图像,完整的信道信息视为需重构的高分辨率图像,提出了一种基于深度学习的两阶段的信道估计方法。第一阶段根据信道输入输出数据维度及特征搭建了一个五层的轻量级反卷积网络,通过少数几层反卷积操作在逐步实现信道数据同尺寸扩张的同时实现信道估计,极大地减少了计算的复杂度;第二阶段构建了一个扩张卷积网络,通过残差学习的方式来估计隐藏在信道图像中的噪声，以进一步抑制信道噪声,提升信道估计的准确度。仿真结果表明,本文所提出的方法在较低的计算复杂度下,能够以更低的估计误差来实现信道估计。
本文结构安排如下:第2节提出了信道估计的系统模型;第3节设计了基于反卷积及扩张卷积的信道估计方法;第4节进行了实验及结果分析;第5节对全文进行了总结。
2 系统模型
在OFDM系统中,二进制数据经过数字调制后进行串并变换,在插入导频信息之后形成新的数据序列{X(k)},然后通过傅里叶逆变换(IDFT)模块将频域信号变为时域信号:
x(n)=IDFT{X(k)}= 
(1)
在IDFT模块之后,为了防止码间干扰,需要在信号中插入循环前缀,经过循环前缀模块处理和并串变换后发送信号xf(n)便通过信道发送出去。信号通过带有噪声的信道之后,接收到的信号可以表示为:
yf(n)=xf(n)⊗h(n)+w(n)
(2)
其中,h(n)是信道状态信息,w(n)是附加的信道噪声。接收端部分首先对接收到的信号yf(n)进行串并变换,然后移除掉循环前缀,接着对信号做傅里叶变换(DFT)变换:
Y(k)=DFT{yf(n)}= 
(3)
经过DFT变换后提取接收信息中的导频信息,通过LS估计算法获得导频信道估计:
HLS=X-1Y
(4)
其中X是提取的导频发送信号,Y为接收的导频信息。LS估计方法结构简单、计算量小,但并未考虑噪声等干扰因素。在考虑噪声的情况下,MMSE估计算法则结合信道的统计特性来最小化接收数据与实际数据的误差的均方和:
(5)
其中RHH表示信道的自相关函数,
则表示噪声功率。MMSE估计方法在一定程度上提高了信道估计性能,方法复杂度也有所提高。由上述方法获得初步的导频信道信息之后,通常采用线性插值或三次样条插值对导频信道信息进行处理以获得完整的信道信息,从而实现信道估计。这种通过插值以获取完整信道估计的方式,会进一步带来较大的估计误差,尤其在含噪及导频数据量少的情况下。
3 基于反卷积网络及扩张卷积网络的信道估计
近年来,为了进一步提升通信性能,相关学者将深度学习应用于无线信道估计。本文将由LS方法获得的初步信道估计作为输入信息,视为等效的二维低分辨率图像,待估计的完整信道信息视为需恢复的高分辨率图像,借鉴图像超分辨的思想,构建了一个反卷积与扩张卷积的两阶段深度神经网络来进行超分辨与噪声抑制,从而实现信道估计,方法框架如图1所示。第一阶段,利用一个浅层的反卷积网络对“低分辨率图像”进行特征提取及信道插值,从而在逐步实现信道数据尺寸放大的同时实现有效的信道估计;为减少噪声影响、改善估计性能,在第二阶段引入了一个扩张卷积网络来进一步抑制信道噪声,从而得到更高质量的“信道图像”,获得更准确的信道信息。
3.1 反卷积信道估计
第一阶段构建的反卷积网络的结构如图2所示,以LS方法获得的初步导频信道信息HLS作为输入,且HLS包含了高分辨率所需要的原始信道信息,通过反卷积网络对输入数据进行超分辨放大后获得含噪的信道信息H1。
该反卷积网络仅包括了5个网络层:前4层为反卷积层,采用了5*5的卷积核,卷积核的个数依次为128、32、8、4,每一层都对前一层得到的数据进行适当放大,并通过ReLU激活函数避免梯度消失;最后一层为卷积层,通过2个大小为1*1的卷积核来减少特征数据维度,使输出信道图像大小与完整信道图像大小尺寸保持一致。
图1 反卷积网络和扩张卷积网络的信道估计流程
Fig.1 Channel estimation process based on deconvolution neural network and dilated neural network
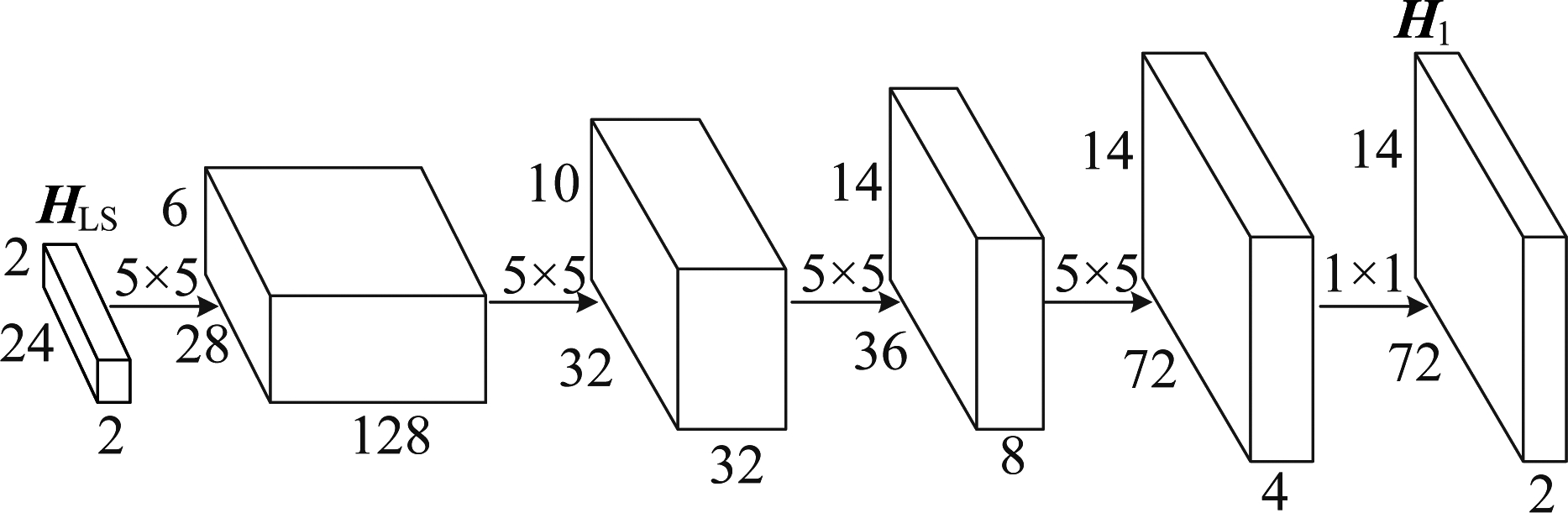
图2 反卷积网络结构图
Fig.2 Deconvolution network structure diagram
如图3所示,不同于卷积操作,该网络中的反卷积作为一种上采样的方法,可以放大数据尺寸,从而逐步实现数据超分辨与信道估计。基于卷积网络的信道估计方法通常需要先对低分辨率信道响应图进行插值放大到输出数据尺寸,再进行多层卷积操作来获得高分辨率信道图像,这往往导致网络参数量及特征数据量较大、计算复杂度较高。而本文所搭建的反卷积网络以反卷积模块为基础,仅通过简单几层反卷积操作在逐步实现信道数据尺寸放大的同时实现信道估计,可有效减小特征数据量及计算复杂度。
3.2 扩张卷积去噪
为了进一步抑制噪声影响,第二阶段借鉴残差学习的思想,构建一个扩张卷积网络来学习信道噪声,从而抑除噪声获得更为准确的信道估计,扩张卷积网络的结构如图4所示。
扩张卷积网络包含了12个网络层,第一层为卷积层,采用64个大小为1*1的卷积核对上一阶段获得的信道估计数据进行处理,并使用ReLU作为激活函数。随后级联10个扩张卷积层+BN+ReLU的基本模块,每层采用64个尺寸大小为3*3的扩张卷积核,扩张卷积也称带孔卷积,即在基础卷积核中注入空洞以增大感受野,这里扩张卷积不仅能学习信道局部相关特征,还能进一步利用更宽频率维度的相关特性获得更为准确的估计。最后一个卷积层使用64个大小为3*3的卷积核用来获得信道噪声估计。扩张卷积网络的基本模块中,BN作为批量归一化可加速网络收敛速度,提升训练稳定性,ReLU作为激活函数能使模型能够更好地挖掘信道特征,拟合训练数据。
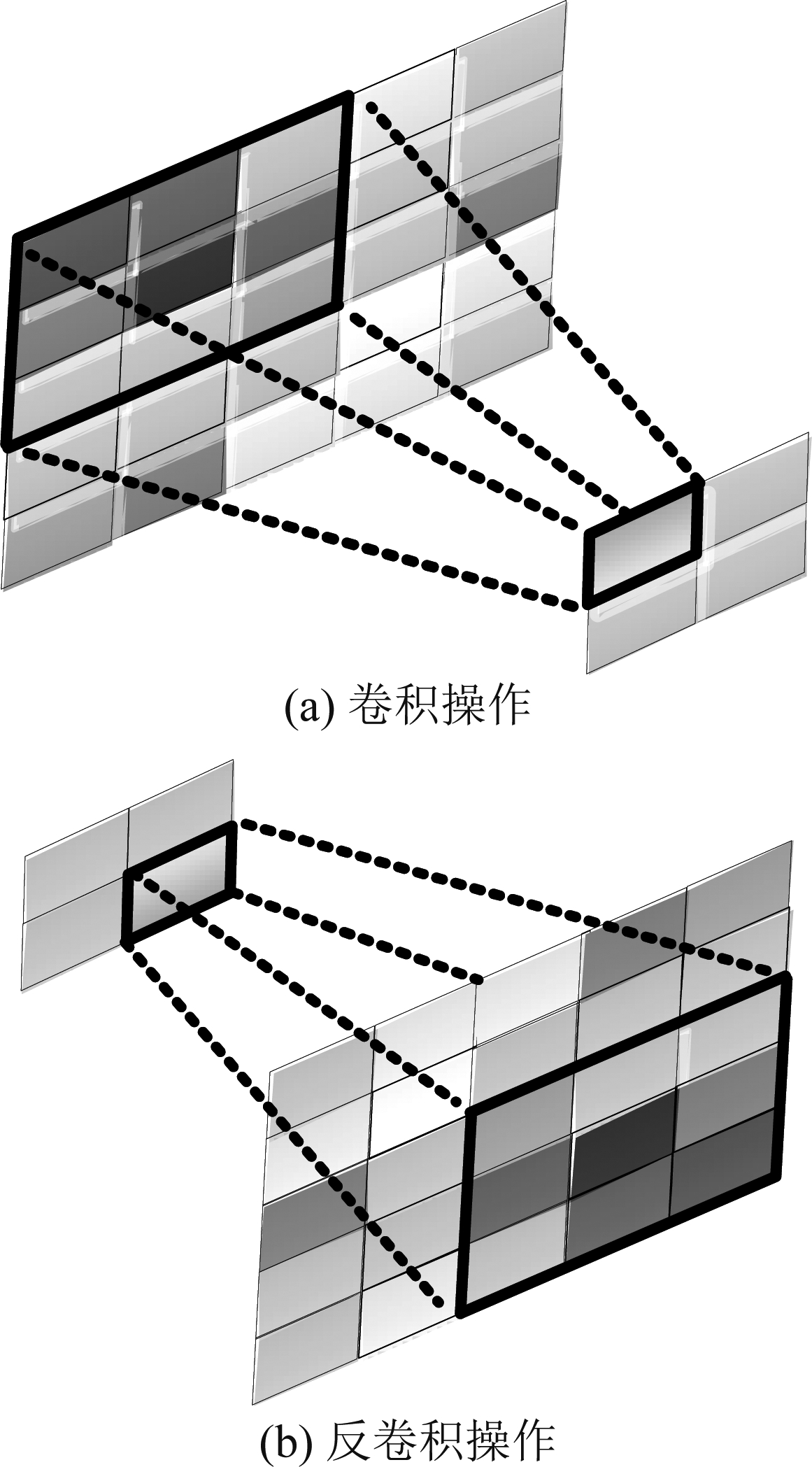
图3 卷积操作和反卷积操作
Fig.3 Convolution operation and Deconvolution operation
这里扩张卷积网络不仅能利用更宽频率维度的相关特性,而且其残差学习的特殊结构能够在噪声水平较低的情况下解决梯度消失问题。即对给定含噪信道:
(6)
其中
是完整的信道信息,Z是噪声,H1是含有噪声的信道信息。残差学习结构的扩张卷积网络通过学习信道噪声,从而从带噪的信道信息中去消减噪声,获得更为准确的信道估计,并防止训练时前层网络的梯度消失问题。
图4 扩张卷积网络结构图
Fig.4 Dilated convolution network structure diagram
3.3 模型训练
本文采用端到端的方式来优化学习模型中的相关参数,根据两阶段的模型本文将训练过程也分为相应的两个阶段:第一阶段对信道估计的反卷积网络进行训练,运用导频信道估计值HLS作为输入数据对模型进行训练,采用自适应矩估计(Adam)优化器和均方误差损失函数(MSE)来训练网络,反卷积网络优化目标可以表示为
(7)
其中,M为所有训练样本总的样本数,W1表示反卷积网络需要优化的参数, f1则代表反卷积网络。为提升系统的耦合度,实现更有效的信道估计,第二阶段对反卷积网络及扩张卷积网络进行联合训练,结合扩张卷积进行信道去噪,实现进一步的信道估计优化,提升系统估计性能。采用与第一阶段相同优化器与损失函数来训练网络,整个网络训练优化目标可以表示为
(8)
其中,W2表示整个网络需要优化的参数, f2则代表反卷积网络及扩张卷积网络。两阶段的训练方式能够获取更好的信道估计与抑噪性能,进一步提升系统的耦合度。
4 实验及结果分析
4.1 实验环境和参数
为验证模型方法的有效性,我们采用维也纳大学开发的LTE-A仿真模拟器[12]获取的无线信道数据来进行仿真实验,该仿真模拟器提供了几个测试模拟场景,被广泛应用于相关研究中以验证不同场景下的信道估计性能[13-14]。实验采用单天线,16QAM的星座调制及SSD接收机工作模式,载波频率和带宽频率分别为2.5 GHz,14 MHz,采用随机生成的噪声。同时,该模拟器参照了链路级模拟器并在实验时选择固定的导频点和位置进行数据提取,导频点的数量为48个。为验证模型的有效性,我们分别选取了无线通信中VehA和AWGN两种最典型的信道模型进行了测试验证,并在不同信噪比下与传统信道估计方法进行了性能对比。
实验中将LTE-A仿真器产生的数据集分为三个部分,数据集分为三个部分:其中80%用于训练集、10%用于验证集、10%用于测试集,大小分别为32000、4000和4000。实验软硬件平台配置如表1所示,网络训练的初始学习率为0.0001,最大迭代次数为1000,中心损失函数的中心学习率设置为0.5,训练批次样本数设定为200。
4.2 实验结果及分析
为了验证算法的有效性,实验分别选取了VehA信道模型和AWGN信道模型产生的数据集进行验证,VehA是一种车载系统信道模型,在车载应用分析和信道建模中被广泛应用。本文算法和传统基于导频序列插值的算法在不同信噪比下的均方误差如图5所示。可以看出,各估计方法的MSE都随SNR的增加呈而下降。LS估计方法[15]均方误差相对较大,MMSE估计方法[16]因考虑了信道的二阶统计特性及噪声相对LS估计方法有一定的性能提升,但需准确获取时延采样点的先验信息。而本文提出的方法在不同信噪比情况下较传统方法具有更低的估计误差,尤其在低信噪比情况下,本文所提的反卷积的信道估计方法在不链接扩张卷积网络的情况下较传统方法都具有较大优势。这是由于基于反卷积的信道估计方法能够学习到信道的时频相关性和信道的分布情况,反卷积操作在不断扩大信道数据尺寸的同时实现了精确的信道估计。随着SNR的增加,反卷积网络性能有所降低,其原因是在高信噪比下噪声和子载波对信道的影响逐渐增强,基于反卷积的信道估计方法不能有效降低传输阶段信道时变造成的估计误差。尽管如此,在引入扩张卷积网络后,结合反卷积和扩张卷积网络的信道估计能够有效地抑制信道噪声,在不同的信噪比下具有更低的估计误差。因此也在某种程度上证明了,我们提出的基于深度学习的两阶段联合训练网络相比于单阶段网络具有更好的信道估计性能。
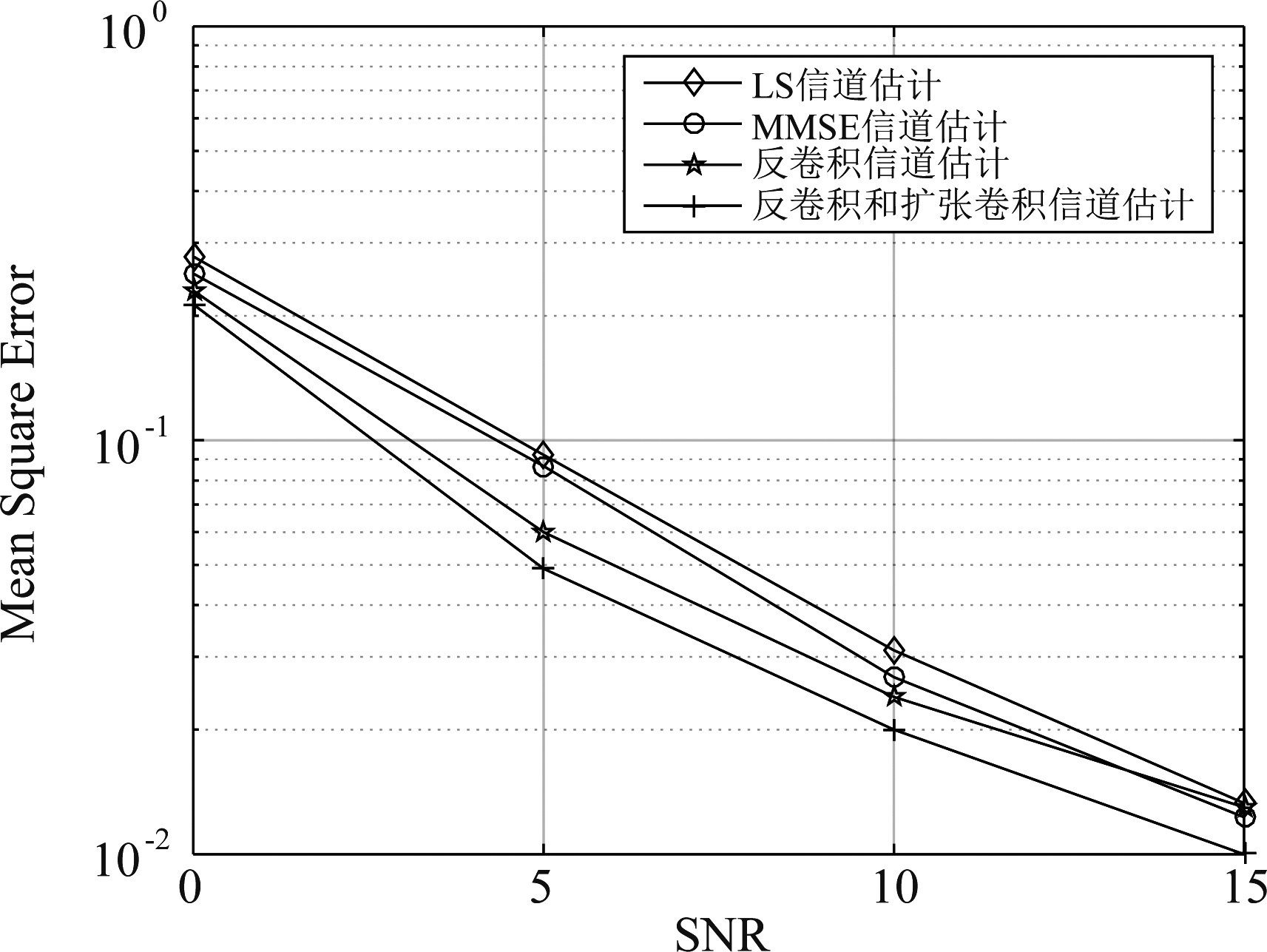
图5 VehA信道模型下各种算法在不同信噪比下 的MSE性能对比
Fig.5 MSE performance comparison of various algorithms under different SNR for VehA channel model
表1 实验环境参数
Tab.1 Experimental environment parameters
处理器内存显卡操作系统框架编程语言Intel Xeor E5-2670@2.3 GHz16GGeForce GTX TITAN XUbuntu 16.04TensorFlowPython3.6
图6 AWGN信道模型下传统算法和本文算法 在不同信噪比下MSE性能对比
Fig.6 MSE performance comparison of various algorithms under different SNR for AWGN channel model
我们对AWGN信道模型进行了进一步实验验证,AWGN信道模型下本文信道估计算法和传统信道估计算法在不同信噪比下的均方误差如图6所示。基于反卷积网络的信道估计算法与传统信道估计算法的MSE性能在低信噪比下相近,且在信噪比较高情况下有更低的估计误差。接入扩张卷积网络后能对高斯白噪声进行较好抑制,在不同信噪比情况下其估计误差远小于传统的基于导频序列的插值方法。当噪声较大时,扩张卷积神经网络能较好的抑制信道噪声,结合反卷积和扩张卷积网络的方法比反卷积网络具有更好的估计性能;随着信噪比的提高,扩张卷积神经网络的作用受到限制,在某些情况下估计性能甚至会低于反卷积网络,这可能是低噪声情况下对反卷积与扩展卷积网络模型的联合训练所带来的。实验结果表明,提出的结合反卷积和扩张卷积网络的信道估计方法可以在AWGN信道受噪声影响较大的情况下,依然可以保持一个稳定的信道估计与抑噪表现。综上所述,本文提出的反卷积网络能充分利用信道的时频相关性,且结合扩张卷积网络可进一步抑制信道噪声,获得更准确的信道估计。
4.3 复杂度及参数量分析
LS和MMSE估计算法的复杂度主要来自于复乘数[17],其复杂度分别表示为Ο(NfNn)和Ο(NfNn(NpfNpn)2+(NpfNpn)3),其中Nf是子载波的数量,Nn代表OFDM符号的数量,Npf和Npn分别代表了沿子载波放置的导频符号数、沿OFDM符号轴放置的导频符号的数量。根据神经网络的复杂度计算模型,某层网络的复杂度可以表示为Ο(M2·K2·Cin·Cout),即复杂度与输入特征图大小M,卷积核尺寸K及输入输出通道数Cin、Cout相关,而整个网络的参数计算量可表示为层内连乘与层间累加
其中D为网络的深度。根据以上计算代入各模型参数得到不同算法的复杂度如表2所示。可以看出,传统估计方法较为简单、复杂度相对较小,但估计性能不理想且难以有效应对噪声。结合深度学习的方法因为设置的网络层数增加了算法的复杂度,但同时能够有效学习信道特性,提升估计性能。在不考虑去噪的情况下,基于反卷积的信道估计算法较现有深度学习方法来说具有更低的复杂度;且不同于卷积网络首先需对数据进行同等插值放大,反卷积网络则直接对输入数据进行逐步扩张。此外,在引入去噪网络后无论是基于卷积的SRCNN网络和反卷积网络都会有复杂度的上升,而本文提出的结合反卷积和扩张卷积的模型综合复杂度相对较低。
表2 算法复杂度比较
Tab.2 Comparison of algorithm complexity
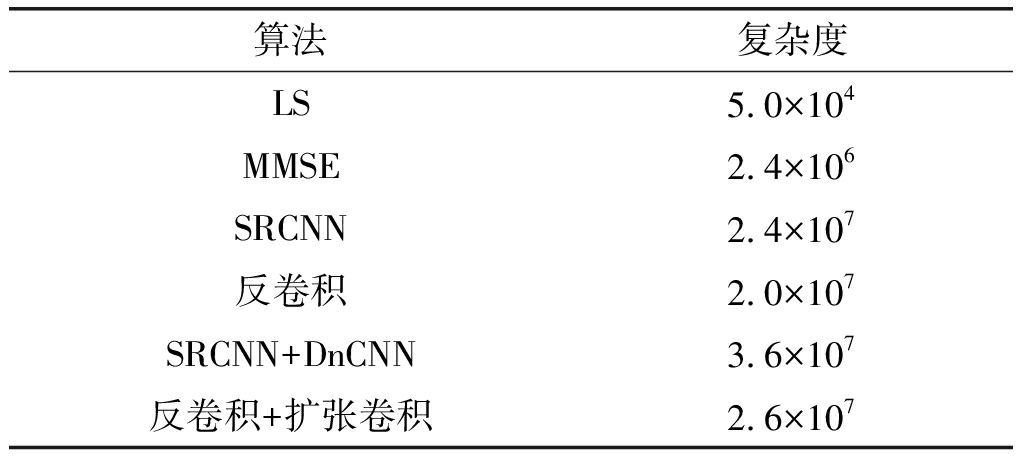
算法复杂度LS5.0×104MMSE2.4×106SRCNN2.4×107反卷积2.0×107SRCNN+DnCNN3.6×107反卷积+扩张卷积2.6×107
5 结论
针对OFDM系统中信道估计问题,本文提出了一种结合反卷积和扩张卷积网络的信道估计方法。具体来说,我们将信道信息视为等效的二维图像,根据无线信道的时频相关性,利用轻量级反卷积网络在逐步实现信道数据尺寸放大的同时实现信道估计,并结合扩张卷积网络来抑制重构噪声,进一步提高信道估计准确度。实验结果表明,在不同的信噪比下,本文算法较其他算法有着更好的信道估计性能,并具有较低的计算复杂度。
[1] COLERI S, ERGEN M, PURI A, et al. Channel estimation techniques based on pilot arrangement in OFDM systems[J]. IEEE Transactions on Broadcasting, 2002, 48(3): 223-229.
[2] 陈国军, 胡捍英. OFDM系统自适应盲信道估计新方法[J]. 信号处理, 2013, 29(6): 777-781.
CHEN Guojun, HU Hanying. New blind adaptive channel estimation schemes based on OFDM systems[J]. Journal of Signal Processing, 2013, 29(6): 777-781.(in Chinese)
[3] LI Y, CIMINI L J, SOLLENBERGER N R. Robust channel estimation for OFDM systems with rapid dispersive fading channels[J]. IEEE Transaction on Communications, 1998, 46(7): 902-915.
[4] WEN Chaokai, SHIH W T, JIN Shi. Deep learning for massive MIMO CSI feedback[J]. IEEE Wireless Communications Letters, 2018, 7(5): 748-751.
[5] LIANG F, SHEN Cong,WU Feng. An iterative BP-CNN architecture for channel decoding[J]. IEEE Journal of Selected Topics in Signal Processing, 2018, 12(1): 144-159.
[6] YE Hao, Li G Y, JUANG B H. Power of deep learning for channel estimation and signal detection in OFDM systems[J]. IEEE Wireless Communications Letters, 2018, 7(1): 114-117.
[7] LEE S, JU H, SHIM B. Pilot assignment and channel estimation via deep neural network[C]∥2018 24th Asia-Pacific Conference on Communications (APCC). Ningbo, China. IEEE, 2018: 454- 458.
[8] SOLTANI M, POURAHMADI V, MIRZAEI A, et al. Deep learning-based channel estimation[J]. IEEE Communications Letters, 2019, 23(4): 652- 655.
[9] CHEN Hui, CHI Nan. Channel estimation based on nonlinear polynomial image super-resolution algorithm for underwater visible light communication[C]∥2019 Asia Communications and Photonics Conference (ACP). Chengdu, China. IEEE, 2019: 1-3.
[10] ZHANG Zhicheng, LIANG Xiaokun, DONG Xu, et al. A sparse-view CT reconstruction method based on combination of DenseNet and deconvolution[J]. IEEE Transactions on Medical Imaging, 2018, 37(6): 1407-1417.
[11] WANG Tianyang, SUN Mingxuan, HU Kaoning. Dilated deep residual network for image denoising[C]∥2017 IEEE 29th International Conference on Tools with Artificial Intelligence(ICTAI). Boston, MA, USA. IEEE, 2017: 1272-1279.
[12] MEHLFÜHRER C, COLOM IKUNO J, 
IMKO M, et al. The Vienna LTE simulators-Enabling reproducibility in wireless communications research[J]. EURASIP Journal on Advances in Signal Processing, 2011(1): 1-14.
[13] XIAO Xiao, TAO Xiaoming, LU Jianhua. Energy-efficient resource allocation in LTE-based MIMO-OFDMA systems with user rate constraints[J]. IEEE Transactions on Vehicular Technology, 2015, 61(1): 185-197.
[14] SCHWARZ S, MEHLFUHRER C, RUPP M. Throughput maximizing multiuser scheduling with adjustable fairness[C]∥2011 IEEE International Conference on Communications(ICC). Kyoto, Japan. IEEE, 2011: 1-5.
[15] LEE Y S, BANG Y J, LEE J H, et al. LS channel estimation performance analysis for RoF channel environment in the OFDM system[C]∥2014 12th International Conference on Optical Internet 2014(COIN). Jeju, Korea (South). IEEE, 2014: 1-2.
[16] IMKO M, MEHLFÜHRER C, WRULICH M, et al. Doubly dispersive channel estimation with scalable complexity[C]∥2010 International ITG Workshop on Smart Antennas(WSA).Bremen,Germany.IEEE,2010:251-256.
[17] LI Lianjun, CHEN Hao, CHANG H H, et al. Deep residual learning meets OFDM channel estimation[J]. IEEE Wireless Communications Letters, 2020, 9(5): 615- 618.
