1 引言
盲源分离广泛应用于信号处理的许多领域,在遥感影像处理、移动通信、生物医学工程、经济学 、声呐和地震信号处理,尤其在语音信号处理领域有着极富吸引力的应用前景。传统的盲源分离技术例如独立成分分析[1],非负矩阵分解 、稀疏成分分析等算法在信号处理、图像处理和语音处理等方向获得了成功的应用。其中,独立分量分析(Independent Component Correlation Algorithm,ICA)[1]通过解线性方程组的估计方式求解信号源,由于其不需要目标语音的语音活动检测(Voice Activity Detection,VAD)和声源波达方向(Direction of Arrival,DOA)等先验信息,因此被广泛应用到盲源分离技术中。但是ICA技术会引入排列问题[2],且无法处理多输入高斯信号。
传统的盲源分离方案多基于时频(Time-Frequency, T-F)信号特征[3],即采用语音信号的幅度谱作为输入,信号恢复时使用输入信号的相位信息。但由于时频信号特征没有利用语音信号的相位信息,因此极大地限制了分离性能的上限。
近年来基于深度学习的语音分离技术逐渐兴起,其中,全卷积单通道实时语音分离网络(Conv-TasNet)[4]、双路径递归神经网络(Dual-Path Recurrent Neural Network, DPRNN)以及双通道U-Net网络性能较优异。基于深度学习的盲源分离方案在单声道的应用中已经取得了很大的进展,但是仍然无法很好解决复杂场景下盲分离算法准确性不高和时延较大的问题。为了解决上述问题,Conv-TasNet使用堆叠的一维扩张卷积来代替长短时间网络(Long Short-term Memory, LSTM)进行分离,卷积操作允许在连续的帧之间进行并行处理,可以极大的加快计算过程,显著提高了分离精度。Conv-TasNet在源失真比(Signal-to-Distortion Ratio, SDR)和平均主观意见分(Mean Opinion Score, MOS)两方面都优于理想的时频幅度掩模的分离精度。但是Conv-TasNet泛化性较差,在实际数据上表现不佳。
通过上述分析,为了解决盲源分离中的排列问题、提高算法的准确性、降低系统的延时,本文提出了一种基于时频域的双通道复数神经网络CgRNN(Complex Gated Recurrent Neural Networks)。所提出的CgRNN对时间循环序列进行改进,利用浮点数类型代替复数域网络隐藏状态的复数类型,实现了传统信号处理和现有深度学习网络的有机融合。
2 复数神经网络结合ICA盲源分离方法框架
2.1 方法原理
所提方法原理框图如图1 所示。在训练阶段,本方法提出的复数网络利用输入的时频数据可以直接对每个频点进行估计。提取输入数据块的复数形式的T-F bin即 X(f, t)特征,通过CgRNN分离模块得到初始化分离矩阵W0( f )。利用W0( f )初始化ICA的分离矩阵,获得最终的分离矩阵W(k)。为了保证分离后矩阵的频域连续性,增加了最小失真原理(Minimal Distortion Principle, MDP)平滑模块。平滑后的输出经过傅里叶反变换后可得分离矩阵的数值滤波器形式。将输入信号X(t)通过FIR滤波器以获取输出信号Y(t)。
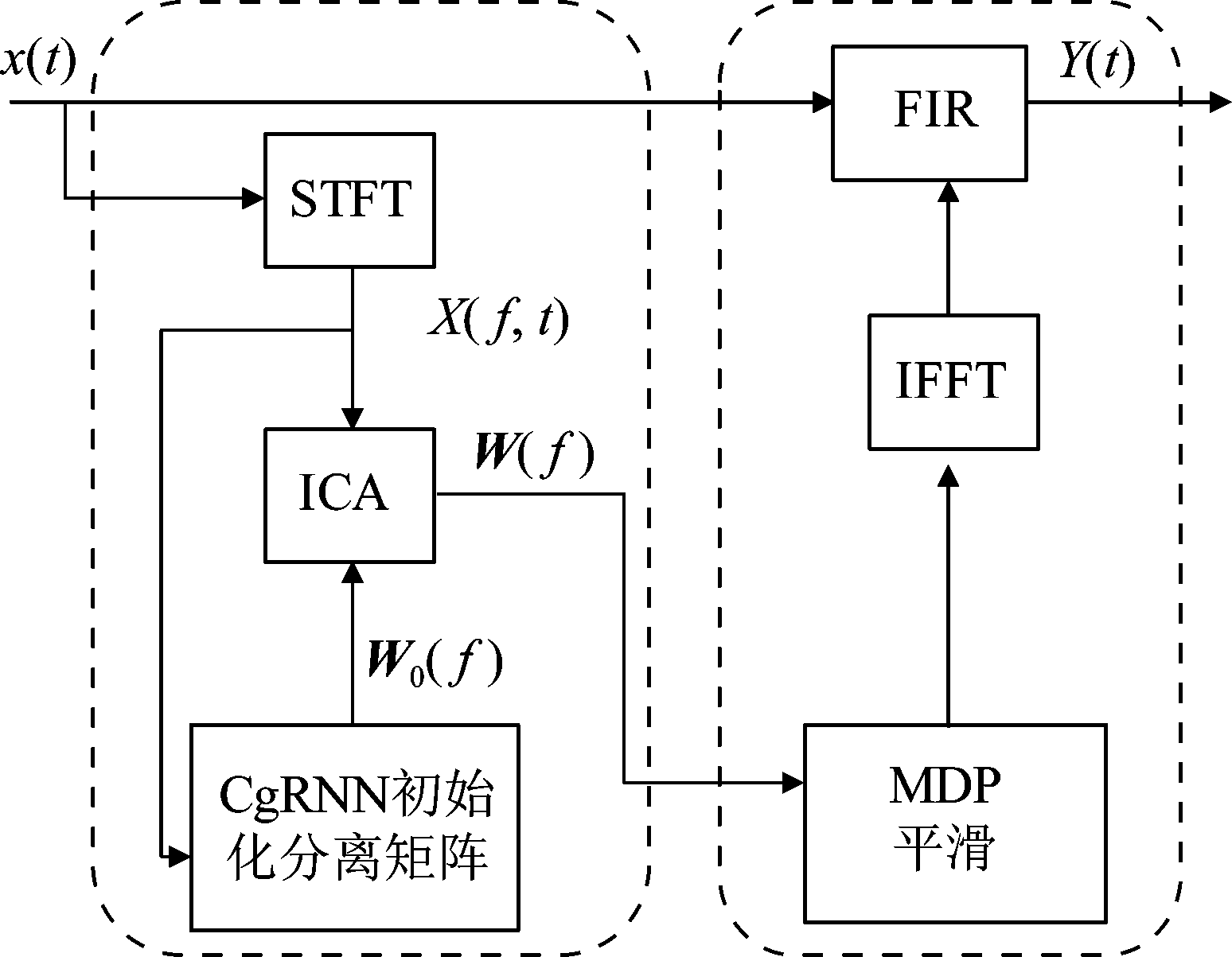
图1 算法流程图
Fig.1 Algorithm flow chart
ICA所处理的数据为一个由混合信号的频谱组成的一个数据块,数据块 x(k, t)表示对应混合信号k频点和时间t上的复数值,详见图2。数据块是由b帧混合信号的复数频谱展开组成,每个频点对应一个分离矩阵W(k),每个数据块包含k个分离矩阵。W(k)为复数网络的学习标签,之后将训练好的网络框架作为算法中的一个模块结合到ICA算法中。
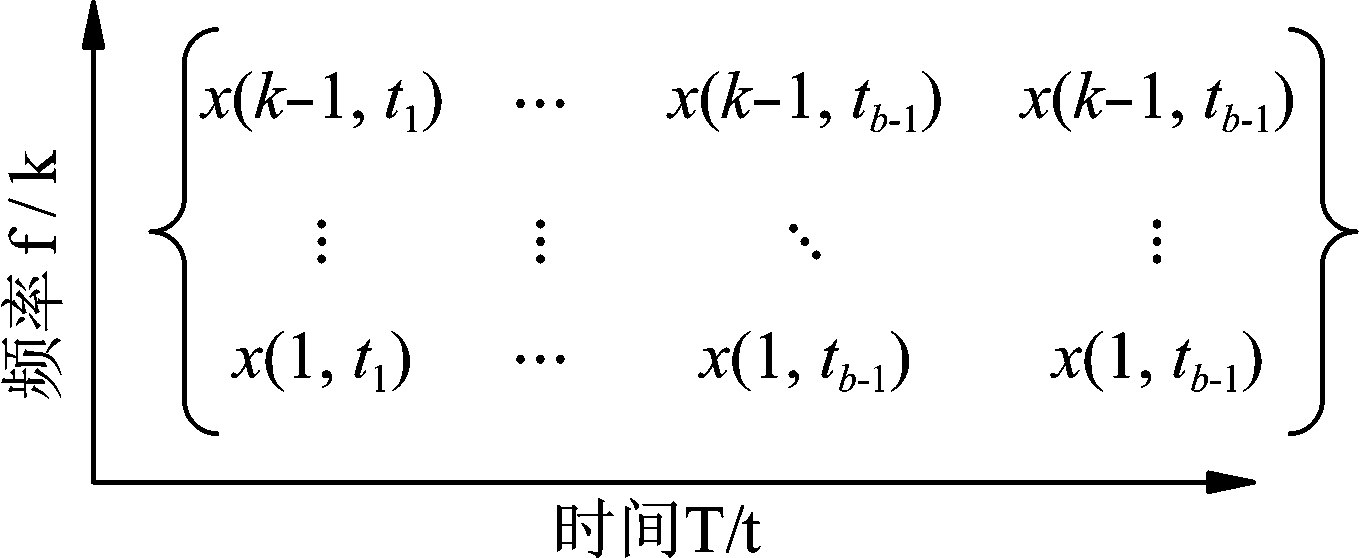
图2 输入数据块
Fig.2 Input data block
本论文提出的算法框架相对传统盲源分离算法有以下明显的优势:
1)降低算法的计算消耗,改善了盲分离算法的实时性。一方面初始化分离矩阵过程不需要先验信息,可以根据输入数据直接给出分离矩阵,使得初始化分离矩阵的算法复杂度下降;另一方面在ICA算法迭代过程中,可以直接获取下一个频点对应的分离矩阵,不需要回传迭代好的分离矩阵,利用神经网络优势可以令所估计的分离矩阵更加贴近真实的分离矩阵。
2)解决了盲源分离过程中的排列问题。传统的盲源分离过程都不可避免地引入排列问题,造成盲源分离输出信号的准确性和稳定性下降,而深度神经网络训练过程中PIT(permutation invariant training)[5]的引入,避免了排列问题,固定了分离后结果的输出顺序,避免了输出顺序混乱,因而算法的准确性得以提高。
利用复数网络可以训练获得性能很好的分离矩阵,因此在一些源信号独立性并非很强的实际应用环境下,依然可以给出很好的分离效果,提高分离的稳定性并且能够处理更加复杂的环境数据。
2.2 复数递归神经网络
复数域信号的表征丰富性使得复数一直以来都是信号处理的首选[6]。对于复数RNN,保范数的状态转移矩阵可以有效的防止梯度消失和爆炸。文献[7]表明,将实数正交权重转移到复数域产生酉RNN可以有效解决实数正交权重难以参数化的问题,并将uRNN的权值构造为分量酉矩阵的乘积。但是该方法不具有全集表示性。文献[8-9]探索了酉矩阵参数化的替代方法。
基于上述研究,本方法提出了基于时频域的双通道复数神经网络CgRNN。CgRNN中引入一个新的复数RNN单元,权重由全维酉矩阵参数化。该复数RNN网络在盲分离任务中性能优于同等参数量的实值网络。使用CgRNN网络根据输入的复数频谱信息,对分离矩阵中每一个复数元素进行估计。使用训练好的模型计算输出信号的分离矩阵,再由ICA算法模块进行分离迭代计算。图3为CgRNN网络结构图。
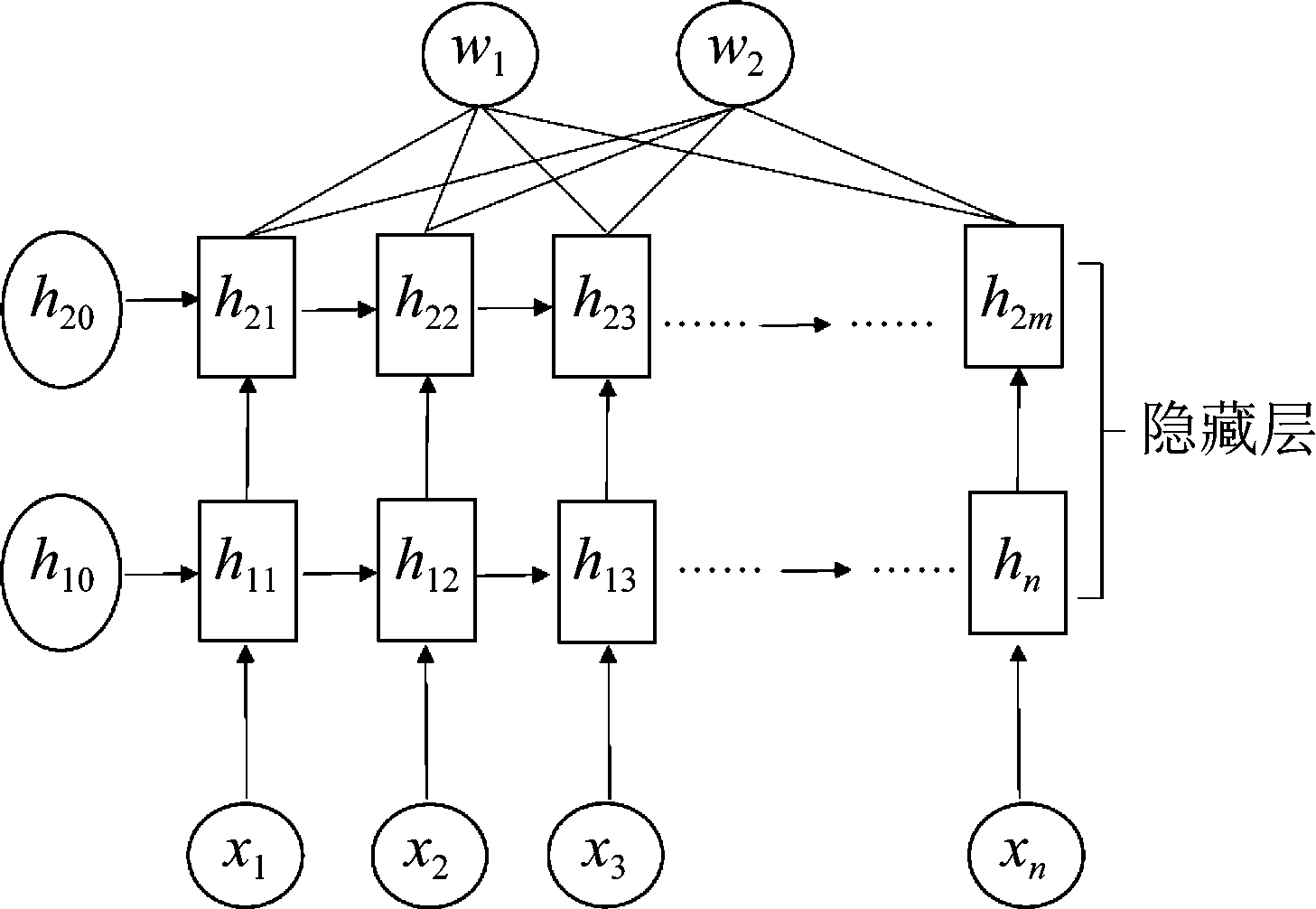
图3 CgRNN网络结构图
Fig.3 CgRNN network structure
在训练阶段,对混合信号进行短时傅里叶变换后获取复数形式的T-F bin特征,将其作为X输入网络进行训练,计算网络输出的估计值W0( f )与真实源的分离矩阵W(k)计算使用PIT方法优化均方误差(Mean squared error,MSE)损失函数,最后获取分离矩阵W(k)。在测试阶段,将测试信号的T-F bin输入之训练好的CgRNN模型,得到估计的W0( f )。
复数网络的主要构件, “复数梯度”和“复数梯度反向传播方法”计算如下:
设z=x+iy,z∈C,其中x=R(z), 且有y=I(z),其极坐标表示如下
z=|z|eiθz
(1)
其中|z|和θ分别表示幅值和相角。
设实值函数u(x, y)和v(x, y)在开集C上连续可微,则当且仅当u和v的偏微分满足柯西-黎曼方程组(2)时, f=u+iv是全纯的。
(2)
z复函数z=f(x,y)的导数为:
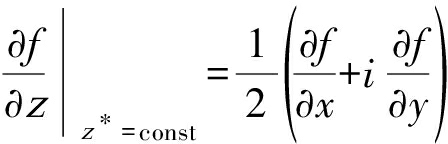
(3)
复数共轭的导函数为:
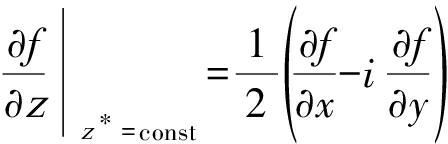
(4)
基于以上的导数,根据链式法则可以得到g(f(z))对z的导数如下:
(5)
其中f*=u(x,y)-iv(x,y)。
因为映射从实数到虚数的表达利用了变量z和它的共轭z*,Wirtinger-Calculusr[10]能够以一种简单而有原则的方式来描述和理论上理解实值损失函数的梯度。
定义RNN如下:
zt=Wht-1+Vxt+b
(6)
ht=fa(zt)
(7)
其中,xt和ht表示了在时间t下的输入和隐藏神经节点向量,fa是一个非线性的激活函数,W和V分别是隐藏状态和输入状态的过渡矩阵。本方法采用了实部和虚部分开激活的方法。复数激活函数fa表达式如下,其中常数b为偏置因子。
fmodReLU(z)=ReLU(|z|+b)e-i·θz= ReLU(|z|+b)z/|z|
(8)
此外本文在实验中比较了递归网络中有界非线性和无界非线性的效果,找到了与通常认为的只有有界非线性应用于RNN的启发式方法相反的额外证据。在实验中,无界非线性表现的更好,但是必须与使用保范数状态转移矩阵的稳定措施相结合。
2.3 复数网络中复数与实数的映射
由于深度学习要求输出的目标值为实数,为了匹配网络输出和目标标签,需进行实数和复数的映射。本研究中使用保留原复数的实部作为实部,其虚部值取0。即
z=x+i·0
(9)
在复数状态下,同样需要将复数映射到实数状态or,使用复数的实部和虚部的线性组合,由Wo和bo分别作为权重和偏置因子,其中![]() 为复数的实部,
为复数的实部,![]() 为该复数对应的虚部。
为该复数对应的虚部。
(10)
使用以上方法解决了复数网络在应用中实数与复数之间的值类型不兼容的问题,可以很好利用实数网络框架搭建成复数网络。
2.4 复数门的选择
通过比较CgRNN和无门uRNN,分析了选通对综合任务的影响。两个网络都使用复数表示和酉状态转移矩阵。作为附加基线,还与TensorFlow的传统GRU进行了比较。本部分选择每个网络的隐藏状态大小均为nh,以确保得到的参数数量(约44k)近似相等。研究中发现CgRNN成功地解决了记忆问题和加性问题。此外,保范数状态的权重矩阵是保证学习过程中稳定性的关键。GRU不具有保范数状态矩阵,导致其稳定性较差。CgRNN实现了与uRNN非常相似的性能,这与将门偏压项初始化为完全打开有关。
对于加性问题,相关的工作[3,11]表明门效应是有益的,这种优势来自于门可以屏蔽网络中不受加性问题影响的无关输入。值得注意的是,加性问题的影响在综合任务中需要综合考虑。
研究[12]比较了CgRNN(nh=80)、交叉熵上的uRNN(nh=140)和标准GRU[12](nh=112)的记忆问题(a)和加性问题(b)。选择每个网络的隐藏状态大小nh,以便近似匹配参数的数量(参数量约44k)。在记忆问题上,保持范数的状态转移矩阵是稳定学习的关键;在加性问题上,有门是重要的。
2.5 复数网络初始化分离矩阵
为了解决ICA算法中的排列问题,本文提出了使用基于PIT和CgRNN初始化盲分离矩阵的方法。混合信号x(k,t)作为输入信息输入到复数网络,使用PIT原则优化MSE损失函数,减小估计值和标签W(k)之间的误差,最终使用估计的复数矩阵初始化ICA算法中的分离矩阵。
3 深度学习结合ICA验证
3.1 实验设置
本研究的数据集详情可见参考文献[12]。该数据集使用两个独立的单声道语音信号对空间的双麦克进行模拟卷积混合生成两麦克的混合语音信号。其中训练数据共5万条,测试数据1万条。将估计后的分离矩阵作为初始化分离矩阵代替RRICA[13]初始化分离矩阵模型。选择源信号干扰比(signal to interference ratio,SIR)和源信号失真比(signal distortion ratio,SDR)等其他参数评价分离后语音信号的质量。
对实验所需的时间序列分帧加窗,其中窗长为4096个频点,窗类型为汉明窗,帧间重叠因子为帧长的75%。对单帧数据进行短时傅里叶分析,为了提高算法的稳健性,信号的观测时长为1 s。
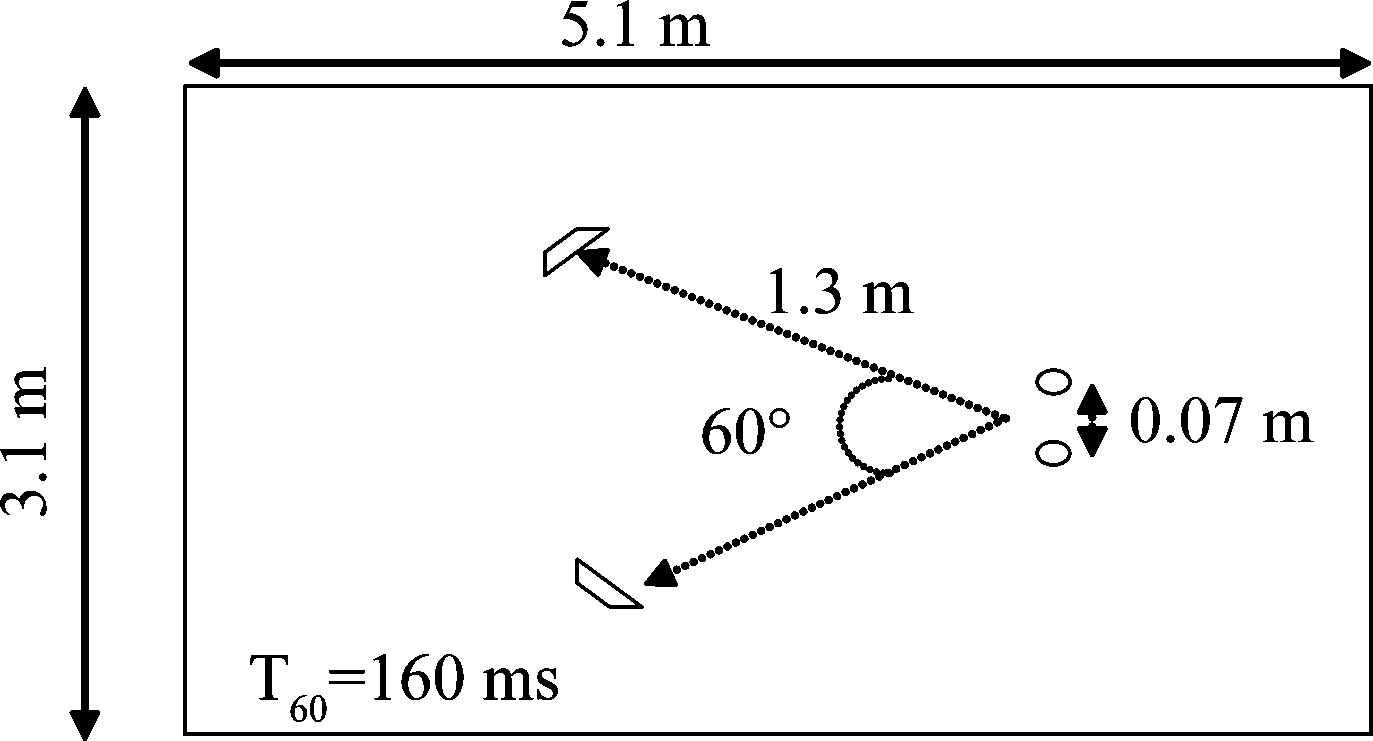
图4 实验场景布局
Fig.4 Layout of experiment scene
实验空间设置如图4所示,使用Lehmann和Johansson的图像源方法[14]产生了脉冲响应,其中假设源麦克风是全向的。麦克风的间距为0.07 m,音频采样频率fs=16 kHz,房间混响时间T60=160 ms。为了能产生在两个麦克风处接受到的信号,两个干净的语音被卷积成脉冲响应,然后在每个信道上获得对所有源信号的卷积混合信号。
图4所示实验场景不受空间混叠的影响,避免了轨迹交叉,弱化了排列的风险。应用最小失真原理(MDP)[11]求解尺度模糊度,采用恰当的平滑方法来减小FFT循环效应引起的峰值。最后利用逆傅里叶变换得到去噪矩阵,即时域的去噪滤波器。根据实验对梯度步长设置为0.1。
3.2 CgRNN初始化分离矩阵实验测试
通过与NLMS[15]方法的对比实验来验证使用复数神经网络初始化分离矩阵的可行性。图5中,横轴为声源到达时间差(TDOA),纵轴表示单位时间,即1 s。变换结果如图5所示,“尖峰”表示了所要估计的TDOA的变换结果。越接近“尖峰”,则意味着对应的横轴越接近真实声源的TDOA值,即完成了对独立声源的估计。

图5 分离矩阵的广义相干变换TDOA时间估计图
Fig.5 TDOA time estimation diagram of generalized coherent transform of separation matrix
图5中(a)和(b)分别为利用NLMS算法和CgRNN网络所估计的分离矩阵的广义相干变换后的TDOA时间估计图。可以看出,(b)图所反映出的声源TDOA估计精度更高(“尖峰”越聚拢),即分离矩阵越接近真实分离过程。进一步说,当应用深度学习时候,其最终状态的分散性要比独立执行ICA使用递归的分散性要小。
3.3 盲分离准确性实验评测
图6和图7表示了估计值和真实声学传播模型间的传播模型误差(Propagation Model Error, PME),其中纵轴表示了PME值,横轴表示了在实验进行中独立分量分析方法分离源信号的迭代次数。ICA处理的信号时长为1 s。对比三种不同的ICA迭代策略:a)牛顿梯度独立分量分析方法;b)递归正则化独立分量分析方法;c)标度牛顿梯度独立分量分析方法[16];d)方法是本论文所提出的深度学习结合的独立分量分析方法。
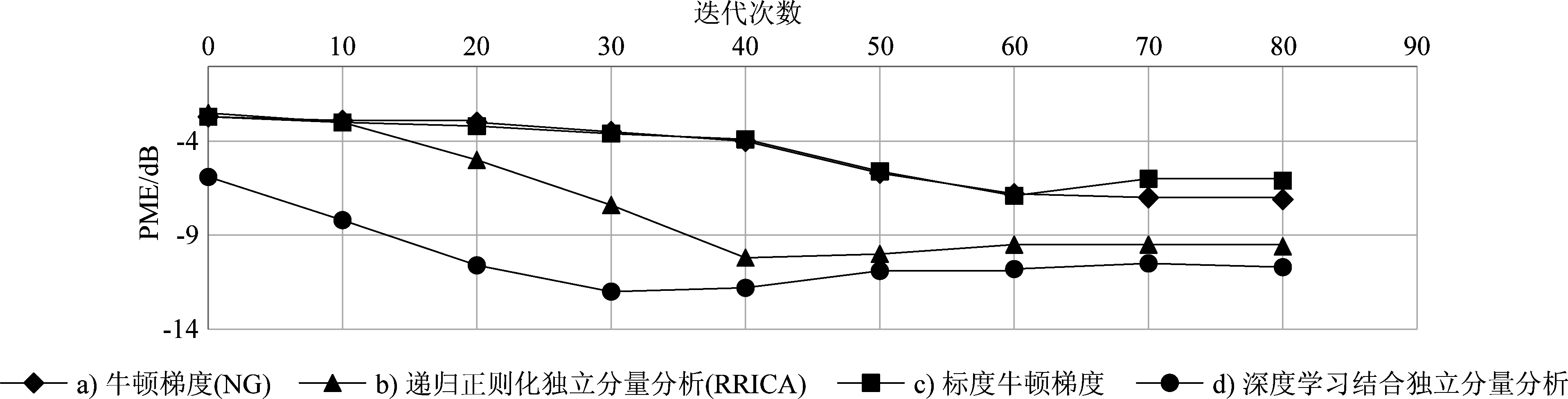
图6 使用PIT进行排列矫正的PME曲线
Fig.6 PME curve after alignment correction using PIT
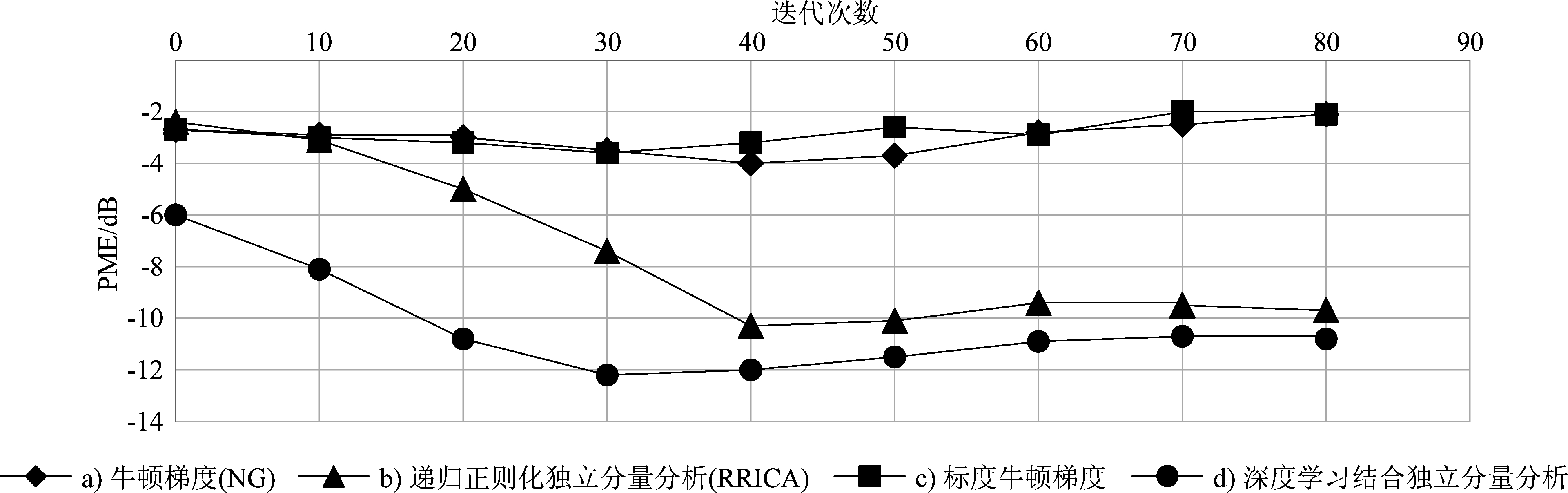
图7 不使用PIT进行排列矫正的PME曲线
Fig.7 PME curve after alignment correction without PIT
观测图6和图7中的PME曲线发现:首先,深度学习的独立分量分析方法可以更快的达到最小值点,相比于递归正则化独立分量分析方法,深度学习的独立分量分析方法节省了近40次迭代计算;其次,深度学习结合的方法可以在初始化阶段PME值相比较下已经最小,一定程度提高了其性能的稳定性,同时也使接下来盲源分离计算更为高效。
图6和图7分别表示在解决了排列问题和未处理排列问题情况下ICA利用牛顿梯度、牛顿梯度加递归正则化、标度牛顿梯度、深度学习加牛顿梯度加递归正则化四种迭代方法处理的结果曲线。由PME曲线可看出,ICA利用标度牛顿梯度、深度学习以及ICA利用牛顿梯度加递归正则化方案可以一定程度上解决排列问题。
3.4 实时性结果分析
为了能够充分的展示给定的实验证据,实验结果基于数据块(图2)和FFT长度上的平均性能进行分析。使用本论文所提出的研究的盲分离算法(Proposed)与其他流行的盲分离算法(ALG)进行比较,所有算法迭代次数均为1000。ALG1:独立向量分析方法(IVA)[17],参数步长0.1;ALG2:时域分离[8]的方法,利用时域滤波器,其尺寸选择是FFT帧长的一半,对角化的矩阵数量为5;ALG3:频域上的Pham 算法[18]。FFT重叠部分为其帧长的75%,傅里叶分析时长为4 s。
以下实验按照上述提出的ALG1(IVA方法)、ALG2、ALG3三种算法,与本论文研究方法(Proposed)在随着信号时间长度变化所处理盲分离性能的SIR和SDR比较,其柱状图如图8。
所有结果都不考虑算法发散的输出信号,图8显示了图4实验配置的最佳性能测试,可以看出本方法在任何信号长度下都表现良好。值得注意的是,在500 ms的情况下,分离源的SIR和SDR几乎等于用9 s数据获得的最佳值的一半。并且即使在观察数据少量的情况下,也不会出现可听的失真。
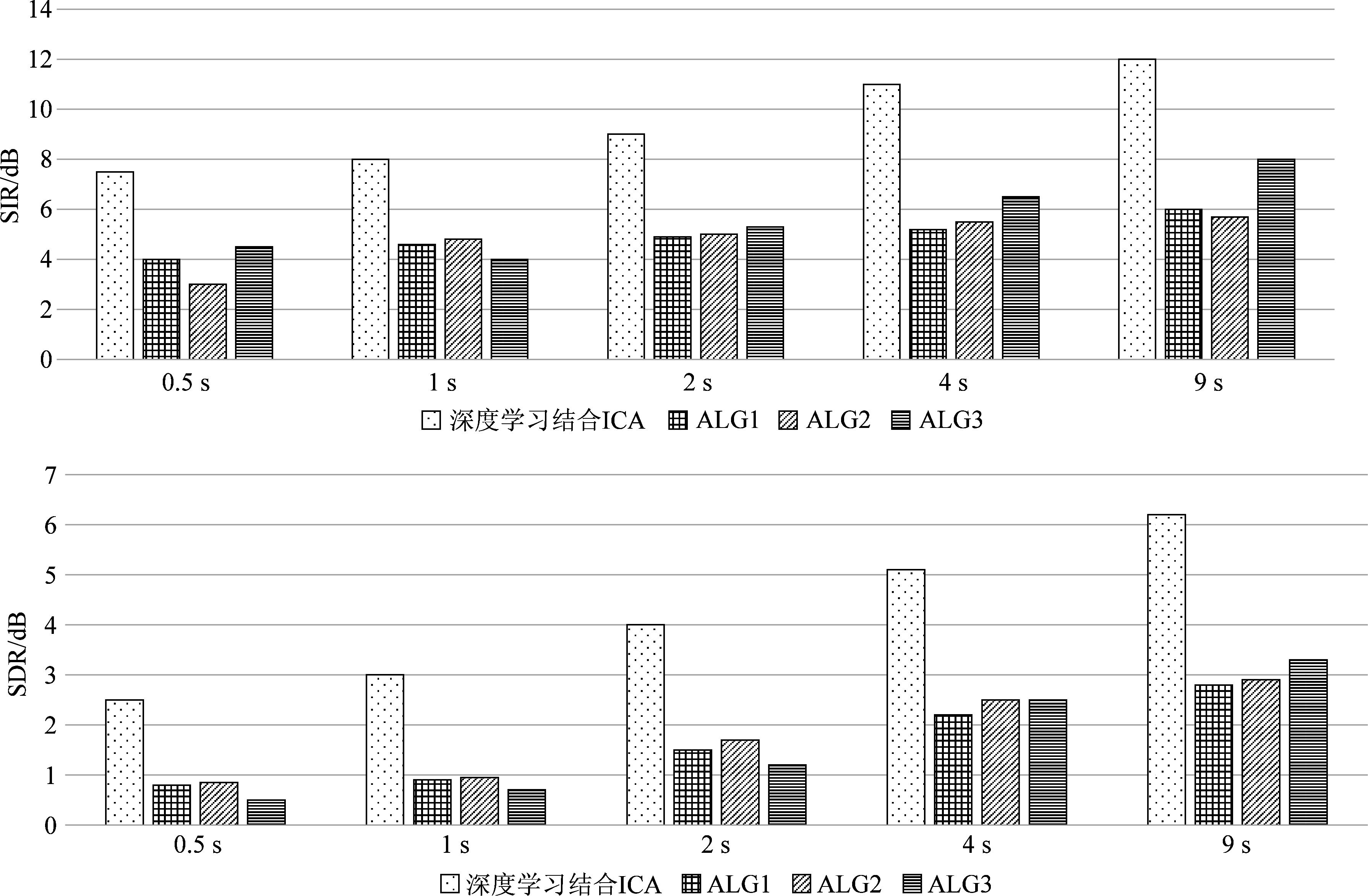
图8 不同时间长度下的SIR和SDR性能
Fig.8 SIR and SDR performance under different time lengths
图8展示了本论文提出的算法框架对比其他三种不同的方法在不同时间长度下的SIR和SDR性能比较。通过图8可得,各个时间长度下,本论文提出的结合深度学习的独立分量分析方法的准确性都更加优异,且信号长度较短时,Proposed的分离性能优于其他三种算法,这为Proposed的实时应用提供了基础。值得注意的是,虽然Proposed在短信号情况下表现优异,但是随着时间长度的增加,其盲源分离性能会更好,这是由于盲分离算法的独立特性本身需要具有足够长的时间长度才能体现的原因。
4 结论
本文研究并提出一种基于传统的信号处理方式结合深度学习进行语音信号盲分离的技术,并且进行充分的实验对比其他ICA算法性能。从实验结果分析可得,本文所提出的方法从分离矩阵的估计的准确性、测试数据盲分离准确性以及稳定性和实时性各个方面都得到了较大的性能提高。尤其在解决传统盲分离的排列问题中,本文方法得到了很好的效果,并且在没有排列矫正的情况下得到了和有理想的排列矫正情况相差无几的性能,同时结合深度学习的方式也显著的降低了时间消耗成本。综合来看,对比其他同类方法,本文所提出的盲分离方法在算法稳定性上表现更好,分离效果更佳,且对于盲分离的实时性应用有显著的意义。
[1] VASILESCU M A O, TERZOPOULOS D. Multilinear independent components analysis[C]∥2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition (CVPR'05). San Diego, CA, USA. IEEE, 2005: 547-553.
[2] SAWADA H, MUKAI R, ARAKI S, et al. A robust and precise method for solving the permutation problem of frequency-domain blind source separation[J]. IEEE Transactions on Speech and Audio Processing, 2004, 12(5): 530-538.
[3] PAL M, ROY R, BASU J, et al. Blind source separation: A review and analysis[C]∥2013 International Conference Oriental COCOSDA held jointly with 2013 Conference on Asian Spoken Language Research and Evaluation (O-COCOSDA/CASLRE). Gurgaon, India. IEEE, 2013.
[4] LUO Yi, MESGARANI N. Conv-TasNet: Surpassing ideal time-frequency magnitude masking for speech separation[J]. IEEE/ACM Transactions on Audio, Speech, and Language Processing, 2019, 27(8): 1256-1266.
[5] YU Dong, KOLB![]() K M, TAN Zhenghua, et al. Permutation invariant training of deep models for speaker-independent multi-talker speech separation[C]∥2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). New Orleans, LA, USA. IEEE, 2017: 241-245.
K M, TAN Zhenghua, et al. Permutation invariant training of deep models for speaker-independent multi-talker speech separation[C]∥2017 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP). New Orleans, LA, USA. IEEE, 2017: 241-245.
[6] LI Hualiang, ![]() T. Complex-valued adaptive signal processing using nonlinear functions[J]. EURASIP Journal on Advances in Signal Processing, 2008, 2008: 765615.
T. Complex-valued adaptive signal processing using nonlinear functions[J]. EURASIP Journal on Advances in Signal Processing, 2008, 2008: 765615.
[7] ARJOVSKY M, SHAH A, BENGIO Y. Unitary evolution recurrent neural networks. Proceedings of The 33rd International Conference on Machine Learning, in Proceedings of Machine Learning Research,2016,48:1120-1128.Available from https:∥proceedings.mlr.press/v48/arjovsky16.html.
[8] HYLAND S, RATSCH G. Learning unitary operators with help from u(n)[A]. In AAAI, 2017: 2050-2058.
[9] JING LI, SHEN YICHEN, ![]() T, et al. Tunable efficient unitary neural networks (EUNN) and their application to RNNs. In ICML, 2017.
T, et al. Tunable efficient unitary neural networks (EUNN) and their application to RNNs. In ICML, 2017.
[10] SCHREIER P J, SCHARF L L. Statistical Signal Processing of Complex-Valued Data: The Theory of Improper and Noncircular Signals. Cambridge: Cambridge University Press,2010. doi:10.1017/CBO9780511815911.
[11] MATSUOKA K. Minimal distortion principle for blind source separation[C]∥Proceedings of the 41st SICE Annual Conference. SICE 2002. Osaka, Japan. IEEE, 2002: 2138-2143.
[12] CHO K, VANMERRIENBOER B, GULCEHRE C, et al. Learning phrase representations using RNN encoder-decoder for statistical machine translation[J]. In EMNLP, 2014: 1078-1082.
[13] NESTA F, SVAIZER P, OMOLOGO M. Convolutive BSS of short mixtures by ICA recursively regularized across frequencies[J]. IEEE Transactions on Audio, Speech, and Language Processing, 2011, 19(3): 624-639.
[14] SAWADA H, ARAKI S, MAKINO S. Measuring dependence of Bin-wise separated signals for permutation alignment in frequency-domain BSS[C]∥2007 IEEE International Symposium on Circuits and Systems. New Orleans, LA, USA. IEEE, 2007: 3247-3250.
[15] CHOI Y S, SHIN H C, SONG W J. Robust regularization for normalized LMS algorithms[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2006, 53(8): 627-631.
[16] DOUGLAS S C, GUPTA M. Scaled natural gradient algorithms for instantaneous and convolutive blind source separation[C]∥2007 IEEE International Conference on Acoustics, Speech and Signal Processing-ICASSP'07. Honolulu, HI, USA. IEEE, 2007: II-637.
[17] KIM T, LEE I, LEE T W. Independent vector analysis: Definition and algorithms[C]∥2006 Fortieth Asilomar Conference on Signals, Systems and Computers. Pacific Grove, CA, USA. IEEE, 2006: 1393-1396.
[18] PHAM D T, SERVIERE C, BOUMARAF H.Blind separation of convolutive audio mixtures using nonstationarity[A]. in Proceedings of ICA, Nara, Japan, Apr. 2003: 981-986.





